Flexibility-Based Evaluation of Variable Generation Acceptability in Korean Power System
Abstract
:1. Introduction
2. Flexibility Index: Ramping Capability Shortage Expectation
2.1. RSE Definition
2.2. Comparison of RSE with Reliability Indices
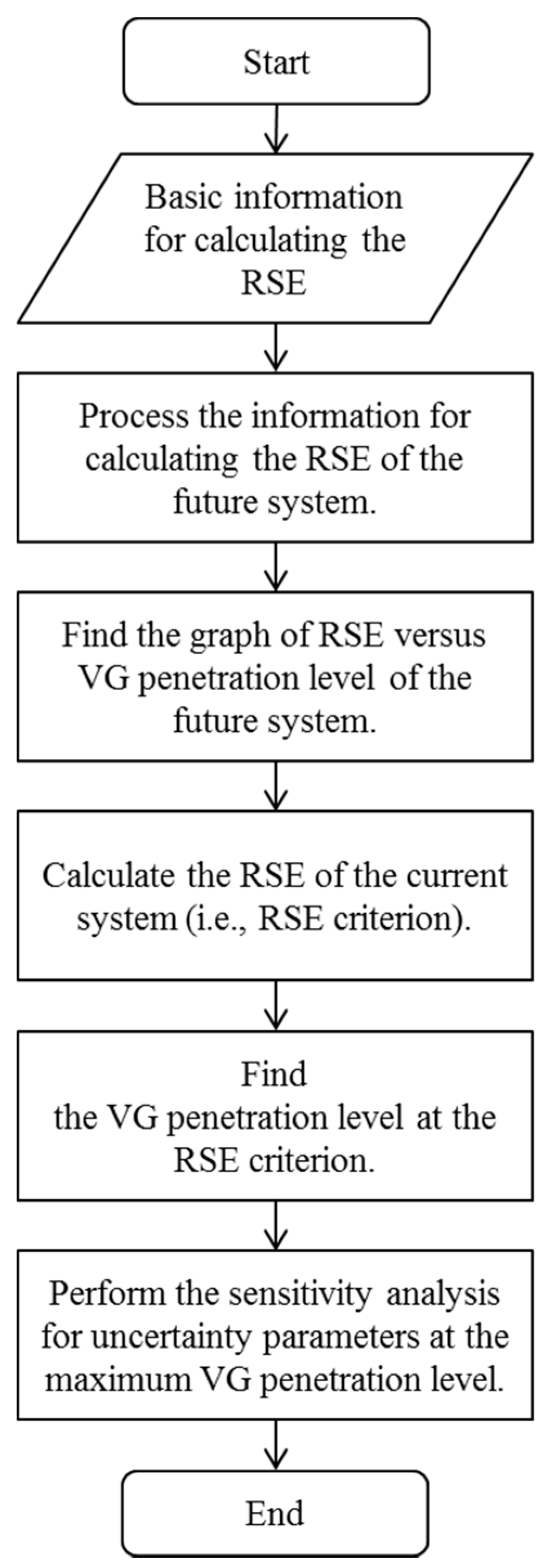
3. Evaluation Procedure of the Variable Generation Acceptability
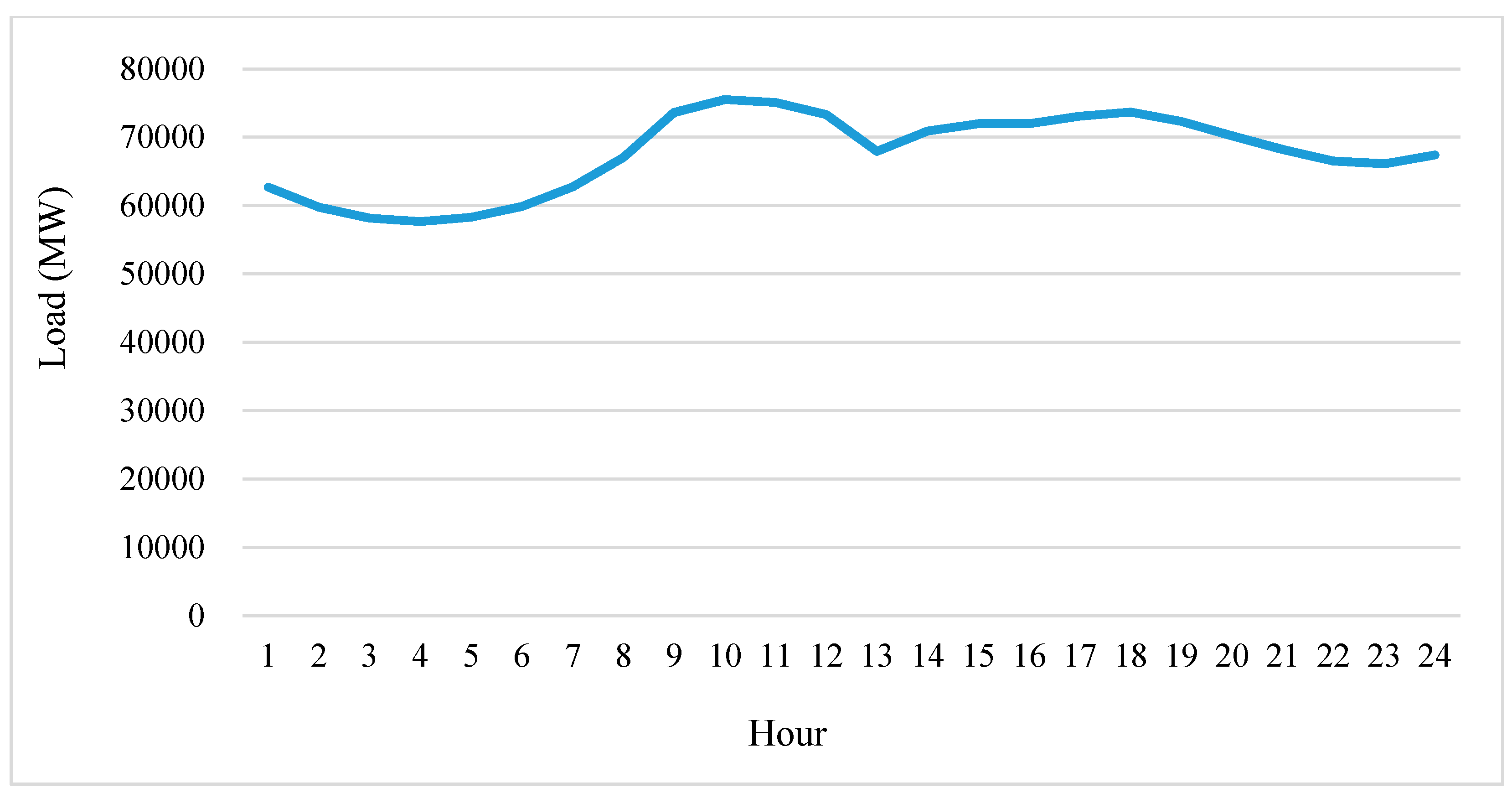
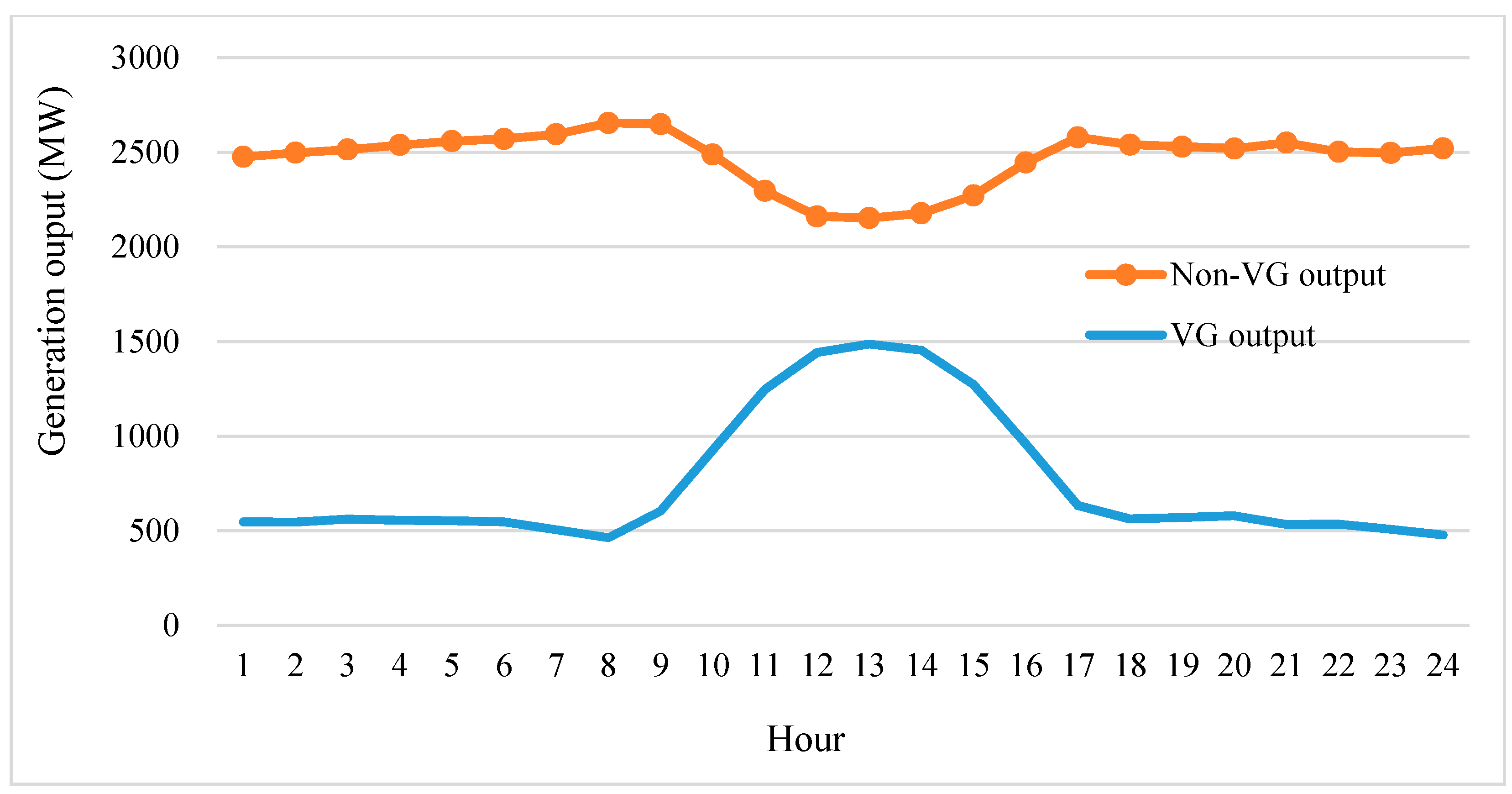
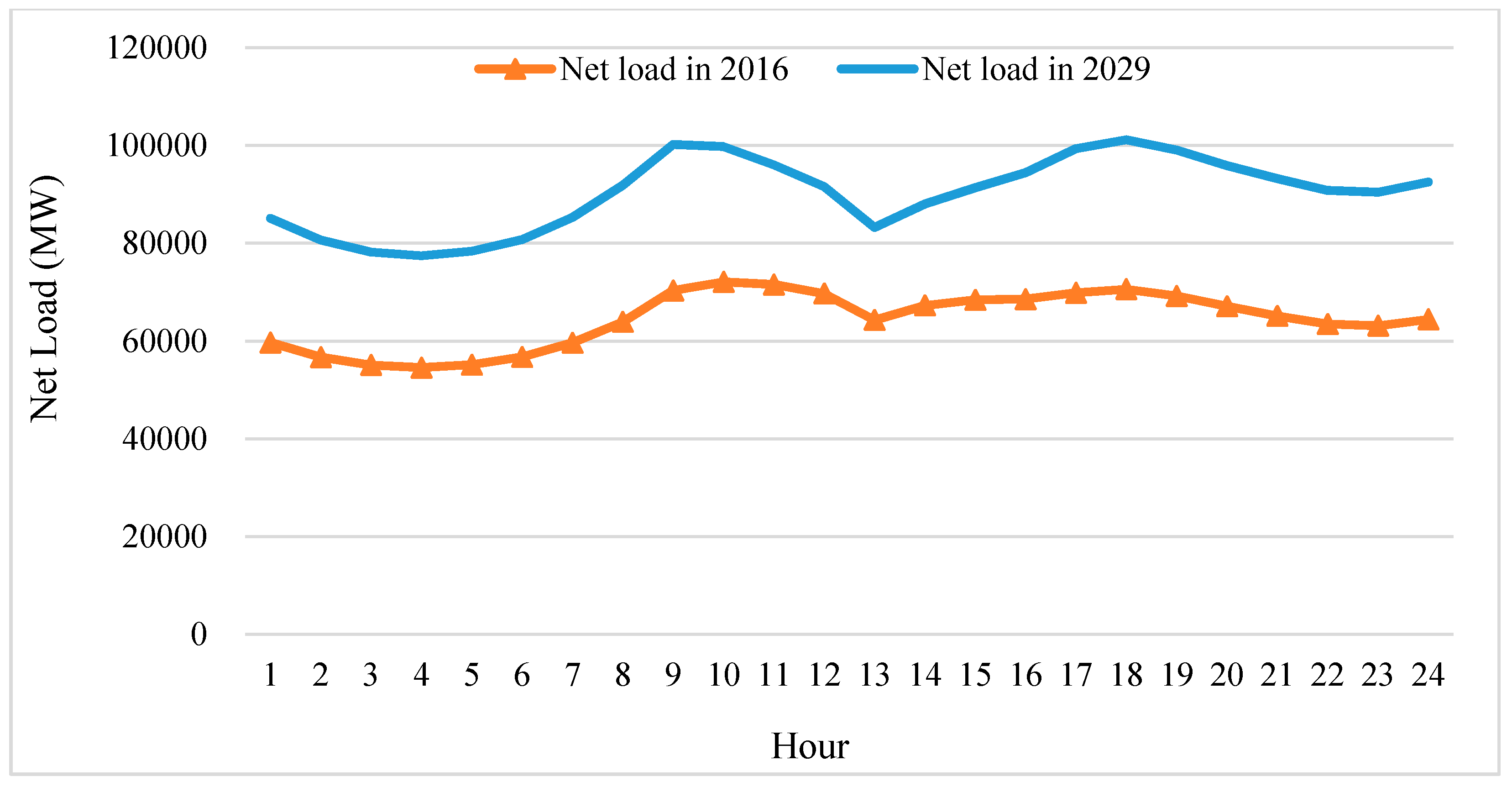
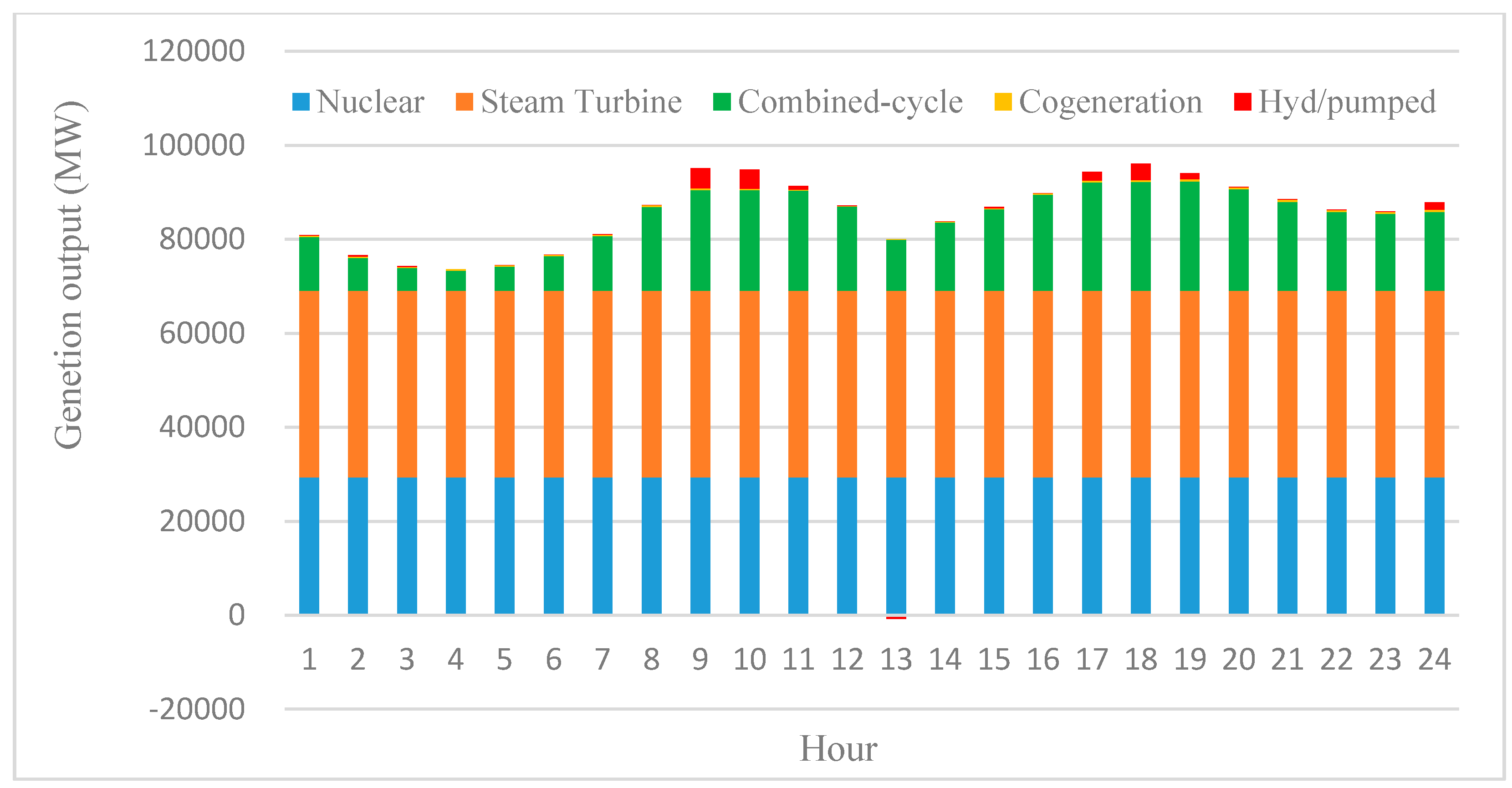
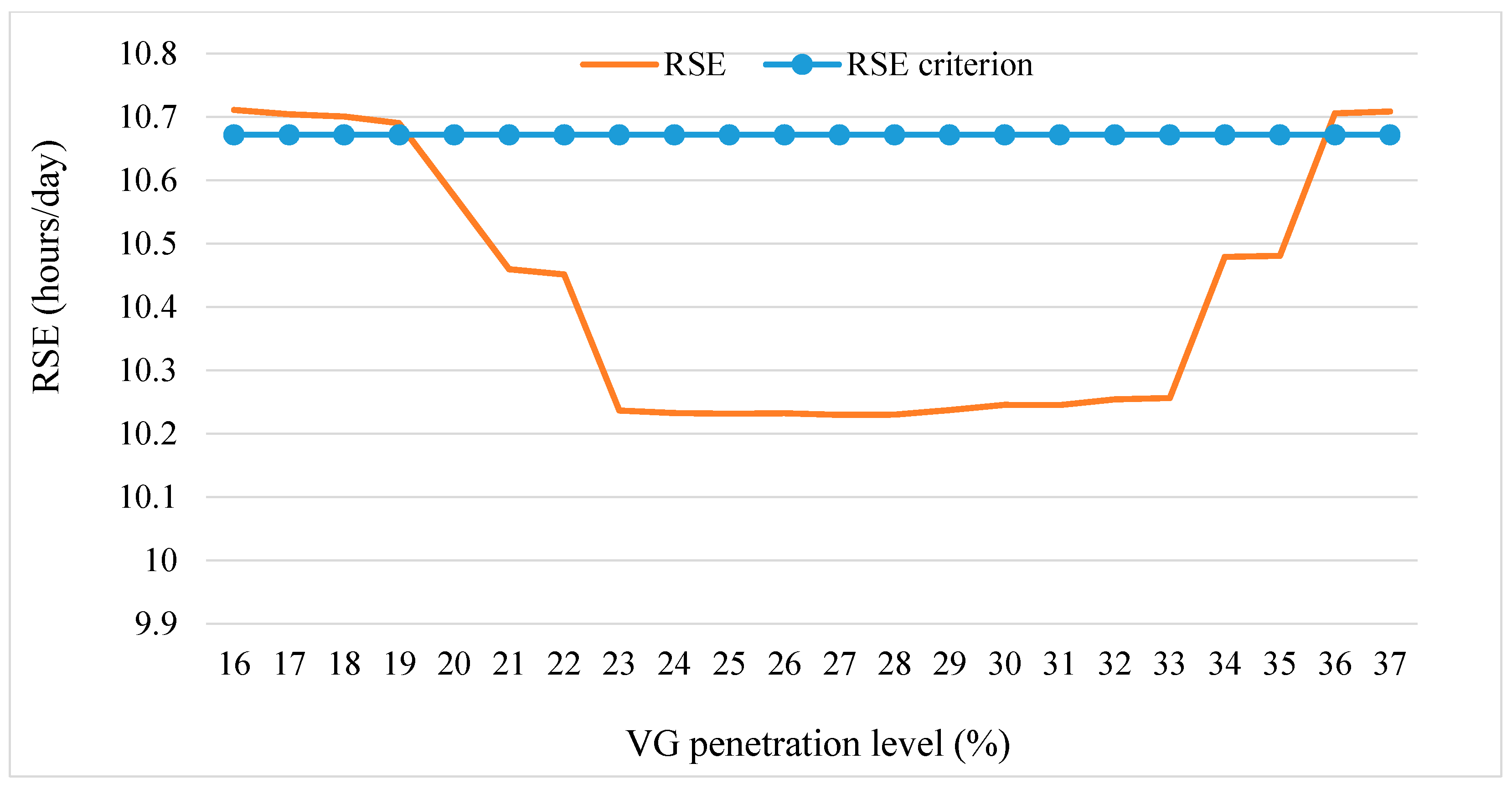
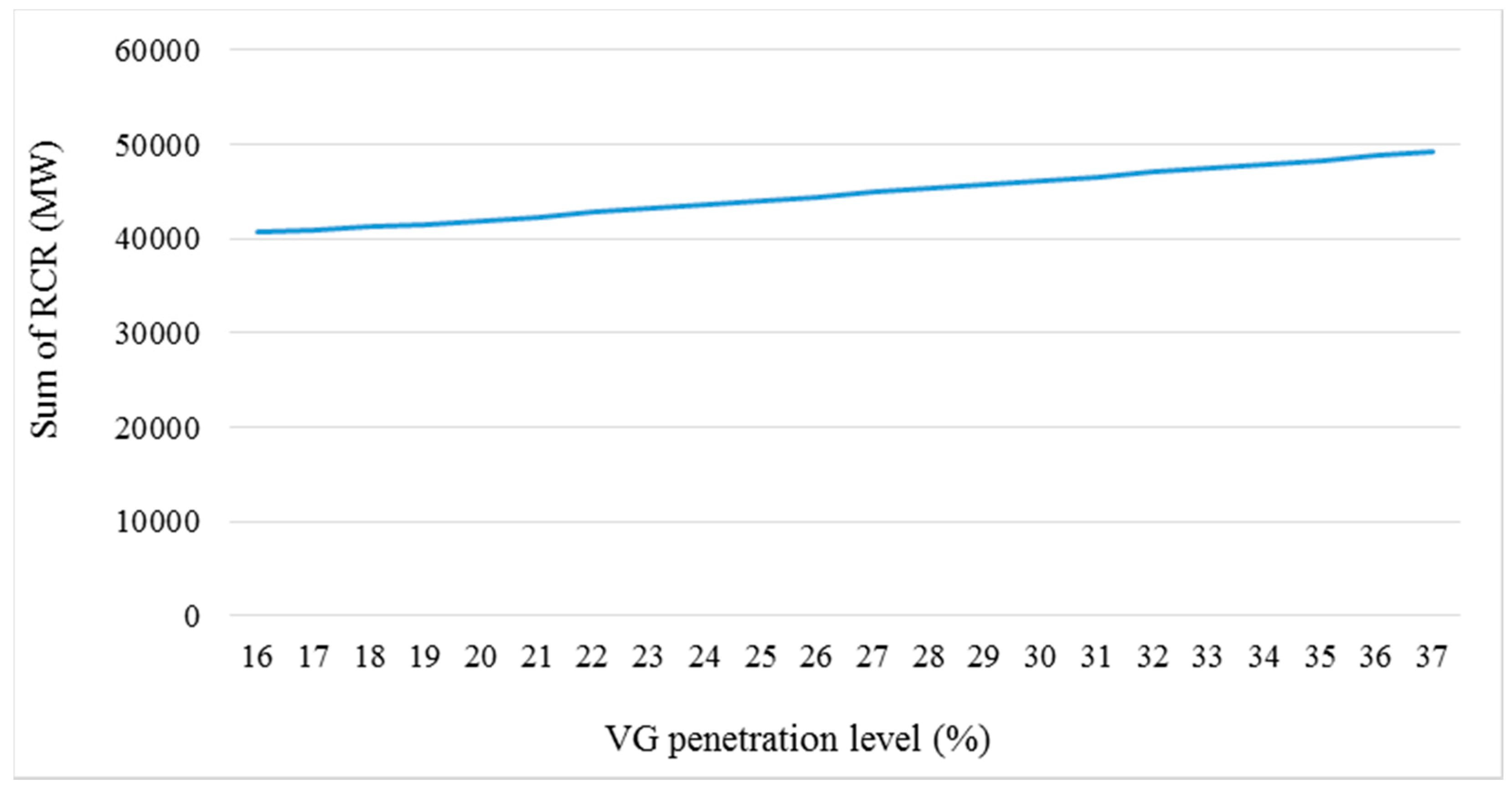
4. Case Study
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Newly Installed Generators from 2017 to 2029 (※ ST: Steam Turbine; CC: Combined Cycle; Nucl.: Nuclear)
| Generator Name | Maximum Output (MW) | Minimum Output (MW) | Coefficient of Cost Function | ||
|---|---|---|---|---|---|
| 2nd-Order (Gcal/MW2) | 1st-Order (Gcal/MW) | Constant (Gcal) | |||
| CC1-GT | 140 | 48 | 0.005454 | 2.489639 | 18.7936 |
| CC2-CC | 200 | 82 | 0.001115 | 1.842653 | 18.01031 |
| CC3-GT | 274 | 184 | 0.00003 | 1.871501 | 157.2697 |
| CC4-GT | 274 | 184 | 0.00003 | 1.871501 | 157.2697 |
| CC3-CC | 400 | 281 | 0.000386 | 1.138112 | 125.5207 |
| CC4-CC | 400 | 281 | 0.000386 | 1.138112 | 125.5207 |
| CC5-GT | 572.6 | 330 | 0.000643 | 1.19617 | 472.335 |
| CC5-CC | 1000 | 542 | 0.000007 | 1.501309 | 100.2745 |
| CC6-GT | 571.6 | 188 | 0.000111 | 2.111027 | 65.73368 |
| CC6-CC | 950 | 439 | 0.000003 | 1.494521 | 70.40799 |
| CC7-GT | 572.6 | 330 | 0.000643 | 1.19617 | 472.335 |
| CC8-GT | 572.6 | 330 | 0.000643 | 1.19617 | 472.335 |
| CC7-CC | 900 | 542 | 0.000007 | 1.501309 | 100.2745 |
| CC8-CC | 900 | 542 | 0.000007 | 1.501309 | 100.2745 |
| CC9-GT | 306.2 | 116 | 0.000003 | 2.461418 | 67.76106 |
| CC9-CC | 470 | 175 | 0.000077 | 1.551216 | 40.38037 |
| CC10-GT | 572.6 | 330 | 0.000643 | 1.19617 | 472.335 |
| CC10-CC | 960 | 542 | 0.000007 | 1.501309 | 100.2745 |
| CC11-GT | 572.6 | 330 | 0.000643 | 1.19617 | 472.335 |
| CC11-CC | 1000 | 542 | 0.000007 | 1.501309 | 100.2745 |
| CC12-GT | 572.6 | 330 | 0.000643 | 1.19617 | 472.335 |
| CC12-CC | 920 | 542 | 0.000007 | 1.501309 | 100.2745 |
| ST1 | 595 | 260 | 0.000136 | 1.863031 | 107.3797 |
| ST2 | 595 | 260 | 0.000136 | 1.863031 | 107.3797 |
| ST3 | 1022 | 609 | 0.000098 | 1.765468 | 199.9551 |
| ST4 | 1022 | 609 | 0.000098 | 1.765468 | 199.9551 |
| ST5 | 1000 | 609 | 0.000098 | 1.765468 | 199.9551 |
| ST6 | 1000 | 609 | 0.000098 | 1.765468 | 199.9551 |
| ST7 | 1000 | 609 | 0.000098 | 1.765468 | 199.9551 |
| ST8 | 1040 | 609 | 0.000098 | 1.765468 | 199.9551 |
| ST9 | 1040 | 609 | 0.000098 | 1.765468 | 199.9551 |
| ST10 | 580 | 260 | 0.000136 | 1.863031 | 107.3797 |
| ST11 | 580 | 260 | 0.000136 | 1.863031 | 107.3797 |
| ST12 | 1040 | 609 | 0.000098 | 1.765468 | 199.9551 |
| ST13 | 1040 | 609 | 0.000098 | 1.765468 | 199.9551 |
| ST14 | 1050 | 609 | 0.000098 | 1.765468 | 199.9551 |
| ST15 | 1050 | 609 | 0.000098 | 1.765468 | 199.9551 |
| ST16 | 1050 | 635 | 0.000025 | 1.899346 | 165.6219 |
| Nucl.1 | 1400 | 795 | 0.000105 | 2.043505 | 267.8154 |
| Nucl.2 | 1400 | 795 | 0.000105 | 2.043505 | 267.8154 |
| Nucl.3 | 1400 | 795 | 0.000105 | 2.043505 | 267.8154 |
| Nucl.4 | 1400 | 795 | 0.000105 | 2.043505 | 267.8154 |
| Nucl.5 | 1500 | 795 | 0.000105 | 2.043505 | 267.8154 |
| Nucl.6 | 1500 | 795 | 0.000105 | 2.043505 | 267.8154 |
| Nucl.7 | 1500 | 795 | 0.000105 | 2.043505 | 267.8154 |
| Nucl.8 | 1500 | 795 | 0.000105 | 2.043505 | 267.8154 |
| Nucl.9 | 1400 | 795 | 0.000105 | 2.043505 | 267.8154 |
| Nucl.10 | 1400 | 795 | 0.000105 | 2.043505 | 267.8154 |
| Nucl.11 | 1400 | 795 | 0.000105 | 2.043505 | 267.8154 |
| Nucl.12 | 1400 | 795 | 0.000105 | 2.043505 | 267.8154 |
| Generator Name | Ramp-Up Rate (MW/min) | Minimum Up Time (h) | Minimum Down Time (h) | Ramp-Up Rate for Start Up (MW/min) | Ramp-Down Rate for Shut Down (MW/min) |
|---|---|---|---|---|---|
| CC1-GT | 7 | 1 | 1 | 7 | 7 |
| CC2-CC | 8.7 | 4 | 3 | 8.7 | 8.7 |
| CC3-GT | 13.1 | 1.3 | 3.8 | 13.1 | 13.1 |
| CC4-GT | 13.1 | 1.3 | 3.8 | 13.1 | 13.1 |
| CC3-CC | 20 | 4 | 3.8 | 20 | 20 |
| CC4-CC | 20 | 4 | 3.8 | 20 | 20 |
| CC5-GT | 22.5 | 3.1 | 4.8 | 22.5 | 22.5 |
| CC5-CC | 36 | 4.2 | 5.3 | 48 | 48 |
| CC6-GT | 22.5 | 1 | 2 | 22.5 | 22.5 |
| CC6-CC | 34.5 | 4 | 3 | 34.5 | 34.5 |
| CC7-GT | 22.5 | 3.1 | 4.8 | 22.5 | 22.5 |
| CC8-GT | 22.5 | 3.1 | 4.8 | 22.5 | 22.5 |
| CC7-CC | 36 | 4.2 | 5.3 | 48 | 48 |
| CC8-CC | 36 | 4.2 | 5.3 | 48 | 48 |
| CC9-GT | 11.5 | 4 | 3 | 11.5 | 11.5 |
| CC9-CC | 18.55 | 4 | 3 | 18.6 | 18.6 |
| CC10-GT | 22.5 | 3.1 | 4.8 | 22.5 | 22.5 |
| CC10-CC | 36 | 4.2 | 5.3 | 48 | 48 |
| CC11-GT | 22.5 | 3.1 | 4.8 | 22.5 | 22.5 |
| CC11-CC | 36 | 4.2 | 5.3 | 48 | 48 |
| CC12-GT | 22.5 | 3.1 | 4.8 | 22.5 | 22.5 |
| CC12-CC | 36 | 4.2 | 5.3 | 48 | 48 |
| ST1 | 15 | 6 | 12 | 15 | 15 |
| ST2 | 15 | 6 | 12 | 15 | 15 |
| ST3 | 12.5 | 8 | 18 | 30.6 | 30.6 |
| ST4 | 12.5 | 8 | 18 | 30.6 | 30.6 |
| ST5 | 12.5 | 8 | 18 | 30.6 | 30.6 |
| ST6 | 12.5 | 8 | 18 | 30.6 | 30.6 |
| ST7 | 12.5 | 8 | 18 | 30.6 | 30.6 |
| ST8 | 12.5 | 8 | 18 | 30.6 | 30.6 |
| ST9 | 12.5 | 8 | 18 | 30.6 | 30.6 |
| ST10 | 15 | 6 | 12 | 15 | 15 |
| ST11 | 15 | 6 | 12 | 15 | 15 |
| ST12 | 12.5 | 8 | 18 | 30.6 | 30.6 |
| ST13 | 12.5 | 8 | 18 | 30.6 | 30.6 |
| ST14 | 12.5 | 8 | 18 | 30.6 | 30.6 |
| ST15 | 12.5 | 8 | 18 | 30.6 | 30.6 |
| ST16 | 10.5 | 7.7 | 20.8 | 1 | 1 |
| Nucl.1 | 0.97 | 8 | 12 | 0.5 | 1.6 |
| Nucl.2 | 0.97 | 8 | 12 | 0.5 | 1.6 |
| Nucl.3 | 0.97 | 8 | 12 | 0.5 | 1.6 |
| Nucl.4 | 0.97 | 8 | 12 | 0.5 | 1.6 |
| Nucl.5 | 0.97 | 8 | 12 | 0.5 | 1.6 |
| Nucl.6 | 0.97 | 8 | 12 | 0.5 | 1.6 |
| Nucl.7 | 0.97 | 8 | 12 | 0.5 | 1.6 |
| Nucl.8 | 0.97 | 8 | 12 | 0.5 | 1.6 |
| Nucl.9 | 0.97 | 8 | 12 | 0.5 | 1.6 |
| Nucl.10 | 0.97 | 8 | 12 | 0.5 | 1.6 |
| Nucl.11 | 0.97 | 8 | 12 | 0.5 | 1.6 |
| Nucl.12 | 0.97 | 8 | 12 | 0.5 | 1.6 |
References
- The Ministry of Trade, Industry and Energy (MOTIE). The 2nd National Energy Master Plan; MOTIE: Sejong, Korea, 2015.
- The Ministry of Trade, Industry and Energy. The 4th New & Renewable Energy Basic Plan; MOTIE: Sejong, Korea, 2014.
- The Ministry of Trade, Industry and Energy. The 7th Basic Plan on Electricity Demand and Supply; MOTIE: Sejong, Korea, 2015.
- Ryan, J.; Ela, E.; Flynn, D.; O’Malley, M. Variable generation, reserves, flexibility and policy interactions. In Proceedings of the 2014 47th Hawaii International Conference on System Sciences (HICSS), Waikoloa, HI, USA, 6–9 January 2014; pp. 2426–2434. [Google Scholar]
- Lin, J.; Cheng, L.; Chang, Y.; Zhang, K.; Shu, B.; Liu, G. Reliability based power systems planning and operation with wind power integration: A review to models, algorithms and applications. Renew. Sustain. Energy Rev. 2014, 31, 921–934. [Google Scholar] [CrossRef]
- Lannoye, E.; Flynn, D.; O’Malley, M. Evaluation of power system flexibility. IEEE Trans. Power Syst. 2012, 27, 922–931. [Google Scholar] [CrossRef]
- Nosair, H.; Bouffard, F. Flexibility envelopes for power system operational planning. IEEE Trans. Sustain. Energy 2015, 6, 800–809. [Google Scholar] [CrossRef]
- Min, C.G.; Park, J.K.; Hur, D.; Kim, M.K. A risk evaluation method for ramping capability shortage in power systems. Energy 2016, 113, 1316–1324. [Google Scholar] [CrossRef]
- Holttinen, H.; Meibom, P.; Orths, A.; Lange, B.; O’Malley, M.; Tande, J.O.; Estanqueiro, A.; Gomez, E.; Söder, L.; Strbac, G.; et al. Impacts of large amounts of wind power on design and operation of power systems, results of IEA collaboration. Wind Energy 2011, 14, 179–192. [Google Scholar] [CrossRef]
- Adams, J.; O’Malley, M.; Hanson, K. Flexibility Requirements and Potential Metrics for Variable Generation: Implications for System Planning Studies; North American Electric Reliability Corporation (NERC): Princeton, NJ, USA, 2010. [Google Scholar]
- Denholm, P.; Hand, M. Grid flexibility and storage required to achieve very high penetration of variable renewable electricity. Energy Policy 2011, 39, 1817–1830. [Google Scholar] [CrossRef]
- Ulam-Orgil, C.; Lee, H.W.; Kang, Y.C. Evaluation of the wind power penetration limit and wind energy penetration in the mongolian central power system. J. Electr. Eng. Technol. 2012, 7, 852–858. [Google Scholar] [CrossRef]
- Huber, M.; Dimkova, D.; Hamacher, T. Integration of wind and solar power in Europe: Assessment of flexibility requirements. Energy 2014, 69, 236–246. [Google Scholar] [CrossRef]
- Xu, Q.; Kang, C.; Zhang, N.; Ding, Y.; Xia, Q.; Sun, R.; Xu, J. A probabilistic method for determining grid-accommodable wind power capacity based on multiscenario system operation simulation. IEEE Trans. Smart Grid 2016, 7, 400–409. [Google Scholar] [CrossRef]
- He, Y.; Xia, T.; Liu, Z.; Zhang, T.; Dong, Z. Evaluation of the capability of accepting large-scale wind power in China. Renew. Sustain. Energy Rev. 2013, 19, 509–516. [Google Scholar] [CrossRef]
- Ela, E.; Kirby, B. ERCOT Event on February 26, 2008: Lessons learned; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2008.
- Lannoye, E.; Flynn, D.; O’Malley, M. Transmission, variable generation, and power system flexibility. IEEE Trans. Power Syst. 2015, 30, 57–66. [Google Scholar] [CrossRef]
- Ma, J.; Silva, V.; Belhomme, R.; Kirschen, D.S.; Ochoa, L.F. Evaluating and planning flexibility in sustainable power systems. In Proceedings of the 2013 IEEE Power and Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- Zhao, J.; Zheng, T.; Litvinov, E. A unified framework for defining and measuring flexibility in power system. IEEE Trans. Power Syst. 2016, 31, 339–347. [Google Scholar] [CrossRef]
- Wang, J.; Botterud, A.; Bessa, R.; Keko, H.; Carvalho, L.; Issicaba, D.; Sumaili, J.; Miranda, V. Wind power forecasting uncertainty and unit commitment. Appl. Energy 2011, 88, 4014–4023. [Google Scholar] [CrossRef]
- Wang, Q.; Guan, Y.; Wang, J. A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output. IEEE Trans. Power Syst. 2012, 27, 206–215. [Google Scholar] [CrossRef]
- Korea Power Exchange. Electric Power Statistics Information System. Available online: http://epsis.kpx.or.kr/epsis/ekesStaticMain.do?cmd=001001&flag=&locale=EN (accessed on 23 February 2017).
- Chung, M.; Lee, S.G.; Park, C.; Park, H.-C.; Im, Y.-H. Development of a combined energy-demands calculator for urban building communities in Korea. Environ. Plan. B 2013, 40, 289–310. [Google Scholar] [CrossRef]
- Marcos, J.; Marroyo, L.; Lorenzo, E.; García, M. Smoothing of PV power fluctuations by geographical dispersion. Prog. Photovolt. Res. Appl. 2012, 20, 226–237. [Google Scholar] [CrossRef]
- Billinton, R.; Allan, R. Reliability Evaluation of Power Systems, 2nd ed.; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Master’s Space (MS). M-Core User’s Manual; MS: Anyang, Korea, 2016. [Google Scholar]
- Korea Power Exchange. Electricity Market Operation Rules; KPX: Naju, Korea, 2016. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Min, C.-G.; Kim, M.-K. Flexibility-Based Evaluation of Variable Generation Acceptability in Korean Power System. Energies 2017, 10, 825. https://doi.org/10.3390/en10060825
Min C-G, Kim M-K. Flexibility-Based Evaluation of Variable Generation Acceptability in Korean Power System. Energies. 2017; 10(6):825. https://doi.org/10.3390/en10060825
Chicago/Turabian StyleMin, Chang-Gi, and Mun-Kyeom Kim. 2017. "Flexibility-Based Evaluation of Variable Generation Acceptability in Korean Power System" Energies 10, no. 6: 825. https://doi.org/10.3390/en10060825
APA StyleMin, C.-G., & Kim, M.-K. (2017). Flexibility-Based Evaluation of Variable Generation Acceptability in Korean Power System. Energies, 10(6), 825. https://doi.org/10.3390/en10060825





