1. Introduction
Ground source heat pump (GSHP) systems are well established means to heat and cool buildings given their greater environmental friendliness and higher energy efficiency with respect to those of other systems [
1]. The closed loop ground borehole heat exchanger (BHE) is the most widely used configuration [
2]. The energy performance of that type’s entire system depends on the thermal performance of the ground heat exchangers which, in turn, depends on the geometry of the BHE, the layout of the borehole field and, obviously, on ground thermal properties. Particular attention must, therefore, be paid to these variables during the design phase.
Data necessary to design a borehole field includes the type of the ground at the installation site as well as the thermal load profile. Ground thermal properties are particularly important to calculate the total length of BHEs. The main parameter is the equivalent thermal conductivity which, for typical sedimentary unconsolidated materials, can range from 1 to 3 W/(m K); the thermal capacity is instead a less variable factor [1.5–2.5 MJ/(m3 K)]. Preliminary measurements of ground thermal conductivity can be obtained from lithology information available for the installation site and from data reported in the literature. This approach, which may prove quite inaccurate, should be used only when the borehole field simply consists of a few BHEs. When the size of the plant-system increases, knowledge of precise ground thermal properties is important to avoid under- or over-sizing the total borehole length which could cause a fall in energy efficiency over the years in the former case and high installation costs in the latter one.
Several analytical models to analyze the heat transfer between the borehole heat exchanger and the surrounding ground are present in literature [
3]. However, the most common procedure to evaluate the equivalent ground thermal conductivity is the Thermal Response Test (TRT) [
4,
5], a simplification of the infinite line source model [
6] which considers the first-order approximation of the exponential integral function of the fluid temperatures measured. TRT measurements must be taken under defined boundary conditions for this interpretation; if any of its assumptions are invalid, the interpretation will lead to an error in the final outcome [
7]. Characterized by simplicity and less computational time, the approach, however, neglects axial heat transfer. Given its simplified approach, it can, in any case, be utilized only for long boreholes with small diameters and to analyze long-term thermal behavior. To this purpose, Conti [
8] recently carried out analyses in order to develop dimensionless criteria to decide the appropriate analytical solution, concluding that the finite line source model [
9] can be used in a wide range of space and time scales. However, also the finite line source model does not consider the effect of the borehole thermal capacitance and the variation of the climate conditions at the ground surface which can significantly affect the thermal behavior of shallow ground heat exchangers.
The cylindrical heat source method is another analytical approach, which was developed by Carslaw and Jaeger [
6], that can be used to consider the finite diameter of the BHE. It represents an exact solution of a cylindrical heat source placed in an infinite homogeneous medium, the ground. In this case as well, the properties of the ground are assumed constant, the axial heat transfer is neglected, and a perfect contact between the cylinder wall and the ground is assumed.
Another method to evaluate the equivalent ground thermal properties is the inverse numerical procedure which uses the TRT measurements as input data [
10,
11]. A more accurate value of the equivalent ground thermal conductivity can be obtained if the numerical model used for that purpose considers the effects of the weather on the earth surface and axial heat transfer as well as the borehole thermal capacitance since these aspects affect the real heat exchange between the heat carrier fluid and the surrounding ground, especially when the borehole depth is low.
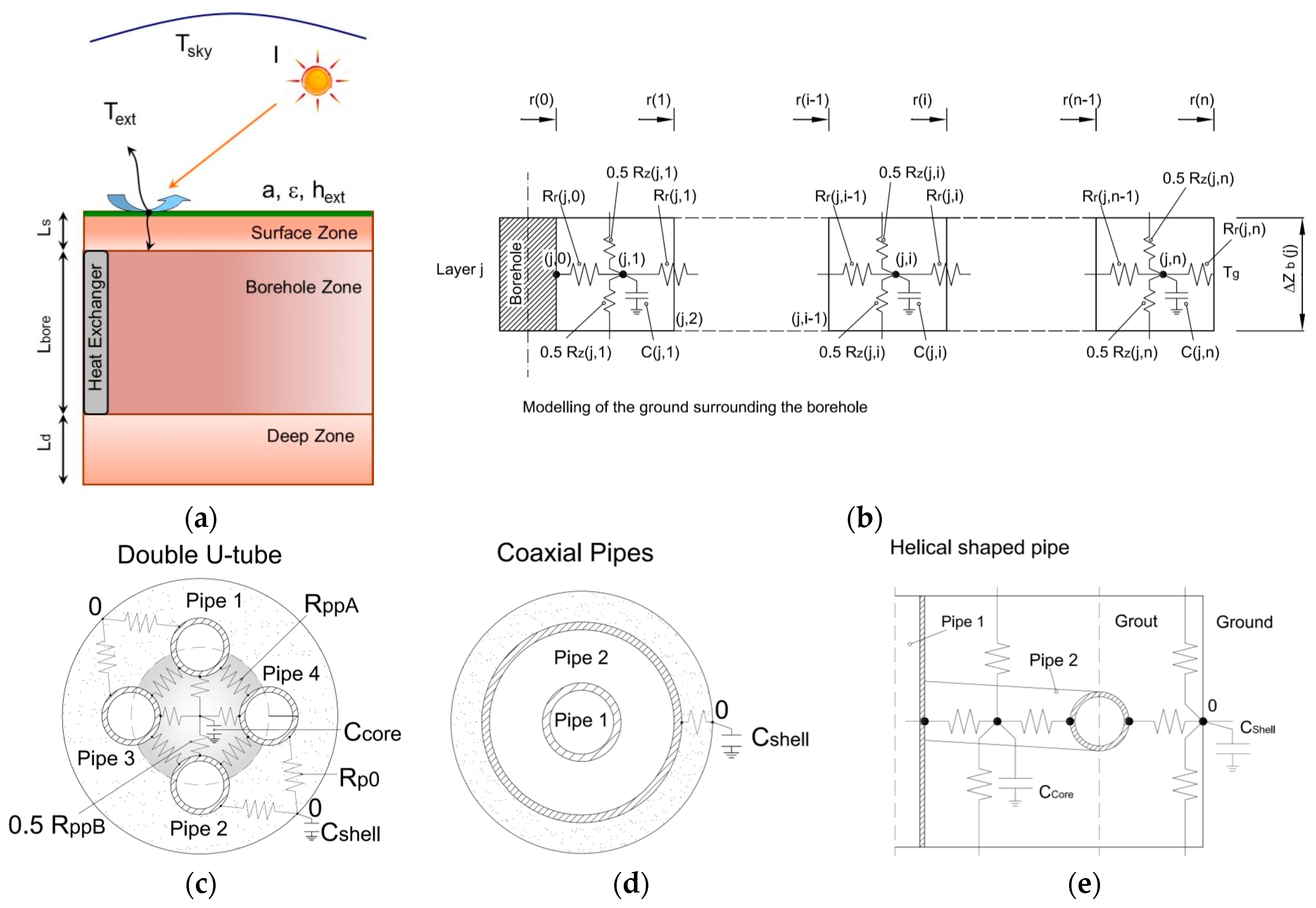
Other, secondary input data that should be used to design a GSHP system is the type of BHE that will be installed. The most commonly used type in practice is the U-tube loop with a single or double U-tube configuration; the former is widely utilized in the United States and Canada while the latter is more common in Europe. Another important model type is the coaxial pipe heat exchanger, which consists of two concentric pipes that can be constructed in different materials. When the outer pipe is in stainless steel, a piling methodology can be used to install the system whenever the ground is clearly an alternation of coarse grain materials such as clay and sand, a solution that would imply reduced installation times.
Many authors have recently been investigating the thermal performances of these BHEs in the attempt to improve the energy performance of heat pumps as well as to reduce the initial cost of installing the boreholes. Wood et al. [
12] compared the energy performance of two loop designs for use with a GSPH of an energy pile installation or a conventional borehole system. Using an experimental facility, two different scenarios were investigated: one with the single U-pipe and the other with a coaxial pipe. They reported that the coaxial loop did not add any performance benefit against a conventional single U-tube configuration. They also concluded that the coaxial loop could potentially reduce drilling costs and facilitate installation.
Aydin and Sisman [
13] conducted an experimental, computational investigation on the effects of multi U-tube boreholes from the point of view of thermal performance (i.e., heat transfer rate per borehole length unit) and of costs. The effect of the number of pipes was, in particular, investigated. The authors concluded that the 2U and 3U-tube configurations had, respectively, 14% and 25% better performance with respect to a single U-tube. From a cost point of view, they concluded that the best solution in their specific Turkish economy was a 2U-tube BHE. Also Conti et al. [
14] compared the single and double U-tube heat exchangers in terms of both heat transfer effectiveness and borehole thermal resistance. Cimmino [
15], recently, developed an analytical tool in order to evaluate the thermal behavior of ground heat exchangers with multiple U-tubes; his model, however, does not consider the borehole thermal capacity. Investigating the effect of the drillhole diameter on the thermal performance of a double U-tube ground heat exchanger, Luo et al. [
16] reported that thermal performance increased with larger drill hole diameters.
Kurevija et al. [
17] investigated the effect of grout thermal conductivity on the long-term energy efficiency of an operating GSHP. Carrying out an energy analysis of a real retrofitting project of a plant system with 16 boreholes spaced 6 m apart, they reported that thermally enhanced grouts are preferable when the ground has high conductivity properties. Zanchini et al. [
18] focused on improving the thermal performance of long coaxial BHEs using detailed models implemented by commercial software [
19]. Their results indicated that the effect of thermal short-circuiting is more relevant when there are higher grout and soil thermal conductivity levels. Those authors also investigated the effect of fluid mass flow rate, and they published [
20] an article reporting the results of a study evaluating the effects of flow direction on the performance of small coaxial BHEs.
Saez Blazquez et al. [
21], who investigated the thermal performance of single/double U-tube and helical shaped pipe heat exchangers using a variety of laboratory tests, concluded that the best thermal performance was found for the latter. Dehghan et al. [
22] carried out a parametric investigation of helical ground heat exchangers in order to define the parameters that influence the thermal performance of an entire GSHP system. Basing their study on 3D numerical simulations, the authors identified the main parameters of helical ground heat exchanger fields, and simulations were carried out for four different configurations. Performance losses due to thermal interactions linked to different BHE spacing and pitch magnitude effects of the helix on the heat transfer ratio were analyzed. The authors concluded that 100% of the variation in the geometrical properties of the helix (pitch and diameter) can affect the thermal performance by about 10%. On the other hand, the minimum distance between the helix appears to be about 7 m to keep the performance loss less than 10%.
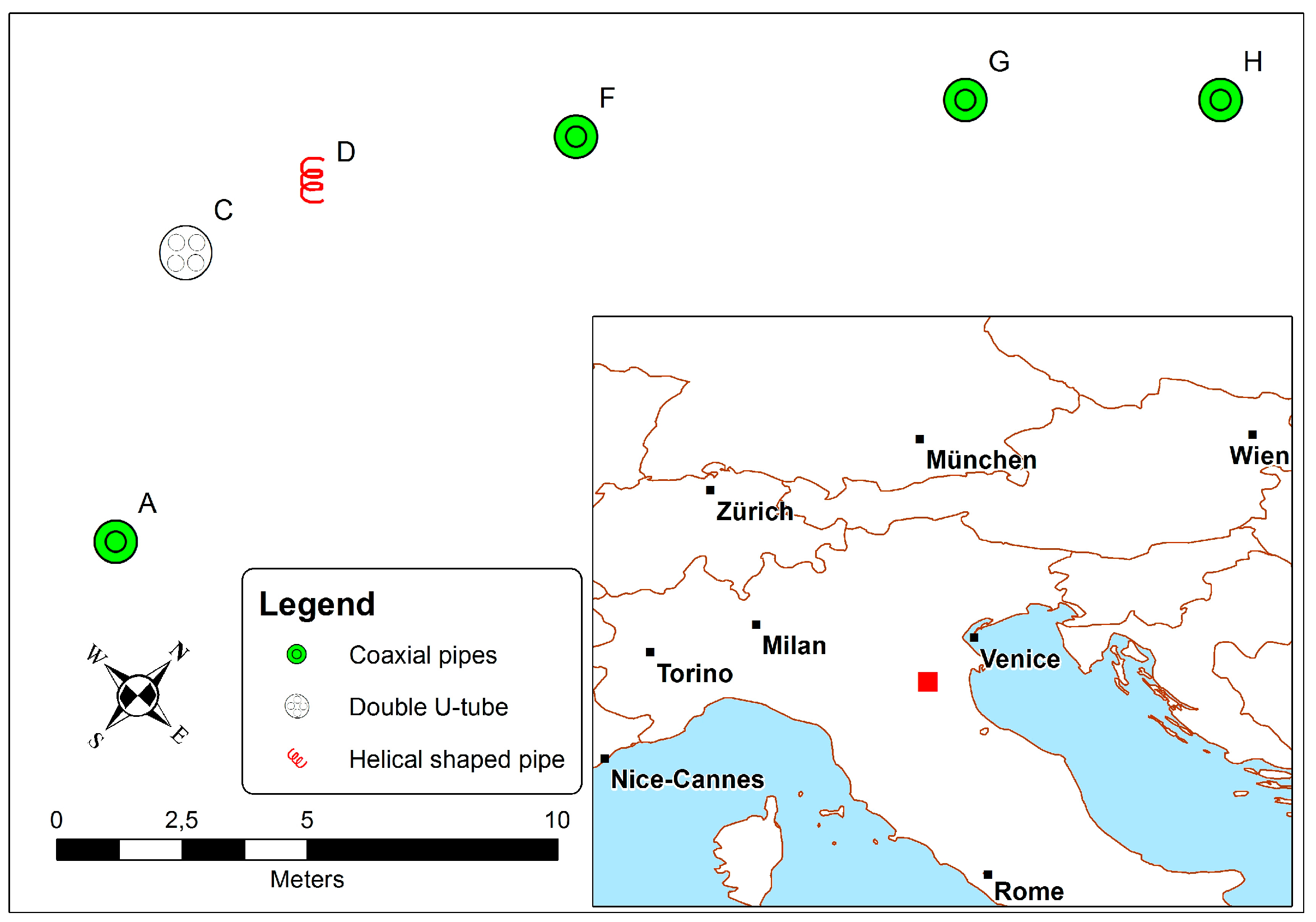
The current study set out to analyze TRTs to evaluate the equivalent ground thermal conductivity, which were carried out on different BHEs located at a single site using both standard interpretations and complete analytical solutions of the infinite line and cylinder source models. The inverse numerical approach was also investigated making use of a detailed numerical model which considers the climatic conditions at the ground surface, axial heat transfer into both the grouting material and ground, and also the borehole thermal capacity. In detail, TRTs were carried out on coaxial pipe, double U-tube and helical shaped pipe BHEs. After the description of the test site and models used (
Section 2), the results of the analysis of the thermal response testing measurements on different borehole heat exchangers are presented (
Section 3).
3. Results and Discussion
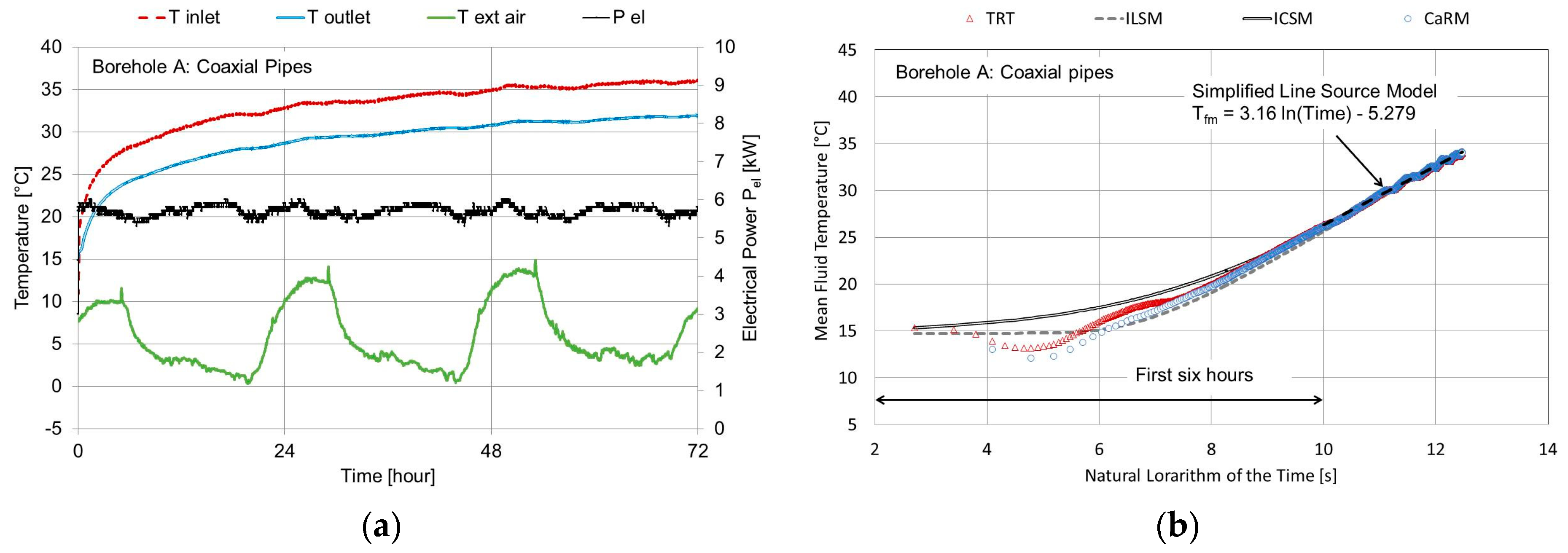
TRT results and their analysis are outlined in this section. As Borehole A, a coaxial BHE, was the longest one (i.e., 96 m long) in the test area, it was used as a reference point for the site’s geological characterization.
Figure 4a outlines the TRT measurements of that BHE. In addition,
Figure 4b shows the analysis carried out in accordance with the common interpretation of the TRT measurements based on the infinite line source approach used to evaluate the equivalent ground thermal conductivity (
λeq) which resulted equal to approximately 1.49 W/(m K) at a depth of 96 m. This value was lower than that (i.e., 1.82 W/(m K)) calculated using information obtained from the data sheets of the drilling operations and values outlined by the standard VDI 4640 [
23]. The uncertainty analysis of the TRT measurements involved a global error of the equivalent thermal conductivity of approximately ±0.15 W/(m K). The fluid volume within that BHE was approximately 286 L; the effect of the thermal capacity of the heat-carrier fluid can be seen in the first section where the mean fluid temperature profile is plotted (
Figure 4b); it initially fell and then started to rise. As can be seen, the greatest difference between the analytical results and the measured values was found during the first six hours of testing; test results were, instead, nearly equivalent over the long-term. The results of CaRM are in agreement also with the short-term experimental values since the model takes into consideration the borehole thermal capacity.
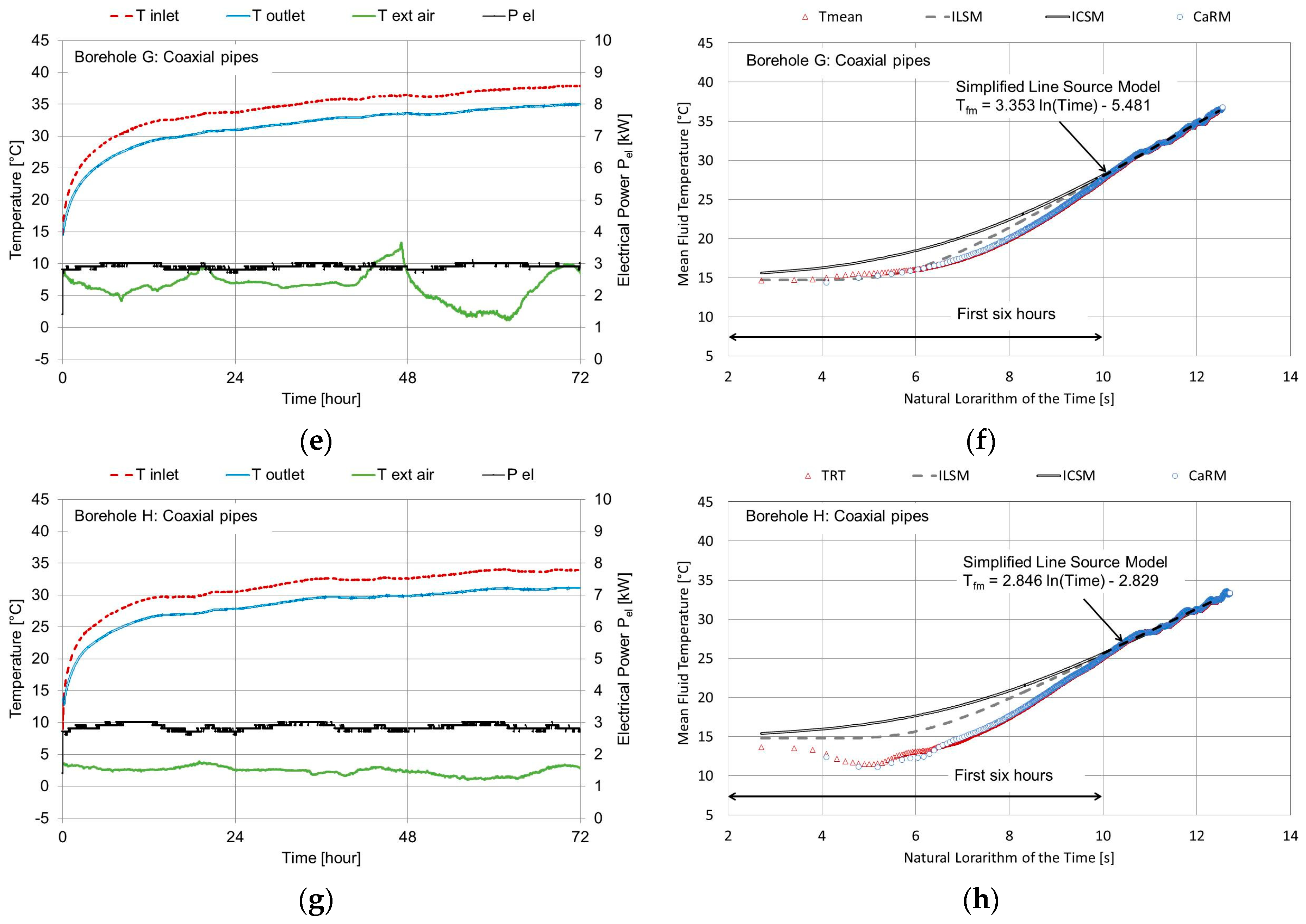
Figure 5 shows the TRT measurements for the 50 m long boreholes.
Figure 5a,b refers to the double U-tube,
Figure 5c,d to Borehole F,
Figure 5e,f to Borehole G, and
Figure 5g,h to Borehole H. The fluid volume is 106 L for the double U-tube; it is 114, 76 and 73 L for Boreholes F, G and H, respectively. The volume fluid flow rate was the same for those BHEs and equal to 2.39 × 10
−4 m
3/s.
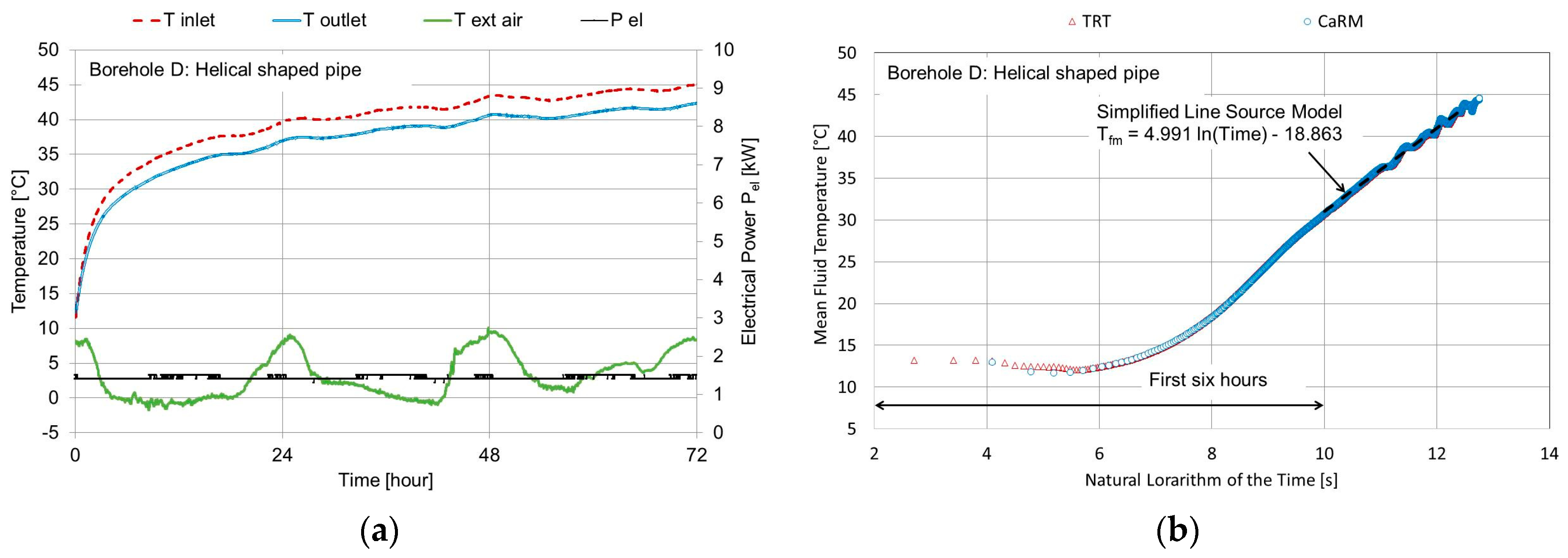
Figure 6 outlines the TRT measurements of the 15 m long helical shaped pipe heat exchanger (Borehole D). The effect of the axial heat conduction cannot be neglected in that particular BHE given its shallow depth and large diameter (i.e., 0.4 m). This explains why the common interpretation based on the infinite line source model (S-ILSM) involves an error in evaluating the equivalent ground thermal conductivity: according to that model, which is the usual one adopted by technicians to calculate the variable, heat transfer takes place only along the radial direction, in which case the result was approximately 1.39 W/(m K). According to the inverse numerical approach, the result was approximately 1.2 W/(m K). The value produced by the numerical procedure was clearly lower since the imposed heat transfer rate moves along both radial and axial directions; it is instead considered a single value in the radial direction by the S-ILSM. As can be seen in
Figure 6b, the mean fluid temperature starts from a value that is lower than that for the 50 m long boreholes (
Figure 5) since the effect of the weather on the ground temperature is higher for the shallow depth of 15 m. The infinite line and cylinder source models were not applied to this BHE because the hypotheses were not clearly satisfied.
Table 7 outlines the equivalent ground thermal conductivity calculated using the common interpretation (S-ILSM), infinite line (ILSM) and cylinder (ICSM) source models as well as the inverse solution via CaRM tool for each BHE investigated. As can be seen, the result of the simplified line source model (S-ILSM) was higher than that found using the complete solution of the infinite line source model (ILSM) since the contribution of the first six hours was neglected. The equivalent thermal conductivity of the ground from the ICSM was less than that via ILSM; in fact, in the ICSM the heat was released at the borehole radius and, consequently, did not take into consideration the contribution of the bore filling material. The minimum
RMSE value was found by means of the CaRM, and this can be seen also in
Figure 4,
Figure 5 and
Figure 6. As can be observed in
Table 7, the equivalent ground thermal conductivity outlined using the interpretation of the infinite line source approach ranged from 1.35 W/(m K) for Borehole G to 1.60 W/(m K) for Borehole C, which is located at the same site and has the same depth. The two BHEs were spaced only about 15 m away from one another but the ground layers could have been diversified leading to different equivalent thermal conductivity values. This result highlights the importance of carrying out TRT measurements at different positions in a borehole field especially when there are several borehole heat exchangers so that any difference in the ground composition can be identified and the mean equivalent thermal conductivity to use during the design process can be found.
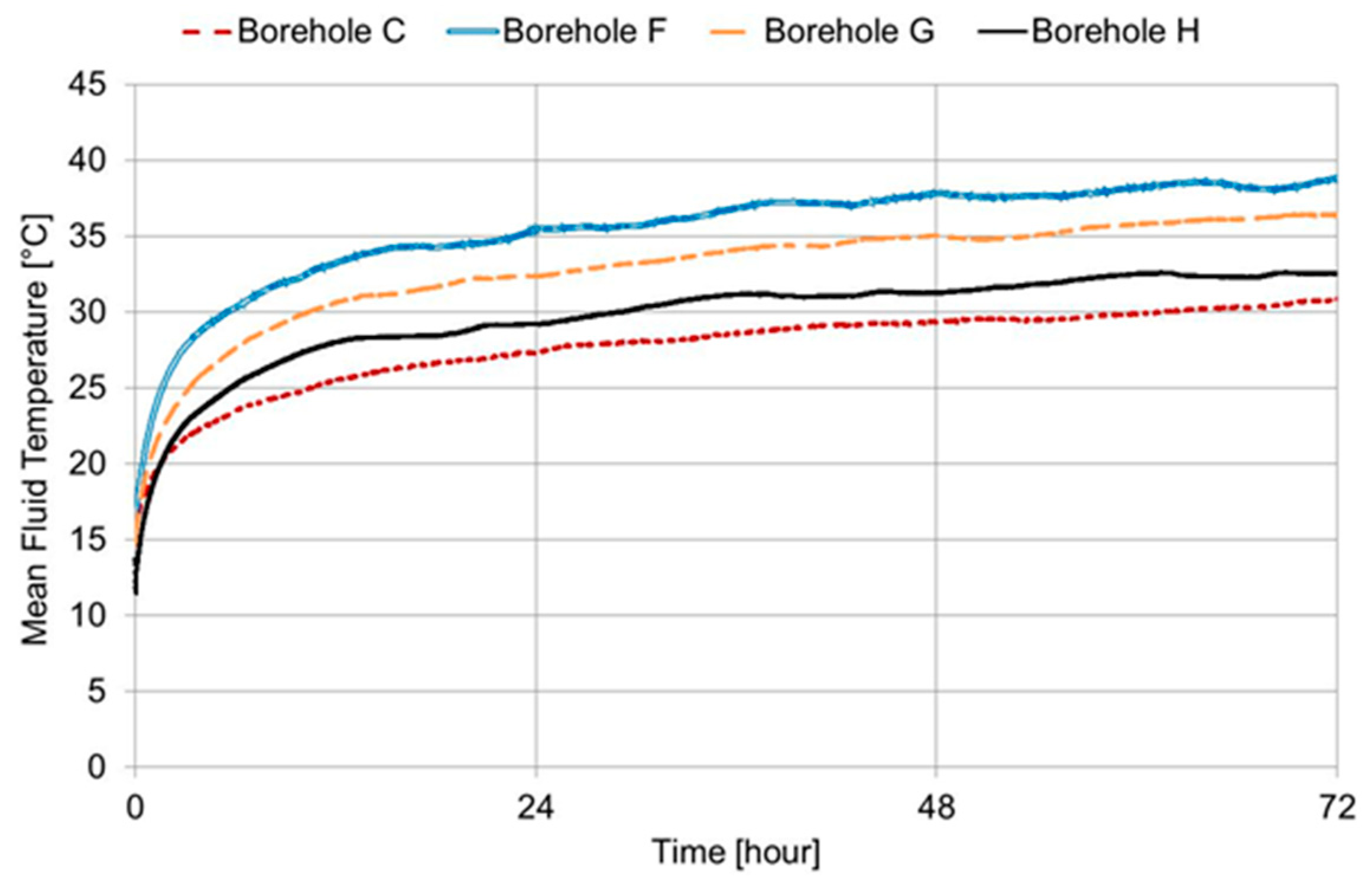
The TRT of the 50 m long BHEs was carried out using both the same heat-injection rate and fluid mass flow rate. As a consequence, the thermal behavior of the BHEs under constant heat injection rate could also be evaluated. The differences between the inlet and outlet mean fluid temperature profiles of the four BHE were thus compared (
Figure 7). As can be seen, after 72 operating hours under a constant heat injection rate, the double U-tube heat exchanger liberated the same heat load with the lowest temperature difference between the heat-carrier fluid inside the pipes and the surrounding ground. The thermal behavior of Borehole H was better than that of Borehole G since it has a larger outer diameter (60.3 versus 50 mm). Borehole F, which had the largest outer diameter (i.e., 101 mm), needed, instead, a higher temperature difference to liberate the heat rate since its thermal resistance was higher than that of Borehole H (see
Table 6); this result largely depended on the material in which the pipes were constructed (PVC for Borehole F and stainless steel for Borehole H).
In order to compare the thermal performance, the global heat transfer coefficient can be calculated as follows:
At the end of the thermal response testing (i.e., after 72 h under constant heat injection rate) the Ub coefficient was approximately 3.7, 2.4, 2.6 and 3.2 W/(m K) for Borehole C, F, G and H, respectively.
4. Conclusions
The current study analyzed the interpretation of thermal response testing using analytical and numerical models. The common method, which uses the first-order approximation of the infinite line source model, was compared with the complete solution of the infinite line and cylinder source models. The inverse numerical procedure was also investigated using a detailed model.
The equivalent thermal conductivity provided by literature data depending on the ground type was about 20% higher than that found using the common interpretation of the TRT measurements conducted on the 96 m long BHE. In addition, the thermal response testing interpretation showed that in that same area the equivalent thermal conductivity ranged from approximately 1.35 to 1.62 W/(m K) for the same BHE depth. The minimum misfit between the experimental and calculated values of the mean fluid temperature was found using the inverse numerical procedure by means of the CaRM simulation tool which considers important phenomena that affect the thermal behavior of the borehole heat exchanger, e.g., the weather conditions at the ground surface, axial heat transfer and borehole thermal capacity. The inverse numerical approach clearly depends on the accuracy of the model used. The main assumption of the analytical models is a constant heat load, which is not easy to replicate in the practice; on the other hand, CaRM tool is able to consider the fluctuations of the heat load and, consequently, the transient thermal behavior. In addition, as the CaRM tool can analyze the short-term behavior of the ground heat exchanger, a lower time span of the thermal response testing can be used, involving a decrease of the test’s costs.
Test results revealed that the thermal behavior of the BHEs when a constant and long-term heat injection rate is applied significantly depends on their total exchanging surface and hence size. When intermittent operating modes of the ground source heat pump system are set, the thermal capacity (of both grouting material and heat carrier fluid) and thermal resistance of the borehole heat exchanger are surely key parameters that could affect the seasonal energy efficiency of the entire system. Therefore, demonstration cases will be realized within the European Cheap-GSHPs project in order to evaluate the energy efficiency of the entire ground source heat pump system under variable operating modes. Considering in particular the coaxial stainless steel pipes, together with energy performance, it is anyway important to consider its easier installation, thanks to the use of a piling methodology that leads to lower costs.