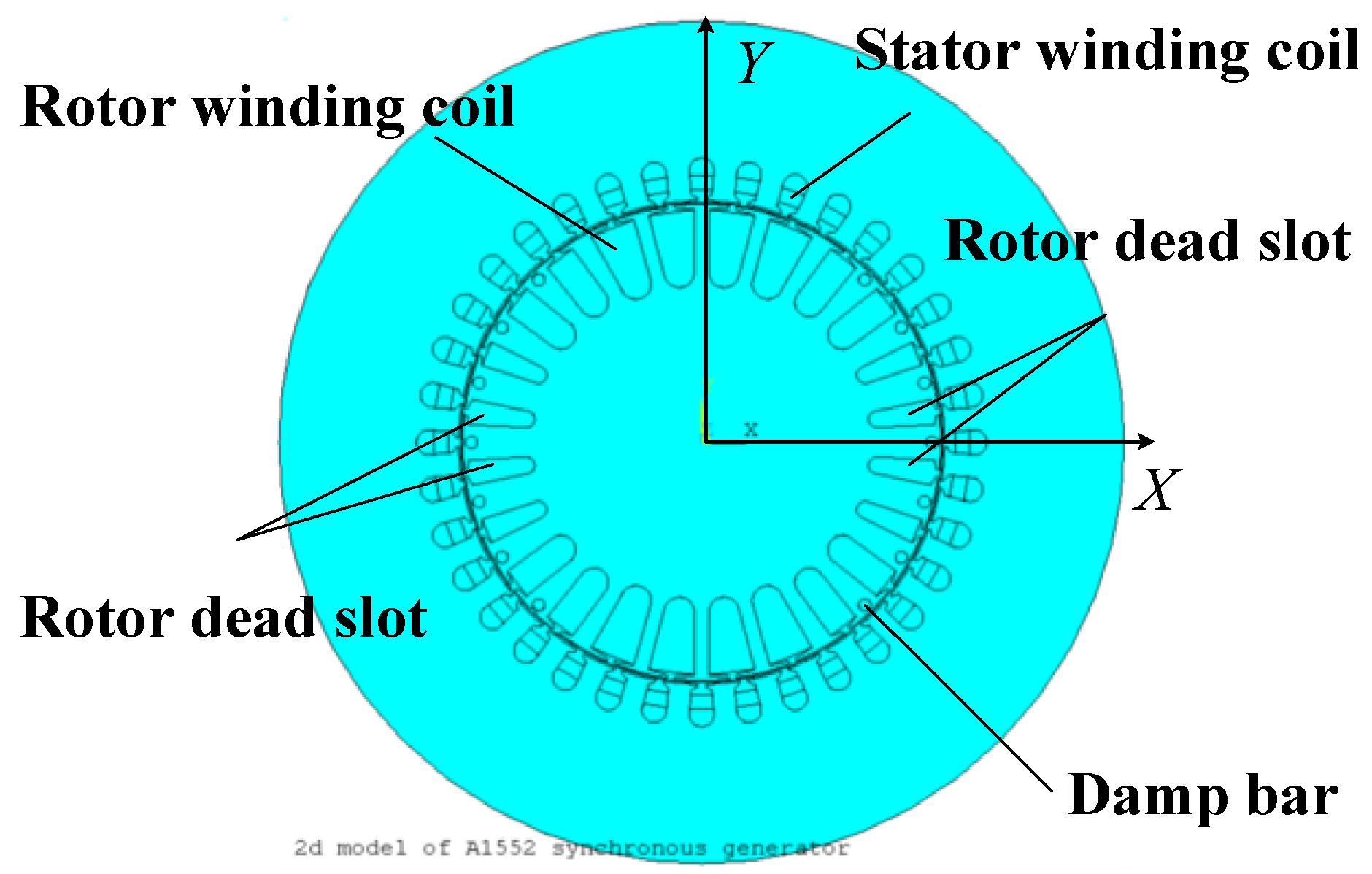
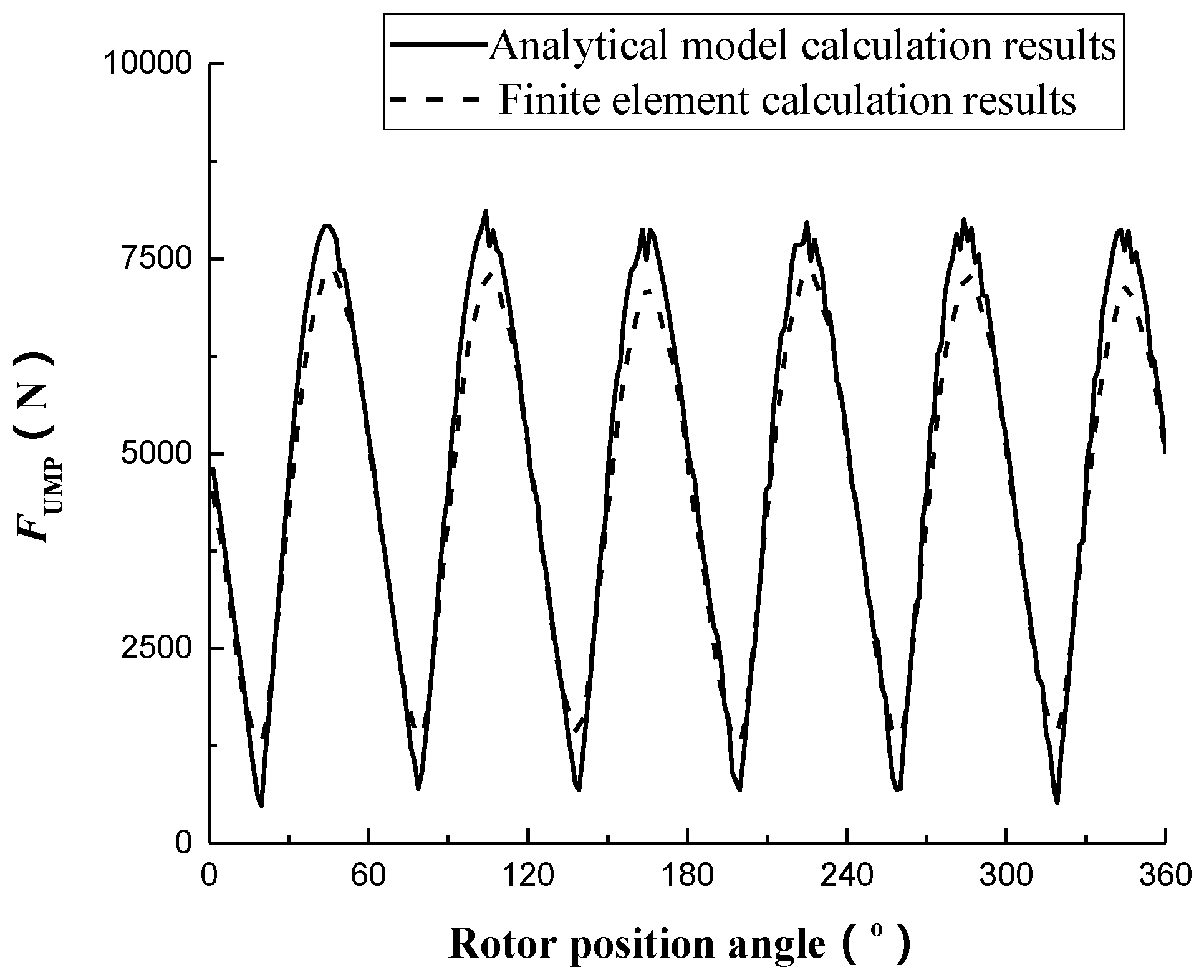
4.1. Effects of Field Winding Short Circuit Position on UMP
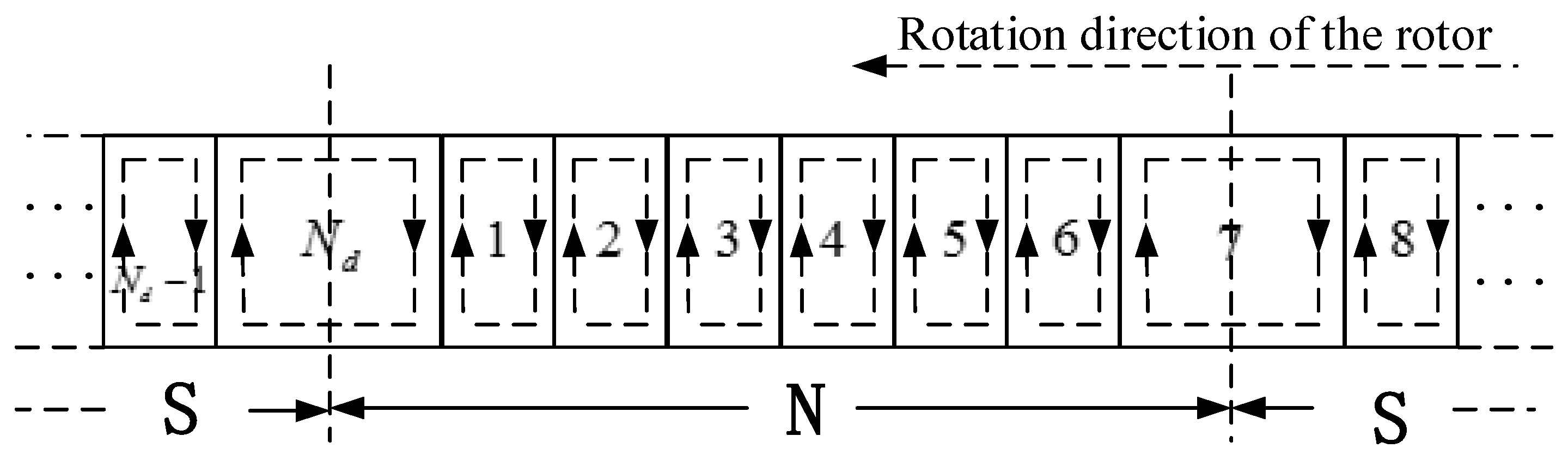
Post-fault MMF is the sum of the MMF produced by the normal field circuit and the MMF produced by the fault additional circuit. When the additional harmonic current of field and damp winding (caused by post-fault stator armature reaction MMF) is not considered, the MMF properties produced by the normal field circuit are the same as those before the faults. Only the effects of the MMF produced by the fault field circuit on the UMP must be analyzed. Fourier decomposition for MMF produced by the fault field concentric coil is carried out:
The rectangular wave MMF is symmetrical around the rotor d-axis, so there is only the cosine term in Equation (20). This calculation is factored into:
where
is the DC component of field current,
w is the number of short circuit turns, and
ky,v is pitch shortening factor of the fault field concentric coils to the
vth harmonic. Its computational formula is as follows:
where
is pitch shortening ratio of the coil.
From Equation (21) we can see that the vth harmonic MMF produced by the fault coil is proportional to the pitch shortening factor ky,v of the coil with regard to the vth harmonic for definite field current and short turns. Therefore, the RMS of the vth harmonic current induced in the stator branch and the amplitude of the space harmonic MMF induced in the air gap are both proportional to ky,v. Each harmonic of fault UMP is generated by magnetic field interactions in the air gap. The amplitude of each harmonic is only affected by ky,v. In the field test, the fundamental component of UMP is measured and observed. This paper takes the fundamental component of UMP as the main research object. UMP thereafter refers to the fundamental component of the UMP.
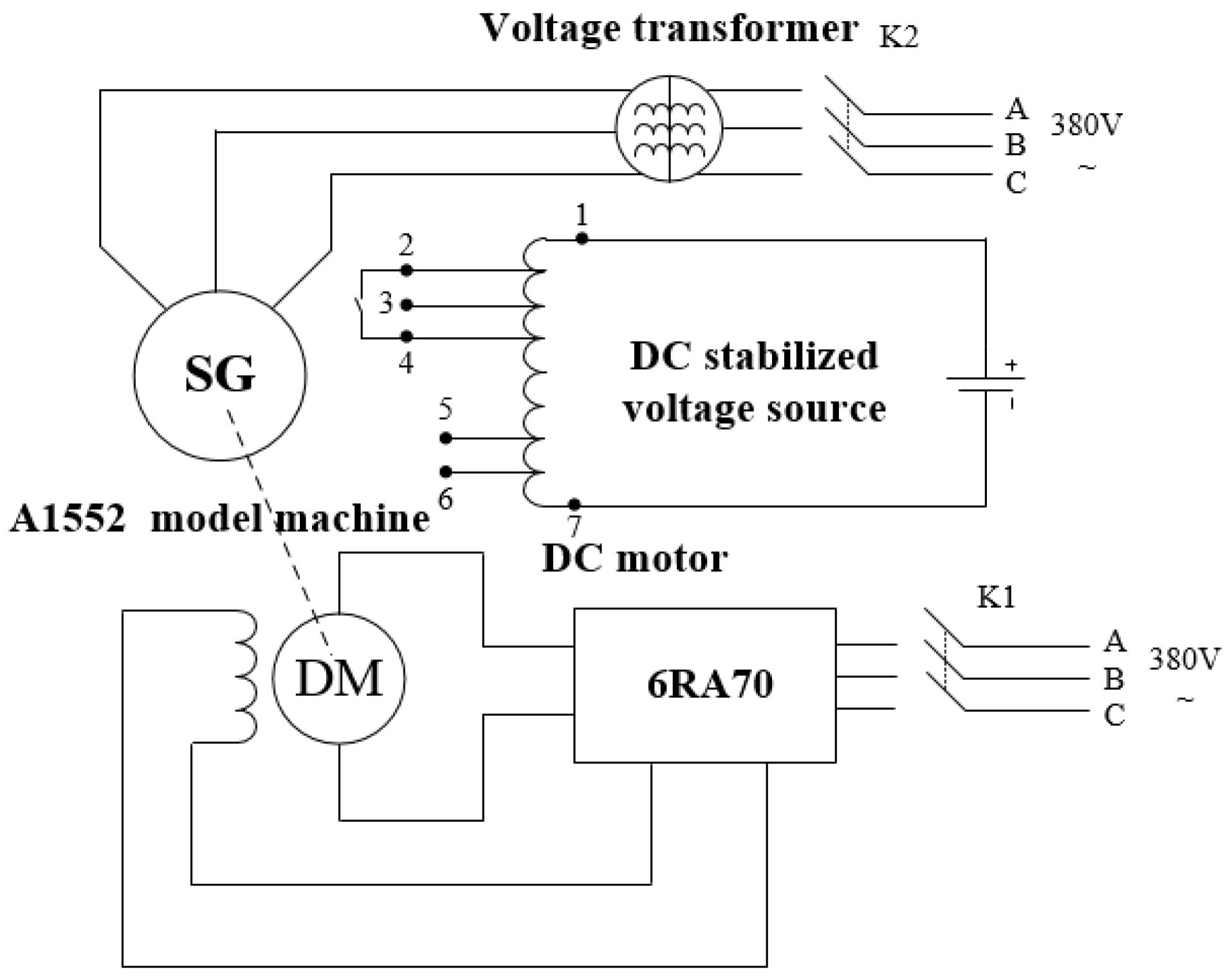
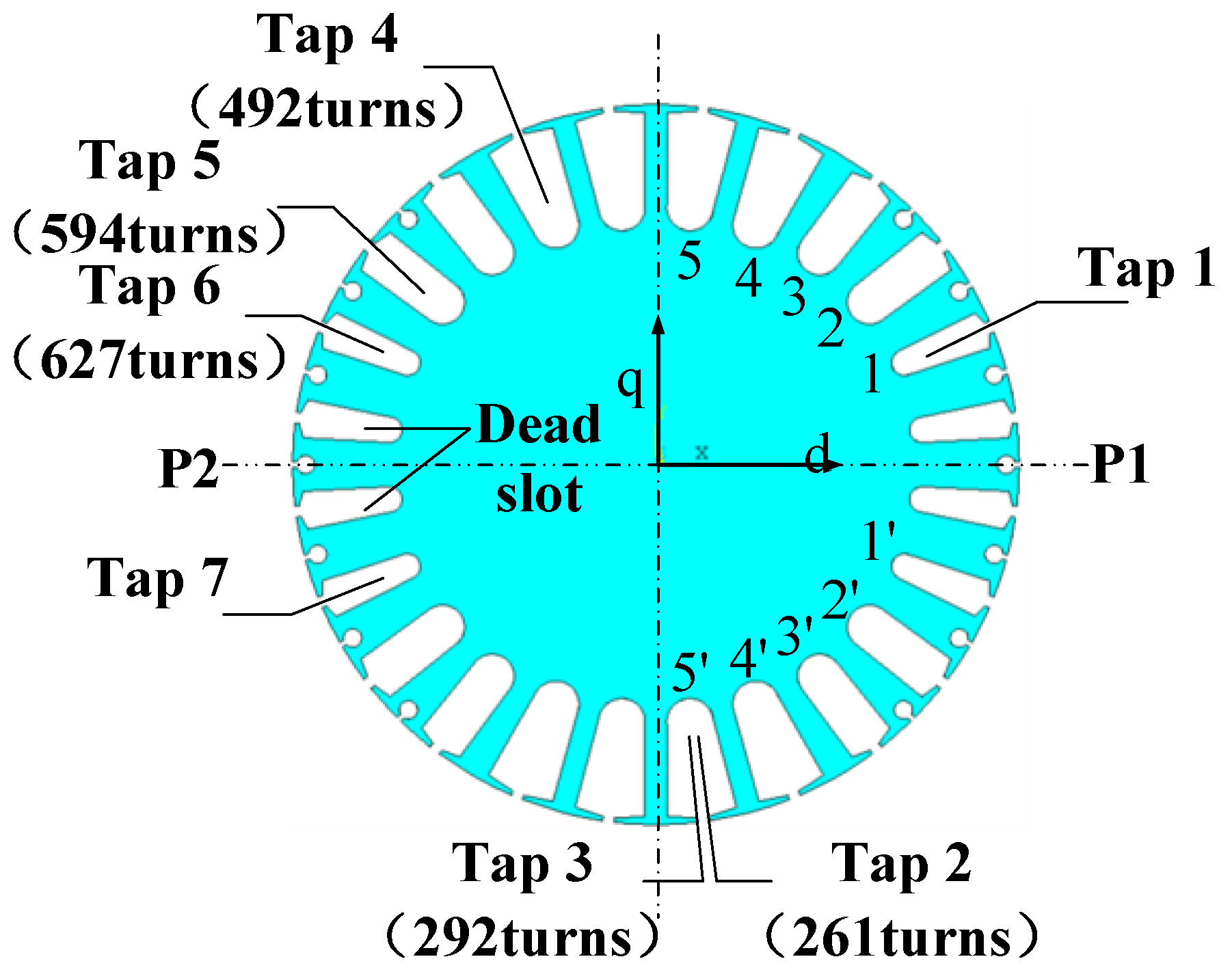
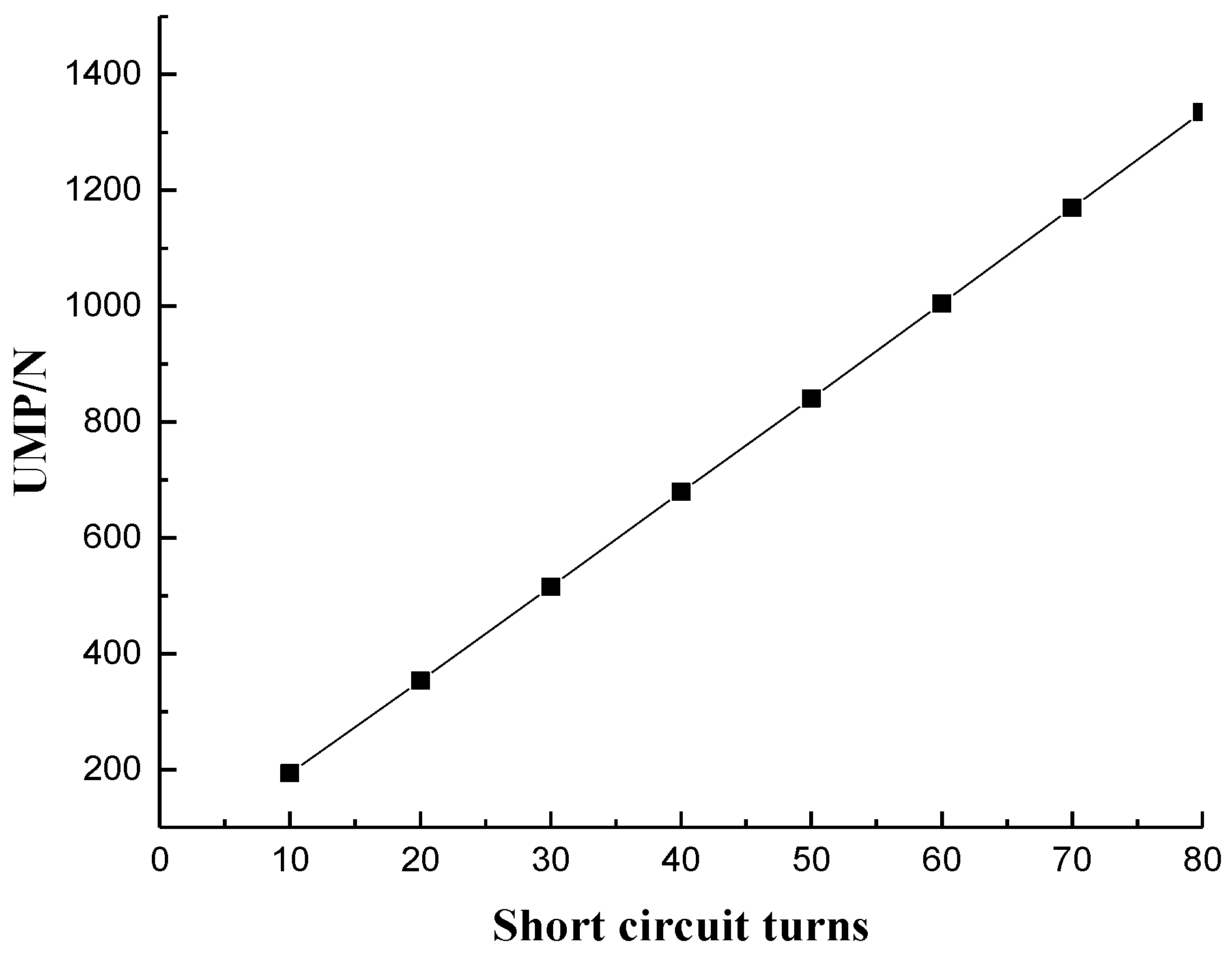
In order to study the influence of short circuit position on UMP, 11–55 foot field concentric coils on 30 turn short circuit faults are respectively calculated. Conditions of operation are grid-connected. The simulation results are shown in
Table 5.
When the two field concentric coils with the same pitch shortening factor ky,2 respectively undergo faults, the values of UMP are similar. The UMP with larger pitch shortening factor ky,1 is slightly less than that with smaller ky,1.
When the field concentric coils with different pitches undergo short circuit faults, UMP is generated by an interaction between the fundamental MMF and the second MMF in the air gap. The fundamental MMF includes the fundamental field MMF and the MMF produced by the stator harmonic current. The fundamental field MMF can be regarded as the sum of the fundamental MMF produced by the normal field circuit and the fundamental MMF produced by the fault additional circuit. The fundamental MMF produced by the fault circuit increased with increasing ky,1, but the fundamental MMF produced by the normal field circuit remained unchanged. The superposition of the two will show a decreasing trend, but the change is minimal overall.
The fundamental current induced in the stator winding and the fundamental MMF produced by the fundamental current will also have the same variation law. The combined fundamental MMF in the air gap will decrease with increasing ky,1, but the overall change is also minimal. The size of the second MMF in the air gap is approximately proportional to ky,2. Therefore, UMP is approximately proportional to pitch shortening factor ky,2 of the fault coil. For the same ky,2, the size of UMP is negatively correlated with ky,1.
4.3. Influence of Generator Running State on UMP
When a field winding inter-turn short circuit fault occurs in a generator, the position of the short circuit and the turn number is fixed in a certain time. With the change of the generator's running state, the UMP on the rotor will change. In order to determine whether or not the field winding inter-turn short circuit fault occurs, it is very important to study the relationship between UMP and the generator’s running state.
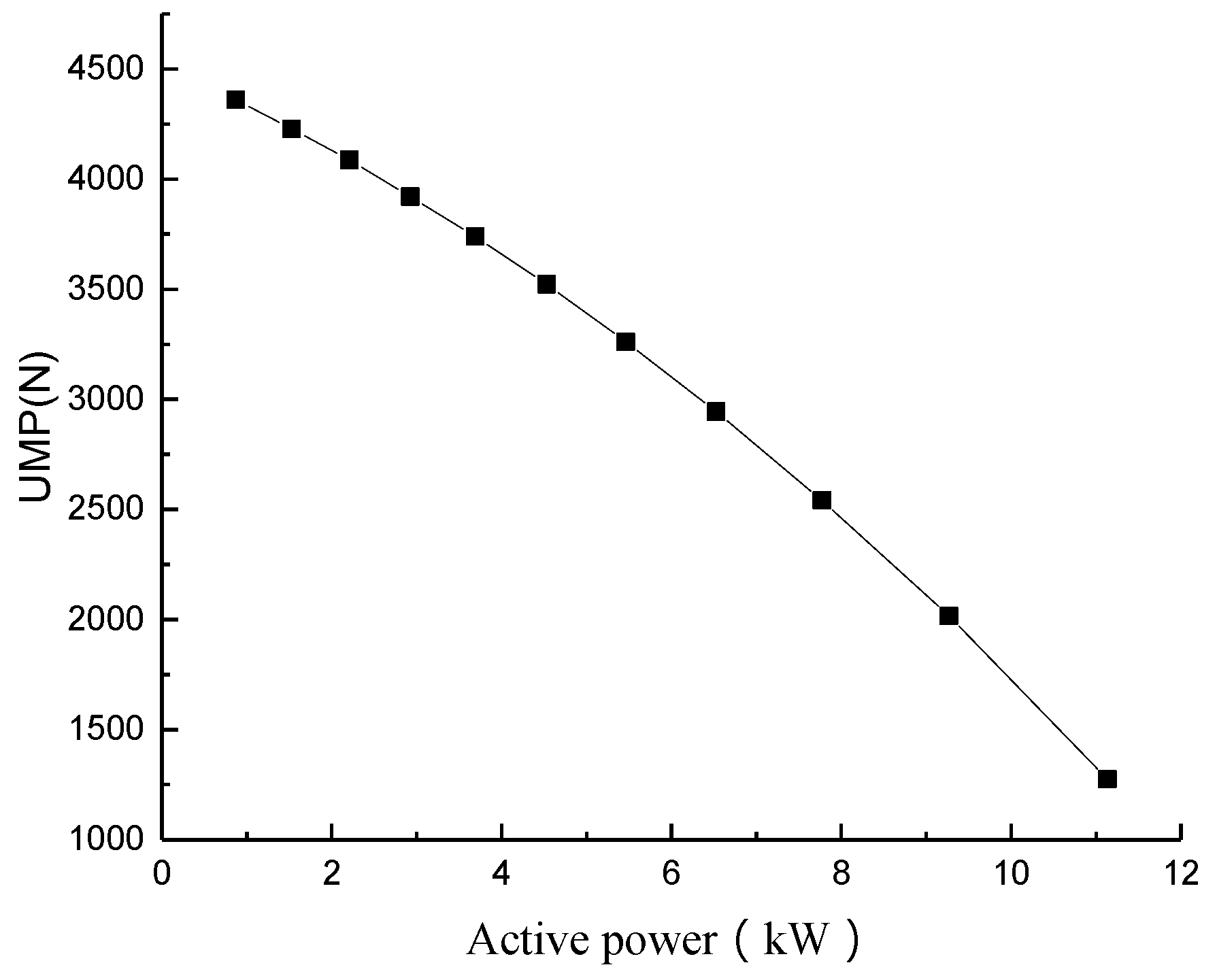
4.3.1. Effect of Output Active Power on UMP
In order to study the effect of active power on UMP, its power factor angle (PFA) is changed. The output active power is also changed, and the reactive power is unchanged according to taps 2–4 short-circuit in the field winding of the machine model. The short circuit faults under these states are calculated.
As shown in
Table 7, the output active power will decrease and UMP will increase with increasing PFA. This is due to the fundamental current of the stator branch reducing with increasing PFA
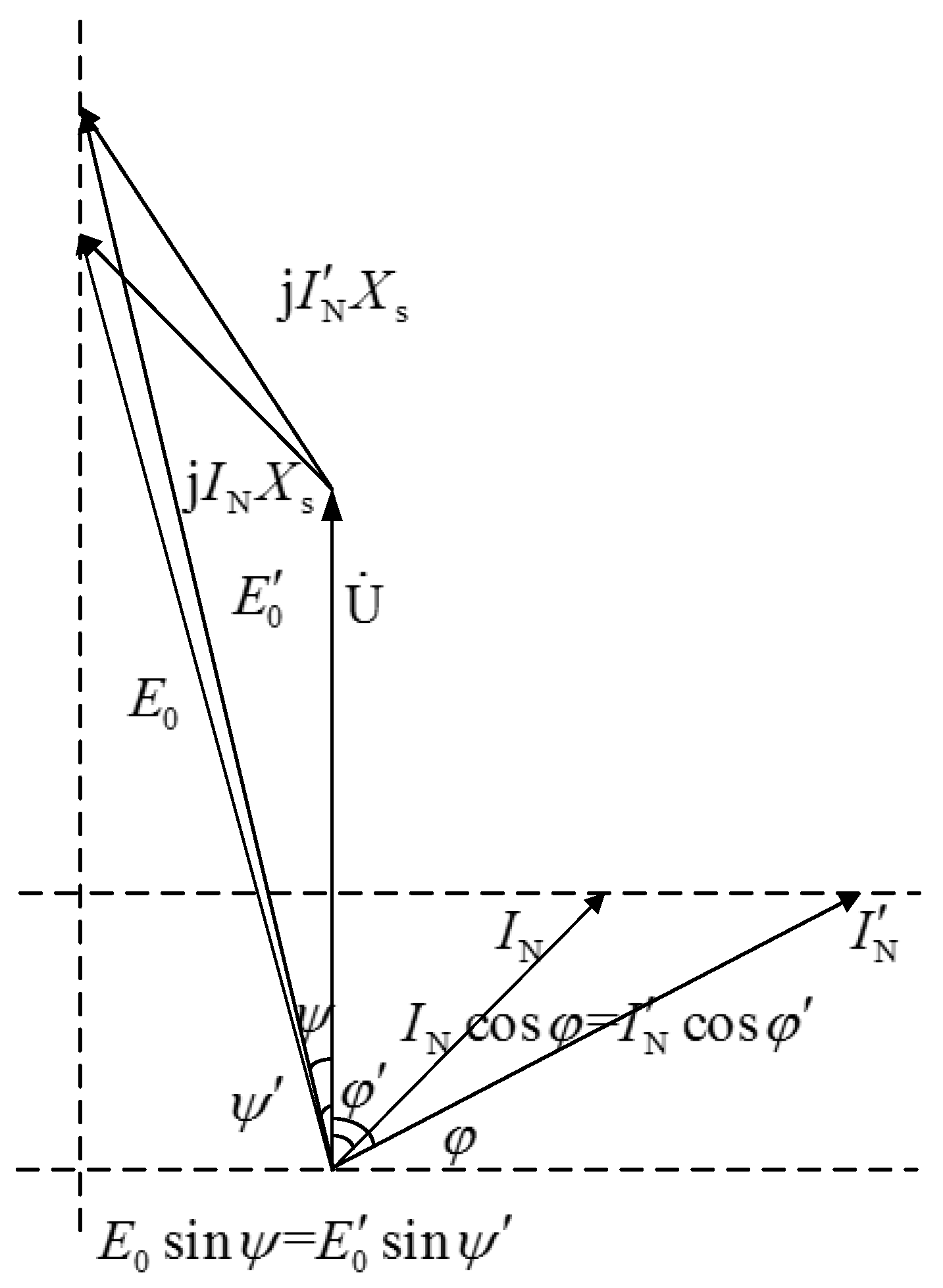
under the premise of constant output reactive power. The size of the secondary harmonic current is essentially invariant. This is because there are no changes in the field current. The fundamental MMF and the secondary MMF produced by the field current, as well as the secondary MMF produced by the stator branch second harmonic current, are all unchanged. Only the fundamental MMF produced by the stator branch fundamental current becomes smaller. Because
, the fundamental MMF of the stator armature plays a demagnetizing role in field MMF. Therefore, the combined MMF in the air gap reduces and UMP decreases.
As seen in
Figure 16, UMP decreases faster with increasing active power. The fundamental MMF produced by the stator branch fundamental current will also increase. Demagnetizing armature reaction will also be stronger, and the saturation degree in the air gap magnetic field will decrease. The higher the air gap saturation, the lower the UMP change rate. The lower the air gap saturation, the greater the UMP change rate.
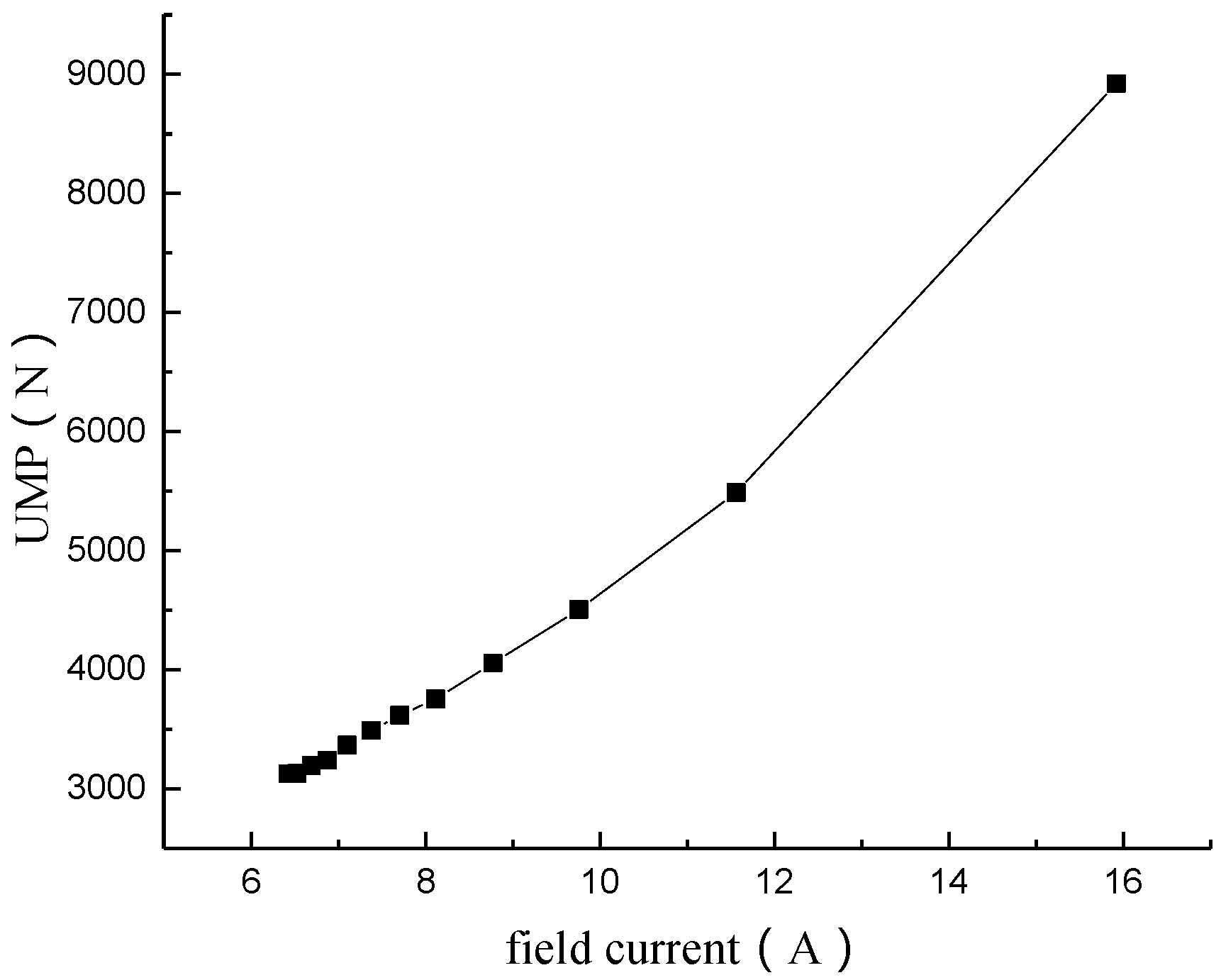
4.3.2. Effect of Field Current on UMP
In order to study the effect of field current on UMP, its PFA is changed so that the field current and output reactive power are also changed. The active power is unchanged under the premise that taps 2–4 short circuit in the field winding of the machine model. The short circuit faults under these states are calculated.
As seen in
Table 8 and
Figure 17 the output reactive power and UMP are increased with increasing PFA. When the PFA increases (
), due to unchanged output active power (
), the fundamental current of the stator branch and the output reactive power are increased (
,
). As the generator voltage
remains unchanged, the field electromotive force becomes larger (
), and the field current also increases (
), as shown in
Figure 18.
The fundamental MMF and the second MMF produced by the rotor and stator will increase with increasing field current. Although the fundamental MMF produced by the stator branch current plays a demagnetizing role compared with the stator fundamental MMF, the influences of the fundamental field MMF on the combined MMF in the air gap are more obvious. UMP will also increase with increasing field current.