Primary and Albedo Solar Energy Sources for High Altitude Persistent Air Vehicle Operation
Abstract
:1. Introduction
2. Energy Requirements and Availability
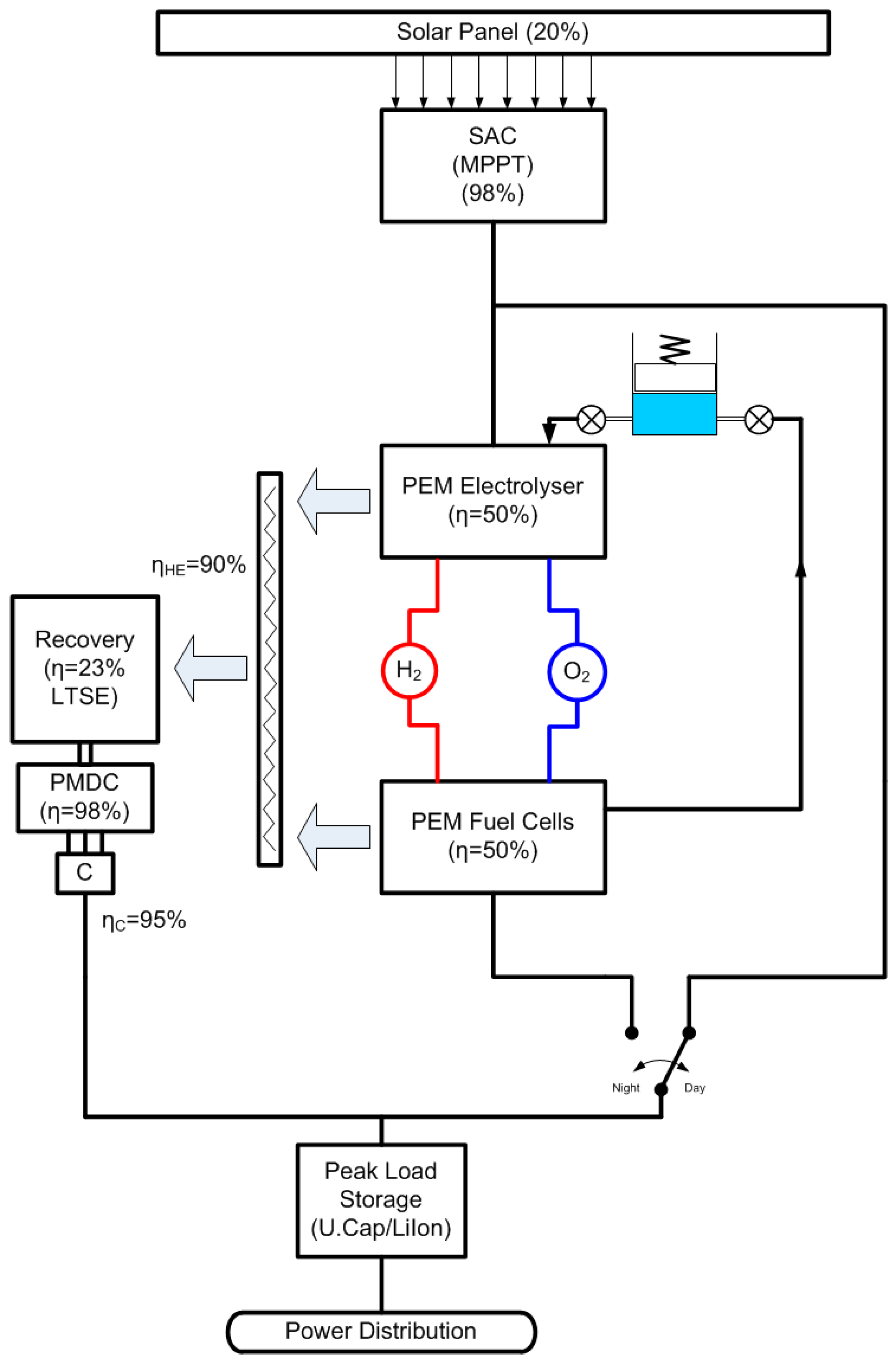
2.1. Energy Harvesting Audit
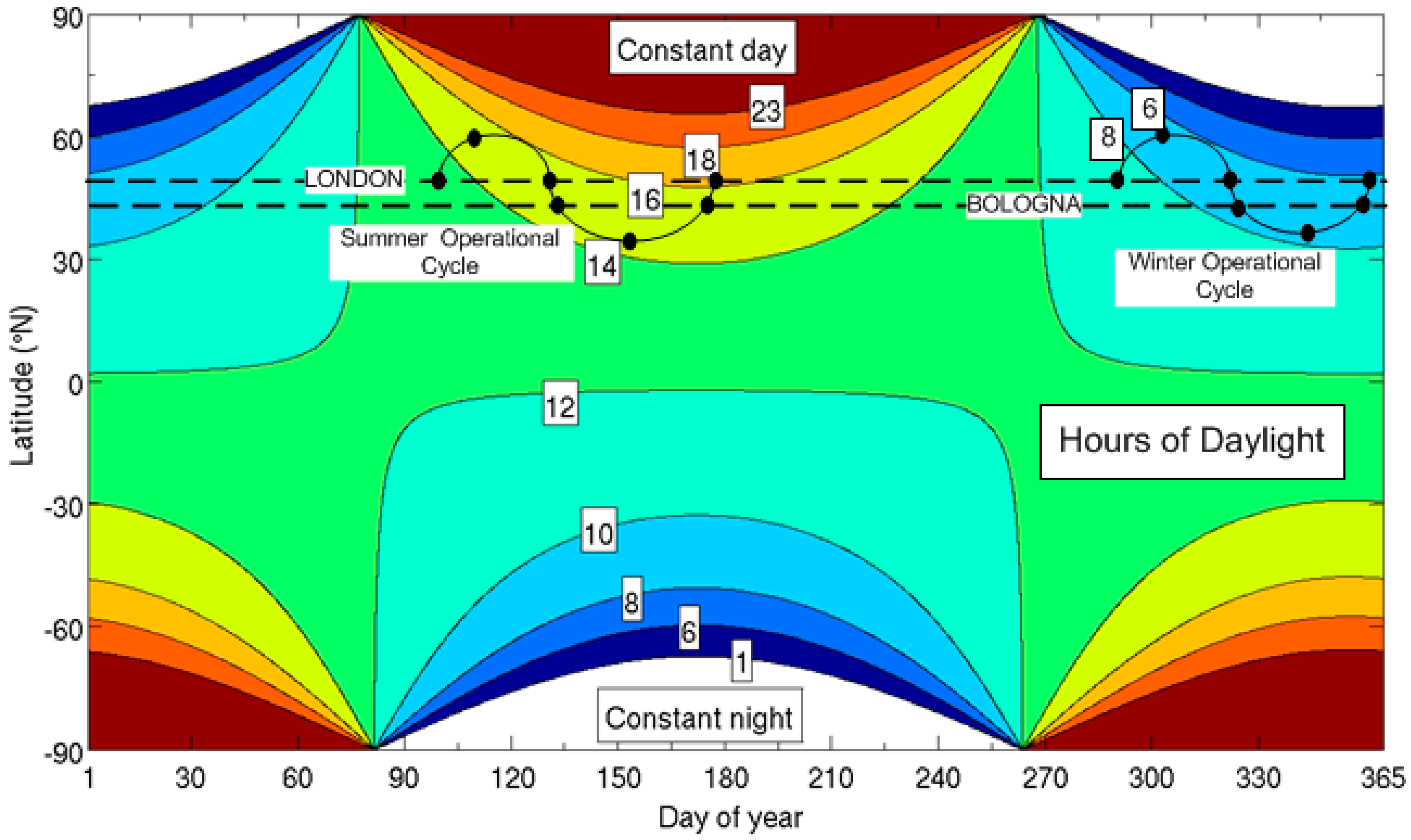
2.2. Day Length
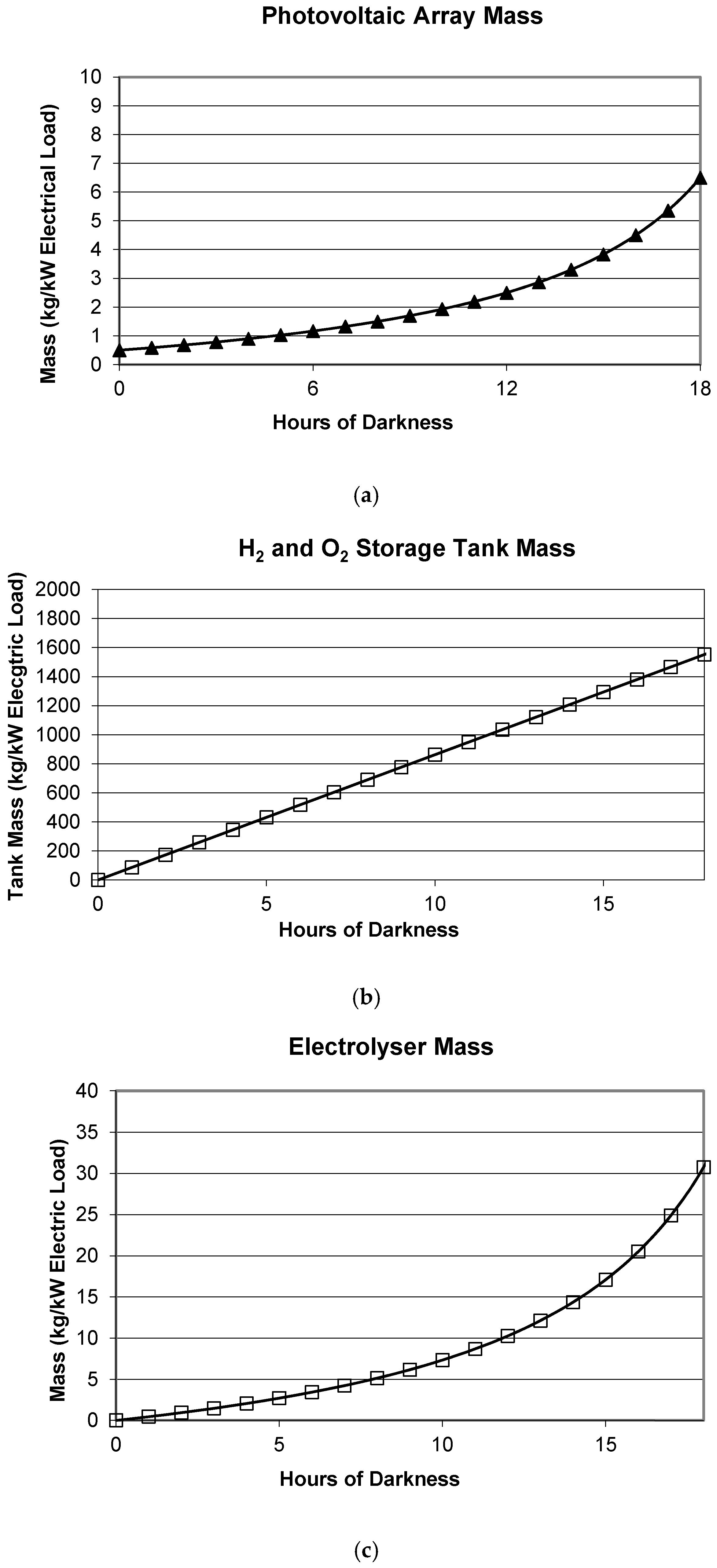
2.3. Impact on System Energy Requirement due to Day Length
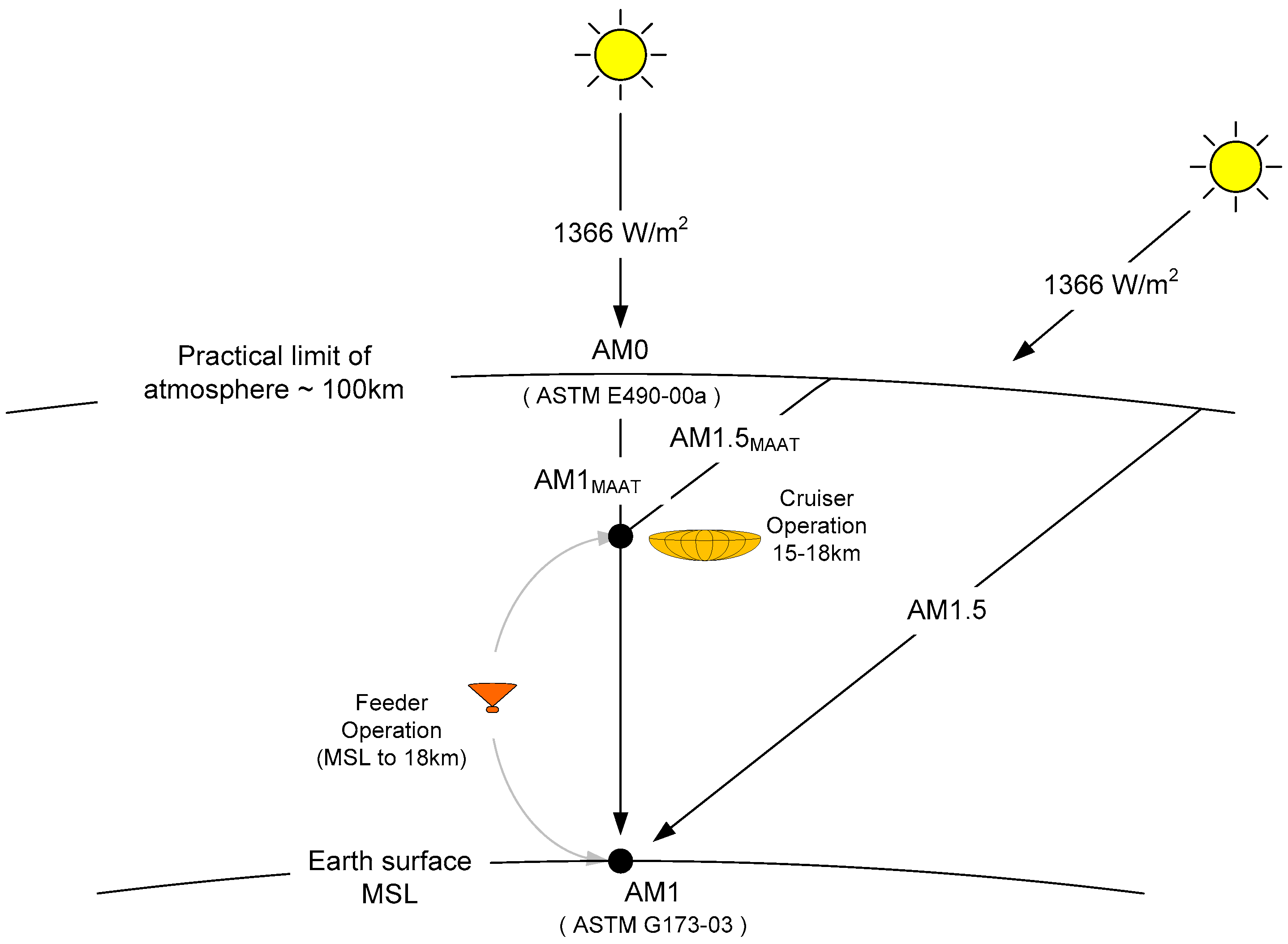
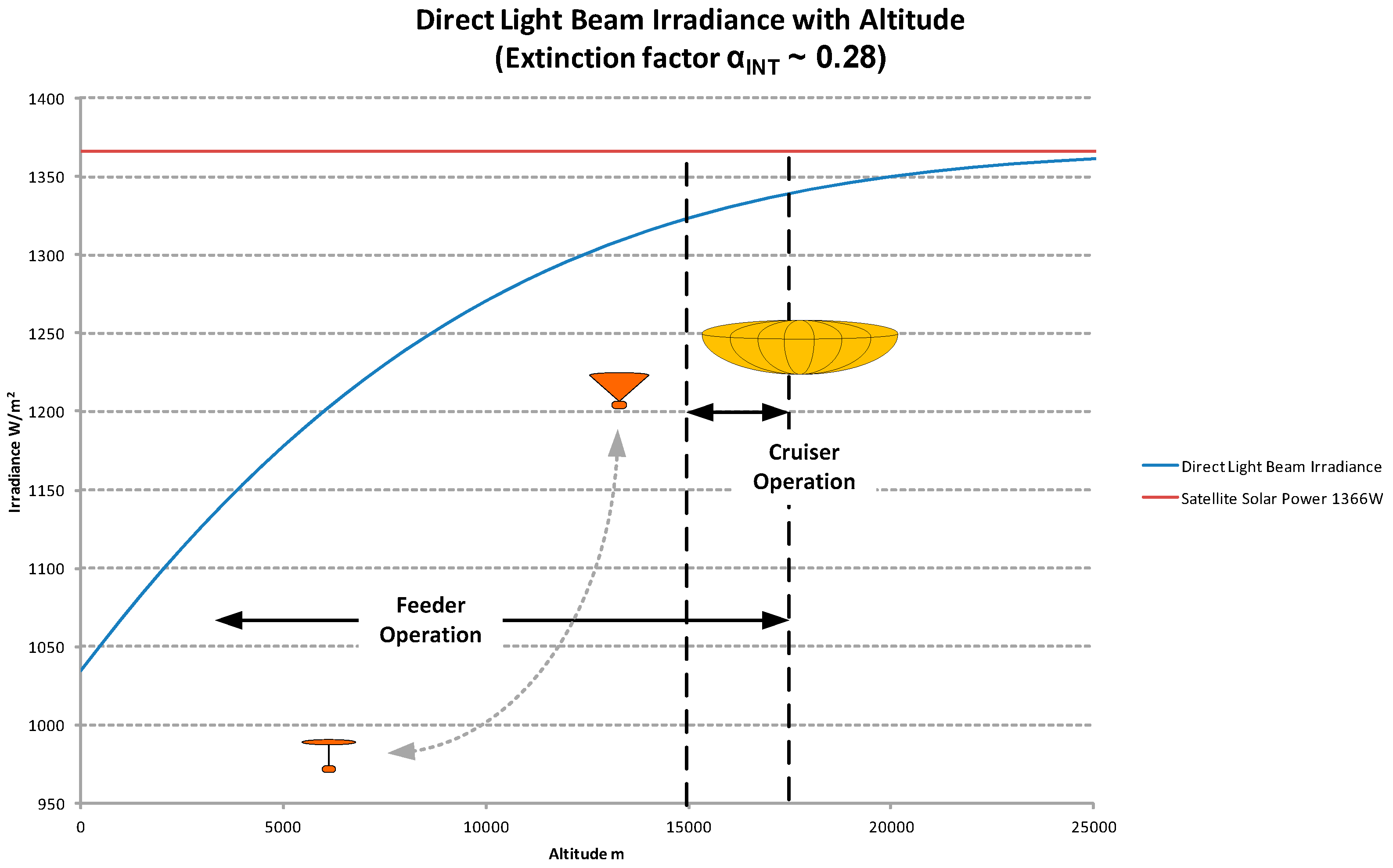
2.4. Energy Harvesting at Stratospheric Altitudes
2.4.1. Harvesting of Direct Insolation
- is the intensity of the light beam after passing through the medium
- is the original light beam intensity
- is the extinction coefficient over the medium thickness h.
- αINT is the total extinction across the whole airmass
- is the extinction coefficient over a section of atmosphere Δh.
- θ is the sun’s zenith angle
- is the cruiser latitude
- δ is the sun’s declination
- γ is the local hour angle.
2.4.2. Harvesting Energy from the Indirect Albedo Effect
- Ae is the earth surface albedo
- Aa is the atmosphere
- Ac is the cloud reflection.
3. Results
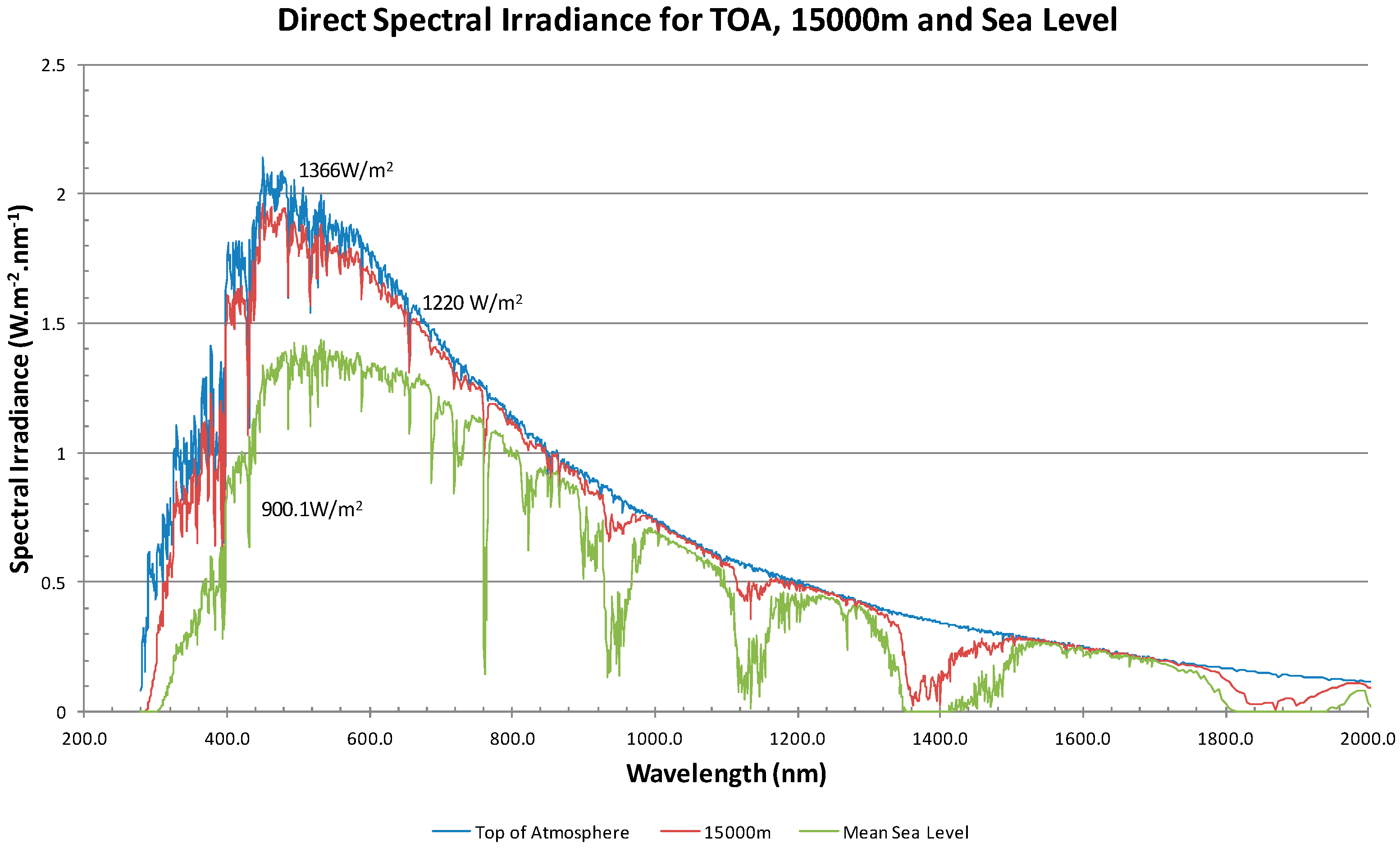
3.1. Available Energy from Direct Insolation
3.2. Available Energy from Indirect Albedo Effect
- (i)
- High types such as Cirrus (Ci), Cirrostratus (Cs) and Cirrocumulus (Cc) typically occur between 6 km and 10 km. They are predominantly formed from ice crystals and have a low reflectivity of around 20%.
- (ii)
- Medium clouds such as Altocumulus (Ac) and Altostratus (As) occur between 2 km and 7 km and have a reflectivity of between 40% and 56%.
- (iii)
- Low cloud types such as Nimbostratus (Ns), Stratocumulus (Sc) and Cumulus (Cu) occur between 1 km and 2 km and have a reflectivity of between 60% and 70%.
- (iv)
- Deep clouds or Cumulonimbus (Cb) occur between 1 km and 10 km and have the characteristic anvil shaped head. They have the highest reflectivity typically lying between 78% and 90%.
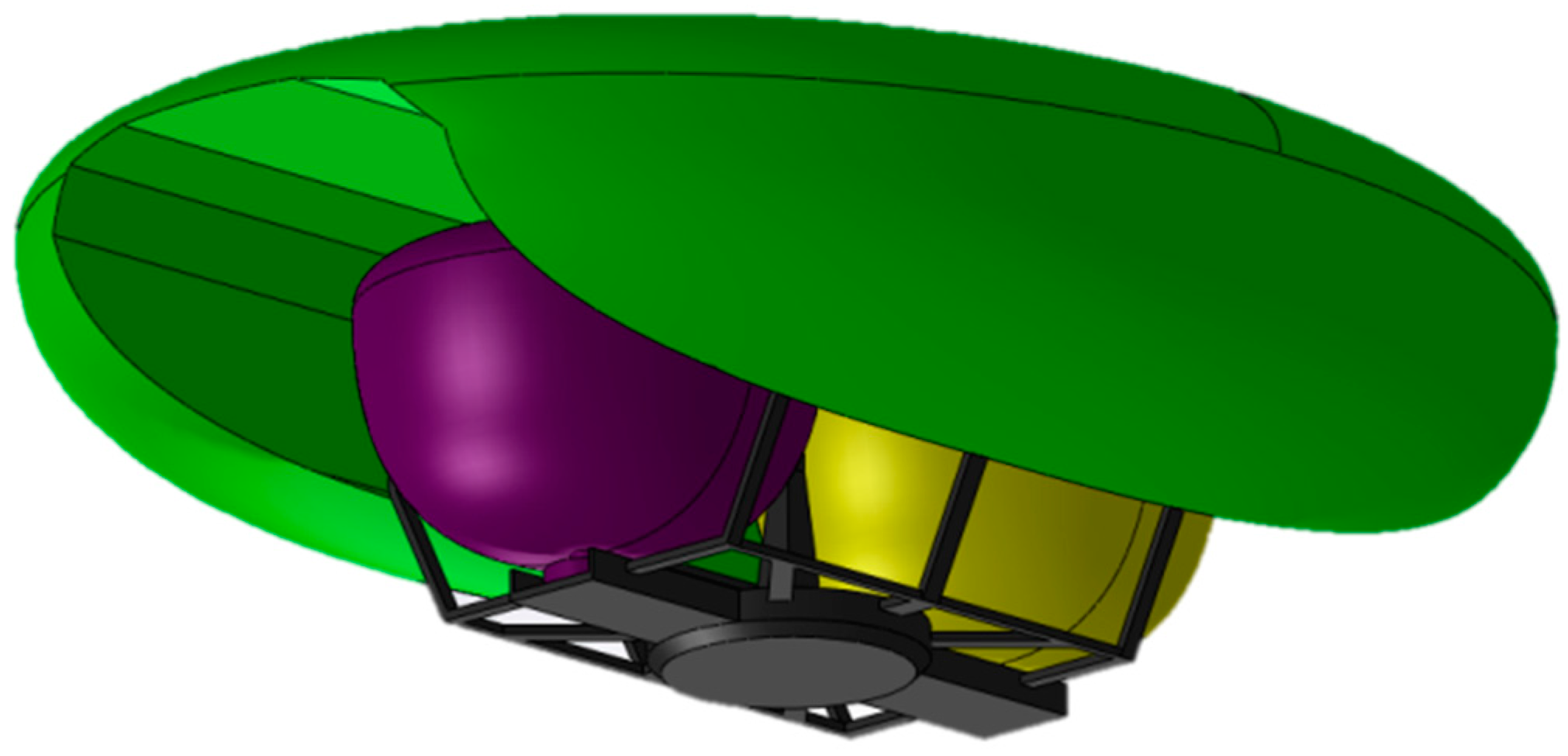
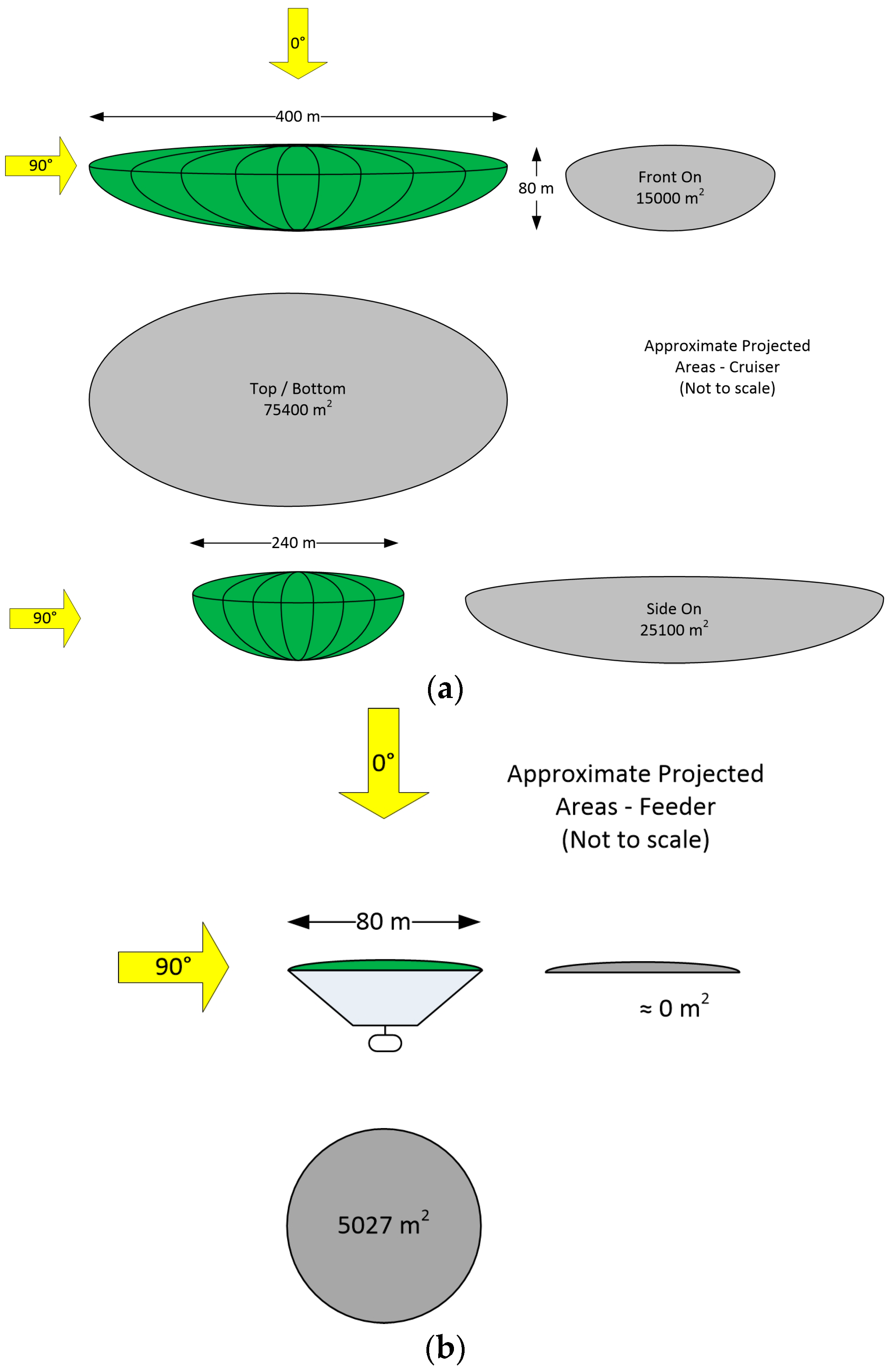
3.3. Impact of Air Vehicle Shape
4. Conclusions
Acknowledgments
| UNIMORE | Italy |
| UBI | Portugal |
| LNC | Germany |
| UH | United Kingdom |
| SFEDU | Russia |
| ENGYS | United Kingdom |
| UniBo | Italy |
| eDL | Uruguay |
| ASKR | Italy |
| VUB | Belgium |
| POLITO | Italy |
Author Contributions
Conflicts of Interest
Abbreviations
| ASTM | American Society for Testing and Materials |
| ATEN | Aerial Transport Elevator Network (Feeder) |
| BOL | Beginning of Life |
| ECS | Environmental Control System |
| EOL | End of Life |
| FC | Fuel Cell |
| HPD | High Power Distribution |
| IFE | In Flight Entertainment |
| LPD | Low Power Distribution |
| MAAT | Multibody Advanced Airship for Transport |
| MPPT | Maximum Power Point Tracker |
| MSL | Mean Sea Level |
| PDC | Power Distribution Circuit |
| PEM | Proton Exchange Membrane |
| PUC | Primary Up Converter |
| PV (A) | Photo-voltaic (Array) |
| SAC | Solar Array Converter |
| SPP | Satellite Peak Power |
| TRU | Transformer Rectifier Unit |
| UAV | Unmanned Air Vehicle |
| UCap | Ultra Capacitor |
References
- Dumas, A.; Trancossi, M. The MAAT Project, Multibody Advanced Airship for Transport, General Overview; Theme [AAT.2011.6.3.-1, AAT.2011.6.2.-1.]; Seventh Framework Programme FP7-EU-Project; LogisticNetwork Consultants GMBH: Hannover, Germany, 2011. [Google Scholar]
- Dumas, A.; Trancossi, M.; Madonia, M.; Giuliani, I. Multibody Advanced Airship for Transport; Paper 2011-01-2786; SAE International: Toulouse, France, 2011. [Google Scholar]
- Dumas, A.; Madonia, M.; Giuliani, I.; Trancossi, M. MAAT Cruiser Feeder Project: Criticalities and Solution Guidelines; Paper 2011-01-2784; SAE International: Toulouse, France, 2011. [Google Scholar]
- The Tissandier Electric Airship. This Day in Aviation 8th October 1883. Available online: www.thisdayinaviation.com/tag/tissandier-electric-airship/ (accessed on 15 November 2016).
- Khoury, G.A.; Mowforth, E. A solar airship, more than a flight of fancy. New Sci. 1978, 79, 100–102. [Google Scholar]
- Choi, S.H.; Elliott, J.R.; King, G.C. Power Budget Analysis for High Altitude Airships. NASA Langley Research Center, Hampton, Virginia 23681-2199. Available online: ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20060012139.pdf (accessed on 15 November 2016).
- QinetiQ News Releases after 14 Nights in the Air, QinetiQ Prepares to Land Its Zephyr Solar Powered Unmanned Aircraft 23/07/2010. Available online: www.qinetiq.com/news/Pages/news.aspx?year=2010 (accessed on 15 November 2016).
- Solar Impulse. Available online: www.solarimpulse.com (accessed on 15 November 2016).
- Glaser, P.E.; Maynard, O.E.; Mackovciak, J.; Ralph, E.L. Feasibility Study of a Satellite Solar Power Station; ADL-C-74830; NASA: Washington, DC, USA, 1974.
- Standard Solar Constant and Zero Air Mass Solar Spectral Irradiance Tables; ASTM International: West Conshohocken, PA, USA, 2014.
- Trenberth, K.E.; Fasullo, T.; Kiehl, J. Earth’s global energy budget. Am. Meteorol. Soc. 2009, 311–323. [Google Scholar] [CrossRef]
- Sunol, A.; Vucinic, D.; De Laet, L. Tensairity concept applied to lighter-than-air vehicles for light-weight structures. In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014. [Google Scholar]
- Dumas, A.; Trancossi, M.; Madonia, M. Energetic design and optimization of a large photovoltaic stratospheric unconventional feeder airship. SAE Int. J. Aerosp. 2012, 5, 354–370. [Google Scholar] [CrossRef]
- Trancossi, M.; Dumas, A.; Cimarelli, A.; Pascoa, J. MAAT cruiser/feeder airship design: Intrinsic stability and energetic flight model. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015. [Google Scholar]
- Pallett, E.H.J. Aircraft Electrical Systems, 3rd ed.; Longman Scientific and Technical: Harlow, UK, 1987. [Google Scholar]
- Majeed, O. Aircraft Environmental Control Systems; Carleton University Aero Lecture 4003: Ottawa, ON, USA, 2010. [Google Scholar]
- Massive 787 System Pressurises Cabin. Available online: http://aviationweek.com/awin/massive-787-electrical-system-pressurizes-cabin (accessed on 12 April 2016).
- KIDSysteme, Technical Data Sky Power. System/Airbus. Available online: http://www.kid-systeme.de/ (accessed on 12 April 2016).
- Burke, K.A. Unitized regenerative fuel cell system development. In Proceedings of the 1st International Energy Conversion Engineering Conference (IECEC), Portsmouth, VA, USA, 17–21 August 2003. [Google Scholar]
- NREL Best Research Cell Efficiencies. Available online: https://en.wikipedia.org/wiki/Solar_cell_efficiency (accessed on 15 November 2016).
- Smith, T.; Bingham, C.; Stewart, P.; Allarton, R.; Stewart, J. Energy harvesting and power network architectures for the multibody advanced airship for transport high altitude cruiser–feeder airship concept. J. Aerosp. Eng. 2013. [Google Scholar] [CrossRef]
- Liou, K.-N. On the absorption, reflection and transmission of solar radiation in cloudy atmospheres. J. Atmosp. Sci. 1976, 33, 798–805. [Google Scholar] [CrossRef]
- Donohoe, A.; Battisti, D.S. Atmospheric and surface contributions to planetary albedo. J. Clim. 2011, 24, 4402–4417. [Google Scholar] [CrossRef]
- Blumthaler, M.; Ambach, W.; Ellinger, R. Increase in solar radiation with altitude. J. Photochem. Photobiol. 1997, 39, 130–134. [Google Scholar] [CrossRef]
- Dumas, A.; Trancossi, M.; Madonia, M.; Anzillotti, S. Effects of altitude on photovoltaic production of hydrogen. In Proceedings of the 5th International Conference on Energy Sustainability, Washignton, DC, USA, 7–10 August 2011; pp. 1–10. [Google Scholar]
- Standard Tables for Reference Solar Spectral Irradiances: Direct Normal and Hemispherical on 37° Tilted Surface; ASTM G173-03(2012); ASTM International: West Conshohocken, PA, USA, 2012.
- Liou, K.N. An Introduction to Atmospheric Radiation (International Geophysics Series), 2nd ed.; Academic: San Diego, CA, USA, 2002; Volume 84. [Google Scholar]
- Rapp-Arraras, I.; Domingo-Santos, M. Extinction, refraction, and delay in the atmosphere. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Aglietti, G.; Redi, S.; Tatnall, A.; Markvart, T. Harnessing high-altitude solar power. IEEE Trans. Energy Convers. 2009, 24, 442–451. [Google Scholar] [CrossRef]
- Young, T. Air mass and refraction. Appl. Opt. 1994, 33, 1108–1110. [Google Scholar] [CrossRef] [PubMed]
- Fritz, S. The albedo of the planet earth and of clouds. J. Metrol. 1949, 6, 277–282. [Google Scholar] [CrossRef]
- Solar Intensity versus AM Coefficient. Available online: https://en.wikipedia.org/wiki/Air_mass_(solar_energy) (accessed on 15 November 2016).
- National Aeronautics and Space Administration. The Earth Science Enterprise Series—Clouds and the Energy Cycle NF-207; Goddard Space Flight Center: Greenbelt, MD, USA, 2017.
| Cruiser Load | Power (kW) |
|---|---|
| Propulsion | ~19.5 MW |
| (72 Pods—rated at circa 270 kW each) | |
| Control Systems | 100 kW |
| Environmental Control Systems | 260 kW |
| (1 kW per pax) | |
| Avionic Systems | 10 kW |
| Lighting | 7.6 kW |
| In Flight Entertainment | 26 kW |
| Galley | 60 kW |
| Situational Awareness | 10 kW |
| Energy storage 1 | Sized for maximum conversion day night scenario |
| (The electrolyser represents a significant mass and will be sized on the predicted excess energy if any) | |
| Total | 20 MW |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smith, T.; Trancossi, M.; Vucinic, D.; Bingham, C.; Stewart, P. Primary and Albedo Solar Energy Sources for High Altitude Persistent Air Vehicle Operation. Energies 2017, 10, 573. https://doi.org/10.3390/en10040573
Smith T, Trancossi M, Vucinic D, Bingham C, Stewart P. Primary and Albedo Solar Energy Sources for High Altitude Persistent Air Vehicle Operation. Energies. 2017; 10(4):573. https://doi.org/10.3390/en10040573
Chicago/Turabian StyleSmith, Tim, Michele Trancossi, Dean Vucinic, Chris Bingham, and Paul Stewart. 2017. "Primary and Albedo Solar Energy Sources for High Altitude Persistent Air Vehicle Operation" Energies 10, no. 4: 573. https://doi.org/10.3390/en10040573
APA StyleSmith, T., Trancossi, M., Vucinic, D., Bingham, C., & Stewart, P. (2017). Primary and Albedo Solar Energy Sources for High Altitude Persistent Air Vehicle Operation. Energies, 10(4), 573. https://doi.org/10.3390/en10040573









