Optimizing the Energy-Efficient Metro Train Timetable and Control Strategy in Off-Peak Hours with Uncertain Passenger Demands

Abstract

How to reduce the energy consumption of metro trains by optimizing both the timetable and control strategy is a major focus. Due to the complexity and difficulty of the combinatorial operation problem, the commonly-used method to optimize the train operation problem is based on an unchanged dwelling time for all trains at a specific station. Here, we develop a simulation-based method to design an energy-efficient train control strategy under the optimized timetable constraints, which assign the dwelling time margin to the running time. This time margin is caused by dynamically uncertain passenger demands in off-peak hours. Firstly, we formulate a dwelling time calculation model to minimize the passenger boarding and alighting time. Secondly, we design an optimal train control strategy with fixed time and develop a time-based model to describe mass-belt train movement. Finally, based on this simulation module, we present numerical examples based on the real-world operation data from the Beijing metro Line 2, in which the energy consumption of one train can be reduced by 21.9%. These results support the usefulness of the proposed approach.

1. Introduction

Metro systems play an important role to relieve urban traffic congestion in public transportation. A major current focus in metro systems is how to reduce the energy consumption. There are two main levels of train energy-efficient operation approaches. A recent emerging research interest is in the field of regenerative energy utilization [1,2,3,4,5,6], which focuses on developing a timetable including the dwelling time at stations and running time at sections (between two adjacent stations) in order to improve the utilization of regenerative energy by synchronizing the operations of accelerating and braking trains [7]. Compared with the upper level of timetable optimization, the lower level of energy-efficient control strategy design at sections has long attracted widespread attention [8,9,10,11,12,13,14,15,16,17,18,19,20,21] to calculate the speed profile with minimum tractive energy consumption under the timetable constraints [22]. The simulation-based method is commonly used to calculate the train traction energy consumption under complex track alignments [23,24,25,26,27] by energy-efficient driving [28,29,30,31]. The energy-efficient timetable and control strategy are closely related, and both of them play a key role in tractive energy consumption. The previous studies typically consider these two levels separately mainly because of the complexity of the combinatorial problem and the difficulty of applying the theory in practice. This has provided an incomplete view of metro system operation.

Currently, there are few studies that have addressed the problem of energy saving considering both the timetable optimization and energy-efficient train control strategy. Ding et al. [32] formulated the train energy-efficient operation as a two-level optimization problem and designed a genetic algorithm to search for the optimal solution, in which the first level is designed to decide the appropriate coasting points for trains at sections, and the second level arranges the train running times at sections for minimizing the tractive energy consumption. Cucala et al. [33] designed a model for energy-efficient driving and timetables, in which the railway operator and administrator requirements are also included. Li and Lo [34] proposed an integrated energy-efficient operation model to jointly optimize the timetable and speed profile with minimum net energy consumption. Huang et al. [21] proposes an energy-efficient approach to reduce the traction energy by optimizing the train operation for multiple sections, considering both the trip time and driving strategy. Although a set of work has been done with a comprehensive view, more realistic work is needed to apply the optimal approach into practice.

A timetable determines the dwelling time at stations and the running time at inter-stations for trains [35]. The dwelling time consists of three parts [36]: the time before the doors open, the period of time during passenger exchange and the time prior to departure after the doors have closed. For the doors, the open and close times are fixed; studies estimated the dwelling time by modelling passengers’ boarding and alighting process [37,38,39,40,41,42]. However, the number of passengers boarding and alighting trains in the off-peak hours is far less than that of the peak. Accordingly, the dwelling time actually for passenger exchange is much shorter than the planned one. The margin time between planned and integrant dwelling time can be assigned to the running time in order to get a more energy-efficient travel pattern.

The current paper extends the previous research in the following aspects:

➢

A more realistic model for the dynamic mathematical model of the metro train is formulated in this paper based on the assumption that a train is considered as a belt with uniformly-distributed mass instead of a mass point model [43].

➢

The timetable optimization model formulated in this paper allows trains to drive as the optimal control strategy with a fixed running time of the section contributed by the reduction of dwelling time at the station, which has a significant reduction in energy consumption (more than 20%).

➢

Compared with [5], when we construct the train movement model, both the track gradients and the curves are taken into account in order to describe train energy consumption more accurately.

The rest of the paper is structured as follows. Section 2 formulates both the timetable optimization module considering passenger boarding and alighting phase and the train operation simulation module in order to calculate the energy consumption of train runs with fixed time. Section 3 describes the optimal function and the constraints of the real-time train energy-saving scheduling problem, meanwhile proposing a simulation-based solution approach for this problem. Section 4 analyzes the sensitivity of the simulation. In Section 5, the performance of the proposed model is evaluated via three case studies. Finally, conclusions and recommendations are provided in Section 6.

2. Mathematical Formulations

In this part, first, we construct an energy-saving optimal timetable module. We define the arrival and departure time of train j at station i as a_i,j and d_i,j, respectively, and the corresponding arrival and departure time in the timetable as a^⁰_i,j and d^⁰_i,j. The running time and the dwelling time of section i (from station i to station i + 1) are expressed as T_R,i,j and T_D,i,j, and according to the timetable, the running time and the dwelling time are T^⁰_R,i,j and T^⁰_D,i,j. The definitions are shown in Figure 1. Then, we develop a time-based train operation simulation module based on a control strategy with fixed running time.

As shown in Figure 1, the actual running time can be obtained by adding the margin time (a_i,j–a^⁰_i,j) to the initial running time, in which the margin time can be calculated by estimating the passengers’ boarding and alighting at the next station i + 1.

For simplistic, we list the assumptions as follows:

(1)

In this manuscript, steady demand within only two periods is considered: peak and off-peak.

(2)

In the off-peak hours, there is no congestion effect, indicating that all passengers who are waiting on a specific station platform can board the train.

(3)

In the off-peak hours we studied, the train departure interval is a constant.

(4)

The train’s departure times at each station are equal to the ones of the initial timetable.

(5)

In this model, the motor efficiency is simplified.

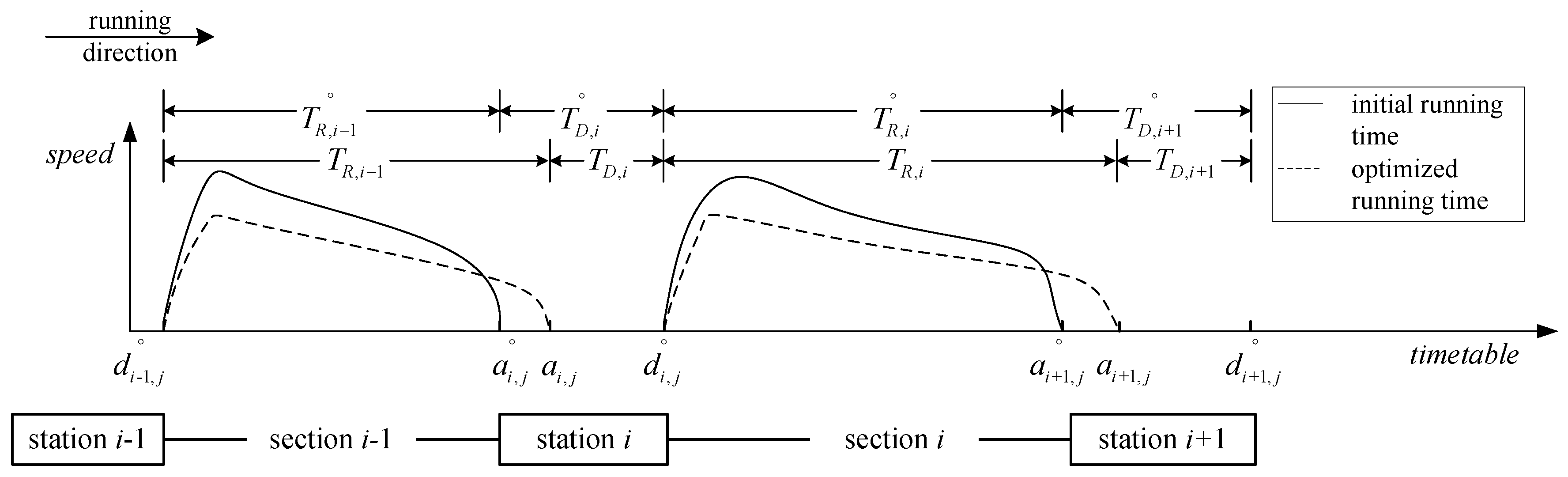
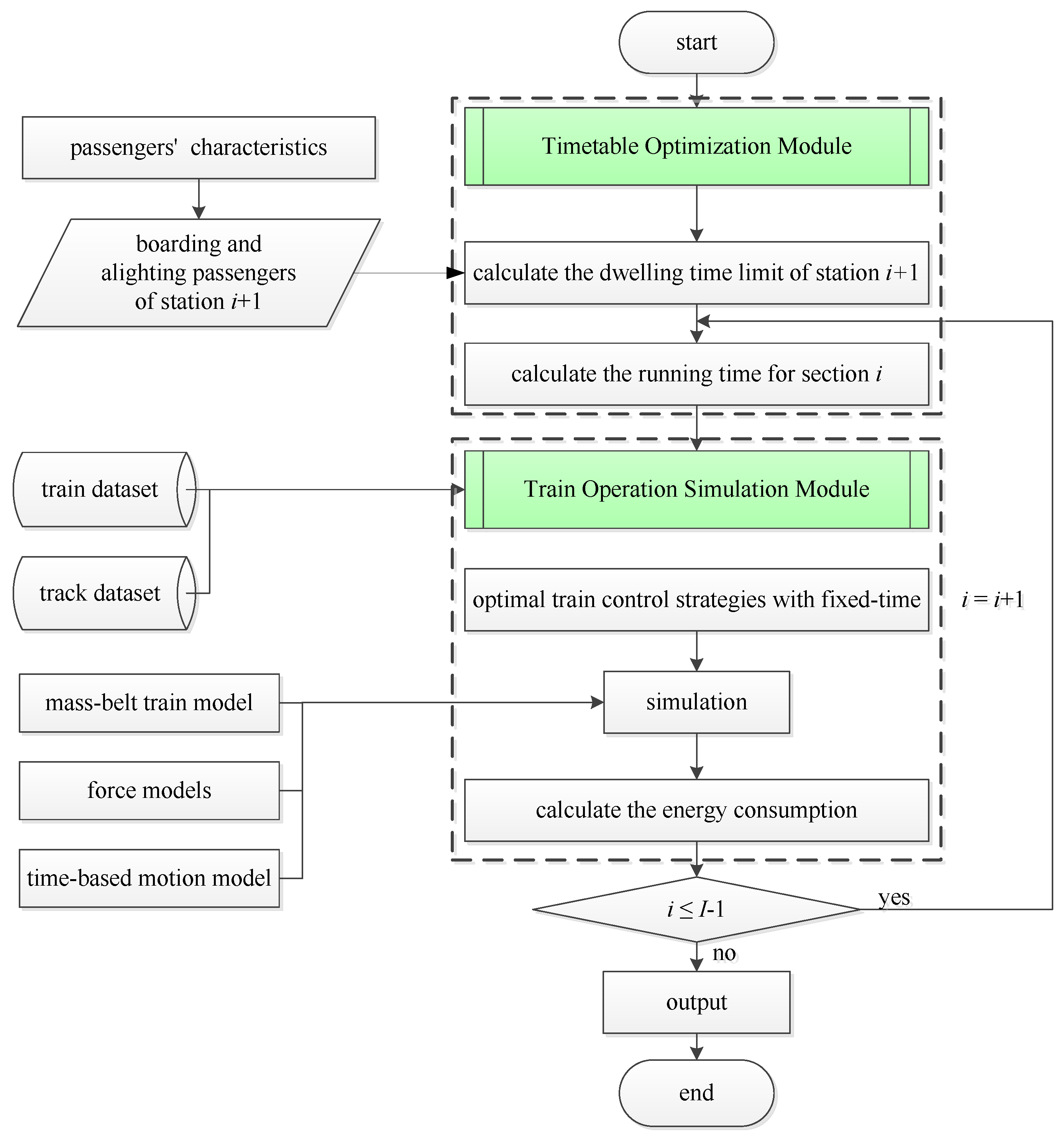
2.1. Timetable Optimization Module

2.1.1. Passenger Characteristics

The passenger arriving and alighting at the metro station for a given period $\left[t_0,t_{final}\right]$ can be modelled by a time-dependent origin-destination table [44,45,46].

$$OD(t)=\left(\begin{array}{ccc}{\kappa }_{1,1}(t)& \cdots & {\kappa }_{1,I}(t)\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\kappa }_{I,I}(t)\end{array}\right)$$

(1)

where κ_i,j(t) is the passenger arriving amount at station i at time t with destination station i’. Additionally, the sum of the amount of arriving passengers at destination i’ for $i\prime \in \left\{i+1,\dots ,I\right\}$ represents the passenger arriving rate λ_i(t) at station i and time t. For a short time period, the passenger arriving rate can be treated as a uniform distribution [47].

When a train j dwells at a given station i according to the timetable at time a^⁰_i,j, the passengers waiting on the platform P_i,j begin to board the train. Additionally, the passengers Q_i,j with trip destination i alight the train during the dwelling time, as well. The timetable dwelling time T^⁰_D,i,j and actual dwelling time T_D,i,j can be described as time window [a^⁰_i,j, d^⁰_i,j] and [a_i,j, d_i,j], respectively. This train will depart station i at time d^⁰_ij and drive to the station i + 1 at time a^⁰_i+1,j with the in-vehicle passengers O_i,j. Note that our study is considering the off-peak hours, thus there are no passengers that cannot board trains. In other words, the scenario in which the passengers have to wait for the next train [48] will not happen. The number of in-vehicle passengers is an important influence factor of train energy consumption.

$$P_{i,j}=\lceil {\displaystyle {\int }_{{d^0}_{i,j-1}}^{{a^0}_{i,j}+T_{D,i,j}}\lambda (t)\mathrm{dt}}\rceil ,\forall i,j$$

(2)

$$Q_{i,j}={\displaystyle \sum _{i=1}^{i-1}{P}_{i,j}\cdot {\gamma }_{i,i\prime }}$$

(3)

$$O_{i,j}=\{\begin{array}{cc}{P}_{i,j}-Q_{i,j},& j=1,2,\cdot \cdot \cdot ,J;i=1\hfill \\ O_{i-1,j}+P_{i,j}-Q_{i,j},& j=1,2,\cdot \cdot \cdot ,J;i=2,\cdot \cdot \cdot ,I\hfill \end{array}$$

(4)

where γ_i,i’ is the ratio describing the passengers boarding the train j at station i who alights at station i’. Thus, γ_i,i’ can be formulated by OD(t):

$${\gamma }_{i,i^{\prime }}=\frac{{\kappa }_{i,i^{\prime }}(t)}{{\displaystyle \sum _{i^{\prime }=i+1}^I{\kappa }_{i,i^{\prime }}(t)}}$$

(5)

2.1.2. Dwelling Time Calculation

Generally speaking, the dwelling time has two components [49]: (i) a fixed time for opening and closing doors; and (ii) door utilization time for boarding and alighting passengers. Thus, the dwelling time is deeply influenced by the passenger flow.

According to the expression that Kim et al. [42] proposed, we propose a polynomial equation to estimate the minimum dwelling time $T_{D,i,j}^{\min }$ for train j at station i as Equation (6).

$$\begin{array}{ll}{T}_{D,i,j}^{\min }& =0.7021Q_{i,j}-0.0068Q_{i,j}^2+0.8417P_{i,j}-0.0083P_{i,j}^2+3.7953\cdot DOC\\ & -2.4495\cdot DO{C}^2+1.0871\cdot DO{C}^3-1.1385\end{array}$$

(6)

where DOC is the degree of crowdedness [50].

Thus, the dwelling time T_D,i,j shall satisfy the constraint as Equation (7).

$$T_{D,i,j}\in \left[T_{D,i,j}^{\min },T_{D,i,j}^{°}\right]$$

(7)

2.2. Train Operation Simulation Module

The train traction energy consumption is mainly affected by the running time in each segment [43,51]. When a train departs from station i before the departure time of the timetable, there will be more running time for the train to drive in the segment, which will lead to less traction energy consumption. In this section, we aim to analyze the energy consumption for trains reducing dwelling time and adding the time margins to the running time. Firstly, in order to calculate the traction energy consumption with time margin addition, we offer a means of optimizing train driving control strategies with a fixed time based on a time-saving pattern. Then, for the sake of accuracy, we describe the train operation model in a single rail segment with a belt with uniformly distributed mass instead of a mass point model.

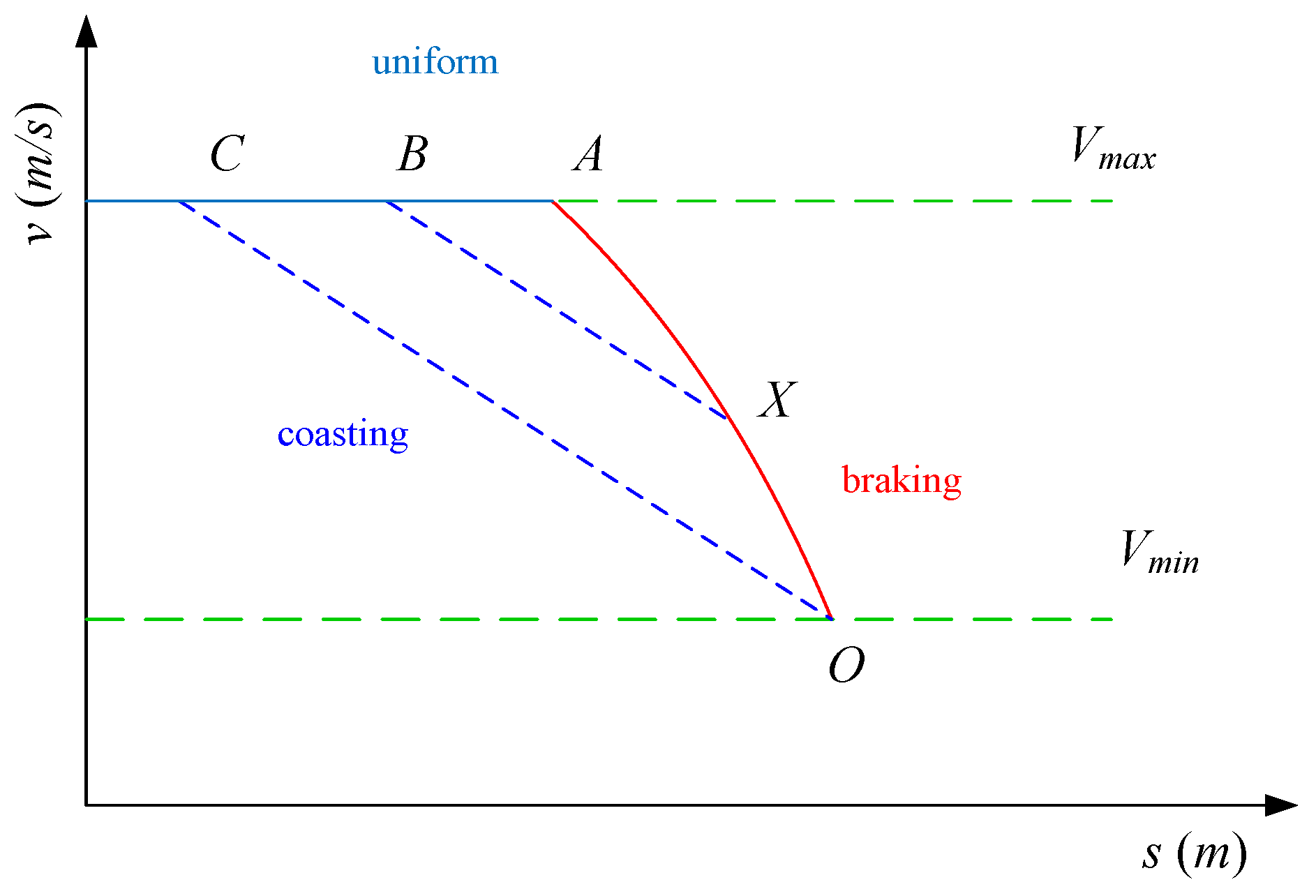
2.2.1. Optimal Train Control Strategies with Fixed Time

In our manuscript, there are six steps to obtain an energy-efficient strategy of one section.

(1)

Generate a driving strategy of a time-saving pattern and the minimized running time of this section.

(2)

Calculate the margin time of the total section as the difference between the running time of the time-saving pattern and the one of the fixed time pattern.

(3)

Divide the section into several subsections by the changes of lines’ speed limits. Previous studies [5,18] have demonstrated that acceleration and coasting are both components of the energy-efficient strategy. Accordingly, the margin time should be allocated to deceleration subsections as much as possible.

(4)

Initialize the speed limit of each subsection, indicating that the speed limit shall reduce to a lower level from the original high one.

(5)

With the limit of the given running time and initial speed of this subsection, calculate a driving strategy and output the actual running time. If the actual running time satisfies the error request, turn to the next subsection.

(6)

Output the results, and end the simulation when all sections have been simulated.

The detailed illustration of Step (5) can be concluded as how to assign the dwelling time T_D,i,j margin of station i to the running time T_R,i,j of section i. Generally speaking, when the train control strategies in each section are given, both the maximum traction and coasting phases are energy efficient already. Thus, the margin time shall be assigned to the braking phase in order to obtain more of an energy-saving effect. The illustration and flowchart of dwelling time margin are shown in Figure 2 and Figure 3, respectively. It is important to note that this method also can be used to the situation in which the speed limit changes from high to low.

As shown in Figure 2, the AO and CO are the braking and coasting curves, respectively, and BXO is the coasting and braking curve where the cut-off point is X.

We define the time margin as T_m; the times of AO, CO, CA and BXO are respectively T_b, T_c, T_u and T_c-b; moreover, the error of calculation is T_error. The main steps are as in Figure 3.

Based on this train control strategy with fixed time, we can calculate the train energy consumption with the approach in the next section.

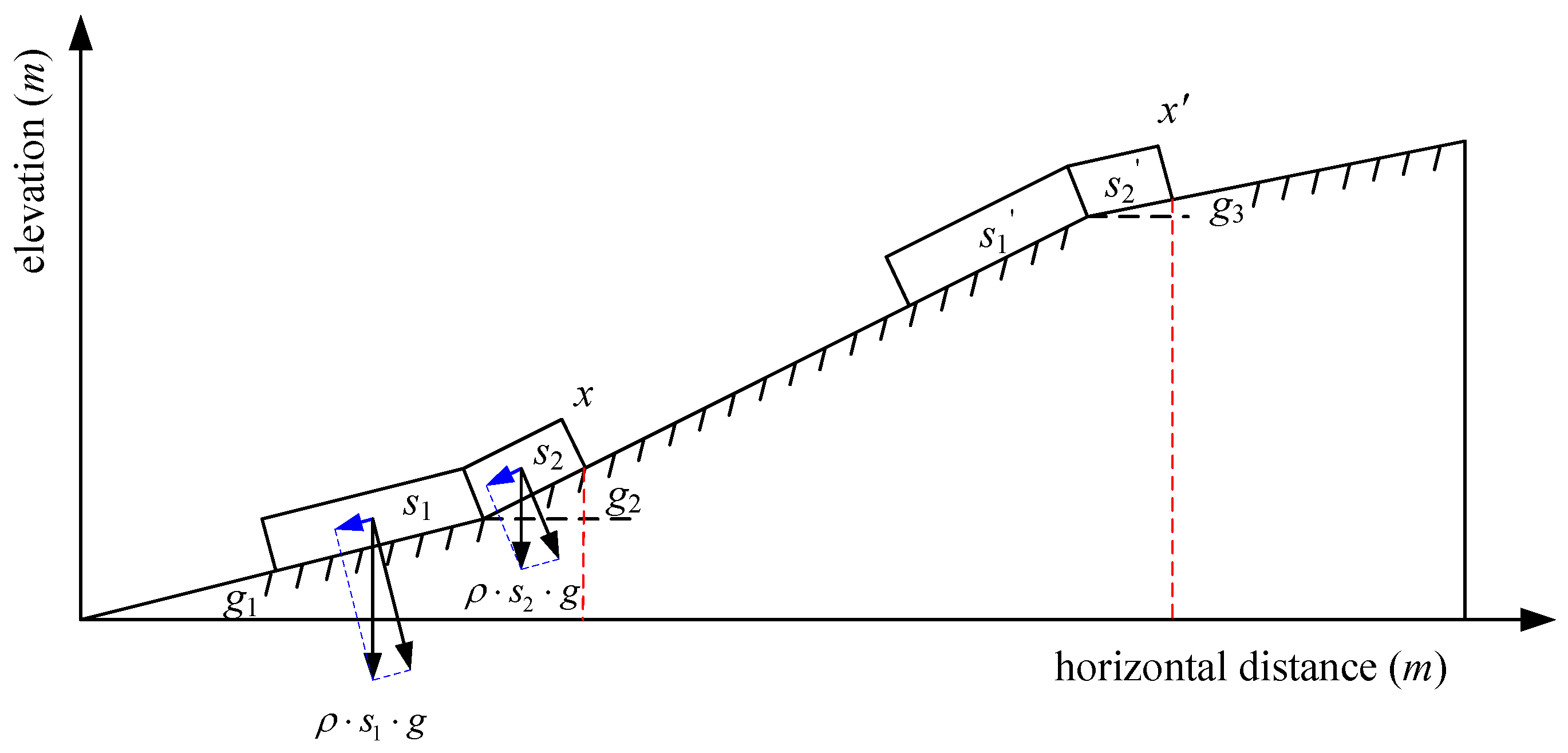
2.2.2. Train Movement Simulation Models

In this paper, the train model is considered as a mass belt instead of a mass point. Thus, the force analysis has to be reformulated. There are two major approaches to simulate train movement, time-based and event-based models [52]. The time-based model requires a highly computational demand as a significant amount of information has to be produced during every update, in which train movement is evaluated at each interval. The full details of train movement are needed when we want to calculate the energy consumption accurately. Thus, we establish a time-based model to describe train movement.

Firstly, we deal with the force analysis based on the mass belt assumption. There are three kinds of force acting on a train driving between successive stations: the traction force T_f, the resistance force R_f and the braking force B_f.

The traction force T_f can be represented as a function of train speed v, which can be simply calculated if the locomotive traction curve is obtained. The specific (per mass unit) traction force t(v) can be represented as a function f(v) related to the speed v.

$$t(v)=f(v)$$

(8)

The resistance force R_f consists of the basic running resistance and the additional resistance. The specific (per mass unit) basic running resistance r(v) is generally calculated as a quadratic equation of train speed v:

$$r(v)=r_0+r_1\cdot v+r_2\cdot v^2$$

(9)

where the coefficients r₁ and r₂ are related to the train mass and the interaction between tracks and train wheels; nevertheless, the coefficient r₀ is related to the aerodynamics of the trains.

The specific (per mass unit) additional resistance w(x) is caused by the track condition consisting of unit gradient resistance w_g, unit curvature resistance w_r and unit tunnel resistance w_t, which can be shown as a function of the position of the train x:

$$w(x)=w_g+w_r+w_t$$

(10)

In this paper, we take the train as a belt with length S. Thus, when the train runs on a track with a continuously varying gradient, the specific (per mass unit) gradient resistance can be calculated as follows:

$$w_g(x)=\frac{1}{M}{\displaystyle \underset{0}{\overset{S}{\int }}\rho \cdot g(x-s)ds}$$

(11)

where M is the train traction weight (containing the mass of both the train M_t and the loading passengers M_p) (kg); ρ is the mass per unit length (kg/m); g(x − s) is the gradient of position (x − s) (‰); S is the train length (m).

Take Figure 4 for example: when the train runs to the position x where the front part (length is s₂) runs to the second slope with gradient g₂ and the tail of the train (length is s₁) still exists on the first slope with gradient g₁, the specific (per mass unit) gradient resistance w_g(x) can be calculated as follows:

$$\begin{array}{ll}{w}_g(x)& =\frac{1}{M}{\displaystyle \underset{0}{\overset{s_1+s_2}{\int }}\rho \cdot g(x-s)ds}\\ & =\frac{\rho \cdot g_1\cdot s_1+\rho \cdot g_2\cdot s_2}{\rho (s_1+s_2)}\\ & =\frac{g_1\cdot s_1+g_2\cdot s_2}{s_1+s_2}\end{array}$$

(12)

Additionally, the specific (per mass unit) gradient resistance w_g(x’) can be calculated in a similar way.

$$\begin{array}{ll}{w}_g(x^{\prime })& =\frac{1}{M}{\displaystyle \underset{0}{\overset{s_1^{\prime }+s_2^{\prime }}{\int }}\rho \cdot g(x-s)ds}\\ & =\frac{\rho \cdot g_2\cdot s_1^{\prime }+\rho \cdot g_3\cdot s_2^{\prime }}{\rho (s_1^{\prime }+s_2^{\prime })}\\ & =\frac{g_2\cdot s_1^{\prime }+g_3\cdot s_2^{\prime }}{s_1^{\prime }+s_2^{\prime }}\end{array}$$

(13)

When the train runs to position x, which is a part of a curve, the specific (per mass unit) curvature resistance w_r can be expressed as Equation (14) considering the train length.

$$w_r(x)=\{\begin{array}{ll}\frac{10.5\cdot \alpha }{L_r(x)},& L_r(x)\ge S\\ \frac{600}{R}\cdot \frac{L_r(x)}{S},& L_r(x)<S\end{array}$$

(14)

where α is the angle of the curve (°); L_r(x) is the length of the curve (m); R is the radius of the curve (m).

The specific (per mass unit) tunnel resistance w_t can be simply calculated by Equation (15).

$$w_t=0.00013\cdot L_t(x)$$

(15)

where L_t(x) is the length of the tunnel (m).

The braking force B_f can be calculated by a function of train speed v; moreover, the specific (per mass unit) braking force b(v) can be shown as a function h(v) related to the speed v.

$$b(v)=h(v)$$

(16)

Thus, the specific force c can be calculated by Equation (17).

$$c=t(v)-r(v)-w(x)-b(v)$$

(17)

2.2.3. Energy Consumption Calculation

A large amount of previous studies [5,15,18,21,53,54,55] have demonstrated that the energy-efficient driving strategies of each section will be maximum traction (MT), coasting (CO) and maximum braking (MB). Additionally, in each phase, train movement is as in Equation (18).

$$\begin{array}{l}{v}_{k+1}=v_k+a_k\cdot \sigma \\ v_k\le V_{\max }\\ l_{k+1}=l_k+(v_k\cdot \sigma +\frac{1}{2}{a}_k\cdot {\sigma }^2)/3.6\\ E_{k+1}=E_k+e_{k+1}\\ e_k=t_k(v)\cdot (l_k-l_{k-1})\end{array}$$

(18)

where v_k and v_k+1 are the initial speeds of the k-th and (k + 1)-th time step, respectively (km/h); V_max is the limit speed (km/h); a_k is the accelerated speed at the k-th time step (km/(h·s)); σ is one time step (s); l_k and l_k+1 are the positions of the k-th and (k + 1)-th time step, respectively (m); E_k and E_k+1 are the accumulative energy consumptions of the k-th and (k + 1)-th time step, respectively (kWh); e_k is the energy consumption of the k-th time step (kWh); t_k(v) is the traction force of the k-th time step (N).

Thus, the total energy consumption E_total can be expressed as follows:

$$E_{total}={\displaystyle \sum _{j=1}^J{\displaystyle \sum _{i=1}^I{\displaystyle \sum _{k=1}^K{e}_k}}}$$

(19)

3. Optimal Model and Solution Method

3.1. Optimal Model

The real running time and dwelling time can be expressed as follows:

$$T_{D,i,j}=d_{i,j}-a_{i,j}$$

(20)

$$T_{R,i,j}=a_{i+1,j}-d_{i,j}$$

(21)

We assume that the trains arriving time at each station are equal to the ones of the initial timetable, in order to ensure safe and reliable operation. Thus, the real arrive time of each train j shall satisfy Equation (22).

$$a_{i+1,j}-a_{i,j}=a_{i+1,j}^{°}-a_{i,j}^{°}$$

(22)

For the train timetable optimal problem in a metro line, the objective model can be expressed as Equation (23) by applying a weighted sum strategy within a given period $\left[t_0,t_{final}\right]$:

$$F_{\mathrm{obj}}=\min E_{\mathrm{total}}$$

(23)

The constraints mainly include the running time constraints, dwelling time constraints, passenger demand constraints and train operation constraints, shown as (2)–(4), (7), (18) and (20)–(22).

3.2. Solution Method

The timetable optimization model with the objective function (23) and Constraints (2)–(4), (7), (18), (20)–(22) is a nonlinear non-convex problem. The complexity of this problem is due to three points: (1) describing the multivariable optimal control strategy of a mass-belt train model with fixed time; (2) solving the optimal objectives with stochastic characters; and (3) dealing with the nonlinear constraints. A simulation-based solution approach is developed to solve this timetable optimization model, and the framework is shown in Figure 5.

As shown in Figure 5, the main steps are as follows.

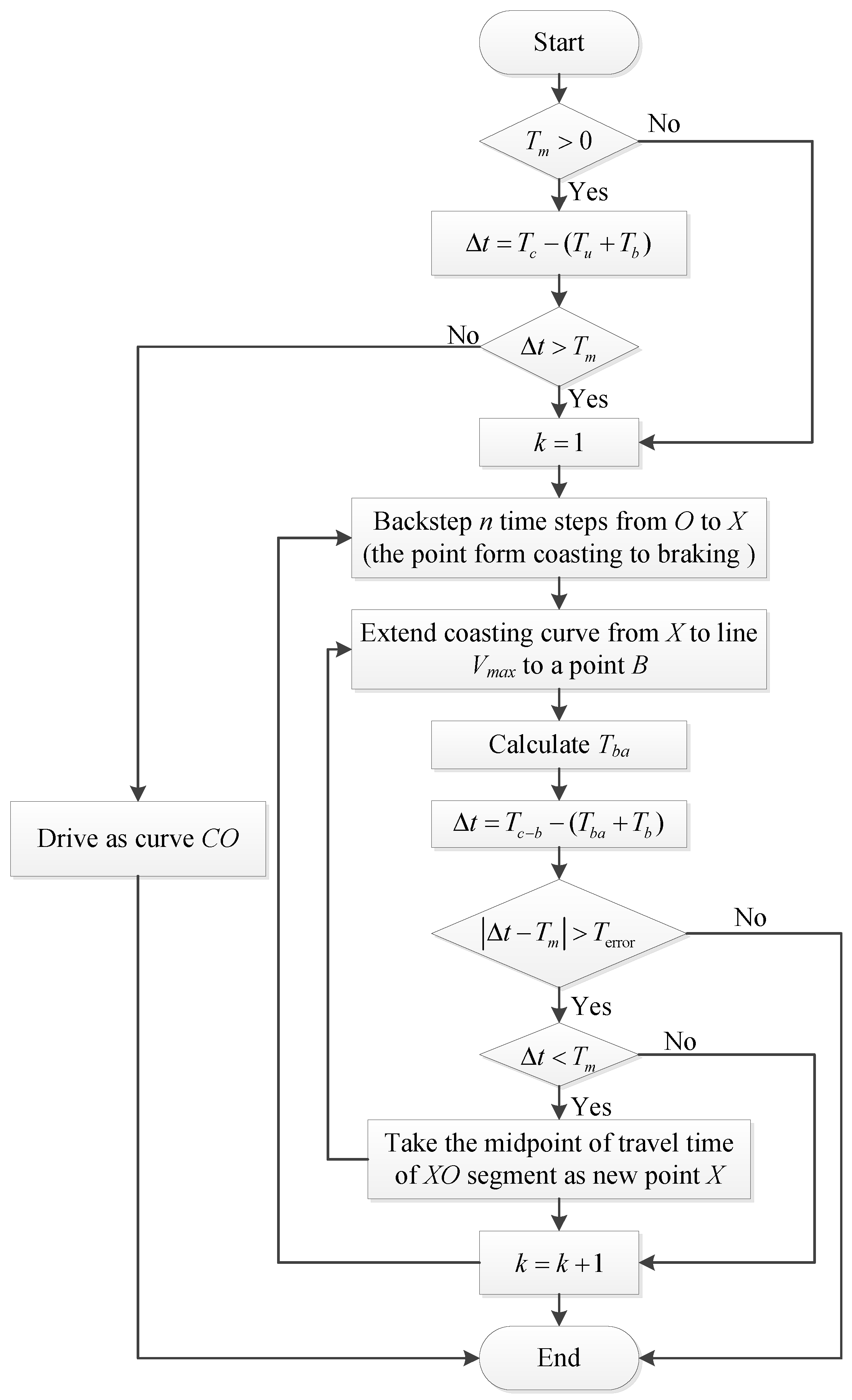
(1)

Calculate the real-time dwelling time margin T_m for station i, ∀ i = 1, 2, …, I.

(2)

A simulation model is then run in section i for a train j with the fixed time margin calculated in (7), where the train control strategies can be obtained with the algorithm presented in Section 2.1.2.

(3)

Calculate the minimize energy consumption E_i,j by using the mass-belt train motion model and the force models according to the condition of section i.

(4)

The simulation process will be executed repeatedly until train j arrives at terminal station I.

4. Sensitivity Analysis of the Simulation

In this section, three numerical examples are established to analyze the sensitivity of the radius curve, gradient, length of grade and speed limit, in order to identify the efficiency and effort of the proposed simulation. Then, we perform a systemic analysis of the accuracy between simulation and measurement values.

4.1. Sensitivity Analysis

We study the metro train energy-saving strategy with the same simulator as our study; some sensitivity analysis can be shown as follows with the parameters: the train traction weight is 150.0 t; the length of the train is 110 m.

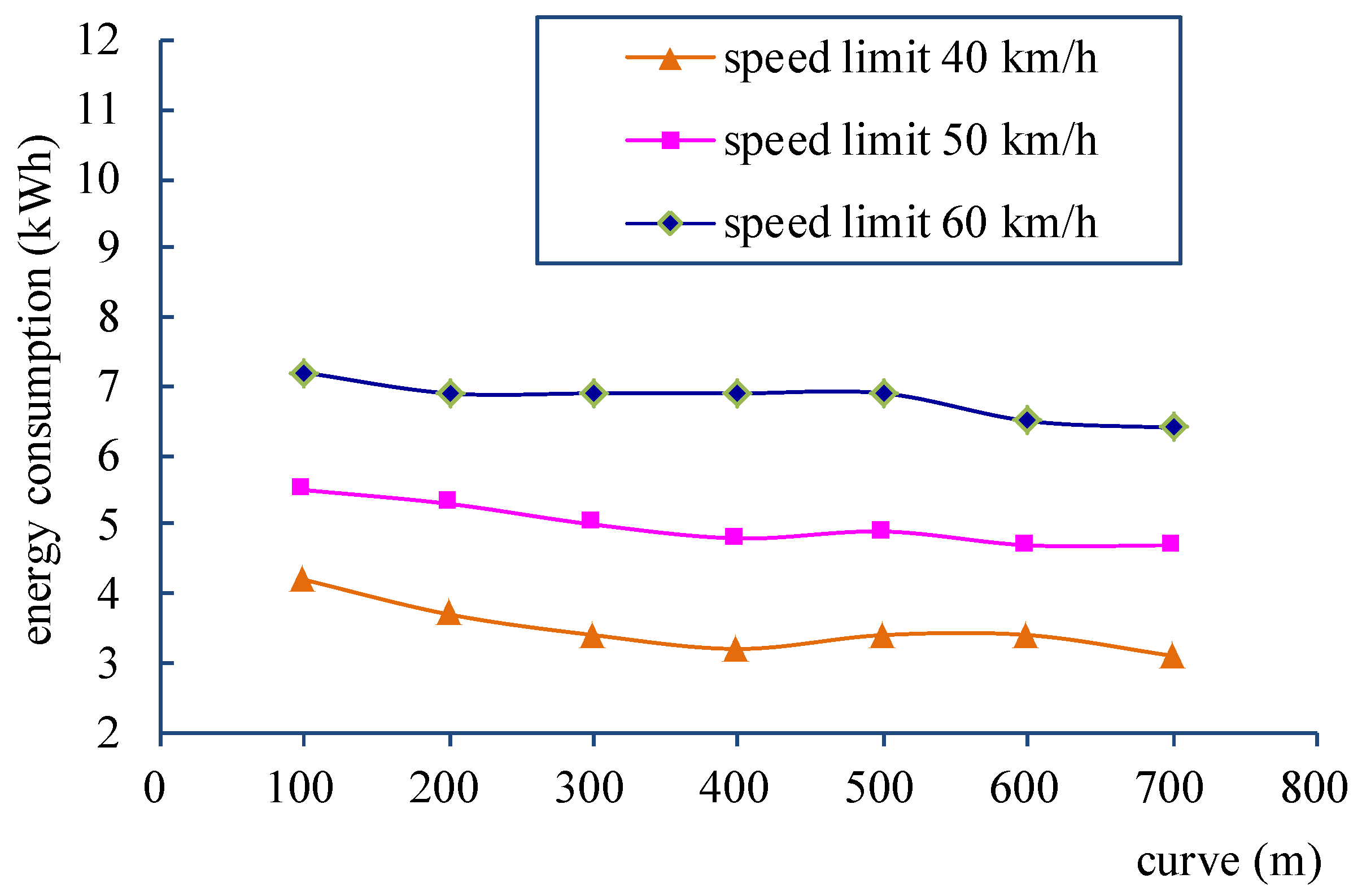
4.1.1. The Curve Sensitivity Analysis

Parameter values used in the simulation have been listed: the curve length is 500 m; the curve radius is increasing from 100 m to 600 m; and the condition of no curve is defined as “∞”. In addition, there are three speed limits: 40 km/h, 50 km/h and 60 km/h. The calculation result is shown in Figure 6.

As shown in Figure 6, the curves of energy consumption indicate similar trends.

(i)

When the radius curve is larger than 500 m, the energy consumption is close to the same one of no radius curve.

(ii)

When the radius curve is smaller than 300 m, the energy consumption is larger.

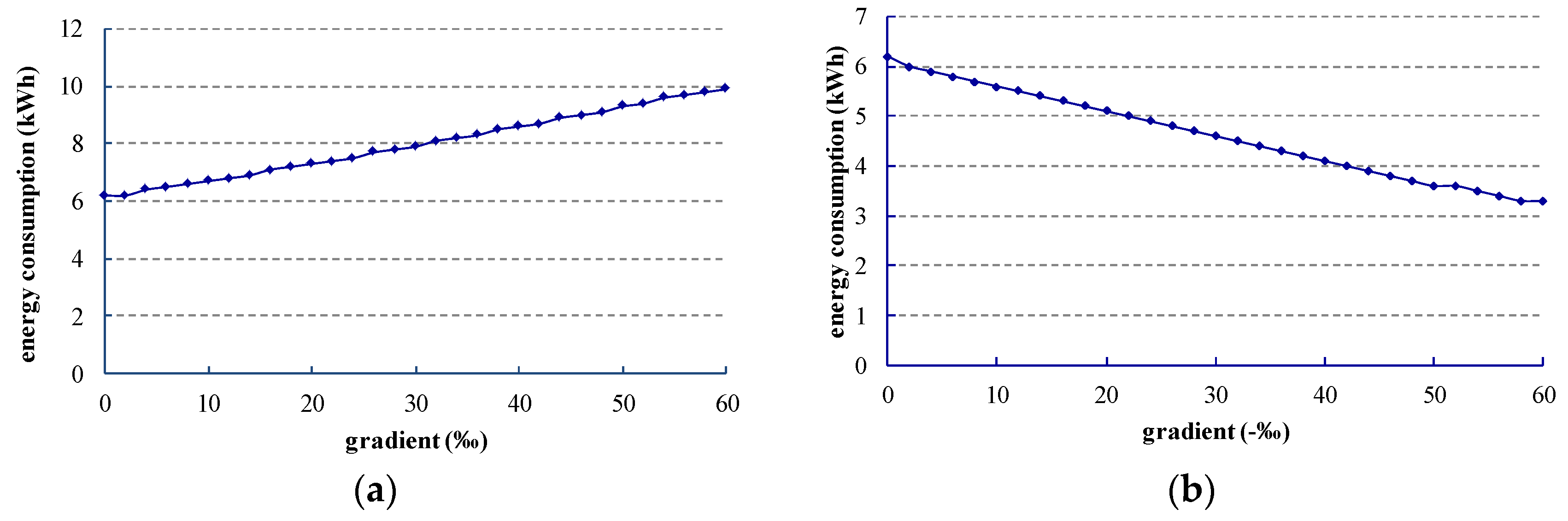
4.1.2. The Gradient Sensitivity Analysis

Parameter values used in the simulation have been listed: the slope length is 300 m; the speed limit is 50 km/h. The energy consumption of the ascending and falling gradient are respectively shown as Figure 7a,b.

As shown in Figure 7, the energy consumption changes linearly with the slope changes with the same grade length and speed limit.

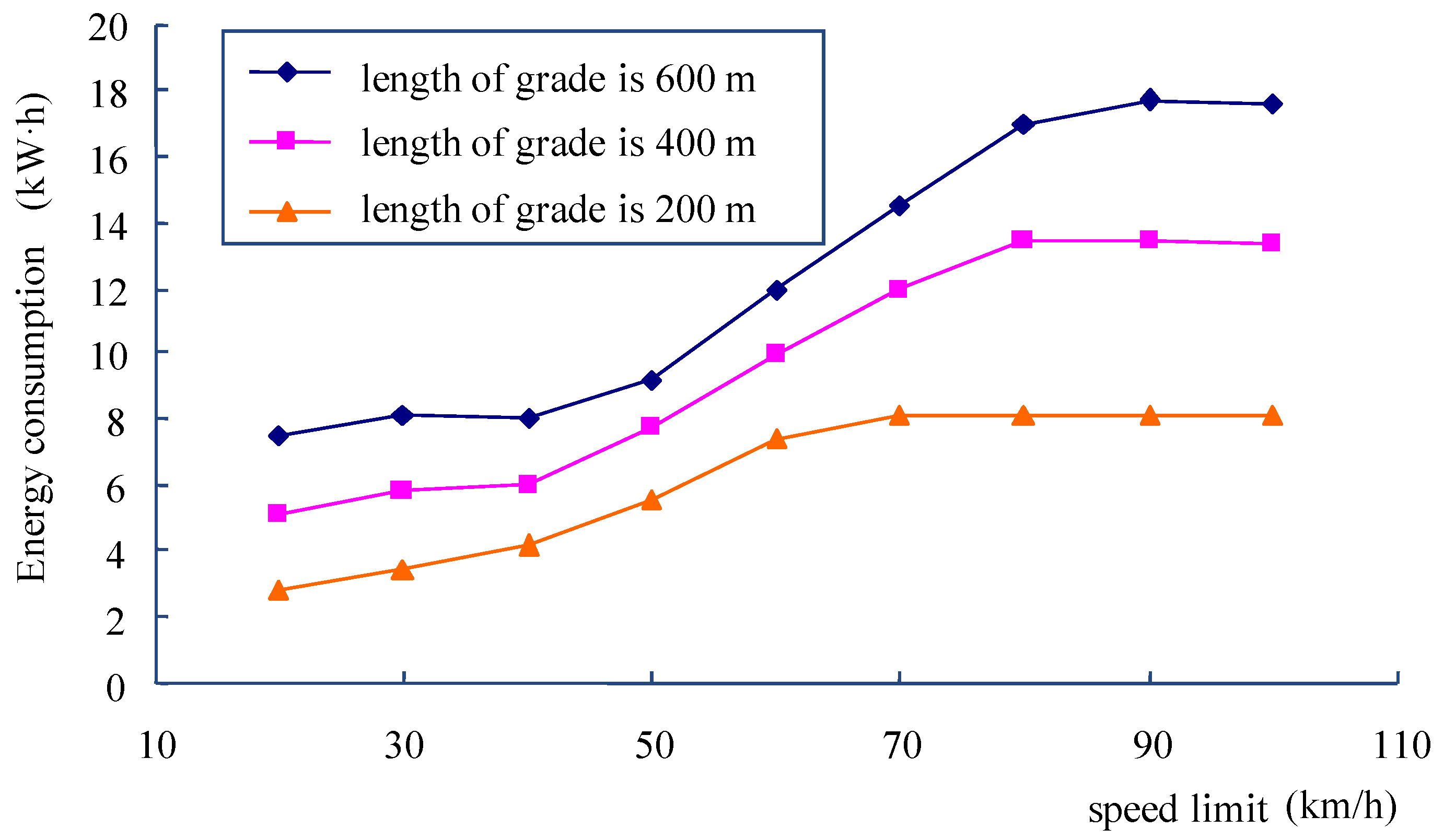
4.1.3. The Length of Grade and Speed Limit Sensitivity Analysis

There are three kinds of grade section lengths, 600, 400 and 200 m, respectively with the same gradient of 30‰. The traction energy consumption of the train from the base to the top of the slope is shown in Figure 8.

As shown in Figure 8, the curves of energy consumption indicate similar trends.

(1)

All curves of energy consumption can be divided into three sections: low speed section, middle speed section and high speed section.

(2)

Based on the 30‰ gradient, the middle sections are respectively 40–90 km/h, 40–80 km/h and 40–70 km/h for the lengths of 600, 400 and 200 m.

(3)

In each speed section, with the increase of speed, the energy consumption increases linearly.

4.2. Accuracy Analysis

There are three kinds of measurement data, AW₀ (194.00 t), AW₂ (279.68 t) and AW₃ (303.20 t), indicating the energy consumption with different load factors. In each kind of measurement data, according to whether regenerative braking energy is used, these still can be divided into two types: the absolute error ε and the percent error δ can be calculated as Equations (24) and (25), respectively.

$$\epsilon =\left|x-a\right|$$

(24)

$$\delta =100\%\times \frac{\epsilon }{\left|a\right|}=100\%\times \left|\frac{x-a}{a}\right|$$

(25)

where x is the simulation value (kWh) and a is the measurement value (kWh).

Both the measurement and simulation values are shown in

Table 1. Traction energy consumption measurement values (kWh).

The Kinds of Energy Consumption		Measurement	Simulation	ε	δ
AW0	Traction energy consumption	375	361.64	13.36	3.56%
	100% regenerative braking energy	206	215.50	9.50	4.61%
AW2	Traction energy consumption	514	530.35	16.35	3.18%
	100% regenerative braking energy	305	308.04	3.04	0.99%
AW3	Traction energy consumption	549	566.10	17.10	3.11%
	100% regenerative braking energy	335	331.08	3.92	1.17%

. Accordingly, we calculate the absolute error and the percent error.

As shown in Table 1, the values of the percent error are all smaller than 5%, indicating that the accuracy of the simulation model proposed is good, and can be applied to the actual operation of the subway system energy-saving strategy analysis.

5. Numerical Examples

In this section, three numerical examples are established to identify the efficiency and effort of the proposed approach for the metro timetable optimization problem. Firstly, we assess the different train energy-efficient performance with different running times within a specified section, aiming to demonstrate the effectiveness of the train control strategy with fixed time. Secondly, we utilize the proposed train movement model considering both the track gradients and the curves to calculate the total energy consumption of Line 2 (inner ring) of the Beijing metro system. For this case, a comparison among the results by different running and dwelling times is given to verify the performance of the energy saving. Last, but not least, we demonstrate how to use the proposed approaches to reduce energy consumption by optimizing the train timetable problem on the real-world Beijing Line 2 (inner ring) with uncertain and dynamic parameters (i.e., passengers’ time-dependent origin-destination demands), which are all taken from historical detected operation data. Note that the timetable, train and track conditions are all collected from the Beijing Mass Transit Railway Operation Corporation (BMTROC, Beijing, China) and not open to public. The train mass is 194.00 t, and the gross load hauled is 279.68 t (assume the passenger’s weight is 60 kg). The train structure is shown in Figure 9.

5.1. A Case of One Single Section’s Energy Consumption

This example considers one specified section of Line 2 (inner ring) named Fuchengmen Station–Fuxingmen Station, the length of which is 1832 m, and the gradients are described in

Table 2. Gradients of section Fuchengmen Station-Fuxingmen Station.

Segment	Grade (‰)	Length (m)
1	3.0	1207.7
2	3.0	140.3
3	−2.0	218.0
4	−8.0	120.0
5	−3.0	121.0
6	4.8	25.0
Total	-	1832.0

. In this case study, the initial running time is 137 s, and the fixed running time changes from 139 s to 153 s, increasing by 2 s. For the sake of simplicity, we assume that the train mass is 194.00 t. The results of energy consumption and train speed profiles are calculated with each running time, which is shown in

Table 3. Energy consumption of section Fuchengmen Station–Fuxingmen Station.

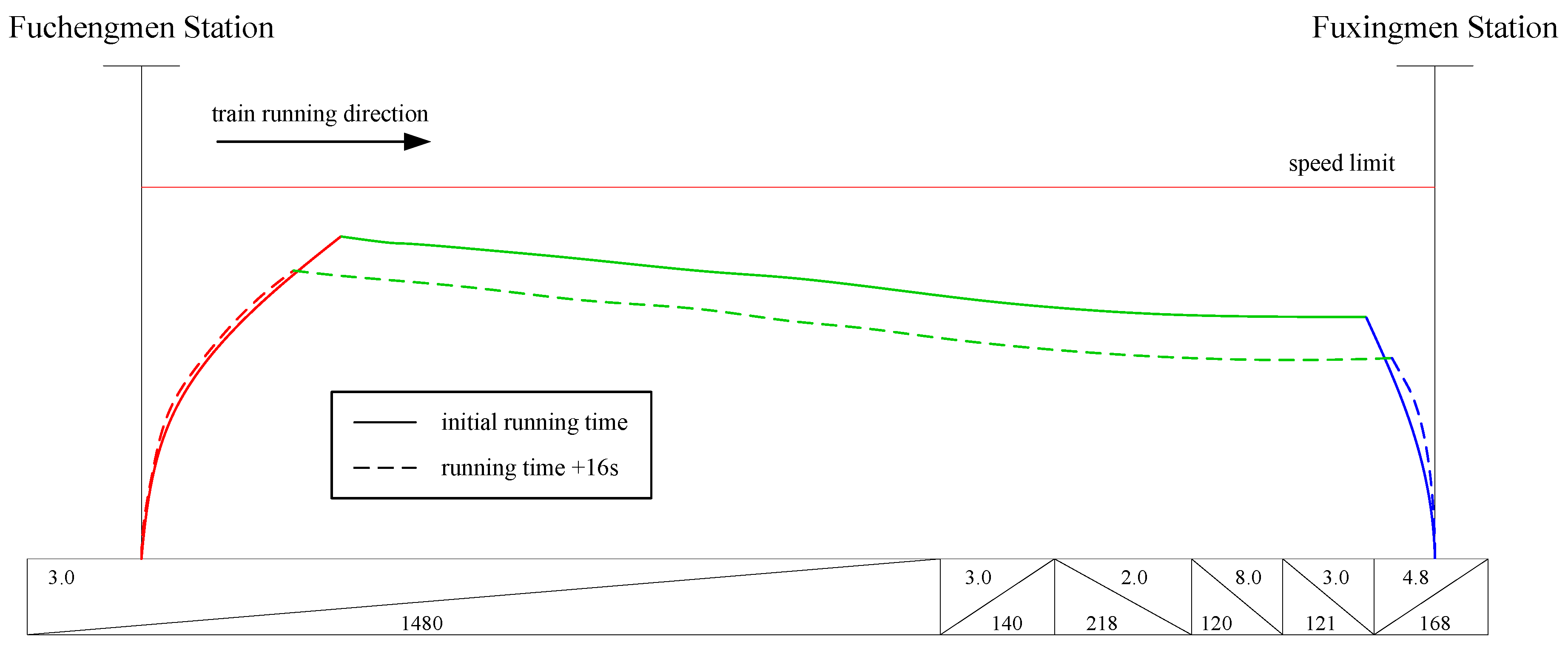
Fixed Running Time (s)	137	139	141	143	145	147	149	151	153
Energy consumption (kWh)	22.99	21.63	21.58	21.45	21.29	21.19	21.15	20.97	20.92
Optimal rate	-	5.9%	0.2%	0.6%	0.7%	0.5%	0.2%	0.9%	0.2%

and Figure 10.

As shown in Table 3, the energy consumption descends with the increase of the fixed running time, with a sharp decrease at the beginning (5.9% optimal rate when the running time is 139 s) and a gradual decline (the optimal rates are no more than 1.0%) when the fixed running time is much larger than that of the initial timetable. From Figure 10, we can see that the coasting speed profiles have a smoothly changing trend when the gradient condition changes, indicating that the utilization of a uniformly-distributed mass-belt model to describe train operation progress is reasonable and practical. Moreover, the speed profile with a longer fixed running time is much lower than that with a shorter time. These results indicate the usefulness of the train control strategy with fixed time.

5.2. The Case of the Whole Line

In the train energy-efficient operation progress, both the train and track condition have been given. However, the number of on-board passengers will strongly affect the train operation performance by changing the train traction mass. In this case study, we identify how much the number of passengers on board will affect the train traction energy consumption by calculating the energy consumption for a train running the whole of Beijing metro Line 2. When the train traction mass increases from 194.00 t to 268.88 t, the energy consumption with each section adding a fixed running time (10 s) is shown in

Table 4. Energy consumption with different train traction mass.

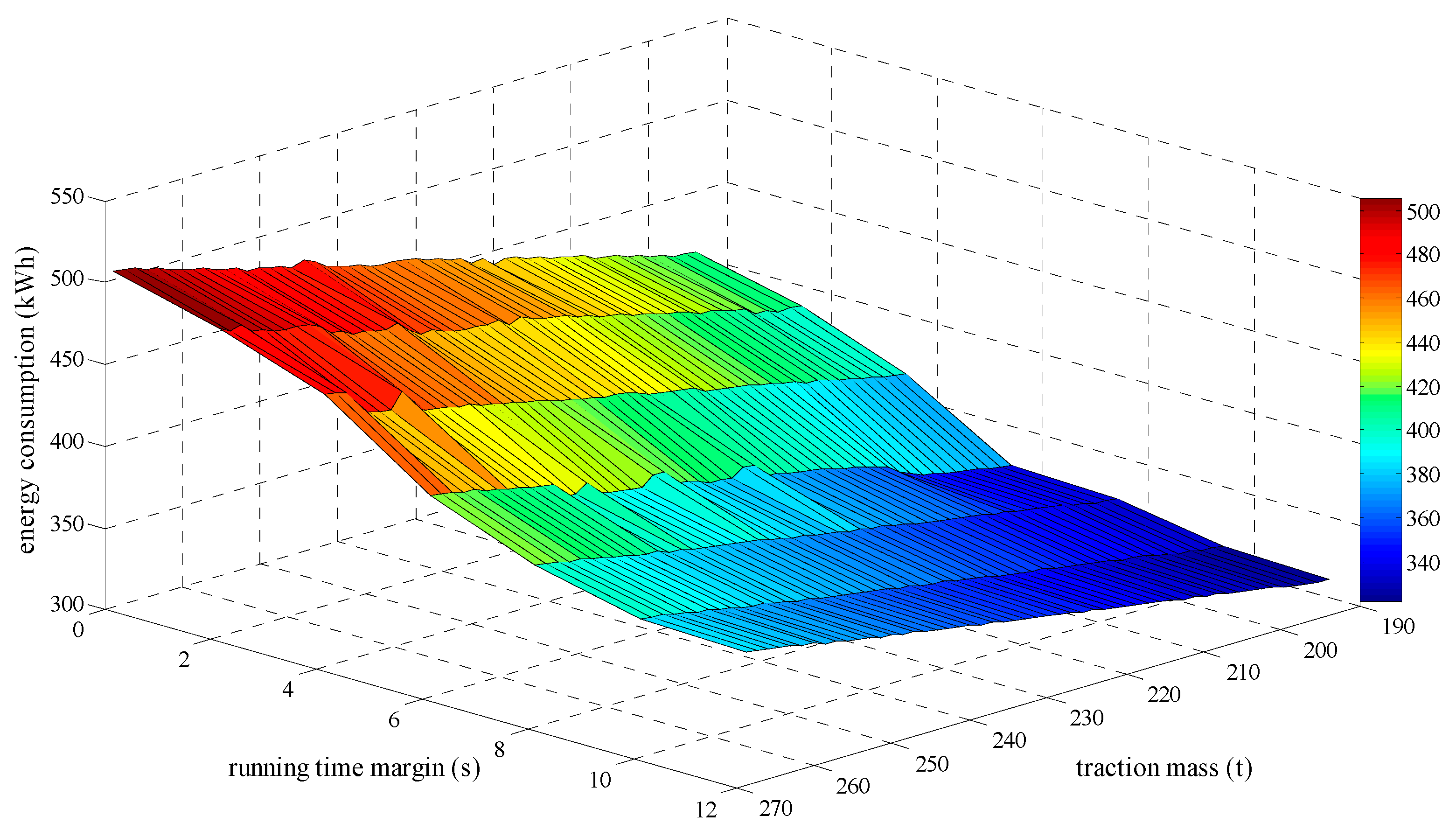
Traction Mass (t)	194.00	195.44	196.88	198.32	199.76	201.20	202.64	204.08	205.52
Energy consumption (kWh)	324.31	325.05	325.71	327.15	327.92	329.85	330.76	332.23	333.17
Traction mass (t)	206.96	208.40	209.84	211.28	212.72	214.16	215.60	217.04	218.48
Energy consumption (kWh)	333.79	335.55	336.28	337.73	338.41	339.82	340.76	342.4	343.08
Traction mass (t)	219.92	221.36	222.80	224.24	225.68	227.12	228.56	230.00	231.44
Energy consumption (kWh)	343.99	345.35	346.46	348.15	348.86	350.13	351.07	352.83	353.43
Traction mass (t)	232.88	234.32	235.76	237.20	238.64	240.08	241.52	242.96	244.40
Energy consumption (kWh)	354.24	356.09	356.79	358.51	359.17	360.83	361.54	362.59	363.97
Traction mass (t)	245.84	247.28	248.72	250.16	251.60	253.04	254.48	255.92	257.36
Energy consumption (kWh)	364.88	366.5	367.15	368.85	369.43	371.31	371.98	372.93	374.83
Traction mass (t)	258.80	260.24	261.68	263.12	264.56	266.00	267.44	268.88
Energy consumption (kWh)	375.61	377.71	378.31	380.27	380.96	382.56	383.25	384.18

. Moreover, the energy consumption is shown in Figure 11 when both the traction mass increases from 194.00 t to 268.88 t and each section running time increases form 2 s to 12 s.

From Table 4, we can conclude that the energy consumption precisely increases with the increase of traction mass. The results illustrate that the energy consumption shows an even lower increasing rate (18.5% = (384.18 − 324.31)/324.31) than the one of traction mass (38.6% = (268.88 − 194.00)/194.00). It seems probable that the presented train operation performance is all optimized by the fixed time train control, which contributes to the low energy consumption.

It is found in Figure 11 that when the running time margin of each station is improved from 0 s to 6 s, the energy consumption of one train with 268.88 t traction mass decreases much more quickly from about 505.93 kWh to approximately 466.85 kWh. Moreover, the effect of the running time margin longer than 6 s on the energy consumption slows down smoothly. In contrast, the energy consumption is evidently linearly increased with the increasing traction mass. Such an increase is accelerated by more traction force or a longer duration of traction applied to achieve the same train speed for a heavier train [43].

5.3. A Real-World Case Study

We consider a real-world case study over the Beijing metro Line 2 (inner ring), which is a loop line consisting of 18 stations and 18 sections with a total length of 23.6 km. In daily operations, the planned cycle time is 2640 s; the minimal headway is h_min = 120 s; and the maximal headway is h_max = 420 s. More details can be found in

Table 5. Basic operation data of Beijing Metro Line 2 (inner ring).

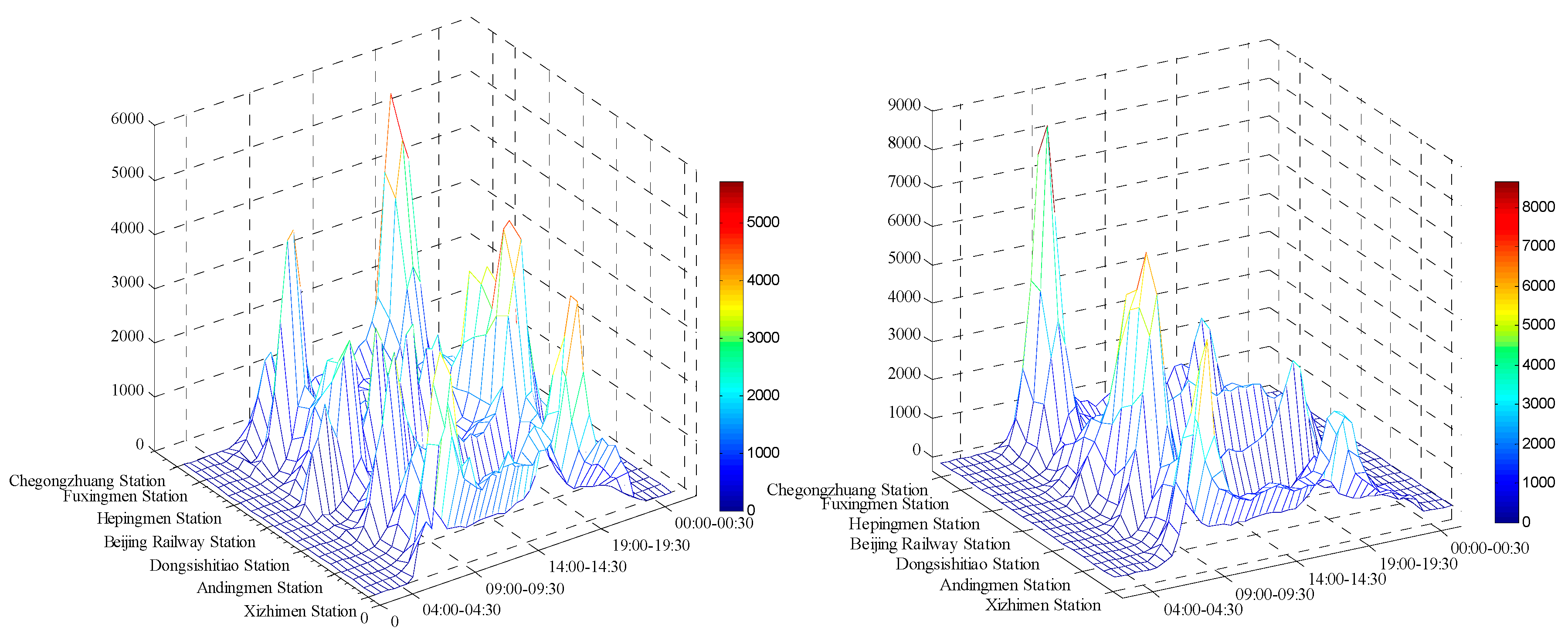
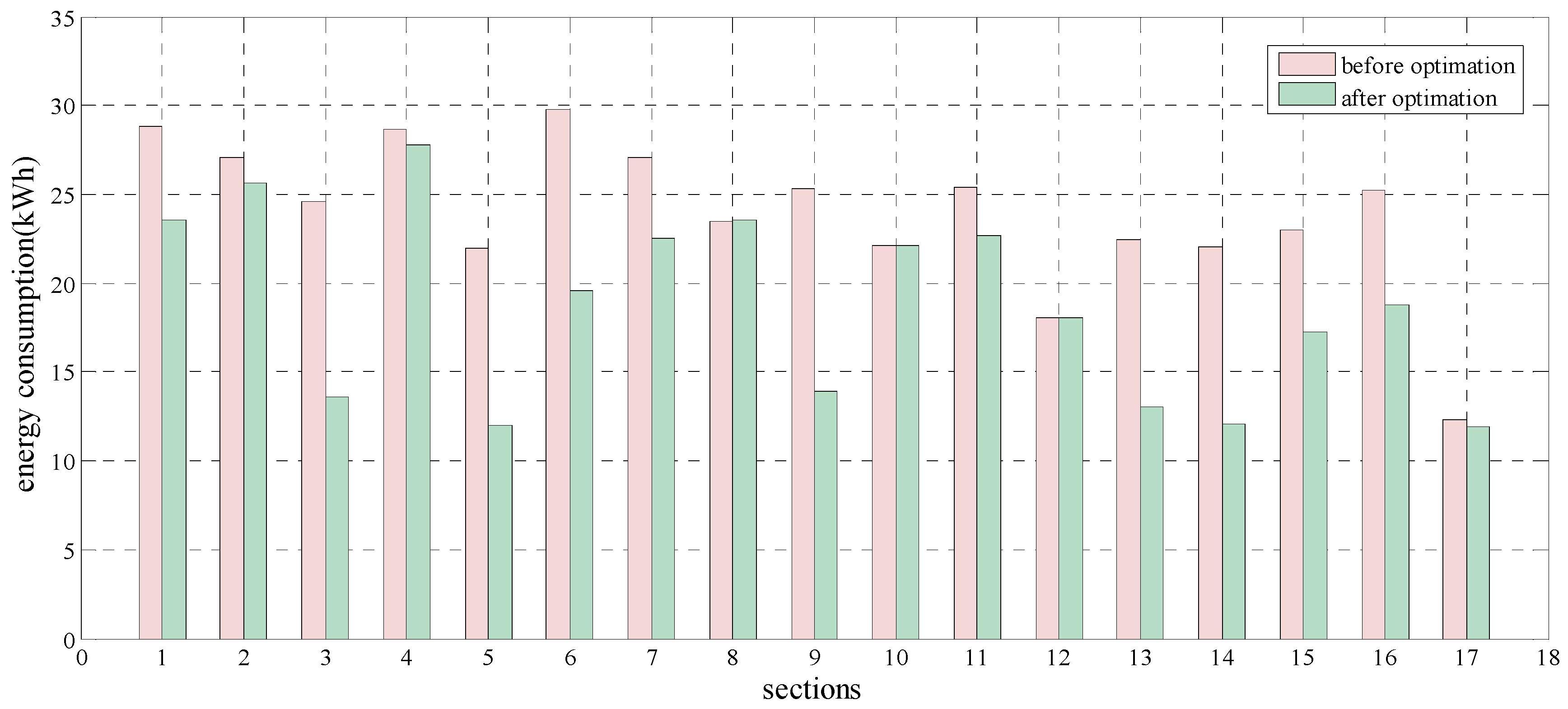
Section	Length (m) *	Running Time (s)	Dwelling Time (s)	Section Passengers
Jianguomen Station–Chaoyangmen Station	1763	123	45	166,945
Chaoyangmen Station–Dongsishitiao Station	1027	88	30	157,873
Dongsishitiao Station–Dongzhimen Station	824	78	50	148,313
Dongzhimen Station–Lama Temple Station	2228	174	45	114,565
Lama Temple Station–Andingmen Station	794	74	30	143,292
Andingmen Station–Guloudajie Station	1237	98	50	145,613
Guloudajie Station–Jishuitan Station	1766	129	50	160,098
Jishuitan Station–Xizhimen Station	1899	166	60	161,824
Xizhimen Station–Chegongzhuang Station	909	87	45	156,004
Chegongzhuang Station–Fuchengmen Station	960	85	30	159,932
Fuchengmen Station–Fuxingmen Station	1832	137	50	157,867
Fuxingmen Station–Changchunjie Station	1234	115	30	109,896
Changchunjie Station–Xuanwumen Station	929	85	30	110,013
Xuanwumen Station–Hepingmen Station	851	82	30	154,568
Hepingmen Station–Qianmen Station	1171	95	30	155,703
Qianmen Station–Chongwenmen Station	1634	123	45	157,306
Chongwenmen Station–Beijing Railway Station	1023	112	60	136,104
Beijing Railway Station–Jianguomen Station	945	101	60	133,743

* Source from http://www.bjsubway.com/station/zjgls/#.

. In this study, we use the real-world passenger demand data collected by the smart card dataset from BMTROC on a weekday of April 2014. Due to the page limitations, we show the number of arriving and departing passengers at each station of Line 2 in Figure 12. It is obvious that the passenger demands are significantly heterogeneous for different stations and different hours, which is corroborated by previous studies [56,57]. In the numerical experiments, we consider the time window from 10:00 to 12:00 in off-peak hours, during which a total of 16 trains are operated. Based on the passenger demand data, we calculate the results of the energy consumption of each section as represented in Figure 13.

In Figure 13, we compare the energy consumption of each section of Line 2 before and after the optimization; it is clearly shows that the energy consumption is obviously decreased after the utilization of the optimal model. As detailed in Figure 13, there are some sections with appreciable energy savings, such as Sections 3, 5, 9, 13 and 14, which are the sections with shorter lengths. Take Section 5 for example: the results illustrate that the energy consumption will show a great decrease from about 21.9 kWh for before optimal to 11.9 kWh for after optimal. In other words, the energy consumption is nearly halved when the running time of this section increases nine seconds. However, this kind of great decrease will not happen in all sections, caused by associated reasons, such as dwelling time margin, gradient condition of the section, and so on. On the whole, the total energy consumption of one train decreases from about 407.3 kWh down to 317.9 kWh. This energy savings rate (21.9%) is much higher than those considering regenerative energy utilization (8.86% in [4], 5.12% in [5] and 8% in [6]) considering the usage of regenerative energy.

6. Conclusions

Based on a dwelling time calculation approach on the basis of representatively dynamic changes of the passenger flow in different time intervals of its daily operation, a metro train timetable and control strategy optimization model is newly developed in this research to reduce the traction energy consumption during off-peak hours. A mass-belt train movement simulation model provides a way of calculating the traction energy consumption with fixed running time considering both the basic running resistance and the additional resistance (such as resistance force caused by track gradients and curves). It has been confirmed that the proposed train simulation model is able to effectively obtain a reasonable driving control strategy with satisfactory optimal energy-saving results. The case studies with the application of the proposed approach show that the newly-developed model is capable of rationally reducing the train traction energy consumption on the basis of meeting the boarding and alighting demand of passengers on the platform. This enables the quick capture of the dwelling time at a station with uncertain and dynamic passenger time-dependent demands, which leads to a longer running time and a lower energy consumption. Furthermore, this approach can be combined with a real-time monitoring of the passengers on station platforms in order to contribute to an off-peak energy-efficient control system.

For the sake of simplicity, we assume that the train arrival time of stations does not change; in other words, the dwelling time margin of station i only can be added to the running time of section i. Therefore, many other different kinds of timetable change assumptions need to be studied with much more optimal scenarios simulated in future research to further validate the results of this research. Furthermore, the comparative analyses of the waiting time value of passengers who arrive at the station during the dwelling time margin and that have to wait for the next train also ought to be made in the future to enrich this work. The good energy-saving effort of this proposed model is obtained on the basis of sacrificing the travel time of a part of the passengers.