A High-Frequency Isolated Online Uninterruptible Power Supply (UPS) System with Small Battery Bank for Low Power Applications
Abstract
:1. Introduction
- (1)
- The number of batteries is not restricted to the dc-link voltage. The volume, weight, and backup time of the battery bank should be designed according to the specific application.
- (2)
- Cost reduction as no extra voltage balancing circuit is required.
- (3)
- Damaged batteries can be isolated or replaced in the battery bank leaving the sensitive system operation uninterrupted. This is a prime function of UPS systems.
- (4)
- Since the discharging currents of the batteries can be profiled individually, hence the stored energy in the batteries can be utilized more efficiently.
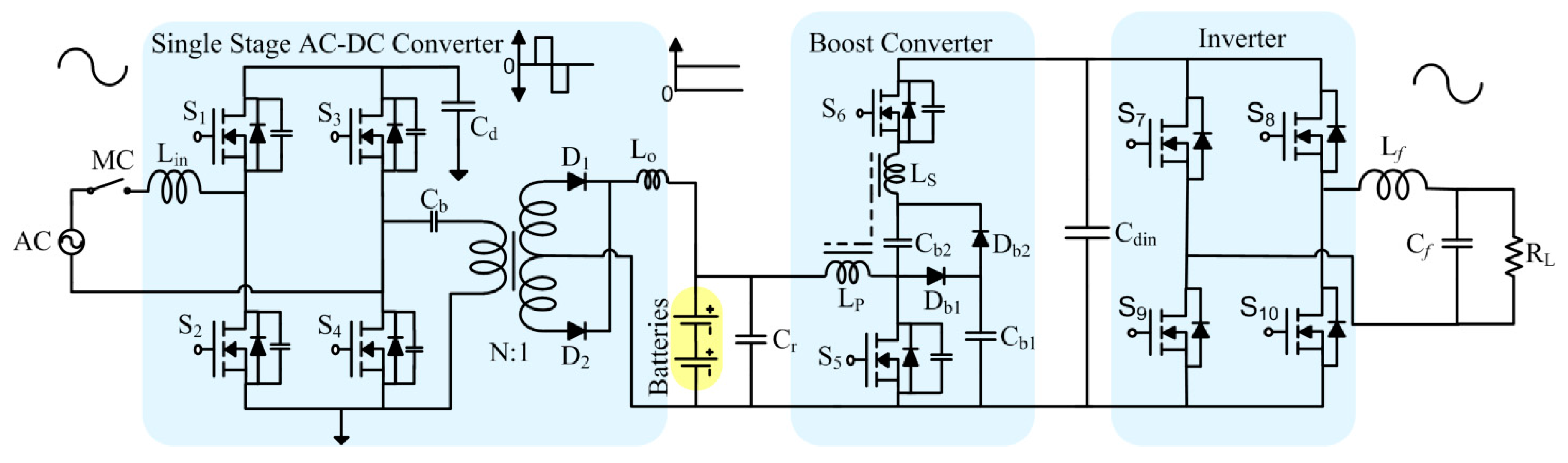
2. Circuit Description
2.1. Modes of Operation
2.1.1. Grid Mode
2.1.2. Battery Mode
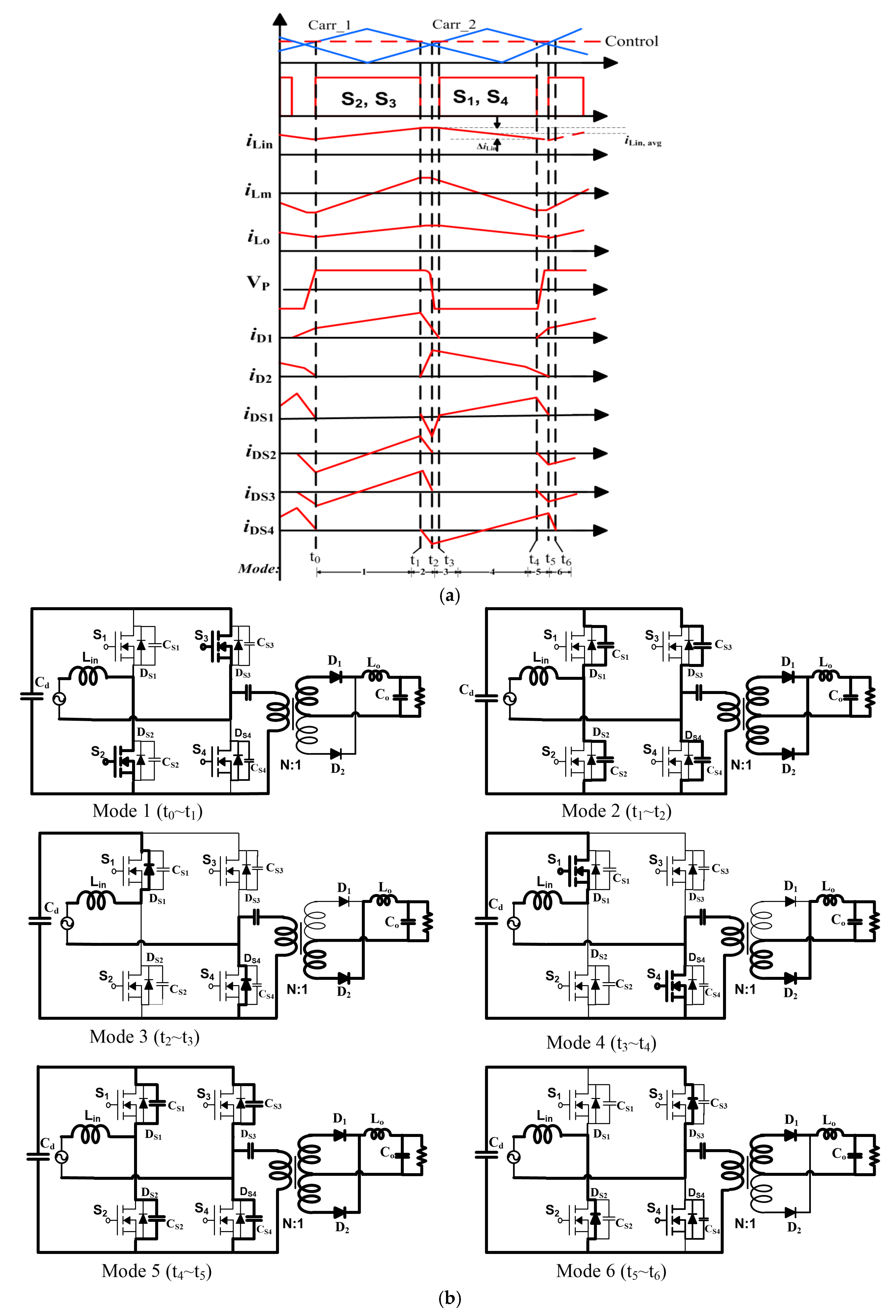
2.2. AC-DC Converter
2.2.1. Mode 1
2.2.2. Mode 2
2.2.3. Mode 3
2.2.4. Mode 4
2.2.5. Mode 5
2.2.6. Mode 6
2.2.7. Continuous condition mode (CCM) of operation of input inductor
2.2.8. Discontinuous conduction mode (DCM) of operation of the input inductor
2.3. Boost Converter
2.3.1. Mode 1 (t0~t1)
2.3.2. Mode 2 (t1~t2)
2.3.3. Mode 3 (t2~t3)
2.3.4. Mode 4 (t3~t4)
2.3.5. Mode 5 (t4~t5)
2.3.6. Mode 6 (t5~t6)
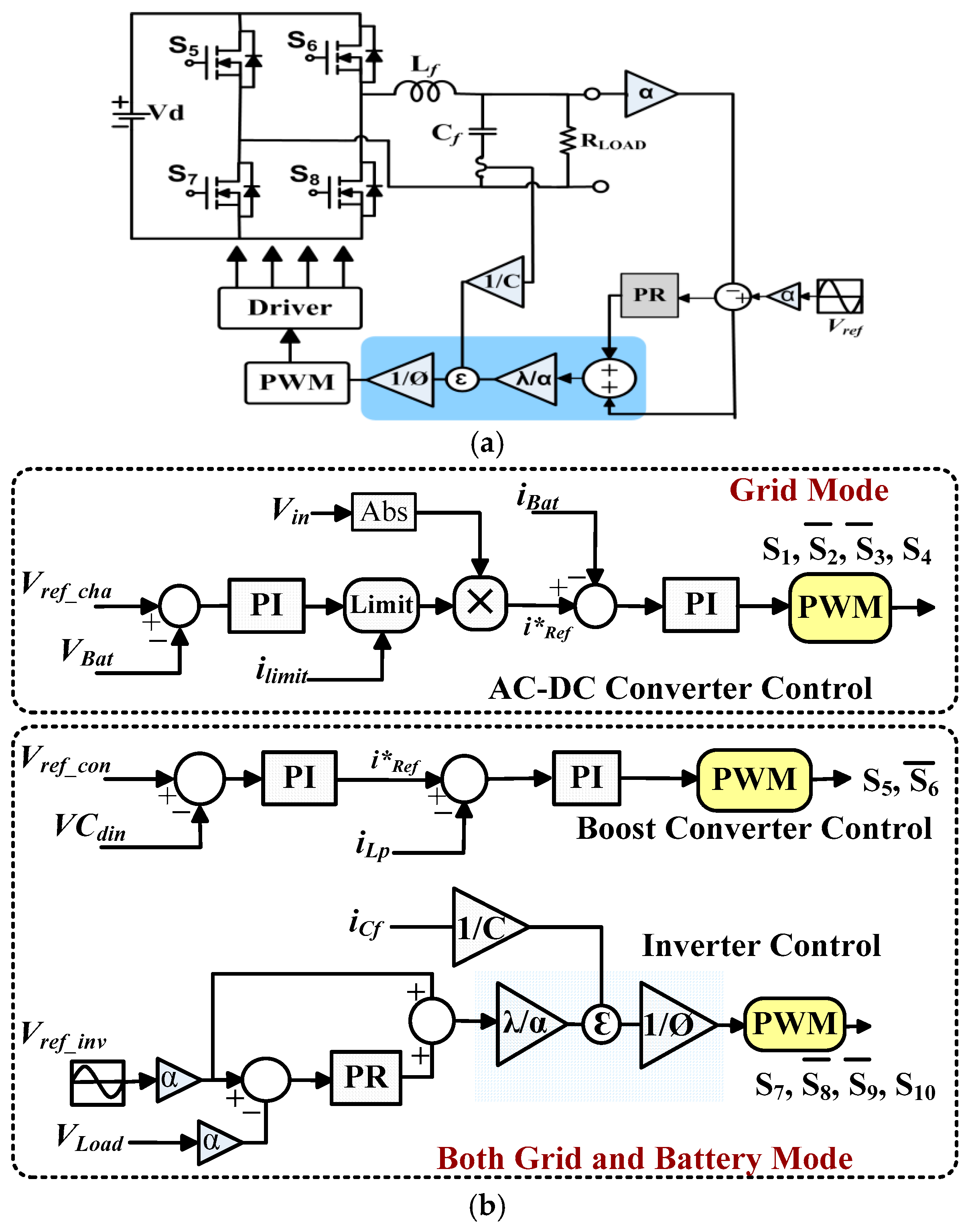
3. Control Strategy
3.1. Inverter Control
3.2. Battery Charger Control
3.3. Boost Converter Control
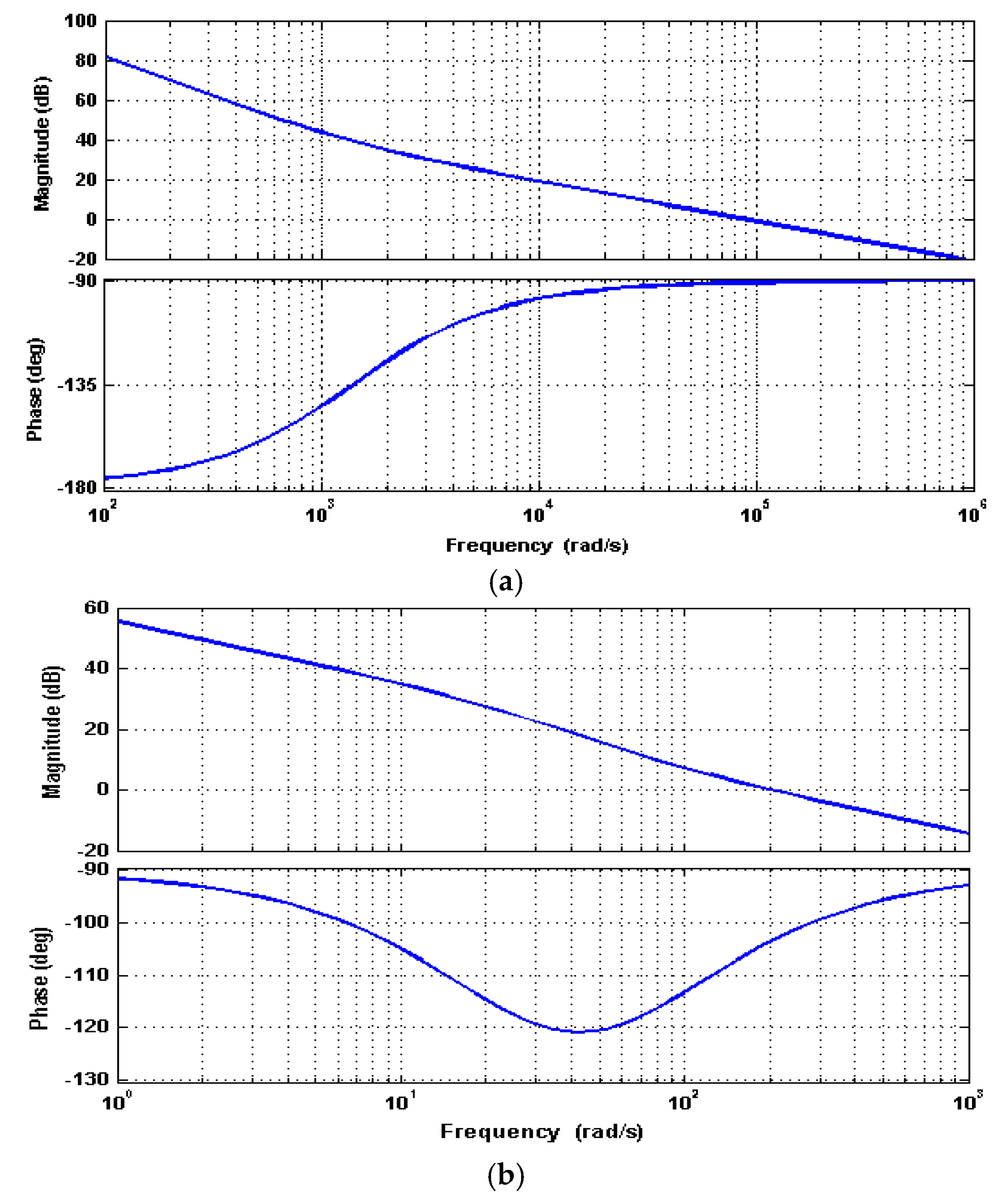
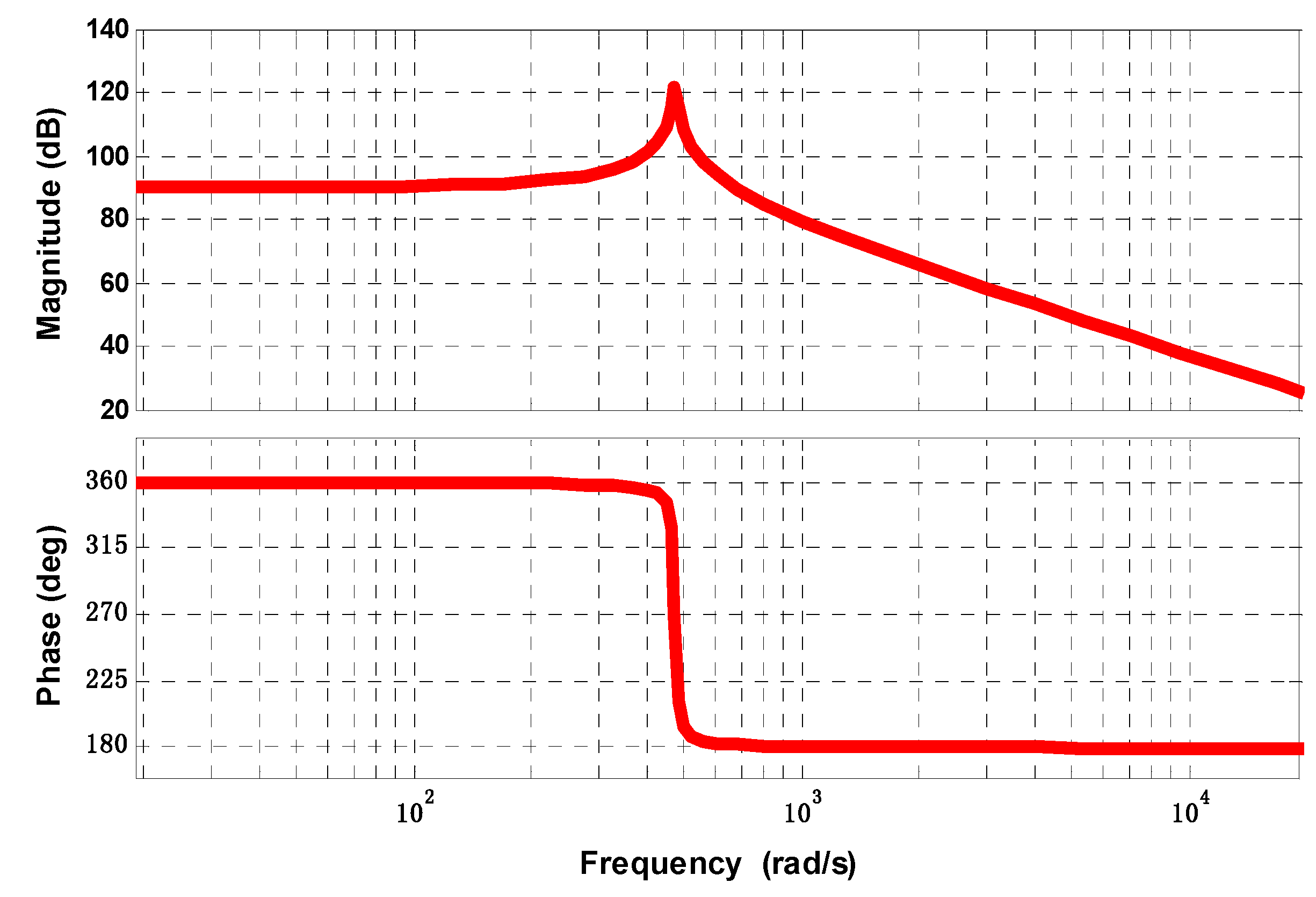
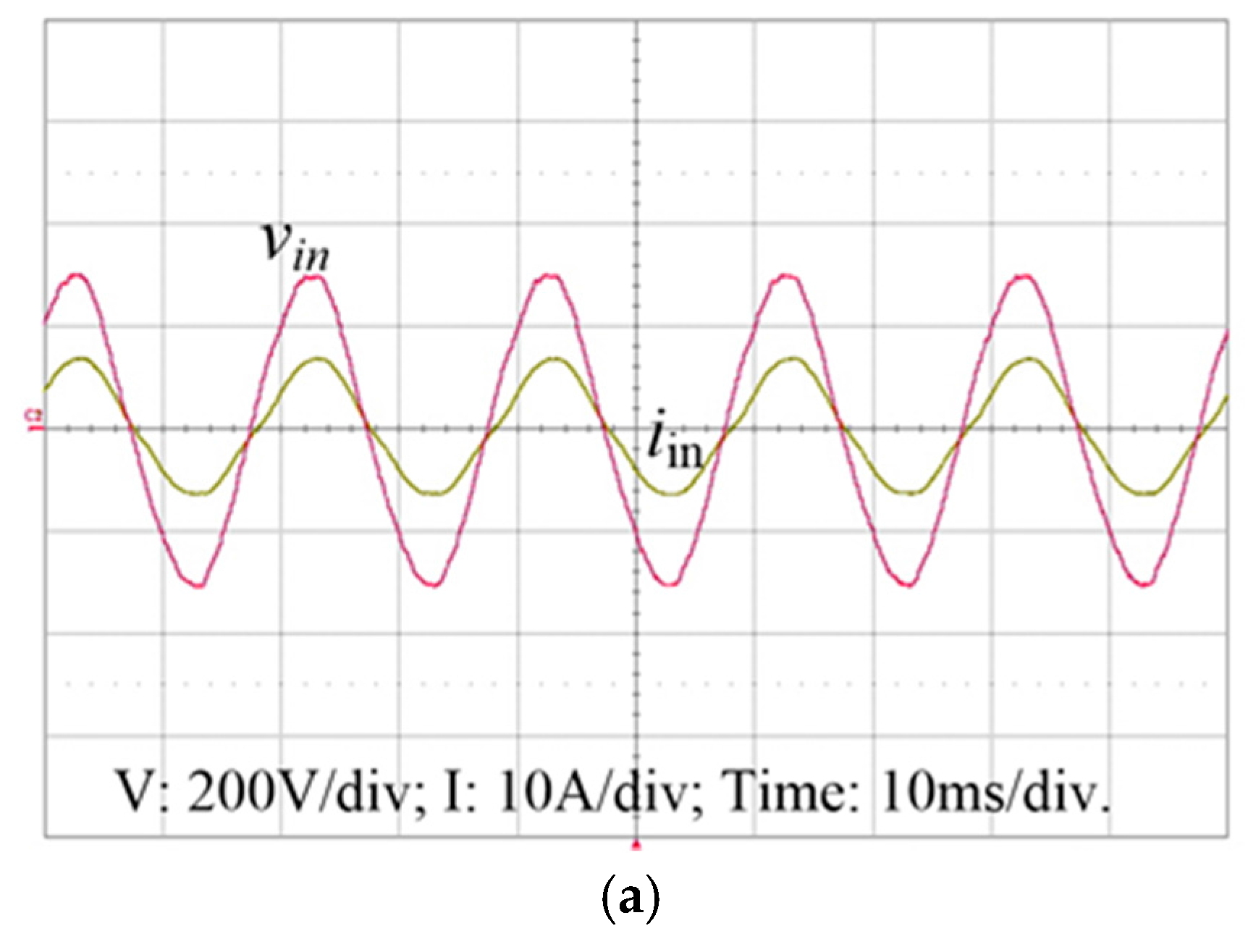
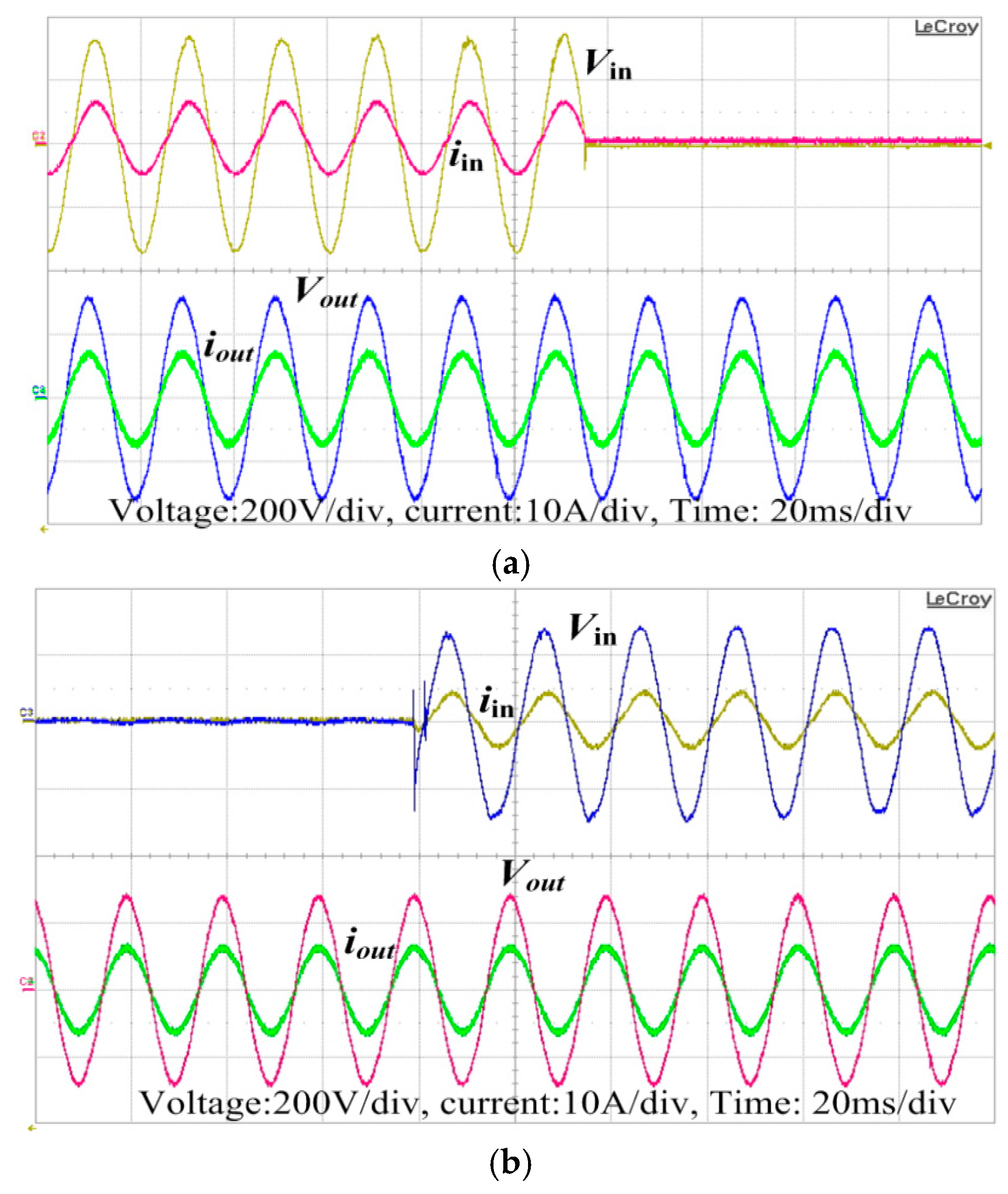
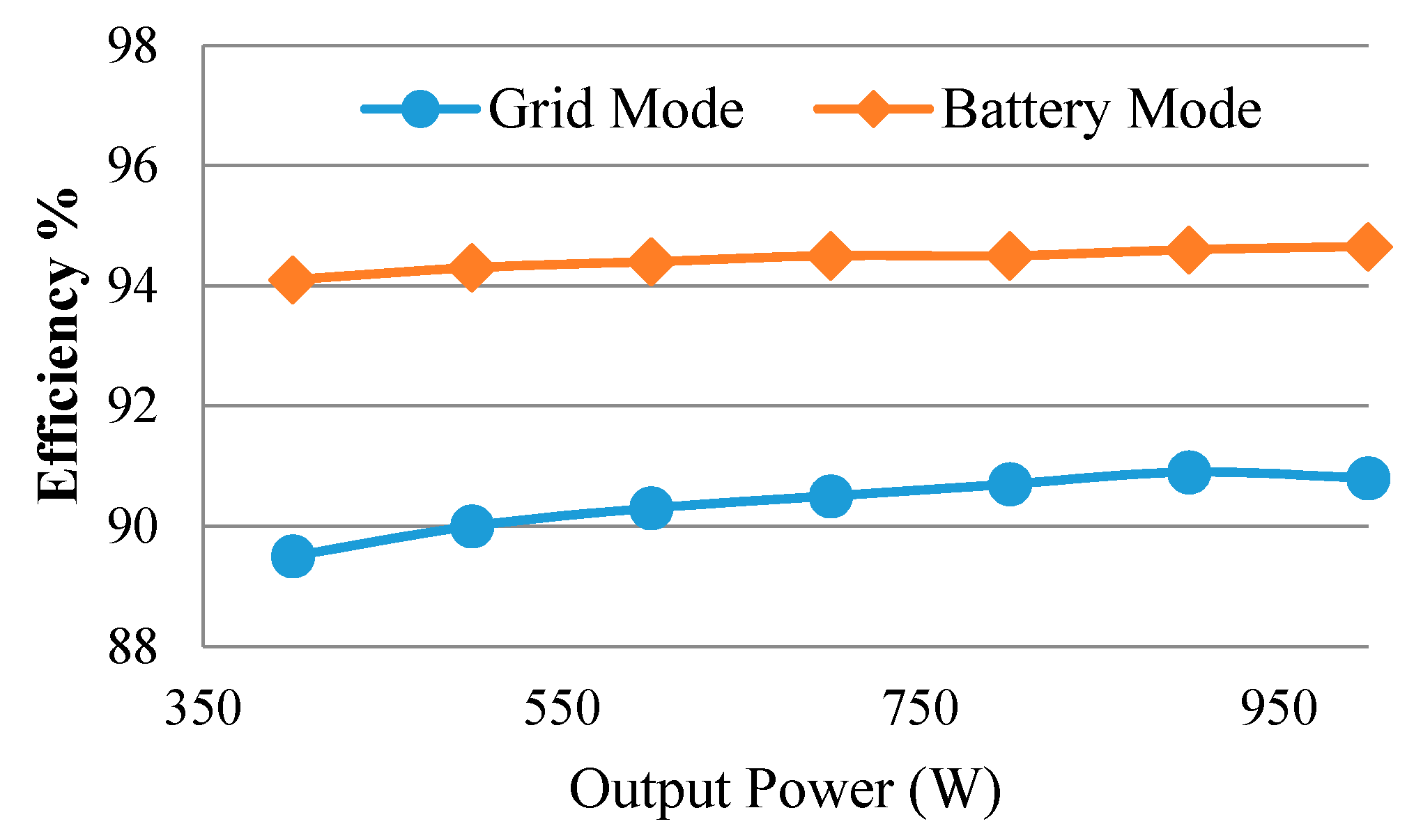
4. Experimental Results
5. Conclusions
Authors Contribution
Acknowledgments
Conflicts of Interest
References
- Lahyani, A.; Venet, P.; Guermazi, A.; Troudi, A. Battery/supercapacitors combination in uninterruptible power supply (UPS). IEEE Trans. Power Electron. 2013, 28, 1509–1522. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.; Xiao, Y. Next-generation multi-functional modular intelligent UPS system for smart grid. IEEE Trans. Ind. Electron. 2013, 60, 3602–3618. [Google Scholar] [CrossRef]
- Branco, C.G.; Torrico-Bascope, R.P.; Cruz, C.M.; de A Lima, F. Proposal of three-phase high-frequency transformer isolation UPS topologies for distributed generation applications. IEEE Trans. Ind. Electron. 2013, 60, 1520–1531. [Google Scholar] [CrossRef]
- Hwang, J.-C.; Chen, J.-C.; Pan, J.-S.; Huang, Y.-C. Measurement method for online battery early faults precaution in uninterrupted power supply system. IET Electr. Power Appl. 2011, 5, 267–274. [Google Scholar] [CrossRef]
- Karve, S. Three of a kind [UPS topologies, IEC standard]. IEE Rev. 2000, 46, 27–31. [Google Scholar] [CrossRef]
- Vázquez, N.; Villegas-Saucillo, J.; Hernández, C.; Rodríguez, E.; Arau, J. Two-stage uninterruptible power supply with high power factor. IEEE Trans. Ind. Electron. 2008, 55, 2954–2962. [Google Scholar]
- Aamir, M.; Kafeel, A.K.; Mekhilef, S. Review: Uninterruptible power supply (UPS) system. Renew. Sust. Energy Rev. 2016, 58, 1395–1410. [Google Scholar] [CrossRef]
- Rodriguez, E.; Vázquez, N.; Hernández, C.; Correa, J. A novel AC UPS with high power factor and fast dynamic response. IEEE Trans. Ind. Electron. 2008, 55, 2963–2973. [Google Scholar] [CrossRef]
- Torrico-Bascope, R.P.; Oliveira, D.S.; Branco, C.G.C.; Antunes, F.L.M. A UPS with 110-V/220-V input voltage and high-frequency transformer isolation. IEEE Trans. Ind. Electron. 2008, 55, 2984–2996. [Google Scholar] [CrossRef]
- Nasiri, A.; Nie, Z.; Bekiarov, S.B.; Emadi, A. An on-line UPS system with power factor correction and electric isolation using BIFRED converter. IEEE Trans. Ind. Electron. 2008, 55, 722–730. [Google Scholar] [CrossRef]
- Hirachi, K.; Yoshitsugu, J.; Nishimura, K.; Chibani, A.; Nakaoka, M. Switched-mode PFC rectifier with high-frequency transformer link for high-power density single phase UPS. In Proceedings of the IEEE 28th Annual IEEE Power Electronics Specialists Conference, (PESC’97 Record), St. Louis, MO, USA, 27 June 1997; Volume 1, pp. 290–296. [Google Scholar]
- De Rooij, M.A.; Ferreira, J.A.; van Wyk, D. A novel unity power factor low-EMI uninterruptible power supply. IEEE Trans. Ind. Electron. 1998, 34, 870–877. [Google Scholar] [CrossRef]
- Park, H.S.; Kim, C.H.; Park, K.B.; Moon, G.W.; Lee, J.H. Design of a charge equalizer based on battery modularization. IEEE Trans. Veh. Technol. 2009, 58, 3216–3223. [Google Scholar] [CrossRef]
- Lee, Y.S.; Cheng, M.W. Intelligent control battery equalization for series connected lithium-ion battery strings. IEEE Trans. Ind. Electron. 2005, 52, 1297–1307. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, M.; Liu, F.; Kang, Y. Instantaneous current-sharing control strategy for parallel operation of UPS modules using virtual impedance. IEEE Trans. Power Electron. 2013, 28, 432–440. [Google Scholar] [CrossRef]
- Yang, S.; Chen, S.; Lin, J. Dynamics analysis of a low-voltage stress single-stage high-power factor correction AC/DC flyback converter. IET Power Electron. 2012, 5, 1624–1633. [Google Scholar] [CrossRef]
- Duarte, J.; Lima, L.R.; Oliveira, L.; Michels, L.; Rech, C.; Mezaroba, M. Single-stage high power factor step-up/step-down isolated AC/DC converter. IET Power Electron. 2012, 5, 1351–1358. [Google Scholar] [CrossRef]
- Ki, S.; Lu, D. Extension of minimum separable switching configuration modelling to single-stage AC/DC converters with direct power transfer. IET Power Electron. 2012, 5, 1154–1163. [Google Scholar] [CrossRef]
- Yang, L.-S.; Liang, T.-J.; Chen, J.-F.; Lin, R.-L. Analysis and design of a novel, single-stage, three-phase AC/DC step-down converter with electrical isolation. IET Power Electron. 2008, 1, 154–163. [Google Scholar] [CrossRef]
- Ma, H.; Ji, Y.; Xu, Y. Design and analysis of single-stage power factor correction converter with a feedback winding. IEEE Trans. Power Electron. 2010, 25, 1460–1470. [Google Scholar] [CrossRef]
- Mahdavi, M.; Farzaneh-Fard, H. Bridgeless CUK power factor correction rectifier with reduced conduction losses. IET Power Electron. 2012, 5, 1733–1740. [Google Scholar] [CrossRef]
- Abasian, A.; Farzaneh-fard, H.; Madani, S. Single stage soft switching AC/DC converter without any extra switch. IET Power Electron. 2014, 7, 745–752. [Google Scholar] [CrossRef]
- Liang, T.-J.; Yang, L.-S.; Chen, J.-F. Analysis and design of a single-phase AC/DC step-down converter for universal input voltage. IET Electr. Power Appl. 2007, 1, 778–784. [Google Scholar] [CrossRef]
- Lai, C.; Shyu, K. A single-stage AC/DC converter based on zero voltage switching LLC resonant topology. IET Electr. Power Appl. 2007, 1, 743–752. [Google Scholar] [CrossRef]
- Lin, J.-L.; Yao, W.-K.; Yang, S.-P. Analysis and design for a novel single-stage high power factor correction diagonal half-bridge forward AC/DC converter. IEEE Trans. Circ. Syst. I Regul. Pap. 2006, 53, 2274–2286. [Google Scholar] [CrossRef]
- Lu, D.-C.; Iu, H.-C.; Pjevalica, V. Single-stage AC/DC boost–forward converter with high power factor and regulated bus and output voltages. IEEE Trans. Ind. Electron. 2009, 56, 2128–2132. [Google Scholar] [CrossRef]
- Choi, W.-Y.; Yoo, J.-S. A bridgeless single-stage half-bridge AC/DC converter. IEEE Trans. Power Electron. 2011, 26, 3884–3895. [Google Scholar] [CrossRef]
- Ribeiro, H.S.; Borges, B.V. High-performance voltage-fed AC–DC full-bridge single-stage power factor correctors with a reduced DC bus capacitor. IEEE Trans. Power Electron. 2014, 29, 2680–2692. [Google Scholar] [CrossRef]
- Das, P.; Pahlevaninezhad, M.; Moschopoulos, G. Analysis and design of a new AC–DC single-stage full-bridge PWM converter with two controllers. IEEE Trans. Ind. Electron. 2013, 60, 4930–4946. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics; Springer Science & Business Media: New York, NY, USA, 2001. [Google Scholar]
- Aamir, M.; Mekhilef, S.; Hee-Jun, K. High-gain zero-voltage switching bidirectional converter with a reduced number of switches. IEEE Trans. Circ. Syst. II Express Briefs 2015, 62, 816–820. [Google Scholar] [CrossRef]
- Zargari, N.; Ziogas, P.; Joos, G. A two switch high performance current regulated DC/AC converter module. IEEE Trans. Ind. Appl. 1995, 31, 583–589. [Google Scholar] [CrossRef]
- Cortes, P.; Ortiz, G.; Yuz, J.I.; Rodriguez, J.; Vazquez, S.; Franquelo, L.G. Model predictive control of an inverter with output LC filter for UPS applications. IEEE Trans. Ind. Electron. 2009, 56, 1875–1883. [Google Scholar] [CrossRef]
- Tamyurek, B. A high-performance SPWM controller for three-phase UPS systems operating under highly nonlinear loads. IEEE Trans. Power Electron. 2013, 28, 3689–3701. [Google Scholar] [CrossRef]
- Komurcugil, H. Rotating-sliding-line-based sliding-mode control for single-phase UPS inverters. IEEE Trans. Ind. Electron. 2012, 59, 3719–3726. [Google Scholar] [CrossRef]
- Abrishamifar, A.; Ahmad, A.A.; Mohamadian, M. Fixed switching frequency sliding mode control for single-phase unipolar inverters. IEEE Trans. Power Electron. 2012, 27, 2507–2514. [Google Scholar] [CrossRef]
- Ullah, W.; Mekhilef, S. Transformer-less 3P3W SAPF (three-phase three-wire shunt active power filter) with line-interactive UPS (uninterruptible power supply) and battery energy storage stage. Energy 2016, 109, 525–536. [Google Scholar]
- International Electro-technical Commission. Uninterruptible Power Systems (UPS)—Methods of Specifying the Performance and Test Requirements; IEC62040-3 Standard; IEC: Geneva, Switzerland, 1999. [Google Scholar]





| Reference | Rated Power | Input/Output Voltage | Battery Bank Voltage | Number of Batteries |
|---|---|---|---|---|
| [8] | 300 VA | 120 | 48 | 4 |
| [9] | 2 kVA | 220 | 108 | 9 |
| [10] | 150 VA | 120 | 48 | 4 |
| [11] | 2 kVA | 110 | 180 | 15 |
| [12] | 3.3 kVA | 220 | 120 | 10 |
| Parameters | Model Predictive Control [33] | SPWM Control [34] | Rotating SMC [35] | Fix-Freq SMC [36] | Proposed Work |
|---|---|---|---|---|---|
| VDC | 529 | 405 | 300 | 360 | 350 |
| VRMS | 150 | 220 | 200 | 220 | 220 |
| Cf (uF) | 40 | 202 | 100 | 9.4 | 6.6 |
| Lf (mH) | 2.4 | 0.03 | 0.250 | 0.357 | 0.84 |
| THD (L) | 2.85% | 1.11% | - | 1.1% | 0.45% |
| THD (NL) | 3.8% | 3.8% | 2.66% | 1.7% | 1.25% |
| TS (ms) | 50 | 60 | - | 0.5 | 0.3 |
| Parameters | Symbol | Value |
|---|---|---|
| Input Voltage | Vin | 220 V |
| Output Voltage | Vout | 220 V |
| Grid Frequency | fr | 50 Hz |
| Output Frequency | fo | 50 Hz |
| Number of Batteries | Vb | 2 Parallel connected (24 V/35 Ah) |
| Maximum Output Power | Po,max | 1 kVA |
| DC-link Voltage | Vd | 360 V |
| Parameters | Symbol | Value |
|---|---|---|
| Input Inductor | Lin | 1.2 mH |
| Switches | S1~S4 | SPP11N60C3 |
| Fast Diodes | D1, D2 | C3D10060A |
| Switching frequency | fs | 50,000 Hz |
| H. F Transformer | T | Lm = 600 uH, TDK core PQ-40/40 |
| DC-Link Capacitor | Cd | 1900 uF |
| Parameters | Symbol | Value |
|---|---|---|
| DC-Link Voltage | Vd_INV | 360 V |
| Battery Bank Voltage | Vb | 24 V |
| Switching Frequency | fs | 30,000 Hz |
| Coupled Inductor | LP, LS | Turns ratio N = 4; Magnetizing Inductor Lm = 107 uH; PQ-5050 core |
| Capacitor | Cb1, Cb2 | Cb1, Cb2 = 2 × 2.2 uF (ceramic), Cd = 1900 uF |
| Switches | S5 ,S6 | IPW60R045CP MOSFET (Infineon Technologies, Santa Clara, CA USA) |
| Diodes | Db1, Db2 | Ultrafast Recovery diode UF5408 |
| Properties | Efficiency | Power Ratings | System Specification | Battery Bank | Size & Weight | |
|---|---|---|---|---|---|---|
| UPS Topology | ||||||
| An On-Line UPS System With Power Factor Correction and Electric Isolation Using BIFRED Converter [10] | - | 150 VA | 110 V | 48 V | Small | |
| Two-Stage Uninterruptible Power Supply With High Power Factor [6] | 84% | 150 VA | 120 V | 60 V | Small | |
| A UPS With 110-V/220-V Input Voltage and High-Frequency Transformer Isolation [9] | 86% | 2 kVA | 110/220 V | 96 V | High | |
| Novel AC UPS With High Power Factor and Fast Dynamic Response [8] | - | 300 VA | 110 V | 48 V | - | |
| Proposed UPS System | 91% | 1 kVA | 220 V | 24 V | Medium | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aamir, M.; Ullah Tareen, W.; Ahmed Kalwar, K.; Ahmed Memon, M.; Mekhilef, S. A High-Frequency Isolated Online Uninterruptible Power Supply (UPS) System with Small Battery Bank for Low Power Applications. Energies 2017, 10, 418. https://doi.org/10.3390/en10040418
Aamir M, Ullah Tareen W, Ahmed Kalwar K, Ahmed Memon M, Mekhilef S. A High-Frequency Isolated Online Uninterruptible Power Supply (UPS) System with Small Battery Bank for Low Power Applications. Energies. 2017; 10(4):418. https://doi.org/10.3390/en10040418
Chicago/Turabian StyleAamir, Muhammad, Wajahat Ullah Tareen, Kafeel Ahmed Kalwar, Mudasir Ahmed Memon, and Saad Mekhilef. 2017. "A High-Frequency Isolated Online Uninterruptible Power Supply (UPS) System with Small Battery Bank for Low Power Applications" Energies 10, no. 4: 418. https://doi.org/10.3390/en10040418
APA StyleAamir, M., Ullah Tareen, W., Ahmed Kalwar, K., Ahmed Memon, M., & Mekhilef, S. (2017). A High-Frequency Isolated Online Uninterruptible Power Supply (UPS) System with Small Battery Bank for Low Power Applications. Energies, 10(4), 418. https://doi.org/10.3390/en10040418







