Tuning the Complexity of Photovoltaic Array Models to Meet Real-time Constraints of Embedded Energy Emulators
Abstract
:1. Introduction
2. Modeling a Photovoltaic Array
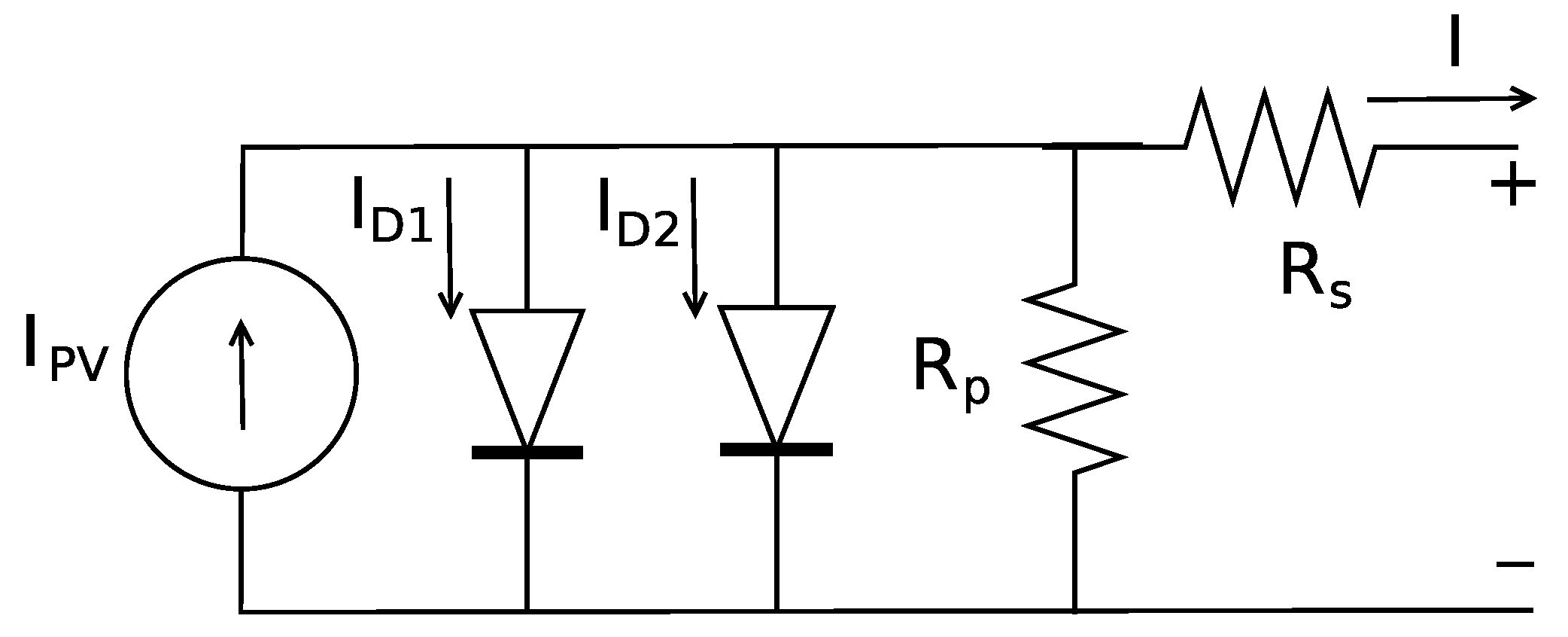
2.1. Models Description
- (1)
- the classic PV effect, by means of current generator and diode ;
- (2)
- the effect of the recombination current in the depletion region, which particularly affects accuracy in the low-voltage region, by means of diode ;
- (3)
- losses due to contact resistance (between silicon and electrodes surfaces) and materials resistance (silicon and electrodes metal), by means of series resistance ;
- (4)
- sensitivity to temperature variation and the effect of leakage current in the PN junction, by means of parallel resistance .
2.2. Numerical Resolution Method
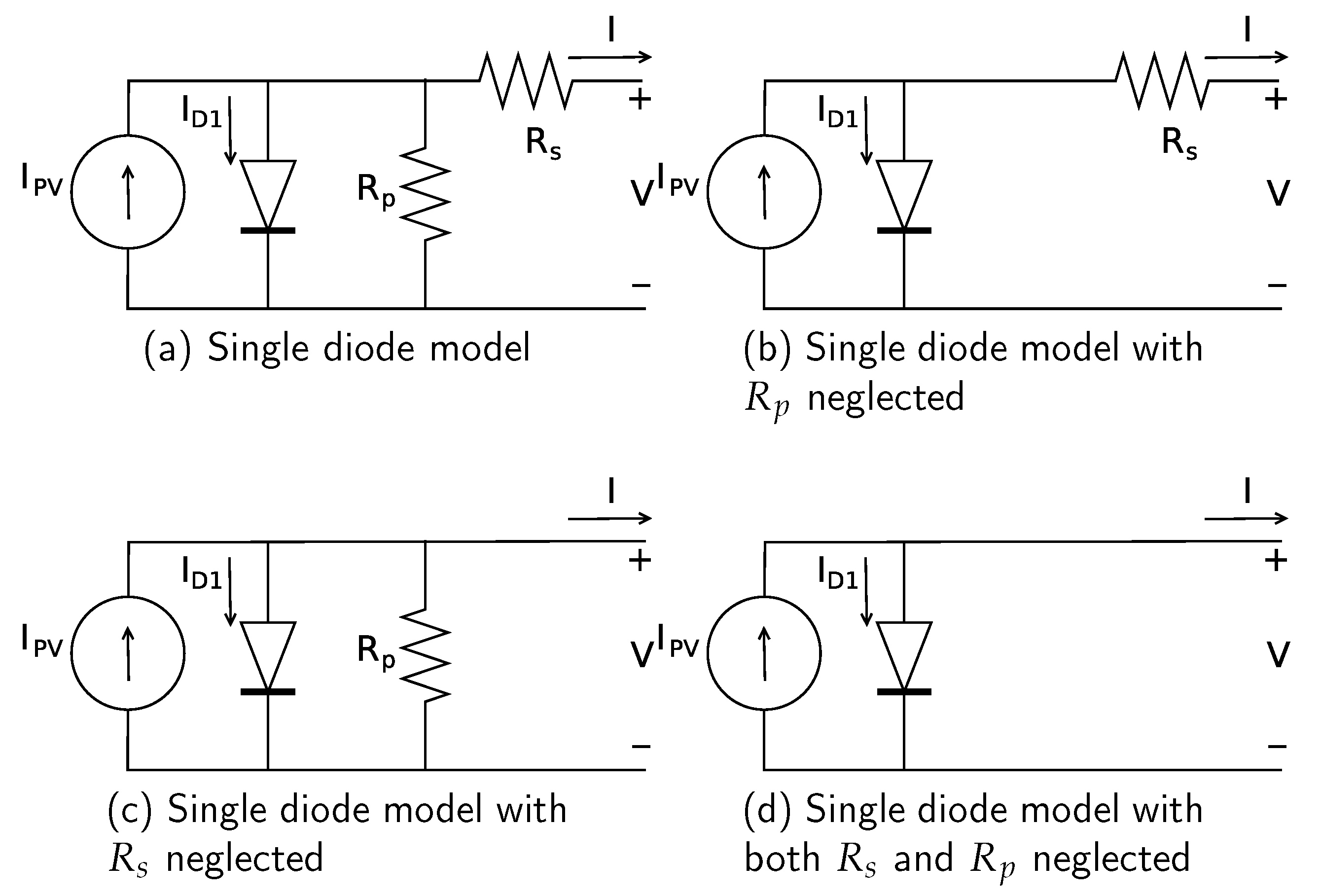
3. Tuning Models Complexity
- For each model to be analyzed:
- -
- the error achieved to reconstruct the Several I–V curve of a particular PV device by means of the model is measured;
- -
- the time required at run-time to resolve the model (i.e., to derive the voltage values to be applied by the emulation board from current values) is measured.
- The two empirically derived metrics are used to build a Pareto curve whose points correspond to the performance of different models when applied to a specific PV array. Indeed, the Pareto curve is a representation (commonly adopted in multi-objective optimization problems) of the achievable trade-offs between the metrics under study.
- The Pareto front is analyzed to obtain the optimal configuration (i.e., the most suitable model for that device).
4. Results and Discussion
4.1. Experimental Set-Up
4.2. Experimental Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| WSN | wireless sensor network |
| EH-WSN | energy harvester wireless sensor network |
| ENO | energy neutral operation |
| PV | photovoltaic |
| STC | standard test conditions |
| ADC | analog to digital converter |
| DAC | digital to analog converter |
| MNE | mean normalized error |
References
- Kansal, A.; Hsu, J.; Zahedi, S.; Srivastava, M.B. Power management in energy harvesting sensor networks. ACM Trans. Embed. Comput. Syst. 2007, 6. [Google Scholar] [CrossRef]
- Jeong, J.; Culler, D. A practical theory of micro-solar power sensor networks. ACM Trans. Sens. Netw. 2012, 9. [Google Scholar] [CrossRef]
- Jeong, J.; Culler, D. Predicting the long-term behavior of a micro-solar power system. ACM Trans. Embed. Comput. Syst. 2012, 11. [Google Scholar] [CrossRef]
- Bogliolo, A.; Freschi, V.; Lattanzi, E.; Murphy, A.L.; Raza, U. Towards a true energetically sustainable WSN: A case study with prediction-based data collection and a wake-up receiver. In Proceedings of 9th IEEE International Symposium on Industrial Embedded Systems (SIES 2014), Pisa, Italy, 18–20 June 2014; pp. 21–28.
- Bogliolo, A.; Lattanzi, E.; Freschi, V. Idleness as a resource in energy-neutral WSNs. In Proceedings of the 2013 1st International Workshop on Energy Neutral Sensing Systems (ENSSys), Rome, Italy, 14 November 2013; ACM: New York, NY, USA, 2013; pp. 1–6. [Google Scholar]
- Raza, U.; Bogliolo, A.; Freschi, V.; Lattanzi, E.; Murphy, A.L. A two-prong approach to energy-efficient WSNs: Wake-up receivers plus dedicated, model-based sensing. Ad Hoc Netw. 2016, 45, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Chou, P.H.; Park, C.; Park, J.; Pham, K.; Liu, J. B#: A battery emulator and power profiling instrument. In Proceedings of the 2003 International Symposium on Low Power Electronics and Design, Seoul, Korea, 25–27 August 2003; pp. 288–293.
- Li, D.J.; Chou, P.H. Maximizing efficiency of solar-powered systems by load matching. In Proceedings of the 2004 International Symposium on Low Power Electronics and Design (ISLPED), Newport Beach, CA, USA, 9–11 August 2004; pp. 162–167.
- Atia, Y.; Zahran, M.; Al-Hossain, A. Solar cell emulator and solar cell characteristics measurements in dark and illuminated conditions. WSEAS Trans. Syst. Control 2011, 6, 125–135. [Google Scholar]
- Lee, W.; Kim, Y.; Wang, Y.; Chang, N.; Pedram, M.; Han, S. Versatile high-fidelity photovoltaic module emulation system. In Proceedings of the International Symposium on Low Power Electronics and Design, Fukuoka, Japan, 1–3 August 2011; pp. 91–96.
- Thale, S.; Wandhare, R.; Agarwal, V. A novel low cost portable integrated solar PV, fuel cell and battery emulator with fast tracking algorithm. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), Denver, CO, USA, 8–3 June 2014; pp. 3138–3143.
- Chen, C.C.; Chang, H.C.; Kuo, C.C.; Lin, C.C. Programmable energy source emulator for photovoltaic panels considering partial shadow effect. Energy 2013, 54, 174–183. [Google Scholar] [CrossRef]
- González-Medina, R.; Patrao, I.; Garcerá, G.; Figueres, E. A low-cost photovoltaic emulator for static and dynamic evaluation of photovoltaic power converters and facilities. Prog. Photovolt. Res. Appl. 2014, 22, 227–241. [Google Scholar] [CrossRef]
- Bobovych, S.; Banerjee, N.; Robucci, R.; Parkerson, J.P.; Schmandt, J.; Patel, C. SunaPlayer. In Proceedings of the 2015 14th International Conference on Information Processing in Sensor Networks (IPSN), Seattle, WA, USA, 13–16 April 2015; ACM Press: New York, NY, USA, 2015; pp. 59–70. [Google Scholar]
- Zhang, H.; Salajegheh, M.; Fu, K.; Sorber, J. Ekho: Bridging the gap between simulation and reality in tiny energy-harvesting sensors. In Proceedings of the 2011 4th Workshop on Power-Aware Computing and Systems (HotPower), Cascasis, Portugal, 23 October 2011; pp. 1–5.
- Hester, J.; Scott, T.; Sorber, J. Ekho: Realistic and repeatable experimentation for tiny energy-harvesting sensors. In Proceedings of the 2014 12th ACM Conference on Embedded Network Sensor Systems (SenSys), Memphis, TN, USA, 3–6 November 2014; pp. 1–15.
- Lattanzi, E.; Freschi, V.; Dromedari, M.; Lorello, L.S.; Peruzzini, R.; Bogliolo, A. A fast and accurate energy source emulator for wireless sensor networks. EURASIP J. Embed. Syst. 2016, 2016. [Google Scholar] [CrossRef]
- Vergura, S. A complete and simplified datasheet-based model of PV cells in variable environmental conditions for circuit simulation. Energies 2016, 9, 326. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Taheri, H. Simple, fast and accurate two-diode model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2011, 95, 586–594. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Syafaruddin. A comprehensive MATLAB Simulink PV system simulator with partial shading capability based on two-diode model. Sol. Energy 2011, 85, 2217–2227. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Taheri, H.; Syafaruddin. Modeling and simulation of photovoltaic (PV) system during partial shading based on a two-diode model. Simul. Model. Pract. Theory 2011, 19, 1613–1626. [Google Scholar] [CrossRef]
- Seyedmahmoudian, M.; Mekhilef, S.; Rahmani, R.; Yusof, R.; Renani, E.T. Analytical modeling of partially shaded photovoltaic systems. Energies 2013, 6, 128–144. [Google Scholar] [CrossRef]
- Di Vincenzo, M.C.; Infield, D. Detailed PV array model for non-uniform irradiance and its validation against experimental data. Sol. Energy 2013, 97, 314–331. [Google Scholar] [CrossRef]
- Park, J.Y.; Choi, S.J. A novel datasheet-based parameter extraction method for a single-diode photovoltaic array model. Sol. Energy 2015, 122, 1235–1244. [Google Scholar] [CrossRef]
- Bastidas, J.D.; Franco, E.; Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G. A model of photovoltaic fields in mismatching conditions featuring an improved calculation speed. Electr. Power Syst. Res. 2013, 96, 81–90. [Google Scholar] [CrossRef]
- Ciulla, G.; Lo Brano, V.; Di Dio, V.; Cipriani, G. A comparison of different one-diode models for the representation of I-V characteristic of a PV cell. Renew. Sustain. Energy Rev. 2014, 32, 684–696. [Google Scholar] [CrossRef]
- Li, Y.; Shi, R. An intelligent solar energy-harvesting system for wireless sensor networks. EURASIP J. Wirel. Commun. Netw. 2015, 2015. [Google Scholar] [CrossRef]
- Brunelli, D.; Dondi, D.; Bertacchini, A.; Larcher, L.; Pavan, P.; Benini, L. Photovoltaic scavenging systems: Modeling and optimization. Microelectron. J. 2009, 40, 1337–1344. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Khouzam, K.; Ly, C.; Koh, C.K.; Ng, P.Y. Simulation and real-time modelling of space photovoltaic systems. In Proceedings of the Conference Record of the Twenty Fourth Photovoltaic Energy Conversion and 1994 IEEE First World Conference on IEEE Photovoltaic Specialists Conference, Waikoloa, HI, USA, 5–9 December 1994; Volume 2, pp. 2038–2041.
- Kuo, Y.C.; Liang, T.J.; Chen, J.F. Novel maximum-power-point-tracking controller for photovoltaic energy conversion system. IEEE Trans. Ind. Electron. 2001, 48, 594–601. [Google Scholar]
- Matagne, E.; Chenni, R.; El Bachtiri, R. A photovoltaic cell model based on nominal data only. In Proceedings of the 2007 International Conference on Power Engineering, Energy and Electrical Drives, Setubal, Portugal, 12–14 April 2007; pp. 562–565.
- Walker, G. Evaluating MPPT converter topologies using a MATLAB PV model. J. Electr. Electron. Eng. 2001, 21, 49–56. [Google Scholar]
- Xiao, W.; Dunford, W.G.; Capel, A. A novel modeling method for photovoltaic cells. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (PESC), Aachen, Germany, 20–25 June 2004; Volume 3, pp. 1950–1956.
- Yusof, Y.; Sayuti, S.H.; Latif, M.A.; Wanik, M.Z.C. Modeling and simulation of maximum power point tracker for photovoltaic system. In Proceedings of the 2004 National Power and Energy Conference (PECon), Kuala Lumpur, Malaysia, 29–30 November 2004; pp. 88–93.
- Glass, M.C. Improved solar array power point model with SPICE realization. In Proceedings of the 31st Intersociety Energy Conversion Engineering Conference (IECEC 96), Washington, DC, USA, 11–16 August 1996; Volume 1, pp. 286–291.
- Kajihara, A.; Harakawa, A. Model of photovoltaic cell circuits under partial shading. In Proceedings of the 2005 IEEE International Conference on Industrial Technology, Hong Kong, China, 14–17 December 2005; pp. 866–870.
- Benavides, N.D.; Chapman, P.L. Modeling the effect of voltage ripple on the power output of photovoltaic modules. IEEE Trans. Ind. Electron. 2008, 55, 2638–2643. [Google Scholar] [CrossRef]
- Quaschning, V.; Hanitsch, R. Numerical simulation of current-voltage characteristics of photovoltaic systems with shaded solar cells. Sol. Energy 1996, 56, 513–520. [Google Scholar] [CrossRef]
- Solarex. MSX-60 and MSX-64 Photovoltaic Modules. Available online: http://www.solarelectricsupply.com/media/custom/upload/Solarex-MSX64.pdf (accessed on 12 October 2016).
- Q.Cells. Hanwha Q Cells Solar Panels. Available online: https://www.q-cells.com/products/solar-panels.html (accessed on 12 October 2016).
- Multicomp. MC-SP0.8-NF-GCS. Available online: http://www.farnell.com/datasheets/925851.pdf (accessed on 12 October 2016).
- Kyocera. KD135SX-UFU. Available online: http://pdf.wholesalesolar.com/module%20pdf%20folder/KD135SX_UPU.pdf (accessed on 12 October 2016).
- Sah, C.T. Fundamentals of Solid-State Electronics; World Scientific: Singapore, 1991. [Google Scholar]

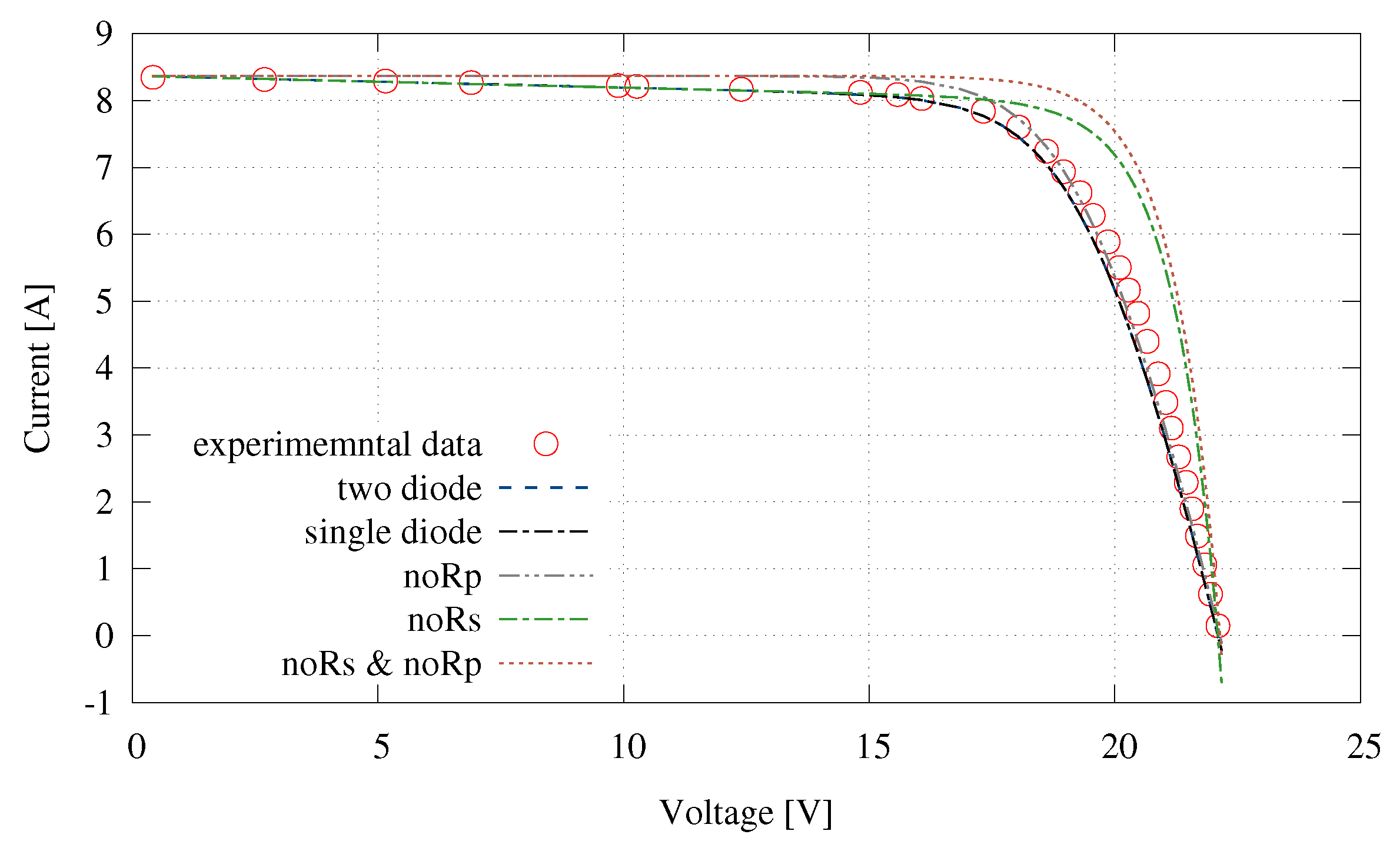
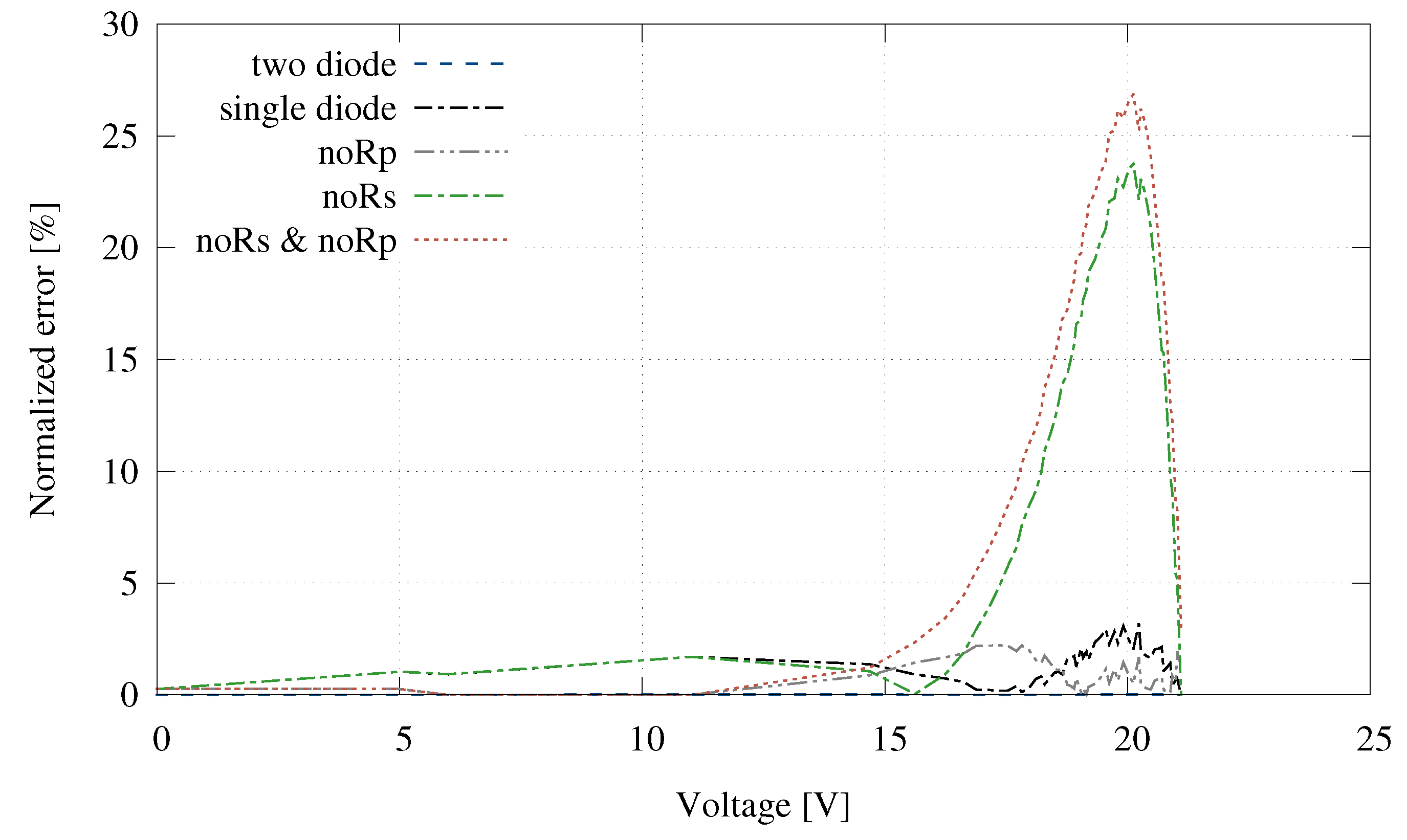
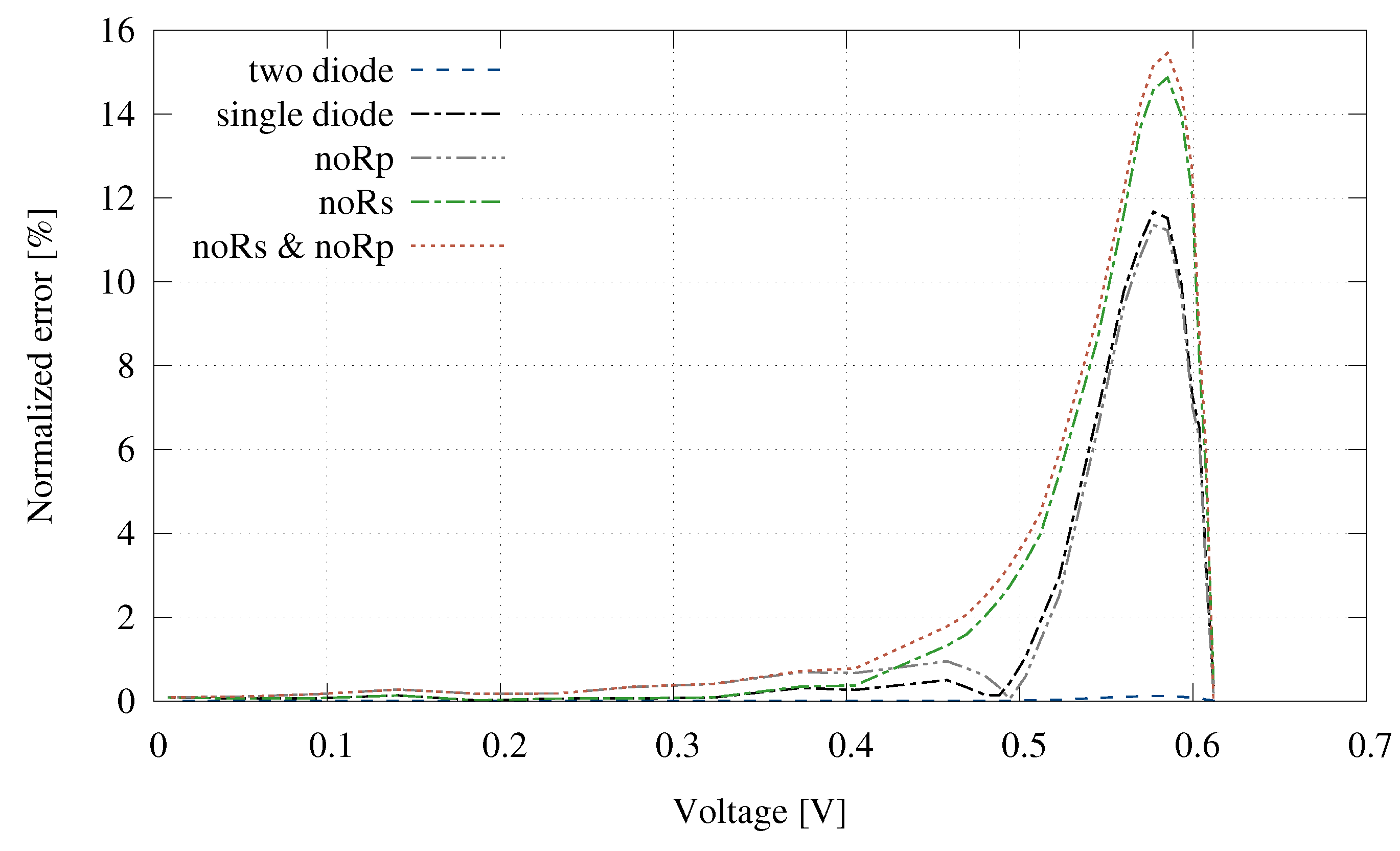
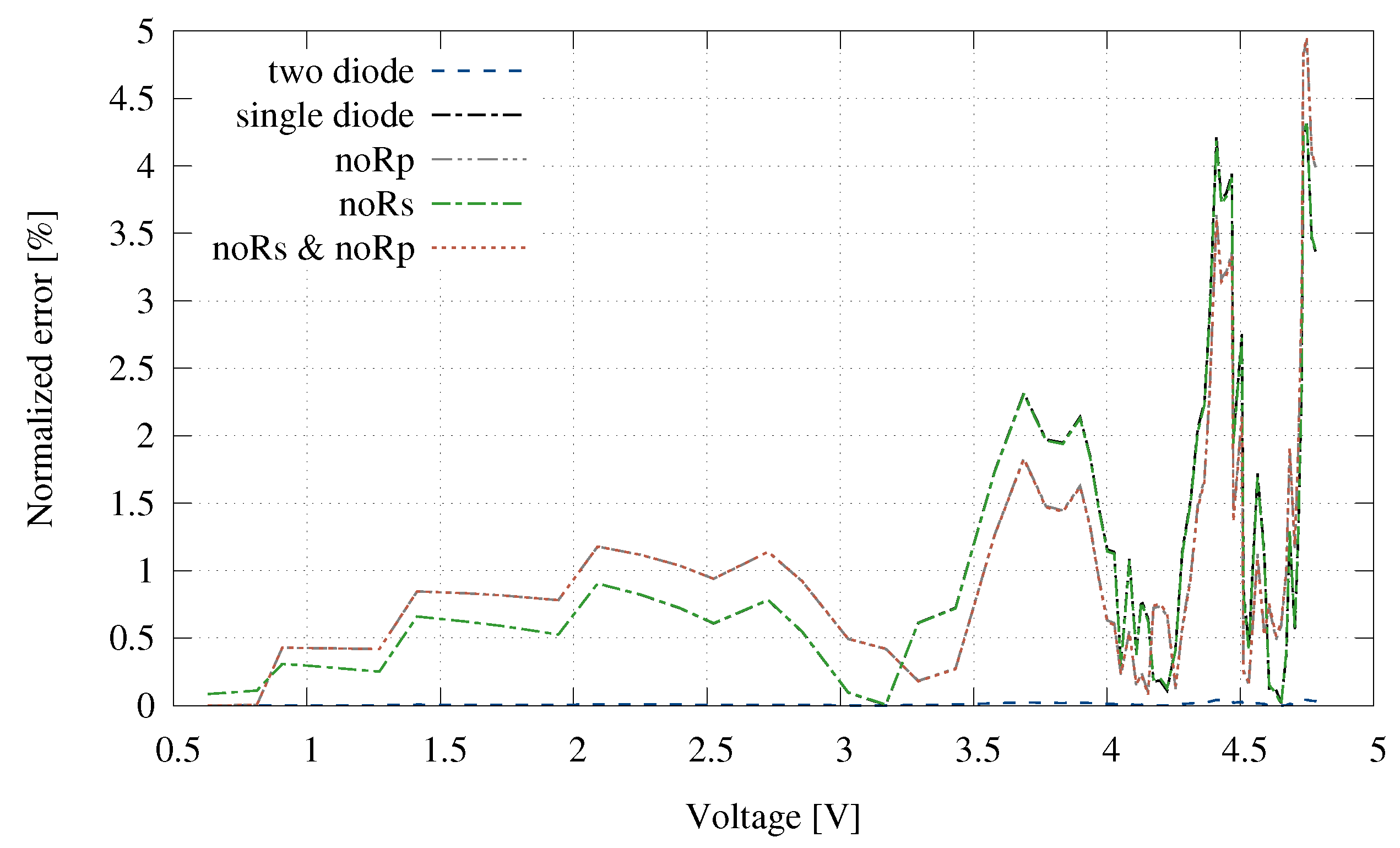
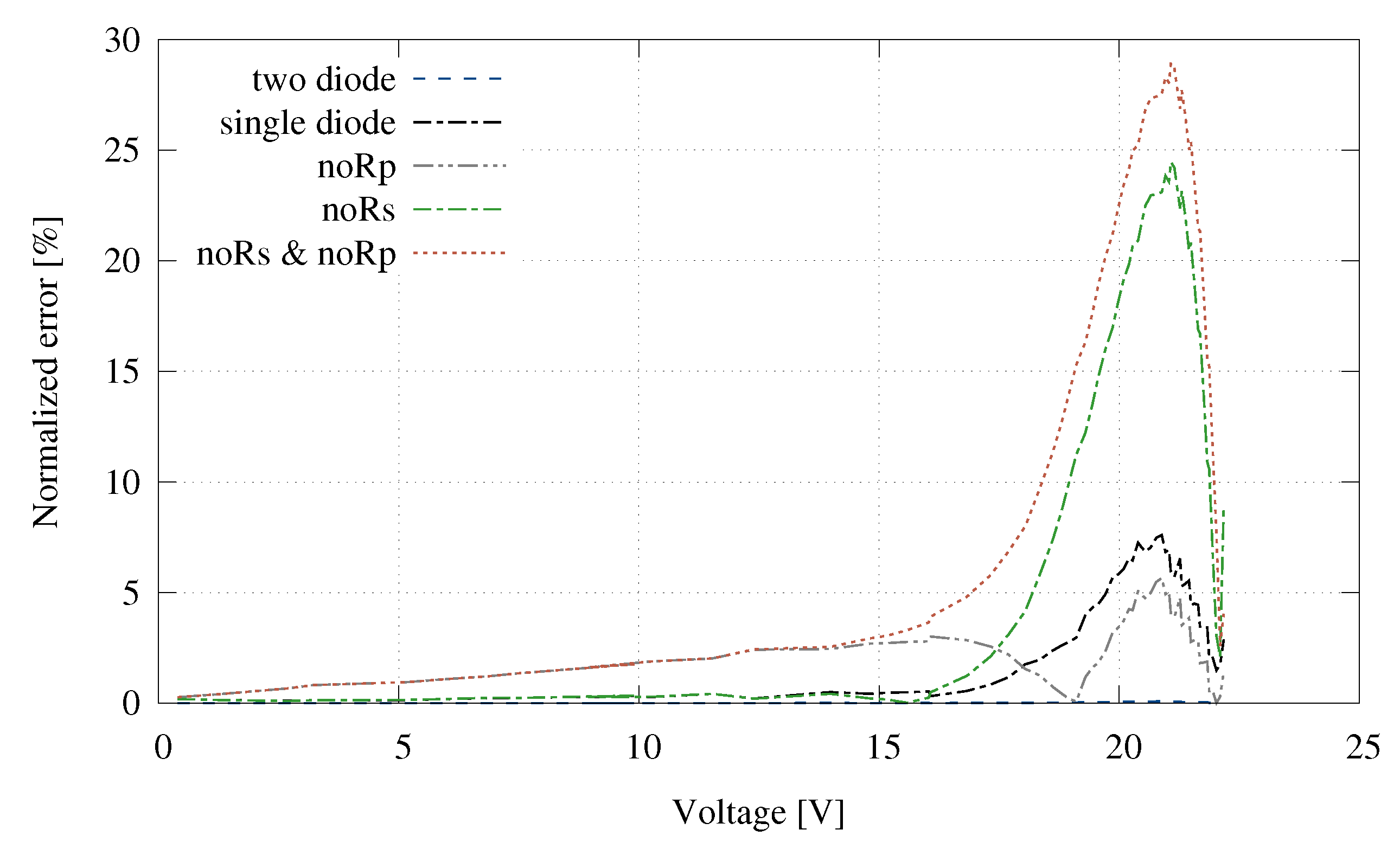
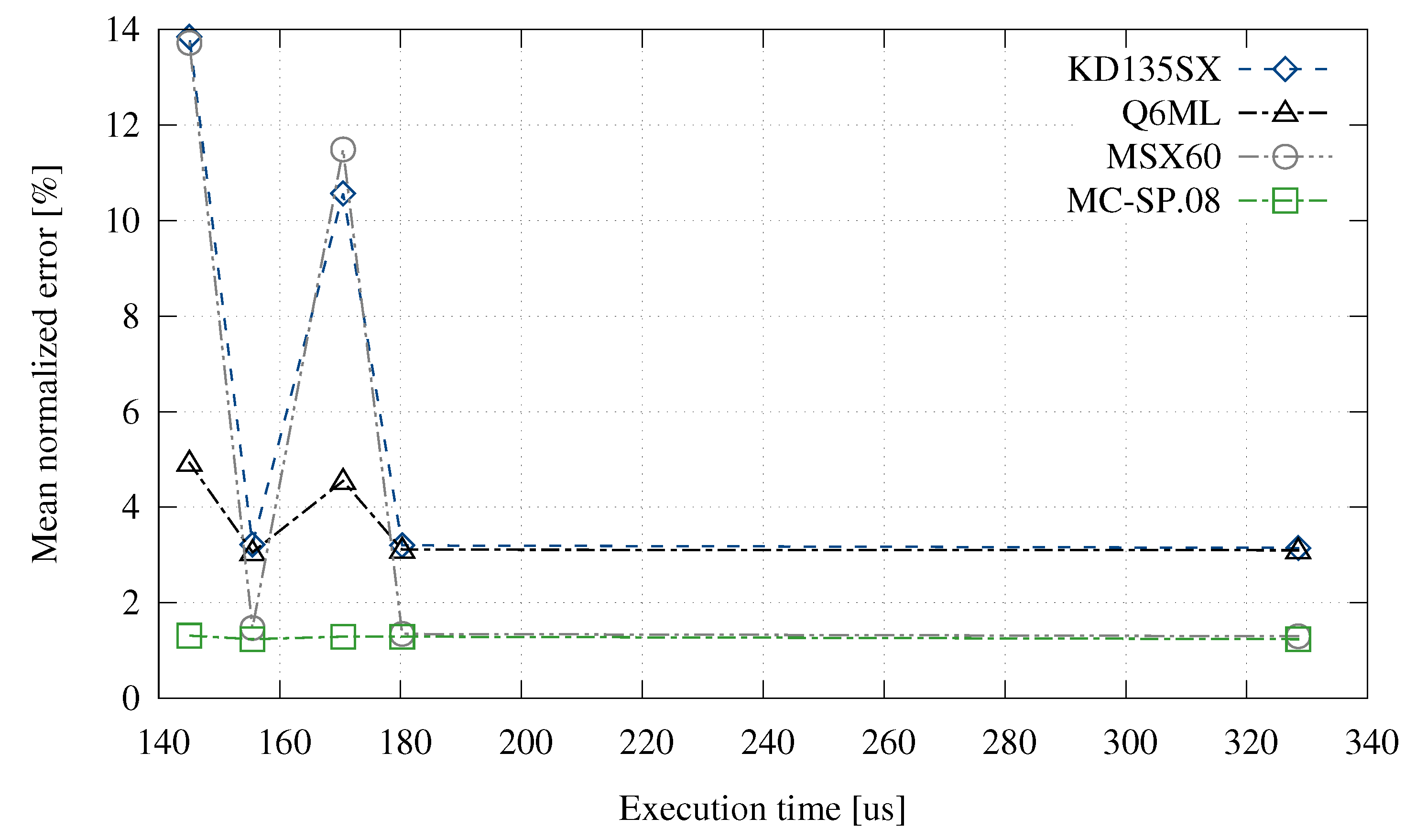
| Parameter | MC-SP.08 | MSX60 | Q6ML | KD135SX |
|---|---|---|---|---|
| (A) | 0.23 | 3.8 | 7.61 | 8.37 |
| (V) | 4.83 | 21.1 | 0.611 | 22.1 |
| (A) | 0.21 | 3.5 | 7.11 | 7.63 |
| (V) | 3.85 | 17.1 | 0.51 | 17.7 |
| = (A) | 1.8 × 10−6 | 4.5 × 10−10 | 3.4 × 10−10 | 3.4 × 10−10 |
| (A) | 0.23 | 3.81 | 7.61 | 8.4 |
| 1.0 | 1.0 | 1.0 | 1.0 | |
| 3.5 | 1.5 | 2.5 | 4.5 | |
| (Ω) | 3320 | 166 | 13 | 56 |
| (Ω) | 0.02 | 0.37 | 0.05 | 0.22 |
| Model | MC-SP.08 | MSX60 | Q6ML | KD135SX | Execution Time (μs) |
|---|---|---|---|---|---|
| MNE (%) | |||||
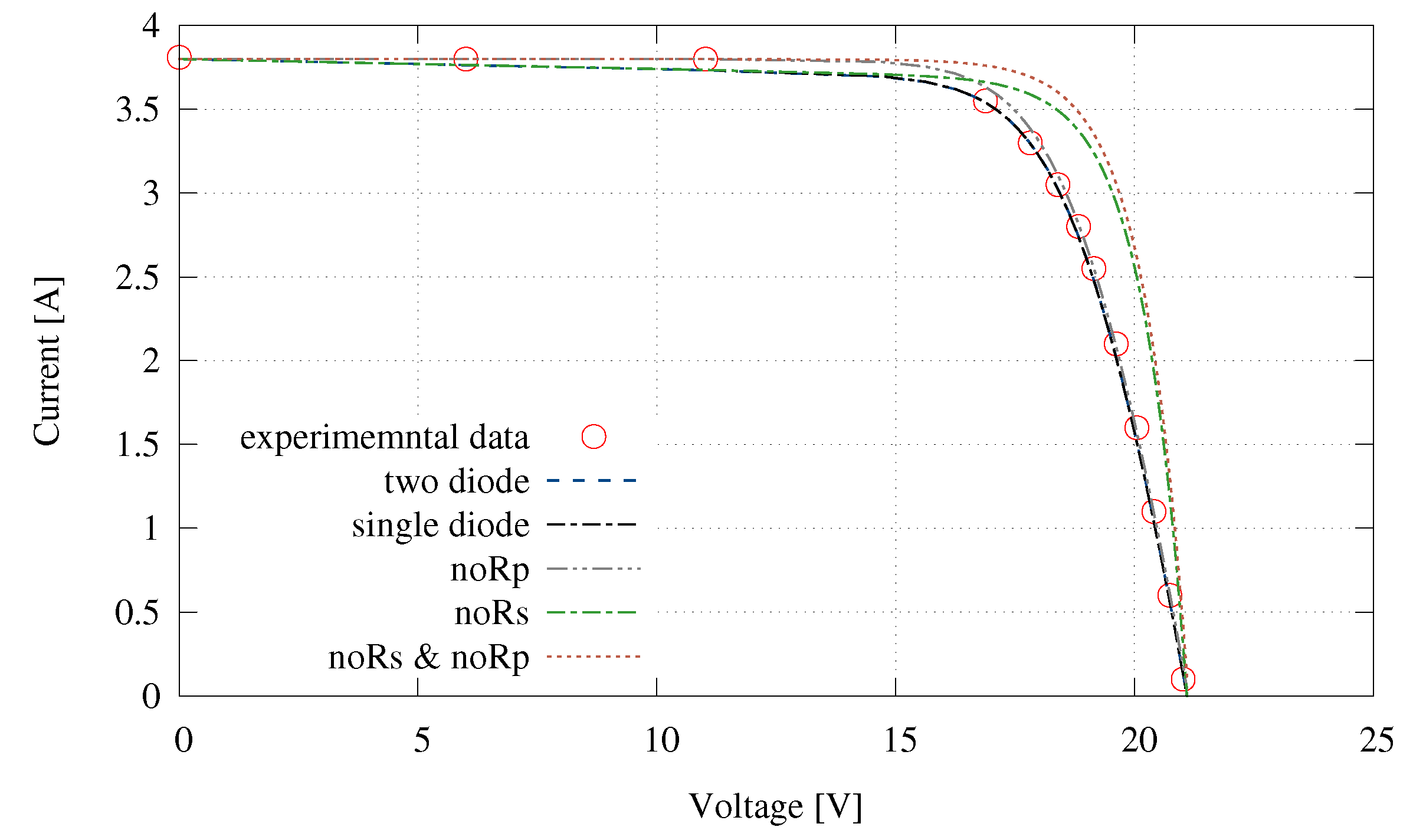
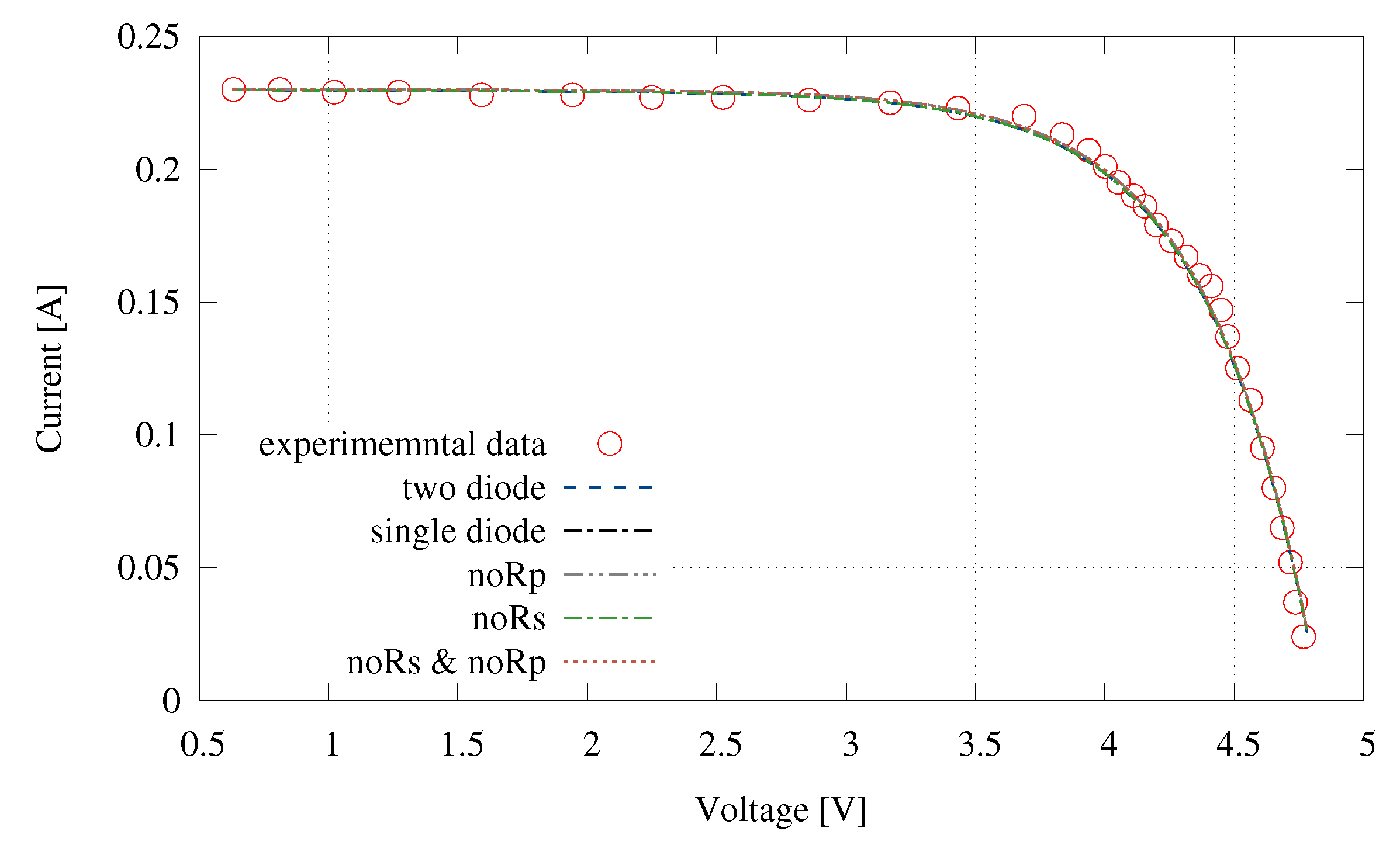
| Complete | 1.24 | 1.30 | 3.10 | 3.15 | 328.5 |
| Single diode | 1.29 | 1.35 | 3.10 | 3.15 | 180.3 |
| No | 1.25 | 1.47 | 3.11 | 3.65 | 155.5 |
| No | 1.29 | 11.49 | 4.55 | 10.57 | 170.5 |
| No & No | 1.30 | 13.72 | 4.93 | 13.85 | 145.1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lattanzi, E.; Dromedari, M.; Freschi, V.; Bogliolo, A. Tuning the Complexity of Photovoltaic Array Models to Meet Real-time Constraints of Embedded Energy Emulators. Energies 2017, 10, 278. https://doi.org/10.3390/en10030278
Lattanzi E, Dromedari M, Freschi V, Bogliolo A. Tuning the Complexity of Photovoltaic Array Models to Meet Real-time Constraints of Embedded Energy Emulators. Energies. 2017; 10(3):278. https://doi.org/10.3390/en10030278
Chicago/Turabian StyleLattanzi, Emanuele, Matteo Dromedari, Valerio Freschi, and Alessandro Bogliolo. 2017. "Tuning the Complexity of Photovoltaic Array Models to Meet Real-time Constraints of Embedded Energy Emulators" Energies 10, no. 3: 278. https://doi.org/10.3390/en10030278
APA StyleLattanzi, E., Dromedari, M., Freschi, V., & Bogliolo, A. (2017). Tuning the Complexity of Photovoltaic Array Models to Meet Real-time Constraints of Embedded Energy Emulators. Energies, 10(3), 278. https://doi.org/10.3390/en10030278








