A Parameter Selection Method for Wind Turbine Health Management through SCADA Data
Abstract
:1. Introduction
2. Methodology
2.1. Mathematical Definition of Copulas
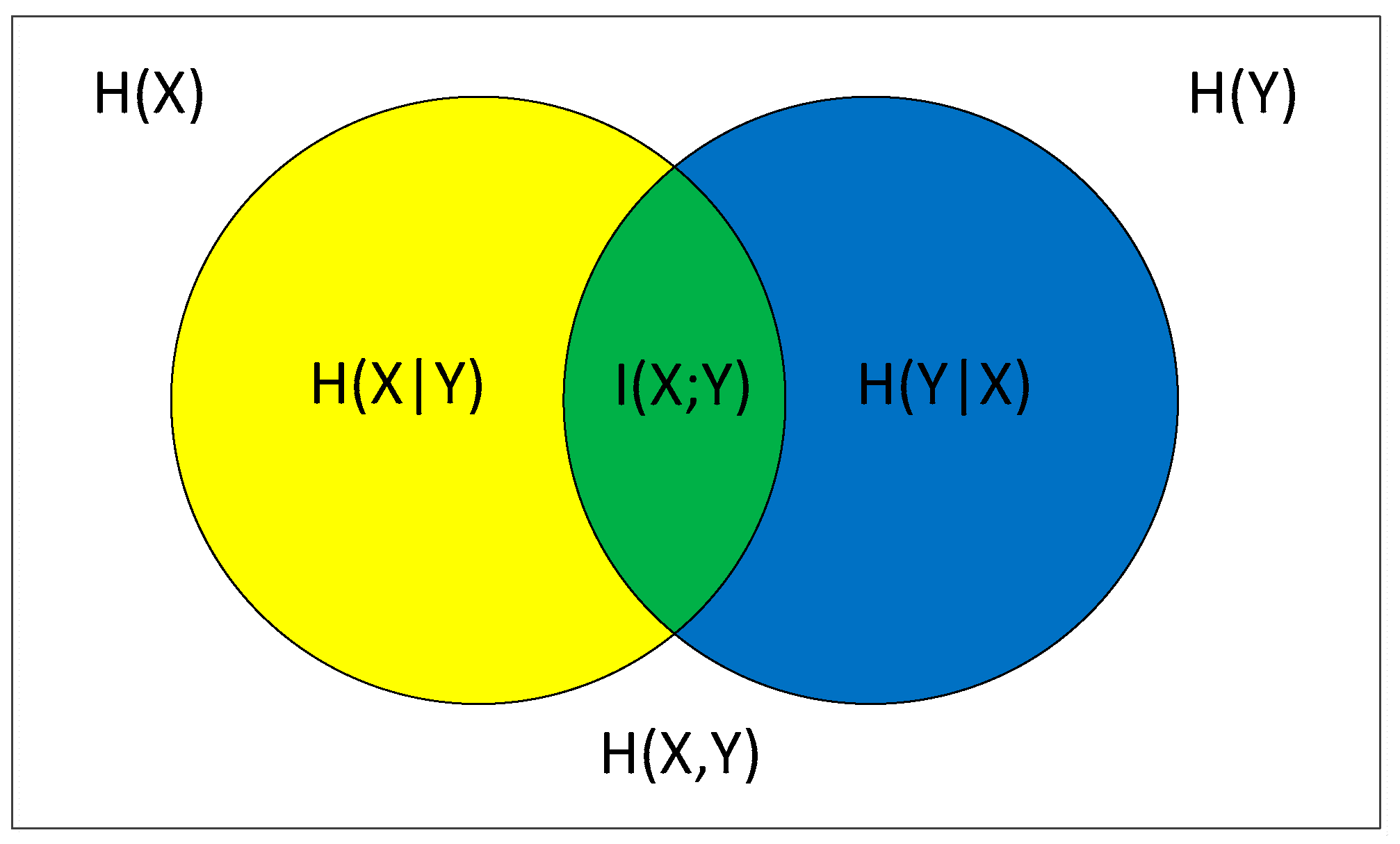
2.2. Mutual Information (MI) and Entropy
2.3. Estimate Mutual Information through Copula
2.4. Empirical Copula-Based Mutual Information Estimation (ECMI)
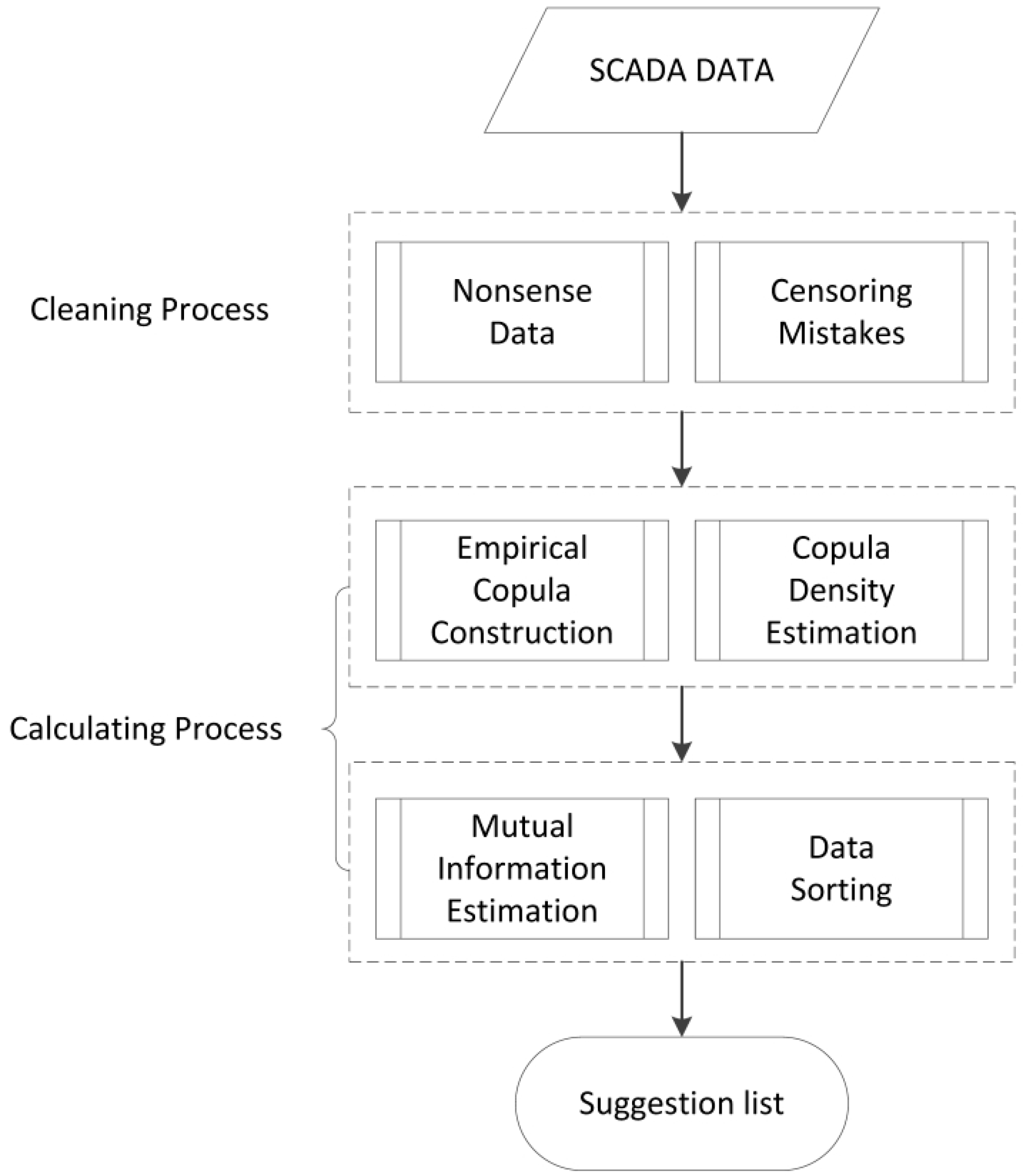
3. Application: Feature Extraction from Wind Turbine SCADA Data
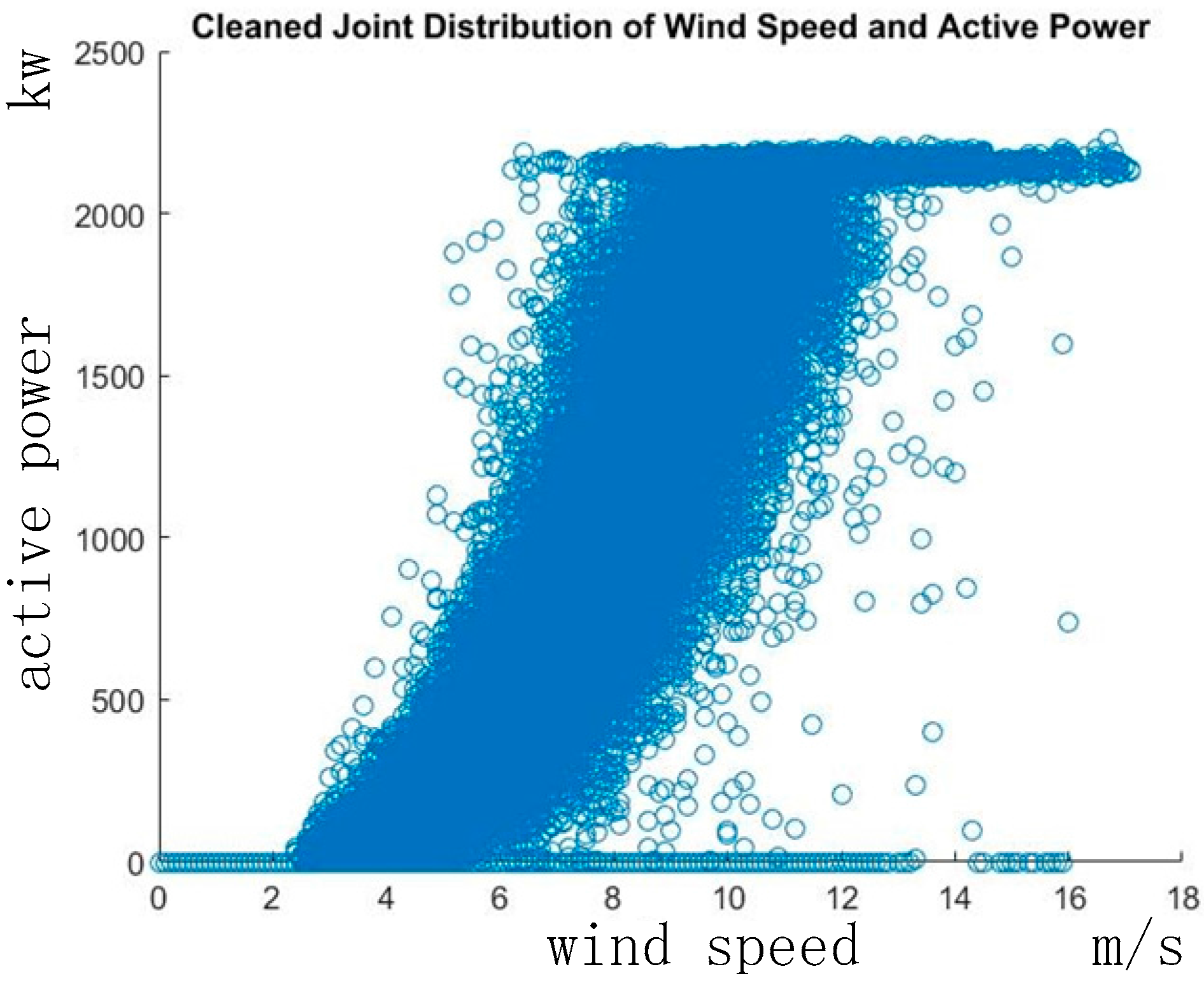
3.1. Scenario Description
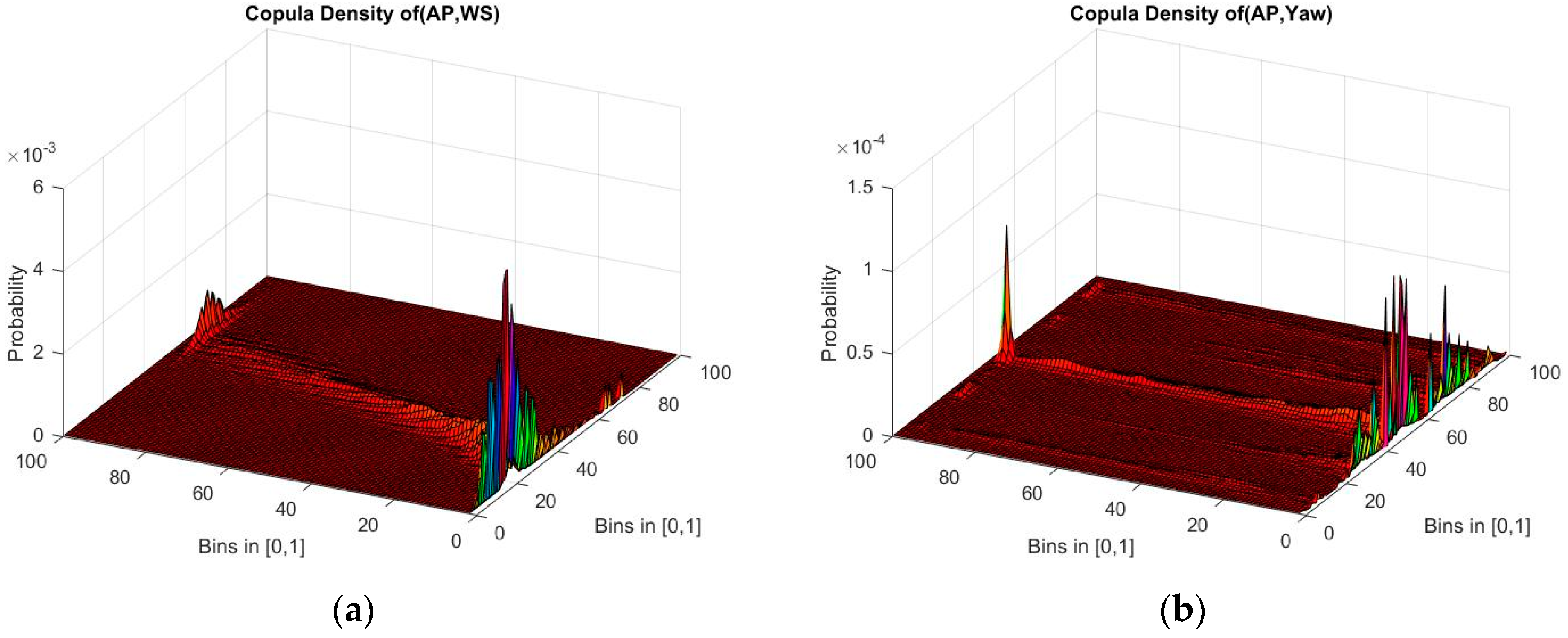
3.2. Results Based on ECMI
3.3. Comparison Study: The Advantages of Mutual Information Based Parameter Selection
- Select 10 parameters which rank higher in the three rank lists.
- Whenever there are several parameters regarding to the same sub component, choose the one which ranks higher.
4. Conclusions
Author Contributions
Conflicts of Interest
References
- European Wind Energy Association. Wind in Power 2015 European Statistics; European Wind Energy Association: Brussels, Belgium, 2016. [Google Scholar]
- Milborrow, D. Operation and maintenance costs compared and revealed. Windstats Newslett. 2006, 19, 1–3. [Google Scholar]
- Yan, Y. Nacelle orientation based health indicator for wind turbines. In Proceedings of the 2015 IEEE Conference on Prognostics and Health Management (PHM), Austin, TX, USA, 22–25 June 2015; pp. 1–7.
- Long, H.; Wang, L.; Zhang, Z.; Song, Z.; Xu, J. Data-Driven Wind Turbine Power Generation Performance Monitoring. IEEE Trans. Ind. Electron. 2015, 62, 6627–6635. [Google Scholar] [CrossRef]
- Sun, P.; Li, J.; Wang, C.; Lei, X. A generalized model for wind turbine anomaly identification based on SCADA data. Appl. Energy 2016, 168, 550–567. [Google Scholar] [CrossRef]
- Lapira, E.; Brisset, D.; Ardakani, H.D.; Siegel, D.; Lee, J. Wind turbine performance assessment using multi-regime modeling approach. Renew. Energy 2012, 45, 86–95. [Google Scholar] [CrossRef]
- Hung, L.P.; Alfred, R.; Hijazi, A.; Hanafi, M. A Review on Feature Selection Methods for Sentiment Analysis. Adv. Sci. Lett. 2015, 21, 2952–2965. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to feature extraction. In Feature Extraction; Springer: Berlin, Germany, 2006; pp. 1–25. [Google Scholar]
- Nevatia, R.; Babu, K.R. Linear feature extraction and description. Comput. Graph. Image Process. 1980, 13, 257–269. [Google Scholar] [CrossRef]
- Hong, Z.-Q. Algebraic feature extraction of image for recognition. Pattern Recognit. 1991, 24, 211–219. [Google Scholar] [CrossRef]
- Li, H.; Jiang, T.; Zhang, K. Efficient and robust feature extraction by maximum margin criterion. IEEE Trans. Neural Netw. 2006, 17, 157–165. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Wen, C.; Li, G.; Chua, C.S. Locality sensitive batch feature extraction for high-dimensional data. Neurocomputing 2016, 171, 664–672. [Google Scholar] [CrossRef]
- Ravishankar, S.; Jain, A.; Mittal, A. Automated feature extraction for early detection of diabetic retinopathy in fundus images. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–26 June 2009; pp. 210–217.
- Pamula, V.R.; Verhelst, M.; van Hoof, C.; Yazicioglu, R.F. A novel feature extraction algorithm for on the sensor node processing of compressive sampled photoplethysmography signals. In Proceedings of the 2015 IEEE Sensors, Busan, Korea, 1–4 November 2015.
- Qian, D.; Wang, B.; Qing, Y.; Zhang, T.; Zhang, Y.; Wang, X.; Nakamura, M. Bayesian Nonnegative CP Decomposition-based Feature Extraction Algorithm for Drowsiness Detection. IEEE Trans. Neural Syst. Rehabil. Eng. 2016. [Google Scholar] [CrossRef] [PubMed]
- Medel, J.; Savakis, A.; Ghoraani, B. A novel time-frequency feature extraction algorithm based on dictionary learning. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016.
- Gopinath, R.; Kumar, C.S.; Vishnuprasad, K.; Ramachandran, K. Feature mapping techniques for improving the performance of fault diagnosis of synchronous generator. Int. J. Progn. Health Manag. 2015, 6, 12. [Google Scholar]
- Wu, F.; Lee, J. Information Reconstruction Method for Improved Clustering and Diagnosis of Generic Gearbox Signals. Int. J. Progn. Health Manag. 2011, 2, 42. [Google Scholar]
- Steuer, R.; Kurths, J.; Daub, C.O.; Weise, J.; Selbig, J. The mutual information: Detecting and evaluating dependencies between variables. Bioinformatics 2002, 18, S231–S240. [Google Scholar] [CrossRef] [PubMed]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin, Germany, 2009; pp. 1–4. [Google Scholar]
- Hardoon, D.R.; Szedmak, S.; Shawe-Taylor, J. Canonical correlation analysis: An overview with application to learning methods. Neural Comput. 2004, 16, 2639–2664. [Google Scholar] [CrossRef] [PubMed]
- Gábor, J.S.; Rizzo, M.L. Brownian distance covariance. Ann. Appl. Stat. 2009, 3, 1236–1265. [Google Scholar]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [PubMed]
- Kinney, J.B.; Atwal, G.S. Equitability, mutual information, and the maximal information coefficient. Proc. Natl. Acad. Sci. USA 2014, 111, 3354–3359. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Durrani, T. Estimation of mutual information using copula density function. Electron. Lett. 2011, 47, 493–494. [Google Scholar] [CrossRef]
- Póczos, B.; Ghahramani, Z.; Schneider, J.G. Copula-based Kernel Dependency Measures. Available online: https://arxiv.org/abs/1206.4682 (accessed on 12 February 2017).
- Sklar, A. Fonctions de Répartition à n Dimensions et Leurs Marges; Université Paris: Paris, Fracne, 1959; Volume 8, pp. 229–231. [Google Scholar]
- Nelson, R.B. An Introduction to Copulas; Springer: Portland, ME, USA, 2006; pp. 7–42. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Carter, T. An Introduction to Information Theory and Entropy; Complex Systems Summer School: Santa Fe, NM, USA, 2007. [Google Scholar]
- Gray, R.M. Entropy and Information. In Entropy and Information Theory; Springer: New York, NY, USA, 2013; pp. 36–37. [Google Scholar]
- Hominal, P.; Deheuvels, P. Estimation non paramétrique de la densité compte-tenu d’informations sur le support. Rev. Stat. Appl. 1979, 27, 47–68. [Google Scholar]
- Charpentier, A.; Fermanian, J.-D.; Scaillet, O. The estimation of copulas: Theory and practice. In Copulas: From Theory to Applications in Finance; Risk Books: London, UK, 2007; pp. 35–62. [Google Scholar]
- Nagler, T.; Czado, C. Evading the curse of dimensionality in multivariate kernel density estimation with simplified vines. J. Multivar. Anal. 2016, 151, 69–89. [Google Scholar] [CrossRef]
- De Vieira, R.; Sanz-Bobi, M. Failure Risk Indicators for a Maintenance Model Based on Observable Life of Industrial Components with an Application to Wind Turbines. IEEE Trans. Reliab. 2013, 62, 569–582. [Google Scholar] [CrossRef]
- Castellani, F.; Astolfi, D.; Sdringola, P.; Proietti, S.; Terzi, L. Analyzing wind turbine directional behavior: SCADA data mining techniques for efficiency and power assessment. Appl. Energy 2017, 185, 1076–1086. [Google Scholar] [CrossRef]

| Rank | Parameter |
|---|---|
| 1. | Generator_Speed |
| 2. | Rotor_Speed |
| 3. | Yaw |
| 4. | Wind_Speed |
| 5. | Pitch_L2 |
| 6. | Pitch_L1 |
| 7. | Pitch_L3 |
| 8. | Generator_Torque |
| 9. | Generator_U1T |
| 10. | Generator_W2T |
| 11. | Generator_V1T |
| 12. | Generator_V2T |
| 13. | Generator_U2T |
| 14. | Generator_W1T |
| 15. | Converter_GridT |
| 16. | Generator_BearingT2 |
| 17. | Generator_Fan2T |
| 18. | Gearbox_BearingT1 |
| 19. | Gearbox_BearingT2 |
| 20. | Gearbox_OilT |
| 21. | Converter_Temperature |
| 22. | Generator_Fan1T |
| 23. | Generator_BearingT1 |
| 24. | Gearbox_EntranceT |
| 25. | Gearbox_BearingT |
| 26. | Nacelle_Temperature |
| 27. | Pitch_1V |
| 28. | Pitch_2V |
| 29. | Pitch_3V |
| 30. | Ambient_Temperature |
| 31. | Converter_LV |
| 32. | Converter_LC |
| 33. | Wind Turbine_State |
| 34. | Gearbox_Oilpressure |
| 35. | Wind_Direction |
| Rank | PCCA | KCCA |
|---|---|---|
| 1. | Converter_L Current | Generator_Torque |
| 2. | Generator_Torque | Converter_L Current |
| 3. | Wind_Speed | Generator_Speed |
| 4. | Generator_U1T | Rotor_Speed |
| 5. | Generator_W2T | Wind_Speed |
| 6. | Generator_V2T | Gearbox_BearingT1 |
| 7. | Generator_U2T | Gearbox_BearingT2 |
| 8. | Generator_V1T | Generator_U1T |
| 9. | Generator_W1T | Generator_W2T |
| 10. | Gearbox_BearingT1 | Generator_U2T |
| 11. | Gearbox_BearingT2 | Generator_V2T |
| 12. | Generator_Speed | Generator_V1T |
| 13. | Rotor_Speed | Generator_W1T |
| 14. | Converter_Temperature | Pitch_L3 |
| 15. | Gearbox_OilT | Pitch_L2 |
| 16. | Generator_Fan2T | Pitch_L1 |
| 17. | Generator_BearingT2 | Gearbox_OilT |
| 18. | Gearbox_EntranceT | Gearbox_Oilpressure |
| 19. | Gearbox_BearingT | Generator_Fan2T |
| 20. | Generator_BearingT1 | Converter_Temperature |
| 21. | Gearbox_Oilpressure | Wind Turbine_State |
| 22. | Pitch_3V | Generator_BearingT2 |
| 23. | Pitch_2V | Gearbox_EntranceT |
| 24. | Pitch_1V | Gearbox_BearingT |
| 25. | Converter_GridT | Generator_BearingT1 |
| 26. | Converter_LV | Generator_Fan1T |
| 27. | Generator_Fan1T | Converter_LV |
| 28. | Wind_Direction | Pitch_3V |
| 29. | Nacelle_Temperature | Pitch_2V |
| 30. | Yaw | Pitch_1V |
| 31. | Ambient_Temperature | Converter_GridT |
| 32. | Wind Turbine_State | Wind_Direction |
| 33. | Pitch_L2 | Yaw |
| 34. | Pitch_L1 | Nacelle_Temperature |
| 35. | Pitch_L3 | Ambient_Temp. |
| No. | PCCA | KCCA | ECMI |
|---|---|---|---|
| 1. | Converter_L Current | Generator_Torque | Generator_Speed |
| 2. | Generator_Torque | Converter_L Current | Rotor_Speed |
| 3. | Wind_Speed | Generator_Speed | Yaw |
| 4. | Generator_U1T | Wind_Speed | Wind_Speed |
| 5. | Gearbox_Bearing T1 | Gearbox_Bearing T1 | Pitch_L2 |
| 6. | Generator_Speed | Generator_U1T | Generator_Torque |
| 7. | Rotor_Speed | Pitch_L3 | Generator_U1T |
| 8. | ConverterTemperature | Gearbox_OilT | GeneratorBearingT2 |
| 9. | Gearbox_OilT | Gearbox_Oilpressure | Generator_Fan2T |
| 10. | Generator_Fan2T | Generator_Fan2T | Gearbox_Bearing T2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, M.; Yi, J.; Mazidi, P.; Cheng, L.; Guo, J. A Parameter Selection Method for Wind Turbine Health Management through SCADA Data. Energies 2017, 10, 253. https://doi.org/10.3390/en10020253
Du M, Yi J, Mazidi P, Cheng L, Guo J. A Parameter Selection Method for Wind Turbine Health Management through SCADA Data. Energies. 2017; 10(2):253. https://doi.org/10.3390/en10020253
Chicago/Turabian StyleDu, Mian, Jun Yi, Peyman Mazidi, Lin Cheng, and Jianbo Guo. 2017. "A Parameter Selection Method for Wind Turbine Health Management through SCADA Data" Energies 10, no. 2: 253. https://doi.org/10.3390/en10020253
APA StyleDu, M., Yi, J., Mazidi, P., Cheng, L., & Guo, J. (2017). A Parameter Selection Method for Wind Turbine Health Management through SCADA Data. Energies, 10(2), 253. https://doi.org/10.3390/en10020253






