Stochastic Optimal Control of Parallel Hybrid Electric Vehicles
Abstract
:1. Introduction
2. Problem Formulation
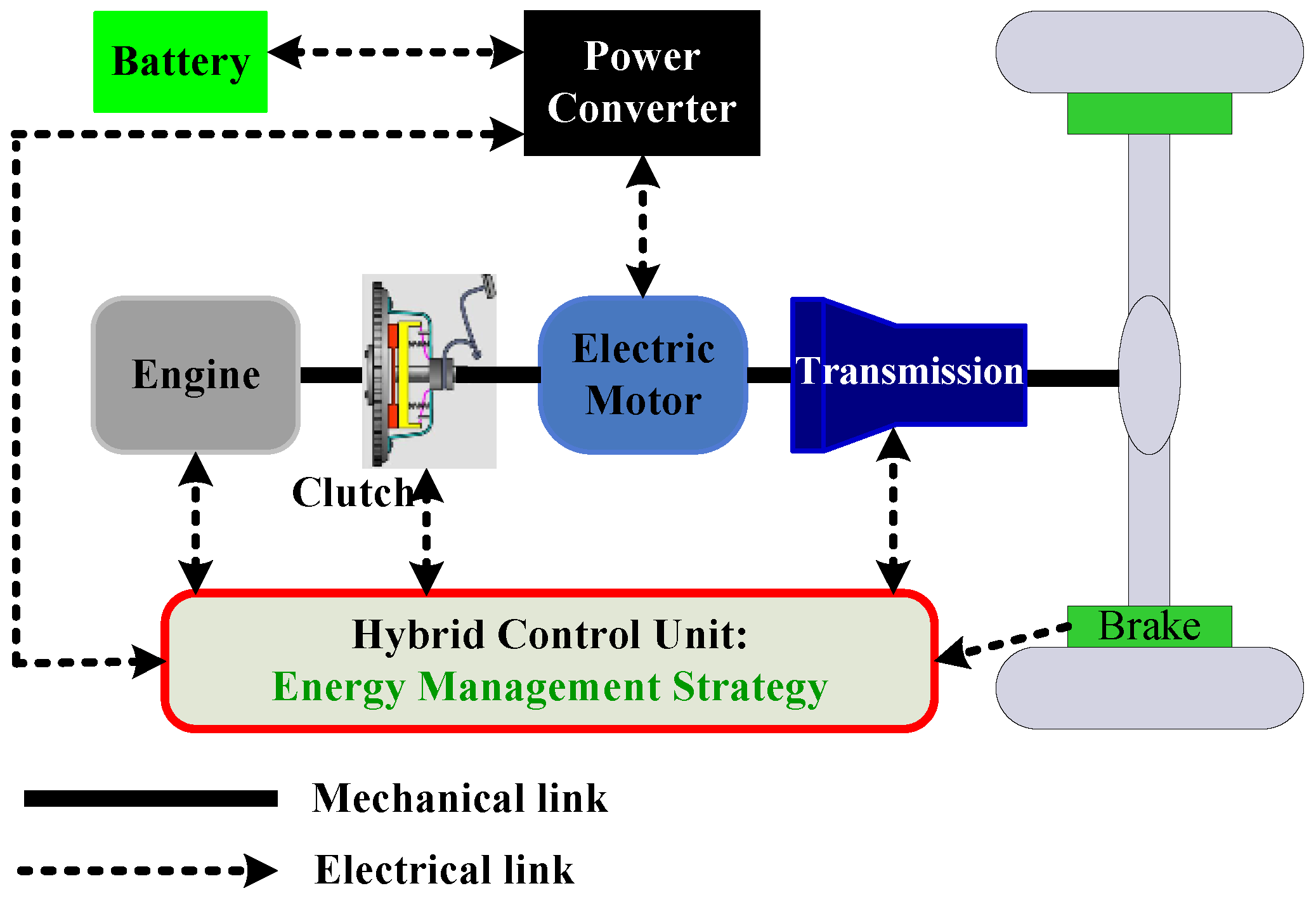
2.1. Parallel HEV System Configuration
2.2. System Equations
2.3. Optimal Control Problem Formulation
3. Problem Implementation
3.1. Dynamic Programming (DP) Method
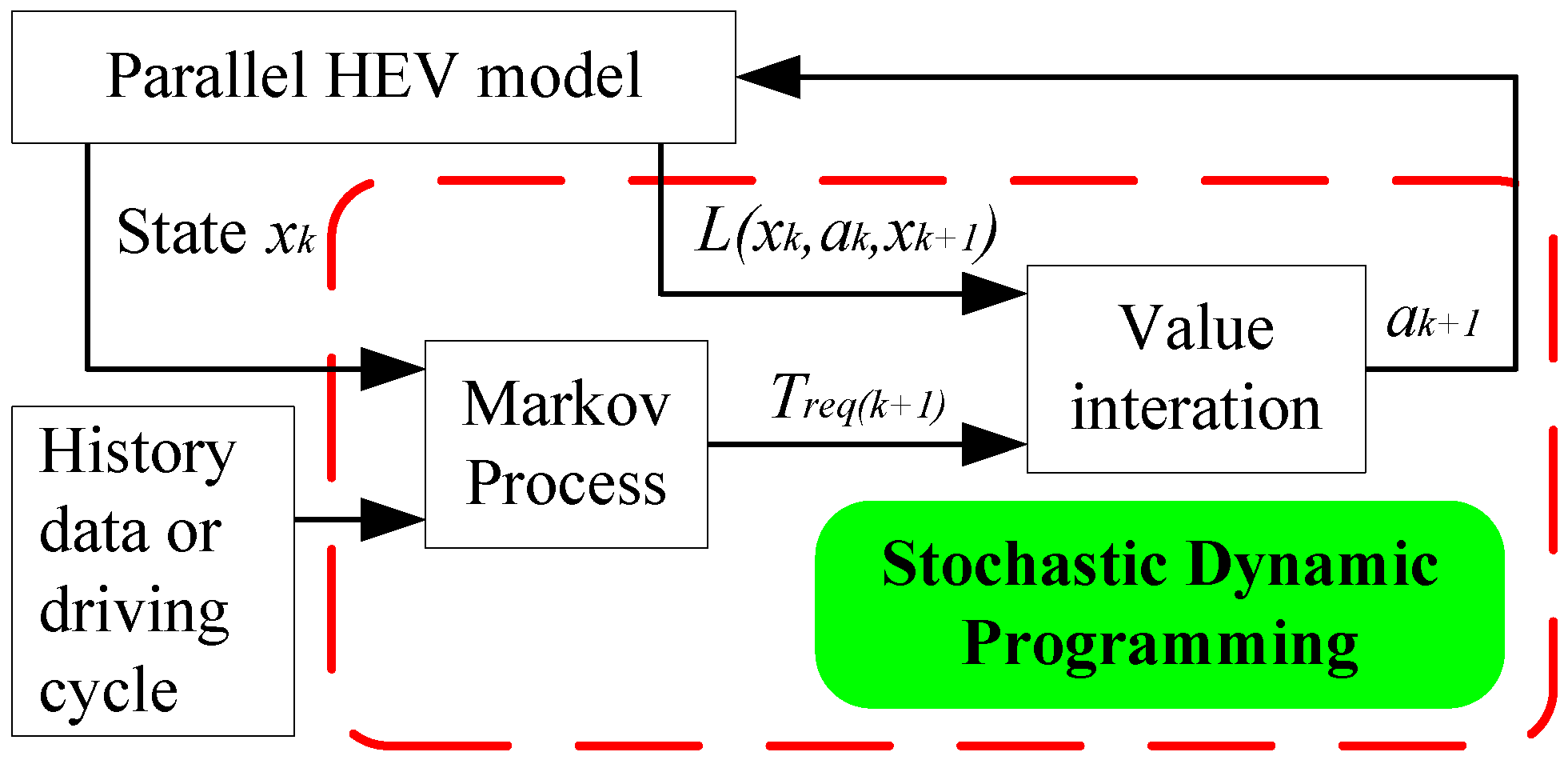
3.2. EMS Based on Stochastic Dynamic Programming (SDP) Approach
3.2.1. SDP Method Description
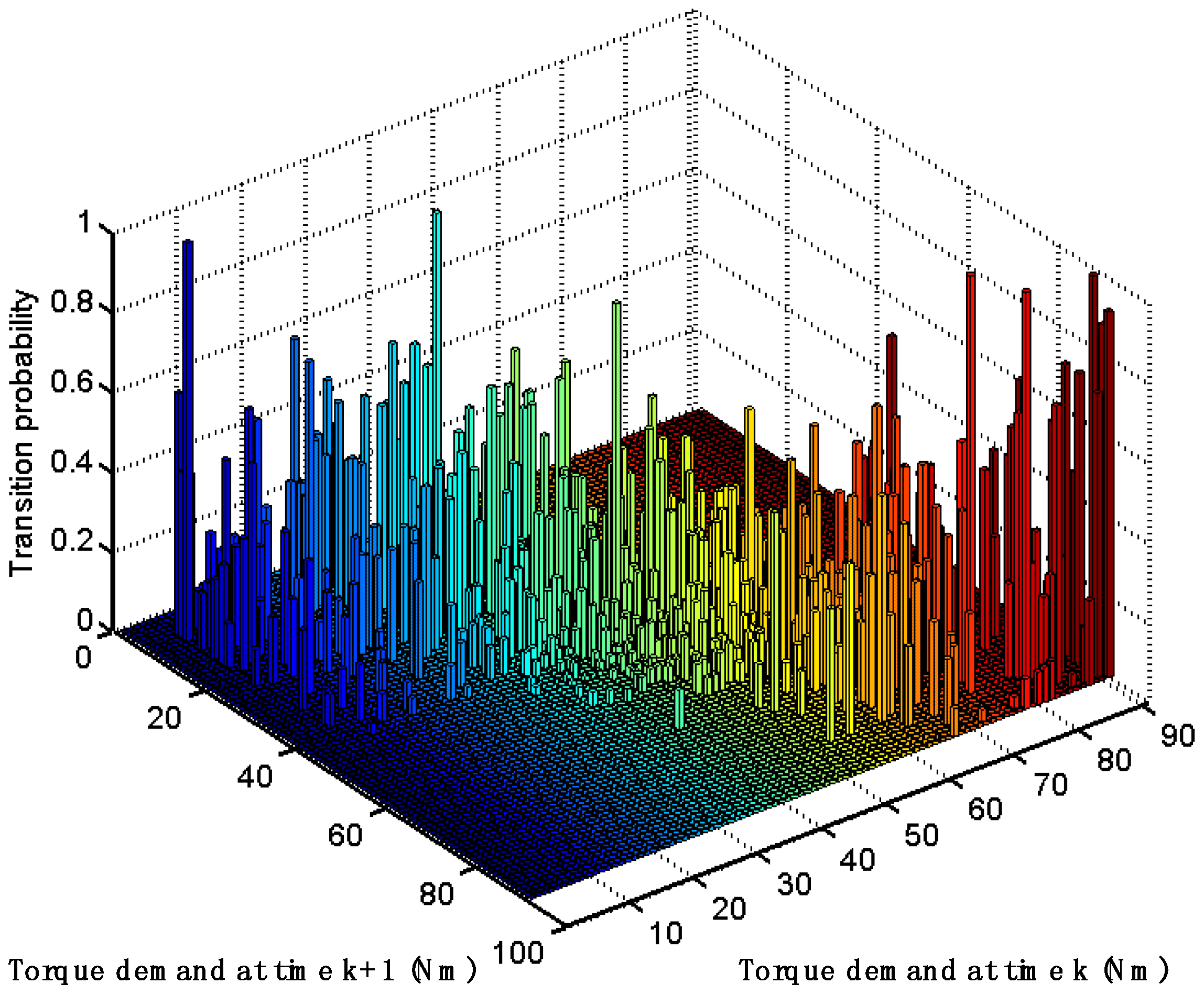
3.2.2. Stochastic Modeling of the Driver Torque Demand
3.2.3. Implementation of the EMS Based on the SDP Approach
4. Performance Evaluation
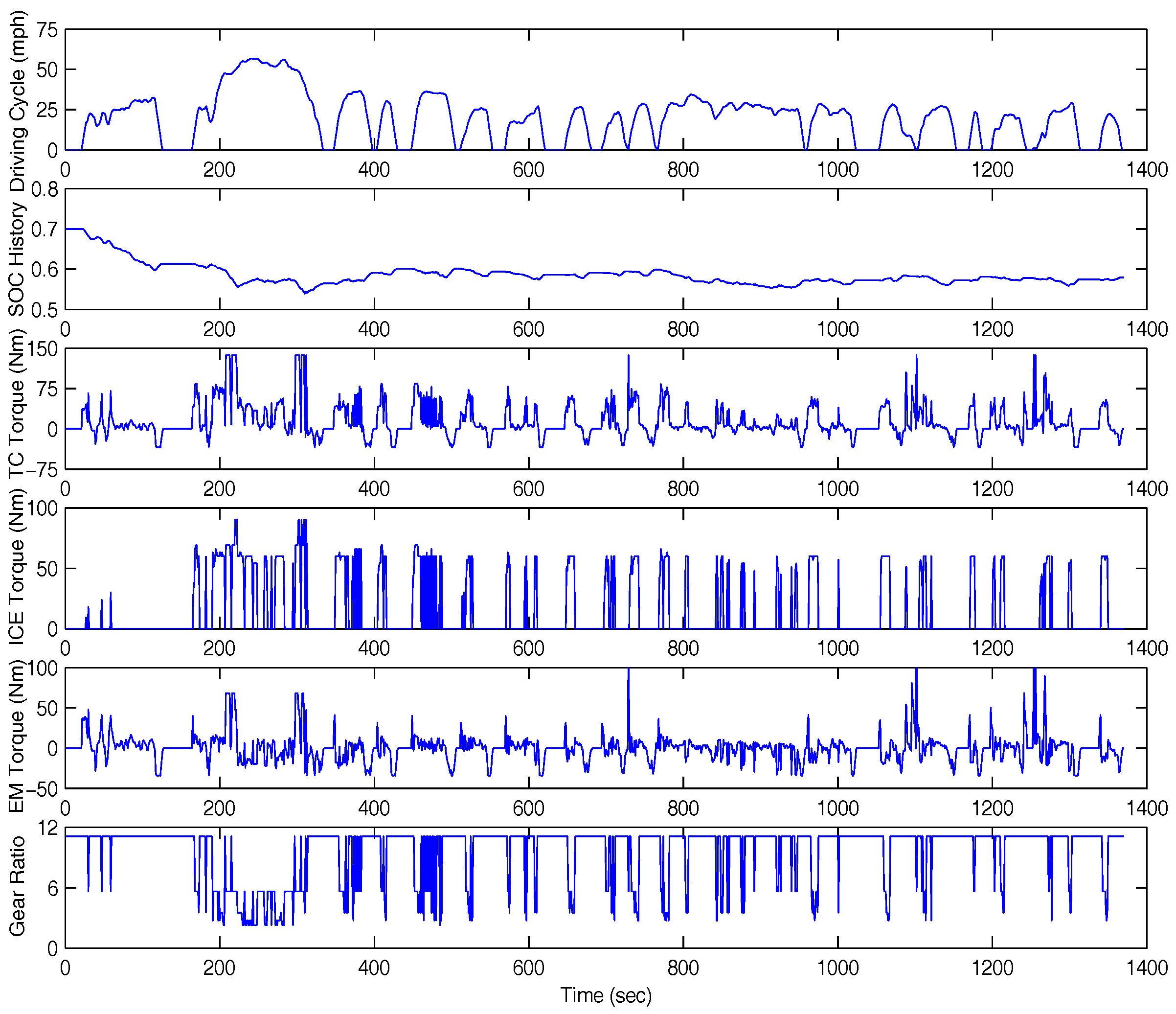
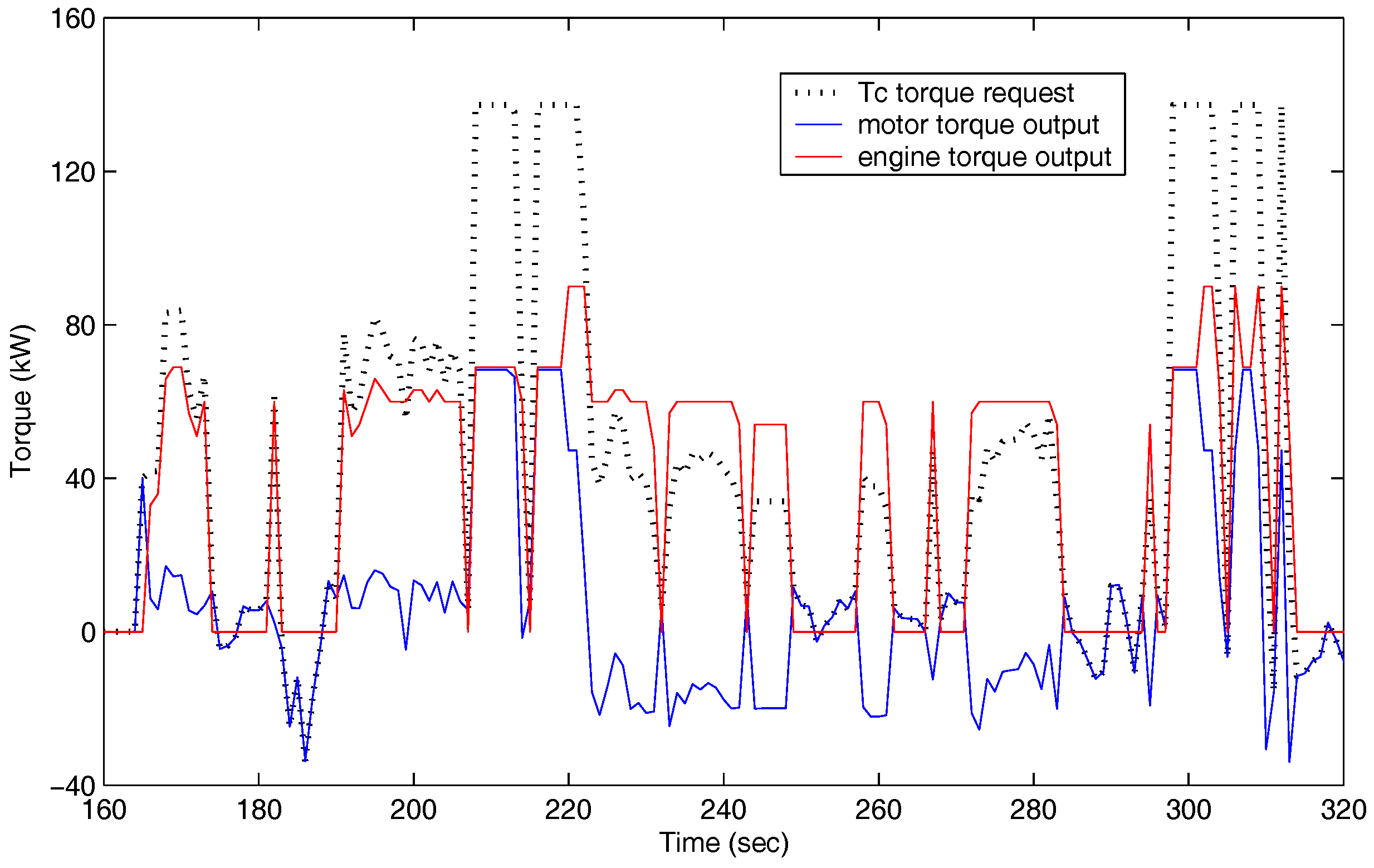
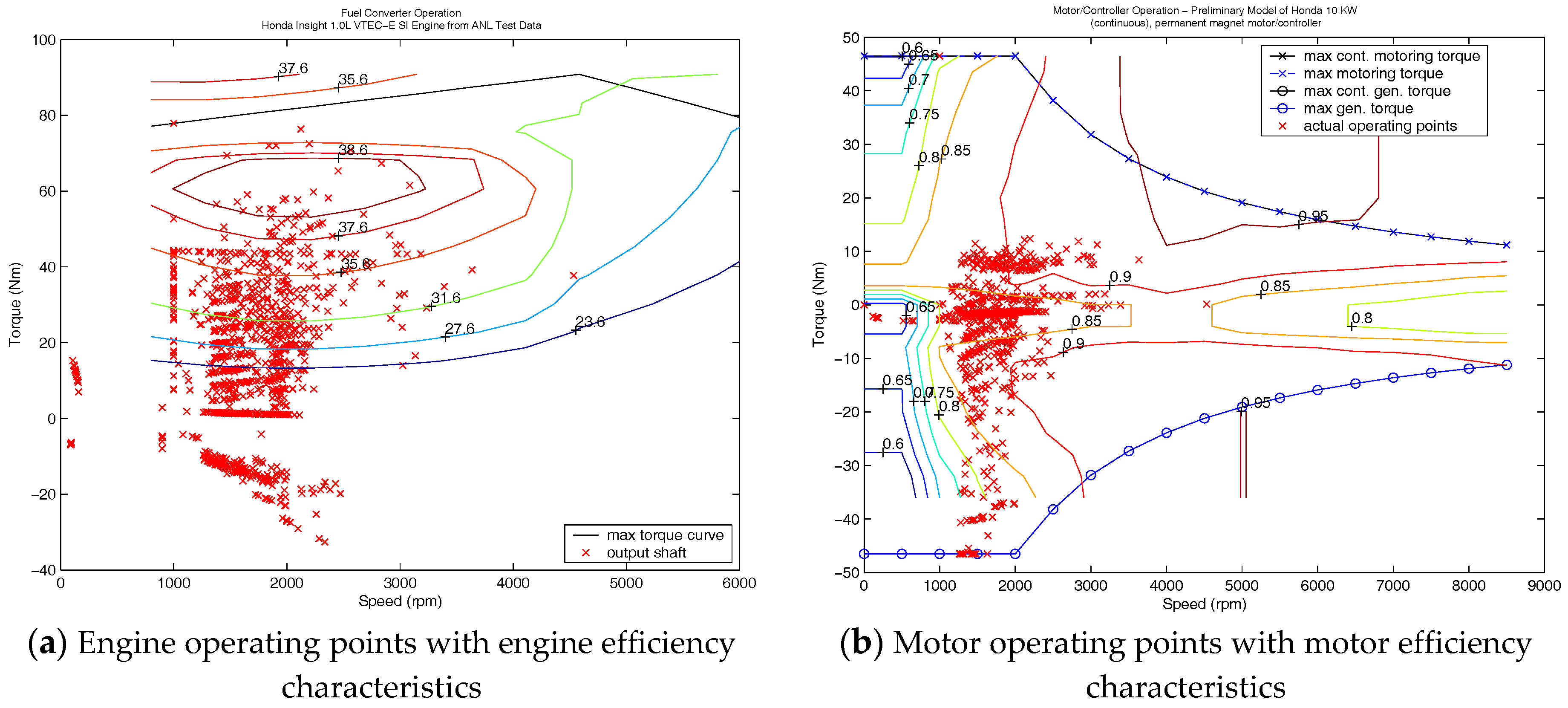
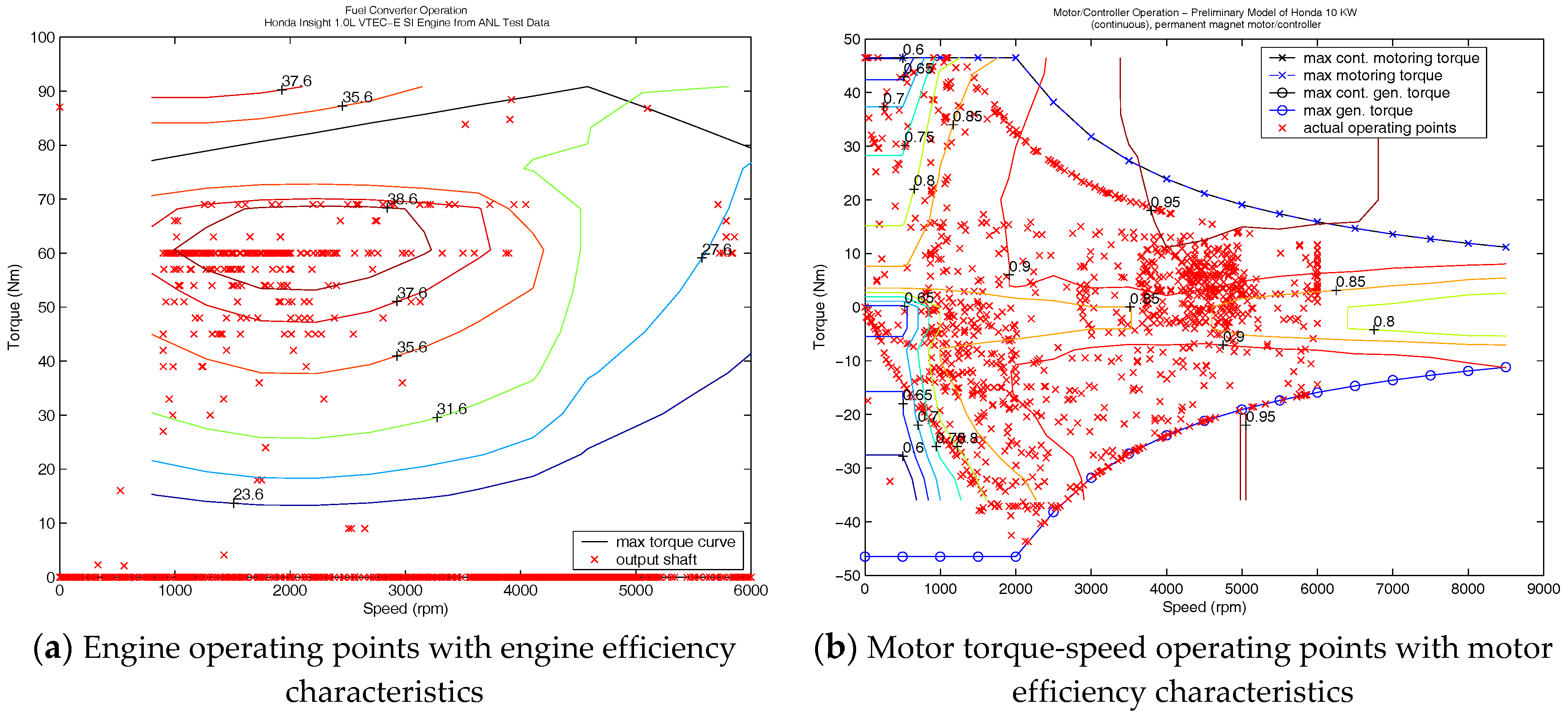
4.1. Simulation Results under the Urban Dynamometer Driving Schedule (UDDS)
4.2. Comparisons of Simulation Results under Different Driving Cycles
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Andreas, A.M. Supervisory power management control algorithms for hybrid electric vehicles: A survey. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1869–1885. [Google Scholar]
- Zhang, P.; Yan, F.W.; Du, C.Q. A comprehensive analysis of energy management strategies for hybrid electric vehicles based on bibliometrics. Renew. Sustain. Energy Rev. 2015, 48, 88–104. [Google Scholar] [CrossRef]
- Jalil, N.; Kheir, A.N.; Salman, M. A rule-based energy management strategy for a series hybrid vehicle. In Proceedings of the 1997 American Control Conference, Albuqueque, NM, USA, 4–6 June 1997; IEEE: New York, NY, USA, 1997; pp. 689–693. [Google Scholar]
- Fernandes Trovão, J.P.; Gameiro Pereirinha, P.J. Control scheme for hybridized electric vehicles with an online power follower management strategy. IET Electr. Syst. Transp. 2015, 5, 12–23. [Google Scholar] [CrossRef]
- Park, J.; Oh, J.; Park, Y.; Lee, K. Optimal power distribution strategy for series-parallel hybrid electric vehicles. In Proceedings of the 1st International Forum on Strategic Technology, Ulsan, Korea, 18–20 October 2006; IEEE: New York, NY, USA, 2007; pp. 37–42. [Google Scholar]
- Zhou, W.H.; Li, M.; Yin, H.; Ma, C.B. An adaptive fuzzy logic based energy management strategy for electric vehicles. In Proceedings of the IEEE 23rd International Symposium on Industrial Electronics, Istanbul, Turkey, 1–4 June 2014; IEEE: New York, NY, USA, 2016; pp. 1778–1783. [Google Scholar]
- Schouten, N.J.; Salman, M.A.; Kheir, N.A. Fuzzy Logic Control for Parallel Hybrid Vehicles. IEEE Trans. Control Syst. Technol. 2002, 10, 460–468. [Google Scholar] [CrossRef]
- Hu, Y.; Li, W.M.; Hui Xu, H.; Xu, G.Q. An online learning control strategy for hybrid electric vehicle based on fuzzy Q-learning. Energies 2015, 8, 11167–11186. [Google Scholar] [CrossRef]
- Won, J.S.; Langari, R. Intelligent energy management agent for a parallel hybrid vehicle-Part II: Torque distribution, charge sustenance strategies, and performance results. IEEE Trans. Veh. Technol. 2005, 54, 935–953. [Google Scholar] [CrossRef]
- Odeim, F.; Roes, J.; Wülbeck, L.; Heinzel, A. Power management optimization of fuel cell/battery hybrid vehicles with experimental validation. J. Power Sources 2014, 252, 333–343. [Google Scholar] [CrossRef]
- Hung, Y.H.; Tung, Y.M.; Chang, C.H. Optimal control of integrated energy management/mode switch timing in a three-power-source hybrid powertrain. Appl. Energy 2016, 173, 184–196. [Google Scholar] [CrossRef]
- Cui, N.X.; Lian, F.X.; Wu, J.; Wang, X.X. Optimization of HEV energy management strategy based on driving cycle modeling. In Proceedings of the 34th Chinese Control Conference, Hangzhou, China, 28–30 July 2015; IEEE: New York, NY, USA, 2015; pp. 7983–7987. [Google Scholar]
- Zou, Y.; Liu, T.; Liu, D.X.; Sun, F.C. Reinforcement learning-based real-time energy management for a hybrid tracked vehicle. Appl. Energy 2016, 171, 372–382. [Google Scholar] [CrossRef]
- Qi, Y.L.; Wang, W.D.; Xiang, C.L. Neural network and efficiency-based control for dual-mode hybrid electric vehicles. In Proceedings of the 34th Chinese Control Conference, Hangzhou, China, 28–30 July 2015; IEEE: New York, NY, USA, 2015; pp. 8103–8108. [Google Scholar]
- Khayyam, H.; Bab-Hadiashar, A. Adaptive intelligent energy management system of plug-in hybrid electric vehicle. Energy 2014, 69, 319–335. [Google Scholar] [CrossRef]
- Kim, N.; Cha, S.; Peng, H. Optimal control of hybrid electric vehicles based on Pontryagin’s Minimum Principle. IEEE Trans. Control Syst. Technol. 2011, 19, 1279–1287. [Google Scholar]
- Ansarey, M.; Panahi, M.S.; Ziarati, H.; Mahjoob, M. Optimal energy management in a dual-storage fuel-cell hybrid vehicle using multi-dimensional dynamic programming. J. Power Sources 2014, 250, 359–371. [Google Scholar] [CrossRef]
- Peng, J.K.; He, H.W.; Xiong, R. Rule based energy management strategy for a series–parallel plug-in hybrid electric bus optimized by dynamic programming. Appl. Energy 2016, 185, 1633–1643. [Google Scholar] [CrossRef]
- Lin, C.C.; Peng, H.; Grizzle, J.W.; Kang, J.M. Power management strategy for a parallel hybrid electric truck. IEEE Trans. Control Syst. Technol. 2003, 11, 839–849. [Google Scholar]
- Opila, D.F.; Wang, X.Y.; McGee, R.; Gillespie, R.B.; Cook, J.A.; Grizzle, J.W. An energy management controller to optimally trade off fuel economy and drivability for hybrid vehicles. IEEE Trans. Control Syst. Technol. 2012, 20, 1490–1505. [Google Scholar] [CrossRef]
- Finesso, R.; Spessa, E.; Venditti, M. Cost-optimized design of a dual-mode diesel parallel hybrid electric vehicle for several driving missions and market scenarios. Appl. Energy 2016, 177, 366–383. [Google Scholar] [CrossRef]
- Stockar, S.; Marano, V.; Canova, M.; Rizzoni, G.; Guzzella, L. Energy-optimal control of plug-in hybrid electric vehicles for real-world driving cycles. IEEE Trans. Veh. Technol. 2011, 60, 2949–2962. [Google Scholar] [CrossRef]
- Zheng, C.H.; Xu, G.Q.; Xu, K.; Pan, Z.M.; Liang, Q. An energy management approach of hybrid vehicles using traffic preview information for energy saving. Energy Convers. Manag. 2015, 105, 462–470. [Google Scholar] [CrossRef]
- Sun, C.; Hu, X.S.; Moura, S.J.; Sun, F.C. Velocity predictors for predictive energy management in hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2015, 23, 1197–1204. [Google Scholar]
- Meyer, R.T.; DeCarlo, R.A.; Jali, N.M.; Ariyur, K.B. Behavioral modeling and optimal control of a vehicle mechanical drive system. In Proceedings of the 2015 American Control Conference, Chicago, IL, USA, 1–3 July 2015; IEEE: New York, NY, USA, 2015; pp. 2266–2271. [Google Scholar]
- Li, L.; You, S.X.; Yang, C.; Yan, B.J.; Song, J.; Chen, Z. Driving-behavior-aware stochastic model predictive control for plug-in hybrid electric buses. Appl. Energy 2016, 162, 868–879. [Google Scholar] [CrossRef]
- Zeng, X.R.; Wang, J.M. A parallel hybrid electric vehicle energy management strategy using stochastic model predictive control with road grade preview. IEEE Trans. Control Syst. Technol. 2015, 23, 2416–2423. [Google Scholar] [CrossRef]
- Negenborn, R.R.; Schutter, B.D.; Wiering, M.A.; Hellendoorn, H. Learning-based model predictive control for Markov decision processes. In Proceedings of the 16th Triennial World Congress, Prague, Czech Republic, 4–8 July 2005; IFAC: New York, NY, USA, 2005; pp. 354–359. [Google Scholar]
- Schori, M.; Boehme, T.J.; Jeinsch, T.; Schultalbers, M. A robust predictive energy management for plug-in hybrid vehicles based on hybrid optimal control theory. In Proceedings of the 2015 American Control Conference, Chicago, IL, USA, 1–3 July 2015; IEEE: New York, NY, USA, 2015; pp. 2278–2284. [Google Scholar]
- Sun, C.; Sun, F.C.; Hu, X.S.; Hedrick, J.K.; Moura, S. Integrating traffic velocity data into predictive energy management of plug-in hybrid electric vehicles. In Proceedings of the 2015 American Control Conference, Chicago, IL, USA, 1–3 July 2015; IEEE: New York, NY, USA, 2015; pp. 2267–2272. [Google Scholar]
- Zeng, X.R.; Wang, J.M. Stochastic optimal control for hybrid electric vehicles running on fixed routes. In Proceedings of the 2015 American Control Conference, Chicago, IL, USA, 1–3 July 2015; IEEE: New York, NY, USA, 2015; pp. 3273–3278. [Google Scholar]
- Lin, C.C.; Peng, H.; Grizzle, J.W. A stochastic control strategy for hybrid electric vehicles. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; IEEE: New York, NY, USA, 2005; pp. 4710–4715. [Google Scholar]
- Fletcher, T.; Thring, R.; Watkinson, M. An energy management strategy to concurrently optimize fuel consumption & PEM fuel cell lifetime in a hybrid vehicle. Int. J. Hydrog. Energy 2016, 41, 21503–21515. [Google Scholar]
- Li, L.; Yan, B.; Yang, C.; Zhang, Y.; Chen, Z.; Jiang, G. Application-oriented stochastic energy management for plug-in hybrid electric bus with AMT. IEEE Trans. Control Syst. Technol. 2016, 65, 4459–4470. [Google Scholar] [CrossRef]
- Vagg, C.; Akehurst, S.; Brace, C.J.; Ash, L. Stochastic dynamic programming in the real-world control of hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2016, 24, 853–866. [Google Scholar] [CrossRef]
- Du, Y.; Zhao, Y.; Wang, Q.; Zhang, Y.; Xia, H. Trip-oriented stochastic optimal energy management strategy for plug-in hybrid electric bus. Energy 2016, 115, 1259–1271. [Google Scholar] [CrossRef]
- Li, L.; Yan, B.; Song, J.; Zhang, Y.; Jiang, G.; Li, L. Two-step optimal energy management strategy for single-shaft series-parallel powertrain. Mechatronics 2016, 36, 147–158. [Google Scholar] [CrossRef]
- Opila, D.F.; Wang, X.; McGee, R.; Gillespie, R.B.; Cook, J.A.; Grizzle, J.W. Real-world robustness for hybrid vehicle optimal energy management strategies incorporating drivability metrics. J. Dyn. Syst. Meas. Control 2014, 136, 061011. [Google Scholar] [CrossRef]
- Moura, S.J.; Fathy, H.K.; Callaway, D.S.; Stein, J.L. A stochastic optimal control approach for power management in plug-in hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2011, 19, 545–555. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, J. A two-level stochastic approach to optimize the energy management strategy for fixed-route hybrid electric vehicles. Mechatronics 2016, 38, 93–102. [Google Scholar] [CrossRef]
- Tate, E.D.; Grizzle, J.W.; Peng, H. Shortest path stochastic control for hybrid electric vehicles. Int. J. Robust Nonlinear Control 2008, 18, 1409–1429. [Google Scholar] [CrossRef]
- Tate, E.D.; Grizzle, J.W.; Peng, H. SP-SDP for fuel consumption and tailpipe emissions minimization in an EVT hybrid. IEEE Trans. Control Syst. Technol. 2010, 18, 673–687. [Google Scholar] [CrossRef]
- Bellman, R.E.; Dreyfus, S.E. Applied Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Dimitri, P.B. Dynamic Programming and Optimal Control Volume I, 3rd ed.; Athena Scientific: Belmont, MA, USA, 1995; pp. 18–19, 404–410. [Google Scholar]
- National Renewable Energy Lab. Evaluation of Range Estimates for Toyota FCHV-Adv under Open Road Driving Conditions. Available online: http://www.nrel.gov/hydrogen/pdfs/toyota_fchv-adv_range_verification.pdf (accessed on 8 February 2017).
| Item | Parameter | Value |
|---|---|---|
| Spark ignition (SI) engine | Displacement (L) | 1.0 |
| Maximum power (kW at 5700 r/min) | 50 | |
| Maximum torque (N∙m at 5600 r/min) | 89.5 | |
| Permanent magnet motor | Maximum power (kW) | 10 |
| Maximum torque (N∙m) | 46.5 | |
| Peak efficiency (%) | 0.96 | |
| Advanced Ni-MH battery | Capacity (Ah) | 6 |
| Nominal cell voltage (V) | 1.2 | |
| Total cells | 120 | |
| Automated transmission | Speed | 5 |
| Gear ratio | 2.2791/2.7606/3.5310/5.6175/11.1066 | |
| Vehicle | Curb weight (kg) | 1000 |
| Parameter | Value |
|---|---|
| Sampling time (s) | 1 |
| Discretization-resolution of SOC | 0.005 |
| Discretization-resolution of ωw | 2 |
| Discretization-resolution of g(k) | 1 |
| Discretization-resolution of Tdem | 10 |
| Discretization-resolution of Te (N∙m) | 1 |
| Discretization-resolution of shift(k) | 1 |
| Weight factor in the cost function α | 0 |
| Weight factor in the cost function λ | 1000 |
| Weight factor in the cost function υ | 0.5 |
| SOC0 | 0.7 |
| SOCref | 0.7 |
| Maximum interation number | 70 |
| EMS | PEACS | DP | SDP |
|---|---|---|---|
| Fuel economy (mpg) | 53.9 | 71.7 | 68.3 |
| Engine efficiency (%) | 24.6 | 37.4 | 35.7 |
| Motoring efficiency (%) | 87.2 | 94.7 | 91.1 |
| Generating efficiency (%) | 79.9 | 95.8 | 93.4 |
| EMS | PEACS | DP | SDP |
|---|---|---|---|
| Fuel economy (mpg) | 52.2 | 60.7 | 58.2 |
| Engine efficiency (%) | 23.4 | 38.2 | 36.1 |
| Motoring efficiency (%) | 81.3 | 90.3 | 87.0 |
| Generating efficiency (%) | 83.8 | 91.7 | 90.5 |
| EMS | PEACS | DP | SDP |
|---|---|---|---|
| Fuel economy (mpg) | 56.3 | 66.5 | 62.1 |
| Engine efficiency (%) | 24.8 | 38.1 | 36.3 |
| Motoring efficiency (%) | 84.2 | 89.7 | 86.1 |
| Generating efficiency (%) | 79.6 | 96.1 | 91.8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, F.; Xu, G.; Hu, Y.; Xu, K.; Li, W. Stochastic Optimal Control of Parallel Hybrid Electric Vehicles. Energies 2017, 10, 214. https://doi.org/10.3390/en10020214
Qin F, Xu G, Hu Y, Xu K, Li W. Stochastic Optimal Control of Parallel Hybrid Electric Vehicles. Energies. 2017; 10(2):214. https://doi.org/10.3390/en10020214
Chicago/Turabian StyleQin, Feiyan, Guoqing Xu, Yue Hu, Kun Xu, and Weimin Li. 2017. "Stochastic Optimal Control of Parallel Hybrid Electric Vehicles" Energies 10, no. 2: 214. https://doi.org/10.3390/en10020214
APA StyleQin, F., Xu, G., Hu, Y., Xu, K., & Li, W. (2017). Stochastic Optimal Control of Parallel Hybrid Electric Vehicles. Energies, 10(2), 214. https://doi.org/10.3390/en10020214





