Mode Shift Control for a Hybrid Heavy-Duty Vehicle with Power-Split Transmission
Abstract
:1. Introduction
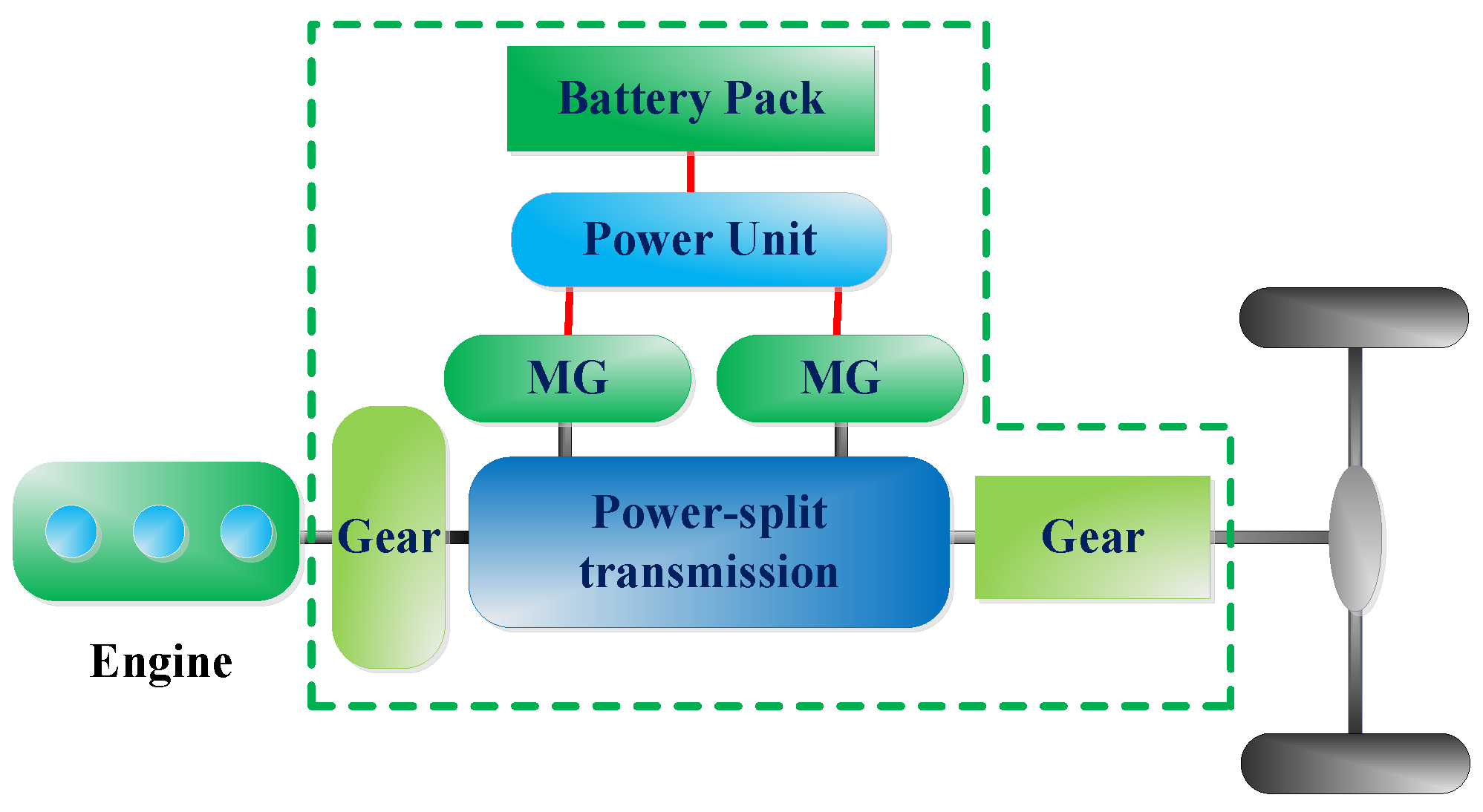
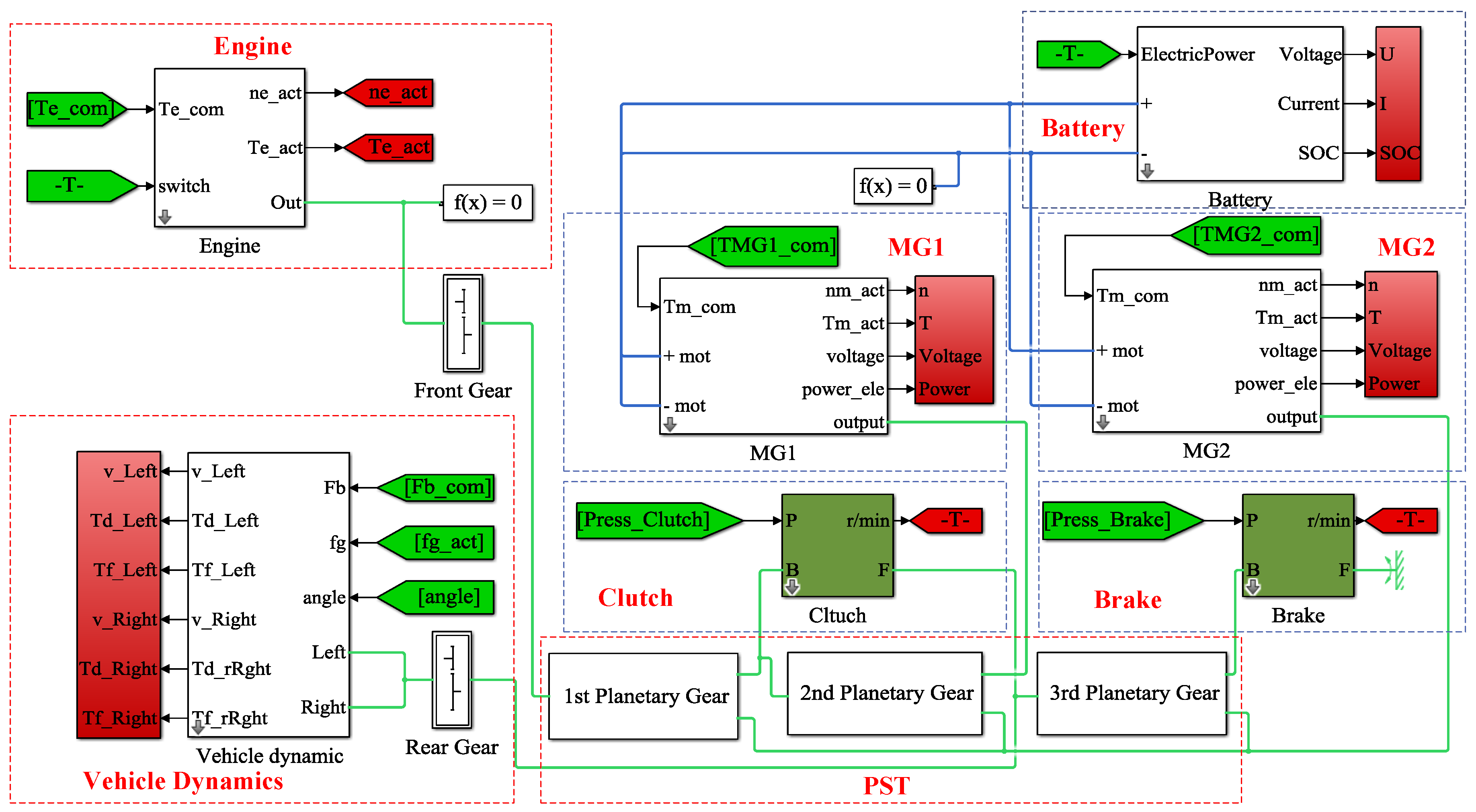
2. Modeling of Hybrid Heavy-Duty Vehicle
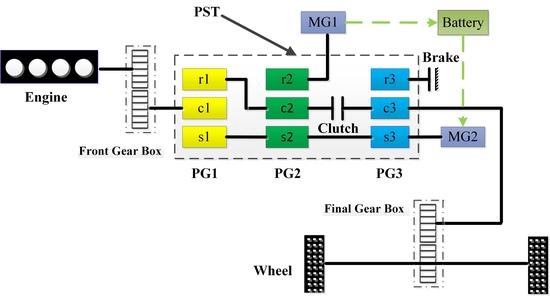
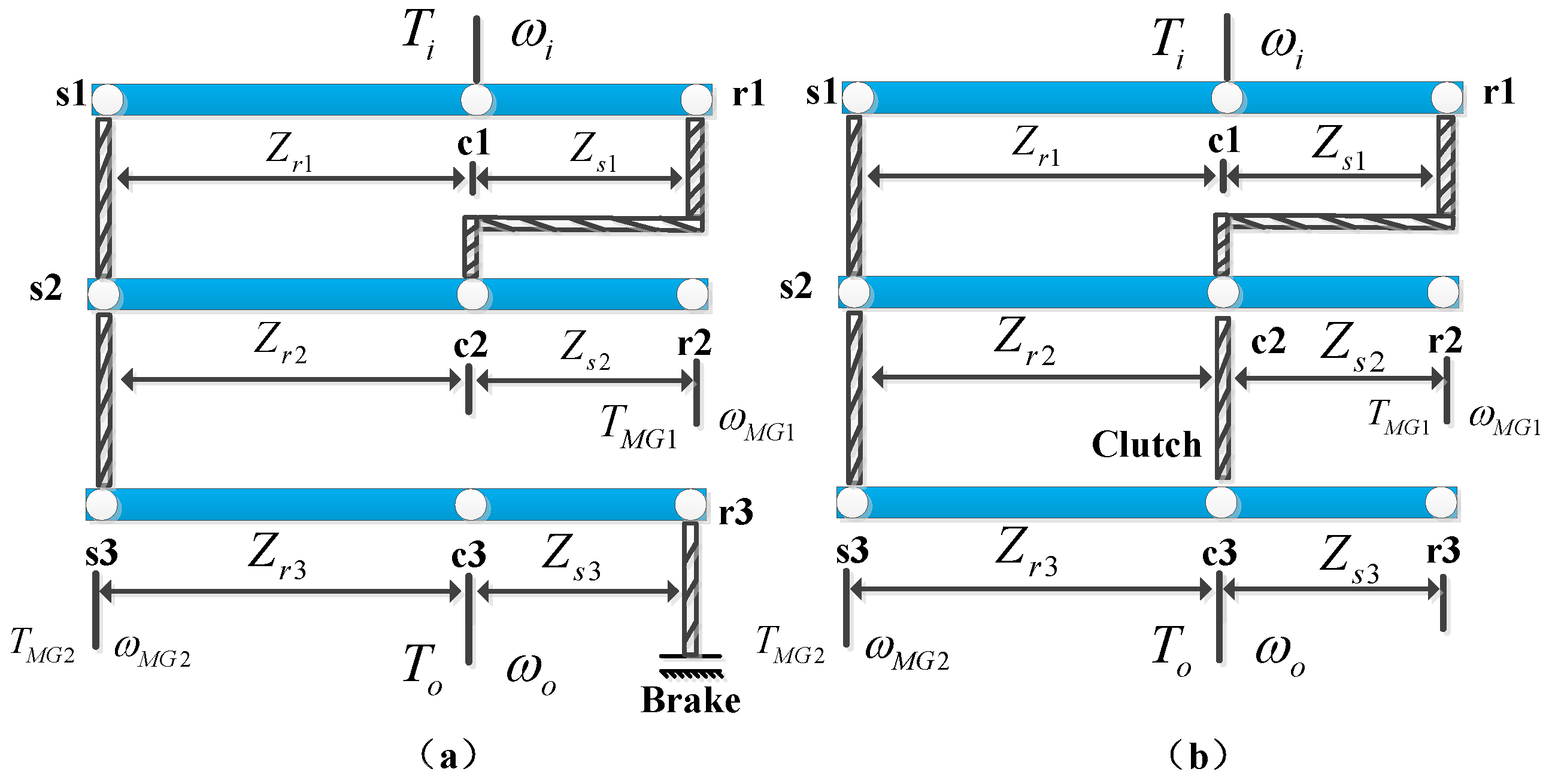
2.1. Introduction to the Hybrid Heavy-Duty Vehicle
2.2. Problem Formulation
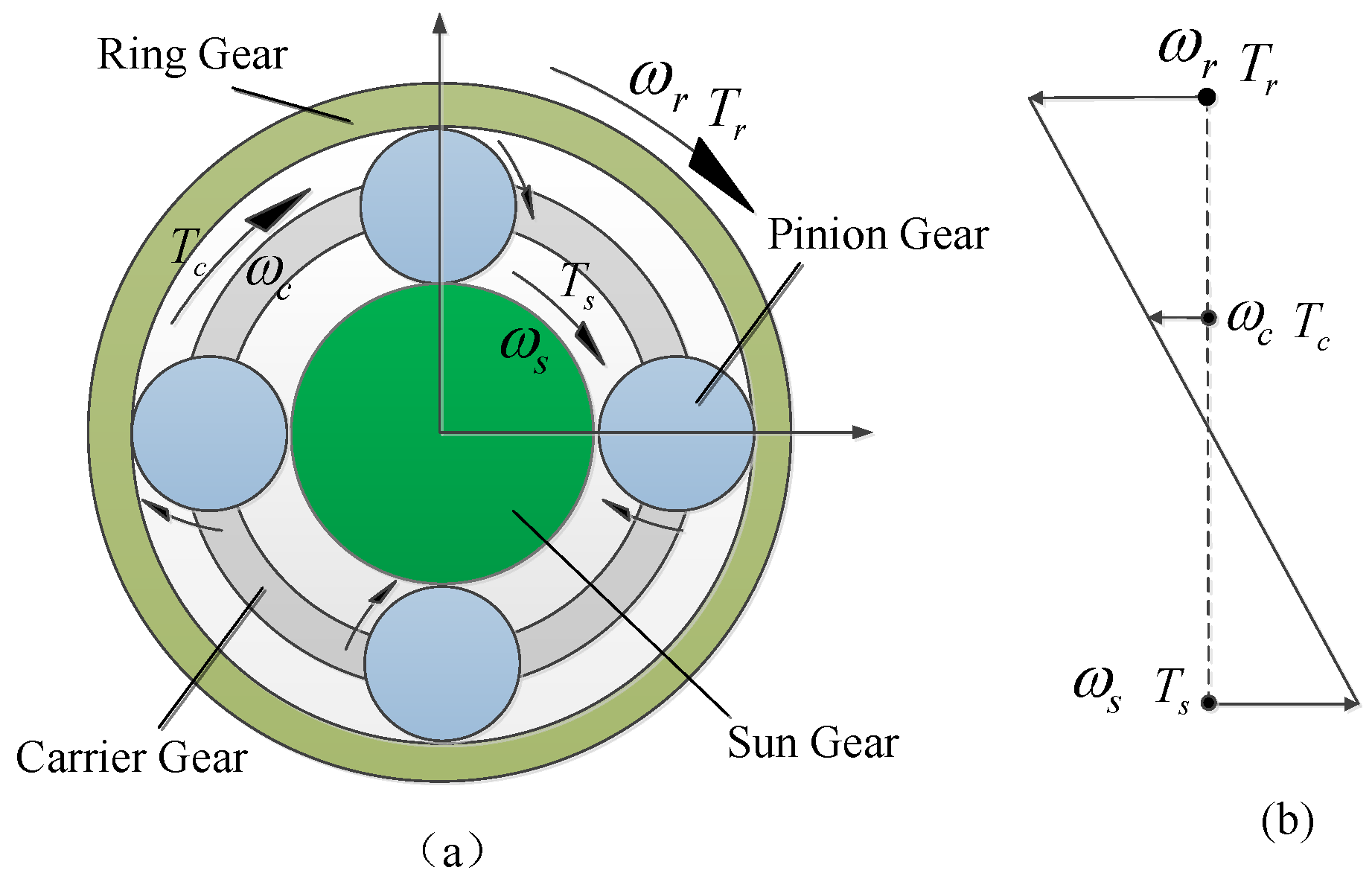
2.3. Speed Equations and Torque Equations
2.4. Dynamic Equations
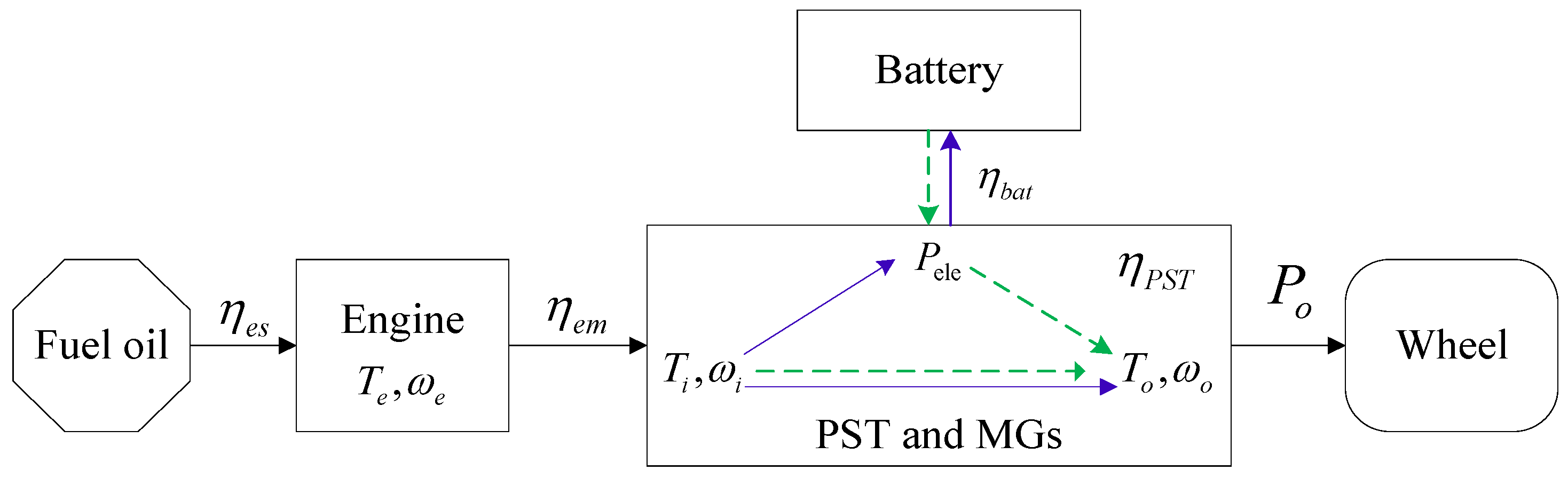
2.5. Engine Model
2.6. Motor-Generator Model
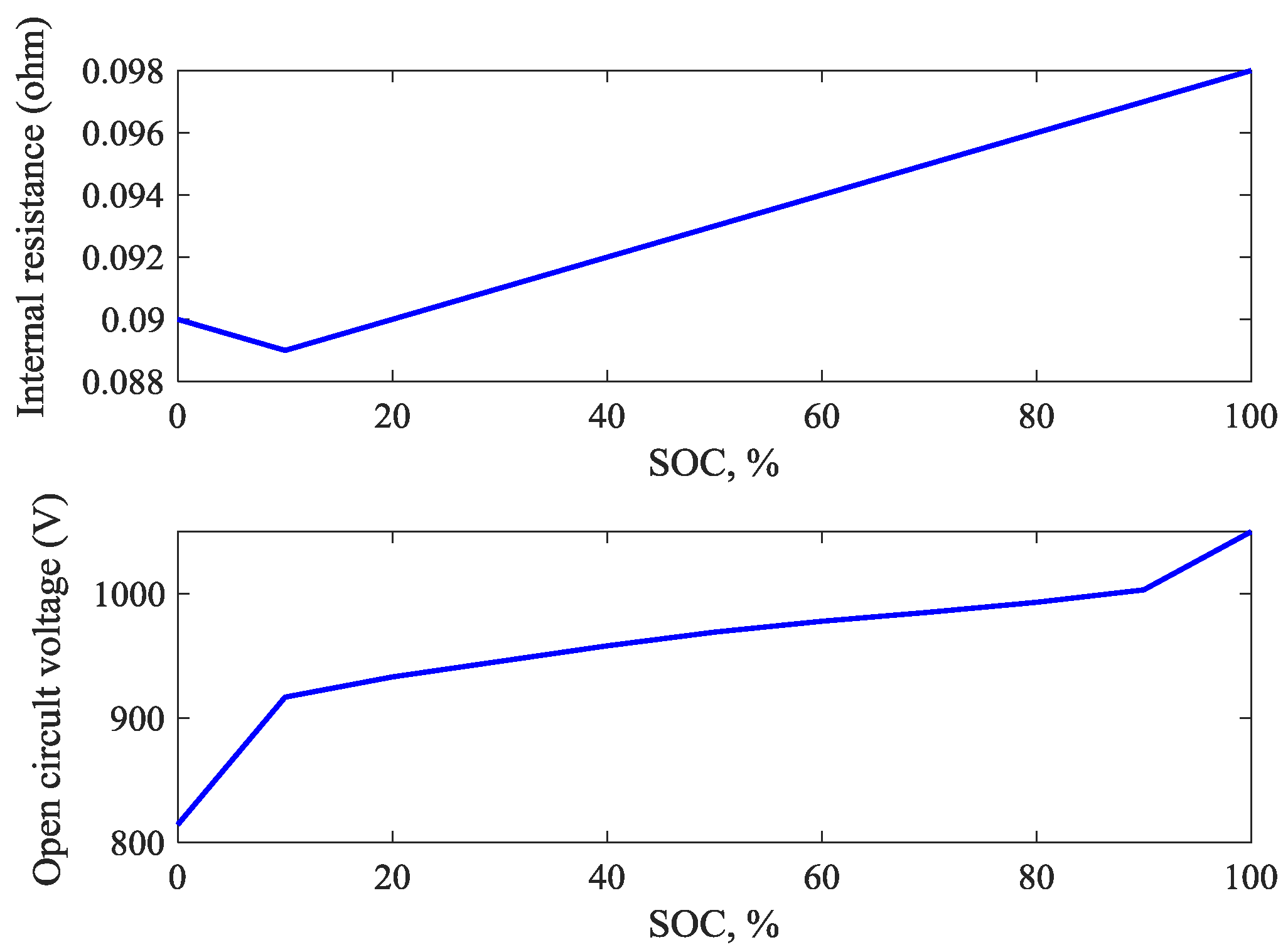
2.7. Battery Model
2.8. Clutch/Brake Model
2.9. Vehicle Dynamics
3. Shift Schedule Design of Hybrid Heavy-Duty Vehicle
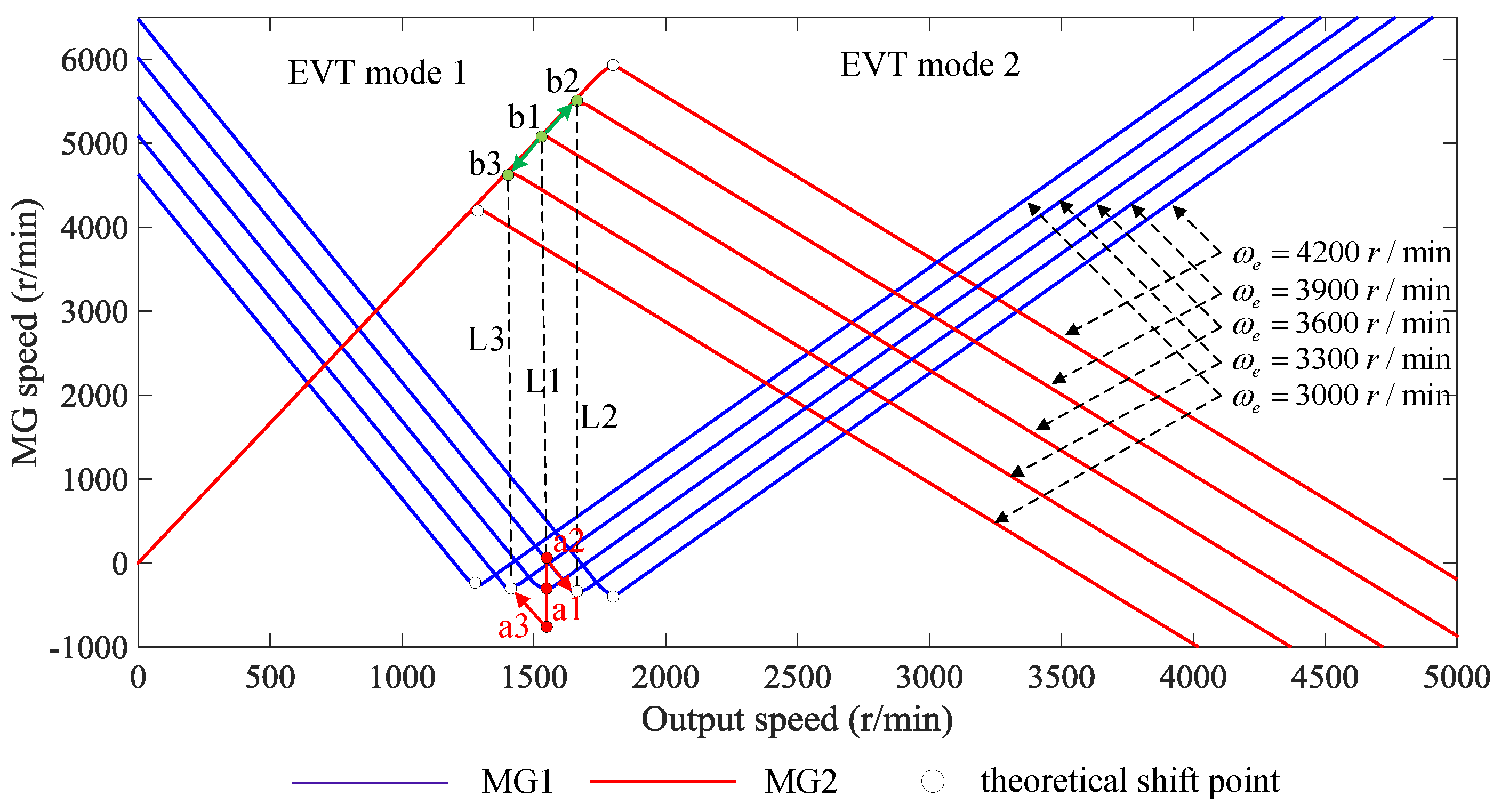
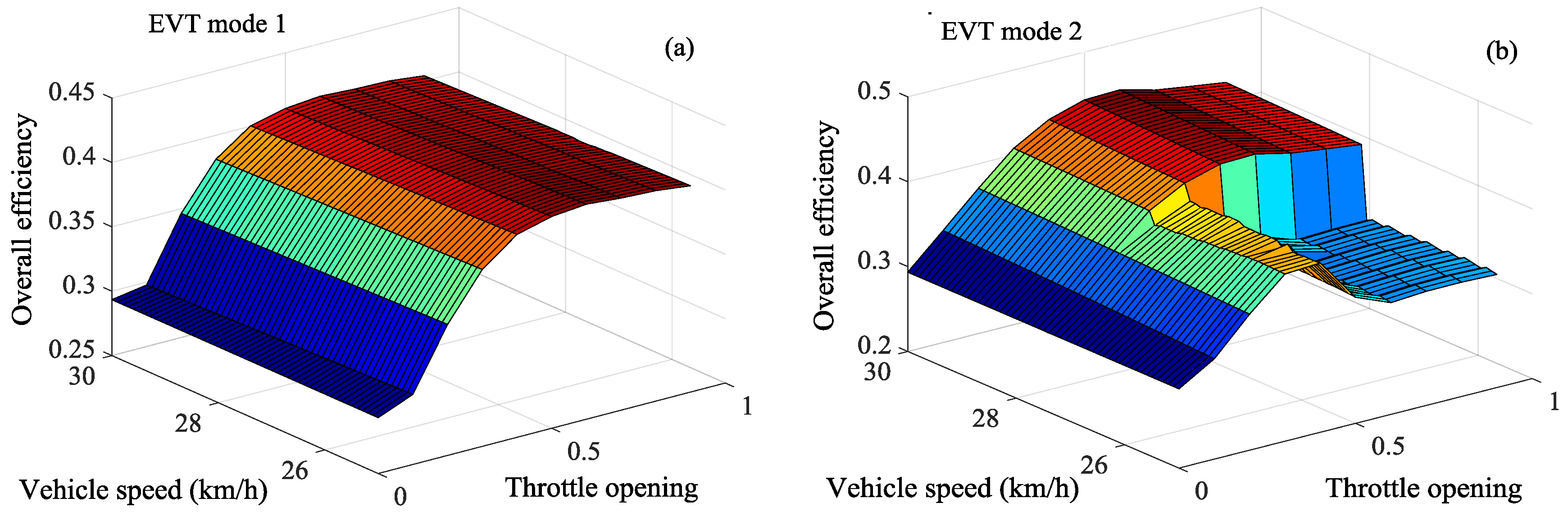
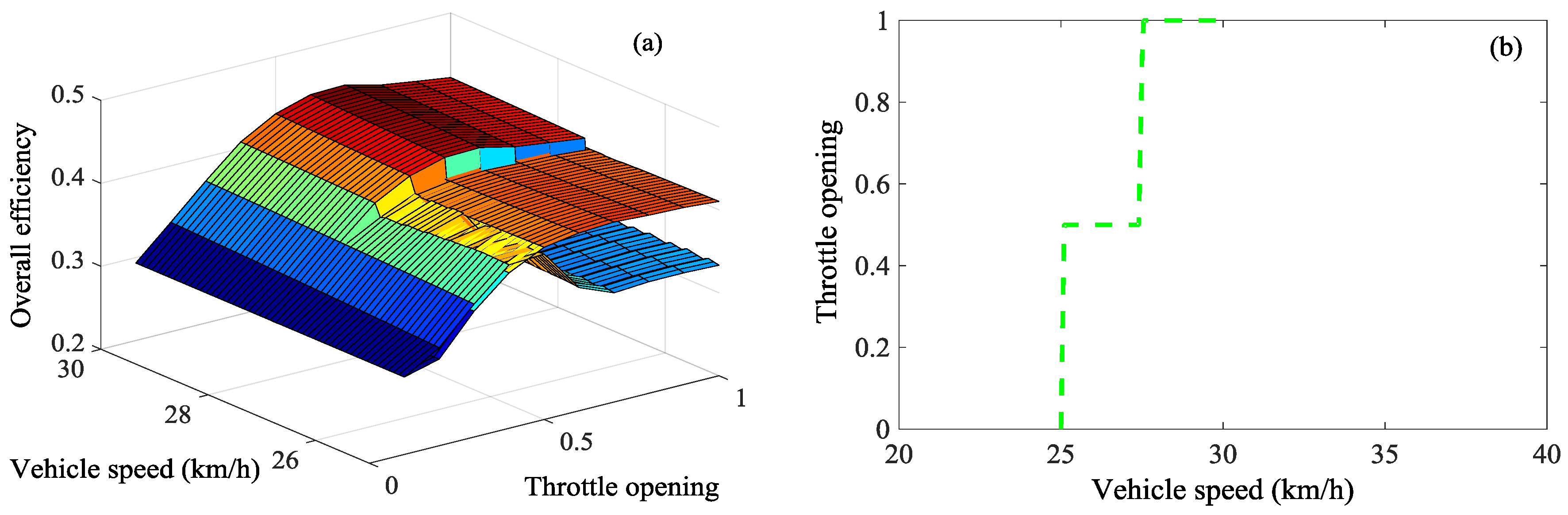
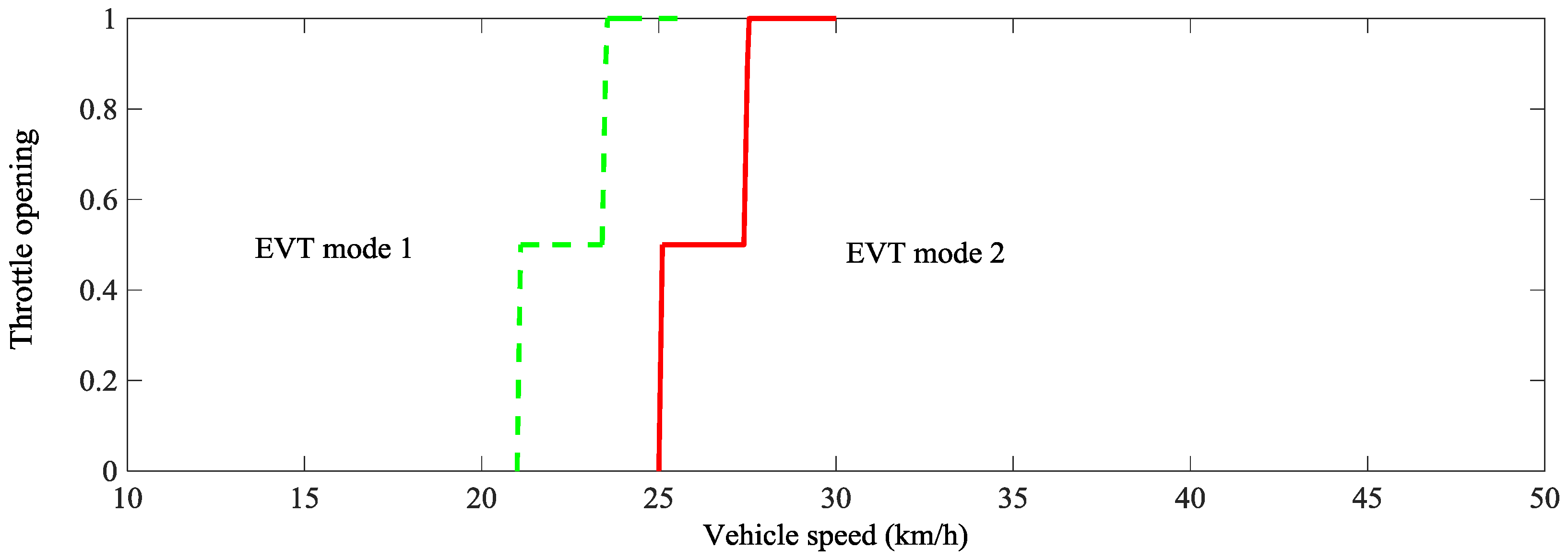
3.1. Shift Point Analysis
3.2. Shift Schedule Design of the Hybrid Heavy-Duty Vehicle
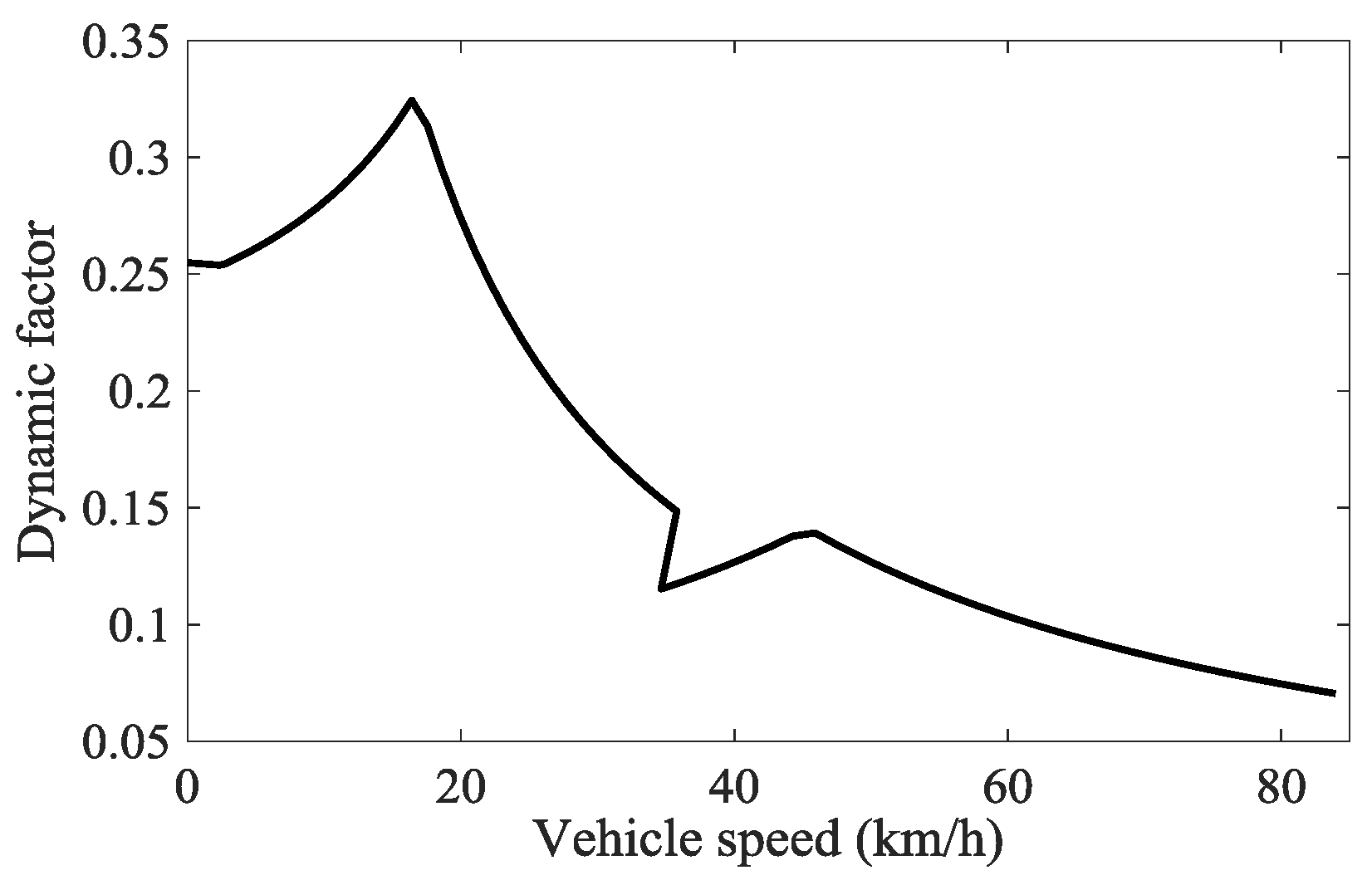
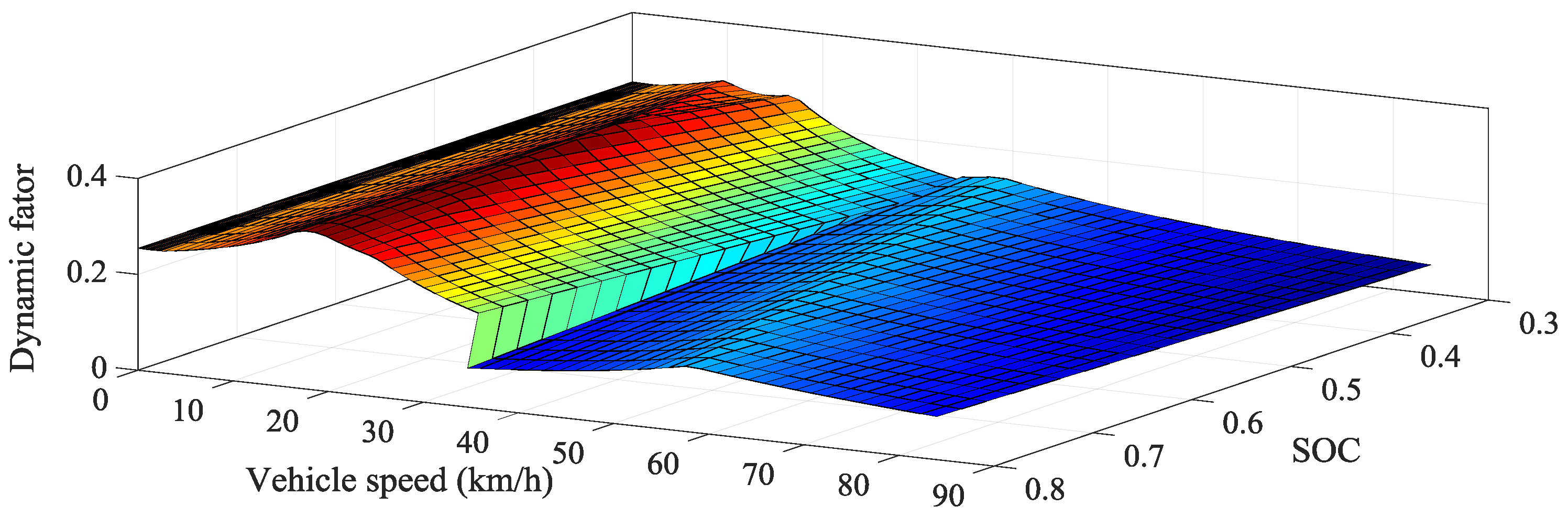
3.2.1. Dynamic Shift Schedule Design
3.2.2. Economic Shift Schedule Design
4. Mode Shift Control Strategy for the Hybrid Heavy-Duty Vehicle
4.1. Shift Schedule Design of the Hybrid Heavy-Duty Vehicle
4.2. Mode Shift Control Strategy
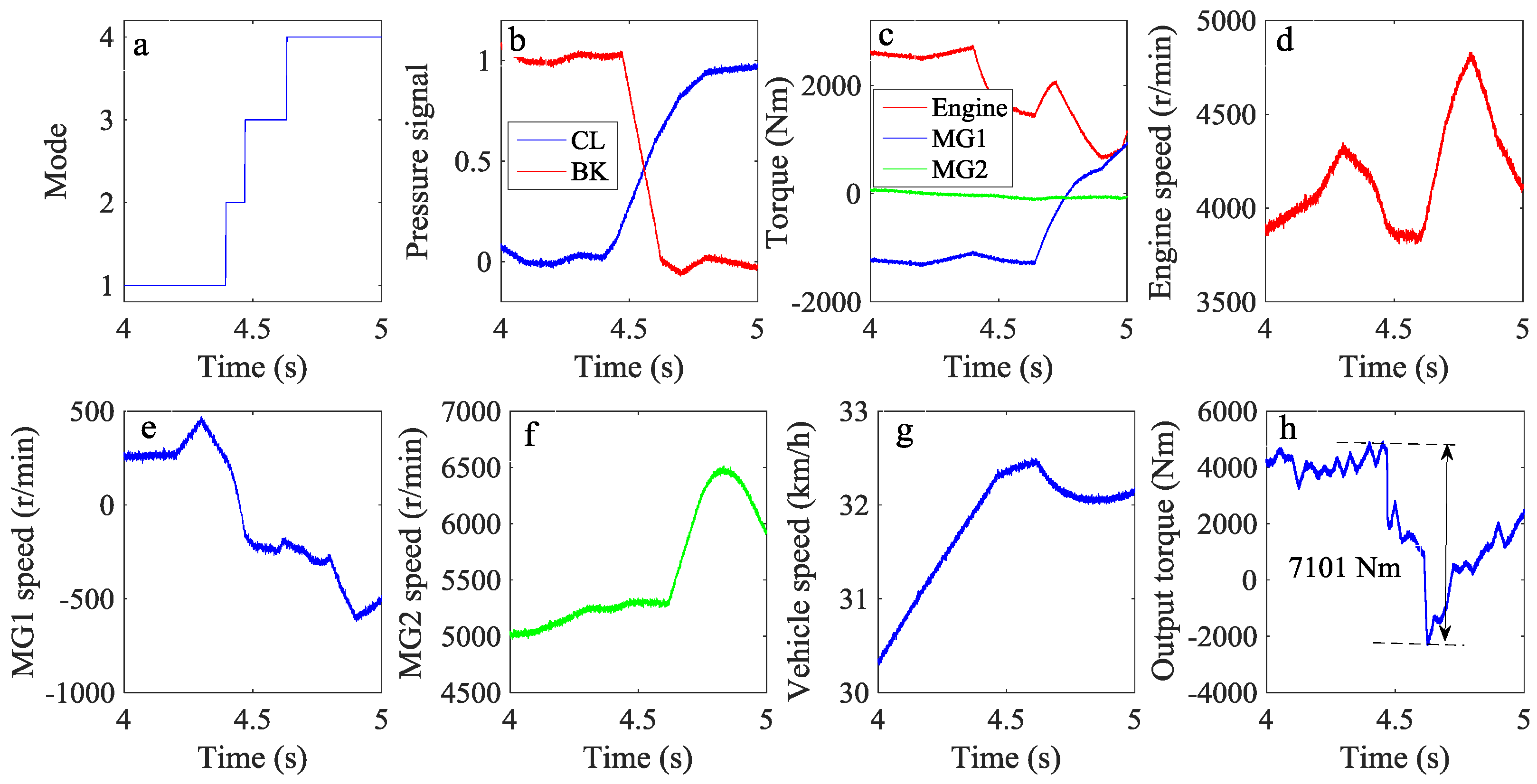
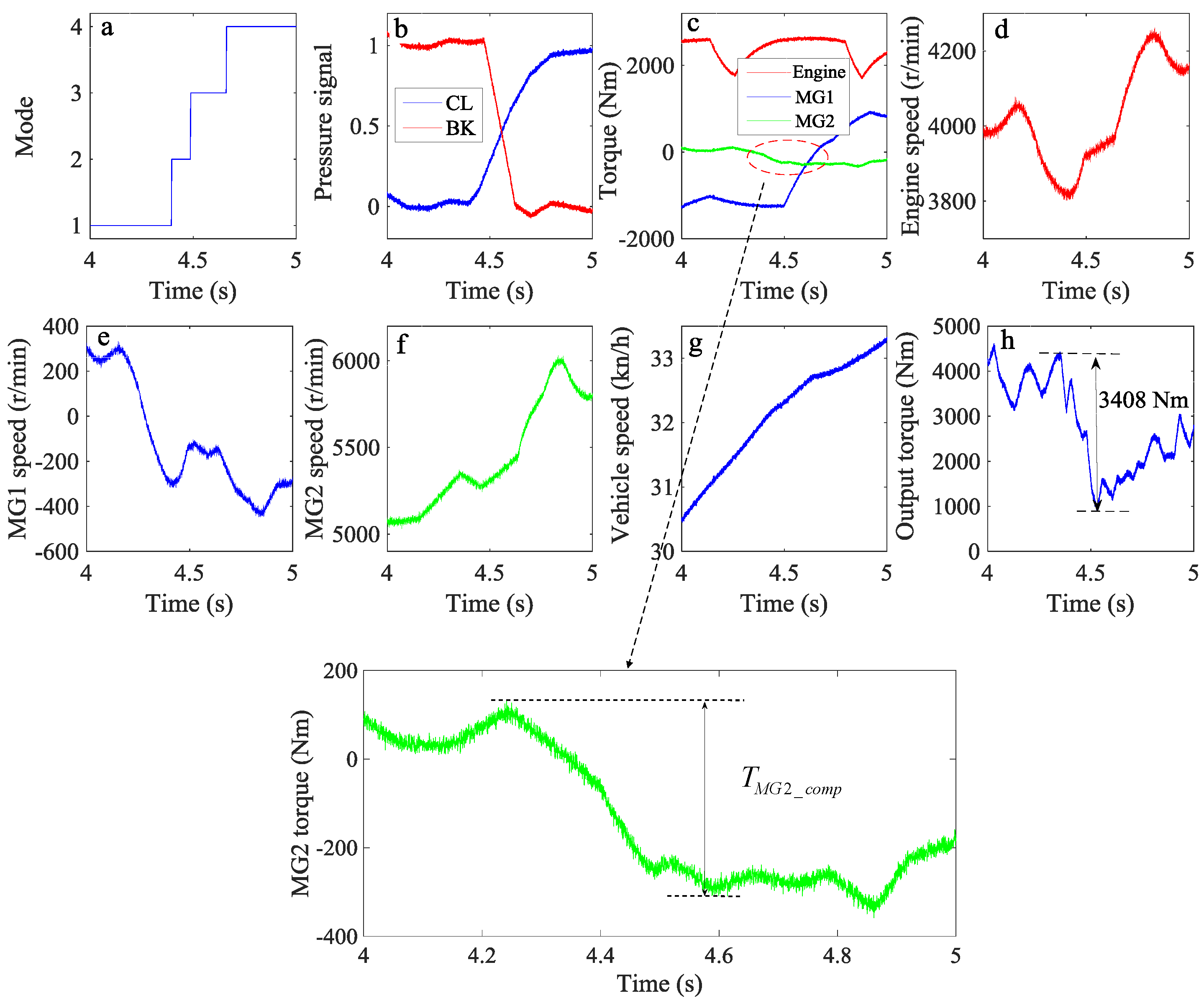
5. Results and Discussion
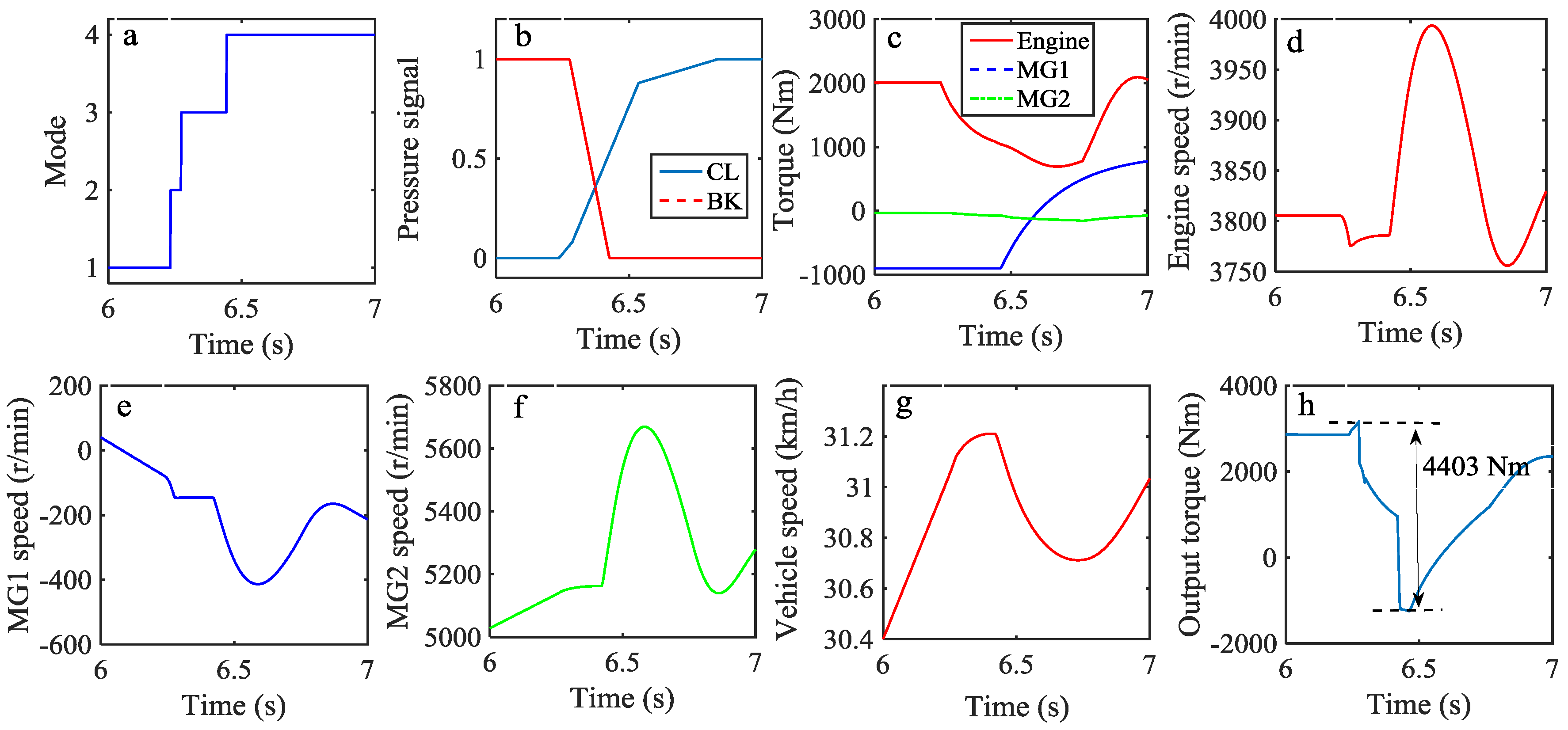
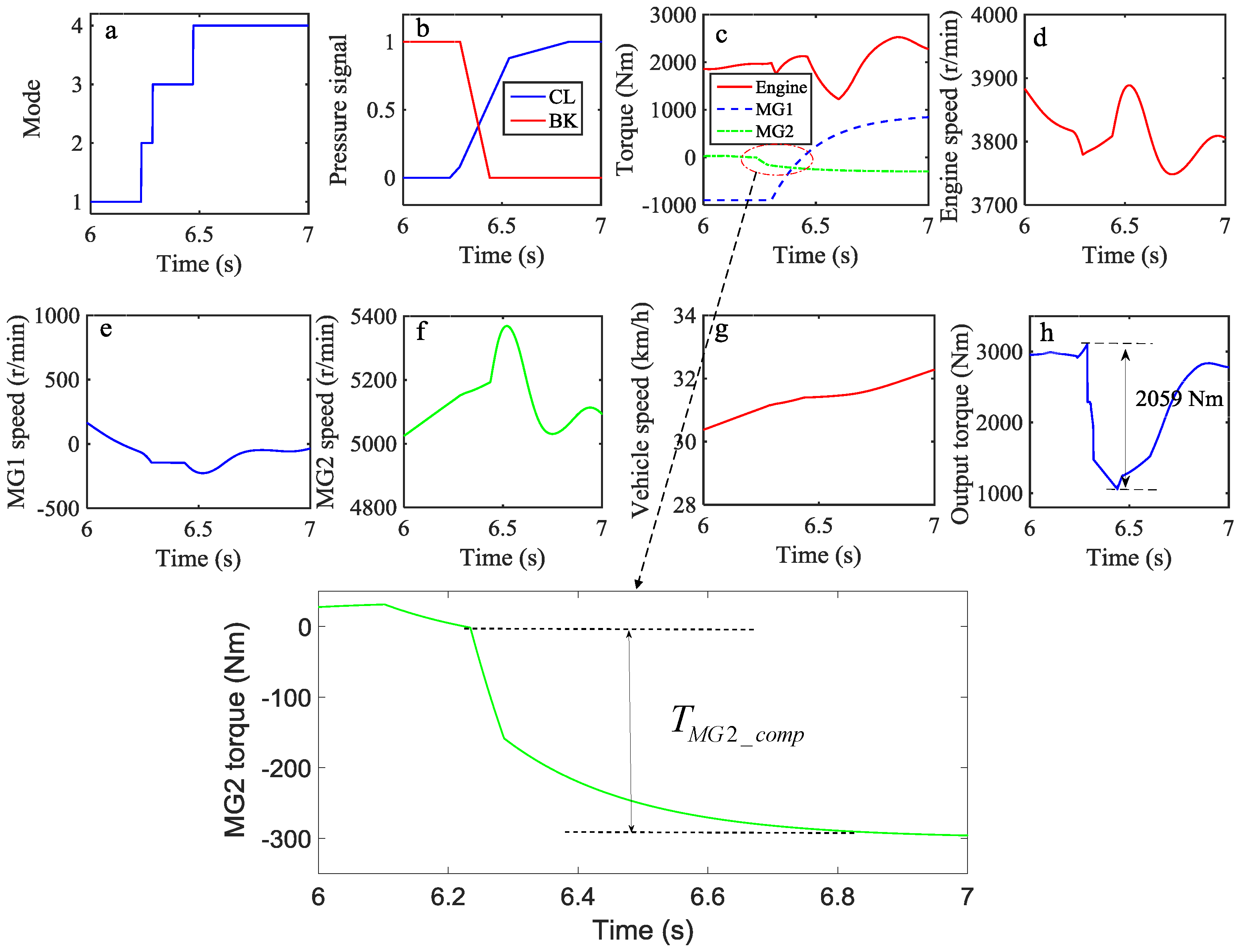
5.1. Simulation Results and Discussion
5.2. Experimental Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Syed, F.U.; Kuang, M.L.; Czubay, J.; Ying, H. Derivation and experimental validation of a power-split hybrid electric vehicle model. IEEE Trans. Veh. Technol. 2006, 55, 1731–1747. [Google Scholar] [CrossRef]
- Li, L.; Yan, B.; Song, J.; Zhang, Y.; Jiang, G. Two-step optimal energy management strategy for single-shaft series-parallel powertrain. Mechatronics 2016, 36, 147–158. [Google Scholar] [CrossRef]
- Mashadi, B.; Emadi, S.A. Dual-mode power-split transmission for hybrid electric vehicles. IEEE Trans. Veh. Technol. 2010, 59, 3223–3232. [Google Scholar] [CrossRef]
- Xiang, C.; Huang, K.; Ma, Y.; Liu, H.; Jia, S. Analysis of characteristics for mode switch of dual-mode electro-mechanical transmission (EMT). In Proceedings of the 2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall), Vancouver, BC, Canada, 14–17 September 2014.
- Zhuang, W.; Zhang, X.; Ding, Y.; Wang, L.; Hu, X. Comparison of multi-mode hybrid powertrains with multiple planetary gears. Appl. Energy 2016, 178, 624–632. [Google Scholar] [CrossRef]
- Xiang, C.; Huang, K.; Ma, Y.; Zhao, Y. Stability analysis for mode switch of multi-mode electro-mechanical transmission (EMT). In Proceedings of the IEEE Transportation Electrification Conference & Expo Asia-Pacific, Beijing, China, 31 August–3 September 2014.
- Wang, W.; Xiang, C.; Liu, H.; Jia, S. A model-predictive-control-based power management strategy for a power-split electromechanical transmission. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 1987–2001. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Xu, J.; Gong, X.; You, C. Energy management for a power-split plug-in hybrid electric vehicle based on dynamic programming and neural networks. IEEE Trans. Veh. Technol. 2014, 63, 1567–1580. [Google Scholar] [CrossRef]
- Ouyang, M.; Zhang, W.; Wang, E.; Yang, F.; Li, J.; Li, Z.; Ye, X. Performance analysis of a novel coaxial power-split hybrid powertrain using a CNG engine and supercapacitors. Appl. Energy 2015, 157, 595–606. [Google Scholar] [CrossRef]
- Zhuang, W.; Zhang, X.; Zhao, D.; Peng, H.; Wang, L. Optimal design of three-planetary-gear power-split hybrid powertrains. Int. J. Automot. Technol. 2016, 17, 299–309. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Mahmoodi-k, M. Development a new power management strategy for power split hybrid electric vehicles. Transp. Res. D Transp. Environ. 2015, 37, 79–96. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Z. Dynamic analysis and multivariable transient control of the power-split hybrid powertrain. IEEE/ASME Trans. Mechatron. 2015, 20, 3085–3097. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Xiong, R.; Xu, J.; You, C. Energy management of a power-split plug-in hybrid electric vehicle based on genetic algorithm and quadratic programming. J. Power Sources 2014, 248, 416–426. [Google Scholar] [CrossRef]
- Xiang, C.; Ding, F.; Wang, W.; He, W. Energy management of a dual-mode power-split hybrid electric vehicle based on velocity prediction and nonlinear model predictive control. Appl. Energy 2017, 189, 640–653. [Google Scholar] [CrossRef]
- Shen, W.; Yu, H.; Hu, Y.; Xi, J. Optimization of Shift Schedule for Hybrid Electric Vehicle with Automated Manual Transmission. Energies 2016, 9, 220. [Google Scholar] [CrossRef]
- Pettersson, M.; Nielsen, L. Gear shifting by engine control. IEEE Trans. Control. Syst. Technol. 2000, 8, 495–507. [Google Scholar] [CrossRef]
- Ying, H.; Xianlei, S.; Shili, X.; Fujun, Z.; Yunshan, G. Design of gear shifting rules on the basis of power performance and fuel economy and experimental study on them. Automob. Technol. 2004, 11, 007. [Google Scholar]
- Yang, C.; Song, J.; Li, L.; Li, S.; Cao, D. Economical launching and accelerating control strategy for a single-shaft parallel hybrid electric bus. Mech. Syst. Signal Process. 2016, 76, 649–664. [Google Scholar] [CrossRef]
- Yang, C.; Jiao, X.; Li, L.; Zhang, Y.; Zhang, L.; Song, J. Robust coordinated control for hybrid electric bus with single-shaft parallel hybrid powertrain. IET Control Theory Appl. 2015, 9, 270–282. [Google Scholar] [CrossRef]
- Pisu, P.; Rizzoni, G. A comparative study of supervisory control strategies for hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2007, 15, 506–518. [Google Scholar] [CrossRef]
- Ngo, V.; Hofman, T.; Steinbuch, M.; Serrarens, A. Predictive gear shift control for a parallel hybrid electric vehicle. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011.
- Zhao, Z.G.; Chen, H.J.; Zhen, Z.X.; Yang, Y.Y. Optimal torque coordinating control of the launching with twin clutches simultaneously involved for dry dual-clutch transmission. Veh. Syst. Dyn. 2014, 52, 776–801. [Google Scholar] [CrossRef]
- Beck, R.; Richert, F.; Bollig, A.; Abel, D.; Saenger, S.; Neil, K.; Noreikat, K.E. Model predictive control of a parallel hybrid vehicle drivetrain. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 12–15 December 2005; pp. 2670–2675.
- Kim, S.; Park, J.; Hong, J.; Lee, M.; Sim, H. Transient Control Strategy of Hybrid Electric Vehicle during Mode Change; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2009. [Google Scholar]
- Zhang, H.; Zhang, Y.; Yin, C. Hardware-in-the-loop simulation of robust mode transition control for a series–Parallel hybrid electric vehicle. IEEE Trans. Veh. Technol. 2016, 65, 1059–1069. [Google Scholar] [CrossRef]
- Shi, G.; Dong, P.; Sun, H.Q.; Liu, Y.; Cheng, Y.J.; Xu, X.Y. Adaptive control of the shifting process in automatic transmissions. Int. J Automot. Technol. 2017, 18, 179–194. [Google Scholar] [CrossRef]
- Chen, L.; Xi, G.; Sun, J. Torque coordination control during mode transition for a series—Parallel hybrid electric vehicle. IEEE Trans. Veh. Technol. 2012, 61, 2936–2949. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, Z.; Zhang, T.; Li, M. Mode transition coordinated control for a compound power-split hybrid car. Mech. Syst. Signal Process. 2017, 87, 192–205. [Google Scholar] [CrossRef]
- Zeng, X.; Yang, N.; Wang, J.; Song, D.; Zhang, N.; Shang, M.; Liu, J. Predictive-model-based dynamic coordination control strategy for power-split hybrid electric bus. Mech. Syst. Signal Process. 2015, 60, 785–798. [Google Scholar] [CrossRef]
- Choi, W.; Kang, J.; Hong, S.; Kim, H. Development of a control algorithm to reduce torque variation for the dual mode HEV during mode shift. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011.
- Yan, F.; Wang, J.; Huang, K. Hybrid electric vehicle model predictive control torque-split strategy incorporating engine transient characteristics. IEEE Trans. Veh. Technol. 2012, 61, 2458–2467. [Google Scholar] [CrossRef]
- Xiang, C.; Wang, Y.; Hu, S.; Wang, W. A new topology and control strategy for a hybrid Battery-Ultracapacitor energy storage system. Energies 2014, 7, 2874–2896. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, J. A parallel hybrid electric vehicle energy management strategy using stochastic model predictive control with road grade preview. IEEE Trans. Control Syst. Technol. 2015, 23, 2416–2423. [Google Scholar] [CrossRef]
- Han, L.J.; Xiang, C.; Yan, W.J.; Qi, Y.L.; Liu, R. Study on system efficiency and power flow optimization for dual-mode hybrid electric vehicle. In Proceedings of the FISITA 2012 World Automotive Congress, Beijing, China, 27 November 2012; pp. 401–415.
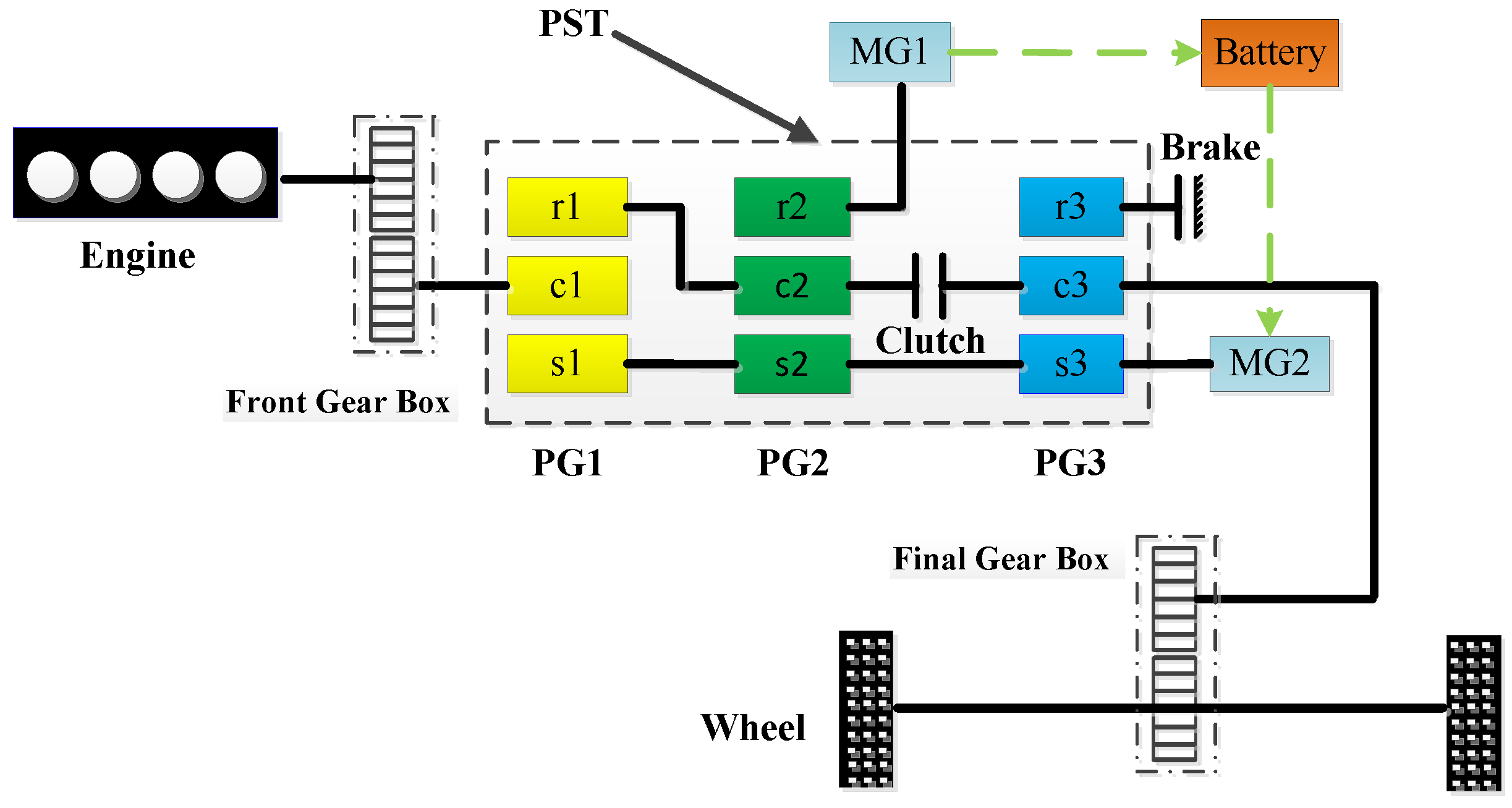


| Mode | MG1 | MG2 | CL | BK |
|---|---|---|---|---|
| EVT Mode 1 | Generator | Motor | Disengaged | Engaged |
| EVT Mode 2 | Motor | Generator | Engaged | Disengaged |
| Components | Parameter | Value |
|---|---|---|
| Engine | Maximum speed | 4250 r/min |
| Maximum torque | 2754 Nm | |
| Motor-generator | Maximum speed | 6050 r/min |
| Maximum torque | 1342 Nm | |
| Battery | Capacity | 70 Ah |
| Bus voltage | 900 V | |
| PGs | K1 | 2.13 |
| K2 | 2.13 | |
| K3 | 2.33 | |
| Vehicle | Mass | 45,000 kg |
| Front gear ratio | 1.4 | |
| Final gear ratio | 4.1 | |
| Clutch brake | Kinetic friction coefficient | 0.06 |
| Static friction coefficient | 0.1 | |
| Pressure | 0–2.5 MPa |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, K.; Xiang, C.; Ma, Y.; Wang, W.; Langari, R. Mode Shift Control for a Hybrid Heavy-Duty Vehicle with Power-Split Transmission. Energies 2017, 10, 177. https://doi.org/10.3390/en10020177
Huang K, Xiang C, Ma Y, Wang W, Langari R. Mode Shift Control for a Hybrid Heavy-Duty Vehicle with Power-Split Transmission. Energies. 2017; 10(2):177. https://doi.org/10.3390/en10020177
Chicago/Turabian StyleHuang, Kun, Changle Xiang, Yue Ma, Weida Wang, and Reza Langari. 2017. "Mode Shift Control for a Hybrid Heavy-Duty Vehicle with Power-Split Transmission" Energies 10, no. 2: 177. https://doi.org/10.3390/en10020177
APA StyleHuang, K., Xiang, C., Ma, Y., Wang, W., & Langari, R. (2017). Mode Shift Control for a Hybrid Heavy-Duty Vehicle with Power-Split Transmission. Energies, 10(2), 177. https://doi.org/10.3390/en10020177