1. Introduction
Inductively coupled wireless power transfer system utilizes time varying electromagnetic fields to transfer energy. It has been widely used in traffic, consumer electronics, underwater, mining equipment, and so on. Compared to the traditional plug-in power supply system, the wireless power transfer (WPT) system can achieve mechanical and electrical isolation, minimize cable and socket applications, and ensure safe operation in harsh environments [
1,
2]. Especially in electric bus and energy storage tram charging, the WPT primary side coil winding can be buried under the existing platform, and achieve station charging. In this manner, the battery capacity and charging time of the tram and bus will be reduced [
3,
4].
The WPT transfer coil is loosely coupled, thus resonance network is required to reduce the reactive power and improve system efficiency. The resonant network, also known as the compensation network, typically resonates with the inductance of the transfer coil, thereby enhancing the transfer efficiency and changing the input and output characteristics. At present, the basic compensation topologies are mainly composed of four types: series-series (SS), series-parallel (SP), parallel-series (PS), and parallel-parallel (PP) [
5], while some more complex compensation topologies are derived on the basis of these four. The hybrid topology on the primary side is proposed in [
6], and can switch between two basic compensation networks to satisfy the constant voltage (CV) and constant current (CC) modes for stationary electric vehicle (EV) charging. In [
7,
8,
9], it is pointed out that LCL type topology can allow the current of the transmitting coil to present a constant current source characteristic, and is suitable for the case of multi-load transfer. In [
10], an LCC resonant network is proposed to adjust the current on the transmitting coil by selecting the capacitor value in series, so that the output characteristics of the constant voltage source can be obtained at the second side. In [
11], a compensation network calculation method is presented to realize the constant voltage or constant current output of the second side under the condition that the coil parameters are determined. In [
12], an S/SP constant voltage gain compensation topology is proposed, and, under full compensation, the voltage gain is independent of mutual inductance. In addition to the output characteristics of resonant networks, some scholars have performed research on the primary capacitance [
13,
14], input impedance [
15], soft switching [
16,
17], the system transfer efficiency optimization method [
18,
19], and the image impedance matching method [
20,
21,
22]. However, most of the above studies did not consider the influence of compensation errors. In practical application, the resonance network is difficult to compensate for perfectly and its good output characteristics may not be as well, as a result, due to the challenge in accurately measuring the mutual inductance and self-inductance of coils, the existence of stray capacitance of the coils, errors of the compensation capacitances, and aging of the compensation capacitors. According the circuit theory, reactive power is present in a system with imperfect compensation. The existence of reactive power increases the stress of the device, and affects the output characteristics of the WPT system. Although there are many ways to improve the compensation accuracy, such as measuring the system’s self-inductance and other parameters as accurately as possible and using high-accuracy capacitors, the cost will raise, especially in mass production. Therefore, it is necessary to study how incomplete compensation affects the output characteristics and how much it affects for the determination of compensation accuracy in the system design.
This paper takes SS topology as an example, and simplifying the causes of incomplete compensation as the accuracy errors of the compensation capacitances. First, according to the circuit equations, the formulas for calculating the power factor and output power, and so on, of the system under incomplete compensation are listed. The changes of output characteristics of the system, such as power factor, output power, coil transfer efficiency, and capacitors’ voltage stress, when the compensation capacitances are in error are analyzed in detail. Although [
20] provides a method to recover both the reactive parts and values of the resistive parts of the load/source impedances, the calculation of the power factor, output power, and other indicators is still rather complex and cumbersome. In view of this situation, as the errors of the compensation capacitors are generally controlled within a relatively small range, the Taylor formula is used to expand the original formulas, so that the simplified formulas can intuitively reflect the influence of the parameters and the errors of the capacitors. In the system design, according to the requirements on output characteristics of the system, the capacitances’ allowable error ranges that can meet the requirements are obtained, which provides the basis for the selection of reasonable capacitance accuracy.
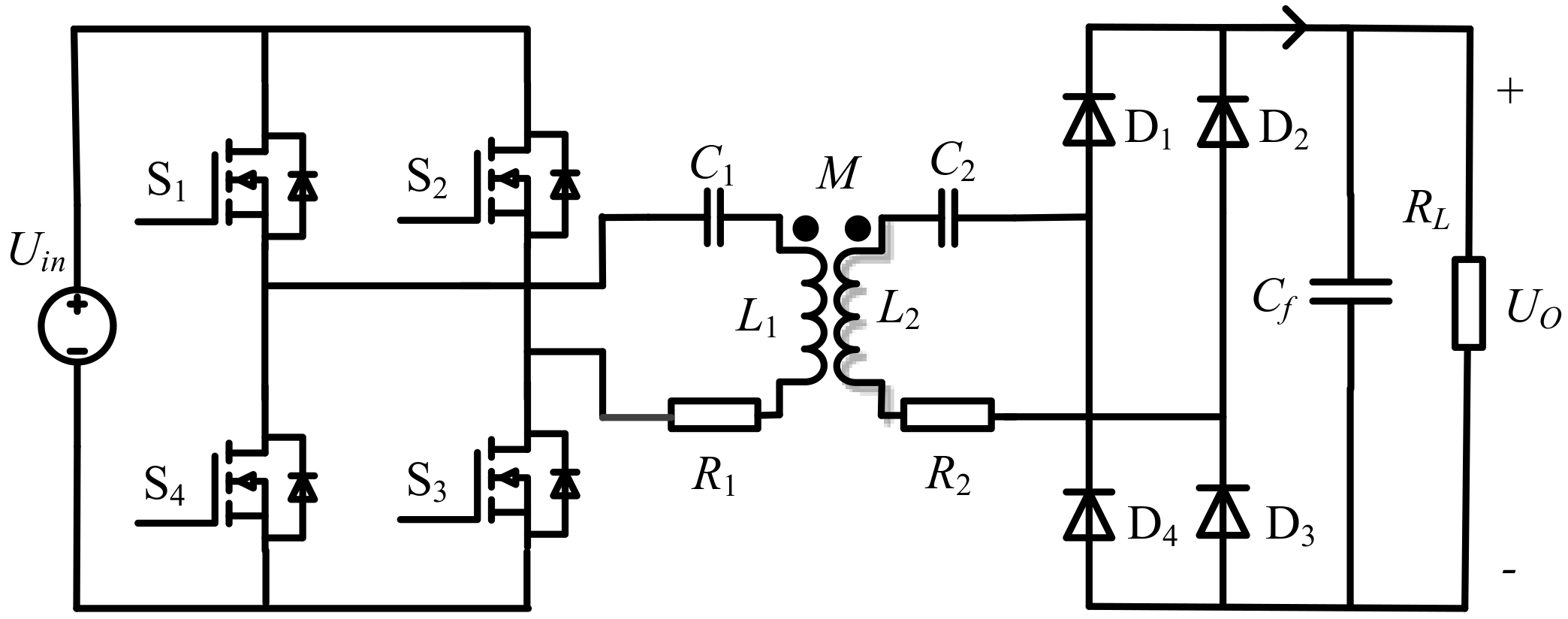
2. Analysis of SS Compensation Topology
A typical schematic diagram of a WPT system with SS topology is shown in
Figure 1.
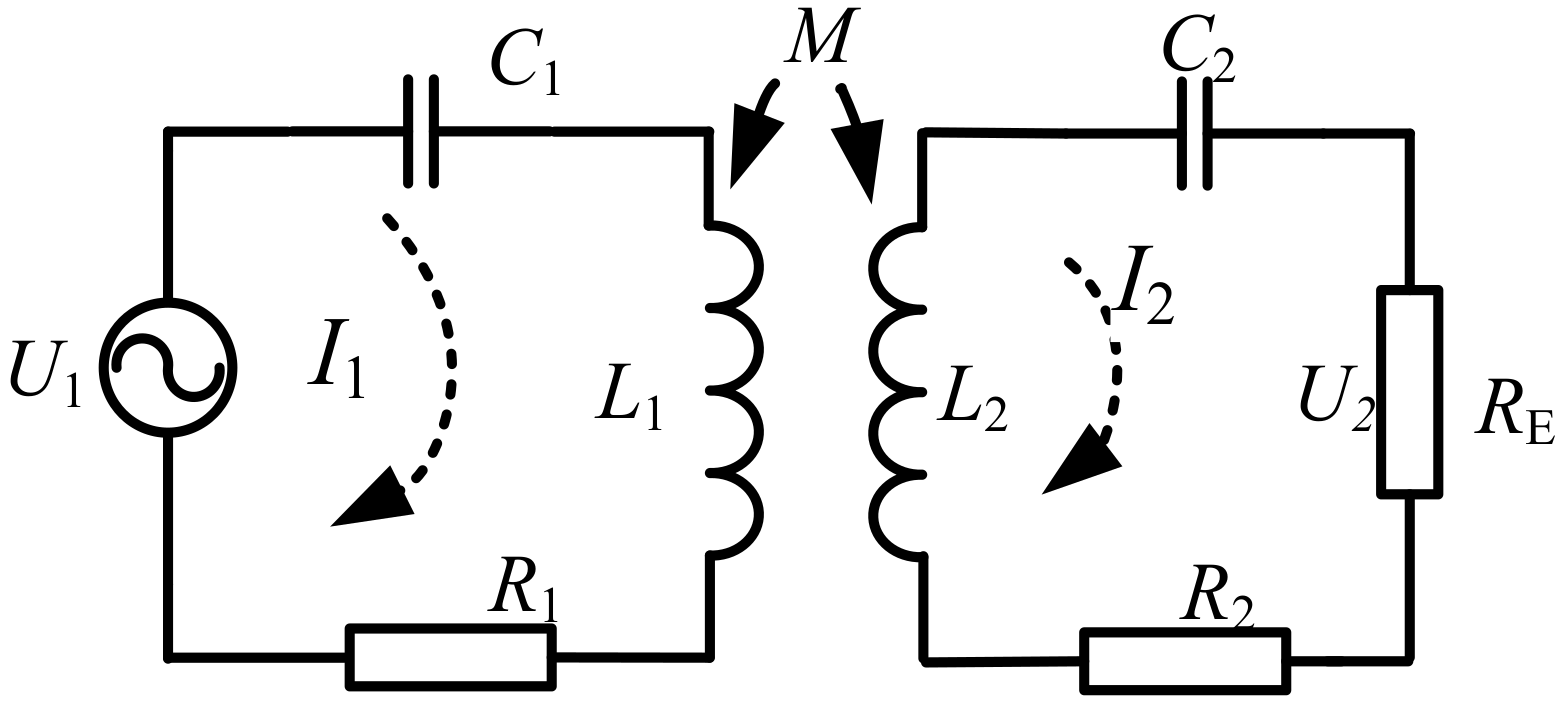
To simplify the analysis,
Figure 1 can be equivalent to a simple model as shown in
Figure 2. Among them,
Uin and
UO is the input and output direct current (DC) voltage,
U1 and
U2 are the root-mean-square (RMS) values of the output voltage of the high frequency inverter and input voltage of the diode rectifier filter circuit,
I1 and
I2 are the RMS values of the output current of the high frequency inverter and input current of the diode rectifier filter circuit. By the Fourier decomposition, only the fundamental harmonic is considered, because high-order harmonic amplitudes are small and these harmonics can hardly be transmitted.
L1 and
L2 are the self-inductances of the loosely coupled transformer, and
M is the coil mutual inductance.
R1 and
R2 are the internal resistances of the primary coil and secondary coil, and
RL and
RE are the load resistance and equivalent resistance, respectively.
By the Fourier decomposition of the square wave,
U1 and
U2 are expressed as:
According to Kirchhoff’s Voltage Law (KVL), the following equations can be obtained:
The relationship between the output equivalent resistance of coupling coils (
RE) and load resistance (
RL) is expressed as follows [
23]:
where
VDth is the threshold voltage, which has a constant value, and
rD is the equivalent resistance of the diode. And the loss on the diodes is usually ignored in the theoretical analysis, so
is considered in the following.
The input current
I1 and output current
I2 can be calculated:
Next the input impedance of the primary side is obtained:
The
ω is the operating angular frequency:
When the operating angular frequency meets Equation (8), the system is fully compensated and the primary input impedance
ZIN is pure resistive. Keeping the secondary under resonance can enhance the power transfer capability and efficiency, while keeping the primary under resonance can decrease the voltage-ampere (VA) rating of the source under the same output power [
18]. It can be seen from Equation (8) that, when the coil self-inductance and system operating frequency are determined, the values of the compensation capacitors are only related to the operating frequency and self-inductance of the coils, and not to the load resistance and mutual inductance between the coils.
Power factor is an important index by which to measure the effect of power transfer, and is defined as the resulting phase between the voltage and current waveforms.
is the input impedance angle of the primary, and
Re[
ZIN] represents the real part of the input impedance. When the system is fully compensated, then
, and
.
Next the output power is obtained:
The coil transfer efficiency can be expressed as follows:
The voltage stress of the compensation capacitor is:
3. Analysis of Influence of Compensation Errors
In practical application, due to the fact that the coils’ parameters are difficult to measure accurately, the capacitors themselves contain errors, for which it is very difficult to perfectly compensate. Therefore, it is necessary to study the influence of incomplete compensation on the output characteristics of the system, then provide the basis for the selection of the capacitances’ accuracy in the system design.
The accurate values of the compensation capacitances, calculated by Equation (8), are expressed by C10 and C20, while the actual values of the compensation capacitances are expressed by C1 and C2, and the ratio between the actual values and exact values the compensation capacitors are represented by k1 and k2, thus C1 = k1C10 and C2 = k2C20 are given.
3.1. Influence on Power Factor
According to Equation (9), the power factor under incomplete compensation can be expressed as follows:
It can be seen from Equation (14) that the calculation formula of the power factor without any treatment is rather complex. It is difficult to see the influence degree of the errors of two compensation capacitors on the power factor of the system. Therefore, next the above formula is dealt with as follows. The following two variables,
e1 and
e2, are defined as follows:
Clearly,
e1 and
e2 can be considered as the relative errors of the two capacitors. Then Equation (14) can be simplified as follows:
Next, it can be seen from Equation (15) that when the errors of compensation capacitors are within a relatively small range, for example, ±10% and ±5%,
e1 and
e2 are both real values close to zero, so that the Taylor formula can be used to expand Equation (16) at
e1 = 0 and
e2 = 0, and the result is as follows:
Ignoring the higher order terms, Equation (17) can be further simplified into:
In the actual system, the following formula should be satisfied:
When the coils internal resistances are neglected, the simplified formula of the power factor can be obtained:
It can be seen from Equation (20) that
ω,
L1,
L2,
M,
RE,
e1 and
e2 are all important factors which affect the power factor. Once the system is determined, there will be an optimal load calculated by Equation (21), in which the maximum coil transfer efficiency is obtained:
Therefore, the errors of the capacitances will have a permissible range within which the power factor can still remain high.
3.2. Influence on Output Power
In the same manner, the influence of the capacitance errors on the output power can be explored. When errors exist, the output power is as follows:
The simplified formula can be obtained as follows, by expanding Equation (22) with the Taylor formula, and ignoring the higher order terms:
Thus the change rate of output power is:
3.3. Influence on Coil Transfer Efficiency
When the capacitances are in error, the coil transfer efficiency is calculated as follows:
Clearly, it can be seen from Equation (25) that, the original formula itself is simple enough, so there is no need to use the Taylor formula to expand it, and the error of the primary series capacitor does not affect the transfer efficiency, only the error of the secondary series capacitor does.
3.4. Influence on Capacitors Voltage Stress
In general, when there are errors in the compensation capacitors, the current in the coils will change, as will the capacitors’ voltage stress. Thus, it is necessary to study the influence of the capacitance errors on the capacitors voltage stress for the actual selection of voltage stress class of the compensation capacitors.
When the two compensation capacitors both contain errors, the voltage stress of
C1 is as follows:
Clearly, the change rate of voltage stress of
C1 is:
And the voltage stress of
C2 is:
The change rate of voltage stress of
C2 is:
Therefore, the change rates of voltage stress of C1 and C2 can be calculated using Equations (27) and (29) when there are errors in the compensation capacitances, which is important for determining the voltage stress class of the compensation capacitors.
4. System Performance Analysis
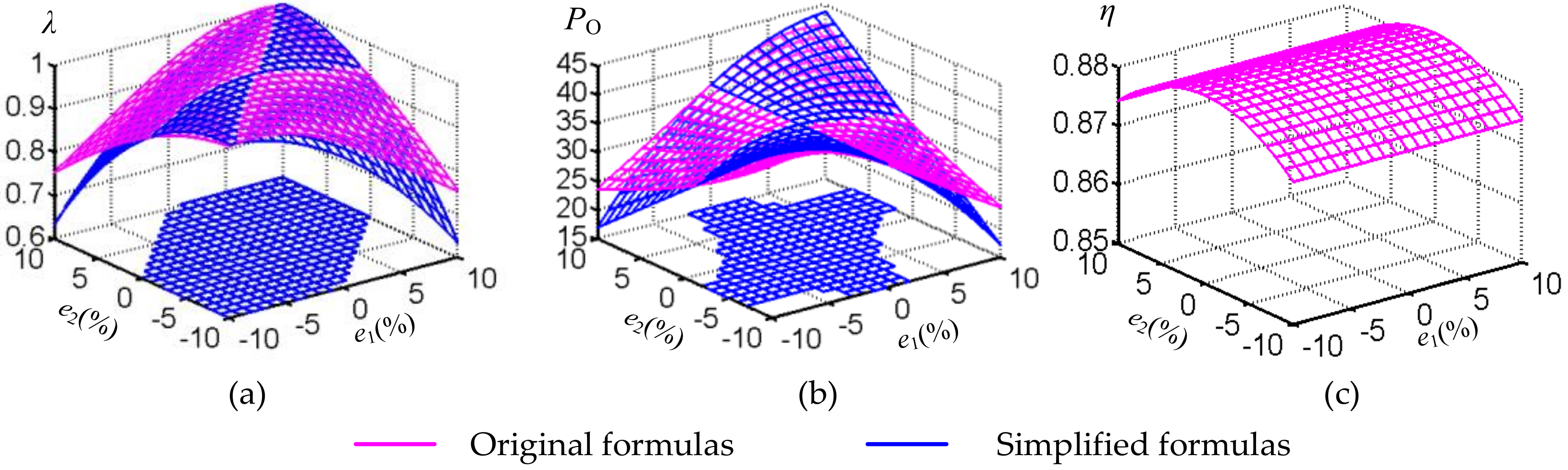
According to the parameters of the actual coils, taking the capacitor precision of ±10% as an example, the power factor, output power, and coil transfer efficiency varying with the capacitance errors are shown in
Figure 3 using the parameters shown in
Table 1.
As shown in
Figure 3a, the power factor remains high when the errors are within a certain range. Taking the power factor of no less than 0.9 as an example, the allowable range of capacitance errors calculated using the simplified formula is drawn, as shown in the shaded area of the XOY plane in
Figure 3a. In some areas, such as in the vicinity of
e1 = 10% and
e2 = −10%, the error between the original and simplified formula is larger than 10%, but the power factor in these regions is low, which will be abandoned. And the error between the original and simplified formula is smaller than 4% when the capacitance errors are within the allowable range calculated using the simplified formula. Thus, it is acceptable to use the Taylor formula to expand the original formula and simplify it. Besides, it can be seen from
Figure 3a that, when two compensation capacitances are both larger and smaller than the exact values, the power factor remains high. The reason is that when the compensation capacitance of the secondary is larger (smaller), the secondary is in a capacitive (inductive) state, that is, the imaginary part of
Z2 is negative (positive), while the reflection impedance reflected to the primary is inductive (capacitive), that is, the imaginary part of
is positive (negative), as shown in Equation (7). Therefore, the equivalent load of the inverter may be turned into pure resistance if the compensation capacitance of the primary is larger (smaller) too, and the high power factor is maintained as a result.
As shown in
Figure 3b, the output power of the system is significantly affected by the capacitance errors when the parameters shown in
Table 1 are employed. When the change rate of the output power of the system is limited to no more than 10%, the allowable error range of the compensation capacitance is shown as the shaded area of the XOY plane in
Figure 3b. The error between the original and simplified formula is smaller than 5% when the capacitance errors are within the allowable range calculated using the simplified formula. So, similarly, the large error in some regions does not affect the final result.
Combined with
Figure 3c and the theoretical calculation formula above, the error of the primary series capacitor does not affect the coil transfer efficiency. Only the error of the secondary series compensation capacitor affects it, and the existence of the error reduces the coil transfer efficiency. When the error of the secondary series compensation capacitor is 10%, the coil transfer efficiency is reduced from 88.2% to 87.4%, which indicates that the coil transfer efficiency is less affected by the error of the secondary series compensation capacitor when the system parameters shown in
Table 1 are employed. Thus, the effect of capacitance errors on coil transfer efficiency is ignored when calculating the allowable capacitance error range.
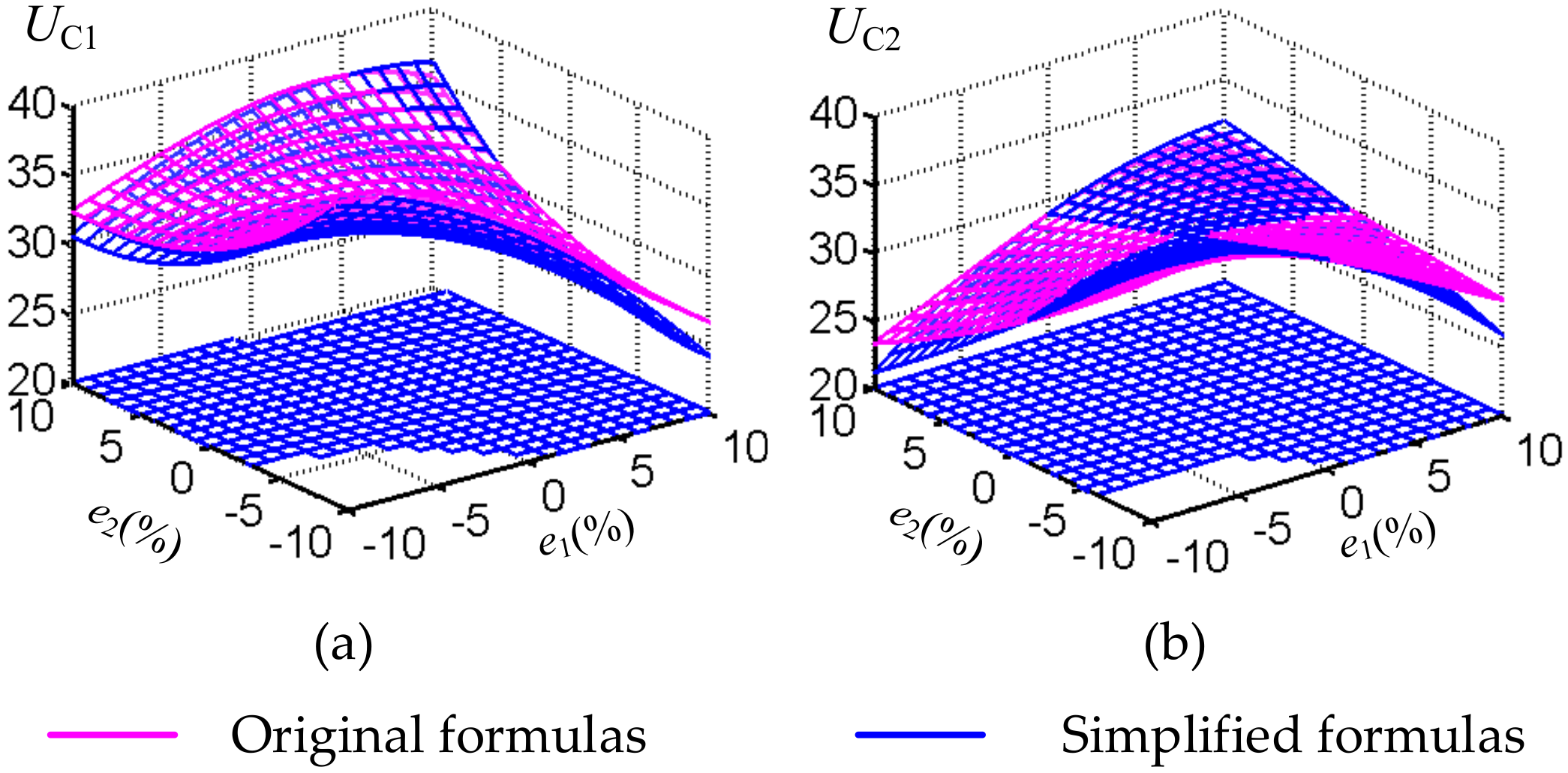
The variation of the voltage stress of the primary series capacitor and secondary series capacitor are shown in
Figure 4a,b. When there are errors in the compensation capacitors, the system will generate reactive power, thereby affecting the current amplitude and the voltage amplitude of the capacitors. In practical use, the withstand voltage level of capacitors is also a factor that cannot be ignored, as it affects the system safety. Therefore, it is necessary to restrict the voltage stress of the compensation capacitors. When the rise rates of the voltage stress of capacitors are limited to no more than 10%, the allowable error ranges of the compensation capacitance are shown as the shaded area of the XOY plane in
Figure 4a,b.
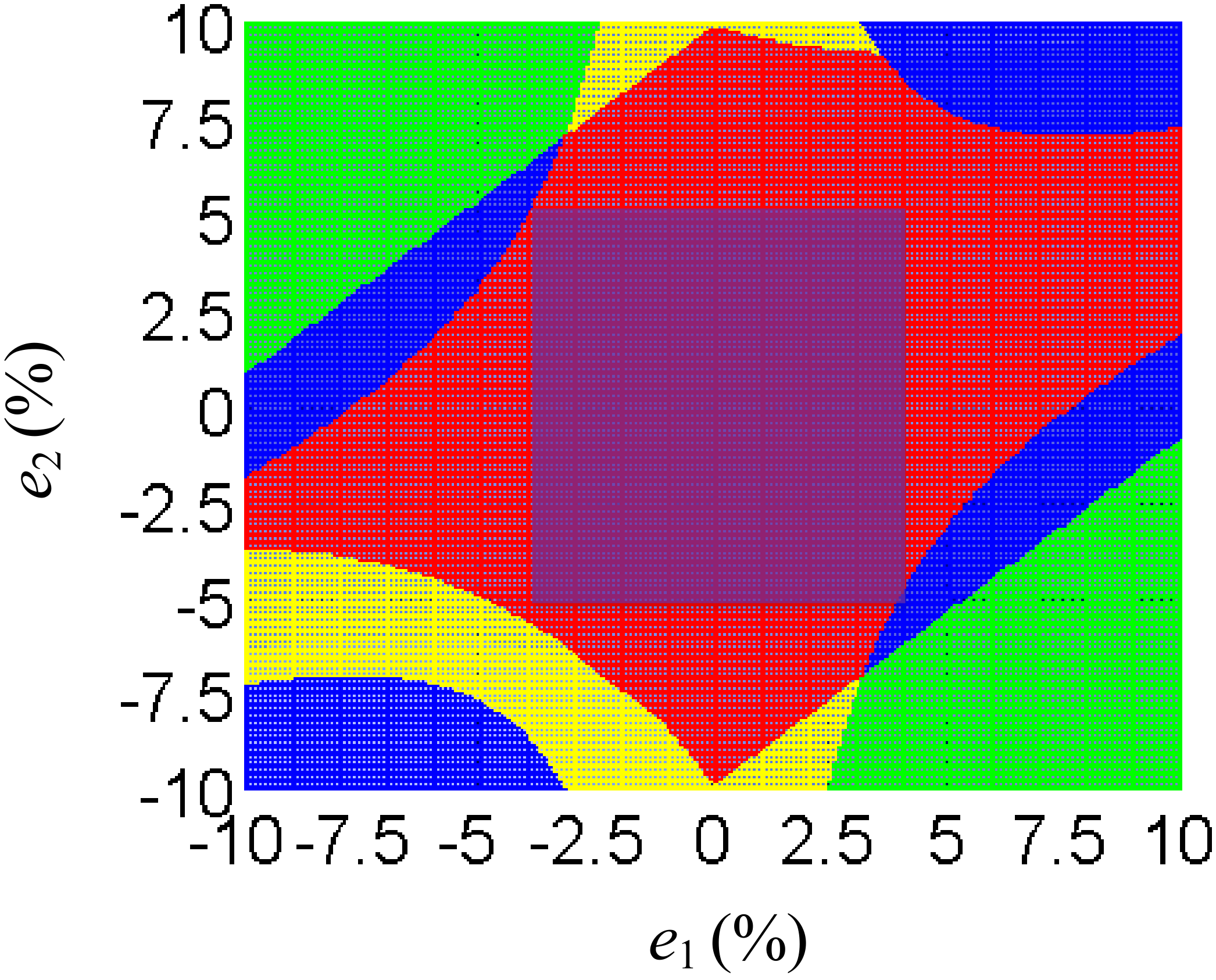
The selection of the accuracy of compensation capacitors should meet the restrictions of the system on power factor, output power, capacitors voltage stress, and other targets. Therefore, in actual use, it is necessary to take the intersection of the shaded area on the XOY plane shown in
Figure 3 and
Figure 4. The allowable error ranges of the compensation capacitances are shown in
Figure 5. The blue and yellow regions are the allowable capacitance error ranges meeting the requirements of power factor and output power, respectively. And the green and cyan regions, which is sheltered, are the allowable capacitance error ranges meeting the requirements of the voltage stress of
C1 and
C2, respectively. The red region is the intersection of all the above allowable range.
In practical application, the selection of two compensation capacitors is independent. Therefore, some areas, where the accuracy requirement of a capacitor is related to another’s, for instance, when e1 = 10%, e2 must be between 3% and 7%, are abandoned. And it can be seen from the red area, e1 = ±3%, e2 = ±7%, and e1 = ±4%, e2 = ±5% and other selections are all acceptable. Obviously, the price of a capacitor rises sharply with the increase of precision. Therefore, e1 = ±4%, e2 = ±5% may a better choice, finally, just like the purple region shows.
5. Experimental Verification
Experimental verification is performed using the experimental platform, as shown in
Figure 6. This platform adopts a TMS320F28335 DSP (TI, Dallas, TX, USA) as the control core and the primary side inverter switch is an FMP65N15T2 (Fuji, Japan), a MOSFET produced by Fuji Electric. The primary and secondary inductors are square coils with a single layer and a turn number of 12, composed of tightly-wound litz wires with a diameter of 3 mm. The length and width of square coils are 25 cm and 18 cm, respectively, and the gap between the primary and secondary is 6.5 cm. The input voltage
U1 and output voltage
U2 are measured using a THDP0200 (Tektronix, OH, USA), and the input current
I1 and output voltage
I2 are measured using a TCP0030A (Tektronix, OH, USA). The phase between the voltage and current waveforms are measured using the phase measurement function of a Tektronix dpo3034 digital phosphor oscilloscope (Tektronix, OH, USA), and the other data are calculated using the measured output voltage and current of the inverter and load. And the system uses the parameters listed in
Table 1 for experimental verification. The actual capacitances values, the mutual inductance, and the self-inductance of coils are measured by a HM8118 LCR bridge (HAMEG, Mainhausen, Germany), and the actual capacitance values of
C1 and
C2 and the calculated values of
e1 and
e2 are listed in
Table 2.
According to the actual capacitance values, the calculated values of
e1 are −10.1%, −5.2%, −0.3%, +4.8%, and +9.8%, respectively, while those of
e2 are −10.0%, −5.3%, +0.3%, +4.4%, and +10.2%. These capacitors are employed, respectively, thus 25 sets of experiments are carried out. When the experiment is carried out, and there is no rectifier in the secondary. Limited by the parameters of the coils, the power level of the confirmatory experiment is very small, only a few dozen watts. And it can be seen from Equation (5) that, the equivalent resistance of coupling coils
RE can be considered to be equal to
only when
is smaller than
and can be ignored, and the loss on the rectifier diodes will not significantly affect the system’s output characteristics. When there is a rectifier in the secondary, the output voltage
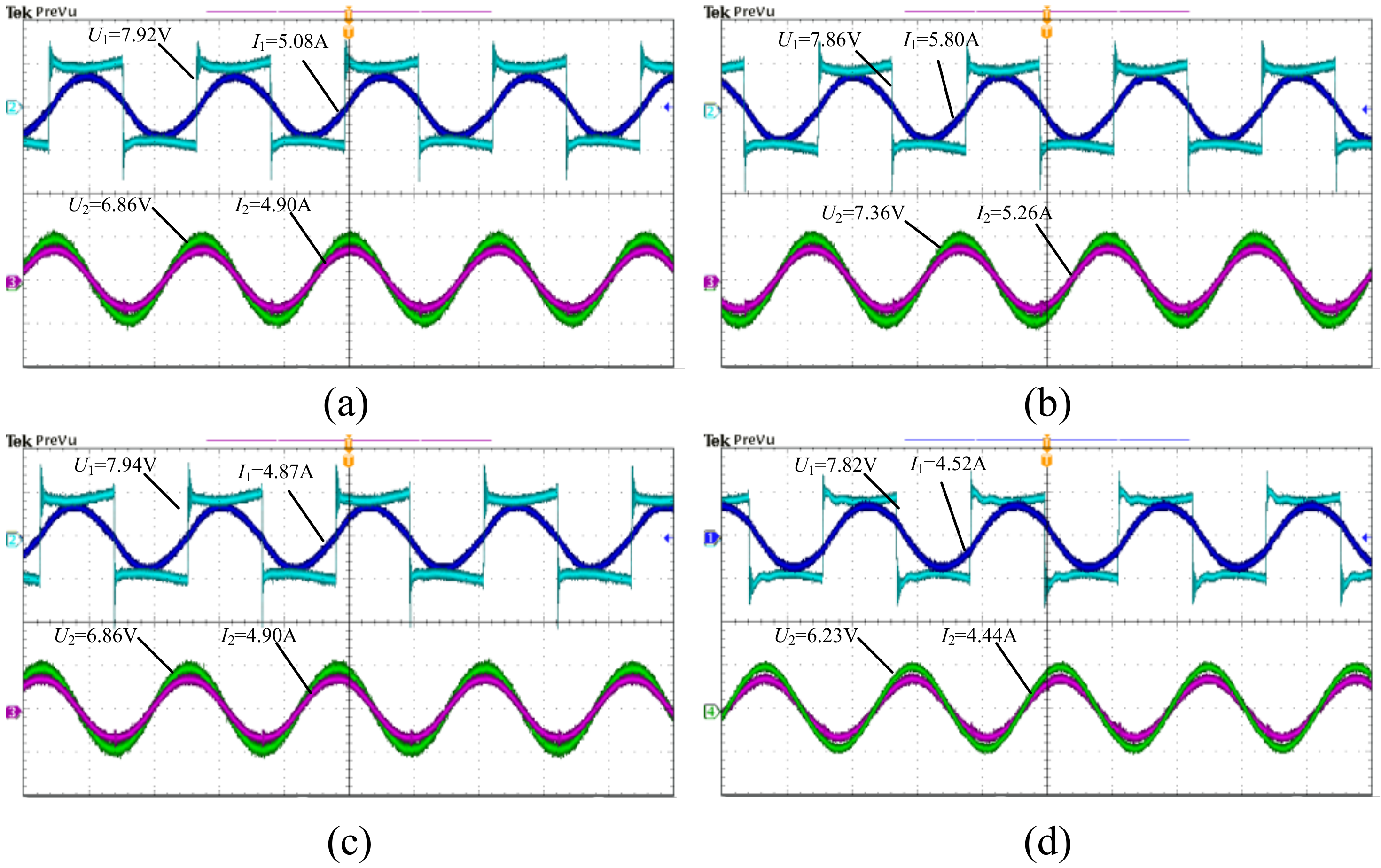
U2 will be a square wave due to the existence of the filter capacitance, which is a sinusoidal wave when there is no rectifier. But high-order harmonic amplitudes are small and these harmonics can hardly be transmitted. So it is feasible to use the resistor without parasitic inductance to be connected to the compensated coil in the experiment. And the output voltage and current waveforms of the inverter and load under the different compensation capacitances errors are shown in
Figure 7, in which the annotation
U1 is the RMS value of the fundamental harmonic of the inverter’s output voltage.
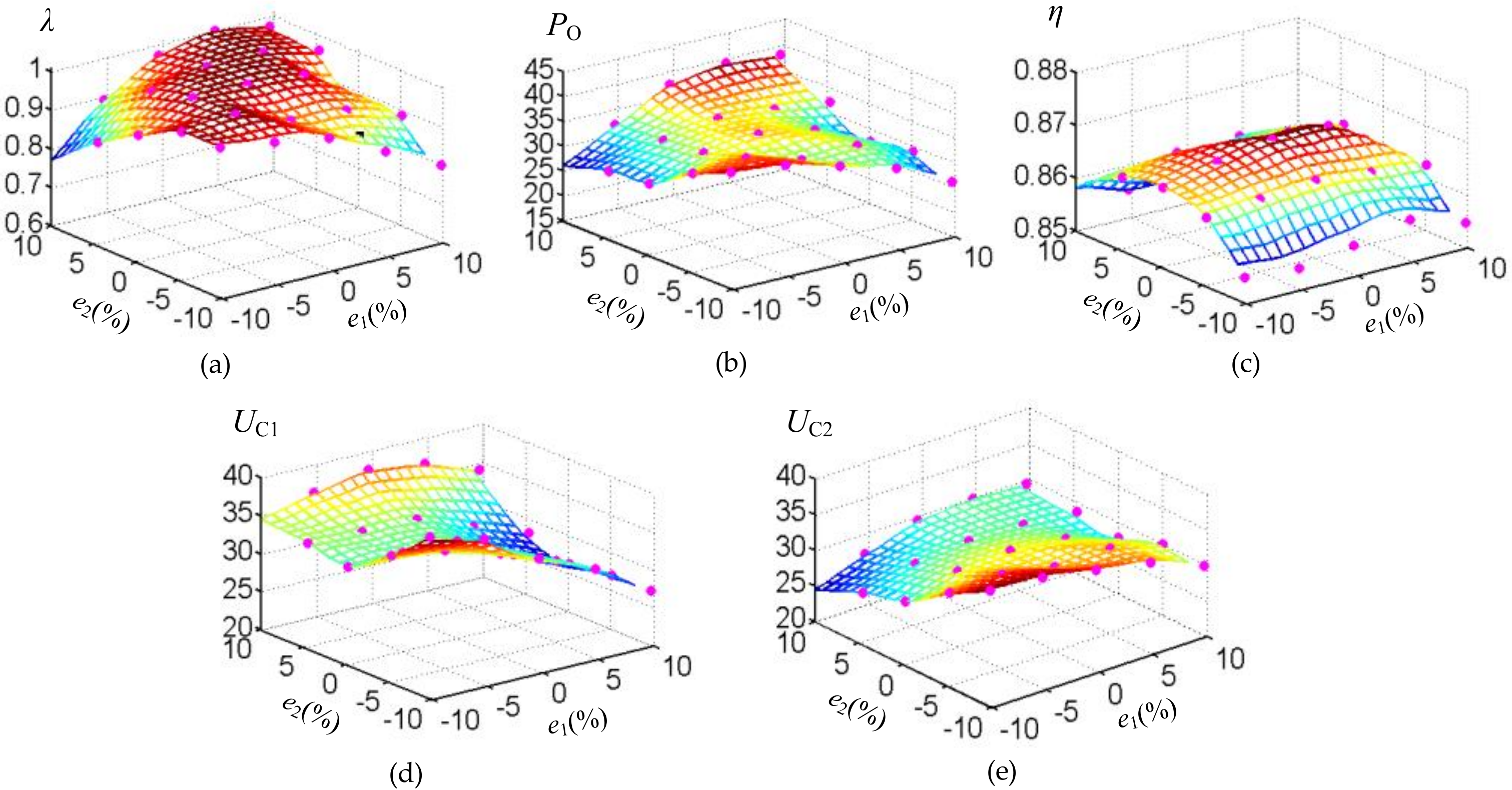
The power factor, output power, and coil transfer efficiency and capacitors’ voltage stress varying with the capacitance errors obtained in the experiments are shown in
Figure 8, in which the data of the magenta points are the calculated results using the measured output voltage and the current of the inverter and load. It can be seen from the experimental results that the power factor, output power, transfer efficiency, and the capacitors’ voltage stress change slowly as the capacitance errors change, thus, the experimental data can be fitted by MATLAB software. The approximate data of the power factor, output power, coil transfer efficiency, and the capacitors’ voltage stress as the capacitance error changes when the capacitance error is within 10% can be obtained, as shown in
Figure 8.
By comparing
Figure 8 with the calculated results of
Section 3, it can be seen that the variation trend of the power factor, output power, coil transfer efficiency, and the capacitors’ voltage stress with capacitance errors is in line with the theoretical calculation results. And the error between the experimental results and theoretical calculation is less than 10%.
The analysis results show that error between the theory and experiment exists in many aspects. First, in the actual circuit, the equivalent load of the inverter, capacitive or inductive, will affect the turn-on and turn-off characteristics of the switches, and this is not considered in the theoretical calculation. When the input DC voltage of the inverter is constant, 10 V in this experiment, the RMS value of the output voltage of the inverter changes slightly with the load’s capacitive or inductive state, as shown in
Figure 7, which will further affect the output power and the capacitors’ voltage stress. In addition, the dead time of the driving pulse of the inverter, approximate treatment in the theoretical calculation formulas, and actual electromagnetic leakage will all affect the transfer characteristics of the system, while these factors are not taken into consideration. Thus, although there is an error between the experimental results and theoretical calculations, the error is within an acceptable range, and the experiment can verify the validity of the theoretical analysis.
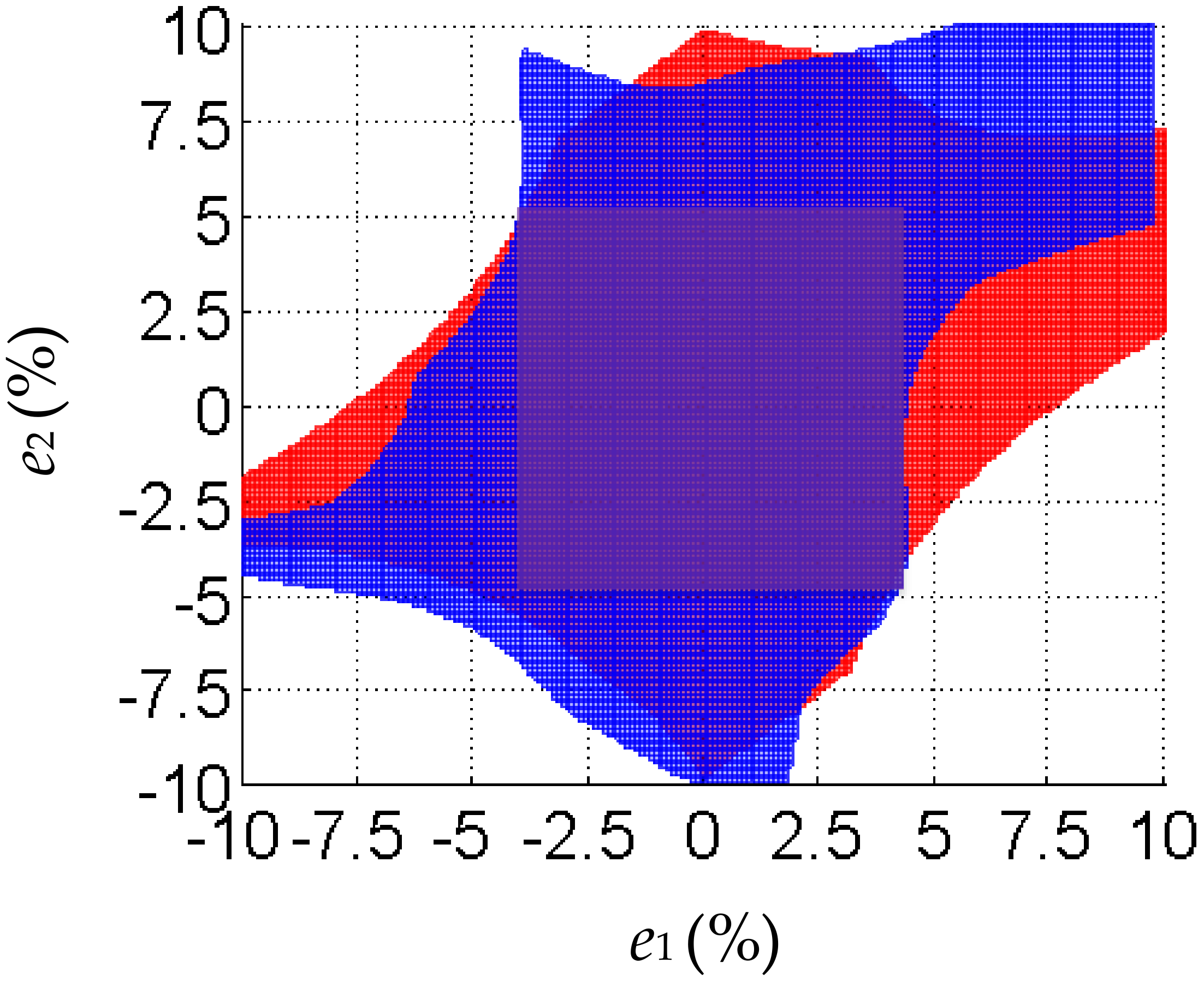
According to the requirements of the system on the power factor, output power change rate, and voltage stress rise rate of the capacitors assumed in
Section 3, the capacitance error range which meets the above requirements in the actual experiment can be obtained. As shown in
Figure 9, the blue area is the allowable capacitance error range of the experimental data, and the red area is the allowable range derived from theoretical calculation. In the upper right corner of
Figure 9, the error between the experimental results and theoretical calculations is larger than other regions, this is because, in this area, the equivalent load of the inverter is capacitive, the RMS value of the fundamental harmonic of the inverter’s output voltage is smaller than 8V in the experiments, resulting in output power, and the voltage stress is less than the theoretical value. When the compensation capacitance of the primary is larger, the equivalent load of the inverter may be turned into pure resistance if the compensation capacitance of the secondary is large, too, just as the analysis in
Section 3 shows, and the output voltage of the inverter may be increased to 8 V again, therefore, the error comes out.
As shown in the figure above, as far as the allowable range satisfying the entire system’s requirements is concerned, the error between the theoretical calculation and actual experiment is within the allowable range, thus proving the validity of the method.