A Combined Electro-Thermal Breakdown Model for Oil-Impregnated Paper
Abstract
:1. Introduction
2. Materials and Methods
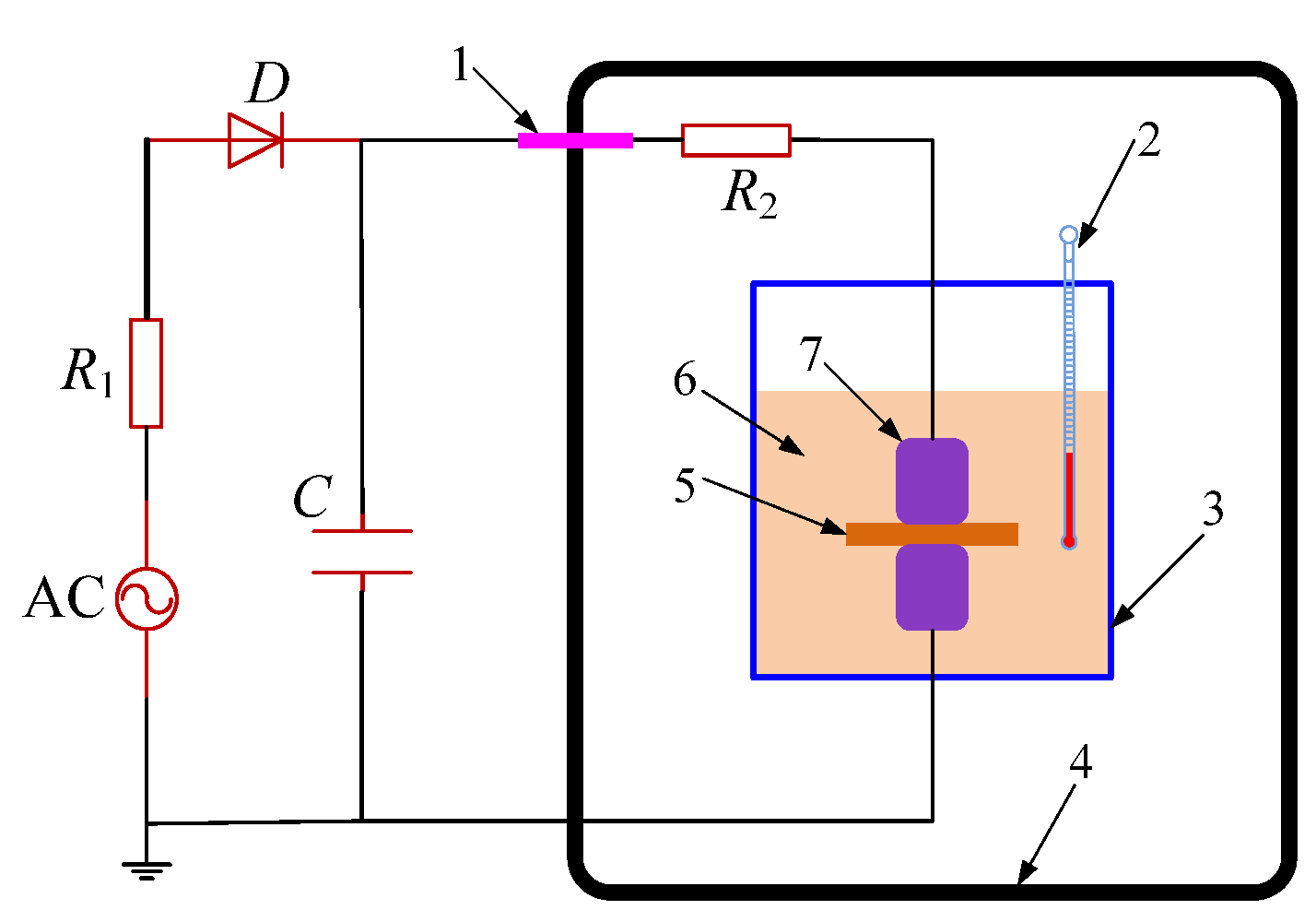
2.1. Electro-Thermal Breakdown Test
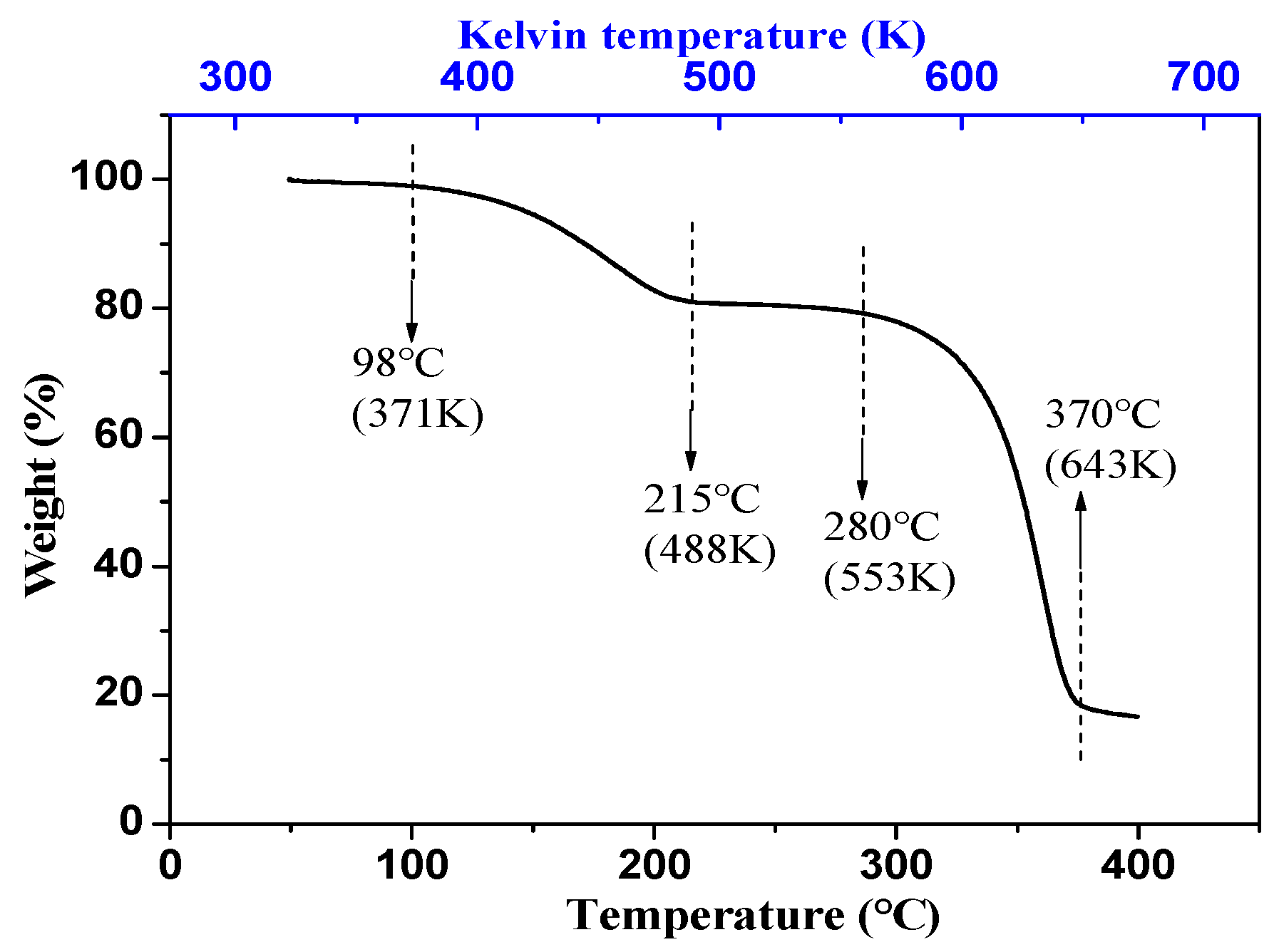
2.2. Thermal Gravimetric Analysis and Conducitivity Measurement
3. Results
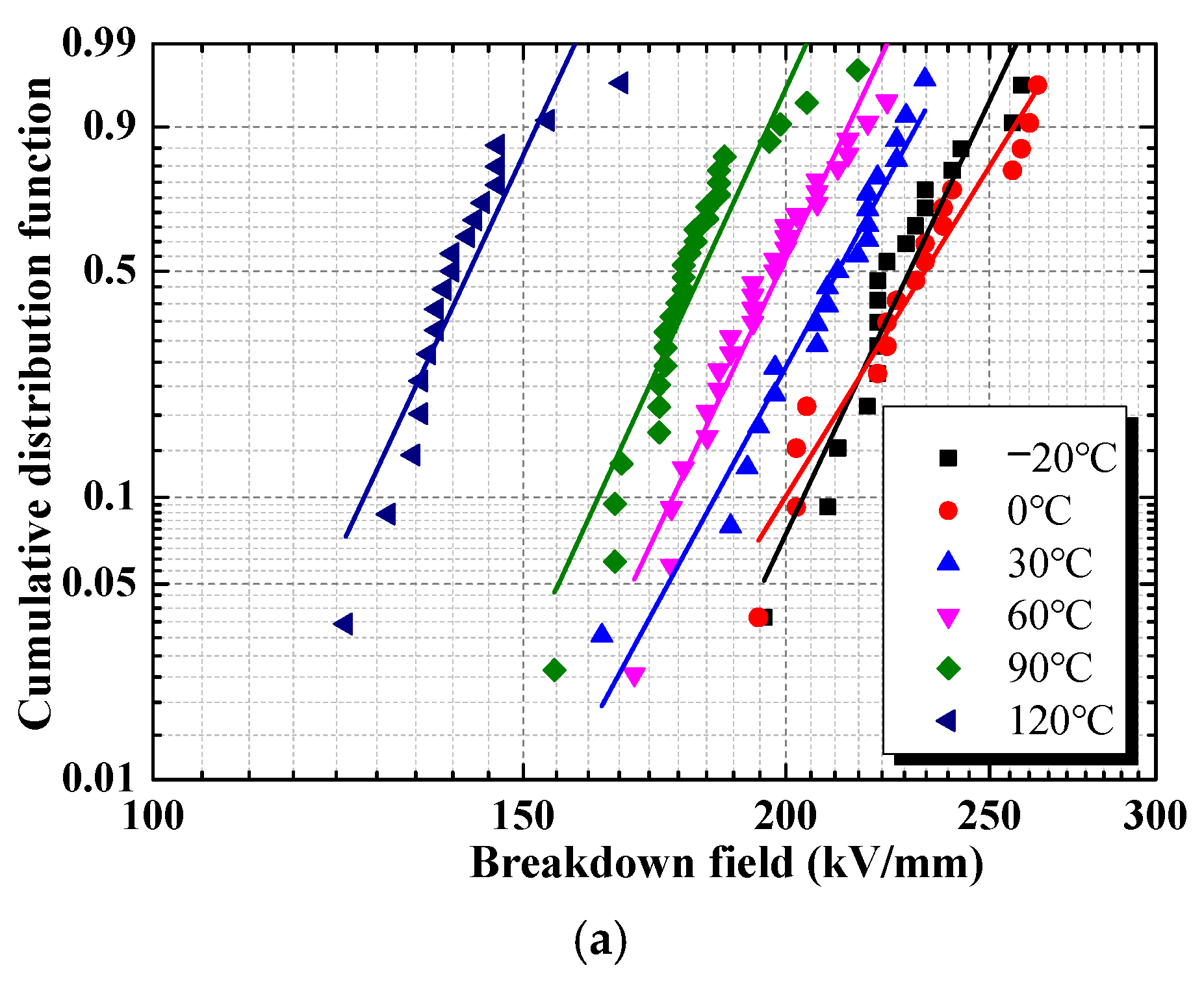
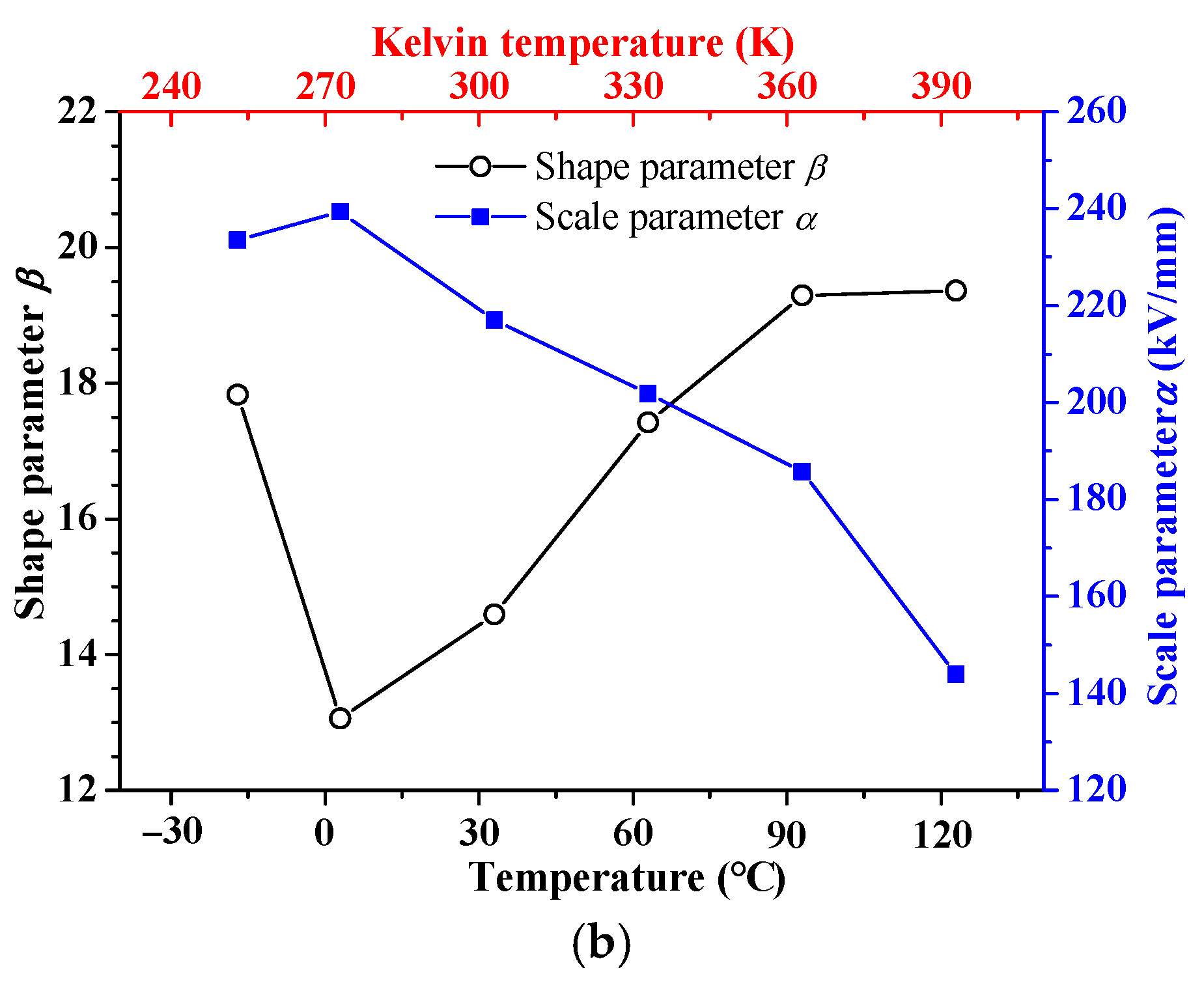
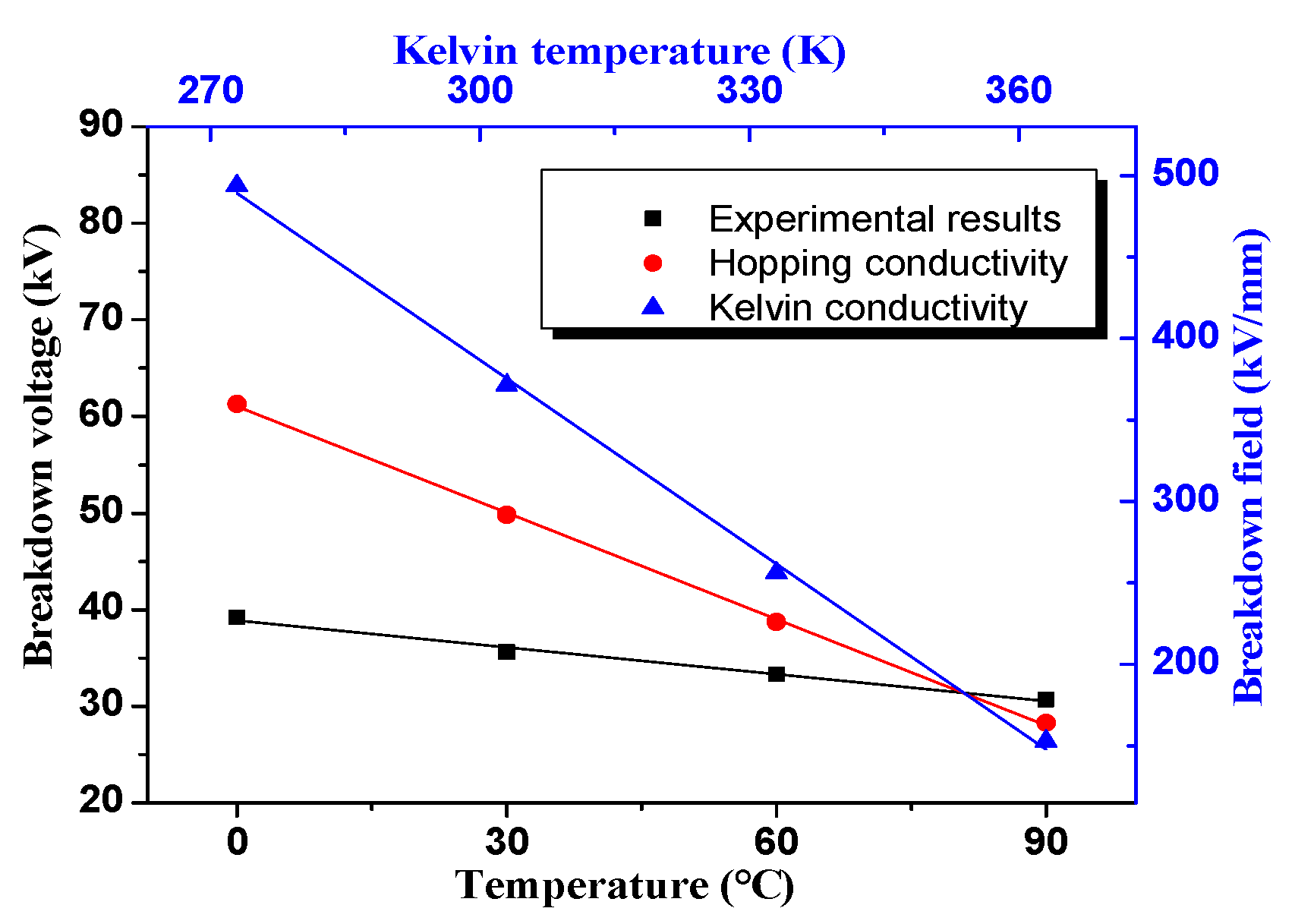
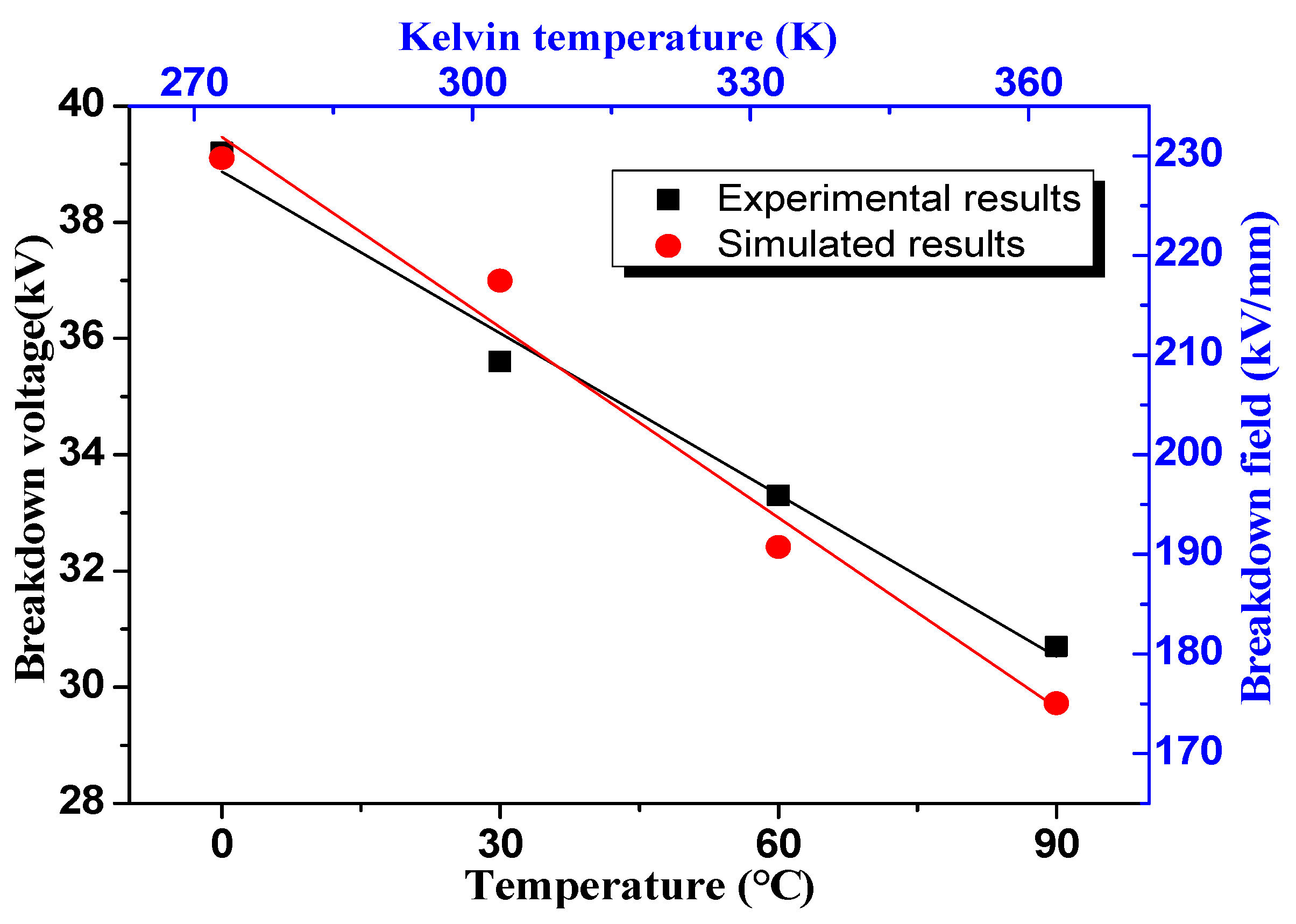
3.1. Breakdown Experiments under Different Temperatures and Thermal Gravimetric Test
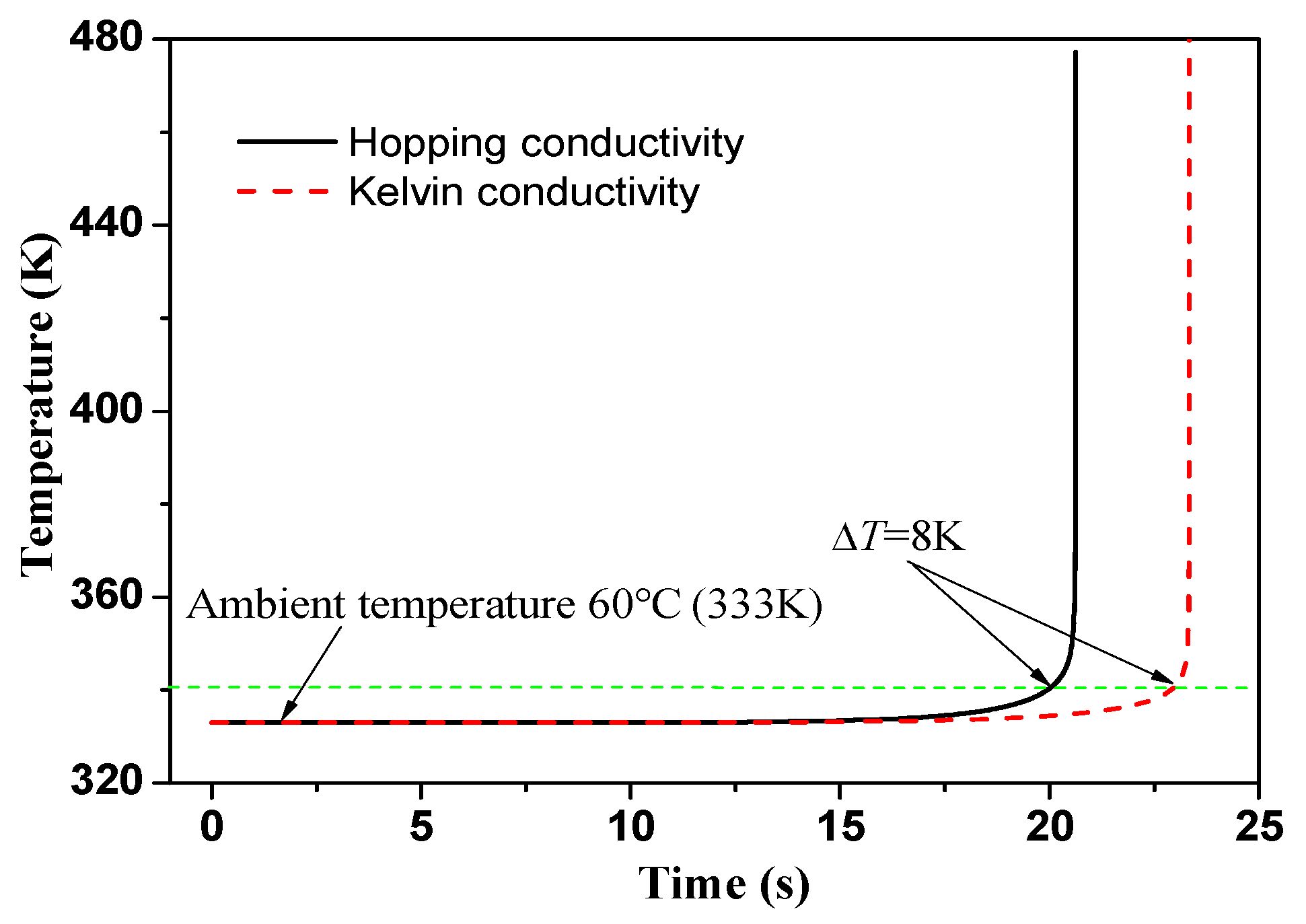
3.2. Thermal Breakdown Simulation
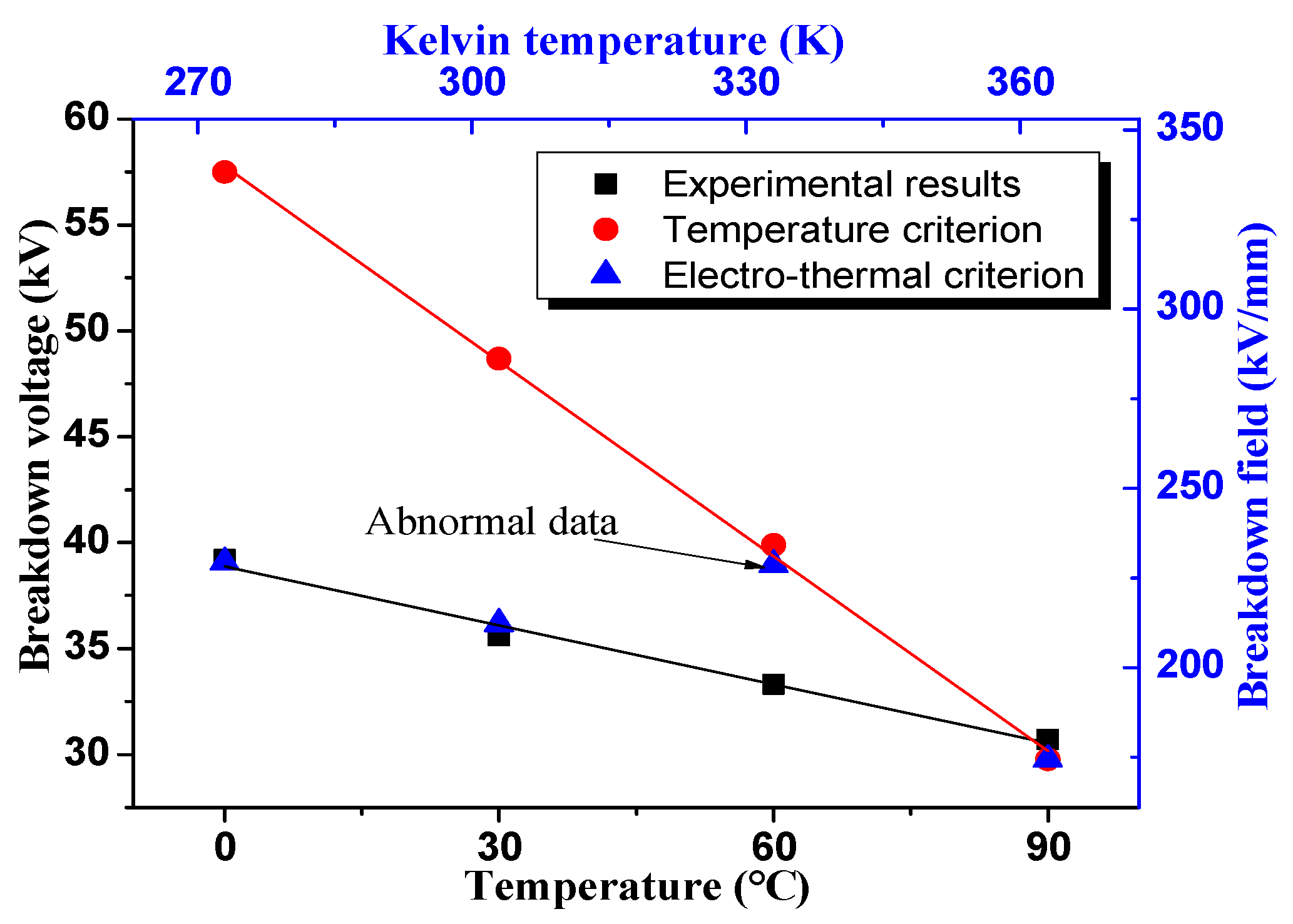
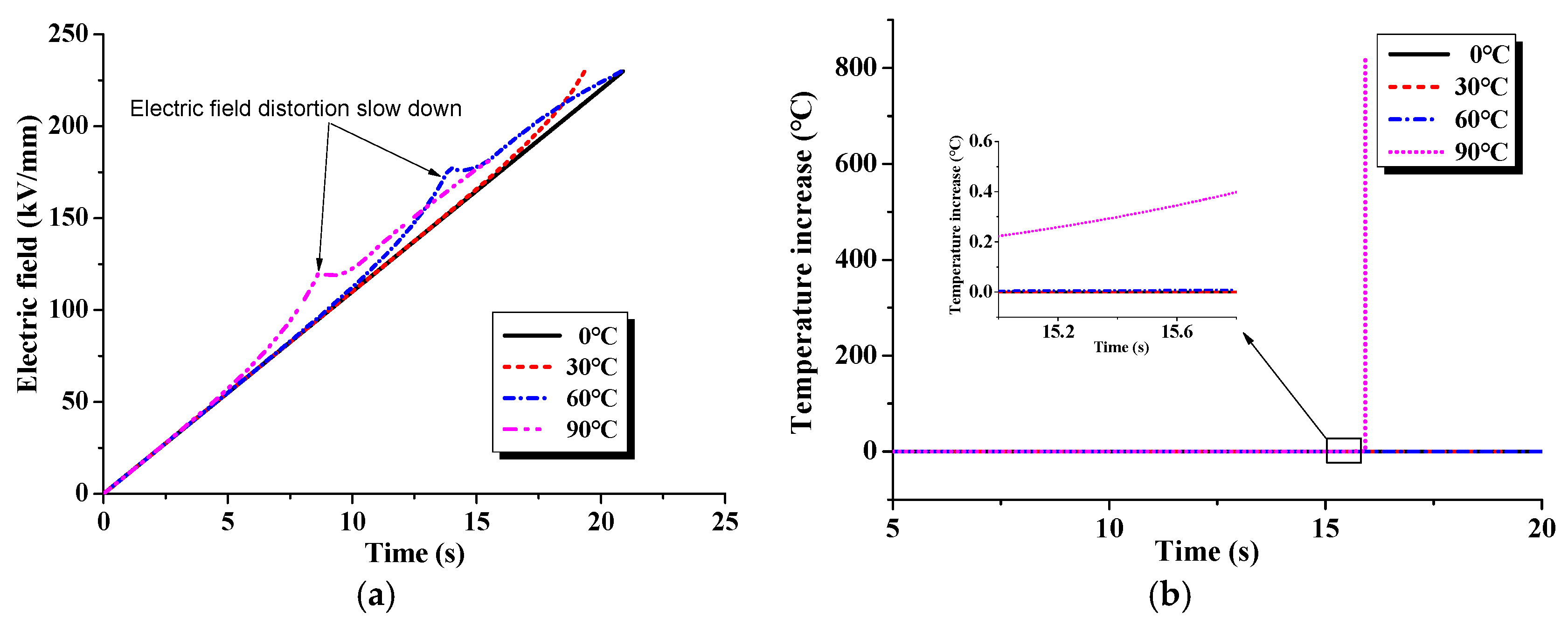
3.3. Electro-Thermal Breakdown Simulation
4. Discussions
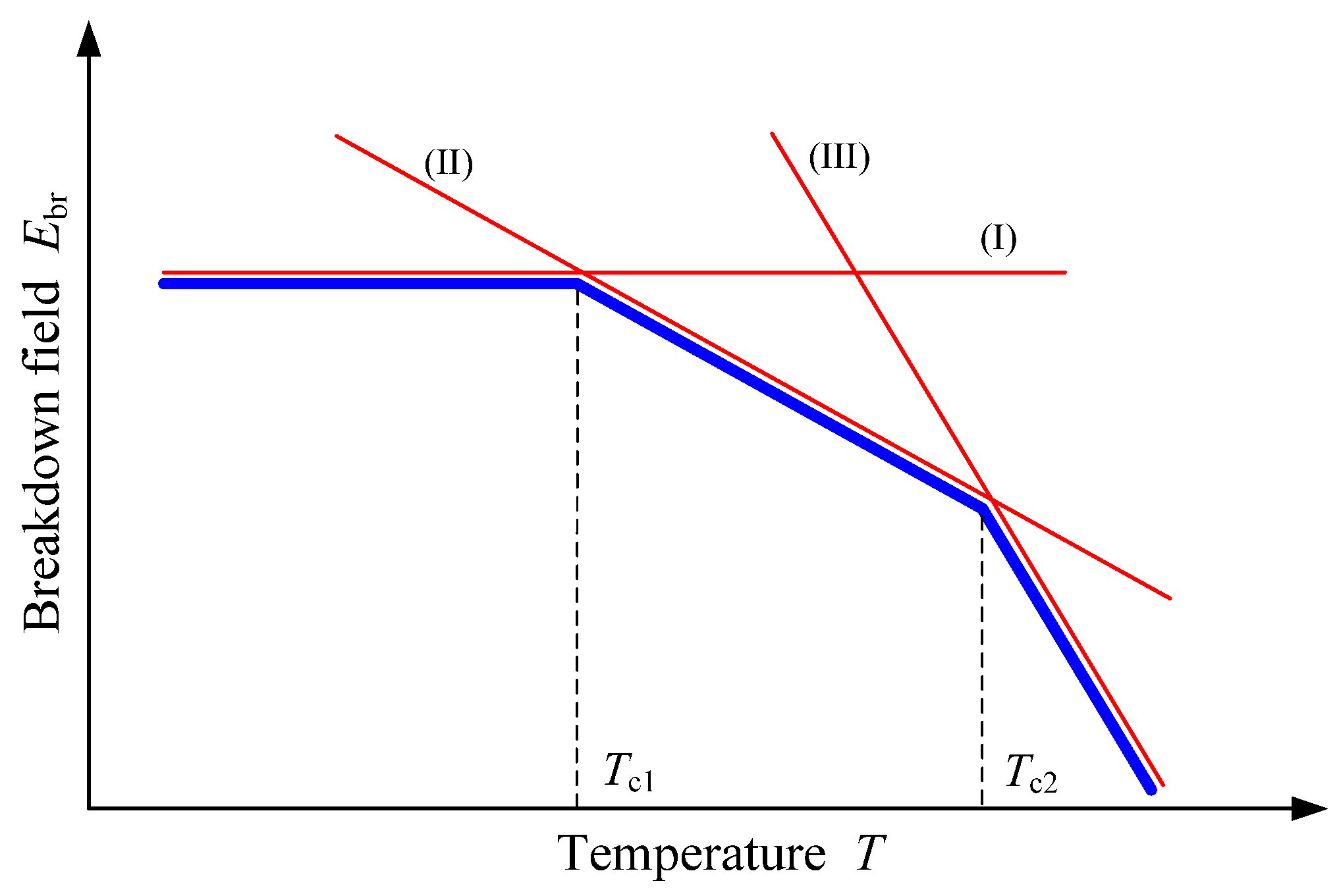
4.1.Thermal Breakdown Simulation
4.2. Electro-Thermal Breakdown Simulation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, Y.; Zhang, Q.; Wang, T.; Li, J.; Guo, C.; Ni, H. Degradation characteristics of oil-immersed pressboard samples induced by partial discharges under DC voltage. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1110–1117. [Google Scholar] [CrossRef]
- Hikita, M.; Nagao, M.; Sawa, G.; Ieda, M. Dielectric breakdown and electrical conduction of poly (vinylidene-fluoride) in high temperature region. J. Phys. D Appl. Phys. 1980, 13, 661. [Google Scholar] [CrossRef]
- Hikita, M.; Sawa, G.; Ieda, M. Electrical breakdown and solid structure of poly(vinylidene-fluoride). J. Phys. D Appl. Phys. 1983, 16, L157. [Google Scholar] [CrossRef]
- Ieda, M.; Nagao, M.; Hikita, M. High-field conduction and breakdown in insulating polymers. Present situation and future prospects. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 934–945. [Google Scholar] [CrossRef]
- Wintle, H. Electrothermal breakdown: Analytic solutions for currents and fields. J. Appl. Phys. 1981, 52, 4181–4185. [Google Scholar] [CrossRef]
- Wei, Y.H.; Mu, H.B.; Deng, J.B.; Zhang, G.J. Effect of space charge on breakdown characteristics of aged oil-paper insulation under dc voltage. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 3143–3150. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Q.; Li, J.; Wang, T.; Dong, W.; Ni, H. Study on micro bridge impurities in oil-paper insulation at DC voltage: their generation, growth and interaction with partial discharge. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 2213–2222. [Google Scholar] [CrossRef]
- Keller, K.J. Formation and annulment of space charges glass and their influence on electric breakdown. Phys. Rev. 1952, 86, 804–805. [Google Scholar] [CrossRef]
- Dissado, L.A.; Mazzanti, G.; Montanari, G.C. The role of trapped space charges in the electrical aging of insulating materials. IEEE Trans. Dielectr. Electr. Insul. 1997, 4, 496–506. [Google Scholar] [CrossRef]
- Zheng, F.; Zhang, Y.; Xiao, C. Relationship between breakdown in polymer dielectrics and space charge. J. Mater. Sci. Eng. 2006, 24, 316–320. [Google Scholar]
- Liao, R.; Hu, E.; Yang, L.; Yuan, Y. Space charge behavior in paper insulation induced by copper sulfide in high-voltage direct current power transformers. Energies 2015, 8, 8110–8120. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, J.; Li, S.; Zhong, L. Origin of thickness dependent dc electrical breakdown in dielectrics. Appl. Phys. Lett. 2012, 100, 222904. [Google Scholar] [CrossRef]
- Choi, D.H.; Randall, C.; Lanagan, M. Combined electronic and thermal breakdown models for polyethylene and polymer laminates. Mater. Lett. 2015, 141, 14–19. [Google Scholar] [CrossRef]
- Boughariou, F.; Chouikhi, S.; Kallel, A.; Belgaroui, E. A new theoretical formulation of coupling thermo-electric breakdown in LDPE film under dc high applied fields. J. Eur. Phys. Plus 2015, 130, 244–251. [Google Scholar] [CrossRef]
- Huang, M.; Zhou, Y.; Chen, W.; Sha, Y.; Jin, F. Influence of voltage reversal on space charge behavior in oil-paper insulation. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 331–339. [Google Scholar] [CrossRef]
- Diaham, S.; Zelmat, S.; Locatelli, M.L.; Dinculescu, S.; Decup, M.; Lebey, T. Dielectric Breakdown of Polyimide Films: Area, Thickness and Temperature Dependence. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 18–27. [Google Scholar] [CrossRef]
- Murakami, Y.; Hozumi, N.; Nagao, M. Surface Temperature Measurement and Analysis of Thermal Breakdown with Ethylene-vinyl Acetate Copolymer in Room-Temperature Region. Jpn. J. Appl. Phys. 2004, 43, 6184. [Google Scholar] [CrossRef]
- Dissado, L.A.; Fothergill, J.C. Electrical Degradation and Breakdown in Polymers; The Redwood Press: Wiltshire, UK, 1992; pp. 49–50. [Google Scholar]
- Jäger, W. Partial Differential Equations: Theory and Numerical Solution; Chapman & Hall/CRC: Boca Raton, FL, USA, 2000; pp. 132–147. [Google Scholar]
- Zhu, Q.; Wang, X.; Wu, K.; Cheng, Y.; Lv, Z.; Wang, H. Space Charge Distribution in Oil Impregnated Papers under Temperature Gradient. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 142–151. [Google Scholar] [CrossRef]
- Le Roy, S.; Segur, P.; Teyssedre, G.; Laurent, C. Description of bipolar charge transport in polyethylene using a fluid model with a constant mobility: Model prediction. J. Phys. D Appl. Phys. 2004, 37, 298–305. [Google Scholar] [CrossRef]
- Tian, J.; Zou, J.; Wang, Y.; Liu, J.; Yuan, J.; Zhou, Y. Simulation of bipolar charge transport with trapping and recombination in polymeric insulators using runge–kutta discontinuous galerkin method. J. Phys. D Appl. Phys. 2008, 41, 195416. [Google Scholar] [CrossRef]
- Zukowski, P.; Koltunowicz, T.N.; Kierczynski, K.; Subocz, J.; Szrot, M.; Gutten, M. Assessment of Water Content in an Impregnated Pressboard based on DC Conductivity Measurements. Theoretical Assumptions. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1268–1275. [Google Scholar] [CrossRef]
- Setayeshmehr, A.; Fofana, I.; Eichler, C.; Akbari, A.; Borsi, H.; Gockenbach, E. Dielectric spectroscopic measurements on transformer oil-paper insulation under controlled laboratory conditions. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1100–1111. [Google Scholar] [CrossRef]
- Wildman, R.A.; Gazonas, G.A. A dynamic electro-thermo-mechanical model of dielectric breakdown in solids using peridynamics. J. Mech. Mater. Struct. 2015, 10, 613–630. [Google Scholar] [CrossRef]
- Tian, J. Simulation of the Space Charge Transport in Insulators under High Electric Field. Doctoral Dissertation, Tsinghua University, Beijing, China, 2009. [Google Scholar]
- Jones, J.P.; Llewellyn, J.P.; Lewis, T.J. The contribution of field-induced morphological change to the electrical aging and breakdown of polyethylene. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 951–966. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, J. Observation of negative differential mobility and charge packet in polyethylene. J. Phys. D Appl. Phys. 2011, 44, 21200121. [Google Scholar] [CrossRef]
- Takahashi, M.; Takenaka, H.; Wada, Y. Electrical conduction of cellulose under DC field. In Proceedings of the 3rd International Conference on Conduction and Breakdown in Solid Dielectrics, Trondheim, Norway, 3–6 July 1989; pp. 182–186. [Google Scholar]

| Symbol | Value | Unit | Symbol | Value | Unit |
|---|---|---|---|---|---|
| a | 2.1 | nm | Cv | 2.5 × 106 | J/(m3·K) |
| ua | 1.1 | eV | J0 | 1.9 × 1013 | A/m2 |
| κ | 0.25 | W/(m·K) |
| Symbol | Meaning | Value | Unit |
|---|---|---|---|
| Net0 | Electron trap density | 100 | C/m3 |
| Nht0 | Hole trap density | 100 | C/m3 |
| Be | Electron trapping coefficient | 7 × 10−3 | s−1 |
| Bh | Hole trapping coefficient | 7 × 10−3 | s−1 |
| Seμ,ht | Recombination coefficient | 4 × 10−3 | m−3 C−1 s−1 |
| Set,hμ | Recombination coefficient | 4 × 10−3 | m−3 C−1 s−1 |
| Set,ht | Recombination coefficient | 4 × 10−3 | m−3 C−1 s−1 |
| ωe | Schottky injection barier | 1.2 | eV |
| ωh | Schottky injection barrier | 1.2 | eV |
| εr | Relative permittivity | 4.4 | — |
| Temperature T ( °C) | 40 | 50 | 70 | 90 | 110 |
|---|---|---|---|---|---|
| Conductivity σ(S/m) | 1.90 × 10−13 | 4.59 × 10−13 | 2.64 × 10−12 | 1.38 × 10−11 | 5.26 × 10−11 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Zhou, Y.; Zhou, Z.; Qi, B. A Combined Electro-Thermal Breakdown Model for Oil-Impregnated Paper. Energies 2017, 10, 2160. https://doi.org/10.3390/en10122160
Huang M, Zhou Y, Zhou Z, Qi B. A Combined Electro-Thermal Breakdown Model for Oil-Impregnated Paper. Energies. 2017; 10(12):2160. https://doi.org/10.3390/en10122160
Chicago/Turabian StyleHuang, Meng, Yuanxiang Zhou, Zhongliu Zhou, and Bo Qi. 2017. "A Combined Electro-Thermal Breakdown Model for Oil-Impregnated Paper" Energies 10, no. 12: 2160. https://doi.org/10.3390/en10122160
APA StyleHuang, M., Zhou, Y., Zhou, Z., & Qi, B. (2017). A Combined Electro-Thermal Breakdown Model for Oil-Impregnated Paper. Energies, 10(12), 2160. https://doi.org/10.3390/en10122160





