Adaptive State Feedback—Theory and Application for Wind Turbine Control
Abstract
:1. Background
2. Problem Formulation
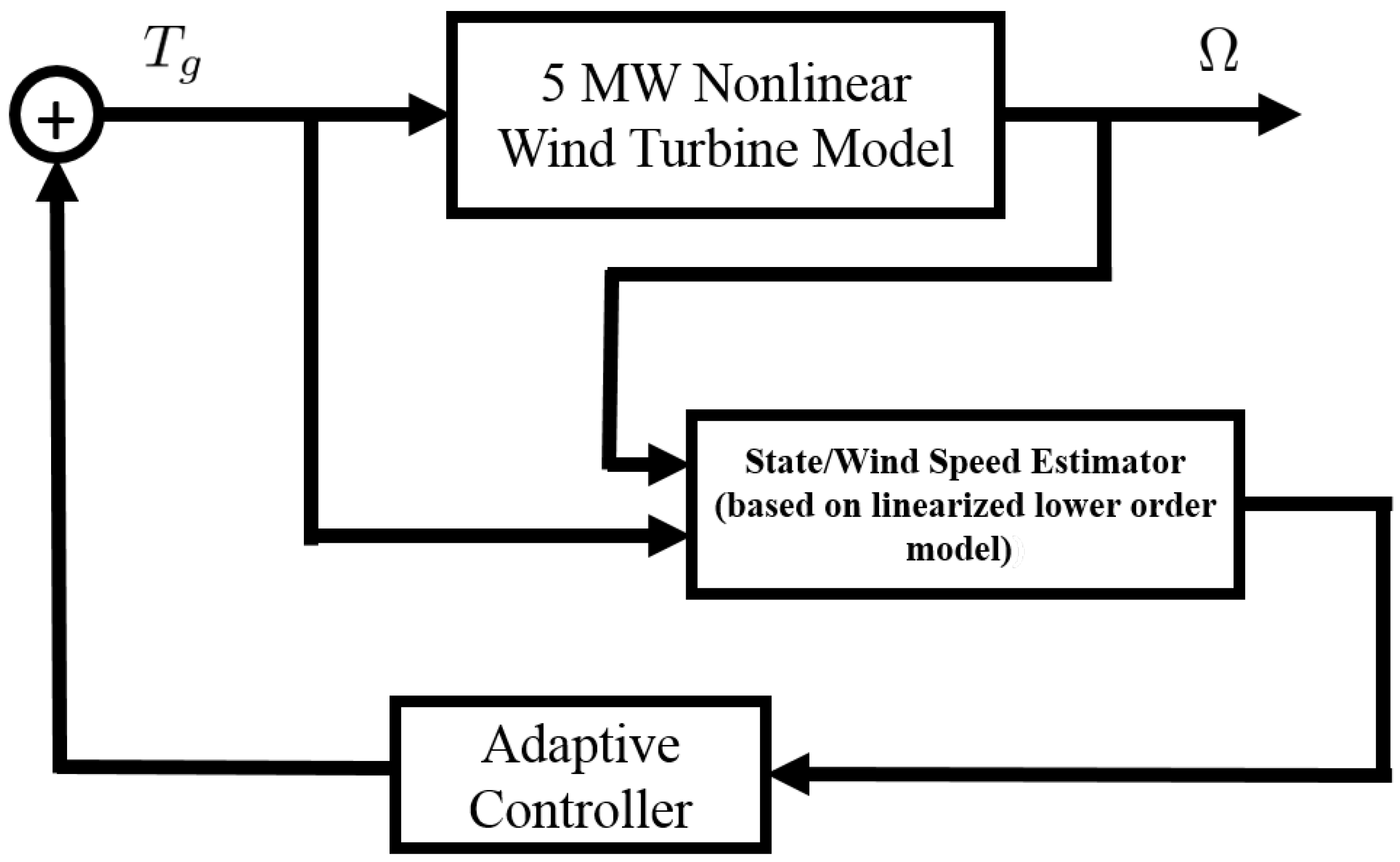
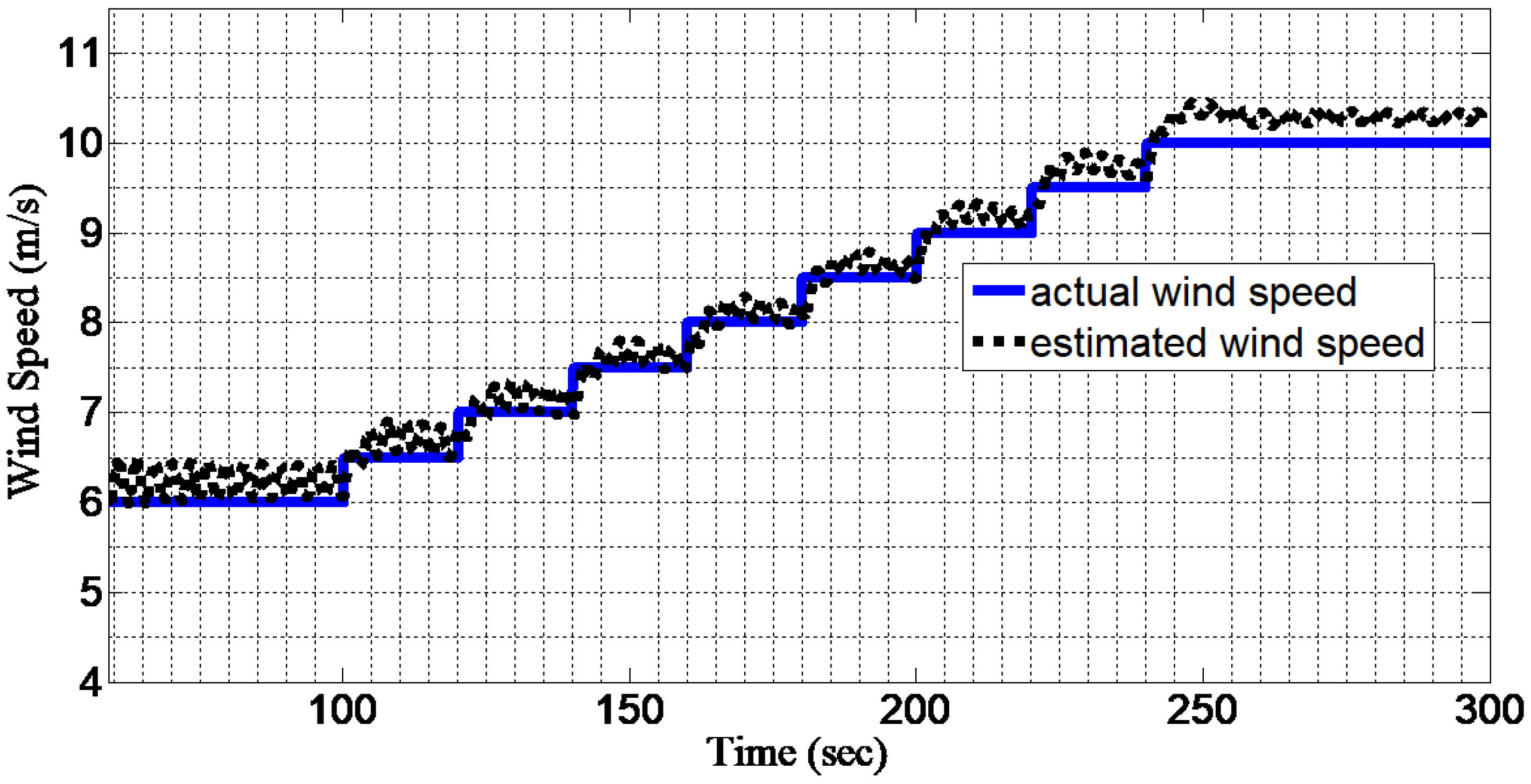
3. System Description and Wind-Speed Estimation
4. Adaptive Controller
Closed-Loop System Formulation
- it is non-minimum-phase;
- the product of system matrices is positive (or ).
- the system is minimum-phase;
- the product of system matrices is positive (or );
- is bounded;
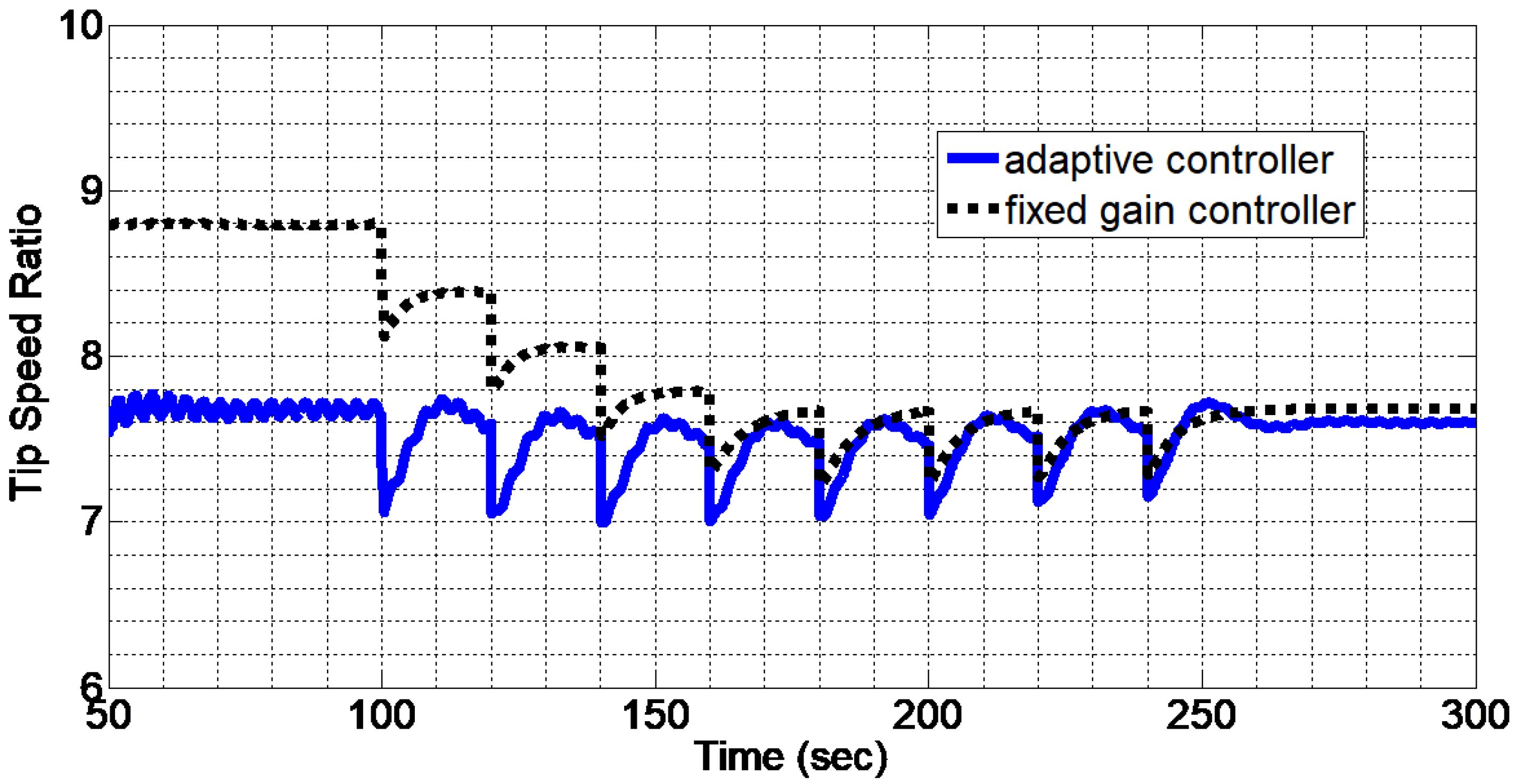
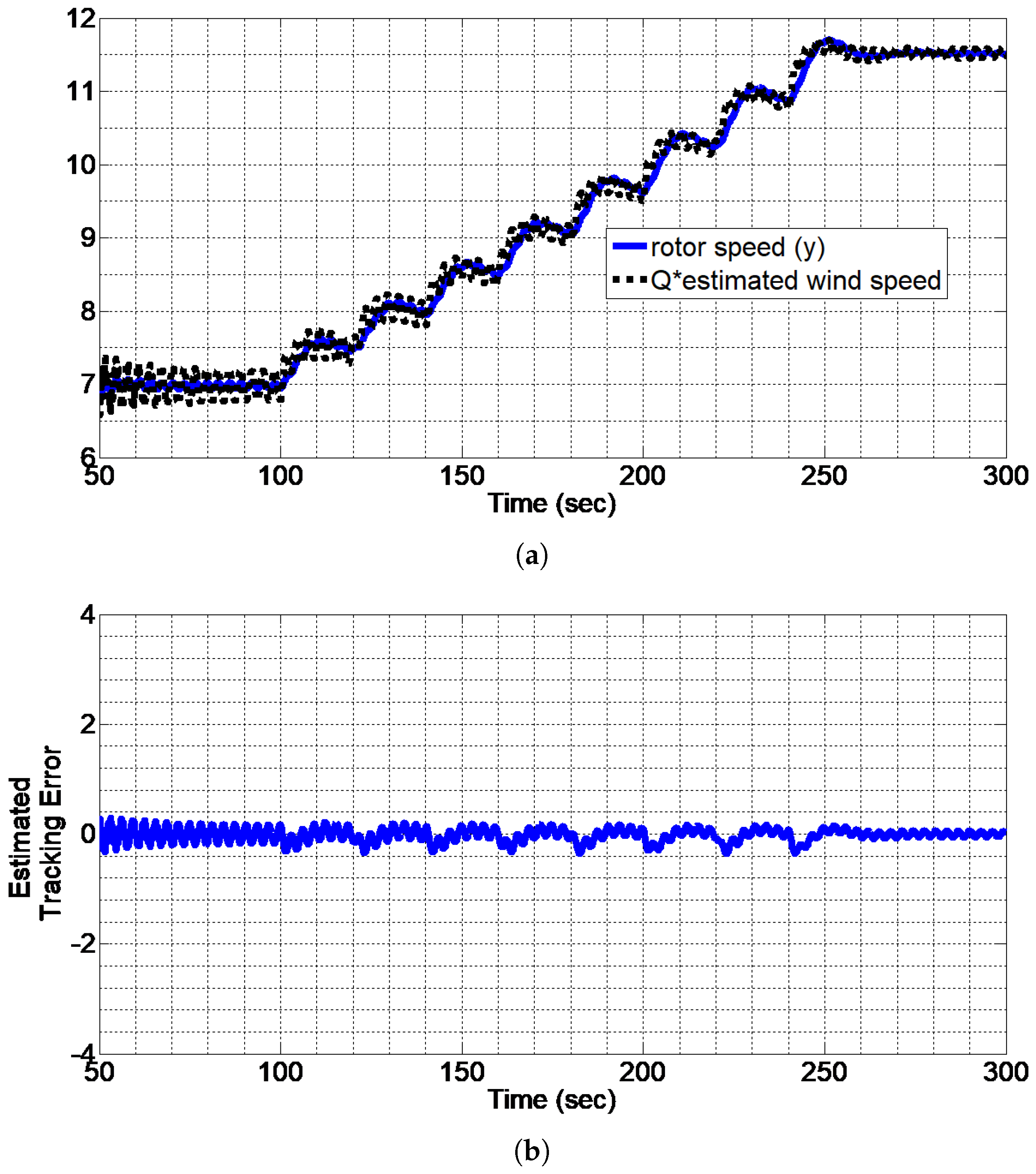
5. Illustration of Adaptive State Feedback
6. Conclusions
Author Contributions
Conflicts of Interest
Appendix A
References
- Laks, J.H.; Pao, L.Y.; Wright, A.D. Control of wind turbines: Past, present, and future. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 2096–2103. [Google Scholar]
- Bossanyi, E. Wind turbine control for load reduction. Wind Energy 2003, 6, 229–244. [Google Scholar] [CrossRef]
- Johnson, K.E.; Pao, L.Y.; Balas, M.J.; Fingersh, L.J. Control of variable-speed wind turbines: Standard and adaptive techniques for maximizing energy capture. IEEE Control Syst. 2006, 26, 70–81. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009.
- Wright, A.D. Modern Control Design for Flexible Wind Turbines; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2004.
- Gao, R.; Gao, Z. Pitch control for wind turbine systems using optimization, estimation and compensation. Renew. Energy 2016, 91, 501–515. [Google Scholar] [CrossRef]
- Sloth, C.; Esbensen, T.; Stoustrup, J. Robust and fault-tolerant linear parameter-varying control of wind turbines. Mechatronics 2011, 21, 645–659. [Google Scholar] [CrossRef]
- Fragoso, S.; Garrido, J.; Vázquez, F.; Morilla, F. Comparative analysis of decoupling control methodologies and H∞ multivariable robust control for variable-speed, variable-pitch wind turbines: Application to a lab-scale wind turbine. Sustainability 2017, 9, 713. [Google Scholar] [CrossRef]
- Schlipf, D.; Schlipf, D.J.; Kühn, M. Nonlinear model predictive control of wind turbines using LIDAR. Wind Energy 2013, 16, 1107–1129. [Google Scholar] [CrossRef]
- Song, D.; Yang, J.; Dong, M.; Joo, Y.H. Model predictive control with finite control set for variable-speed wind turbines. Energy 2017, 126, 564–572. [Google Scholar] [CrossRef]
- Jaramillo-Lopez, F.; Kenne, G.; Lamnabhi-Lagarrigue, F. A novel online training neural network-based algorithm for wind speed estimation and adaptive control of PMSG wind turbine system for maximum power extraction. Renew. Energy 2016, 86, 38–48. [Google Scholar] [CrossRef]
- Narayana, M.; Sunderland, K.M.; Putrus, G.; Conlon, M.F. Adaptive linear prediction for optimal control of wind turbines. Renew. Energy 2017, 113, 895–906. [Google Scholar] [CrossRef]
- Hatami, A.; Moetakef-Imani, B. Innovative adaptive pitch control for small wind turbine fatigue load reduction. Mechatronics 2016, 40, 137–145. [Google Scholar] [CrossRef]
- Wen, J.T.Y.; Balas, M.J. Robust adaptive control in Hilbert space. J. Math. Anal. Appl. 1989, 143, 1–26. [Google Scholar] [CrossRef]
- Fuentes, R.J.; Balas, M.J. Direct adaptive rejection of persistent disturbances. J. Math. Anal. Appl. 2000, 251, 28–39. [Google Scholar] [CrossRef]
- Fuentes, R.J.; Balas, M.J. Robust model reference adaptive control with disturbance rejection. In Proceedings of the 2002 American Control Conference, Anchorage, AK, USA, 8–10 May 2002; Volume 5, pp. 4003–4008. [Google Scholar]
- Balas, M.; Fuentes, R.; Erwin, R. Adaptive control of persistent disturbances for aerospace structures. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Dever, CO, USA, 14–17 August 2000; p. 3952. [Google Scholar]
- Matras, A.L.; Flowers, G.T.; Fuentes, R.; Balas, M.; Fausz, J. Suppression of persistent rotor vibrations using adaptive techniques. J. Vib. Acoust. 2006, 128, 682–689. [Google Scholar] [CrossRef]
- Frost, S.A.; Balas, M.J.; Wright, A.D. Direct adaptive control of a utility-scale wind turbine for speed regulation. Int. J. Robust Nonlinear Control 2009, 19, 59–71. [Google Scholar] [CrossRef]
- Balas, M.; Li, Q.; Peterman, R. Adaptive disturbance tracking control for large horizontal axis wind turbines in variable speed region II operation. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; p. 248. [Google Scholar]
- Balas, M.; Thapa, K.; Li, Q. Adaptive disturbance tracking control for large horizontal axis wind turbines with disturbance estimator in Region II operation. In Proceedings of the ASME Wind Symposium, Orlando, FL, USA, 4–7 January 2011. [Google Scholar]
- Magar, K.S.T.; Balas, M.J.; Frost, S.A. Adaptive Disturbance Tracking Control With Wind Speed Reduced Order State Estimation for Region II Control of Large Wind Turbines. In Proceedings of the ASME 2012 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Stone Mountain, GA, USA, 19–21 September 2012; pp. 329–333. [Google Scholar]
- Magar, K.T.; Balas, M.J.; Frost, S.A. Direct adaptive torque control for maximizing the power captured by wind turbine in partial loading condition. Wind Energy 2016, 19, 911–922. [Google Scholar] [CrossRef]
- Balas, M.; Fuentes, R. A non-orthogonal projection approach to characterization of almost positive real systems with an application to adaptive control. In Proceedings of the American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 2, pp. 1911–1916. [Google Scholar]
- Wilson, R.E.; Lissaman, P. Applied Aerodynamics of Wind Power Machines; Oregon State University: Corvallis, OR, USA, 1974. [Google Scholar]
- Wang, N.; Johnson, K.E.; Wright, A.D. FX-RLS-based feedforward control for LIDAR-enabled wind turbine load mitigation. IEEE Trans. Control Syst. Technol. 2012, 20, 1212–1222. [Google Scholar] [CrossRef]
- Johnson, C. Theory of disturbance-accommodating controllers. Control Dyn. Syst. 1976, 12, 387–489. [Google Scholar]
- Thapa Magar, K.; Balas, M.; Feng, Y.; Frost, S. Adaptive Pitch Control for Speed Regulation of Floating Offshore Wind Turbine: Preliminary Study. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013; p. 454. [Google Scholar]
- Li, N. Adaptive Control of Flow Over Wind Turbine Blade. Ph.D. Thesis, University of Wyoming, Laramie, WY, USA, 2013. [Google Scholar]
- Yuan, Y.; Tang, J. Adaptive pitch control of wind turbine for load mitigation under structural uncertainties. Renew. Energy 2017, 105, 483–494. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Buhl, M.L., Jr. Development and verification of a fully coupled simulator for offshore wind turbines. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thapa Magar, K.; Balas, M.; Frost, S.; Li, N. Adaptive State Feedback—Theory and Application for Wind Turbine Control. Energies 2017, 10, 2145. https://doi.org/10.3390/en10122145
Thapa Magar K, Balas M, Frost S, Li N. Adaptive State Feedback—Theory and Application for Wind Turbine Control. Energies. 2017; 10(12):2145. https://doi.org/10.3390/en10122145
Chicago/Turabian StyleThapa Magar, Kaman, Mark Balas, Susan Frost, and Nailu Li. 2017. "Adaptive State Feedback—Theory and Application for Wind Turbine Control" Energies 10, no. 12: 2145. https://doi.org/10.3390/en10122145
APA StyleThapa Magar, K., Balas, M., Frost, S., & Li, N. (2017). Adaptive State Feedback—Theory and Application for Wind Turbine Control. Energies, 10(12), 2145. https://doi.org/10.3390/en10122145



