Electrical-Loss Analysis of Power-Split Hybrid Electric Vehicles
Abstract
:1. Introduction
2. Model
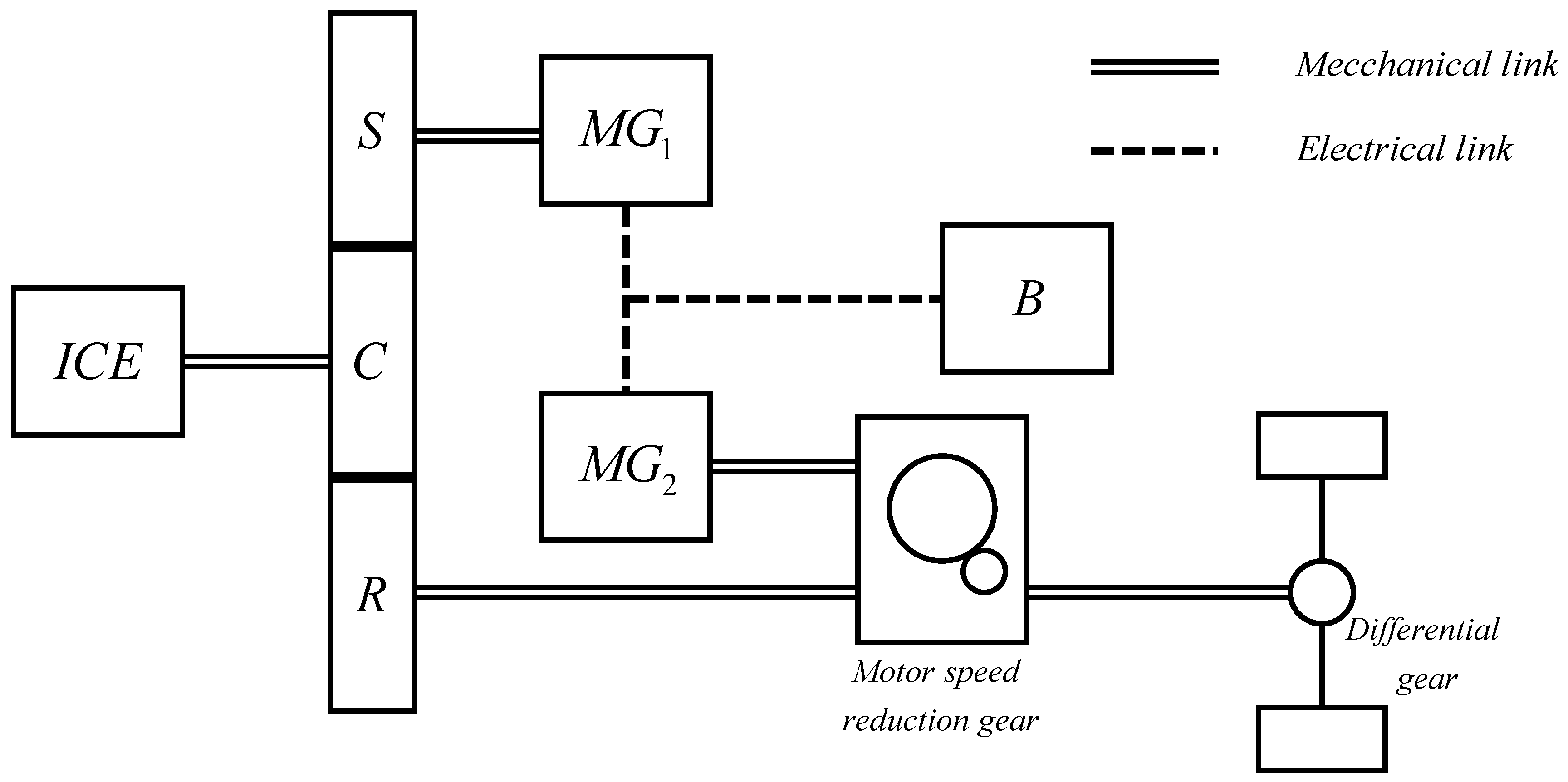
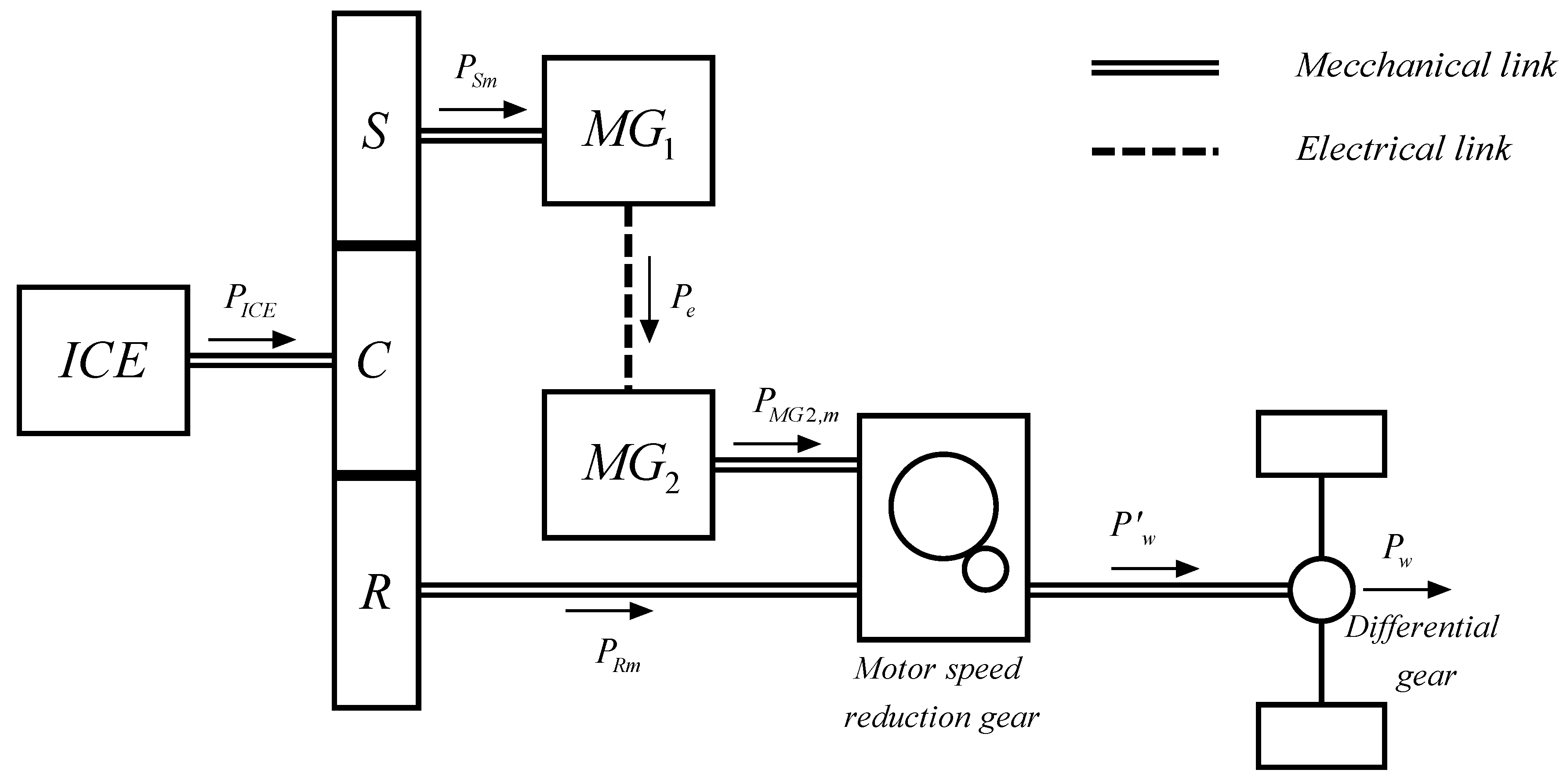
2.1. Power Split Device Energy Model
2.2. Electrical Losses and Internal Combustion Engine Modeling
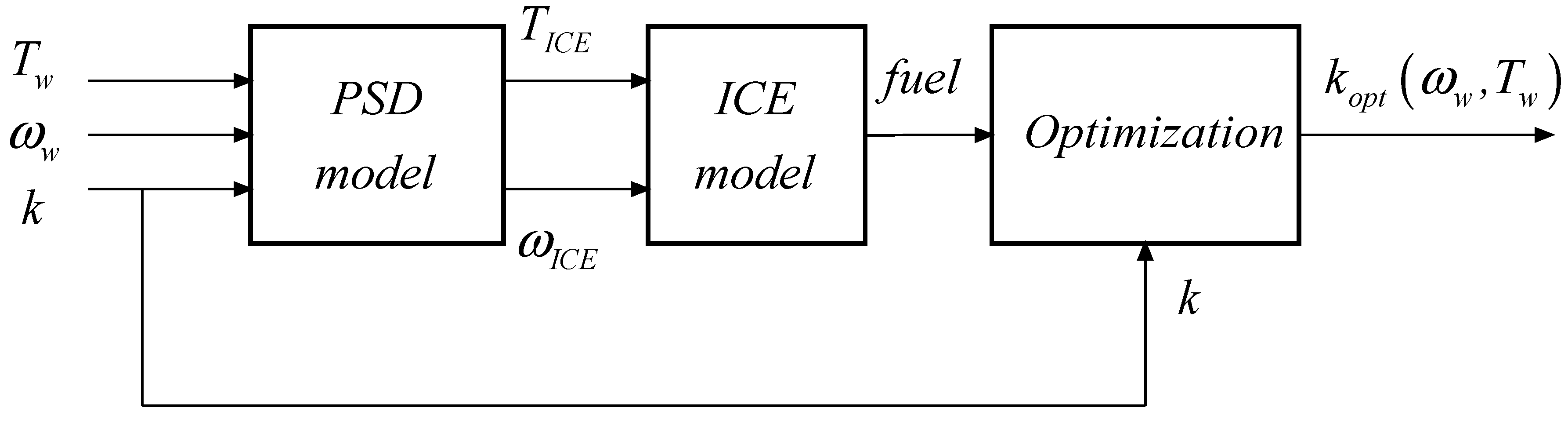
2.3. CVT Powertrain Efficiency Optimization
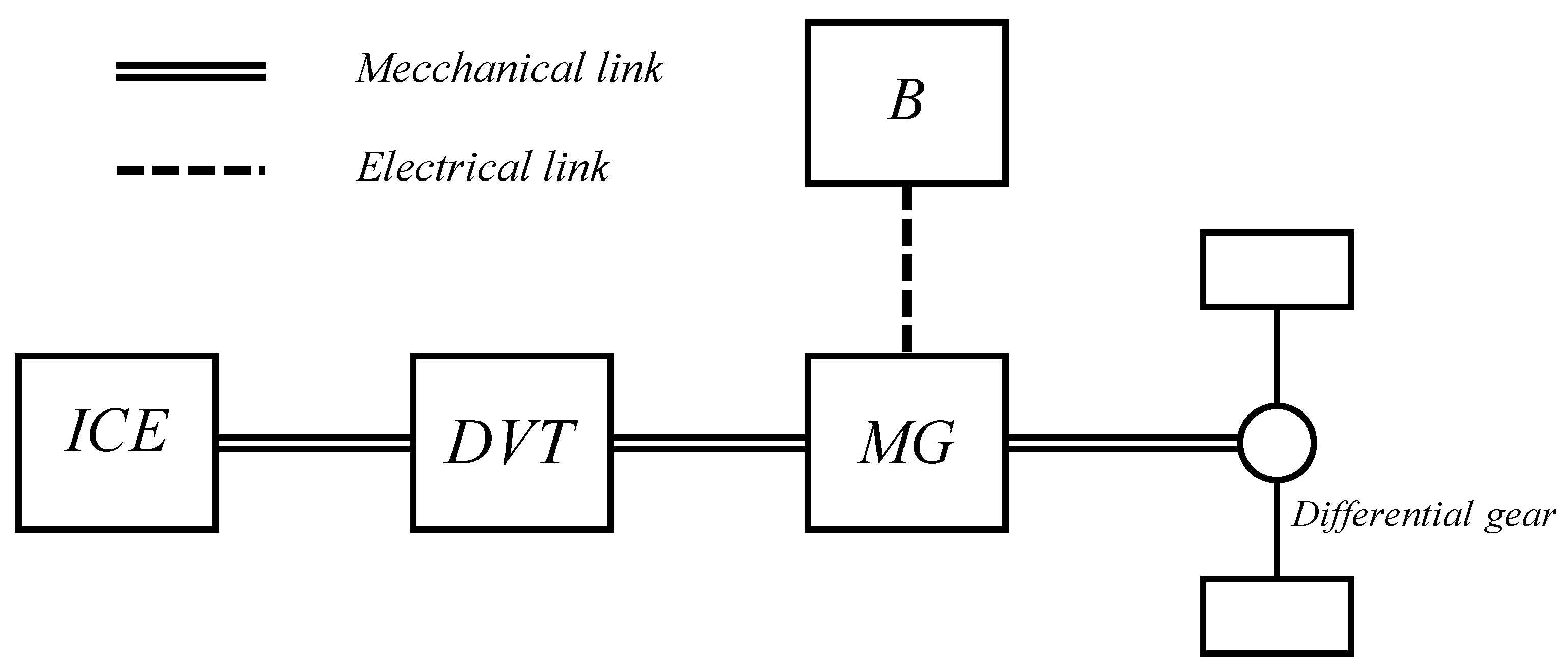
2.4. DVT Powertrain Effciency Optimazation
2.5. MATLAB/Simulink Model
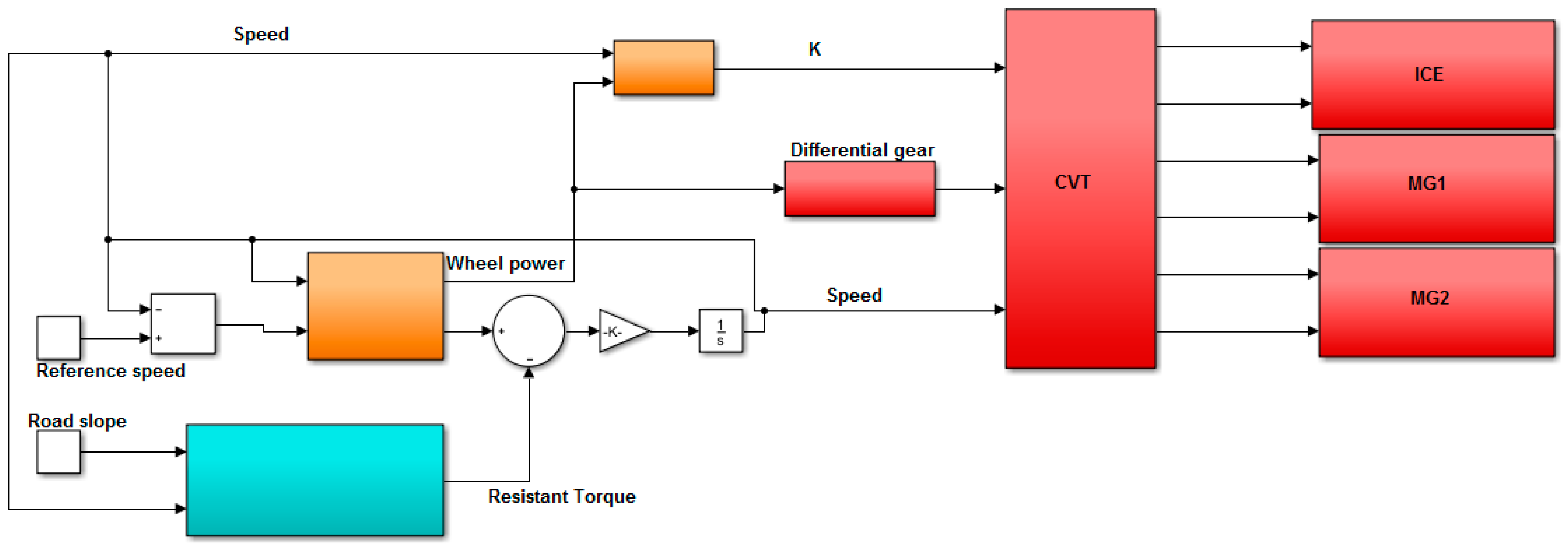
2.5.1. Power Split-Device Vehicle MATLAB Simulink Model
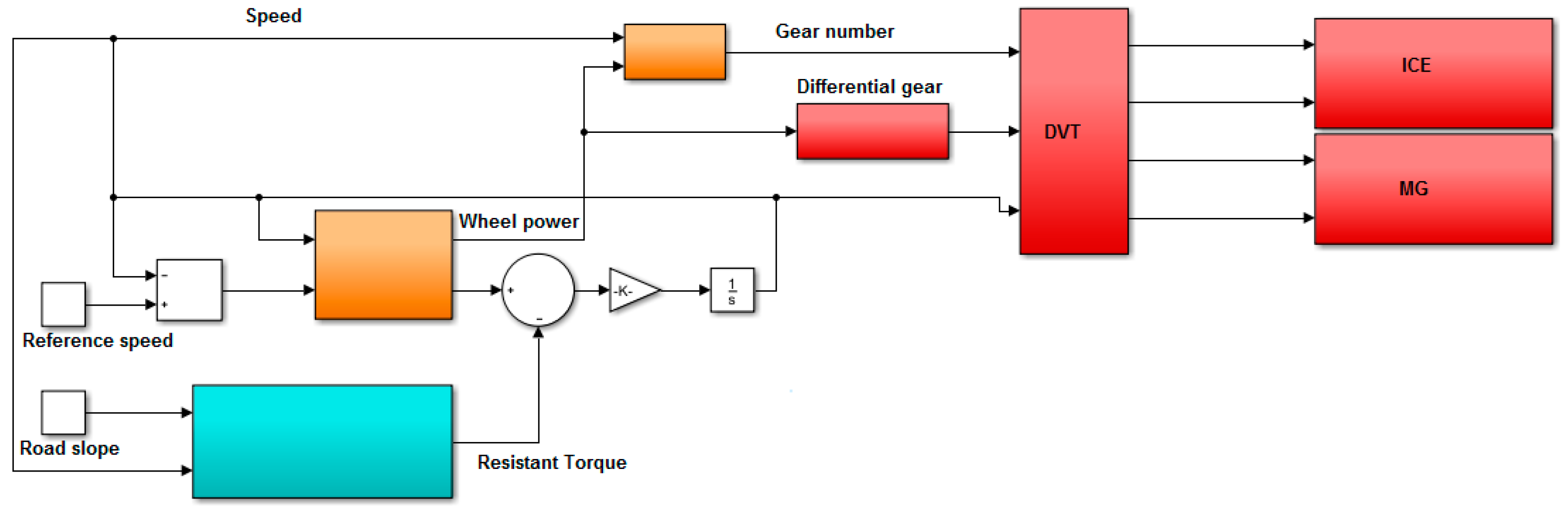
2.5.2. DVT MATLAB/Simulink Model
2.6. Vehicle Features
2.7. Road Mission Features
3. Results
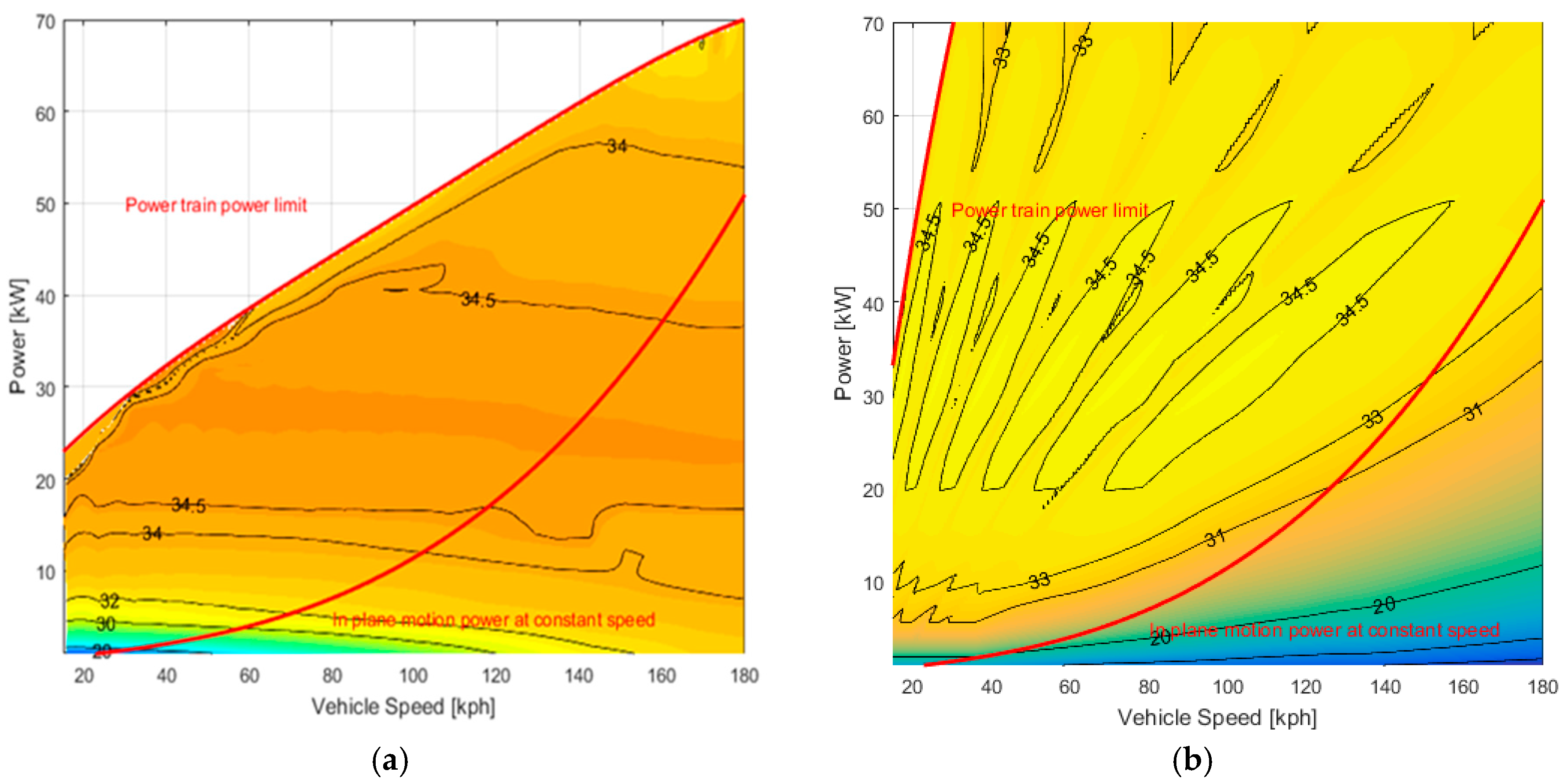
3.1. Electrical Losses in Power-Split Device
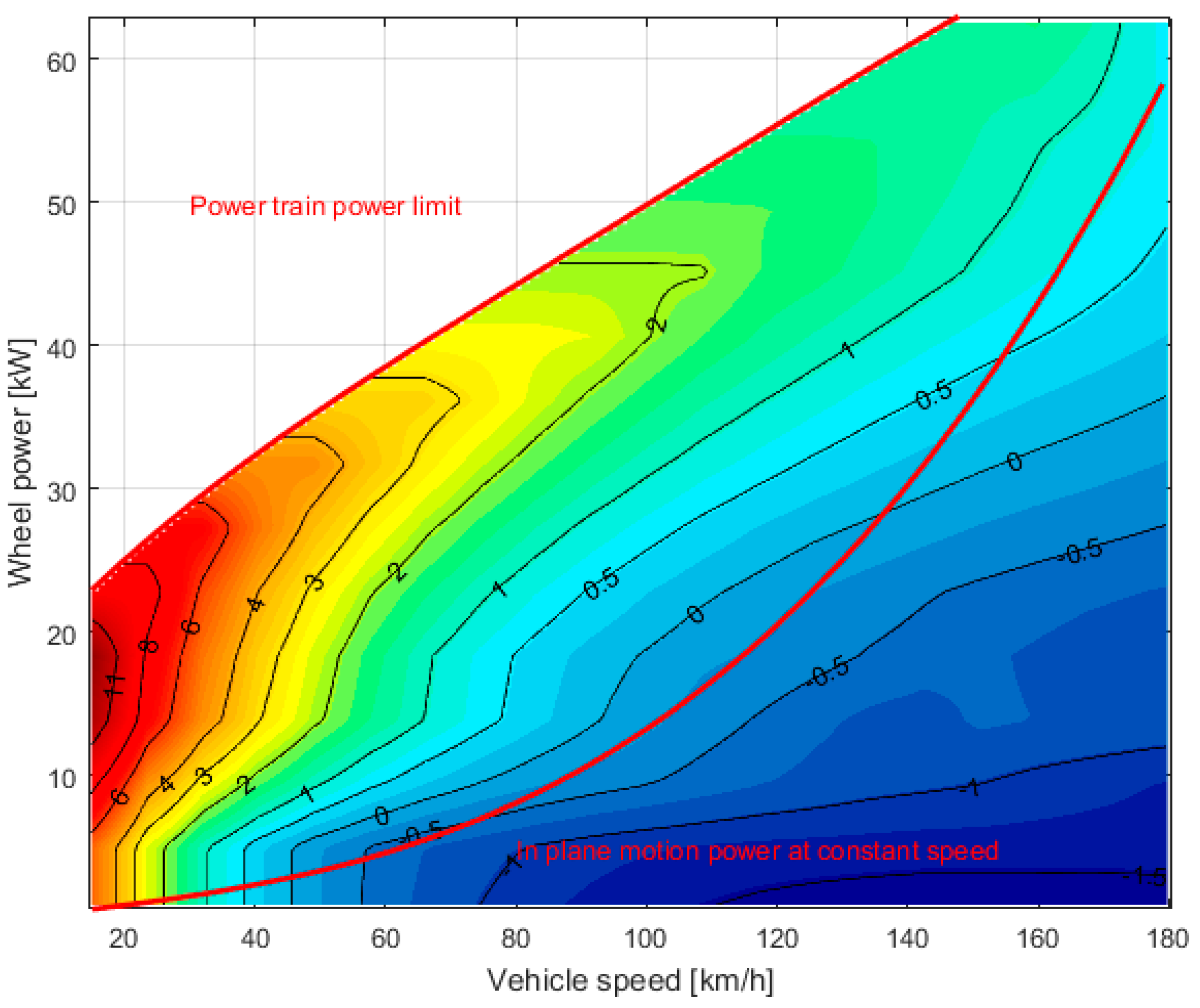
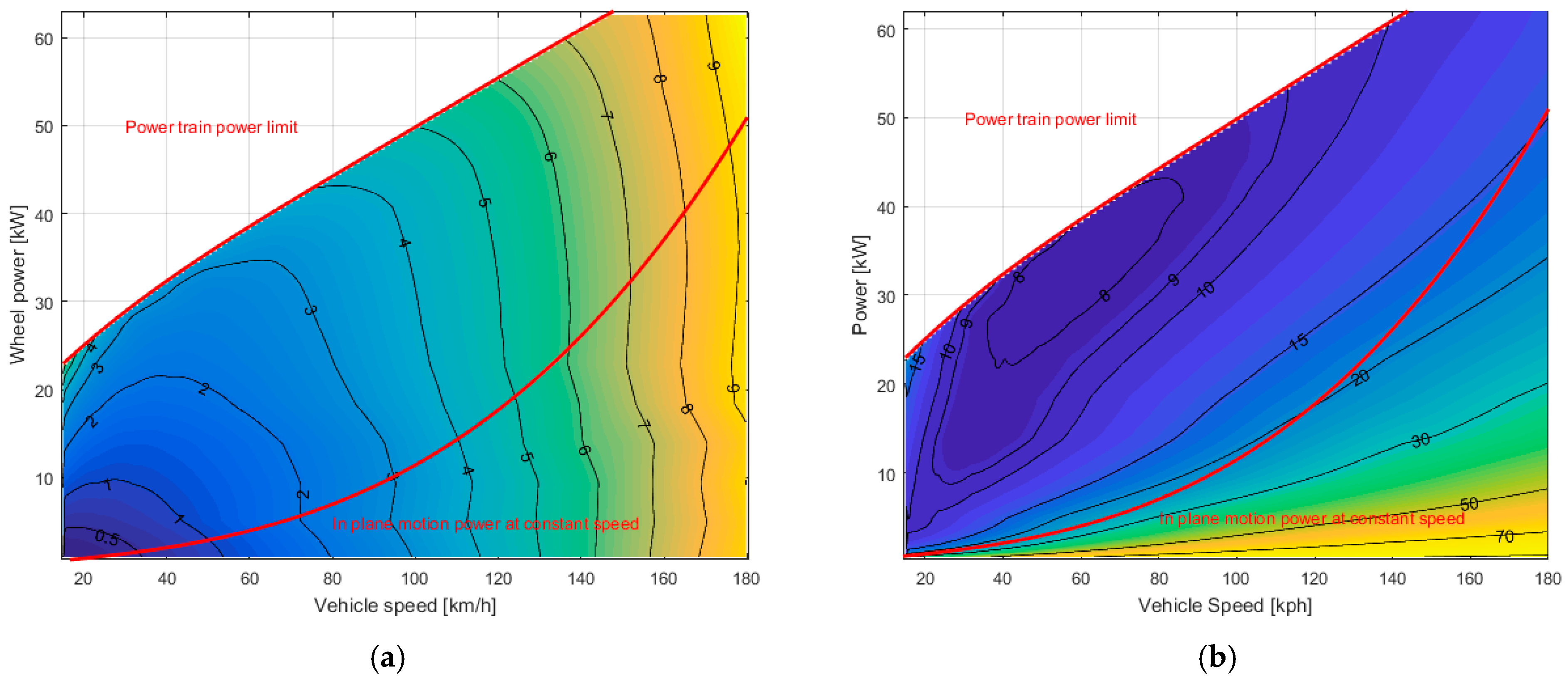
3.1.1. Electrical Losses in Power-Split Device over Different Operating Condition
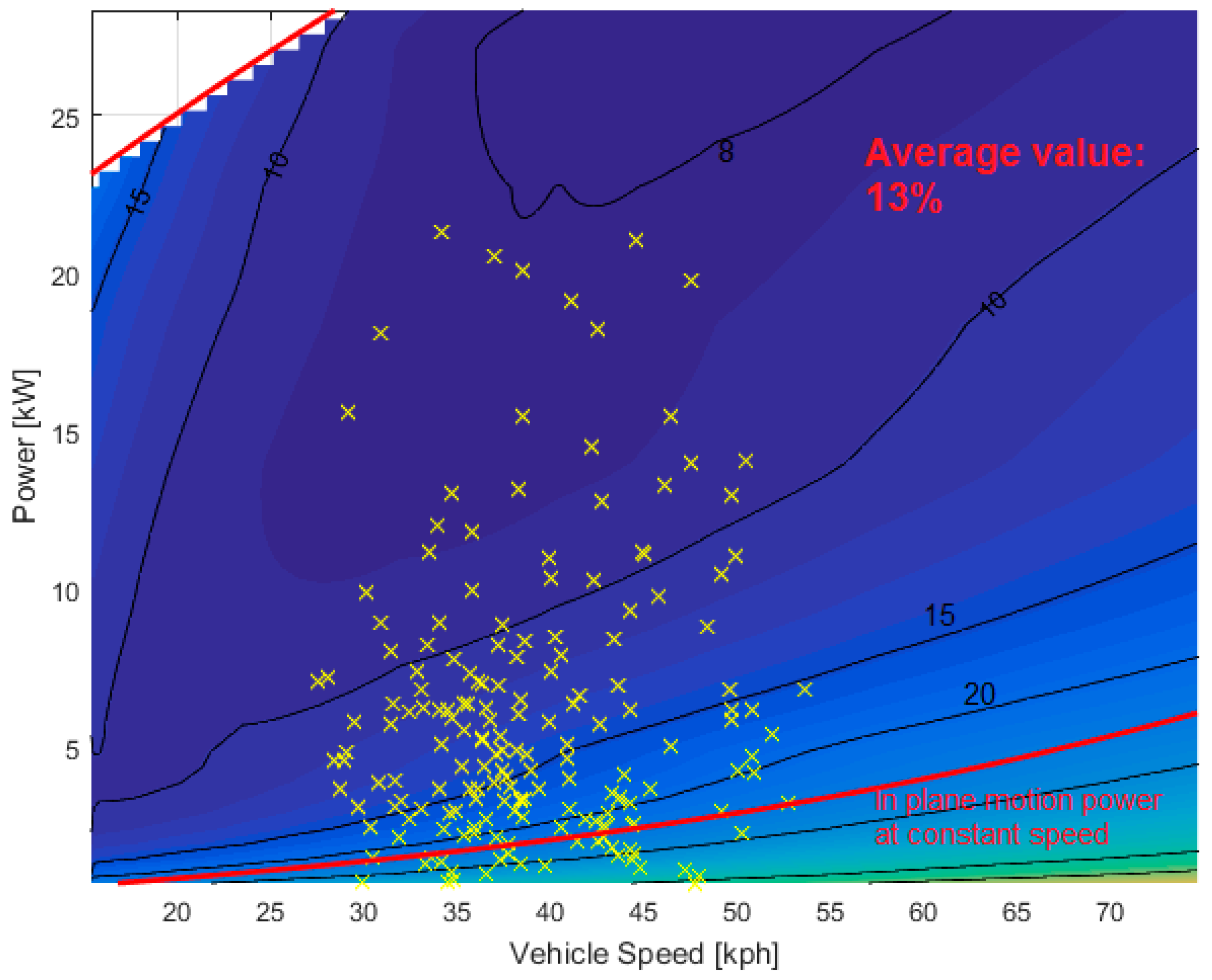
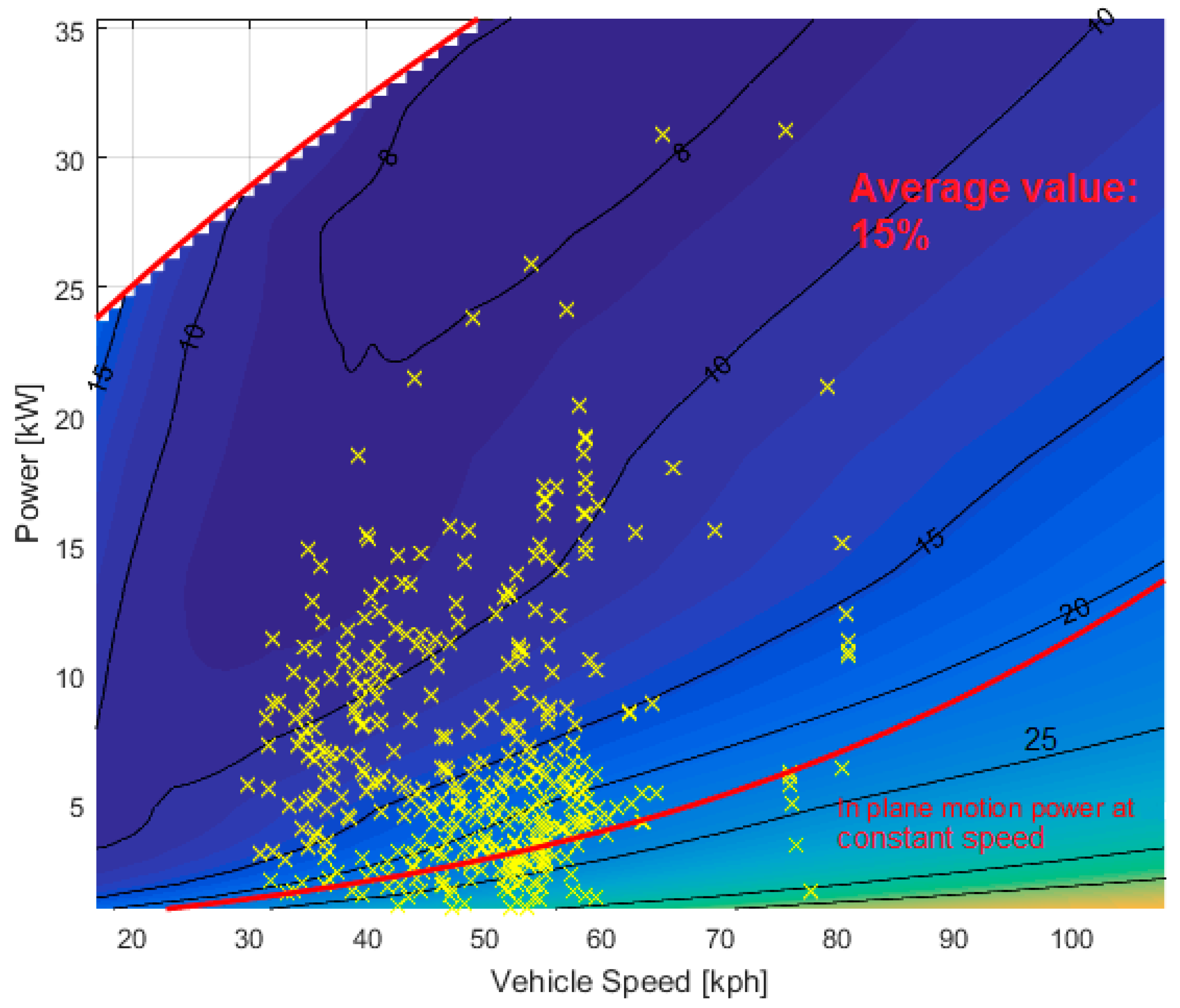
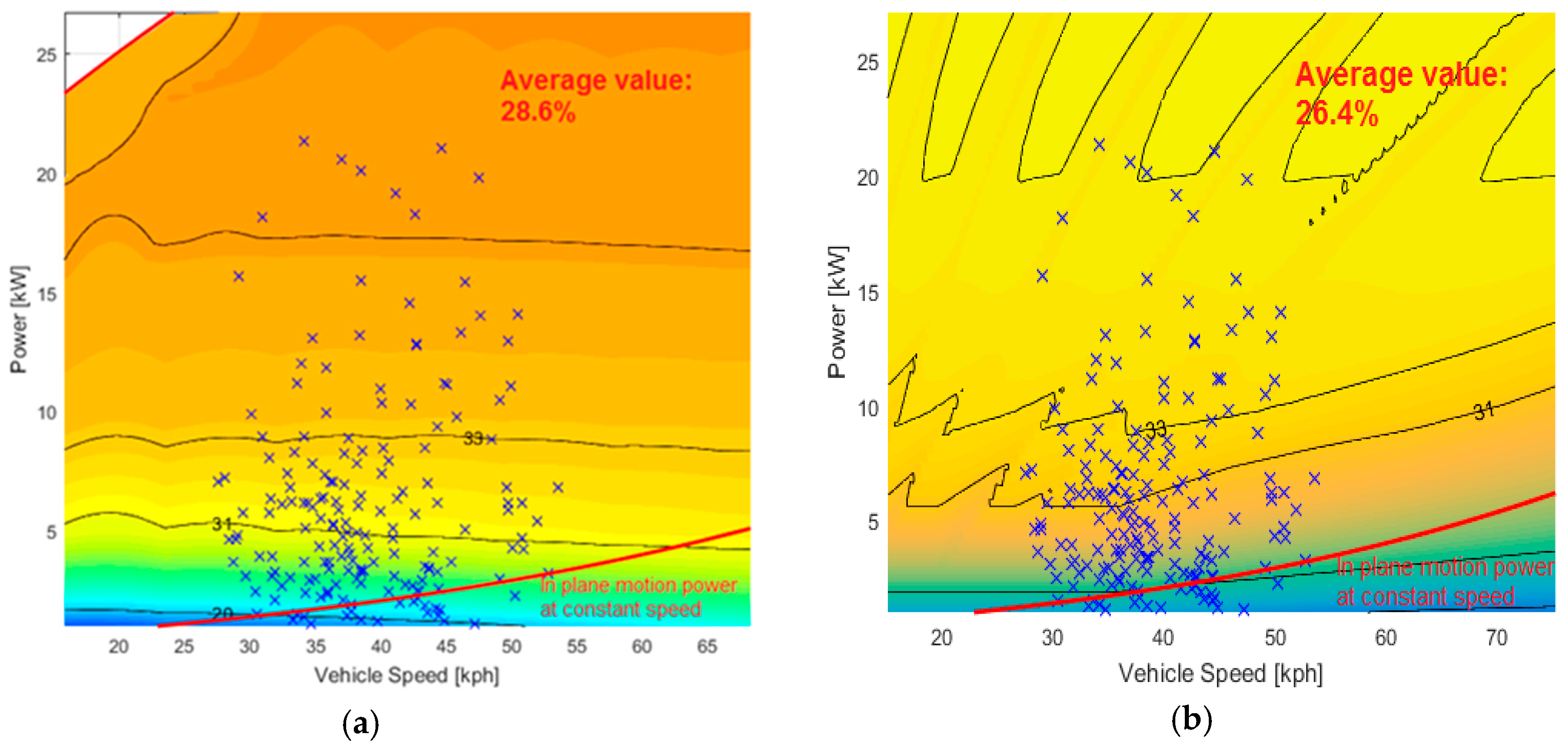
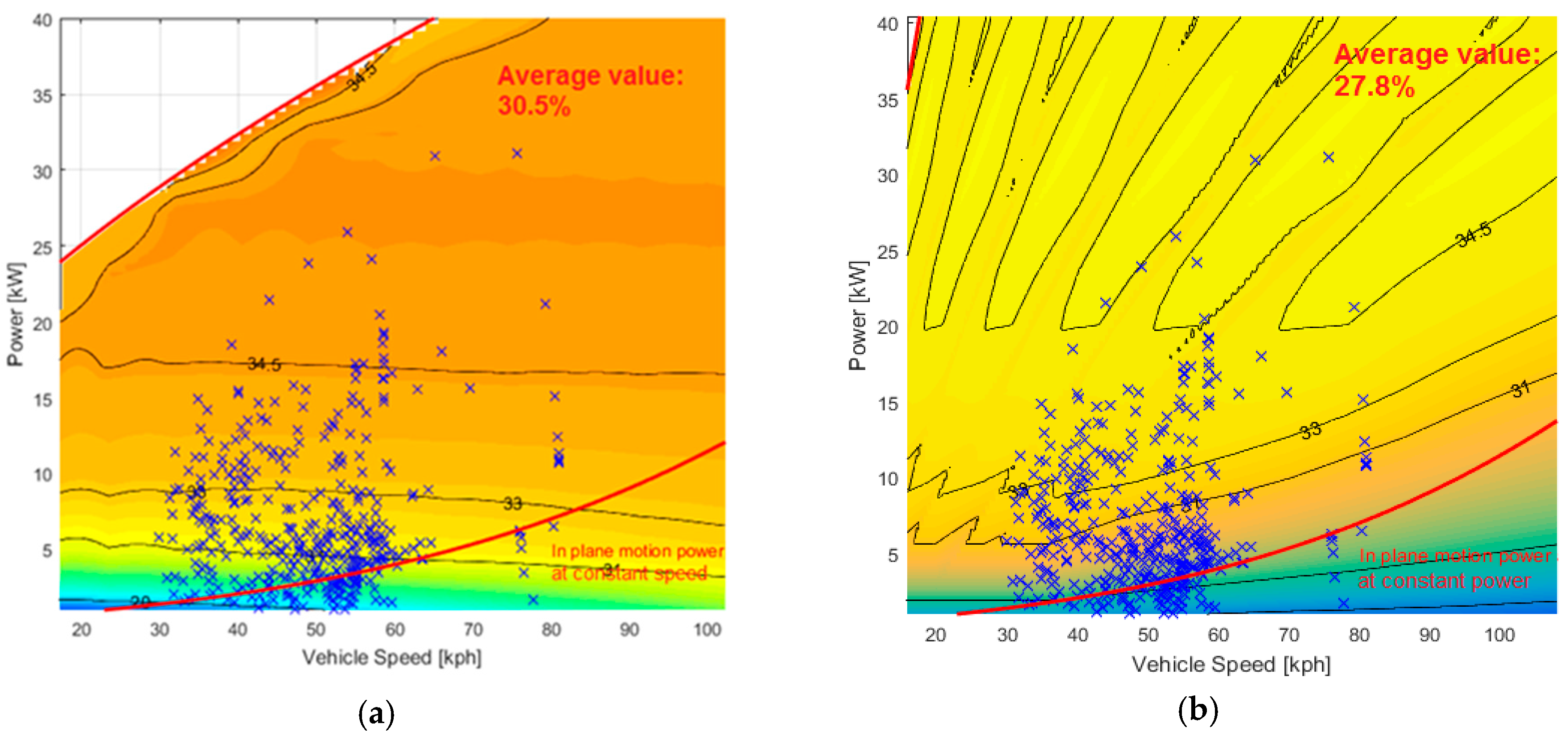
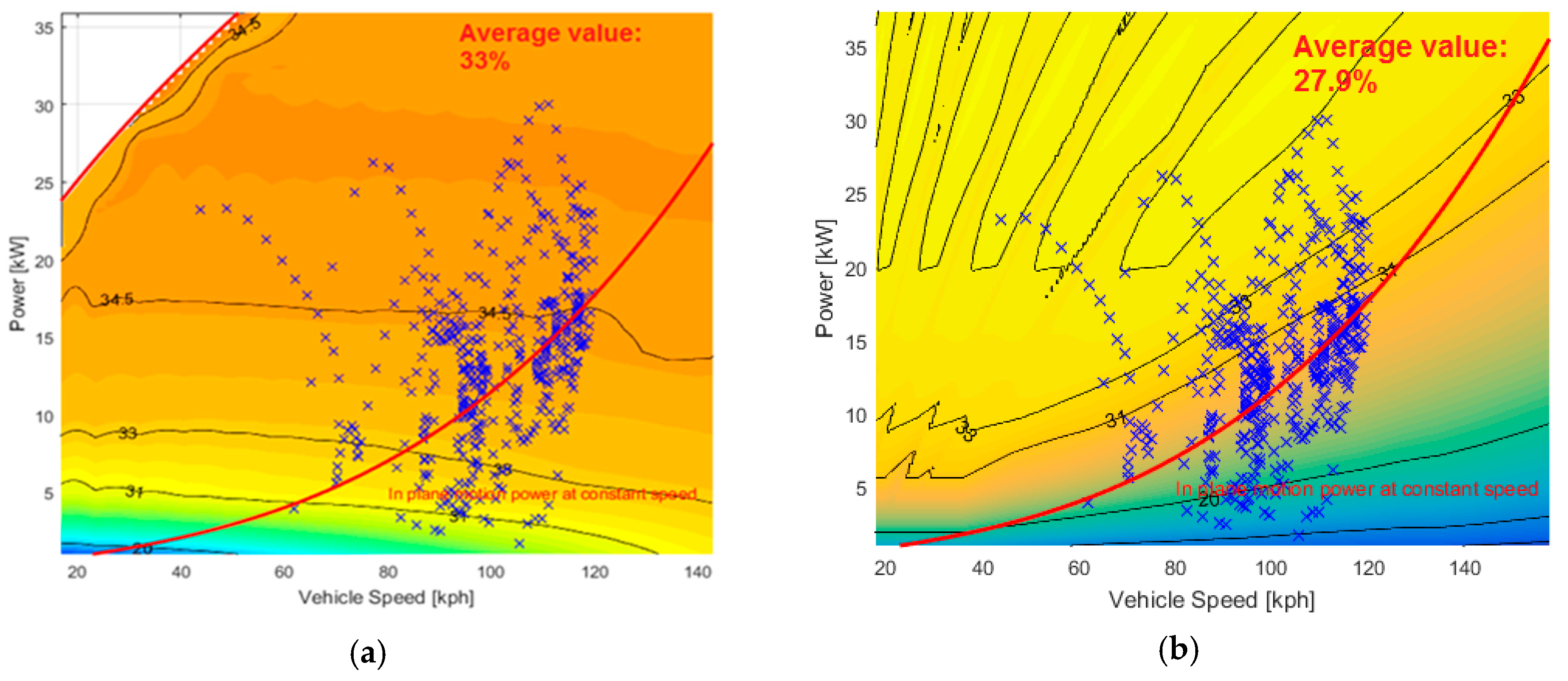
3.1.2. Electrical Losses in Power-Split Device over Different Real-Road Missions
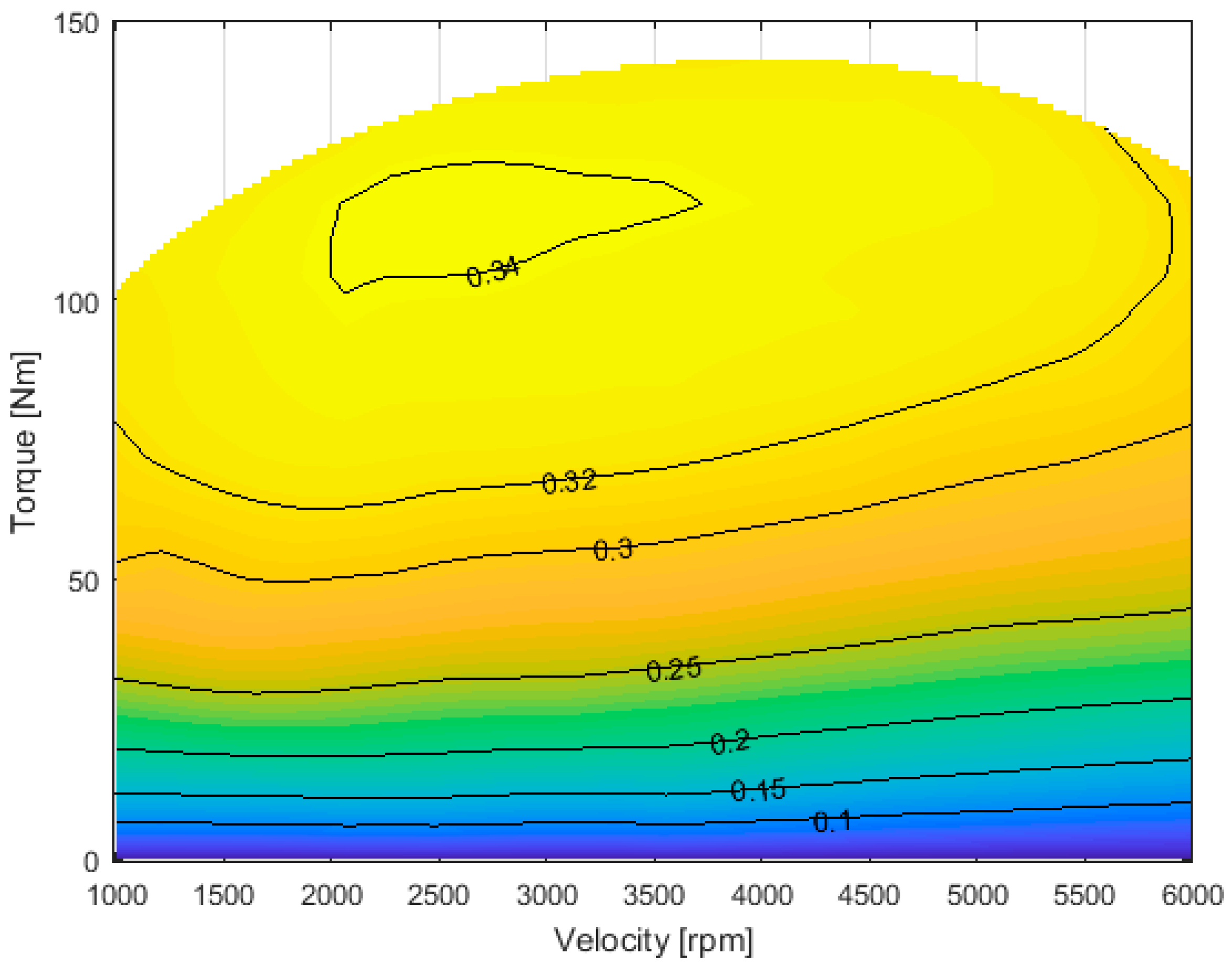
3.2. ICE Efficiency
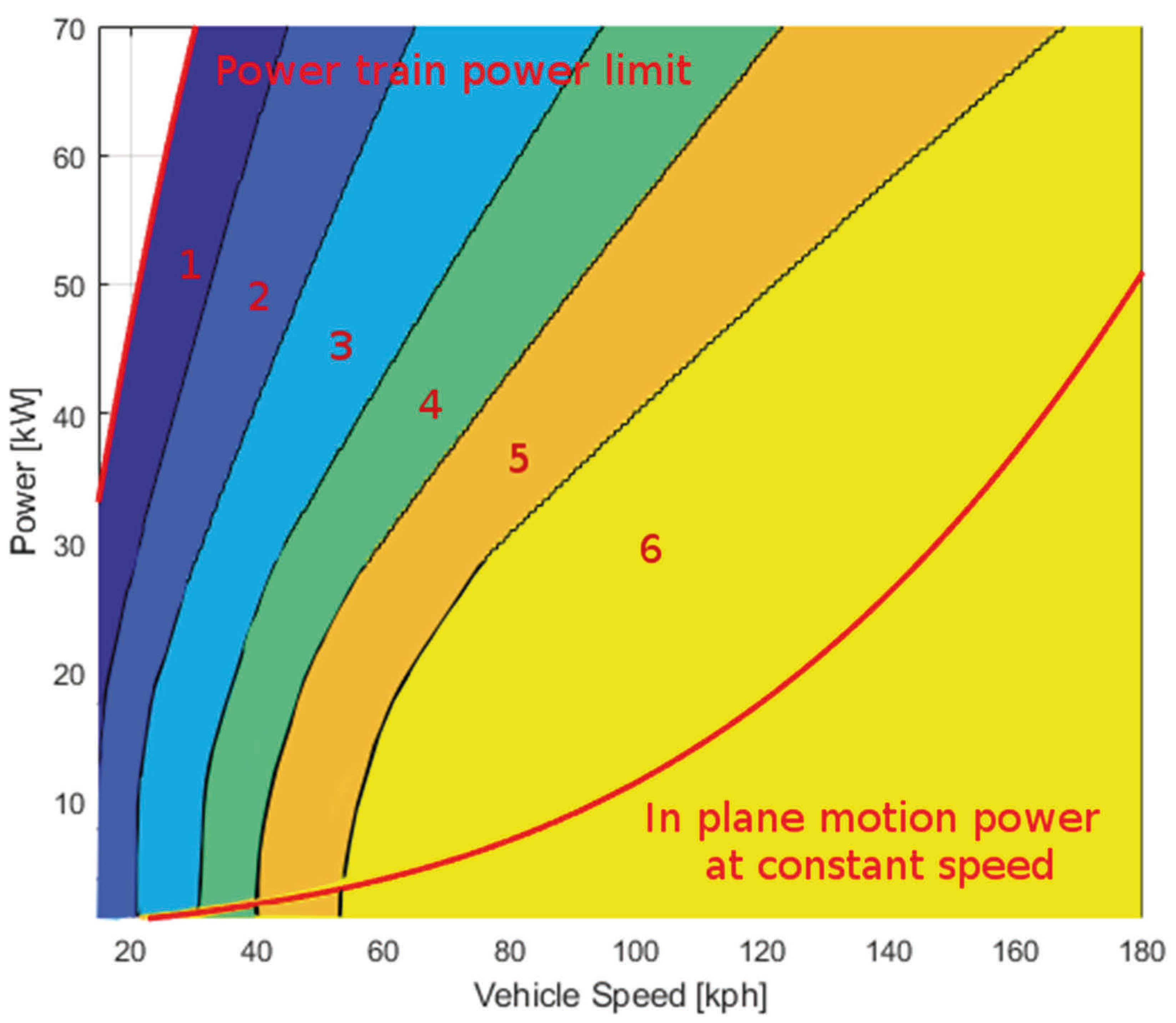
3.2.1. ICE Efficiency over Different Operating Condition
3.2.2. ICE Efficiency over Different Real Road Mission
3.3. Powertrain Global Efficiency
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xia, C.; Du, Z.; Zhang, C. A single-degree-of-freedom energy optimization strategy for power-split hybrid electric vehicles. Energies 2017, 10, 896. [Google Scholar] [CrossRef]
- Lee, H.; Park, Y.I.; Cha, S.W. Power management strategy of hybrid electric vehicle using power split ratio line control strategy based on dynamic programming. In Proceedings of the 2015 15th International Conference on Control, Automation and Systems (ICCAS), Busan, Korea, 13–16 October 2015; pp. 1739–1742. [Google Scholar]
- Fan, J.; Zhang, J.; Shen, T. Map-based power-split strategy design with predictive performance optimization for parallel hybrid electric vehicles. Energies 2015, 8, 9946–9968. [Google Scholar] [CrossRef]
- Lee, S.; Choi, J.; Jeong, K.; Kim, H. A study of fuel economy improvement in a plug-in hybrid electric vehicle using engine on/off and battery charging power control based on driver characteristics. Energies 2015, 8, 10106–10126. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Xu, J.; Gong, X.; You, C. Energy management for a power-split plug-in hybrid electric vehicle based on dynamic programming and neural networks. IEEE Trans. Veh. Technol. 2014, 63, 1567–1580. [Google Scholar] [CrossRef]
- Abdelsalam, A.A.; Cui, S. A fuzzy logic global power management strategy for hybrid electric vehicles based on a permanent magnet electric variable transmission. Energies 2012, 5, 1175–1198. [Google Scholar] [CrossRef]
- Burress, T.A.; Coomer, C.L.; Campbell, S.L.; Seiber, L.E.; Marlino, L.D.; Staunton, R.H.; Cunningham, J.P. Evaluation of the 2007 Toyota Camry Hybrid Synergy Drive System; ORNL/TM2007/190, Revised; UT-Battelle, Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2008.
- Burress, T.A.; Coomer, C.L.; Campbell, S.L.; Wereszczak, A.A.; Cunningham, J.P.; Marlino, L.D. Evaluation of the 2008 Lexus LS 600h Hybrid Synergy Drive System; ORNL/TM-2008/185; UT-Battelle, Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2009.
- Burress, T.A.; Campbell, S.L.; Coomer, C.L.; Ayers, C.W.; Wereszczak, A.A.; Cunningham, J.P.; Marlino, L.D.; Seiber, L.E.; Lin, H.T. Evaluation of the 2010 Toyota Prius Hybrid Synergy Drive System; Technical Report ORNL/TM2010/253; Oak Ridge National Laboratory (ORNL), Power Electronics and Electric Machinery Research Facility: Oak Ridge, TN, USA, 2011.
- Son, H.; Park, K.; Hwang, S.; Kim, H. Design methodology of a power split type plug-in hybrid electric vehicle considering drivetrain losses. Energies 2017, 10, 437. [Google Scholar] [CrossRef]
- Pellegrino, G.; Vagati, A.; Guglielmi, P.; Boazzo, B. Performance comparison between surface-mounted and interior pm motor drives for electric vehicle application. IEEE Trans. Ind. Electron. 2012, 59, 803–811. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Soong, W.L.; Pellegrino, G.; Armando, E. Efficiency maps of electrical machines. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 2791–2799. [Google Scholar]
- Kim, H.; Chen, H.; Zhu, J.; Maksimović, D.; Erickson, R. Impact of 1.2kv SiC-MOSFET EV traction inverter on urban driving. In Proceedings of the 2016 IEEE 4th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Fayetteville, AR, USA, 7–9 November 2016; pp. 78–83. [Google Scholar]
- Passalacqua, M.; Lanzarotto, D.; Repetto, M.; Marchesoni, M. Advantages of using supercapacitors and silicon carbide on hybrid vehicle series architecture. Energies 2017, 10, 920. [Google Scholar] [CrossRef]
- Königstein, A.; Grebe, U.D.; Wu, K.-J.; Larsson, P.-I. Differentiated analysis of downsizing concepts. MTZ Worldw. 2008, 69, 4–11. [Google Scholar] [CrossRef]
- Adachi, S.; Hagihara, H. The Renewed 4-Cylinder Engine Series for Toyota Hybrid System. In Proceedings of the 33rd International Vienna Motor Symposium, Vienna, Austria, 26–27 April 2012; pp. 1–24. [Google Scholar]



| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| MG1 | motor-generator 1 | MG2 torque | |
| MG2 | motor-generator 2 | Differential gear ratio | |
| Electrical Power | Differential gear efficiency | ||
| ICE power | Motor speed reduction gear ratio | ||
| MG1 Electrical loss | motor speed reduction gear efficiency | ||
| MG2 Electrical loss | wheel rotational speed | ||
| Sun gear mechanical power | sun gear rotational speed | ||
| Ring gear mechanical power | ring gear rotational speed | ||
| MG2 mechanical power | ICE rotational speed | ||
| Drive shaft mechanical power | Willis constant | ||
| Wheel power | Sun–Ring gear ratio | ||
| Sun gear torque | ICE torque | ||
| Ring gear torque | Power split device efficiency | ||
| Wheel torque |
| Vehicle Feature | CVT | DVT |
|---|---|---|
| Vehicle mass (g) | 1450 | 1450 |
| Rolling coefficient | 0.01 | 0.01 |
| Drag coefficient | 0.25 | 0.25 |
| Vehicle front area (m2) | 2.3 | 2.3 |
| Wheel radius (m) | 0.3 | 0.3 |
| Differential gear ratio | 3.45 | 10.8 |
| Differential efficiency | 0.97 | 0.97 |
| Gear efficiency | 0.95 | 0.95 |
| Air density (kg/m3) | 1.22 | 1.22 |
| ICE power (kW) | 72 | 72 |
| ICE maximum torque (Nm) | 142 | 142 |
| MG2 maximum torque (Nm) | 163 | 163 |
| MG2 base speed (rpm) | 3000 | 3000 |
| MG2 maximum speed (rpm) | 17,000 | 17,000 |
| MG1 maximum torque (Nm) | 43 | - |
| MG1 base speed (rpm) | 5000 | - |
| MG1 maximum speed (rpm) | 10,000 | - |
| DC-link voltage (V) | 650 | 650 |
| Road Mission | Average Speed (km/h) | Maximum Speed (km/h) | Length (km) | Elevation (m) | Maximum Road Slope (%) |
|---|---|---|---|---|---|
| US06 | 78 | 130 | 13 | - | - |
| UDDS | 31 | 90 | 12 | - | - |
| HWFET | 78 | 97 | 16.5 | - | - |
| Urban | 24 | 57 | 11.4 | 20 | negligible |
| Extra-urban | 45 | 80 | 36 | 300 | 9 |
| Highway | 104 | 130 | 22 | - | - |
| Road Missions | CVT | DVT |
|---|---|---|
| US06 | 26.0% | 28.1% |
| UDDS | 23.4% | 24.9% |
| HWFET | 23.3% | 24.9% |
| Urban | 22.4% | 23.0% |
| Extra-urban | 23.5% | 24.8% |
| Highway | 23.9% | 25.5% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonfiglio, A.; Lanzarotto, D.; Marchesoni, M.; Passalacqua, M.; Procopio, R.; Repetto, M. Electrical-Loss Analysis of Power-Split Hybrid Electric Vehicles. Energies 2017, 10, 2142. https://doi.org/10.3390/en10122142
Bonfiglio A, Lanzarotto D, Marchesoni M, Passalacqua M, Procopio R, Repetto M. Electrical-Loss Analysis of Power-Split Hybrid Electric Vehicles. Energies. 2017; 10(12):2142. https://doi.org/10.3390/en10122142
Chicago/Turabian StyleBonfiglio, Andrea, Damiano Lanzarotto, Mario Marchesoni, Massimiliano Passalacqua, Renato Procopio, and Matteo Repetto. 2017. "Electrical-Loss Analysis of Power-Split Hybrid Electric Vehicles" Energies 10, no. 12: 2142. https://doi.org/10.3390/en10122142
APA StyleBonfiglio, A., Lanzarotto, D., Marchesoni, M., Passalacqua, M., Procopio, R., & Repetto, M. (2017). Electrical-Loss Analysis of Power-Split Hybrid Electric Vehicles. Energies, 10(12), 2142. https://doi.org/10.3390/en10122142








