The Future of the European Electricity Grid Is Bright: Cost Minimizing Optimization Shows Solar with Storage as Dominant Technologies to Meet European Emissions Targets to 2050
Abstract
:1. Introduction
2. Method
2.1. The Power Plant Database
2.2. The Solar Technology Model
2.3. The Electricity Investment Model
2.4. The Scenario
3. Results and Discussion
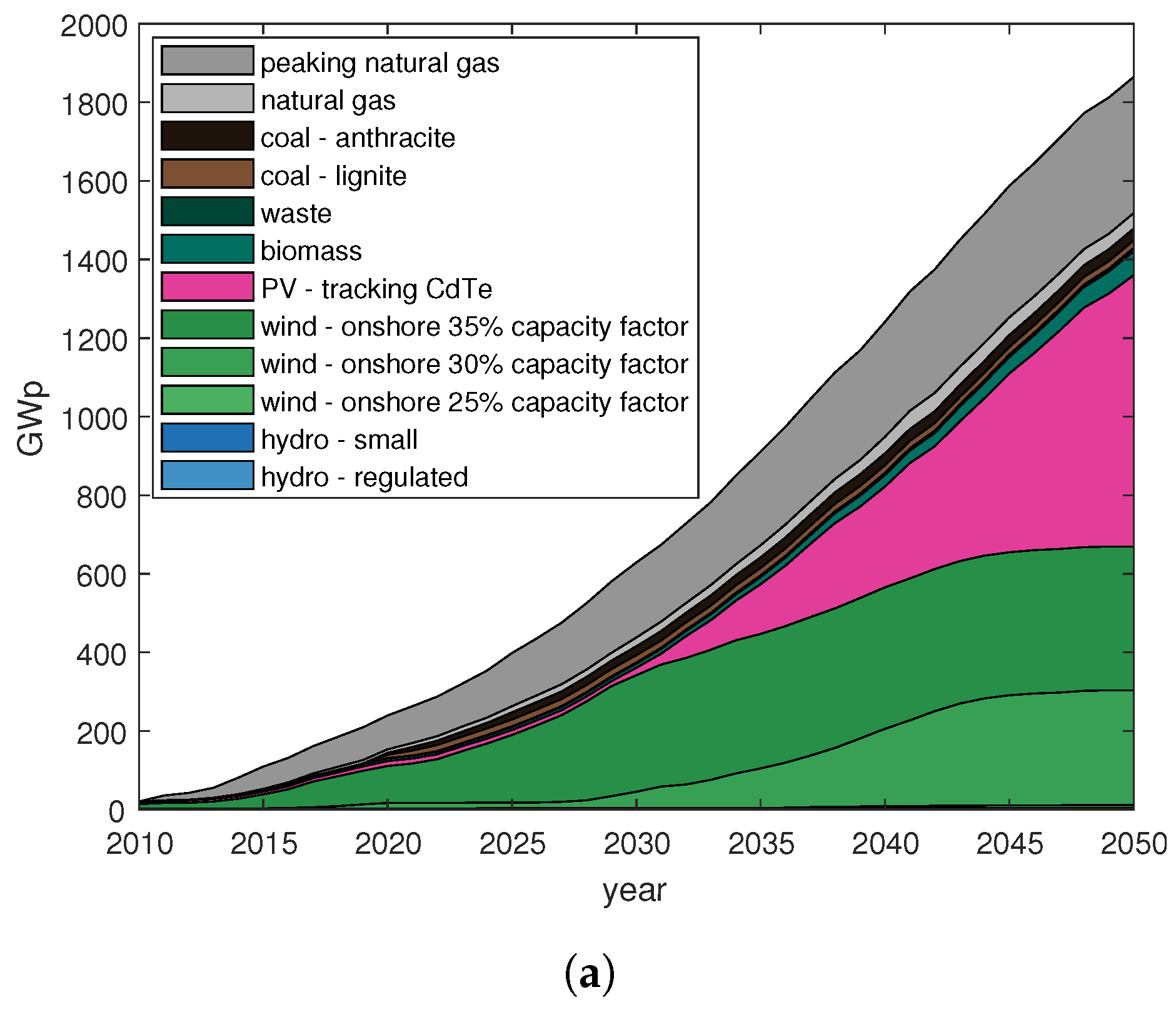
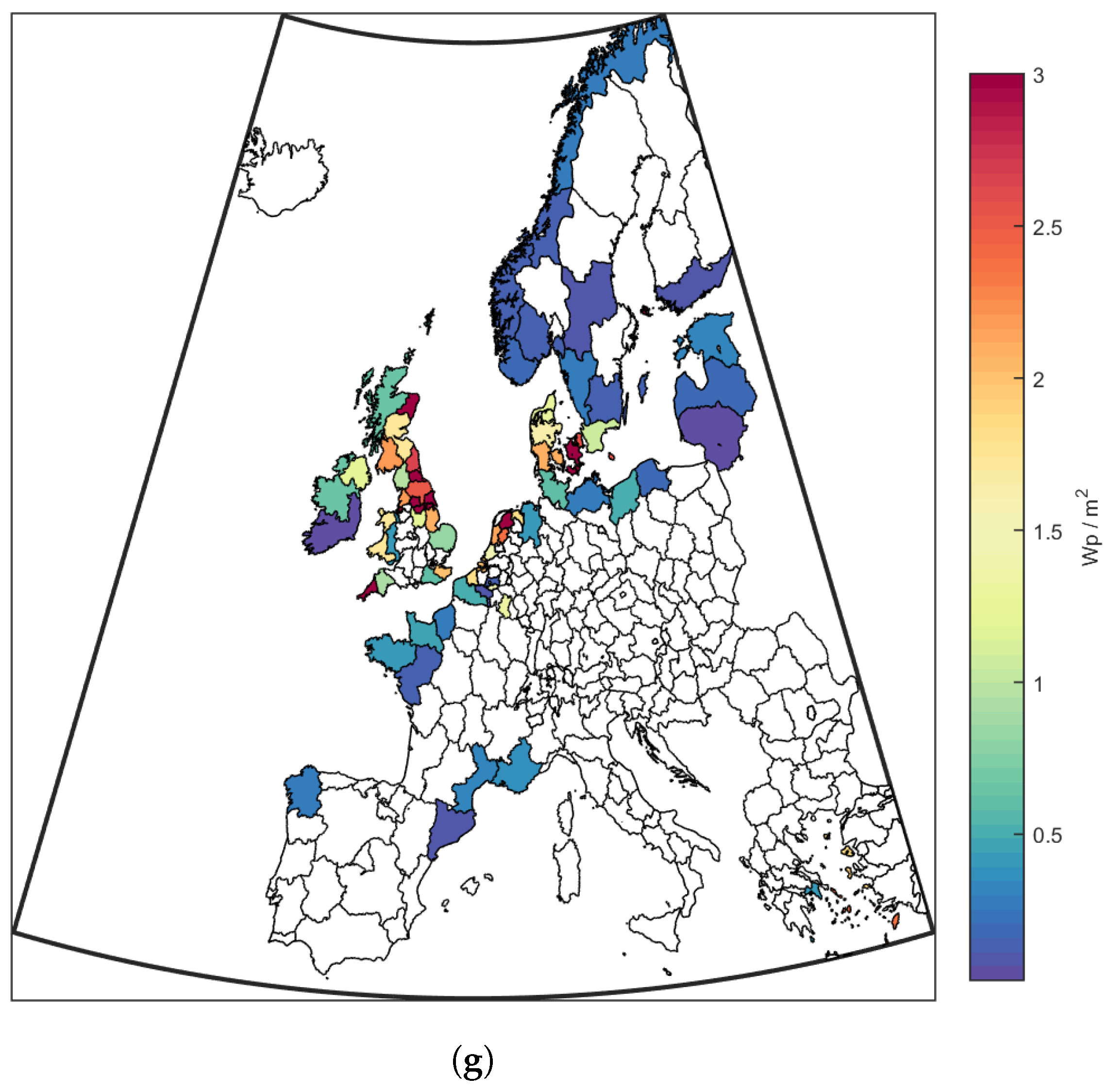
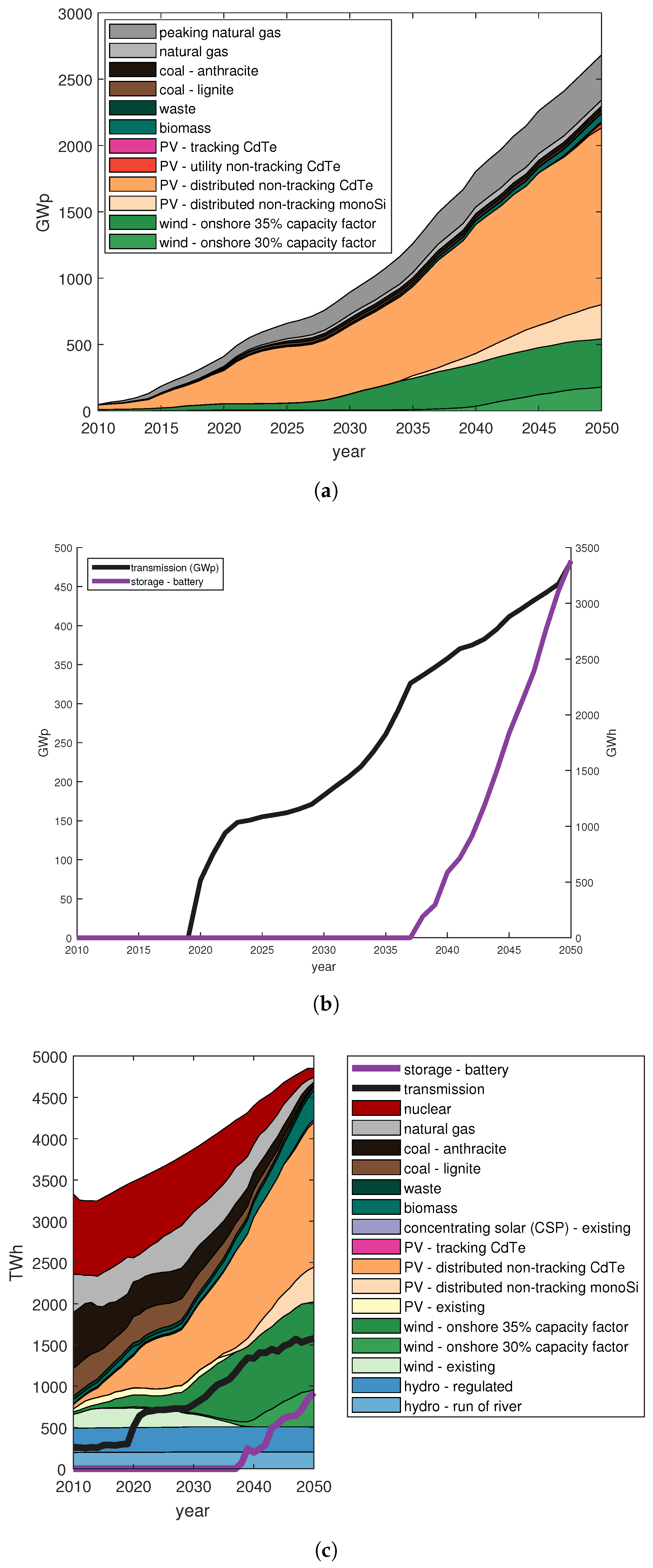
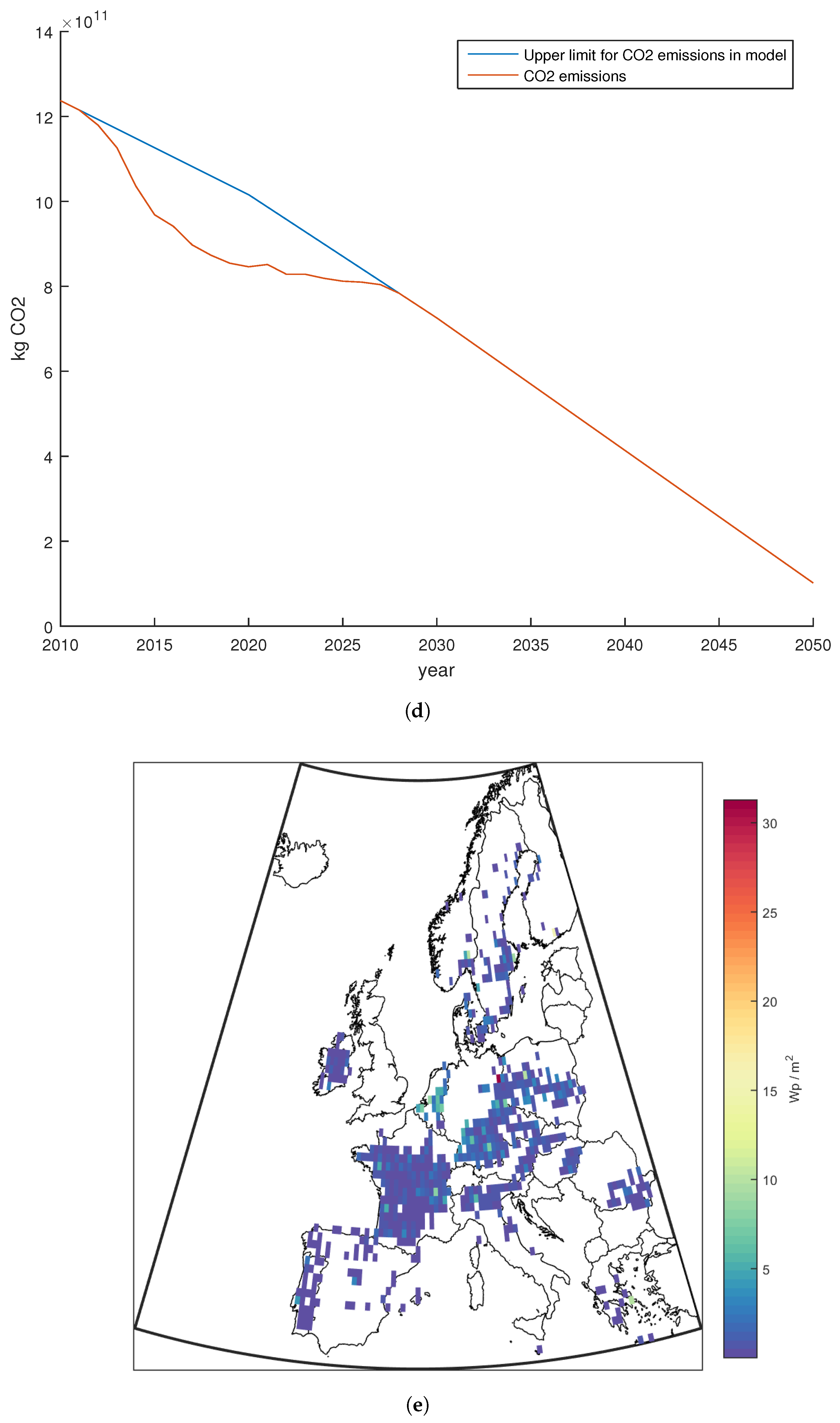
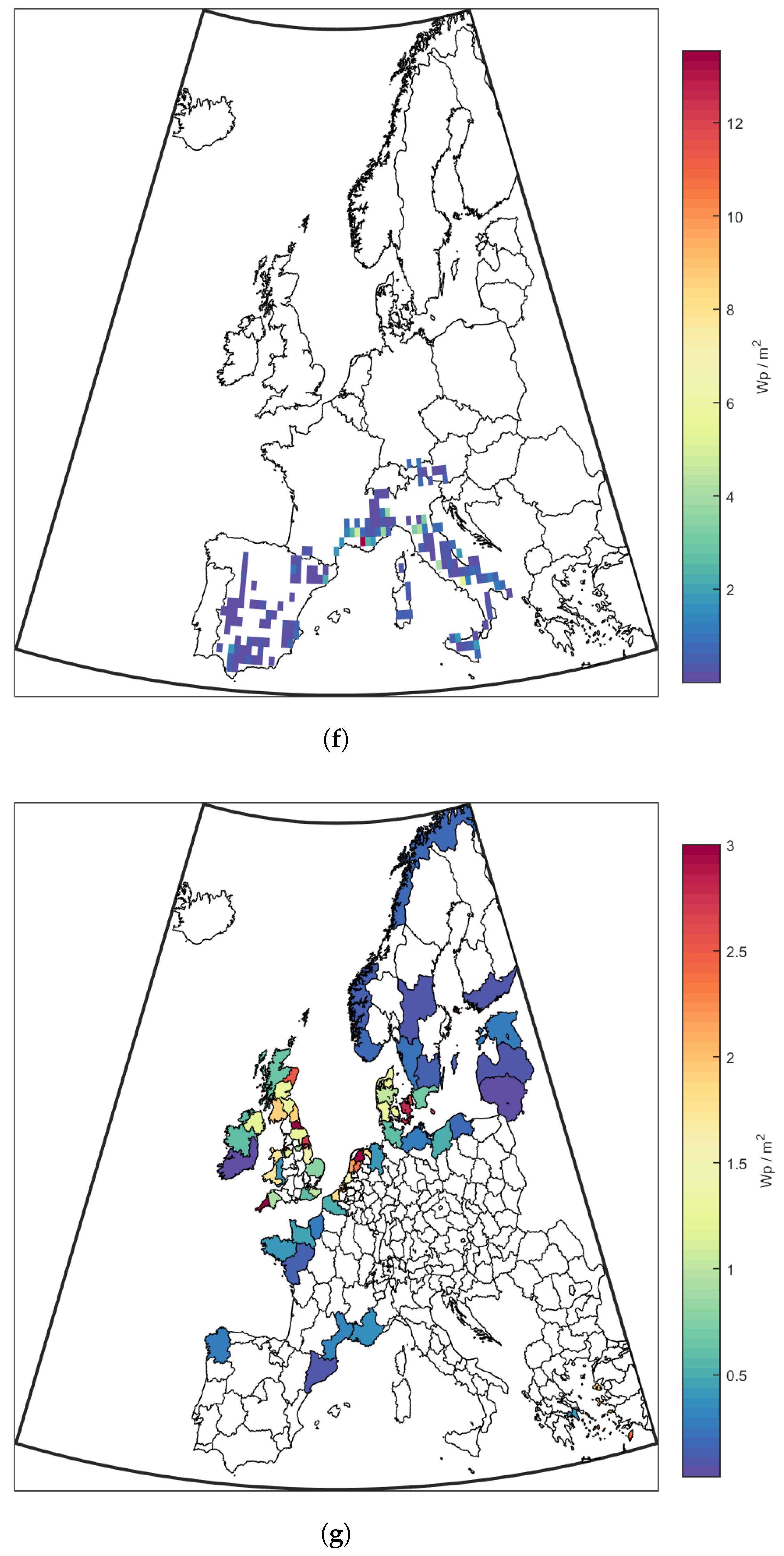
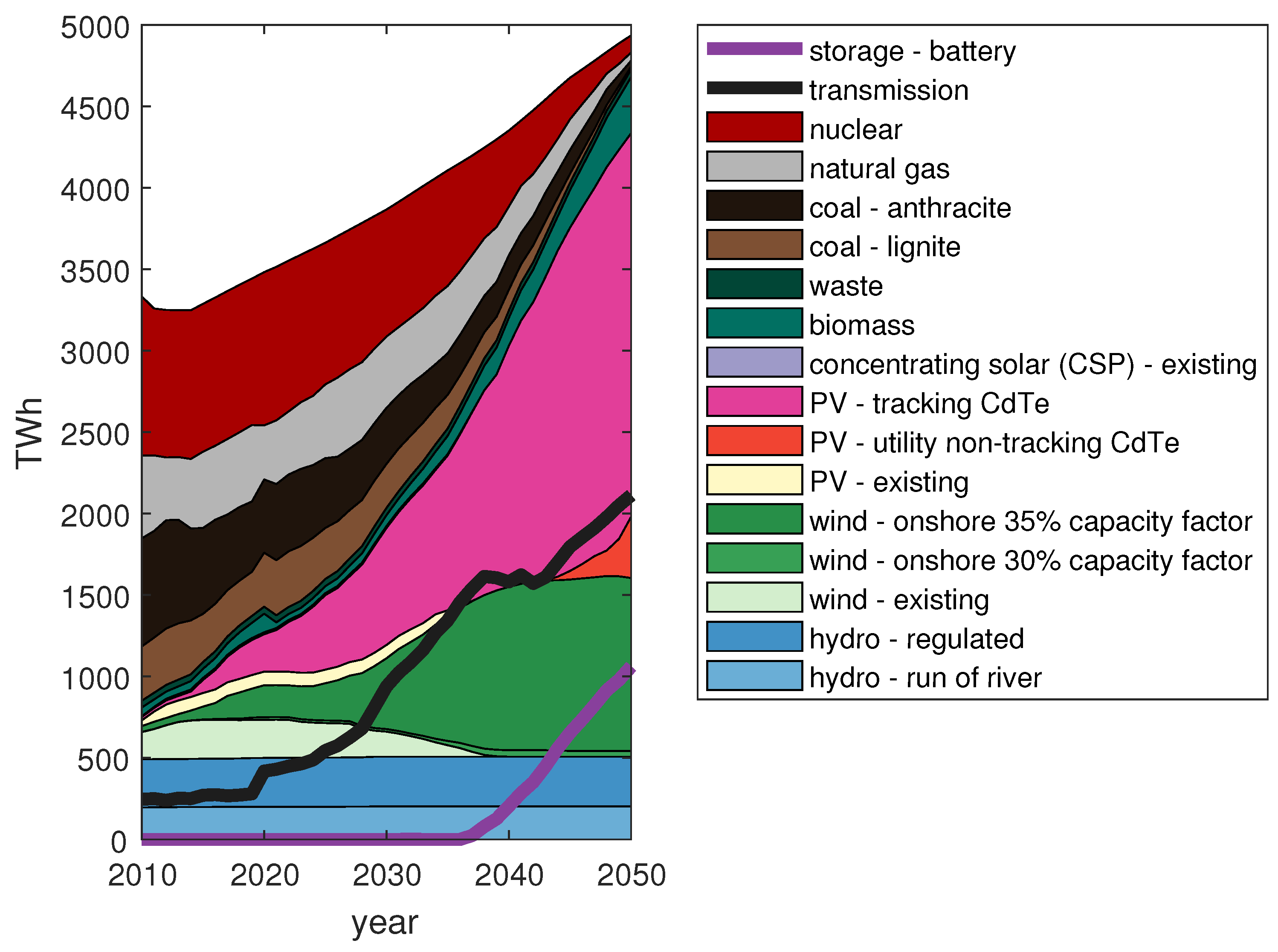
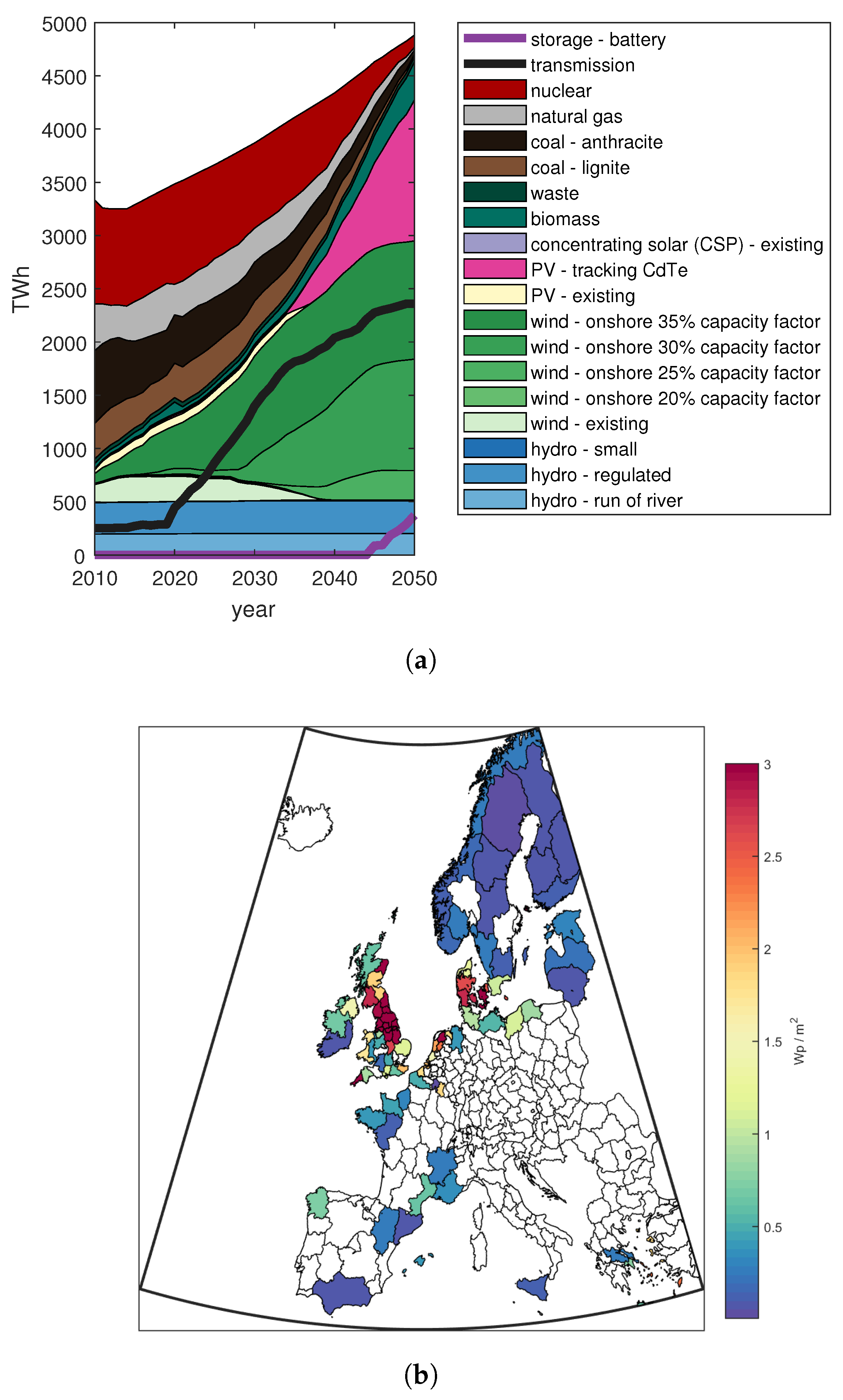
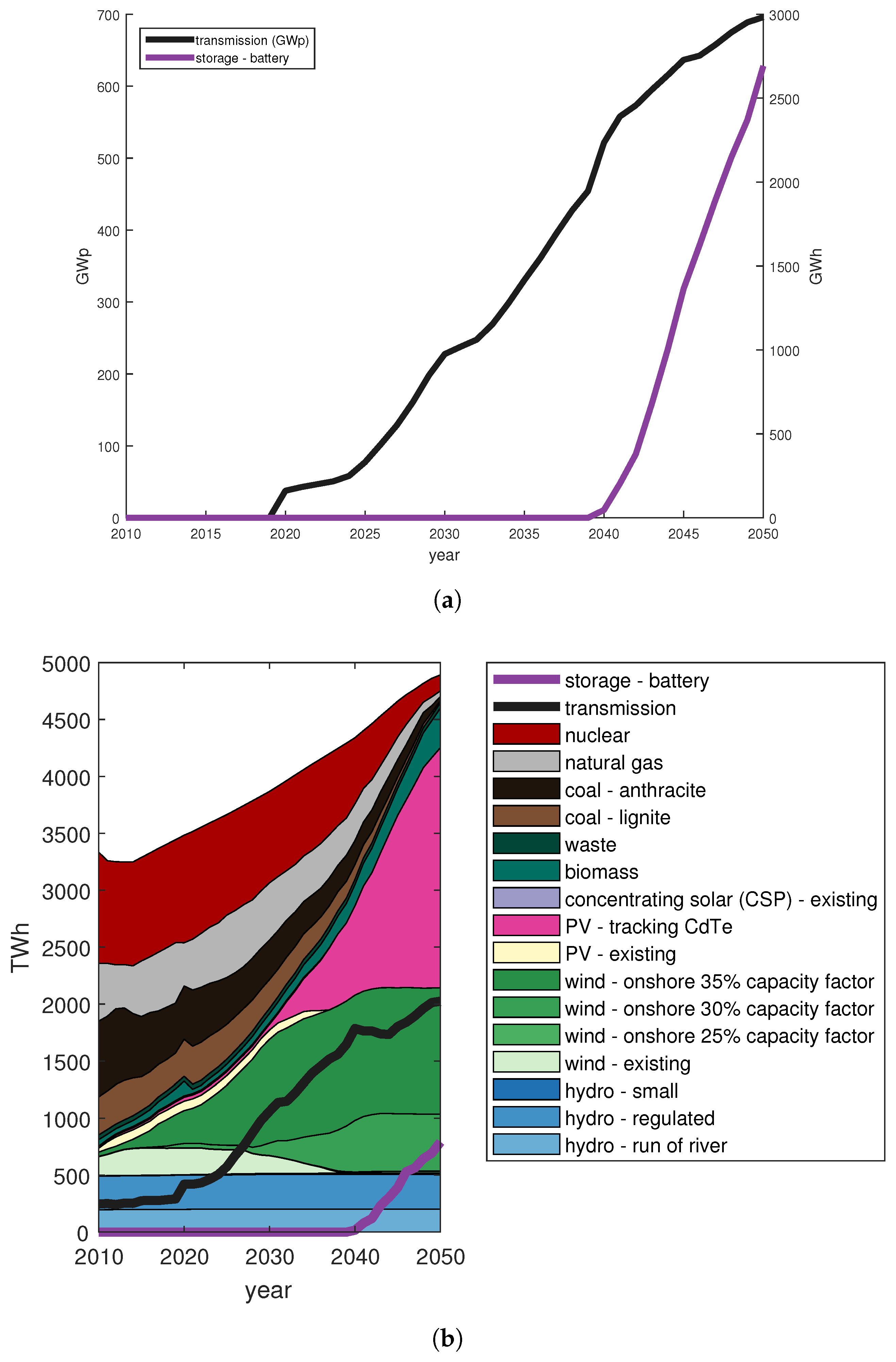
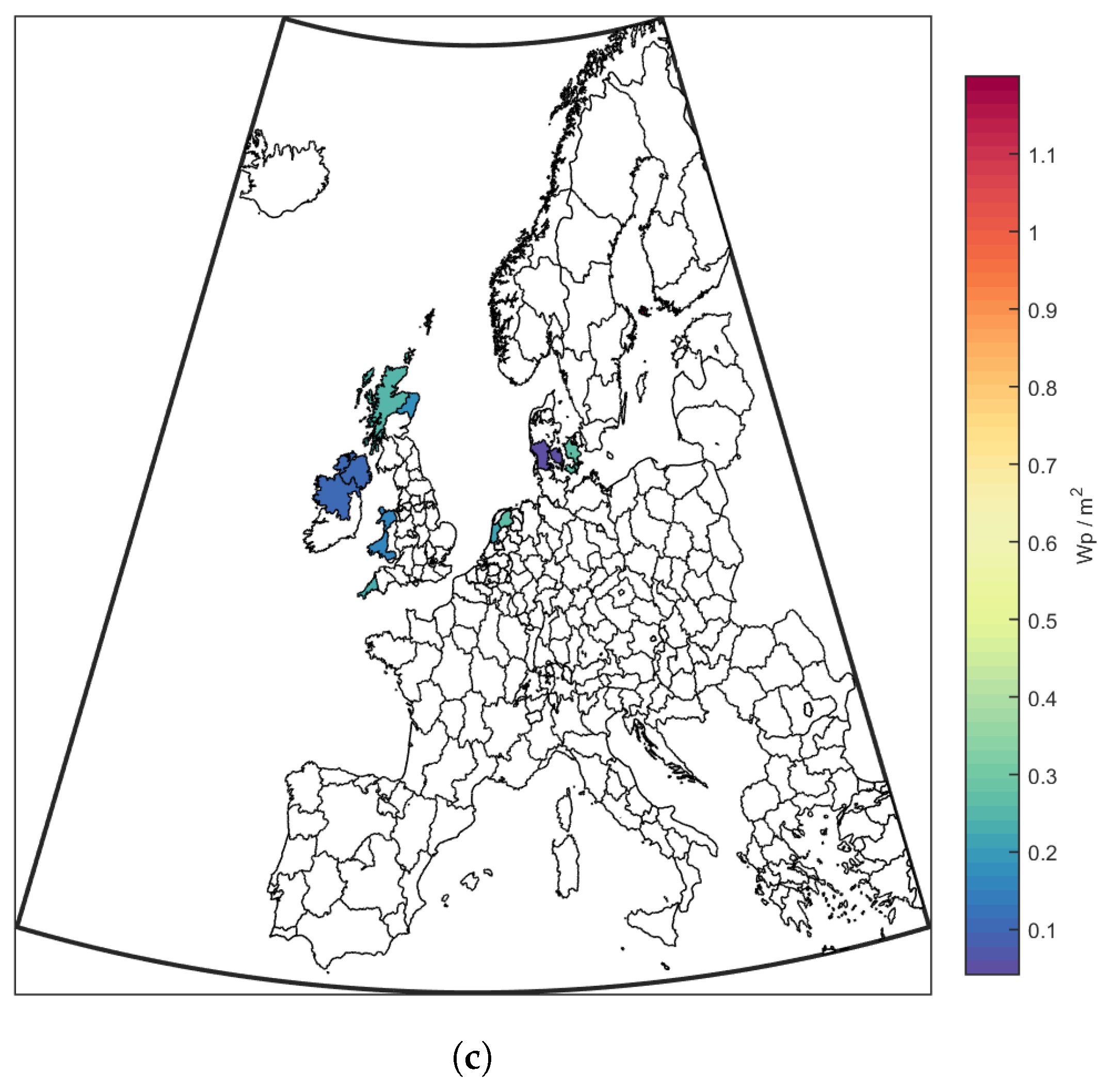
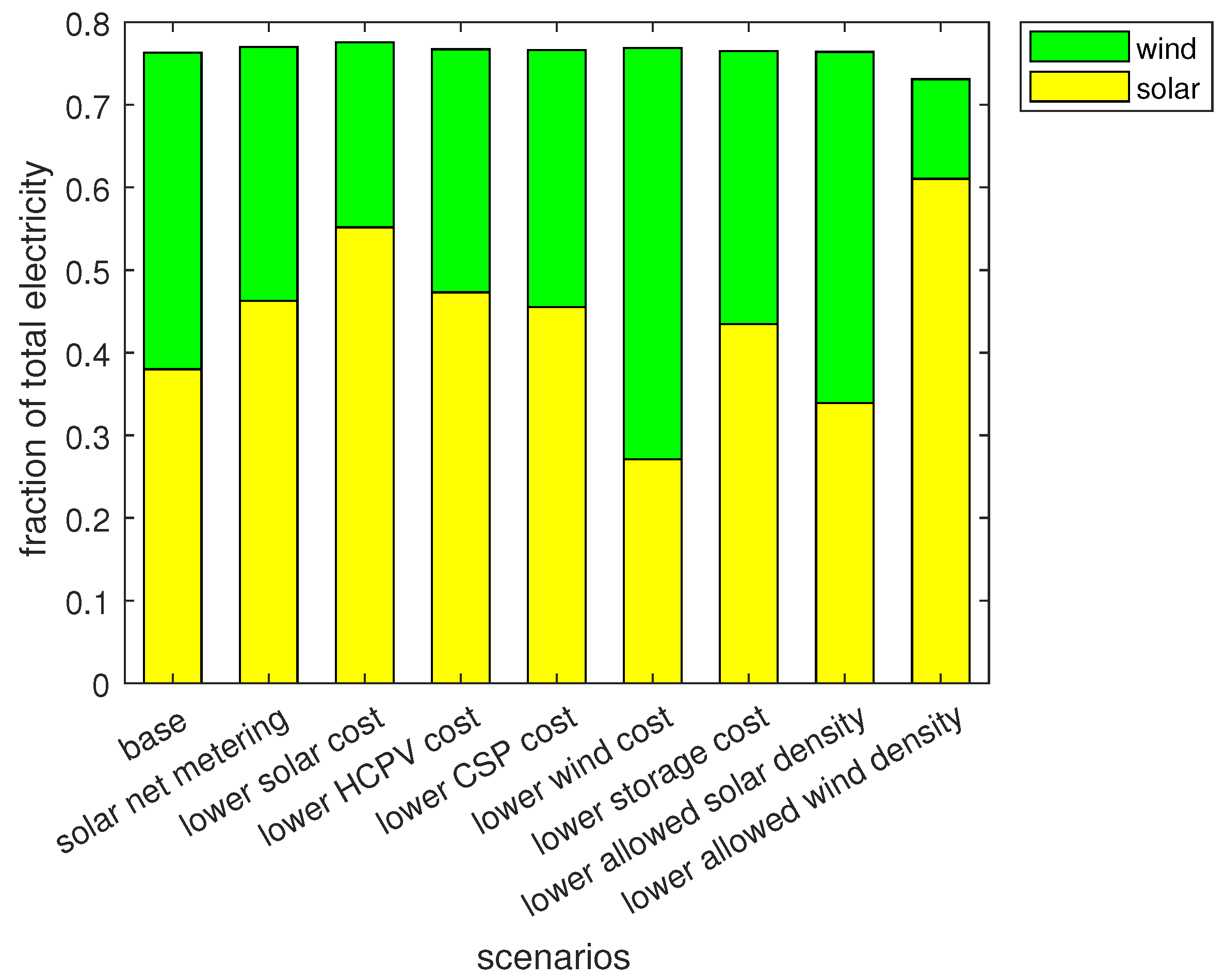
3.1. Base Case
3.2. Sensitivity with Solar Net Metering
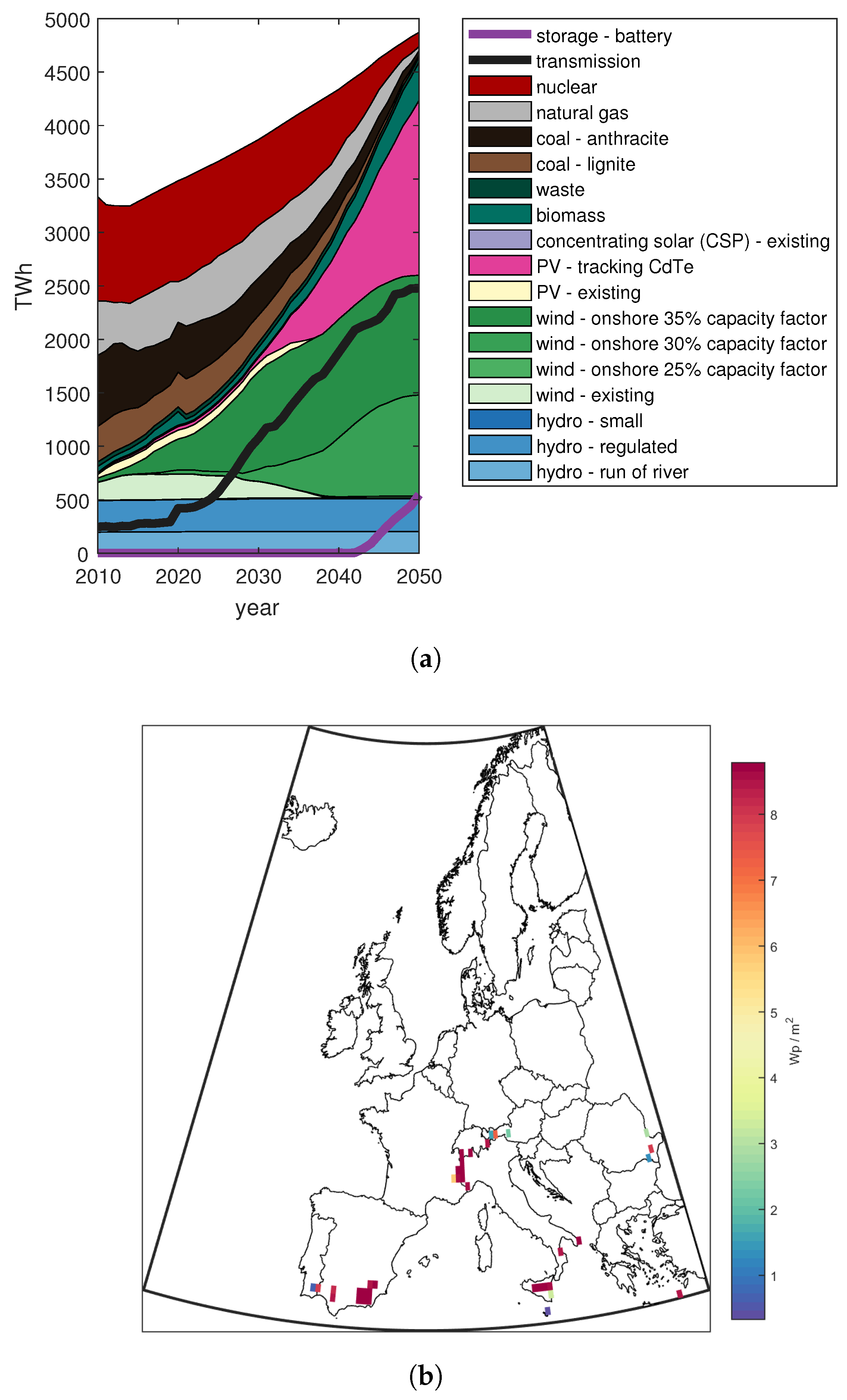
3.3. Sensitivity with Lower Solar Costs
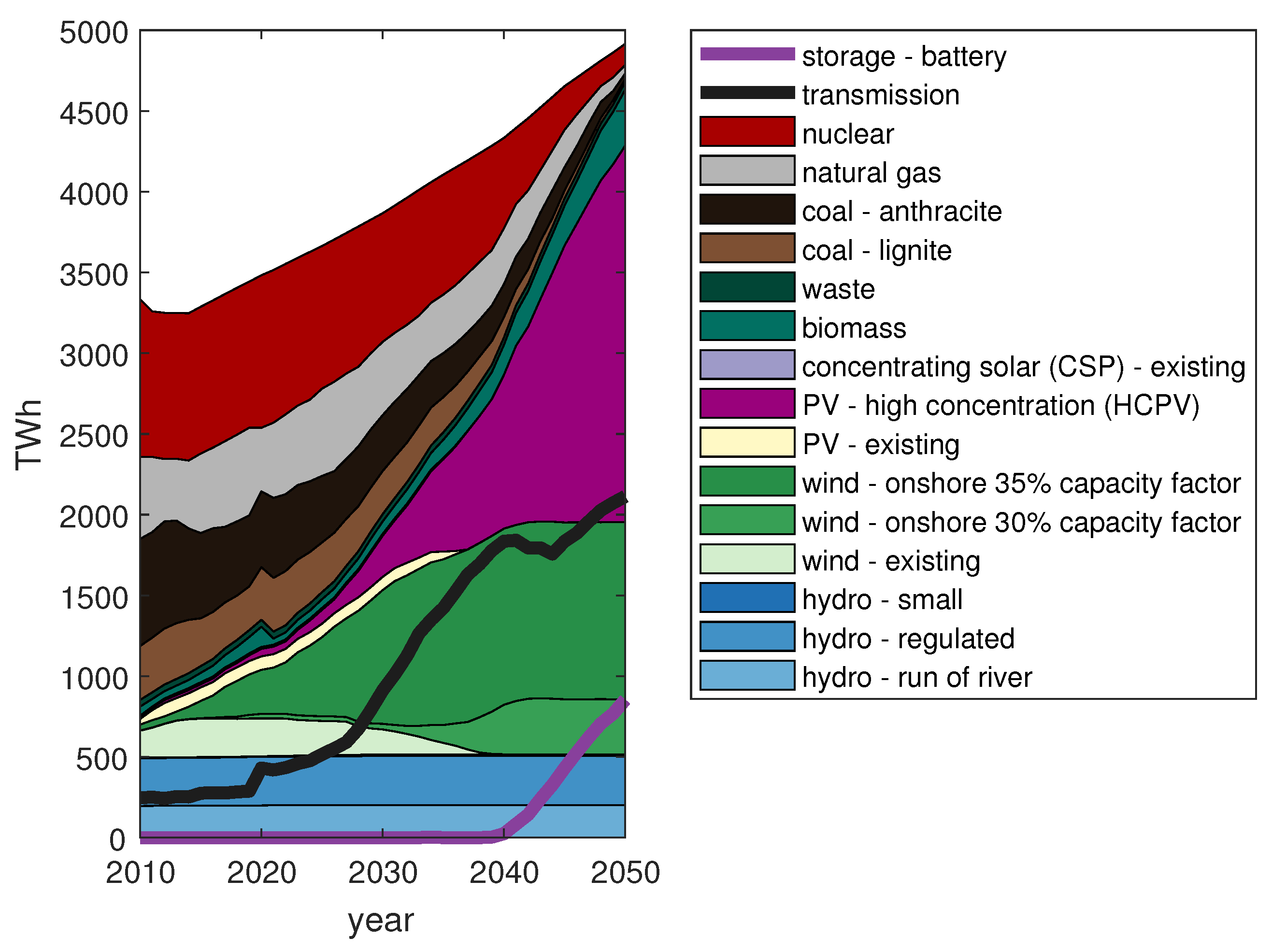
3.4. Sensitivity with Lower HCPV Cost
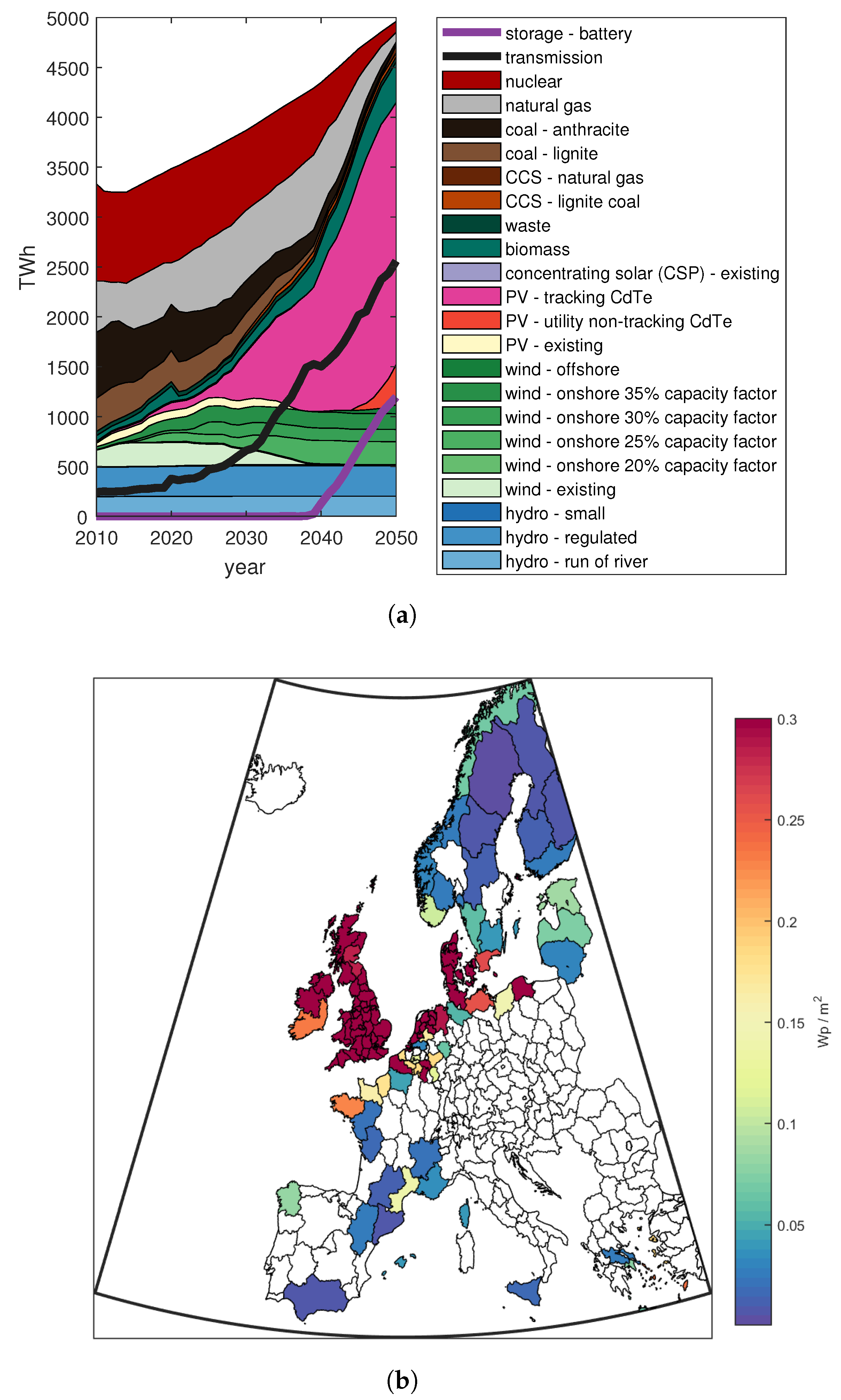
3.5. Sensitivity with Lower CSP Cost
3.6. Sensitivity with Lower Wind Cost
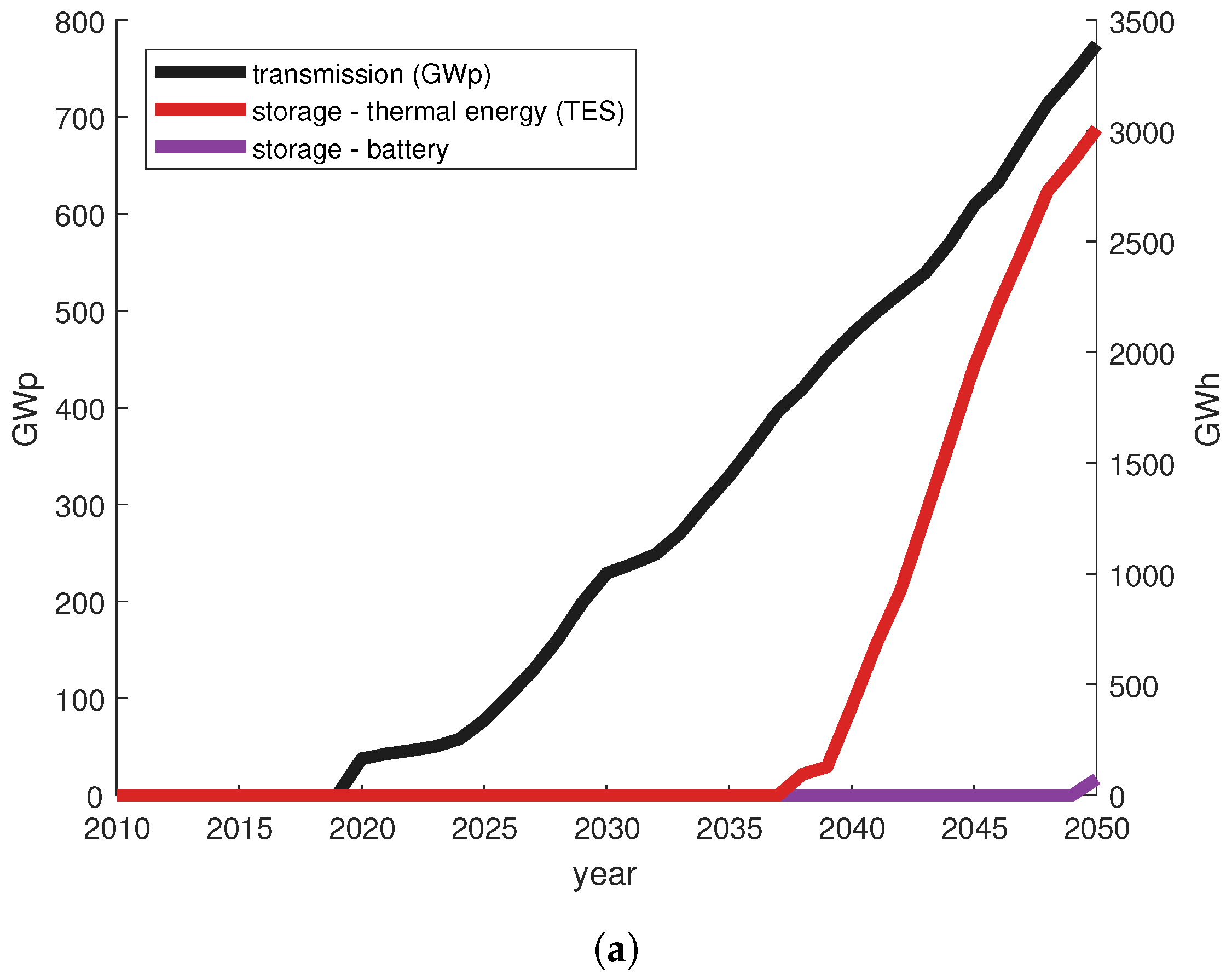
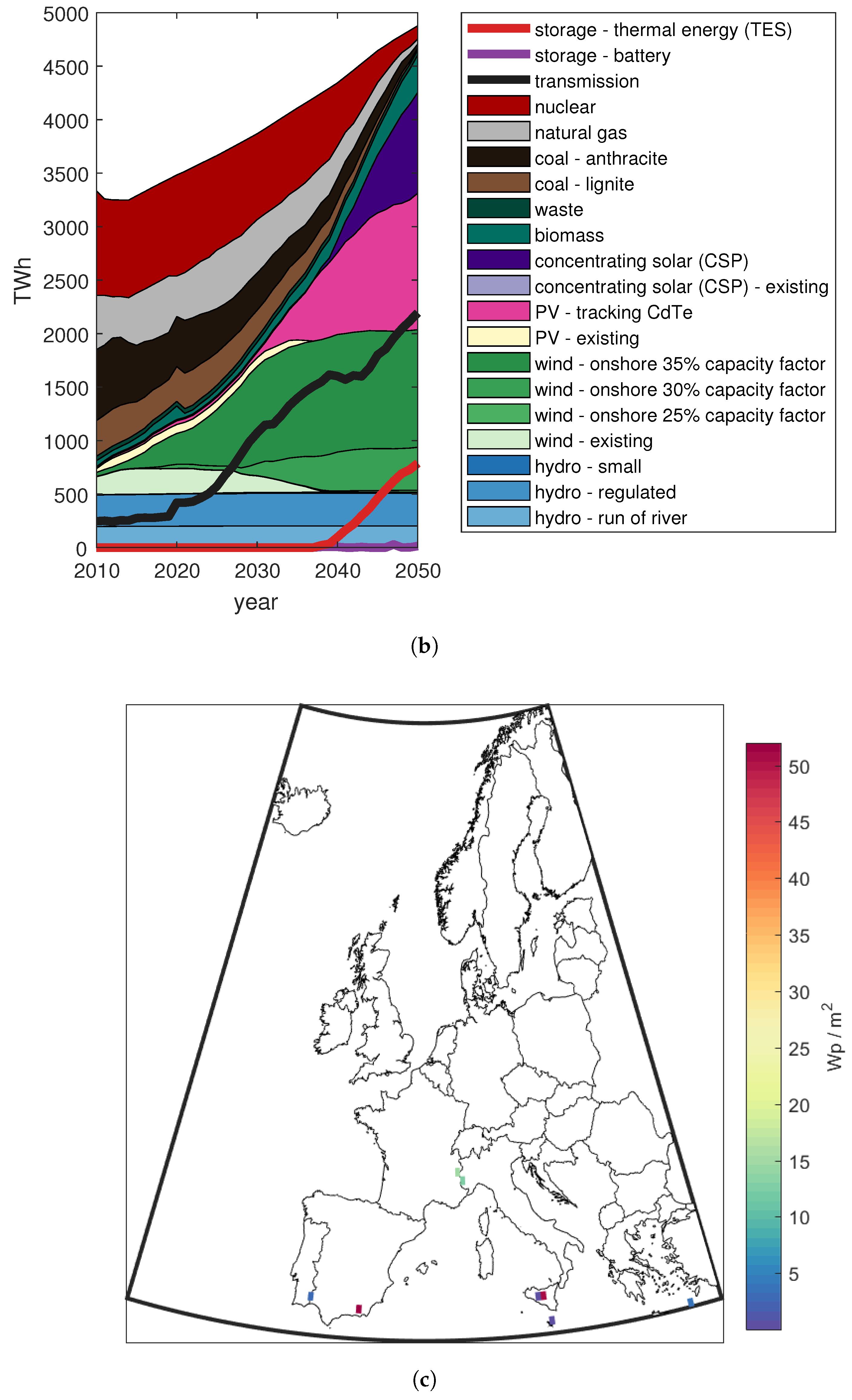
3.7. Sensitivity with Lower Storage Cost
3.8. Sensitivity with Lower Allowed Installed Solar Density and Wind
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. Technology Input Data
| Generation Technology | Technical Lifetime (years) | Costs | Efficiency (%) | Annual Availability (%) | |
|---|---|---|---|---|---|
| Investment (€/kW) | Fixed O&M (€/kW, year) | ||||
| Nuclear | 60 | 5148 | 154.4 | 39–42 | 85 |
| Anthracite | |||||
| Condensing | 40 | 1560 | 33.5 | 47–55 | 85 |
| CHP | 40 | 1560 | 33.5 | 35–45 | 85 |
| BP | 40 | 1560 | 33.5 | 81–84 | 85 |
| Lignite | |||||
| Condensing | 40 | 1560 | 33.5 | 46–56 | 85 |
| CHP | 40 | 1560 | 33.5 | 35–45 | 85 |
| BP | 40 | 1560 | 33.5 | 81–84 | 85 |
| Natural gas | |||||
| CCGT | 30 | 780 | 19.5 | 60–70 | 85 |
| CHP | 30 | 1014 | 30.4 | 48–57 | 85 |
| GT | 30 | 390 | 15.6 | 35–45 | 85 |
| BP | 30 | 1014 | 30.4 | 81–84 | 85 |
| Biomass | |||||
| Condensing | 40 | 1856 | 64.7 | 40–49 | 85 |
| CHP | 40 | 3151 | 118.6 | 29–39 | 85 |
| BP | 40 | 3151 | 118.6 | 81–84 | 85 |
| Waste | |||||
| CHP | 40 | 6630 | 251.9 | 16–21 | 85 |
| Generation Technology | Costs | Efficiency (%) | Annual Availability (%) | Capture Efficiency (%) | |
|---|---|---|---|---|---|
| Investment (€/kW) | Fixed O&M (€/kW, year) | ||||
| Anthracite | 3003 | 90.5 | 35–43 | 85 | 87.7 |
| Lignite | 3003 | 90.5 | 35–43 | 85 | 88.9 |
| Natural gas | 1800 | 35.1 | 46–53 | 85 | 88.5 |
| Biomass co-fire | |||||
| Anthracite | 3463 | 107.6 | 34–41 | 85 | 87.7 |
| Lignite | 3463 | 107.6 | 34–41 | 85 | 88.9 |
| Generation Technology | Costs 2012 | Costs 2020 | Costs 2050 | |||
|---|---|---|---|---|---|---|
| Investment (€/kW) | Fixed O&M (€/kW, year) | Investment (€/kW) | Fixed O&M (€/kW, year) | Investment (€/kW) | Fixed O&M (€/kW, year) | |
| Wind power | ||||||
| Onshore | 1386 | 35.5 | 1343 | 34.1 | 1192 | 29.5 |
| Offshore | 3918 | 136.9 | 3341 | 116.9 | 1838 | 64.6 |
| Solar power | ||||||
| Non-concentrating PV | ||||||
| Building | 2439 | 25.2 | 2011 | 24.2 | 976 | 20.6 |
| Utility | 1867 | 19.2 | 1529 | 18.4 | 724 | 15.7 |
| Tracking | 2081 | 21.5 | 1754 | 21.1 | 923 | 19.7 |
| HCPV , tracking | 2800 | 28.8 | 2294 | 27.6 | 1085 | 23.5 |
| CSP, tracking | 5570 | 222.8 | 4739 | 189.5 | 2586 | 103.2 |
| Storage Technology | Technical Lifetime (years) | Investment Cost (€/kWh) | Round-Trip Efficiency (%) | ||
|---|---|---|---|---|---|
| 2012 | 2020 | 2050 | |||
| TES | 25 | 129 | 77 | 11 | 0.95 |
| Battery | 10 | 274 | 183 | 41 | 0.9 |
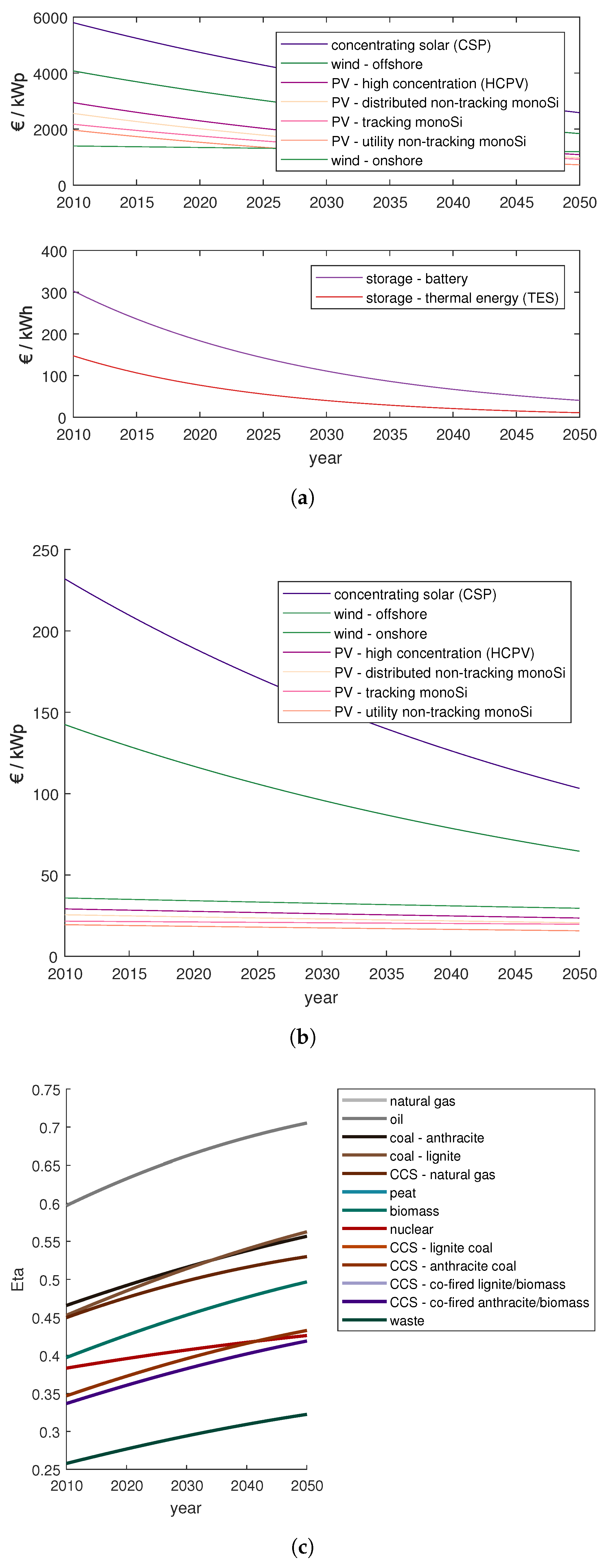
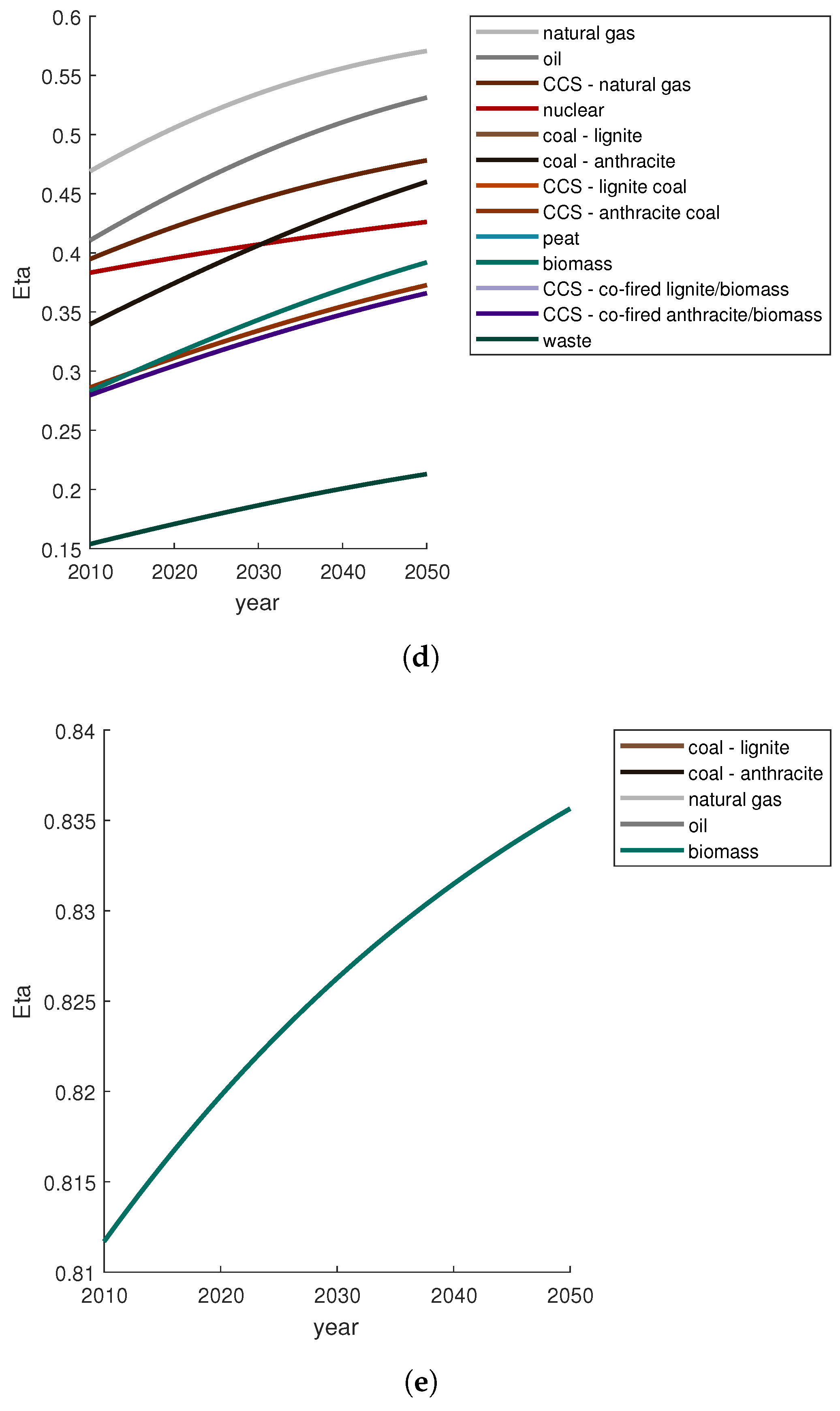
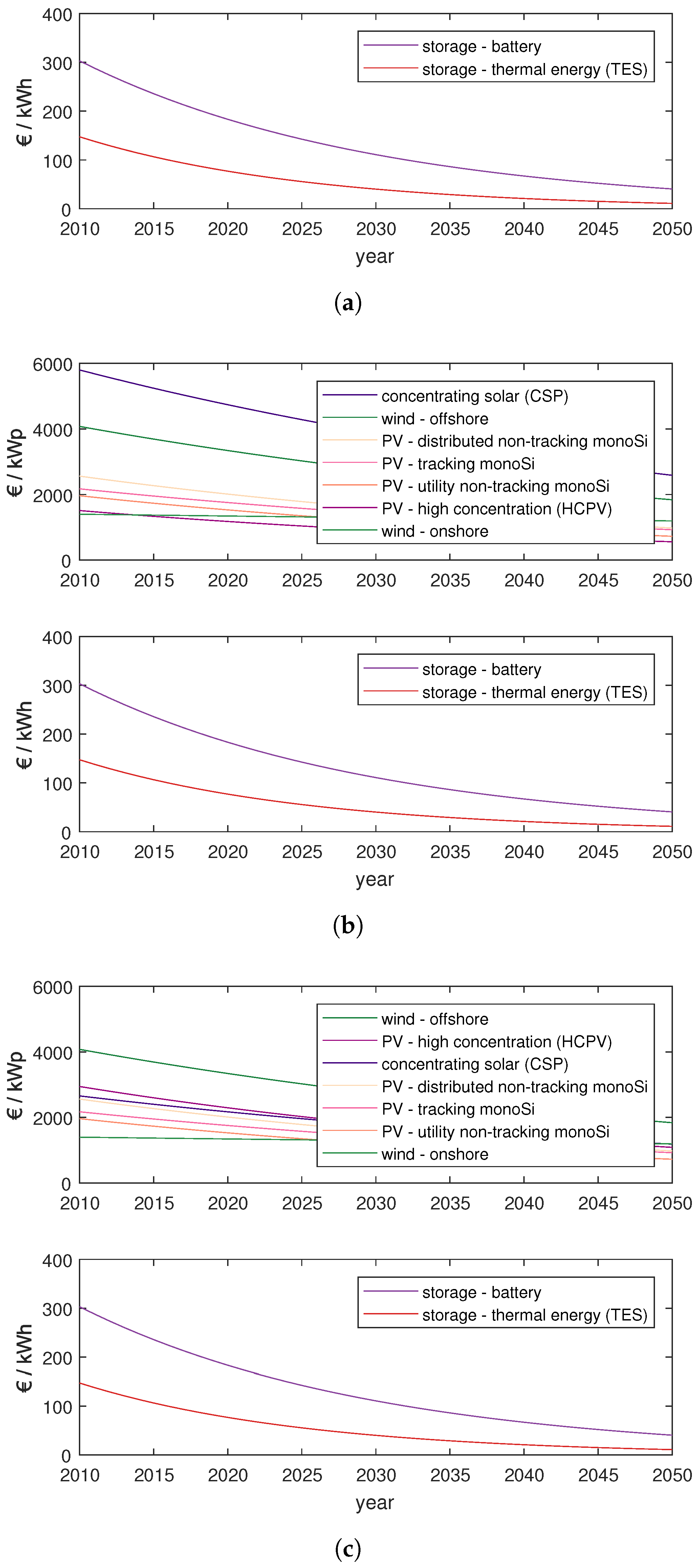
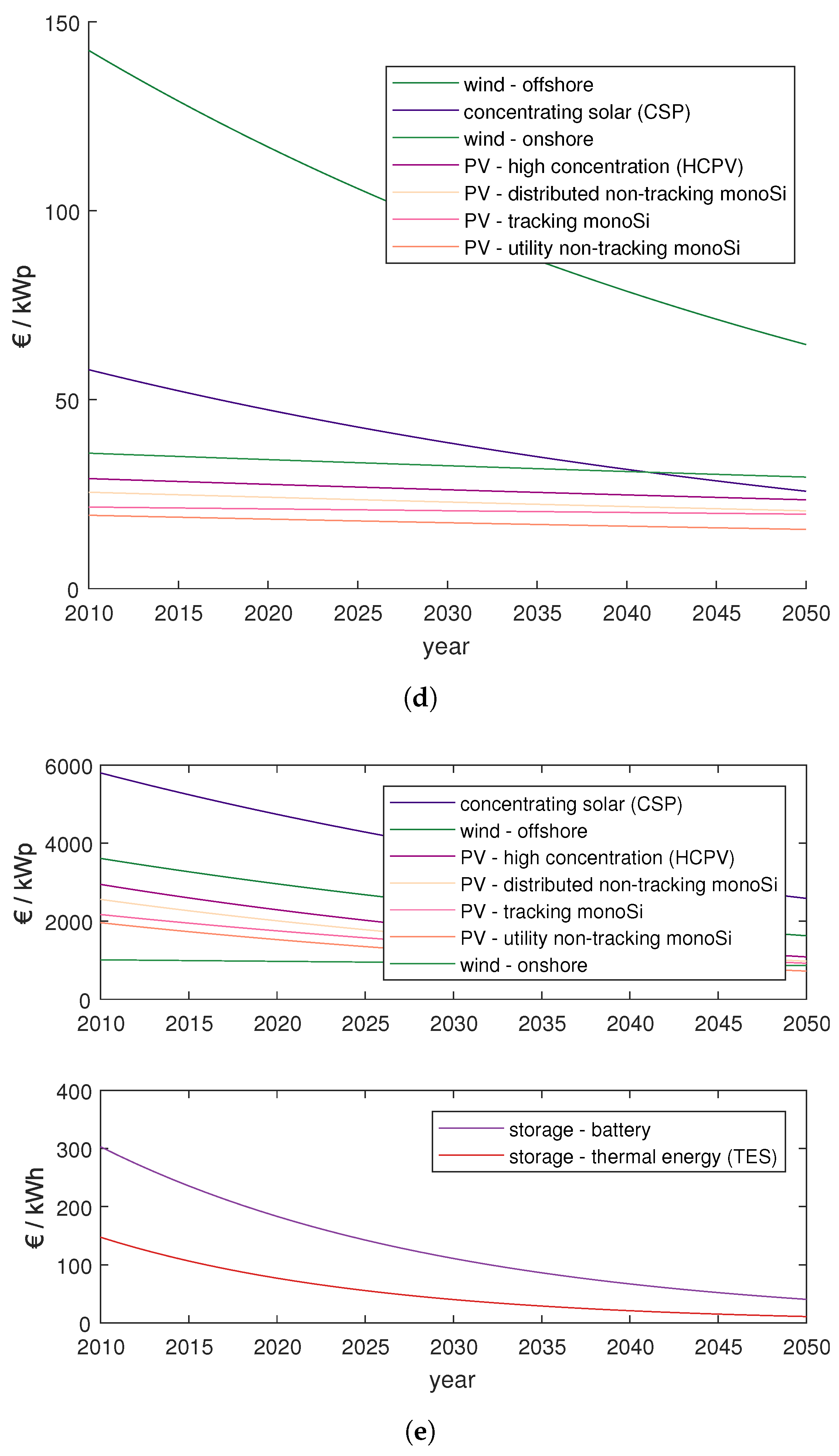
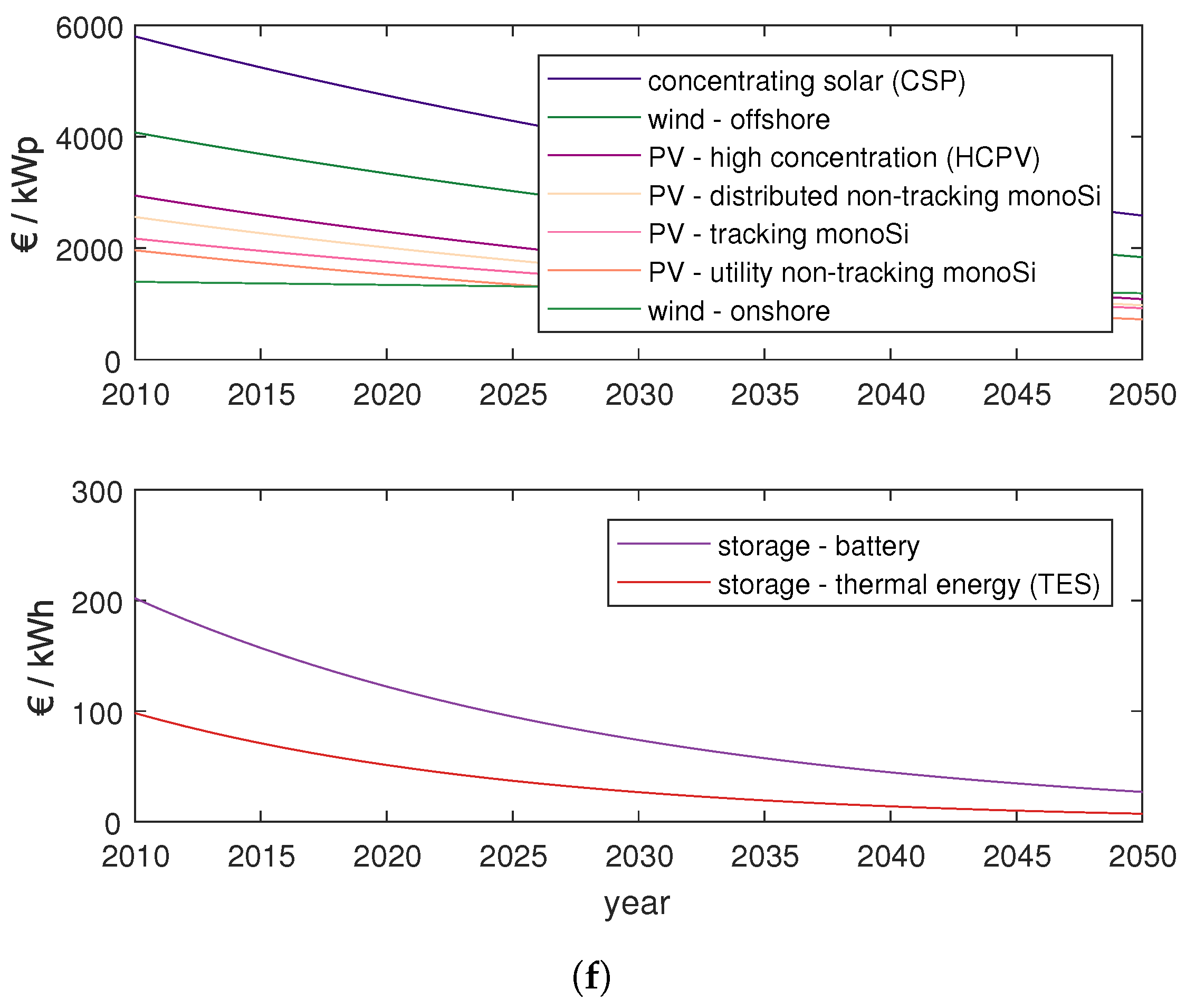
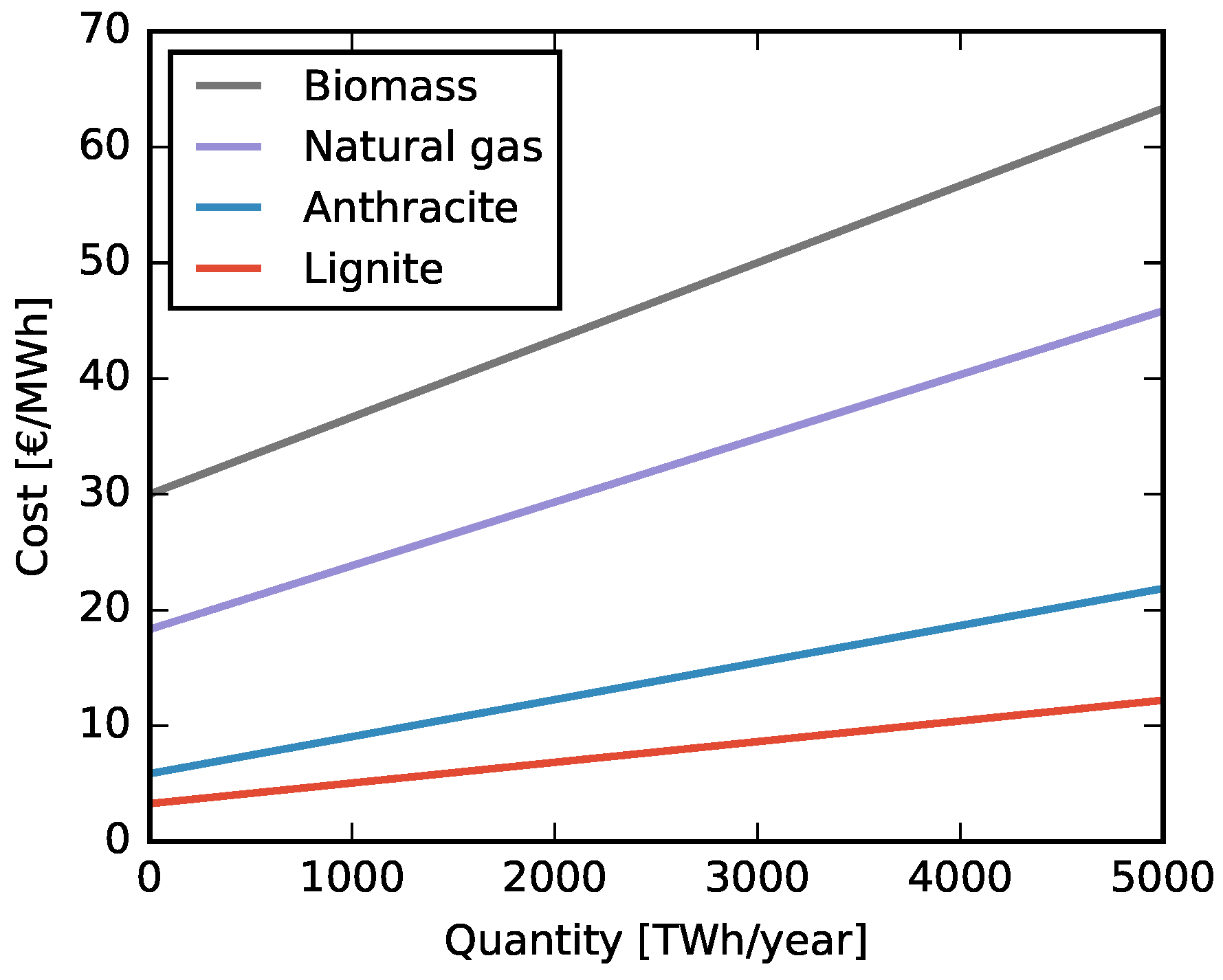
Appendix A.2. Fuel Supply Curves
References
- Pietzcker, R.C.; Stetter, D.; Manger, S.; Luderer, G. Using the sun to decarbonize the power sector: The economic potential of photovoltaics and concentrating solar power. Appl. Energy 2014, 135, 704–720. [Google Scholar] [CrossRef]
- Fürsch, M.; Hagspiel, S.; Jägemann, C.; Nagl, S.; Lindenberger, D.; Tröster, E. The role of grid extensions in a cost-efficient transformation of the European electricity system until 2050. Appl. Energy 2013, 104, 642–652. [Google Scholar] [CrossRef]
- Berrill, P.; Arvesen, A.; Scholz, Y.; Gils, H.C.; Hertwich, E.G. Environmental impacts of high penetration renewable energy scenarios for Europe. Environ. Res. Lett. 2016, 11, 014012. [Google Scholar] [CrossRef]
- Mileva, A.; Nelson, J.H.; Johnston, J.; Kammen, D.M. Sunshot solar power reduces costs and uncertainty in future low-carbon electricity systems. Environ. Sci. Technol. 2013, 47, 9053–9060. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Smith, S.J.; Kyle, G.P.; Stackhouse, P.W. Modeling the potential for thermal concentrating solar power technologies. Energy Policy 2010, 38, 7884–7897. [Google Scholar] [CrossRef]
- Viebahn, P.; Lechon, Y.; Trieb, F. The potential role of concentrated solar power (CSP) in Africa and Europe—A dynamic assessment of technology development, cost development and life cycle inventories until 2050. Energy Policy 2011, 39, 4420–4430. [Google Scholar] [CrossRef]
- Peters, M.; Schmidt, T.S.; Wiederkehr, D.; Schneider, M. Shedding light on solar technologies—A techno-economic assessment and its policy implications. Energy Policy 2011, 39, 6422–6439. [Google Scholar] [CrossRef]
- Denholm, P.; Margolis, R.M. Evaluating the limits of solar photovoltaics (PV) in electric power systems utilizing energy storage and other enabling technologies. Energy Policy 2007, 35, 4424–4433. [Google Scholar] [CrossRef]
- Kjärstad, J.; Johnsson, F. The European power plant infrastructure—Presentation of the Chalmers energy infrastructure database with applications. Energy Policy 2007, 35, 3643–3664. [Google Scholar] [CrossRef]
- Norwood, Z.; Kammen, D. Life cycle analysis of distributed concentrating solar combined heat and power: Economics, global warming potential and water. Environ. Res. Lett. 2012, 7, 044016. [Google Scholar] [CrossRef]
- Norwood, Z.; Nyholm, E.; Otanicar, T.; Johnsson, F. A Geospatial Comparison of Distributed Solar Heat and Power in Europe and the U.S. PLoS ONE 2014, 9, e112442. [Google Scholar] [CrossRef] [PubMed]
- Odenberger, M.; Unger, T.; Johnsson, F. Pathways for the North European electricity supply. Energy Policy 2009, 37, 1660–1677. [Google Scholar] [CrossRef]
- Göransson, L.; Goop, J.; Unger, T.; Odenberger, M.; Johnsson, F. Linkages between demand-side management and congestion in the European electricity transmission system. Energy 2014, 69, 860–872. [Google Scholar] [CrossRef]
- Eurostat. Electricity Prices Components for Domestic Consumers, from 2007 Onwards—Annual Data [nrg_pc_204_c]. 2015. Available online: http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=nrg_pc_204_c&lang=en (accessed on 10 September 2015).
- Eurostat. Electricity Prices for Domestic Consumers, from 2007 Onwards—Bi-Annual Data [nrg_pc_204]. 2015. Available online: http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=nrg_pc_204&lang=en (accessed on 10 September 2015).
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts (ECMWF). ERA-Interim. 2016. Available online: http://www.ecmwf.int/en/research/climate-reanalysis/era-interim. (accessed on 2 September 2016).
- Nilsson, K.; Unger, T. Bedömning av en Europeisk Vindkraftpotential med GIS-Analys; Project Report; Profu AB: Mölndal, Sweden, 2014. (In Swedish) [Google Scholar]
- European Commission. Energy Roadmap 2050; Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions, COM(2011) 885 Final; European Commission: Brussels, Belgium, 2011. [Google Scholar]
- Eurelectric. Power Choices Reloaded: Europe’s Lost Decade? 2013. Available online: http://www.eurelectric.org/media/79057/power_choices_2013_final-2013-030-0353-01-e.pdf (accessed on 31 August 2016).
- European Commission. National Action Plans. 2015. Available online: https://ec.europa.eu/energy/en/topics/renewable-energy/national-action-plans (accessed on 10 September 2015).
- International Energy Agency. WEIO 2014—Power Generation Investment Assumptions. 2014. Available online: http://www.worldenergyoutlook.org/media/weowebsite/2014/weio/WEIO2014PGAssumptions.xlsx (accessed on 10 September 2015).
- Nykvist, B.; Nilsson, M. Rapidly falling costs of battery packs for electric vehicles. Nat. Clim. Chang. 2015, 5, 329–332. [Google Scholar] [CrossRef]
- European Solar Thermal Electricity Association. SET-Plan—Solar Thermal Electricity European Industrial Initiative (STE-EII). 2013. Available online: https://setis.ec.europa.eu/system/files/Solar%20CSP%20EII%202013-2015%20IP_0.pdf (accessed on 10 September 2015).
- GTM Research. Solar Balance-of-System: To Track or Not to Track, Part I. 2012. Available online: http://www.greentechmedia.com/articles/read/Solar-Balance-of-System-To-Track-or-Not-to-Track-Part-I (accessed on 10 September 2015).
- U.S. Energy Information Administration. Levelized Cost and Levelized Avoided Cost of New Generation Resources in the Annual Energy Outlook 2017. Technical Report; 2017. Available online: https://www.eia.gov/outlooks/aeo/pdf/electricity_generation.pdf (accessed on 6 September 2017).
- Kost, C.; Mayer, J.N.; Thomsen, J.; Hartmann, N.; Senkpiel, C.; Philipps, S.; Nold, S.; Lude, S.; Saad, N.; Schlegl, T. Levelized Cost of Electricity Renewable Energy Technologies. 2013. Available online: https://www.ise.fraunhofer.de/en/publications/veroeffentlichungen-pdf-dateien-en/studien-und-konzeptpapiere/study-levelized-cost-of-electricity-renewable-energies.pdf (accessed on 10 September 2015).
- Hansen, J.; Sato, M.; Kharecha, P.; Beerling, D.; Berner, R.; Masson-Delmotte, V.; Pagani, M.; Raymo, M.; Royer, D.L.; Zachos, J.C. Target atmospheric CO2: Where should humanity aim? arXiv, 2008; arXiv:0804.1126. [Google Scholar]
- Magné, B.; Chateau, J.; Dellink, R. Global implications of joint fossil fuel subsidy reform and nuclear phase-out: An economic analysis. Clim. Chang. 2014, 123, 677–690. [Google Scholar] [CrossRef]
- International Energy Agency; Nuclear Energy Agency. Projected Costs of Generating Electricity—2015 Edition. Technical Report NEA No. 7057. 2015. Available online: https://www.iea.org/publications/freepublications/publication/projected-costs-of-generating-electricity-2015-edition.html (accessed on 6 September 2017).

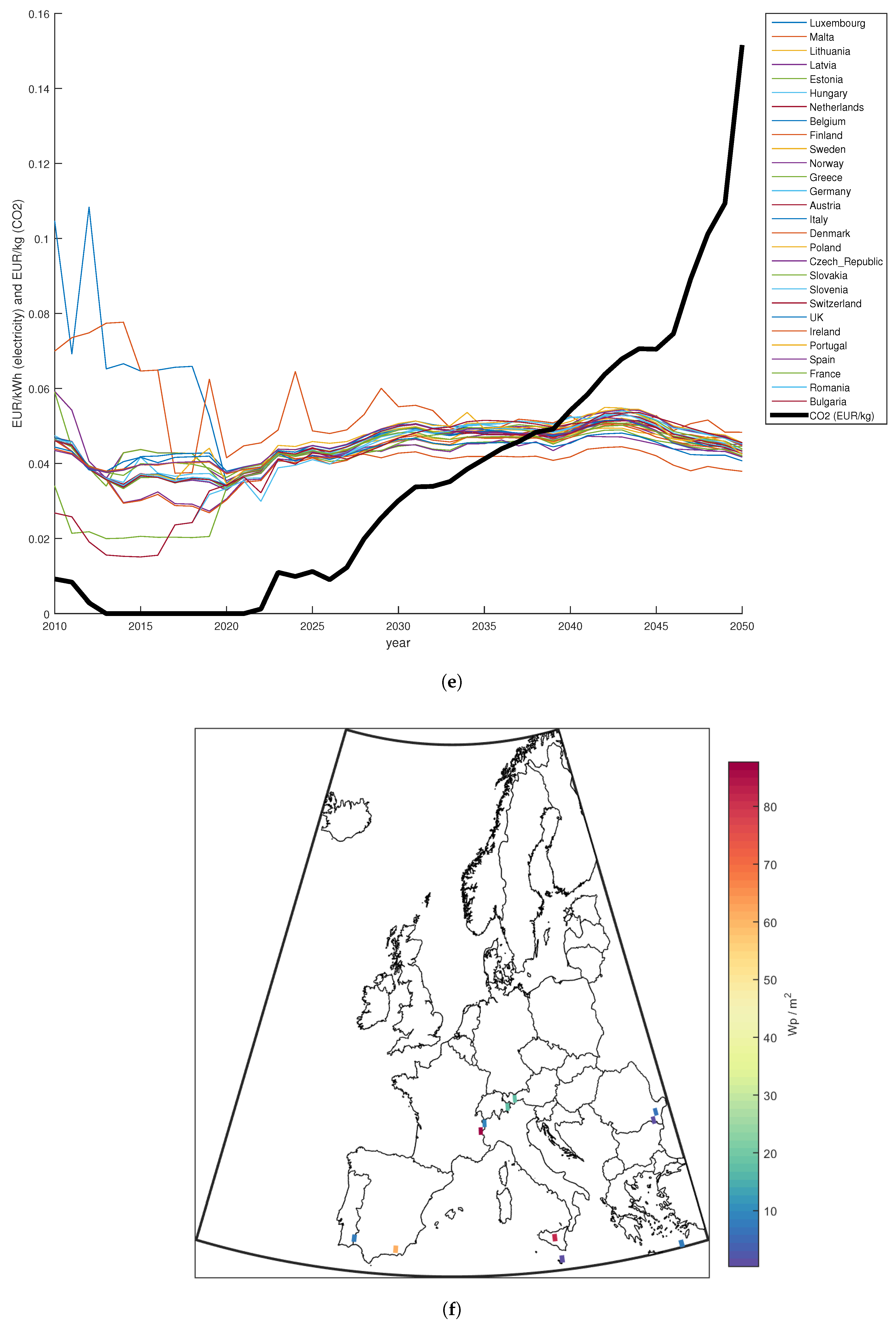
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Norwood, Z.; Goop, J.; Odenberger, M. The Future of the European Electricity Grid Is Bright: Cost Minimizing Optimization Shows Solar with Storage as Dominant Technologies to Meet European Emissions Targets to 2050. Energies 2017, 10, 2080. https://doi.org/10.3390/en10122080
Norwood Z, Goop J, Odenberger M. The Future of the European Electricity Grid Is Bright: Cost Minimizing Optimization Shows Solar with Storage as Dominant Technologies to Meet European Emissions Targets to 2050. Energies. 2017; 10(12):2080. https://doi.org/10.3390/en10122080
Chicago/Turabian StyleNorwood, Zack, Joel Goop, and Mikael Odenberger. 2017. "The Future of the European Electricity Grid Is Bright: Cost Minimizing Optimization Shows Solar with Storage as Dominant Technologies to Meet European Emissions Targets to 2050" Energies 10, no. 12: 2080. https://doi.org/10.3390/en10122080
APA StyleNorwood, Z., Goop, J., & Odenberger, M. (2017). The Future of the European Electricity Grid Is Bright: Cost Minimizing Optimization Shows Solar with Storage as Dominant Technologies to Meet European Emissions Targets to 2050. Energies, 10(12), 2080. https://doi.org/10.3390/en10122080





