A Novel Method of Statistical Line Loss Estimation for Distribution Feeders Based on Feeder Cluster and Modified XGBoost
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Description and Preprocessing
2.2. K-medoids Algorithm with Weighting Distance for Clustering Distribution Feeders
2.2.1. Selecting Variables for Clustering Distribution Feeders
2.2.2. K-Medoids Algorithm with Weighting Distance
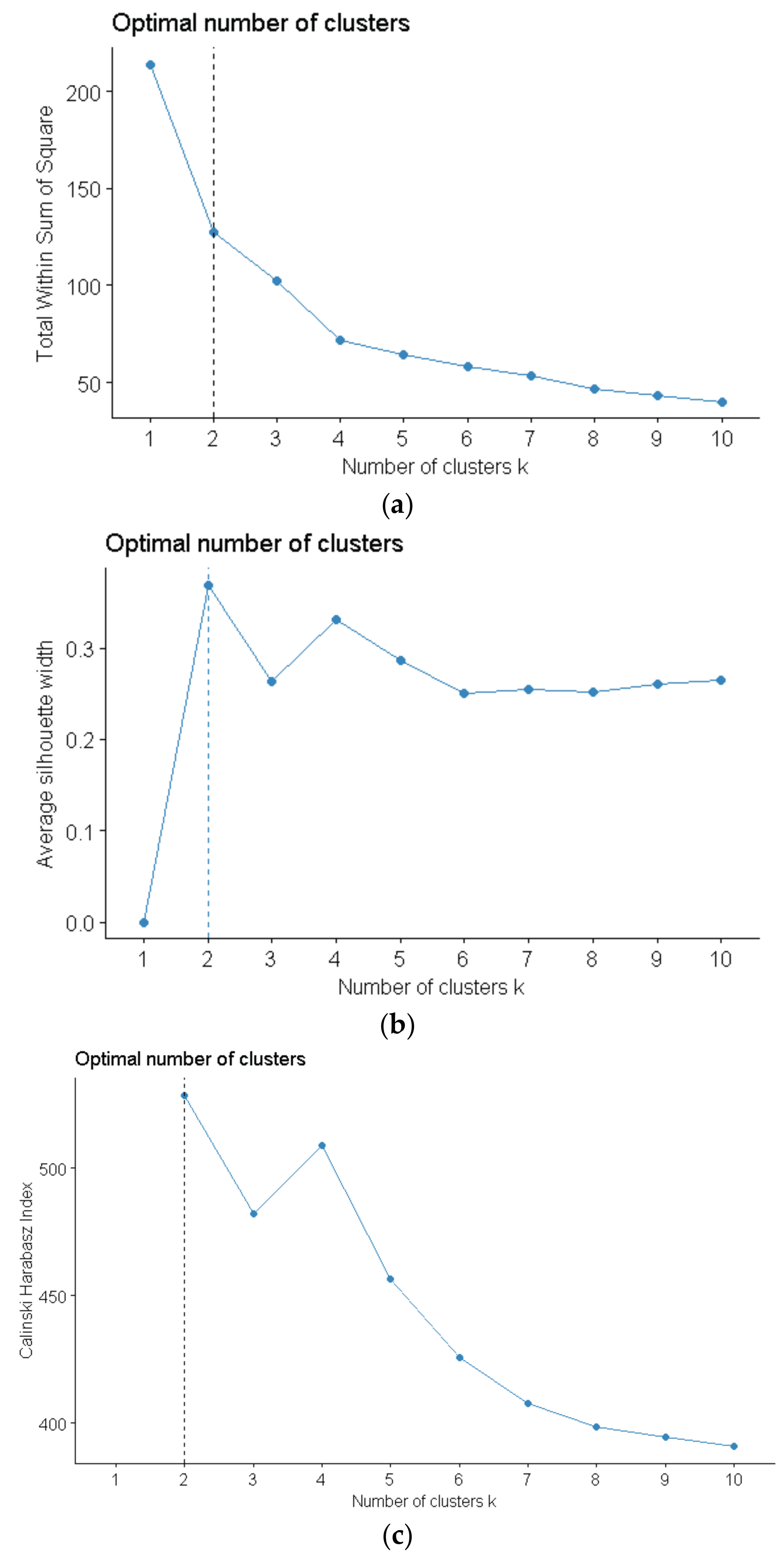
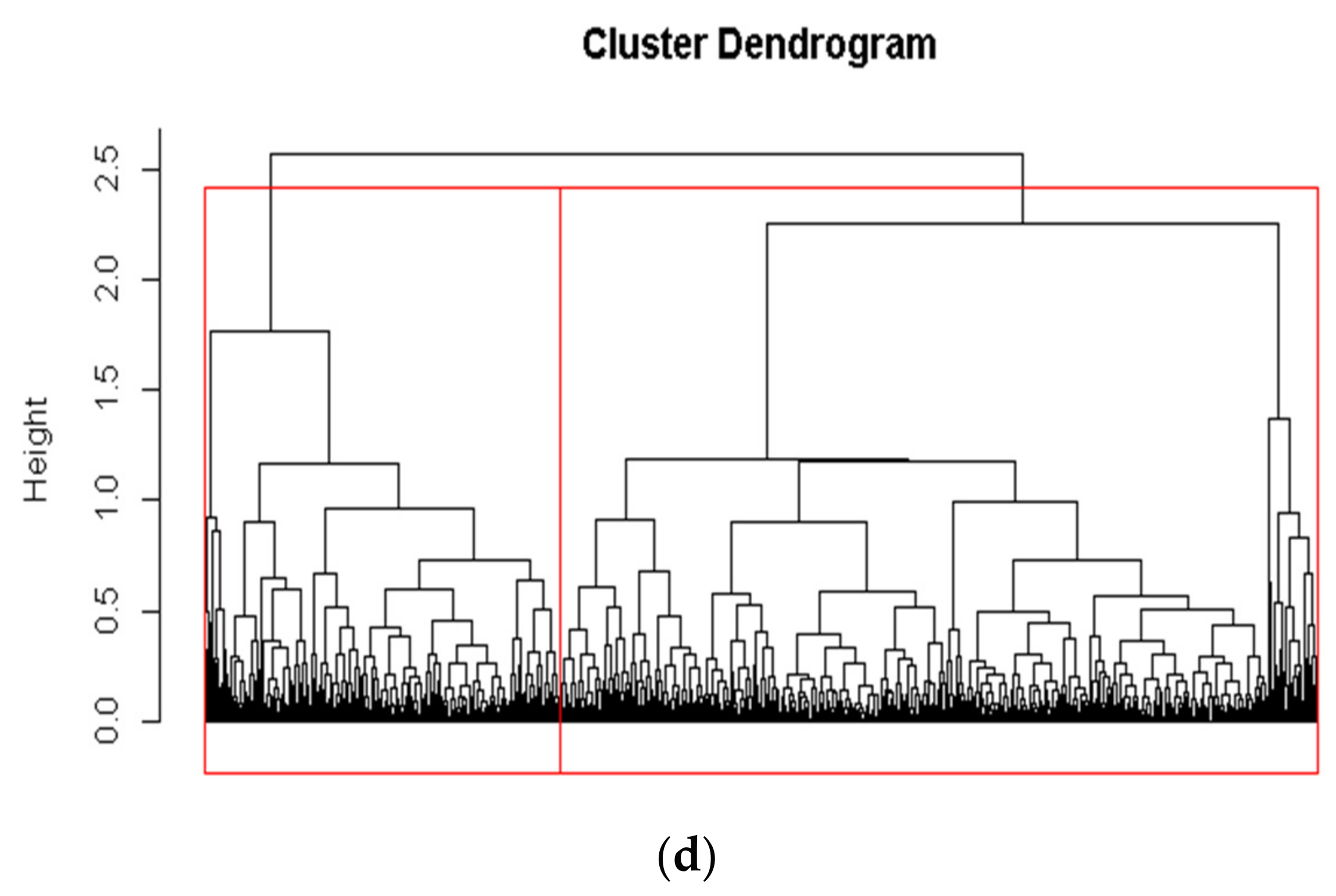
2.2.3. Determining the Optimal Number of Clusters
2.3. XGBoost Algorithm Modified by Theoretical Value for the Estimation of Statistical Line Loss
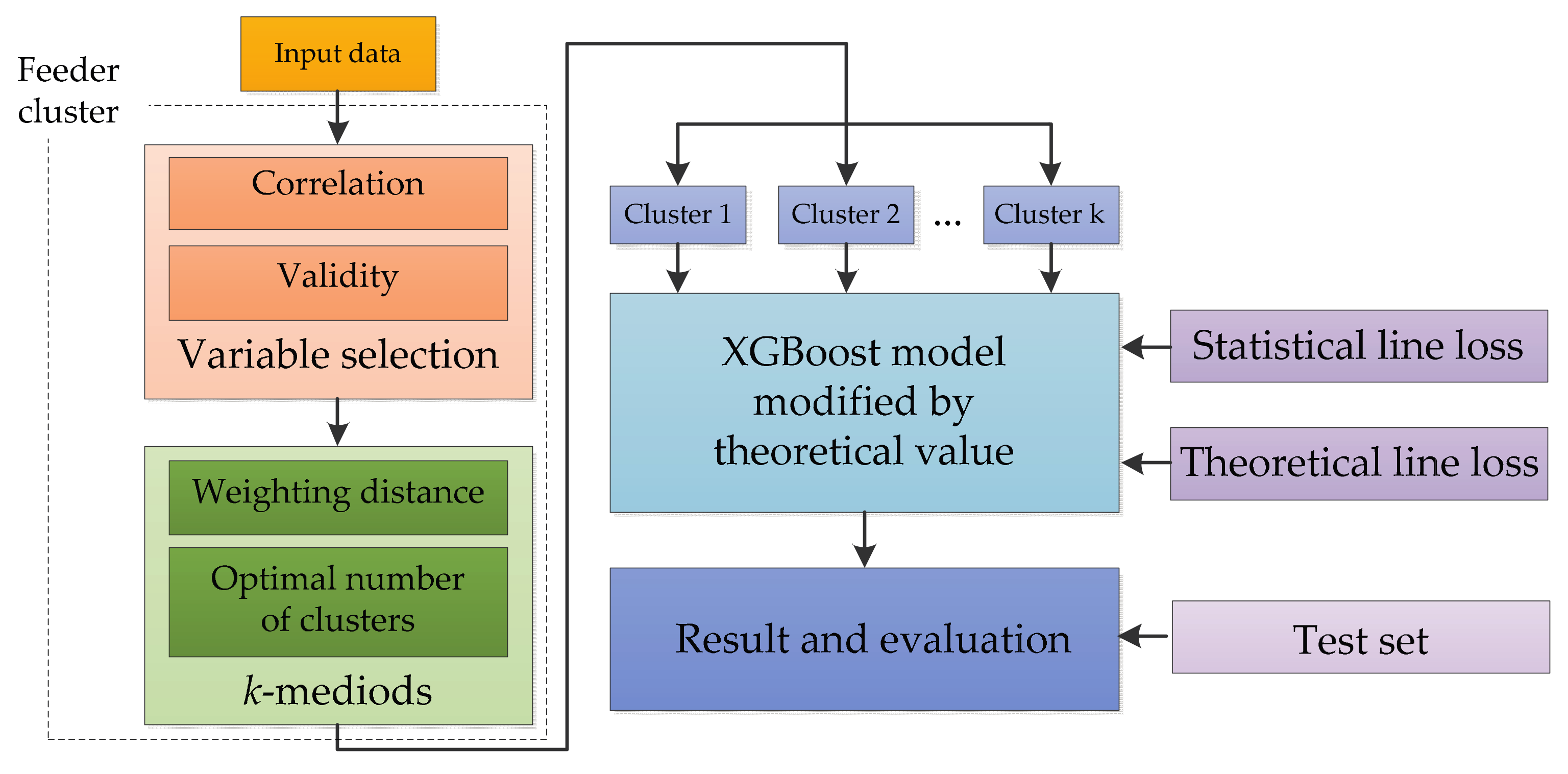
2.4. The Full Procedure of the Estimation of Statistical Line Loss of Distribution Feeders
- Feeder cluster. Select variables for clustering distribution feeders by analyzing the correlation and validity of variables, then cluster the input samples using k-medoids algorithm with weighting distance.
- Model training. Determine the model parameters for each cluster by training the XGBoost model that is modified by theoretical value, taking the clustering result, statistical, and theoretical line loss as input data.
- Prediction and evaluation. Predict the statistical line loss in the test set using the aforementioned model and evaluate the performance of the model.
3. Results and Discussion
3.1. Distribution Feeder Cluster
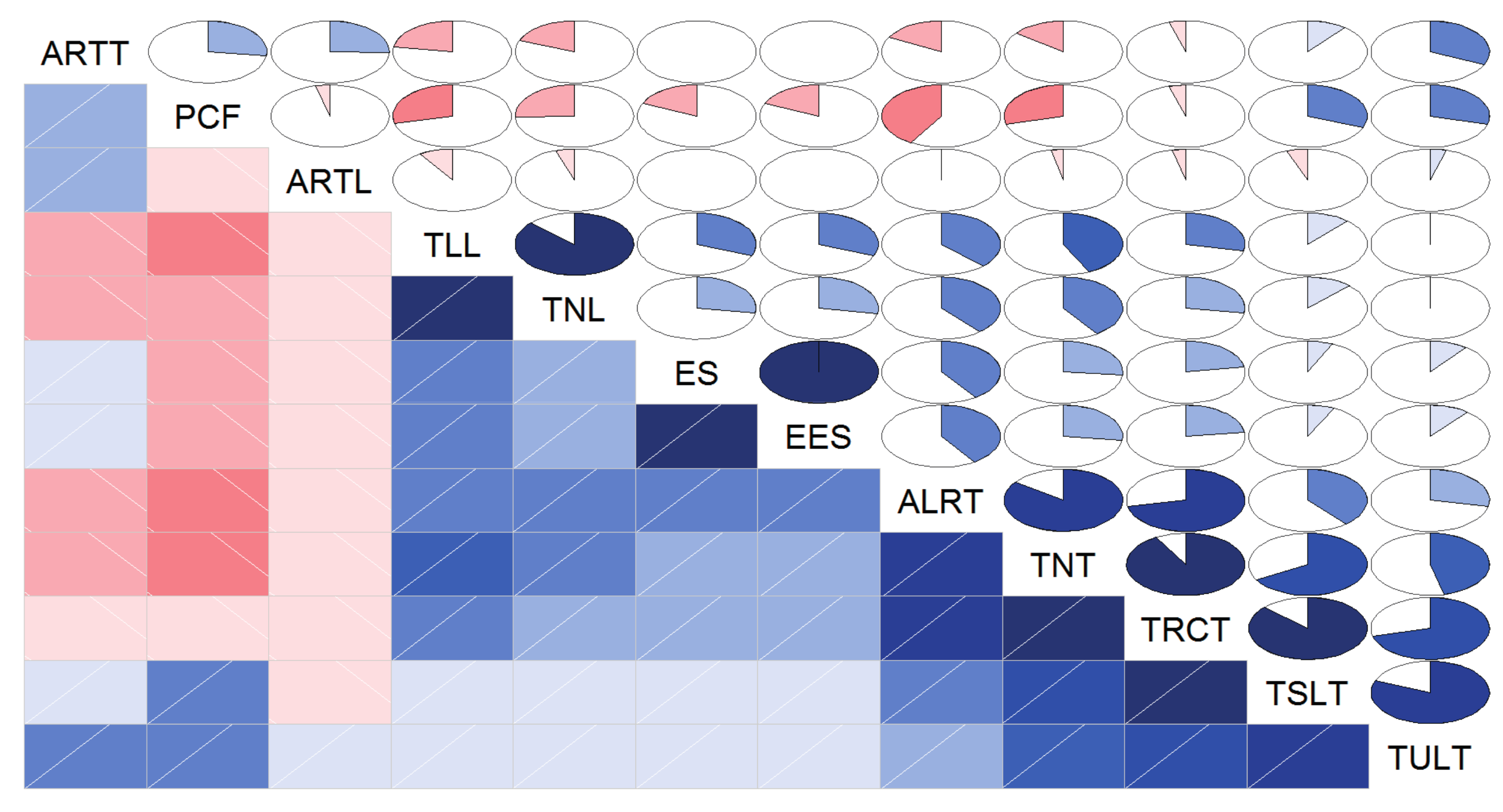
3.1.1. Correlation of Variables for Clustering Distribution Feeders
3.1.2. Validity of Variables for Clustering Distribution Feeders
3.1.3. The Results of Distribution Feeders Cluster with Optimal Number of Clusters
3.2. Estimation of Statistical Line Loss of Distribution Feeders
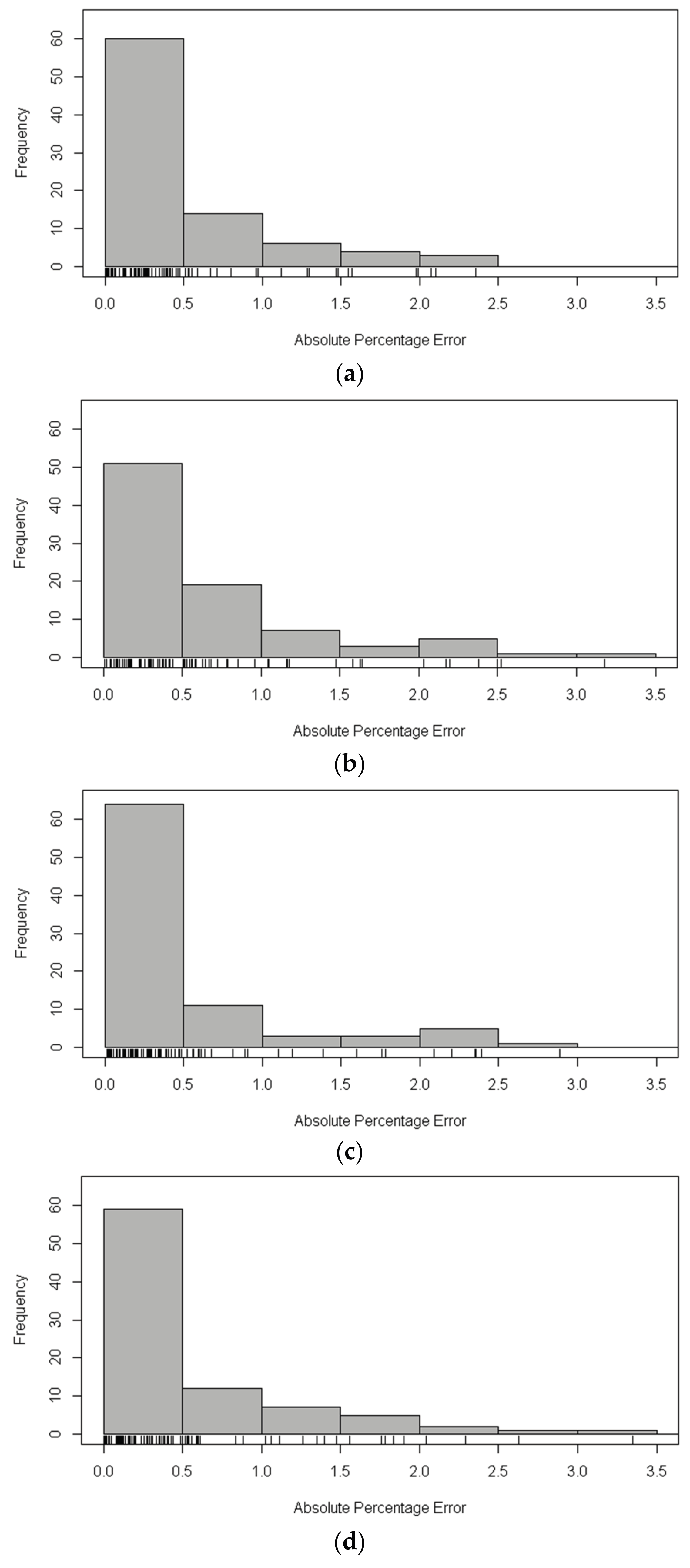
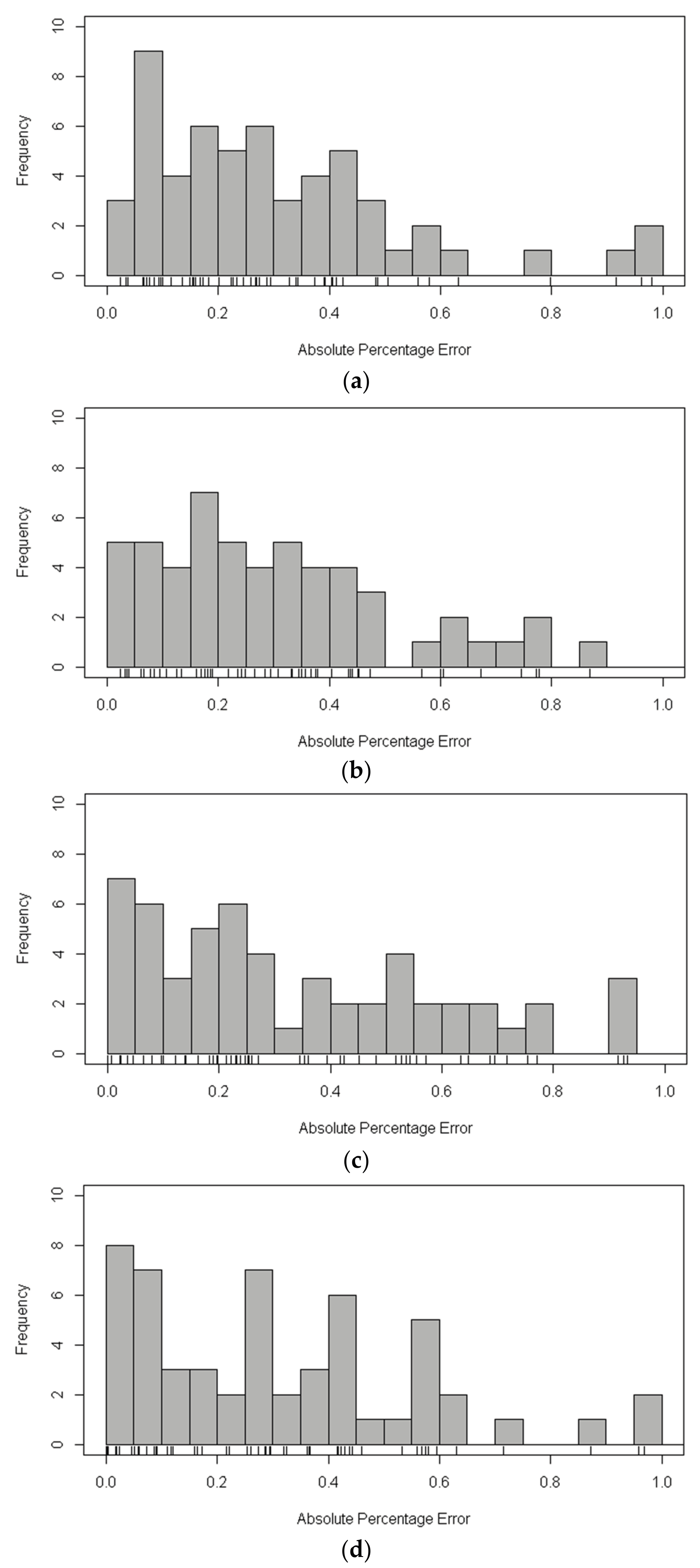
3.2.1. The Evaluation of XGBoost Model for Estimation of Statistical Line Loss
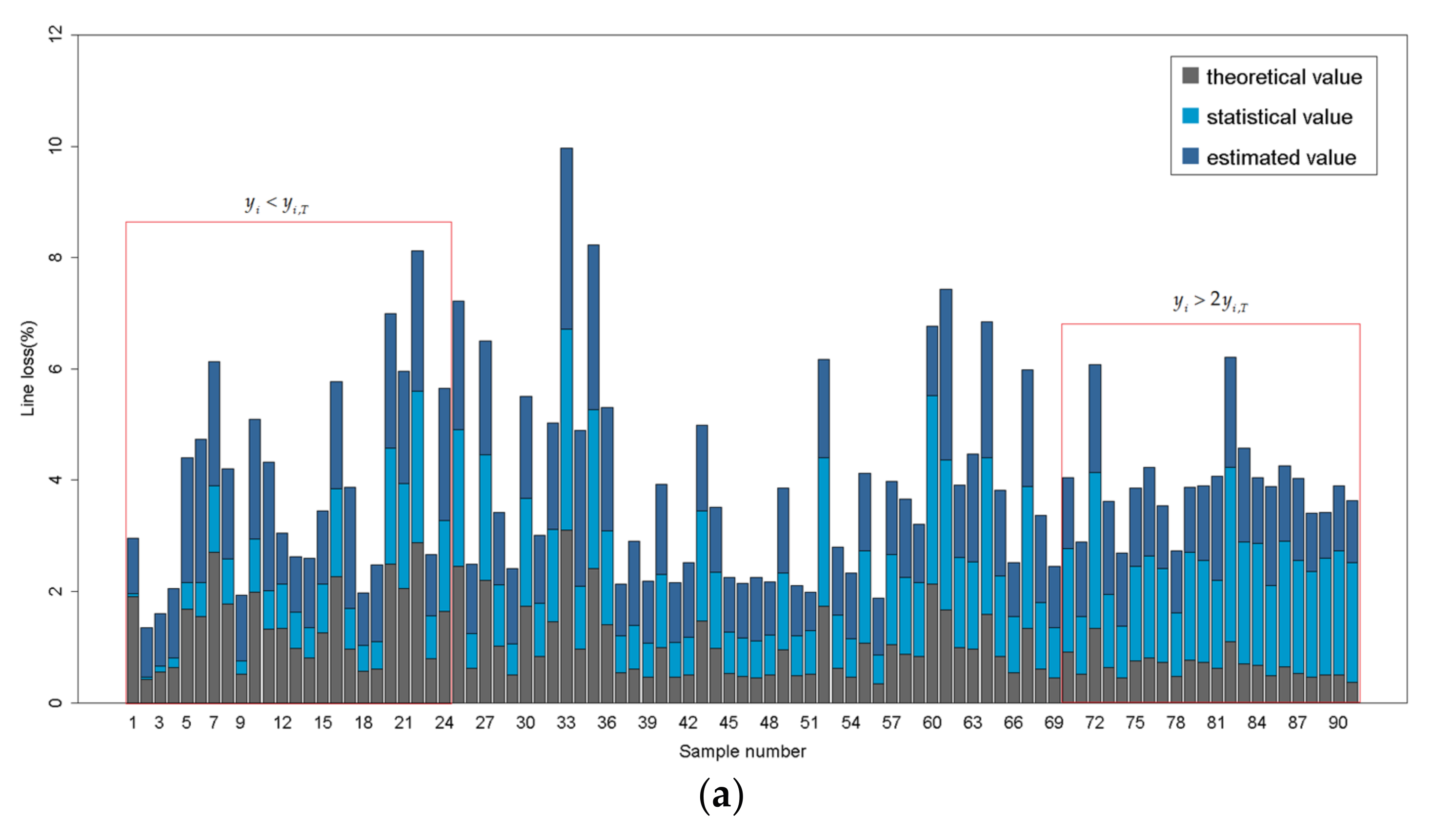
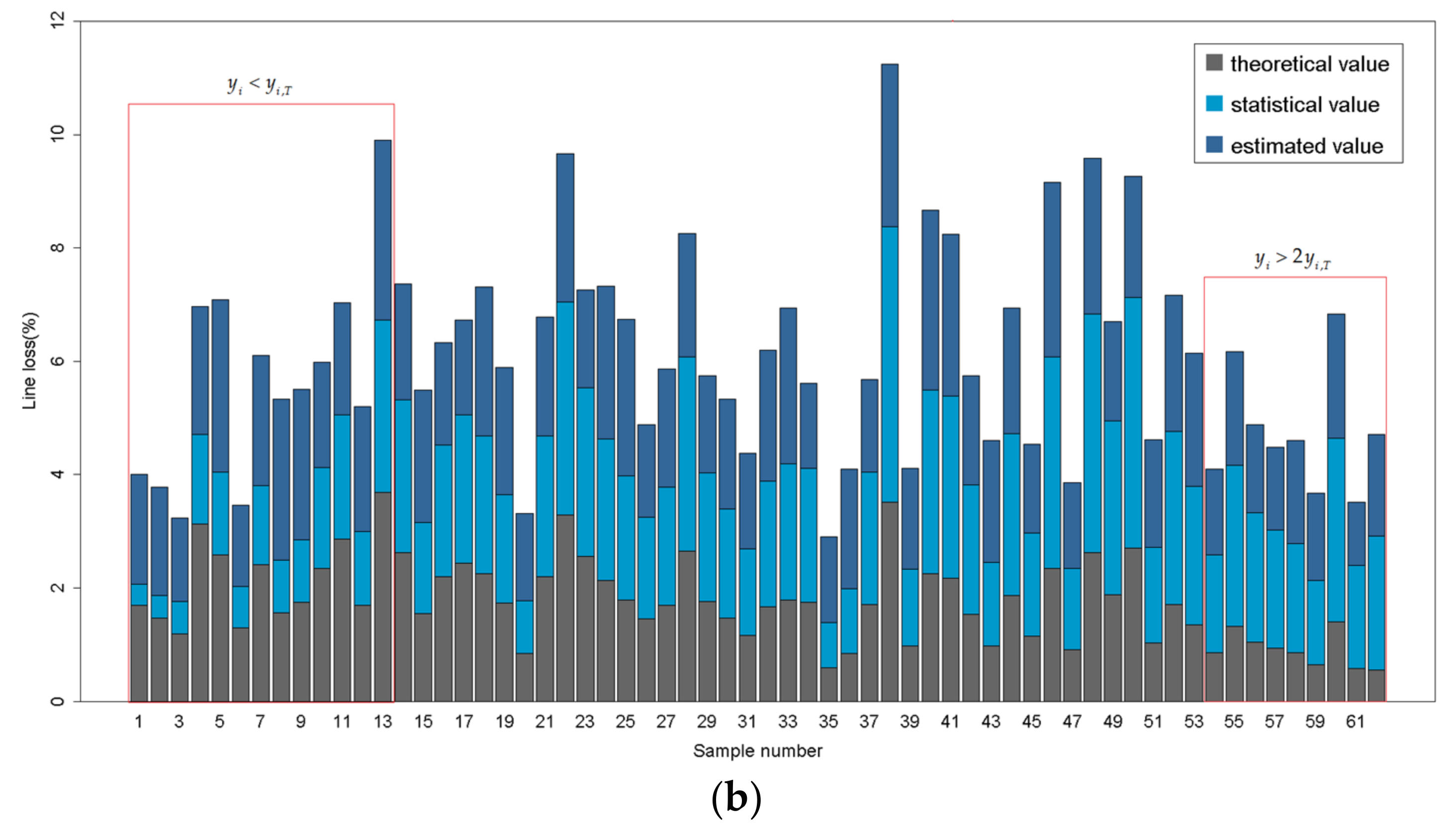
3.2.2. Estimation of Statistical Line Loss Using XGBoost Model Modified by Theoretical Value
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yu, W.; Xiong, Y.; Zhou, X.; Zhao, G.; Chen, N. Analysis on technical line losses of power grids and countermeasures to reduce line losses. Power Syst. Technol. 2006, 30, 54–57. [Google Scholar] [CrossRef]
- Flaten, D.L. Distribution system losses calculated by percent loading. IEEE Trans. Power Syst. 1988, 3, 1263–1269. [Google Scholar] [CrossRef]
- Shenkman, A.L. Energy loss computation by using statistical techniques. IEEE Trans. Power Deliv. 1990, 5, 254–258. [Google Scholar] [CrossRef]
- Taleski, R.; Rajicic, D. Energy summation method for energy loss computation in radial distribution networks. IEEE Trans. Power Syst. 1996, 11, 1104–1111. [Google Scholar] [CrossRef]
- Mikic, O.M. Variance-based energy loss computation in low voltage distribution networks. IEEE Trans. Power Syst. 2007, 22, 179–187. [Google Scholar] [CrossRef]
- Queiroz, L.M.O.; Roselli, M.A.; Cavellucci, C.; Lyra, C. Energy losses estimation in power distribution systems. IEEE Trans. Power Syst. 2012, 27, 1879–1887. [Google Scholar] [CrossRef]
- Fu, X.; Chen, H.; Cai, R.; Xuan, P. Improved LSF method for loss estimation and its application in DG allocation. IET Gener. Transm. Distrib. 2016, 10, 2512–2519. [Google Scholar] [CrossRef]
- Ibrahim, K.A.; Au, M.T.; Gan, C.K.; Tang, J.H. System wide MV distribution network technical losses estimation based on reference feeder and energy flow model. Int. J. Electr. Power Energy Syst. 2017, 93, 440–450. [Google Scholar] [CrossRef]
- Dortolina, C.; Nadira, R. The loss that is unknown is no loss at all: A top-down/bottom-up approach for estimating distribution losses. IEEE Trans. Power Syst. 2005, 20, 1119–1125. [Google Scholar] [CrossRef]
- Oliveira, M.E.; Padilha-Feltrin, A. A top-down approach for distribution loss evaluation. IEEE Trans. Power Deliv. 2009, 24, 2117–2124. [Google Scholar] [CrossRef]
- Armaulia Sanchez, V.; Lima, D.A.; Ochoa, L.F.; Oliveira, M.E. Statistical Top-Down Approach for Energy Loss Estimation in Distribution Systems. In Proceedings of the 2015 IEEE Eindhoven Powertech, Eindhoven, The Netherlands, 29 June–2 July 2015. [Google Scholar]
- Dashtaki, A.K.; Haghifam, M.R. A new loss estimation method in limited data electric distribution networks. IEEE Trans. Power Deliv. 2013, 28, 2194–2200. [Google Scholar] [CrossRef]
- Grigoras, G.; Scarlatache, F. Energy Losses Estimation in Electrical Distribution Networks with a Decision Trees-based Algorithm. In Proceedings of the 2013 8th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 23–25 May 2013. [Google Scholar]
- Lezhniuk, P.; Bevz, S.; Piskliarova, A. Evaluation and Forecast of Electric Energy Losses in Distribution Networks Applying Fuzzy-Logic. In Proceedings of the 2008 IEEE Power & Energy Society General Meeting, Pittsburgh, PA, USA, 20–24 July 2008; Volumes 1–11, pp. 3279–3282. [Google Scholar]
- Zheng, H.; Yuan, J.; Chen, L. Short-term load forecasting using EMD-LSTM neural networks with a Xgboost algorithm for feature importance evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
- Urraca, R.; Martinez-de-Pison, E.; Sanz-Garcia, A.; Antonanzas, J.; Antonanzas-Torres, F. Estimation methods for global solar radiation: Case study evaluation of five different approaches in central Spain. Renew. Sustain. Energy Rev. 2017, 77, 1098–1113. [Google Scholar] [CrossRef]
- Chen, W.; Fu, K.; Zuo, J.; Zheng, X.; Huang, T.; Ren, W. Radar emitter classification for large data set based on weighted-xgboost. IET Radar Sonar Navig. 2017, 11, 1203–1207. [Google Scholar] [CrossRef]
- Aler, R.; Galvan, I.M.; Ruiz-Arias, J.A.; Gueymard, C.A. Improving the separation of direct and diffuse solar radiation components using machine learning by gradient boosting. Sol. Energy 2017, 150, 558–569. [Google Scholar] [CrossRef]
- Baker, J.; Pomykalski, A.; Hanrahan, K.; Guadagni, G. Application of Machine Learning Methodologies to Multiyear Forecasts of Video Subscribers. In Proceedings of the 2017 Systems and Information Engineering Design Symposium (SIEDS), Charlottesville, VA, USA, 28 April 2017; pp. 100–105. [Google Scholar]
- Ge, Y.; He, S.; Xiong, J.; Brown, D.E. Customer Churn Analysis for a Software-as-a-service Company. In Proceedings of the 2017 Systems and Information Engineering Design Symposium (SIEDS), Charlottesville, VA, USA, 28 April 2017; pp. 106–111. [Google Scholar]
- Zhang, Y.; Huang, Q.; Ma, X.; Yang, Z.; Jiang, J. Using Multi-features and Ensemble Learning Method for Imbalanced Malware Classification. In Proceedings of the 2016 IEEE Trustcom/BigDataSE/ISPA, Tianjin, China, 23–26 August 2016; pp. 965–973. [Google Scholar]
- Ayumi, V. Pose-based Human Action Recognition with Extreme Gradient Boosting. In Proceedings of the 14th IEEE Student Conference on Research and Development (SCORED), Kuala Lumpur, Malaysia, 13–14 December 2016. [Google Scholar]
- Lei, T.; Chen, F.; Liu, H.; Sun, H.; Kang, Y.; Li, D.; Li, Y.; Hou, T. ADMET evaluation in drug discovery. Part 17: Development of quantitative and qualitative prediction models for chemical-induced respiratory toxicity. Mol. Pharm. 2017, 14, 2407–2421. [Google Scholar] [CrossRef] [PubMed]
- Mustapha, I.B.; Saeed, F. Bioactive molecule prediction using extreme gradient boosting. Molecules 2016, 21, 983. [Google Scholar] [CrossRef] [PubMed]
- Sheridan, R.P.; Wang, W.M.; Liaw, A.; Ma, J.; Gifford, E.M. Extreme gradient boosting as a method for quantitative structure-activity relationships. J. Chem. Inf. Model. 2016, 56, 2353–2360. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Liu, C.; Li, Y.; Liu, N. A boosted decision tree approach using Bayesian hyper-parameter optimization for credit scoring. Expert Syst. Appl. 2017, 78, 225–241. [Google Scholar] [CrossRef]
- Xia, Y.; Liu, C.; Liu, N. Cost-sensitive boosted tree for loan evaluation in peer-to-peer lending. Electron. Commer. Res. Appl. 2017, 24, 30–49. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Broderick, R.J.; Williams, J.R. Clustering Methodology for Classifying Distribution Feeders. In Proceedings of the 2013 IEEE 39th Photovoltaic Specialists Conference (PVSC), Tampa, FL, USA, 16–21 June 2013; pp. 1706–1710. [Google Scholar]
- Cale, J.; Palmintier, B.; Narang, D.; Carroll, K. Clustering Distribution Feeders in the Arizona Public Service Territory. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), Denver, CO, USA, 8–13 June 2014; pp. 2076–2081. [Google Scholar]
- Dehghani, F.; Dehghani, M.; Nezami, H.; Saremi, M. Distribution Feeder Classification Based on Self Organized Maps (Case Study: Lorestan Province, Iran). In Proceedings of the 2015 20th Conference on Electrical Power Distribution Networks Conference (EPDC), Zahedan, Iran, 28–29 April 2015; pp. 27–31. [Google Scholar]
- Van der Laan, M.; Pollard, K.; Bryan, J. A new partitioning around medoids algorithm. J. Stat. Comput. Simul. 2003, 73, 575–584. [Google Scholar] [CrossRef]
- Kwedlo, W. A clustering method combining differential evolution with the K-means algorithm. Pattern Recognit. Lett. 2011, 32, 1613–1621. [Google Scholar] [CrossRef]
- Kishor, D.R.; Venkateswarlu, N.B. A Behavioral Study of Some Widely Employed Partitional and Model-Based Clustering Algorithms and Their Hybridizations. In Advances in Intelligent Systems and Computing, Proceedings of the International Conference on Data Engineering and Communication Technology, (ICDECT 2016) Volume 2, Pune, India, 10–11 March 2016; Satapathy, S.C., Bhateja, V., Joshi, A., Eds.; Springer: Singapore, 2017; Volume 469, pp. 587–601. [Google Scholar]
- Maulik, U.; Bandyopadhyay, S. Performance evaluation of some clustering algorithms and validity indices. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1650–1654. [Google Scholar] [CrossRef]
- Schepers, J.; Ceulemans, E.; Van Mechelen, I. Selecting among multi-mode partitioning models of different complexities: A comparison of four model selection criteria. J. Classif. 2008, 25, 67–85. [Google Scholar] [CrossRef]
- De Amorim, R.C.; Hennig, C. Recovering the number of clusters in data sets with noise features using feature rescaling factors. Inf. Sci. 2015, 324, 126–145. [Google Scholar] [CrossRef]
- Lord, E.; Willems, M.; Lapointe, F.-J.; Makarenkov, V. Using the stability of objects to determine the number of clusters in datasets. Inf. Sci. 2017, 393, 29–46. [Google Scholar] [CrossRef]
- Chiang, M.M.-T.; Mirkin, B. Intelligent choice of the number of clusters in k-means clustering: An experimental study with different cluster spreads. J. Classif. 2010, 27, 3–40. [Google Scholar] [CrossRef]
- Mur, A.; Dormido, R.; Duro, N.; Dormido-Canto, S.; Vega, J. Determination of the optimal number of clusters using a spectral clustering optimization. Expert Syst. Appl. 2016, 65, 304–314. [Google Scholar] [CrossRef]
- Martinez-Penaloza, M.-G.; Mezura-Montes, E.; Cruz-Ramirez, N.; Acosta-Mesa, H.-G.; Rios-Figueroa, H.-V. Improved multi-objective clustering with automatic determination of the number of clusters. Neural Comput. Appl. 2017, 28, 2255–2275. [Google Scholar] [CrossRef]
- Langfelder, P.; Zhang, B.; Horvath, S. Defining clusters from a hierarchical cluster tree: The Dynamic Tree Cut package for R. Bioinformatics 2008, 24, 719–720. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Kabacoff, R. R in Action, 2nd ed.; Shelter Island: New York, NY, USA, 2015; pp. 125–127, 271–276. [Google Scholar]
- Javier Martinez-de-Pison, F.; Fraile-Garcia, E.; Ferreiro-Cabello, J.; Gonzalez, R.; Pernia, A. Searching Parsimonious Solutions with GA-PARSIMONY and XGBoost in High-Dimensional Databases. In Advances in Intelligent Systems and Computing, Proceedings of the International Joint Conference SOCO’16-CISIS’16-ICEUTE’16, Saint Sebastian, Spain, 19–21 October 2016; Grana, M., LopezGuede, J.M., Etxaniz, O., Herrero, A., Quintian, H., Corchado, E., Eds.; Springer: Cham, Switzerland, 2017; Volume 527, pp. 201–210. [Google Scholar]
| Variables | Description | Variables | Description |
|---|---|---|---|
| SLLR | Statistical Line Loss Rate of a Feeder | TLLR | Theoretical Line Loss Rate of a feeder |
| EES | Electrical Energy Supply of a Feeder | ES | Electricity Sales Belonging to a Feeder |
| TNT | Total Number of Transformers Belonging to a Feeder | TRCT | Total Rated Capacity of Transformers Belonging to a Feeder |
| TSLT | Total Short Circuit Loss of Transformers Belonging to a Feeder | TULT | Total Unload Loss of Transformers Belonging to a Feeder |
| ALRT | Average Load Rate of Transformers Belonging to a Feeder | ARTT | Average Run Time of Transformers Belonging to a Feeder |
| TNL | Total Number of Lines Belonging to a Feeder | TLL | Total Length of Lines Belonging to a Feeder |
| PCF | Proportion of Cable in a Feeder | ARTL | Average Run Time of Lines Belonging to a Feeder |
| Indexes | TRCT (kW) | EES (kWh) | ARTT (m) | TLL (m) | PCF | ARTL (m) |
|---|---|---|---|---|---|---|
| 1.11 × 10−4 | 7.81 × 10−7 | 4.21 × 10−3 | 1.26 × 10−5 | 6.51 × 10−2 | 1.76 × 10−5 | |
| 20,440.0 | 2,830,644.8 | 240.0 | 26,846.0 | 1.0 | 656.5 | |
| 2.271 | 2.210 | 1.010 | 0.337 | 0.065 | 0.011 |
| Quantiles | TRCT | EES | ARTT | TLL |
|---|---|---|---|---|
| Minimum | 0.01109 | 0.00867 | 0.00414 | 0.00070 |
| 1st Quantile | 0.17738 | 0.18435 | 0.27452 | 0.03647 |
| Median | 0.44345 | 0.31386 | 0.39634 | 0.05655 |
| Mean | 0.51787 | 0.39373 | 0.40414 | 0.06303 |
| 3rd Quantile | 0.75247 | 0.53603 | 0.52078 | 0.08275 |
| Maximum | 2.27710 | 2.20318 | 0.99676 | 0.31182 |
| Medoids | Cluster 1 | Cluster 2 |
|---|---|---|
| TRCT (kW) | 2260 | 7454 |
| EES (kWh) | 336,377 | 549,426 |
| ARTT (m) | 92.4 | 91.3 |
| TLL (m) | 7814 | 5651 |
| Index | Calculation Formula |
|---|---|
| RMSE | |
| MAPE | |
| APE |
| Method | Cluster 1 | Cluster 2 | ||
|---|---|---|---|---|
| RMSE | MAPE | RMSE | MAPE | |
| XGBoost | 0.6979 | 0.9452 | 0.7840 | 0.4585 |
| decision tree | 0.7884 | 1.0434 | 0.8621 | 0.5321 |
| neural network | 0.7616 | 1.0605 | 0.8586 | 0.4912 |
| random forests | 0.7174 | 0.9990 | 0.8382 | 0.5027 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Dong, P.; Tian, Y. A Novel Method of Statistical Line Loss Estimation for Distribution Feeders Based on Feeder Cluster and Modified XGBoost. Energies 2017, 10, 2067. https://doi.org/10.3390/en10122067
Wang S, Dong P, Tian Y. A Novel Method of Statistical Line Loss Estimation for Distribution Feeders Based on Feeder Cluster and Modified XGBoost. Energies. 2017; 10(12):2067. https://doi.org/10.3390/en10122067
Chicago/Turabian StyleWang, Shouxiang, Pengfei Dong, and Yingjie Tian. 2017. "A Novel Method of Statistical Line Loss Estimation for Distribution Feeders Based on Feeder Cluster and Modified XGBoost" Energies 10, no. 12: 2067. https://doi.org/10.3390/en10122067
APA StyleWang, S., Dong, P., & Tian, Y. (2017). A Novel Method of Statistical Line Loss Estimation for Distribution Feeders Based on Feeder Cluster and Modified XGBoost. Energies, 10(12), 2067. https://doi.org/10.3390/en10122067




