Characterisation of Ground Thermal and Thermo-Mechanical Behaviour for Shallow Geothermal Energy Applications
Abstract
1. Introduction
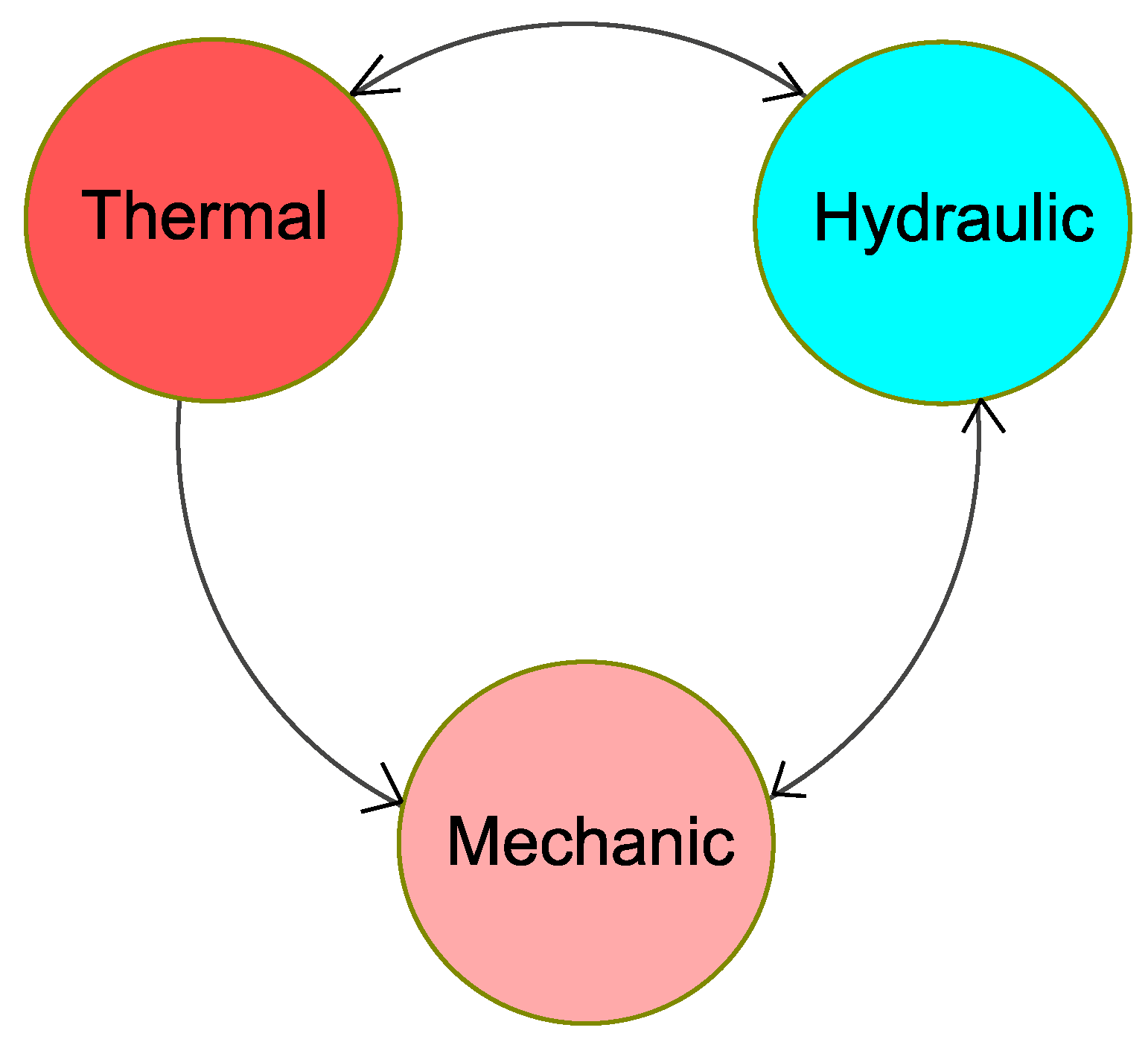
2. Thermo-Hydro-Mechanical Processes in Soil and Rocks
3. Laboratory Thermal Testing of Soils and Rocks
3.1. Steady-State Methods
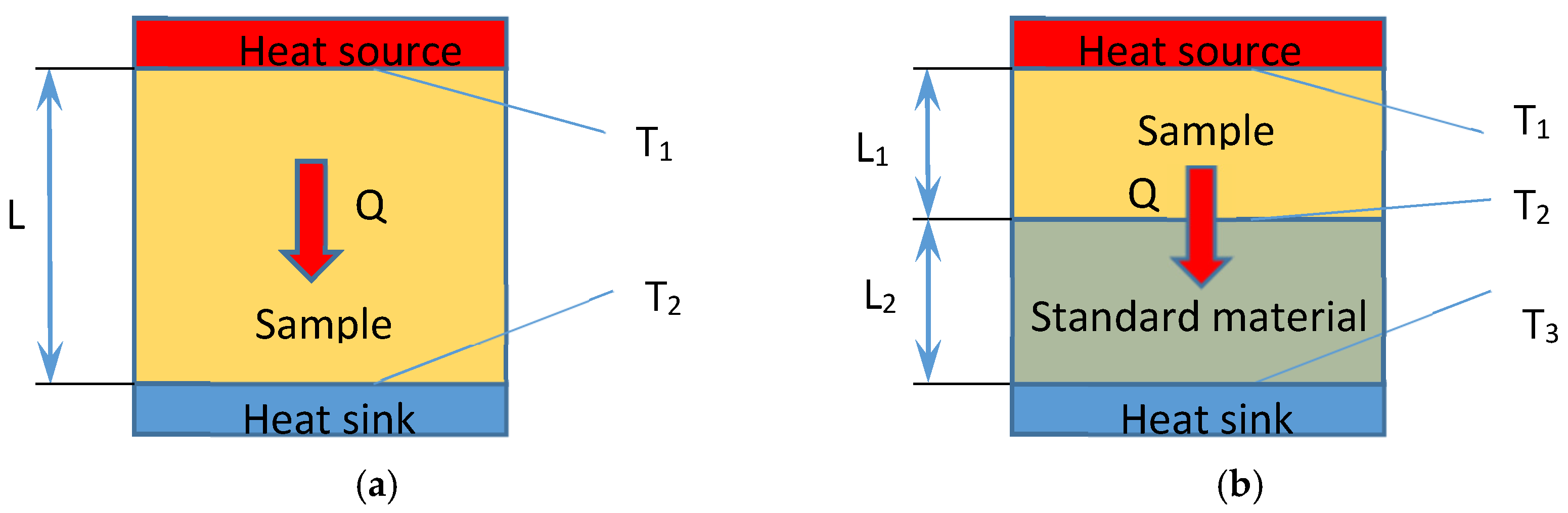
3.1.1. Absolute Techniques
3.1.2. Comparative Cut-Bar Technique
3.2. Transient Methods
3.2.1. Needle-Probe Method
3.2.2. Transient Plane Source (TPS) Method
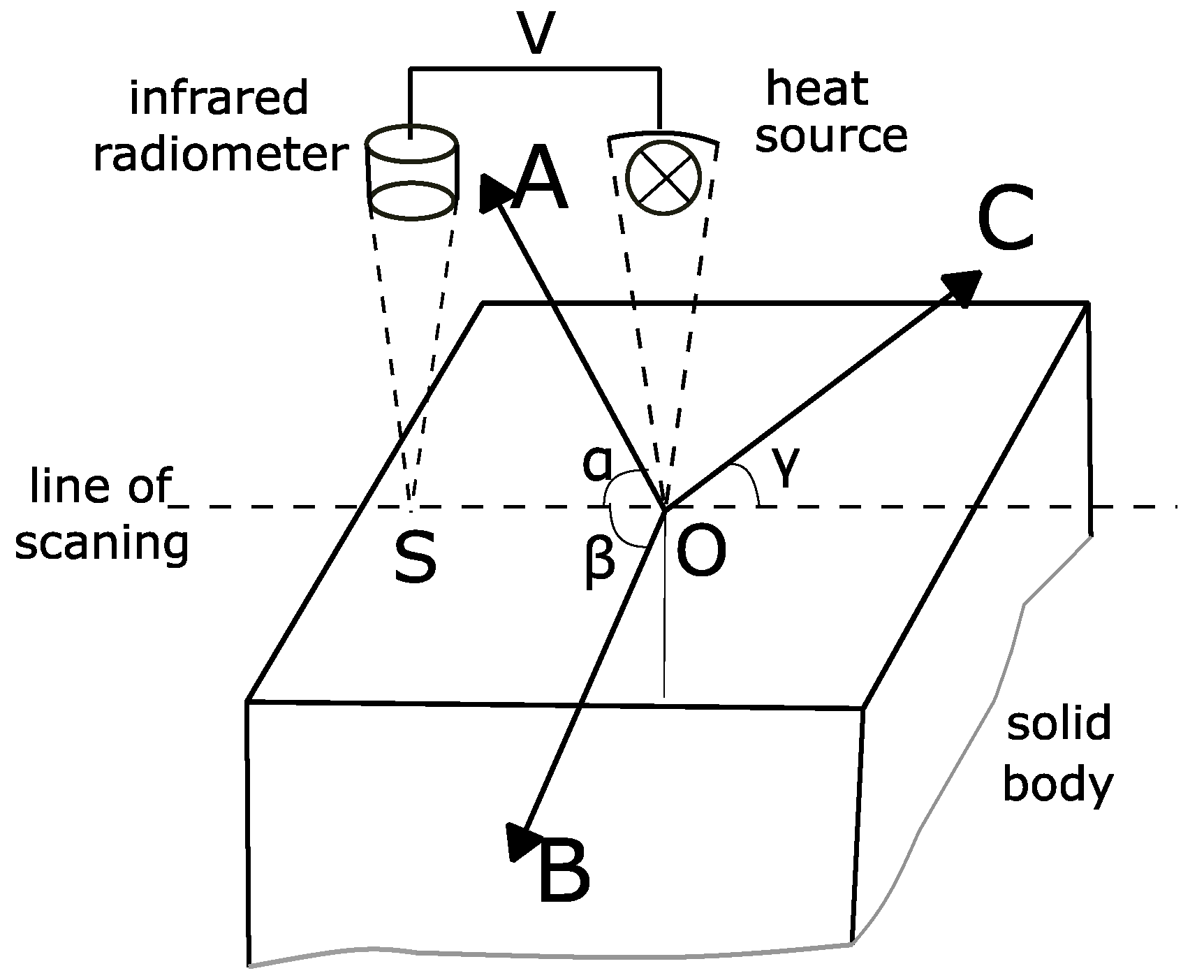
3.2.3. Optical Scanning Technique
3.3. Comparison of Methods
4. In Situ Thermal Testing (Thermal Response Tests)
4.1. Undisturbed Ground Temperature
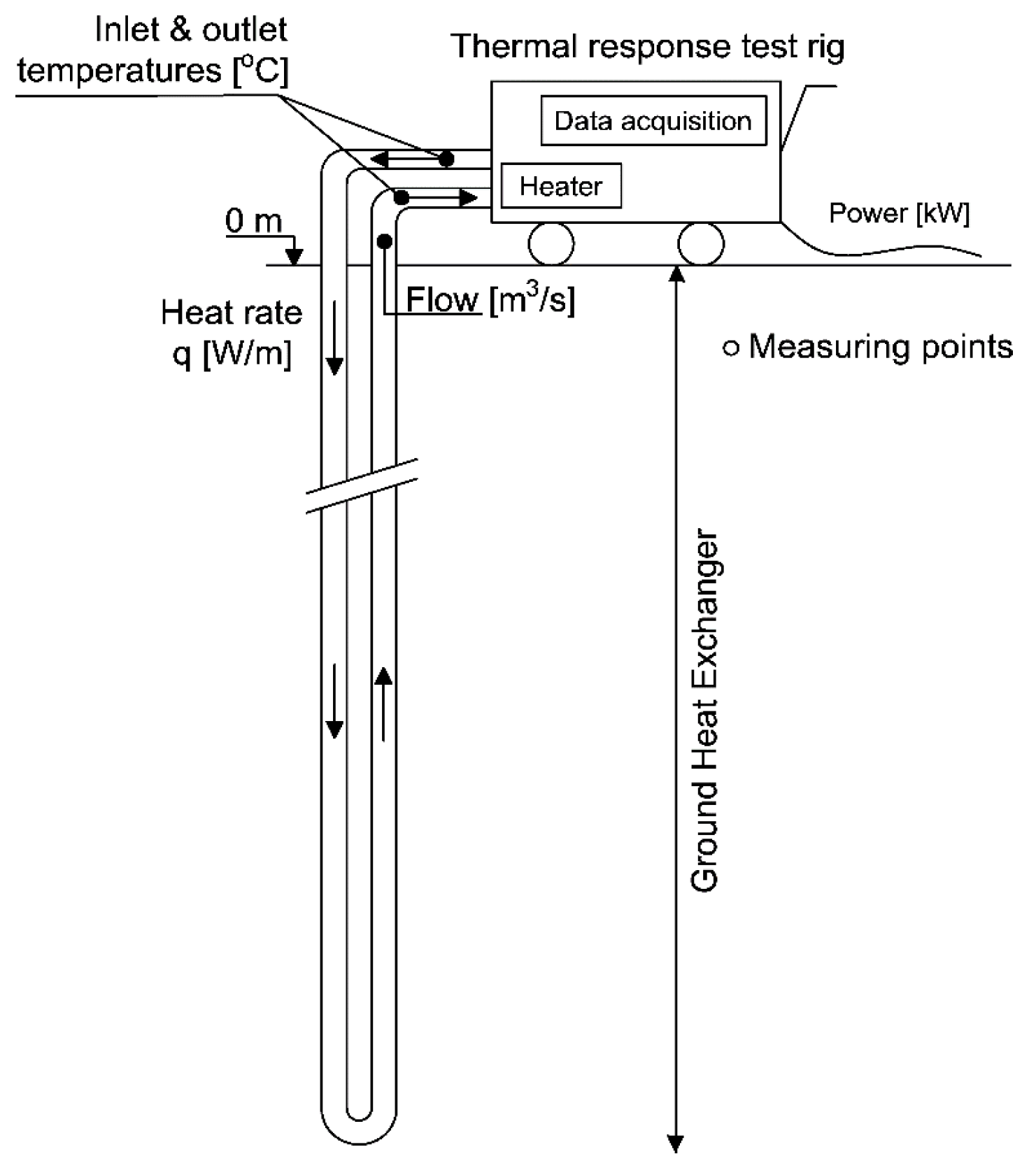
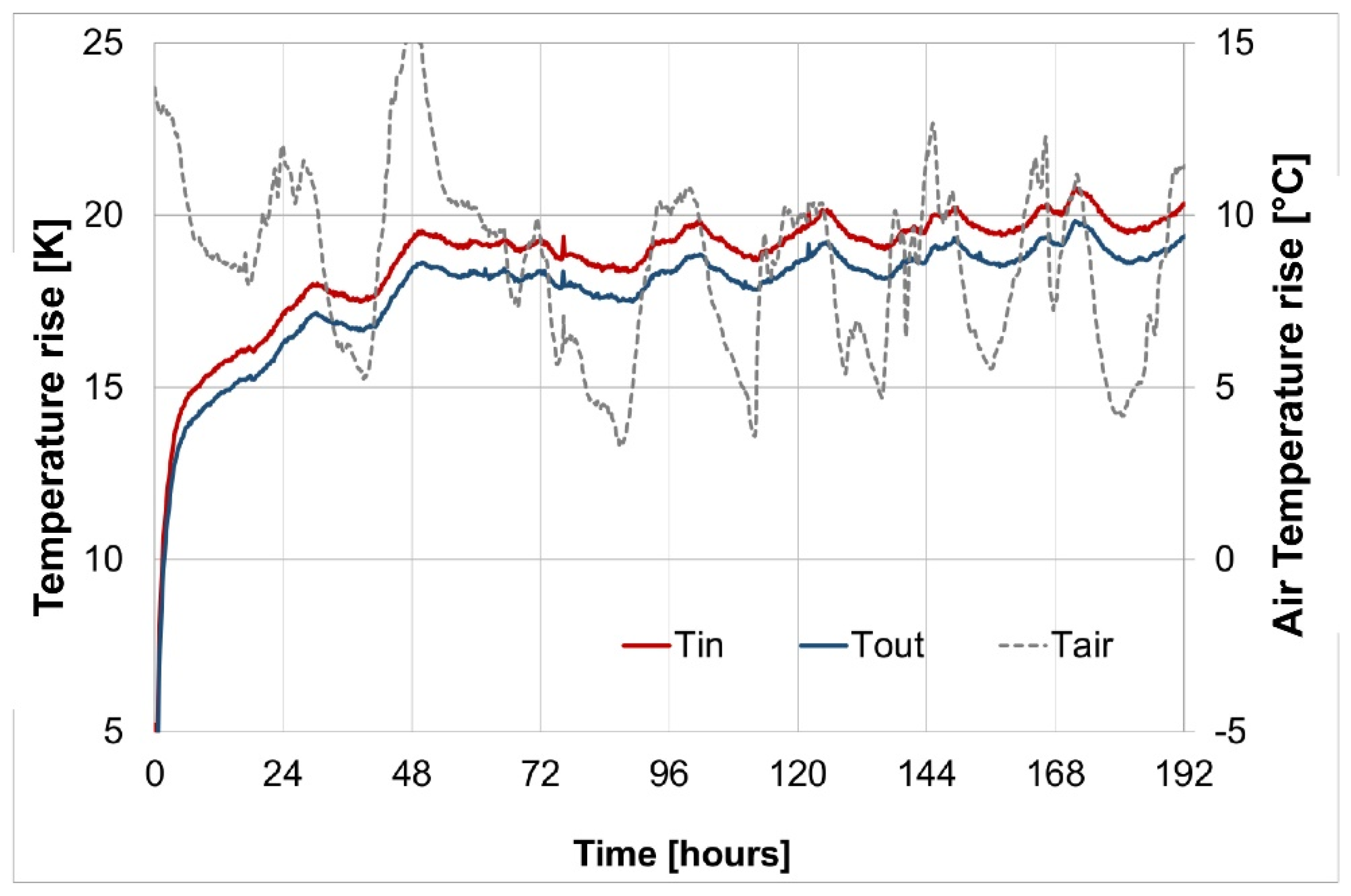
4.2. Thermal Response Testing
4.3. Distributed and Enhanced Thermal Response Testing
4.4. Thermal Response Testing of Foundation Pile Heat Exchangers
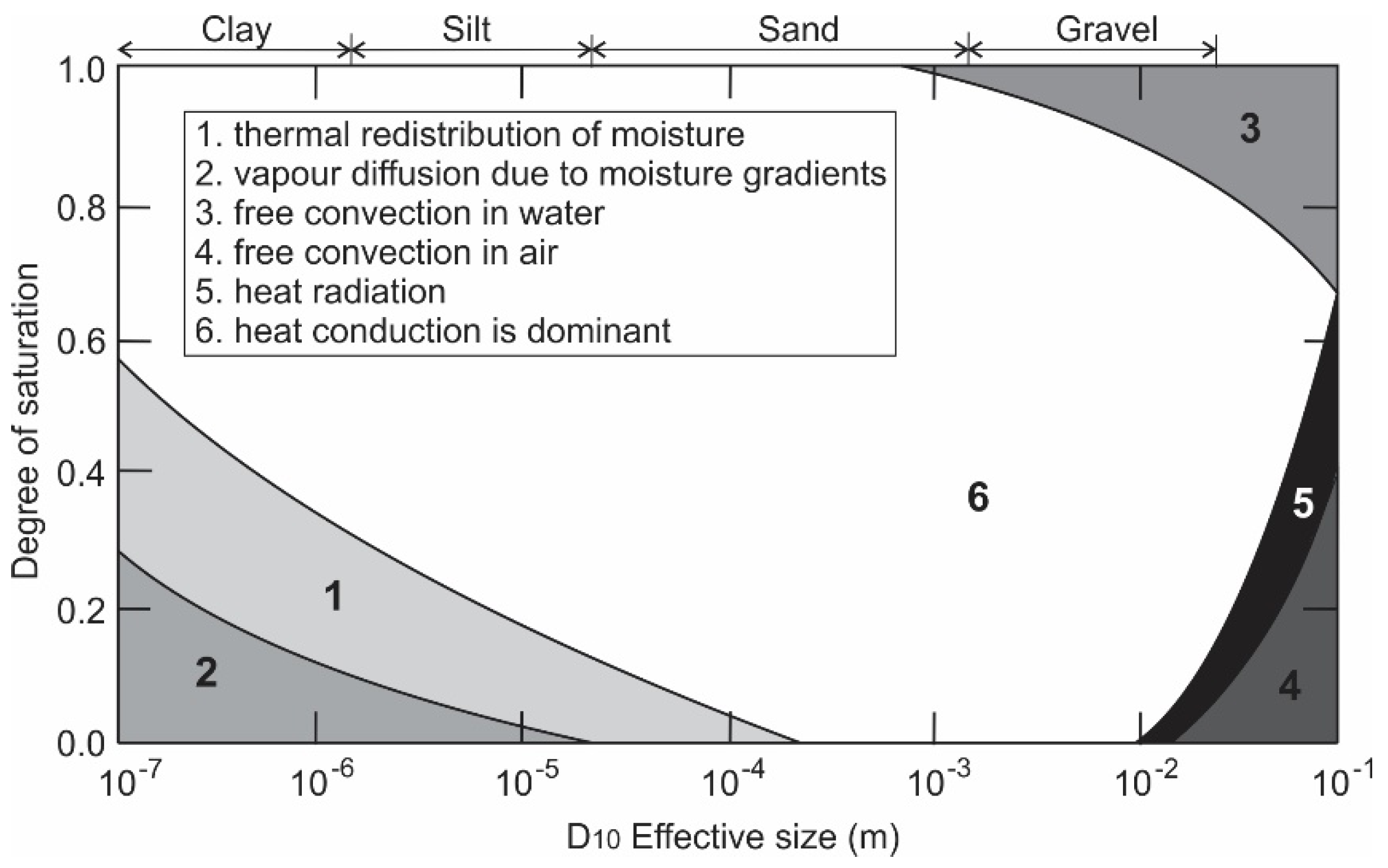
5. Scale in Thermal Properties Measurement
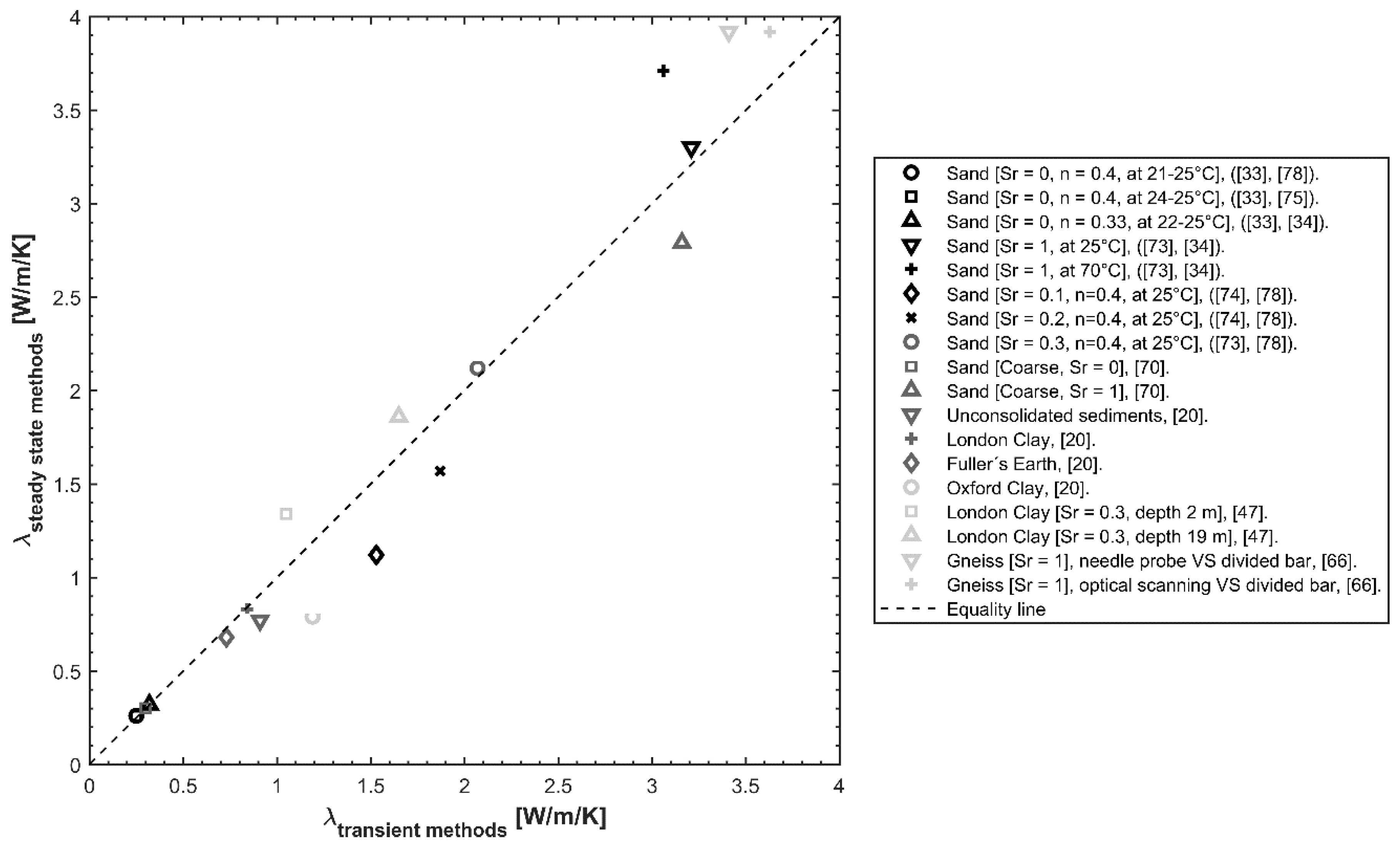
5.1. Comparison between Laboratory and Field Thermal Characterisation
5.1.1. True Scale Effects
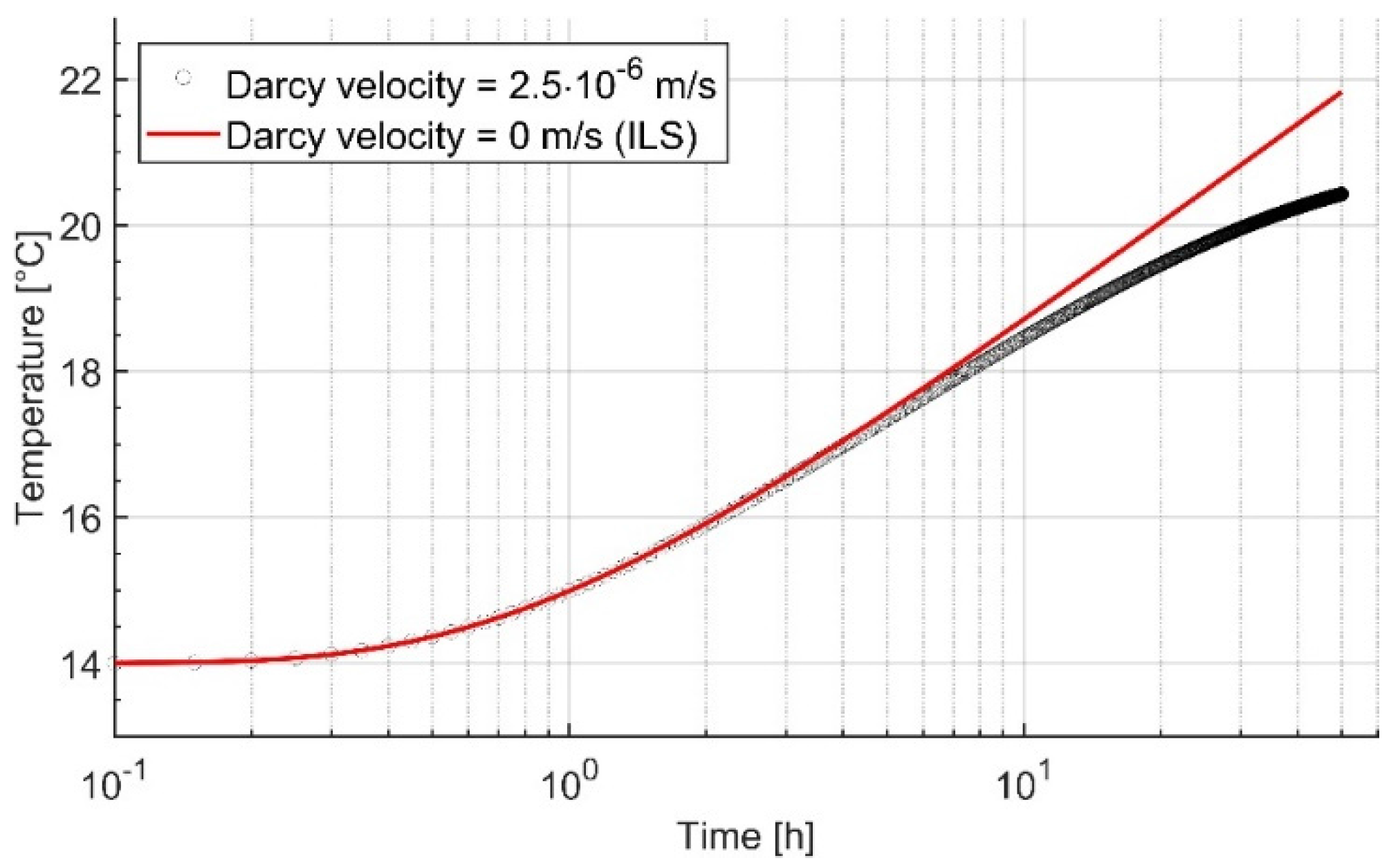
5.1.2. Groundwater Effects
5.1.3. Sampling Issues
5.1.4. Error Sources from In Situ Test Data
5.2. Example Characterisation
5.3. Upscaling from Field to Regional Scale
6. Characterisation of Thermo-Hydro-Mechanical (THM) Soil Behaviour
6.1. Relevant Coupling Effects in Energy Geostructures
6.2. Effect of Temperature on Soil Mechanical Behaviour
6.3. Laboratory THM Characterisation
6.3.1. THM Response by Triaxial Tests
6.3.2. THM Response by Shear Tests
6.3.3. THM Response by Oedometric Tests
6.4. Basic Parameters Needed for Thermo-Mechanical Modelling
7. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of interest
Abbreviations
| Acronyms | |
| 1U | Single U pipe heat exchanger |
| 2U | Double U pipe heat exchanger |
| 3U | Three U pipe heat exchanger |
| APGE | Auger Pressure Grouted Energy |
| AR | Aspect Ratio |
| ASHRAE | American Society of Heating, Refrigerating, and Air-Conditioning |
| BHE | Borehole Heat Exchanger |
| CaRM | Capacity Resistance Model |
| CCM | Composite Cylindrical Model |
| CPT | Cone Penetration Test |
| CSM | Cylinder Source Model |
| DTRT | Distributed Thermal Response Test |
| DTS | Distributed Temperature Sensing |
| ETRT | Enhanced Thermal Response Test |
| FDTR | Frequency Domain Thermoreflectance Technique |
| FEA | Finite Element Analysis |
| FEM | Finite Element Method |
| FLS | Finite Line Source |
| GHE | Ground Heat Exchanger |
| GIS | Geographical Information System |
| GPM | Geothermal Properties Measurement |
| GPM | Geothermal Properties Measurement |
| ILS | Infinite Line Source |
| LVDT | Linear Variable Differential Transformers |
| OCR | Over-Consolidation Ratio |
| SGE | Shallow Geothermal Energy |
| TC | Thermal Conductivity |
| TEP | TRT Evaluation Program |
| TG | Thermal Grout |
| THM | Thermo-Hydro-Mechanical |
| TPS | Transient Plane Source |
| TRT | Thermal Response Test |
| W | W-shape pipe heat exchanger |
| Nomenclature | |
| ∆ | increment or change operator (-) |
| A, B, C | main axes of thermal conductivity with angles α, β, γ (rad or °) to line of scanning, respectively |
| Ai | area normal to the direction of the heat flow (m2) |
| D10 | 10% of the sample is passing the 1.4 millimeter size (-) |
| E | void ratio (-) |
| K and Kf | bulk modulus of the soil skeleton and Biot’s modulus, respectively (-) |
| Li | length of the material (m) |
| M | critical state parameter |
| N | porosity (-) |
| O | area of the heat spot (m2) |
| Q | heat flow (W) |
| q | heat rate (W·m−1) |
| qc | cone resistance (MPa) |
| rb | ground heat exchanger radius (m) |
| Rb | thermal resistance of the ground heat exchanger (K·m·W−1) |
| Rf | friction ratio (%) |
| S | detection area of the radiometer |
| Sr | degree of saturation |
| Tambient and Tair | ambient temperature during the TRT (K or °C) |
| Ti | temperature (K or °C) |
| Tin or Tinjection | inlet temperature to the ground heat exchangers during the TRT (K or °C) |
| Tout | outlet temperature from the ground heat exchangers during the TRT (K or °C) |
| TR | reference temperature (K) |
| U | excess pore pressure (kPa) |
| V | velocity of scanning (m·s−1) |
| X | direction coordinate or distance (m) |
| α | thermal diffusivity (m2·s−1], defined as α = λ/ρcp |
| β | volumetric free thermal expansion coefficient (K−1) |
| βg and βw | volumetric thermal expansion coefficients of the soil particles and water, respectively (K−1) |
| εv | volumetric strain (-) |
| εvT | volumetric thermal expansion (-) |
| ζ | rate of water per unit volume flowing into or out of the soil voids (ζ > 0 for water flowing out of the voids) |
| λ | thermal conductivity (W·m−1·K−1) |
| λR | reference thermal conductivity (W·m−1·K−1) |
| ρcp | volumetric heat capacity (J·m−3·W−1) |
| σ’v | effective vertical stress (kPa) |
| σi | principal stresses (kPa) |
Appendix A
| Method | Limitations | Advantages |
|---|---|---|
| Guarded hot plate | (1) Large sample required. (2) Method not designed with soils in mind. (3) Presence of contact resistance that is difficult to evaluate or eliminate. (4) Overestimates the thermal conductivity of coarse saturated soils as it includes the effect of buoyancy-driven flow. (5) Moisture migration may occur in unsaturated soils. (6) Long duration tests. | (1) Standardised method [231] for rocks. (2) More suited to dried samples. (3) Possibility to measure thermal conductivity at different temperatures without needing external chambers. |
| Thermal cell | (1) Overestimates the thermal conductivity due to uncontrolled heat losses. (2) Long test durations. (3) Potential for moisture migration in unsaturated soils. | (1) Larger thermally activated zone than transient methods. (2) Suitable for any soil. (3) Sample sizes and shape suited to routine site investigation practice. |
| Divided bar | (1) It is a comparative method. (2) Similar problems to guarded hot plate including long duration and potential for moisture migration. | (1) Larger thermally activated zone than transient methods. (2) Well suited for rock testing. |
| Thermal needle probe | (1) Need stable applied current. (2) Small sample volume is thermally activated; hence many tests may be needed in heterogeneous soils. (3) Not appropriate when soil grain size is large relative to needle. (4) The samples need to be large enough to avoid the effect of boundaries. (5) Contact resistance errors created when hole is drilled into rock samples or hard soils. | (1) Standardised method [46]. (2) Very rapid test; minimising moisture migration and hence suitable for partially saturated samples. (3) Portable version for in situ measurements. (4) Different needle sizes available to adapt to smaller samples. |
| Thermal dual needle probe | (1) Same as limitations of the thermal needle probe, but requires extra care to ensure that insertion does not change separation of needle. | (1) As for the thermal needle probe, but it is not standardised. (2) It can also determine thermal diffusivity. |
| Transient plane source | (1) Requires complex decision-making to select adequate sensors, power and measuring times. (2) Hard to create a smooth surface in in some soil types. (3) It is not standardised for soil and rock samples. | (1) A wide range of sample sizes can be measured as there are different sizes of sensors. (2) Applicable to all types of soils and rocks. (3) Fast measurements. (4) Volumetric heat capacity can also be determined. (5) There is no need to drill the samples as the probe remains in contact with the surface. |
| Optical scanning technique | (1) It is not a standardised method for soils and rocks. (2) Not well suited to soils given the requirement for smooth polished surfaces. | (1) Well suited for use with rocks. (2) Allows measuring the variations of the thermal conductivity along a scanning line on the sample. (3) Gives indications of the heterogeneity of the material. |
| Pile Type, Length (m)/Diameter or Size (m) | Pipe Configuration | TRT Duration | Interpretation Methodology | Pile Thermal Resistance (m.K.W−1) | Soil Thermal Conductivity (W.m−1.K−1) | Reference |
|---|---|---|---|---|---|---|
| Auger pile, 25.8/0.88 | - | 160 h | ILS * | 0.080 | 2.40 | [232] |
| Auger pile, 23/0.6 | 2U * | 20 h | ILS * | - | 1.52 | [233] |
| Driven precast, 15/0.27x0.27 | 1U * | 30 h | ILS * | 0.170 | 2.56 | [234] |
| Driven steel tube, 17/0.244 | 1U * | 30 h | ILS * | 0.110 | 2.37 | |
| Auger pile APGE *, 18.3/0.305 | 2U * | 96 h | ILS * initial 10 h neglected | - | 2.91 | [235] |
| Auger pile APGE *, 18.3/0.305 | 1U * | 67 h | ILS * initial 10 h neglected | - | 2.98 | |
| Auger pile APGE *, 18.3/0.457 | 2U * | 100 h | ILS * initial 10 h neglected | - | 2.92 | |
| Auger pile APGE *, 18.3/0.457 | 1U * | 110 h | ILS * initial 10 h neglected | - | 3.27 | |
| Hollow precast pile, 13.25/0.4 | W * | 14 h | 72 h 3D FEM * simulation | 0.131 | 2.46 | [163] |
| Hollow precast pile, 13.75/0.4 | 3U * | 0.098 | 2.53 | |||
| Auger pile, 6/0.30 | 1U * | 9.5 h | ILS * | - | 2.87 | [174] |
| GPM * | - | 2.94 | ||||
| 10 h recovery | Recovery data | - | 2.60 | |||
| Auger pile, 14.2/0.25 | 1U * | 13 h | ILS * | - | 3.23 | |
| 6 h recovery | Recovery data | - | 3.53 | |||
| Auger pile cement/sand, 30.5/0.254 | 1U * | 48–60 h | ILS *, FLS *, CSM * | 0.230 | 1.95–1.96–1.94 | [236] |
| Auger pile cement/sand, 30.5/0.254 | 2U * | 48–60 h | ILS *, FLS *, CSM * | 0.120 | 2.02–2.02–2.03 | |
| Auger pile cement/sand, 30.5/0.254 | 1U * | 48–60 h | ILS *, FLS *, CSM * | 0.220 | 1.95–1.96–1.92 | |
| Auger pile cement, 30.5/0.254 | 1U * | 48–60 h | ILS *, FLS *, CSM * | 0.190 | 1.99–1.98–1.96 | |
| Auger pile TG *, 18.3/0.305 | 2U * | 94 h | ILS * time superposition | - | 2.50 | [152] with data from [235] |
| Auger pile APGE *, 18.3/0.305 | 2U * | 96 h | ILS * time superposition | - | 2.80 | |
| Auger pile APGE *, 18.3/0.457 | 2U * | 100 h | ILS * time superposition | - | 2.60 | |
| Auger pile 18.3/0.305 | 2U * | 96 h | G-function time superposition | 0.061 | 3.10 | [237] with data from [235] |
| Auger pile 18.3/0.305 | 1U * | 67 h | G-function time superposition | 0.104 | 2.98 | |
| Auger pile 18.3/0.457 | 2U * | 100 h | G-function time superposition | 0.104 | 3.18 | |
| Auger pile 18.3/0.457 | 1U * | 110 h | G-function time superposition | 0.135 | 3.77 | |
| Auger pile, 26.8/0.3 | 1U * | 34.25 days multi stage TRT | G-functions | 0.125 | 2.4 | [166] |
| ILS * | 0.125 | 2.6 | ||||
| Auger pile, 16.1/0.6 | 1U * | 72 h | ILS * | - | 4.19 | [238] |
| 3U * | 216 h | ILS * | - | 3.75 | ||
| 3U * | 1248 h | ILS * | - | 4.99 | ||
| Auger pile, 45/0.6 | W * | 48 h | ILS * | - | 2.96 | [157] |
| CCM * | - | 2.42 | ||||
| Auger pile, 18/0.42 | W * | 96 h | ILS * | 0.370 | 2.78 | [239] |
| Auger pile, 15.2/0.61 | 2U * | 498 h | ILS * | - | 1.90–2.10 | [173] |
| Auger pile, 15.2/0.61 | 2U * | 498 h | Based on thermistor measurements in boreholes | - | 2.00–2.30 | [240] |
| Driven precast, 15/0.3x0.3 | W * | 96 h | 2D FEM * simulation | 0.062 | 2.41 | [168] |
| Auger pile, 16.1/0.6 | 1U * | 72 h | 2D FEM * | - | 1.80 | [241] |
| Driven precast, 10/0.27x0.27 | 1U * | 275 h | ILS * | 0.191 | 2.74 | [242] |
| Micro-pile, 12/0.18 | - | 96 h | ILS * | 0.300 | 0.90 | [243] |
| Driven precast, 17/0.35x0.35 | 2U * | 120 h | ILS * | 0.160 | 2.70 | [175] |
| Auger pile, 20/0.62 | 2U * | 110 h | CaRM * | - | 1.50 | [160] |
| Reference | Hole Diameter | Depth | AR | Ground Conditions | Lab Method | Field Method | Tinjection > Tambient ? | Comments |
|---|---|---|---|---|---|---|---|---|
| [107] | 0.15 | 100 | 658 | Clastic sedimentary sequence | Needle probe (93 measurements on core) | TRT, line-source | Yes | DTRT also carried out with higher resulting average effective thermal conductivity |
| [145] | 0.136 | 86 to 99 | 632 to 728 | Shale, siltstone, and sandstone | Needle probe (on dry cuttings) | TRT, line source and FEA | Varies | Four boreholes, varying test lengths including one long-term test |
| [176] | >0.15 | 110 or 200 | >500 | Clay, silt, sand mudstone | Transient strip heat source | TRT, line source | ? | 22 TRT on 11 boreholes, 337 samples tested |
| [170] | ? | ? | ? | Sedimentary, volcanic, and metamorphic rocks | 1D transient source [244] | TRT, line source | ? | 57 boreholes tested and laboratory results from 1398 rock cores |
| [177] | 0.126 | 18.3 | 145 | Sand | Needle probe | TRT, line source | Yes | Laboratory sand box |
| [108] | 0.25 | 30 | 120 | Sand and gravel with clay layers | Needle probe | TRT, line source | Varies | |
| [47] | 0.3 | 26 | 87 | Stiff fissured clay | Needle probe | TRT, line source | Yes | Values from first stage of multi-stage TRT |
| [152] | 0.305 and 0.457 | 18.3 | 60 and 40 | Sandy clay and dense sand | Needle probe | TRT, line source | Yes | |
| [174] | 0.25 | 14.5 | 58 | Sand and gravel | Needle probe | TRT, line source and GPM | ? | Short duration in situ test |
| [175] | 0.35 | 17.4 | 50 | Organic clay, sands, and gravels | Needle and dual needle probes | TRT, line source | ? | Square cross-section pile |
| [163] | 0.4 | 13.25 | 33 | Weathered granite | Needle probe | TRT, FEA | ? | Spun concrete pile |
| [172] | 0.6 | 16.1 | 27 | Sand and clayey sand | Needle probe | TRT, line source | Yes | |
| [173] | 0.61 | 15.2 | 25 | Sand, sandstone | Needle probe | TRT, line source | Yes | Four piles, each test corrected for long header pipes |
References
- European Technology and Innovation Platform, Renewable Heating and Cooling. Geothermal Energy Pannel. Available online: http://www.rhc-platform.org/structure/geothermal-technology-panel/ (accessed on 6 July 2017).
- Rees, S. Advances in Ground Source Heat Pump Systems; Woodhead Publishing: Sawston, UK, 2016; ISBN 978-0-08-100311-4. [Google Scholar]
- Brandl, H. Energy foundations and other thermo-active ground structures. Geotechnique 2006, 56, 81–122. [Google Scholar] [CrossRef]
- Adam, D.; Markiewicz, R. Energy from earth-coupled structures, foundations, tunnels and sewers. Géotechnique 2009, 59, 229–236. [Google Scholar] [CrossRef]
- Bidarmaghz, A.; Narsilio, G.; Johnston, I. Numerical Modelling of Ground Heat Exchangers with Different Ground Loop Configurations for Direct Geothermal Applications. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013. [Google Scholar]
- Batini, N.; Rotta Loira, A.F.; Conti, P.; Testi, D.; Grassie, W.; Laloui, L. Energy and geotechnical behaviour of energy piles for different design solutions. Appl. Therm. Eng. 2015, 86, 199–213. [Google Scholar] [CrossRef]
- Alberti, L.; Angelotti, A.; Antelmi, M.; La Licata, I. A Numerical Study on the Impact of Grouting Material on Borehole Heat Exchangers Performance in Aquifers. Energies 2017, 10, 703. [Google Scholar] [CrossRef]
- Delaleux, F.; Py, X.; Olives, R.; Dominguez, A. Enhancement of geothermal borehole heat exchangers performances by improvement of bentonite grouts conductivity. Appl. Therm. Energy 2012, 33–34, 92–99. [Google Scholar] [CrossRef]
- Di Donna, A.; Barla, M. The role of ground conditions on energy tunnels’ heat exchange. Environ. Geotech. 2016, 3, 214–224. [Google Scholar] [CrossRef]
- Wołoszyn, J.; Gołas, A. Sensitivity analysis of efficiency thermal energy storage on selected rock mass and grout parameters using design of experiment method. Energy Convers. Manag. 2014, 87, 1297–1304. [Google Scholar] [CrossRef]
- Low, J. Thermal Conductivity of Soils for Energy Foundation Applications. Ph.D. Thesis, University of Southampton, Southampton, UK, 2015. [Google Scholar]
- Laloui, L.; Nuth, M.; Vulliet, L. Experimental and numerical investigations of the behaviour of heat exchanger pile. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 763–781. [Google Scholar] [CrossRef]
- Rees, S.; Adjali, M.; Zhou, Z.; Davies, M.; Thomas, H. Ground heat transfer effects on the thermal performance of earth-contact structures. Renew. Sustain. Energy Rev. 2000, 4, 213–265. [Google Scholar] [CrossRef]
- Thirumaleshwar, M. Fundamentals of Heat and Mass Transfer; Pearson Education: Delhi, India, 2009; ISBN 8177585193. [Google Scholar]
- De Vries, D.A. Simultaneous transfer of heat and moisture in porous media. Trans. Am. Geophys. Union 1958, 39, 909–916. [Google Scholar] [CrossRef]
- De Vries, D.A. Thermal properties of soils. In Physics of Plant Environment, 2nd ed.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1966. [Google Scholar]
- De Vries, D.A. Heat transfer in soils. In Heat and Mass Transfer in the Biosphere. Part 1. Transfer Processes in Plant Environment; De Vries, D.A., Afghan, N.H., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 1974. [Google Scholar]
- Woodside, W.; Messner, J.H. Thermal conductivity of porous media. I. Unconsolidated Sands. J. Appl. Phys. 1961, 32, 1688–1699. [Google Scholar] [CrossRef]
- Farouki, O.T. Thermal Properties of Soils; No. CRREL-MONO-81-1; U.S. Army Corps of Engineers, Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1981. [Google Scholar]
- Midttømme, K.; Roaldset, E. Thermal conductivity of sedimentary rocks: Uncertainties in measurement and modelling. Geol. Soc. Lond. Spec. Publ. 1999, 158, 45–60. [Google Scholar] [CrossRef]
- Hellstrom, G. Ground Heat Storage, Thermal Analysis of Duct Storage Systems; Department of Mathematical Physics, University of Lund: Lund, Sweden, 1991. [Google Scholar]
- Liebel, H.T. Influence of Groundwater on Measurements of Thermal Properties in Fractured Aquifers. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2012. [Google Scholar]
- Campanella, R.G.; Mitchell, J.K. Influence of temperature variations on soil behavior. J. Soil Mech. Found. Div. 1968. [Google Scholar]
- Hueckel, T.; Baldi, G. Thermoplasticity of saturated clays: Experimental constitutive study. J. Geotech. Eng. Div. 1990, 116, 1778–1796. [Google Scholar] [CrossRef]
- Cekerevac, C.; Laloui, L. Experimental study of the thermal effects on the mechanical behaviour of a clay. Int. J. Numer. Anal. Methods Geomech. 2004, 28, 209–228. [Google Scholar] [CrossRef]
- Laloui, L.; Olgun, C.G.; Sutman, M.; McCartney, J.S.; Coccia, C.J.; Abuel-Naga, H.M.; Bowers, G.A. Issues involved with thermoactive geotechnical systems: Characterization of thermomechanical soil behavior and soil-structure interface behavior. J. Deep Found. Inst. 2014, 8, 108–112. [Google Scholar] [CrossRef]
- Jensen, C.; Xing, C.; Folsom, C.; Ban, H.; Phillips, J. Design and validation of a high-temperature comparative thermal-conductivity measurement system. Int. J. Thermophys. 2012, 33, 311–329. [Google Scholar] [CrossRef]
- ASTM International. Standard Test Method for Steady-State Heat Flux Measurements and Thermal Transmission Properties by Means of the Guarded-Hot-Plate Apparatus; ASTM C177–13; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar] [CrossRef]
- British Standards Institution (BSI). Thermal Performance of Building Materials and Products. Determination of Thermal Resistance by Means of Guarded Hot Plate and Heat Flow Meter Methods. Products of High and Medium Thermal Resistance; BS EN 12667:2001; British Standards Institution (BSI): London, UK, 2001. [Google Scholar]
- International Organization for Standardization. Thermal Insulation—Determination of Steady-State Thermal Resistance and Related Properties—Guarded Hot Plate Apparatus; ISO 8302:1991; International Organization for Standardization: Geneva, Switzerland, 1991. [Google Scholar]
- Salmon, D. Thermal conductivity of insulations using guarded hot plates, including recent developments and sources of reference materials. Meas. Sci. Technol. 2001, 12. [Google Scholar] [CrossRef]
- Zhao, D.; Qian, X.; Gu, X.; Jajja, S.A.; Yang, R. Measurement Techniques for Thermal Conductivity and Interfacial Thermal Conductance of Bulk and Thin Film Materials. J. Electron. Packag. 2016, 138. [Google Scholar] [CrossRef]
- Tarnawski, V.R.; Momose, T.; Leong, W.H.; Bovesecchi, G.; Coppa, P. Thermal conductivity of standard sands. Part I. Dry-state conditions. Int. J. Thermophys. 2009, 30, 949–968. [Google Scholar] [CrossRef]
- Nikolaev, I.V.; Leong, W.H.; Rosen, M.A. Experimental investigation of soil thermal conductivity over a wide temperature range. Int. J. Thermophys. 2013, 34, 1110–1129. [Google Scholar] [CrossRef]
- Hiraiwa, Y.; Kasubuchi, T. Temperature dependence of thermal conductivity over a wide range of temperature (5–75 °C). Eur. J. Soil Sci. 2000, 51, 211–218. [Google Scholar] [CrossRef]
- Low, J.E.; Loveridge, F.A.; Powrie, W. Error analysis of the thermal cell for soil thermal conductivity measurement. In Proceedings of the Institution of Civil Engineers ICE—Geotechnical Engineering; ICE Publishing: London, UK, 2017; Volume 170, pp. 191–200. [Google Scholar] [CrossRef]
- Clarke, B.G.; Agab, A.; Nicholson, D. Model specification to determine thermal conductivity of soils. In Proceedings of the Institution of Civil Engineers—Geotechnical Engineering; ICE publishing: London, UK, 2008; Volume 161, pp. 161–168. [Google Scholar] [CrossRef]
- Alrtimi, A.; Rouainia, M.; Haigh, S. Thermal conductivity of a sandy soil. Appl. Therm. Eng. 2016, 106, 551–560. [Google Scholar] [CrossRef]
- ASTM International. Standard Test Method for Thermal Conductivity of Solids Using the Guarded-Comparative-Longitudinal Heat Flow Technique; ASTM E1225-13; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar] [CrossRef]
- Barry-Macaulay, D.; Bouazza, A.; Singh, R.M.; Wang, B.; Ranjith, P.G. Thermal conductivity of soils and rocks from the Melbourne (Australia) region. Eng. Geol. 2013, 164, 131–138. [Google Scholar] [CrossRef]
- Schmidt, A.J.; Cheaito, R.; Chiesa, M. A frequency-domain thermoreflectance method for the characterization of thermal properties. Rev. Sci. Instrum. 2009, 80, 094901. [Google Scholar] [CrossRef] [PubMed]
- Van der Held, E.F.M.; Van Drunen, F.G. A method of measuring the thermal conductivity of liquids. Physica 1949, 15, 865–881. [Google Scholar] [CrossRef]
- Blackwell, J.H. A transient-flow method for determination of thermal constants of insulating materials in bulk Part I—Theory. J. Appl. Phys. 1954, 25, 137–144. [Google Scholar] [CrossRef]
- Teka, Thermophysical Instruments-Geothermal Investigation. 2017. Available online: http://www.te-ka.de/index.php/en/ (accessed on 6 July 2017).
- Isomet. Portable Heat Transfer Analyser. Available online: http://appliedp.com/produkty/isomet/ (accessed on 29 November 2017).
- ASTM International. Standard Test Method for Determination of Thermal Conductivity of Soil and Soft Rock by Thermal Needle Probe Procedure; ASTM D5334–14; ASTM International: West Conshohocken, PA, USA, 2000. [Google Scholar] [CrossRef]
- Low, J.; Loveridge, F.; Powrie, W. A comparison of laboratory and in situ methods to determine soil thermal conductivity for energy foundations and other ground heat exchanger applications. Acta Geotech. 2015, 10, 209–218. [Google Scholar] [CrossRef]
- Kasubuchi, T. Development of in-situ soil water measurement by heat-probe method. Jpn. Agric. Res. Q. 1992, 26, 178–181. [Google Scholar]
- Campbell, G.S.; Calissendorff, C.; Williams, J.H. Probe for measuring soil specific heat using a heat-pulse method. Soil Sci. Soc. Am. J. 1991, 55, 291–293. [Google Scholar] [CrossRef]
- Bilskie, J.R. Dual Probe Methods for Determining Soil Thermal Properties: Numerical Laboratory Study. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 1994. [Google Scholar]
- Rajeev, P.; Kodikara, J. Estimating apparent thermal diffusivity of soil using field temperature time series. Geomech. Geoengin. 2016, 11, 28–46. [Google Scholar] [CrossRef]
- Lockmuller, N.; Redgrove, J.; Kubicar, L.U. Measurement of thermal conductivity with the needle probe. High Temp. High Press. 2003, 35, 127–138. [Google Scholar] [CrossRef]
- Valente, A.; Morais, R.; Tuli, A.; Hopmans, J.W.; Kluitenberg, G.J. Multi-functional probe for small-scale simultaneous measurements of soil thermal properties, water content, and electrical conductivity. Sens. Actuators 2006, 132, 70–77. [Google Scholar] [CrossRef]
- Assael, M.J.; Antoniadis, K.D.; Wakeham, W.A. Historical evolution of the transient hot-wire technique. Int. J. Thermophys. 2010, 31, 1051–1072. [Google Scholar] [CrossRef]
- Merckx, B.; Dudoignon, P.; Garnier, J.P.; Marchand, D. Simplified transient hot-wire method for effective thermal conductivity measurement in geo materials: Microstructure and saturation effect. Adv. Civ. Eng. 2012, 2012. [Google Scholar] [CrossRef]
- International Organization for Standardization. Plastics—Determination of Thermal Conductivity and Thermal Diffusivity—Part 2: Transient Plane Heat Source (Hot Disc) Method; ISO 22007–2:2015; International Organization for Standardization: Geneva, Switzerland, 2015. [Google Scholar]
- Gustafsson, S.; Thermetrol, A.B. Device for Measuring Thermal Properties of a Test Substance-the Transient Plane Source (TPS) Method. U.S. Patent 5,044,767, 1991. [Google Scholar]
- Gustafsson, S.E. Transient plane source techniques for thermal conductivity and thermal diffusivity measurements of solid materials. Rev. Sci. Instrum. 1991, 62, 797–804. [Google Scholar] [CrossRef]
- Mikulić, D.; Milovanović, B. TCi System for Non-Destructive Determination of Thermal Properties of Materials. In Proceedings of the 10th European Conference on Non-Destructive Testing, Moscow, Russia, 7–11 June 2010; ICNDT: Northampton, UK, 2010; pp. 1364–1373. [Google Scholar]
- Thermtest Inc. Thermtest Thermophysical Instruments. Available online: https://thermtest.com/tps-global (accessed on 6 July 2017).
- C-Therm Technologies Ltd. TCi Thermal Conductivity Analyzer. Available online: http://ctherm.com/products/tci_thermal_conductivity/ (accessed on 6 July 2017).
- Suleiman, B.M. Thermal Conductivity of Saturated samples using the Hot-Disk Technique. In Proceedings of the 4th WSEAS International Conference on Heat Transfer, Thermal Engineering and Environment, Elounda, Greece, 21–23 August 2006. [Google Scholar]
- Florides, G.; Theofanous, E.; Iosif-Stylianou, I.; Tassou, S.; Christodoulides, P.; Zomeni, Z.; Tsiolakis, E.; Kalogirou, S.; Messaritis, V.; Pouloupatis, P.; et al. Modeling and assessment of the efficiency of horizontal and vertical ground heat exchangers. Energy 2013, 58, 655–663. [Google Scholar] [CrossRef]
- Stylianou, I.I.; Tassou, S.; Christodoulides, P.; Panayides, I.; Florides, G. Measurement and analysis of thermal properties of rocks for the compilation of geothermal maps of Cyprus. Renew. Energy 2016, 88, 418–429. [Google Scholar] [CrossRef]
- Stylianou, I.I.; Florides, G.; Tassou, S.; Tsiolakis, E.; Christodoulides, P. Methodology for estimating the ground heat absorption rate of Ground Heat Exchangers. Energy 2017, 127, 258–270. [Google Scholar] [CrossRef]
- Popov, Y.A.; Pribnow, D.F.C.; Sass, J.H.; Williams, C.F.; Burkhardt, H. Characterization of rock thermal conductivity by high-resolution optical scanning. Geothermics 1999, 28, 253–276. [Google Scholar] [CrossRef]
- Haffen, S.; Geraud, Y.; Diraison, M.; Dezayes, C. Determining fluid flow zones in a geothermal reservoir from thermal conductivity and temperature. Geothermics 2013, 46, 32–41. [Google Scholar] [CrossRef]
- Liu, S.; Feng, C.; Wang, L.; Li, C. Measurement and analysis of thermal conductivity of rocks in the Tarim Basin, Northwest China. Acta Geol. Sin. (Engl. Ed.) 2011, 85, 598–609. [Google Scholar] [CrossRef]
- Mitchell, J.K.; Kao, T.C. Measurement of soil thermal resistivity. J. Geotech. Geoenviron. Eng. 1978, 104, 1307–1320. [Google Scholar]
- Slusarchuk, W.A.; Foulger, P.H. Development and Calibration of a Thermal Conductivity Probe Apparatus for Use in the Field and Laboratory. National Research Council of Canada, Division of Building Research; Technical Paper No. 388; National Research Council Canada: Ottawa, ON, Canada, 1973.
- Tarnawski, V.R.; Momose, T.; Leong, W.H. Thermal conductivity of standard sands II. Saturated conditions. Int. J. Thermophys. 2011, 32, 984–1005. [Google Scholar] [CrossRef]
- Tarnawski, V.R.; McCombie, M.L.; Momose, T.; Sakaguchi, I.; Leong, W.H. Thermal conductivity of standard sands. Part III. Full range of saturation. Int. J. Thermophys. 2013, 34, 1130–1147. [Google Scholar] [CrossRef]
- Woodside, W.; Cliffe, J.B. Heat and moisture transfer in closed systems of two granular materials. Soil Sci. 1959, 87, 75–82. [Google Scholar] [CrossRef]
- Kersten, M.S. Thermal Properties of Soils; Bulletin 28; University of Minnesota, Institute of Technology, Engineering Experiment Station: Minneapolis, MN, USA, 1949; Volume LII. [Google Scholar]
- Jackson, R.D.; Taylor, S.A. Thermal conductivity and diffusivity. In Methods of Soil Analysis: Part 1—Physical and Mineralogical Methods; Klute, A., Ed.; Soil Science Society of America, American Society of Agronomy: Madison, WI, USA, 1986. [Google Scholar]
- Sass, J.H.; Lachenbruch, A.H.; Munroe, R.J. Thermal conductivity of rocks from measurements on fragments and its application to heat-flow determinations. J. Geophys. Res. 1971, 76, 3391–3401. [Google Scholar] [CrossRef]
- Moench, A.F.; Evans, D.D. Thermal conductivity and diffusivity of soil using a cylindrical heat source. Soil Sci. Soc. Am. J. 1970, 34, 377–381. [Google Scholar] [CrossRef]
- Bligh, T.P.; Smith, E.A. Thermal conductivity measurements of soils in the field and laboratory using a thermal conductivity probe. Energy Effic. Build. Syst. Rep. 1983, 25, 275. [Google Scholar]
- Jorand, R.; Vogt, C.; Marquart, G.; Clauser, C. Effective thermal conductivity of heterogeneous rocks from laboratory experiments and numerical modelling. J. Geophys. Res. Solid Earth 2013, 118, 5225–5235. [Google Scholar] [CrossRef]
- Smits, K.M.; Sakaki, T.; Limsuwat, A.; Illangasekare, T.H. Thermal conductivity of sands under varying moisture and porosity in drainage–wetting cycles. Vadose Zone J. 2010, 9, 172–180. [Google Scholar] [CrossRef]
- Johansen, O. Thermal Conductivity of Soils; Draft Translated: 637; U.S. Army Corps of Engineering, Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1977. [Google Scholar]
- Côté, J.; Konrad, J.M. A generalized thermal conductivity model for soils and construction materials. Can. Geotech. J. 2005, 42, 443–458. [Google Scholar] [CrossRef]
- Côté, J.; Konrad, J.M. Assessment of structure effects on the thermal conductivity of two-phase porous geomaterials. Int. J. Heat Mass Trans. 2009, 52, 796–804. [Google Scholar] [CrossRef]
- Antilén, M.; Escudey, M.; Förster, J.E.; Moraga, N.; Marty, D.; Fudym, O. Application of the hot disk method to the thermophysical characterization of soils. J. Chil. Chem. Soc. 2003, 48, 27–29. [Google Scholar] [CrossRef]
- Mogensen, P. Fluid to Duct Wall Heat Transfer in Duct System Heat Storage. In Proceedings of the International Conference on Subsurface Heat Storage in Theory and Practice, Stockholm, Sweden, 6–8 June 1983; Swedish Council for Building Research: Stockholm, Sweden, 1983; pp. 652–657. [Google Scholar]
- Gehlin, S. Thermal Response Test: Method Development and Evaluation. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2002. [Google Scholar]
- VDI-Standards. VDI 4640 blatt 3 utilization of the subsurface for thermal purposes. In Underground Thermal Energy Storage; VDI-Gessellschaft Energie und Umwelt (GEU): Berlin, Germany, 2001. [Google Scholar]
- Spitler, J.D.; Gehlin, S.E.A. Thermal response testing for ground source heat pump systems—An historical review. Renew. Sustain. Energy Rev. 2015, 50, 1125–1137. [Google Scholar] [CrossRef]
- Witte, H.J.L. In situ estimation of ground thermal properties. In Advances in Ground-Source Heat Pump Systems; Rees, S., Ed.; Woodhead Publishing: Sawston, UK, 2016. [Google Scholar]
- Zhang, C.; Guo, Z.; Liu, Y.; Cong, X.; Peng, D. A review on thermal response test of ground-coupled heat pump systems. Renew. Sustain. Energy Rev. 2014, 40, 851–867. [Google Scholar] [CrossRef]
- Li, M.; Lai, A.C. Review of analytical models for heat transfer by vertical ground heat exchangers (GHEs): A perspective of time and space scales. Appl. Energy 2015, 151, 178–191. [Google Scholar] [CrossRef]
- Microgeneration Installation Standard. MIS 3005 Microgeneration Installation Standard: Requirements for MCS Contractors Undertaking the Supply, Design, Installation, Set to Work, Commissioning and Handover of Microgeneration Heat Pump Systems, Issue 4.3; Microgeneration Installation Standard, Department of Energy and Climate Change: London, UK, 2008. [Google Scholar]
- Recknagel, H.; Sprenger, E.; Schramek, E.-R. Génie Climatique [Taschenbuch für Heizung und Klimatechnik]; Bodson, A., Caradec, C., Pastureau, S., Petit, N., Eds.; Clima & Confort: Dunod, Paris, France, 2013. [Google Scholar]
- Javed, S. Design of ground source heat pump systems. Thermal Modelling and Evaluation of Borehole Heat Transfer. Ph.D. Thesis, Chalmers University of Technology, Göteborg, Sweden, 2012. [Google Scholar]
- Kavanaugh, S.P.; Rafferty, K.D.; American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE). Ground-Source Heat Pumps: Design of Geothermal Systems for Commercial and Institutional Buildings; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 1997. [Google Scholar]
- Kurevija, T.; Vulin, D.; Macenić, M. Impact of geothermal gradient on ground source heat pump system modeling. Rud. Geol. Naft. Zb. 2014, 28, 39–45. [Google Scholar]
- Dehkordi, S.E.; Schincariol, R.A. Effect of thermal-hydrogeological and borehole heat exchanger properties on performance and impact of vertical closed-loop geothermal heat pump systems. Hydrogeol. J. 2014, 22, 189–203. [Google Scholar] [CrossRef]
- Radioti, G.; Sartor, K.; Charlier, R.; Dewallef, P.; Nguyen, F. Effect of undisturbed ground temperature on the design of closed-loop geothermal systems: A case study in a semi-urban environment. Appl. Energy 2017, 200, 89–105. [Google Scholar] [CrossRef]
- Kavanaugh, S.P.; Xie, L.; Martin, C. TRP-1118—Investigation of Methods for Determining Soil and Rock Formation Thermal Properties from Short Term Field Test; Final Report; American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE): Atlanta, GA, USA, 2000. [Google Scholar]
- Javed, S.; Fahlén, P. Thermal response testing of a multiple borehole ground heat exchanger. Int. J. Low-Carbon Technol. 2011, 6, 141–148. [Google Scholar] [CrossRef]
- Gehlin, S.; Nordell, B. Determining undisturbed ground temperature for thermal response test. ASHRAE Trans. 2003, 109, 151–156. [Google Scholar]
- Taniguchi, M.; Uemura, T. Effects of urbanization and groundwater flow on the subsurface temperature in Osaka, Japan. Phys. Earth Planet. Inter. 2005, 152, 305–313. [Google Scholar] [CrossRef]
- Banks, D. An Introduction to Thermogeology. Ground Source Heating and Cooling; Blackwell Publishing: Oxford, UK, 2008; ISBN 978-0-470-67034-7. [Google Scholar]
- Ferguson, G.; Woodbury, A.D. Urban heat island in the subsurface. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Zhu, K.; Blum, P.; Ferguson, G.; Balke, K.D.; Bayer, P. The geothermal potential of urban heat islands. Environ. Res. Lett. 2010, 5. [Google Scholar] [CrossRef]
- Menberg, K.; Bayer, P.; Zosseder, K.; Rumohr, S.; Blum, P. Subsurface urban heat islands in German cities. Sci. Total Environ. 2013, 442, 123–133. [Google Scholar] [CrossRef] [PubMed]
- Soldo, V.; Borović, S.; Lepoša, L.; Boban, L. Comparison of different methods for ground thermal properties determination in a clastic sedimentary environment. Geothermics 2016, 61, 1–11. [Google Scholar] [CrossRef]
- Witte, H.J.L.; van Gelder, G.J.; Spitler, J.D. In Situ Measurement of Ground Thermal Conductivity: A Dutch Perspective. ASHRAE Trans. 2002, 108, 263–272. [Google Scholar]
- Wang, H.; Qi, C.; Du, H.; Gu, J. Improved method and case study of thermal response test for borehole heat exchangers of ground source heat pump system. Renew. Energy 2010, 35, 727–733. [Google Scholar] [CrossRef]
- Javed, S.; Nakos, H.; Claesson, J. A method to evaluate thermal response tests on groundwater-filled boreholes. ASHRAE Trans. 2012, 118, 540–549. [Google Scholar]
- Acuña, J.; Palm, B. Distributed thermal response tests on pipe-in-pipe borehole heat exchangers. Appl. Energy 2013, 109, 312–320. [Google Scholar] [CrossRef]
- Raymond, J.; Lamarche, L. Development and numerical validation of a novel thermal response test with a low power source. Geothermics 2014, 51, 434–444. [Google Scholar] [CrossRef]
- Dornstädter, J.; Heidinger, P.; Heinemann-Glutsch, B. Erfahrungen aus der Praxis mit dem Enhanced Geothermal Response Test (EGRT). In Proceedings of the Der Geothermiekongress 2008, Karlsruhe, Germany, 11–13 November 2008; pp. 271–279. [Google Scholar]
- Poulsen, S.E.; Alberdi-Pagola, M. Interpretation of ongoing thermal response tests of vertical (BHE) borehole heat exchangers with predictive uncertainty based stopping criterion. Energy 2015, 88, 157–167. [Google Scholar] [CrossRef]
- Ingersoll, L.R.; Zobel, O.J.; Ingersoll, A.C. Heat Conduction with Engineering, Geological, and Other Applications; The University of Wisconsin Press: Madison, WI, USA, 1954. [Google Scholar]
- Carlslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1959; ISBN 0-19-853368-3. [Google Scholar]
- American Society of Heating, Refrigerating and Air-Conditioning Engineer (ASHRAE). 2007 ASHRAE Handbook—Heating, Ventilating, and Air-Conditioning Applications (I-P Edition); American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2007. [Google Scholar]
- Beier, R.A.; Smith, M.D. Minimum duration of in-situ tests on vertical boreholes. ASHRAE Trans. 2003, 109, 475–486. [Google Scholar]
- Shonder, J.A.; Beck, J. A New Method to Determine the Thermal Properties of Soil Formations From in Situ Field Tests; Report ORNL/TM-2000/97; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2000.
- Austin, W.; Yavuzturk, C.; Spitler, J.D. Development of an In-Situ System and Analysis Procedure for Measuring Ground Thermal Properties. ASHRAE Trans. 2000, 106, 365–379. [Google Scholar]
- Nakos, H. Response Testing and Evaluation of Groundwater-Filled Boreholes: Development and Validation of a New Calculation Tool. Master’s Thesis, Chalmers University of Technology, Göteborg, Sweden, 2011. [Google Scholar]
- Javed, S.; Claesson, J. New analytical and numerical solutions for the short-term analysis of vertical ground heat exchangers. ASHRAE Trans. 2011, 117, 3–12. [Google Scholar]
- Marcotte, D.; Pasquier, P. On the estimation of thermal resistance in borehole thermal conductivity test. Renew. Energy 2008, 33, 2407–2415. [Google Scholar] [CrossRef]
- Javed, S.; Spitler, J.; Fahlén, P. An experimental investigation of the accuracy of thermal response tests used to measure ground thermal properties. ASHRAE Trans. 2011, 117, 13–21. [Google Scholar]
- Javed, S.; Spitler, J. Accuracy of borehole thermal resistance calculation methods for grouted single U-tube ground heat exchangers. Appl. Energy 2017, 187, 790–806. [Google Scholar] [CrossRef]
- Lamarche, L.; Kajl, S.; Beauchamp, B. A review of methods to evaluate borehole thermal resistances in geothermal heat-pump systems. Geothermics 2010, 39, 187–200. [Google Scholar] [CrossRef]
- Spitler, J.D.; Javed, S.; Ramstad, R.K. Natural convection in groundwater-filled boreholes used as ground heat exchangers. Appl. Energy 2016, 164, 352–365. [Google Scholar] [CrossRef]
- Witte, H.J.L. Error analysis of thermal response tests. Appl. Energy 2013, 109, 302–311. [Google Scholar] [CrossRef]
- Javed, S. Thermal response testing: Results and experiences from a ground source heat pump test facility with multiple boreholes. In Proceedings of the 11th REHVA World Congress (Clima 2013), Prague, Czech Republic, 16–19 June 2013. [Google Scholar]
- Bandos, T.V.; Montero, Á.; Córdoba, P.F.D.; Urchueguía, J.F. Improving parameter estimates obtained from thermal response tests: Effect of ambient air temperature variations. Geothermics 2011, 40, 136–143. [Google Scholar] [CrossRef]
- Sanner, B.; Mands, E.; Sauer, M.; Grundmann, E. Technology, development status, and routine application of Thermal Response Test. In Proceedings of the European Geothermal Congress 2007, Unterhaching, Germany, 30 May–1 June 2007. [Google Scholar]
- Diao, N.; Li, Q.; Fang, Z. Heat transfer in ground heat exchangers with groundwater advection. Int. J. Therm. Sci. 2004, 43, 1203–1211. [Google Scholar] [CrossRef]
- Raymond, J.; Therrien, R.; Gosselin, L.; Lefebvre, R. Numerical analysis of thermal response tests with a groundwater flow and heat transfer model. Renew. Energy 2011, 36, 315–324. [Google Scholar] [CrossRef]
- Wagner, V.; Blum, P.; Kübert, M.; Bayer, P. Analytical approach to groundwater-influenced thermal response tests of grouted borehole heat exchangers. Geothermics 2013, 46, 22–31. [Google Scholar] [CrossRef]
- Verdoya, M.; Chiozzi, P. Influence of groundwater flow on the estimation of subsurface thermal parameters. Int. J. Earth Sci. 2016, 1–8. [Google Scholar] [CrossRef]
- Beier, R.A.; Smith, M.D. Removing Variable Heat Rate Effects from Borehole Tests. ASHRAE Trans. 2003, 109, 463–474. [Google Scholar]
- Sauer, M. Evaluating improper response test data by using superposition of line source approximation. In Proceedings of the European Geothermal Congress EGC 2013, Pisa, Italy, 3–8 June 2013. [Google Scholar]
- Hu, P.; Meng, Q.; Sun, Q.; Zhu, N.; Guan, C. A method and case study of thermal response test with unstable heat rate. Energy Build. 2012, 48, 199–205. [Google Scholar] [CrossRef]
- Spitler, J.; Rees, S.; Yavuzturk, C. More Comments on In-Situ Borehole Thermal Conductivity Testing; The Source: Barrie, ON, Canada, 1999; Volume 12, pp. 4–6. [Google Scholar]
- Gehlin, S.; Hellstrom, G. Influence on thermal response test by groundwater flow in vertical fractures in hard rock. Renew. Energy 2003, 28, 2221–2238. [Google Scholar] [CrossRef]
- Fujii, H.; Hiroaki, O.; Itoi, R. Thermal Response Tests Using Optical Fiber Thermometers. GRC Trans. 2006, 30, 545–551. [Google Scholar]
- Florides, G.; Kalogirou, S. First in situ determination of the thermal performance of a U-pipe borehole heat exchanger, in Cyprus. Appl. Therm. Eng. 2008, 28, 157–163. [Google Scholar] [CrossRef]
- Acuña, J.; Mogensen, P.; Palm, B. Distributed thermal response test on a U-pipe borehole heat exchanger. In Proceedings of the 11th International Conference on Thermal Energy Storage Effstock 2009, Stockholm, Sweden, 14–17 June 2009; Academic Conferences Publishing: Stockholm, Sweden, 2009. [Google Scholar]
- Loveridge, F.; Holmes, G.; Powrie, W.; Roberts, T. Thermal response testing through the chalk aquifer. In Proceedings of the Institution of Civil Engineers ICE—Geotechnical Engineering; ICE publishing: London, UK, 2013; Volume 166, pp. 197–210. [Google Scholar] [CrossRef]
- Radioti, G.; Delvoie, S.; Charlier, R.; Dumont, G.; Nguyen, F. Heterogeneous bedrock investigation for a closed-loop geothermal system: A case study. Geothermics 2016, 62, 79–92. [Google Scholar] [CrossRef]
- Heske, C.; Kohlsch, O.; Dornstädter, J.; Heidinger, P. Der Enhanced-Geothermal-Response Test als Auslegungsgrundlage und Optimierungstool. Geothermische Standorterkundung: Sonderheft Oberflächennahe Geothermie. Bbr Fachmagazin für Brunnen- und Leitungsbau 2011, 62, 36–43. (In German) [Google Scholar]
- Liebel, H.T.; Huber, K.; Frengstad, B.S.; Ramstad, R.K.; Brattli, B. Temperature footprint of a thermal response test can help to reveal thermogeological information. Nor. Geol Unders. Bull. 2011, 451, 20–31. [Google Scholar]
- Fujii, H.; Okubo, H.; Nishi, K.; Itoi, R.; Ohyama, K.; Shibata, K. An improved thermal response test for U-tube ground heat exchanger based on optical fiber thermometers. Geothermics 2009, 38, 399–406. [Google Scholar] [CrossRef]
- Hausner, M.B.; Suarez, F.; Glander, K.E.; Van De Giesen, N.; Selker, J.S.; Tyler, S.W. Calibrating single-ended fiber-optic raman spectra distributed temperature sensing data. Sensors 2011, 11, 10859–10879. [Google Scholar] [CrossRef] [PubMed]
- Raymond, J.; Lamarche, L. Simulation of thermal response tests in a layered subsurface. Appl. Energy 2013, 109, 293–301. [Google Scholar] [CrossRef]
- Brandl, H. Thermo-active Ground-Source Structures for Heating and Cooling. Procedia Eng. 2013, 57, 9–18. [Google Scholar] [CrossRef]
- Loveridge, F.; Brettmann, T.; Olgun, G.; Powrie, W. Assessing the applicability of thermal response testing to energy piles. In Proceedings of the Global Perspectives on the sustainable Execution of Foundations Works, Stockholm, Sweden, 21–23 May 2014. [Google Scholar]
- GSHP Association. Thermal Pile: Design, Installation & Materials Standards; Ground Source Heat Pump Association National Energy Centre: Milton Keynes, UK, 2012; p. 85. [Google Scholar]
- Loveridge, F.; Powrie, W. Temperature response functions (G-functions) for single pile heat exchangers. Energy 2013, 57, 554–564. [Google Scholar] [CrossRef]
- Claesson, J.; Javed, S. An analytical method to calculate borehole fluid temperatures for time-scales from minutes to decades. ASHRAE Trans. 2011, 117, 279–288. [Google Scholar]
- Bandos, T.V.; Campos-Celador, Á.; López-González, L.M.; Sala-Lizarraga, J.M. Finite cylinder-source model for energy pile heat exchangers: Effects of thermal storage and vertical temperature variations. Energy 2014, 78, 639–648. [Google Scholar] [CrossRef]
- Hu, P.; Zha, J.; Lei, F.; Zhu, N.; Wu, T. A composite cylindrical model and its application in analysis of thermal response and performance for energy pile. Energy Build. 2014, 84, 324–332. [Google Scholar] [CrossRef]
- Man, Y.; Yang, H.; Diao, N.; Liu, J.; Fang, Z. A new model and analytical solutions for borehole and pile ground heat exchangers. Int. J. Heat Mass Transfer 2010, 53, 2593–2601. [Google Scholar] [CrossRef]
- Maragna, C.; Rachez, X. Innovative Methodology to Compute the Temperature Evolution of Pile Heat Exchangers. In Proceedings of the World Geothermal Congress, Melbourne, Australia, 19–25 April 2015. [Google Scholar]
- Zarrella, A.; Emmi, G.; Zecchin, R.; de Carli, M. An appropriate use of the thermal response test for the design of energy foundation piles with U-tube circuits. Energy Build. 2017, 134, 259–270. [Google Scholar] [CrossRef]
- De Carli, M.; Tonon, M.; Zarrella, A.; Zecchin, R. A computational capacity resistance model (CaRM) for vertical ground-coupled heat exchangers. Renew. Energy 2010, 35, 1537–1550. [Google Scholar] [CrossRef]
- Franco, A.; Moffat, R.; Toledo, M.; Herrera, P. Numerical sensitivity analysis of thermal response tests (TRT) in energy piles. Renew. Energy 2016, 86, 985–992. [Google Scholar] [CrossRef]
- Park, H.; Lee, S.R.; Yoon, S.; Choi, J.C. Evaluation of thermal response and performance of PHC energy pile: Field experiments and numerical simulation. Appl. Energy 2013, 103, 12–24. [Google Scholar] [CrossRef]
- Cecinato, F.; Loveridge, F.A.; Gajo, A.; Powrie, W. A new modelling approach for piled and other ground heat exchanger applications. In Proceedings of the XVI European Conference on Soil Mechanics and Geotechnical Engineering 2015, Edinburgh, UK, 13–17 September 2015; ICE Institution of Civil Engineers: London, UK, 2015. [Google Scholar]
- Cecinato, F.; Loveridge, F.A. Influences on the thermal efficiency of energy piles. Energy 2015, 82, 1021–1033. [Google Scholar] [CrossRef]
- Loveridge, F.; Powrie, W.; Nicholson, D. Comparison of two different models for pile thermal response test interpretation. Acta Geotech. 2014, 9, 367–384. [Google Scholar] [CrossRef]
- Ozudogru, T.; Brettmann, T.; Guney Olgun, C.; Martin, I.J.; Senol, A. Thermal Conductivity Testing of Energy Piles: Field Testing and Numerical Modeling. In Proceedings of the GeoCongress 2012, State of the Art and Practice in Geotechnical Engineering, Oakland, CA, USA, 25–29 March 2012. [Google Scholar]
- Alberdi-Pagola, M.; Poulsen, S.E. Thermal response testing and performance of quadratic cross section energy piles (Vejle, Denmark). In Proceedings of the XVI European Conference on Soil Mechanics and Geotechnical Engineering 2015, Edinburgh, UK, 13–17 September 2015; ICE Institution of Civil Engineers: London, UK, 2015. [Google Scholar]
- Schulze-Makuch, D.; Carlson, D.A.; Cherkauer, D.S.; Malik, P. Scale Dependency of Hydraulic Conductivity in Heterogeneous Media. Water 1999, 37, 904–919. [Google Scholar] [CrossRef]
- Liebel, H.T.; Huber, K.; Frengstad, B.S.; Kalskin Ramstad, R.; Brattli, B. Rock core samples cannot replace thermal response tests—A statistical comparison based on thermal conductivity data from the Oslo Region (Norway). In Zero Emission Buildings, Proceedings of the Renewable Energy 682 Research Conference, Trondheim, Norway, 7–8 June 2010; Haase, M., Hestnes, A.G., Eds.; Renewable Energy Conference & Tapir Academic Press: Trondheim, Norway, 2010; pp. 145–154. [Google Scholar]
- Radioti, G. Shallow Geothermal Energy: Effect of In Situ Conditions on Borehole Heat Exchanger Design and Performance. Ph.D. Thesis, University of Liège, Liège, Belgium, 2016. [Google Scholar]
- Bouazza, A.; Wang, B.; Singh, R.M. Soil effective thermal conductivity from energy pile thermal tests. In Coupled Phenomena in Environmental Geotechnics, Proceedings of the International Symposium, Torino, Italy, 1–3 July 2013; Taylor & Francis: London, UK, 2013; pp. 211–219. [Google Scholar]
- Murphy, K.D.; Mccartney, J.S.; Henry, K.S. Impact of horizontal run-out length on the thermal response of full-scale energy foundations. In Geo-Congress 2014 Technical Papers: Geo-Characterization and Modeling for Sustainability; ASCE: Reston, VA, USA, 2014; pp. 2715–2724. [Google Scholar]
- Hemmingway, P.; Long, M. Energy piles: Site investigation and analysis. In Proceedings of the Institution of Civil Engineers—Geotechnical Engineering; ICE publishing: London, UK, 2013; Volume 166, pp. 561–575. [Google Scholar]
- Badenes, B.; de Santiago, C.; Nope, F.; Magraner, T.; Urchueguia, J.; de Groot, M.; Pardo de Santayana, F.; Arcos, J.L.; Martin, F. Thermal characterization of a geothermal precast pile in Valencia (Spain). In Proceedings of the European Geothermal Congress 2016, Strasbourg, France, 19–24 September 2016. [Google Scholar]
- Zhang, Y.; Gao, P.; Yu, Z.; Fang, J.; Li, C. Characteristics of ground thermal properties in Harbin, China. Energy Build. 2014, 69, 51–259. [Google Scholar] [CrossRef]
- Beier, R.A.; Smith, M.D.; Spitler, J.D. Reference data sets for vertical boreholes ground heat exchanger models and thermal response tests analysis. Geothermics 2011, 40, 79–85. [Google Scholar] [CrossRef]
- Graham, J. The 2003 R.M. Hardy Lecture: Soil parameters for numerical analysis in clay. Can. Geotech. J. 2006, 43, 187–209. [Google Scholar] [CrossRef]
- Dong, Y.; McCartney, J.S.; Lu, N. Critical review of thermal conductivity models for unsaturated soils. Geotech. Geol. Eng. 2015, 33, 207–221. [Google Scholar]
- Allani, M.; Van Lysebetten, G.; Huybrechts, N. Experimental and numerical study of the thermo-mechanical behaviour of energy piles for Belgian practice. In Advances in Laboratory Testing and Modelling of Soils and Shales (ATMSS), 1st ed.; Ferrari, A., Laloui, L., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 405–412. ISBN 978-3-319-52773-4. [Google Scholar]
- Sanner, B. Overview of shallow geothermal systems. In Geotrainet Training Manual for Designers of Shallow Geothermal Systems; McCorry, M., Jones, G.L.L., Eds.; European Federation of Geologists: Brussels, Belgium, 2011; pp. 7–14. [Google Scholar]
- Morpher-Busch, L. Instructions for Using the Thermomap Viewer. 2013. Available online: http://geoweb2.sbg.ac.at/thermomap/Instruction_Manual_Map_Viewer.pdf (accessed on 20 Febuary 2017).
- Cérmak, V.; Rybach, L. Thermal conductivity and specific heat of minerals and rock. In Geophysics—Physical Properties of Rocks, Landolt-Bornstein Numerical Data and Functional Relationships in Science and Technology; New Series, Group V; Springer: Berlin, Germany, 1982; pp. 305–343. [Google Scholar]
- Yavari, N.; Tang, M.; Pereira, J.M.; Hassen, G. Effect of temperature on the shear strength of soils and the soil–structure interface. Can. Geotech. J. 2016, 53, 1186–1194. [Google Scholar] [CrossRef]
- Eriksson, L. Temperature effects on consolidation properties of sulphide clays. In Proceedings of the 12th International Conference on Soil Mechanics and Foundation Engineering, Rio de Janeiro, Brazil, 13–18 August 1989; Taylor & Francis: Rotterdam, The Netherlands, 1989. [Google Scholar]
- Leroueil, S.; Marques, M.E.S. Importance of strain rate and temperature effects in geotechnical engineering. In Measuring and Modelling Time Dependent Soil Behaviour; Geotechnical Special Publication (Book 61); Sheahan, T.C., Kaliakin, V.N., Eds.; American Society of Civil Engineers: New York, NY, USA, 1996. [Google Scholar]
- Vardoulakis, I. Dynamic thermo-poro-mechanical analysis of catastrophic landslides. Géotechnique 2002, 52, 151–171. [Google Scholar] [CrossRef]
- Cecinato, F.; Zervos, A.; Veveakis, E. A thermomechanical model for the catastrophic collapse of large landslides. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 1507–1535. [Google Scholar] [CrossRef]
- Cecinato, F.; Zervos, A. Influence of thermomechanics in the catastrophic collapse of planar landslides. Can. Geotech. J. 2012, 49, 207–225. [Google Scholar] [CrossRef]
- Alonso, E.E.; Zervos, A.; Pinyol, N.M. Thermo-poro-mechanical analysis of landslides: From creeping behaviour to catastrophic failure. Géotechnique 2015, 66, 202–219. [Google Scholar] [CrossRef]
- Rice, J. Heating and weakening of faults during earthquake slip. J. Geophys. Res. 2006, 111, B5. [Google Scholar] [CrossRef]
- Sulem, J.; Lazar, P.; Vardoulakis, I. Thermo-PoroMechanical Properties of Clayey Gouge and Application to Rapid Fault Shearing. Int. J. Num. Anal. Meth. Geomech. 2007, 31, 523–540. [Google Scholar] [CrossRef]
- Filimonov, M.; Vaganova, N. Simulation of thermal stabilization of soil around various technical systems operating in permafrost. Appl. Math. Sci. 2013, 7, 7151–7160. [Google Scholar] [CrossRef]
- Uzer, A. Evaluation of Freezing-Thawing Cycles for Foundation Soil Stabilization. Soil Mech. Found. Eng. 2016, 53, 202–209. [Google Scholar] [CrossRef]
- Makusa, G.; Mácsik, J.; Holm, G.; Knutsson, S. Laboratory test study on the effect of freeze–thaw cycles on strength and hydraulic conductivity of high water content stabilized dredged sediments. Can. Geotech. J. 2016, 53, 1038–1045. [Google Scholar] [CrossRef]
- Maranha, J.; Pereira, C.; Vieira, A. Thermo-Viscoplastic Subloading Soil Model for Isotropic Stress and Strain Conditions. In Advances in Laboratory Testing and Modelling of Soils and Shales (ATMSS), 1st ed.; Ferrari, A., Laloui, L., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 405–412. ISBN 978-3-319-52773-4. [Google Scholar]
- Hueckel, T.; Pellegrini, R. Thermoplastic modelling of undrained failure of saturated clay due to heating. Soils Found. 1991, 31, 1–16. [Google Scholar] [CrossRef]
- Laloui, L.; Cekerevac, C. Thermo-plasticity of clays: An isotropic yield mechanism. Comput. Geotech. 2003, 30, 649–660. [Google Scholar] [CrossRef]
- Vieira, A.; Maranha, J.R. Thermoplastic analysis of a thermoactive pile in a normally consolidated Clay. Int. J. Geomech. 2017, 17, 04016030. [Google Scholar] [CrossRef]
- Mitchell, J.K. Fundamentals of Soil Behavior, 2nd ed.; Wiley InterScience: New York, NY, USA, 1993; p. 592. ISBN 978-0-471-46302-3. [Google Scholar]
- Laloui, L.; Di Donna, A. Understanding the behaviour of energy geo-structures. In Proceedings of the Institution of Civil Engineers ICE—Civil Engineering; Institution of Civil Engineers: London, UK, 2011; Volume 164, pp. 184–191. [Google Scholar]
- Bourne-Webb, P. Observed response of energy geostructures. In Energy geostructures: Innovation in underground Engineering; Laloui, L., Di Donna, A., Eds.; Wiley: Hoboken, NJ, USA; ISTE: London, UK, 2013; pp. 45–77. ISBN 978-1-84821-572-6. [Google Scholar]
- Cekerevac, C. Thermal Effects on the Mechanical Behaviour of Saturated Clays: An Experimental and Constitutive Study. Ph.D. Thesis, École Polytechnique Federal de Lausanne, Lausanne, Switzerland, 2003. [Google Scholar]
- Di Donna, A.; Laloui, L. Response of soil subjected to thermal cyclic loading: Experimental and constitutive study. Eng. Geol. 2015, 190, 65–76. [Google Scholar] [CrossRef]
- Gens, A. Soil-environment interactions in geotechnical engineering. Géotechnique 2010, 60, 3–74. [Google Scholar] [CrossRef]
- François, B.; Laloui, L. ACMEG-TS: A constitutive model for unsaturated soils under non-isothermal conditions. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1955–1988. [Google Scholar] [CrossRef]
- Bolzon, G.; Schrefler, B. Thermal effects in partially saturated soils: A constitutive model. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 861–877. [Google Scholar] [CrossRef]
- Voight, B.; Faust, C. Frictional heat and strength loss in some rapid landslides. Géotechnique 1982, 32, 43–54. [Google Scholar] [CrossRef]
- Vardoulakis, I. Catastrophic landslides due to frictional heating of the failure plane. Mech. Cohesive-Frict. Mater. 2000, 5, 443–467. [Google Scholar] [CrossRef]
- Laloui, L.; Francois, B. ACMEG-T: Soil thermoplasticity model. J. Eng. Mech. 2009, 135, 932–944. [Google Scholar] [CrossRef]
- Robinet, J.C.; Pasquiou, A.; Jullien, A.; Belanteur, N.; Plas, F. Expériences de laboratoire sur le comportement thermo-hydro-mécanique de matériaux argileux remaniés gonflants et non gonflants. Revue Française de Géotechnique 1997, 81, 53–80. [Google Scholar] [CrossRef]
- Burghignoli, A.; Desideri, A.; Miliziano, S. A laboratory study on the thermomechanical behaviour of clayey soils. Can. Geotech. J. 2000, 37, 764–780. [Google Scholar] [CrossRef]
- Stewart, M.A.; MacCartney, J.S. Centrifuge Modeling of Soil-Structure Interaction in Energy Foundations. J. Geotech. Geoenviron. Eng. 2013, 140. [Google Scholar] [CrossRef]
- Graham, J.; Tanaka, N.; Crilly, T.; Alfaro, M. Modified Cam-Clay modelling of temperature effects in clays. Can. Geotech. J. 2001, 38, 608–621. [Google Scholar] [CrossRef]
- Hueckel, T.; François, B.; Laloui, L. Explaining thermal failure in saturated clays. Géotechnique 2009, 59, 197–212. [Google Scholar] [CrossRef]
- Abuel-Naga, M.; Bergado, T.; Bouazza, A. Thermally induced volume change and excess pore water pressure of soft Bangkok clay. Eng. Geol. 2007, 89, 144–154. [Google Scholar] [CrossRef]
- Hueckel, T.; Pellegrini, R.; Del Olmo, C. A constitutive study of thermo-elasto-plasticity of deep carbonatic clays. Int. J. Numer. Anal. Methods Geomech. 1998, 22, 549–574. [Google Scholar] [CrossRef]
- Baldi, G.; Hueckel, T.; Peano, A.; Pellegrini, R. Developments in Modelling of Thermo-Hydro-Geomechanical Behaviour of Boom Clay and Clay-Based Buffer Materials; Report 13365/2 EN; Commission of European Communities: Brussels, Belgium, 1991.
- Towhata, I.; Kuntiwattanakul, P.; Seko, I.; Ohishi, K. Volume change of clays induced by heating as observed in consolidation tests. Soils Found. 1993, 33, 170–183. [Google Scholar] [CrossRef]
- Plum, R.L.; Esrig, M.I. Some Temperature Effects on Soil Compressibility and Pore Water Pressure; Highway Research Board Special Report 103; Highway Research Board: Washington, DC, USA, 1969; pp. 231–242. [Google Scholar]
- Demars, K.R.; Charles, R.D. Soil volume changes induced by temperature cycling. Can. Geotech. J. 1982, 19, 188–194. [Google Scholar] [CrossRef]
- Sultan, N.; Delage, P.; Cui, Y.J. Temperature effects on the volume change behavior of Boom clay. Eng. Geol. 2002, 64, 135–145. [Google Scholar] [CrossRef]
- Abuel-Naga, H.M.; Bergado, D.T.; Soralump, S.; Rujicipat, P. Thermal consolidation of soft Bangkok clay. Int. J. Lowl. Technol. 2005, 17, 13–22. [Google Scholar]
- Baldi, G.; Hueckel, T.; Pellegrini, R. Thermal volume changes of the mineral-water system in low-porosity clay soils. Can. Geotech. J. 1988, 25, 807–825. [Google Scholar] [CrossRef]
- Di Donna, A.; Ferrari, A.; Laloui, L. Experimental investigation of the soil-concrete interface: Physical mechanisms, cyclic mobilisation and behaviour at different temperatures. Can. Geotech. J. 2015, 53, 659–672. [Google Scholar] [CrossRef]
- Marques, M.E. Influence of Strain RATE and Temperature in Natural Clays Compaction. Master’s Thesis, Université Laval, Laval, QC, Canada, 1996. (In Portuguese). [Google Scholar]
- Boudali, M.; Leroueil, S.; Srinivasa Murthy, B.R. Viscous behaviour of natural clays. In Proceedings of the 13th International Conference Soil Mechanics and Foundation Engineering ICSMFE, New Delhi, India, 5–10 January 1994. [Google Scholar]
- Di Donna, A.; Laloui, L. Soil response under the thermo mechanical conditions imposed by energy geostructures. In Energy Geostructures: Innovation in Underground Engineering; Laloui, L., Di Donna, A., Eds.; Wiley: Hoboken, NJ, USA; ISTE: London, UK, 2013; pp. 45–77. ISBN 978-1-84821-572-6. [Google Scholar]
- Laloui, L.; Cekerevac, C.; Francois, B. Constitutive modelling of the thermo-plastic behaviour of soils. Eur. J. Environ. Civ. Eng. 2005, 9, 635–650. [Google Scholar]
- Kuntiwattanakul, P. Effect of High Temperature on Mechanical Behaviour of Clays. Ph.D. Thesis, University of Tokyo, Tokyo, Japan, 1991. [Google Scholar]
- Standard Test Method for Calculating Thermal Diffusivity of Rock and Soil; ASTM D4612–16; ASTM International: West Conshohocken, PA, USA, 2016. [CrossRef]
- Swiss Federal Office of Energy (BFE). Innovative Improvements of Thermal Response Tests; Final Report Project 101-690; BFE: Ittigen, Switzerland, 2008; 68p. [Google Scholar]
- Amis, A.; Bourne-Webb, P.; Amatya, B.; Soga, K.; Davidson, C. The effects of heating and cooling energy piles under working load at Lambeth College. In Proceedings of the 33rd Annual and 11th International DFI Conference, New York, NY, USA, 15–17 October 2008. [Google Scholar]
- Lennon, D.J.; Watt, E.; Suckling, T.P. Energy piles in Scotland. In Proceedings of the 5th International Confernence on Deep Foundations on Bored and Auger Piles, Ghent, Belgium, 20 August 2008; Van Impe, W.F., Van Impe, P., Eds.; Taylor & Francis Group: London, UK, 2009. [Google Scholar]
- Brettman, T.P.E.; Amis, T.; Kapps, M. Thermal conductivity analysis of geothermal energy piles. In Proceedings of the 2010 Geotechnical Challenges in Urban Regeneration Conference, London, UK, 26–28 May 2010. [Google Scholar]
- Abdelaziz, S.L.A.M. Deep Energy Foundations: Geotechnical Challenges and Design Considerations. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, Virginia, February 2013. [Google Scholar]
- Loveridge, F.; Olgun, C.G.; Brettmann, T.; Powrie, W. The Thermal Behaviour of Three Different Auger Pressure Grouted Piles Used as Heat Exchangers. Geotech. Geol. Eng. 2014, 33, 1–17. [Google Scholar] [CrossRef]
- Baycan, S.; Haberfield, C.; Chapman, G.; Wang, B.; Bouazza, A.; Singh, R.; Barry-Macaulay, D. Field investigation of a geothermal energy pile: Initial observations. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013. [Google Scholar]
- You, S.; Cheng, X.; Guo, H.; Yao, Z. In-situ experimental study of heat exchange capacity of CFG pile geothermal exchangers. Energy Build. 2014, 79, 23–31. [Google Scholar] [CrossRef]
- Murphy, K.D.; McCartney, J.S.; Henry, K.S. Evaluation of thermo-mechanical and thermal behavior of full-scale energy foundations. Acta Geotech. 2014, 10, 179–195. [Google Scholar] [CrossRef]
- Yu, K.; Singh, R.; Bouazza, A.; Bui, H. Determining soil thermal conductivity through numerical simulation of a heating test on a heat exchanger pile. Geotech. Geol. Eng. 2015, 33, 239–252. [Google Scholar] [CrossRef]
- Carlsson, S. Energipålar-Termiskt Responstest på Prefabricerad Energipåle i Betong. Master’s Thesis, Lund University, Lund, Sweden, 2015. [Google Scholar]
- Ronchi, F.; Salciarini, D.; Cavalagli, N.; Tamagnini, C. Numerical Model of Energy Foundation Behavior: The Prototype of a Geothermal Micro-pile. Procedia Eng. 2016, 158, 326–331. [Google Scholar] [CrossRef]
- Middleton, M.F. A transient method of measuring the thermal properties of rocks. Geophysics 1993, 58, 357–365. [Google Scholar] [CrossRef]







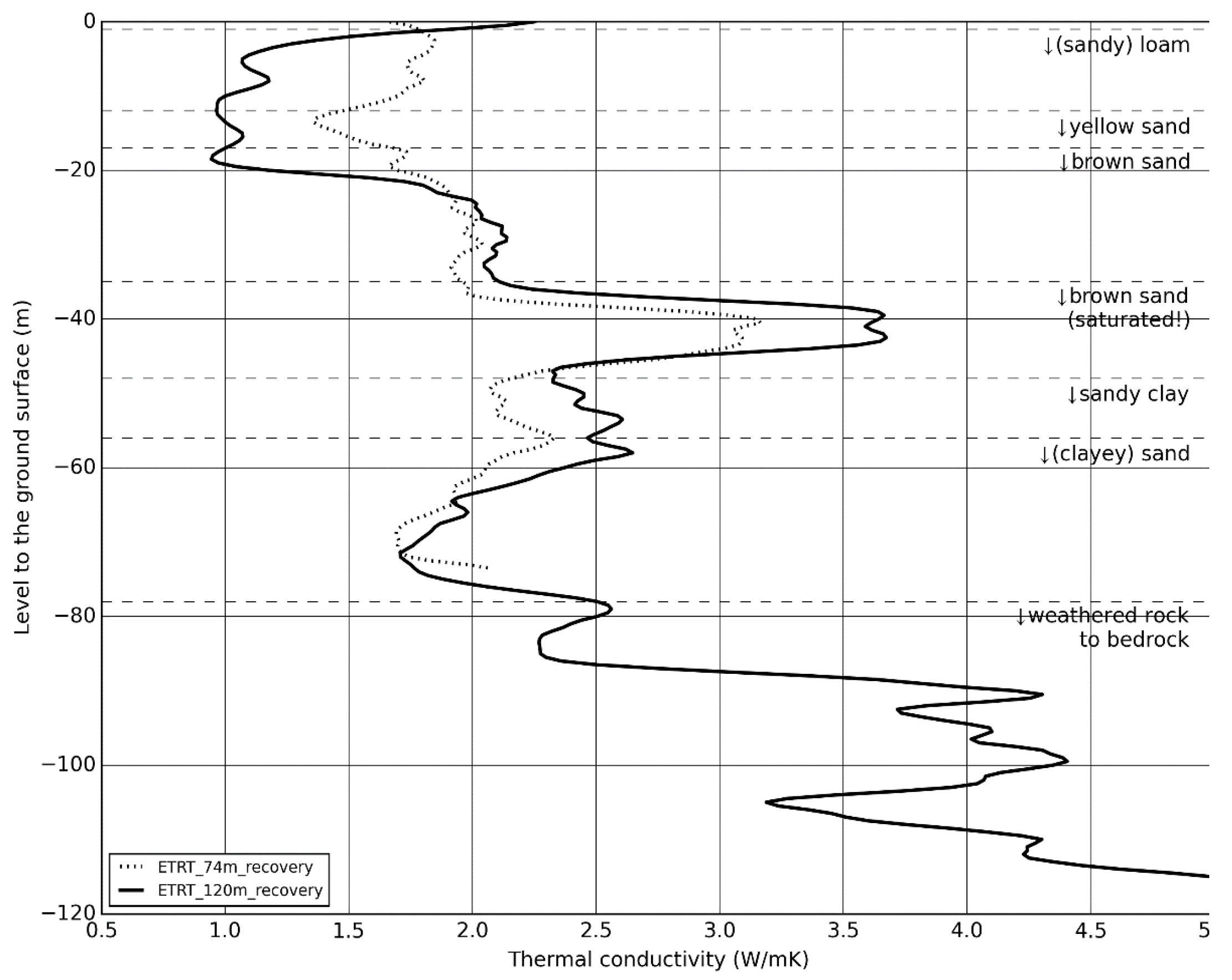
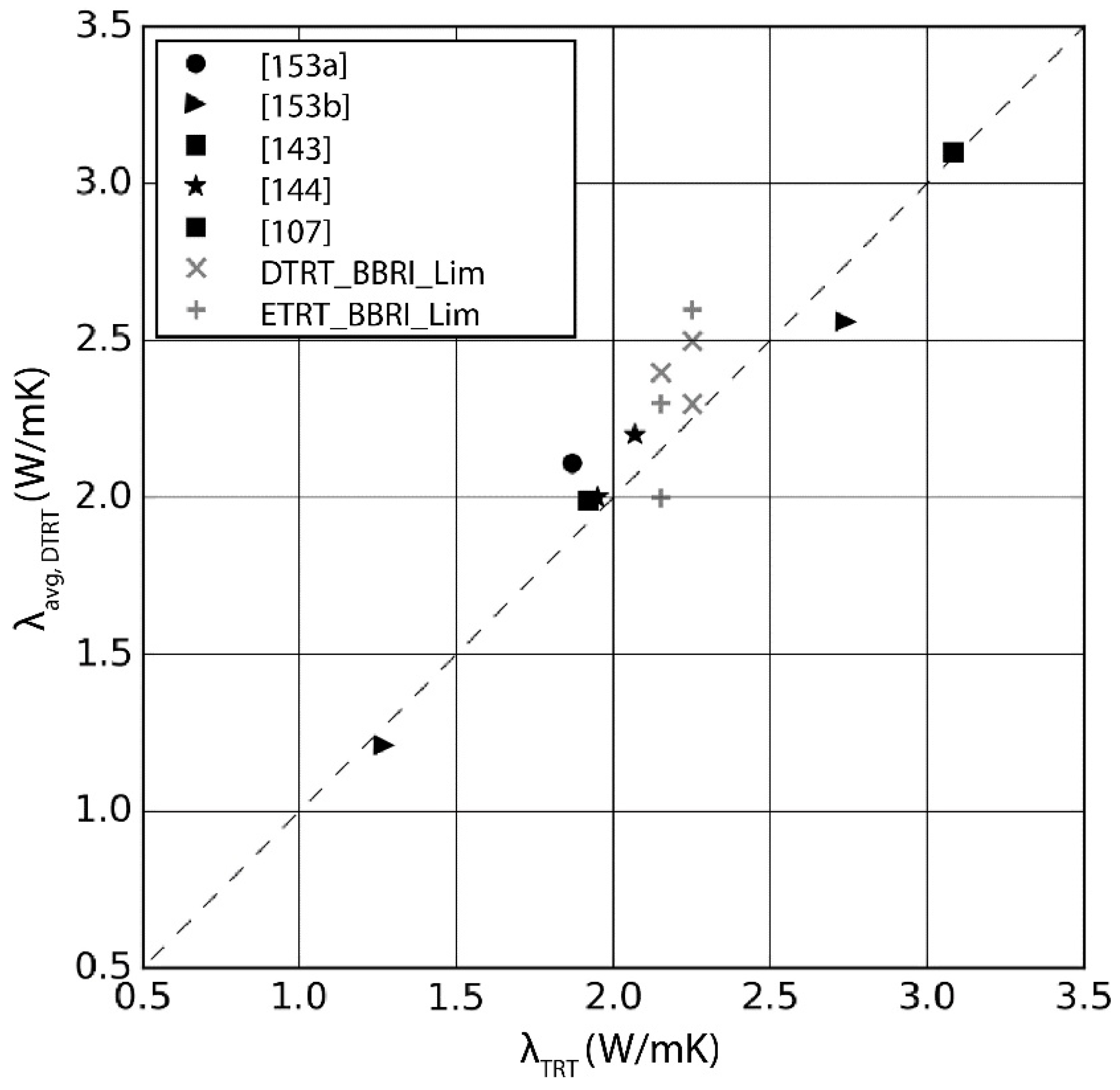
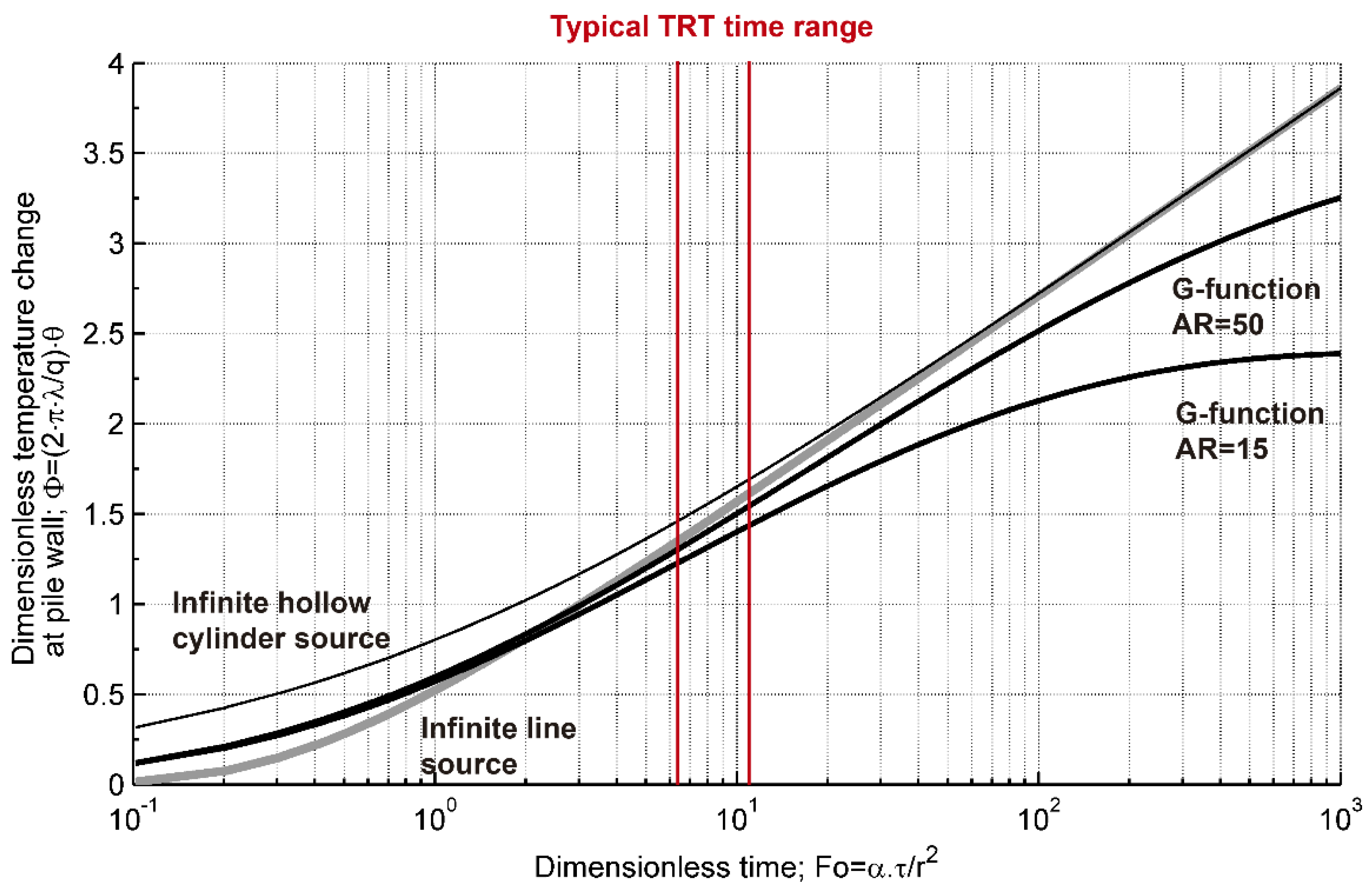
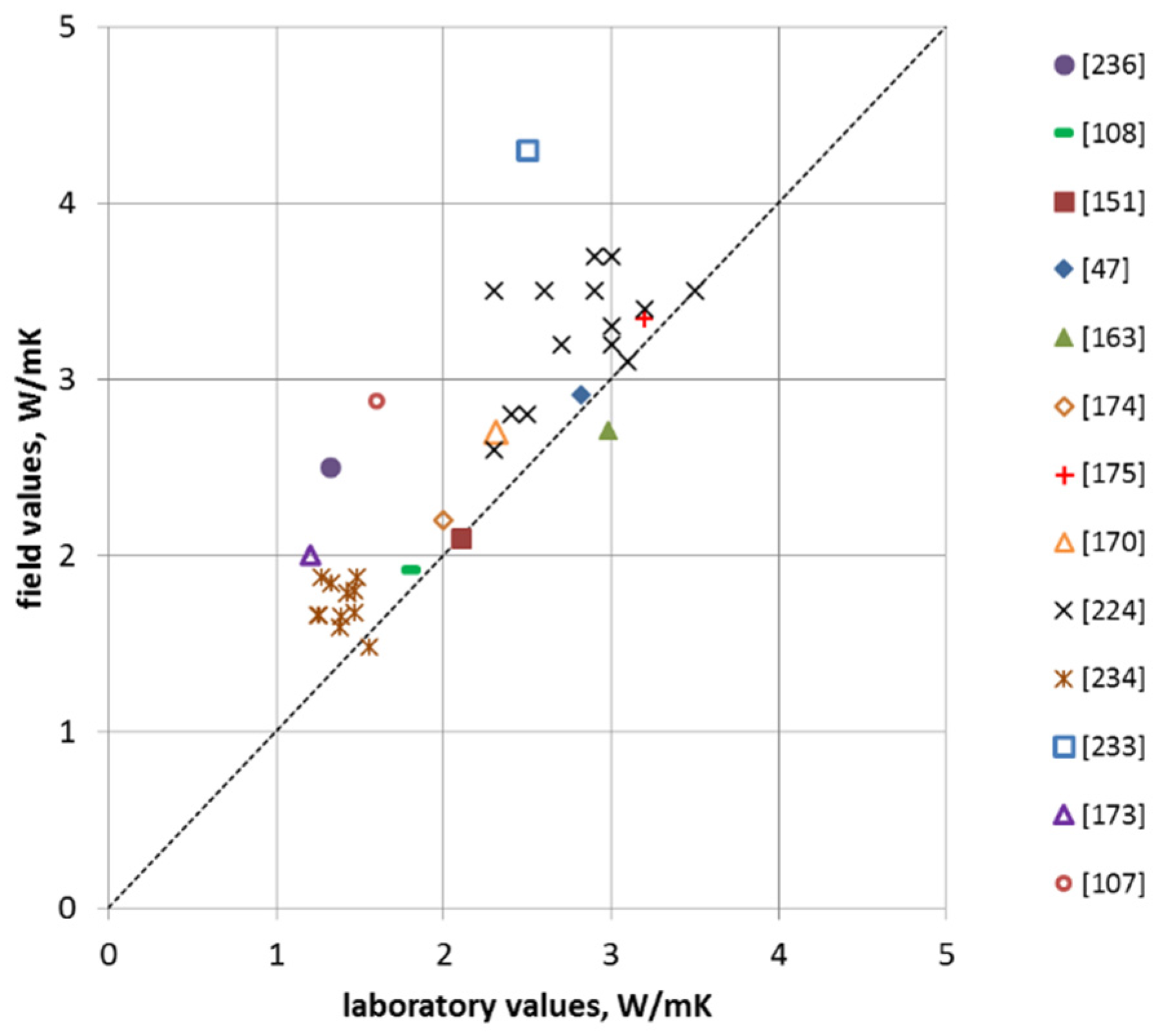
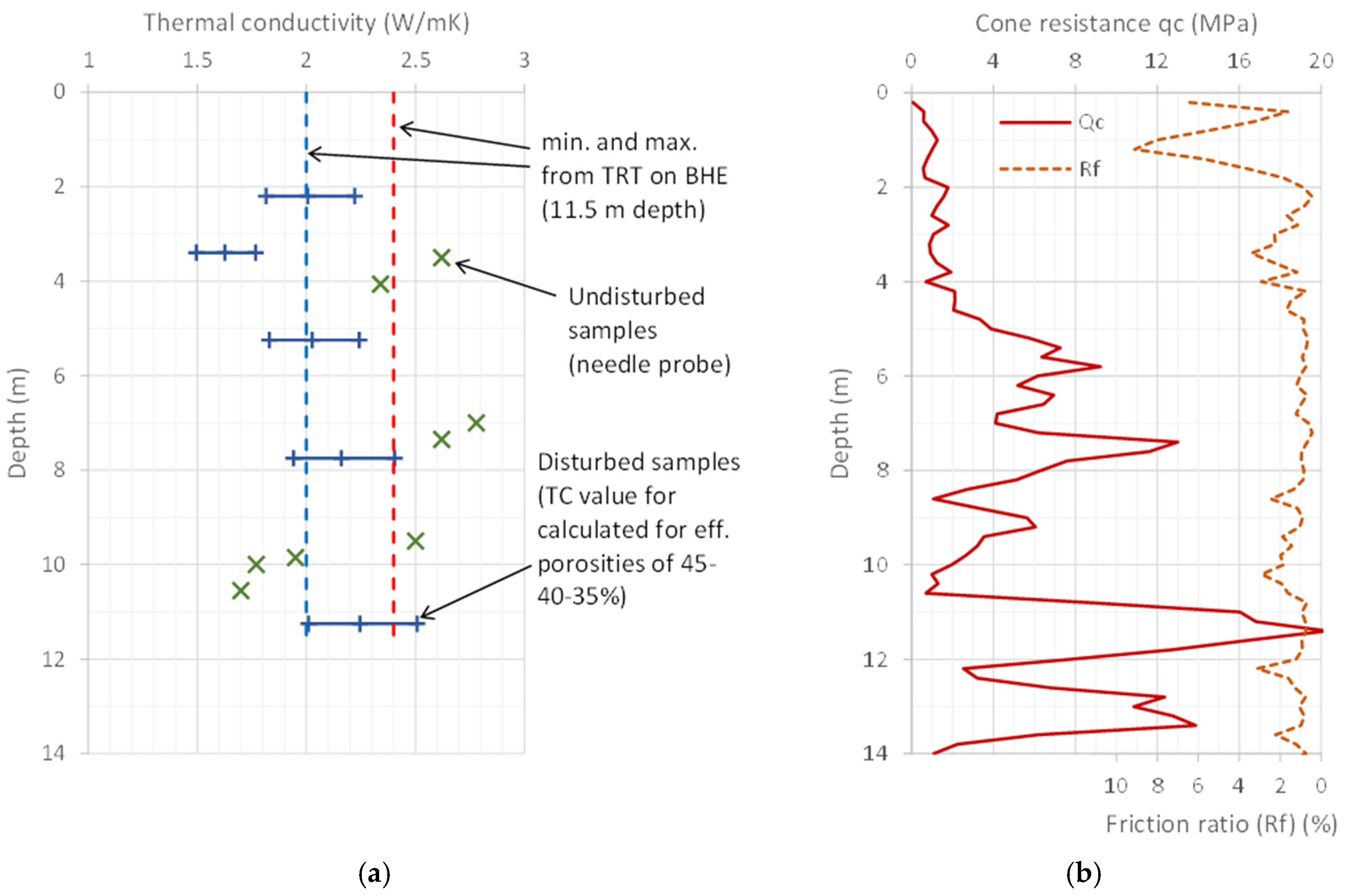
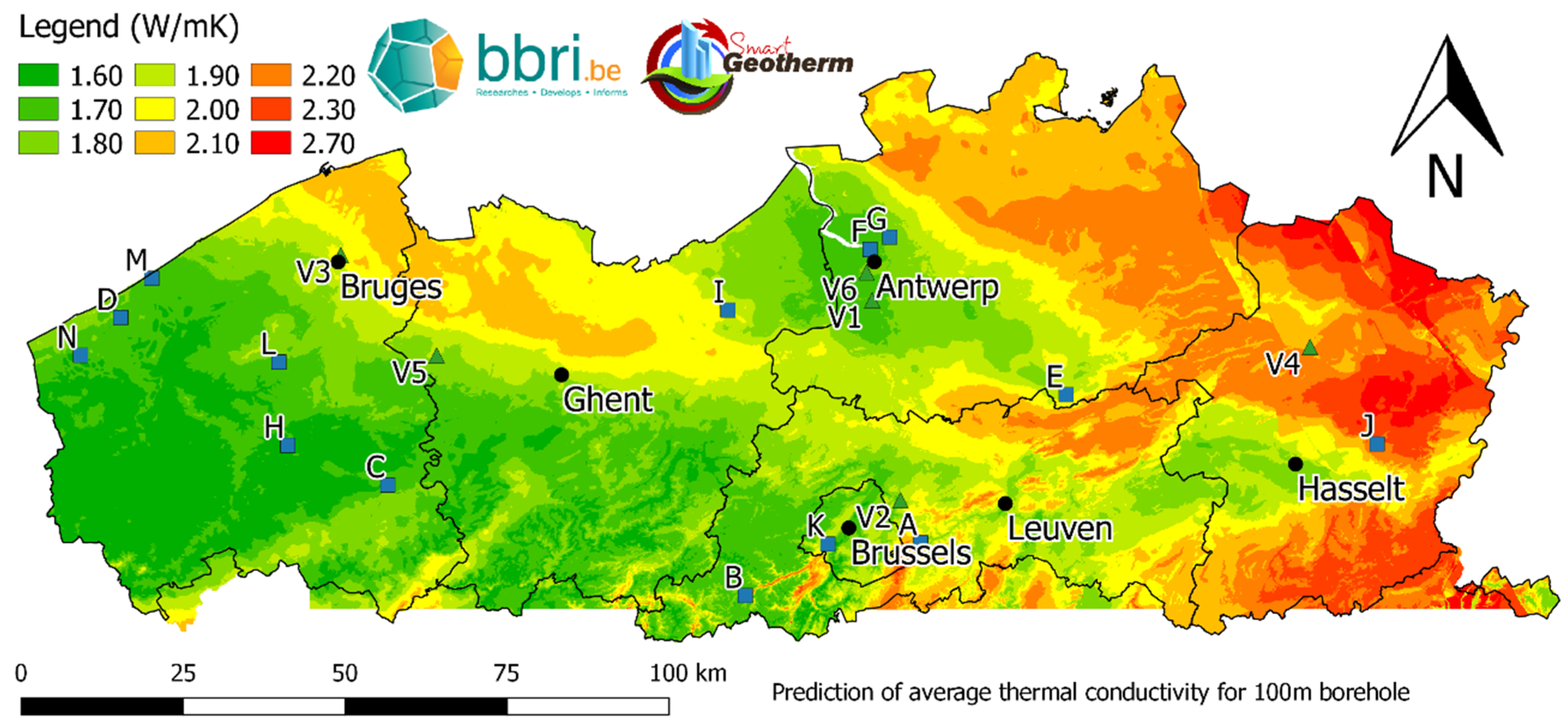
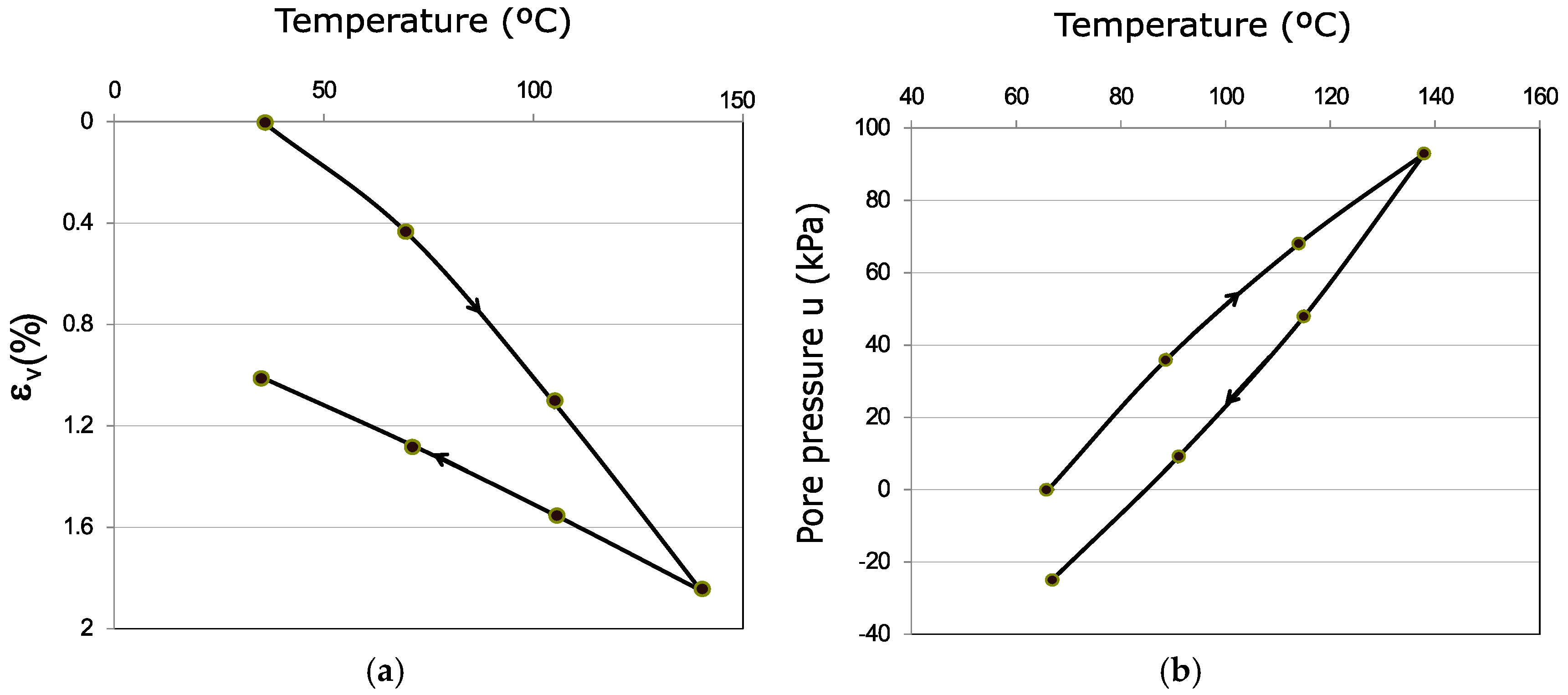
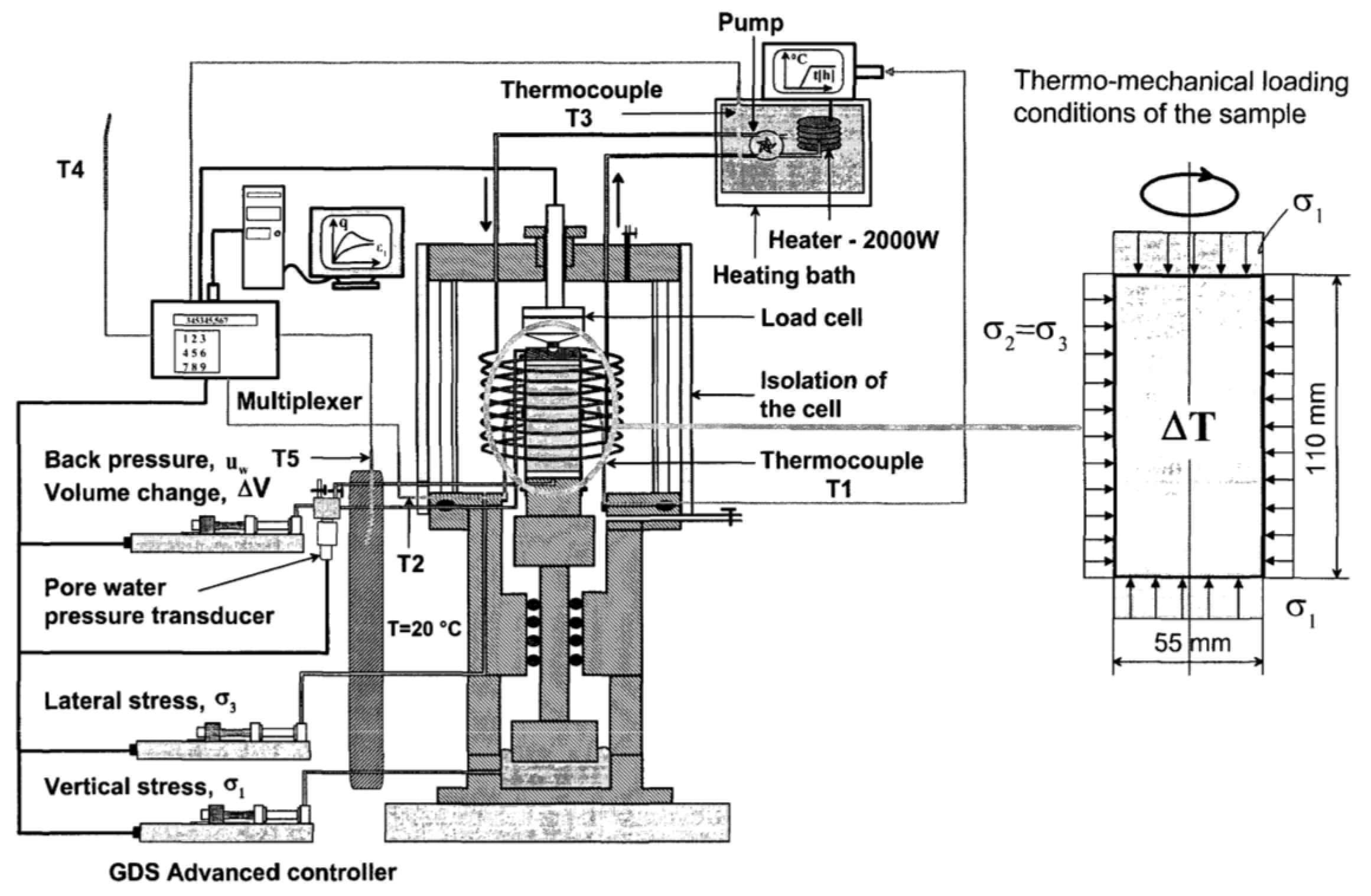

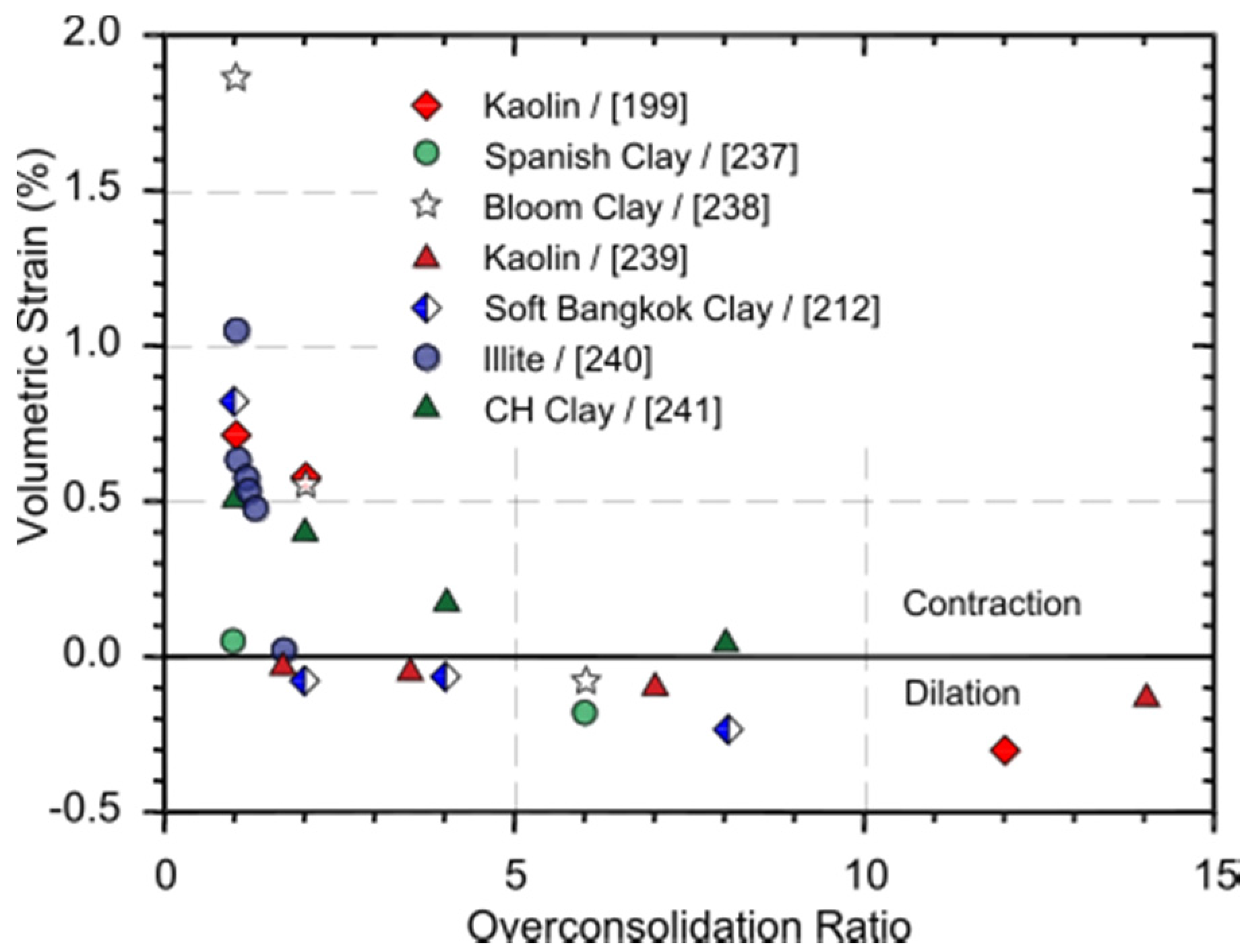
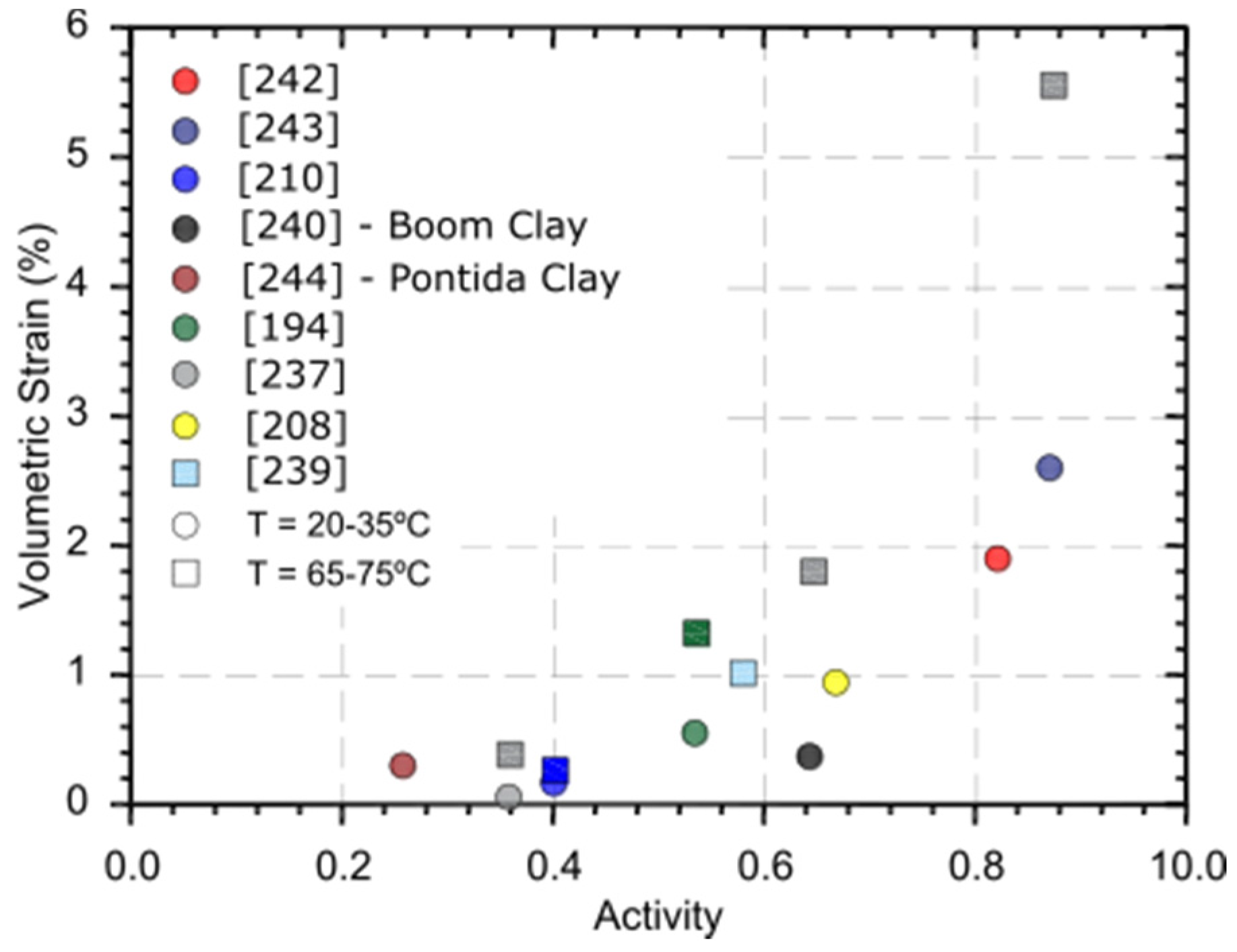
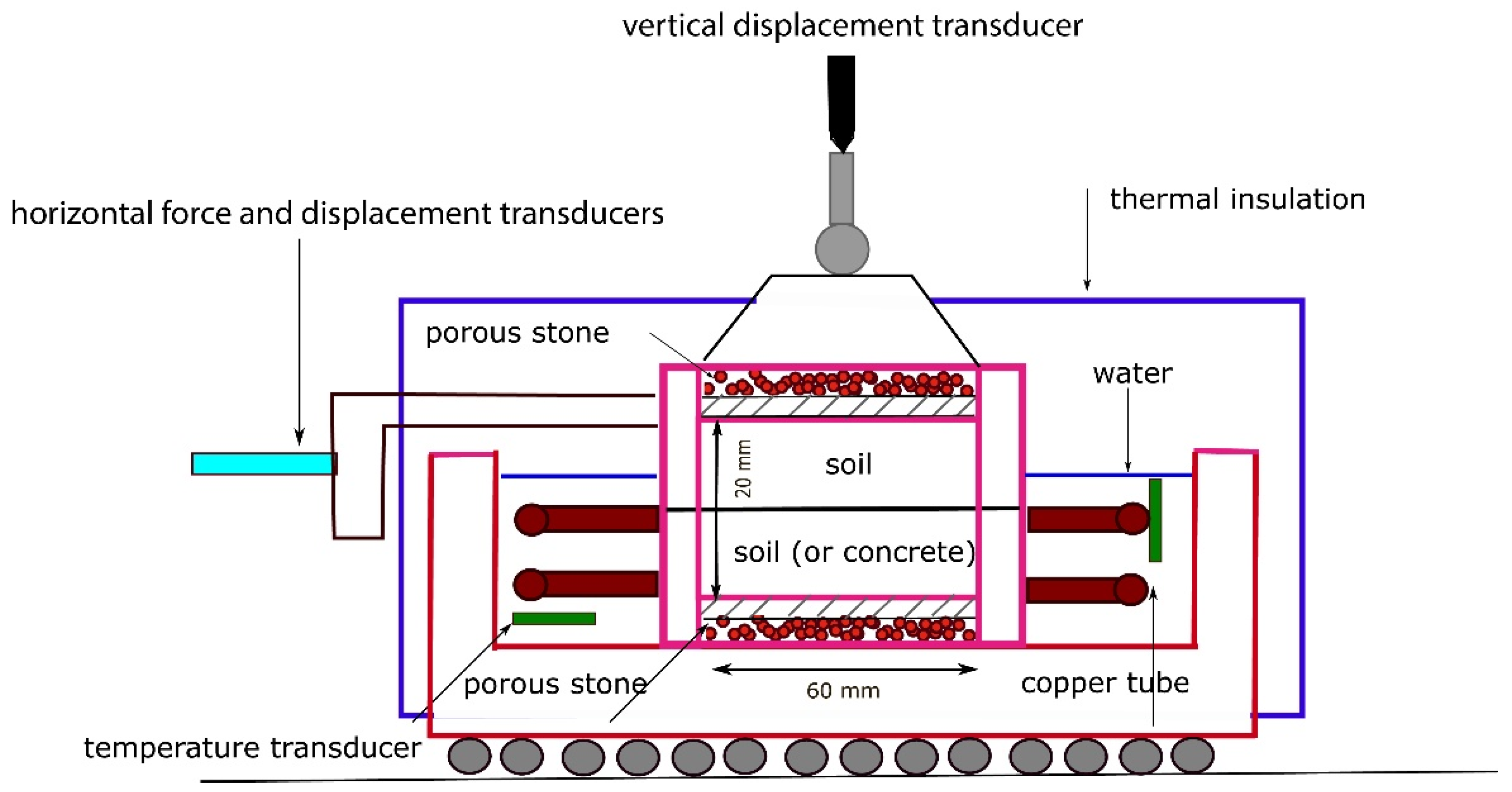
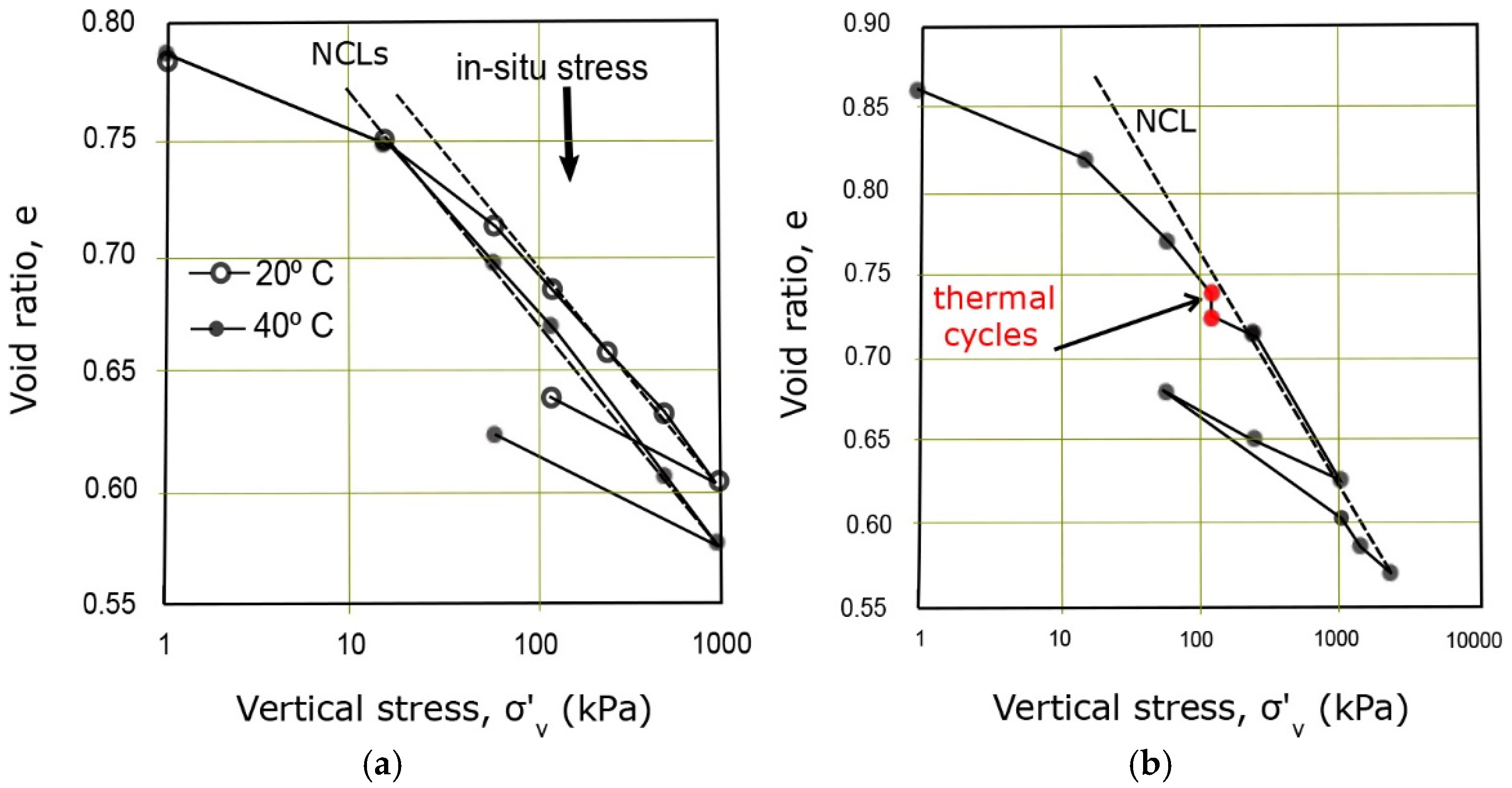
| Parameter | Borehole 74-m-Deep | Borehole 120-m-Deep | ||
|---|---|---|---|---|
| Standard TRT | Enhanced TRT | Standard TRT | Enhanced TRT | |
| Injected power | 53 W/m | 28 W/m | 56 W/m | 23.1 W/m |
| Flow rate | 0.26 l/s | - | 0.25 l/s | - |
| Heating phase duration | 136 h | 84 h | 117 h | 96 h |
| Recovery phase duration | - | 60 h | - | 124 h |
| Average thermal conductivity | 2.1–2.2 W·m−1·K−1 | 2.0 W·m−1·K−1 | 2.2–2.3 W·m−1·K−1 | 2.6 W·m−1·K−1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vieira, A.; Alberdi-Pagola, M.; Christodoulides, P.; Javed, S.; Loveridge, F.; Nguyen, F.; Cecinato, F.; Maranha, J.; Florides, G.; Prodan, I.; et al. Characterisation of Ground Thermal and Thermo-Mechanical Behaviour for Shallow Geothermal Energy Applications. Energies 2017, 10, 2044. https://doi.org/10.3390/en10122044
Vieira A, Alberdi-Pagola M, Christodoulides P, Javed S, Loveridge F, Nguyen F, Cecinato F, Maranha J, Florides G, Prodan I, et al. Characterisation of Ground Thermal and Thermo-Mechanical Behaviour for Shallow Geothermal Energy Applications. Energies. 2017; 10(12):2044. https://doi.org/10.3390/en10122044
Chicago/Turabian StyleVieira, Ana, Maria Alberdi-Pagola, Paul Christodoulides, Saqib Javed, Fleur Loveridge, Frederic Nguyen, Francesco Cecinato, João Maranha, Georgios Florides, Iulia Prodan, and et al. 2017. "Characterisation of Ground Thermal and Thermo-Mechanical Behaviour for Shallow Geothermal Energy Applications" Energies 10, no. 12: 2044. https://doi.org/10.3390/en10122044
APA StyleVieira, A., Alberdi-Pagola, M., Christodoulides, P., Javed, S., Loveridge, F., Nguyen, F., Cecinato, F., Maranha, J., Florides, G., Prodan, I., Van Lysebetten, G., Ramalho, E., Salciarini, D., Georgiev, A., Rosin-Paumier, S., Popov, R., Lenart, S., Erbs Poulsen, S., & Radioti, G. (2017). Characterisation of Ground Thermal and Thermo-Mechanical Behaviour for Shallow Geothermal Energy Applications. Energies, 10(12), 2044. https://doi.org/10.3390/en10122044








