2. Fennoscandia Basement Wellbore Temperature Events at 1.5 km
Geothermal heat energy extracted from Fennoscandia basement rock can replace the current fossil-fuel demand made by the several hundred district heating plants supplying hot water to as many as a million homes throughout Finland. For Fennoscandia basement with geothermal gradient ~19 °C/km, supply of significant geothermal energy to district heating plants requires EGS couplets at depths ~5–7 km. At a district heating plant in Espoo, immediately west of Helsinki, a 2 km deep 100 mm diameter pilot well, OTN1, was drilled, cored, and logged in advance of deeper drilling. Currently, two adjacent 305 mm diameter wellbores, OTN2 and OTN3, now reach 3.3 and 5.5 km depths.
Pilot well OTN1 logs are observed to follow the power-spectral trend (i), and core poroperm properties for twenty core samples from depth intervals at 300 m and 1300 m follow poroperm spatial correlation (ii). Well-core porosity is typically less than 1%, and permeability of order 1–10 μD (10
−18–10
−17 m
2). As discussed below, the empirical poroperm relation κ(x,y,z) ∝ exp(αφ(x,y,z)) valid for the measured value of α ~ 500 for OTN1 is similar to values found for porosity-permeability data from the KTB well and the Borrowdale volcanics at the UK Sellafield nuclear facility. This discussion places OTN1 well-log spatial fluctuation and well-core poroperm data in a wider basement rock context provided by KTB, Fennoscandia and UK Nirex metamorphic basement rock data [
24,
25,
26,
27,
28].
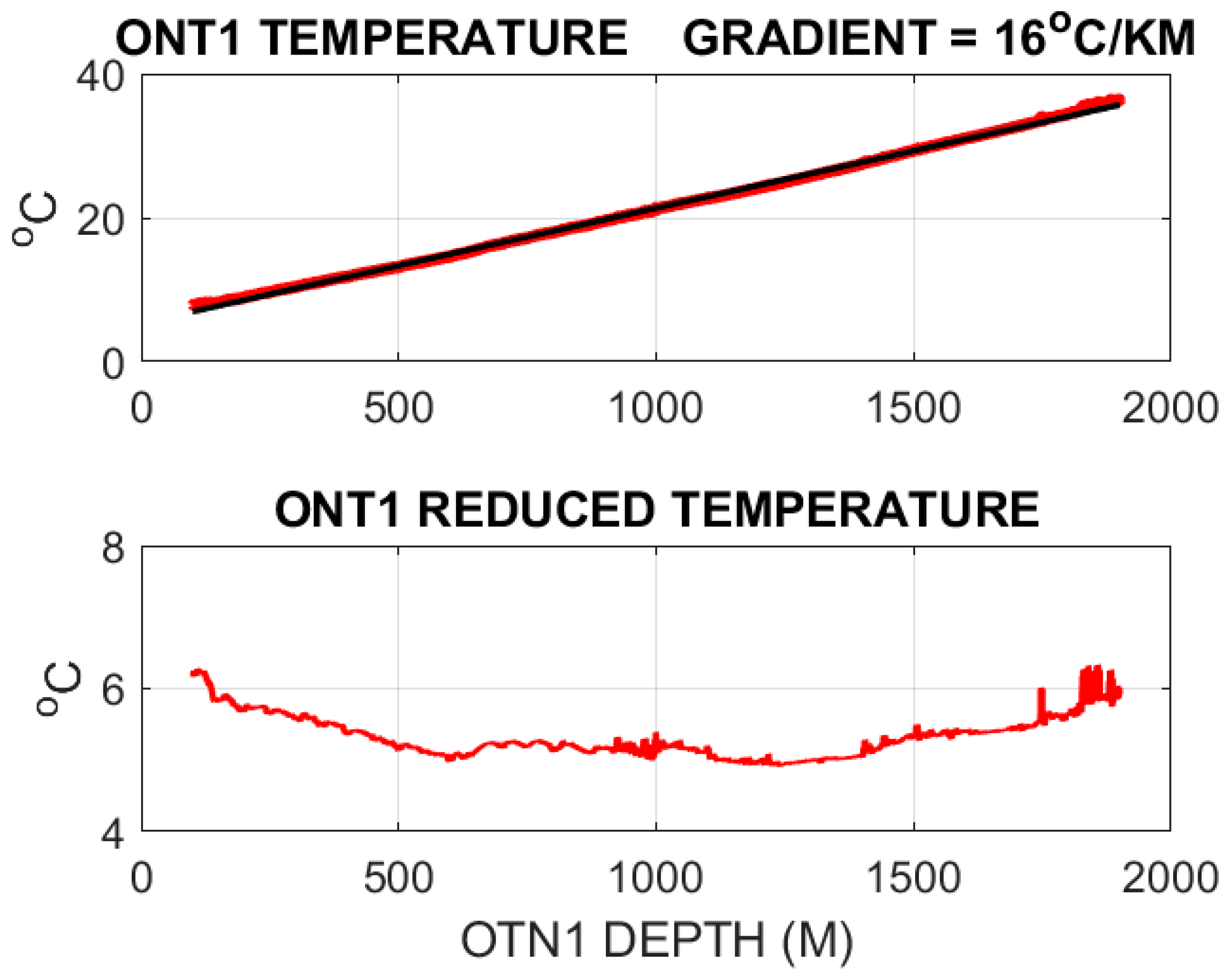
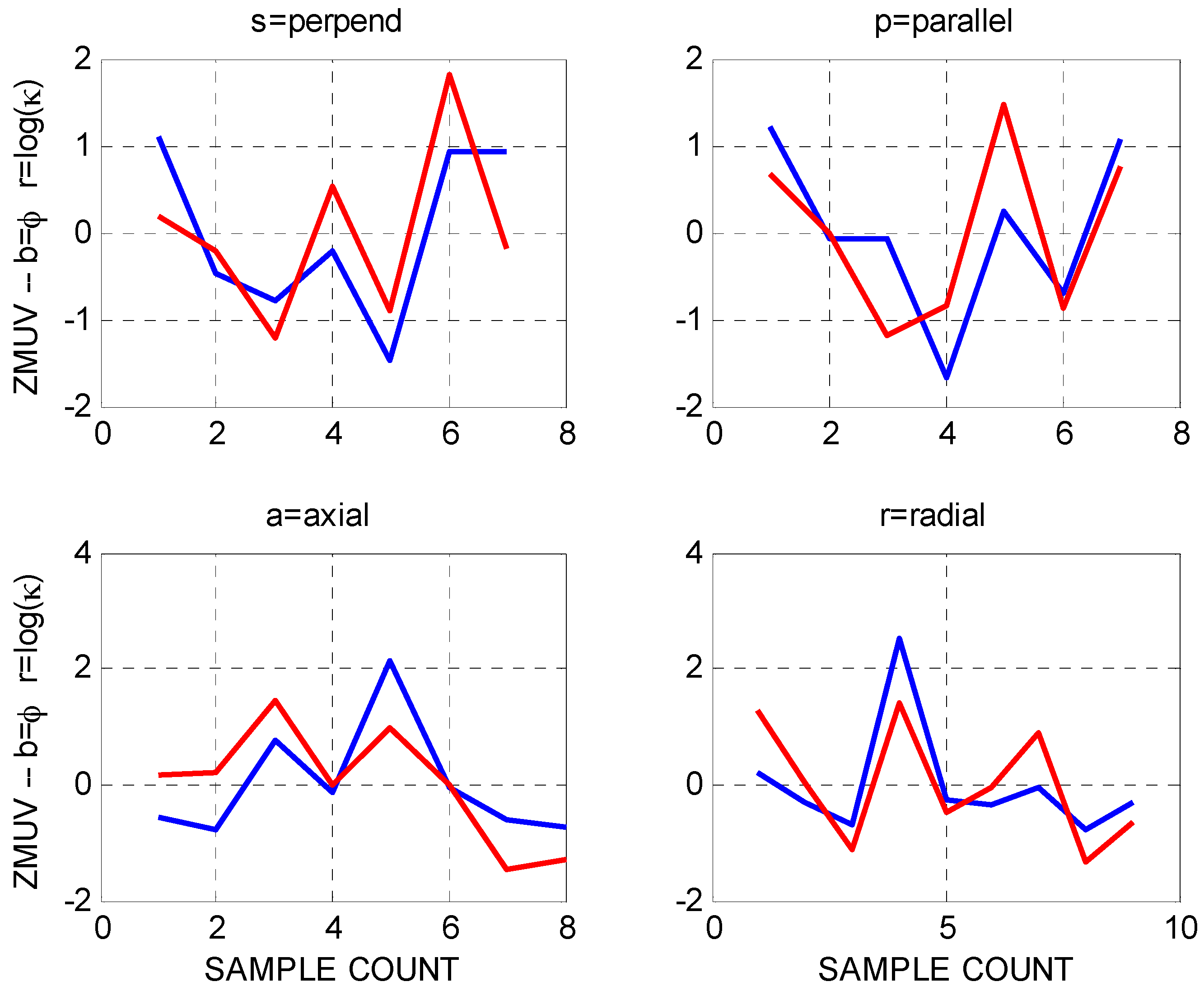
Figure 1 and
Figure 2 display the OTN1 pilot well open-hole temperature and reduced temperature profiles run five months after drilling completion (no successive temperature logs were run to detect time-evolving temperature levels). The upper panel of
Figure 1 shows a uniform temperature gradient perturbed at the near-surface due to groundwater circulation, and at depth due to a section of unusually heterogeneous rock (with possible depth-related instrument effects). Removing the uniform temperature gradient (black line in upper plot), the lower
Figure 1 panel highlights the effects of near-surface groundwater circulation to depth ~600 m, and shows discrete wellbore intervals of considerable temperature fluctuation at 800–1100 m and 1750–1850 m. These intervals are associated with a complex, highly fractured and attenuative mafic gneissic rock; well core inspection indicates an intensely foliated amphibore/hornblende-biotite gneiss. Our present interest lies in the more uniform granites between 1120 m to 1700 m, where the reduced temperature profile shows a series of sharp isolated positive temperature events.
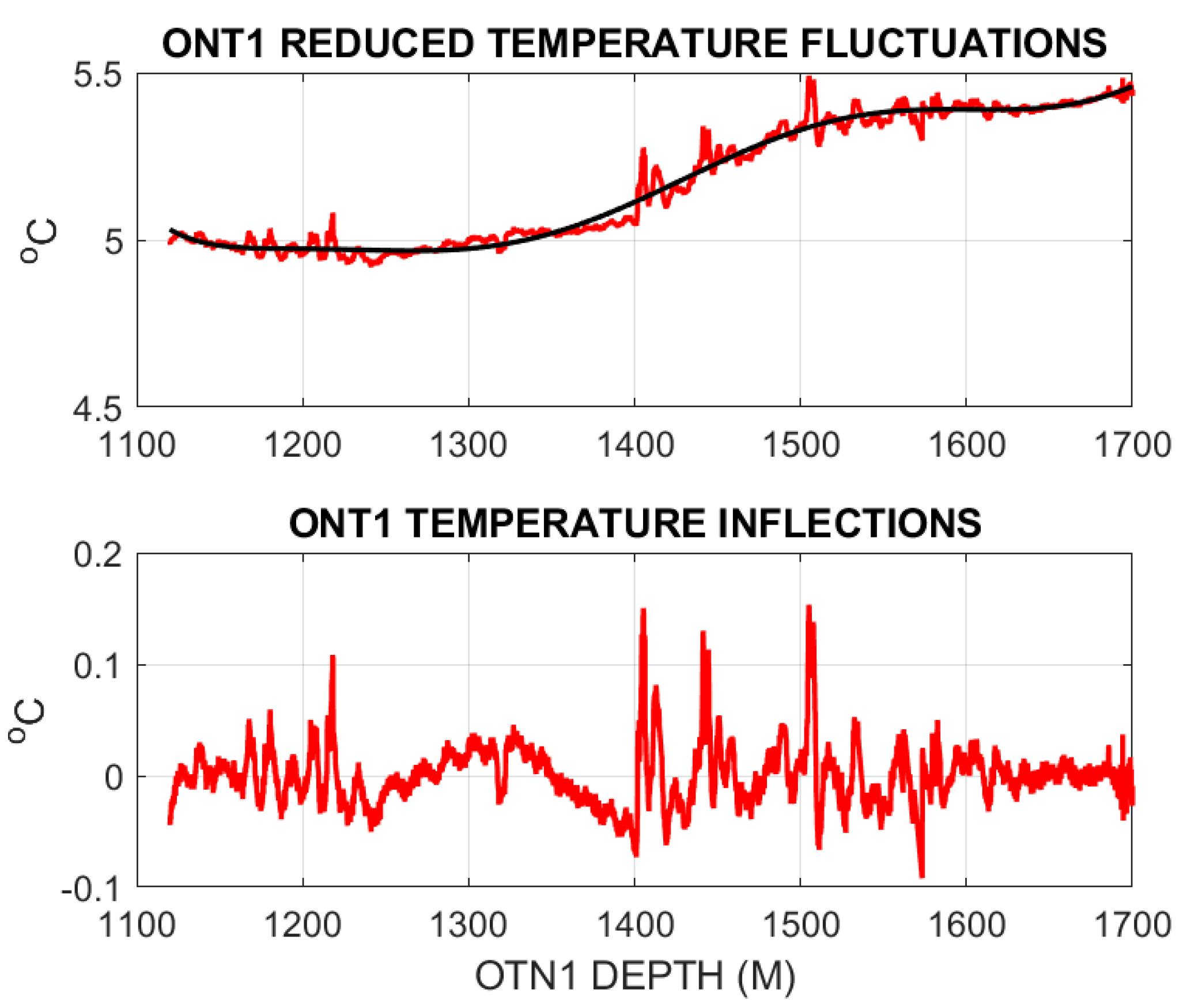
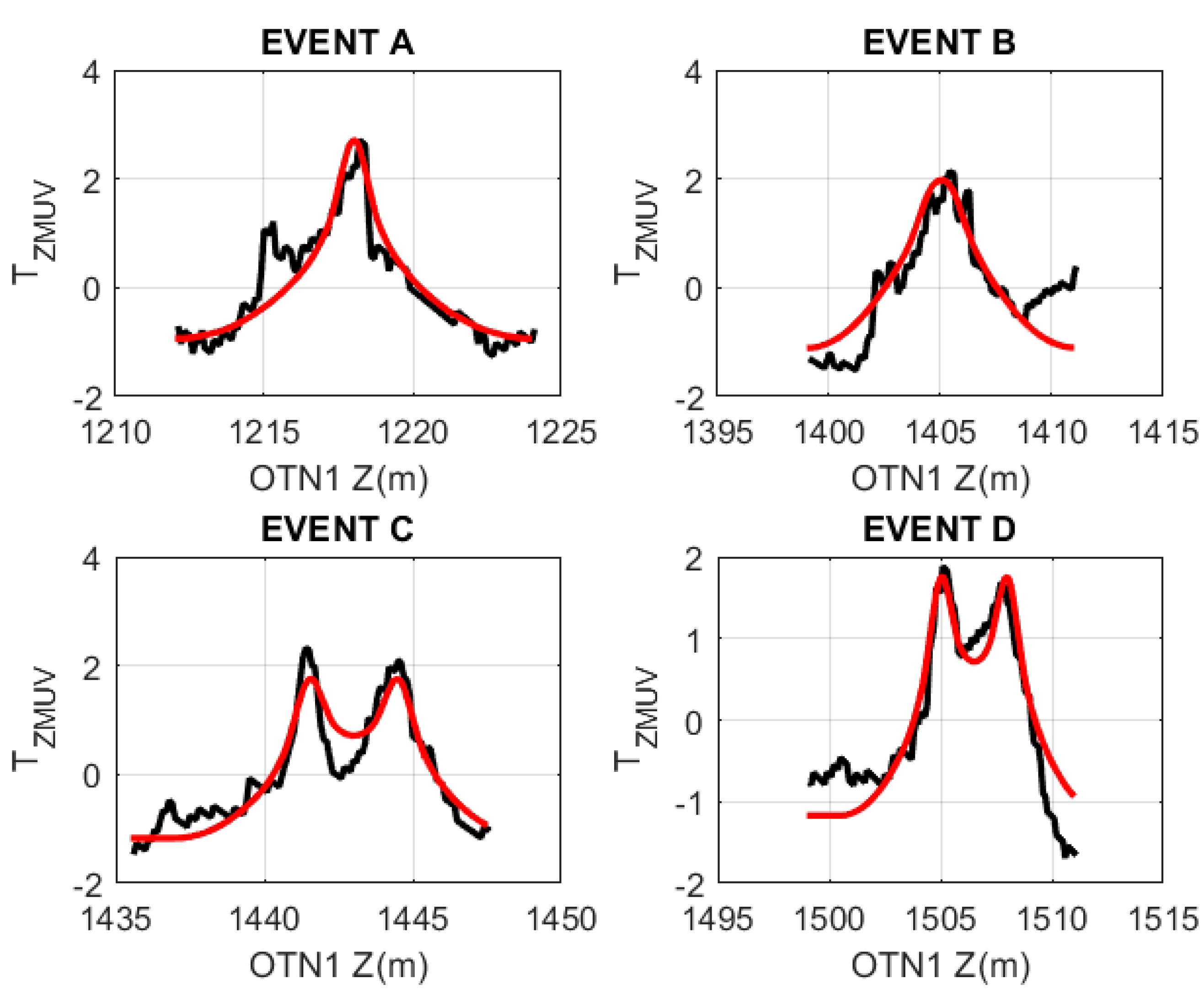
Figure 2 expands the
Figure 1 wellbore depth scale over the OTN1 1120–1700 m granite interval, detailing the discrete 0.05–0.1 °C temperature events of interest. A dozen or so 0.05–0.10 °C positive temperature excursions visually assessed to be ~5–7-m in axial extent occur over a 600-m span. The lower panel of
Figure 2 displays the discrete temperature deviations relative to the upper-panel polynomial curve fit to the reduced temperature trace.
The
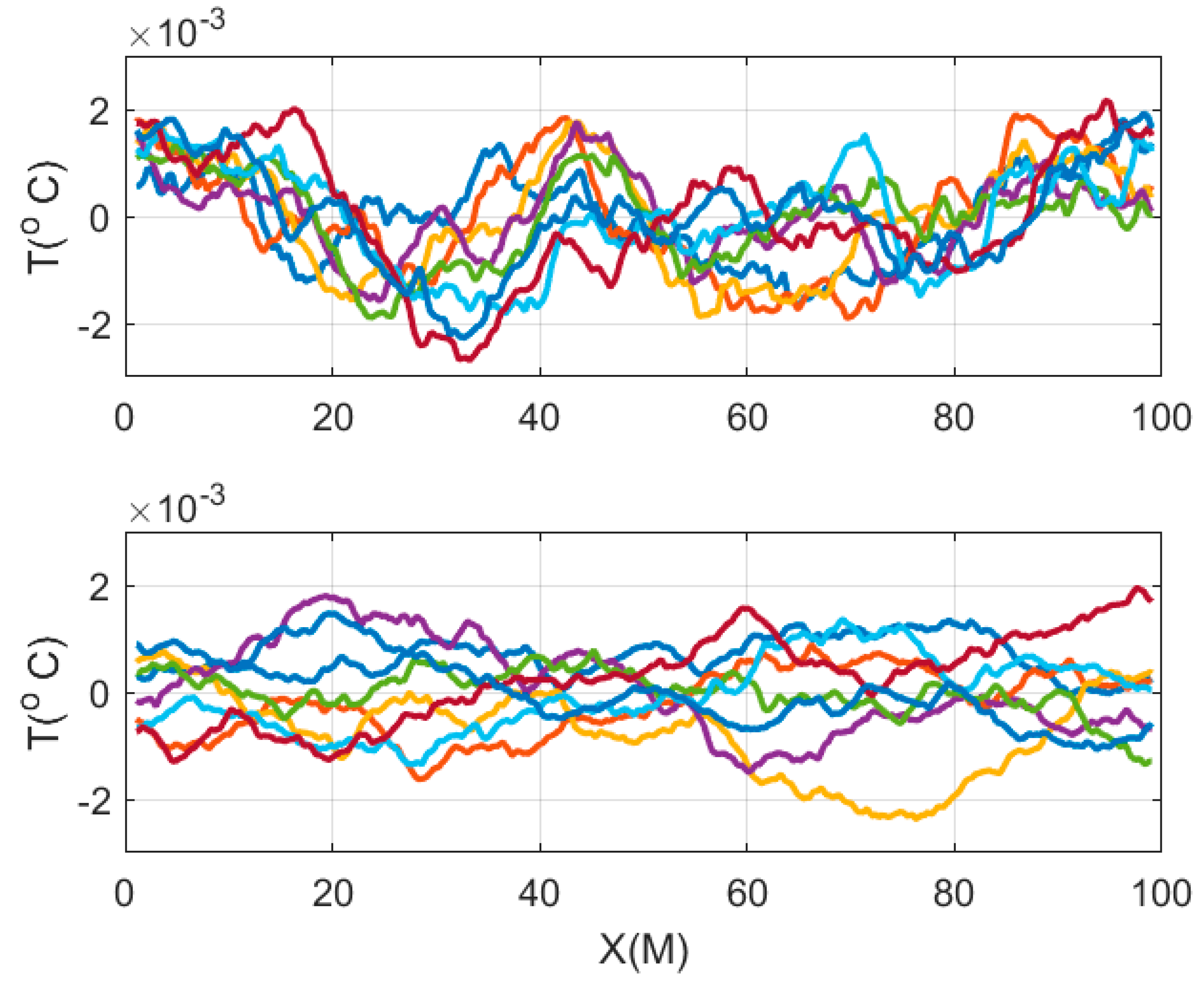
Figure 2 OTN1 wellbore thermal fluctuations are unlikely to be caused by spatial variations in the thermal conductivity properties of rock. Spatial fluctuations of thermal conductivity for Fennoscandia basement rock measured over Hm intervals along a 2.5 km deep regional wellbore are restricted to 1% deviation from the mean [
28]. Using the spectral character of the thermal conductivity data sequence to construct a representative 2D distribution of thermal conductivity spatial fluctuations,
Figure 3 indicates that temperature fluctuations expected from thermal conductivity fluctuations are unlikely to exceed 0.005 °C. The
Figure 2 thermal deviations are 10 to 20 times the level attributable to spatial variations in thermal conductivity.
Our working hypothesis for the physical process leading to the
Figure 2 OTN1 temperature events is that isolated fracture-connectivity structures in the crust intersect the wellbore and feed warmer crustal water into the cooler wellbore fluid column over a period of months between drilling and logging of OTN1. Such circumstances are quantified in [
5,
6]. We assume that after a period of months the crust-wellbore fluid flow system is approaching a steady state in which the amplitude and spatial distribution of the temperature incursions change slowly.
Figure 4 shows a 2D planar flow geometry illustrating the concept of, and modelling procedure for, steady-state heat transport by a fluid in a porous medium that can cause OTN1 temperature events. Adapting the planar crustal fluid flow context of [
29] and Equation (A4) of
Appendix A,
Figure 4 color distributions represent a steady-state temperature field determined by fluid flow driven by a planar pressure field moving fluid across a lateral crustal section bounded on the bottom by a fixed crustal temperature and on the top by a fixed fluid temperature. The
Figure 4 planar fluid-solid interface thus plays the role of the OTN1 wellbore interface within the basement rock.
In the
Figure 4 lateral crustal section, a channel ~5% of the section length has higher crustal permeability to permit warmer crustal fluid at higher pressure to flow into the cooler fluid at lower pressure. Representing OTN1 temperature events, the
Figure 4 flow channel transports heat at a greater rate than in the crustal section on either side of the flow channel. Where the warmer crustal fluid enters the cooler fluid layer, fluid temperatures rise above the background level. Zero-flow conditions at the crustal section edges replicate indefinite lateral continuation of planar flow. The resultant steady-state wellbore interface temperature profile in the lower panel shows that, away from the localized fluid transport channel, leaking crustal fluids can generate small temperature fluctuations on the flanks of the central temperature event; such disseminated temperature fluctuations along the wellbore may be present in the
Figure 2 wellbore temperature data. Given the conceptual nature of the
Figure 4 2D flow representation of OTN1 3D flow structures, the physical dimensions and associated flow and temperature fields are arbitrary.
The
Figure 4 2D conceptual representation of OTN1 temperature events illustrates the global mesh nature of the 3D finite element computations discussed below. As access to deep crustal fluids is generally via a wellbore, slow or rapid percolation passage of wellbore fluid into or out of a surrounding crustal rock volume can be defined entirely by a stochastic permeability distribution within a global volumetric mesh. For illustration purposes, the
Figure 4 wellbore fluid is included in the flow simulation as a high-permeability flow component embedded in the global mesh across the rectangular model domain. Finite element computation simulates heat advection through the crustal-section flow-channel in parallel with heat conduction in the crust and the wellbore fluid. Inspection of
Figure 4 shows that the spatially variable fluid flow geometry will give a variable value for the planar-flow Peclet number, P
e ≡ v
0ρCL/K, where v
0 = fluid flow velocity, ρC = volumetric heat capacity of water, L = layer thickness, and K = thermal conductivity of rock, across the crustal section [
29]. The relation of Peclet number to fluid flow velocity links observed temperature distributions to crustal fluid flow structures.
The
Figure 4 2D mesh construction is for heat advection concept and computational mesh illustration purposes only. The following 3D wellbore-centric fluid flow computations treat the narrow-gauge wellbores as geometric flow boundaries outside the global mesh construction. As in
Figure 4 for 2D flow, 3D model axial variation of wellbore-centric radial flow Peclet number computed for OTN1 temperature events converts observed wellbore axial temperature distributions into estimates of radial heat advective fluid flow for fracture-connectivity flow structures. Axial temperature distributions along wellbore profiles embodied in axially-varyings Peclet numbers thus become a diagnostic tool for investigating wellbore-centric fluid flow processes in crustal rock.
3. 3D Global Mesh Finite Element Modelling of Basement Rock Wellbore Temperature Events
Empirical crustal property (i) establishes the existence of spatially-correlated poroperm structures at all scales and at all drilling-accessed depths in the crust. In parallel, empirical crustal flow properties (ii) and (iii) establish the poro-connectivity flow mechanics at all scales for wellbore-accessed crustal volumes. On the strength of empirics (i)–(iii), we interpret the
Figure 2 set of wellbore-logged basement rock thermal event structures in terms of the ‘canonical’ or ‘type’ crust-to-wellbore or wellbore-to-crust fluid flow constructs sketched in
Figure 4.
Given the broad evidentiary base for ambient crustal flow properties (i)–(iii), it is logical to expect that when a wellbore intersects naturally-occurring flow structures, fluid at crustal confining pressures in the long-range spatially-correlated fracture-connectivity network flows into the hydrostatically under-pressured wellbore. If the intercepted flow structure is sufficiently large scale, heat will be advected into the wellbore by the inflowing fluid for a long enough period to be observed by wellbore logging. Comprehensive evidence for persistent Dm-scale crust-to-wellbore advective inflow is given in [
5,
6] for a Hm-scale tight gas sandstone crustal volume.
The steady-state rate at which crustal fluids flow from the crust into a wellbore,
v(x,y,z), is given by Darcy’s law in terms of permeability distribution κ(x,y,z) and constant dynamic viscosity of water µ:
for appropriate fluid pressure boundary conditions in the crustal volume.
Conservation of mass requires that steady-state Darcy flow velocity has vanishing divergence,
·
v = 0, yielding the defining flow equation for finite-element solvers:
The finite element method for solving differential equations allows for essentially arbitrary spatial variation of material properties such as κ(x,y,z) [
30,
31,
32]. As illustrated in
Figure 4, our application of this finite element solver capability assumes that a single global numerical mesh spans the entire flow model.
If Darcy fluid flow carries heat through a medium of mean porosity φ, the combined steady-state conducted and advected heat energy flow is:
for K = Fourier’s thermal conductivity for rock and ρC = fluid volumetric heat capacity. Conservation of steady-state thermal energy,
·
q = 0, then couples the spatially-variable temperature field T(x,y,z) to the spatially-variable Darcy fluid velocity flow field
v(x,y,z) for the given crustal temperature and fluid pressure boundary conditions. This coupling leads to the defining steady-state equation for a nonlinear finite-element solver:
where the conservation of mass condition
·v = 0 is observed, and D = K/ρC ~ 0.7 × 10
−6 m
2/s is the essentially constant thermal diffusivity of the rock-fluid system for rock thermal conductivity K ~ 3 W/m∙°C and fluid volumetric heat capacity ρC ~ 4.28 MJ/m
3∙°C.
Where long-range spatially-correlated fracture-connectivity percolation networks intersect a wellbore, Darcy flow can be approximated as essentially wellbore-centric radial,
v(x,y,z) ~
v(r) =
v(r
0)r
0/r. The 3D steady-state flow condition (4) then reduces to a 2D analytical form in wellbore-centric radius r,
given in terms of radial flow boundaries at r
0 < r
1 characterized by boundary temperatures T
0 and T
1, with Peclet number P
e = r
0φv
0/D (
Appendix A). Analytic expression (5) serves to check 3D solutions of non-linear thermal energy conservation constraint Equation (4), while at the same time yielding an estimate of advective fluid flow rate for the crustal fracture-connectivity flow system, φv
0 ~ P
eD/r
0.
The degree of advection heat transport relative to conductive heat transport for a given model flow structure determines the shape to the axial temperature along the wellbore. Matching the observed axial temperature profile in turn constrains the effective steady-state flow velocity of the crustal fluid leaking into the wellbore without having to know explicitly the permeability or pressure boundary conditions. Modeling axial temperature profiles interpreted as sequences of 2D wellbore-centric radial flow Peclet numbers thus has the potential to calibrate EGS wellbore-centric flow stimulation processes.
We use Matlab 3D partial differential equation solvers to model steady-state axial temperature profiles constrained by the mass conservation (2) and heat energy conservation (4). The Matlab 3D solvers [
32] have two forms for a scalar field variable u(x,y,z):
and:
Equation (6) is equivalent to an elliptical partial differential equation, and Equation (7) generalises (6) by allowing coefficients terms c(x,y,z) and a(x,y,z) and source term f(x,y,z) to depend on the field variable u(x,y,z) and its spatial derivatives, u
x, u
x and u
z. The key feature of finite-element modelling employed here is its tractability to essentially arbitrary position-dependent coefficients, e.g., c(x,y,z) for (6), and c(x,y,z,u,u
x,u
x,u
z) for (7), to meet the conditions imposed by stochastic poroperm media [
30,
31,
32].
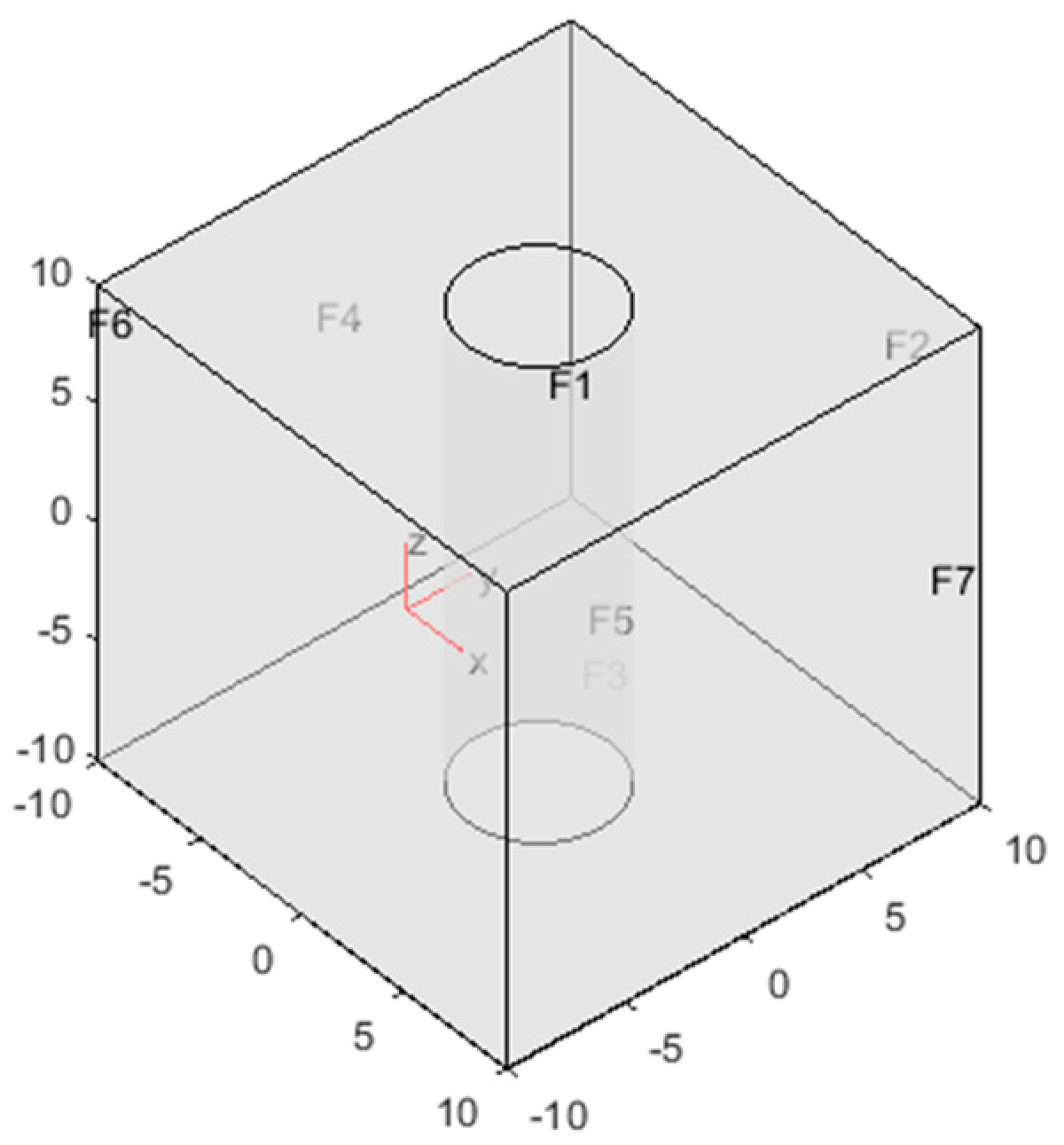
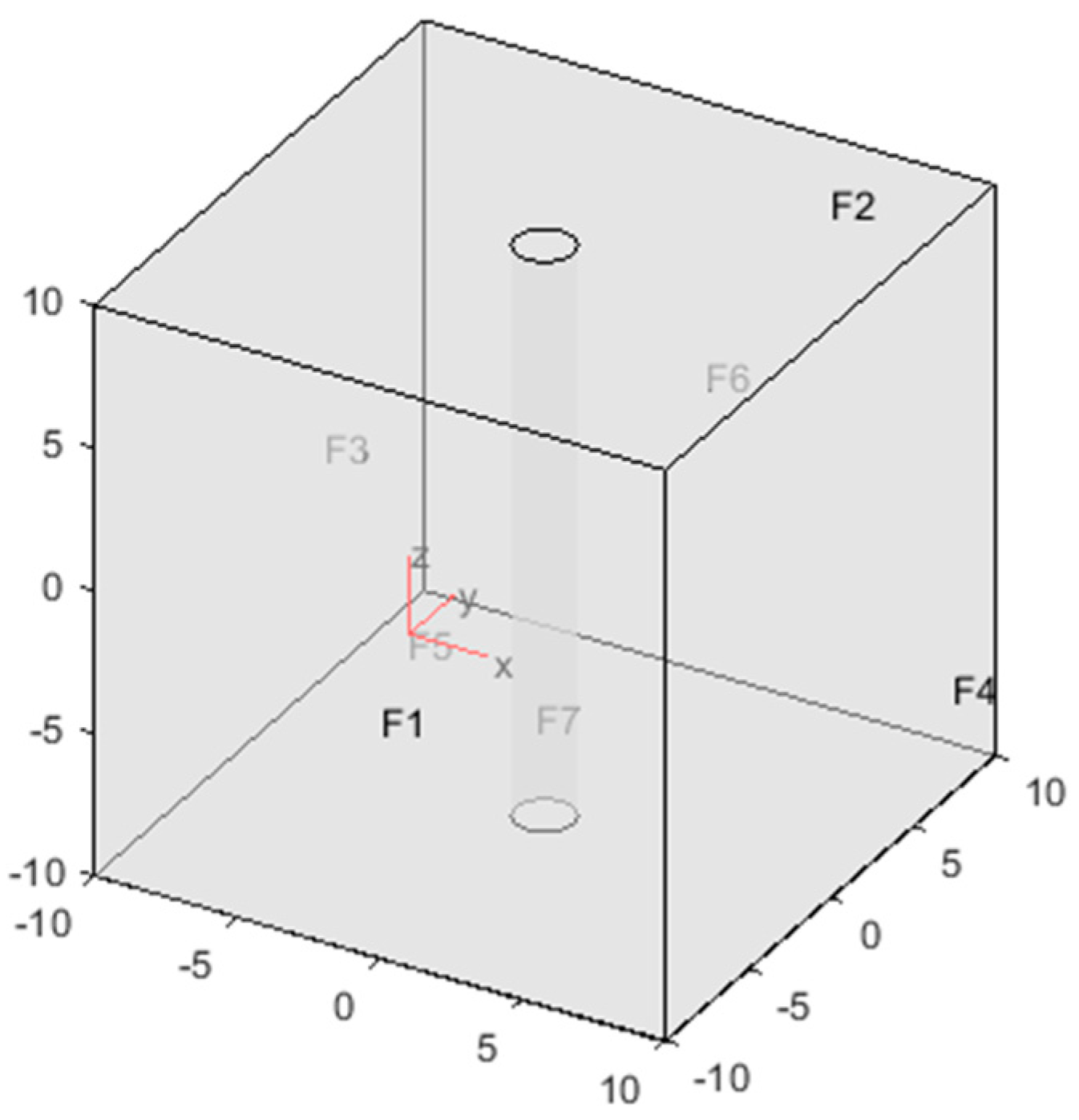
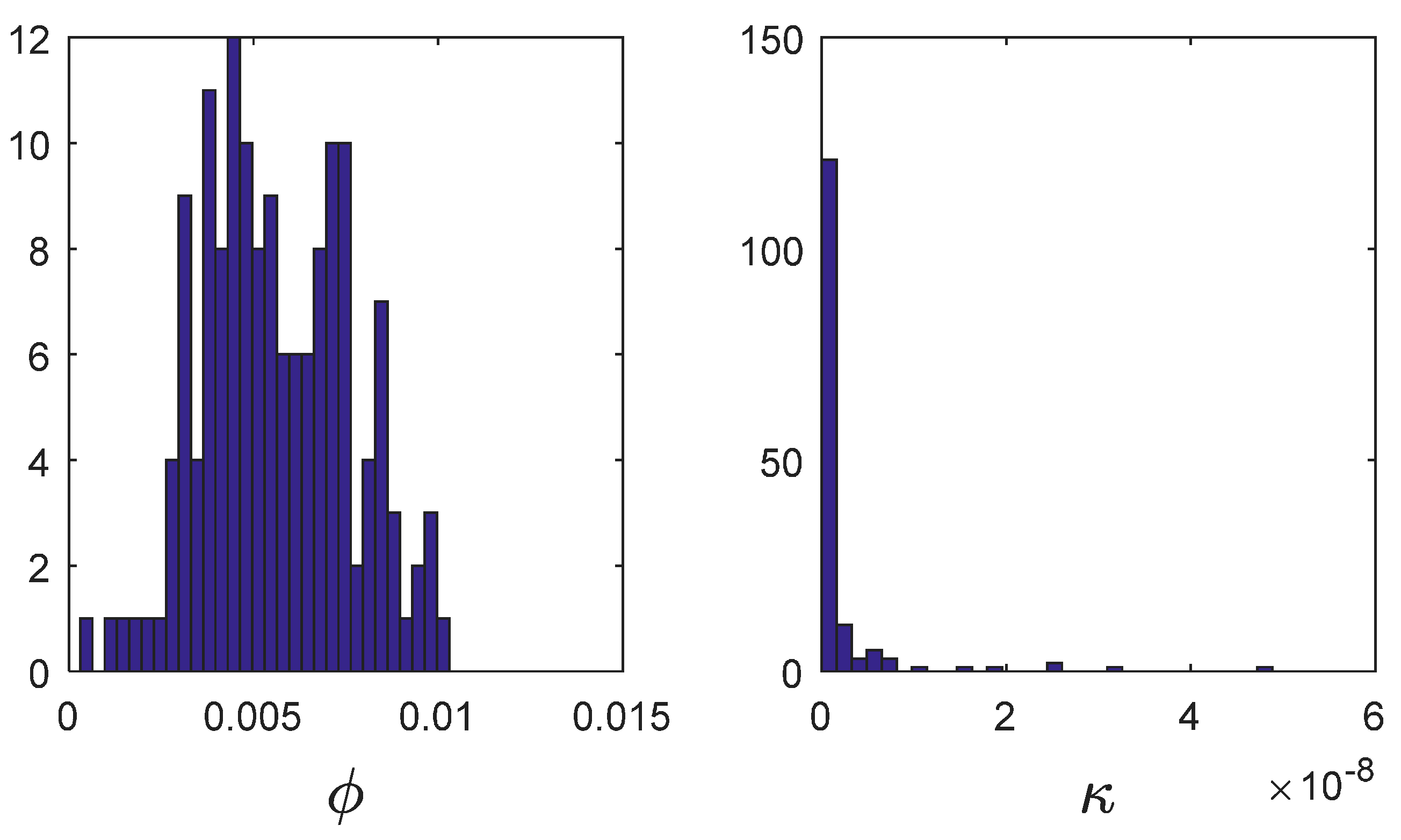
Figure 5 pictures the model geometry for wellbore-centric flow/transport simulation of
Figure 2 OTN1 temperature data. Internally, the model volume is characterized by a spatially-correlated stochastic distribution of porosity φ(x,y,z) and its associated permeability field κ(x,y,z) ~ exp(αφ(x,y,z)).
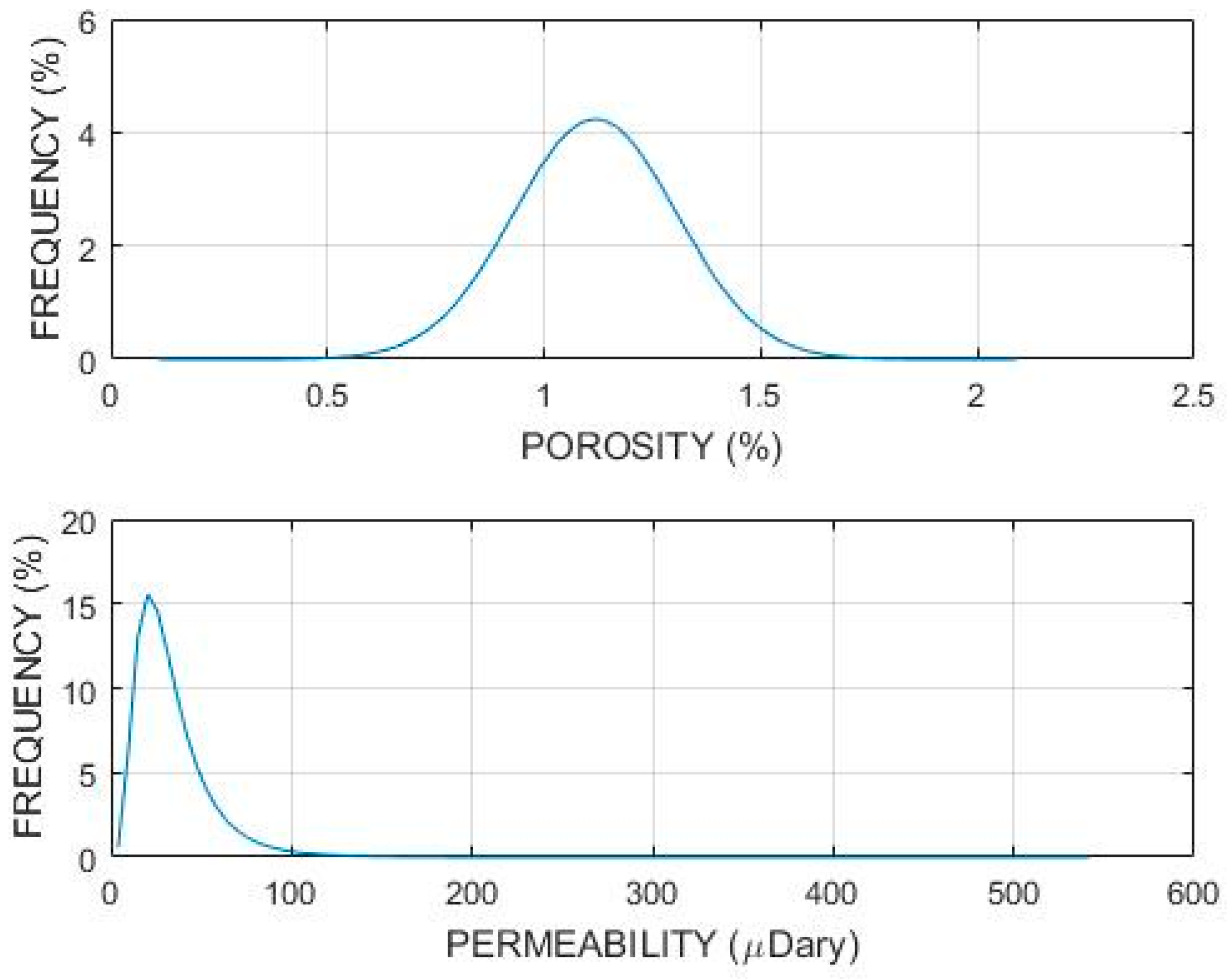
Figure 6 shows the distribution frequency of porosity and permeability values in
Figure 5 model crustal volumes. Model volumes have essentially uniform pressure and temperature conditions on each side; for modelling simplicity, zero-flux boundary conditions are set on the top and bottom faces. As illustrated in
Figure 4 for 2D, we can inset at will in the
Figure 5 crustal volume geometric flow structures to give enhanced percolation via greater fracture connectivity along the flow structure. Where inserted flow structures intersect the model volume external boundaries, we assume the structures connect to the surrounding crust to deliver heat energy at the external boundary.
Figure 7 displays how external crustal heat energy input to the model volume is represented by setting a fixed temperature increment at the intersection of the flow structure with the model external faces.
Solutions to constraint conditions (6) and (7) determine how the incremental heat energy at the model external surfaces is expressed as temperature along the internal wellbore. In matching computed temperature profiles to observed
Figure 2 temperature events, we provide a physical description of the fluid flow and heat transport process between the central wellbore and the enclosing crustal volume. By calibrating this model to OTN1 temperature events, we can explore hypothetical scenarios of EGS stimulation in which high pressure wellbore fluids enter into existing and/or relic fracture-connectivity structures in the surrounding crust.
The scalar field variables represented by finite element scale field u(x,y,z) are, for (6), pressure P(x,y,z), for solving the Darcy flow constraint Equation (2), and for (7), temperature T(x,y,z), for solving the thermal energy constraint Equation (4). For pressure fields u = P(x,y,z), (6) is used with coefficient term c(x,y,z) representing permeability κ(x,y,z), with coefficient term a(x,y,z) and source term f(x,y,z) set to zero. For temperature fields u = T(x,y,z), (7) is used with coefficient term c(x,y,z,u,ux,ux,uz) set to unity, coefficient term a(x,y,z,u,ux,ux,uz) set to zero, and source term set to the advective flow of heat, f(x,y,z,T,Tx,Tx,Tz) = 1/D φv(x,y,z)·T(x,y,z).
The
Figure 5 computation volume is discretized by 161 nodes on a side. With a notional physical dimension of 20 m per side, the nodal spatial resolution is Δx = Δy = Δz = 12.5 cm. Ambient poroperm properties within the crustal domain are numerical realisations of a 3D stochastic spatial connectivity distribution representing porosity φ(x,y,z) and associated permeability κ(x,y,z) ~ exp(αφ(x,y,z)) given by crustal empirics (I)–(III).
Figure 6 shows the degree of spatial heterogeneity typical of the power-law scaling spatial fluctuation amplitudes: ~6 octaves for the normally distributed porosity about mean porosity φ ~ 1.2% and ~9 octaves for the lognormally distributed permeability generated by fracture-connectivity parameter α ~ 300 introduced in empirical condition (III).
The wellbore interior boundary surface is assigned a boundary flux distribution. As our modelling task is to compute an interior temperature distribution on the basis of an exterior temperature distribution, we assign the wellbore a heat flux boundary condition which generates an associated temperature distribution T0(r0,z) = 1/h q0(r0,z) on the basis of the computed heat delivered to the wellbore. For present purposes, the heat transfer coefficient h is taken to be a free model parameter.
Model wellbore radii can range from a 5-node diameter (30 cm radius) as in
Figure 5 to the 17- and 50-node (1 m and 3 m, respectively) diameter model wellbores discussed below. Modelling with a range of wellbore radii within the fixed node-count numerical volume checks for possible computational effects of a small wellbore defined by few nodes, and possible effects on wellbore axial temperature distribution due to the radial distance over which influx fluids travel from the exterior crustal boundary to the interior wellbore boundary.
To compute Darcy flow velocity v(x,y,z), the wellbore is assumed to be at hydrostatic pressure. Fluid in the crustal volume will be subject to higher pressure, most probably given by the minimum principal stress. Given the fluid-flow empirics (I)–(III), almost all fluid will ultimately be connected through a global fracture-connectivity pathway, and hence the fluid pressure will be approximately in equilibrium with the minimum principal stress. As the minimum horizontal principal stress, σh ~ 22 MPa/km·zkm, exceeds hydrostatic pressure, Ph ~ 10 MPa/km·zkm, wherever in the crustal volume there is a geometric feature of elevated fracture-connectivity parameter α that connects the surrounding crust to the interior wellbore, we can assume that fluid pressure σh outside the model cube drives fluid from the crust into the wellbore.
In consideration of wellbore temperature log data in
Figure 2 and observations of localized wellbore temperature effects elsewhere [
5,
6,
7,
8], we can suppose that fluids flowing into a newly drilled wellbore bring heat crustal heat into the wellbore fluid. Fracture-connectivity pathways leaking fluid into a wellbore can be expected to generate positive temperature events at sites where fracture-connectivity structures intersect the wellbore. Positive temperature inflections in
Figure 2 characterize OTN1 data; the conceptual
Figure 4 illustrates a positive temperature deflection.
In line with the expected transport of heat from the crust into a wellbore,
Figure 7 illustrates an appropriate model external boundary condition temperature distribution. The incremented boundary temperature field corresponds to a 0.6 m-thick horizontal flow structure of higher poro-connectivity parameter α which conveys fluids from the surrounding crustal volume to the central wellbore. The axial dimension 0.6 m refers to the model grid thickness of a presumed radially extensive heterogeneous body of crustal rock that supports percolation flow into the wellbore from a laterally extended flow structure embedded in the crust. The dimension 0.6 m is computationally wide enough to give node-support to the flow and transport processes within the flow structure. The flow structure thickness is consistent with the rock-fluid interaction empirics (I)–(III) expressed in the introduction. With this empirics-based conceptual framework, we ignore flow models presumed to conduct fluid as Poiseuille or ‘pipe flow’ between idealised smooth/featureless planar surfaces. Thus 0.6 meters refers only to to a radial zone of spatially erratic percolation flow in low-porosity/low-permeability rock with considerably more poro-connectivity than found in the ambient crust.
Figure 8 and
Figure 9 display quadrant section contour plots for the temperature and heat transport solutions to (7) generated by the 0.6 m-thick percolation flow structure pictured in
Figure 7.
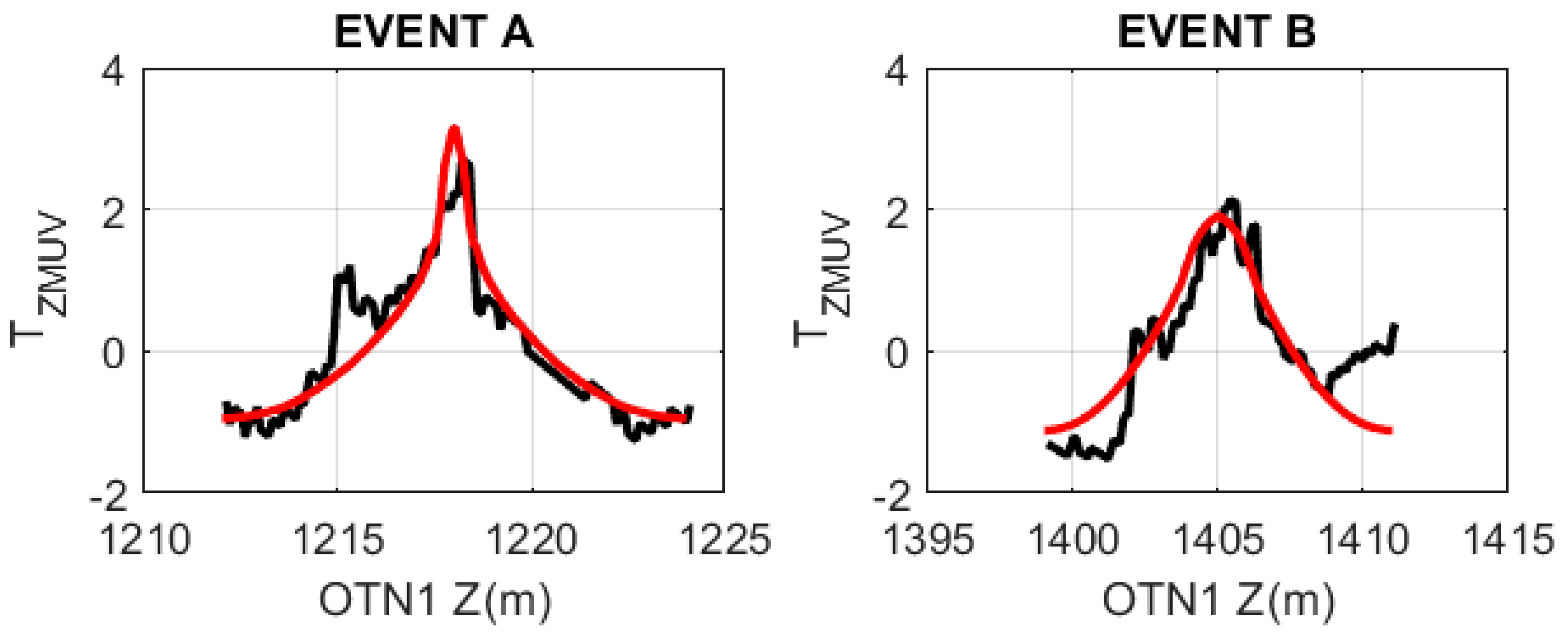
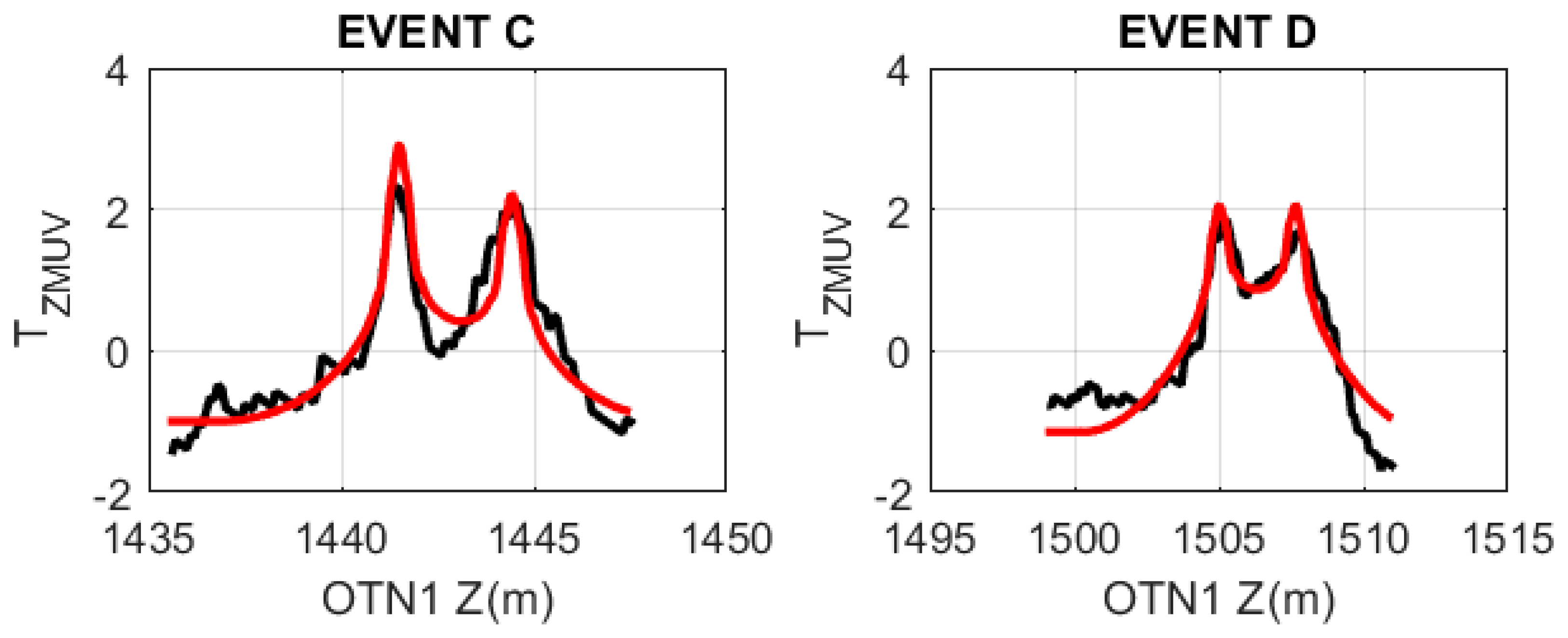
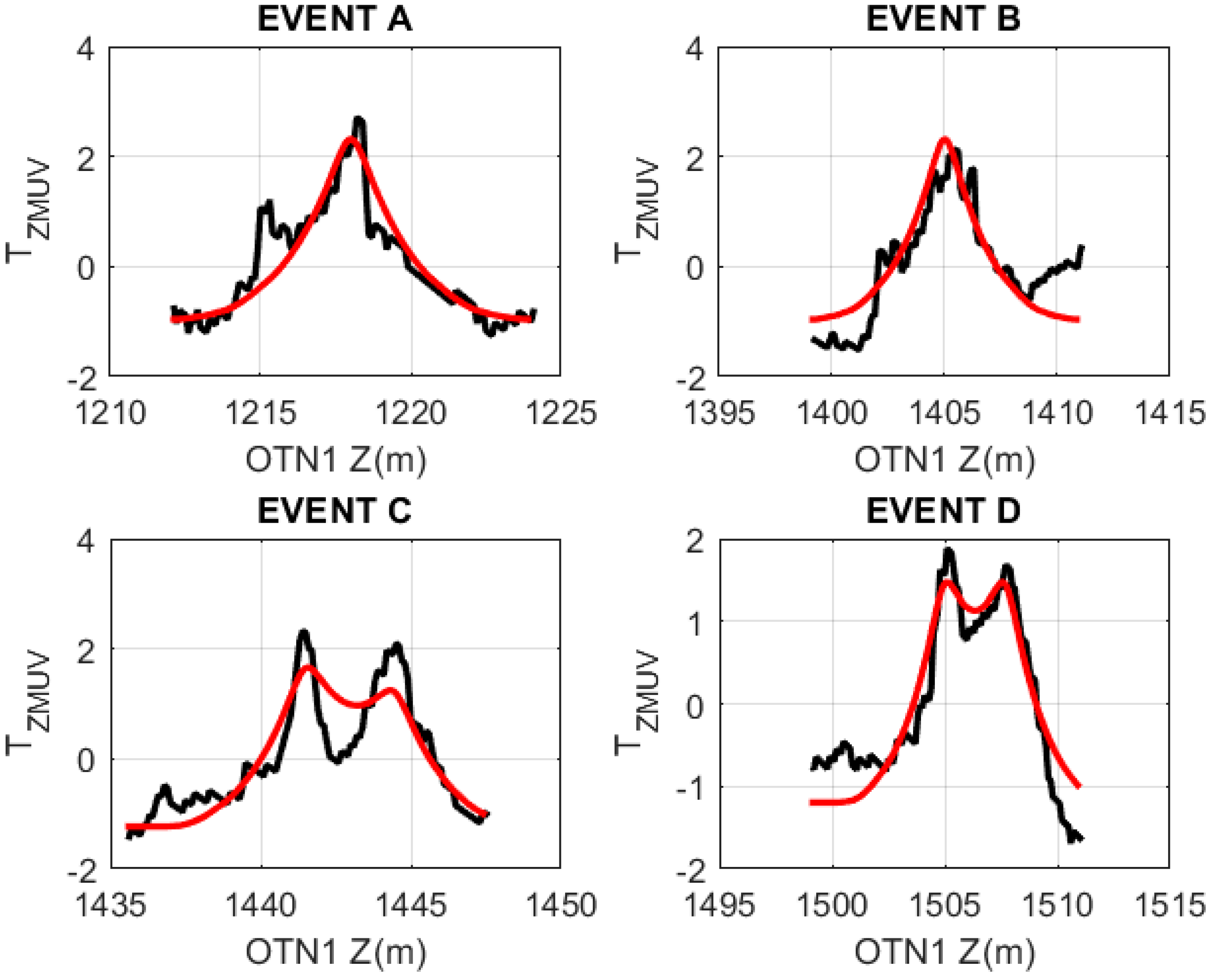
Figure 10 shows model wellbore axial temperature profile matches to significant OTN1 temperature events in the 1120 m–1700 m interval of granite basement given in
Figure 2. Except for the upper-right temperature event of
Figure 10, the
Figure 7,
Figure 8 and
Figure 9 model flow simulation percolation structures have 0.6 m thicknesses. It is found that a 2–3 m-thick model flow structure is required to match the broader (more axially extensive) temperature event at 1405 m depth seen in the
Figure 10 upper-right wellbore temperature profile.
The
Figure 10 advection flow model wellbore temperature profiles computed by (7) for
Figure 7-like flow-structure geometry and boundary conditions provide plausible shapes to fit to the
Figure 2 observed OTN1 wellbore temperature profiles. Agreement between the model and observed profiles indicate that axial temperature diffusion by conduction combined with radial advective heat transfer via 0.6-m-thick flow structures into a 30 cm-radius wellbore provide reasonable approximations to the diffusion-advection process hypothesized for fracture-connectivity fluid percolation structures observed in Fennoscandia basement rock at depths to 2.5 km.
4. 2D Wellbore-Centric Radial Flow Peclet Number Characterization of 3D Temperature Models
Figure 7,
Figure 8,
Figure 9 and
Figure 10 describe the steady-state 3D wellbore-centric temperature field around a vertical wellbore when heat-transporting fluid flows into the wellbore from horizontal flow structures as given in
Figure 7. For wellbore levels at or near horizonal flow structures, the radial temperature distribution is dominated by thermal advection (high Peclet numbers), while at wellbore axial offsets away from horizontal flow structures, the radial temperature field is dominated by thermal conduction (low Peclet numbers).
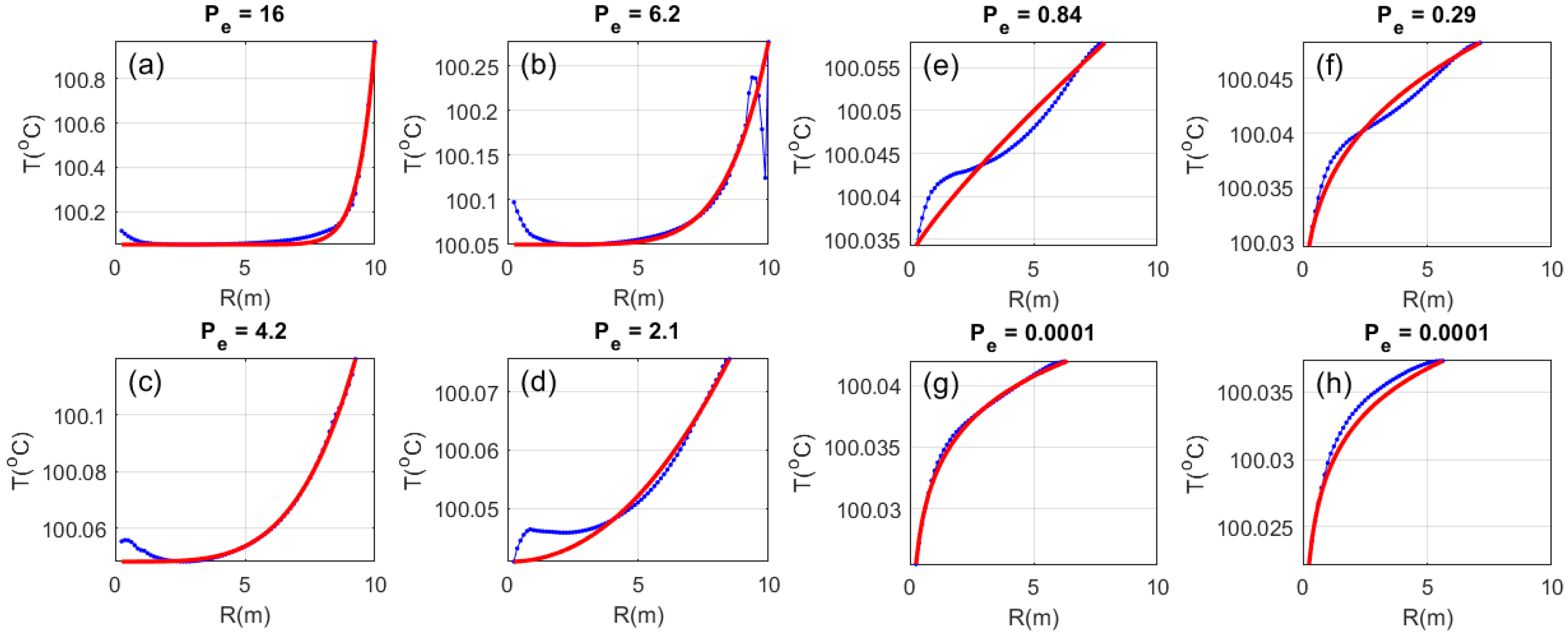
Figure 11 shows the axial changes in model radial temperature profiles (blue dots) for the 1218m OTN1 temperature event A shown in upper left plot of
Figure 10. Model radial temperature profiles T
0 < T(r) < T
1 for r
0 < r < r
1 at successive depths along the wellbore axis are approximated by best-fits (red traces) to steady-state radial temperature distribution (5) for free parameter Peclet number P
e = r
0φv
0/D:
as the Darcy flow heat transport rates φv
0 vary with depth along the wellbore interval in crustal rock of mean porosity φ and thermal diffusivity D ~0.7 × 10
−6 m
2/s (
Appendix A).
Figure 11 assumes an ambient wellbore temperature T
0 ~ 100 °C and external ambient crustal temperature T
1 ~ 100 °C + ΔT, ΔT ~ 0.05 °C except near the advective flow horizon when ΔT = 1 °C (see
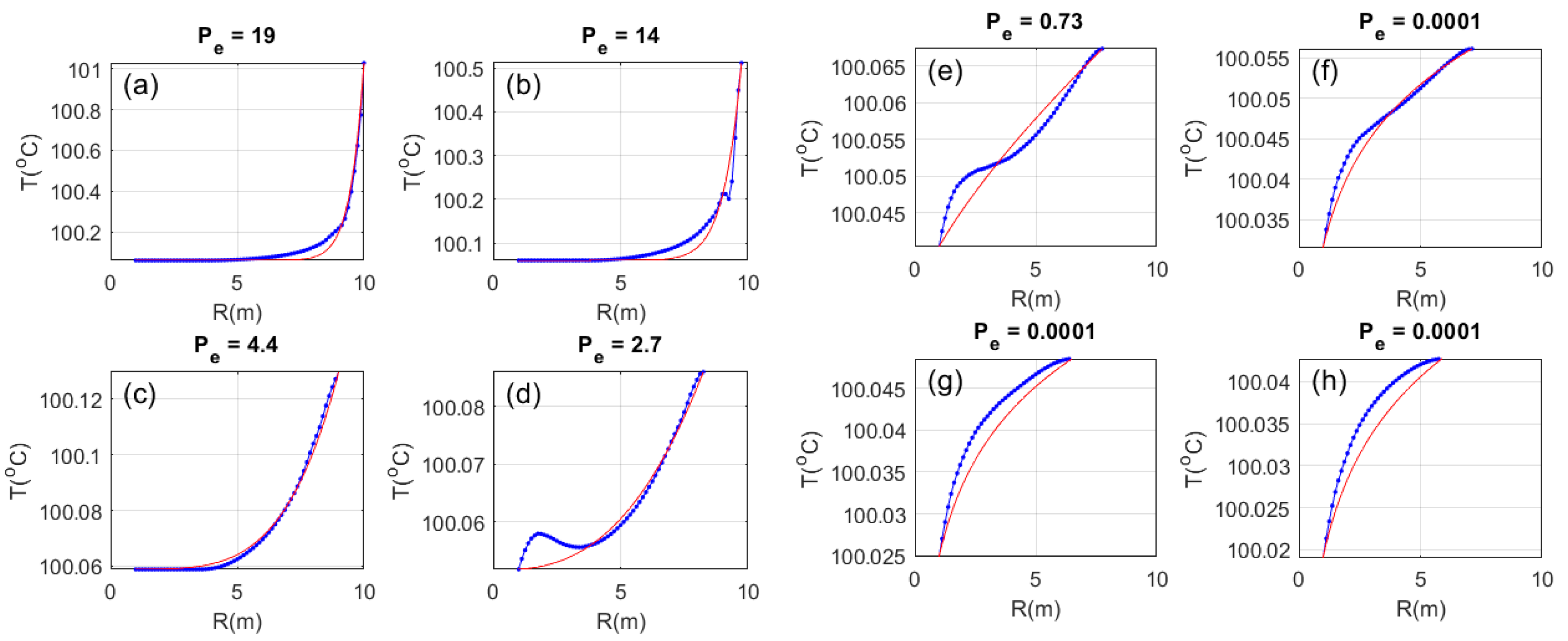
Figure 7). Equation (5) is fit to the
Figure 8 numerical model radial temperature distributions for the sequence of wellbore depths (a–h) in
Figure 11. Beginning at the upper-left plot (a), successive axial offsets from the horizontal fracture-connectivity flow structure are described by decreasing Peclet numbers in plots (b–h) as thermal advection heat transfer decreases relative to thermal conduction heat transfer. The 2D analytic approximations (5) for optimized Peclet number closely fit the numerical model temperature profiles. The
Figure 11 agreement between a sequence of 2D analytic expression (5) optimized for Peclet number, and the
Figure 7,
Figure 8,
Figure 9 and
Figure 10 3D numerical model temperature distribution, validate the finite-element numerical procedure (7).
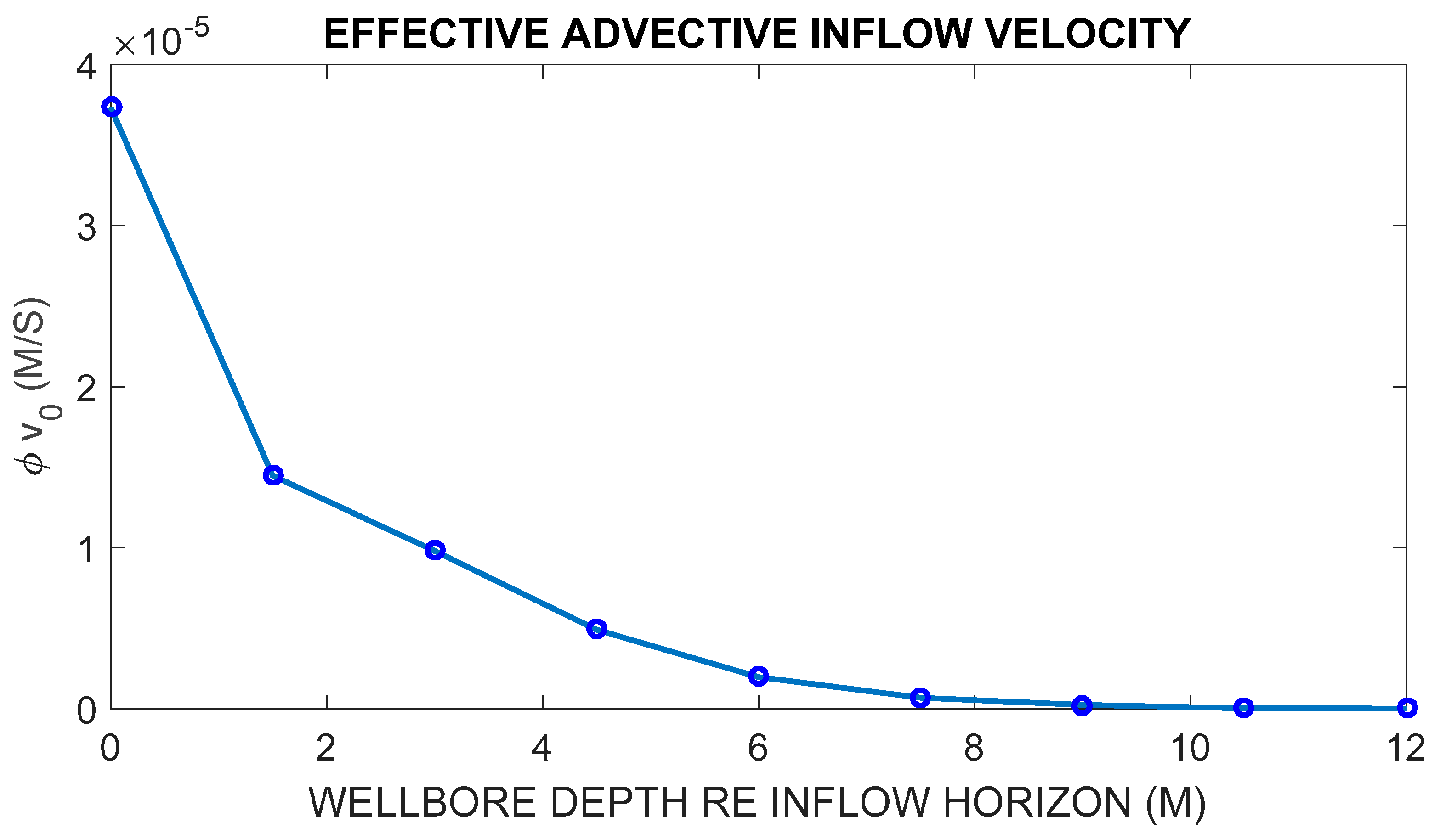
Figure 12 characterizes the effective Darcy fluid inflow parameter φv
0 = P
eD/r
0 at offsets along the wellbore axis from the advective heat inflow horizon.
The relation of wellbore-centric model Peclet numbers in
Figure 11 to axial temperature profiles in
Figure 10 is governed in part by the ratio of the inner and outer model radii r
1/r
0. The heat advection flow computation for
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11 and
Figure 12 assumes model radius r
1 = 10 m enclosing a wellbore radius r
0 = 30 cm, giving model/wellbore radius ratio r
1/r
0 = 33. The steady-state advective heat transfer temperature field (5) indicates that for Peclet numbers of interest, e.g., P
e > ~3, wellbore-centric heat transfer for large values of r
1/r
0 is essentially decoupled from the external boundary. As we are primarily interested in interpreting wellbore axial temperature events in terms of fluid inflow from crustal domain fracture-connectivity structures, we look at the degree of spatial resolution that the
Figure 2 OTN1 wellbore temperature events can give for the scale of flow structures away from the wellbore.
While the steady-state heat flux temperature field (5) formally returns a value T
1 for radius r = r
1 for all values of Peclet number P
e, for radii much larger than the wellbore radius but smaller than the model radius, r
0/r
1 << r/r
1 < 1, (5) reduces to:
For values of the model exterior temperature T1 differing little from the wellbore temperature T0, T(r) ~ T0 for most of the radial extent away from the wellbore, and as a result the value of the external boundary temperature T1 has little influence on the wellbore temperature profile.
Expressing system steady-state advective heat flow (3) in terms of (5) gives:
from which the wellbore temperature T
0 is directly dependent on the crustal heat inflow q
1 at the model external boundary:
While Equation (10) is analytically straightforward, for numerical solutions it is preferable to give a temperature rather than a heat flux boundary condition. We can, accordingly, use (10) to infer the magnitude of the heat influx at the model boundary from the given numerical value of the wellbore temperature T0.
The physical and numerical implications of Equations (8)–(10) motivate examining the model wellbore temperature profile for a smaller model/wellbore radius ration, r
1/r
0 = 3 (
Figure 13). Computing the axial temperature profile for a model wellbore radius r
0 = 3 m in an r
1 = 10 m model volume tests the extent to which the r
1/r
0 influences model axial temperature distributions.
Figure 14 shows that if the external radial temperature boundary is not sufficiently far away from the wellbore heat flux boundary, the model axial temperature distribution is overly affected by the radial temperature boundary condition and the model cannot match the observed axial temperature profile. The
Figure 13 wellbore radius geometry shows that the external temperature boundary must be sufficiently far from the wellbore internal heat flux boundary to allow sufficient heat to be thermally conducted away from the advective heat influx flow structure in order to match observation.
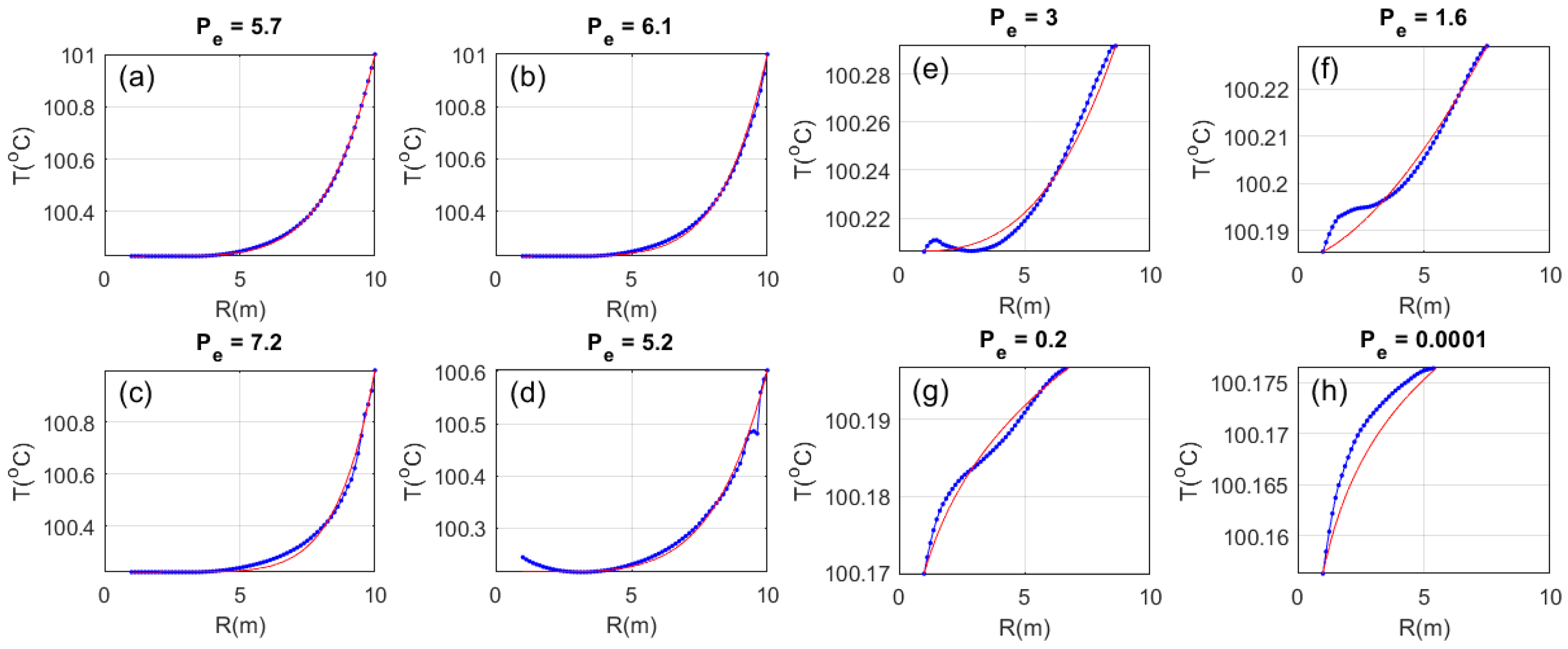
Figure 15 results for the
Figure 13 wellbore model are to be compared with
Figure 10.
Figure 10 versus
Figure 15 model fits to OTN1 wellbore axial temperature profiles quantifies the effect of an order of magnitude wellbore/model radius ratio r
1/r
0 difference, 33 to 3.3. For 0.6 m thick advective fluid inflow fracture-connectivity horizons, the 30 cm wellbore temperature profiles are more sharply peaked than the 3 m wellbore temperature profiles. In particular, the lower panels of
Figure 10 and
Figure 14 show that model temperature profiles for adjacent 0.6 m inflow horizons follow the observed temperature contours for a 30 cm wellbore while model profiles for a 3 m wellbore cannot follow these contours. We conclude on the basis of the latter condition that 0.6 m-thick fracture-connectivity inflow structures draining into an r
0 = 30 cm wellbore must extend deeper into the crust than r
1 = 1 m.
Figure 14 and
Figure 16 indicate that a 1 m radius wellbore model, r
1/r
0 = 10, does not match the OTN1 temperature profile for the adjacent inflow horizons shown in the lower-left panel of
Figure 16. The 1 m model wellbore matches the lower-right panel better than does the 3 m model wellbore but does not require a narrower gauge wellbore model. From the
Figure 11,
Figure 15 and
Figure 16 model/data matches, we can infer that, within the limits of our 161-node 3D computational spatial resolution, crustal penetration of a 0.6 m-thick fracture-connectivity inflow structures is greater than 3 m and is consistent with being a great as 10 m.
The effect of thickening the fracture-connectivity structures draining into a wellbore is illustrated in
Figure 17 and
Figure 18 for a 1 m radius wellbore.
Figure 17 essentially duplicates for a 1 m radius wellbore what
Figure 11 shows for a 30 cm radius wellbore for a 0.6 m-thick inflow structure. After large Peclet numbers, P
e ~ 15, at the location of the inflow structure, at 10 m offsets from the inflow structure effective advective heat transport is reduced to the level the level of thermal conduction, P
e < 1.
Figure 18 shows, however, that the effect of increasing the thickness of the inflow structure to 2–3 m reduces the Peclet number near the inflow structure, P
e ~ 5, and extends the axial effect of heat advective flow beyond 10 m. A thick advective heat influx structure spreads the axial temperature profile along the wellbore. The axial temperature spreading effect seen in the Peclet numbers of
Figure 18 corresponds to the broader OTN1 temperature event pictured in the upper-right panels of
Figure 10,
Figure 15 and
Figure 16.
From 2D steady-state wellbore-centric flow and temperature expressions (9) and (10), r1q1 = r0q0 = KPeΔT0 gives the rate at which heat energy leaves the model crustal volume due to radial heat flow in Peclet number Pe ~ 10 fracture-connectivity structures producing OTN1 temperature excursions ΔT0 ~ 0.05–0.1 °C. Advective heat energy leaving the model crustal volume via wellbore-centric fluid inflow structures of thickness ℓ is then ΔQad = q0 2πr0 ℓ = 2π Pe KℓΔT0. For Pe = 10 and ℓ = 1 m, ΔQad = 2π × 103 W/m/°C 1 m 0.1 °C ~20 W for each temperature event. A similar degree of wellbore-centric heat, ΔQcd ~20 W, exits from the crustal volume due to conduction, Pe ~ 1, intervals of wellbore length ℓ = 10 m.
The heat energy of a crustal volume of size 103 m3 and heat capacity 840 J/kg/°C × 2200 kg/m3 at 100 °C ambient temperature is E = 100 GJ. At a prospective loss of heat energy on order of 40 W due to OTN1 advection temperature events and associated heat conduction, the model crustal volume loses heat energy ΔE ~ 40 W·3 × 107 s ~1.2 GJ at the rate of 1% per year. As the advectively lost heat of the OTN1 temperature events is easily replaced by thermal conduction at the model boundaries, the observed heat rate loss is consistent with a steady-state thermal condition. Advective heat flow into the model volume via a wellbore-centric flow structure occurs at a rate, q1 = KPeΔT0/r1 ~ 0.3 W/m2, about 6 times the nominal crustal heat flow of 50 mW/m2. Given that the OTN1 temperature ‘events’ are an observed phenomenon that are an order of magnitude greater than can be expected from purely thermal conductivity variations, the above given numbers illustrate that the model-implied heat flows attributed by our working hypothesis for the origin of the temperature ‘events’ are not out of line with ambient crustal heat flow. I.e., 0.05–0.1 °C wellbore temperature deviations can be seen as localized advective temperature ‘events’ that are not suspiciously large deviations from geothermal gradient heat flow.
Further to
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10 and
Figure 11 temperature modelling results, spatially averaged fluid flow velocity estimates proceed from model Peclet numbers, v
0 ~ P
eD/φr
0 at the wellbore and v
1 ~ P
eD/φr
1 at the model periphery. For a model P
e ~ 10 advective flow system with 10 m external radius in a crustal medium of mean ambient porosity φ ~ 0.01 and thermal diffusivity D ~ 0.7 × 10
−6 m
2/s, the external crustal inflow fluid flow velocity v
1 ~ 0.7 × 10
−4 m/s. These inferred model fluid flow rates can be put into context with reference to convective heat transport, which typically involves fluid flow rates in excess of 10
−7 m/s [
33]. Fluid flow rates of order 10
−7 m/s can be inferred from temperature data for planar crustal fluid flow [
29]. The model flow rates are thus consistent with wellbore-stimulated localized enhanced flow/transport processes giving rise to localized temperature deflections of order 0.05–0.1 °C.
From Darcy’s law (1), the associated model permeability of the fracture-conductivity flow structure generating OTN1 temperature events, κm ~ vµ/∂rP, is given by wellbore-crust pressure differential ΔP/Δr and fluid viscosity µ ~ 0.5 × 10−3 Pa·s. Estimating the wellbore-crust pressure differential ΔP as the difference between wellbore hydrostatic pressure Ph ~ 10 MPa/km·1.5 km and crustal pore pressure given by the minimum principal stress σh ~ Pp ~ 22 MPa/km·1.5 km for crustal minimum principal stress at 1.5 km depth, κm ~ 0.7 × 10−4 m/s⋅0.5 ×·10−3 Pa∙s × 10 m/(12 × 1.5 × 106 Pa) ~2 × 10−14 m2 ~ 0.02 Darcy.
The fracture connectivity parameter associated with the fracture-connectivity flow structures generating observed temperature events is then κ
m ~ κ exp(α
mφ) for φ ~ 0.01 and κ ~ 1 μDarcy is then α
m ~ 1000. If we associate an effective ambient value for poro-connectivity α ~ 500 (Figures 25–29 [
24,
25,
26,
27]), then an OTN1 temperature event model flow structure poro-connectivity α
m ~ 1000 is of order twice the ambient value is nominally characteristic of Peclet number P
e ~ 10 flow structures.
5. Wellbore Temperature Event Modelling as Assessment of EGS Stimulation of Basement Rock
Fennoscandia basement rock wellbore OTN1 temperature event modelling pictured in
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12,
Figure 13,
Figure 14,
Figure 15,
Figure 16,
Figure 17 and
Figure 18 suggests a canonical or type concept of basement rock fracture-connectivity permeability that is amenable to detailed numerical investigation of wellbore-centric fluid processes in Dm-scale crustal volumes characterised by spatially-correlated poroperm distributions. Porosity spatial correlation is defined by empirical condition (i) that a wellbore porosity sequence φ(ξ) within the crustal volume has a Fourier power-spectrum S
φ(k) that scales inversely with spatial wavenumber k, S
φ(k) ∝ 1/k
β, β ~ 1. The spatially-correlated normal distributions of porosity φ(x,y,z) give the associated permeability κ(x,y,z) ∝ exp(αφ(x,y,z)) fields a lognormal distribution for sufficiently large parameter α in accord with empirical conditions (ii) and (iii).
Our present wellbore-centric flow modelling results can be placed in a wider basement rock permeability stimulation context:
OTN1 solute-transport galvanic well-log profiles parallel OTN1 basement rock temperature profiles.
Deep basement well-log and well-core data supporting spatial-correlation empirics (I)–(III) imply general application to EGS basement rock stimulation.
Crustal deformation energetics appear to favour spatially-correlated granularity over planar continuum flow structures, implying wide application of the present modelling construct.
Wellbore-centric flow modelling provides a simple calculus for the physical scales needed for successful EGS commercial outcomes.
5.1. OTN1 Basement Rock Solute Transport Events
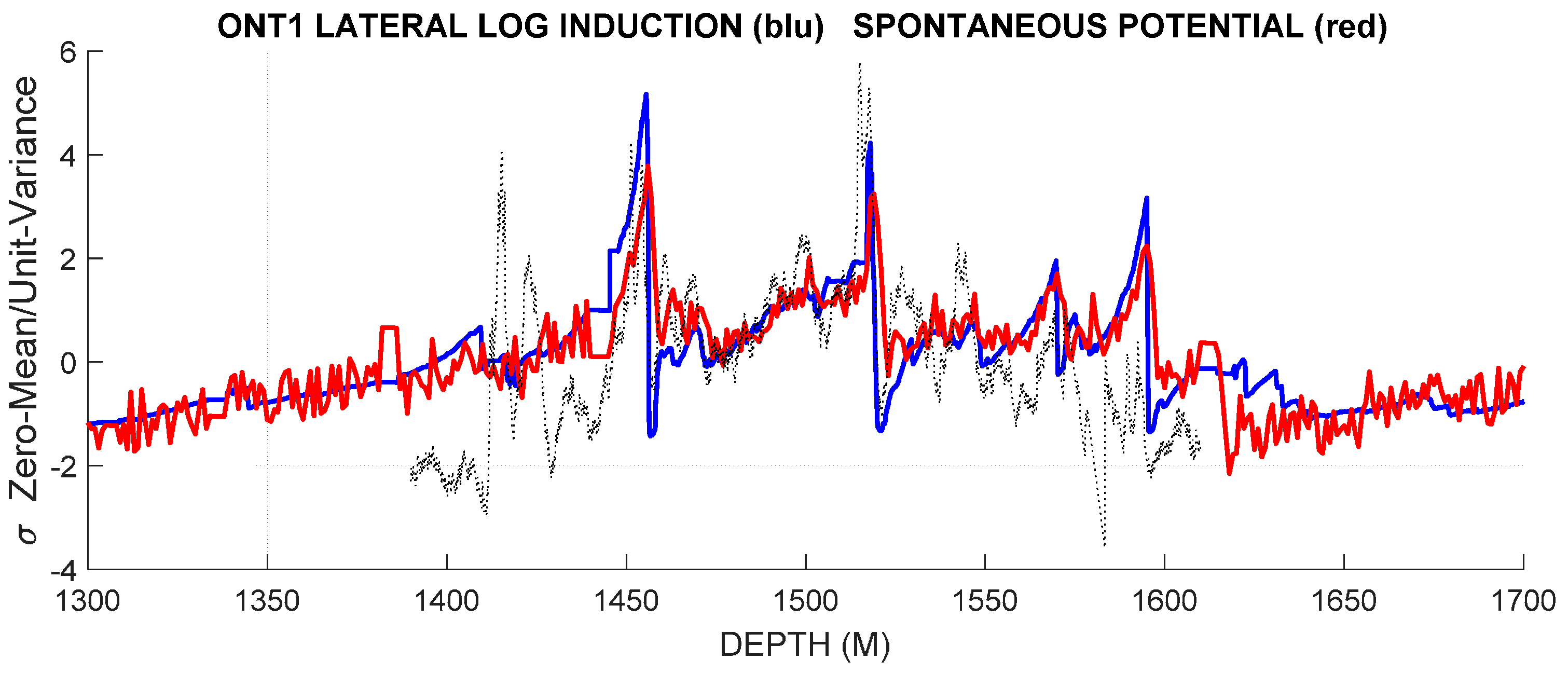
It is plausible that the episodes of fluid influx into the OTN1 well that transport heat to the wellbore fluid also register as electrical conductivity fluctuations responding to increases solute content and/or solute transport that registers as a spontaneous potential signal.
Figure 19 indicates considerable spatial correlation between the OTN1 temperature profile from
Figure 2 (black dots) and two OTN1 galvanic profiles, lateral log induction (blue trace) and spontaneous potential (red trace). As solute concentrations obey a gradient law similar to Fourier’s law of heat transport, temperature modelling is similar to fluid solute concentration modelling. However, while the gradient flow principle is the same, brine concentrations are affected by local rock mineralogy with no parallel in thermal properties, hence a one-to-one correspondence between temperature and solute wellbore fluid inflow events is not expected.
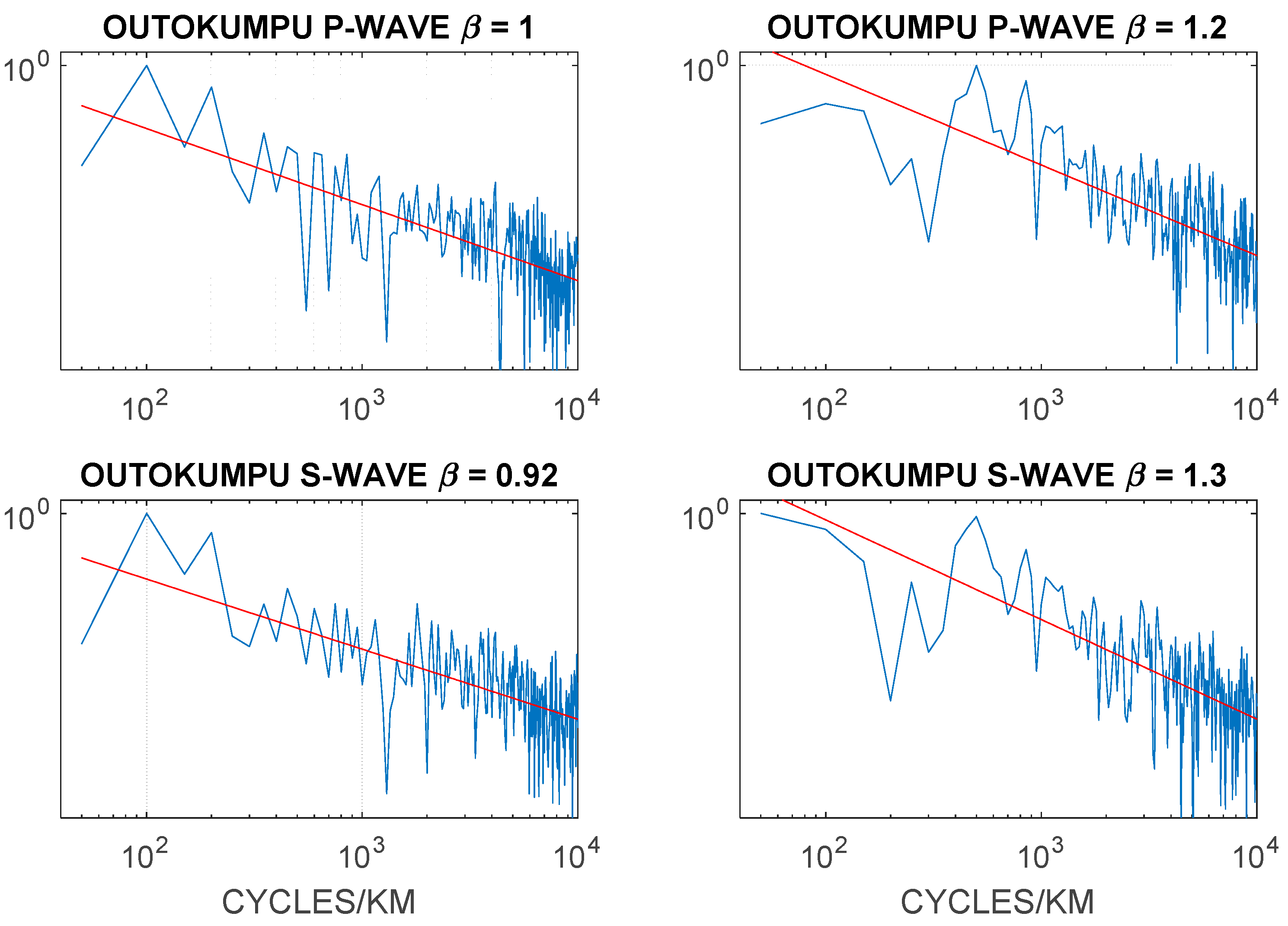
Fluid solute and electrical conductivity studies at the 2.5 km deep Outokumpu mining district wellbore [
28] reveal the total dissolved solids range from 15 g to 50 g per liter for SO
4 and Mg species [
34], with electrical conductivities ranging between 10 mS/cm and 50 mS/cm steadily growing over a period of years since drilling [
35].
5.2. Basement Rock Well-Log and Well-Core Empirics for KTB, Fennoscandia and Borrowdale Metamorphic Rock
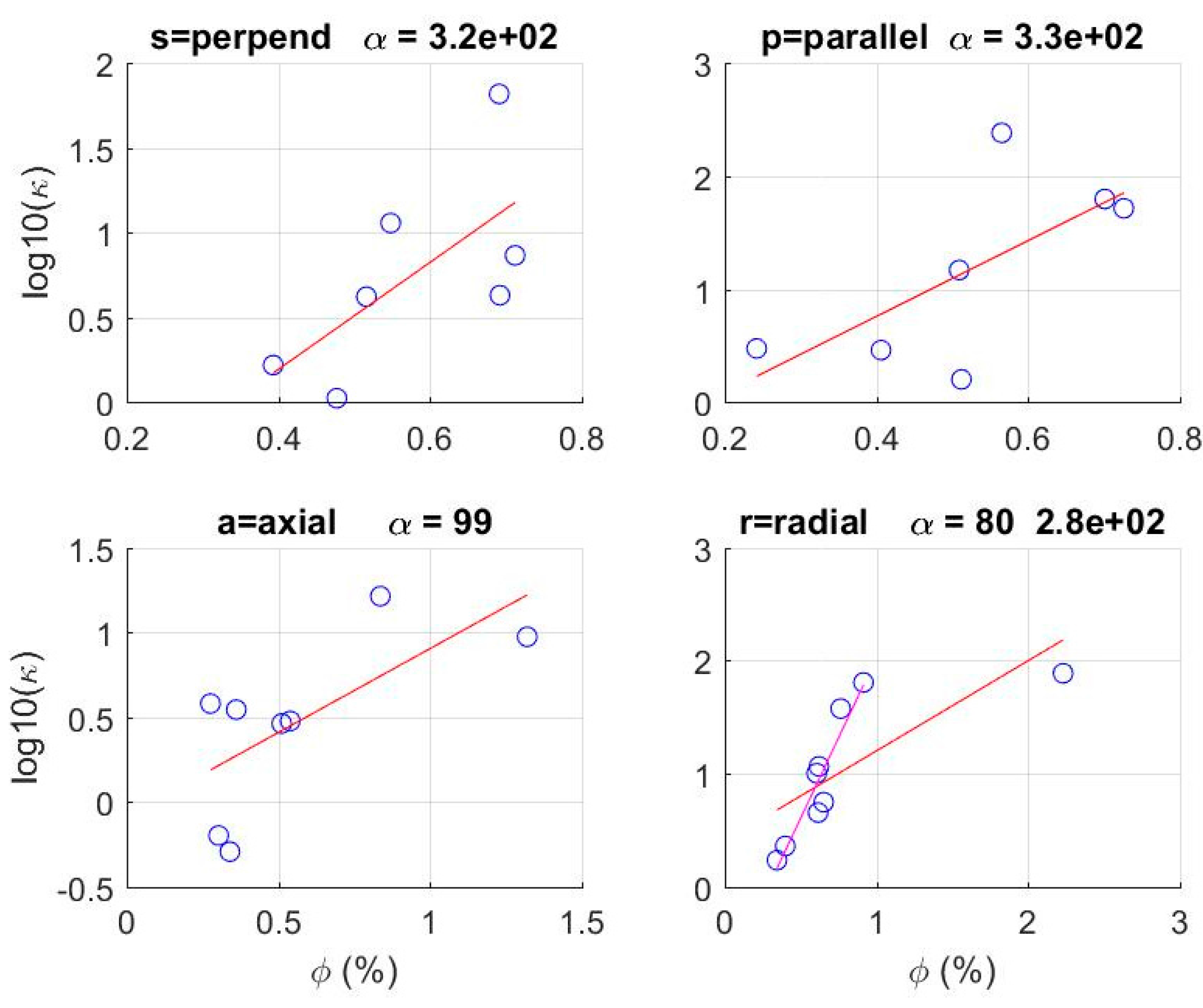
Compaction of spatially-uncorrelated porous media presents no conceptual difficulties. Upon increasing compaction, pore fluid driven out of a rock comprising spatially-uncorrelated grain populations leaves disordered grains squeezed together to fill pore voids with cements filling remaining interstices and no change in the degree of spatial organization e.g., [
36]. Less obvious is the effect of increased compaction on spatially-correlated porous media: what becomes of the spatial-correlation flow structures evident at 1–5 km depths in reservoir rock worldwide when compaction reduces fluid content at sub-reservoir 5–10 km depths? Are spatial correlation flow structure empirics (i)–(iii) destroyed by continued compaction or are correlation structures preserved as relic or fossilised forms at increasing depth?
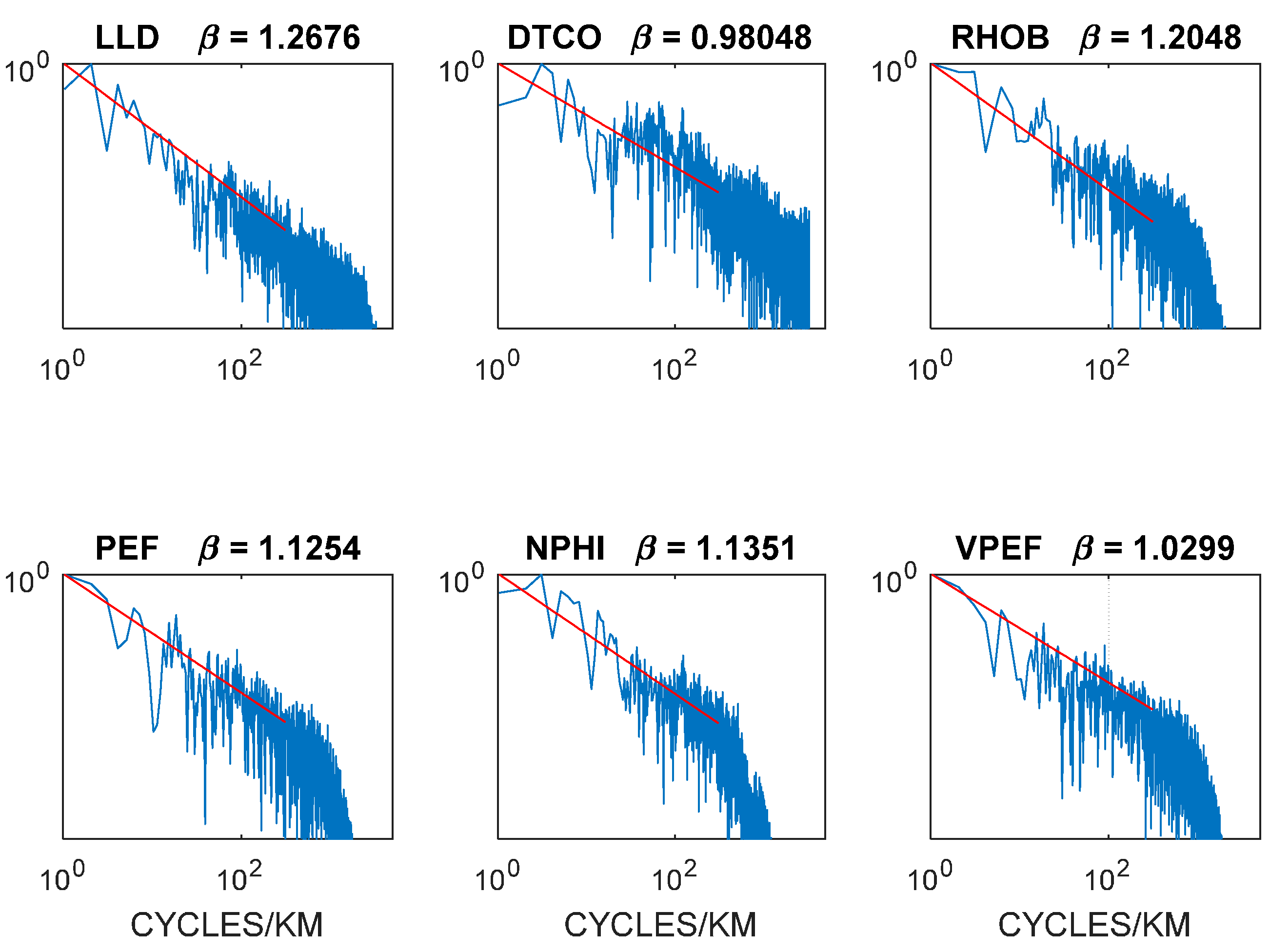
KTB well-log spatial fluctuation data at 6–8 km depths indicate that crustal compaction processes preserve the spatial fluctuation heterogeneity and power-law spectral scaling, S(k) ∝ 1/k
β, β ~1, observed at 1–5 km depths (
Figure 20 and
Figure 21; [
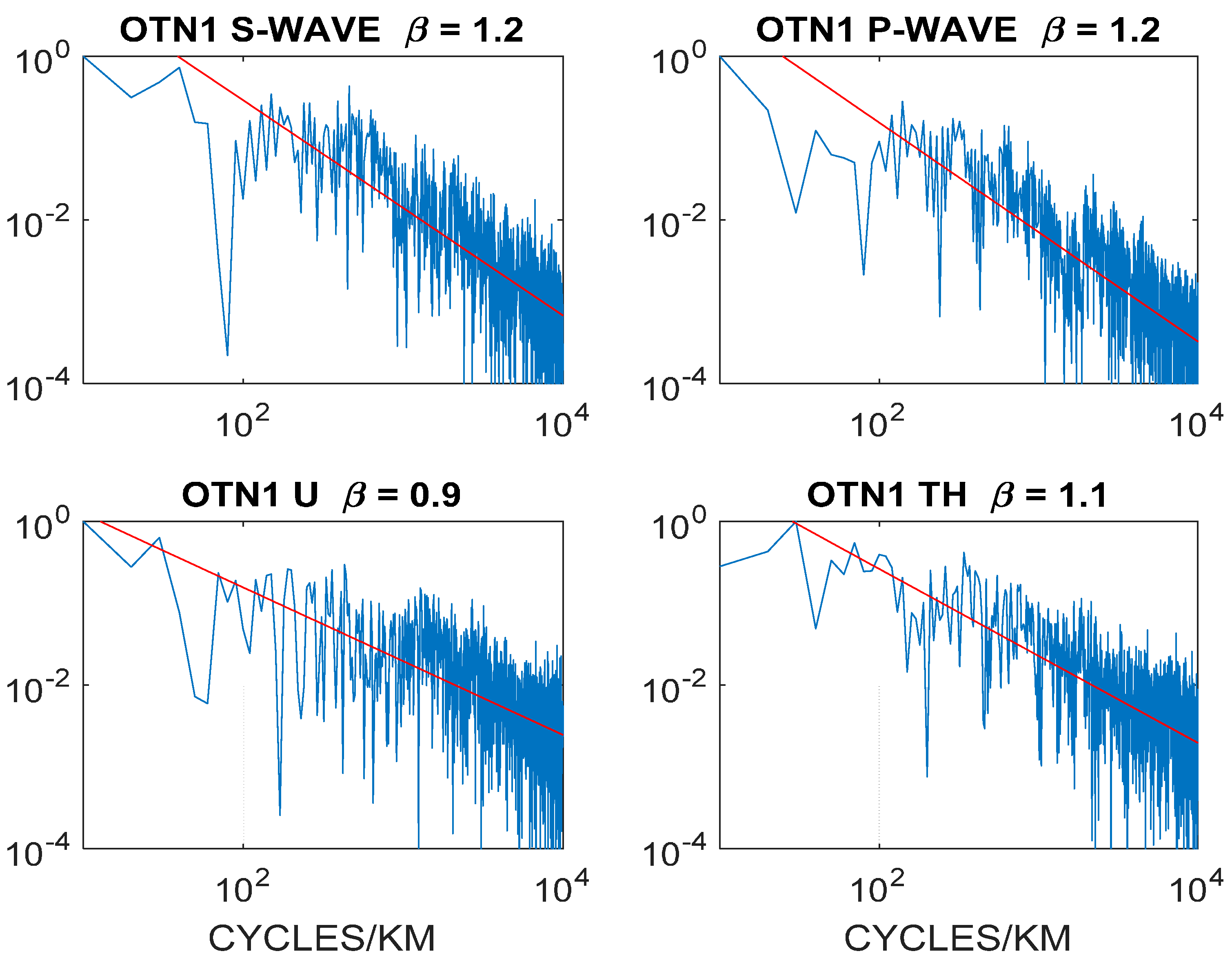
24]). It is also seen that OTN1 and Outokumpu mining district Fennoscandia basement rock subject to past high-grade metamorphism preserves S(k) ∝ 1/k
β, β ~ 1, spatial correlation spectral scaling to 2.5 km depths (
Figure 22 and
Figure 23; [
28]).
Further, KTB well core from 4 km to 5.5 km depth (
Figure 24 and
Figure 25; [
24]) and well-flow data from highly metamorphosed low-porosity/low-permeability Borrowdale Volcanics Group (BVG) in Cumbria UK (
Figure 26,
Figure 27 and
Figure 28; [
25,
26,
27]) preserve the spatial-correlation poroperm relation κ(x,y,z) ∝ exp(αφ(x,y,z)) introduced as crustal fluid-rock interaction empirical relation (III). KTB well-core data and BVG field data yield empirical values for the poro-connectivity parameter α in the poroperm relation κ ∝ exp(αφ) that is valid for low porosity basement rock. It is observed that as porosity declines with increasing compaction, φ → 0.01, basement rock fluid flow continues to follow fracture-connectivity percolation flow paths characterized by increasing values of poro-connectivity parameter α → 300–700.
5.3. Crustal Deformation Energetics for Spatially-Correlated Crustal Fluid Flow Granularity
Well-log, well-core, and well-productivity empirics focus on the granular rather than the spatially-averaged effective continuum nature of crustal rock. Key features of rock granularity emerge from considering the empirical spatial fluctuation relation between well-core porosity and well-core permeability, δφ ∝ δlog(κ) [
5,
6,
14,
15,
16,
17].
Consider characterizing the porosity of a sample rock volume by a number n of grain-scale defects associated with the pore population. The grain-scale defects are cement bond failures that allow pores to communicate their fluid content with adjacent pores. Such defects are logically associated with pores as pores have the lowest elastic modulus and hence are subject to the greatest local strains within a crustal volume undergoing deformation during tectonic stress loading. In this granularity construct, grain-scale defect connectivity offers a simple quantitative account of crustal rock permeability associated with fluid percolation between pores.
For a sample rock volume with n defects, spatial connectivity between defects within the sample scales as the combinatorial factor n! = n(n − 1)(n − 2)(n − 3) … 1. Permeability associated with defect connectivity is thus quantified as κ ∝ n! A well-known mathematical relation, log(n!) ~n(log(n) − 1), quantifies the effect of incrementing the defect population of a sample volume by a small number δn << n. For porosity increment n → n + δn, the incremented permeability is δlog(n!) = log((n + δn)!) − δlog(n!) ~(n + δn)log(n + δn) − 1) − n(log(n) − 1), giving δlog(n!) ~δn log(n). This relation exactly expresses the empirical property of well-core poroperm sequences, δφ ∝ δlog(κ). For porosity proportional to defect number, φ ∝ n, and permeability proportional to defect connectivity factor n!, κ ∝ n!, cement bond defect connectivity in a granular medium gives a direct mechanism for the essentially universally observed properties of well-core poroperm spatial correlation (II) and its associated lognormality of crustal permeability distributions at core scale and well-production at field scale (III).
Placing EGS-type stimulation in wellbore-centric fluid pressurization context, the above granularity construct quantifies the effect on inter-granular fluid flow of introducing a single grain-scale defect into a poroperm structure, n → n + 1. The incremental effect differs for Poiseuille flow versus granular percolation: adding a single defect to a conduit between continuum dislocation surfaces has a smaller effect than adding a single defect to disseminated/granular-connectivity structures of empirics (i)–(iii).
For a fluid of dynamic viscosity μ driven by pressure gradient P’, Poiseuille volumetric flow per unit breadth of the flow front is Q (m2/s) = P’ Δ3/12 μ (Pa/m m3/Pa·s). The corresponding fluid velocity is v (m/s) = P’ Δ2/12 μ. For a gap Δ comprising a number n defects in the continuum flow structure, the mean gap increment is δΔ ~ Δ/n. It follows from (v + δv)/v = 1 + δv/v = (Δ + δΔ)2/Δ2 ~ 1 + 2δΔ/Δ, that adding a single defect to the medium increases the gap by Δδ and increases fluid velocity by δv/v ~ 2/n.
For the disseminated empirical granular medium with fluid velocity v ∝ exp(αφ), the equivalent increment gives (κ + δκ)/κ = 1 + δκ/κ ∝ exp(αδφ) ~ 1 + αδφ, whence for φ = nδφ, δκ/κ = δv/v ~ αδφ = αφ/n. For standard reservoir formations with porosity in the range 0.1 < φ < 0.3, the empirical values of α, 20 < α < 40, give αφ ~ 6 ± 2 fluid velocity increment factor for aquifer formations. For basement rock with porosity an order of magnitude smaller, φ ~ 0.01, the value of α increases by an order of magnitude, 300 < α < 700, giving an empirical estimate of fluid velocity increment factor αφ ~ 5 for basement formations.
Allowing for rough surfaces at large confining stresses in the deep crust, the effective exponent characteristic of Poiseuille flow mechanics significantly increases [
34]. If fracture surface roughness is included within the flow conduit, exponents for the effective Poiseuille flow factor Δ
m are modelled to increase from 3 to ~5–10 [
38,
39]. The increased exponent heightens the effect of increments in defect population on fluid flow in tight rock.
For wellbore-fluid stimulation of crustal permeability,
Table 1 indicates that creating a grain-scale defect in a crustal volume produces greater flow effect if the defect is embedded in a granular percolation flow structure than if the defect contributes to a conduit gap in the smooth continuum flow structures of the discrete fracture concept of EGS stimulation. It follows that energy expended by wellbore pressurization is more effective in dissipating wellbore fluid pressure fronts if defects generated by fluid pressures contribute to granularity flow structures than if they contribute to continuum flow structures. If the observed effect of large confining stresses is taken into account, the empirical granularity picture is consistent with rough fracture surfaces expected at the limit of thin flow conduit gaps.
Given the extensive evidence of well-log, well-core, and well-flow empirics (i)–(iii) as the ambient condition of crustal rock, we may argue that wellbores penetrating crustal media will typically encounter localised disseminated/granularity rather than planar geometric/continuum flow surfaces associated with discrete fracture displacement structures.
We can interpret
Table 1 further to argue that the ambient crustal empirics (i)–(iii) result from the implied energetics of defect insertion through rock-fluid interaction. Rock stress involving fluids is more easily dissipated if fluid permeability stimulation proceeds through spatially-correlated fracture-connectivity granularity rather than through spatially-uncorrelated effective-medium planar continuum displacements. For generating ambient crustal fluid-rock flow conditions, the fact that porosity increments require doing work against confining stresses means that it is energetically favourable for defect enhancement to proceed in a spatially-correlated granularity medium than in a spatially-uncorrelated continuum medium. Discrete fracture systems may thus be seen to characterize crustal tectonic settings in which solid-rock displacement rates due to far-field tectonic plate motion exceed the rate at which fluid pressures can dissipate through slower fracture-connectivity mechanisms. EGS mechanisms based on local wellbore-centric fluid pressurization rather than elastic stress generated by far-field tectonics may thus couple more readily to the slower ambient-crust defect injection processes leading to spatially-correlated granularity than to the faster defect injection processes leading to discrete-fracture displacements.
5.4. EGS Couplet Scale Dimensions
The irreducible statement of EGS principle is to pass fluid from an injector wellbore through an ambient hot crustal volume to a producer wellbore at a sufficient rate over a sufficient length of time that the recovered heat energy covers the cost of: (a) drilling sufficiently deep wells to access sufficient temperature and (b) stimulating the wellbore-centric crustal volumes to sufficient radius to access a sufficient crustal volume.
The scale-sufficiency conditions for an EGS wellbore-centric flow doublet are simply quantified by considering the radial transfer of heat energy via wellbore fluid injected into the surrounding crust. For wellbore radius r
0 and length ℓ in a crustal volume of porosity φ, fluid of temperature T
0 and volumetric heat capacity ρC injected or produced at radial velocity v
0 steadily transfers Q = 2πr
0φv
0 ℓ ρCT
0 watts of heat energy from/to the wellbore to/from the crust. The crustal temperature surrounding an injector wellbore grows as a function of radius and time from the initial crustal temperature as:
for D ≡ K/ρC the thermal diffusivity of the crustal medium, ν = P
e/2 one-half the Peclet number P
e ≡ r
0φv
0/D, and J
ν(:) and Y
ν(:) the order ν Bessel functions of the first and second kind respectively [
40].
Peclet number P
e = r
0φv
0/D = r
0φv
0ρC/K links the crustal temperature growth to the rate at which the wellbore supplies heat:
For a given injection of heat energy Q, the system Peclet number of resultant temperature field diminishes in proportion to the wellbore length ℓ and fluid temperature T0. For a maximally stimulated wellbore that supports Pe ~ 5 heat transport across every meter of wellbore length for crustal rock temperature 100 °C, the total wellbore-centric heat extraction rate is Q ~ 10 MW per km of wellbore.
Figure 29 shows the temperature growth curve T(r,t) as a function of Peclet number. A km-long EGS wellbore doublet capable of producing Q ~ 10 MW heat energy for 30 years from crust at 100 °C requires a wellbore doublet radially offset by a distance ~50 m. An EGS wellbore doublet separated by 50 m thus requires that each wellbore be effectively stimulated to a 25 m radius.
6. Summary/Conclusions
Despite abundant well-log, well-core, and well-flow counter-evidence, the working assumption that fluid flow in geological formations is effectively uniform due to spatial averaging over uncorrelated poroperm fluctuations has remained in place since the mid-19th century observations and innovations of Darcy and Dupuit [
33,
41,
42,
43,
44,
45,
46,
47,
48,
49]. This stasis is essentially a practical matter: for both groundwater and hydrocarbon crustal fluids, it has been found cost effective to ignore manifest fluid flow heterogeneity by the simple practice of drilling more wells.
Groundwater wells are shallow and therefore inexpensive. The considerable value of hydrocarbon fluids means that, first, a relatively few high-flow/high-profit oil/gas wells tend to cover the cost of many low-flow oil/gas wells, and, second, the population of many low-flow wells that accompany the few high-flow wells are generally profitable for considerable lengths of time [
19].
Geothermal energy provision, in contrast, lacks the well-cost offsets afforded groundwater and hydrocarbon reservoir fluids. In natural convective geothermal systems with high fluid temperatures and permeabilities, the excessively large flow-rate demand to power turbines means that crustal flow heterogeneity cannot be cost-effectively solved by the rubric of spatial averaging [
21]. Subsurface imaging is required to achieve ‘smart-drilling’ practice to keep well costs down in tapping naturally convective geothermal flow systems [
18]. In low-porosity/low-permeability basement rock geothermal systems, the high cost of drilling and the limited technical means of EGS permeability enhancement for wellbore-to-wellbore flow mean that net fluid through-put remains generally non-commercial for power-production [
1,
2].
Balancing the negatives of basement rock EGS geothermal heat energy provision are the positives of great abundance of carbon-free heat energy for direct use purposes. The accessible heat energy in a 50 m thick crustal section 5 km below any of Finland’s district heating plants with a 5-km municipal service radius is of the order E = πR
2ℓ ρC T ~0.75 × 10
18 J ~ 150 million BOE, the energy content of a sizeable conventional oil field [
49]. The heat energy content accessible to a single fully-stimulated P
e ~ 5 EGS doublet of 50 m offset and 3 km horizontal extent to produce 30 MW heat energy extraction is ~1000 times the annual energy consumption of currently operating district heating plants. From
Figure 29, conductive recharge of an EGS 30 MW doublet heat extraction crustal volume can supply heat to the injector-producer wellbore pair for ~30 years.
Our OTN1 wellbore temperature event modeling assessment of naturally occurring basement rock fracture-connectivity flow systems suggests that the necessary condition of ‘full stimulation’ for EGS wellbore doublets is that every 3–5 m interval of wellbore supports a P
e ~ 5–10 fracture-connectivity flow path between the doublet pair. Model estimates of natural flow stimulation through naturally enhanced poro-connectivity parameter α indicates that doubling the poro-connectivity from ambient crust value α ~500 derived from well-core data (e.g.,
Figure 24,
Figure 25,
Figure 26,
Figure 27 and
Figure 28, [
24,
25,
26,
27]) to α ~1000 achieves the necessary stimulation goal for wellbore-centric flow systems of order 10-meter radius.
Cross-well fracture-connectivity paths may be a narrow Pe ~ 10–15 flow structure or broader Pe ~ 5 flow structures, but radial cross-well fluid flow must occur along the entire length ℓ of the injection-production wellbore pair to achieve full EGS heat production. In this definition of fully-stimulated EGS wellbore production Q, we use a conservative estimate Q = 2πPeKℓ’T0 where the effective length unit of wellbore heat production is 3 m, so that ℓ’ = ℓ/3. Additionally, to produce ~10 MW from fully-stimulated wellbore-pairs for 30 years, the radial cross-well flow-connectivity flow structures must be of order 50 m path length, equating to ~25 m stimulation radius for each wellbore. Development of the full axial-stimulation and the 25 m radial-stimulation conditions indicated by OTN1 temperature event assessment for deep crustal basement EGS are currently very much works in progress.