Principal Mismatch Patterns Across a Simplified Highly Renewable European Electricity Network
Abstract
1. Introduction
2. Modelling and Methods
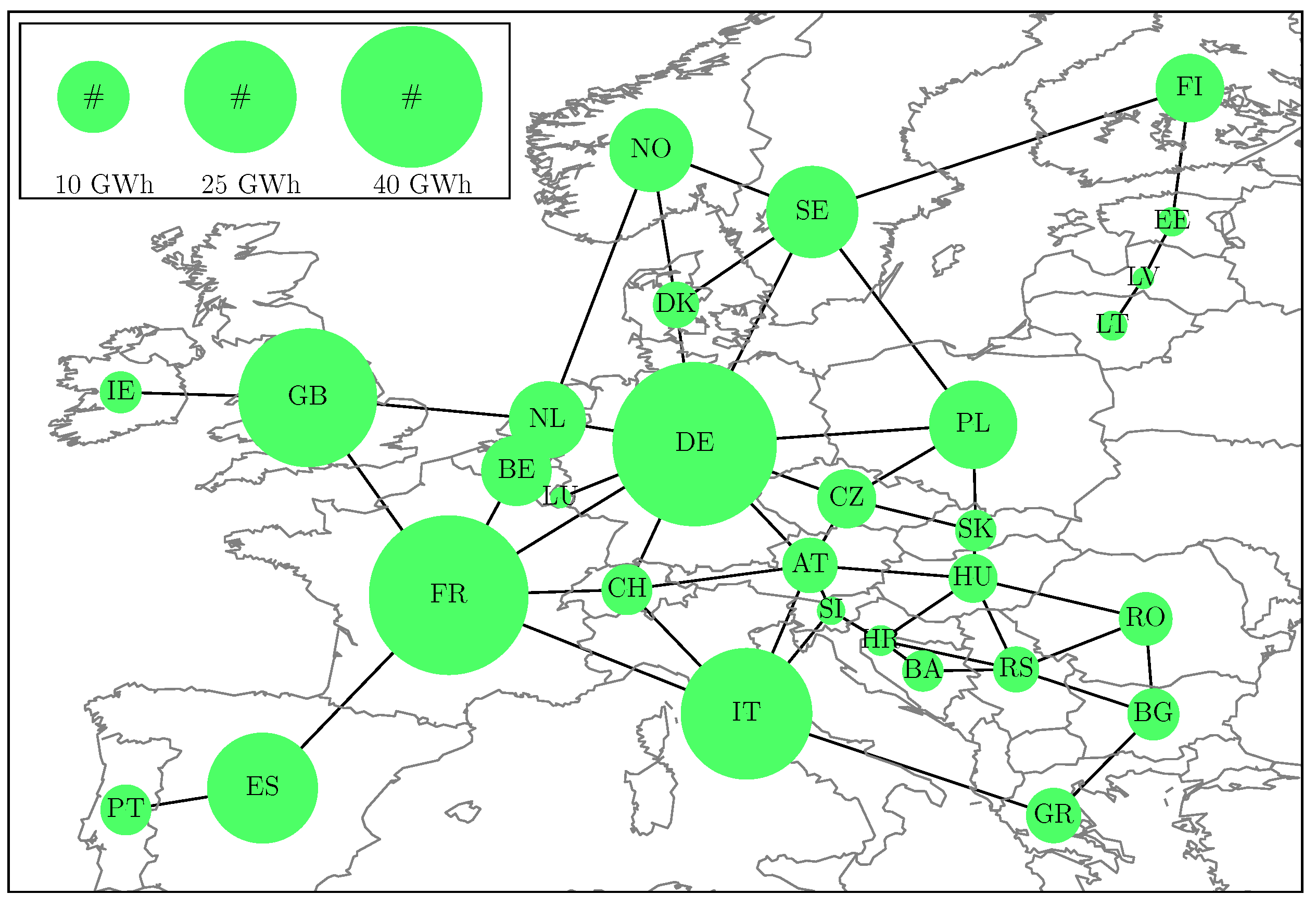
2.1. Modelling of a Simplified Highly Renewable European Electricity Network
2.2. Infrastructure Measures
2.3. Principal Component Analysis
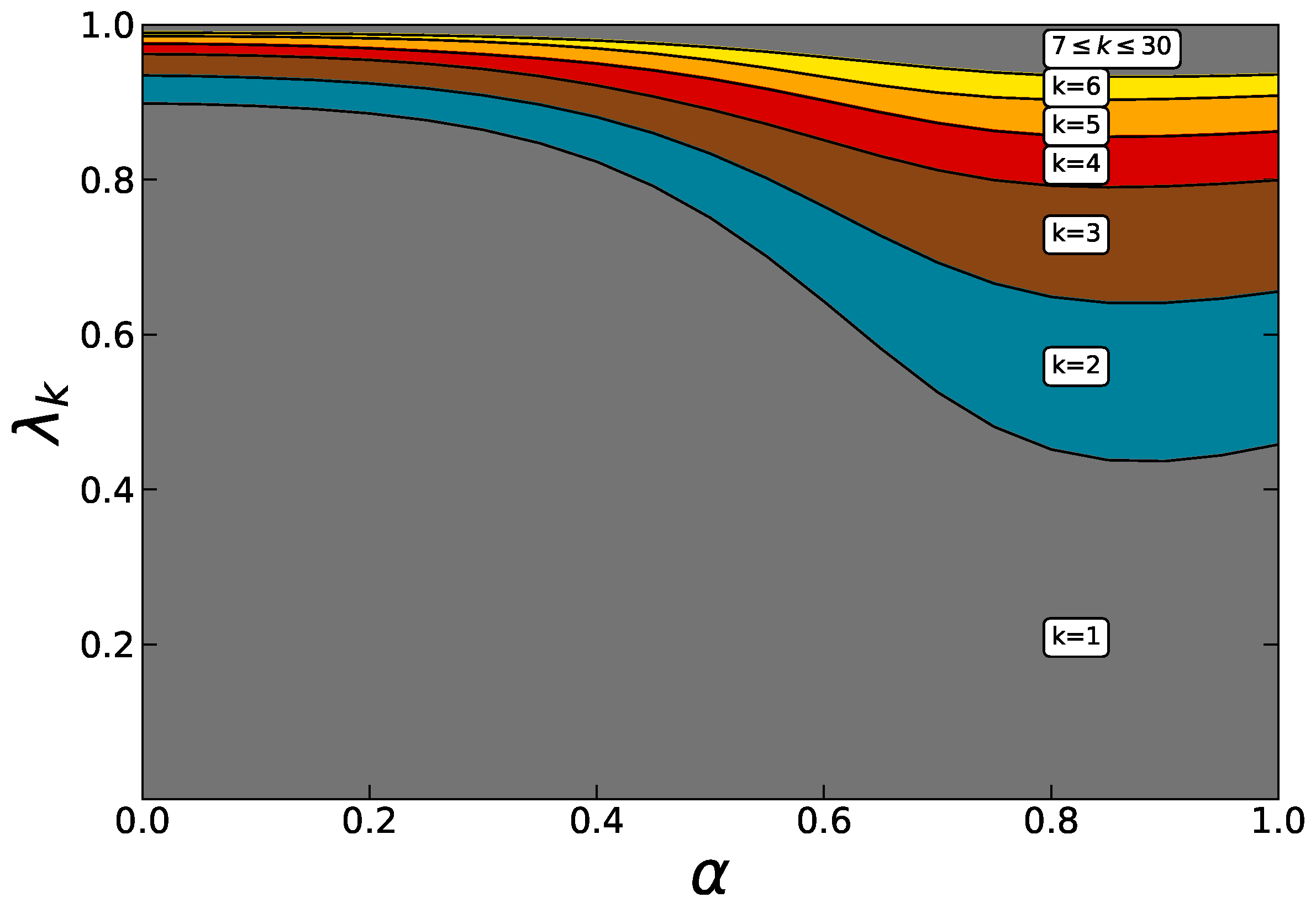
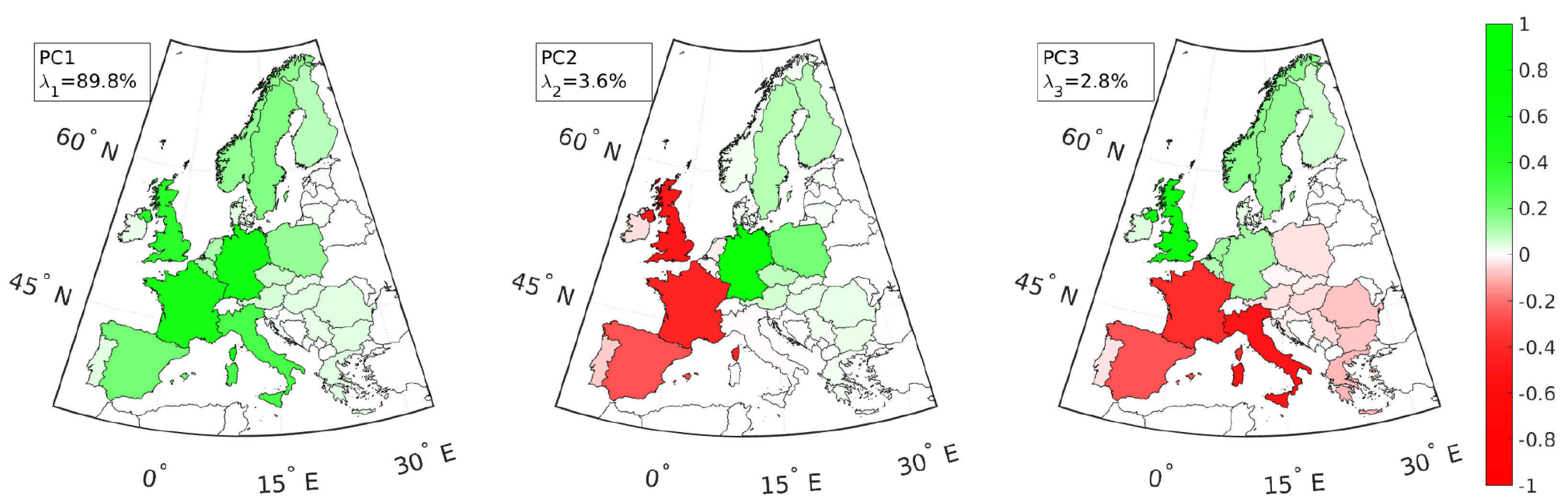
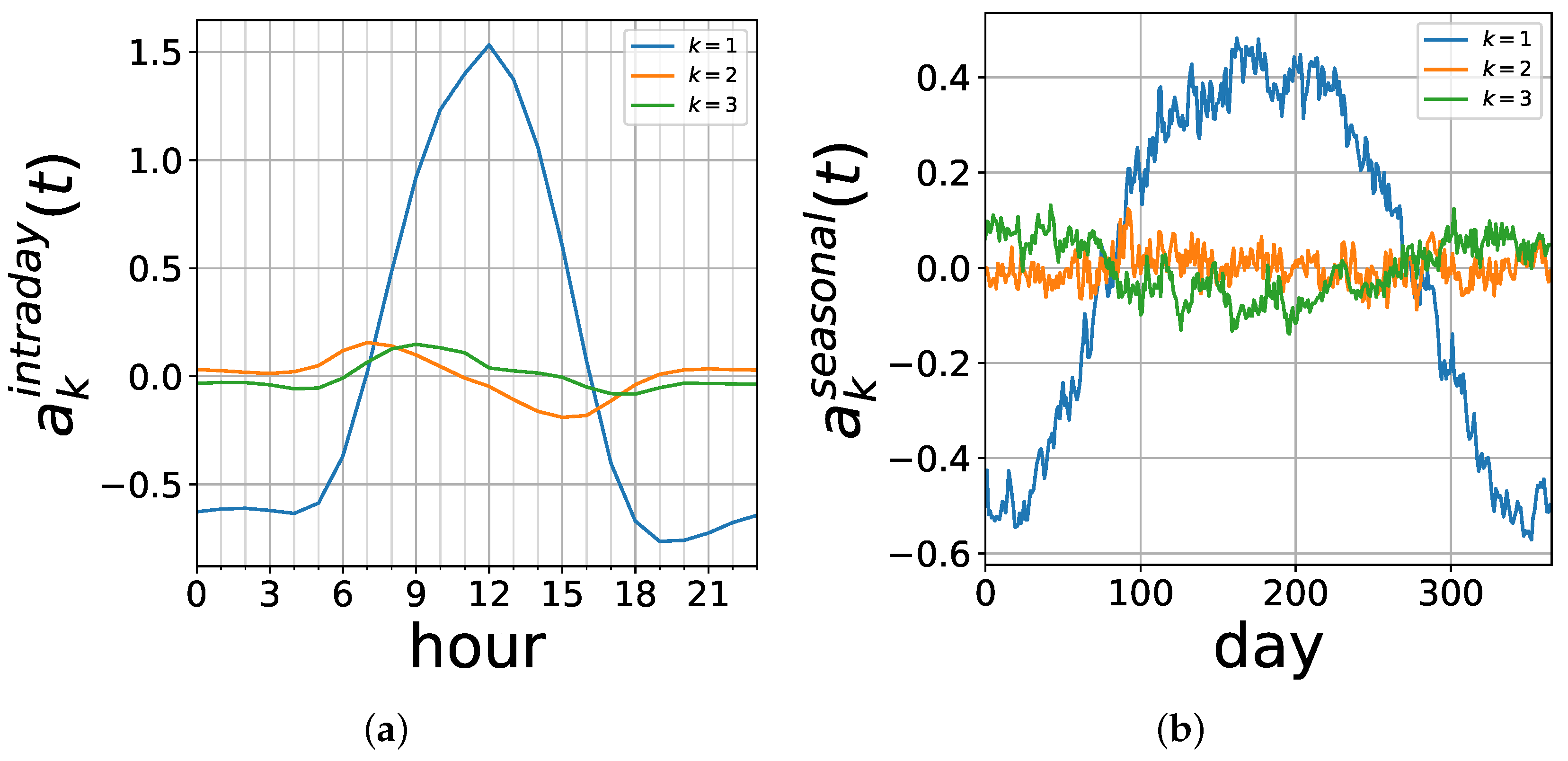
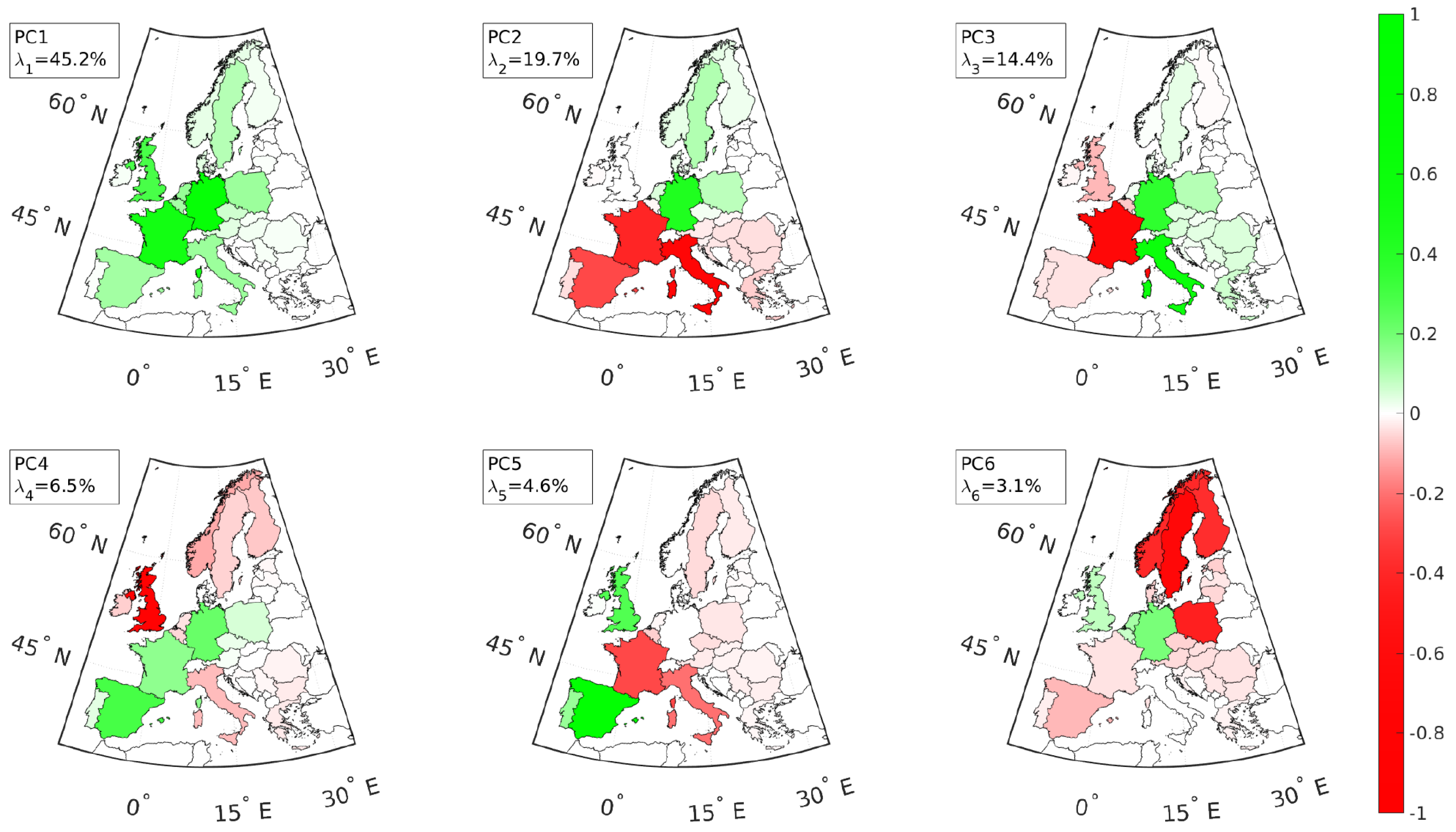
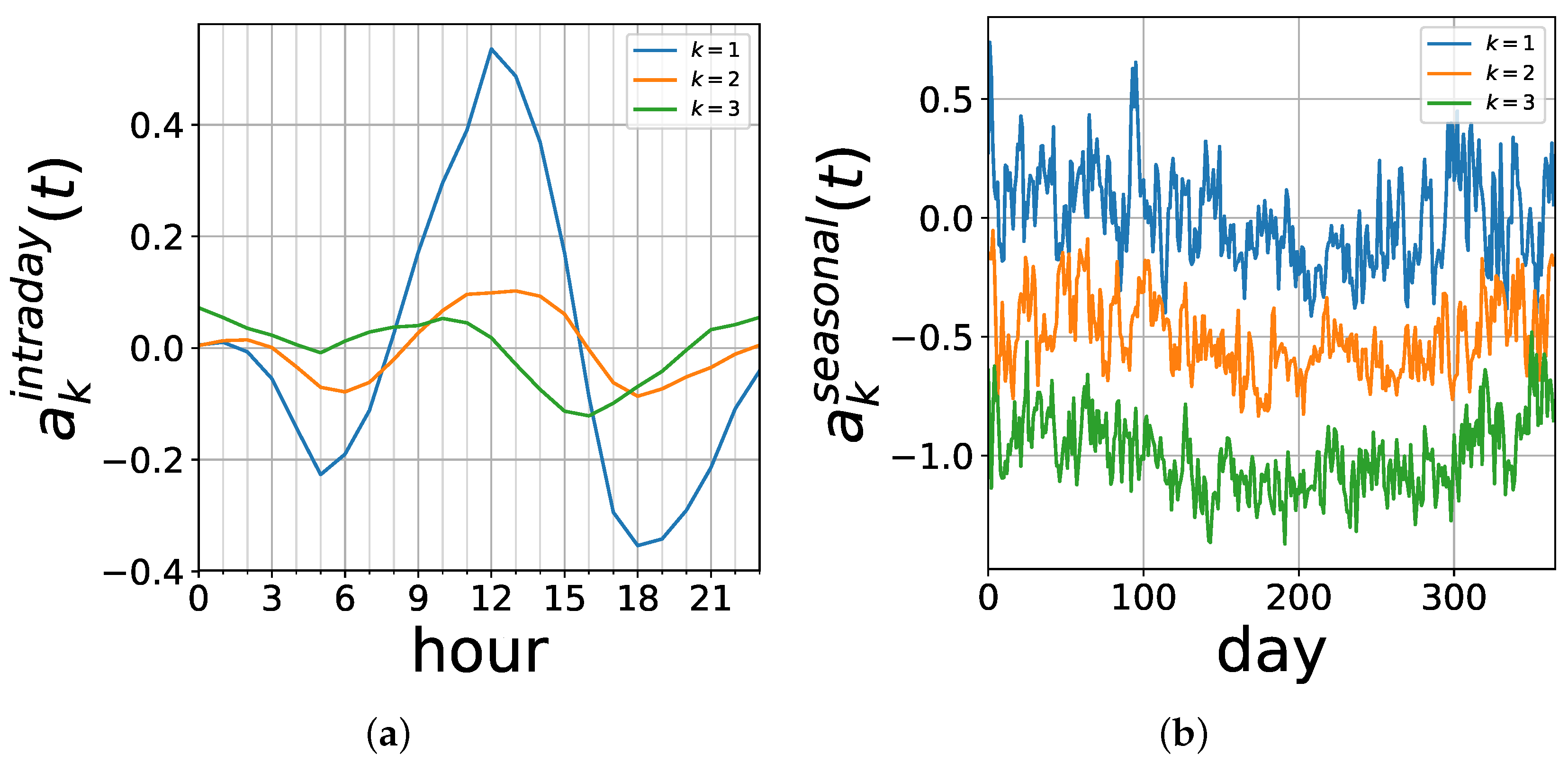
3. Results: Principal Mismatch Components
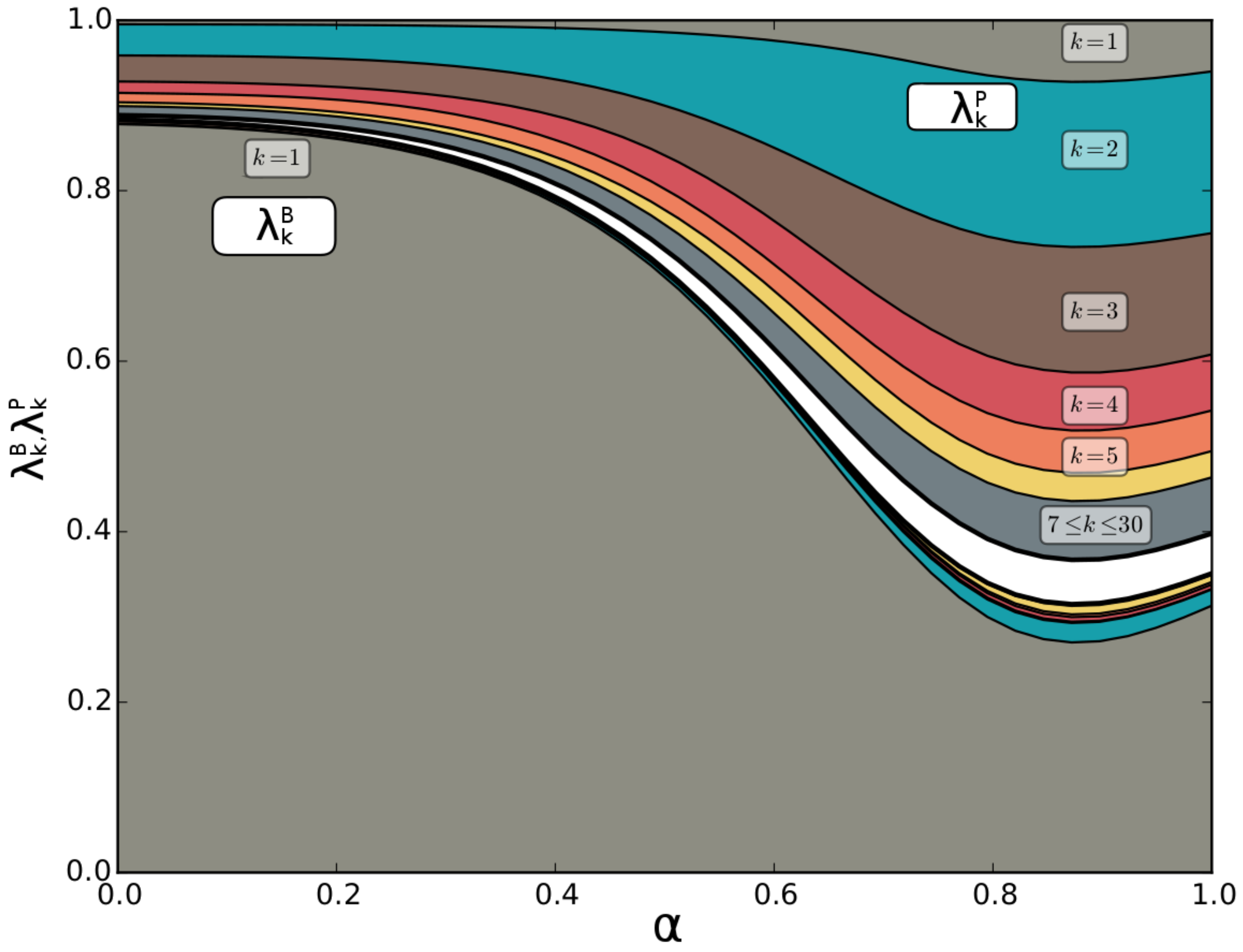
4. Discussion: Contribution of Principal Mismatch Patterns to the Balancing and Transmission Infrastructures
5. Conclusions and Outlook
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PCA | Principal Component Analysis |
References
- Graabak, I.; Korpås, M. Variability characteristics of European wind and solar power resources—A review. Energies 2016, 9, 449. [Google Scholar] [CrossRef]
- Engeland, K.; Borga, M.; Creutin, J.D.; François, B.; Ramos, M.H.; Vidal, J.P. Space-time variability of climate variables and intermittent renewable electricity production—A review. Renew. Sustain. Energy Rev. 2017, 79, 600–617. [Google Scholar] [CrossRef]
- Holttinen, H. Wind power variations in the Nordic countries. Wind Energy 2005, 8, 173–195. [Google Scholar] [CrossRef]
- Apt, J. The spectrum of power from wind turbines. J. Power Sources 2007, 169, 369–374. [Google Scholar] [CrossRef]
- Milan, P.; Wächter, M.; Peinke, J. Turbulent character of wind energy. Phys. Rev. Lett. 2013, 110, 138701. [Google Scholar] [CrossRef] [PubMed]
- Grams, C.; Beerli, R.; Pfenninger, S.; Staffell, I.; Wernli, H. Balancing Europe’s wind-power output through spatial deployment informed by weather regimes. Nat. Clim. Chang. 2017, 7, 557–562. [Google Scholar] [CrossRef] [PubMed]
- Holttinen, H.; Milligan, M.; Kirby, B.; Acker, T.; Neimane, V.; Molinski, T. Using standard deviation as a measure of increased operational reserve requirement for wind power. Wind Energy 2008, 32, 355–378. [Google Scholar] [CrossRef]
- Holttinen, H.; Meibom, P.; Orths, B.; Lange, M.; O’Malley, M.; Tande, J.O.L.; Estanquerio, A.; Gomez, E.; Söder, L.; Strbac, G.; et al. Impacts of large amounts of wind power on design and operation of power systems—Results of IEA collaboration. Wind Energy 2011, 14, 179–192. [Google Scholar] [CrossRef]
- Tarroja, B.; Mueller, F.; Eichman, J.D.; Samuelsen, S. Metrics for evaluating the impacts of intermittent renewable generation on utility load-balancing. Energy 2012, 42, 546–562. [Google Scholar] [CrossRef]
- Lannoye, E.; Flynn, D.; O’Malley, M. Evaluation of power system flexibility. IEEE Trans. Power Syst. 2012, 27, 922–931. [Google Scholar] [CrossRef]
- Huber, M.; Dimkova, D.; Hamacher, T. Integration of wind and solar power in Europe: Assessment of flexibility requirements. Energy 2014, 69, 236–246. [Google Scholar] [CrossRef]
- Ulbig, A.; Andersson, G. Analyzing operational flexibility of electric power systems. Int. J. Electr. Power Energy Syst. 2015, 72, 155–164. [Google Scholar] [CrossRef]
- Schlachtberger, D.P.; Becker, S.; Schramm, S.; Greiner, M. Backup flexibility classes in emerging large-scale renewable electricity systems. Energy Convers. Manag. 2016, 125, 336–346. [Google Scholar] [CrossRef]
- Kiss, P.; Jánosi, I.M. Limitations of wind power availability over Europe: A conceptual study. Nonlinear Process. Geophys. 2008, 15, 803–813. [Google Scholar] [CrossRef]
- Baïle, R.; Muzy, J.F. Spatial intermittency of surface layer wind fluctuations at mesoscale range. Phys. Rev. Lett. 2010, 105, 254501. [Google Scholar] [CrossRef] [PubMed]
- Widén, J. Correlations between large-scale solar and wind power in a future scenario for Sweden. IEEE Trans. Sustain. Energy 2011, 2, 177–184. [Google Scholar] [CrossRef]
- Roques, F.; Hiroux, C.; Saguan, M. Optimal wind power deployment in Europe—A portfolio approach. Energy Policy 2010, 38, 3245–3256. [Google Scholar] [CrossRef]
- Rombauts, T.; Delarue, E.; D’haeseleer, W. Optimal-portfolio-theory-based allocation of wind power—Taking into account cross-border transmission-capacity constraints. Renew. Energy 2011, 36, 2374–2387. [Google Scholar] [CrossRef]
- Thomaidas, N.S.; Santos-Alamillos, F.J.; Pozo-Vazquez, D.; Usaola-Garcia, J. Optimal management of wind and solar energy resources. Comput. Oper. Res. 2016, 66, 284–291. [Google Scholar] [CrossRef]
- Hagspiel, S.; Papamannouil, A.; Schmid, M.; Andersson, G. Copula-based modeling of stochastic wind power in Europe and implications for the Swiss power grid. Appl. Energy 2012, 96, 33–44. [Google Scholar] [CrossRef]
- Czisch, G. Szenarien zur zukünftigen Stromversorgung. Ph.D. Thesis, Universität Kassel, Kassel, Germany, 2005. [Google Scholar]
- Heide, D.; Von Bremen, L.; Greiner, M.; Hoffmann, C.; Speckmann, M.; Bofinger, S. Seasonal optimal mix of wind and solar power in a future, highly renewable Europe. Renew. Energy 2010, 35, 2483–2489. [Google Scholar] [CrossRef]
- Heide, D.; Greiner, M.; Von Bremen, L.; Hoffmann, C. Reduced storage and balancing needs in a fully renewable European power system with excess wind and solar power generation. Renew. Energy 2011, 36, 2515–2523. [Google Scholar] [CrossRef]
- Schaber, K.; Steinke, F.; Hamacher, T. Transmission grid extensions for the integration of variable renewable energies in Europe: Who benefits where? Energy Policy 2012, 43, 123–135. [Google Scholar] [CrossRef]
- Schaber, K.; Steinke, F.; Mühlich, P.; Hamacher, T. Parametric study of variable renewable energy integration in Europe: Advantages and costs of transmission grid extensions. Energy Policy 2012, 42, 498–508. [Google Scholar] [CrossRef]
- Rodriguez, R.A.; Becker, S.; Andresen, G.; Heide, D.; Greiner, M. Transmission needs across a fully renewable European power system. Renew. Energy 2014, 63, 467–476. [Google Scholar] [CrossRef]
- Becker, S.; Rodríguez, R.A.; Andresen, G.B.; Schramm, S.; Greiner, M. Transmission grid extensions during the build-up of a fully renewable pan-European electricity supply. Energy 2014, 64, 404–418. [Google Scholar] [CrossRef]
- Becker, S.; Frew, B.A.; Andresen, G.B.; Zeyer, T.; Schramm, S.; Greiner, M.; Jacobson, M.Z. Features of a fully renewable US electricity system: Optimized mixes of wind and solar PV and transmission grid extensions. Energy 2014, 72, 443–458. [Google Scholar] [CrossRef]
- Gils, H.C.; Scholz, Y.; Pregger, T.; De Tena, D.L.; Heide, D. Integrated modelling of variable renewable energy-based power supply in Europe. Energy 2017, 123, 173–188. [Google Scholar] [CrossRef]
- Andresen, G.B.; Sœndergaard, A.A.; Greiner, M. Validation of Danish wind time series from a new global renewable energy atlas for energy system analysis. Energy 2015, 93, 1074–1088. [Google Scholar] [CrossRef]
- Staffell, I.; Pfenninger, S. Using bias-corrected reanalysis to simulate current and future wind power output. Energy 2016, 114, 1224–1239. [Google Scholar] [CrossRef]
- Pfenninger, S.; Staffell, I. Long-term patterns of European PV output using 30 years of validated hourly reanalysis and satellite data. Energy 2016, 114, 1251–1265. [Google Scholar] [CrossRef]
- Rasmussen, M.G.; Andresen, G.B.; Greiner, M. Storage and balancing synergies in a fully or highly renewable pan-European power system. Energy Policy 2012, 51, 642–651. [Google Scholar] [CrossRef]
- Steinke, F.; Wolfrum, P.; Hoffmann, C. Grid vs. storage in a 100% renewable Europe. Renew. Energy 2013, 50, 826–832. [Google Scholar] [CrossRef]
- Jensen, T.V.; Greiner, M. Emergence of a phase transition for the required amount of storage in highly renewable electricity systems. Eur. Phys. J. Spec. Top. 2014, 223, 2475–2481. [Google Scholar] [CrossRef]
- Bussar, C.; Moos, M.; Alvarez, R.; Wolf, P.; Thien, T.; Chen, H.; Cai, Z.; Leuthold, M.; Sauer, D.U.; Moser, A. Optimal allocation and capacity of energy storage systems in a future European power system with 100% renewable energy generation. Energy Procedia 2014, 46, 40–47. [Google Scholar] [CrossRef]
- Bussar, C.; Stöcker, P.; Cai, Z.; Moraes, L.; Alvarez, R.; Chen, H.; Breuer, C.; Moser, A.; Leuthold, M.; Sauer, D.U. Large-scale integration of renewable energies and impact on storage demand in a European renewable power system of 2050. Energy Procedia 2015, 73, 145–153. [Google Scholar] [CrossRef]
- Weitemeyer, S.; Kleinhans, D.; Vogt, T.; Agert, C. Integration of renewable energy sources in future power systems: The role of storage. Renew. Energy 2015, 75, 14–20. [Google Scholar] [CrossRef]
- Budischak, C.; Sewell, D.; Thomson, H.; Mach, L.; Veron, D.E.; Kempton, W. Cost-minimized combinations of wind power, solar power and electrochemical storage, powering the grid up to 99.9% of the time. J. Power Sources 2013, 225, 60–74. [Google Scholar] [CrossRef]
- Rodríguez, R.A.; Becker, S.; Greiner, M. Cost-optimal design of a simplified, highly renewable pan-European electricity system. Energy 2015, 83, 658–668. [Google Scholar] [CrossRef]
- Eriksen, E.H.; Schwenk-Nebbe, L.J.; Tranberg, B.; Brown, T.; Greiner, M. Optimal heterogeneity in a simplified highly renewable European electricity system. Energy 2017, 133, 913–928. [Google Scholar] [CrossRef]
- Schlachtberger, D.; Brown, T.; Schramm, S.; Greiner, M. The benefits of cooperation in a highly renewable European electricity network. Energy 2017, 134, 469–481. [Google Scholar] [CrossRef]
- Haken, H. Principles of Brain Functioning; Springer: Berlin, Germany, 1996. [Google Scholar]
- Von Bremen, L.; Saleck, N.; Heinemann, D. Enhanced regional forecasting considering single wind farm distribution for upscaling. J. Phys. Conf. Ser. 2007, 75, 012040. [Google Scholar] [CrossRef]
- Burke, D.J.; O’Malley, M.J. A study of Principal Component Analysis applied to spatially distributed wind power. IEEE Trans. Power Syst. 2011, 26, 2084–2092. [Google Scholar] [CrossRef]
- Rodriguez, R.A.; Dahl, M.; Becker, S.; Greiner, M. Localized vs. synchronized exports across a highly renewable pan-European transmission network. Energy Sustain. Soc. 2015, 5, 21. [Google Scholar] [CrossRef]
- WEPROG. Available online: http://www.weprog/ (accessed on 18 September 2017).
- Boßmann, T.; Staffell, I. The shape of future electricity demand: Exploring load curves in 2050s Germany and Britain. Energy 2015, 90, 1317–1333. [Google Scholar] [CrossRef]
- Wenz, L.; Levermann, A.; Auffhammer, M. North-south polarization of European electricity consumption under future warming. Proc. Nalt. Acad. Sci. USA 2017, 114, E7910–E7918. [Google Scholar] [CrossRef] [PubMed]
- Wood, A.J.; Wollenberg, B.F.; Sheblé, G.B. Power Generation, Operation and Control; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Schäfer, M.; Tranberg, B.; Hempel, S.; Schramm, S.; Greiner, M. Decompositions of injection patterns for nodal flow allocation in renewable electricity networks. Eur. Phys. J. B 2017, 90, 144. [Google Scholar] [CrossRef]
- Schmid, P. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Deladreue, S.; Brouaye, F.; Bastard, P.; Péligry, L. Using two multivariate methods for line congestion study in transmission systems under uncertainty. IEEE Trans. Power Syst. 2003, 18, 353–358. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Mathiesen, B. Smart Energy Europe: The technical and economic impact of one potential 100% renewable energy scenario for the European Union. Renew. Sustain. Energy Rev. 2016, 60, 1634–1653. [Google Scholar] [CrossRef]

| , | |||||||
|---|---|---|---|---|---|---|---|
| 0.0301 | 0.0281 | 0.0272 | 0.0258 | 0.0238 | 0.0195 | 0.0136 | |
| 0.0101 | 0.0101 | 0.0098 | 0.0098 | 0.0096 | 0.0095 | 0.0089 | |
| 0.1402 | 0.1388 | 0.1371 | 0.1368 | 0.1365 | 0.1348 | 0.1318 | |
| 0.686 | 0.682 | 0.659 | 0.656 | 0.650 | 0.643 | 0.613 | |
| 0.0184 | 0.0164 | 0.0154 | 0.0139 | 0.0119 | 0.0077 | 0.0020 | |
| 0.0120 | 0.0101 | 0.0091 | 0.0074 | 0.0061 | 0.0040 | 0.0007 | |
| 1.812 | 1.486 | 1.372 | 1.250 | 1.156 | 0.904 | 0.356 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raunbak, M.; Zeyer, T.; Zhu, K.; Greiner, M. Principal Mismatch Patterns Across a Simplified Highly Renewable European Electricity Network. Energies 2017, 10, 1934. https://doi.org/10.3390/en10121934
Raunbak M, Zeyer T, Zhu K, Greiner M. Principal Mismatch Patterns Across a Simplified Highly Renewable European Electricity Network. Energies. 2017; 10(12):1934. https://doi.org/10.3390/en10121934
Chicago/Turabian StyleRaunbak, Mads, Timo Zeyer, Kun Zhu, and Martin Greiner. 2017. "Principal Mismatch Patterns Across a Simplified Highly Renewable European Electricity Network" Energies 10, no. 12: 1934. https://doi.org/10.3390/en10121934
APA StyleRaunbak, M., Zeyer, T., Zhu, K., & Greiner, M. (2017). Principal Mismatch Patterns Across a Simplified Highly Renewable European Electricity Network. Energies, 10(12), 1934. https://doi.org/10.3390/en10121934





