An Interval Fuzzy-Stochastic Chance-Constrained Programming Based Energy-Water Nexus Model for Planning Electric Power Systems
Abstract
:1. Introduction
2. Study System
2.1. Problem Statement
2.2. System Description
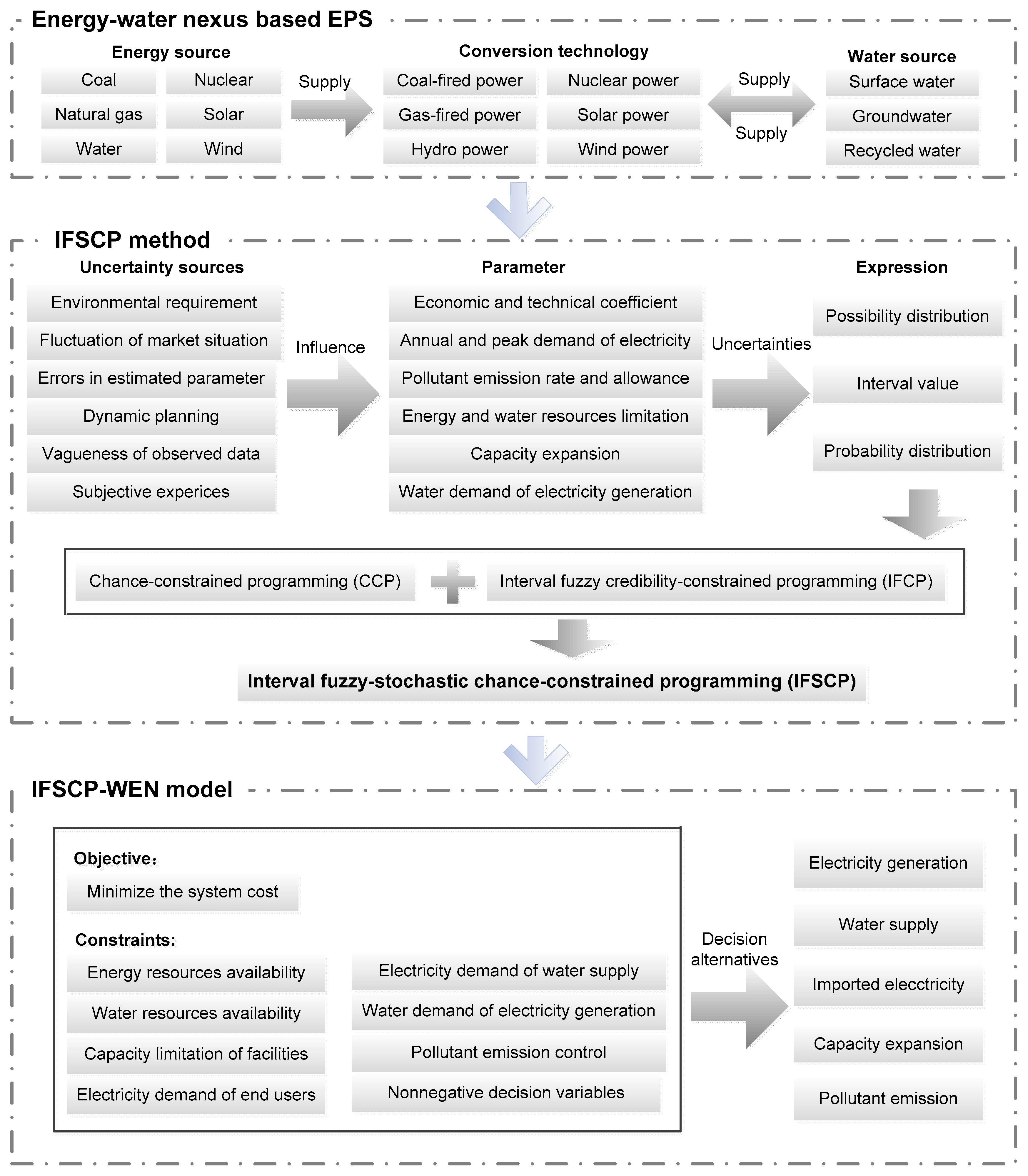
3. Development of IFSCP-WEN
3.1. IFSCP Method
3.2. IFSCP-WEN Modeling Formulation
- (1)
- Energy resources availability:
- (2)
- Water resources availability:
- (3)
- Capacity limitation of facilities:
- (4)
- Electricity demand of end users:
- (5)
- Electricity demand for water supply:
- (6)
- Water demand for electricity generation:
- (7)
- Pollutant emission control constraints:
- (8)
- Capacity expansion constraints:
- (9)
- Non-negative constraint:
3.3. Data Analysis
4. Result Analysis and Discussion
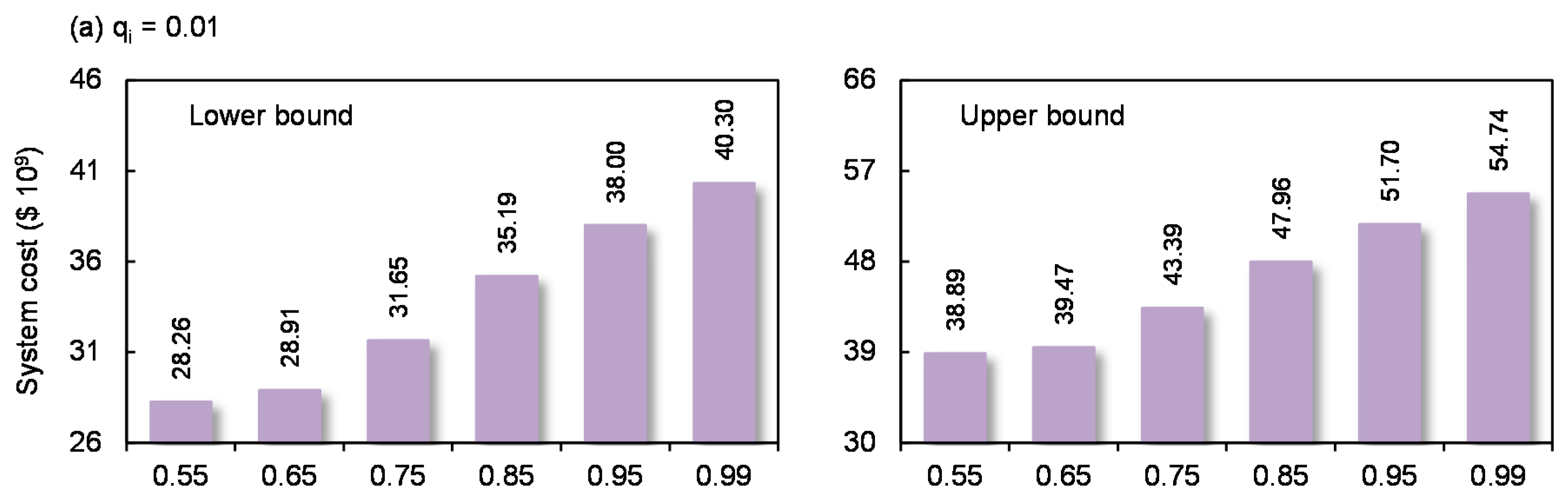
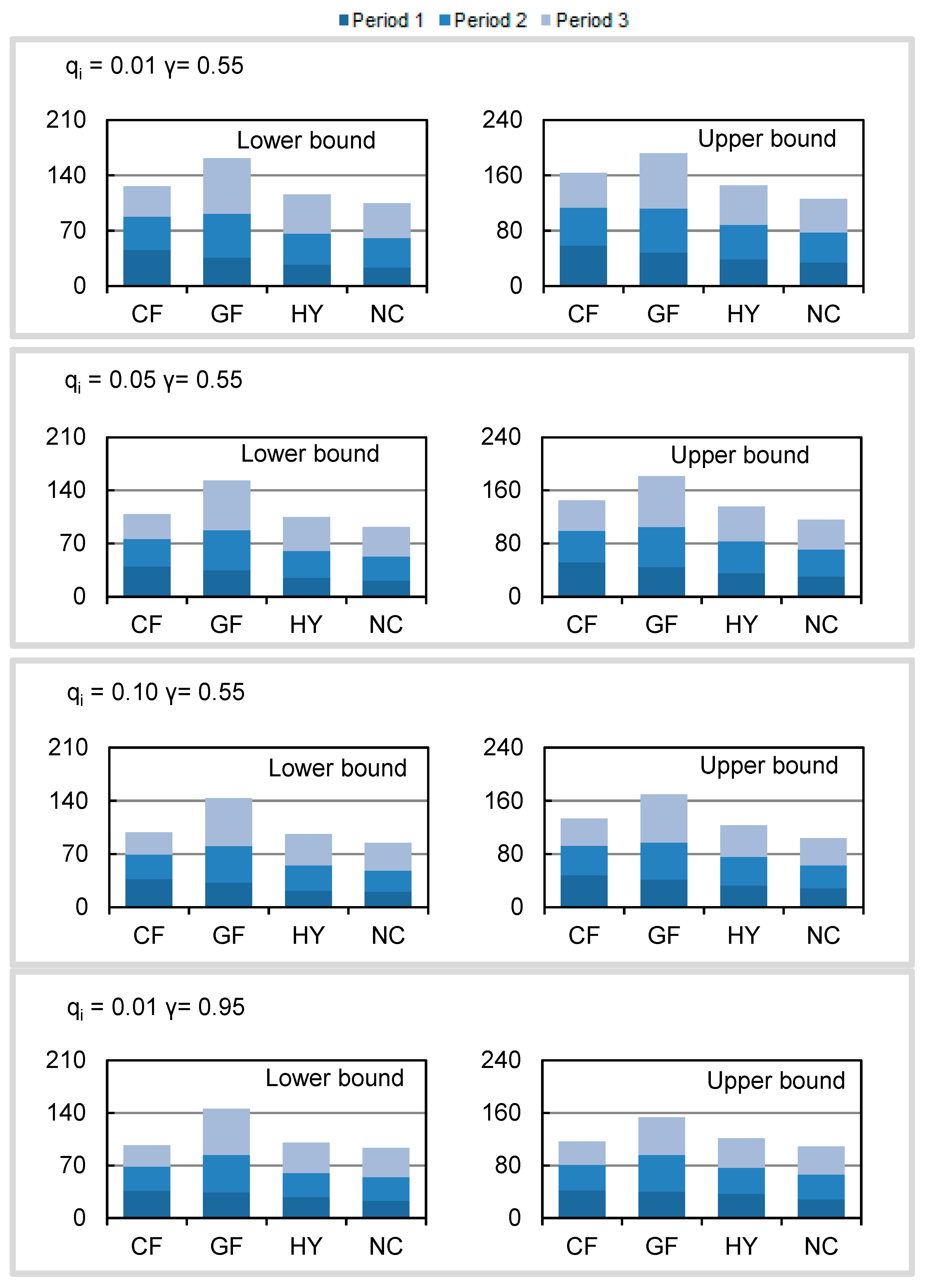
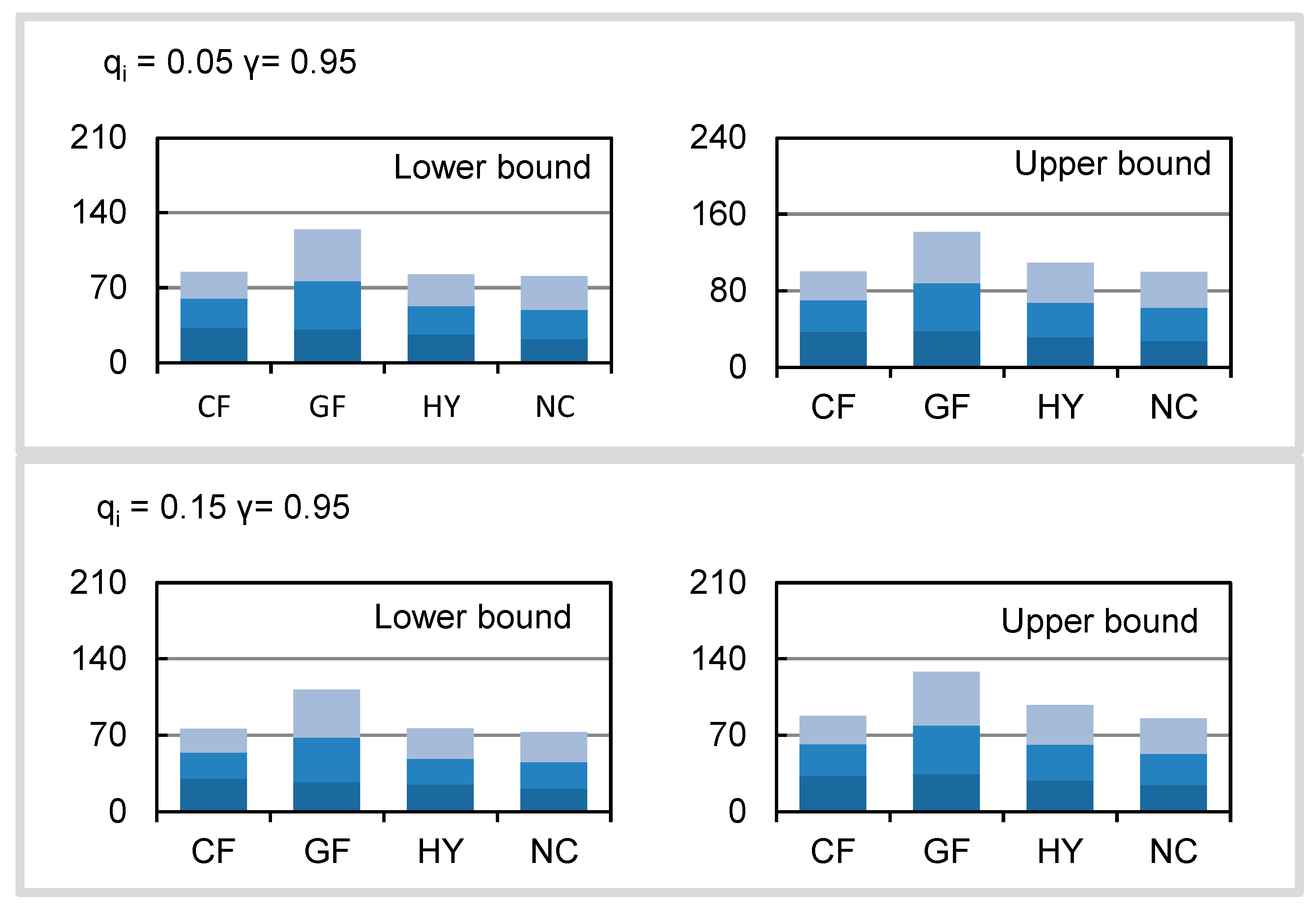
4.1. System Cost
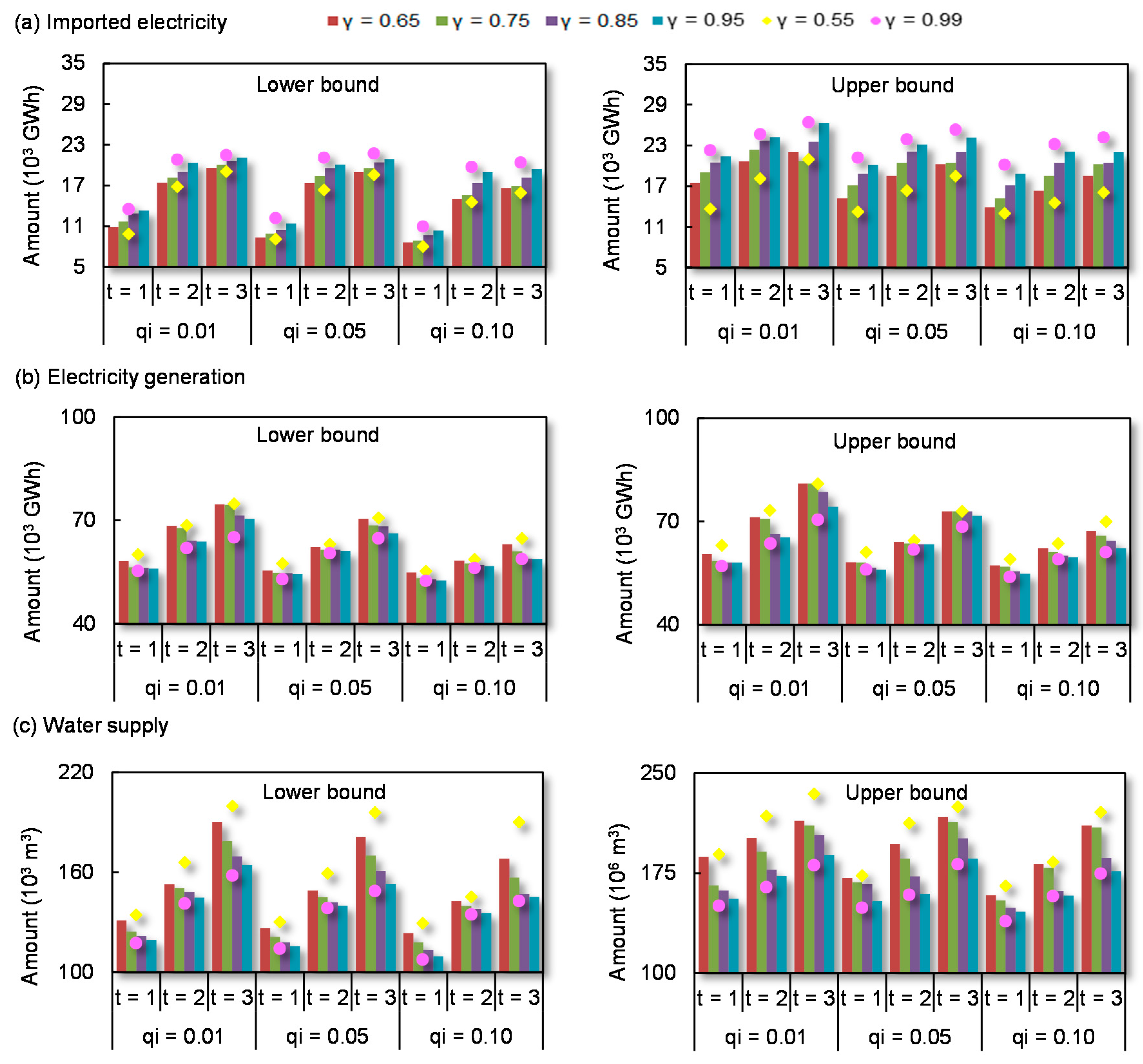
4.2. Electricity and Water Supply Patterns
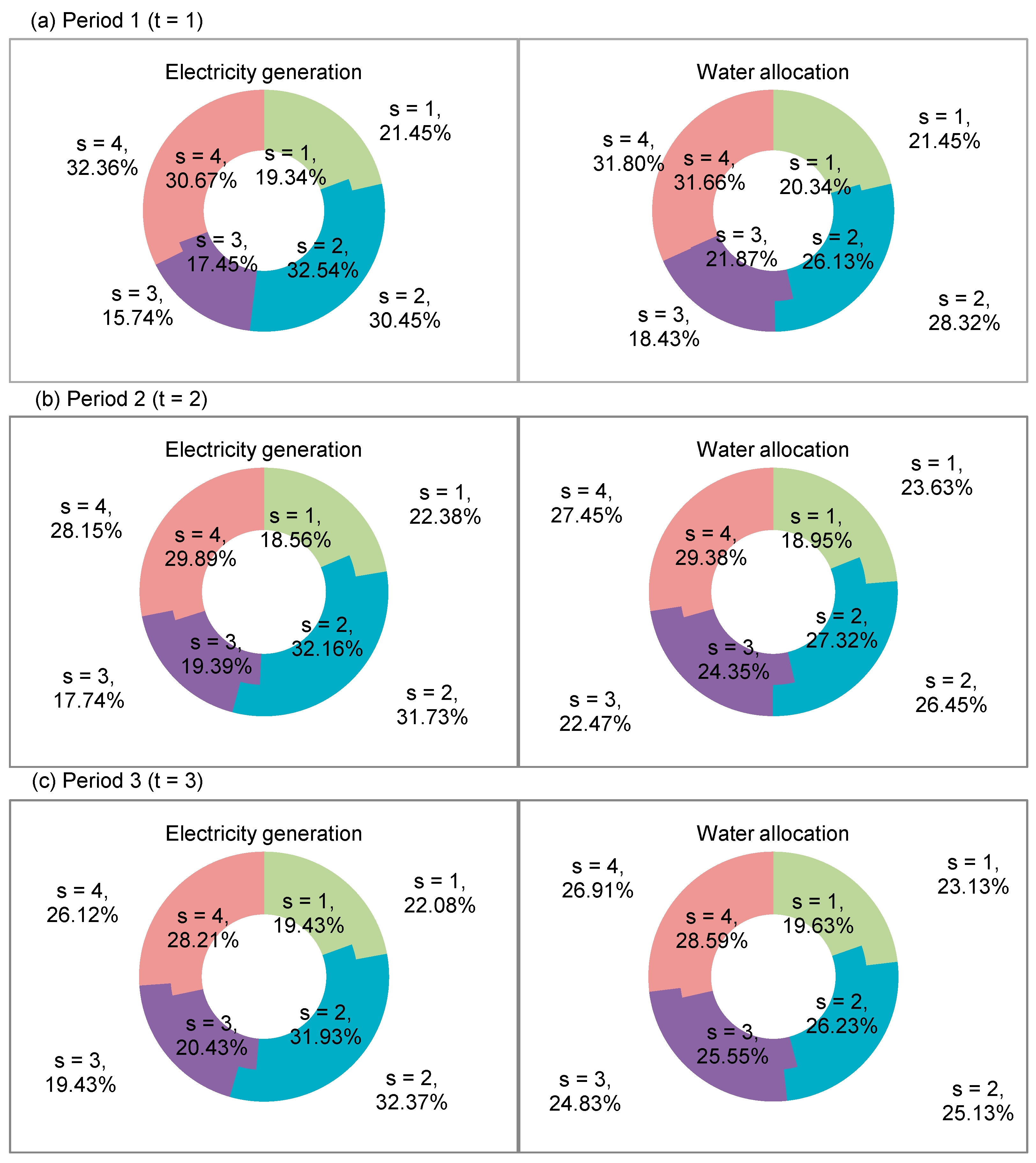
4.3. Distribution of Electricity Generation
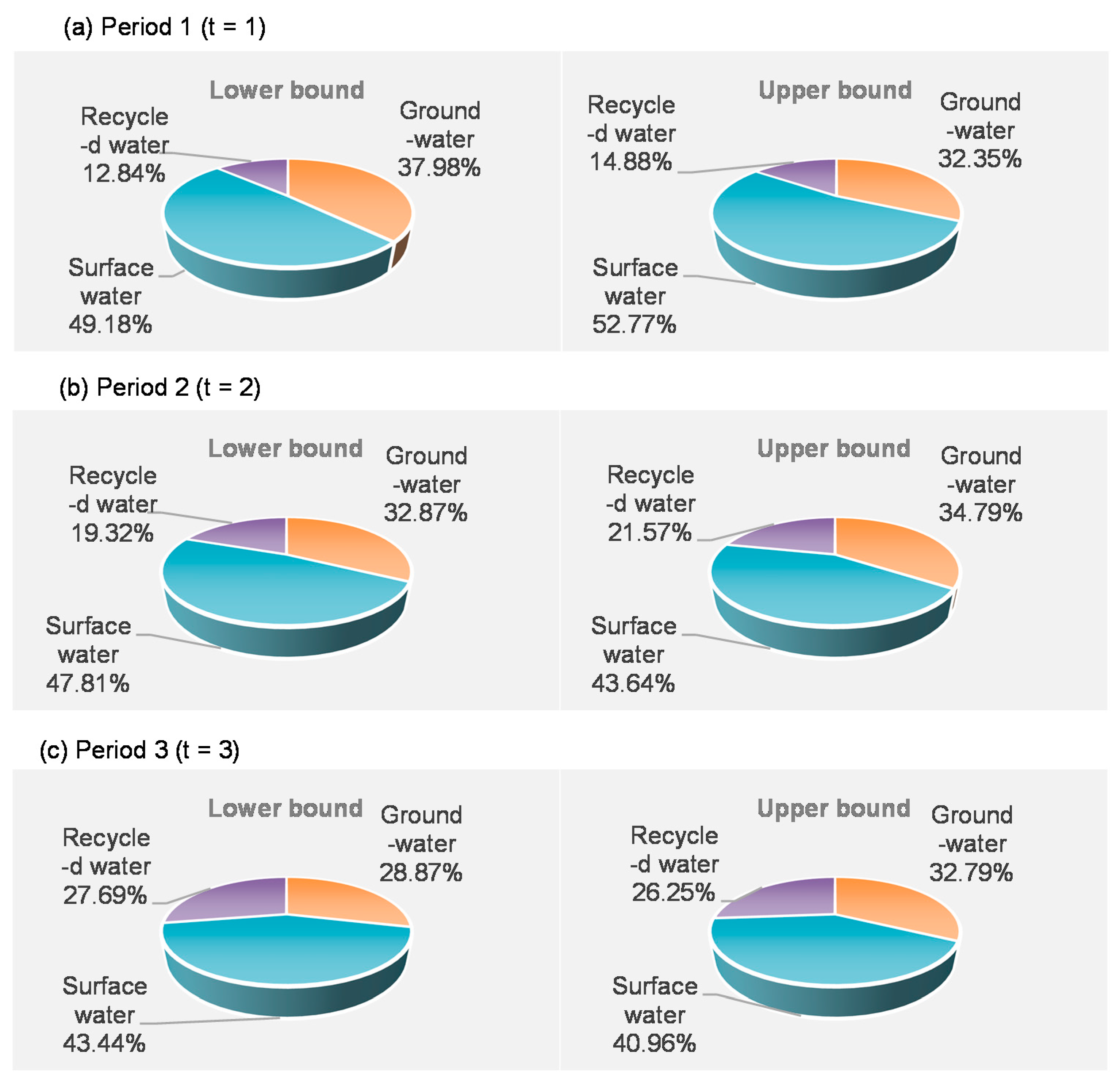
4.4. Water Allocation for Electricity Generation
4.5. Pollutant Emissions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Solution Method
Appendix B. Nomenclatures for Parameters and Variables
| system cost over the planning horizon ($) | |
| N | type of generating facility; n = 1 (coal-fired); n = 2 (natural gas-fired); n =3 (hydro); n = 4 (nuclear); n = 5 (solar); n = 6 (wind) |
| T | time period; t = 1, 2, 3 |
| S | season; s = 1 (spring); s = 2 (summer); s = 3 (autumn); s = 4 (winter) |
| unit cost for purchasing energy resource n in period t ($/TJ) | |
| amount of electricity generation via utility n in season s of period t (GWh) | |
| consumption rate of utility n (TJ/GWh) | |
| cost for importing electricity in season s of period t ($/GWh) | |
| imported electricity in season s of period t (GWh) | |
| fixed cost for electricity generation by utility n in period t ($/GW) | |
| expanded capacity for utility n in period t (GW) | |
| 0–1 variables for identifying whether or not utility n needs to be expanded in period t | |
| variable cost for generating electricity via utility n in period t ($/GWh) | |
| service time of utility n in season s of period t (h) | |
| fixed cost for expanding capacity for utility n in period t ($) | |
| variable cost for expanding capacity for utility n in period t ($/GW) | |
| environmental facilities cost for SO2 emission in period t ($/GW) | |
| cost for emission of SO2 in period t ($/GWh) | |
| environmental facilities cost for NOx emission in period t ($/GW) | |
| cost for emission of NOx in period t ($/GWh) | |
| environmental facilities cost for PM10 emission in period t ($/GW) | |
| cost for emission of PM10 in period t ($/GWh) | |
| financial subsidy in period t ($/GWh) | |
| available resource for utility n in period t (TJ) | |
| unit cost of groundwater for electricity generation ($/m3) | |
| groundwater for electricity generation by utility n in season s of period t (m3) | |
| available groundwater in season s of period t (m3) | |
| unit cost of surface water for electricity generation ($/m3) | |
| surface water for electricity generation by utility n in season s of period t (m3) | |
| available surface water in season s of period t (m3) | |
| unit cost of recycled water for electricity generation ($/m3) | |
| recycled water for electricity generation by utility n in season s of period t (m3) | |
| available recycled water in season s of period t (m3) | |
| residual capacity for utility n (GW) | |
| base-load electricity demand in period t (GWh) | |
| peak-electricity demand in season s of period t (GWh) | |
| unit amount of electricity for pumping groundwater in season s of period t (GWh/m3) | |
| unit amount of electricity for extracting surface water in season s of period t (GWh/m3) | |
| unit amount of electricity for delivering water in season s of period t (GWh/m3) | |
| available electricity for extracting and delivering water in season s of period t (GWh) | |
| unit amount of electricity for treating wastewater in season s of period t (GWh/m3) | |
| unit amount of electricity for recycling water in season s of period t (GWh/m3) | |
| available electricity for recycled water in season s of period t (GWh) | |
| consumption rate of electricity for collecting, treating and delivering water (%) | |
| unit water demand per unit of electricity generation (m3/GWh) | |
| emission amount of SO2 in utility n in period t (tonne/GWh) | |
| emission amount of NOX in utility n in period t (tonne/GWh) | |
| emission amount of PM10 in facility n in period t (tonne/GWh) | |
| allowed amount of SO2 in period t (tonne) | |
| allowed amount of NOX in period t (tonne) | |
| allowed amount of PM10 in period t (tonne) | |
| maximum capacity for electricity generation facility n (GW) |
References
- World Energy Outlook Report; International Energy Agency: Paris, France, 2010. Available online: http://www.worldenergyoutlook.org (accessed on 14 November 2017).
- Yoon, S.G.; Kang, S.G. Economic microgrid planning algorithm with electric vehicle charging demands. Energies 2017, 10, 1487. [Google Scholar] [CrossRef]
- Nair, S.; George, B.; Malano, H.M.; Arora, M.; Nawarathna, B. Water-energy-greenhouse gas nexus of urban water systems: Review of concepts, state-of-art and methods. Resour. Conserv. Recycl. 2014, 89, 1–10. [Google Scholar] [CrossRef]
- Ozturk, I. Sustainability in the food-energy-water nexus: Evidence from BRICS (Brazil, the Russian Federation, India, China, and South Africa) countries. Energy 2015, 93, 999–1010. [Google Scholar] [CrossRef]
- DeNooyer, T.A.; Peschel, J.M.; Zhang, Z.X.; Stillwell, A.S. Integrating water resources and power generation: The energy-water nexus in Illinois. Appl. Energy 2016, 162, 363–371. [Google Scholar] [CrossRef]
- Vilanova, M.R.N.; Balestier, J.A.P. Exploring the energy-water nexus in Brazil: The electricity use for water supply. Energy 2015, 85, 415–432. [Google Scholar] [CrossRef]
- Gleick, P.H. Water and Energy. Annu. Rev. Energy Environ. 1994, 19, 267–299. [Google Scholar] [CrossRef]
- Yang, J.; Chen, B. Energy-water nexus of wind power generation systems. Appl. Energy 2016, 169, 1–13. [Google Scholar] [CrossRef]
- Davies, E.G.R.; Kyle, P.; Edmonds, J.A. An integrated assessment of global and regional water demands for electricity generation to 2095. Adv. Water Resour. 2013, 52, 296–313. [Google Scholar] [CrossRef]
- Santhosh, A.; Farid, A.M.; Youcef-Toumi, K. Real-time economic dispatch for the supply side of the energy-water nexus. Appl. Energy 2014, 122, 42–52. [Google Scholar] [CrossRef]
- Li, P.; Chen, B.; Li, Z.L.; Jing, L. ASOC: A novel agent-based simulation-optimization coupling approach-algorithm and application in offshore oil spill responses. J. Environ. Inform. 2016, 28, 90–100. [Google Scholar]
- Khan, Z.; Linares, P.; García-González, J. Integrating water and energy models for policy driven applications. A review of contemporary work and recommendations for future developments. Renew. Sustain. Energy Rev. 2017, 67, 1123–1138. [Google Scholar] [CrossRef]
- Bazilian, M.; Rogner, H.; Howells, M.; Hermann, S.; Arent, D.; Gielen, D.; Pasquale, S.; Alexander, M.; Paul, K.; Richard, S.J.T.; et al. Considering the energy, water and food nexus: Towards an integrated modelling approach. Energy Policy 2011, 39, 7896–7906. [Google Scholar] [CrossRef]
- Dubreuil, A.; Assoumou, E.; Bouckaert, S.; Selosse, S.; Maizi, N. Water modeling in an energy optimization framework—The water-scarce middle east context. Appl. Energy 2013, 101, 268–279. [Google Scholar] [CrossRef]
- Vliet Van, M.T.H.; Vögele, S.; Rübbelke, D. Water constraints on European power supply under climate change: Impacts on electricity prices. Environ. Res. Lett. 2013, 8, 1345–1346. [Google Scholar] [CrossRef]
- Liu, L.; Hejazi, M.; Patel, P.; Kyle, P.; Davies, E.; Zhou, Y.Y.; Clarke, L.; Edmonds, J. Water demands for electricity generation in the U.S.: Modeling different scenarios for the energy-water nexus. Technol. Forecast. Soc. Chang. 2015, 94, 318–334. [Google Scholar] [CrossRef]
- Lubega, W.N.; Farid, A.M. Quantitative engineering systems modeling and analysis of the energy-water nexus. Appl. Energy 2014, 135, 142–157. [Google Scholar] [CrossRef]
- Santhosh, A.; Farida, A.M.; Youcef-Toumic, K. The impact of storage facility capacity and ramping capabilities on the supply side economic dispatch of the energy-water nexus. Energy 2014, 66, 363–377. [Google Scholar] [CrossRef]
- Gjorgiev, B.; Sansavini, G.; Gjorgiev, B.; Sansavini, G.; Gjorgiev, B.; Sansavini, G. Electrical power generation under policy constrained energy-water nexus. Appl. Energy 2017. [Google Scholar] [CrossRef]
- Nie, S.; Li, Y.P.; Liu, J.; Huang, C.Z. Risk management of energy system for identifying optimal power mix with financial-cost minimization and environmental-impact mitigation under uncertainty. Energy Econ. 2017, 61, 313–329. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Yang, Z.F.; Nie, S.L. IFMP: Interval-fuzzy multistage programming for water resources management under uncertainty. Resour. Conserv. Recycl. 2008, 52, 800–812. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, G. Optimal water resource planning under fixed budget by interval-parameter credibility constrained programming. Eng. Optim. 2011, 43, 879–889. [Google Scholar] [CrossRef]
- Marufuzzaman, M.; Eksioglua, S.D.; Huang, E. Two-stage stochastic programming supply chain model for biodiesel production via wastewater treatment. Comput. Oper. Res. 2014, 49, 1–17. [Google Scholar] [CrossRef]
- Seddighi, A.H.; Ahmadi-Javid, A. Integrated multiperiod power generation and transmission expansion planning with sustainability aspects in a stochastic environment. Energy 2015, 86, 9–18. [Google Scholar] [CrossRef]
- Ghalelou, A.N.; Fakhri, A.P.; Nojavan, S.; Majidi, M.; Hatami, H. A stochastic self-scheduling program for compressed air energy storage (CAES) of renewable energy sources (RESs) based on a demand response mechanism. Energy Convers. Manag. 2016, 120, 388–396. [Google Scholar] [CrossRef]
- Taylan, O.; Kaya, D.; Demirbas, A. An integrated multi attribute decision model for energy efficiency processes in petrochemical industry applying fuzzy set theory. Energy Convers. Manag. 2016, 117, 501–512. [Google Scholar] [CrossRef]
- Theo, W.L.; Lim, J.S.; Alwi, S.R.W.; Rozali, N.E.M.; Ho, W.S.; Abdul-Manan, Z. An MILP model for cost-optimal planning of an on-grid hybrid power system for an eco-industrial park. Energy 2016, 116, 1423–1441. [Google Scholar] [CrossRef]
- Wu, Y.N.; Xie, C.; Xu, C.; Li, F. A decision framework for electric vehicle charging station site selection for residential communities under an intuitionistic fuzzy environment: A case of Beijing. Energies 2017, 10, 1270. [Google Scholar] [CrossRef]
- Tan, Q.L.; Ding, Y.H.; Zhang, Y.M. Optimization model of an efficient collaborative power dispatching system for carbon emissions trading in China. Energies 2017, 10, 1405. [Google Scholar] [CrossRef]
- Soares, M.P.; Street, A.; Valladão, D.M. On the solution variability reduction of stochastic dual dynamic programming applied to energy planning. Eur. J. Oper. Res. 2017, 258, 743–760. [Google Scholar] [CrossRef]
- Dai, C.; Cai, Y.P.; Ren, W.; Xie, Y.F.; Guo, H.C. Identification of optimal placements of best management practices through an interval-fuzzy possibilistic programming model. Agric. Water Manag. 2016, 165, 108–121. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Huang, Y.F.; Zhou, Y.F. A multistage fuzzy-stochastic programming model for supporting sustainable water resources allocation and management. Environ. Model. Softw. 2009, 24, 786–797. [Google Scholar] [CrossRef]
- Li, Y.F.; Li, Y.P.; Huang, G.H.; Chen, X. Energy and environmental systems planning under uncertainty—An inexact fuzzy-stochastic programming approach. App. Energy 2010, 87, 3189–3211. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H. Electric-power systems planning and greenhouse-gas emission management under uncertainty. Energy Convers. Manag. 2012, 57, 173–182. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.P.; Huang, G.H. Mathematical modeling for water quality management under interval and fuzzy uncertainties. J. Appl. Math. 2013, 2013, 731568. [Google Scholar] [CrossRef]
- Khan, U.T.; Valeo, C. Short-term peak flow rate prediction and flood risk assessment using fuzzy linear regression. J. Environ. Inform. 2016, 28, 71–89. [Google Scholar]
- Yu, L.; Li, Y.P.; Huang, G.H. A fuzzy-stochastic simulation-optimization model for planning electric power systems with considering peak-electricity demand: A case study of Qingdao, China. Energy 2016, 98, 190–203. [Google Scholar] [CrossRef]
- Hamiche, A.M.; Stambouli, A.B.; Flazi, S. A review of the energy-water nexus. Renew. Sustain. Energy Rev. 2016, 65, 319–331. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Nie, S.L. Planning water resources management system using a fuzzy-boundary interval-stochastic programming method. Adv. Water Resour. 2010, 33, 1105–1117. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Fan, S. Density forecasting for long-term peak electricity demand. IEEE Trans. Power Syst. 2010, 25, 1142–1153. [Google Scholar] [CrossRef]
- Statistics Bureau of Qingdao Municipality. Qingdao Statistical Yearbook in 2014; China Statistical Press: Qingdao, China, 2015. (In Chinese) [Google Scholar]

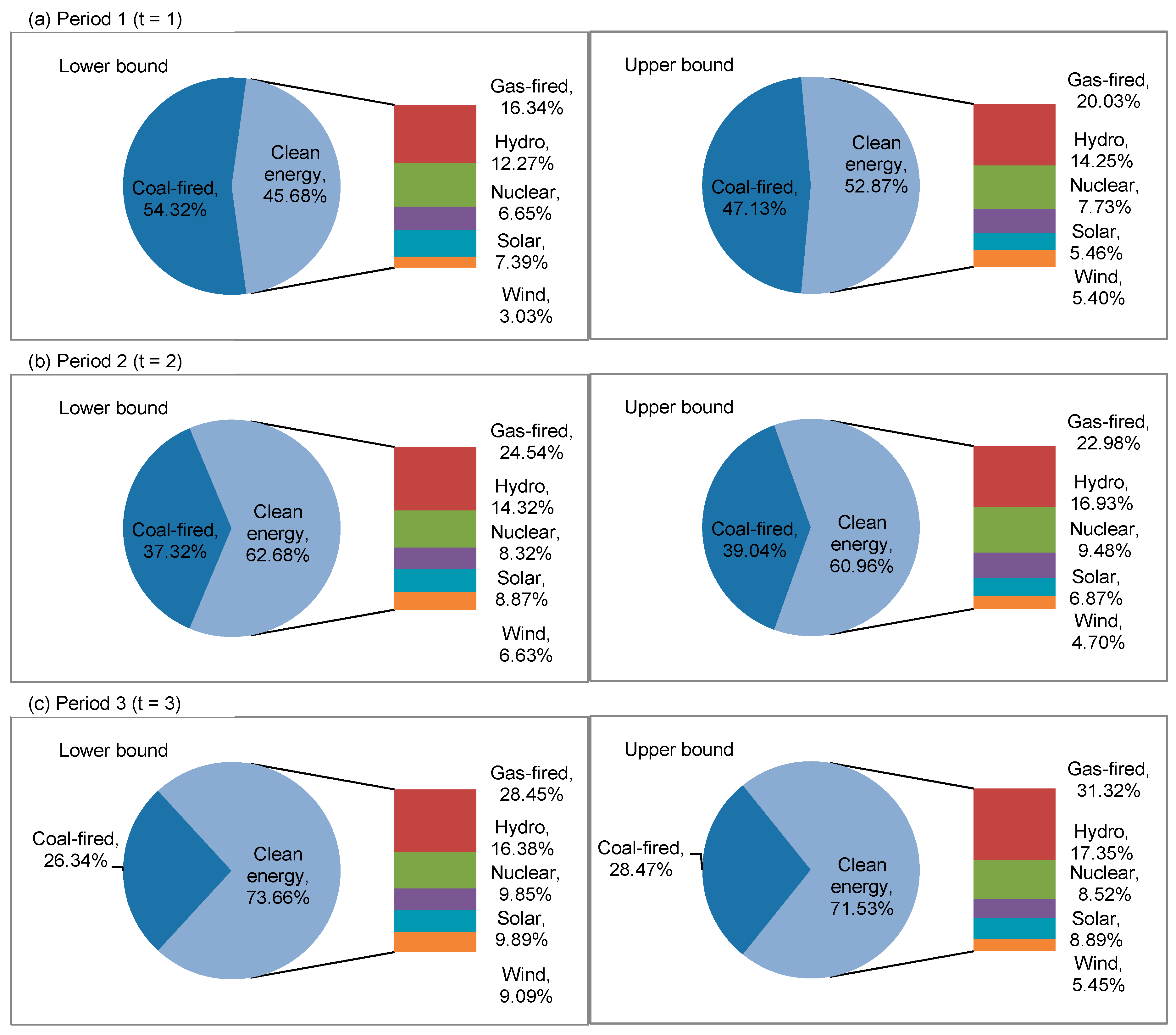

| Technology | Period | ||
|---|---|---|---|
| t = 1 | t = 2 | t = 3 | |
| Fixed cost for electricity generation (106 $/GW) | |||
| Coal-fired | [(22.45, 23.38, 25.24), (28.06, 30.12, 33.07)] | [(21.24, 22.91, 24.43), (27.17, 28.38, 32.11)] | [(20.98, 22.44, 23.68), (25.83, 26.92, 31.54)] |
| Gas-fired | [(33.16, 35.68, 37.75), (40.32, 42.81, 44.93)] | [(30.23, 33.17, 35.22), (37.44, 39.81,41.75)] | [(29.23, 31.23,33.74), (35.78, 37.47, 39.87)] |
| Hydro | [(71.47, 73.36, 75.13), (86.71, 88.03, 89.94)] | [(67.34, 69.38, 71.03), (81.54, 83.26,85.76)] | [(63.35, 65.43, 67.76), (75.87, 78.51, 80.65)] |
| Nuclear | [(115.33, 119.21, 121.74), (140.27, 143.04, 145.84)] | [(111.74, 113.17, 115.83), (133.23, 135.81, 137.34)] | [(104.34, 107.39, 110.54), (126.43, 128.87, 131.43)] |
| Solar | [(67.43, 70.26, 72.54), (81.74, 84.31, 86.47)] | [(63.54, 66.71, 68.95), (77.98, 80.06, 82.97)] | [(60.76, 63.36, 66.02), (72.43, 75.96, 78.42)] |
| Wind | [(55.54, 59.25, 62.54), (68.43, 71.21, 74.04)] | [(52.54, 56.26, 59.75), (63.03, 67.51, 71.75)] | [(51.17, 53.38, 55.93), (61.42, 64.06, 66.84)] |
| Variable cost for electricity generation (103 $/GWh) | |||
| Coal-fired | [(1.34, 1.59, 1.84), (1.72, 1.91, 2.11)] | [(1.31, 1.56, 1.59), (1.85, 1.88, 1.91)] | [(1.49, 1.52, 1.55), (1.81, 1.84, 1.87)] |
| Gas-fired | [(2.14, 2.19, 2.24), (2.58, 2.63, 2.68)] | [(2.03, 2.08, 2.13), (2.46, 2.51, 2.55)] | [(1.92, 1.97, 2.02), (2.31, 2.36, 2.41)] |
| Hydro | [(7.21, 7.25, 7.29), (8.63, 8.67, 8.71)] | [(6.81, 6.85, 6.89), (8.17, 8.21, 8.25)] | [(6.44, 6.48, 6.52), (7.71, 7.75, 7.79)] |
| Nuclear | [(7.17, 7.21, 7.25), (8.53, 8.57, 8.61)] | [(6.83, 6.87, 6.91), (8.18, 8.22, 8.26)] | [(6.45, 6.49, 6.53), (7.74, 7.79, 7.83)] |
| Solar | [(7.74, 7.79, 7.83), (9.32, 9.36, 9.40)] | [(7.55, 7.59, 7.63), (9.26, 9.30, 9.34)] | [(7.43, 7.47, 7.51), (9.11, 9.15, 9.19)] |
| Wind | [(9.42, 9.47, 9.52), (11.29, 11.34, 11.39)] | [(9.01, 9.06, 9.11), (10.81, 10.86, 10.91)] | [(8.61, 8.66, 8.71), (10.33, 10.38, 10.43)] |
| Technology | Period | ||
|---|---|---|---|
| t = 1 | t = 2 | t = 3 | |
| Unit Water Demand of Electricity Generation (103 m3/GWh) | |||
| Coal-fired | [(1.22, 1.26.1.32), (1.48, 1.53, 1.58)] | [(1.14, 1.21, 1.27), (1.41, 1.46, 1.52)] | [(1.07, 1.14, 1.19), (1.32, 1.37, 143)] |
| Gas-fired | [(1.71, 1.76, 1.82), (2.14, 2.23, 2.29)] | [(1.62, 1.69, 1.74), (2.03, 2.14, 2.22)] | [(1.52, 1.59, 1.65), (1.85, 1.94, 2.03)] |
| Hydro | [(2.78, 2.84, 2.93), (3.21, 3.53, 3.71)] | [(2.21, 2.47, 2.63), (3.13, 3.26, 3.45)] | [(2.24, 2.48, 2.75), (2.85, 2.94, 3.12)] |
| Nuclear | [(1.84, 1.89, 1.93), (2.29, 2.37, 2.45)] | [(1.63, 1.72, 1.79), (2.07, 2.15, 2.21)] | [(1.57, 1.62, 1.68), (1.83, 1.95, 2.03)] |
| Unit Amount of Electricity for Extracting Water (10-6 GWh/m3) | |||
| Surface water | [(0.76, 0.81, 0.86), (0.89, 0.94, 0.99)] | [(0.71, 0.78, 0.83), (0.84, 0.89, 0.94)] | [(0.63, 0.75, 0.79), (0.81, 0.85, 0.89)] |
| Groundwater | [(0.36, 0.42, 0.48), (0.51, 0.57, 0.63)] | [(0.32, 0.38, 0.44), (0.47, 0.53, 0.59)] | [(0.27, 0.33, 0.39), (0.42, 0.48, 0.54)] |
| Unit Amount of Electricity for Delivering Water (10-6 GWh/m3) | |||
| Surface water | [(1.21 1.23, 1.25), (1.31, 1.33, 1.35)] | [(1.17, 1.19, 1.21), (1.25, 1.27, 1.29)] | [(1.14, 1.16, 1.18), (1.22, 1.24, 1.26)] |
| Groundwater | [(1.21 1.23, 1.25), (1.31, 1.33, 1.35)] | [(1.17, 1.19, 1.21), (1.25, 1.27, 1.29)] | [(1.14, 1.16, 1.18), (1.22, 1.24, 1.26)] |
| Recycled water | [(0.23, 0.26, 0.29), (0.31, 0.34, 0.37)] | [(0.19, 0.22, 0.25), (0.27, 0.30, 0.33)] | [(0.14, 0.17, 0.20), (0.23, 0.26, 0.29)] |
| Unit Amount of Electricity for Treating Water(10-6 GWh/m3) | |||
| Recycled water | [(0.12, 0.13, 0.14), (0.16, 0.17, 0.18)] | [(0.10, 0.11, 0.12), (0.14, 0.15, 0.16)] | [(0.09, 0.10, 0.11), (0.13, 0.14, 0.15)] |
| Technology | Period | ||
|---|---|---|---|
| t = 1 | t = 2 | t = 3 | |
| Annual Electricity Demand (103 GWh) | |||
| = 0.01 | [69.84, 74.34] | [76.39, 79.03] | [81.42, 85.03] |
| = 0.05 | [65.38,67.43] | [71.34, 75.23] | [76.27, 79.49] |
| = 0.10 | [55.73,63.69] | [65.84, 69.32] | [71.43, 74.43] |
| Electricity Demand in Summer (103 GWh) | |||
| = 0.10 | [28.94, 32.48] | [34.18, 37.49] | [39.43, 42.55] |
| = 0.05 | [24.04, 27.03] | [29.75, 33.07] | [35.94, 38.94] |
| = 0.01 | [19.43, 23.57] | [24.43, 27.03] | [29.74, 34.43] |
| Electricity Demand in Winter (103 GWh) | |||
| = 0.01 | [22.53, 27.84] | [28.39, 31.38] | [35.57, 38.15] |
| = 0.05 | [19.37, 21.33] | [23.03, 26.14 ] | [31.28, 34.47] |
| = 0.10 | [15.46, 18.47] | [20.03, 24.07] | [26.54, 30.74] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, Y.; Huang, G.; Suo, C.; Yin, S. An Interval Fuzzy-Stochastic Chance-Constrained Programming Based Energy-Water Nexus Model for Planning Electric Power Systems. Energies 2017, 10, 1914. https://doi.org/10.3390/en10111914
Liu J, Li Y, Huang G, Suo C, Yin S. An Interval Fuzzy-Stochastic Chance-Constrained Programming Based Energy-Water Nexus Model for Planning Electric Power Systems. Energies. 2017; 10(11):1914. https://doi.org/10.3390/en10111914
Chicago/Turabian StyleLiu, Jing, Yongping Li, Guohe Huang, Cai Suo, and Shuo Yin. 2017. "An Interval Fuzzy-Stochastic Chance-Constrained Programming Based Energy-Water Nexus Model for Planning Electric Power Systems" Energies 10, no. 11: 1914. https://doi.org/10.3390/en10111914
APA StyleLiu, J., Li, Y., Huang, G., Suo, C., & Yin, S. (2017). An Interval Fuzzy-Stochastic Chance-Constrained Programming Based Energy-Water Nexus Model for Planning Electric Power Systems. Energies, 10(11), 1914. https://doi.org/10.3390/en10111914






