1. Introduction
Wind power, as one of the most developed energy generation modes, has been increasing in the modern power system, more conventional synchronous generators which enjoy the ability of frequency support are replaced by wind turbine generators (WTGs). Unlike conventional synchronous generators, WTGs are connected to the power grid through power electronic converters, and as a result, the system frequency is decoupled from the rotor speed of the WTGs [
1]. In addition, WTGs usually operate over the maximum power point tracking curve so that there is no available reserve power. Therefore, WTGs do not provide inherent inertia, and do not respond to system frequencies when a disturbance occurs; they pose a great challenge to the frequency stability in a power system with a high wind power penetration level [
2,
3,
4]. Thus, WTGs should assist in system frequency regulation to maintain the frequency stability of power systems with increased wind power.
To solve the frequency stability problem caused by decreased inertia in a power system with increased wind power, a large amount of research has been conducted to enable wind power to participate in system frequency regulation, so as to improve inertial response [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16]. The most common idea is to establish a supplementary control loop between system frequency and an extra active power reference; as a result, the coupling relation between frequency deviation and active power is established. These methods can generally be divided into three control modes: virtual inertial control [
5,
6,
7,
8], power reserve control [
9,
10,
11,
12], combined virtual inertial control and power reserve control [
13,
14,
15,
16]. The above research can effectively improve the frequency control ability of wind turbines themselves. However, relatively little literature focuses on the dynamic frequency response characteristics of wind power integrated power systems [
17,
18]. A frequency domain model, including governors, networks and load characteristics is developed in [
17] to analyze the power system frequency response to wind power fluctuations of different frequencies. The researchers in [
18] develop an assessment method on the impact of wind power injection on power system frequency deviations. However, the above studies consider the wind turbine as a negative load, ignoring the internal dynamic response characteristics of the wind turbine. Simultaneously, these are static frequency evaluation methods, and hence, it is difficult to efficaciously reflect the dynamic frequency response characteristics of high-wind integrated power systems. Recently, the research on dynamic frequency characteristics for traditional power systems have received the attention of many researchers. A quintessential low-order system frequency response (SFR) model is widely used in power system frequency analysis due to its simple and clear calculation [
19], which can effectively analyze and evaluate the frequency dynamics of power system disturbances, and can help technology policy makers to develop relevant emergency control strategies to maintain the frequency stability of the system.
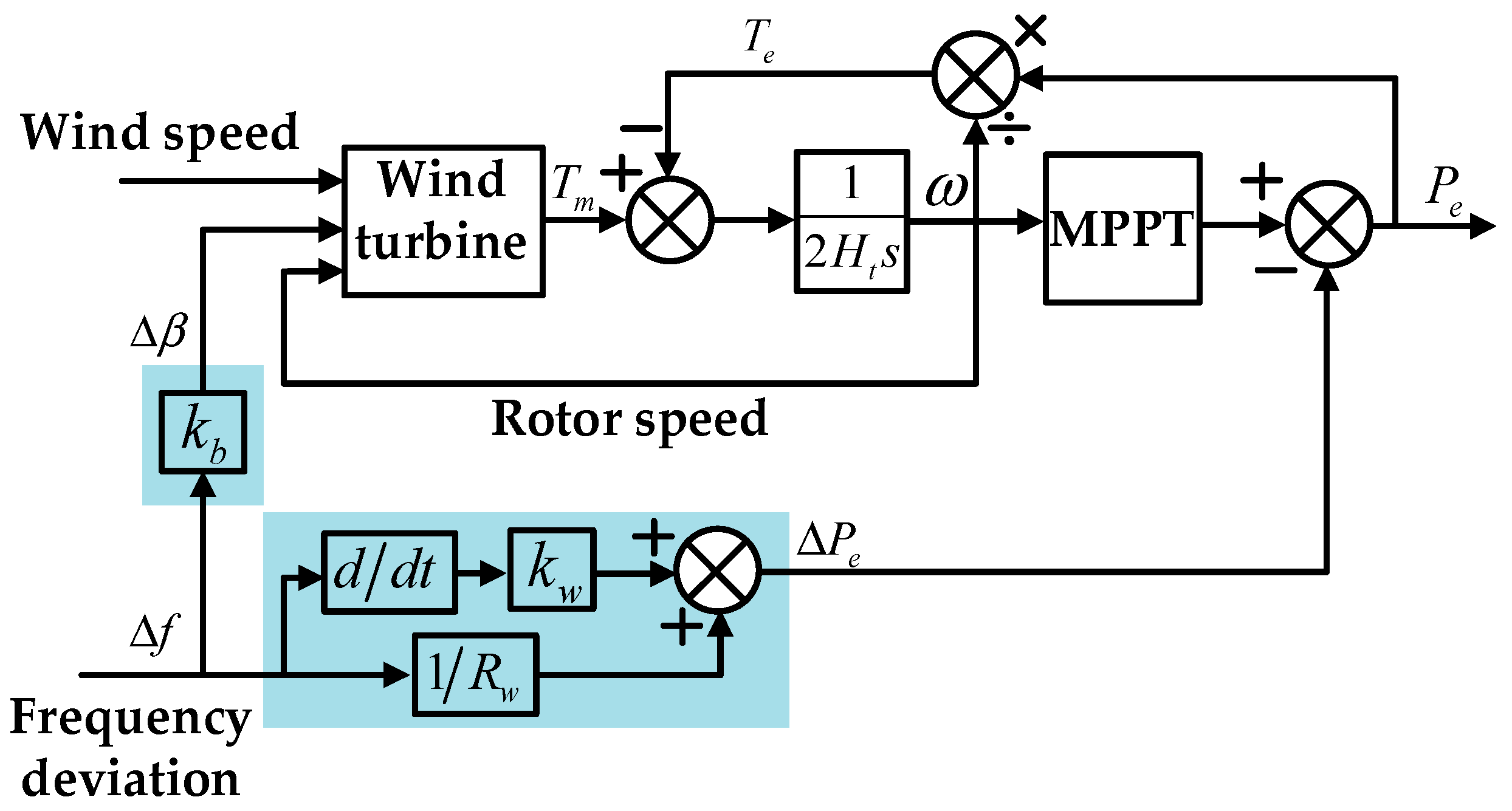
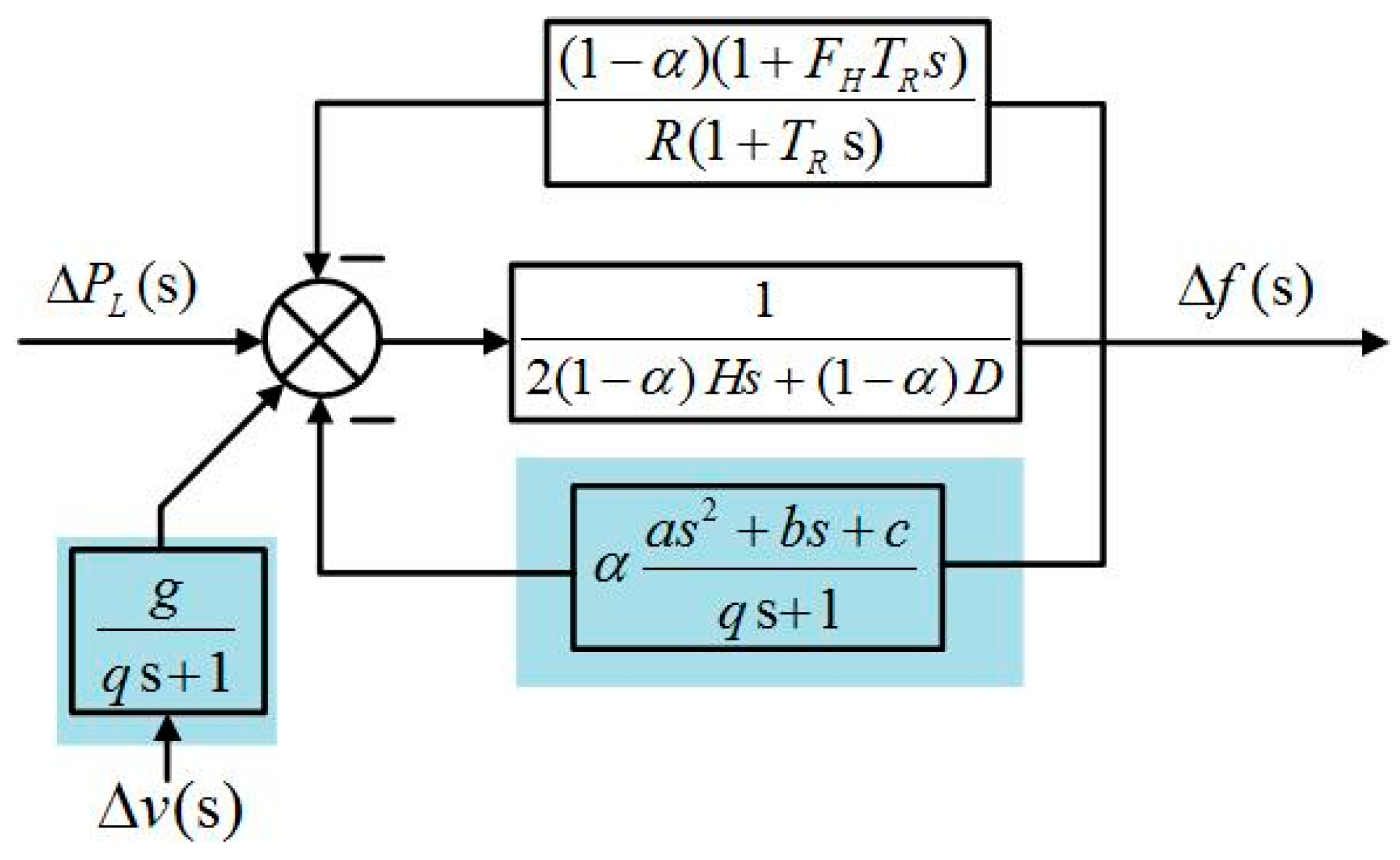
With large-scale wind power into the grid, the traditional SFR model is no longer suitable for high permeability wind power systems, research into the dynamic frequency response characteristics of high-wind integrated power systems becomes a crucial subject to be studied. Hence, it is indispensable to investigate the SFR model for power systems with high penetrated wind power. There are three main contributions in this paper. Firstly, the combined frequency control strategy of WTG based on the virtual inertia control and the pitch-control-based deloading control is introduced. Secondly, the reduced-order model of WTG is deduced by employing small signal analysis theory, and an extended SFR model that takes the wind power into account based on the reduced-order model of WTG and the traditional SFR model. Afterwards, the stability of the extended SFR model is analyzed. Finally, analytical tests and evaluations of the extended SFR model are given.
4. Verification of the Extended SFR Model
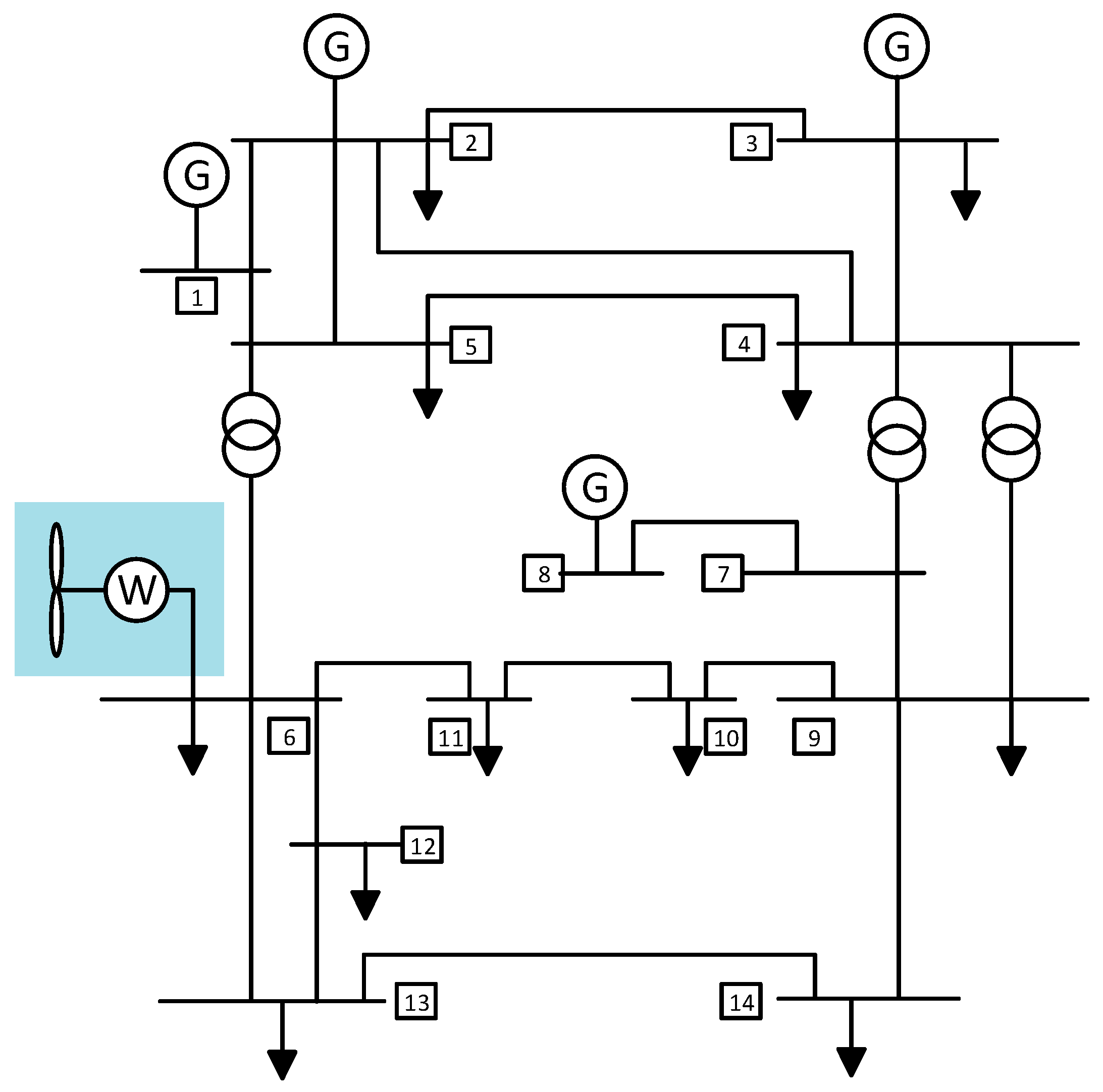
In order to verify the validity of the proposed extended SFR model, the IEEE-14 bus system is chosen as a case study. The wiring diagram is shown in
Figure 7; system total load power is 220 MW and generator nodes are 1, 2, 3, 6 and 8. Using the unit substitution method, the 6# synchronous generator is replaced by wind turbines to maintain the power flow balance of the system, the ratio of wind turbine capacity to total generator capacity is 30%, namely
α = 0.3, and it is assumed that the wind turbines are replaced by a dynamic aggregate wind turbine generator [
23,
24]. The synchronous generators are made of thermal power units, and both of them are equipped with a prime mover governor system. The wind power adopts permanent magnet direct drive wind turbine, and the wind turbine adopts the frequency regulation control strategy shown in
Figure 1. The operating data and parameters for the extended SFR model for the high-wind integrated power system, such as wind turbine generators and traditional generators, are mentioned in
Appendix A.
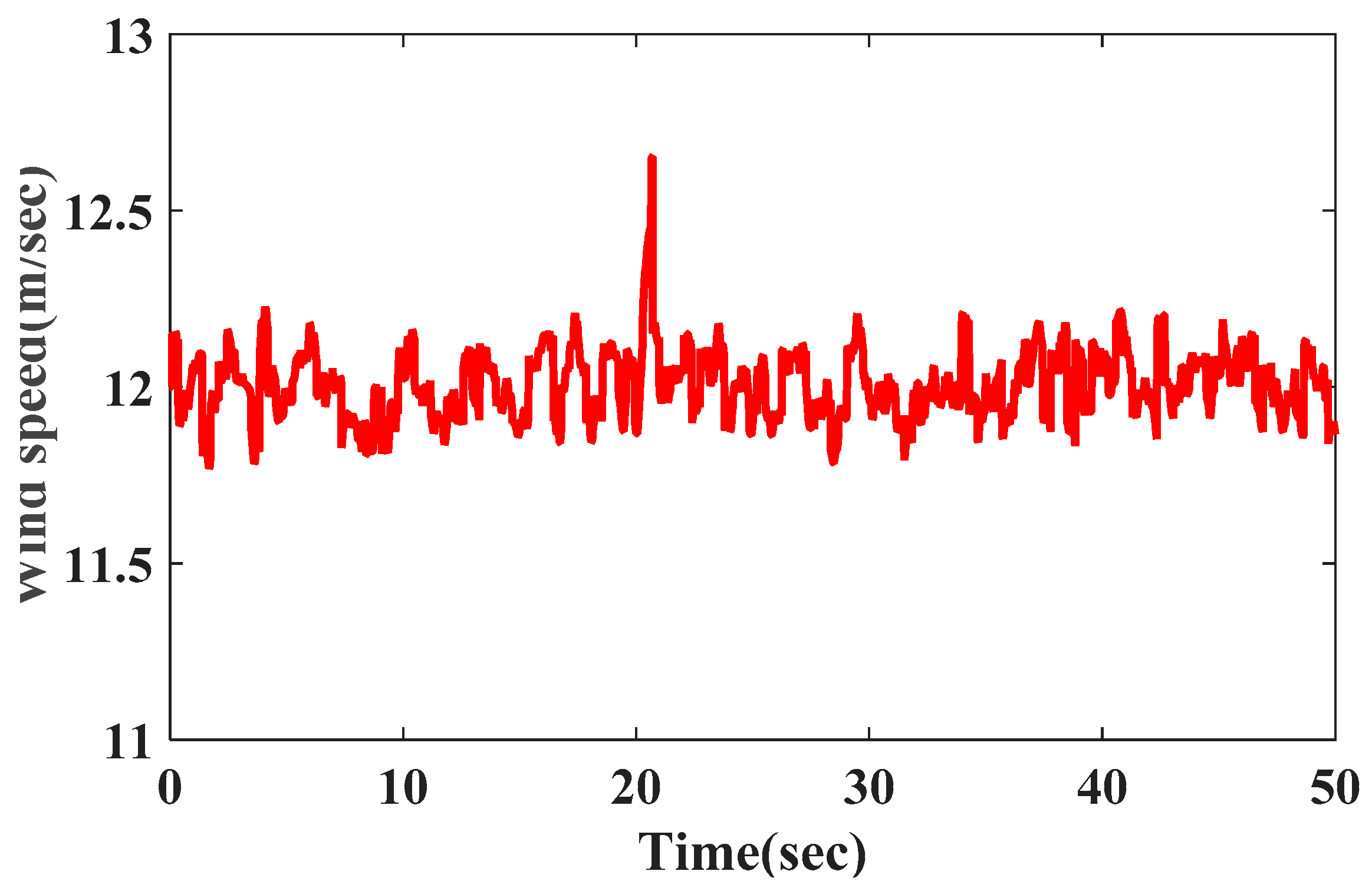
For wind power generation, the output power of WTG is affected by wind speed. Therefore, the impact of wind speed should not be neglected when analyzing the dynamic frequency response of high-wind integrated power systems. However, the wind speed is uncontrollable, and the output power of the WTG fluctuates with the fluctuation of the wind speed, so the resulting in frequency fluctuates. In order to make wind speed closer to reality in the case study, the mathematical model of stochastic fluctuating wind speed is applied, the wind speed is composed of base wind speed, gust wind speed, ramp wind speed and noise wind speed [
25,
26], as shown in
Figure 8. And it is assumed that a 0.2 pu load disturbance occurs at
t = 5 s in the simulation.
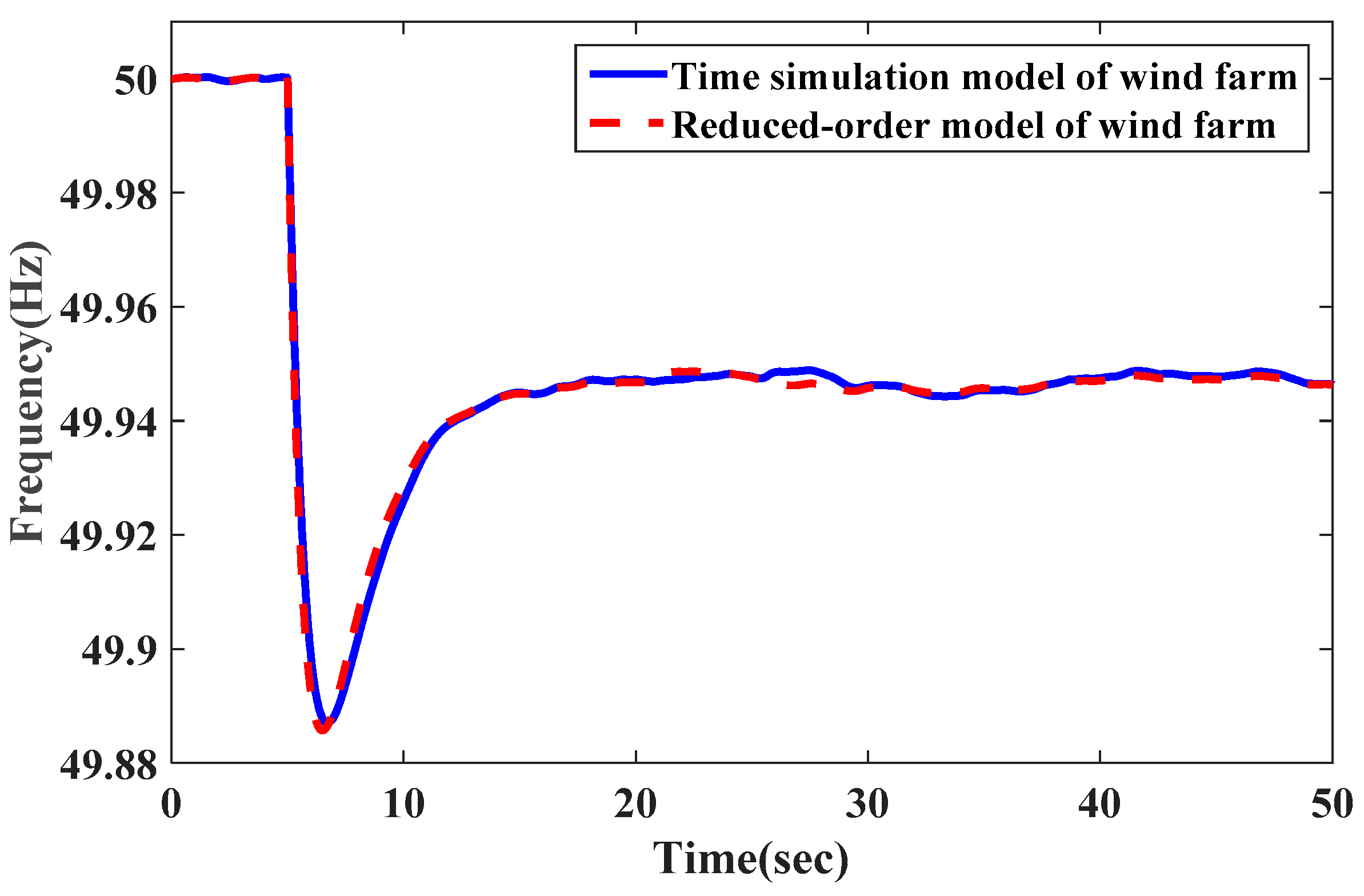
The system frequency response of the reduced-order model and the detailed time simulation model of wind farms are depicted and compared in
Figure 9. It can be seen that the curves of the frequency obtained from the reduced-order model and time simulation model of wind farms are in good agreement; the system frequencies of wind farms based on the reduced-order model are accurately simulated in comparison to the time simulation model. That means the reduced-order model can represent real time frequency dynamic response of the wind farm.
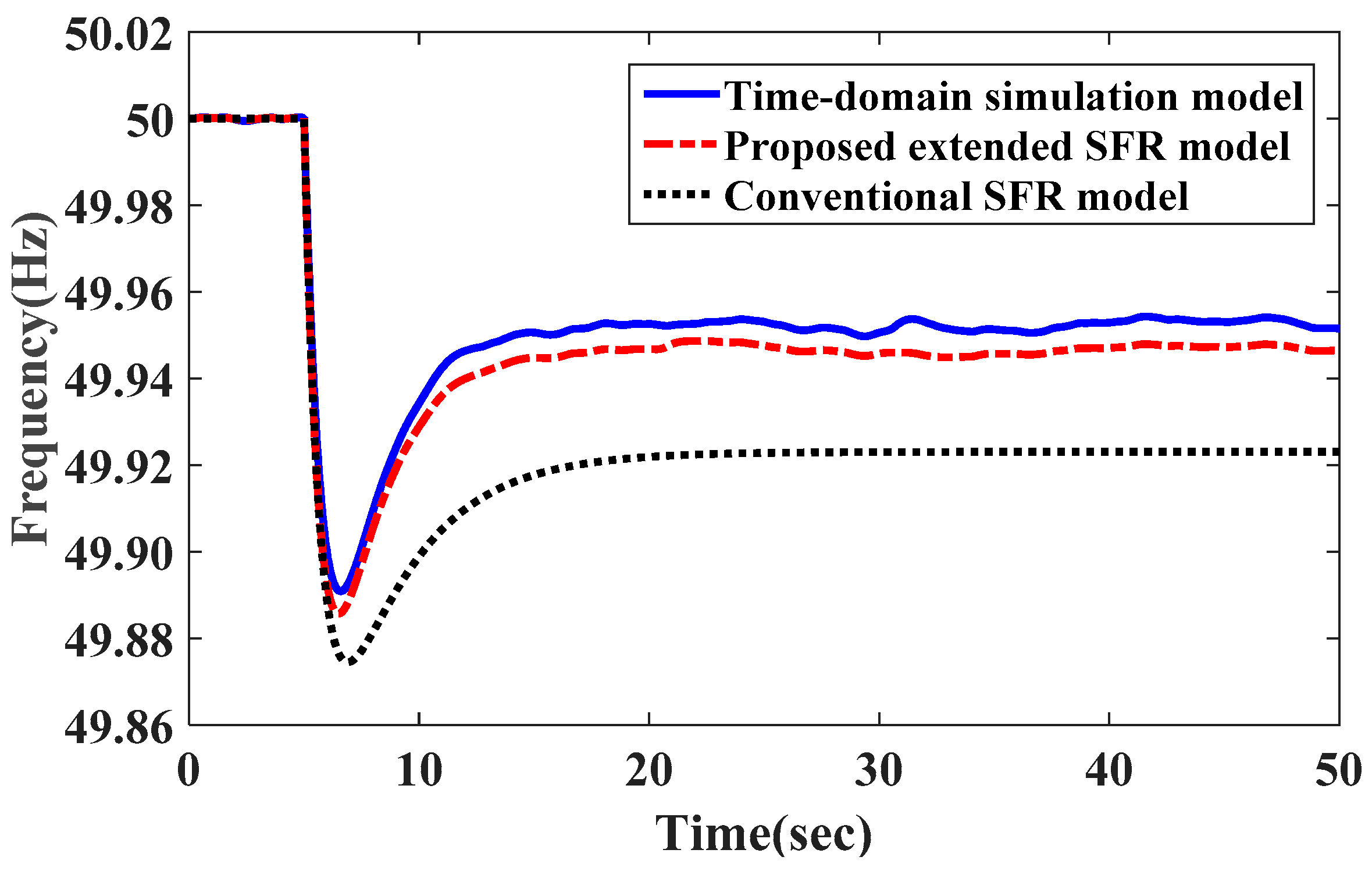
The system frequency response of the extended SFR model, the conventional SFR model and the detailed time simulation model based on test system, as shown in
Figure 7, are also depicted and compared in
Figure 10. Although the extended SFR model ignores the topological structure of the network and cannot reflect the dynamic power of the branch, the initial frequency response, the minimum frequency and the frequency steady-state value of the extended SFR model have higher simulation accuracy. Compared with the whole time domain simulation results, the maximum error in the frequency drop is less than 0.005 Hz, and the frequency steady value error is less than 0.006 Hz; thus, the extended SFR model method can calculate the frequency response process of the system. Compared with the conventional SFR model (proposed in [
18]), the proposed extended SFR model exhibits a smaller frequency nadir error and steady-state frequency error. It can also more efficaciously reflect the dynamic response characteristics of wind turbines.
The WTG responds to the system frequency by controlling electromagnetic torque
Te or mechanical torque
Tm. The electromagnetic torque control in this paper refers to the virtual inertial control, and the mechanical torque control is the pitch-control-based deloading control.
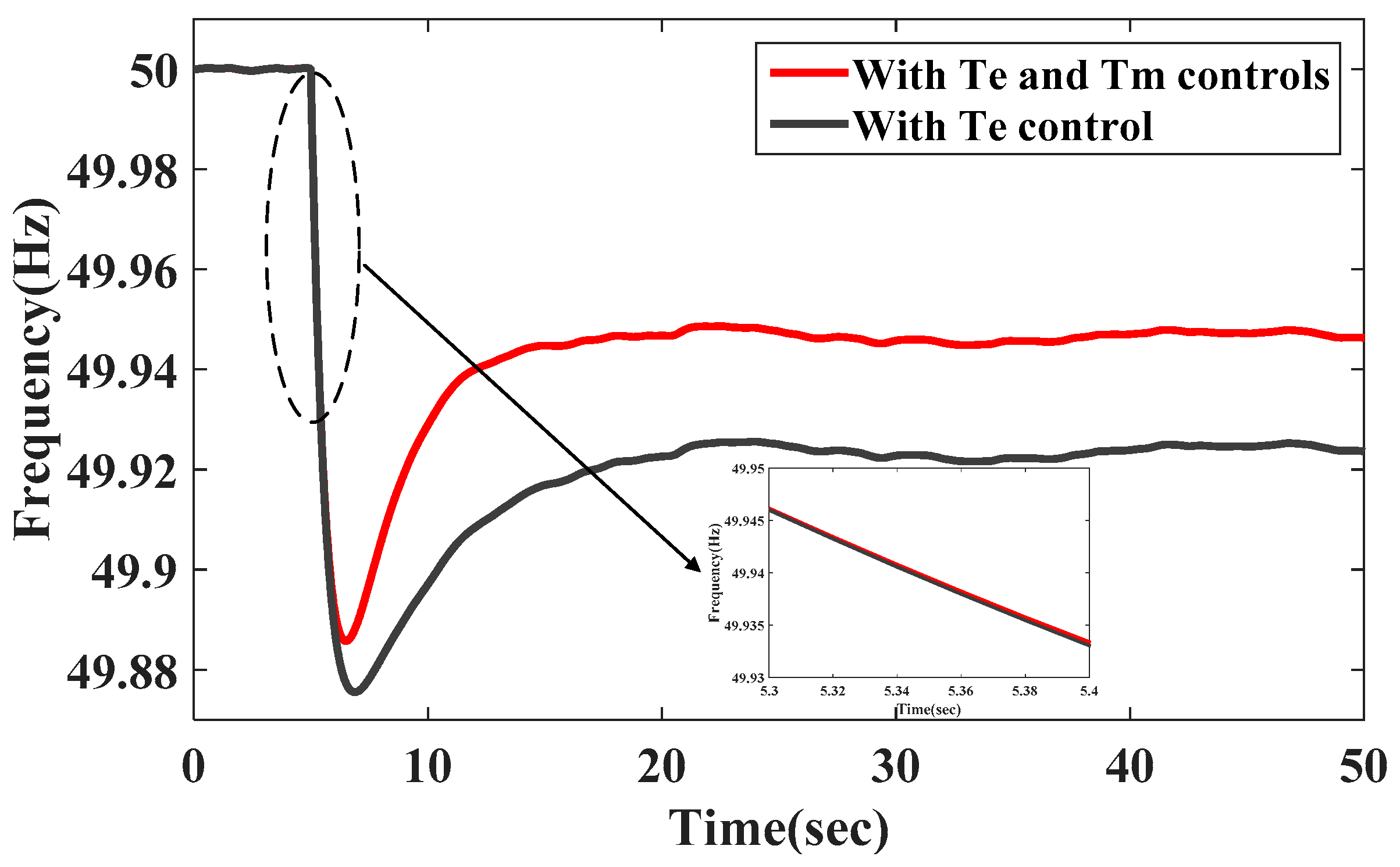
Figure 11 shows the dynamic frequency response and the additional power of the system with different torque control. Based on the extended SFR model, it can be seen that the frequency dynamic characteristics after disturbance can be improved when combined with
Te control and
Tm control; as a result, the minimum frequency and the steady-state frequency value are improved. When only the
Te control is applied in the extended SFR model, the minimum frequency is 49.875 Hz, and the quasi steady state value is 49.925 Hz. When the
Tm control is added, the system minimum frequency is 49.885, and the steady-state frequency value is 49.948 Hz. In addition, it can be seen that the control of adding
Tm does not affect the initial rate of frequency change (see the enlarged diagram in
Figure 11).
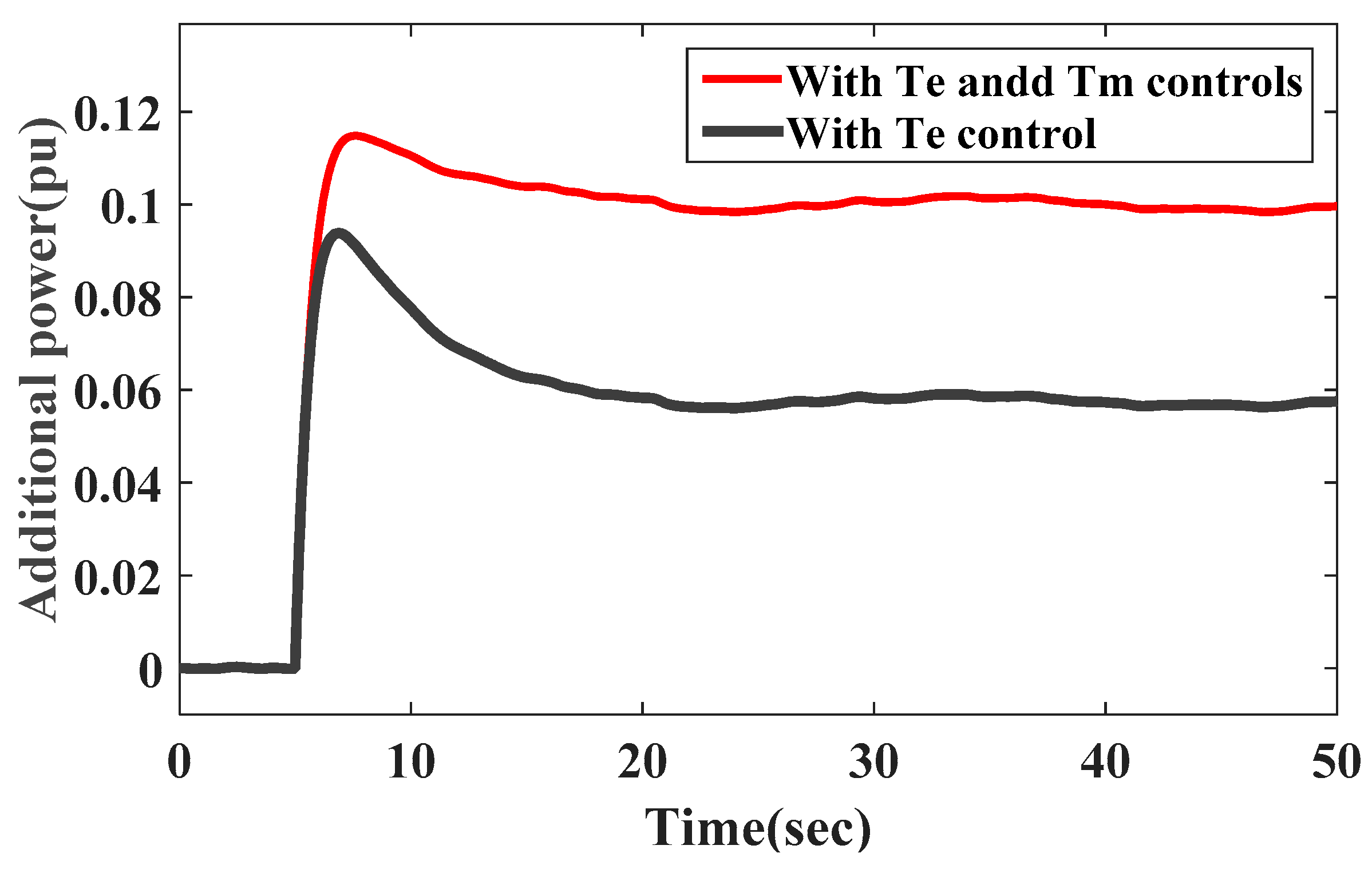
Figure 12 shows the additional power-per-unit value of the WTG; after adding
Tm control, the wind turbine can release a certain reserve power according to the change of the frequency. This part of the reserve power accelerates the rotor, thereby reducing the steady-state frequency deviation.
From the analysis in
Section 3, it is suggested that parameters of virtual inertia control, such as
kw,
Rw and pitch-control-based deloading control
kb, will affect the frequency dynamic response characteristics of the power system. Therefore, in order to evaluate the impact of parameters
kw,
Rw and
kb on system specific frequency response, different values of parameter
kw,
Rw and
kb are considered in
Figure 13,
Figure 14 and
Figure 15. It is assumed that all load disturbances and wind speeds are the same in the simulation scenario.
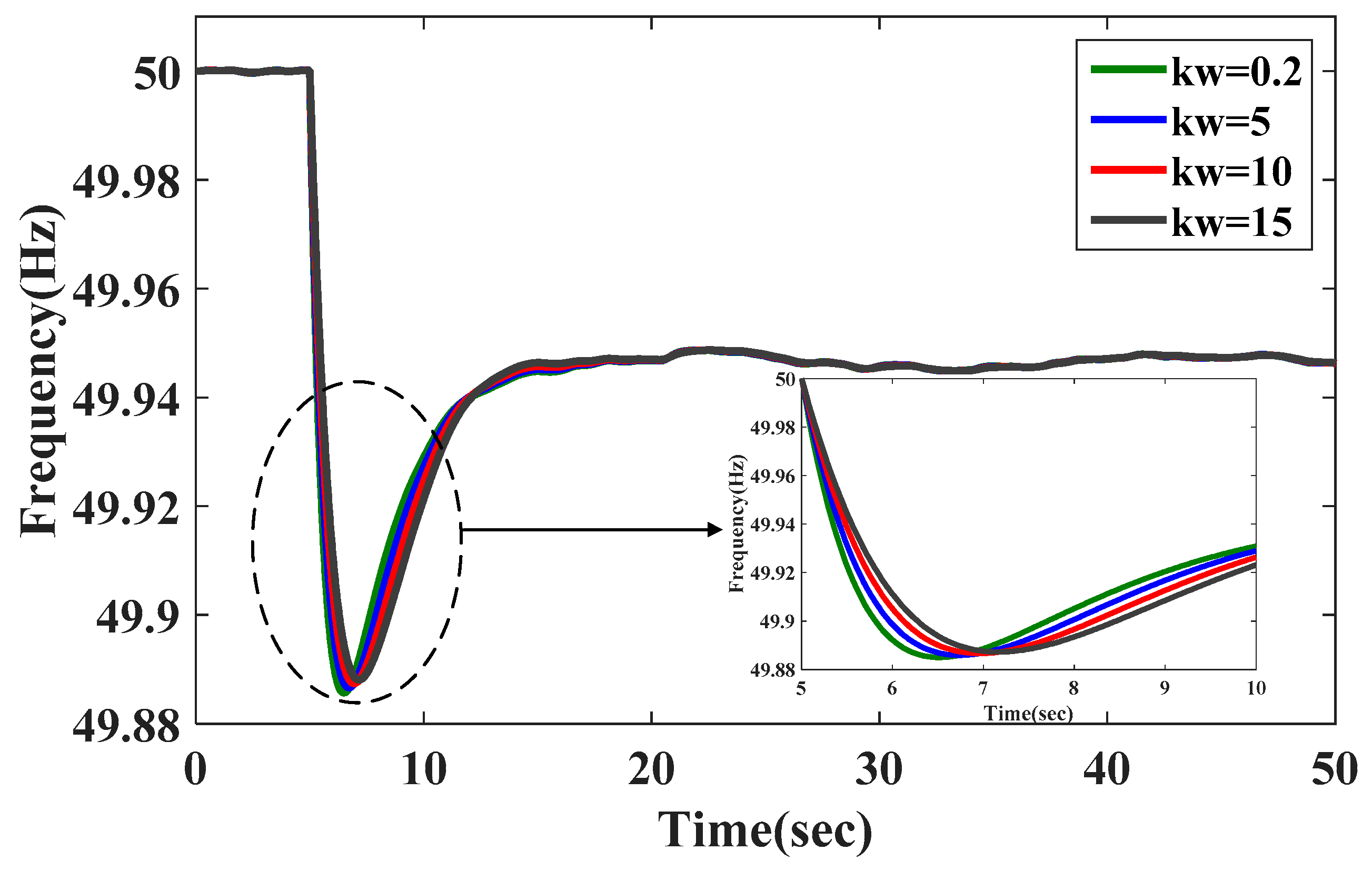
From
Figure 13, it can be seen that
kw has almost no impact on the steady-state frequency value of the perturbed system, but affects the initial frequency change rate, the minimum frequency and the arrival time of minimum frequency of the perturbed system. The minimum frequency is comparatively higher when the value of
kw is larger, and the initial frequency change rate becomes slower and the arrival time of the minimum frequency is later at higher value of
kw. That means the frequency change rate is sensitive to the change of parameter
kw; the simulation result is consistent with the analysis of (26) and
Figure 3. Also, as can be seen from
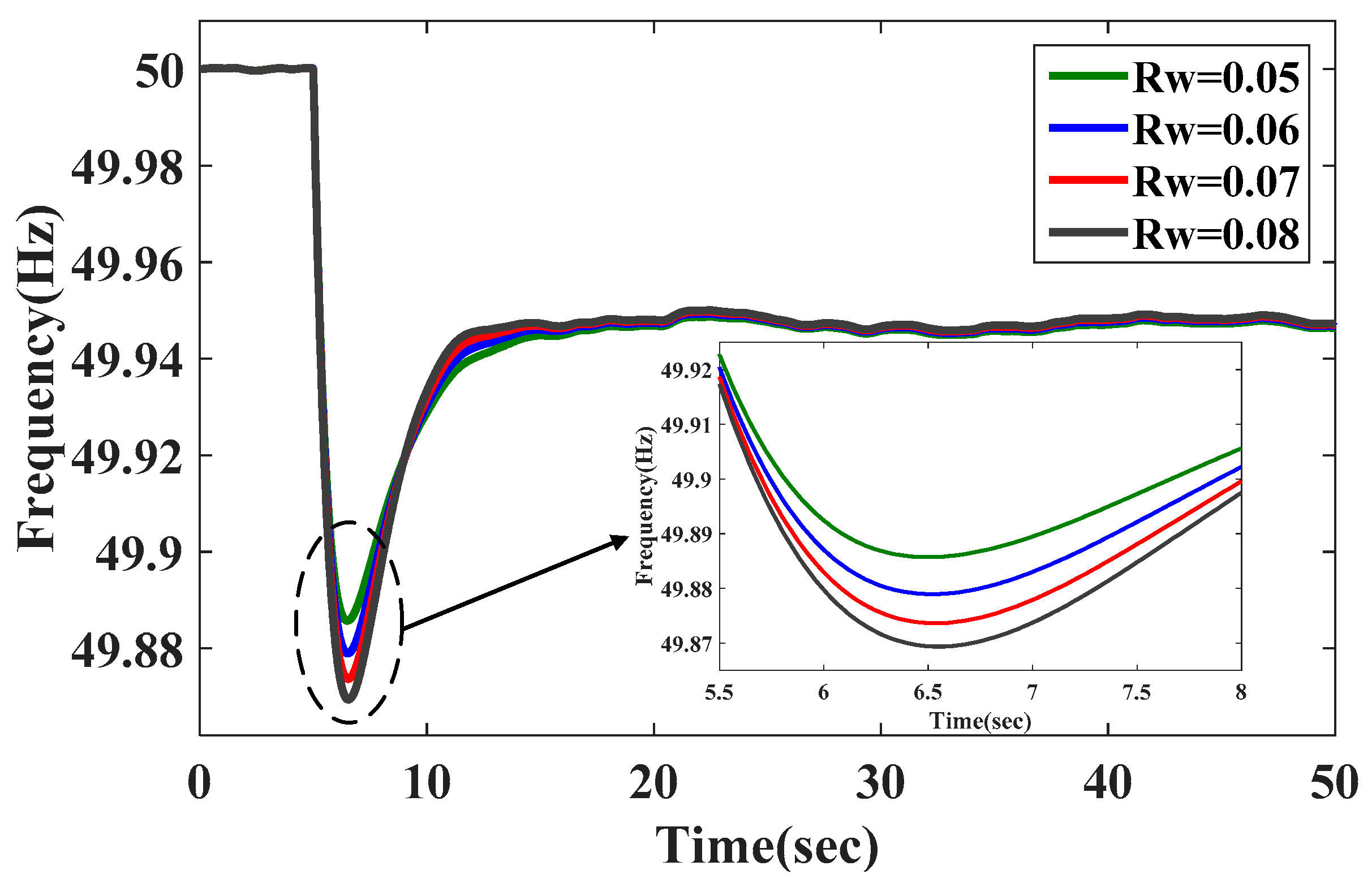
Figure 14,
Rw mainly affects the minimum frequency; the minimum frequency is comparatively higher when the value of
Rw is less; it has little effect on the rate of the frequency change, and also has a slight effect on the steady-state frequency value. This demonstrates that the inertial control of WTG can make a contribution to the frequency stabilization, and the larger
kw and smaller
Rw can play a greater role. However, the improvement in steady-state frequency deviation is not particularly good.
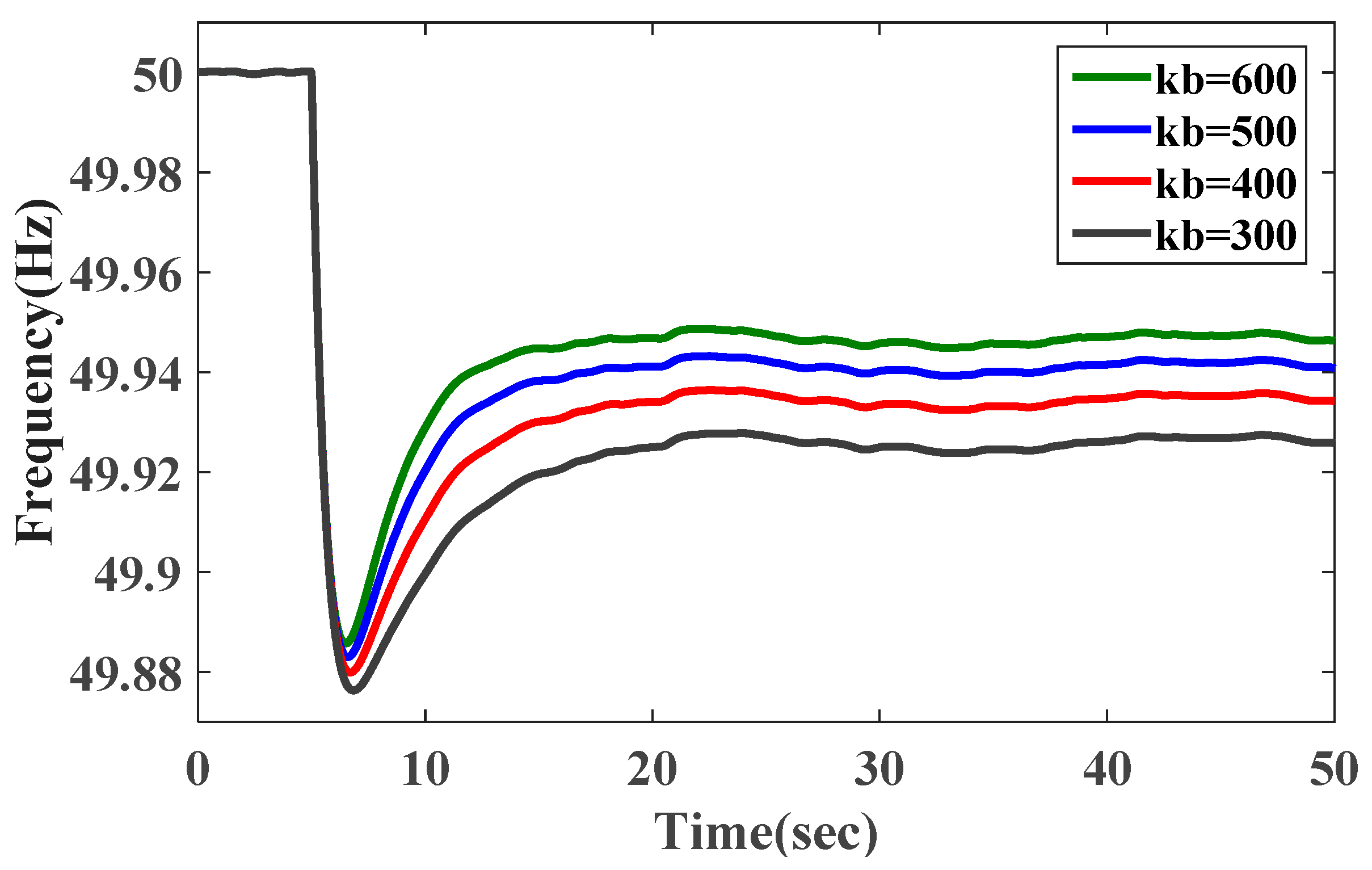
The impact of parameter
kb on frequency dynamic response is shown in
Figure 15, where
kb represents the proportional relationship between the frequency deviation and the pitch angle deviation. It can be seen that
kb does not affect the initial frequency change rate, but has a greater impact on the minimum frequency and the steady-state frequency values. With an increase of parameter
kb, the initial frequency change rate of each frequency response curve is coincident, and the minimum frequency and the steady-state frequency values are higher. That means the minimum frequency and the steady-state frequency values are sensitive to the change of parameter
kb. That is mainly because a higher
kb setting will result in a larger reserve power controlled by pitch-control-based deloading control. The simulation result is also consistent with the analysis of (27) and
Figure 4.
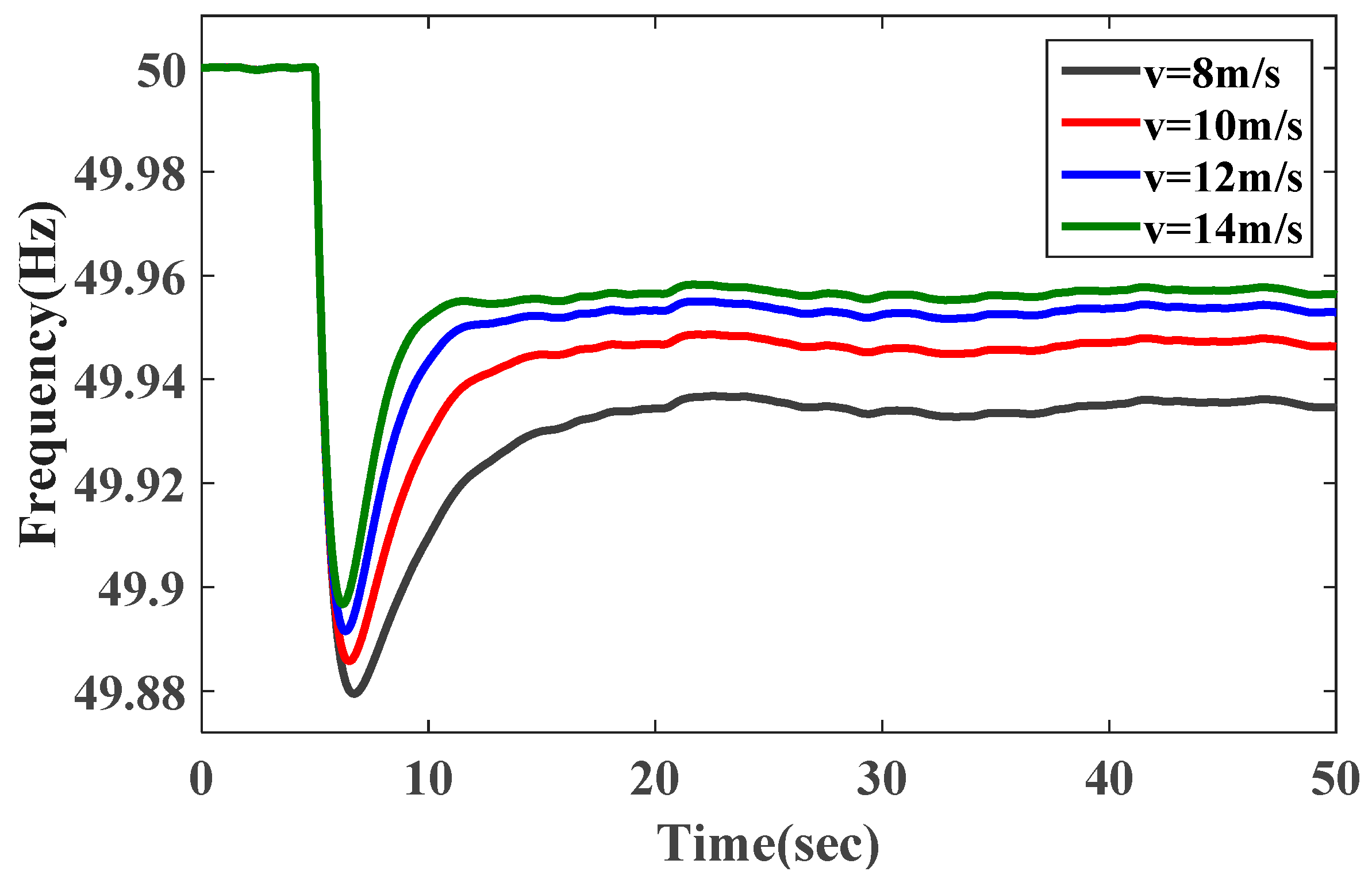
As mentioned above, the fluctuation of wind speed results into frequency variation. The impact of initial operating wind speed
v on frequency dynamic response is shown in
Figure 16. It can be seen that an increase in initial operating wind speed
v improves the frequency dynamics, which can be particularly reflected by the dynamic indices of the minimum frequency and the steady-state frequency values. This is mainly because a higher initial operating wind speed
v setting will also result in a larger output power of WTG and the change of the reserve power controlled by pitch-control-based deloading control.
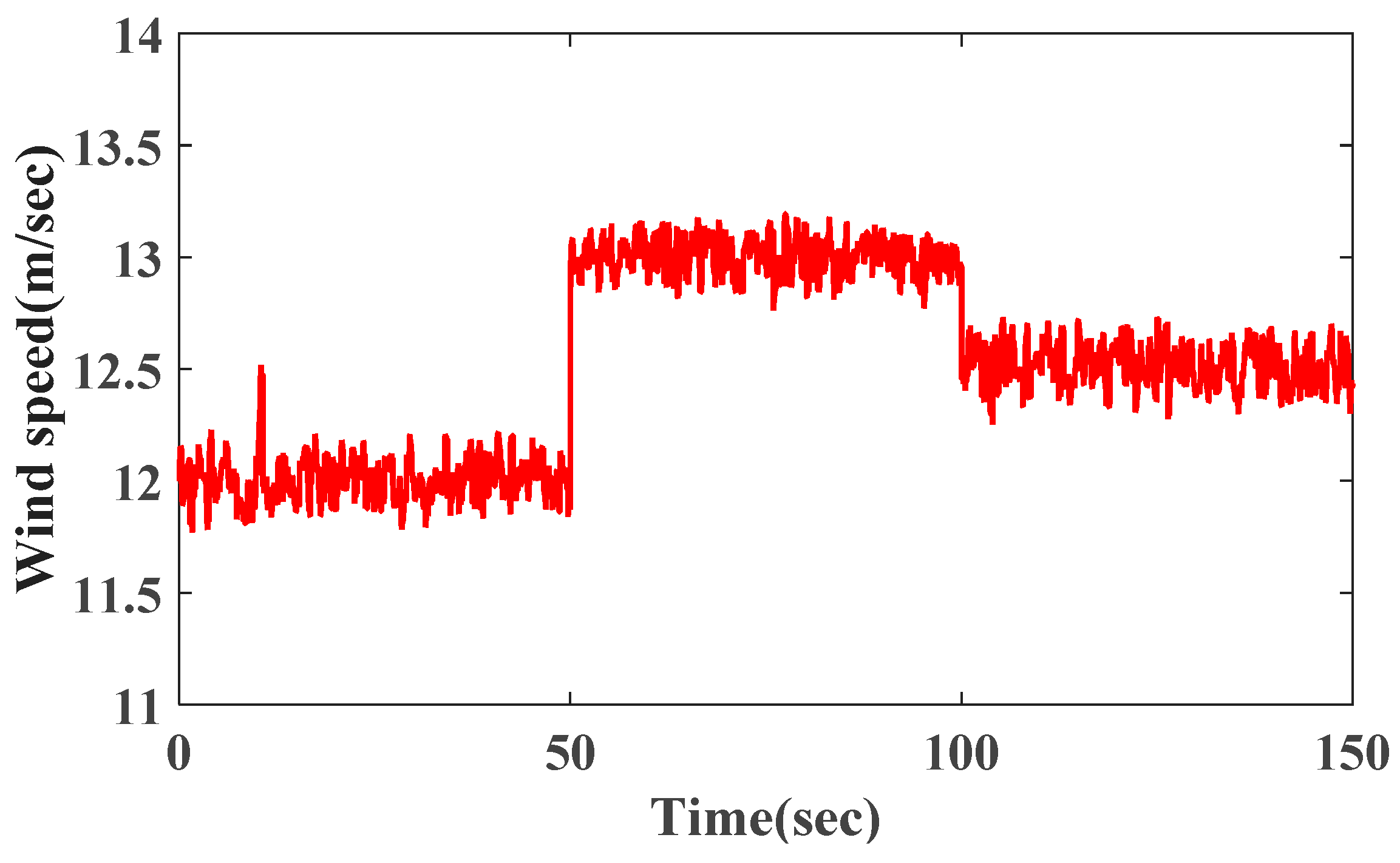
The above analysis is based on load disturbance. In fact, the wind speed may change suddenly in the area where the wind resource fluctuates greatly. Meanwhile, according to
Figure 2 and (25), sudden disturbance of wind speed will also affect the dynamic response frequency. The step wind speed model for WTG is considered as shown in
Figure 17; it is also composed of base wind speed, gust wind speed, ramp wind speed and noise wind speed in order to present more realistic results [
25,
26]. It is assumed that the initial average operating wind speed is 12 m/s, which is the rated wind speed. The wind speed suddenly increased to 13 m/s at
t = 50 s and suddenly decreased to 12.5 m/s at
t = 100 s, as shown in
Figure 17. Meanwhile, assume that only the wind speed disturbance occurs (∆
Pd = 0). The frequency response and the active power response of the system under wind speed conditions shown in
Figure 17 are shown in
Figure 18 and
Figure 19, respectively.
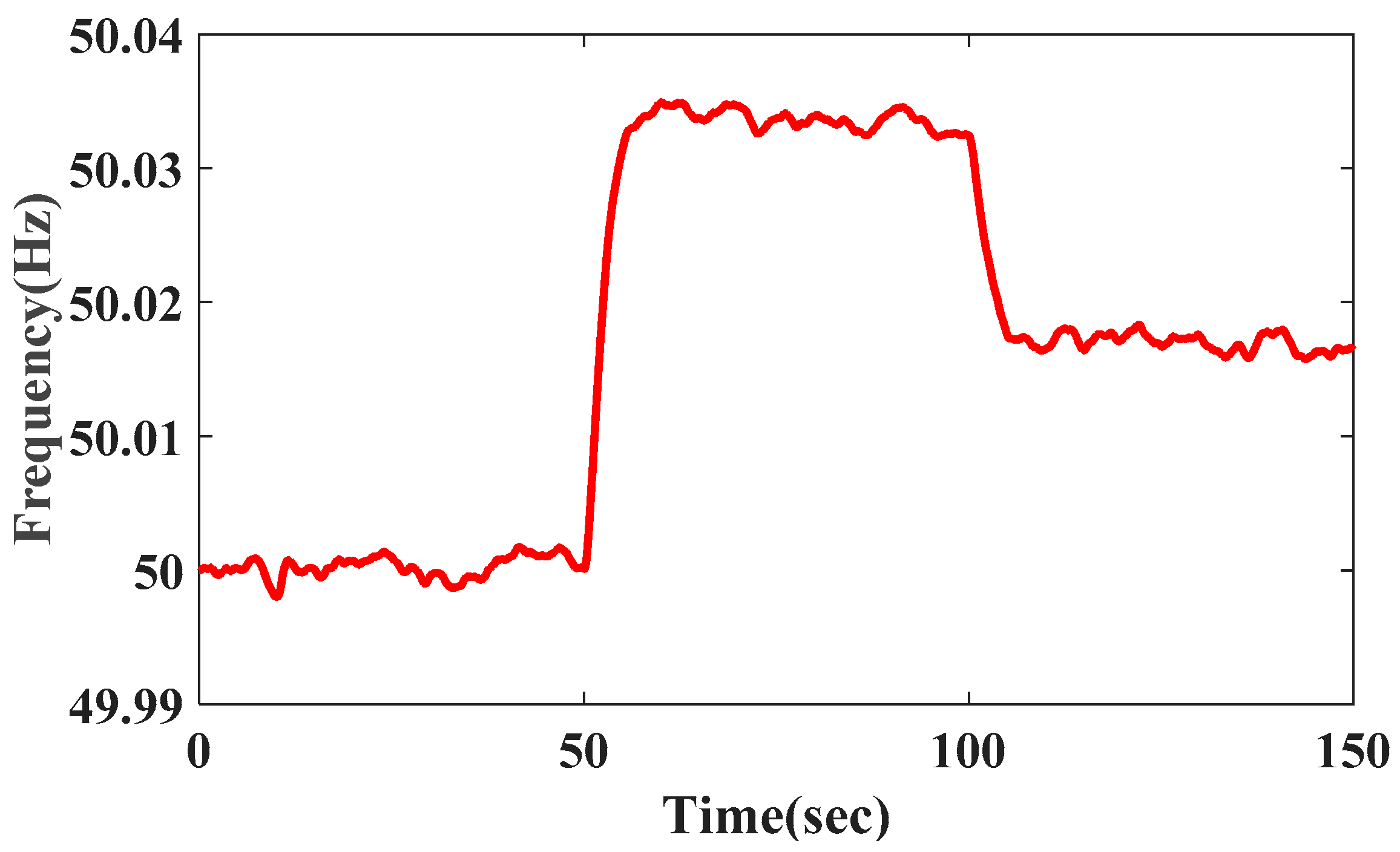
It can be observed from the
Figure 18 that the frequency response trends are the same as the wind speed; namely, the sudden increase in wind speed will increase the value of system frequency. Conversely, the sudden decrease of wind speed will reduce the value of system frequency. But the frequency response is smoother (i.e., dip value is less) with a sudden disturbance in wind speed as compared to a sudden disturbance in load. That is mainly because the output power of WTG varies with the change of wind speed. The transfer function expression between the wind speed variation and output power variation of WTG is a first-order system as shown in Equation (21), which acts like a first-order low-pass filter, thus the inertial damping will be acted.
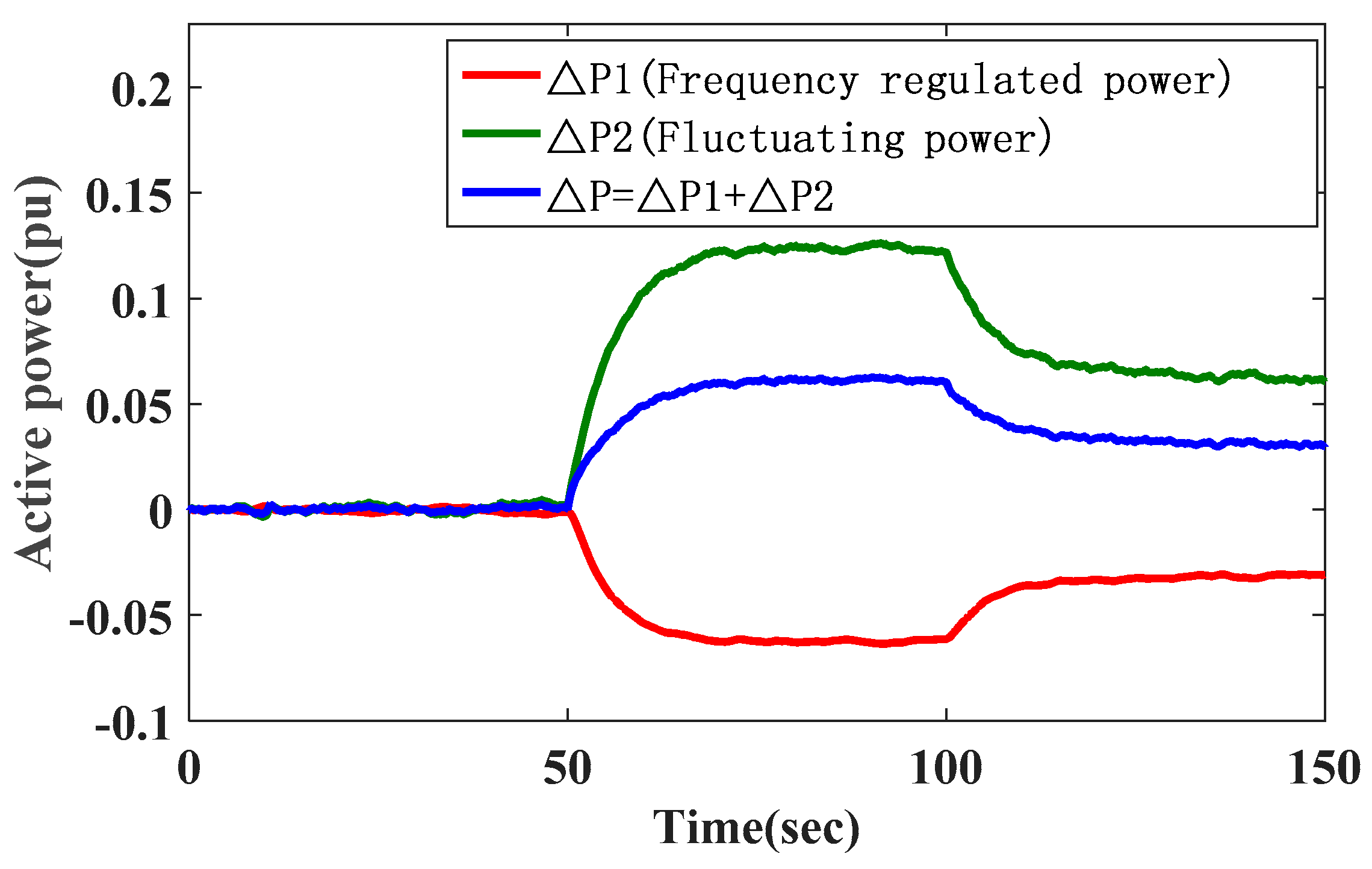
Figure 19 shows that the sudden change in wind speed will change the power of two parts: one is the output power of the WTG itself (Δ
P1), and another is the power released by the wind turbine (Δ
P2) participating in frequency regulation. It is worth mentioning that the change in direction of Δ
P1 and Δ
P2 is reversed, and the magnitude of the change of Δ
P2 is larger than Δ
P1; thus, it is concluded that the variation of wind speed will bring frequency deviation of the system.
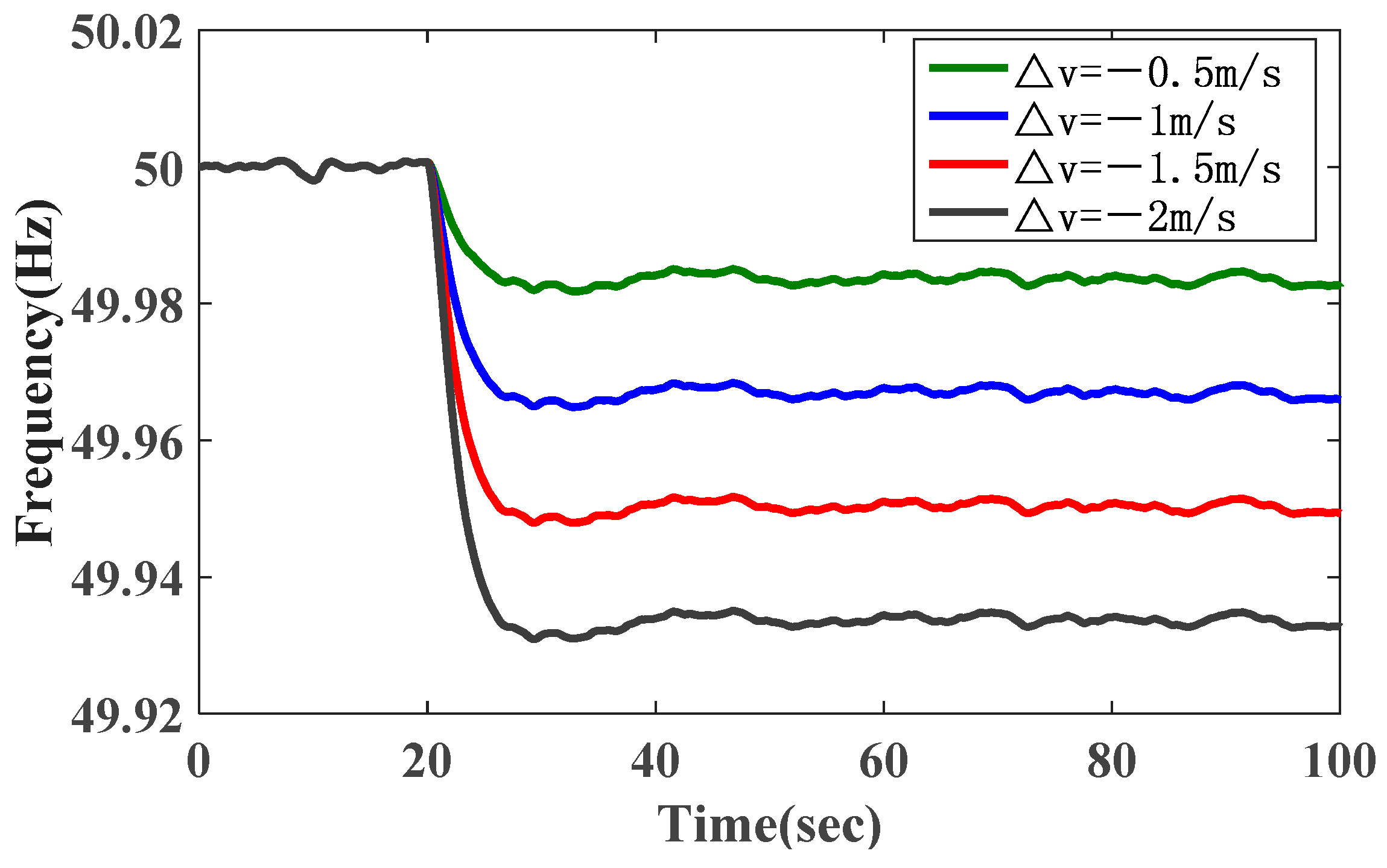
In addition, the frequency response for varying values of wind speed
v is shown in
Figure 20, it can be noticed that the dynamic response characteristics of frequency become worse when the wind speed is more abrupt. The result is extremely similar to varying the parameter Δ
Pd, the difference is that the frequency response is smoother (i.e., dip value is less) than mentioned above.