An Affine Arithmetic-Based Power Flow Algorithm Considering the Regional Control of Unscheduled Power Fluctuation
Abstract
:1. Introduction
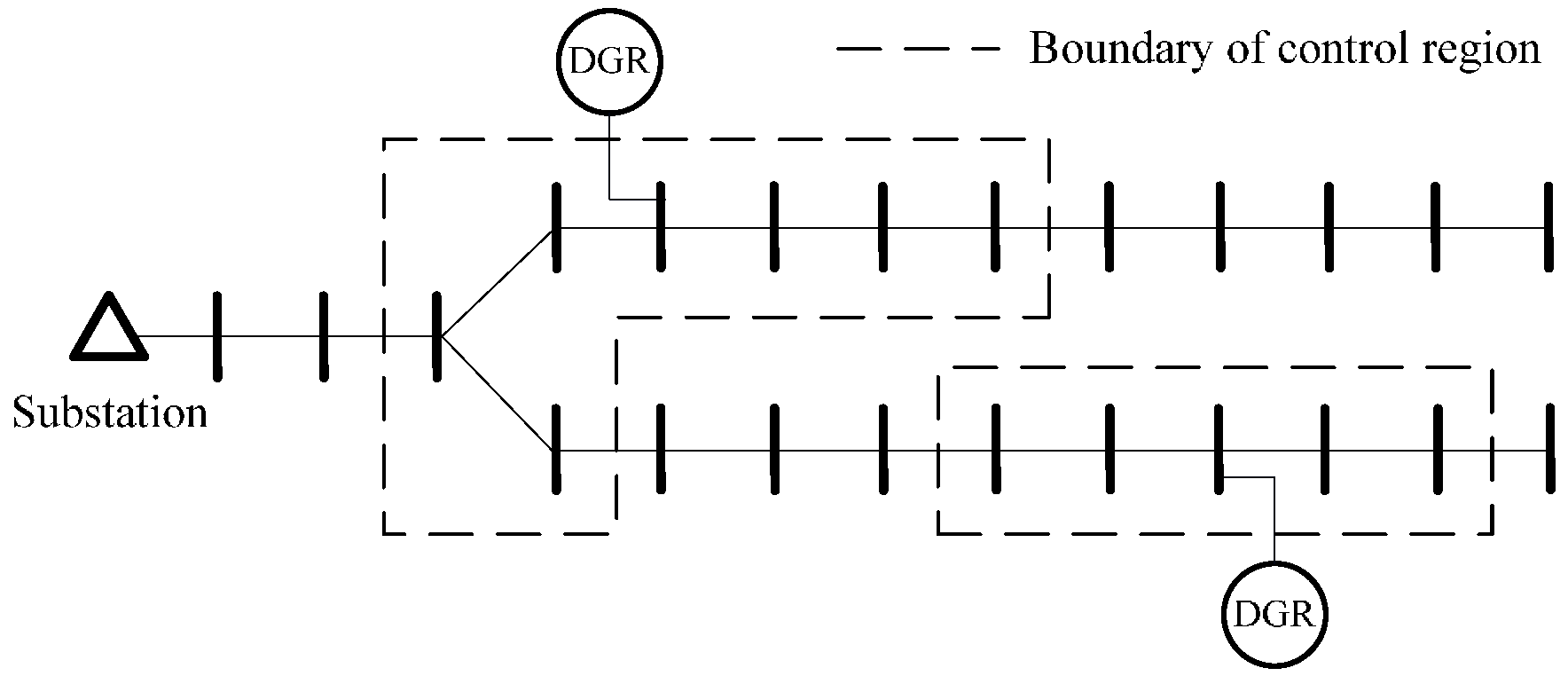
2. Regional Control of Unscheduled Power Fluctuation
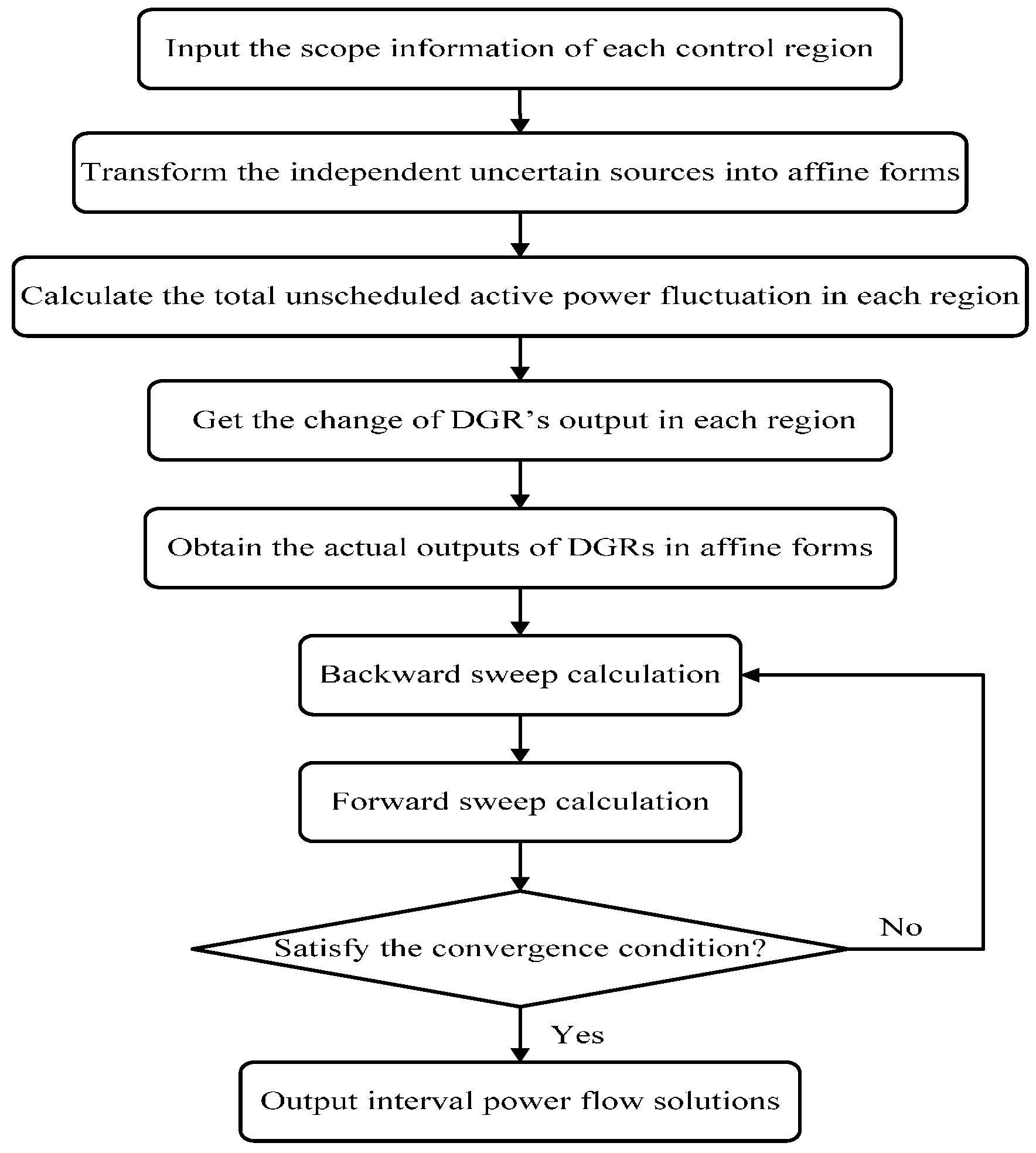
3. Proposed Affine Arithmetic-Based Modeling Method and Power Flow Algorithm
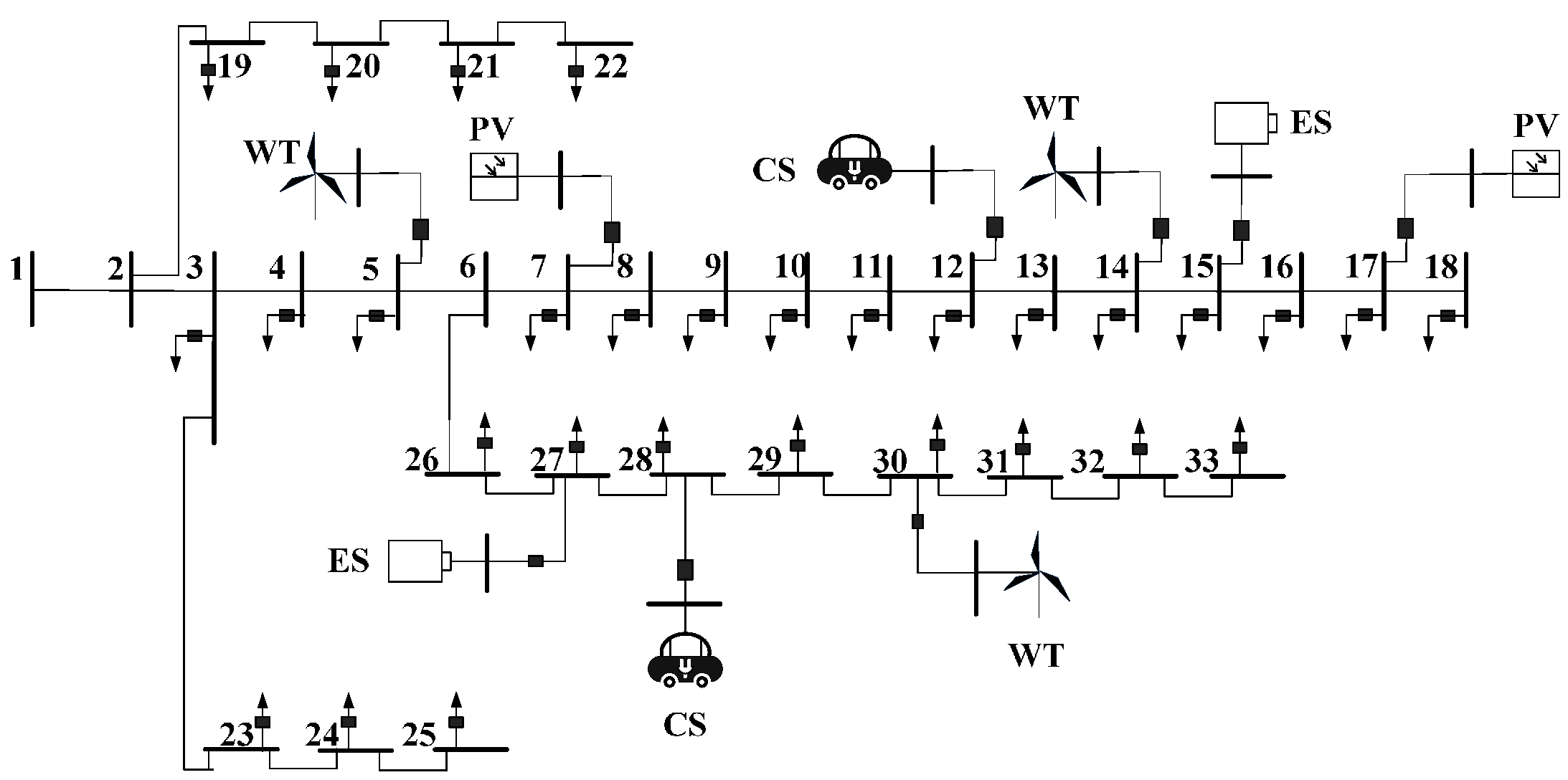
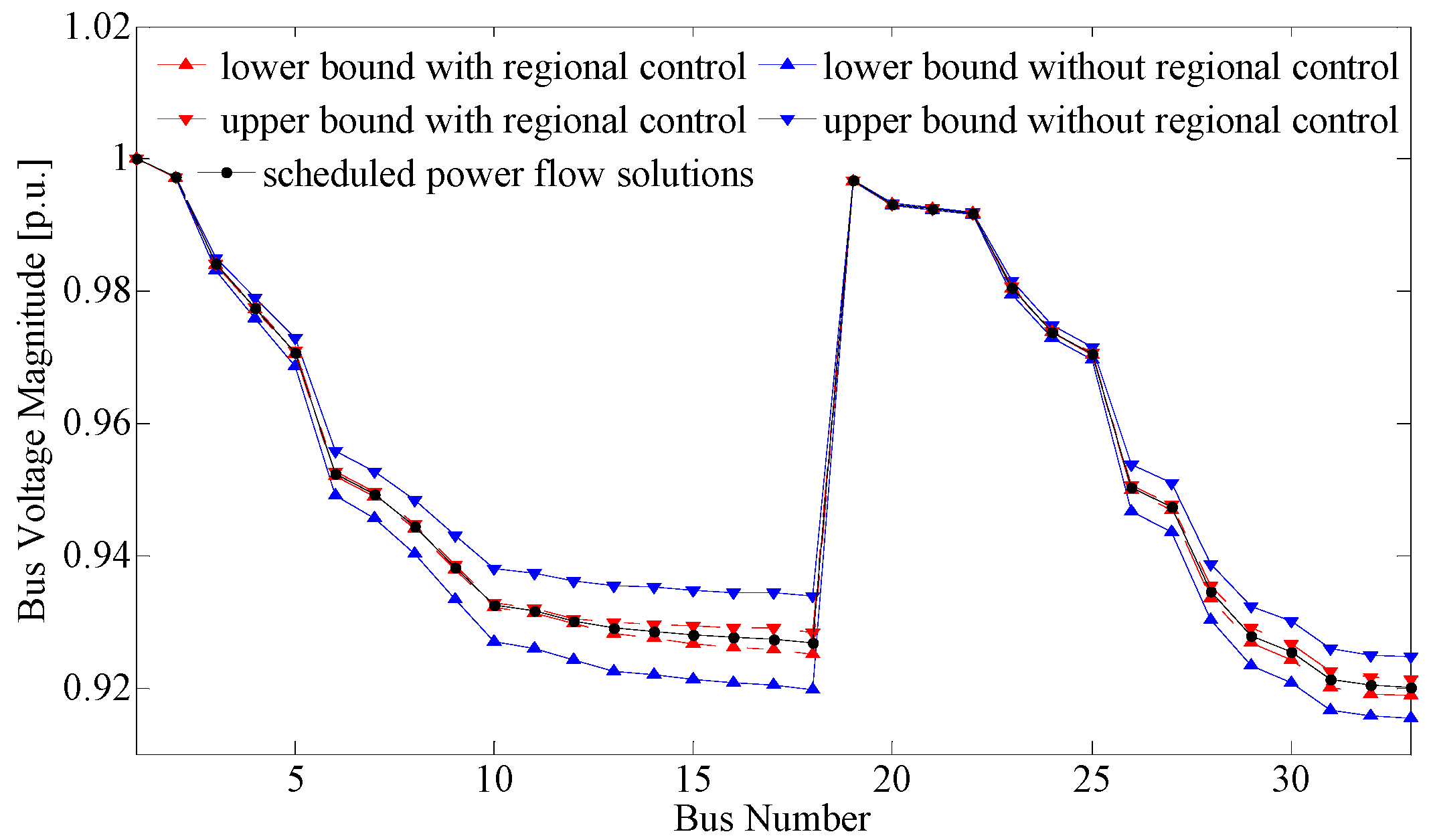
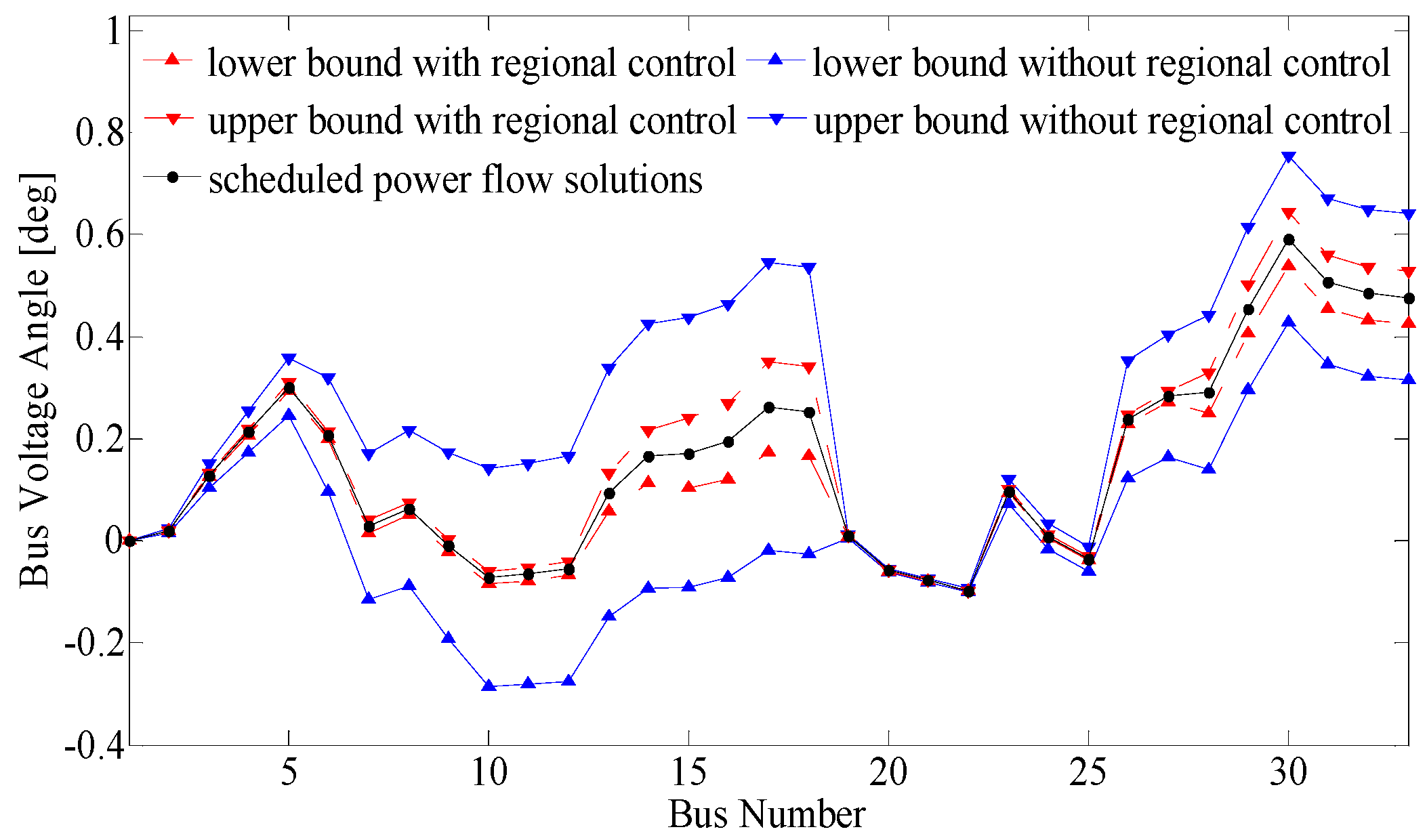
4. Case Study
- (1)
- WT, PV, CS and ES stand for wind turbine, photovoltaic module, electric vehicle charging station, and energy storage, respectively. WT, PV, and CS are uncertain sources. ES is regarded as the DGR.
- (2)
- At the moment under study, uncertain sources of the same type are assumed to have the same predicted output or demand. The predicted active power injection to the corresponding bus from WT, PV, and CS are 300 kW, 200 kW, and −500 kW, respectively. The prediction errors of all the uncertain sources are set as ±10%.
- (3)
- The maximum charging or discharging power of ES is assumed to be ±100 kW, and no charging or discharging performance occurs at the moment.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yang, N.C. Three-phase power flow calculations by direct ZLOOP method for microgrids with electric vehicle charging demands. IET Gener. Transm. Distrib. 2013, 7, 1002–1010. [Google Scholar] [CrossRef]
- Ou, T.C.; Tsao, T.P.; Lin, W.M.; Hong, C.M.; Lu, K.H.; Tu, C.S. A novel power flow analysis for microgrid distribution system. In Proceedings of the 8th IEEE Conference on Industrial Electronics and Applications (ICIEA), Melbourne, Australia, 19–21 June 2013; pp. 1550–1555. [Google Scholar]
- Das, B. Radial distribution system power flow using interval arithmetic. Int. J. Electr. Power Energy Syst. 2002, 24, 827–836. [Google Scholar] [CrossRef]
- Vaccaro, A.; Canizares, C.A.; Villacci, D. An affine arithmetic-based methodology for reliable power flow analysis in the presence of data uncertainty. IEEE Trans. Power Syst. 2010, 25, 624–632. [Google Scholar] [CrossRef]
- Gu, W.; Luo, L.; Ding, T.; Meng, X.; Sheng, W. An affine arithmetic-based algorithm for radial distribution system power flow with uncertainties. Int. J. Electr. Power Energy Syst. 2014, 58, 242–245. [Google Scholar] [CrossRef]
- Jupe, S.C.E.; Taylor, P.C.; Michiorri, A. Coordinated output control of multiple distributed generation schemes. IET Renew. Power Gener. 2010, 4, 283–297. [Google Scholar] [CrossRef]
- Pandi, V.R.; Al-Hinai, A.; Feliachi, A. Coordinated control of distributed energy resources to support load frequency control. Energy Convers. Manag. 2015, 105, 918–928. [Google Scholar] [CrossRef]
- Pandi, V.R.; Al-Hinai, A.; Feliachi, A. Adaptive coordinated feeder flow control in distribution system with the support of distributed energy resources. Int. J. Electr. Power Energy Syst. 2017, 85, 190–199. [Google Scholar] [CrossRef]
- Ou, T.C.; Hong, C.M. Dynamic operation and control of microgrid hybrid power systems. Energy 2014, 66, 314–323. [Google Scholar] [CrossRef]
- Ou, T.C. A novel unsymmetrical faults analysis for microgrid distribution systems. Int. J. Electr. Power Energy Syst. 2012, 43, 1017–1024. [Google Scholar] [CrossRef]
- Ou, T.C. Ground fault current analysis with a direct building algorithm for microgrid distribution. Int. J. Electr. Power Energy Syst. 2013, 53, 867–875. [Google Scholar] [CrossRef]
- Wang, S.; Han, L.; Wu, L. Uncertainty tracing of distributed generations via complex affine arithmetic based unbalanced three-phase power flow. IEEE Trans. Power Syst. 2015, 30, 3053–3062. [Google Scholar] [CrossRef]
- Luo, L.; Zhu, J.; Yang, S.; Wang, K.; Yao, J.; Gu, W. Interval Arithmetic based Influence Analysis on Power Flow caused by Integration of Wind Power and Electric Vehicles. In Proceedings of the 19th World Congress of the International Federation of Automatic Control (IFAC), Cape Town, South Africa, 24–29 August 2014; pp. 2758–2763. [Google Scholar]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
| Scenario Type | Voltage Magnitude (p.u.) | Voltage Angle (degrees) | ||
|---|---|---|---|---|
| Maximum Deviation | Average Deviation | Maximum Deviation | Average Deviation | |
| With regional control | 0.0016 | 5.8667 × 10−4 | 0.0882 | 2.5423 × 10−2 |
| Without regional control | 0.0070 | 3.5262 × 10−3 | 0.2843 | 1.2892 × 10−1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, L.; Gu, W.; Wang, Y.; Chen, C. An Affine Arithmetic-Based Power Flow Algorithm Considering the Regional Control of Unscheduled Power Fluctuation. Energies 2017, 10, 1794. https://doi.org/10.3390/en10111794
Luo L, Gu W, Wang Y, Chen C. An Affine Arithmetic-Based Power Flow Algorithm Considering the Regional Control of Unscheduled Power Fluctuation. Energies. 2017; 10(11):1794. https://doi.org/10.3390/en10111794
Chicago/Turabian StyleLuo, Lizi, Wei Gu, Yonghui Wang, and Chunxi Chen. 2017. "An Affine Arithmetic-Based Power Flow Algorithm Considering the Regional Control of Unscheduled Power Fluctuation" Energies 10, no. 11: 1794. https://doi.org/10.3390/en10111794
APA StyleLuo, L., Gu, W., Wang, Y., & Chen, C. (2017). An Affine Arithmetic-Based Power Flow Algorithm Considering the Regional Control of Unscheduled Power Fluctuation. Energies, 10(11), 1794. https://doi.org/10.3390/en10111794




