A Maximum Power Transfer Tracking Method for WPT Systems with Coupling Coefficient Identification Considering Two-Value Problem
Abstract
1. Introduction
2. Coupling Coefficient Identification and Maximum Power Transfer Tracking
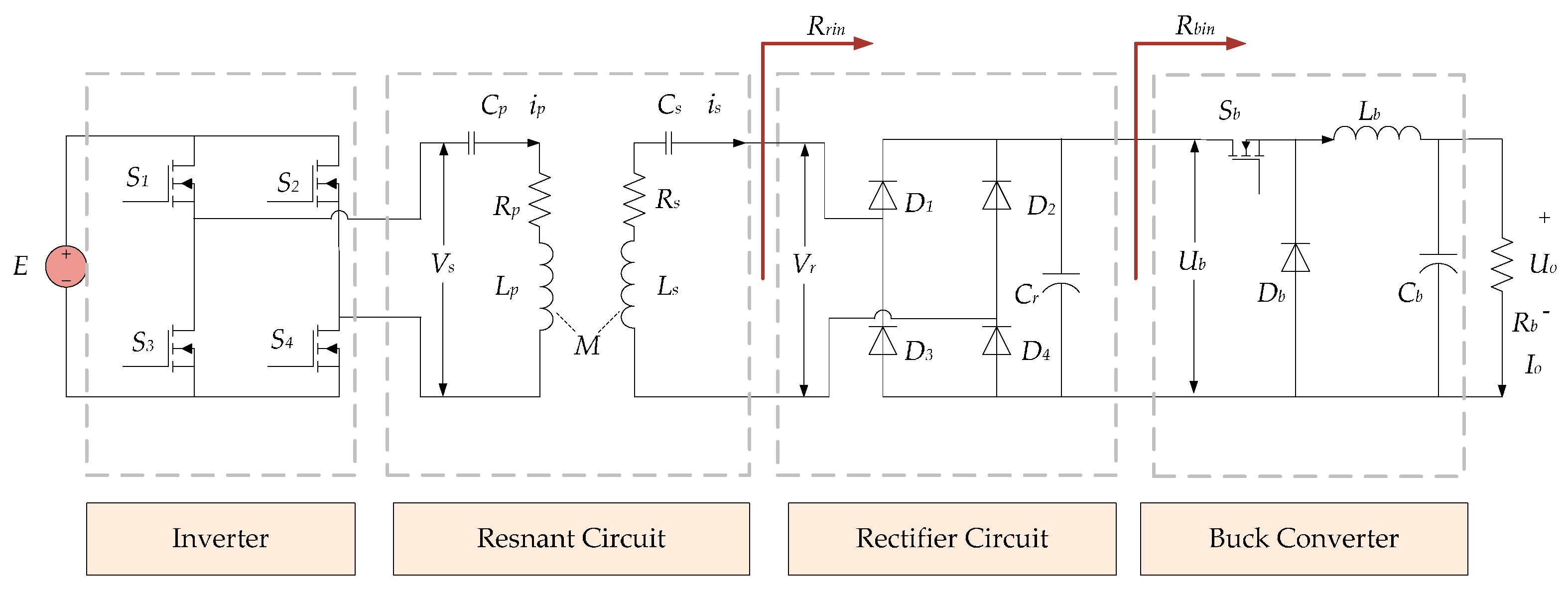
2.1. System Topology
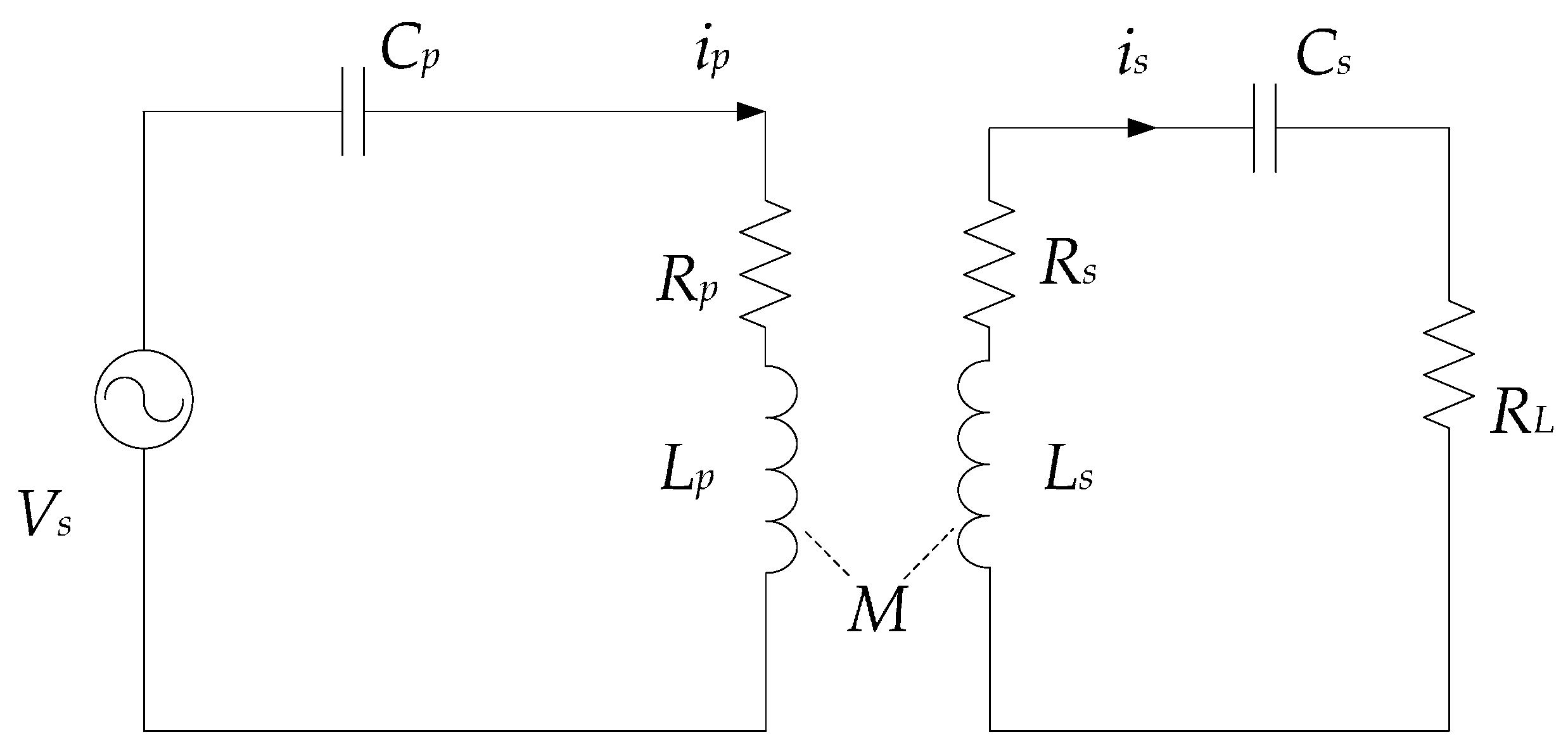
2.2. Identification of the Coupling Coefficient
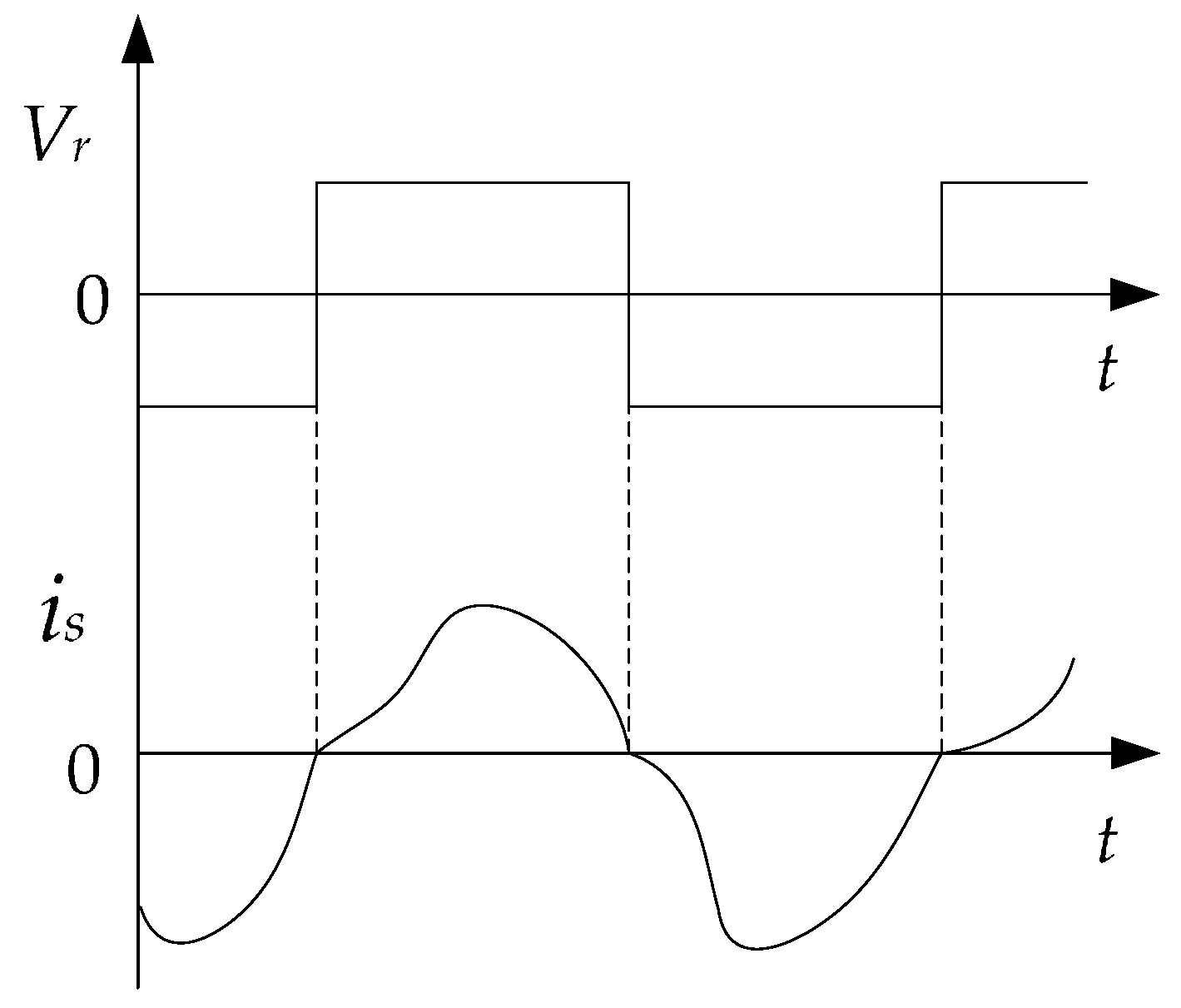
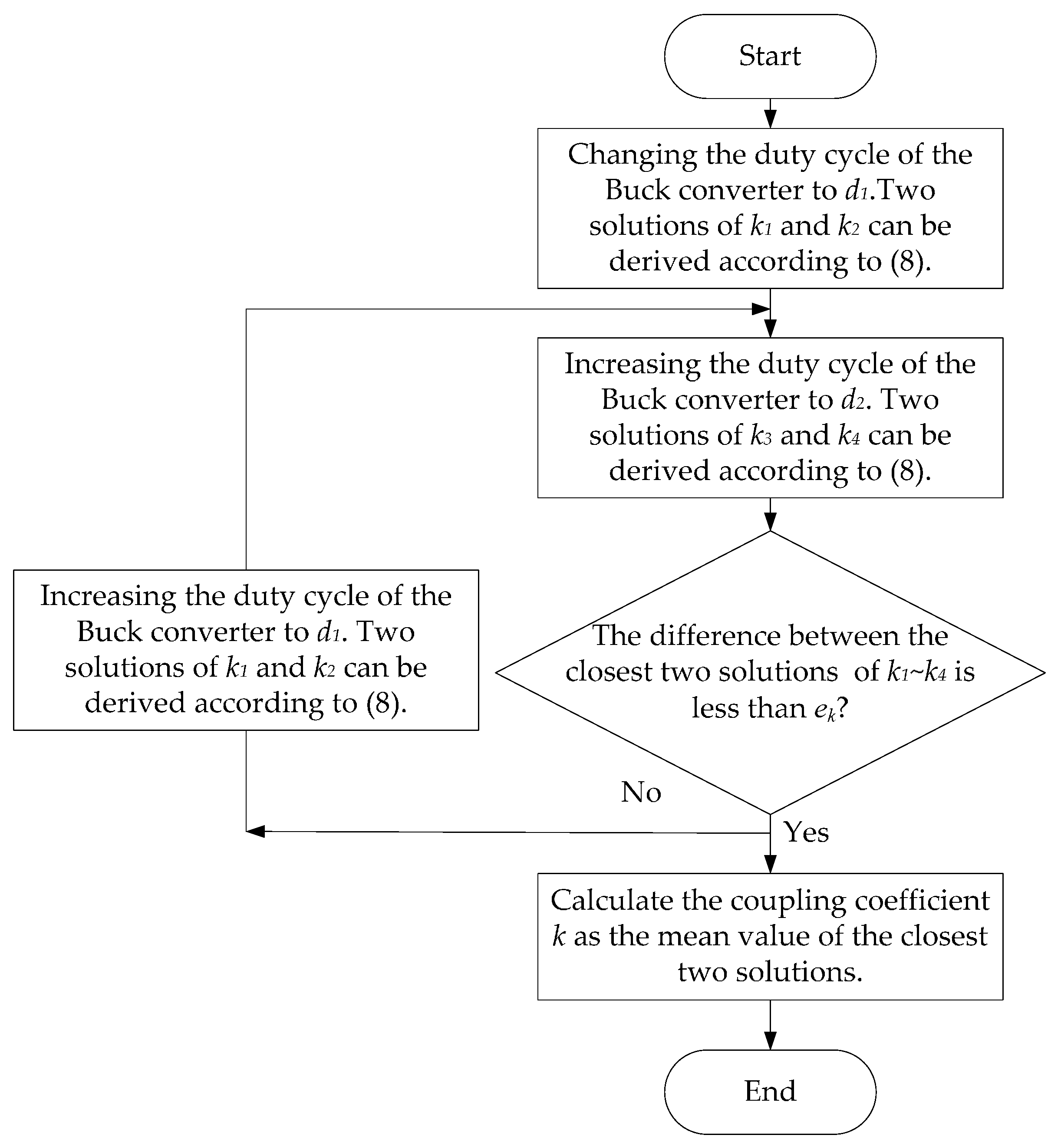
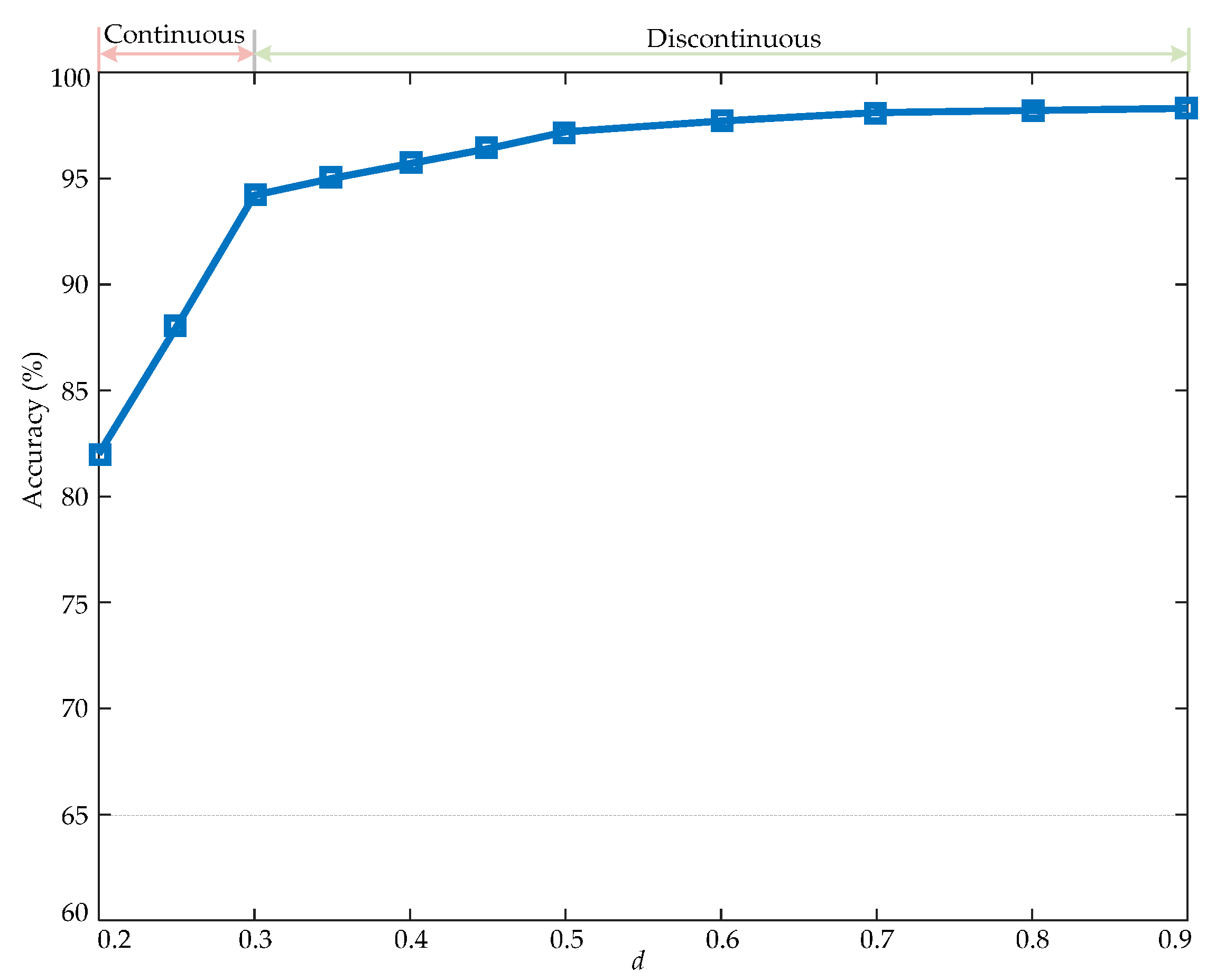
2.3. Dealing with the Two-Value Issue When Identifing the Coupling Coefficient
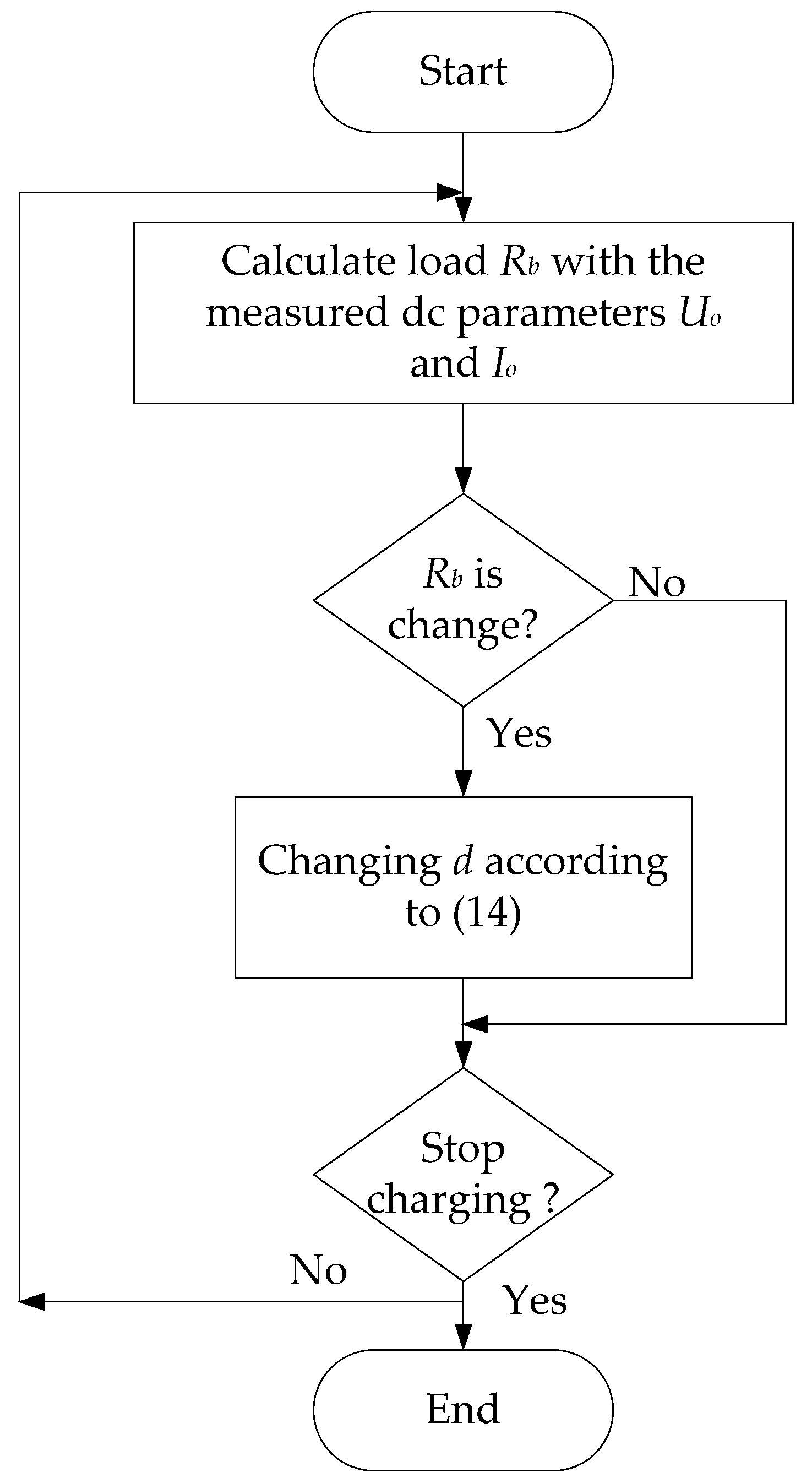
2.4. Maximum Power Transfer Tracking
3. Simulation Analysis
3.1. System Parameters and the Control Structure
3.2. Analysis of the Coupling Coefficient Identification and Maximum Power Transfer Tracking
4. Experimental Analysis
4.1. Experimental Setup
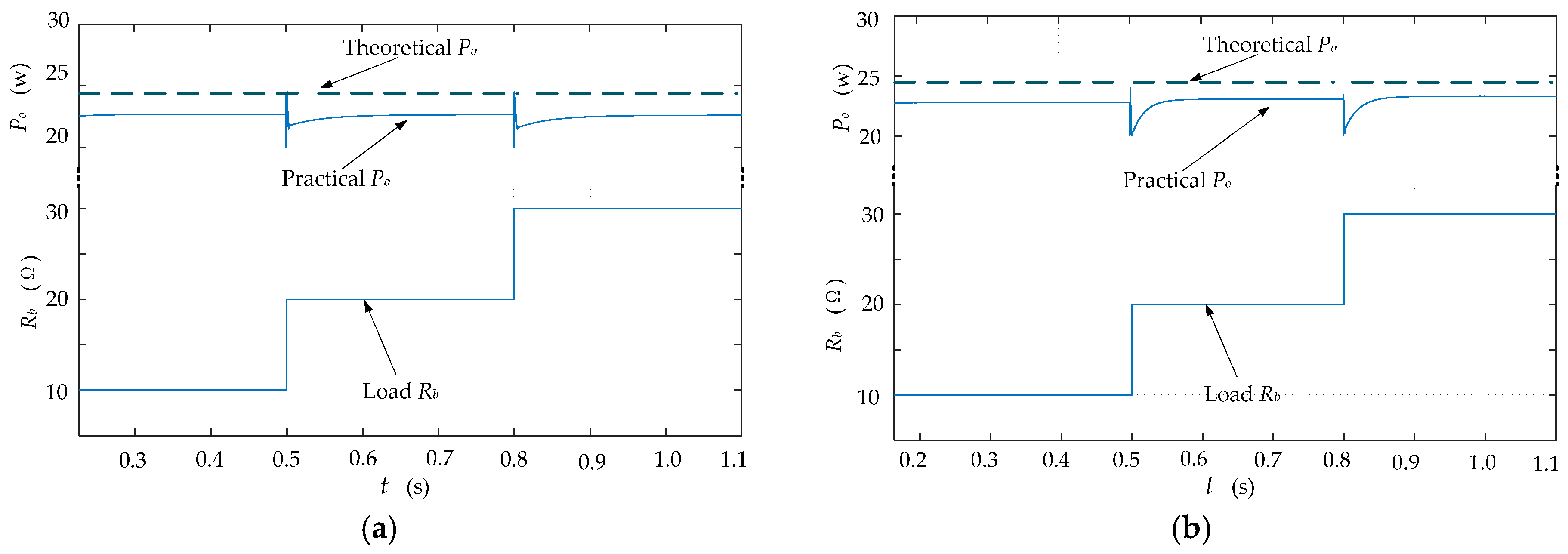
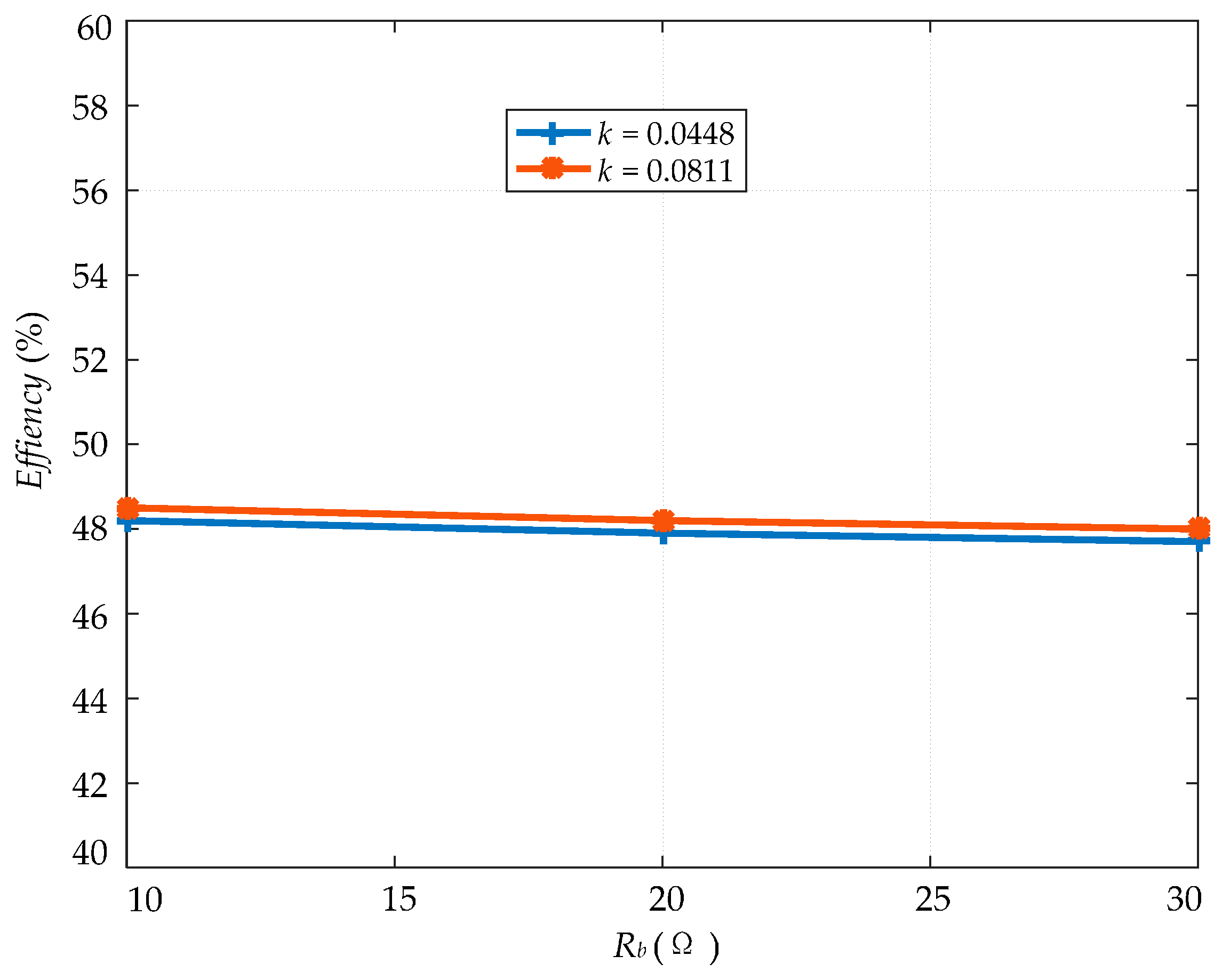
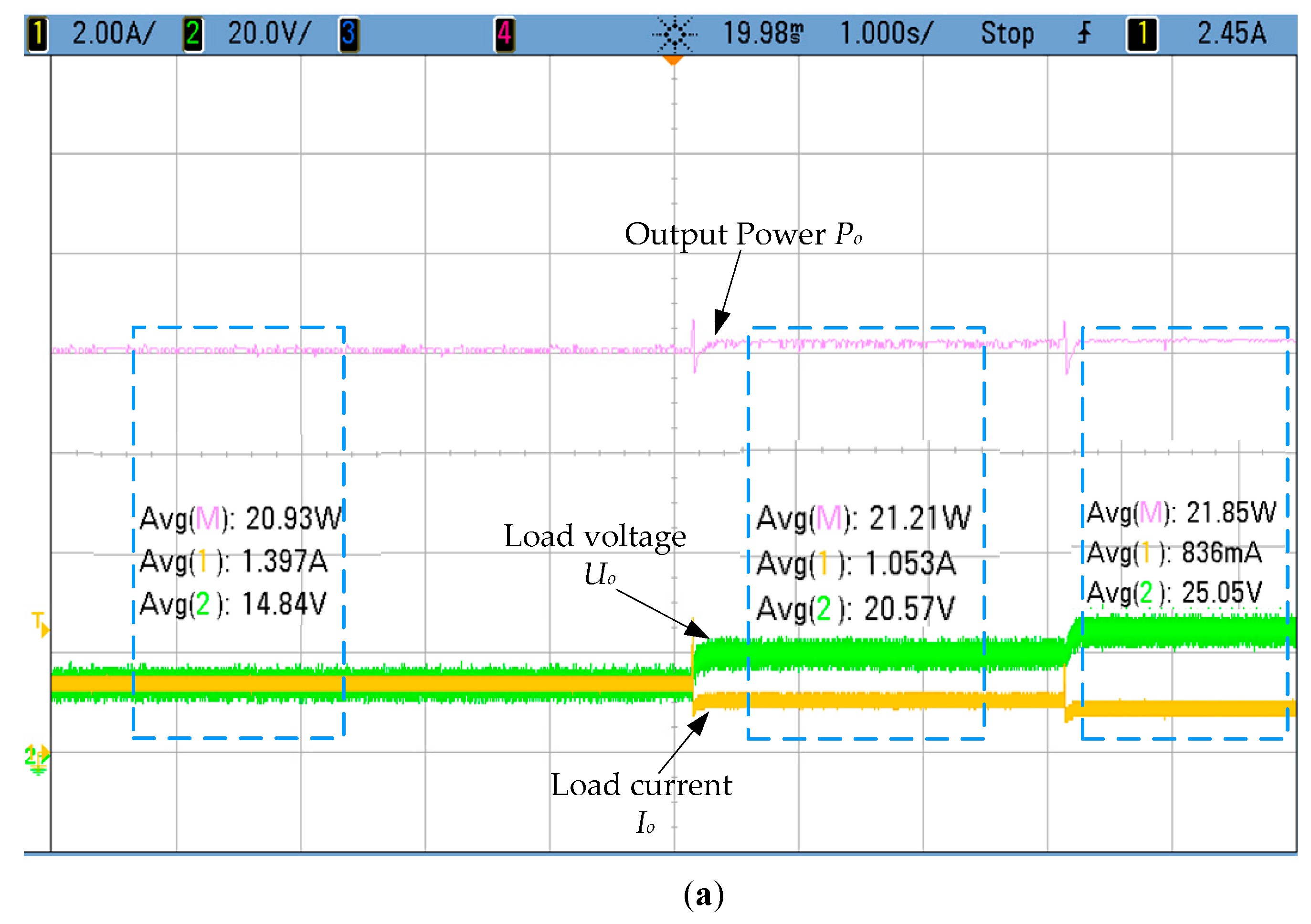
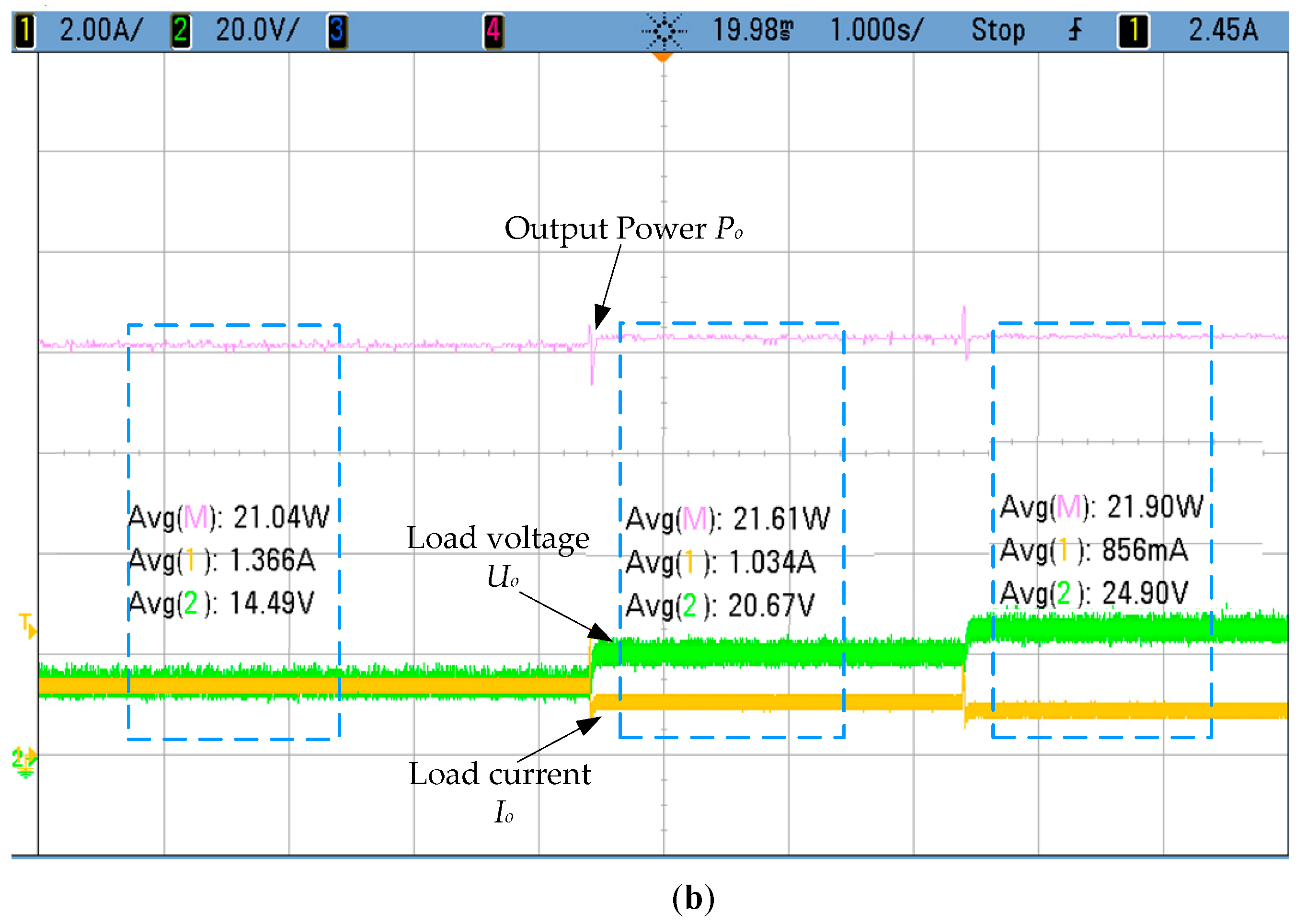
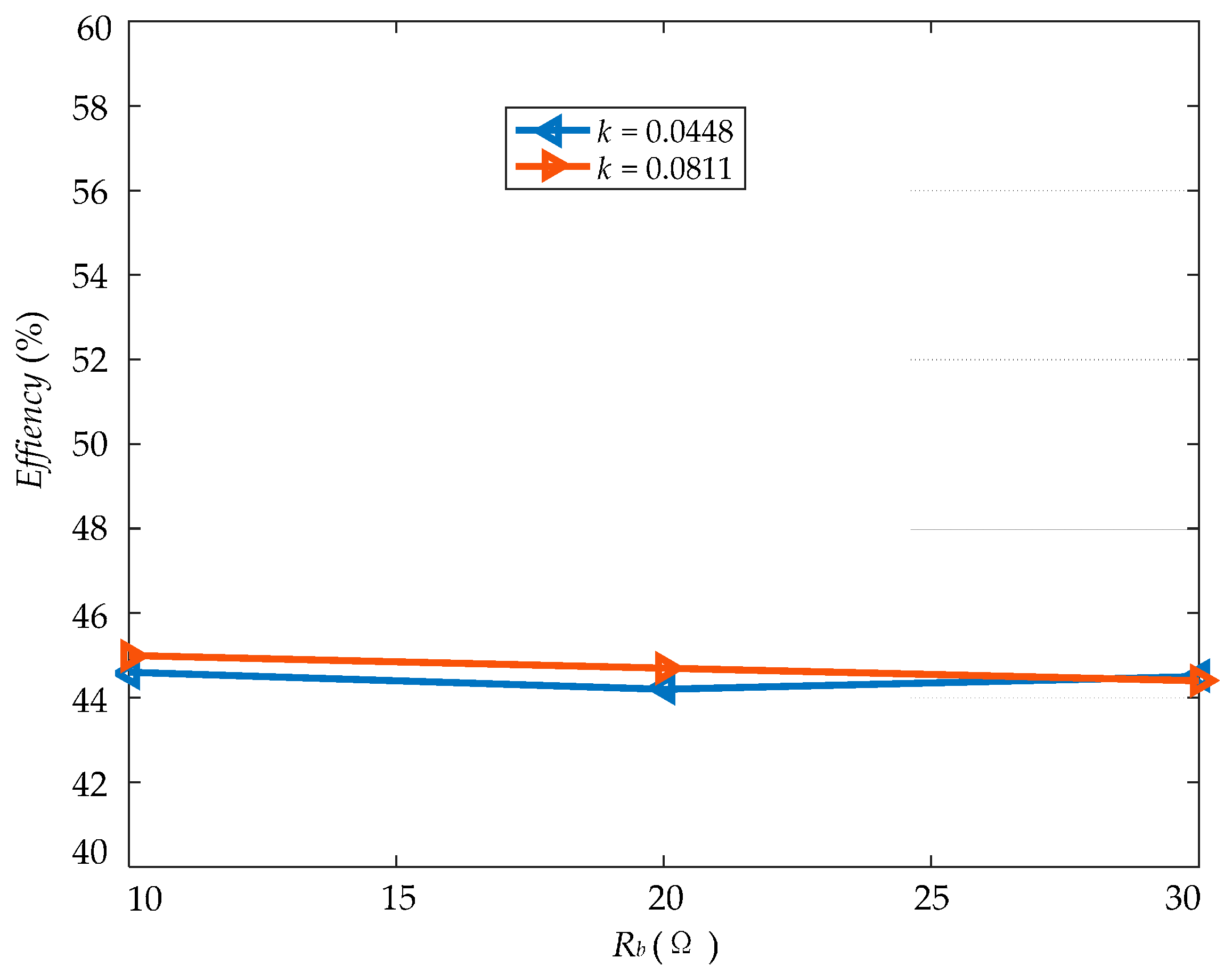
4.2. Experimental Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dai, X.; Li, X.F.; Li, Y.L.; Hu, A.P. Impedance Matching Range Extension Method for Maximum Power Transfer Tracking in IPT System. IEEE Trans. Power Electron. 2017. [Google Scholar] [CrossRef]
- Jawad, A.M.; Nordin, R.; Gharghan, S.K.; Jawad, H.M.; Ismail, M. Opportunities and Challenges for Near-Field Wireless Power Transfer: A Review. Energies 2017, 10, 1022. [Google Scholar] [CrossRef]
- Jiang, C.; Chau, K.T.; Liu, C.; Lee, C.H.T. An Overview of Resonant Circuits for Wireless Power Transfer. Energies 2017, 10, 894. [Google Scholar] [CrossRef]
- Dai, X.; Jiang, J.; Li, Y.; Yang, T. A Phase-Shifted Control for Wireless Power Transfer System by Using Dual Excitation Units. Energies 2017, 10, 1000. [Google Scholar] [CrossRef]
- Zhong, W.X.; Hui, S.Y.R. Maximum Energy Efficiency Tracking for Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2015, 30, 4025–4034. [Google Scholar] [CrossRef]
- Covic, G.A.; Boys, J.T. Inductive Power Transfer. Proc. IEEE 2013, 101, 1276–1289. [Google Scholar] [CrossRef]
- Hui, S.Y.R.; Zhong, W.X.; Lee, C.K. A Critical Review of Recent Progress in Mid-Range Wireless Power Transfer. IEEE Trans. Power Electron. 2014, 29, 4500–4511. [Google Scholar] [CrossRef]
- Wei, X.; Wang, Z.; Dai, H. A Critical Review of Wireless Power Transfer Via Strongly Coupled Magnetic Resonances. Energies 2014, 7, 4316–4341. [Google Scholar] [CrossRef]
- Li, W.; Zhao, H.; Li, S.; Deng, J.; Kan, T.; Mi, C.C. Integrated LCC Compensation Topology for Wireless Charger in Electric and Plug-In Electric Vehicles. IEEE Trans. Ind. Electron. 2015, 62, 4215–4225. [Google Scholar] [CrossRef]
- Zhang, W.; Mi, C.C. Compensation Topologies of High-Power Wireless Power Transfer Systems. IEEE Trans. Veh. Technol. 2016, 65, 4768–4778. [Google Scholar] [CrossRef]
- Wang, C.S.; Covic, G.A.; Stielau, O.H. Power Transfer Capability and Bifurcation Phenomena of Loosely Coupled Inductive Power Transfer Systems. IEEE Trans. Power Electron. 2004, 51, 148–157. [Google Scholar] [CrossRef]
- Pawellek, A.; Oeder, C.; Duerbaum, T. Comparison of Resonant LLC and LCC Converters for Low-Profile Applications. In Proceedings of the 14th European Conference on Power Electronics and Applications (EPE)/ECCE Europe Conference on Power Electronics and Adjustable Speed Drives, Birmingham, UK, 30 August 1–September 2011; pp. 1–10. [Google Scholar]
- Li, X.F.; Tang, C.S.; Dai, X.; Deng, P.Q.; Su, Y.G. An Inductive and Capacitive Combined Parallel Transmission of Power and Data for Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2017. [Google Scholar] [CrossRef]
- Su, Y.G.; Zhang, H.Y.; Wang, Z.H.; Hu, A.P.; Chen, L.; Sun, Y. Steady-State Load Identification Method of Inductive Power Transfer System Based on Switching Capacitors. IEEE Trans. Power Electron. 2015, 30, 6349–6355. [Google Scholar] [CrossRef]
- Dai, X.; Li, X.F.; Li, Y.L.; Hu, A.P. Maximum Efficiency Tracking for Wireless Power Transfer Systems with Dynamic Coupling Coefficient Estimation. IEEE Trans. Power Electron. 2017. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, A.P.; Madawala, U.K. Maximum Power Transfer and Efficiency Analysis of Different Inductive Power Transfer Tuning. In Proceedings of the 10th IEEE Conference on Industrial Electronics and Applications, Auckland, New Zealand, 15–17 July 2015; pp. 655–660. [Google Scholar]
- Li, H.L.; Hu, A.P.; Covic, G.A.; Tang, C.S. Optimal Coupling Condition of IPT System for Achieving Maximum Power Transfer. Electron. Lett. 2009, 45, 76–77. [Google Scholar] [CrossRef]
- Xiao, C.; Liu, Y.; Cheng, D.; Wei, K. New Insight of Maximum Transferred Power by Matching Capacitance of a Wireless Power Transfer System. Energies 2017, 10, 688. [Google Scholar] [CrossRef]
- Zhong, W.X.; Hui, S.Y.R. Maximum Energy Efficiency Operation of Series-Series Resonant Wireless Power Transfer Systems Using On-Off Keying Modulation. IEEE Trans. Power Electron. 2017. [Google Scholar] [CrossRef]
- Li, H.C.; Li, J.; Wang, K.; Chen, W.; Yang, X. A Maximum Efficiency Point Tracking Control Scheme for Wireless Power Transfer Systems Using Magnetic Resonant Coupling. IEEE Trans. Power Electron. 2015, 30, 3998–4008. [Google Scholar] [CrossRef]
- Fu, M.F.; Ma, C.; Zhu, X. A Cascaded Boost-Buck Converter for High-Efficiency Wireless Power Transfer Systems. IEEE Trans. Ind. Inf. 2014, 10, 1972–1980. [Google Scholar] [CrossRef]
- Kobayashi, D.; Imura, T.; Hori, Y. Real-time Coupling Coefficient Estimation and Maximum Efficiency Control on Dynamic Wireless Power Transfer for Electric Vehicles. In Proceedings of the IEEE PELS Workshop on Emerging Technologies: Wireless Power (WoW), Daejeon, Korea, 5–6 June 2015; pp. 1–6. [Google Scholar]
- Jiwariyavej, V.; Imura, T.; Hori, Y. Coupling Coefficients Estimation of Wireless Power Transfer System via Magnetic Resonance Coupling Using Information from Either Side of the System. IEEE J. Emerg. Sel. Topics Power Electron. 2014, 3, 191–200. [Google Scholar] [CrossRef]
- Yin, J.; Parisini, T.; Hui, S.Y. Front-End Monitoring of the Mutual Inductance and Load Resistance in a Series–Series Compensated Wireless Power Transfer System. IEEE Trans. Power Electron. 2016, 31, 7339–7352. [Google Scholar] [CrossRef]
- Forsyth, A.J.; Ward, G.A.; Mollow, S.V. Extended Fundamental Frequency Analysis of the LCC Resonant Converter. IEEE Trans. Power Electron. 2003, 18, 1286–1292. [Google Scholar] [CrossRef]


| Items | Parameter | Value | Parameter | Value |
|---|---|---|---|---|
| Resonant circuits | Lp | 365.96 µH | Ls | 363.68 µH |
| Rp | 0.83 Ω | Rs | 0.51 Ω | |
| Cp | 34.25 nF | Cs | 34.30 nF | |
| Litz-wire coils | Diameter | 14 cm | Number of turns | 25 |
| Frequencies | f | 45 kHz | fb | 100 kHz |
| Buck converter | Lb | 120 µH | Cb | 470 µF |
| Input source | E | 10 V |
| Reference k | Identified k | Accuracy |
|---|---|---|
| 0.0448 | 0.0474 | 94.16% |
| 0.0811 | 0.0839 | 96.59% |
| 0.0930 | 0.0962 | 96.67% |
| 0.1500 | 0.1531 | 97.93% |
| 0.2000 | 0.2037 | 98.15% |
| 0.2500 | 0.2546 | 98.16% |
| Separation Distance | Reference k | Motivating d1 | Motivating d2 | Identified k | Accuracy |
|---|---|---|---|---|---|
| 6 cm | 0.0811 | d1 = 0.5 k1 = 0.0877; k2 = 0.0183 | d2 = 0.6 k3 = 0.0854; k4 = 0.0098 | 0.0866 | 93.2% |
| 9 cm | 0.0448 | d1 = 0.5 k1 = 0.0484; k2 = 0.0332 | d2 = 0.6 k3 = 0.0464; k4 = 0.0207 | 0.0474 | 94.2% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, X.; Li, X.; Li, Y.; Deng, P.; Tang, C. A Maximum Power Transfer Tracking Method for WPT Systems with Coupling Coefficient Identification Considering Two-Value Problem. Energies 2017, 10, 1665. https://doi.org/10.3390/en10101665
Dai X, Li X, Li Y, Deng P, Tang C. A Maximum Power Transfer Tracking Method for WPT Systems with Coupling Coefficient Identification Considering Two-Value Problem. Energies. 2017; 10(10):1665. https://doi.org/10.3390/en10101665
Chicago/Turabian StyleDai, Xin, Xiaofei Li, Yanling Li, Pengqi Deng, and Chunsen Tang. 2017. "A Maximum Power Transfer Tracking Method for WPT Systems with Coupling Coefficient Identification Considering Two-Value Problem" Energies 10, no. 10: 1665. https://doi.org/10.3390/en10101665
APA StyleDai, X., Li, X., Li, Y., Deng, P., & Tang, C. (2017). A Maximum Power Transfer Tracking Method for WPT Systems with Coupling Coefficient Identification Considering Two-Value Problem. Energies, 10(10), 1665. https://doi.org/10.3390/en10101665





