Newton Power Flow Methods for Unbalanced Three-Phase Distribution Networks
Abstract
:1. Introduction
- Radial or weakly meshed (radial network with a few simple loops) structure:In general, a transmission network is operated in a meshed structure, whereas a distribution network is operated in a radial structure where there are no loops in the network and each bus is connected to the source via exactly one path.
- High ratio:Transmission lines of the distribution network have a wide range of resistance R and reactance X values. Therefore, ratios in the distribution network are relatively high compared to the transmission network.
- Multi-phase power flow and unbalanced loads:A single-phase representation is used for power flow analysis on transmission network which is assumed to be a balanced network. Unlike the transmission network, a distribution network must use a three-phase power flow analysis due to the unbalanced loads.
- Distributed generations:Unlike conventional power plants connected to the transmission network, DGs have fluctuating power output that is difficult to predict and control since it is strongly dependent on weather conditions.
- Modification of conventional power flow solution methods [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]:Methods in this category are generally a proper modification of existing methods such as GS, NR and FDLF.
- Backward–forward sweep (BFS)-based algorithms [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61]:BFS-based algorithms generally take an advantage of the radial network topology. The method is an iterative process in which at each iteration two computational steps are performed, a forward and a backward sweep. The forward sweep is mainly the node voltage calculation and the backward sweep is the branch current or power, or the admittance summation.
2. Power System Model
- : the voltage magnitude
- : the voltage phase angle
- : the active power
- : the reactive power
2.1. Load Model
- Constant power (PQ):The powers (P and Q) are independent of variations in the voltage magnitude :
- Constant current (I):The powers (P and Q) vary directly with the voltage magnitude :
- Constant impedance (Z):The powers (P and Q) vary with the square of the voltage magnitude :
- Polynomial (Po):The relation between powers (P and Q) and voltage magnitudes is described by a polynomial equation:where , , and , , are constant parameters of the model and satisfy the following equations:
- Exponential:The relation between powers (P and Q) and voltage magnitudes is described by an exponential equation:where n is a constant parameter of the model.
2.2. Load Connection
2.3. Generator Model
- The constant power factor model (PQ bus):The active power P output and power factor are specified and the reactive power Q is determined by these two variables.
- The variable reactive power model (PQ bus):The active power P output is specified and the reactive power Q is determined by applying a predetermined polynomial function.
- The constant voltage model (PV bus):The active power P output and voltage magnitude are specified.
2.4. Transformer Model
- Divide the self admittance matrix of the primary by :
- Divide the self admittance matrix of the secondary by :
- Divide the mutual admittance matrices by : ,
3. Power Flow Problem
4. Newton Power Flow Solution Methods
4.1. The Power Mismatch Function
4.2. The Current Mismatch Function
4.2.1. Polar Current Mismatch Version (NR-c-pol)
4.2.2. Representation of PV Buses for NR-c-pol
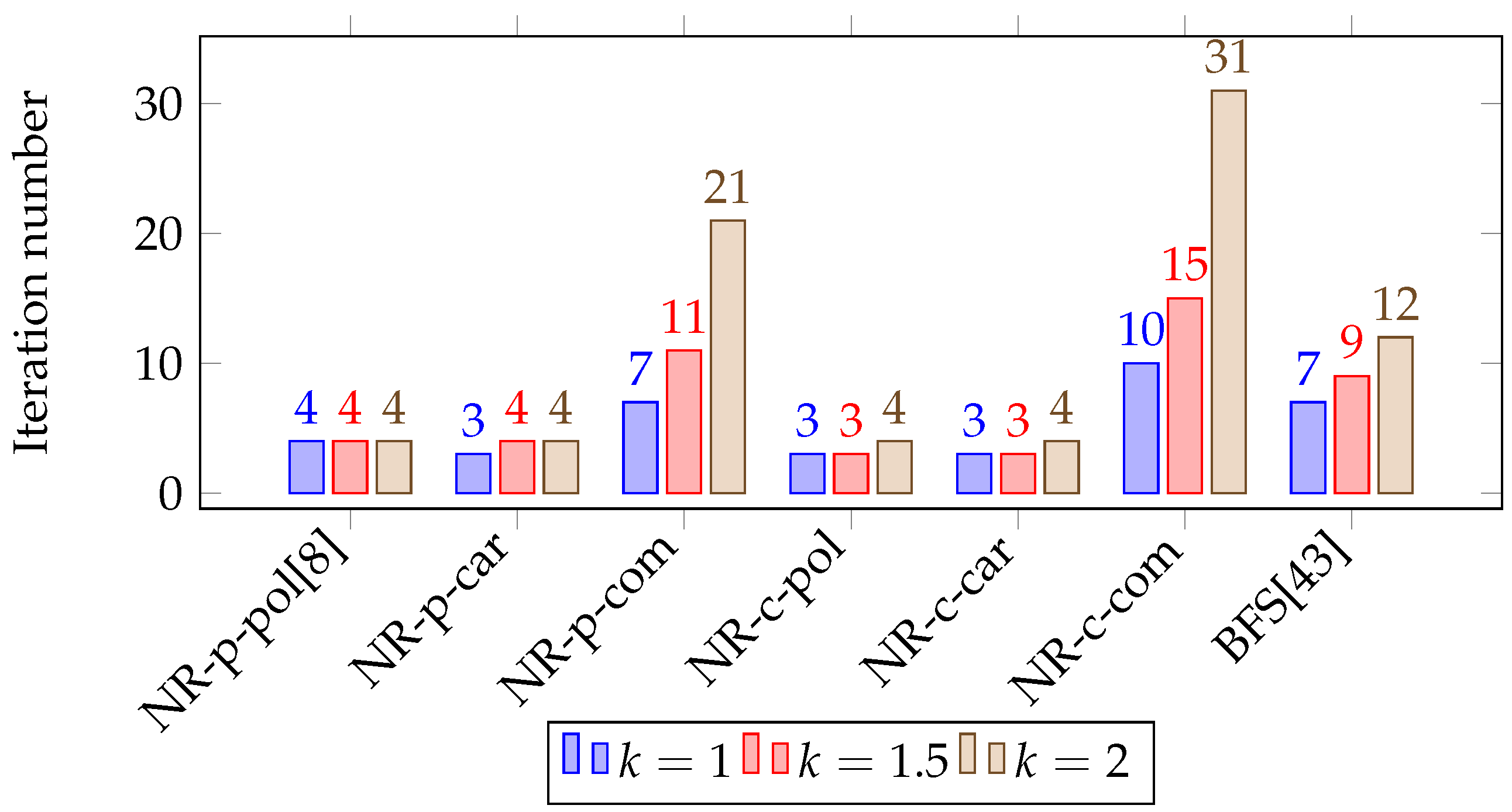
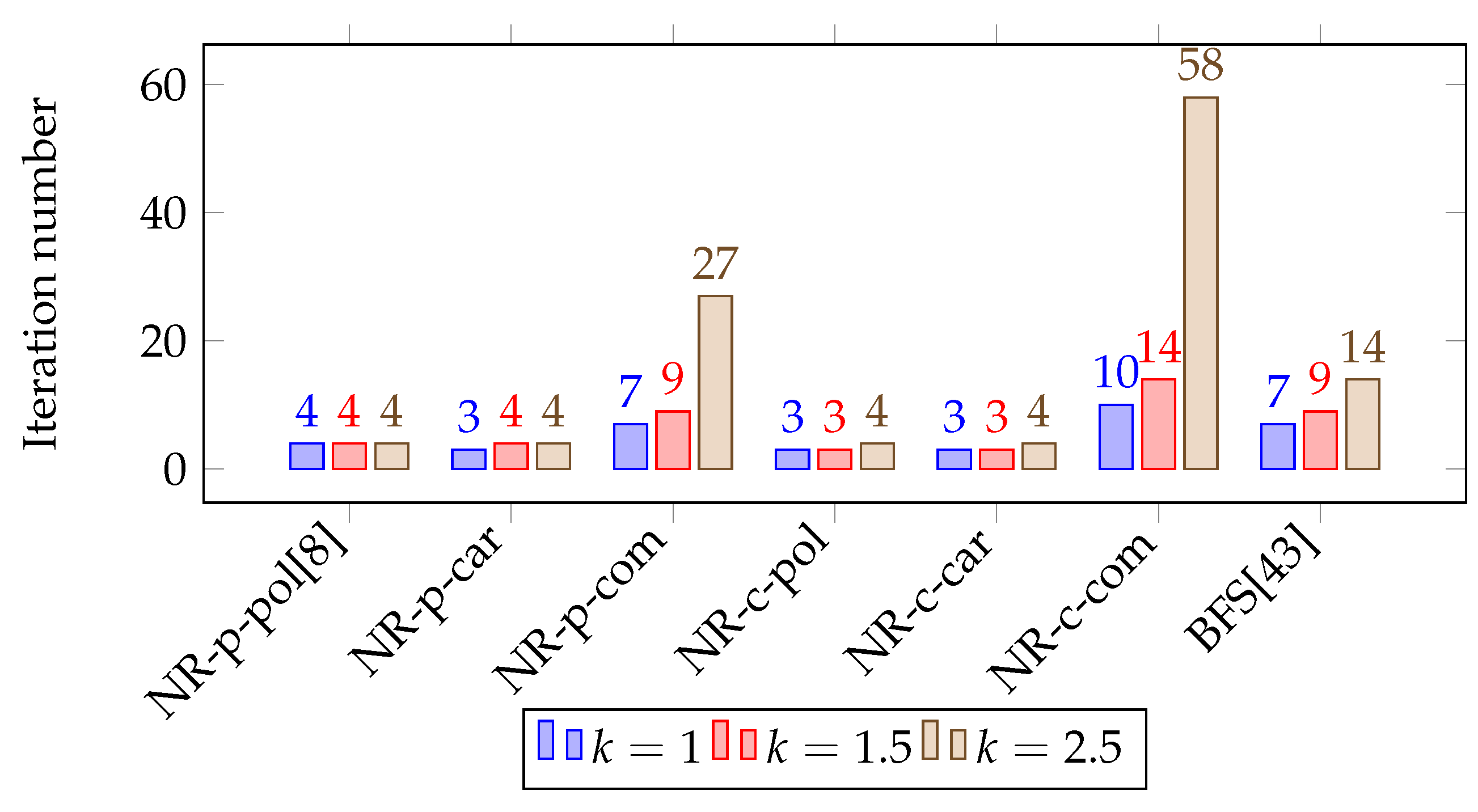
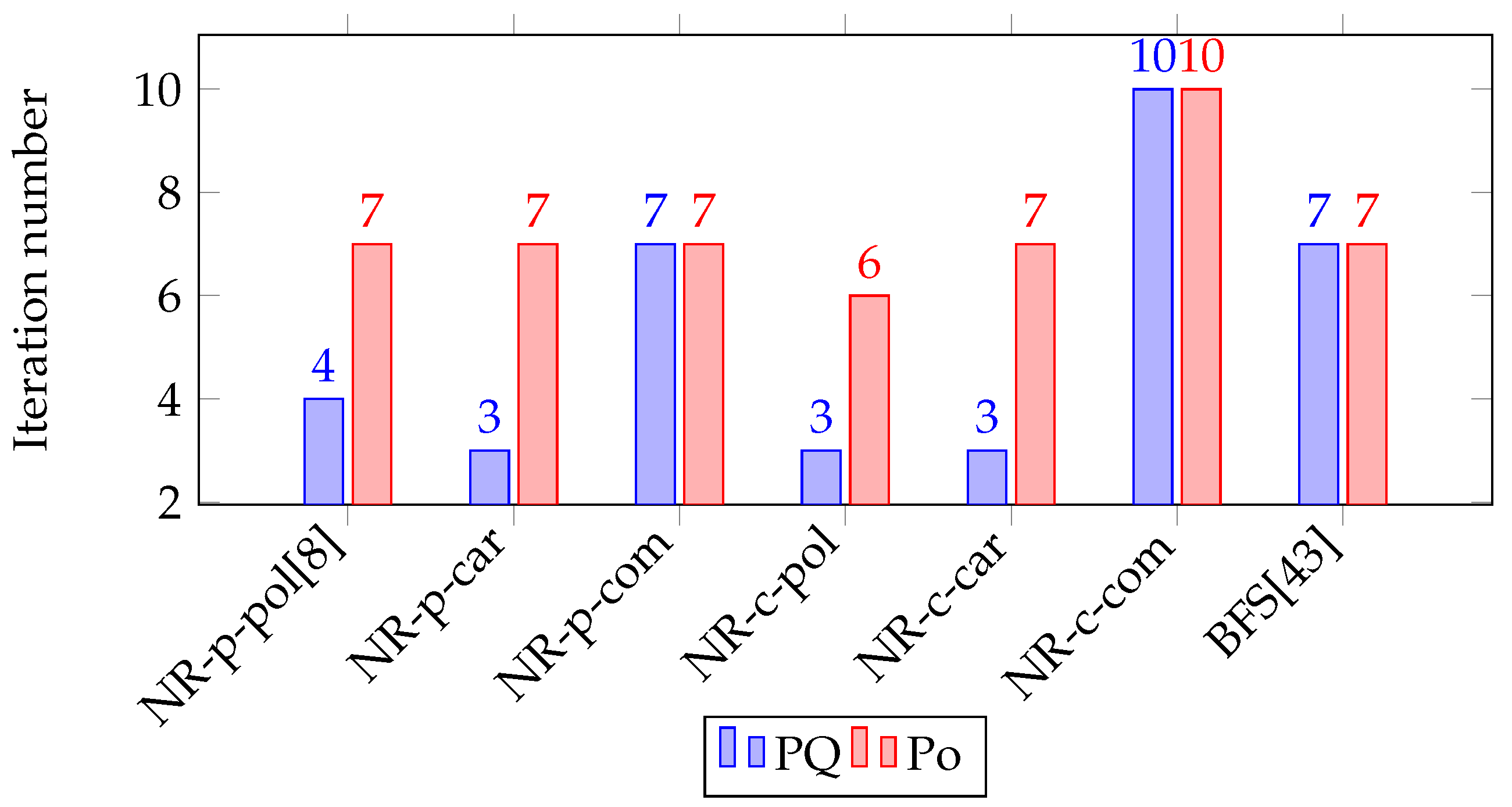
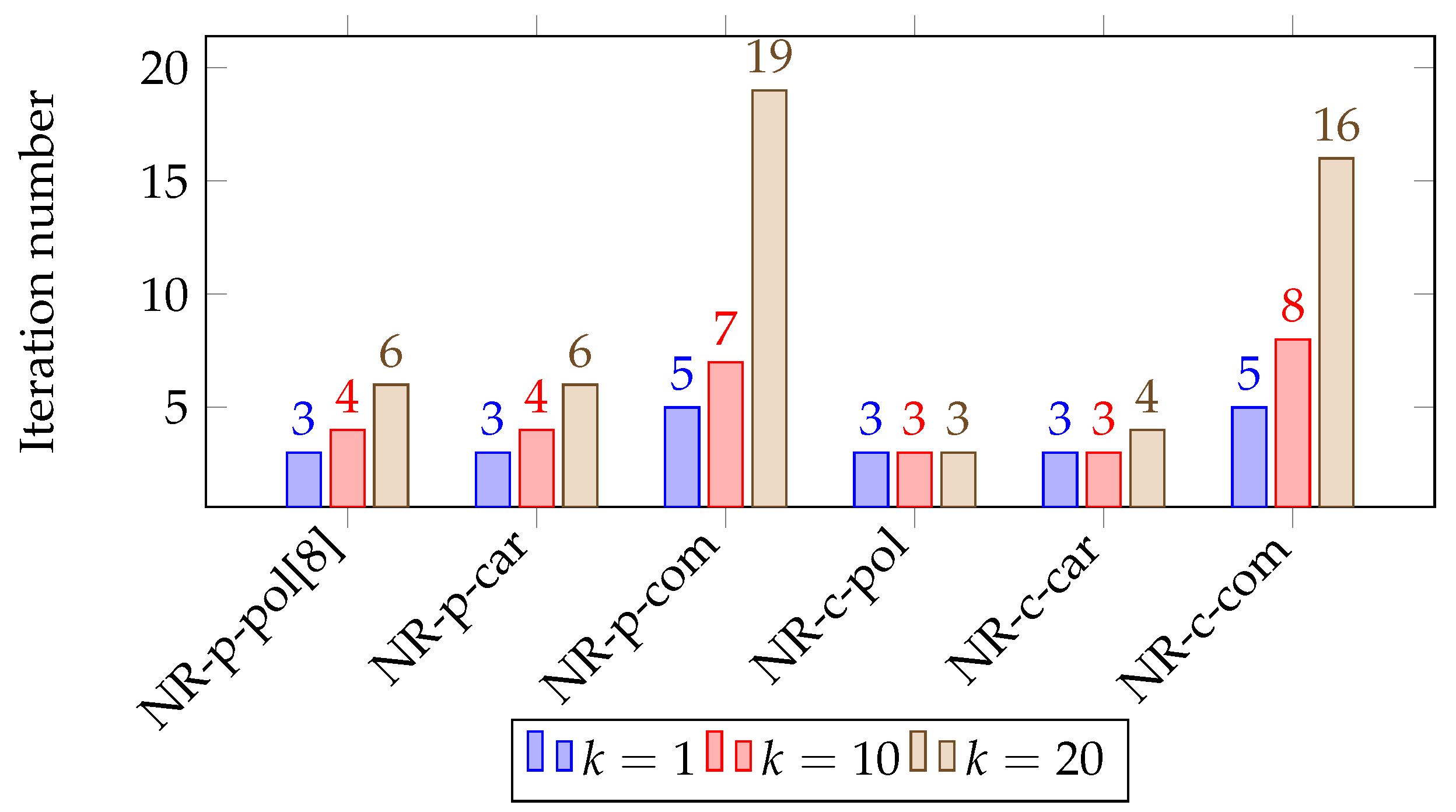
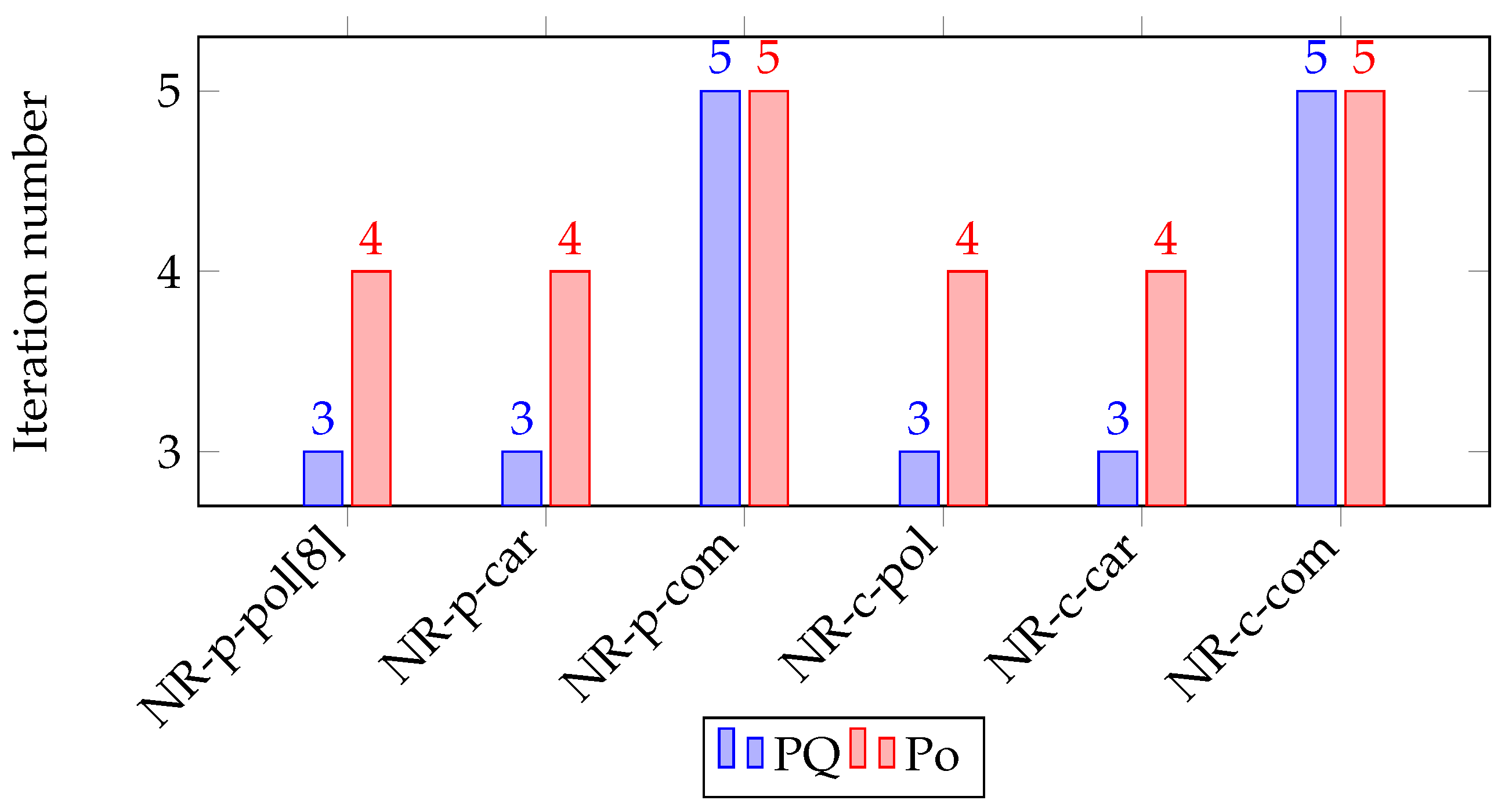
5. Numerical Experiment
5.1. Single-Phase Problems
5.2. Three-Phase Problems
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BFS | backward-forward sweep |
| DG | distributed generation |
| DSO | distribution system operators |
| FDLF | fast-decoupled load flow |
| GS | Gauss–Seidel |
| NR | Newton power flow method |
| NR-p-pol | polar power mismatch version of NR |
| NR-p-car | Cartesian power mismatch version of NR |
| NR-p-com | complex power mismatch version of NR |
| NR-c-pol | polar current mismatch version of NR |
| NR-c-car | Cartesian current mismatch version of NR |
| NR-c-com | complex current mismatch version of NR |
| TSO | transmission system operator |
| SG | smart grid |
References
- Schavemaker, P.; van der Sluis, L. Electrical Power System Essentials; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Keyhani, A.; Marwali, M. Smart Power Grids 2011; Power Systems; Springer: Berlin, Germany, 2012. [Google Scholar]
- Budka, K.; Deshpande, J.; Thottan, M. Communication Networks for Smart Grids: Making Smart Grid Real; Computer Communications and Networks; Springer: Berlin, Germany, 2014. [Google Scholar]
- Thomas, M.; McDonald, J. Power System SCADA and Smart Grids; Taylor & Francis: Abingdon, UK, 2015. [Google Scholar]
- Balamurugan, K.; Srinivasan, D. Review of power flow studies on distribution network with distributed generation. In Proceedings of the 2011 IEEE Ninth International Conference on Power Electronics and Drive Systems, Singapore, 5–8 December 2011; pp. 411–417. [Google Scholar]
- Martinez, J.A.; Mahseredjian, J. Load flow calculations in distribution systems with distributed resources. A review. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–29 July 2011; pp. 1–8. [Google Scholar]
- Stevenson, W.D. Elements of Power System Analysis; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Tinney, W.F.; Hart, C.E. Power flow solution by Newton’s method. IEEE Trans. Power Appar. Syst. 1967, PAS-86, 1449–1460. [Google Scholar] [CrossRef]
- Stott, B.; Alsaç, O. Fast decoupled load flow. IEEE Trans. Power Appar. Syst. 1974, PAS-93, 859–869. [Google Scholar] [CrossRef]
- Iwamoto, S.; Tamura, Y. A load flow calculation method for Ill-conditioned power systems. IEEE Trans. Power Appar. Syst. 1981, PAS-100, 1736–1743. [Google Scholar] [CrossRef]
- Tripathy, S.C.; Prasad, G.D.; Malik, O.P.; Hope, G.S. Load-flow solutions for ill-conditioned power systems by a newton-like method. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 3648–3657. [Google Scholar] [CrossRef]
- Reddy, S.; Suresh, S.S.K.; Kumar, S.V.J. Load flow solution for ill-conditioned power systems using runge-kutta and Iwamoto methods with facts devices. J. Theor. Appl. Inf. Technol. 2009, 5, 693–703. [Google Scholar]
- Chiang, H.D. A decoupled load flow method for distribution power networks: Algorithms, analysis and convergence study. Int. J. Electr. Power Energy Syst. 1991, 13, 130–138. [Google Scholar] [CrossRef]
- Chen, T.H.; Chen, M.S.; Hwang, K.J.; Kotas, P.; Chebli, E.A. Distribution system power flow analysis—A rigid approach. IEEE Trans. Power Deliv. 1991, 6, 1146–1152. [Google Scholar] [CrossRef]
- Chen, T.H.; Chen, M.S.; Inoue, T.; Kotas, P.; Chebli, E.A. Three-phase cogenerator and transformer models for distribution system analysis. IEEE Trans. Power Deliv. 1991, 6, 1671–1681. [Google Scholar] [CrossRef]
- Zhang, F.; Cheng, C.S. A modified Newton method for radial distribution system power flow analysis. IEEE Trans. Power Syst. 1997, 12, 389–397. [Google Scholar] [CrossRef]
- Nguyen, H.L. Newton-Raphson method in complex form. IEEE Trans. Power Deliv. 1997, 12, 1355–1359. [Google Scholar] [CrossRef]
- Da Costa, V.M.; Martins, N.; Pereira, J.L.R. Developments in the Newton Raphson power flow formulation based on current injections. IEEE Trans. Power Syst. 1999, 14, 1320–1326. [Google Scholar] [CrossRef]
- Garcia, P.A.N.; Pereira, J.L.R.; Carneiro, S.; da Costa, V.M.; Martins, N. Three-phase power flow calculations using the current injection method. IEEE Trans. Power Syst. 2000, 15, 508–514. [Google Scholar] [CrossRef]
- Lin, W.M.; Teng, J.H. Three-phase distribution network fast-decoupled power flow solutions. Int. J. Electr. Power Energy Syst. 2000, 22, 375–380. [Google Scholar] [CrossRef]
- Teng, J.H.; Chang, C.Y. A novel and fast three-phase load flow for unbalanced radial distribution systems. IEEE Trans. Power Deliv. 2002, 17, 1238–1244. [Google Scholar] [CrossRef]
- Teng, J.H. A modified Gauss-Seidel algorithm of three-phase power flow analysis in distribution networks. Int. J. Electr. Power Energy Syst. 2002, 24, 97–102. [Google Scholar] [CrossRef]
- Vieira, J.; Freitas, W.; Morelato, A. Phase-decoupled method for three-phase power-flow analysis of unbalanced distribution systems. IEE Proc. Gener. Transm. Distrib. 2004, 151, 568–574. [Google Scholar] [CrossRef]
- Chen, T.H.; Yang, N.C. Loop frame of reference based three-phase power flow for unbalanced radial distribution systems. Electr. Power Syst. Res. 2010, 80, 799–806. [Google Scholar] [CrossRef]
- Sun, H.; Nikovski, D.; Ohno, T.; Takano, T.; Kojima, Y. A fast and robust load flow method for distribution systems with distributed generations. Energy Procedia 2011, 12, 236–244. [Google Scholar] [CrossRef]
- Lagace, P.J. Power flow methods for improving convergence. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 1387–1392. [Google Scholar]
- Abdelaziz, M.M.A.; Farag, H.E.; El-Saadany, E.F.; Mohamed, Y.A.R.I. A novel and generalized three-phase power flow algorithm for islanded microgrids using a Newton trust region method. IEEE Trans. Power Syst. 2013, 28, 190–201. [Google Scholar] [CrossRef]
- Idema, R.; Lahaye, D. Computational Methods in Power System Analysis; Atlantis Studies in Scientific Computing in Electromagnetics; Atlantis Press: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Li, C.; Chaudhary, S.K.; Vasquez, J.C.; Guerrero, J.M. Power flow analysis algorithm for islanded LV microgrids including distributed generator units with droop control and virtual impedance loop. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition, Fort Worth, TX, USA, 16–20 March 2014; pp. 3181–3185. [Google Scholar]
- Wang, L.; Chen, C.; Shen, T. Improvement of power flow calculation with optimization factor based on current injection method. Discrete Dyn. Nat. Soc. 2014, 2014, 437567. [Google Scholar] [CrossRef]
- Milano, F. Analogy and convergence of Levenberg’s and Lyapunov-based methods for power flow analysis. IEEE Trans. Power Syst. 2016, 31, 1663–1664. [Google Scholar] [CrossRef]
- Mumtaz, F.; Syed, M.; Al Hosani, M.; Zeineldin, H. A novel approach to solve power flow for islanded microgrids using modified Newton-Raphson with droop control of DG. IEEE Trans. Sustain. Energy 2016, 7, 493–503. [Google Scholar] [CrossRef]
- Pourbagher, R.; Derakhshandeh, S.Y. A powerful method for solving the power flow problem in the ill-conditioned systems. Int. J. Electr. Power Energy Syst. 2018, 94, 88–96. [Google Scholar] [CrossRef]
- Cheng, C.S.; Shirmohammadi, D. A three-phase power flow method for real-time distribution system analysis. IEEE Trans. Power Deliv. 1995, 10, 671–679. [Google Scholar] [CrossRef]
- Thukaram, D.; Banda, H.W.; Jerome, J. A robust three phase power flow algorithm for radial distribution systems. Electr. Power Syst. Res. 1999, 50, 227–236. [Google Scholar] [CrossRef]
- Ranjan, R.; Venkatesh, B.; Chaturvedi, A.; Das, D. Power flow solution of three-phase unbalanced radial distribution network. Electr. Power Compon. Syst. 2004, 32, 421–433. [Google Scholar] [CrossRef]
- Khushalani, S.; Solanki, J.M.; Schulz, N.N. Development of three-phase unbalanced power flow using PV and PQ models for distributed generation and study of the impact of DG models. IEEE Trans. Power Deliv. 2007, 22, 1019–1025. [Google Scholar] [CrossRef]
- Moghaddas-Tafreshi, S.; Mashhour, E. Distributed generation modeling for power flow studies and a three-phase unbalanced power flow solution for radial distribution systems considering distributed generation. Electr. Power Syst. Res. 2009, 79, 680–686. [Google Scholar] [CrossRef]
- Shirmohammadi, D.; Hong, H.; Semlyen, A.; Luo, G. A compensation-based power flow method for weakly meshed distribution and transmission networks. IEEE Trans. Power Deliv. 1988, 3, 753–762. [Google Scholar] [CrossRef]
- Luo, G.X.; Semlyen, A. Efficient load flow for large weakly meshed networks. IEEE Trans. Power Syst. 1990, 5, 1309–1316. [Google Scholar] [CrossRef]
- Haque, M.H. Efficient load flow method for distribution systems with radial or mesh configuration. IEE Proc. Gener. Transm. Distrib. 1996, 143, 33–38. [Google Scholar] [CrossRef]
- Haque, M. A general load flow method for distribution systems. Electr. Power Syst. Res. 2000, 54, 47–54. [Google Scholar] [CrossRef]
- Teng, J.H. A direct approach for distribution system load flow solutions. IEEE Trans. Power Deliv. 2003, 18, 882–887. [Google Scholar] [CrossRef]
- Rajicic, D.; Ackovski, R.; Taleski, R. Voltage correction power flow. IEEE Trans. Power Deliv. 1994, 9, 1056–1062. [Google Scholar] [CrossRef]
- Zhu, Y.; Tomsovic, K. Adaptive power flow method for distribution systems with dispersed generation. IEEE Trans. Power Deliv. 2002, 17, 822–827. [Google Scholar] [CrossRef]
- Teng, J.H. Modelling distributed generations in three-phase distribution load flow. IET Proc. Gener. Transm. Distrib. 2008, 2, 330–340. [Google Scholar] [CrossRef]
- Augugliaro, A.; Dusonchet, L.; Favuzza, S.; Ippolito, M.; Sanseverino, E.R. A new backward/forward method for solving radial distribution networks with PV nodes. Electr. Power Syst. Res. 2008, 78, 330–336. [Google Scholar] [CrossRef]
- Ghosh, S.; Das, D. Method for load-flow solution of radial distribution networks. IEE Proc. Gener. Transm. Distrib. 1999, 146, 641–648. [Google Scholar] [CrossRef]
- Samuel Mok, S.; Elangovan, C.L.; Salama, M. A new approach for power flow analysis of balanced radial distribution systems. Electr. Mach. Power Syst. 2000, 28, 325–340. [Google Scholar]
- Aravindhababu, P.; Ganapathy, S.; Nayar, K. A novel technique for the analysis of radial distribution systems. Int. J. Electr. Power Energy Syst. 2001, 23, 167–171. [Google Scholar] [CrossRef]
- Liu, J.; Salama, M.; Mansour, R. An efficient power flow algorithm for distribution systems with polynomial load. Int. J. Electr. Eng. Educ. 2002, 39, 371–386. [Google Scholar] [CrossRef]
- Cespedes, R. New method for the analysis of distribution networks. IEEE Trans. Power Deliv. 1990, 5, 391–396. [Google Scholar] [CrossRef]
- Jasmon, G.; Lee, L. Distribution network reduction for voltage stability analysis and loadflow calculations. Int. J. Electr. Power Energy Syst. 1991, 13, 9–13. [Google Scholar] [CrossRef]
- Das, D.; Nagi, H.; Kothari, D. Novel method for solving radial distribution networks. IEE Proc. Gener. Transm. Distrib. 1994, 141, 291–298. [Google Scholar] [CrossRef]
- Das, D.; Kothari, D.; Kalam, A. Simple and efficient method for load flow solution of radial distribution networks. Int. J. Electr. Power Energy Syst. 1995, 17, 335–346. [Google Scholar] [CrossRef]
- Haque, M. Load flow solution of distribution systems with voltage dependent load models. Electr. Power Syst. Res. 1996, 36, 151–156. [Google Scholar] [CrossRef]
- Afsari, M.; Singh, S.; Raju, G.; Rao, G. A fast power flow solution of radial distribution networks. Electr. Power Compon. Syst. 2002, 30, 1065–1074. [Google Scholar] [CrossRef]
- Mekhamer, S.; Soliman, S.; Moustafa, M.; El-Hawary, M. Load flow solution of radial distribution feeders: A new contribution. Int. J. Electr. Power Energy Syst. 2002, 24, 701–707. [Google Scholar] [CrossRef]
- Ranjan, R.; DAS. Simple and efficient computer algorithm to solve radial distribution networks. Electr. Power Compon. Syst. 2003, 31, 95–107. [Google Scholar] [CrossRef]
- Eminoglu, U.; Hocaoglu, M.H. A new power flow method for radial distribution systems including voltage dependent load models. Electr. Power Syst. Res. 2005, 76, 106–114. [Google Scholar] [CrossRef]
- Satyanarayana, S.; Ramana, T.; Sivanagaraju, S.; Rao, G. An efficient load flow solution for radial distribution network including voltage dependent load models. Electr. Power Compon. Syst. 2007, 35, 539–551. [Google Scholar] [CrossRef]
- Stott, B. Review of load-flow calculation methods. Proc. IEEE 1974, 62, 916–929. [Google Scholar] [CrossRef]
- Srinivas, M.S. Distribution load flows: A brief review. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting, Singapore, 23–27 January 2000; Volume 2, pp. 942–945. [Google Scholar]
- Eminoglu, U.; Hocaoglu, M.H. Distribution systems forward/backward sweep-based power flow algorithms: A review and comparison study. Electr. Power Compon. Syst. 2008, 37, 91–110. [Google Scholar] [CrossRef]
- Sereeter, B.; Vuik, C.; Witteveen, C. On a Comparison of Newton-Raphson Solvers for Power Flow Problems; Report 17-7; Delft Institute of Applied Mathematics, Delft University of Technology: Delft, The Netherlands, 2017. [Google Scholar]
- Van Ness, J.E.; Griffin, J.H. Elimination methods for load-flow studies. Trans. Am. Inst. Electr. Eng. Part III 1961, 80, 299–302. [Google Scholar] [CrossRef]
- Lindén, K.; Segerqvist, I. Modelling of Load Devices and Studying Load/System Characteristics; Technical Report; Chalmers University of Technology: Gothenburg, Sweden, 1992. [Google Scholar]
- Subrahmanyam, J.; Radhakrishna, C. A simple approach of three phase distribution system modeling for power flow calculations. Int. J. Energy Power Eng. 2010, 3, 3. [Google Scholar]
- Electric Power Research Institute (EPRI). Engineering Guide for Integration of Distributed Generation and Storage into Power Distribution Systems; Technical Report; EPRI: Palo Alto, CA, USA, 2000. [Google Scholar]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Optimal capacitor placement on radial distribution systems. IEEE Trans. Power Deliv. 1989, 4, 725–734. [Google Scholar] [CrossRef]
- Kersting, W.H. Radial distribution test feeders. In Proceedings of the 2001 IEEE Power Engineering Society Winter Meeting, Columbus, OH, USA, 28 January–1 February 2001; Volume 2, pp. 908–912. [Google Scholar]
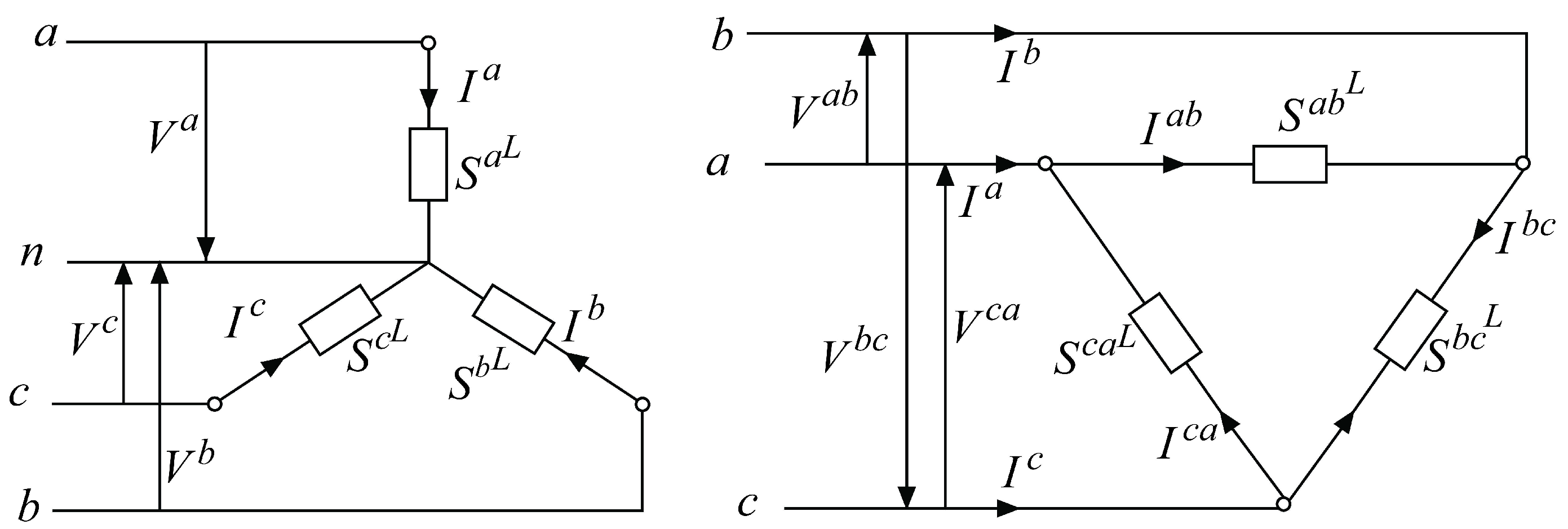
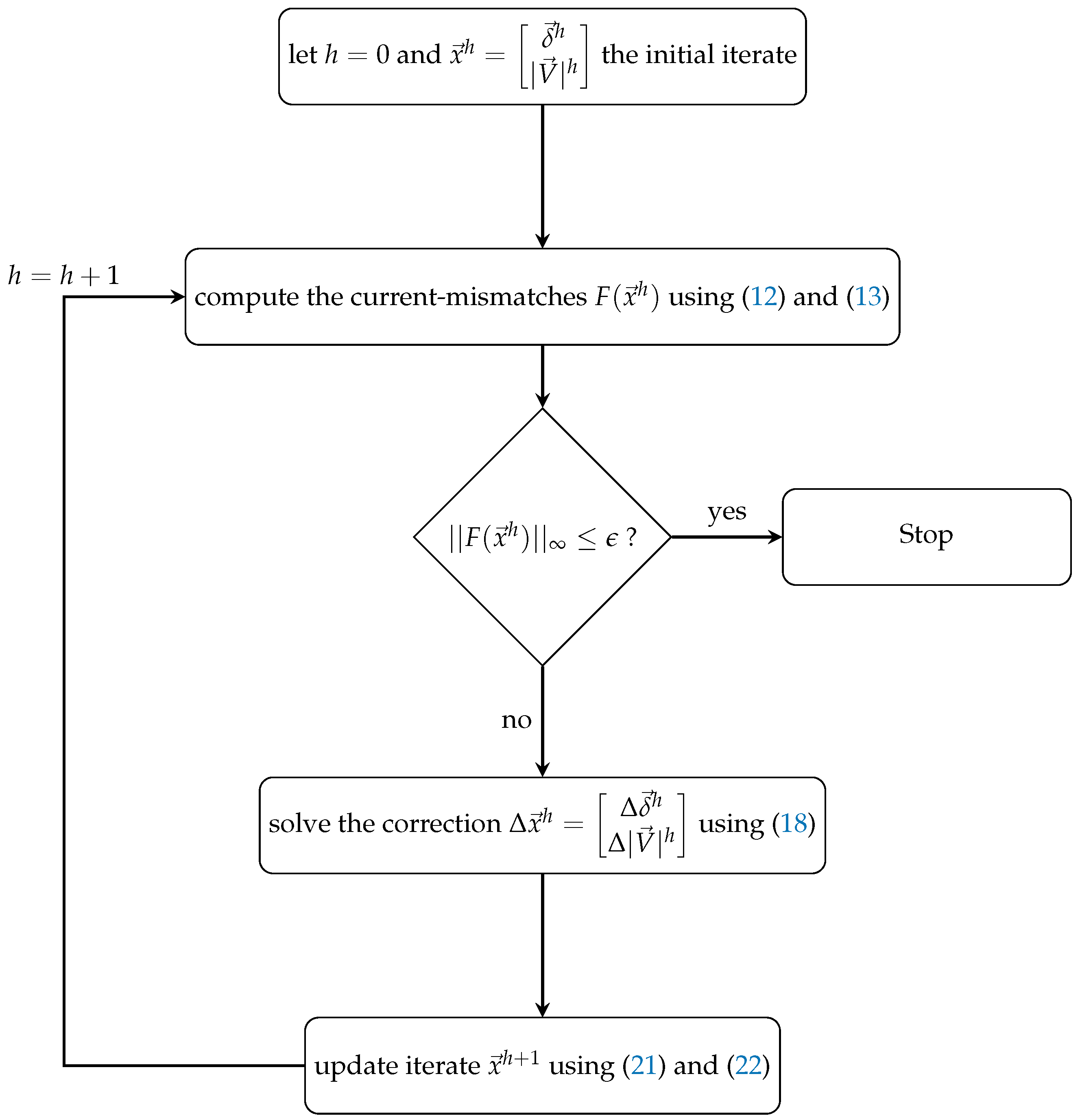
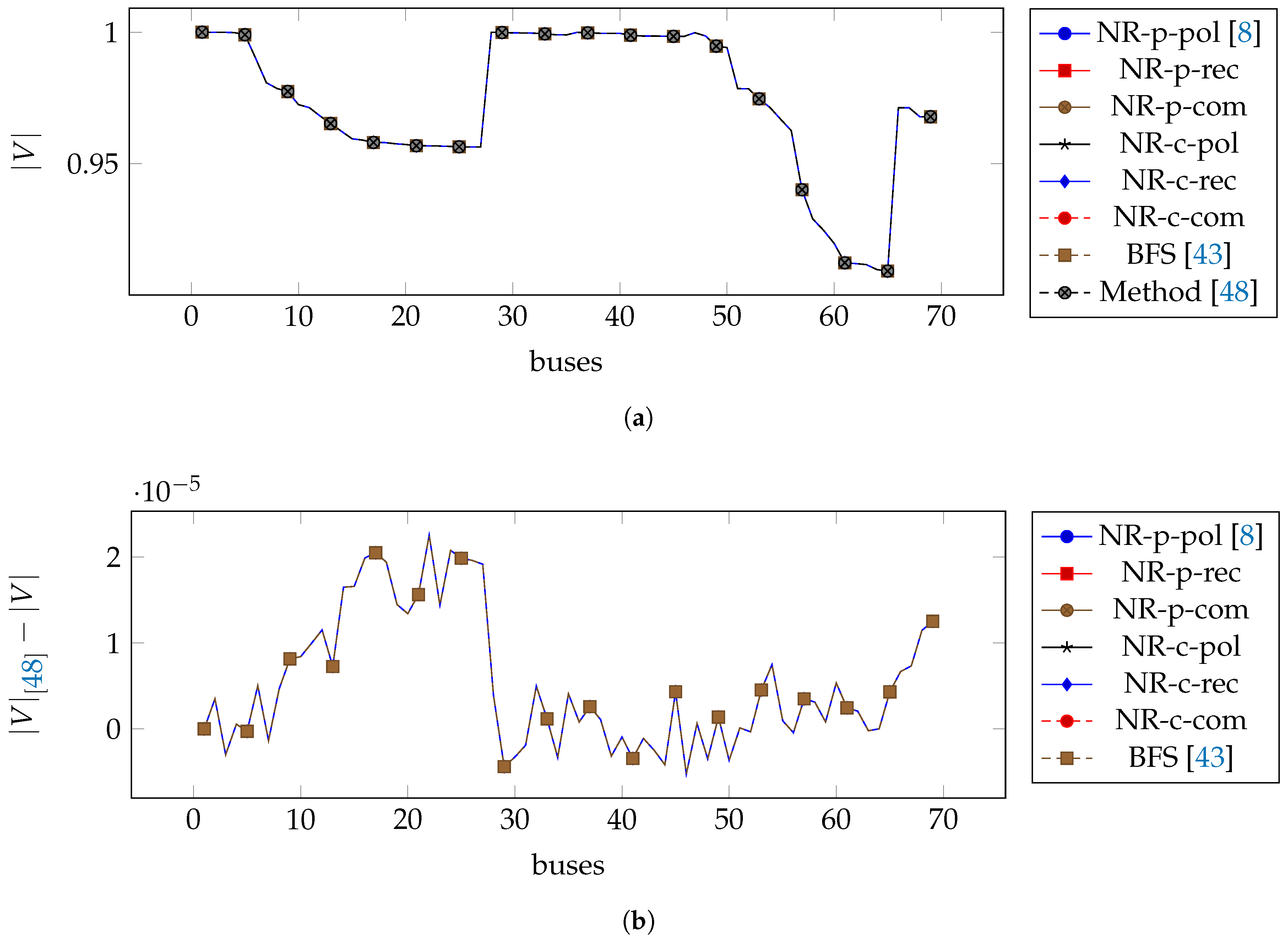

| Bus Type | Number of Buses | Known | Unknown |
|---|---|---|---|
| slack node or swing bus | 1 | ||
| generator node or PV bus | |||
| load node or PQ bus |
| Transformer Connection | Self Admittance | Mutual Admittance | |||
|---|---|---|---|---|---|
| Bus | Bus | ||||
| Wye-G | Wye-G | ||||
| Wye-G | Wye | ||||
| Wye-G | Delta | ||||
| Wye | Wye-G | ||||
| Wye | Wye | ||||
| Wye | Delta | ||||
| Delta | Wye-G | ||||
| Delta | Wye | ||||
| Delta | Delta | ||||
| Methods | Test Cases | |||||
|---|---|---|---|---|---|---|
| DCase33 | DCase69 | |||||
| Iter | Time | Iter | Time | |||
| NR-p-pol [8] | 3 | 0.0123 | 4 | 0.0131 | ||
| NR-p-car | 3 | 0.0067 | 3 | 0.0069 | ||
| NR-p-com | 6 | 0.0058 | 7 | 0.0060 | ||
| NR-c-pol | 3 | 0.0087 | 3 | 0.0090 | ||
| NR-c-car | 3 | 0.0073 | 3 | 0.0077 | ||
| NR-c-com | 7 | 0.0068 | 10 | 0.0084 | ||
| BFS [43] | 7 | 0.0102 | 7 | 0.0104 | ||
| Methods | Test Cases | |||||
|---|---|---|---|---|---|---|
| DCase13 | DCase37 | |||||
| Iter | Time | Iter | Time | |||
| NR-p-pol [8] | 3 | 0.0116 | 2 | 0.0134 | ||
| NR-p-car | 3 | 0.0067 | 2 | 0.0069 | ||
| NR-p-com | 5 | 0.0055 | 3 | 0.0055 | ||
| NR-c-pol | 3 | 0.0087 | 2 | 0.0094 | ||
| NR-c-car | 3 | 0.0073 | 2 | 0.0079 | ||
| NR-c-com | 5 | 0.0067 | 3 | 0.0065 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sereeter, B.; Vuik, K.; Witteveen, C. Newton Power Flow Methods for Unbalanced Three-Phase Distribution Networks. Energies 2017, 10, 1658. https://doi.org/10.3390/en10101658
Sereeter B, Vuik K, Witteveen C. Newton Power Flow Methods for Unbalanced Three-Phase Distribution Networks. Energies. 2017; 10(10):1658. https://doi.org/10.3390/en10101658
Chicago/Turabian StyleSereeter, Baljinnyam, Kees Vuik, and Cees Witteveen. 2017. "Newton Power Flow Methods for Unbalanced Three-Phase Distribution Networks" Energies 10, no. 10: 1658. https://doi.org/10.3390/en10101658
APA StyleSereeter, B., Vuik, K., & Witteveen, C. (2017). Newton Power Flow Methods for Unbalanced Three-Phase Distribution Networks. Energies, 10(10), 1658. https://doi.org/10.3390/en10101658





