Effect of Injection Site on Fault Activation and Seismicity during Hydraulic Fracturing
Abstract
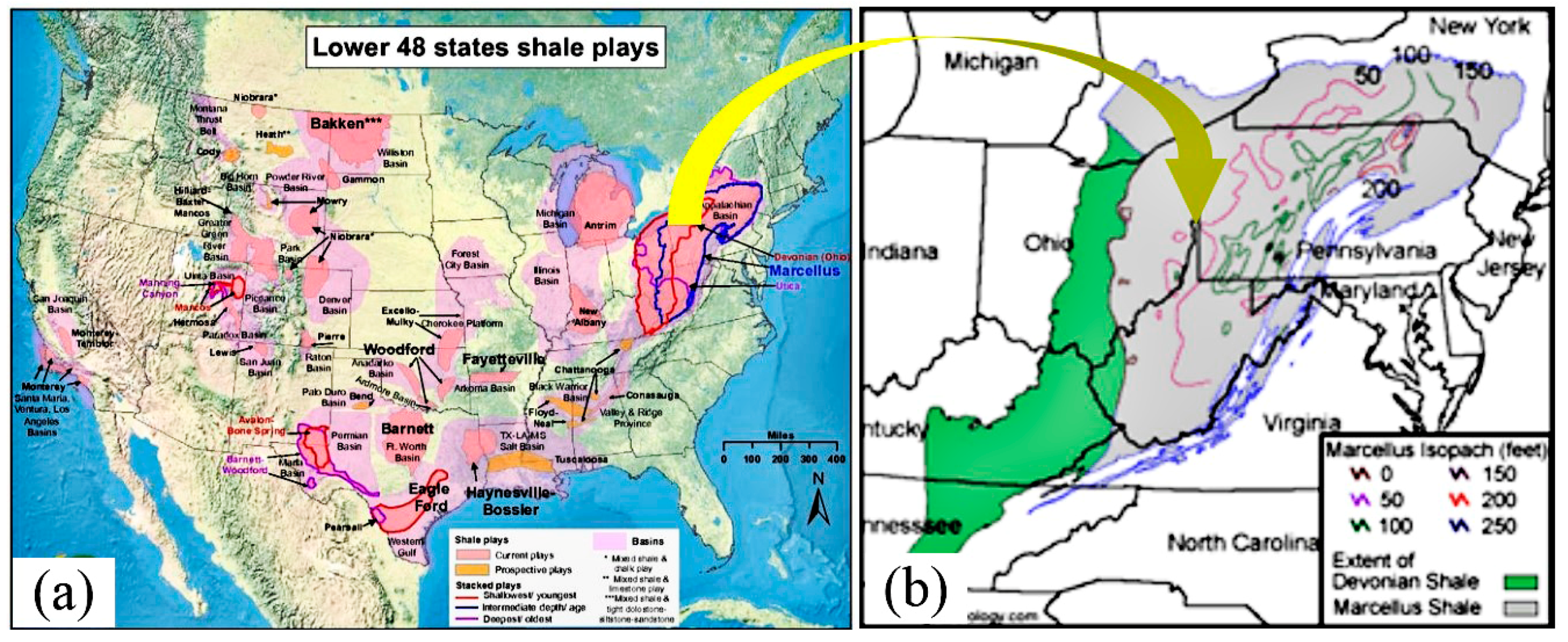
:1. Introduction
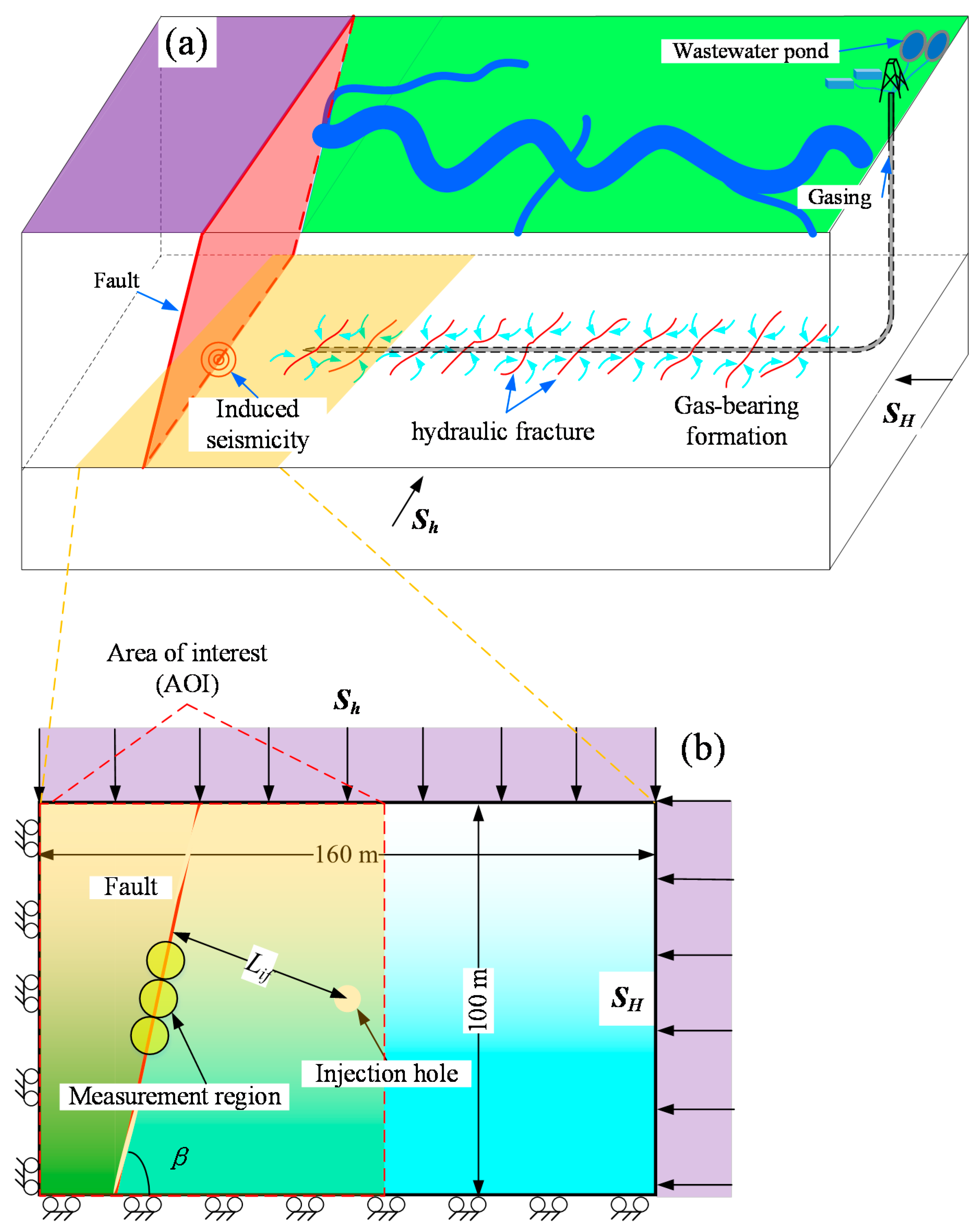
2. Numerical Simulation Procedure
2.1. Coupled Hydro-Mechanical Model
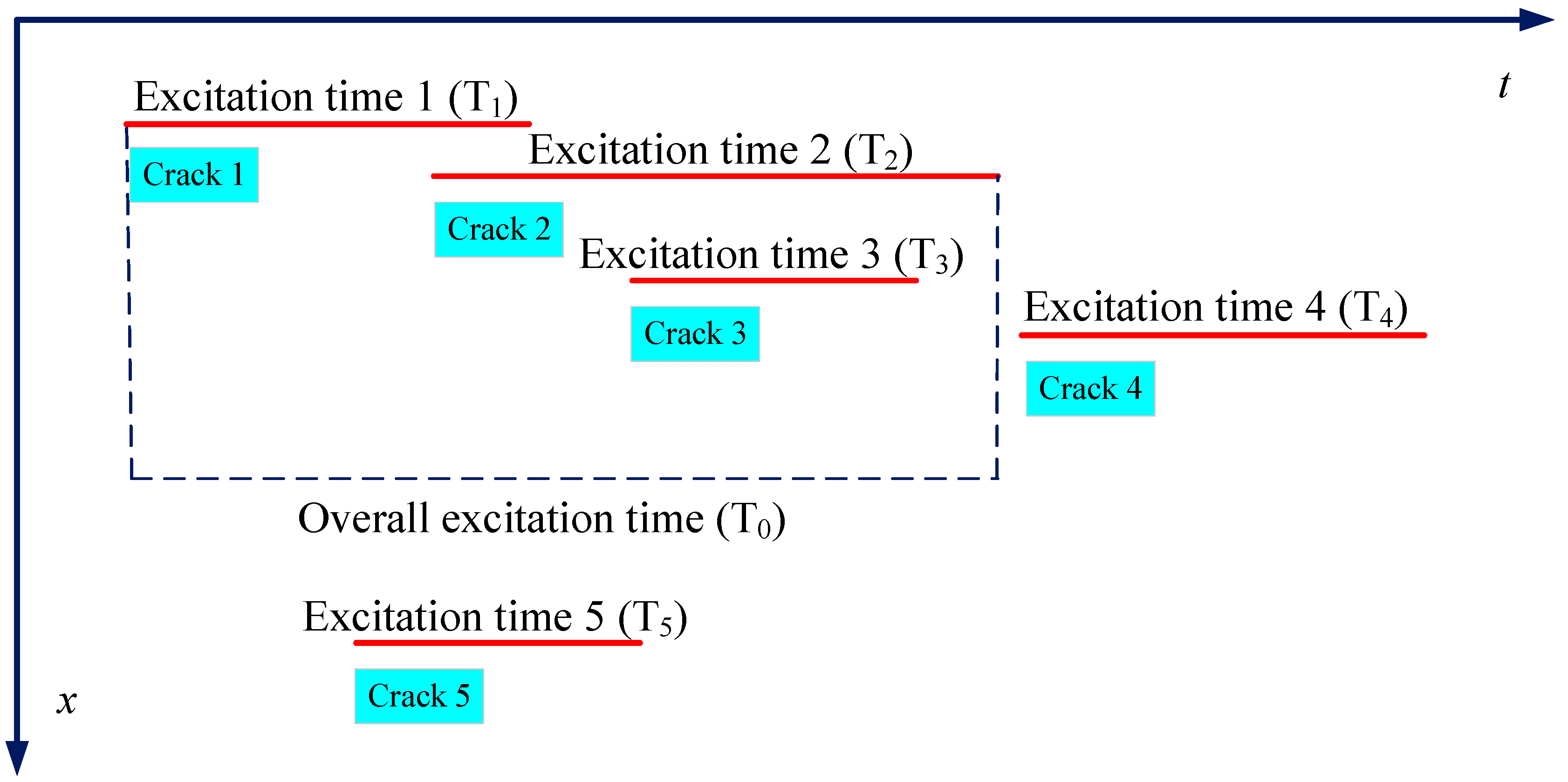
2.2. Moment Tensor Method
3. Model Steps and Validation
3.1. Model Steps
3.2. Model Validation
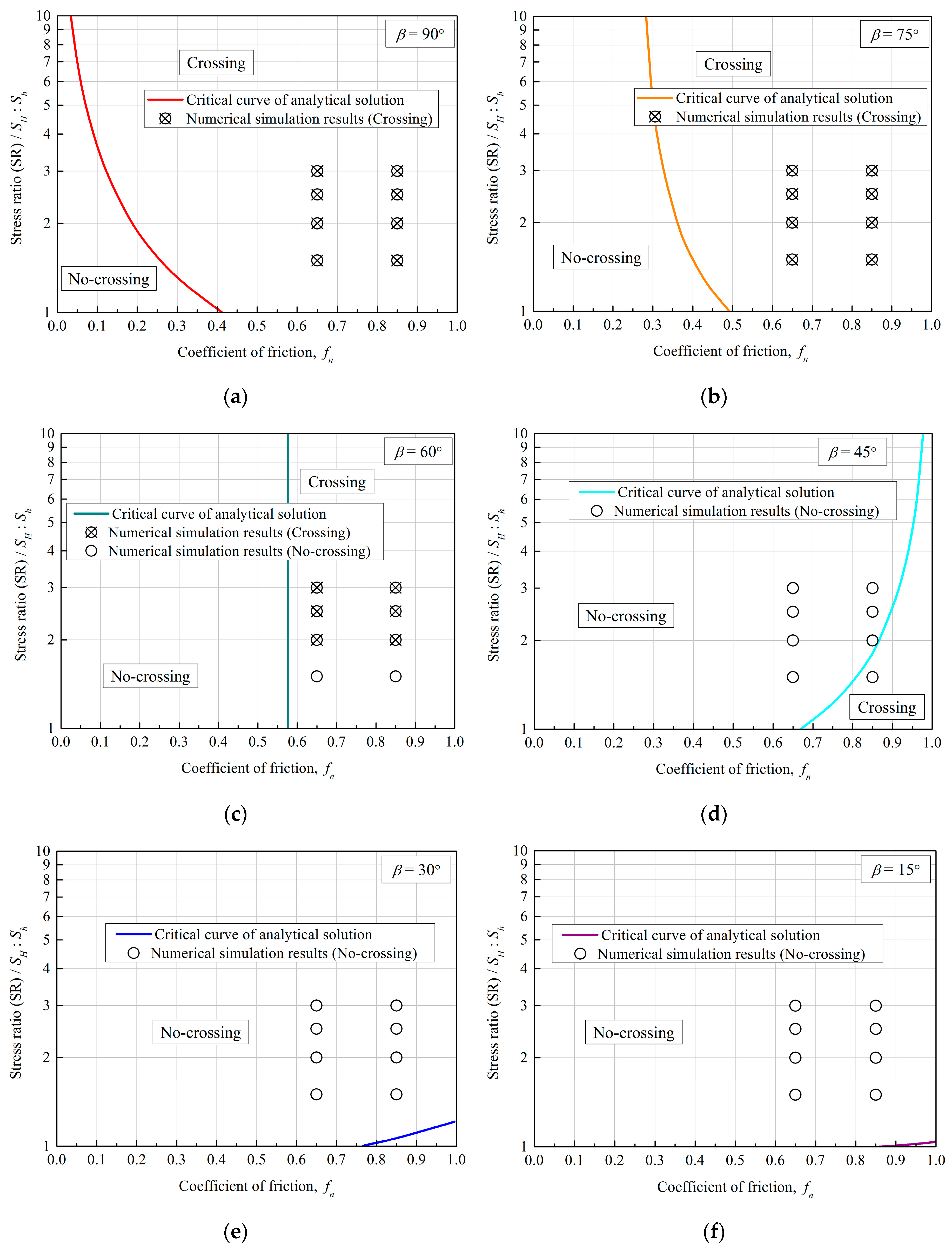
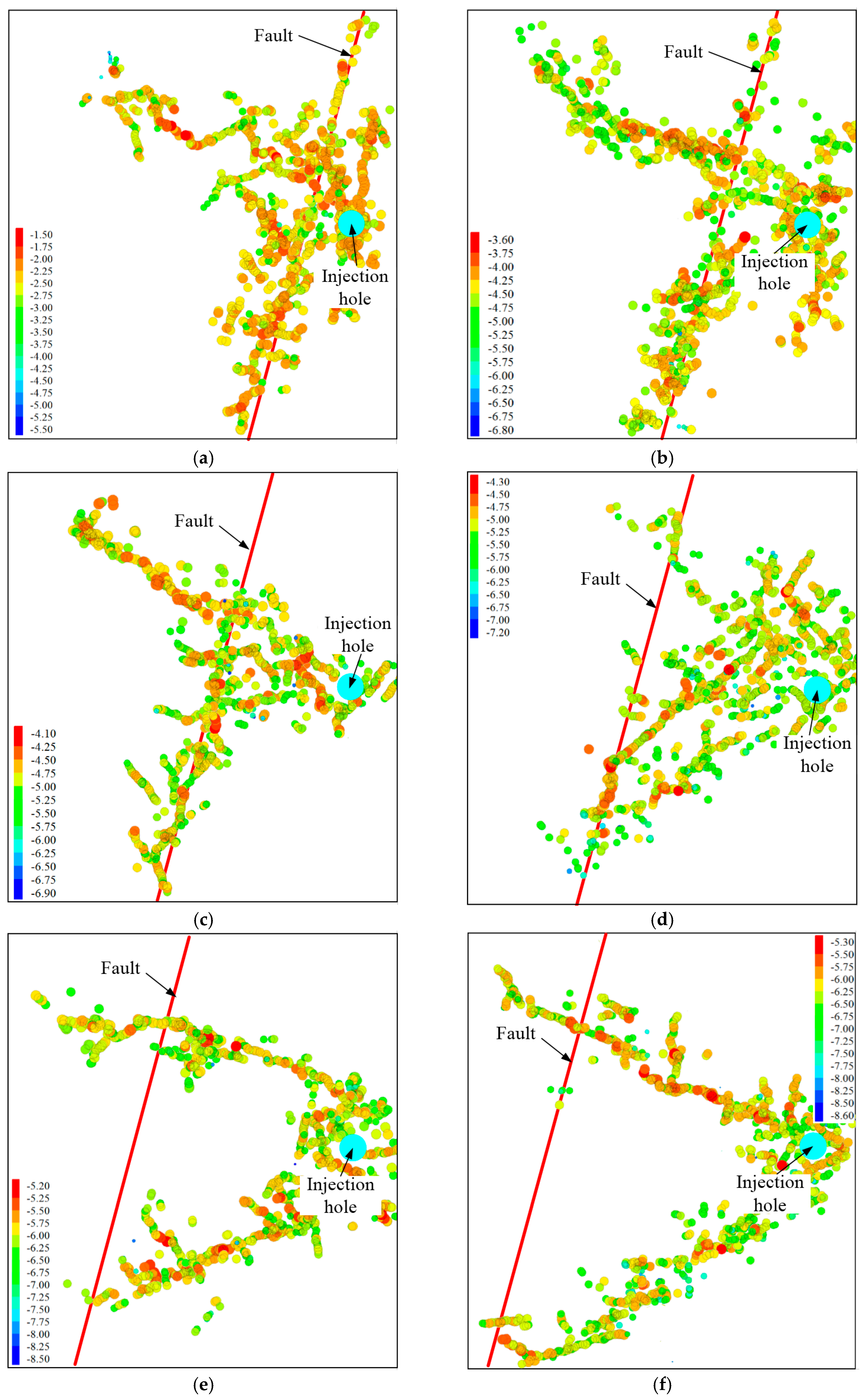
4. Results and Analysis
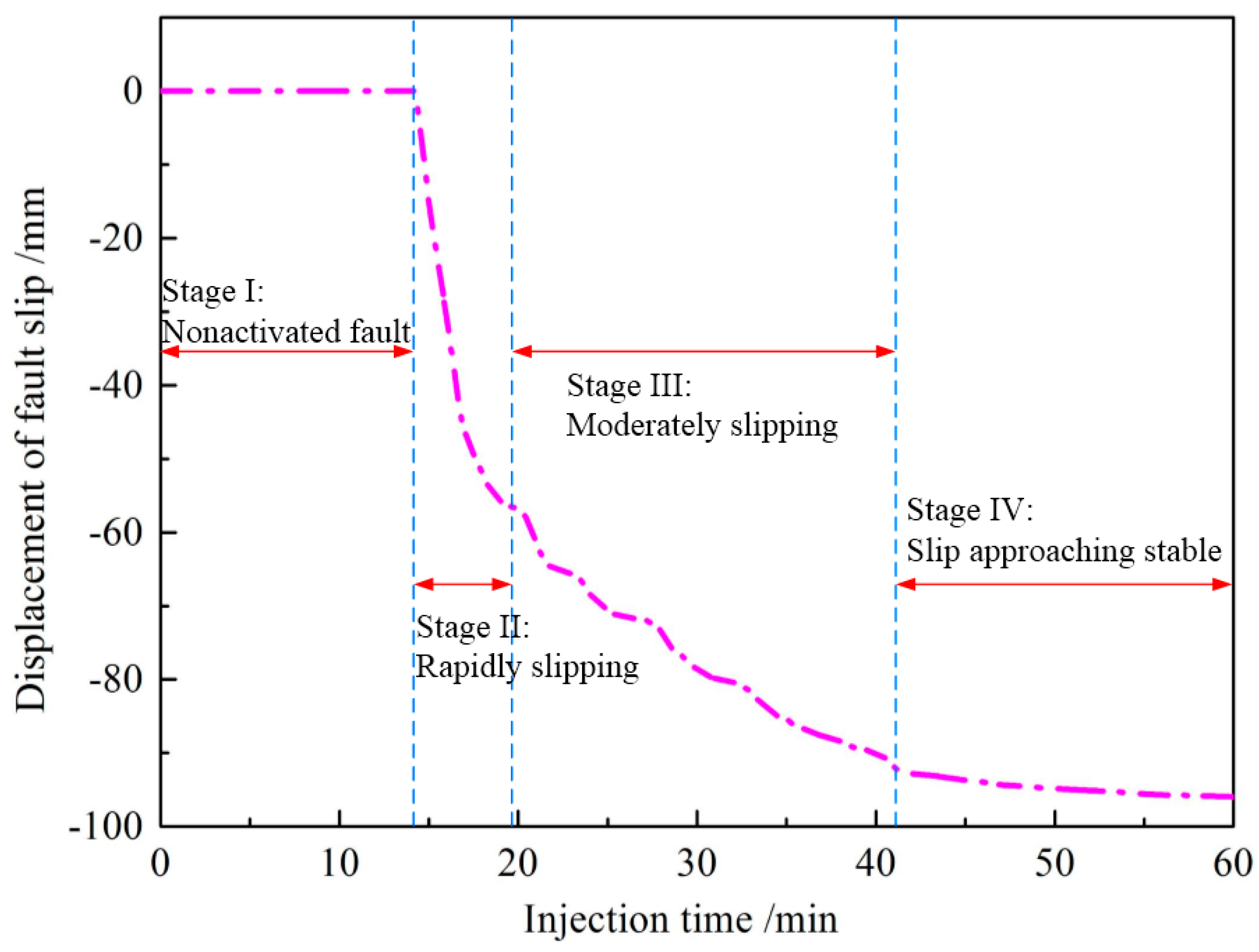
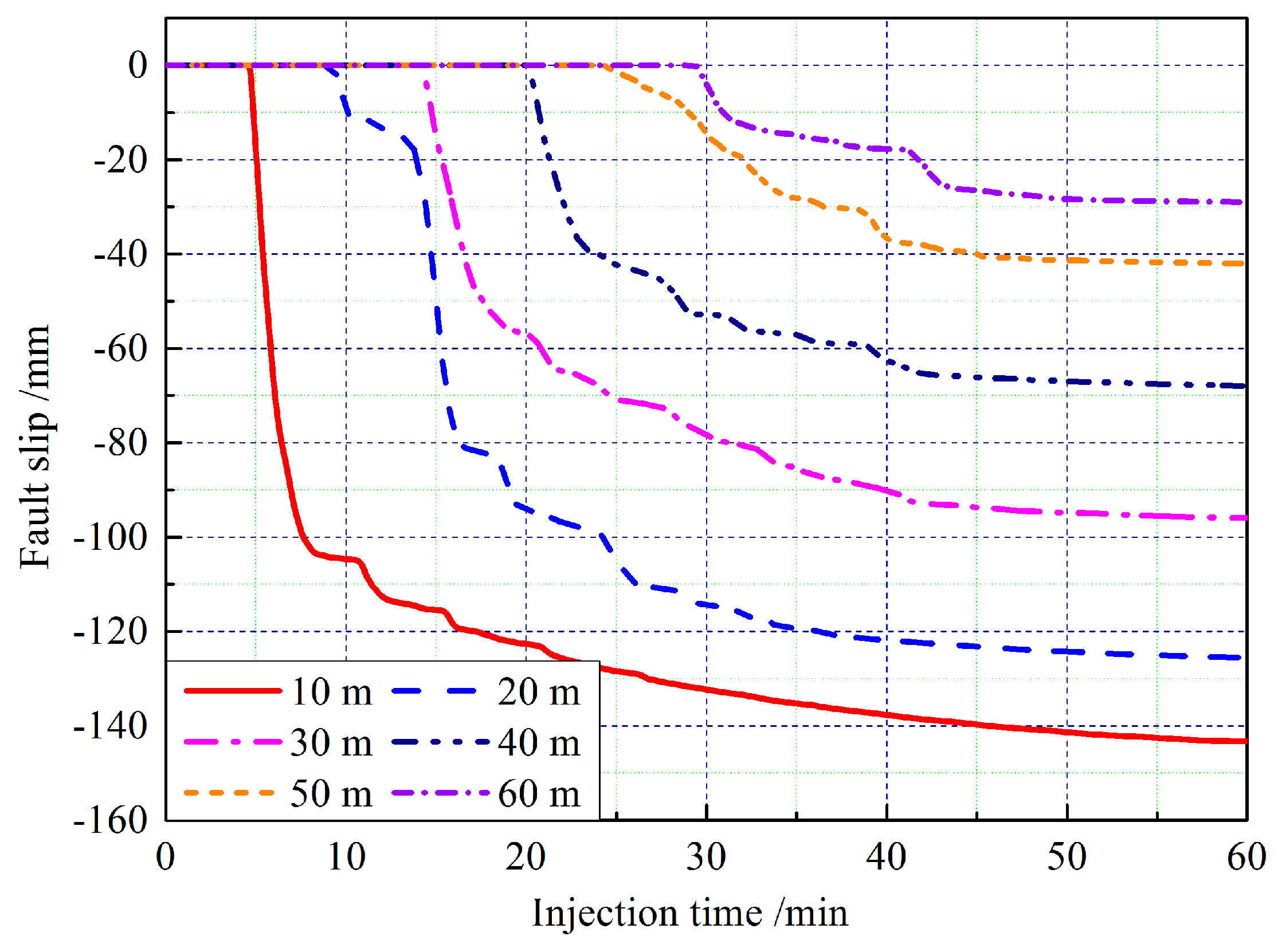
4.1. Fault Slip Displacement
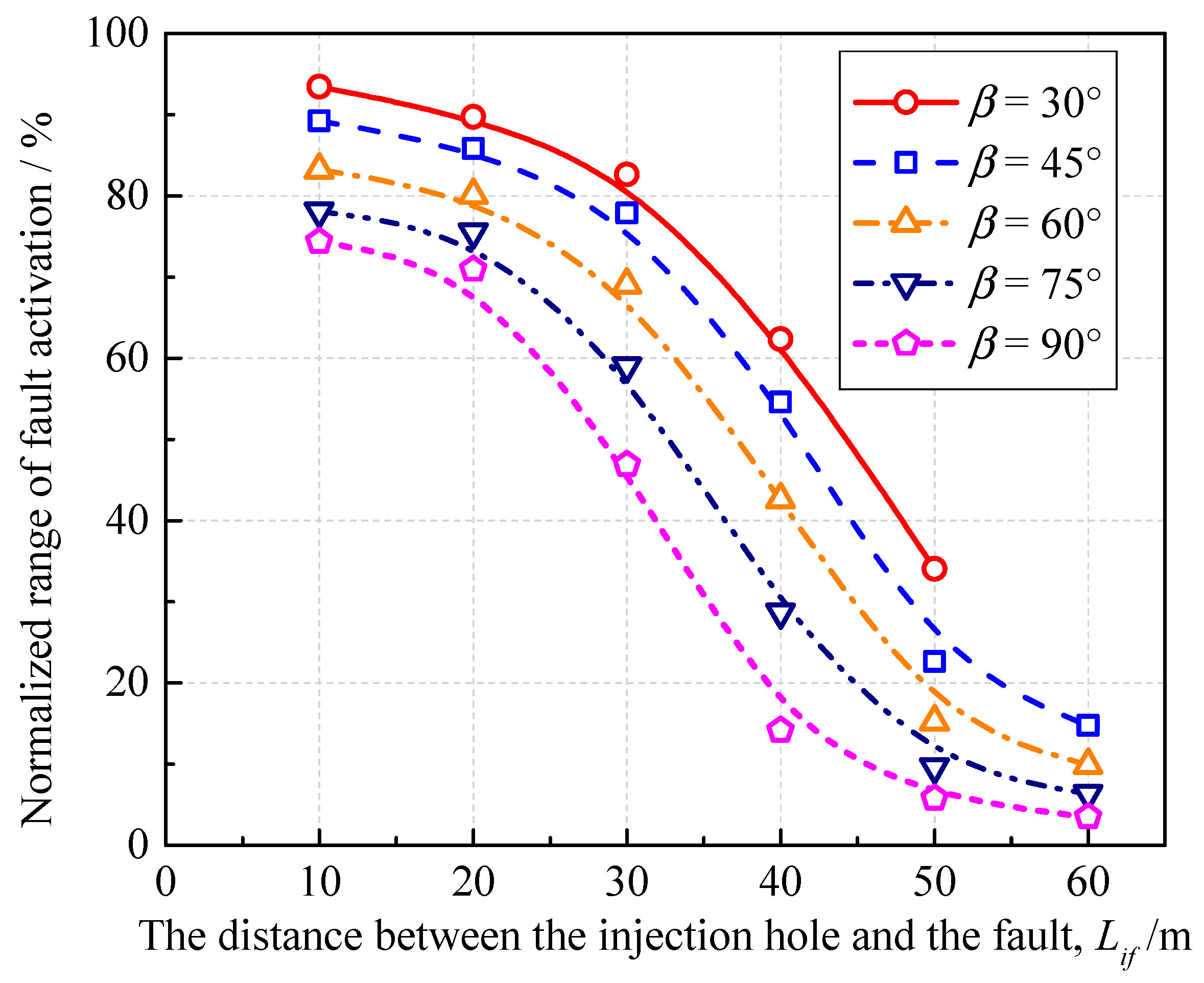
4.2. The Normalized Range of Fault Activation
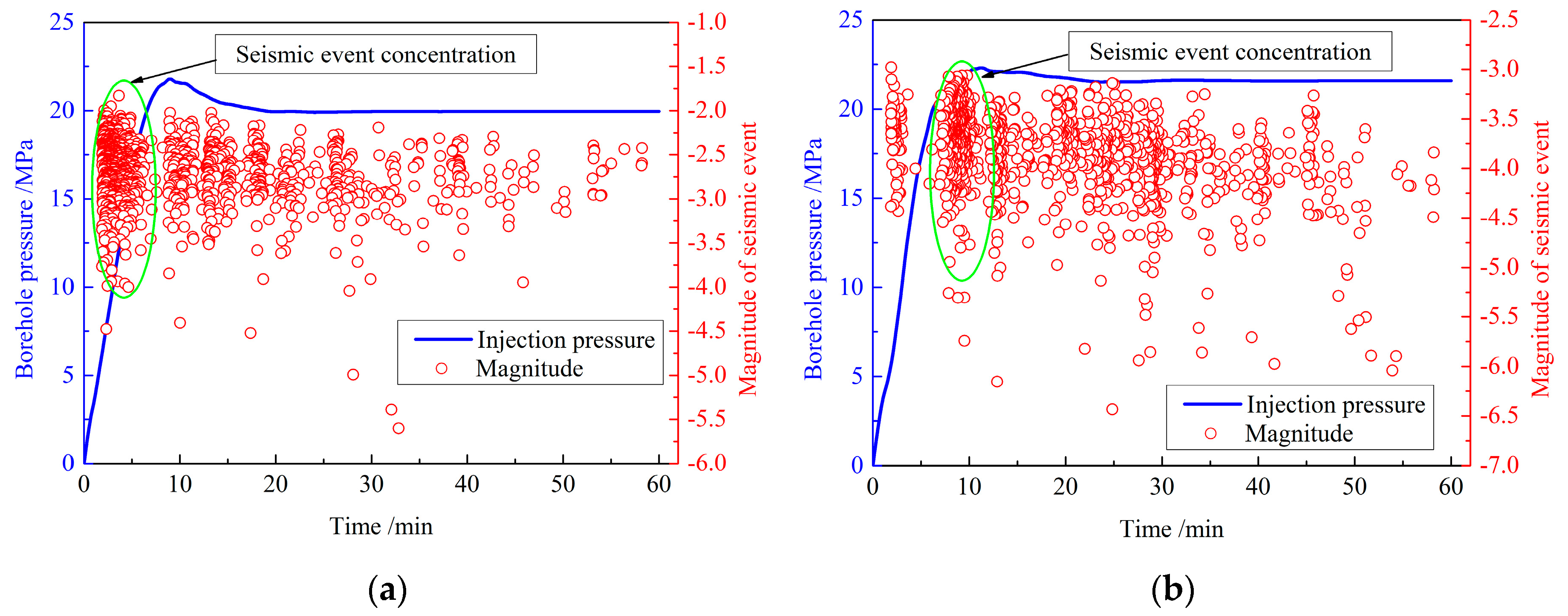
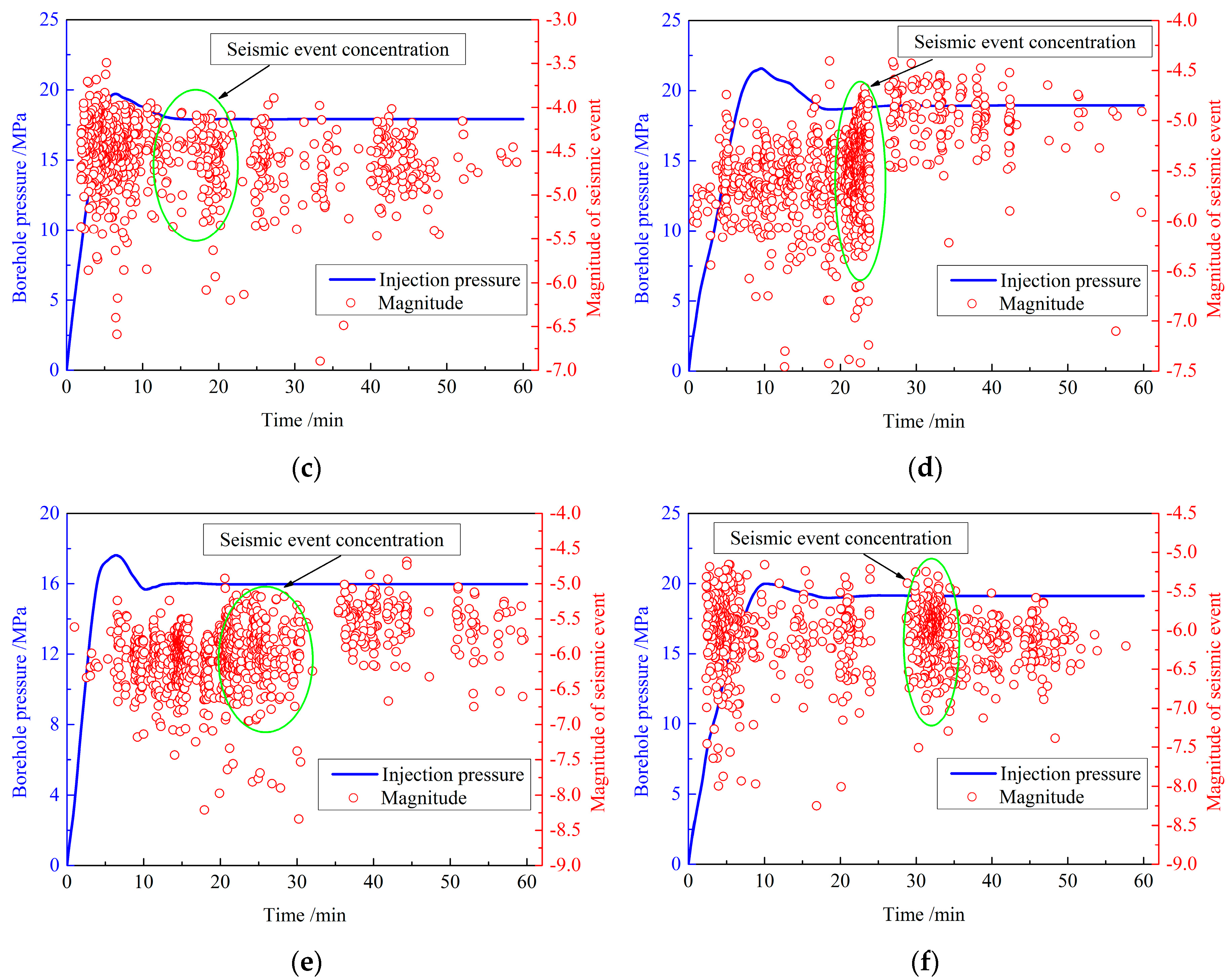
4.3. Injection Pressure Distribution
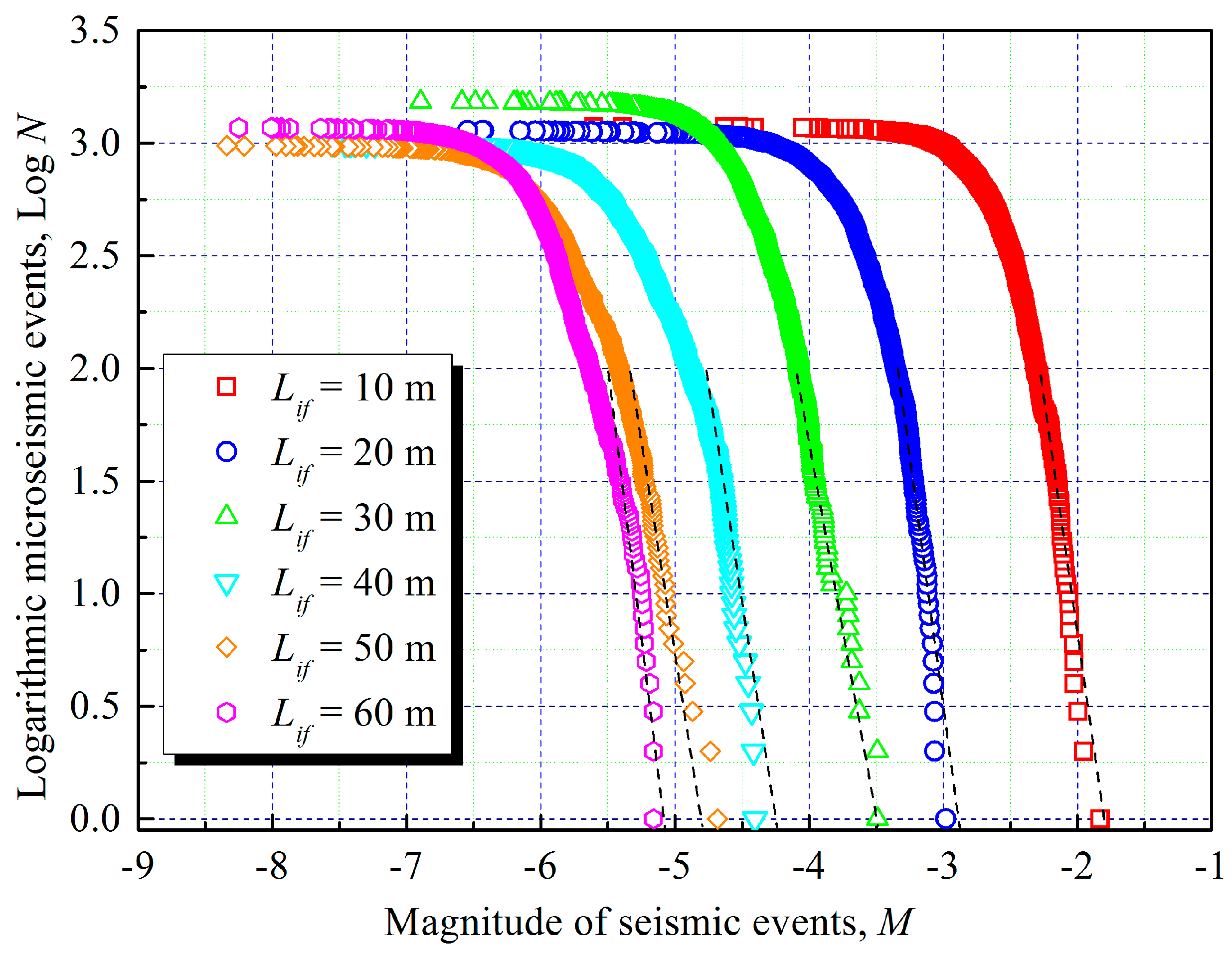
4.4. Cumulative Frequency of Seismic Events
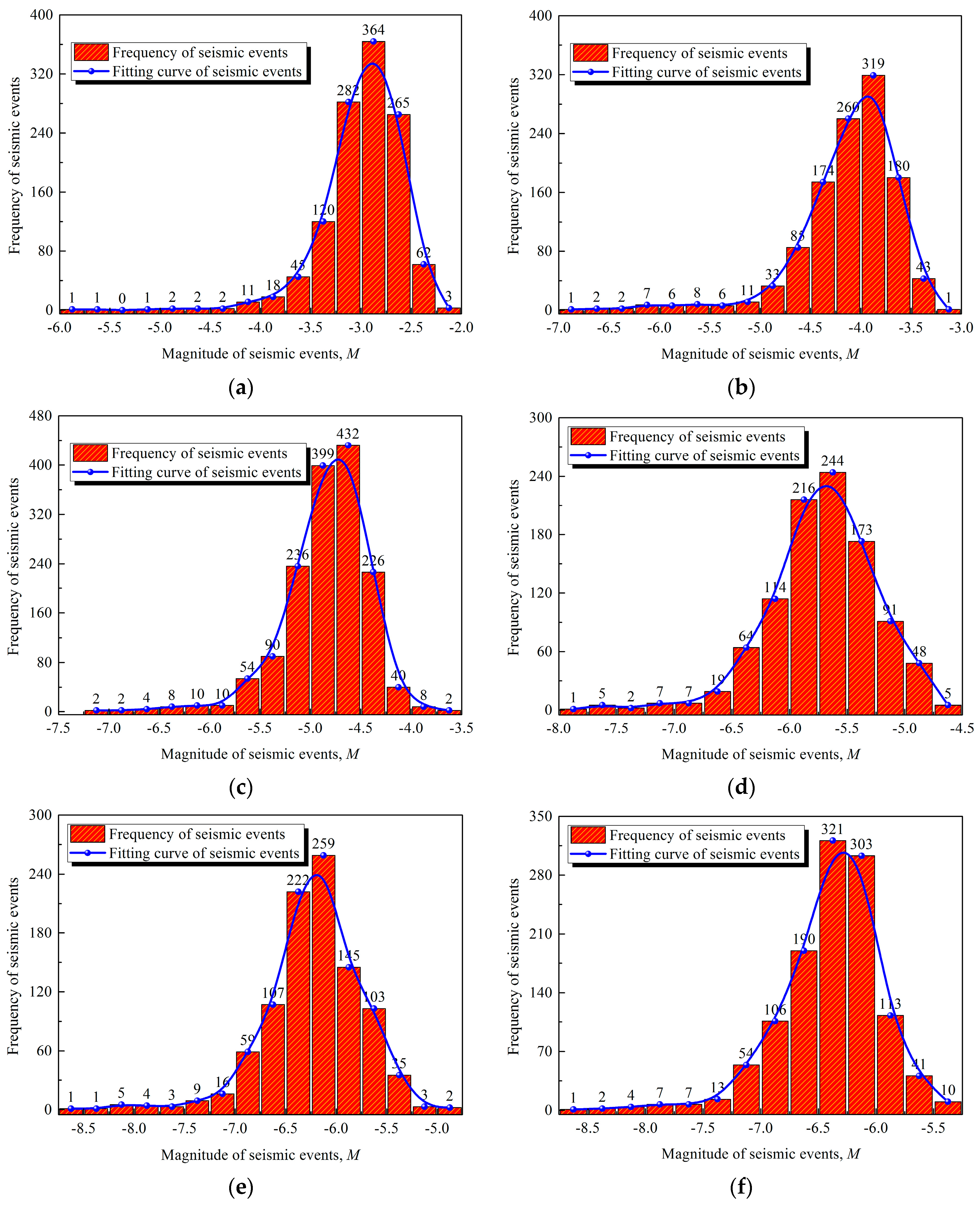
4.5. Magnitude Distribution of Seismic Events
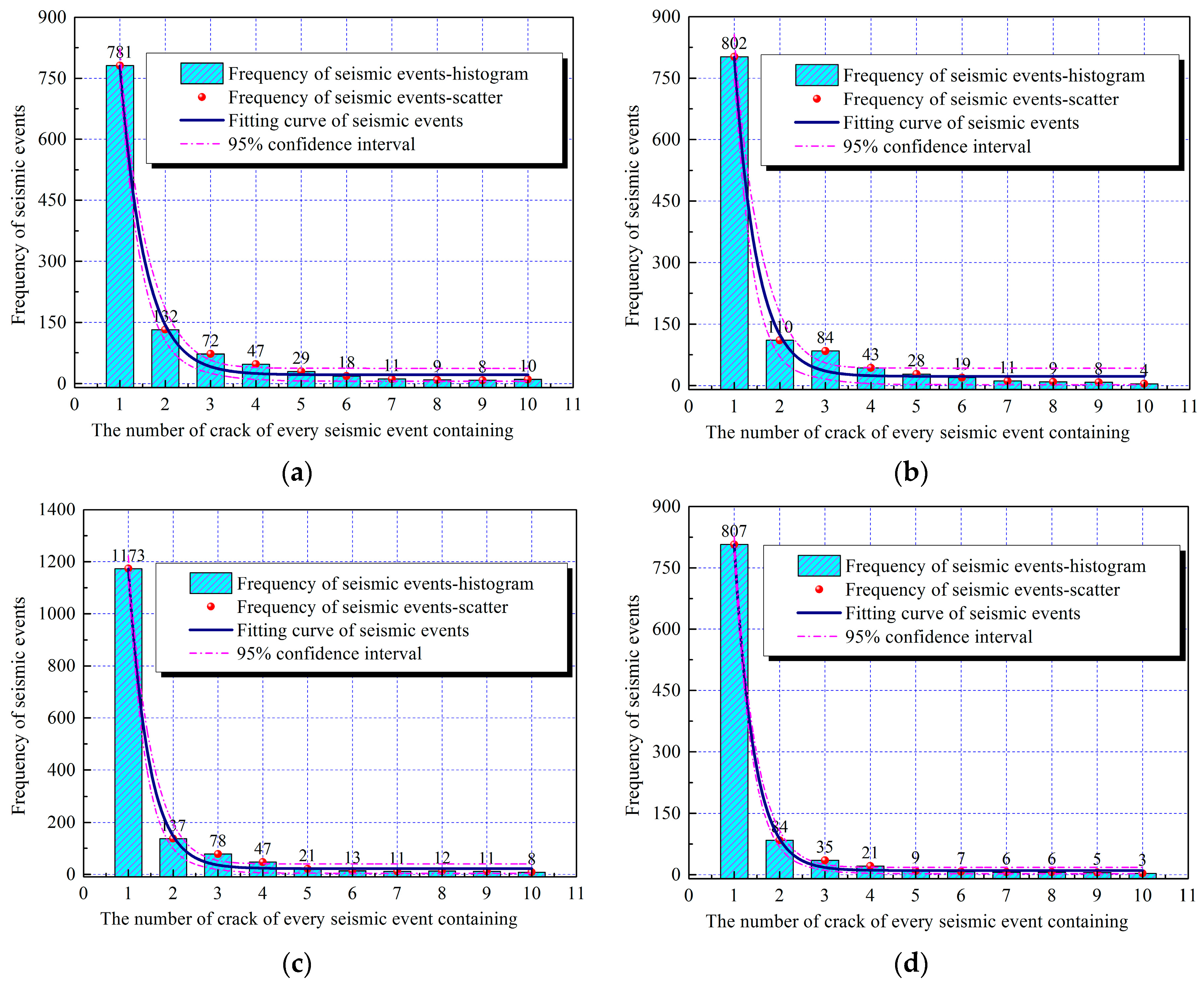
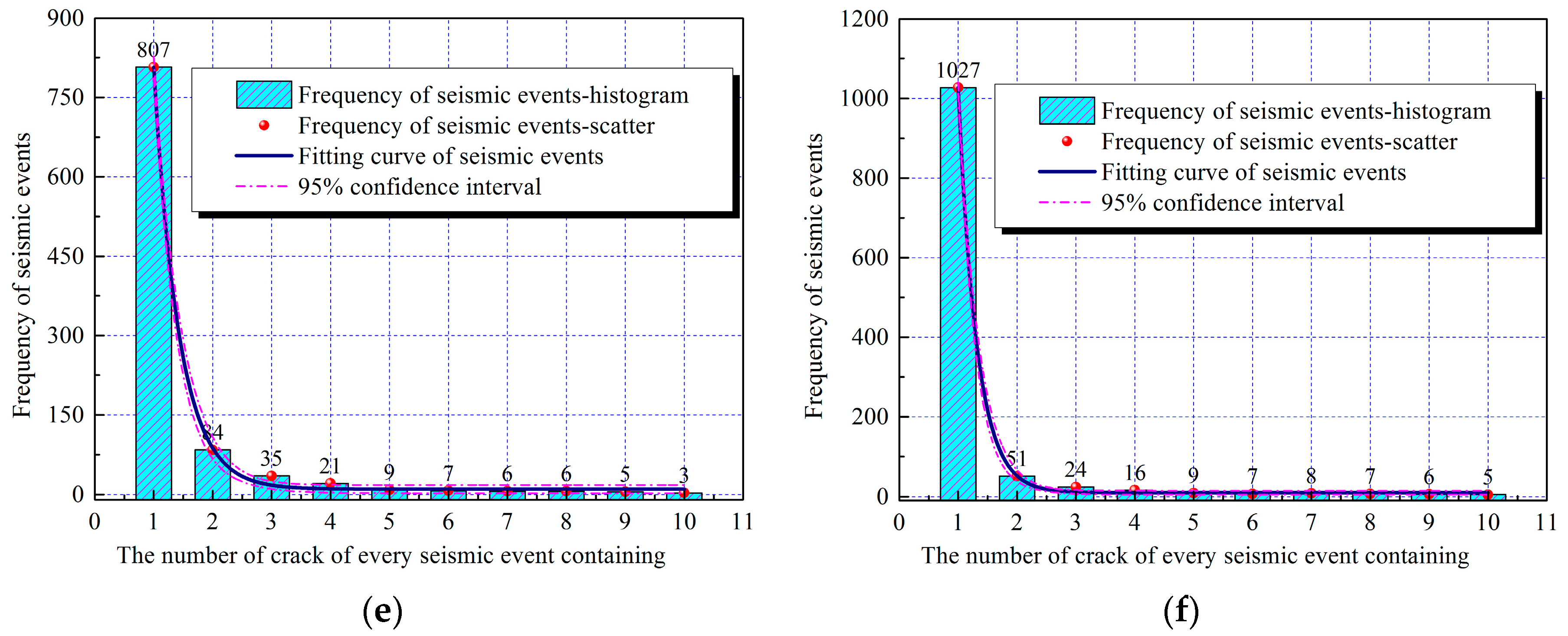
4.6. Seismic Events Containing the Crack Number
5. Discussion
6. Conclusions
- (1)
- The fault slip displacement and activation range increased at first, and then remained stable with an increase in the distance between the injection hole and the fault. In addition, there is a critical distance and interaction between the injection-induced stress disturbance, and fault slip was gentle when the actual distance between the injection hole and fault was larger than the threshold distance.
- (2)
- There was a linear relationship between the magnitude and the logarithmic frequency of the seismic events in a concentration zone. The b-value decreased with the increase in the distance between the injection hole and the fault. When Lif was relatively large (Lif ≥ 50 m), the b-value declined by more than 50%, which meant that no large-magnitude seismic event and affected area was generated within this distance range.
- (3)
- Seismic event frequency presented a normal distribution within the different magnitude ranges, and a negative exponential distribution was observed between the crack number contained in the seismic events and the seismic event frequency. In the case of the shortest Lif (Lif = 10 m), seismic event magnitudes concentrated in ranges from –3.5 to –1.5. In addition, the frequency of seismic events containing one crack was the lowest, while that of the seismic events containing more than 10 cracks was highest.
- (4)
- The injection rate, properties of the rock reservoir, and boundary conditions remained unchanged, resulting in small variations in the magnitude of borehole pressure (18–22 MPa). However, the distribution of injection pressure was quite sensitive to the change in the distance between the injection hole and the fault. Therefore, the interaction between the HFN and the fault induced by unstable injection pressure can result in the largest number of cracks.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Huang, S.; Liu, D.; Yao, Y.; Gan, Q.; Cai, Y.; Xu, L. Natural fractures initiation and fracture type prediction in coal reservoir under different in-situ stresses during hydraulic fracturing. J. Nat. Gas Sci. Eng. 2017, 43, 69–80. [Google Scholar] [CrossRef]
- Nagel, N.B.; Sanchez-Nagel, M.A.; Zhang, F.; Garcia, X.; Lee, B. Coupled Numerical Evaluations of the Geomechanical Interactions between a Hydraulic Fracture Stimulation and a Natural Fracture System in Shale Formations. Rock Mech. Rock Eng. 2013, 46, 581–609. [Google Scholar] [CrossRef]
- Fu, P.; Johnson, S.M.; Carrigan, C.R. An explicitly coupled hydro-geomechanical model for simulating hydraulic fracturing in arbitrary discrete fracture networks. Int. J. Numer. Anal. Methods 2013, 37, 2278–2300. [Google Scholar] [CrossRef]
- Wang, W.; Li, X.; Lin, B.; Zhai, C. Pulsating hydraulic fracturing technology in low permeability coal seams. Int. J. Min. Sci. Technol. 2015, 25, 681–685. [Google Scholar] [CrossRef]
- Rammay, M.H.; Awotunde, A.A. Stochastic optimization of hydraulic fracture and horizontal well parameters in shale gas reservoirs. J. Nat. Gas Sci. Eng. 2016, 36, 71–78. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Wang, H.; Liu, H.; Wu, H. Comparison of consecutive and alternate hydraulic fracturing in horizontal wells using XFEM-based cohesive zone method. J. Pet. Sci. Eng. 2016, 143, 14–25. [Google Scholar] [CrossRef]
- Omar, M.A.Z.; Rahman, M.M. Modeling Pinpoint Multistage Fracturing with 2D Fracture Geometry for Tight Oil Sands. Pet. Sci. Technol. 2011, 29, 1203–1213. [Google Scholar] [CrossRef]
- Tian, S.; Li, G.; Huang, Z.; Niu, J.; Xia, Q. Investigation and Application for Multistage Hydrajet-Fracturing with Coiled Tubing. Pet. Sci. Technol. 2009, 27, 1494–1502. [Google Scholar] [CrossRef]
- Verdon, J.P.; Kendall, J.M.; Horleston, A.C.; Stork, A.L. Subsurface fluid injection and induced seismicity in southeast Saskatchewan. Int. J. Greenh. Gas Control 2016, 54, 429–440. [Google Scholar] [CrossRef]
- Bao, X.; Eaton, D.W. Fault activation by hydraulic fracturing in western Canada. Science 2016, 354, 1406–1409. [Google Scholar] [CrossRef] [PubMed]
- Chang, M.; Huang, R. Observations of hydraulic fracturing in soils through field testing and numerical simulations. Can. Geotech. J. 2016, 53, 343–359. [Google Scholar] [CrossRef]
- Mrdjen, I.; Lee, J. High volume hydraulic fracturing operations: Potential impacts on surface water and human health. Int. J. Environ. Health Res. 2016, 26, 361–380. [Google Scholar] [CrossRef] [PubMed]
- Ito, T.; Hayashi, K. Role of Stress-controlled Flow Pathways in HDR Geothermal Reservoirs. Pure Appl. Geophys. 2003, 160, 1103–1124. [Google Scholar] [CrossRef]
- Renshaw, C.E.; Pollard, D.D. An Experimentally Verified Criterion for Propagation Across Unbounded Frictional Interfaces in Brittle, Linear Elastic Materials. Int. J. Rock Mech. Min. Sci. 1995, 32, 234–249. [Google Scholar] [CrossRef]
- Anderson, G.D. Effects of Friction on Hydraulic Fracture Growth Near Unbonded Interfaces in Rocks. Soc. Pet. Eng. J. 1981, 21, 21–29. [Google Scholar] [CrossRef]
- Weng, X. Modeling of complex hydraulic fractures in naturally fractured formation. J. Unconv. Oil Gas Resour. 2015, 9, 114–135. [Google Scholar] [CrossRef]
- Blanton, T.L. An experimental study of interaction between hydraulically induced and pre-existing fractures. SPE unconventional gas recovery symposium. Soc. Pet. Eng. 1982. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, M.; Jin, Y.; Zhang, G. Analysis of fracture propagation behavior and fracture geometry using a tri-axial fracturing system in naturally fractured reservoirs. Int. J. Rock Mech. Min. Sci. 2008, 45, 1143–1152. [Google Scholar] [CrossRef]
- Daneshy, A.A. Hydraulic Fracture Propagation in the Presence of Planes of Weakness. SPE European Spring Meeting. Soc. Pet. Eng. 1974. [Google Scholar] [CrossRef]
- Gu, H.; Weng, X. Criterion for fractures crossing frictional interfaces at non-orthogonal angles. In Proceedings of the 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium: American Rock Mechanics Association, Salt Lake City, UT, USA, 27–30 June 2010. [Google Scholar]
- Gu, H.; Weng, X.; Lund, J.B.; Mack, M.G.; Ganguly, U.; Suarez-Rivera, R. Hydraulic fracture crossing natural fracture at nonorthogonal angles: A criterion and its validation. SPE Prod. Oper. 2012, 27, 20–26. [Google Scholar] [CrossRef]
- Cheng, W.; Jin, Y.; Chen, M. Reactivation mechanism of natural fractures by hydraulic fracturing in naturally fractured shale reservoirs. J. Nat. Gas Sci. Eng. 2015, 23, 431–439. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Zhang, B. Analysis of Fracturing Network Evolution Behaviors in Random Naturally Fractured Rock Blocks. Rock Mech. Rock Eng. 2016, 49, 4339–4347. [Google Scholar] [CrossRef]
- Wasantha, P.L.P.; Konietzky, H.; Weber, F. Geometric nature of hydraulic fracture propagation in naturally-fractured reservoirs. Comput. Geotech. 2017, 83, 209–220. [Google Scholar] [CrossRef]
- Yuan, B.; Wood, D.A.; Yu, W. Stimulation and hydraulic fracturing technology in natural gas reservoirs: Theory and case studies (2012–2015). J. Nat. Gas Sci. Eng. 2015, 26, 1414–1421. [Google Scholar] [CrossRef]
- Zeng, Q.; Yao, J. Numerical simulation of fracture network generation in naturally fractured reservoirs. J. Nat. Gas Sci. Eng. 2016, 30, 430–443. [Google Scholar] [CrossRef]
- Merrill, T.W.; Schizer, D.M. The Shale Oil and Gas Revolution, Hydraulic Fracturing, and Water Contamination: A Regulatory Strategy. Columbia Law and Economics Working Paper No. 440. Available online: https://ssrn.com/abstract=2221025 (accessed on 13 October 2017).
- Hatzenbuhler, H.; Centner, T. Regulation of Water Pollution from Hydraulic Fracturing in Horizontally-Drilled Wells in the Marcellus Shale Region, USA. Water 2012, 4, 983–994. [Google Scholar] [CrossRef]
- Lebeau, M.; Konrad, J. A new capillary and thin film flow model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- De Pater, C.J.; Baisch, S. Geomechanical Study of Bowland Shale Seismicity. Synthesis Report. Available online: https://www.politiekemonitor.nl/9353000/1/j4nvgs5kjg27kof_j9vvioaf0kku7zz/viu9lvhwcewb/f=/blg137575.pdf (accessed on 16 October 2017).
- Holland, A. Examination of Possibly Induced Seismicity from Hydraulic Fracturing in the Eola Field; Oklahoma Geological Survey: Garvin County, OK, USA, 2011. [Google Scholar]
- Skoumal, R.J.; Brudzinski, M.R.; Currie, B.S. Earthquakes Induced by Hydraulic Fracturing in Poland Township, Ohio. Bull. Seismol. Soc. Am. 2015, 105, 189–197. [Google Scholar] [CrossRef]
- Fisher, K.; Warpinski, N. Hydraulic fracture-height growth: Realdata. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Witherspoon, P.A.; Wang, J.S.; Iwai, K.; Gale, J.E. Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zimmermann, G.; Zang, A. Numerical Investigation on Stress Shadowing in Fluid Injection-Induced Fracture Propagation in Naturally Fractured Geothermal Reservoirs. Rock Mech. Rock Eng. 2015, 48, 1439–1454. [Google Scholar] [CrossRef]
- Itasca Consulting Group. PFC2D Manual, version 5.0; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2014. [Google Scholar]
- Lisjak, A.; Liu, Q.; Zhao, Q.; Mahabadi, O.K.; Grasselli, G. Numerical simulation of acoustic emission in brittle rocks by two-dimensional finite-discrete element analysis. Geophys. J. Int. 2013, 195, 423–443. [Google Scholar] [CrossRef]
- Heinze, T.; Galvan, B.; Miller, S.A. A new method to estimate location and slip of simulated rock failure events. Tectonophysics 2015, 651–652, 35–43. [Google Scholar] [CrossRef]
- Liang, S.; Elsworth, D.; Li, X.; Yang, D. Topographic influence on stability for gas wells penetrating longwall mining areas. Int. J. Coal Geol. 2014, 132, 23–36. [Google Scholar] [CrossRef]
- Rummel, F.; Baumgärtner, J. Hydraulic fracturing stress measurements in the GPK1 borehole, Soultz sous Forêts. Geotherm. Sci. Technol. 1991, 3, 119–148. [Google Scholar]
- Outlook, A.E. Energy information administration. Dep. Energy 2010, 92010, 1–15. [Google Scholar]
- Chong, Z.; Karekal, S.; Li, X.; Hou, P.; Yang, G.; Liang, S. Numerical investigation of hydraulic fracturing in transversely isotropic shale reservoirs based on the discrete element method. J. Nat. Gas Sci. 2017, 46, 398–420. [Google Scholar] [CrossRef]
- Wang, T.; Hu, W.; Elsworth, D.; Zhou, W.; Zhou, W.; Zhao, X.; Zhao, L. The effect of natural fractures on hydraulic fracturing propagation in coal seams. J. Pet. Sci. Eng. 2017, 150, 180–190. [Google Scholar] [CrossRef]
- Shivakumar, K.; Rao, M.V.M.S. Application of fractals to the study of rock fracture and rockburst-associated seismicity. In New Delhi: Application of Fractals in Earth Sciences; AA Balkema: Avereest, The Netherlands; USA/Oxford: New York, NY, USA; IBH Pub. Co.: Delhi, India, 2000; pp. 171–188. [Google Scholar]
- Shivakumar, K.; Rao, M.V.M.S.; Srinivasan, C.; Kusunose, K. Multifractal Analysis of the Spatial Distribution of Area Rockbursts at Kolar Gold Mines. Int. J. Rock Mech. Min. Sci. 1996, 33, 167–172. [Google Scholar] [CrossRef]
- Chong, Z.; Li, X.; Hou, P.; Chen, X.; Wu, Y. Moment tensor analysis of transversely isotropic shale based on the discrete element method. Int. J. Min. Sci. Technol. 2017, 27, 507–515. [Google Scholar] [CrossRef]
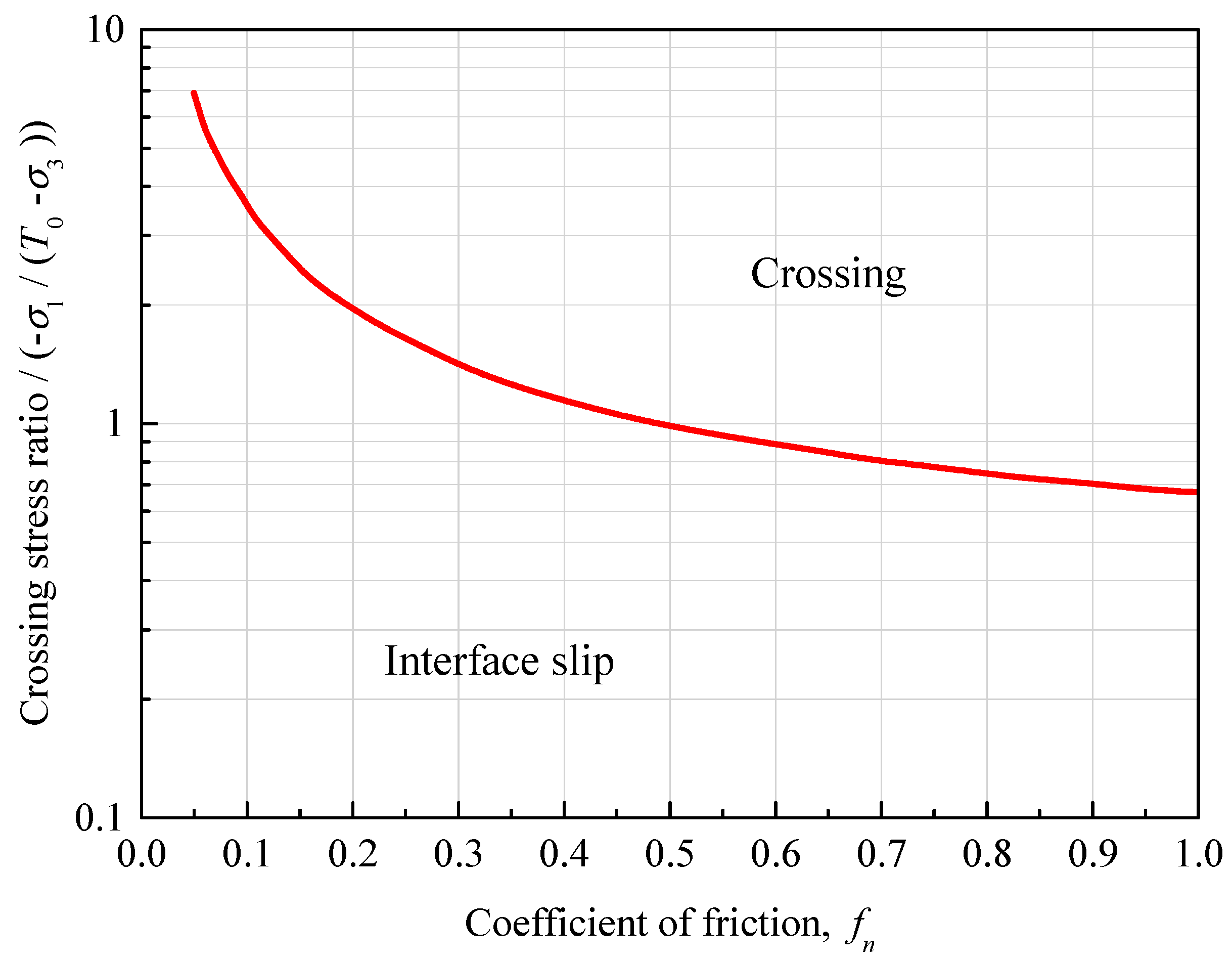
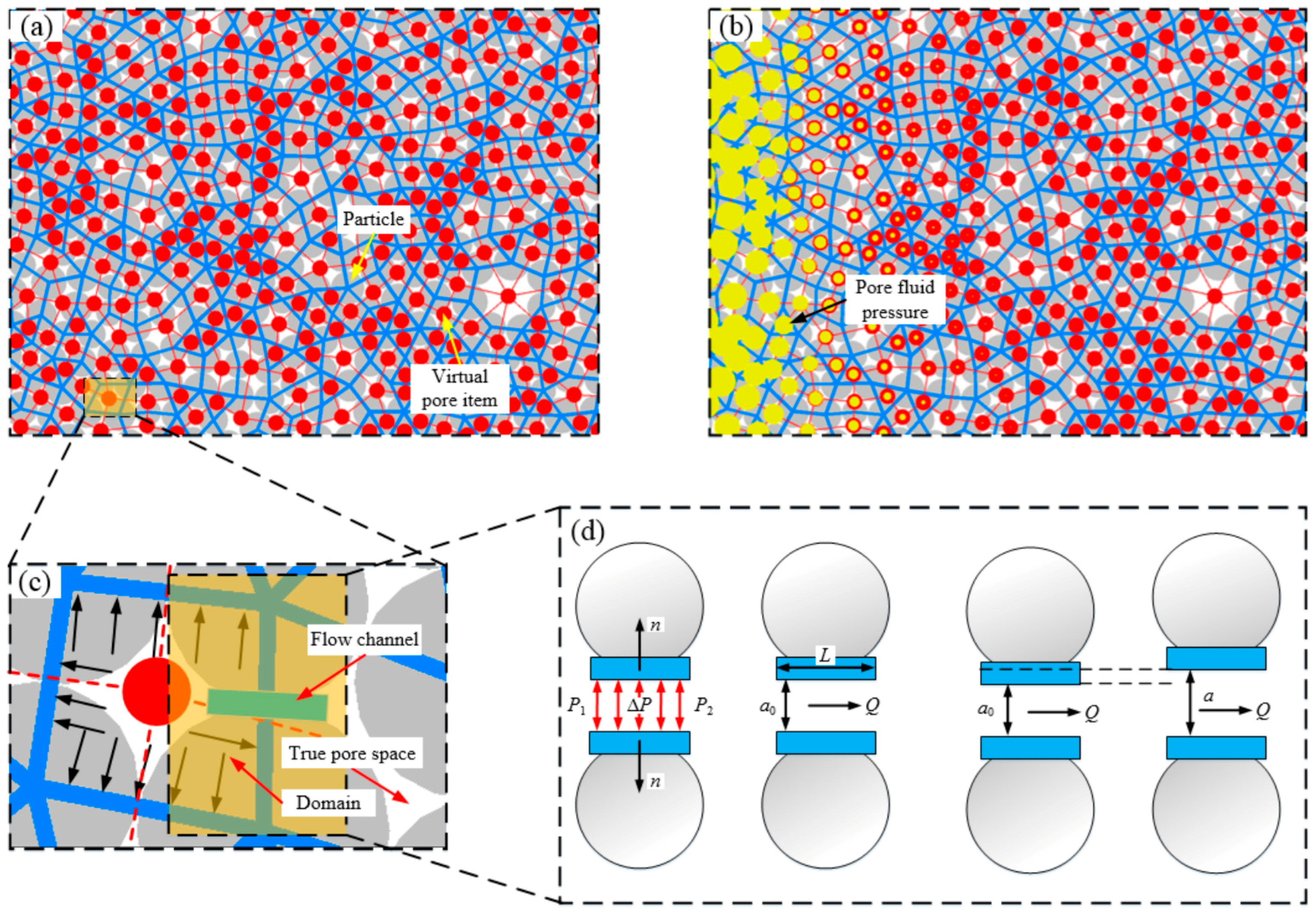
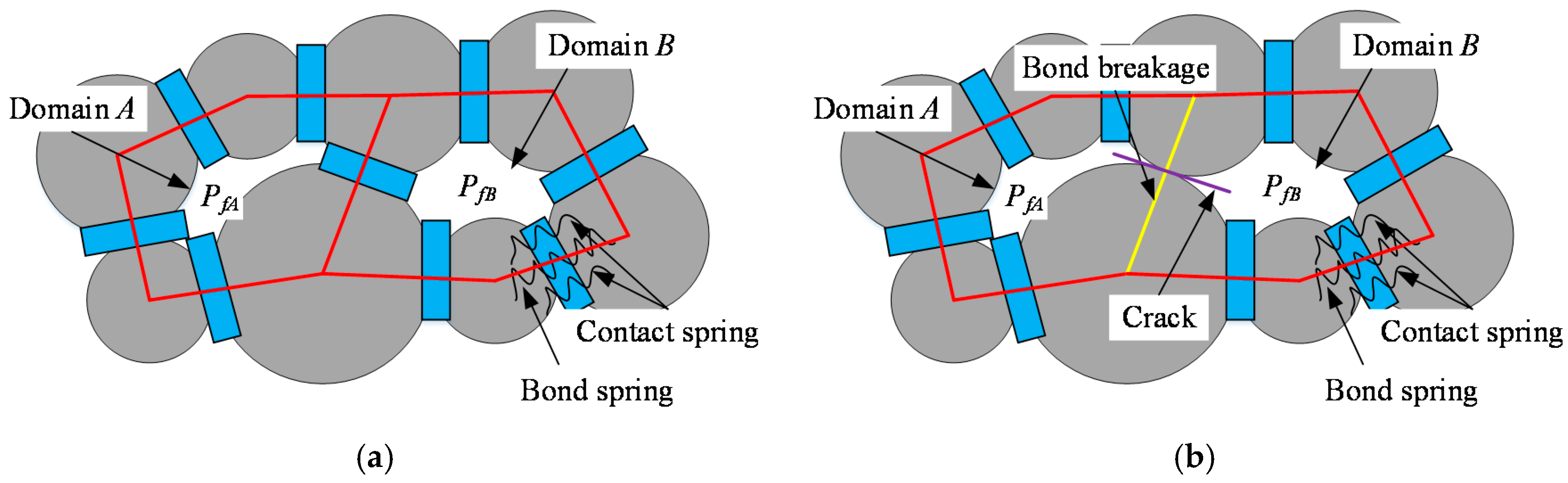


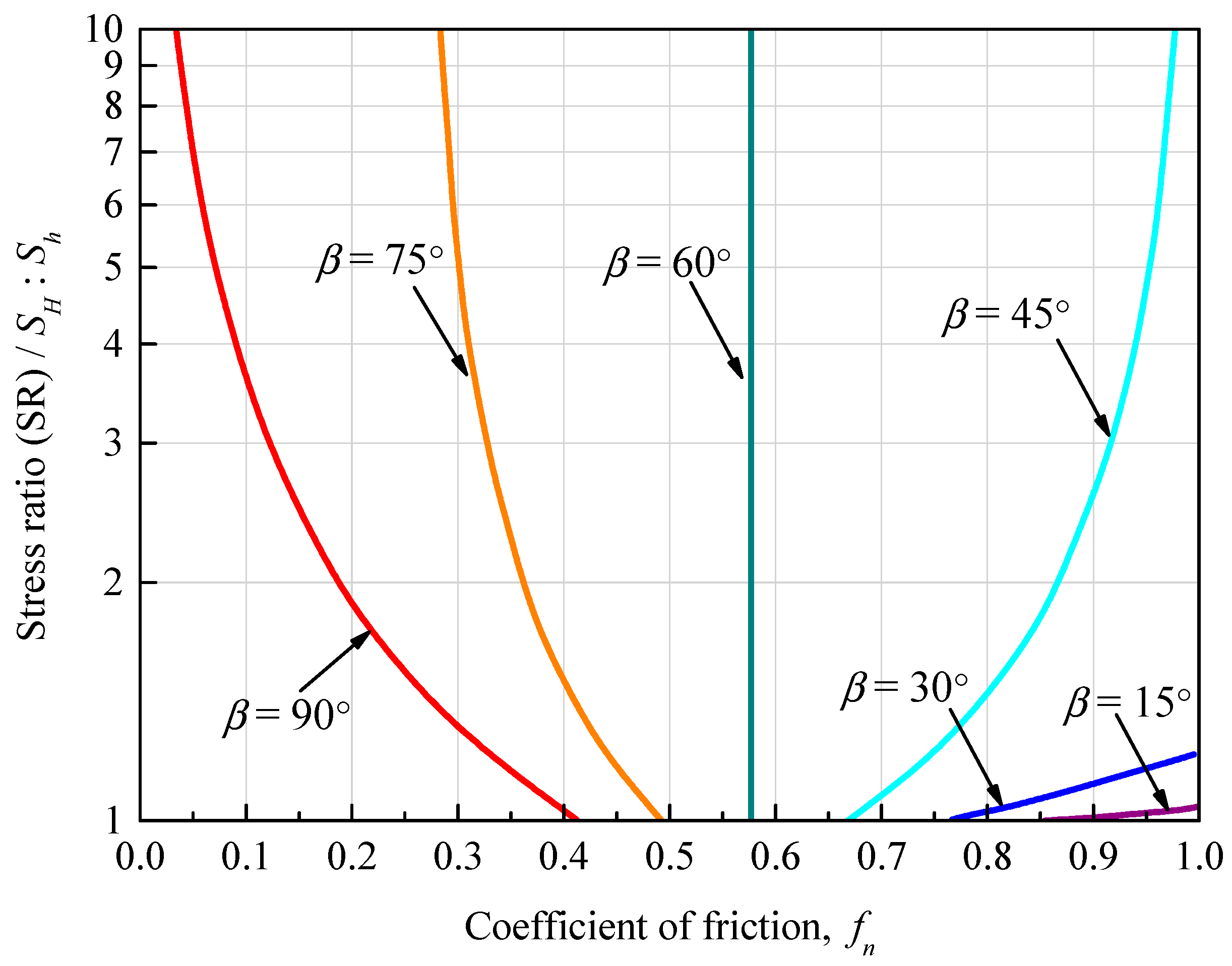
| Parameters | Unit | Values |
|---|---|---|
| Rock Matrix | ||
| Particle density | kg/m3 | 2700 |
| Particle friction coefficient | - | 0.10 |
| Young’s modulus of the particle | GPa | 15.2 |
| Young’s modulus of the parallel bond | GPa | 15.2 |
| Normal stiffness of the parallel bond (mean) | MPa | 100.6 |
| Normal stiffness of the parallel bond (std deviation) | MPa | 25 |
| Shear stiffness of the parallel bond (mean) | MPa | 131.5 |
| Shear stiffness of the parallel bond (std deviation) | MPa | 30 |
| Fault Properties | ||
| Normal stiffness | GPa/m | 60 |
| Shear stiffness | GPa/m | 60 |
| Tensile strength | MPa | 0 |
| Cohesion | MPa | 0 |
| Friction angle | ° | 29.5 |
| Dilation angle | ° | 0 |
| Fluid Properties and Operational Parameters | ||
| Injection rate | m3·s−1 | 2.0 × 10−6 |
| Fluid bulk modulus | GPa | 2.2 |
| Fluid dynamic viscosity | Pa·s | 1.1 × 10−4 |
| Initial hydraulic aperture | m | 3.2 × 10−5 (PB and SJ) |
| Infinite hydraulic aperture | m | 3.2 × 10−6 (PB and SJ) |
| Parameters | Unit | Values |
|---|---|---|
| Normal stiffness | GPa/m | 45 |
| Shear stiffness | GPa/m | 45 |
| Tensile strength | MPa | 6.2 |
| Cohesion | MPa | 4.8 |
| Friction angle | ° | 23.5 |
| Dilation angle | ° | 0 |
| The Distance between the Injection Hole and the Fault (m) | 10 | 20 | 30 | 40 | 50 | 60 | |
|---|---|---|---|---|---|---|---|
| Stage I | Duration (min) | 4.70 | 9.34 | 14.28 | 20.16 | 24.32 | 29.44 |
| Displacement (mm) | 0 | 0 | 0 | 0 | 0 | 0 | |
| Stage II | Duration (min) | 4.24 | 7.9 | 7.02 | 6.96 | 6.06 | 5.90 |
| Displacement (mm) | 104.11 | 81.96 | 63.09 | 42.41 | 16.07 | 15.13 | |
| Stage III | Duration (min) | 30.48 | 22.54 | 19.98 | 14.96 | 12.6 | 9.19 |
| Displacement (mm) | 33.29 | 39.83 | 29.28 | 22.98 | 22.97 | 11.28 | |
| Stage IV | Duration (min) | 20.58 | 20.22 | 18.72 | 17.92 | 17.02 | 15.47 |
| Displacement (mm) | 5.87 | 3.77 | 3.57 | 2.54 | 2.95 | 2.57 | |
| Accumulative displacement (mm) | 143.27 | 125.56 | 95.94 | 67.93 | 41.99 | 28.98 | |
| The Distance between the Injection Hole and the Fault (m) | a-Value | b-Value |
|---|---|---|
| 10 | −11.79 | 2.52 |
| 20 | −8.928 | 2.96 |
| 30 | −20.23 | 3.65 |
| 40 | −9.07 | 4.85 |
| 50 | −16.26 | 6.01 |
| 60 | −21.48 | 7.20 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chong, Z.; Li, X.; Chen, X. Effect of Injection Site on Fault Activation and Seismicity during Hydraulic Fracturing. Energies 2017, 10, 1619. https://doi.org/10.3390/en10101619
Chong Z, Li X, Chen X. Effect of Injection Site on Fault Activation and Seismicity during Hydraulic Fracturing. Energies. 2017; 10(10):1619. https://doi.org/10.3390/en10101619
Chicago/Turabian StyleChong, Zhaohui, Xuehua Li, and Xiangyu Chen. 2017. "Effect of Injection Site on Fault Activation and Seismicity during Hydraulic Fracturing" Energies 10, no. 10: 1619. https://doi.org/10.3390/en10101619
APA StyleChong, Z., Li, X., & Chen, X. (2017). Effect of Injection Site on Fault Activation and Seismicity during Hydraulic Fracturing. Energies, 10(10), 1619. https://doi.org/10.3390/en10101619