A New Technique for Reducing Size of a WPT System Using Two-Loop Strongly-Resonant Inductors
Abstract
:1. Introduction
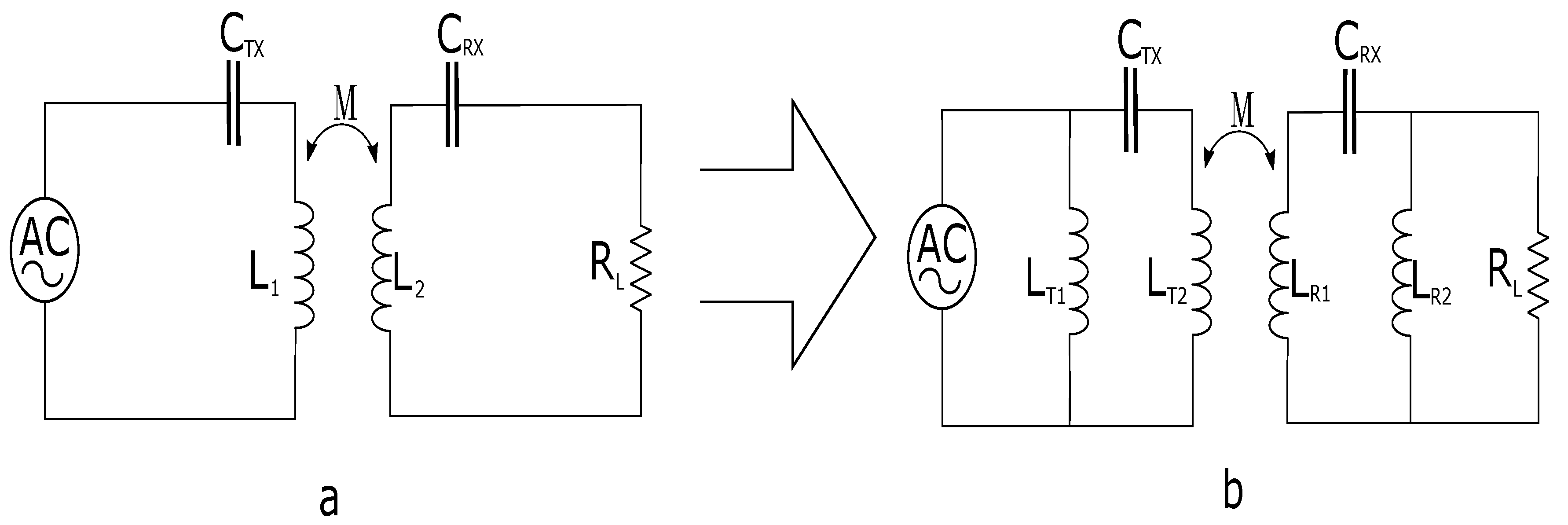
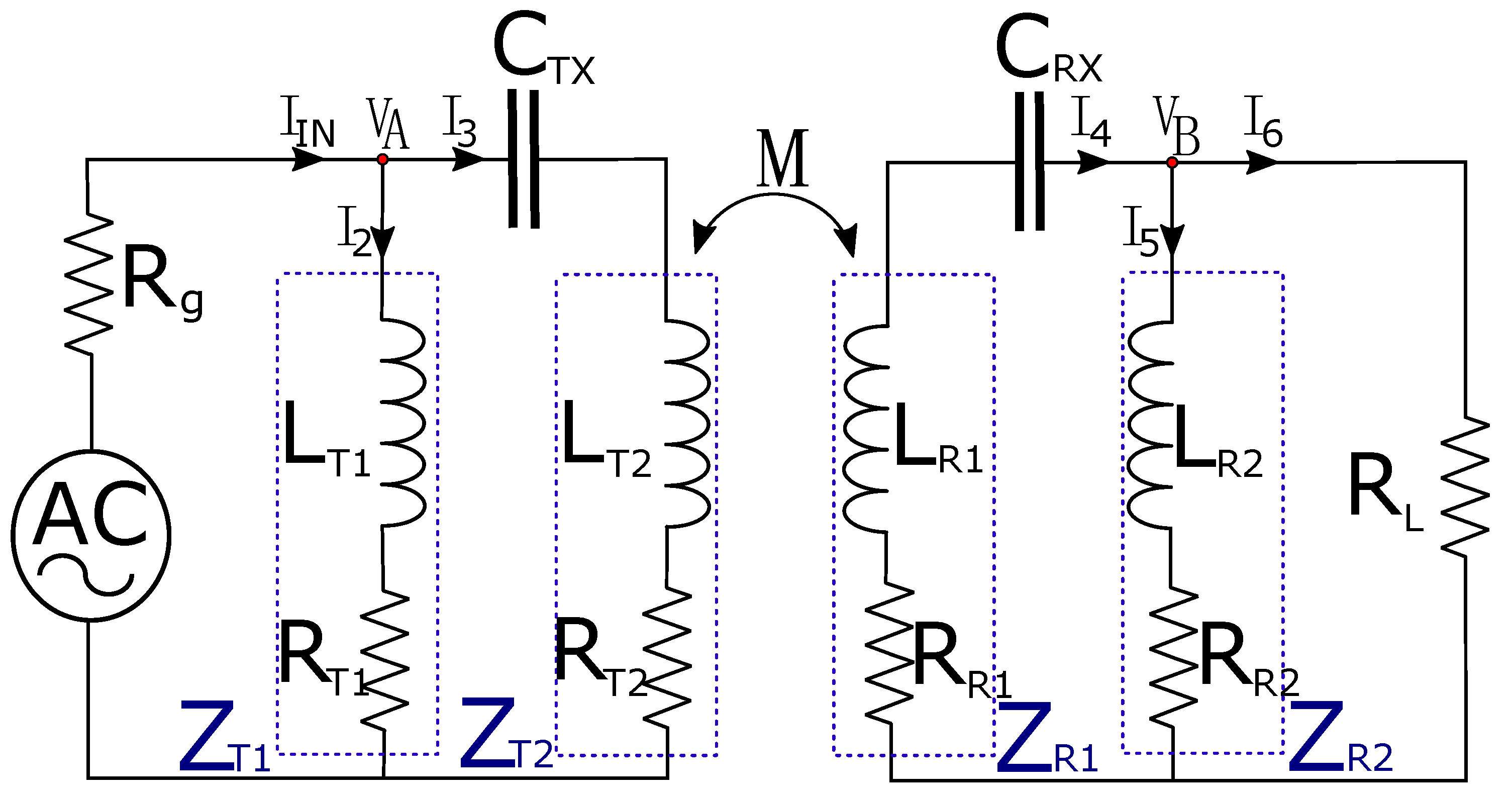
2. Theoretical Analysis of Strongly-Coupled WPT Systems
3. Numerical Analysis
3.1. High Q Coil System Specifications
3.2. Low Q Coil System Specifications without Additional Inductor
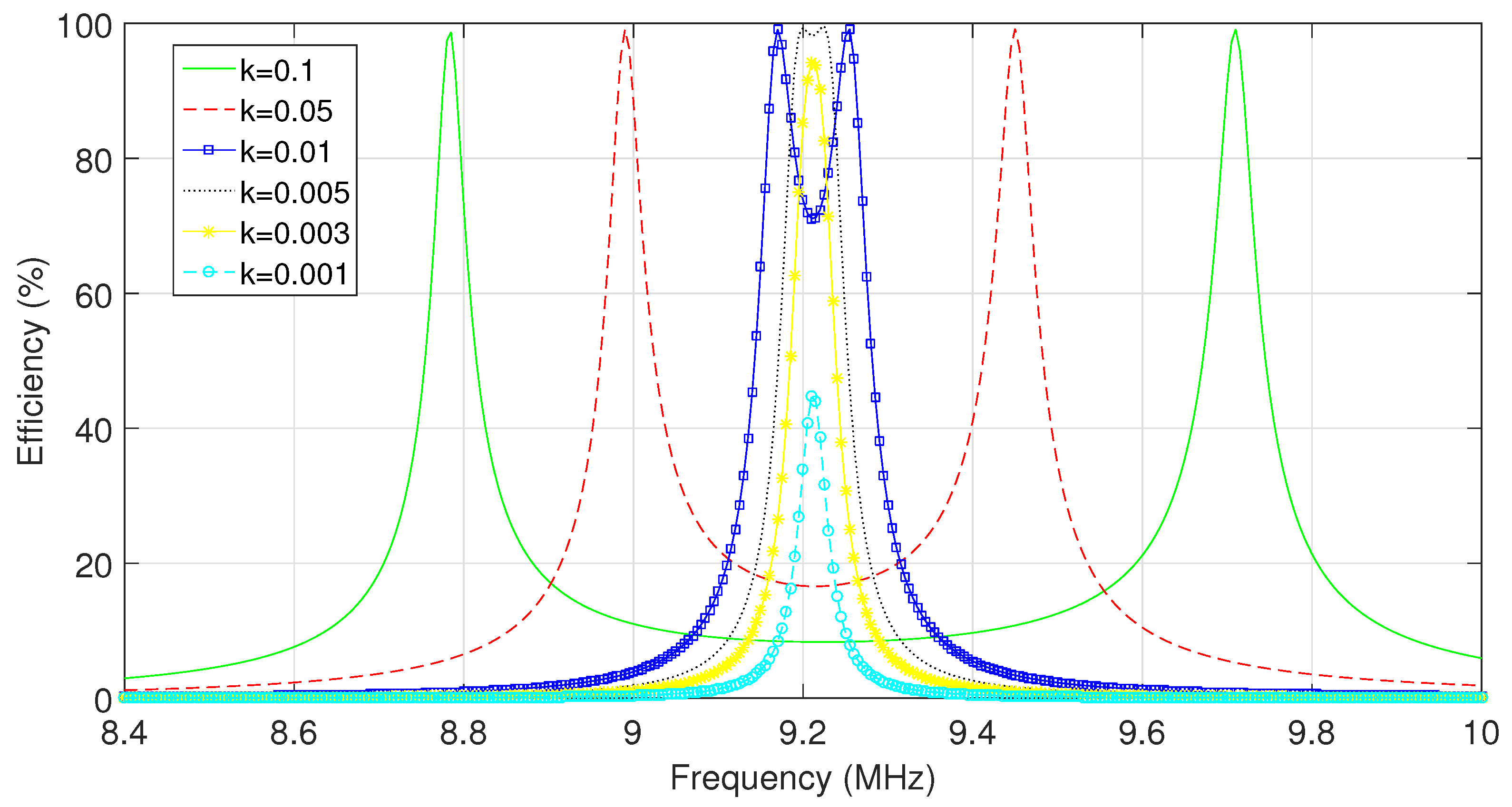
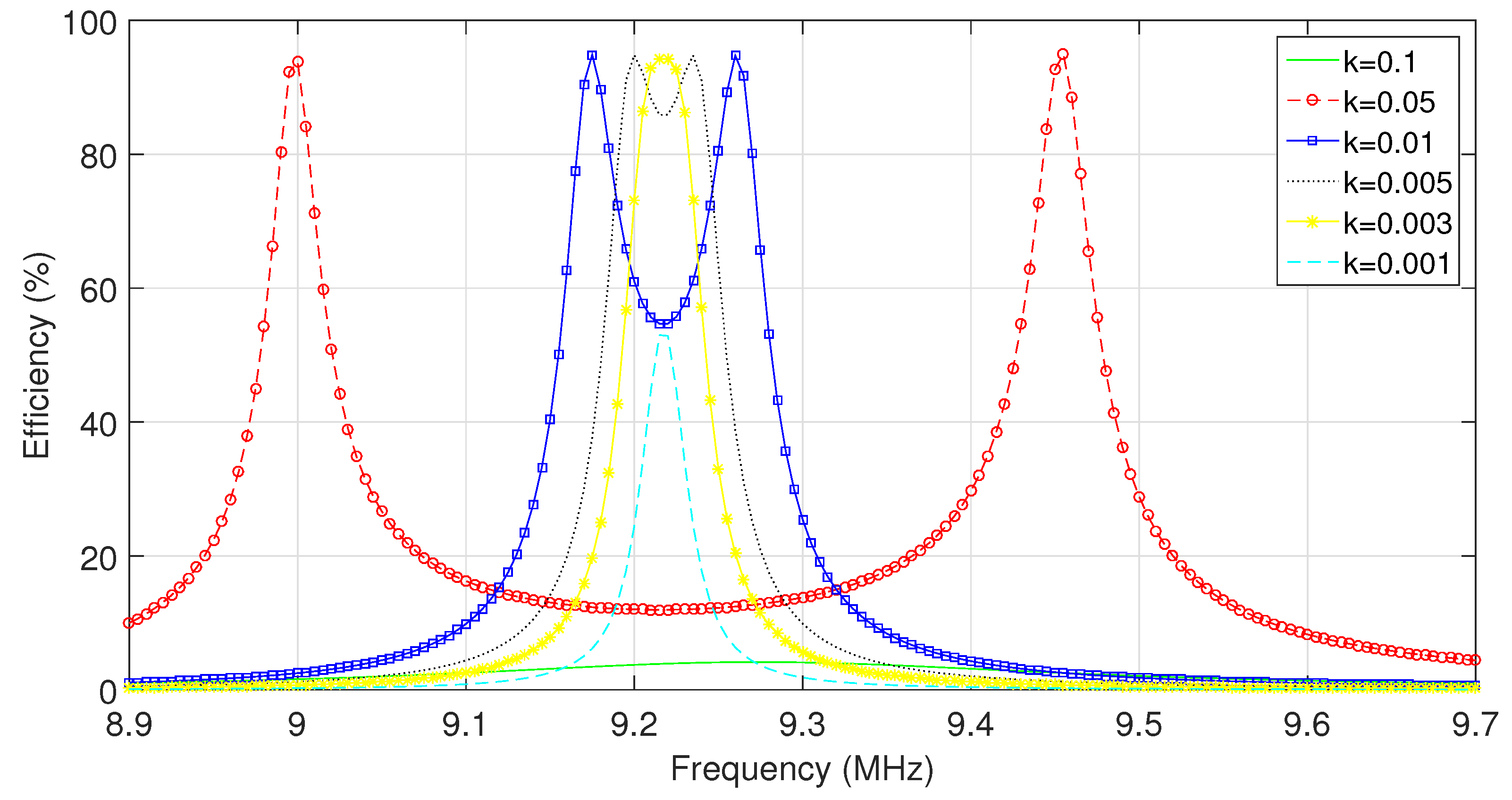
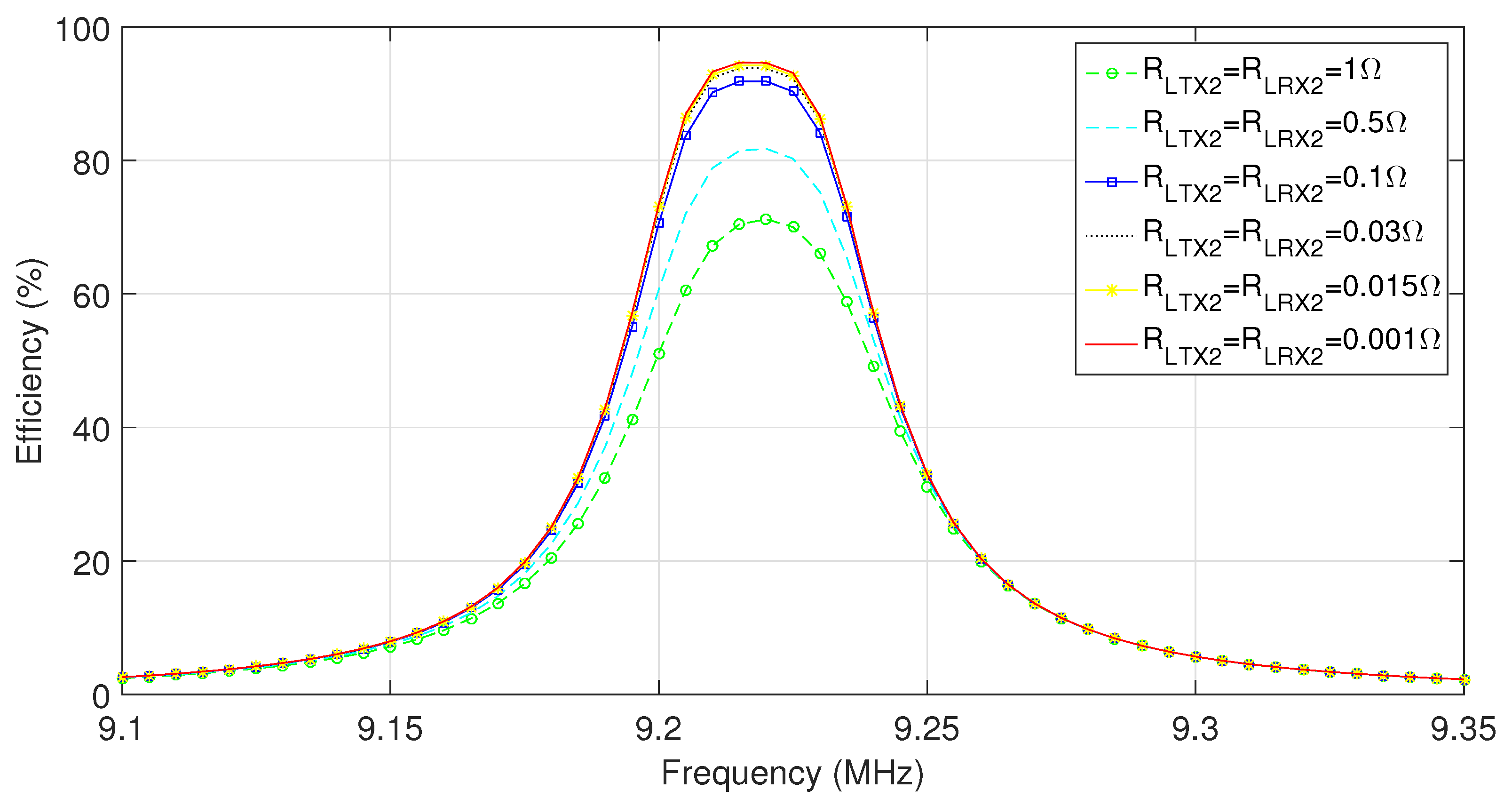
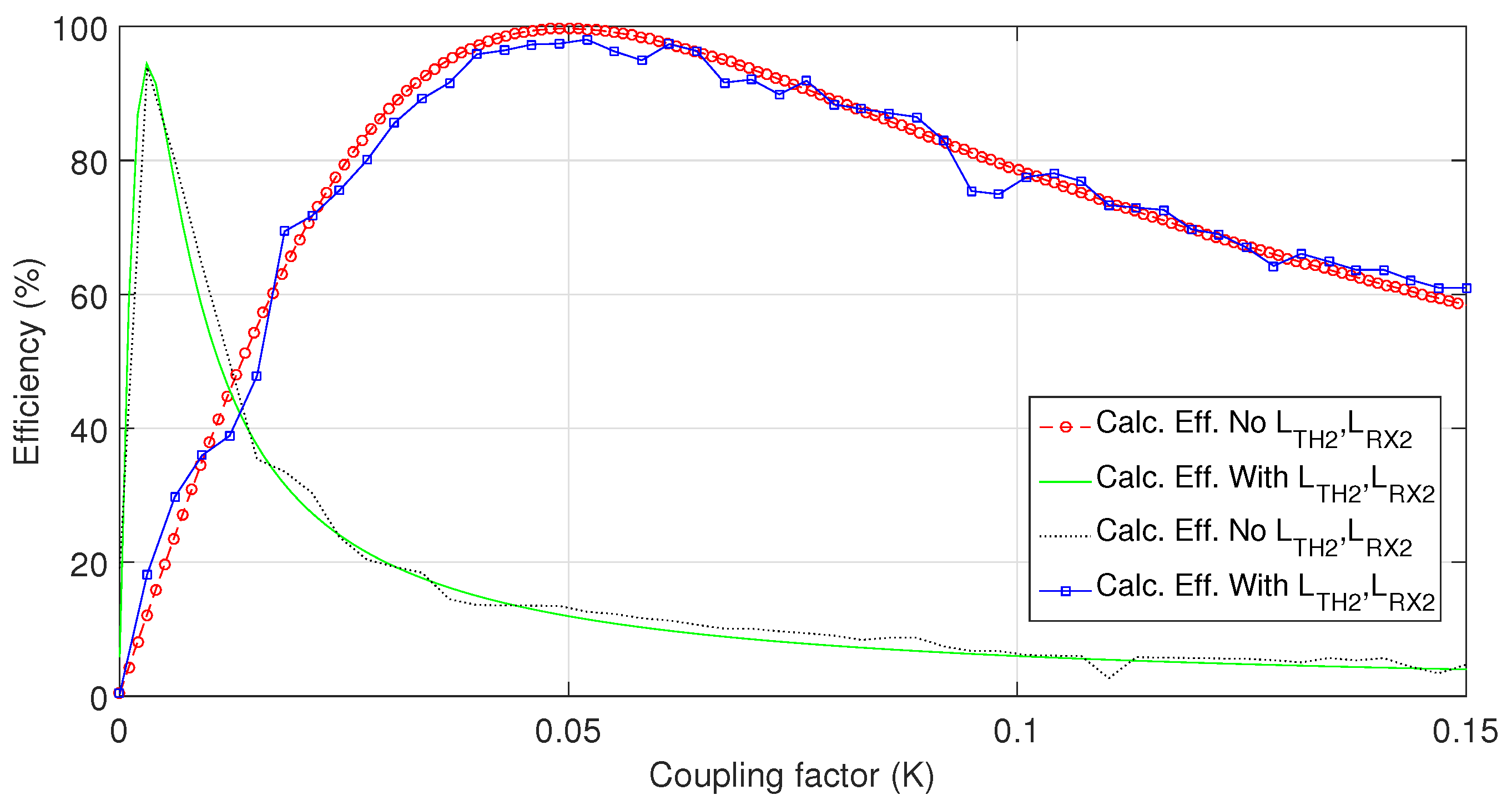
3.3. Effect of the Additional Coil Resistance on the System Efficiency
4. Experimental Setup
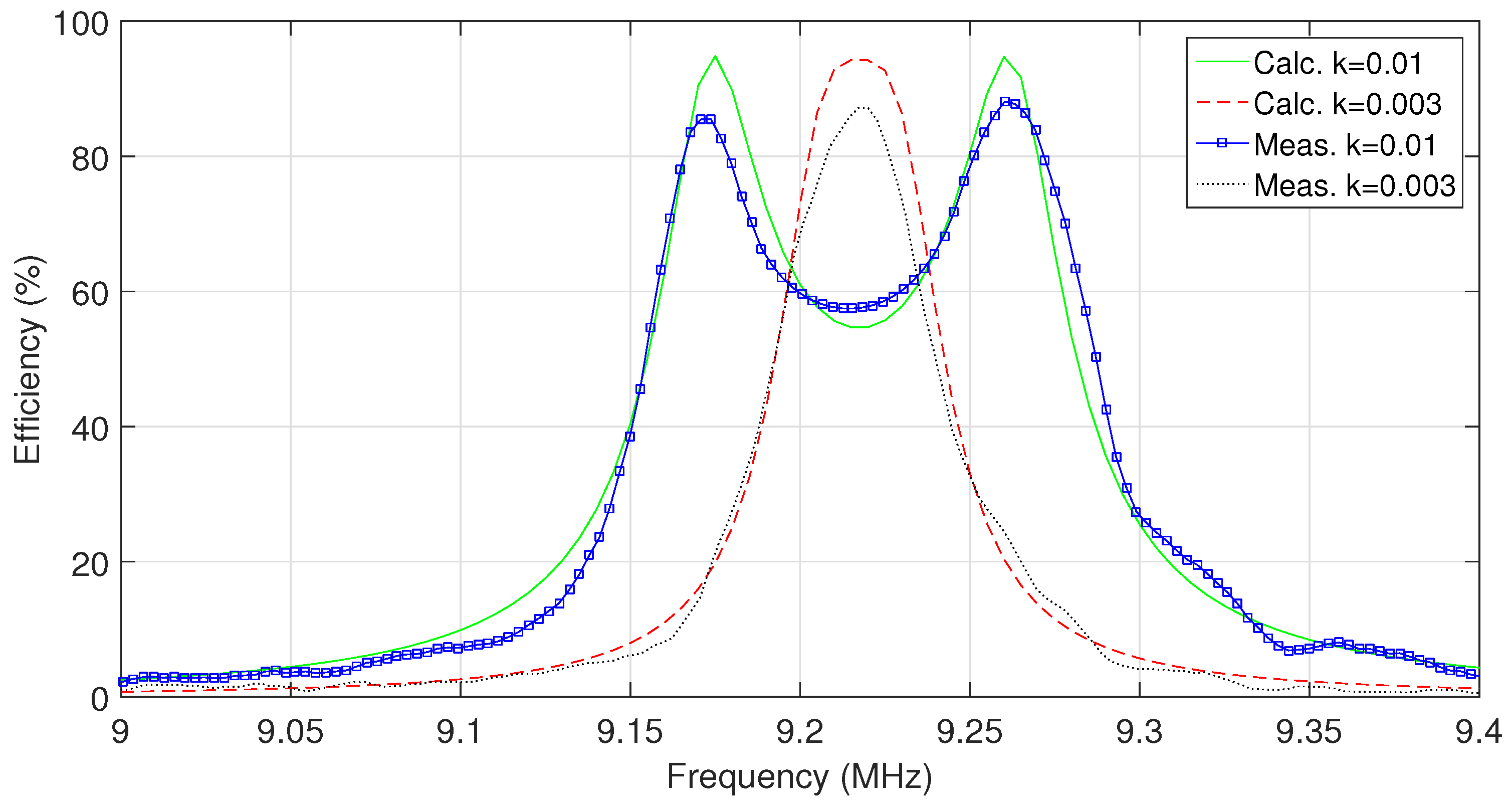
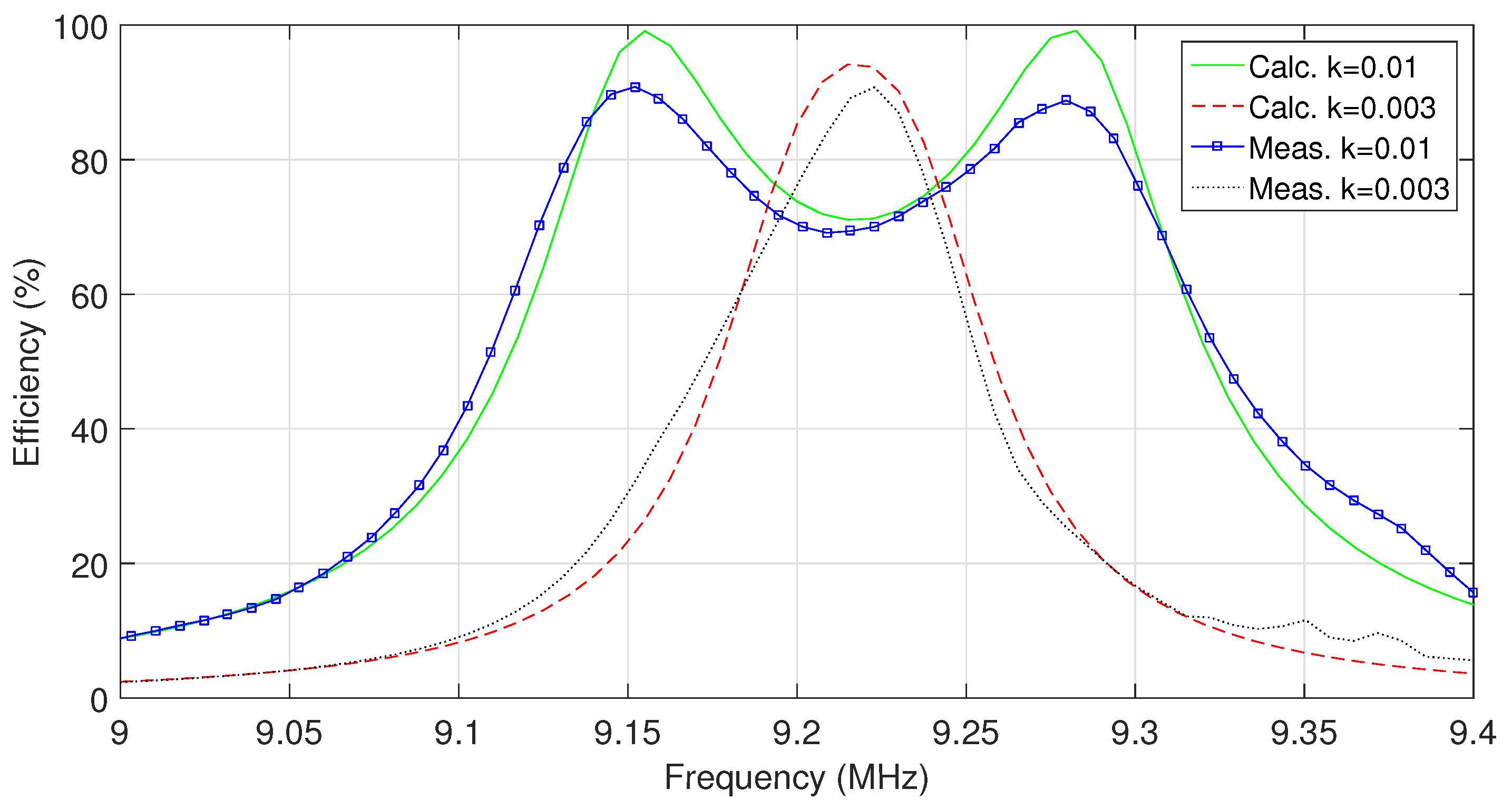
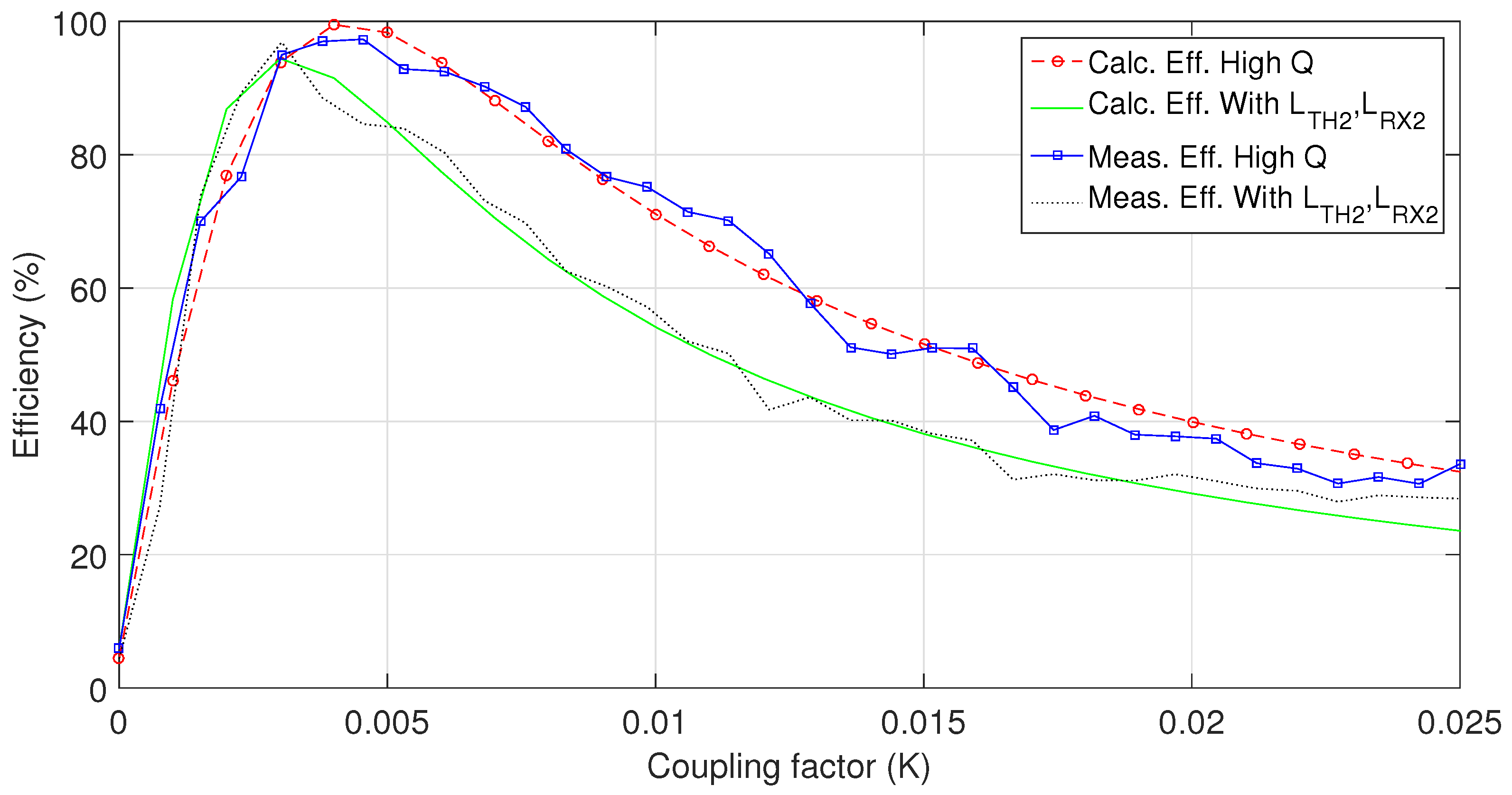
4.1. System Design and Measurements
4.2. System Maximum Efficiency
5. Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rabie, K.M.; Adebisi, B.; Rozman, M. Outage probability analysis of WPT systems with multiple-antenna access point. In Proceedings of the 2016 10th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Prague, Czech Republic, 20–22 July 2016; pp. 1–5. [Google Scholar]
- Rabie, K.M.; Adebisi, B.; Alouini, M.S. Wireless power transfer in cooperative DF relaying networks with log-normal fading. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Lin, J.C. Wireless power transfer for mobile applications, and health effects [telecommunications health and safety]. IEEE Antennas Propag. Mag. 2013, 55, 250–253. [Google Scholar] [CrossRef]
- Dickinson, R.M. Power in the sky: Requirements for microwave wireless power beamers for powering high-altitude platforms. IEEE Microw. Mag. 2013, 14, 36–47. [Google Scholar] [CrossRef]
- Raible, D.E.; Dinca, D.; Nayfeh, T.H. Optical frequency optimization of a high intensity laser power beaming system utilizing VMJ photovoltaic cells. In Proceedings of the 2011 International Conference on Space Optical Systems and Applications (ICSOS), Santa Monica, CA, USA, 11–13 May 2011; pp. 232–238. [Google Scholar]
- Lu, Y.; Ma, D.B. Wireless power transfer system architectures for portable or implantable applications. Energies 2016, 9, 1087. [Google Scholar] [CrossRef]
- Kim, S.; Ho, J.S.; Chen, L.Y.; Poon, A.S. Wireless power transfer to a cardiac implant. Appl. Phys. Lett. 2012, 101, 073701. [Google Scholar] [CrossRef]
- Kilinc, E.G.; Conus, G.; Weber, C.; Kawkabani, B.; Maloberti, F.; Dehollain, C. A system for wireless power transfer of micro-systems in-vivo implantable in freely moving animals. IEEE Sens. J. 2014, 14, 522–531. [Google Scholar] [CrossRef]
- Cook, N.P.; Sieber, L.; Widmer, H. Short Range Efficient Wireless Power Transfer. U.S. Patent 12,427,318, 21 April 2009. [Google Scholar]
- Xie, L.; Shi, Y.; Hou, Y.T.; Lou, A. Wireless power transfer and applications to sensor networks. IEEE Wirel. Commun. 2013, 20, 140–145. [Google Scholar]
- Jawad, A.M.; Nordin, R.; Gharghan, S.K.; Jawad, H.M.; Ismail, M. Opportunities and challenges for near-field wireless power transfer: A review. Energies 2017, 10, 1022. [Google Scholar] [CrossRef]
- Costanzo, A.; Dionigi, M.; Mastri, F.; Mongiardo, M.; Monti, G.; Russer, J.A.; Russer, P.; Tarricone, L. Conditions for a load-independent operating regime in resonant inductive WPT. IEEE Trans. Microw. Theory Tech. 2017, 65, 1066–1076. [Google Scholar] [CrossRef]
- Fotopoulou, K.; Flynn, B.W. Wireless power transfer in loosely coupled links: Coil misalignment model. IEEE Trans. Magn. 2011, 47, 416–430. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Cheng, Y.; Li, X.; Xing, G. QiLoc: A Qi wireless charging based system for robust user-initiated indoor location services. In Proceedings of the 2015 12th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), Seattle, WA, USA, 22–25 June 2015; pp. 480–488. [Google Scholar]
- Liu, X. Qi standard wireless power transfer technology development toward spatial freedom. IEEE Circuits Syst. Mag. 2015, 15, 32–39. [Google Scholar] [CrossRef]
- Van Wageningen, D.; Staring, T. The Qi wireless power standard. In Proceedings of the 14th International Power Electronics and Motion Control Conference EPE-PEMC 2010, Ohrid, Macedonia, 6–8 September 2010; pp. S15-25–S15-32. [Google Scholar]
- Kim, J.; Son, H.C.; Kim, D.H.; Park, Y.J. Optimal design of a wireless power transfer system with multiple self-resonators for an LED TV. IEEE Trans. Consum. Electron. 2012, 58. [Google Scholar] [CrossRef]
- Geng, Y.; Li, B.; Yang, Z.; Lin, F.; Sun, H. A high efficiency charging strategy for a supercapacitor using a wireless power transfer system based on inductor/capacitor/capacitor (LCC) compensation topology. Energies 2017, 10, 135. [Google Scholar] [CrossRef]
- Haldi, R.; Schenk, K.; Nam, I.; Santi, E. Finite-element-simulation-assisted optimized design of an asymmetrical high-power inductive coupler with a large air gap for EV charging. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 3635–3642. [Google Scholar]
- Wen, F.; Huang, X. Optimal magnetic field shielding method by metallic sheets in wireless power transfer system. Energies 2016, 9, 733. [Google Scholar] [CrossRef]
- RamRakhyani, A.K.; Mirabbasi, S.; Chiao, M. Design and optimization of resonance-based efficient wireless power delivery systems for biomedical implants. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 48–63. [Google Scholar] [CrossRef] [PubMed]
- Rozman, M.; Fernando, M.; Adebisi, B.; Rabie, K.M.; Kharel, R.; Ikpehai, A.; Gacanin, H. Combined conformal strongly-coupled magnetic resonance for efficient wireless power transfer. Energies 2017, 10, 498. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljačić, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Somani, S.; Shaqfeh, E.S.; Prakash, J.R. Effect of solvent quality on the coil- stretch transition. Macromolecules 2010, 43, 10679–10691. [Google Scholar] [CrossRef]
- Junaid, A.B.; Konoiko, A.; Zweiri, Y.; Sahinkaya, M.N.; Seneviratne, L. Autonomous wireless self-charging for multi-rotor unmanned aerial vehicles. Energies 2017, 10, 803. [Google Scholar] [CrossRef]
- Dai, Z.; Wang, J.; Long, M.; Huang, H. A witricity-based high-power device for wireless charging of electric vehicles. Energies 2017, 10, 323. [Google Scholar] [CrossRef]
- Hwang, K.; Cho, J.; Kim, D.; Park, J.; Kwon, J.H.; Kwak, S.I.; Park, H.H.; Ahn, S. An autonomous coil alignment system for the dynamic wireless charging of electric vehicles to minimize lateral misalignment. Energies 2017, 10, 315. [Google Scholar] [CrossRef]
- Jiang, C.; Chau, K.T.; Liu, C.; Lee, C.H.T. An overview of resonant circuits for wireless power transfer. Energies 2017, 10, 894. [Google Scholar] [CrossRef]
- Liu, D.; Hu, H.; Georgakopoulos, S.V. Misalignment sensitivity of strongly coupled wireless power transfer systems. IEEE Trans. Power Electron. 2017, 32, 5509–5519. [Google Scholar] [CrossRef]
- Sample, A.P.; Meyer, D.T.; Smith, J.R. Analysis, experimental results, and range adaptation of magnetically coupled resonators for wireless power transfer. IEEE Trans. Ind. Electron. 2011, 58, 544–554. [Google Scholar] [CrossRef]
- Vijayakumaran Nair, V.; Choi, J.R. An efficiency enhancement technique for a wireless power transmission system based on a multiple coil switching technique. Energies 2016, 9, 156. [Google Scholar] [CrossRef]
- Kiani, M.; Jow, U.M.; Ghovanloo, M. Design and optimization of a 3-coil inductive link for efficient wireless power transmission. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 579–591. [Google Scholar] [CrossRef] [PubMed]
- Jow, U.M.; Ghovanloo, M. Design and optimization of printed spiral coils for efficient transcutaneous inductive power transmission. IEEE Trans. Biomed. Circuits Syst. 2007, 1, 193–202. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Kang, S.; Kim, Y.; Jung, C. Small-sized metallic and transparent film resonators for MR-WPT system. Electron. Lett. 2016, 52, 650–652. [Google Scholar] [CrossRef]
- Hu, H.; Liu, D.; Georgakopoulos, S.V. Miniaturized strongly coupled magnetic resonant systems for wireless power transfer. In Proceedings of the 2016 IEEE International Symposium on Antennas and Propagation (APSURSI), Fajardo, Puerto Rico, 26 June–1 July 2016; pp. 155–156. [Google Scholar]
- Nguyen, V.T.; Kang, S.H.; Jung, C.W. Wireless power transfer for mobile devices with consideration of ground effect. In Proceedings of the 2015 IEEE Wireless Power Transfer Conference (WPTC), Boulder, CO, USA, 13–15 May 2015; pp. 1–4. [Google Scholar]
- Fujita, T.; Yasuda, T.; Akagi, H. A wireless power transfer system with a double-current rectifier for EVs. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–7. [Google Scholar]
- Mahdavifard, M.; Poorfakhraei, A.; Tahami, F. A novel method for reduction of coil weight and size in wireless power transfer. In Proceedings of the 2017 8th Power Electronics, Drive Systems Technologies Conference (PEDSTC), Mashhad, Iran, 14–16 February 2017; pp. 395–400. [Google Scholar]
- Theilmann, P.T.; Asbeck, P.M. An analytical model for inductively coupled implantable biomedical devices with ferrite rods. IEEE Trans. Biomed. Circuits Syst. 2009, 3, 43–52. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Georgakopoulos, S.V. Analysis and design of conformal SCMR WPT systems with multiple resonators. In Proceedings of the 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI), Memphis, TN, USA, 6–11 July 2014; pp. 1347–1348. [Google Scholar]
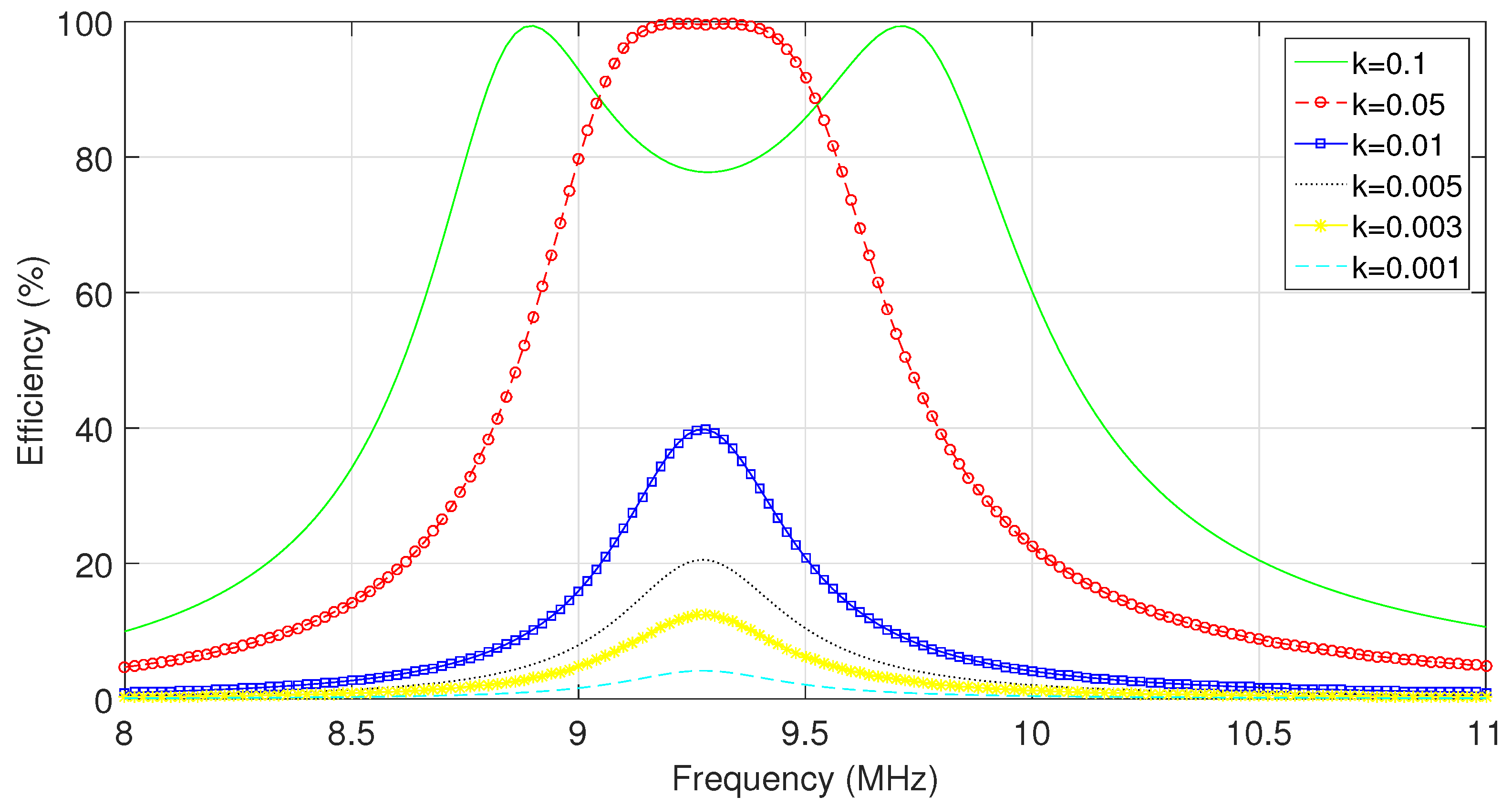
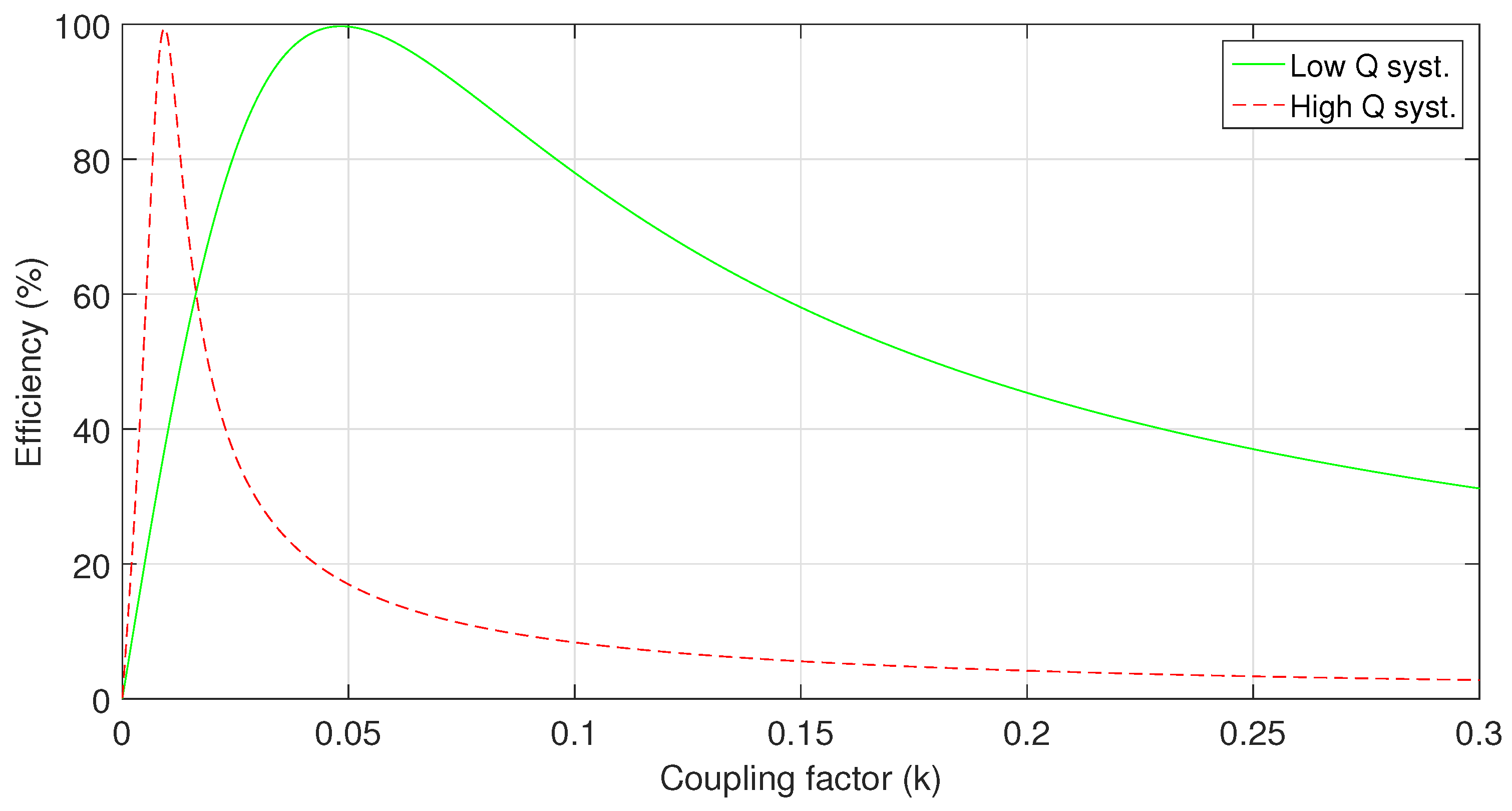
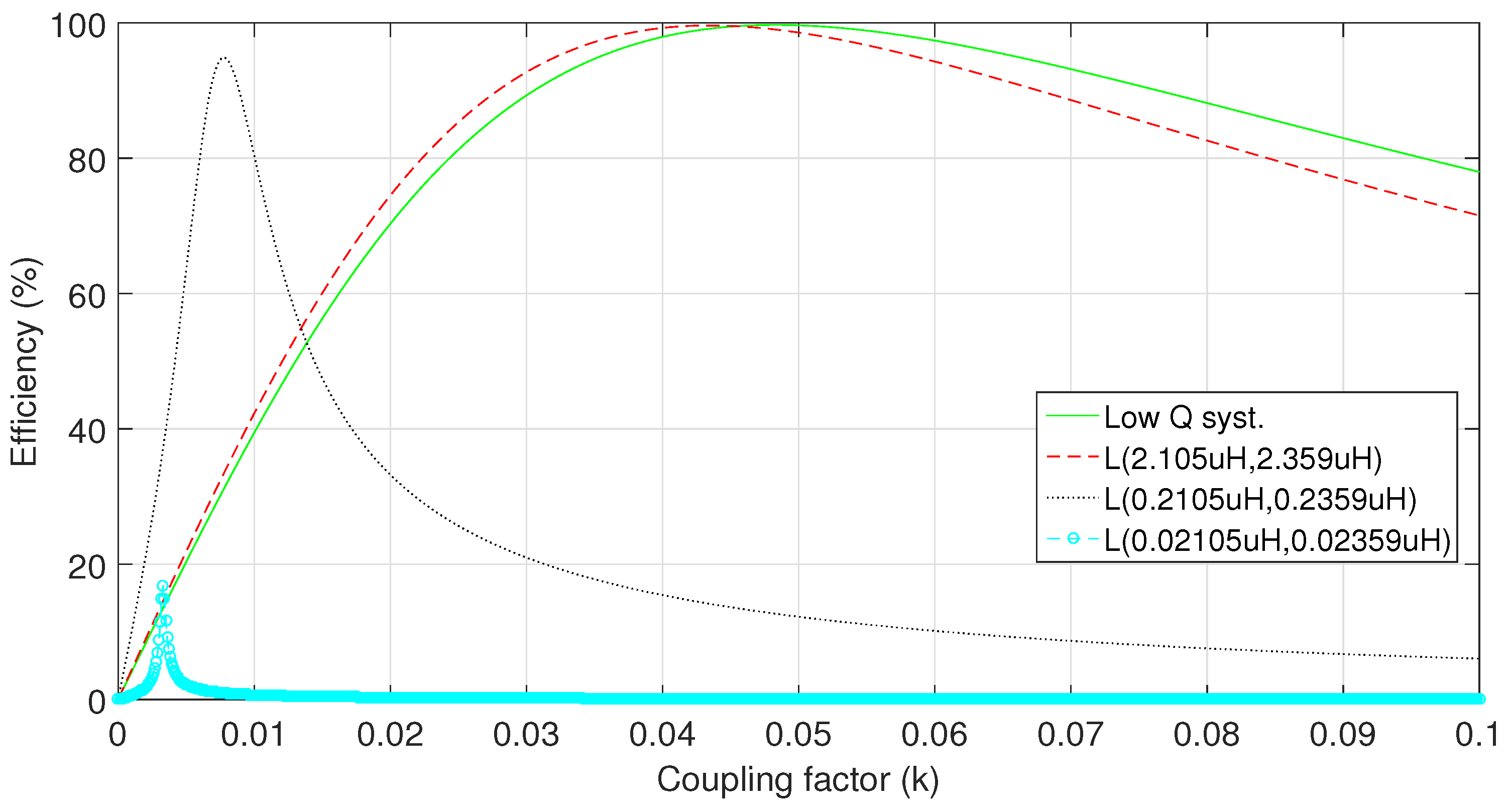
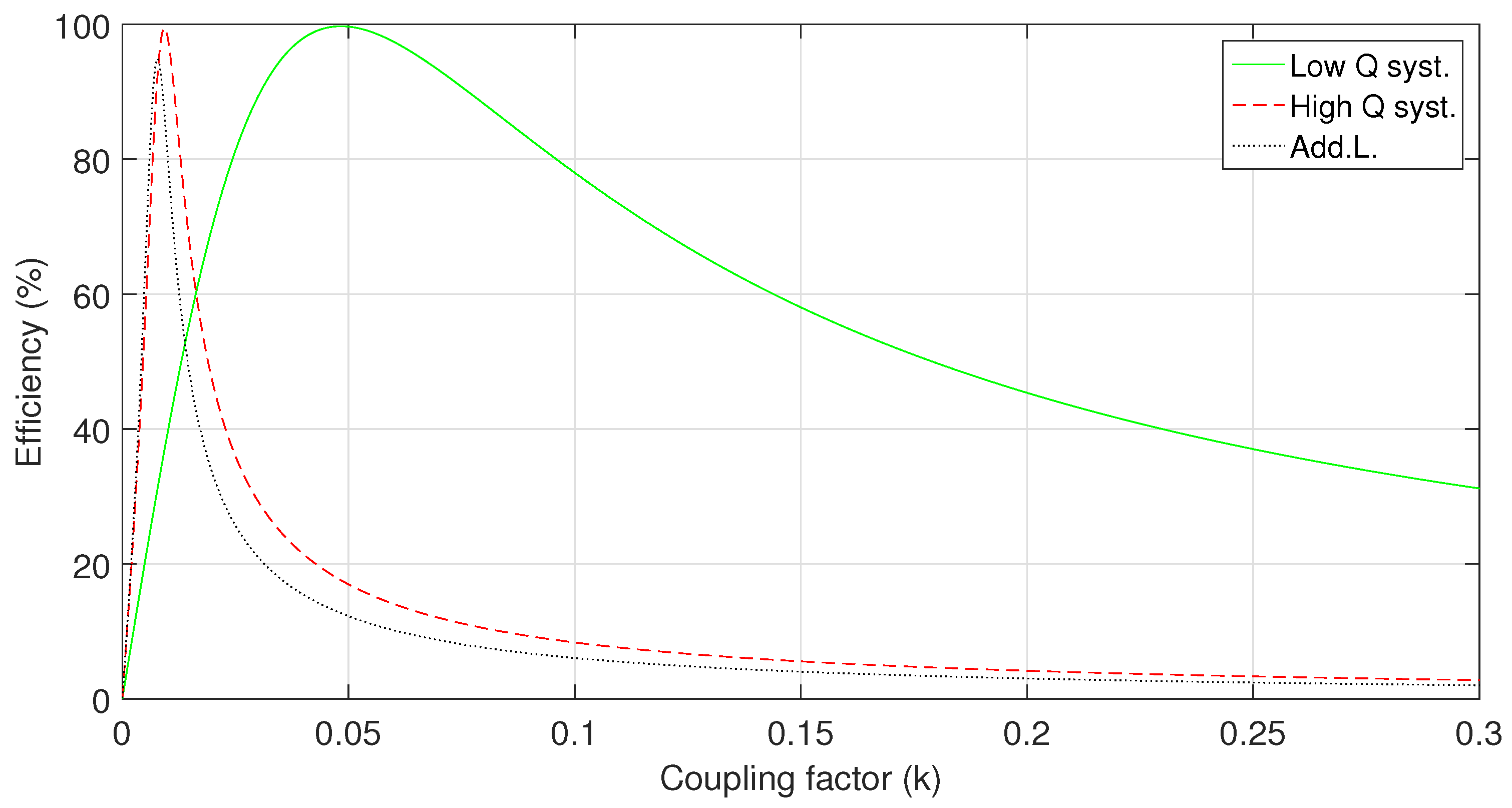

| 0.48 | 0.48 |
| (a) b | (b) b |
| Capacitance | Inductance | Resistance | Resistance |
|---|---|---|---|
| = 1.6 pF | = 186.6 H | = 0.15Ω | = 50Ω |
| = 1.3 pF | = 229.6 H | = 0.15Ω | = 50Ω |
| Capacitance | Inductance | Resistance | Resistance |
|---|---|---|---|
| = 18 pF | = 16.37 H | = 0.15Ω | = 50Ω |
| = 15 pF | = 19.65 H | = 0.15Ω | = 50Ω |
| Capacitance | Inductance | Resistance | Resistance |
|---|---|---|---|
| = 18 pF | = 16.37 H | = 0.15Ω | = 50Ω |
| = 15 pF | = 0.2105 H | = 0.15Ω | = 50Ω |
| = 19.65 H | = 0.15Ω | ||
| = 0.2359 H | = 0.15Ω |
| Conv. | Mod. | Diff. % | Conv. | Mod. | Diff. % | |
|---|---|---|---|---|---|---|
| Length | 15 mm | 3 mm | 80% | 20 mm | 4 mm | 80% |
| Weight | 7.37 g | 1.58 g | 78.6% | 8.63 g | 1.78 g | 79.4% |
| Turns | 41 | 8 | 80.5% | 48 | 48 | 81% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rozman, M.; Fernando, M.; Adebisi, B.; Rabie, K.M.; Collins, T.; Kharel, R.; Ikpehai, A. A New Technique for Reducing Size of a WPT System Using Two-Loop Strongly-Resonant Inductors. Energies 2017, 10, 1614. https://doi.org/10.3390/en10101614
Rozman M, Fernando M, Adebisi B, Rabie KM, Collins T, Kharel R, Ikpehai A. A New Technique for Reducing Size of a WPT System Using Two-Loop Strongly-Resonant Inductors. Energies. 2017; 10(10):1614. https://doi.org/10.3390/en10101614
Chicago/Turabian StyleRozman, Matjaz, Michael Fernando, Bamidele Adebisi, Khaled M. Rabie, Tim Collins, Rupak Kharel, and Augustine Ikpehai. 2017. "A New Technique for Reducing Size of a WPT System Using Two-Loop Strongly-Resonant Inductors" Energies 10, no. 10: 1614. https://doi.org/10.3390/en10101614
APA StyleRozman, M., Fernando, M., Adebisi, B., Rabie, K. M., Collins, T., Kharel, R., & Ikpehai, A. (2017). A New Technique for Reducing Size of a WPT System Using Two-Loop Strongly-Resonant Inductors. Energies, 10(10), 1614. https://doi.org/10.3390/en10101614








