Estimating the Value of Price Risk Reduction in Energy Efficiency Investments in Buildings
Abstract
:1. Introduction
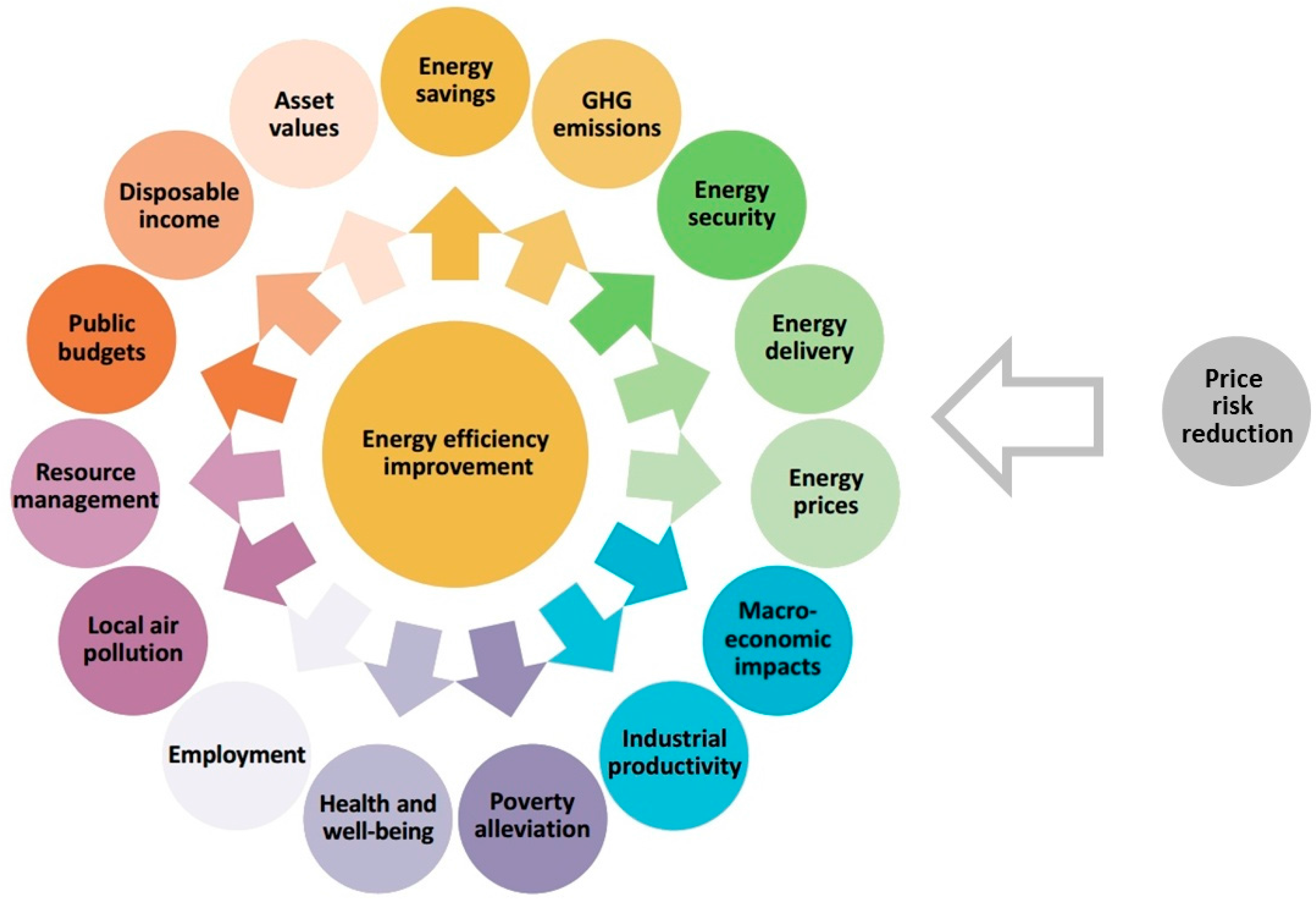
1.1. Rationale for Price Risk Reduction
1.2. Review of Price Risk Valuation Methods
2. Methods
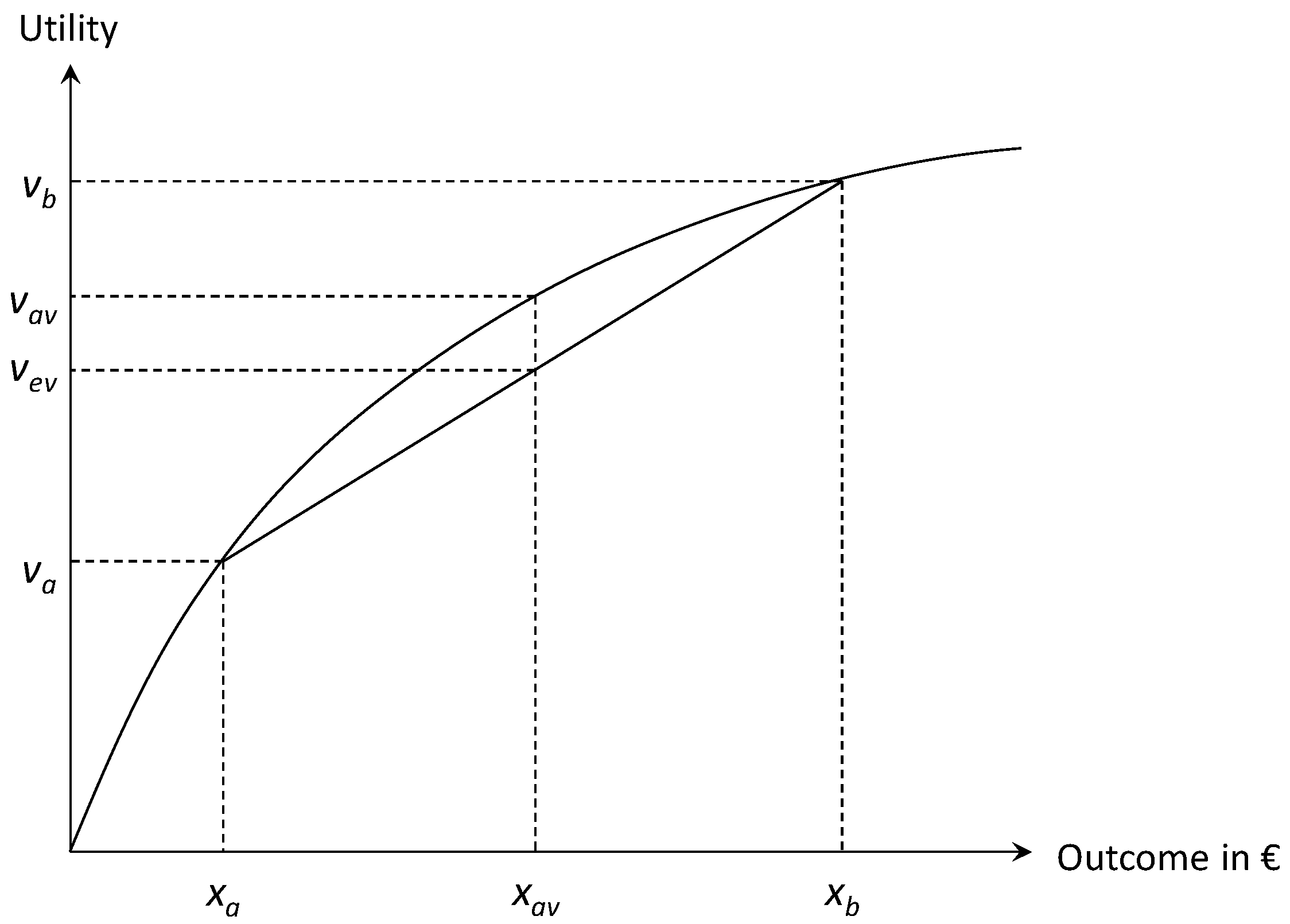
2.1. Calculating the Value of Price Risk Reduction
2.2. Electricity Price
2.3. Case Buildings and Energy Consumption
- Business as usual (BAU), with direct electric radiators as the only source of heat;
- BAU + fireplace, with a fireplace supplementing the radiators;
- BAU + heat pump, with an air source heat pump supplementing the radiators; and
- BAU + solar collectors, with roof-mounted solar heat collectors supplementing the radiators.
3. Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Al-Sunaidy, A.; Green, R. Electricity deregulation in OECD countries. Energy 2006, 31, 769–787. [Google Scholar] [CrossRef]
- Kokkonen, A. Sähkölämmityksen Tehostamisohjelma Elvari Loppuraportti; Motiva: Helsinki, Finland, 2015. [Google Scholar]
- Laustsen, J. Energy Efficiency Requirements in Building Codes, Energy Efficiency Policies for New Buildings; International Energy Agency: Paris, France, 2008. [Google Scholar]
- Gillingham, K.; Newell, R.G.; Palmer, K. Energy Efficiency Economics and Policy. Annu. Rev. Resour. Econ. 2009, 1, 597–620. [Google Scholar] [CrossRef]
- Brown, M. Obstacles to Energy Efficiency. In Encyclopedia of Energy; Cleveland, C., Ed.; Elsevier: San Diego, CA, USA, 2004; pp. 465–475. [Google Scholar]
- Klemick, H.; Wolverton, A. Energy-efficiency gap. In Encyclopedia of Energy; Cleveland, C., Ed.; Elsevier: San Diego, CA, USA, 2004. [Google Scholar]
- Abadie, L.M.; Chamorro, J.M.; González-Eguino, M. Valuing uncertain cash flows from investments that enhance energy efficiency. J. Environ. Manag. 2013, 116, 113–124. [Google Scholar] [CrossRef] [PubMed]
- Jackson, J. Promoting energy efficiency investments with risk management decision tools. Energy Policy 2010, 38, 3865–3873. [Google Scholar] [CrossRef]
- Tuominen, P.; Reda, F.; Dawoud, W.; Elboshy, B.; Elshafei, G.; Negm, A. Economic appraisal of energy efficiency in buildings using cost-effectiveness assessment. Proced. Econ. Financ. 2015, 21, 422–430. [Google Scholar] [CrossRef]
- Vine, E.; Mills, E.; Chen, A. Energy-efficiency and renewable energy options for risk management and insurance loss reduction. Energy 2000, 25, 131–147. [Google Scholar] [CrossRef]
- Thompson, P. Evaluating energy efficiency investments: Accounting for risk in the discounting process. Energy Policy 1997, 25, 989–996. [Google Scholar] [CrossRef]
- Weinsziehr, T.; Skumatz, L. Evidence for Multiple Benefits or NEBs: Review on Progress and Gaps from the IEA Data and Measurement Subcommittee. In Proceedings of the International Energy Policy & Programme Evaluation Conference, Amsterdam, The Netherlands, 7–9 June 2016. [Google Scholar]
- Ürge-Vorsatz, D.; Novikova, A.; Sharmina, M. Counting good: Quantifying the co-benefits of improved efficiency in buildings. In Proceedings of the ECEEE 2009 Summer Study, Stockholm, Sweden, 1–6 June 2009. [Google Scholar]
- International Energy Agency. Capturing the Multiple Benefits of Energy Efficiency; International Energy Agency: Paris, France, 2014. [Google Scholar]
- U.S. Environmental Protection Agency. Assessing the Multiple Benefits of Clean Energy; U.S. Environmental Protection Agency: Washington, DC, USA, 2011.
- Tuominen, P.; Holopainen, R.; Eskola, L.; Jokisalo, J.; Airaksinen, M. Calculation method and tool for assessing energy consumption in the building stock. Build. Environ. 2014, 75, 153–160. [Google Scholar] [CrossRef]
- Conchar, M.; Zinkhan, G.; Peters, C.; Olavarrieta, S. An Integrated Framework for the Conceptualization of Consumers’ Perceived Risk. J. Acad. Mark. Sci. 2004, 32, 418–436. [Google Scholar] [CrossRef]
- Electricity Authority. Managing Electricity Price Risk; Electricity Authority: Wellington, New Zeeland, 2012. [Google Scholar]
- Mas-Colell, A.; Whinston, M.; Green, J. Microeconomic Theory; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Black, J.; Hashimzade, N.; Myles, G. A Dictionary of Economics; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Bank for International Settlements. A Glossary of Terms Used in Payments and Settlement Systems; Bank for International Settlements: Basel, Switzerland, 2003. [Google Scholar]
- James, T. Energy Markets: Price Risk Management and Trading; John Wiley & Sons: Singapore, 2012. [Google Scholar]
- Profeta, C.; Roynette, B.; Yor, M. Option Prices as Probabilities: A New Look at Generalized Black-Scholes Formulae; Springer: Berlin, Germany, 2010. [Google Scholar]
- Brennan, M.; Schwartz, E. Evaluating natural resource investments. J. Bus. 1985, 2, 135–157. [Google Scholar] [CrossRef]
- Woo, C.-K.; Horowitz, I.; Hoang, K. Cross hedging and forward-contract pricing of electricity. Energy Econ. 2001, 23, 1–15. [Google Scholar] [CrossRef]
- Deng, S.; Oren, S. Electricity derivatives and risk management. Energy 2006, 31, 940–953. [Google Scholar] [CrossRef]
- Black, F. The pricing of commodity contracts. J. Financ. Econ. 1976, 3, 167–179. [Google Scholar] [CrossRef]
- Zvi, B.; Kane, A.; Marcus, A. Investments; McGraw-Hill/Irwin: New York, NY, USA, 2008. [Google Scholar]
- Statistics Finland. Energian hinnat. Available online: http://stat.fi/til/ehi/tau.html (accessed on 20 September 2017).
- Eydeland, A.; Wolyniec, K. Energy and Power Risk Management: New Developments in Modelling, Pricing and Hedging; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Nord Pool. Elspot Prices. Available online: http://www.nordpoolspot.com/Market-data1/Elspot/Area-Prices/ (accessed on 1 April 2014).
- Energy Authority. Sähkön hintatilastot. Available online: http://www.energiavirasto.fi/sahkon-hintatilastot (accessed on 12 May 2014).
- Energiapolar. Polar Spot Hinnat ja Ehdot. Available online: https://www.energiapolar.fi/loader.aspx?id=4f88ac11-60ba-4160-8d5a-9f86a1e2a168 (accessed on 12 May 2014).
- Vilhola, J.; Heljo, J. Lämmitystapojen kehitys 2002–2012; Tampere University of Technology: Tampere, Finland, 2012. [Google Scholar]
- Tiihonen, A. Asumisväljyys Lisääntyy Hitaasti; Statistics Finland: Helsinki, Finland, 2011. [Google Scholar]
- Ministry of the Environment. D3 Energy Management in Buildings, Regulations and Guidelines 2010; Ministry of the Environment: Helsinki, Finland, 2010.
- Motiva. Lämmitystapojen Vertailulaskuri. Available online: http://lammitysvertailu.eneuvonta.fi (accessed on 21 March 2014).
- Bank of Finland. Monetary Financial Institutions Annual Review 2013; Bank of Finland: Helsinki, Finland, 2014. [Google Scholar]
| Price Component | Amount (c/kWh) | Source |
|---|---|---|
| Electricity spot price | 4.34 | [31] |
| Electricity tax | 1.39 | [32] |
| Value-added tax | 0.97 | [31] |
| Power company price marginal | 0.25 | [33] |
| Transmission fee | 3.16 | [31] |
| Total consumer price | 10.11 | - |
| Indicator | BAU | BAU + Fireplace | BAU + Heat Pump | BAU + Solar |
|---|---|---|---|---|
| Investment cost (€) | 4000 | 9500 | 6000 | 10,000 |
| Electricity consumption (kWh/a) | 16,387 | 13,984 | 13,488 | 14,370 |
| Other heat sources (kWh/a) | 0 | 2403 | 2899 | 2017 |
| Cost Type | BAU | BAU + Fireplace | BAU + Heat Pump | BAU + Solar |
|---|---|---|---|---|
| Variable cost | 1655 | 1612 | 1362 | 1451 |
| Capital cost | 269 | 639 | 403 | 605 |
| Total cost | 1924 | 2251 | 1765 | 2056 |
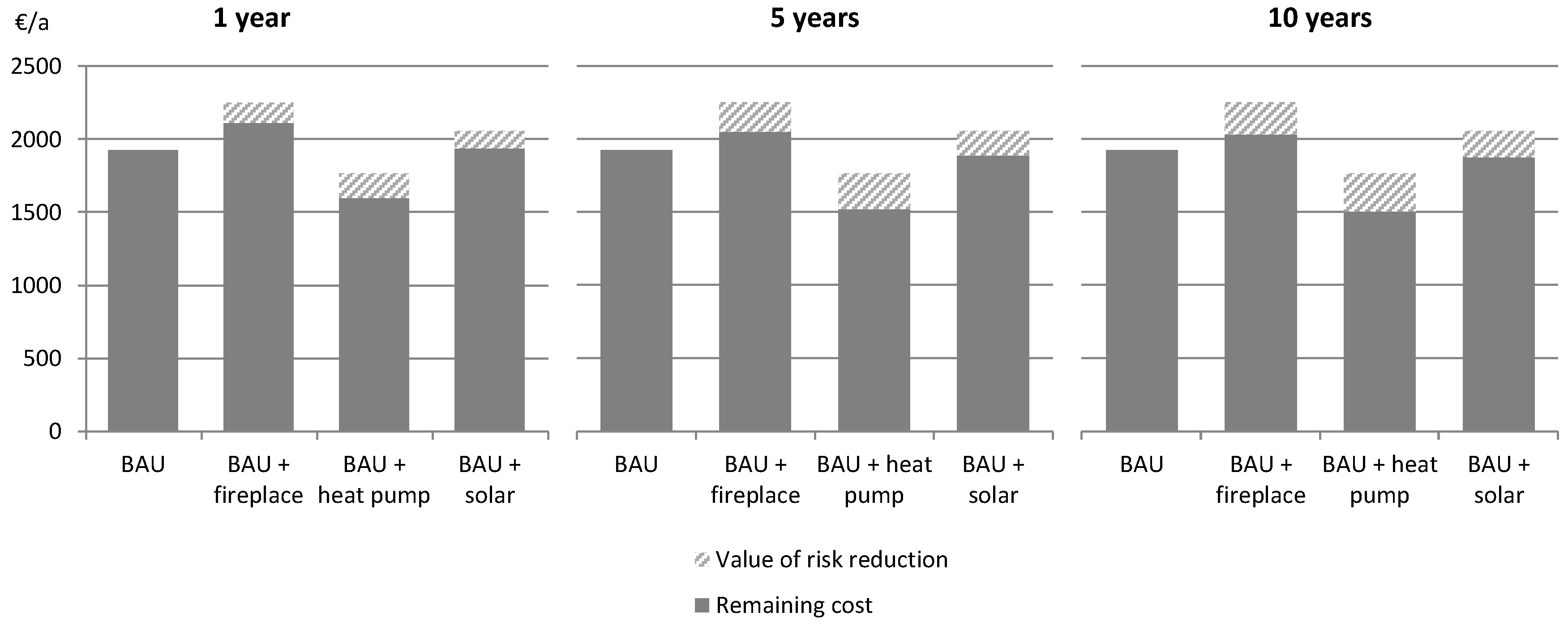
| Time Period | Type of Cost or Value | BAU | BAU + Fireplace | BAU + Heat Pump | BAU + Solar |
|---|---|---|---|---|---|
| - | Total annualized cost | 1924 | 2251 | 1765 | 2056 |
| 1 year | Value of risk reduction | 0 | −140 | −168 | −117 |
| Remaining cost | 1924 | 2111 | 1597 | 1939 | |
| Relative value | 0% | 6% | 10% | 6% | |
| 5 years | Value of risk reduction | 0 | −204 | −247 | −172 |
| Remaining cost | 1924 | 2047 | 1518 | 1884 | |
| Relative value | 0% | 9% | 14% | 8% | |
| 10 years | Value of risk reduction | 0 | −218 | −263 | −183 |
| Remaining cost | 1924 | 2033 | 1502 | 1873 | |
| Relative value | 0% | 10% | 15% | 9% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuominen, P.; Seppänen, T. Estimating the Value of Price Risk Reduction in Energy Efficiency Investments in Buildings. Energies 2017, 10, 1545. https://doi.org/10.3390/en10101545
Tuominen P, Seppänen T. Estimating the Value of Price Risk Reduction in Energy Efficiency Investments in Buildings. Energies. 2017; 10(10):1545. https://doi.org/10.3390/en10101545
Chicago/Turabian StyleTuominen, Pekka, and Tuomas Seppänen. 2017. "Estimating the Value of Price Risk Reduction in Energy Efficiency Investments in Buildings" Energies 10, no. 10: 1545. https://doi.org/10.3390/en10101545
APA StyleTuominen, P., & Seppänen, T. (2017). Estimating the Value of Price Risk Reduction in Energy Efficiency Investments in Buildings. Energies, 10(10), 1545. https://doi.org/10.3390/en10101545




