Abstract
This paper develops a path for the global energy system up to 2050, presenting a new application of the open-source energy modeling system (OSeMOSYS) to the community. It allows quite disaggregate energy and emission analysis: Global Energy System Model (GENeSYS-MOD) uses a system of linear equations of the energy system to search for lowest-cost solutions for a secure energy supply, given externally defined constraints, mainly in terms of CO2-emissions. The general algebraic modeling system (GAMS) version of OSeMOSYS is updated to the newest version and, in addition, extended and enhanced to include e.g., a modal split for transport, an improved trading system, and changes to storages. The model can be scaled from small-scale applications, e.g., a company, to cover the global energy system. The paper also includes an application of GENeSYS-MOD to analyze decarbonization scenarios at the global level, broken down into 10 regions. Its main focus is on interdependencies between traditionally segregated sectors: electricity, transportation, and heating; which are all included in the model. Model calculations suggests that in order to achieve the 1.5–2 °C target, a combination of renewable energy sources provides the lowest-cost solution, solar photovoltaic being the dominant source. Average costs of electricity generation in 2050 are about 4 €cents/kWh (excluding infrastructure and transportation costs).
1. Introduction
Energy system modeling is an important tool to inform the scientific debate and the policy discussion about different pathways available to reach certain objectives, such as environmental objectives in terms of greenhouse gas emissions. Energy system models have been around for about five decades, inspired by the combination of computer capacities and an increased interest in energy issues in the wake of the first oil crisis (1973); since then, one observes a rapid increase in the number of models and the complexity thereof (see for a survey Connolly et al. []).
In general, energy system models can be classified into two different classes of models: techno-economic, also called process-orientated or bottom-up models, and macroeconomic models []. While the former can offer a respectable amount of resolution analyzing the impact of specific technologies for their respective energy system, they lack in depicting relevant macroeconomic coherence. Techno-economic energy system models saw a rise in the early 1970s after the first oil crisis to analyze the possibilities of more efficient final energy use []. Since then, the focus shifted towards a more long-term approach to identify challenges and developments in the broader picture of climate change []. Some of today’s most known techno-economic models are from the MARKAL/TIMES family of models, e.g., NEMS, PRIMES, or MESSAGE. While some of these models were originally developed as pure optimization models, they already try to bridge the gap between techno-economic and macroeconomic models [,,,]. These partial equilibrium models commonly focus on energy demand and supply markets, allowing for a broader representation of technological aspects than purely macroeconomic models [].
Taking a rather top-down perspective, computable general equilibrium models (CGE) assume a certain market structure, and dynamic of the economy, e.g., competitive or oligopolistic, and then add a certain level of technological detail. Thus, the Emission Prediction and Policy Analysis (EPPA) -model of Massachusetts Institute of Technology (MIT) is a CGE-model assuming a competitive economy and covering a high level of sectoral and macroeconomic detail [].
Adopting a more pragmatic approach, simulation models are designed to replicate the functioning of specific energy markets, without being bound to some predefined, theoretical structural form. Two examples of such simulation models are the World Energy Model (WEM; for more information see: http://www.worldenergyoutlook.org/weomodel/) used by the International Energy Agency (IEA), amongst others to calculate scenarios for the World Energy Outlook (WEO), and Prospective Outlook on Long-term Energy Systems (POLES), developed by the University of Grenoble (France), used extensively by the European Commission for long-term scenario work []. A simple form of simulation models consists of the accounting framework models []. The long-range energy alternatives planning model (LEAP), developed by the Stockholm Environment Institute, belongs to this group. In fact, a link between OSeMOSYS and LEAP is established to extend the existing accounting framework [].
While the choice of the model structure is a very important issue, the choice of technical detail and assumptions is another driver. For example, results of an energy model will largely diverge depending on whether sector coupling is possible or not, whether certain technologies are available or not, and whether price developments are properly anticipated. In that respect, one observes a critical moment in energy system modeling of low-carbon futures, driven by the unexpected cost decrease of renewable energies and storage technologies. Traditionally, energy system models relied on the trio of fossil fuels with carbon capture, nuclear energy, and renewables; the two former ones providing backup capacity in case of no wind and no sun. This pattern is now challenged by the availability of low-cost storage technologies and other flexibility options (such as demand-side management, high-voltage grid interconnections, etc.), providing the necessary flexibility to balance intermittent renewables []. The recent controversy about renewables-based energy scenarios highlights this issue, see Clack et al. [] and Jacobson, et al. [].
This paper contributes to the debate by presenting a new energy system model with a high level of sectoral detail that can be used—among others—for global climate policy scenarios. The model, called GENeSYS-MOD, is a full-fledged energy system originally based on the open-source energy modeling system, called OSeMOSYS. The model uses a system of linear equations of the energy system to search for lowest-cost solutions for a secure energy supply, given externally defined constraints on greenhouse-gas (GHG) emissions. In particular, it takes into account increasing interdependencies between traditionally segregated sectors, e.g., electricity, transportation, and heating. OSeMOSYS itself is used in a variety of research to provide insights about regional energy systems and their transition towards renewable energies (Moura et al. [] implemented a version called SAMBA, where the South American energy system is depicted. Others like Rogan et al. [] tackle national energy system, in this case analyzing the Irish one over the period 2009–2020. Recently, Lyseng et al. [] modeled the Alberta power system, analyzing the impact of carbon prices, loads and costs getting a solution of how a decarbonization until 2030 can be achieved). We provide a translation of the initial model, written in GNU MathProg (GMPL), into the widely used and available GAMS software. We also extended the code and implemented additional functionalities, e.g., a modal split for the transportation sector or relative investment limits for the single model periods. Last but not least, both the code and the data used by GENeSYS-MOD are open-access and freely available to the scientific community.
The paper is structured in the following way: the next section lays out the model and its various aspects. Section 3 presents the model implementation, and its global application. Fuels and technologies, as well as their availabilities and limitations are described. Section 4 presents the results, and Section 5 concludes (this paper results from a graduate study project convened by Roman Mendelevitch, Pao-Yu Oei, and Franziska Holz, at Berlin University of Technology, in the summer semester 2016, see Burandt et al. [] for details. We are grateful for previous work in the OSeMOSYS open-source community, without which our work would not have been possible. Earlier versions of the paper were presented and discussed at the 10th TransAtlantic Infraday (November 2016, Washington, DC, USA), the 40th International Conferences of the International Association for Energy Economics (IAEE, Singapore, June 2017), the 10th Annual Internationale Energiewirtschaftstagung IEWT (February 2017, Vienna, Austria), DIW’s internal cluster seminar on climate and energy policy (December 2016), as well as the OSeMOSYS working group (June 2017). We thank participants at these conferences, in particular Dawud Ansari, Wolf-Peter Schill, and Christian Breyer for comments; the usual disclaimer applies).
2. GENeSYS-MOD: Model Description
GENeSYS-MOD has been developed by our team based on the OSeMOSYS, originally coded in GNU MathProg. In addition to a full-fledged conversion of the current version of OSeMOSYS into the GAMS software, we have extended the model significantly. This section describes both the basic structure we have taken over, as well as the additions; we also provide the framework for the application to the global energy system.
2.1. The Model
GENeSYS-MOD is based on the version of OSeMOSYS created by Noble [], has been updated to the newest version of OSeMOSYS, and will be regularly updated from there. GENeSYS-MOD uses the CPLEX-solver (version 12.7.1.0) for its calculations. Just like OSeMOSYS, GENeSYS-MOD consists of multiple blocks of functionality (see Figure 1), which work as separate entities that can be changed or extended. To soften the limitations of a linear model, we implemented an additional block, called ‘Transportation’, implementing a modal split for the distribution of passenger or freight kilometers of a particular type of transportation (e.g., passenger road traffic). Additionally, we added trade costs, losses and capacities for fuels between regions, changed the endogenous calculation of storages, and reformulated the renewable energy target equations. A list of all sets, as well as all relevant parameters, can be found in Appendix A.1.
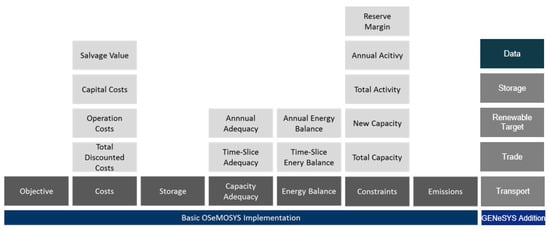
Figure 1.
Blocks of functionality of GENeSYS-MOD (the illustration is based on Howells et al. []).
The model calculates the optimal flows of energy carriers, services, or their proxies that are produced in the production sector, and converted through a network of transformation technologies to meet the set demands (energy carrier proxies are an abstract kind of energy carriers (e.g., passenger kilometers).
To achieve this, the model distinguishes between fuels and technologies. Energy carriers and services are called fuels in the model and hence are referred like this from this point on. Each fuel represents a specific energy carrier, a group of similar ones or their proxies. Furthermore, fuels are produced, transformed and used by technologies. Additionally, technologies represent all kinds of energy using, producing or transforming techniques (e.g., plants, storages or residual fuel users).
The technologies can run in different modes of operation if applicable, e.g., a plant can be defined to produce either electric power in one mode of operation, or heat in the other one. To simulate the loss of energy when converting certain fuels into another type, technologies have a defined InputActivityRatio and OutputActivityRatio. Technologies with only one of these ratios defined are either supply or demand nodes.
2.1.1. Objective Function
The objective function minimizes the net present cost of an energy system to meet the given demands for energy carriers and services. This is done by summing up the total discounted costs of each technology (t) in each year (y) and region (r). Furthermore, the total discounted trade costs of importing fuels in each region are summed up and added to the objective value:
2.1.2. Costs
Costs incur when building new capacities of technologies (DiscountedCapitalInvestmenty,r,t), maintaining capacities or using them (DiscountedOperatingCostty,r,t) (see Equation (2)):
These parameters are defined for each year, technology, and region in the model. The operation of and investment in a non-storage technology is specified by three kinds of costs. First, a technology has a given capital cost. These costs are calculated on an annual basis and are determined by the level of new installed capacity by a per-unit cost to determine the capital investment into new capacities. Furthermore, GENeSYS-MOD uses salvage costs to calculate the salvage value of technologies that have exceeded their operational life or are being replaced. Thus, the salvage value is determined by the year of installment, the operational life and a globally defined discount rate. OSeMOSYS offers an implementation of a sinking fund deprecation method and a straight-line depreciation method (the sinking fund deprecation method is an advanced deprecation method in which the estimated salvage value from the deprecation is invested into a fund and the resulting discounted values are used to calculate further salvage rates; the straight-line deprecation method is a simple, linear deprecation method, allocating the same amount or percentage of an asset's cost to each year), our model assumes the sinking fund deprecation method as default. Lastly, there are operational costs for each technology, divided in variable and fixed costs. Furthermore, the total annual operating costs are discounted back with a globally defined discount rate to the first year modeled to make costs comparable. A global discount rate of 5% was assumed for the calculations of our model. The emission penalty can be determined exogenously (e.g., a given carbon prices), or endogenously (by determining the shadow price resulting from the CO2-emission constraints). The discounted operating costs are then summed up with the discounted capital investment, emissions penalty, and salvage value.
2.1.3. Storage
The current implementation of storages in OSeMOSYS is based on general storage assumptions described by Welsch et al. []. This implementation has been changed in order to facilitate an endogenous calculation of storage capacities. Instead of setting a StorageMaxChargeRate, an Energy-Power-Ratio has been implemented for storages, with the maximum storage capacity being a variable instead. Different types of storage have different operation lifetimes, maximal and minimal ratios, and costs. The model calculates the cost of investments per unit of storage capacity and combines it with the salvage value that is computed for the end of the modeling period. Both costs are used to incorporate the storage equations into the objective function. Equations (3) and (4) define the rates for charging and discharging for each time slice:
2.1.4. Transportation
The ‘Transportation’ block introduces a modal split for transportation technologies. First, the demand of a certain fuel is split by the defined modal types into several demands per modal type. Furthermore, technologies can be tagged with modal types to define which technology can cover this split demand. Lastly, the tagged technologies must produce at least the amount of the split demand:
The following example illustrates this idea: The model has two types of passenger cars and a cheap rail technology defined. Each car is assigned to the modal type “passenger cars” and the rail is assigned to the “rail” type. Furthermore, all technologies produce “passenger kilometers” as a fuel (as mentioned before, everything a technology uses, produces, or transforms is considered a fuel in the model. This includes both regular fuels, such as power, but also services, such as passenger kilometers). Without further restrictions, the model would only use the rail technology due to its lowest costs. This, however, is unrealistic as cars will still be the best option for less frequented routes which cannot be properly included in the model due to a relatively broad geographical coverage. If our modal split function is now included in the model, we can define that at least 20% of the “passenger kilometers” must be fulfilled by the modal type “passenger cars”. Thus, we are not implementing strict limitations of the use of technologies, but set up lower bounds. Therefore, we can reproduce a more realistic result of the transportation sector and overcome some of the inherent disadvantages of a Linear Program (LP).
2.1.5. Trade
To implement trade costs in our model, we had to split the pre-existing trade variable into separate export and import variables. The total trade costs for each time slice, year and region are then calculated by summing up the trade costs for each fuel that is imported into a given region from another region, as seen in Equation (8). To incorporate these costs into the objective function, they are furthermore discounted back to the starting year of the model run and then added to the total discounted costs. Also, trade losses, as well as maximum trade capacities for power trade have been implemented in the model equations. Equation (9) demonstrates the inclusion of losses that occur on exports, equation 10 presents the maximum capacity constraint for an electricity trade route, which has to be satisfied for all time slices:
3. Model Application and Implementation
GENeSYS-MOD includes a multitude of supply and transformation technologies to satisfy the different demand needs that, in combination, form the global energy system. Its possible flows, technologies (symbolized by boxes), and demands (shaded boxes) are illustrated in Figure 2.
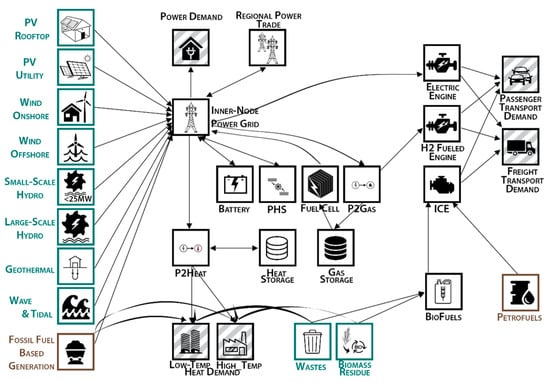
Figure 2.
Layout of GENeSYS-MOD.
3.1. Regional Disaggregation and Trade
In its current form, GENeSYS-MOD addresses global energy issues, and for this purpose it splits the world into ten regions: Africa, China, Europe, Former Soviet Union, India, Middle East, North America, Oceania, Rest of Asia and South America (see Appendix A.3 for a list of countries in each of the regions). These regions represent geographical clusters of countries in which energy is both produced and consumed (see Figure 3 for a graphical representation). At the same time, the regions act as nodes connecting with other regions to allow for trading. All parameters, e.g., on demand and production potentials (e.g., such as the potential area in which onshore wind generators could be built), and other parameters such as costs and efficiency are defined for each region. Regions are able to trade fuels via the set TradeRoutes, which define which regions are able to trade a certain type of fuel with one another. Because of the large distances between regions, we disabled the trading of power for our model calculations.
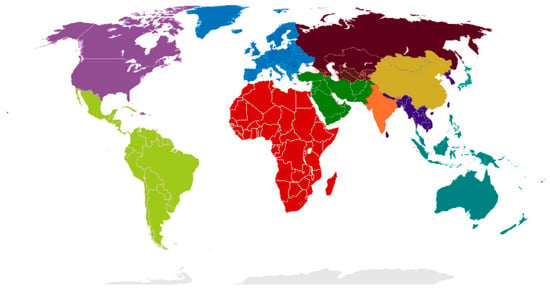
Figure 3.
Regional disaggregation of GENeSYS-MOD.
3.2. Demand and Fuel Disaggregation
GENeSYS-MOD distinguishes three groups of final demand: electricity, heat, and mobility. They are then split up into low temperature heat (used for water and room heating and cooling) and high temperature heat (process heat over 100 °C) in the heat sector, and passenger and freight transport demands in the mobility sector. Other fuels in the model are used for transformation purposes (e.g., hydrogen or biomass), serve as an input (such as the conventional fossil fuels coal, natural gas, or oil), or are used to define certain technical restrictions. These ‘area input fuels’ can be used to limit the use of certain technologies (such as PV cells) by available suitable land on a regional basis, which may serve as a superior indicator to capacity-based calculations.
As such, we defined the following fuels for our final demands (see Table 1).

Table 1.
Fuel disaggregation.
3.3. Modeling Period and Investment Restrictions
The modeling period covers the years 2020 to 2050 in 5-year-steps. The year 2015 is used as base year with existing capacities. There are no fixed investment limits for technologies. Instead, we opted for a percentage-based approach in order to reproduce investment rates more realistically. Therefore, the investment is limited by the total amount invested, as well as the maximum capacity potential.
3.4. Time Disaggregation
GENeSYS-MOD presents most results on an annual basis, but it offers a much more disaggregated approach with respect to time periods and time dependent data, such as, for example, the power demand per region or the use of storages. This is accomplished by dividing the year into several time slices, which can be defined by the model user to suit the needs of the application. One year is thus divided into seasons, which then contain day types (e.g., weekday/weekend) and daily time brackets (e.g., day/night), all defined as fractions of a year.
For this model specification, we chose to use three seasons (intermediate, summer, winter—with intermediate combining the seasons of autumn and spring), one day type, and two daily time brackets (day, night). The daily time bracket “day” is set to 16 h (⅔ of one day), while “night” is 8 h long (⅓). Multiplying these fractions for each combination (calculation example: ) gives us a total of six different time slices. Table 2 presents the fraction per year for all the time slices used (given in % of one year).

Table 2.
Time disaggregation (% of one year).
3.5. Emissions
GENeSYS-MOD is mainly targeted at greenhouse gas emissions from the energy sector, and therefore monitors CO2 in particular detail. CO2 constraints can be defined at the regional level, but also at the global level. For the applications used in this paper, we choose the global approach with a CO2 budget corresponding to the 1.5–2 °C target; according to IPCC [], about 550–1300 Gt CO₂ may be emitted between 2011 and 2050. Considering the global emissions between 2011–2014, as well as taking into account non-energy emissions (such as from industry, or land use and land-use change), we opted for a budget of 650 Gt of CO2 for the GENeSYS-MOD global model calculations.
The emission values per energy carrier per petajoule have been calculated, based on NEI [], Edenhofer et al. [] (for nuclear energy production) and EIA [] (for coal, gas and oil). All emissions can then be calculated for each technology based on their fuel consumption.
3.6. Storage
GENeSYS-MOD has been designed with attention to storage requirements, in particular in the electricity sector. Storages are connected on a technology basis, meaning each technology that wants to store or use stored energy must be connected by defining the link between them. Also, storages do not store specific fuels, but are generic “energy depots”, whose input is defined by the output fuel of the technology. A list of all implemented technologies and storage technologies can be found in Appendix A.2.
3.7. Modal Split for Transportion
The modal split for the transportation sector is exogenously given, and based on calculations that are based on data from the 450 ppm scenario from the World Energy Outlook [], using a regional differentiation. While the modal split is strictly defined for 2015, these bounds are consecutively lowered to let the model find the optimal solution.
3.8. Input Data
This section provides the main data sources required for the subsequent model calculations. As the scenarios focus on low-carbon technologies, particular weight is placed on renewable sources in this section; this will be different when we address other questions using GENeSYS-MOD, e.g., the optimal selection of coal vs. natural gas utilization.
3.8.1. Fossil Fuel Availability and Prices
Current energy systems are mainly based on conventional resources like coal, gas, oil, and nuclear power []. GENeSYS-MOD can use conventional fuels and their corresponding technologies, and invest into new capacities. Existing capacities of conventional and renewable technologies are considered by the model as residual capacities, and phased out as their lifetime expires []. The annual production of the conventional energy resources published in the World Energy Outlook [] is taken as a constant limit in the model. Carbon capture is not being considered, since it is not commercially available and is unlikely to be so in the future.
3.8.2. Renewable Technologies and Potentials
● Solar
With worldwide average annual growth rates of solar power supply of 46.2% since 1990, solar power it is one of the main drivers of any low-carbon transformation []. The technical potential of solar power is very high, but it is highly dependent on regional and temporal circumstances.
We consider two different technologies for power generation purposes: photovoltaics (PV) and concentrated solar power (CSP). The former makes use of direct radiation as well as radiation reflected by the clouds, and therefore results in a steadier energy inflow. Similar to Jacobson et al. [], we consider residential and commercial photovoltaic panels on the one hand, and utility plants at open areas on the other hand. The potentials of these technologies with respect to different regions are adopted from Jacobson et al. [] and illustrated in Table 3. Sites with less than 4kWh/m2/d are excluded, as are sites with too high slope, urban areas, or protected areas.

Table 3.
Solar PV—Regional Potential.
The conditions for using concentrated solar, on the other hand, are more constraining. CSP requires a high intensity of direct radiation, and produces low efficiency values with lower radiation. We consider sites with more than 2000 kWh/(m2·year), corresponding to capacity factors of about 20–25% []. This occurs mainly in regions such as Africa, the Middle East and Oceania.
● Wind
The availability of wind can vary strongly, both during the day but also seasonally, with availabilities up to 50% higher in winter months, e.g., in Europe []. In addition, the availability of wind power can also be constrained by environmental factors, such as the exclusion of high altitude winds []. As a result, we only consider locations where the average wind speed in 10 meters height exceeds 4 m/s [].
Our model differentiates between onshore and offshore wind. Onshore wind technology is already reasonably mature compared to other renewable energy sources, with its efficiency being close to the theoretical optimum. Most wind turbine systems have hub heights around 100 meters with rotor diameters of 50–100 m []. The potentially suitable area for onshore plants is directly given by the calculation of Jacobson et al. []. However, the potentially suitable area for offshore plants was calculated by a reverse calculation of the total GW (Gigawatt) potential given by Arent et al. []. Therefore, we used their assumption of a power density of 5 MW/km2. The latter, in combination with the stated regional potential for wind power in GW, allows the calculation of the possible suitable area, which is shown in Table 4.

Table 4.
Wind—Regional Potential.
● Biofuels
If all possible sources of residues and waste would be used, the world’s total technical annual potential is estimated to be more than 100 EJ per year []. Since it is difficult to estimate the regional potential of residues and forest products, we refer to solid biomass waste. This includes renewable urban waste, but also food wastes that are produced at the first stages of the supply chain. Furthermore, we only consider second-generation biomass for energy production. Compared to first-generation energy crops (e.g., wheat, corn, beet or palm oil), they have an important advantage because they are non-food materials. This means that agricultural by-products like cereal straw, sugarcane bagasse, or forest residues are used and biofuels do not compete directly with food production.
The share of food losses and waste (inclusive animal excrements) of the total energetic biomass potential is 42% []. Therefore, food losses and waste offer a potential of around 11.7 EJ. Some important differences exist between different regions depending on their grade of industrialization. In highly developed countries like North America or Europe, the annual per capita food loss and waste is 280–300 kg. On the other hand, in less-developed countries, the figure is lower, at 120 and 170 kg []. In accordance with the IEA [], we assume that 40% of the collected waste could be used for power production. Thus, we calculated different regional potentials based on data from Gustavsson []. Cost assumptions for biomass and their evolution from 2015 to 2050 are adopted from Sims et al. [] and Havlík et al. []. The resulting potentials are shown in Table 5. Costs are reduced from 14.5 €/GJ in 2015 to 2.2 €/GJ in 2050 due to technical improvements.

Table 5.
Biomass—Regional Potential.
● Hydropower
Hydropower is the energy transported by the water on its way from a higher to a lower level, and therefore has the highest density in regions with high slope and a constant supply of water. The greater the amount of water the river transports and the steeper the gradient of its stream course, the higher the potential in this area. Most of hydropower potentials are located in mountainous regions []. The global annual amount of water transported this way is estimated to be 47.000 km3, of which 28.000 km3 is on the surface. This sums up to around 40.000 TWh/year theoretical hydropower generation []. Regions like Asia, especially China, South America, and Africa show the most hydropower resources. Compared to solar and wind, hydropower is more predictable and constant over the years, but there are seasonal fluctuations caused by rain or melting snow. The regional potentials of hydropower are calculated using data from [,] and are represented in Table 6. For the resulting potentials, an even distribution of small and large-scale hydro has been assumed.

Table 6.
Hydropower—Regional and Economical Potential.
● Geothermal
Geothermal energy can provide a regular supply, but it is relatively expensive compared to other sources, although advances in drilling technologies and more effective reservoir management have been lowering costs significantly in the recent past []. The technical potential of geothermal energy is abundant, and it is broadly available []. The geothermal resources are caused by three important components: (i) the energy flow within the Earth crust (magma, water, steam, gases); (ii) the heat flow due to conduction; and (iii) the energy that is stored in rocks and fluids within the earth crust []. The most promising geothermal sources are located near plate margins and geologically active regions. Most of the existing geothermal plants for power plants are located in regions with high temperatures of the crust surface, high rock permeability, or a naturally existing water-steam resource [,,].
Some early research projects indicate a high potential of geothermal recourses for the energy sector. The EPRI [] stated that within the first three kilometers of the continental earth crust exists sufficient heat to provide sufficient energy for the next 100,000 years. Nevertheless, not all the theoretically existing energy can be used directly in terms of heat or to generate electricity, both for technical and economic reasons. The resulting regional potentials for geothermal power generation, based on [,] are shown in Table 7.

Table 7.
Geothermal—Regional Potential.
● Others
Renewable, synthetically produced gas, such as hydrogen, can be used to provide low and high-temperature heat, as well electric power. Furthermore, liquefied hydrogen gas can be used as fuel in the transportation sector. Thus, hydrogen can play a major role in a low-carbon transformation.
Hydrogen gas can be used in combined heat and power plants (CHP) to produce electricity and heat []. Renewable hydrogen gas CHPs are modeled according to the characteristics of the natural gas CHP technology, with hydrogen as input instead. Because hydrogen can only be generated by using expensive electrolysis technologies, power and heat generated by hydrogen is rather expensive.
In the transportation sector, hydrogen can be used in fuel-cell-driven electric vehicles (FCEV) via gaseous hydrogen. FCEV provide long range services up to 900 km per refueling []. However, this long range is achieved through a decreased overall efficiency in comparison to battery-driven electric vehicles. Additionally, other long-range transportation technologies can use liquefied hydrogen, such as freight cargo trucks or aircraft.
3.9. Cost Assumptions
Since the model identifies the least-cost combination for the energy system, cost parameters, especially their assumptions for the future, are crucial and a main driver of the results. Hence, it is essential to understand the relations and implications of those costs and verify results by testing for their sensitivity. The different types of cost considered in GENeSYS-MOD are: (1) cost for building capacities and running those, (2) emission penalties, and (3) costs for trading fuels between regions.
Most of our cost assumptions and data originate from Schröder et al. [], Gulagi et al. [], and Breyer et al. []. Also, price estimates from the 450 ppm scenario of the World Energy Outlook [] are taken as fuel prices for fossil fuels in our model. Emission penalties are currently not considered in this model setup, as we opted for a global carbon budget instead. For more information about the different costs consult Burandt et al. []. The capex of different electricity generating technologies can be found in Appendix A.4.
4. Scenario Definition and Results
4.1. Scenario Definition
GENeSYS-MOD was designed to develop and compare different scenarios for the global energy system, but for our first application, we have chosen a rather simple structure: we are interested in the cost-optimal energy mix that respects a global CO2-target calibrated for a 1.5–2 °C world, as explained above: defined here as a CO2-budget of 650 Gt for 2015 to 2050 (consistent with a 1.5°C scenario). All technologies described in the previous section are available.
Also, a sensitivity analysis concerning various parameters and assumptions has been made (costs of renewable power generating technologies, storage costs, fossil fuel costs, and demand growth), showing that our results are robust and that the model behaves accordingly.
4.2. Results
4.2.1. The Global Energy System
Figure 4 shows the results for the basic run of GENeSYS-MOD, applied to the global energy system. Our investigation of whether a globally sustainable 100% renewable energy supply is possible by 2050 results in the finding that it is technically and economically feasible, with a resulting shadow price for CO2 of about 32€ per ton CO2. This shows that a switch towards 100% renewables can be achieved with very low costs, as renewable technologies become increasingly competitive.
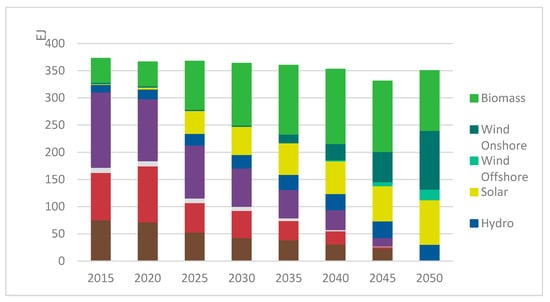
Figure 4.
Development of the global energy mix (final energy supply) with a CO2-budget of 650 Gt.
The global energy system shifts from a world almost entirely reliant on the fossil fuel sources oil, coal, and natural gas, to a fully decarbonized energy system in 2050. While starting out slowly, the growth of renewables, especially biomass, solar and wind quickly picks up and reaches a stage of about 50% of the energy mix being renewable as soon as 2030. This transformation varies strongly from sector to sector, as well as on a regional basis.
4.2.2. Electricity
The energy system experiences a very strong sector coupling of the power with both the heat and transportation sectors. This can be observed via the vastly rising generation of power, more than tripling by 2050 compared to 2015 values. Figure 5 shows the development of the power generation mix between 2015–2050 at the global level. While conventional sources still account for over 2/3 of consumption in 2015, and even over 80% when including hydropower, the energy mix changes structurally from 2025 on, mainly due to solar photovoltaics becoming economically competitive. Since low-carbon electricity generation technologies are available at low costs, the electricity sector is the first to decarbonize, and freeing up CO2-emissions for the heat and transportation sectors. Natural gas loses market shares relatively early (2025), and the use of coal is also significantly reduced. Due to possible sunk costs, rising fossil fuel prices (especially for natural gas), and increased competitiveness of renewables, no new fossil-fueled power plants are constructed. Instead, existing capacities are being utilized, depending on their remaining lifetimes. Coal remains the largest fossil fuel source for power generation, although still quickly declining in overall amounts after 2020.
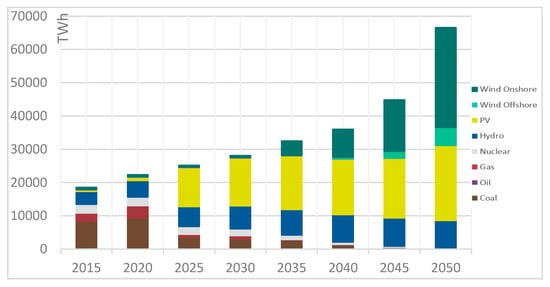
Figure 5.
Development of global power generation.
Somewhat surprisingly, wind picks up market shares relatively late, i.e., in the 2030s (onshore wind) or even after 2035 for offshore wind. This is due to optimal solar potentials being exhausted, which gives wind power the opportunity to enter the mix. The contribution of hydropower increases slightly, with most optimal potentials already being utilized beforehand. Hydropower makes up a share of about 13% of the final power generation profile.
Figure 6 presents the regional power generation mixes in 2050, demonstrating regional differences in our model results.
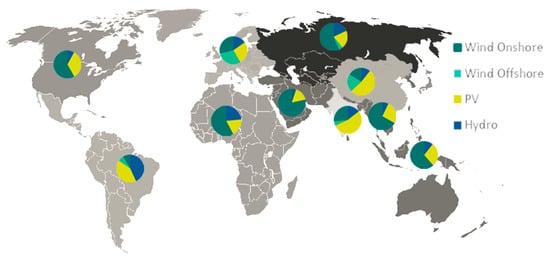
Figure 6.
Power generation profiles in 2050.
4.2.3. Heat
The energy mix in the heating sector shows quite a different decarbonization pathway. Figure 7 shows the model results for the high temperature heat production from 2015–2050. After a first expansion of natural gas, replacing oil as a fuel by 2020, both natural gas and coal diminish their share significantly in the 2020s and, much more so, in the 2030s and 2040s. Biomass takes over the lion’s share of the fossil fuels until 2035, when hydrogen and electric furnaces start to become economically viable.
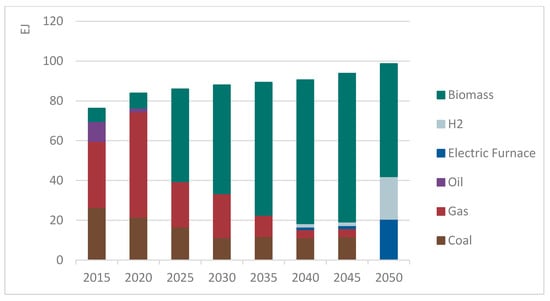
Figure 7.
Development of global high-temperature heat production.
A similar trend is observed for low temperature heat generation (see Figure 8), with biomass and electric heating meeting most of the heating demands for 2050. Overall, low temperature heating sees an earlier electrification than its high temperature counterpart.
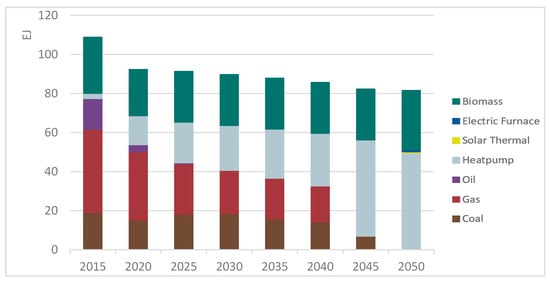
Figure 8.
Development of global low-temperature heat generation.
Until quite late in the modeling period, fossil fuels remain a major energy source for heating in both high and low temperature heat generation. Natural gas and coal are the main contributors, both being used as late as 2040 and 2045, before finally being replaced by renewables. This is due to the need for an expanded power system, which has to be constructed beforehand, as well as heat generation from fossil fuels being more efficient than its use for power generation.
4.2.4. Transportation
Figure 9 and Figure 10 show the modal share for freight and passenger transportation, respectively. The shift towards renewable fuel sources happens somewhat gradually, depending on the region. On a global scale, freight transportation by road in 2050 is achieved via biofuels and hydrogen, whilst ships utilize biofuels as their energy source. Biofuels are utilized as a transitional fuel source for road-based freight transportation, seeing some early utilization, before hydrogen joins the mix in 2045. The year 2030 poses the year where renewables become increasingly competitive and cost-efficient, which can be observed via a stronger shift away from their fossil counterparts around 2030/2035 across all sectors.
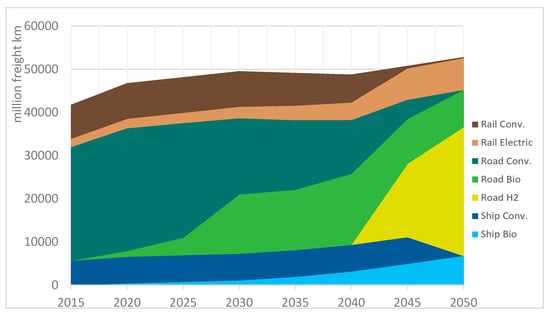
Figure 9.
Development of freight transportation services.
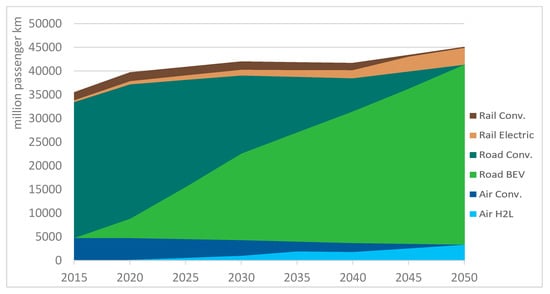
Figure 10.
Development of passenger transportation services.
4.2.5 Global CO2 Emissions
Figure 11 shows the development of global CO2-emissions between 2015 and 2050, distinguished by fossil fuel source (coal, natural gas, oil). Both coal- and oil-based emissions are constantly declining over the years. By contrast, CO2-emissions from natural gas increase between 2015 and 2020, before declining. The period between 2020 and 2025 marks the largest reduction in coal-based emissions, showing a large jump from over 15 Gt to just under 10 Gt CO2 in 2025. Overall, the binding emissions budget, combined with increasing efficiency and reduced cost of renewable technologies, sparks the strong decline of emissions towards 2050.
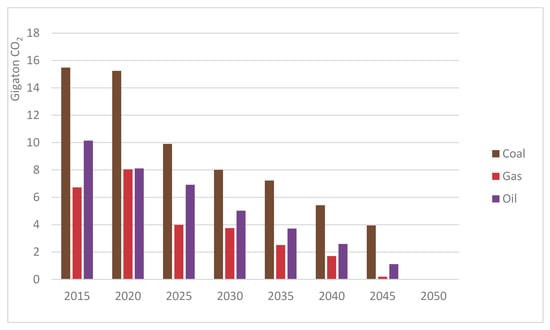
Figure 11.
Global emissions per fossil energy carrier in billion tons.
4.2.6. Average Costs
Figure 12 shows the average costs of electricity generation by the dominating technologies in 2050. The average price per kilowatt-hour for energy supply in 2050 is just above 4 ct/kWh. Solar PV (1.7–3.2 ct/kWh) and hydro (2–2.6 ct/kWh) are the cheapest options for generating electricity, followed by wind onshore (2.9–5 ct/kWh), and wind offshore with 6.4 to 10 ct/kWh. Technologies such as tidal, geothermal, or wave energy plants have been omitted due to their almost nonexistent role in the final energy mix.
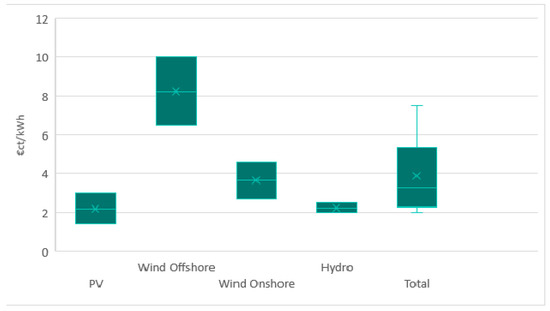
Figure 12.
Costs of power generation per technology in 2050 in €cent/kWh.
5. Conclusions
Energy system modeling has developed significantly over the last decade, and it is now facing new challenges, as lower-carbon transformation scenarios with higher shares of renewables have to be scrutinized. In this paper, we present a new energy system model, called GENeSYS-MOD, that is specifically designed to calculate global longer-term scenarios for a low-carbon world. GENeSYS-MOD was developed on the basis of the OSeMOSYS, with additional functionalities added (e.g., for storage and transportation). We also provide a translation of the original GNU MathProg version into the GAMS software. GENeSYS-MOD minimizes the total costs for supplying 10 regions of the world with energy (electricity, heat, mobility), such that certain environmental constraints, e.g., CO2 budgets, are respected. The modeling period consists of the years from 2020 to 2050 in 5-year steps, with 2015 as a baseline. Additionally, we split the year into several time periods to simulate different seasons and daytimes and the concomitant fluctuation of renewable energy production. To investigate the interaction between the various sectors, we consider three major types of demand: power, heat, and transport.
After a detailed description of the model, its implementation and the input data, as well as assumptions, the new model is used to calculate low-carbon scenarios for the global energy system, commensurate with reaching the 1.5–2 °C target, here defined as a global CO2 budget of 650 Gt for the period 2015–2050. The results of this base period (2015) serve as verification of the functionality of our model as well as a baseline for renewable energy targets. We then allow investments into technologies and the construction of new plants for the calculations of the path towards the year 2050.
The model results suggest a reorientation of the energy system, driven mainly by the climate constraint and decreasing costs of renewable energy sources. As the carbon constraint becomes more binding, less fossil fuels are used to supply energy, and a gradual shift towards renewable sources is observed, accompanied by sector coupling to the benefit of electricity consumption, and some new technological trends, such as the introduction of hydrogen in the transportation sector. The energy mix in 2050 is based on wind and solar power, biomass, and hydropower as the main energy sources. To a smaller degree, geothermal and tidal power plants provide energy as well. Depending on the region, some fossil fuels are phased out as early as 2035 with most fossil fuels being replaced by 2045.
Since the two main sources of renewable energy in our model, wind, and solar power, produce energy in the form of electricity, we observe a strong sector-coupling of the power sector with both the heat and transport sector. In the heating sector, heat pumps, and direct heating with electricity convert power into heat. In the transport sector, electricity is directly used in battery electric vehicles and electric rails as well as converted into hydrogen to provide mobility where the direct use of electricity is not possible. In conclusion, the energy system drastically changes from a dependency on natural gas, crude oil and coal to a system based on wind and solar power as well as biomass within 35 years. This increases overall power consumption over our modeling period, more than tripling the overall production of power compared to 2015.
All models should provide insight, not blunt numbers, and we need to point out shortcomings and future refinements of GENeSYS-MOD as well. At the current, quite aggregate level, we are not considering regional specificities, for example resulting from specific preferences with respect to certain technologies which are not modeled in our normative approach. Also, work needs to continue on the regional and temporal breakdown, in particular given the high share of fluctuating renewables. Issues like hourly storage and more granular time slices have yet to be considered (a case study on the transformation of the energy system in India (with a 10-node-approach) has been done and was published earlier this year []. Current projects include model applications for India, Europe, and China).
Renewable energy generation has the problem of the potentially high fluctuation which is inherently given for technologies like wind turbines or solar plants. Providing sustainable energy despite depending on external influences like weather is one of the major challenges when considering renewable energies. These issues are not sufficiently represented in our model, since the current implementation only makes use of six time slices and ten regions. Since we operate on a fairly accurate time-basis for things like energy or heat demand, but on a very large scale with our regional setup, data collection can become quite challenging, often leading to the need for assumptions to calculate certain values. Especially with the fluctuating nature of renewable energy sources and the implementation of storage systems, more detailed data is needed.
To be able to better simulate the fluctuating nature of renewables, adding more time slices and day types might increase model accuracy. Especially (short-term) storages and their implementation profit from smaller timeframes with different demand and supply factors. Also, possibly problematic events such as multiple days with very low wind or sun hours might be simulated as a result. Thus, while our current results indicate that a 100% renewable energy system by 2050 can be achieved and show first directions towards its realization, further research can improve upon these findings and present more insights about the exact measures needed to reach an optimal outcome.
Acknowledgments
We acknowledge support by the German Research Foundation and the Open Access Publication Funds of Technische Universität Berlin.
Author Contributions
Konstantin Löffler, Karlo Hainsch, Thorsten Burandt lead the coding and modeling efforts, as well as data research and writing the paper. Additionally, Konstantin Löffler managed the reviewing and editing process. Pao-Yu Oei contributed to the model implementation, as well as supervision, proof-reading, and the editing process. Christian von Hirschhausen and Claudia Kemfert initiated the research, supervised the model creation and implementation, supported the data input and policy backgrounds, and contributed to writing the text.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. List of Sets and Parameters
| Set Name (Abbreviation) | Set Description |
| Daylytimebracket (lh) | Allows for day/night differentiation, i.e., splits a single day into brackets |
| Daytype (ld) | Allows to model different days like weekday/weekend |
| Emissions (e) | Emissions produced by the different technologies |
| Fuel (f) | Fuels enter or leave technologies. Demands are always for specific fuels. |
| Modaltype (mt) | Allows for the modal split in the transportation sector. |
| Mode of Operation (m) | Technologies might operate in different modes, enabling different input-output combinations |
| Region (r) | The different (aggregated) regions considered. |
| Season (ls) | Allows a differentiation for yearly seasons (e.g., summer/winter). |
| Storage (s) | The set of different storage technologies. |
| Technology (t) | Everything that processes energy in any form is considered a technology. |
| Timeslice (l) | Timeslices are a combination of ls, ld and lh. Hence, one timeslice could be “summer weekend day”. |
| Year (y) | The set of the different modeled years. |
| Parameter Name | Parameter Description |
| Amount of demand that can be satisfied at any time of the year, not time-slice dependent. | |
| Amount of emissions allowed in a year and region. | |
| Amount of emissions not produced by modeled technologies in a given year. | |
| Maximum time a technology may run in a year. | |
| Maximum time a technology may run in a time-slice. | |
| Conversion factor of capacities [GW] into activity [PJ]. Assumes provision of 1 [GW] over one year. | |
| Capital costs for storage technologies. | |
| Capital cost for all technologies. | |
| Assigns DailyTimeBracket to time-slice. | |
| Assigns DayType to time-slice. | |
| Assigns Season to time-slice. | |
| Length of a DailyTimeBracket in one day as a fraction of the year. | |
| Amount of days per week in which a DayType occurs. | |
| Amount of emissions produced by a technology for producing 1 [PJ] of energy. | |
| Penalty for emitting emissions. | |
| Fixed O&M costs for a technology. | |
| Describes coupled with OutputActivityRatio the efficiency of a technology. | |
| Percentage of storage capacity that must not be deceeded. | |
| Assigns the share of a mean of transportation for one demand fuel. | |
| Amount of emissions that must not be exceeded over the whole modeling period. | |
| Amount of emissions that is not produced by a modeled technology in whole modeling period. | |
| Operational life of storage technologies. | |
| Operational life of all technologies. | |
| Describes coupled with InputActivityRatio the efficiency of a technology. | |
| Tags fuels that do not produce emissions. | |
| Tags technologies that do not produce emissions. | |
| Tags whether more than the actual demand has to be produced of a given fuel. | |
| Tags which technologies can contribute to the reserve margin. | |
| Sets the amount of reserve margin that has to be produced. | |
| Capacities that exist in addition to the endogenously built capacities. | |
| Storage Capacities that exist in addition to the endogenously built capacities. | |
| Annual demand of fuels which are time-slice dependent. | |
| Assigns a share of SpecifiedAnnualDemand to the different time-slices. | |
| Amount of stored energy at the beginning of the modeling period. | |
| Maximum charge amount of a storage within one hour | |
| Maximum discharge amount of a storage within one hour | |
| Assigns different transportation technologies to the modal type. | |
| Technologies that can use a fuel from a storage. | |
| Technologies that can provide a fuel for a storage. | |
| Maximum amount of investments into a technology in a year. | |
| Maximum amount of used capacity in a year. | |
| Minimum amount of investments into a technology in a year. | |
| Minimum amount of used capacity in a year. | |
| Variable costs for trading a fuel between regions. | |
| Tags possible trade routes between regions. | |
| Variable O&M costs for using a technology. | |
| Share of a time-slice in one year. |
Appendix A.2. List of Technologies and Storages
| Technology | Description |
| Area_DistrictHeating_avg | Usable area for centralized heating (average) |
| Area_DistrictHeating_inf | Usable area for centralized heating (inferior) |
| Area_DistrictHeating_opt | Usable area for centralized heating (optimal) |
| Area_PV_Commercial | Usable area for commercial rooftop PV systems |
| Area_Solar_Roof | Usable area for private rooftop PV systems |
| BIOFLREFINERY | Refinery for biomass to biofuel conversion |
| C_Coal | Coal resource node |
| C_Gas | Gas resource node |
| C_Nuclear | Nuclear material resource node |
| C_Oil | Crude oil resource node |
| ELYSER | Hydrogen-producing elyser |
| FRT_Rail_ELC | Freight rail transport; Electric train |
| FRT_Rail_Petro | Freight rail transport; Petro-fueled |
| FRT_Road_Bio | Freight road transport; Biofuels |
| FRT_Road_Conv | Freight road transport; Conventional fuels |
| FRT_Road_H2 | Freight road transport; Hydrogen-based |
| FRT_Ship_Bio | Freight ship transport; Biofuels |
| FRT_Ship_Conv | Freight ship transport; Conventional fuels |
| FUEL_CELL | Fuel cell |
| H2TL | Hydrogen liquefaction |
| P_Coal | Coal-based power plant |
| P_Gas | Natural gas-based power plant |
| P_Nuclear | Nuclear power plant |
| P_Oil | Oil power plant |
| PSNG_Air_Conv | Passenger air transport; Conventional fuels |
| PSNG_Air_H2L | Passenger air transport; Liquid hydrogen |
| PSNG_Rail_ELC | Passenger rail transport; Electric train |
| PSNG_Rail_Petro | Passenger rail transport; Petro-fueled |
| PSNG_Road_BEV | Passenger road transport; Battery electric vehicle |
| PSNG_Road_Bio | Passenger road transport; Biofuels |
| PSNG_Road_FCEV | Passenger road transport; Fuel cell electric vehicle |
| PSNG_Road_ICE | Passenger road transport; Internal combustion engine |
| Res_BioMass | Biomass resource node |
| Res_CSP | Concentrated solar power plant |
| Res_CSP_Storage | Concentrated solar power plant with integrated storage |
| Res_Hydro_Large | Large-scale hydro (>25MW) |
| Res_Hydro_Small | Small-scale hydro |
| Res_PV_Commercial | Rooftop-PV on commercial buildings |
| Res_PV_Residential | Residential rooftop PV systems |
| Res_PV_Utility_avg | Utility-scale PV (average) |
| Res_PV_Utility_inf | Utility-scale PV (inferior) |
| Res_PV_Utility_opt | Utility-scale PV (optimal) |
| Res_Thermal_Geo | Geothermal power generation |
| Res_Thermal_Solar | Solar-based heat generation |
| Res_Tidal | Tidal power plant |
| Res_Wave | Wave power plant |
| Res_Wind_Offshore_avg | Offshore wind plant (average) |
| Res_Wind_Offshore_inf | Offshore wind plant (inferior) |
| Res_Wind_Offshore_opt | Offshore wind plant (optimal) |
| Res_Wind_Onshore_avg | Onshore wind plant (average) |
| Res_Wind_Onshore_inf | Onshore wind plant (inferior) |
| Res_Wind_Onshore_opt | Onshore wind plant (optimal) |
| ST_Battery_Lion | Dummy-Technology for battery storage |
| ST_H2 | Dummy-Technology for hydrogen storage |
| ST_Heat_cen | Dummy-Technology for central heat storage |
| ST_Heat_dec | Dummy-Technology for decentral heat storage |
| ST_PSP | Dummy-Technology for pump storage |
| ST_PSP_Residual | Dummy-Technology for residual pump storage capacities |
| T_heat_high_bio | High-temperature heat generation (biomass) |
| T_heat_high_coal | High-temperature heat generation (coal) |
| T_heat_high_elfur | High-temperature heat generation (electric furnace) |
| T_heat_high_gas | High-temperature heat generation (natural gas) |
| T_heat_high_oil | High-temperature heat generation (oil) |
| T_heat_high_res-gas | High-temperature heat generation (hydrogen) |
| T_heat_low_bio | Low-temperature heat generation (biomass) |
| T_heat_low_bio_cen | Low-temperature heat generation (biomass; centralized) |
| T_heat_low_bio_chp | Low-temperature heat generation (biomass; combined heat-power-plant) |
| T_heat_low_bio_chp_cen | Low-temperature heat generation (biomass; centralized; combined heat-power-plant) |
| T_heat_low_coal | Low-temperature heat generation (coal) |
| T_heat_low_coal_cen | Low-temperature heat generation (coal; centralized) |
| T_heat_low_coal_chp_cen | Low-temperature heat generation (coal; centralized; combined heat-power-plant) |
| T_heat_low_elfur | Low-temperature heat generation (electric furnace) |
| T_heat_low_elfur_cen | Low-temperature heat generation (electric furnace; centralized) |
| T_heat_low_gas | Low-temperature heat generation (natural gas) |
| T_heat_low_gas_cen | Low-temperature heat generation (natural gas; centralized) |
| T_heat_low_gas_chp_cen | Low-temperature heat generation (natural gas; centralized; combined heat-power-plant) |
| T_heat_low_heatpump | Low-temperature heat generation (heatpump) |
| T_heat_low_heatpump_cen | Low-temperature heat generation (heatpump; centralized) |
| T_heat_low_oil | Low-temperature heat generation (oil) |
| T_heat_low_oil_cen | Low-temperature heat generation (oil; centralized) |
| T_heat_low_oil_chp_cen | Low-temperature heat generation (oil; centralized; combined heat-power-plant) |
| T_heat_low_res-gas | Low-temperature heat generation (hydrogen) |
| T_heat_low_res-gas_cen | Low-temperature heat generation (hydrogen; centralized) |
| T_heat_low_res-gas_chp | Low-temperature heat generation (hydrogen; combined-heat-power-plant) |
| T_heat_low_res-gas_chp_cen | Low-temperature heat generation (hydrogen; centralized; combined heat-power-plant) |
| Storages | |
| S_Battery_Lion | Lithium-Ion battery |
| S_CSP_storage | Storage-technology connected to CSP with storage |
| S_H2 | Hydrogen (gas) storage |
| S_Heat_cen | Heat storage for central heating |
| S_Heat_dec | Heat storage for decentral heating |
| S_PSP | (Hydro) Pump-storage-plant |
Appendix A.3. List of Countries, Grouped by Region
| Africa | ||
| Algeria | Ethiopia | Niger |
| Angola | Gabon | Nigeria |
| Benin | Gambia (Islamic Republic of) | Rwanda |
| Botswana | Ghana | Sao Tome and Principe |
| Burkina Faso | Guinea | Senegal |
| Burundi | Guinea Bissau | Sierra Leone |
| Cabo Verde | Kenya | Somalia |
| Cameroon | Lesotho | South Africa |
| Central African Republic | Liberia | South Sudan |
| Chad | Libya | Sudan |
| Comoros | Madagascar | Swaziland |
| Congo | Malawi | Togo |
| Côte D'Ivoire | Mali | Tunisia |
| Democratic Republic of the Congo | Mauritania | Uganda |
| Djibouti | Mauritius | United Republic of Tanzania |
| Egypt | Morocco | Zambia |
| Equatorial Guinea | Mozambique | Zimbabwe |
| Eritrea | Namibia | |
| Asia-Rest | ||
| Bangladesh | Malaysia | Singapore |
| Bhutan | Maldives | Sri Lanka |
| Brunei Darussalam | Myanmar | Thailand |
| Cambodia | Nepal | Timor-Leste |
| Indonesia | Philippines | Viet Nam |
| Lao People’s Democratic Republic | Seychelles | |
| China | ||
| China | Mongolia | |
| Europe | ||
| Albania | Germany | Norway |
| Andorra | Greece | Poland |
| Austria | Hungary | Portugal |
| Belarus | Iceland | Romania |
| Belgium | Ireland | San Marino |
| Bosnia and Herzegovina | Italy | Serbia |
| Bulgaria | Latvia | Slovakia |
| Croatia | Liechtenstein | Slovenia |
| Cyprus | Lithuania | Spain |
| Czech Republic | Luxembourg | Sweden |
| Denmark | Malta | Switzerland |
| Estonia | Monaco | The former Yugoslav Republic of Macedonia |
| Finland | Montenegro | Ukraine |
| France | Netherlands | United Kingdom of Great Britain and Northern Ireland |
| India | ||
| India | ||
| Middle East | ||
| Afghanistan | Kuwait | Syrian Arab Republic |
| Bahrain | Lebanon | Turkey |
| Iran (Islamic Republic of) | Oman | United Arab Emirates |
| Iraq | Pakistan | Yemen |
| Israel | Qatar | |
| Jordan | Saudi Arabia | |
| North America | ||
| Canada | Mexico | United States of America |
| Ocenania | ||
| Australia | Micronesia (Federated States of) | Samoa |
| Democratic People’s Republic of Korea | Nauru | Solomon Islands |
| Fiji | New Zealand | Tonga |
| Japan | Palau | Tuvalu |
| Kiribati | Papua New Guinea | Vanuatu |
| Marshall Islands | Republic of Korea | |
| FSU | ||
| Armenia | Kyrgyzstan | Uzbekistan |
| Azerbaijan | Russian Federation | Republic of Moldova |
| Georgia | Tajikistan | |
| Kazakhstan | Turkmenistan | |
| South America | ||
| Antigua and Barbuda | Dominica | Panama |
| Argentina | Dominican Republic | Paraguay |
| Bahamas | Ecuador | Peru |
| Barbados | El Salvador | Saint Kitts and Nevis |
| Belize | Grenada | Saint Lucia |
| Bolivia (Plurinational State of) | Guatemala | Saint Vincent and the Grenadines |
| Brazil | Guyana | Suriname |
| Chile | Haiti | Trinidad and Tobago |
| Colombia | Honduras | Uruguay |
| Costa Rica | Jamaica | Venezuela, Bolivarian Republic of |
| Cuba | Nicaragua | |
Appendix A.4. Capital Cost Development of Electricity-Generating Technologies (in million €/GW)
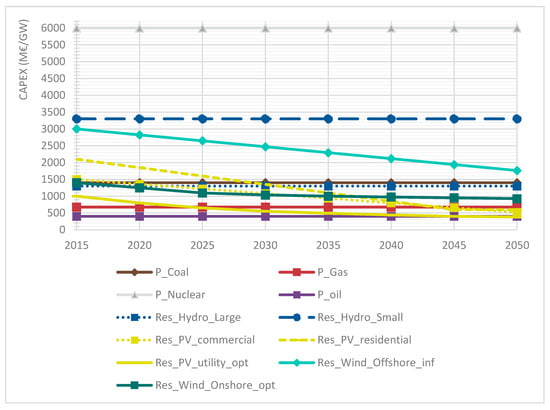
Figure A1.
Capital Cost development of power-generating technologies.
References
- Connolly, D.; Lund, H.; Mathiesen, B.V.; Leahy, M. A review of computer tools for analysing the integration of renewable energy into various energy systems. Appl. Energy 2010, 87, 1059–1082. [Google Scholar] [CrossRef]
- Herbst, A.; Toro, F.; Reitze, F.; Jochem, E. Introduction to energy systems modelling. Swiss J. Econ. Stat. 2012, 148, 111–135. [Google Scholar]
- Bhattacharyya, S.C.; Timilsina, G.R. A review of energy system models. Int. J. Energy Sect. Manag. 2010, 4, 494–518. [Google Scholar] [CrossRef]
- Seebregts, A.; Gary, G.; Koen, S. Energy/environmental modeling with the MARKAL family of models. In Operations Research Proceedings 2001; Chamoni, P., Leisten, R., Martin, A., Minnemann, J., Stadtler, H., Eds.; Springer-Verlag: Duisburg, Germany, 2001; Volume 2001, pp. 75–82. ISBN 978-3-540-43344-6. [Google Scholar]
- EIA The National Energy Modeling System: An Overview. Available online: https://www.eia.gov/outlooks/aeo/nems/overview/index.html (accessed on 19 September 2017).
- IIASA MESSAGE. Available online: http://www.iiasa.ac.at/web/home/research/researchPrograms/Energy/MESSAGE.en.html (accessed on 11 July 2017).
- E3MLab. PRIMES Model; E3Mlab, National Technocal University of Athens: Athens, Greece, 2016. [Google Scholar]
- Yang, Z.; Eckaus, R.S.; Ellerman, A.D.; Jacoby, H.D. The MIT Emissions Prediction and Policy Analysis (EPPA) Model; Joint Program on the Science and Policy of Global Change: Cambridge, MA, USA, 1996; p. 49. [Google Scholar]
- Criqui, P. International Markets and Energy Prices: The POLES Model. In Models for Energy Policy; Lesourd, J.-B., Percebois, J., Valette, F., Eds.; Routledge Studies in the History of Economic Modelling; Routledge: Abingdon, UK, 1996; pp. 14–29. ISBN 978-0-415-12975-6. [Google Scholar]
- Mundaca, L.; Neij, L. A multi-criteria evaluation framework for tradable white certificate schemes. Energy Policy 2009, 37, 4557–4573. [Google Scholar] [CrossRef]
- Heaps, C. An introduction to LEAP. Stockh. Environ. Inst. 2008, 1–16. Available online: https://www.energycommunity.org/documents/LEAPIntro.pdf (accessed on 19 September 2017).
- SSRN, Wind Providing Balancing Reserves—An Application to the German Electricity System of 2025. Available online: https://papers.ssrn.com/soL3/papers.cfm?abstract_id=2952288 (accessed on 9 September 2017).
- Clack, C.T.M.; Qvist, S.A.; Apt, J.; Bazilian, M.; Brandt, A.R.; Caldeira, K.; Davis, S.J.; Diakov, V.; Handschy, M.A.; Hines, P.D.H.; et al. Evaluation of a proposal for reliable low-cost grid power with 100% wind, water, and solar. Proc. Natl. Acad. Sci. USA 2017, 114, 6722–6727. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, M.Z.; Delucchi, M.A.; Cameron, M.A.; Frew, B.A. The United States can keep the grid stable at low cost with 100% clean, renewable energy in all sectors despite inaccurate claims. Proc. Natl. Acad. Sci. USA 2017, 114, E5021–E5023. [Google Scholar] [CrossRef] [PubMed]
- Moura, G.; Howells, M.; Legey, L. SAMBA, The open source South American Model Base. A Brazilian Perspective on Long Term Power Systems Investment and Integration; Technical Report; Royal Institute of Technology: Stockholm, Sweden, 2015. [Google Scholar]
- Rogan, F.; Cahill, C.J.; Daly, H.E.; Dineen, D.; Deane, J.P.; Heaps, C.; Welsch, M.; Howells, M.; Bazilian, M.; Gallachóir, B.P.Ó. LEAPs and Bounds—An Energy Demand and Constraint Optimised Model of the Irish Energy System. Energy Effic. 2014, 7, 441–466. [Google Scholar] [CrossRef]
- Lyseng, B.; Rowe, A.; Wild, P.; English, J.; Niet, T.; Pitt, L. Decarbonising the Alberta power system with carbon pricing. Energy Strategy Rev. 2016, 10, 40–52. [Google Scholar] [CrossRef]
- Burandt, T.; Hainsch, K.; Löffler, K.; Böing, H.; Erbe, J.; Kafemann, I.-V.; Kendziorski, M.; Kruckelmann, J.; Rechtlitz, J.; Scherwath, T. Designing a Global Energy System based on 100% Renewables for 2050-Insights from the Open-source Energy Modelling System (OSeMOSYS) 2016. Available online: https://ideas.repec.org/p/diw/diwwpp/dp1678.html (accessed on 9 September 2017).
- Noble, K. OSeMOSYS: The Open Source Energy Modeling System—A Translation into the General Algebraic Modeling System (GAMS); KTH: Stockholm, Sweden, 2012; Available online: http://www.osemosys.org/uploads/1/8/5/0/18504136/osemosys_in_gams_wp_desa_2012.pdf (accessed on 19 September 2017).
- Howells, M.; Rogner, H.; Strachan, N.; Heaps, C.; Huntington, H.; Kypreos, S.; Hughes, A.; Silveira, S.; DeCarolis, J.; Bazillian, M.; et al. OSeMOSYS: The Open Source Energy Modeling System: An introduction to its ethos, structure and development. Energy Policy 2011, 39, 5850–5870. [Google Scholar] [CrossRef]
- Welsch, M.; Howells, M.; Bazilian, M.; DeCarolis, J.F.; Hermann, S.; Rogner, H.H. Modelling elements of Smart Grids–Enhancing the OSeMOSYS (Open Source Energy Modelling System) code. Energy 2012, 46, 337–350. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Summary for Policymakers. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, NY, USA, 2014. [Google Scholar]
- NEI Comparison of Lifecycle Emissions of Energy Technologies. Available online: http://www.nei.org/Issues-Policy/Protecting-the-Environment/Life-Cycle-Emissions-Analyses/Comparison-of-Lifecycle-Emissions-of-Selected-Ener (accessed on 19 September 2017).
- Renewable Energy Sources and Climate Change Mitigation: Special Report of the Intergovernmental Panel on Climate Change; Edenhofer, O.; Pichs Madruga, R.; Sokona, Y.; UNEP; WMO; IPCC; PIK (Eds.) Cambridge University Press: Cambridge, NY, USA, 2012; ISBN 978-1-107-02340-6. [Google Scholar]
- EIA International Energy Outlook 2016. Available online: https://www.eia.gov/outlooks/ieo/pdf/0484(2016).pdf (accessed on 19 September 2017).
- World Energy Outlook 2015; International Energy Agency (Ed.) OECD: Paris, France, 2015; ISBN 978-92-64-24365-1. Available online: http://www.worldenergyoutlook.org/media/weowebsite/2015/WEO2015_Chapter01.pdf (accessed on 19 September 2017).
- Farfan, J.; Breyer, C. Structural changes of global power generation capacity towards sustainability and the risk of stranded investments supported by a sustainability indicator. J. Clean. Prod. 2017, 141, 370–384. [Google Scholar] [CrossRef]
- OECD, Renewables Information 2016. Available online: http://www.oecd-ilibrary.org/energy/renewables-information-2016_renew-2016-en;jsessionid=lxmv0jej2xlb.x-oecd-live-03 (accessed on 22 September 2017).
- Jacobson, M.Z.; Delucchi, M.A.; Bauer, Z.A.F.; Goodman, S.C.; Chapman, W.E.; Cameron, M.A.; Bozonnat, C.; Chobadi, L.; Clonts, H.A.; Enevoldsen, P.; et al. 100% Clean and Renewable Wind, Water, and Sunlight All-Sector Energy Roadmaps for 139 Countries of the World. Joule 2017, 108–121. [Google Scholar] [CrossRef]
- Trieb, F.; Schillings, C.; O’Sullivan, M.; Pregger, T.; Hoyer-Klick, C. Global Potential of Concentrating Solar Power. In Proceedings of the SolarPaces Conference, Berlin, Germany, 15–18 September 2009. [Google Scholar]
- Archer, C.L.; Jacobson, M. Evaluation of global wind power. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Marvel, K.; Kravitz, B.; Caldeira, K. Geophysical limits to global wind power. Nat. Clim. Chang. 2012, 3, 118–121. [Google Scholar] [CrossRef]
- Hau, E. Windkraftanlagen; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-72150-5. [Google Scholar]
- Schröder, A.; Kunz, F.; Meiss, J.; Mendelevitch, R.; Hirschhausen, C. Current and Prospective Costs of Electricity Generation until 2050; DIW: Berlin, Germany, 2013.
- Arent, D.; Sullivan, P.; Heimiller, D.; Lopez, A.; Eurek, K.; Badger, J.; Jorgensen, H.E.; Kelly, M. Improved Offshore Wind Resource Assessment in Global Climate Stabilization Scenarios; Technical Report; NREL: Golden, CO, USA, 2012; p. 24.
- Sims, R.E.H.; Mabee, W.; Saddler, J.N.; Taylor, M. An overview of second generation biofuel technologies. Bioresour. Technol. 2010, 101, 1570–1580. [Google Scholar] [CrossRef] [PubMed]
- Mühlenh, J. Reststoffe Für Bioenergie Nutzen-Potenziale, Mobilisierung Und Umweltbilanz; Agentur für Erneuerbare Energien: Berlin, Germany, 2013; p. 45. [Google Scholar]
- Gustavsson, J. Global Food Losses and Food Waste: Extent, Causes and Prevention: Study Conducted for the International Congress “Save Food!”; Technical Report; Food and Agriculture Organization of the United Nations: Rome, Italy, 2011; ISBN 978-92-5-107205-9. [Google Scholar]
- International Energy Agency (IEA). Energy Technology Perspectives 2016-Towards Sustainable Urban Energy Systems; International Energy Agency (IEA): Paris, France, 2016; ISBN 978-92-64-25233-2. [Google Scholar]
- Havlík, P.; Schneider, U.A.; Schmid, E.; Böttcher, H.; Fritz, S.; Skalský, R.; Aoki, K.; Cara, S.D.; Kindermann, G.; Kraxner, F.; et al. Global land-use implications of first and second generation biofuel targets. Energy Policy 2011, 39, 5690–5702. [Google Scholar] [CrossRef]
- Handbook of Energy. Vol. 1: Diagrams, Charts, and Tables; Cleveland, C.J.; Morris, C. (Eds.) Elsevier: Amsterdam, The Netherlands, 2013; ISBN 978-0-08-046405-3. [Google Scholar]
- Younger, P. Geothermal Energy: Delivering on the Global Potential. Energies 2015, 8, 11737–11754. [Google Scholar] [CrossRef]
- EPRI Geothermal Power: Issues, Technologies, and Opportunities for Research, Development, Demonstration, and Deployment 2010. Available online: https://www.epri.com/#/pages/product/1020783/ (accessed on 19 September 2017).
- Stefánsson, V. Estimate of the World Geothermal Potential. In Geothermal Training in Iceland 20th Anniversary Workshop; The United Nations University: Reykjavik, Iceland, 1998; pp. 111–120. [Google Scholar]
- Geothermal Energy: Utilization and Technology; Dickson, M.; UNESCO (Eds.) UNESCO: Paris, France, 2003; ISBN 978-92-3-103915-7. [Google Scholar]
- Rybach, L. Geothermal Power Growth 1995–2013—A Comparison with Other Renewables. Energies 2014, 7, 4802–4812. [Google Scholar] [CrossRef]
- Geothermal Legacy Collection, EPRI Geothermal Energy Prospects for the Next 50 Years. EPRI ER-611-SR Special Report 1978. Available online: http://www.osti.gov/geothermal/servlets/purl/5027376 (accessed on 22 September 2017).
- Gawell, K.; Reed, M.; Wright, M. Preliminary Report: Geothermal Energy, the Potential for Clean Power from the Earth; Geothermal Energy Association: Washington, DC, USA, 1999. [Google Scholar]
- Geothermal Energy: International Market Update 2010. Available online: http://www.geo-energy.org/pdf/reports/GEA_International_Market_Report_Final_May_2010.pdf (accessed on 19 September 2017).
- Fraunhofer ISE. 100% Erneuerbare Energien für Strom und Wärme in Deutschland; Fraunhofer-Institut für Solare Energiesysteme ISE: Freiburg, Germany, 2012; p. 37. [Google Scholar]
- International Energy Agency (IEA). Technology Roadmap-Hydrogen and Fuel Cells; Technology Roadmap; International Energy Agency (IEA): Paris, France, 2015; p. 81. [Google Scholar]
- Gulagi, A.; Bogdanov, D.; Breyer, C. The Demand for Storage Technologies in Energy Transition Pathways Towards 100% Renewable Energy for India. In Proceedings of the 11th International Renewable Energy Storage Conference, Düsseldorf, Germany, 14–16 March 2017. [Google Scholar]
- Breyer, C.; Bogdanov, D.; Gulagi, A.; Aghahosseini, A.; Barbosa, L.S.N.S.; Koskinen, O.; Barasa, M.; Caldera, U.; Afanasyeva, S.; Child, M.; et al. On the role of solar photovoltaics in global energy transition scenarios: On the role of solar photovoltaics in global energy transition scenarios. Prog. Photovolt. Res. Appl. 2017, 25, 727–745. [Google Scholar] [CrossRef]
- Decarbonizing the Indian Energy System until 2050: An Application of the Open Source Energy Modeling System OSeMOSYS. Available online: https://www.researchgate.net/publication/318966842_Decarbonizing_the_Indian_Energy_System_until_2050_-_An_Application_of_the_Open_Source_Energy_Modeling_System_OSeMOSYS (accessed on 22 September 2017).
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).