Zonal Voltage Control Combined Day-Ahead Scheduling and Real-Time Control for Distribution Networks with High Proportion of PVs
Abstract
1. Introduction
2. Reactive Power-Voltage Sensitivity Based the Optimal Network Partition
2.1. Basic Concepts and Descriptions
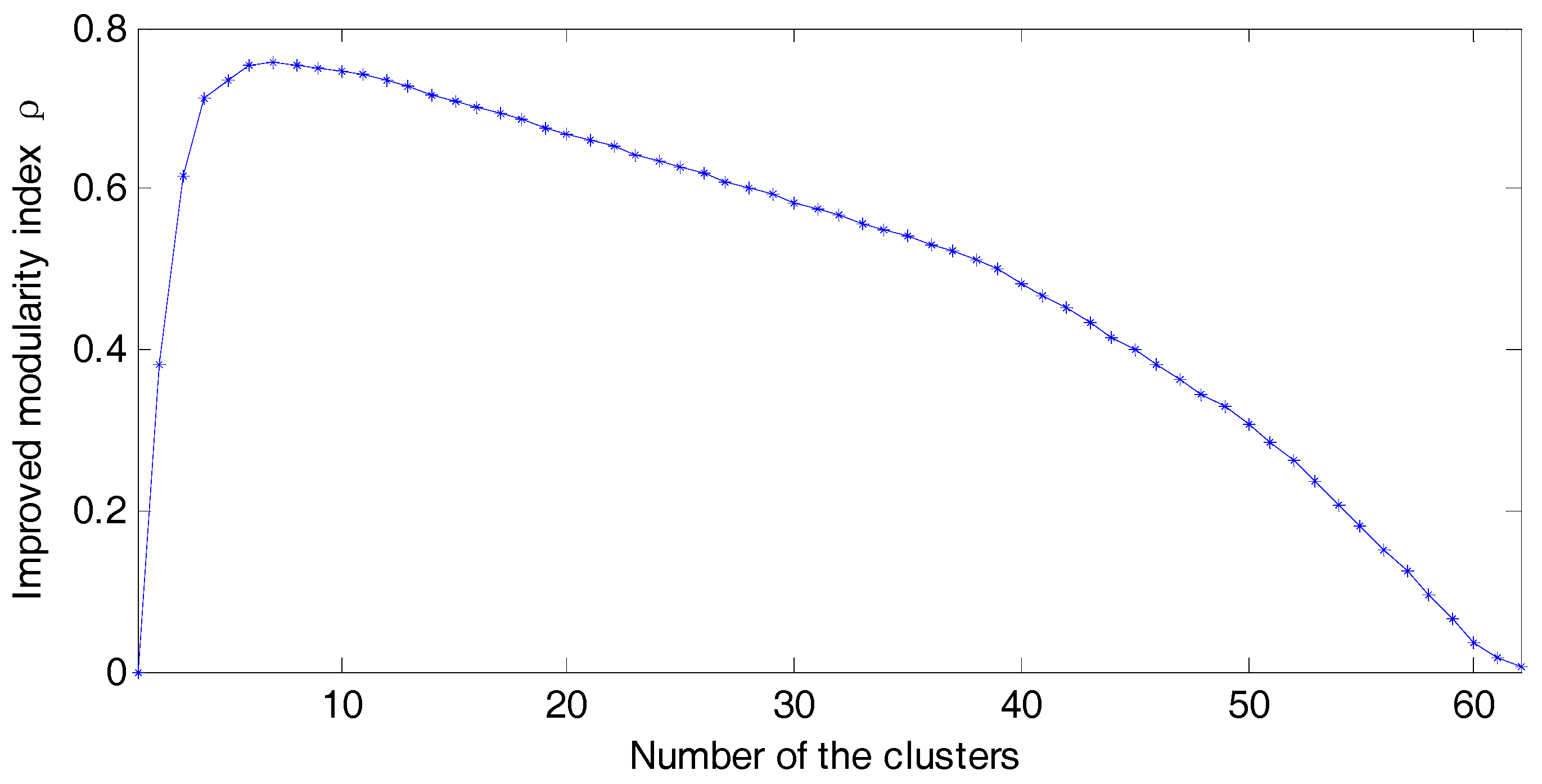
2.2. Improved Modularity Index
2.3. Network Partition Optimization Algorithm
- Step 1:
- Obtain the complete forecast data of PV output and load demand one day ahead.
- Step 2:
- Collect the forecast data for the initial time, initialize the network partition so that each sub-network has only one node, and compute the initial improved modularity index ρim of each sub-network using (8).
- Step 3:
- For each node i, another node j is randomly selected from the remaining nodes to form a new sub-network (i, j). The modularity index of the new partition is calculated. Measure the modularity variation Δρ = − ρim for each possible partition where a pair of nodes is merged. The nodes i and j will be grouped into the same sub-community if the modularity variation reaches the highest value, and the total value of modularity will be updated.
- Step 4:
- Treat the newly formed sub-networks as individual nodes, and conduct the network merge process by repeating Step 3. The network is updated with the newly formed sub-communities.
- Step 5:
- The process is stopped when nodes can no longer be merged into any sub-network and the modularity does not increase. The optimal partition, the sub-network sets and the associated modularity indices are obtained.
- Step 6:
- Obtain the forecast data of the next period, and repeat the partitioning procedure until partitioning of the distribution network is completed for all periods.
3. Day-Ahead Optimal Scheduling of Distribution Networks
3.1. Operation Cost Model of the Distribution Network
3.1.1. OLTC Model
3.1.2. PV Model
3.1.3. Distributed SC Model
3.1.4. Grid Losses Model
3.2. Objective Function and Problem Solving
- OLTC constraints: Equations (10)–(11).
- PV constraints: Equations (13)–(14).
- SC constraints: Equation (16).
- Network constraints:
4. Real-Time Optimal Control of Distribution Networks
5. Case Study
5.1. Case Study System
5.2. Distribution Network Partition
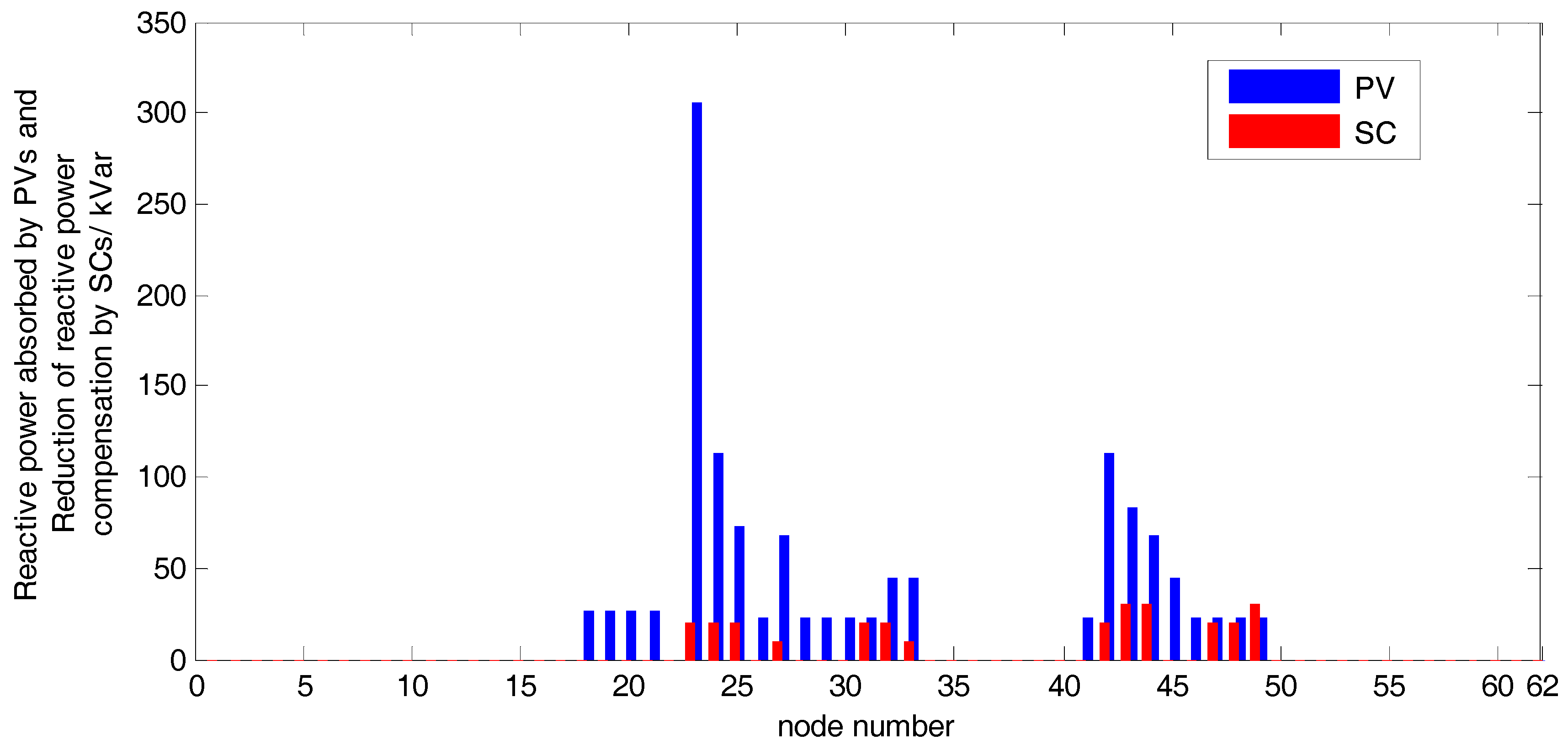
5.3. Result of the Two-Level Voltage Control Method
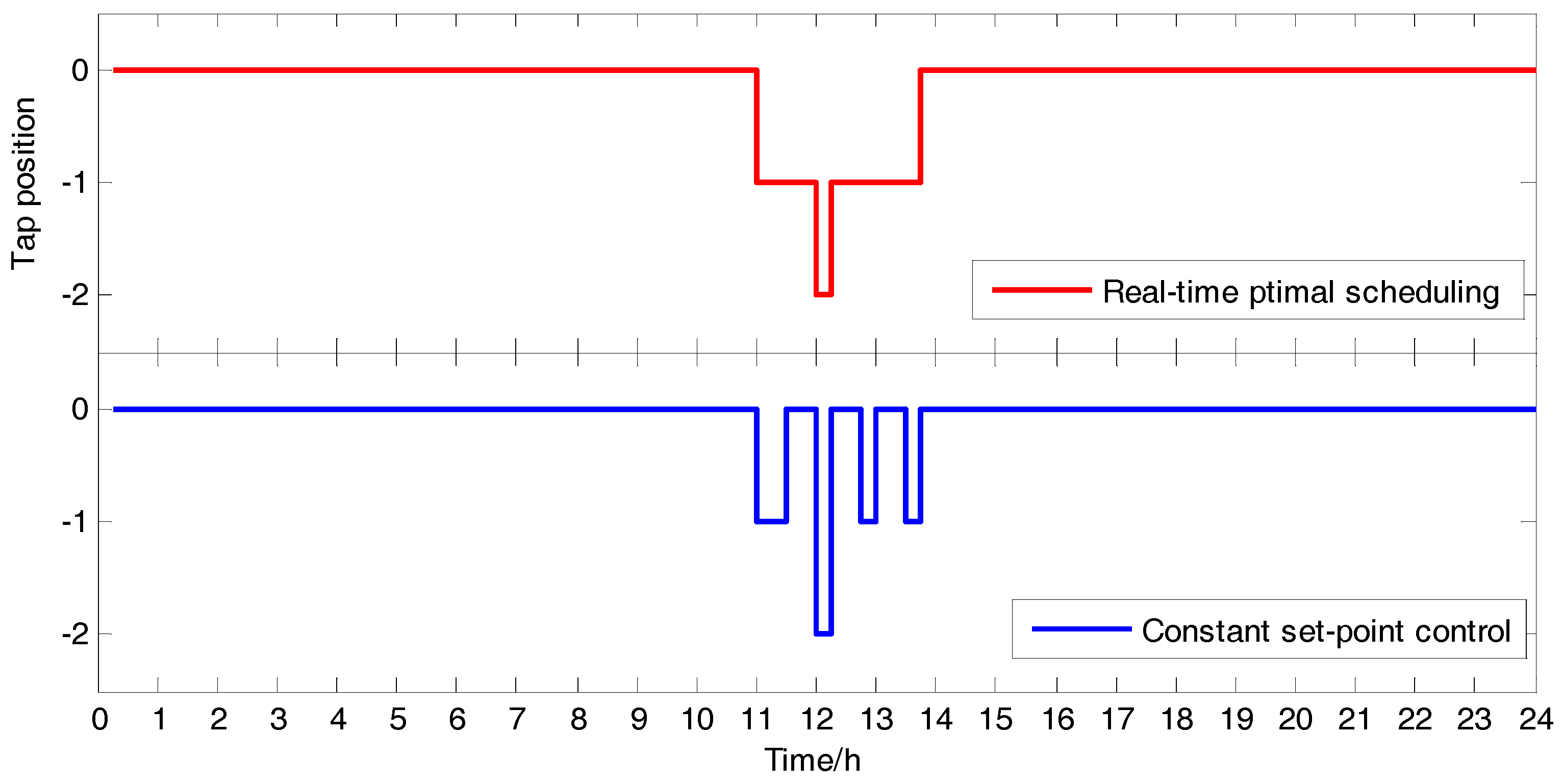
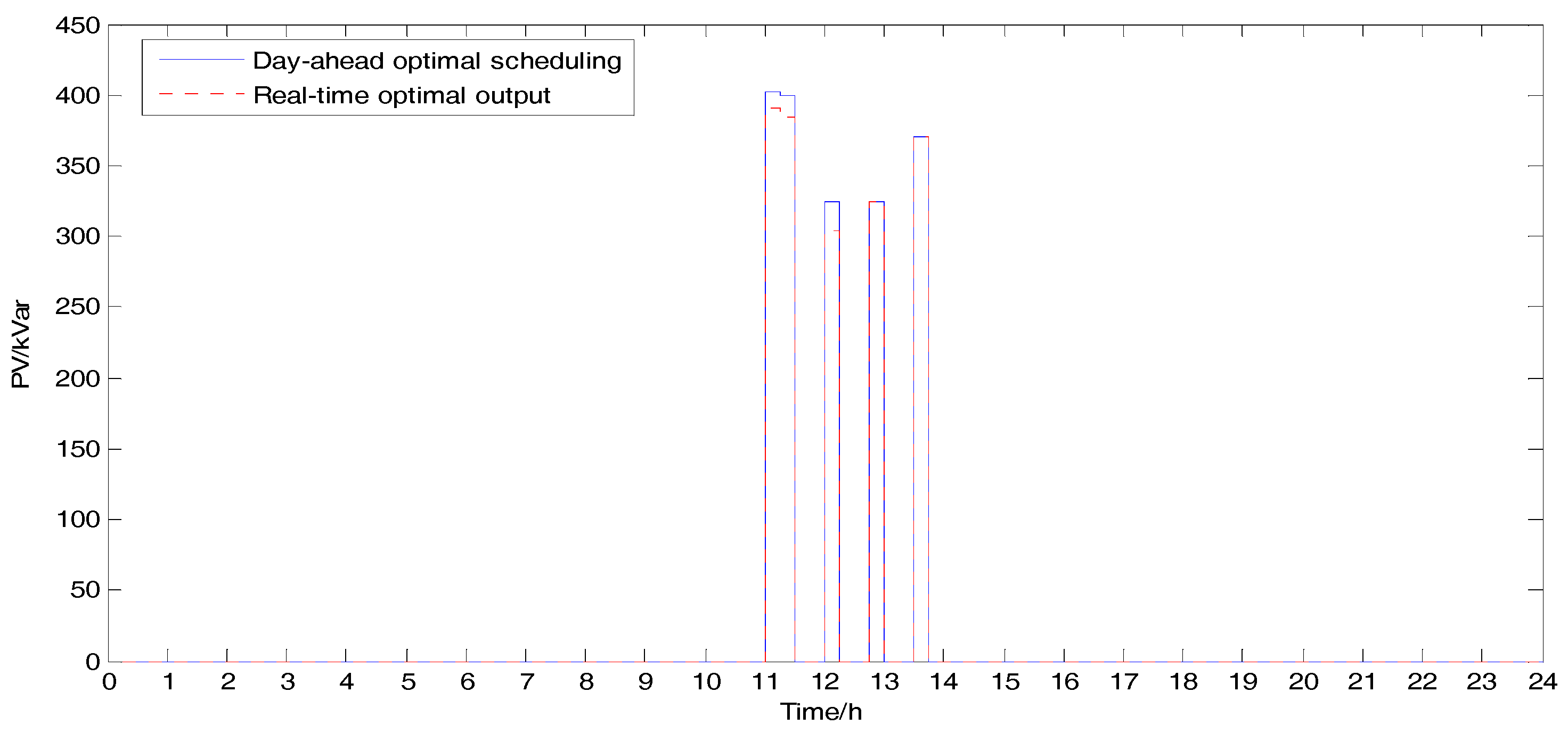
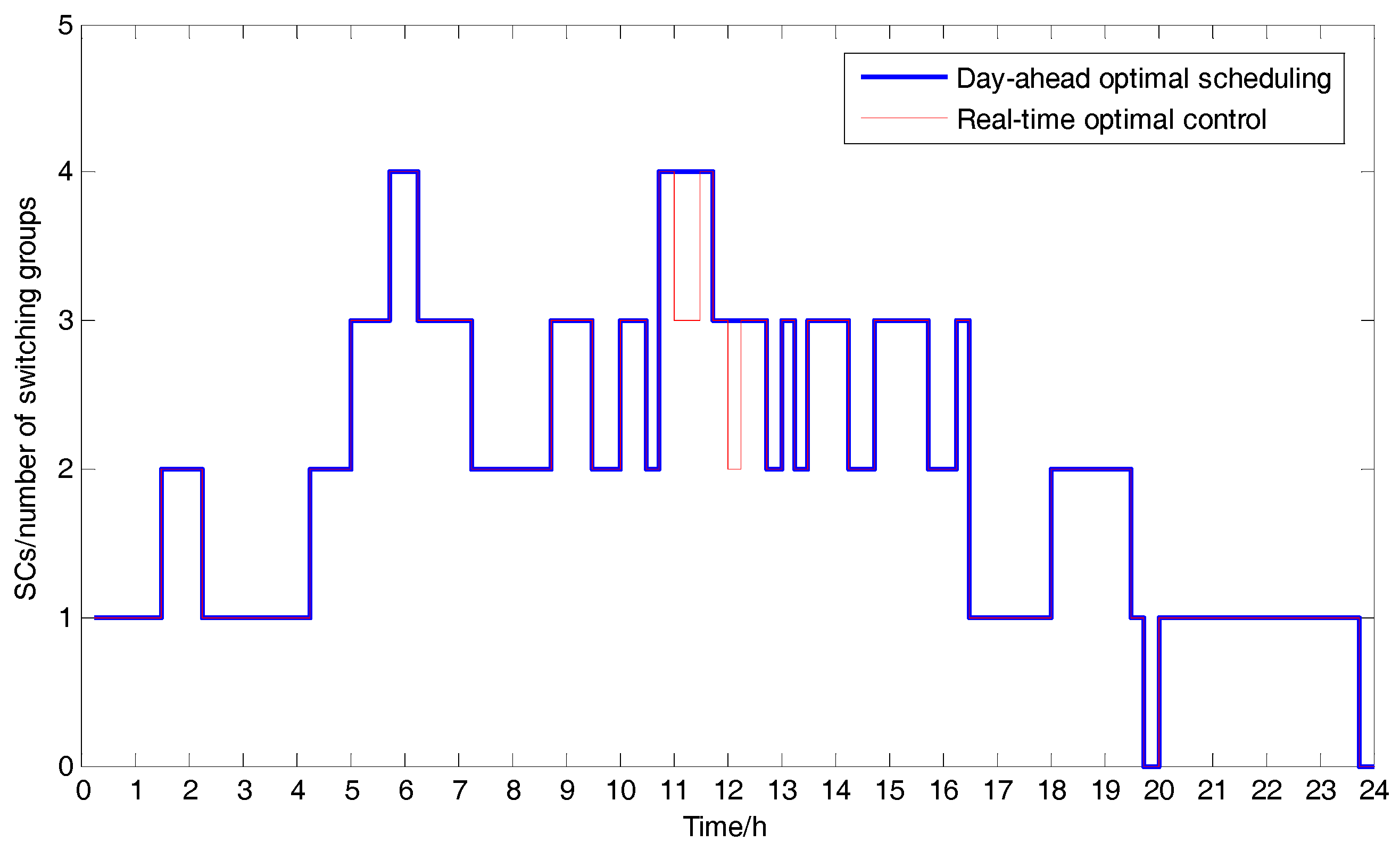
5.4. Real-Time Voltage Optimal Voltage Control
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| A | weighted adjacency matrix of the network |
| Aij | weighted value of the edge between nodes i and j |
| ki | the sum of all the weighted values of the links connected with node i |
| m | the total edge weight |
| ΔP | the changes in the injections of active power |
| ΔQ | the changes in the injections of reactive power |
| Δδ | the incremental change in phase angle |
| ΔU | the incremental change in voltage magnitude |
| SPU | voltage magnitude sensitivity with respect to active power |
| SQU | voltage magnitude sensitivity with respect to reactive power |
| SPδ | voltage phase angle sensitivity with respect to active power |
| SQδ | voltage phase angle sensitivity with respect to reactive power |
| Qsupplied | the total reactive power supported by the PVs and SCs in the sub-network Ck |
| γ | reactive power balance degree |
| β | intra-partition coupling degree |
| ρ | conventional modularity index |
| ρim | improved modularity index |
| Δvi | the incremental voltage change of node i |
| the reactive-voltage sensitivity of ith PV unit on the ith node in sub-network Ck | |
| Cinstall | the maintenance cost of OLTC |
| NOLTC | the maximum allowable number of OLTC operations without maintenance |
| tapOLTC(t) | tap-position of OLTC at time t |
| tapOLTC(t − 1) | tap-position of OLTC at time t − 1 |
| TapOLTC,min | the lower boundary of the tap-position |
| TapOLTC,max | the upper boundary of the tap-position |
| T_OLTC | the total tap operations within a day |
| TTOmax | the maximum allowable tap operations |
| cPV | the compensation factor of inverter losses due to the reactive power utilization |
| CK | the Kth sub-network |
| nPV | the numbers of PVs within CK |
| QPV,n(t) | the absorbed/injected value of utilized reactive power from a PV inverter in node n at the time t |
| Qmax,n | maximum reactive power capacity of the PV inverter in node n |
| PPV,n | the active power of each PV inverter in node n at time t |
| LSC | the maintenance cost caused by the SC tap-changing |
| SSC | the capacity of one group SC |
| QSC,n(t) | reactive power regulated by SC in node n at time t |
| QSC,n(t − 1) | reactive power regulated by SC in node n at time t − 1 |
| cLOSS | the grid loss compensation cost |
| Iline,n(t) | the current of line n at time t |
| Zline,n | impedance of line n |
| PGi | active power generated by conventional generators |
| QGi | reactive power generated by conventional generators |
| PPVi | the active power generated by PV units |
| QPVi | the reactive power generated by PV units |
| PDi | active power demand of loads |
| QDi | reactive power demand of loads |
| Vi | the voltage magnitudes of node i |
| Bij | susceptance of the branch consisting of nodes i and j |
| Gij | conductance of the branch consisting of nodes i and j |
| θij | the phase difference of node i and node j |
| QSC,i | reactive power generated by distributed SCs |
| d | index of generations |
| xd | the positions of the particles at the dth generation |
| xd+1 | the positions of the particles at the d+1th generation |
| vd | corresponding velocities of the particles of the dth generation |
| vd+1 | corresponding velocities of the particles of the d + 1th generation |
| c0 | the inertia weight factor |
| c1, c2 | the acceleration constants |
| gi,t | current position of the particle i in these particles at iteration t. |
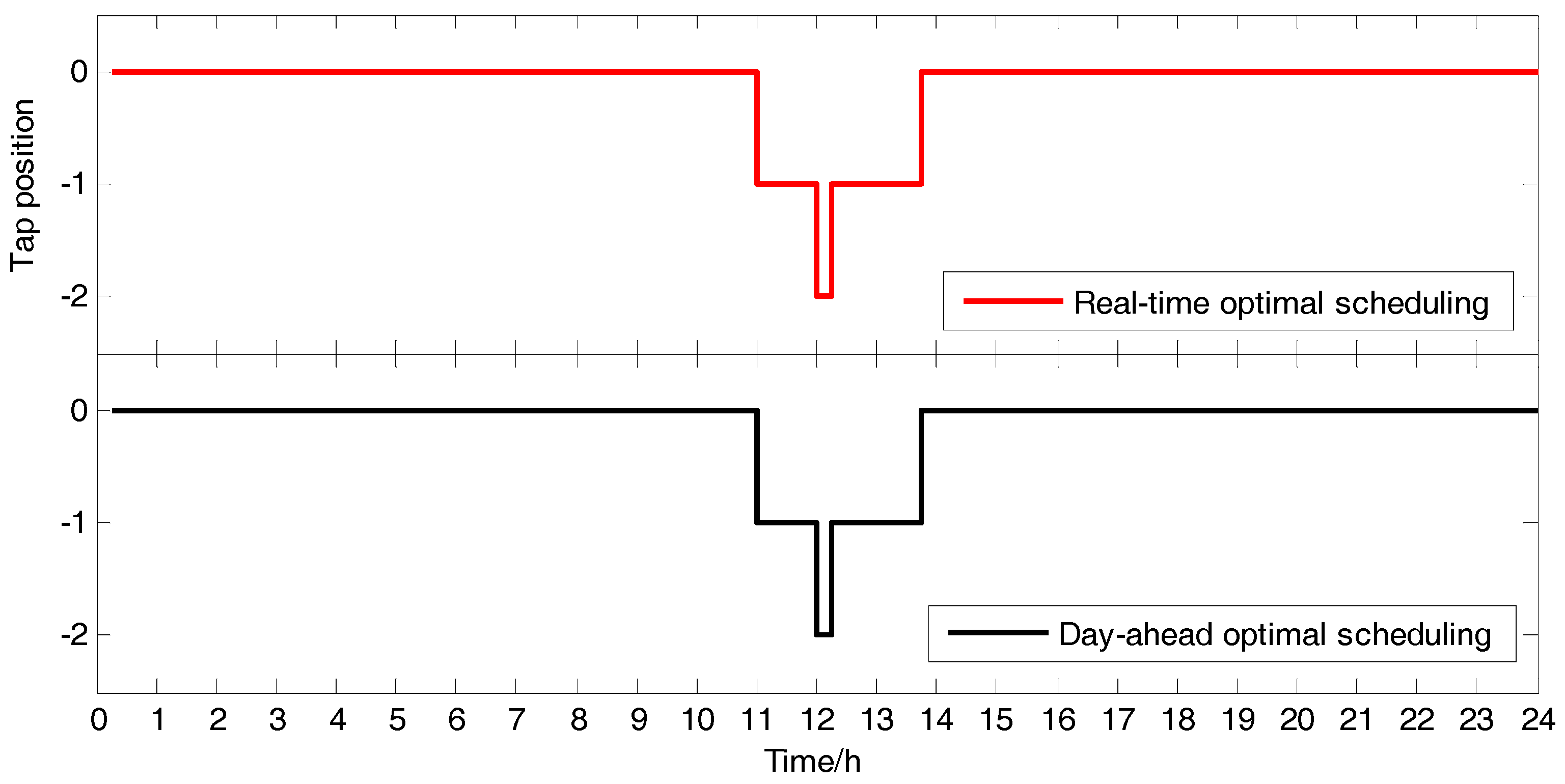
| (t) | Tap-position of OLTC at time t in real-time optimal control |
| (t) | Tap-position of OLTC at time t in day-ahead optimal scheduling |
| (t) | reactive power regulated by a PV inverter in node n at the time t in real-time optimal control |
| (t) | reactive power regulated by a PV inverter in node n at the time t in day-ahead optimal scheduling |
| (t) | reactive power regulated by SC in node n at time t in real-time optimal control |
| (t) | reactive power regulated by SC in node n at time t in day-ahead optimal scheduling |
Appendix A
| From | To | Line Impedance (Ω/km) | Line Type | Length (km) |
|---|---|---|---|---|
| 1 | 2 | 0.0754 + j0.085 | DL-300 | 0.92 |
| 1 | 3 | 0.0754 + j0.085 | DL-300 | 0.86 |
| 1 | 4 | 0.0754 + j0.085 | DL-300 | 0.89 |
| 2 | 5 | 0.32 + j0.119 | JKLY-70 | 0.05 |
| 5 | 6 | 0.32 + j0.119 | JKLY-70 | 0.14 |
| 6 | 7 | 0.32 + j0.119 | JKLY-70 | 0.25 |
| 7 | 8 | 0.32 + j0.119 | JKLY-70 | 0.12 |
| 5 | 9 | 0.32 + j0.119 | JKLY-70 | 0.23 |
| 9 | 10 | 0.32 + j0.119 | JKLY-70 | 0.12 |
| 10 | 11 | 0.32 + j0.119 | JKLY-70 | 0.14 |
| 11 | 12 | 0.32 + j0.119 | JKLY-70 | 0.21 |
| 12 | 13 | 0.32 + j0.119 | JKLY-70 | 0.19 |
| 13 | 14 | 0.32 + j0.119 | JKLY-70 | 0.24 |
| 9 | 15 | 0.32 + j0.119 | JKLY-70 | 1.12 |
| 15 | 16 | 0.32 + j0.119 | JKLY-70 | 0.23 |
| 16 | 17 | 0.32 + j0.119 | JKLY-70 | 0.21 |
| 17 | 18 | 0.32 + j0.119 | JKLY-70 | 0.19 |
| 18 | 19 | 0.32 + j0.119 | JKLY-70 | 0.09 |
| 19 | 20 | 0.32 + j0.119 | JKLY-70 | 0.11 |
| 20 | 21 | 0.32 + j0.119 | JKLY-70 | 0.15 |
| 15 | 22 | 0.32 + j0.119 | JKLY-70 | 1.33 |
| 22 | 23 | 0.32 + j0.119 | JKLY-70 | 0.34 |
| 23 | 24 | 0.32 + j0.119 | JKLY-70 | 0.23 |
| 24 | 25 | 0.32 + j0.119 | JKLY-70 | 0.13 |
| 25 | 26 | 0.32 + j0.119 | JKLY-70 | 0.07 |
| 26 | 27 | 0.32 + j0.119 | JKLY-70 | 0.12 |
| 27 | 28 | 0.32 + j0.119 | JKLY-70 | 0.13 |
| 28 | 29 | 0.32 + j0.119 | JKLY-70 | 0.06 |
| 26 | 30 | 0.32 + j0.119 | JKLY-70 | 0.12 |
| 30 | 31 | 0.32 + j0.119 | JKLY-70 | 0.18 |
| 30 | 31 | 0.32 + j0.119 | JKLY-70 | 0.34 |
| 34 | 32 | 0.32 + j0.119 | JKLY-70 | 0.23 |
| 32 | 33 | 0.32 + j0.119 | JKLY-70 | 0.21 |
| 3 | 34 | 0.099 + j0.093 | JKLY-185 | 0.05 |
| 34 | 35 | 0.099 + j0.093 | JKLY-185 | 0.34 |
| 35 | 36 | 0.099 + j0.093 | JKLY-185 | 0.23 |
| 36 | 37 | 0.099 + j0.093 | JKLY-185 | 0.31 |
| 37 | 38 | 0.099 + j0.093 | JKLY-185 | 0.22 |
| 38 | 39 | 0.099 + j0.093 | JKLY-185 | 0.12 |
| 39 | 40 | 0.099 + j0.093 | JKLY-185 | 0.19 |
| 40 | 41 | 0.099 + j0.093 | JKLY-185 | 1.12 |
| 41 | 42 | 0.099 + j0.093 | JKLY-185 | 0.35 |
| 42 | 43 | 0.099 + j0.093 | JKLY-185 | 0.34 |
| 43 | 44 | 0.099 + j0.093 | JKLY-185 | 0.18 |
| 44 | 45 | 0.099 + j0.093 | JKLY-185 | 0.13 |
| 45 | 46 | 0.099 + j0.093 | JKLY-185 | 0.25 |
| 46 | 47 | 0.099 + j0.093 | JKLY-185 | 0.24 |
| 47 | 48 | 0.099 + j0.093 | JKLY-185 | 0.16 |
| 48 | 49 | 0.099 + j0.093 | JKLY-185 | 0.32 |
| 4 | 50 | 0.32 + j0.119 | JKLY-70 | 0.06 |
| 50 | 51 | 0.32 + j0.119 | JKLY-70 | 0.32 |
| 51 | 52 | 0.32 + j0.119 | JKLY-70 | 0.28 |
| 52 | 53 | 0.32 + j0.119 | JKLY-70 | 0.26 |
| 53 | 54 | 0.32 + j0.119 | JKLY-70 | 0.29 |
| 54 | 55 | 0.32 + j0.119 | JKLY-70 | 1.03 |
| 55 | 56 | 0.32 + j0.119 | JKLY-70 | 0.12 |
| 56 | 57 | 0.32 + j0.119 | JKLY-70 | 0.09 |
| 57 | 58 | 0.32 + j0.119 | JKLY-70 | 0.23 |
| 58 | 59 | 0.32 + j0.119 | JKLY-70 | 0.36 |
| 59 | 60 | 0.32 + j0.119 | JKLY-70 | 0.34 |
| 60 | 61 | 0.32 + j0.119 | JKLY-70 | 0.28 |
| 61 | 62 | 0.32 + j0.119 | JKLY-70 | 0.22 |
| Bus No. | Load (kW + j kVar) | Bus No. | Load (kW + j kVar) |
|---|---|---|---|
| 1 | 0 | 32 | 100.784 + j15.001 |
| 2 | 20.008 + j6.423 | 33 | 50.147 + j15.331 |
| 3 | 32.112 + j5.221 | 34 | 10.334 + j0.356 |
| 4 | 24.445 + j6.889 | 35 | 1212.768 + j223.489 |
| 5 | 14.565 + j11.235 | 36 | 1222.636 + j343.321 |
| 6 | 1345.55 + j460.228 | 37 | 338.492 + j27.128 |
| 7 | 24.142 + j4.421 | 38 | 121.464 + j22.788 |
| 8 | 353.018 + j96.561 | 39 | 126.418 + j32.336 |
| 9 | 18.334 + j5.214 | 40 | 314.048 + j23.834 |
| 10 | 591.154 + j140.336 | 41 | 119.422 + j22.218 |
| 11 | 542.785 + j175.564 | 42 | 154.296 + j36.647 |
| 12 | 260.592 + j23.833 | 43 | 260.592 + j30.833 |
| 13 | 152.645 + j30.001 | 44 | 699.356 + j75.389 |
| 14 | 150.088 + j50.362 | 45 | 129.378 + j78.331 |
| 15 | 14.332 + j4.365 | 46 | 299.663 + j65.227 |
| 16 | 111.506 + j10.369 | 47 | 599.153 + j25.233 |
| 17 | 100.587 + j63.245 | 48 | 552.632 + j85.336 |
| 18 | 110.114 + j10.336 | 49 | 541.088 + j120.333 |
| 19 | 90.223 + j36.102 | 50 | 30.231 + j12.244 |
| 20 | 110.004 + j42.331 | 51 | 1117.921 + j332.145 |
| 21 | 100.753 + j14.557 | 52 | 1197.551 + j351.214 |
| 22 | 6.331 + j1.254 | 53 | 1307.672 + j110.221 |
| 23 | 426.991+ j85.933 | 54 | 116.778 +j22.214 |
| 24 | 622.155+ j120.383 | 55 | 120.345 + j56.333 |
| 25 | 738.499 + j145.361 | 56 | 117.672 + j42.351 |
| 26 | 12.366 + j2.366 | 57 | 100.447 + j10.236 |
| 27 | 110.568 + j36.688 | 58 | 325.661 + j145.361 |
| 28 | 100.888 + j34.444 | 59 | 101.352 + j31.224 |
| 29 | 200.963 + j80.382 | 60 | 100.398 + j45.14 |
| 30 | 103.224 + j36.225 | 61 | 114.872 + j32.331 |
| 31 | 100.355 + j15.253 | 62 | 500.231 + j112.454 |
References
- Hosenuzzaman, M.; Rahim, N.A.; Selvaraj, J.; Hasanuzzaman, M.; Malek, A.B.M.A.; Nahar, A. Global prospects, progress, policies, and environmental impact of solar photovoltaic power generation. Renew. Sustain. Energy Rev. 2015, 41, 284–297. [Google Scholar] [CrossRef]
- Saponara, S.; Fanucci, L.; Bernardo, F.; Falciani, A. Predictive Diagnosis of High-Power Transformer Faults by Networking Vibration Measuring Nodes with Integrated Signal Processing. IEEE Trans. Instrum. Meas. 2016, 65, 1749–1760. [Google Scholar] [CrossRef]
- Lee, J.H. Model predictive control: Review of the three decades of development. Int. J. Control Autom. Syst. 2011, 9, 415. [Google Scholar] [CrossRef]
- Saponara, S.; Bacchillone, T. Network Architecture, Security Issues, and Hardware Implementation of a Home Area Network for Smart Grid. J. Comput. Netw. Commun. 2012, 2012, 285–293. [Google Scholar] [CrossRef]
- Mcdaniel, P.; Mclaughlin, S. Security and Privacy Challenges in the Smart Grid. IEEE Secur. Priv. 2009, 7, 75–77. [Google Scholar] [CrossRef]
- Ding, M.; Wang, W.; Wang, X.; Song, Y.; Chen, D.; Sun, M. A Review on the Effect of Large-scale PV Generation on Power Systems. Proc. CSEE 2014, 34, 1–14. [Google Scholar]
- Kekatos, V.; Wang, G.; Conejo, A.J.; Giannakis, G.B. Stochastic reactive power management in microgrids with renewables. IEEE Trans. Power Syst. 2014, 30, 3386–3395. [Google Scholar] [CrossRef]
- Smith, J.W.; Sunderman, W.; Dugan, R.; Seal, B. Smart inverter volt/var control functions for high penetration of PV on distribution systems. In Proceedings of the IEEE/PES Power Systems Conference and Exposition (PSCE), Phoenix, AZ, USA, 20–23 March 2011; pp. 1–6. [Google Scholar]
- Alyami, S.; Wang, Y.; Wang, C.; Zhao, J. Adaptive Real Power Capping Method for Fair Overvoltage Regulation of Distribution Networks With High Penetration of PV Systems. IEEE Trans. Smart Grid 2014, 5, 2729–2738. [Google Scholar] [CrossRef]
- Jahangiri, P.; Aliprantis, D.C. Distributed volt/var control by PV inverters. IEEE Trans. Power Syst. 2013, 28, 3429–3439. [Google Scholar] [CrossRef]
- Dall’Anese, E.; Dhople, S.V.; Giannakis, G.B. Optimal dispatch of photovoltaic inverters in residential distribution systems. IEEE Trans. Sustain. Energy 2014, 5, 487–497. [Google Scholar] [CrossRef]
- Efkarpidis, N.; Rybel, T.D.; Driesen, J. Optimization control scheme utilizing small-scale distributed generators and OLTC distribution transformers. Sustain. Energy Grids Netw. 2016, 8, 74–84. [Google Scholar] [CrossRef]
- Yang, H.T.; Chen, Y.T.; Liao, J.T.; Yang, C.-T. Over-voltage mitigation control strategies for distribution system with high PV penetration. In Proceedings of the IEEE, International Conference on Intelligent System Application to Power Systems, Porto, Portugal, 11–16 September 2015. [Google Scholar]
- Biserica, M.; Foggia, G.; Chanzy, E.; Passelergue, J.C. Network partition for coordinated control in active distribution networks. In Proceedings of the IEEE Powertech, Grenoble, France, 16–20 June 2013. [Google Scholar]
- Xu, Y.; Jiang, W.; Cheng, X. Partitioning for reactive voltage based on spectral clustering and pilot nodes selection. Power Syst. Prot. Control 2016, 44, 73–78. [Google Scholar]
- Hu, Z.; Wang, X.; Wang, X.; Chen, H. A Two-Layered Network Partitioning Approach for Optimal Reactive Power Dispatching. Power Syst. Technol. 2004, 28, 37–41. [Google Scholar]
- Wei, Z.; Liu, J.; Cheng, F.; Song, Q.; Deng, J.; Chen, X. Fast powernetwork partitioning method in Mvar control space based on community wining. Proc. CSEE 2011, 31, 166–172. [Google Scholar]
- Long, C.; Procopiou, A.T.; Ochoa, L.F.; Bryson, G.; Randles, D. Performance of OLTC-based control strategies for LV networks with photovoltaics. In Proceedings of the IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Chen, Y.; Strothers, M.; Benigni, A. Day-ahead optimal scheduling of PV inverters and OLTC in distribution feeders. In Proceedings of the IEEE Power and Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Gao, C. Voltage Control in Distribution Networks Using On-Load Tap Changer Transformers. Ph.D. Thesis, University of Bath, Bath, UK, 2013. [Google Scholar]
- Long, C.; Ochoa, L.F. Voltage Control of PV-Rich LV Networks: OLTC-Fitted Transformer and Capacitor Banks. IEEE Trans. Power Syst. 2015, 31, 4016–4025. [Google Scholar] [CrossRef]
- Agalgaonkar, Y.P.; Pal, B.C.; Jabr, R.A. Distribution Voltage Control Considering the Impact of PV Generation on Tap Changers and Autonomous Regulators. IEEE Trans. Power Syst. 2013, 29, 182–192. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, H.; Wang, J.; Begovic, M. Inverter-Less Hybrid Voltage/Var Control for Distribution Circuits with Photovoltaic Generators. IEEE Trans. Smart Grid 2014, 5, 2718–2728. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2004, 69, 066133. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Zeng, L.; Wang, L. Maximum penetration of DG based on voltage sensitivity. East China Electr. Power 2013, 41, 1175–1180. [Google Scholar]
- Oshiro, M.; Tanaka, K.; Senjyu, T.; Toma, S.; Yona, A.; Saber, A.Y.; Funabashi, T.; Kim, C.-H. Optimal voltage control in distribution systems using PV generators. Int. J. Electr. Power Energy Syst. 2011, 33, 485–492. [Google Scholar] [CrossRef]
- Zhao, B.; Guo, C.X.; Cao, Y.J. Improved particle swam optimization algorithm for OPF problems. In Proceedings of the Power Systems Conference and Exposition, New York, NY, USA, 10–13 October 2004; pp. 233–238. [Google Scholar]
- Zhao, B.; Guo, C.X.; Cao, Y.J. An improved particle swarm optimization algorithm for optimal reactive power dispatch. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 16 June 2005; pp. 272–279. [Google Scholar]




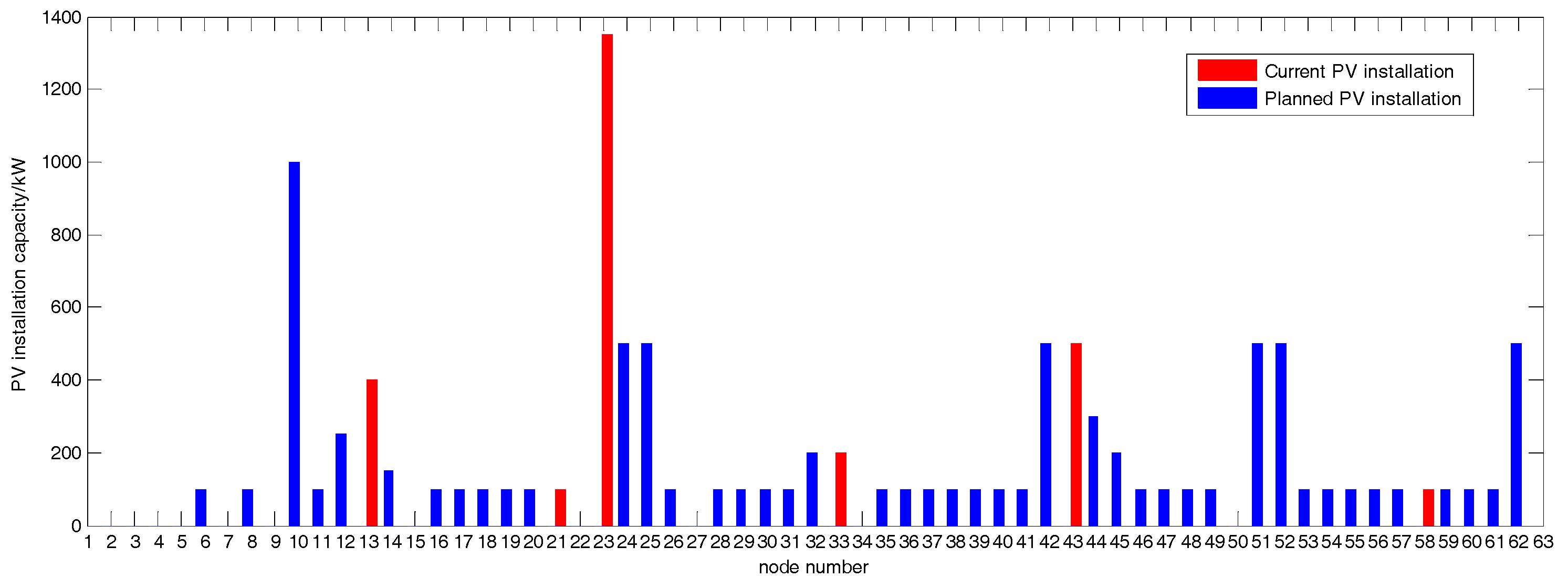



| Node Number | 13 | 21 | 23 | 33 | 43 | 58 |
| Installed Capacity (kW) | 400 | 100 | 1350 | 200 | 500 | 100 |
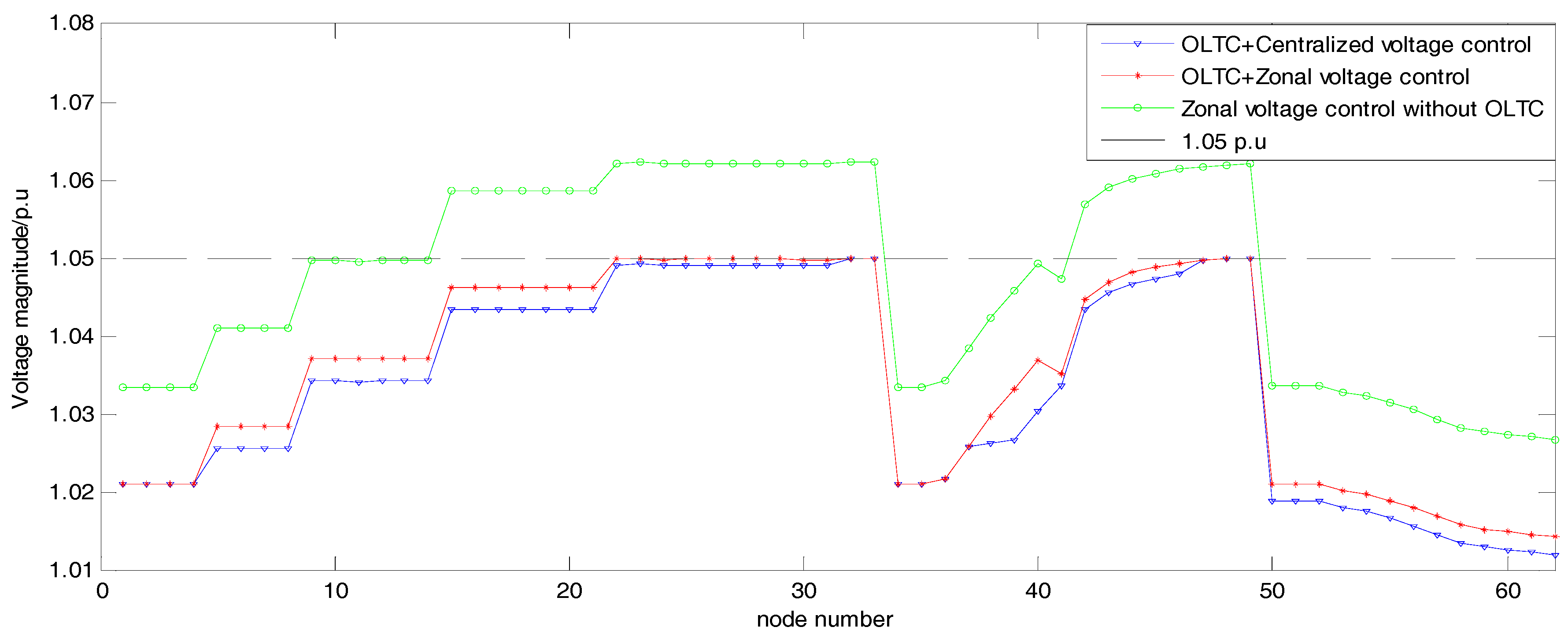
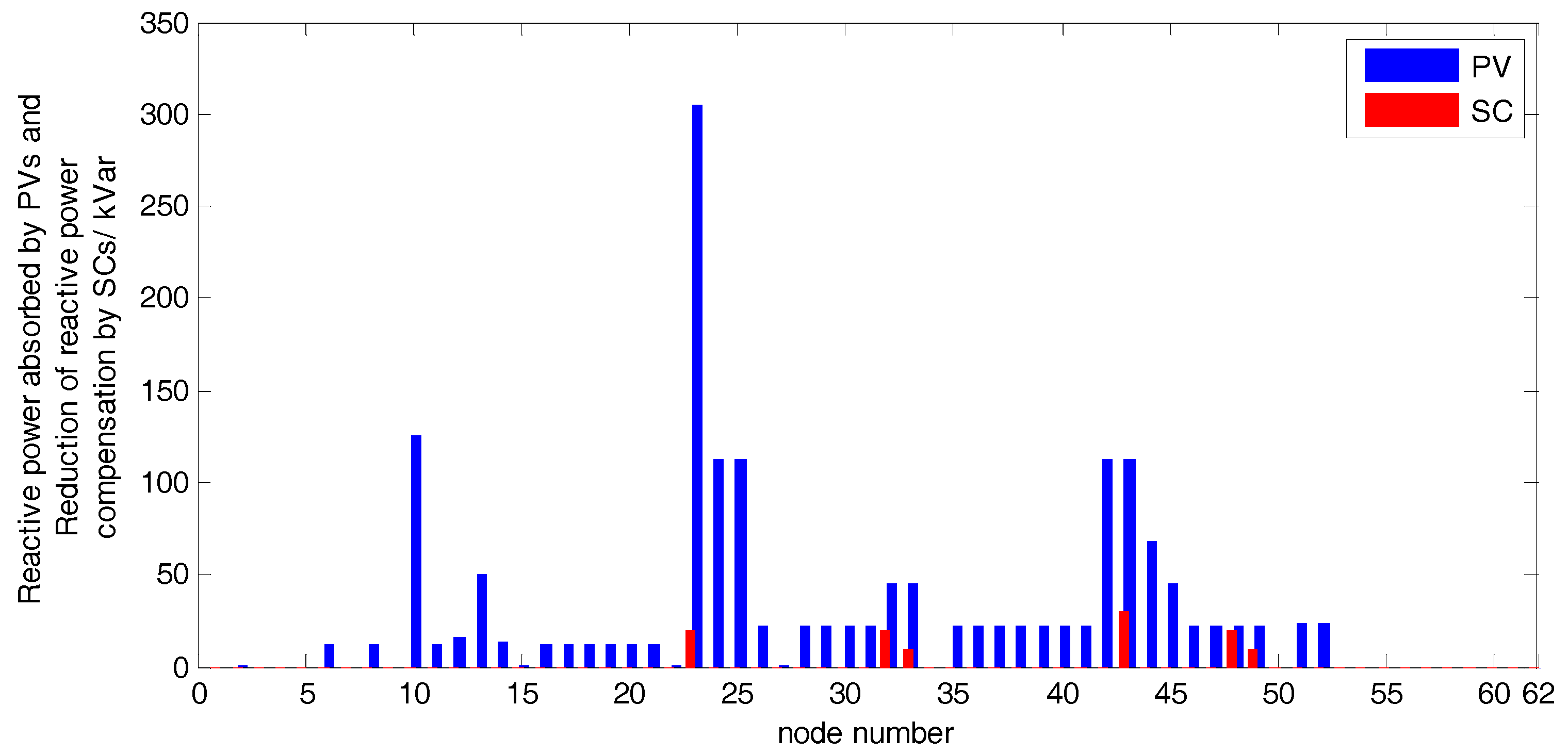
| Case | PV (kVar) | SC (kVar) | Total Cost (USD) |
|---|---|---|---|
| Zonal voltage control without an OLTC | 1483 | 790 | 300.53/$ |
| OLTC + Zonal voltage control | 1290 | 270 | 176.15/$ |
| Case | PV (kVar) | SC (kVar) | Total Cost (USD) | Time (s) |
|---|---|---|---|---|
| OLTC + Centralized voltage control | 1674 | 110 | 169.41/$ | 30.61 |
| OLTC + Zonal voltage control | 1290 | 270 | 176.15/$ | 4.32 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, C.; Zhao, B.; Ding, M.; Li, Z.; Ge, X. Zonal Voltage Control Combined Day-Ahead Scheduling and Real-Time Control for Distribution Networks with High Proportion of PVs. Energies 2017, 10, 1464. https://doi.org/10.3390/en10101464
Xiao C, Zhao B, Ding M, Li Z, Ge X. Zonal Voltage Control Combined Day-Ahead Scheduling and Real-Time Control for Distribution Networks with High Proportion of PVs. Energies. 2017; 10(10):1464. https://doi.org/10.3390/en10101464
Chicago/Turabian StyleXiao, Chuanliang, Bo Zhao, Ming Ding, Zhihao Li, and Xiaohui Ge. 2017. "Zonal Voltage Control Combined Day-Ahead Scheduling and Real-Time Control for Distribution Networks with High Proportion of PVs" Energies 10, no. 10: 1464. https://doi.org/10.3390/en10101464
APA StyleXiao, C., Zhao, B., Ding, M., Li, Z., & Ge, X. (2017). Zonal Voltage Control Combined Day-Ahead Scheduling and Real-Time Control for Distribution Networks with High Proportion of PVs. Energies, 10(10), 1464. https://doi.org/10.3390/en10101464




