Energy Rebound as a Potential Threat to a Low-Carbon Future: Findings from a New Exergy-Based National-Level Rebound Approach
Abstract
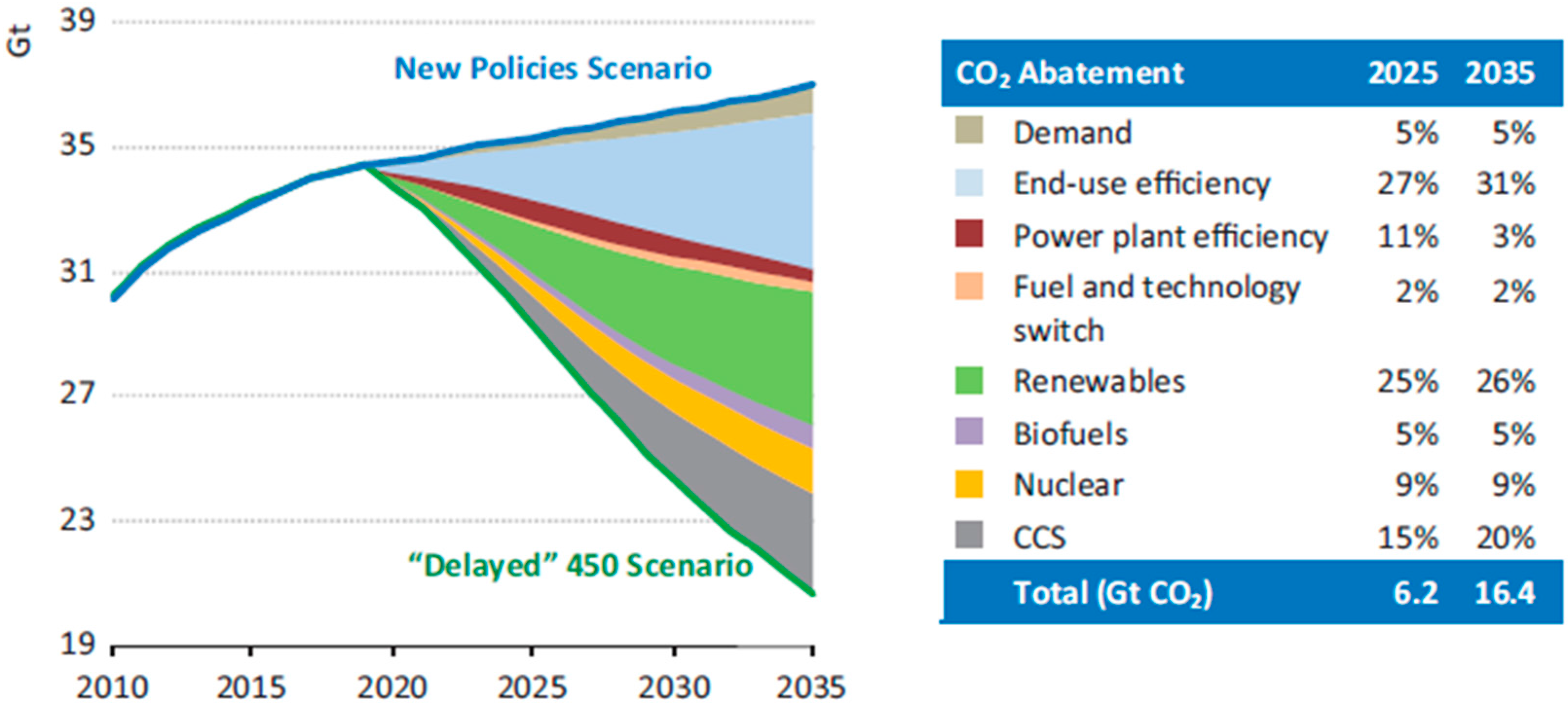
:1. Introduction: A Low Carbon Future—Under Threat from Energy Rebound
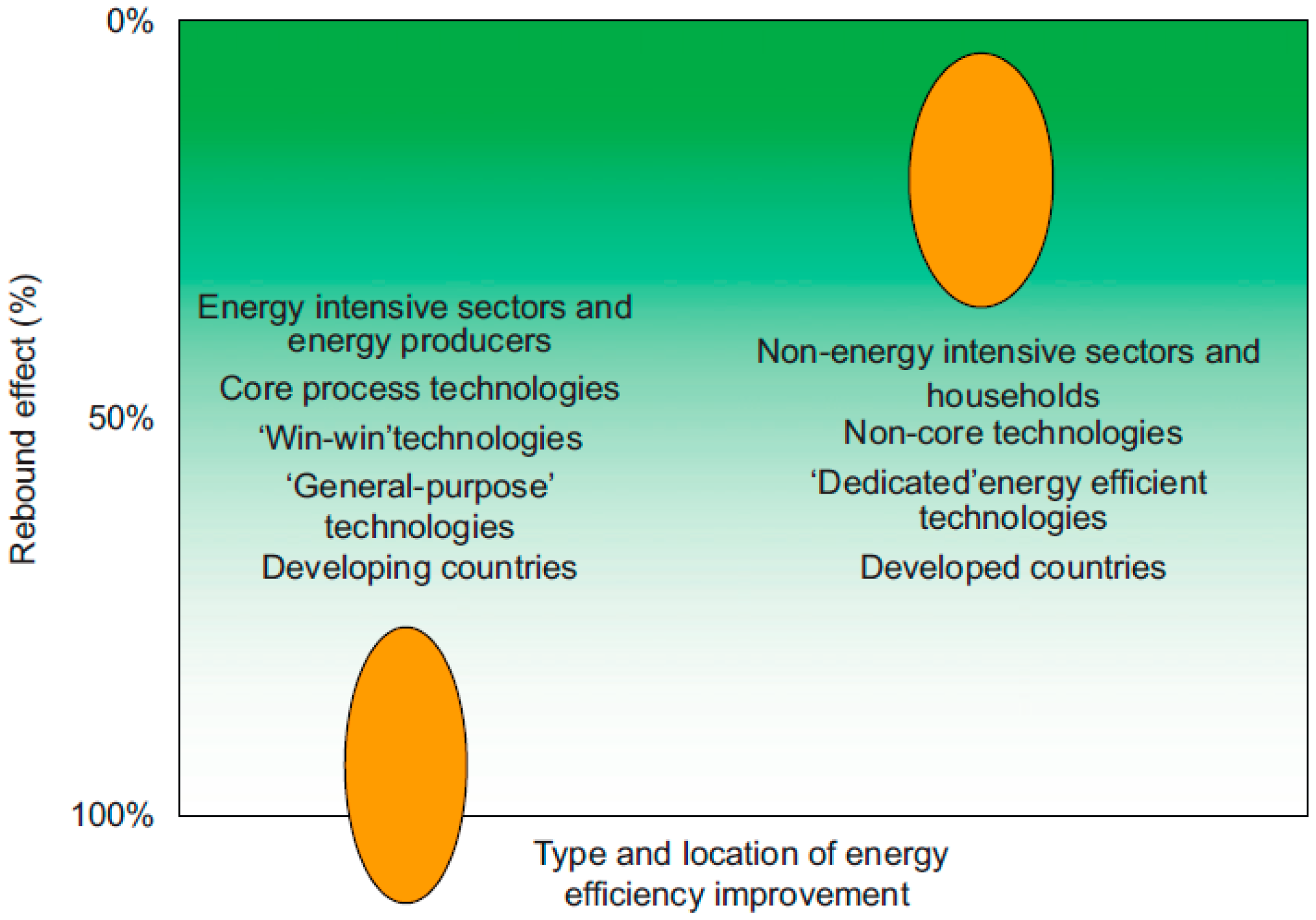
1.1. Concepts: Energy Efficiency and Energy Rebound
1.2. The Issue: More Empirical National Energy Rebound Studies Are Required
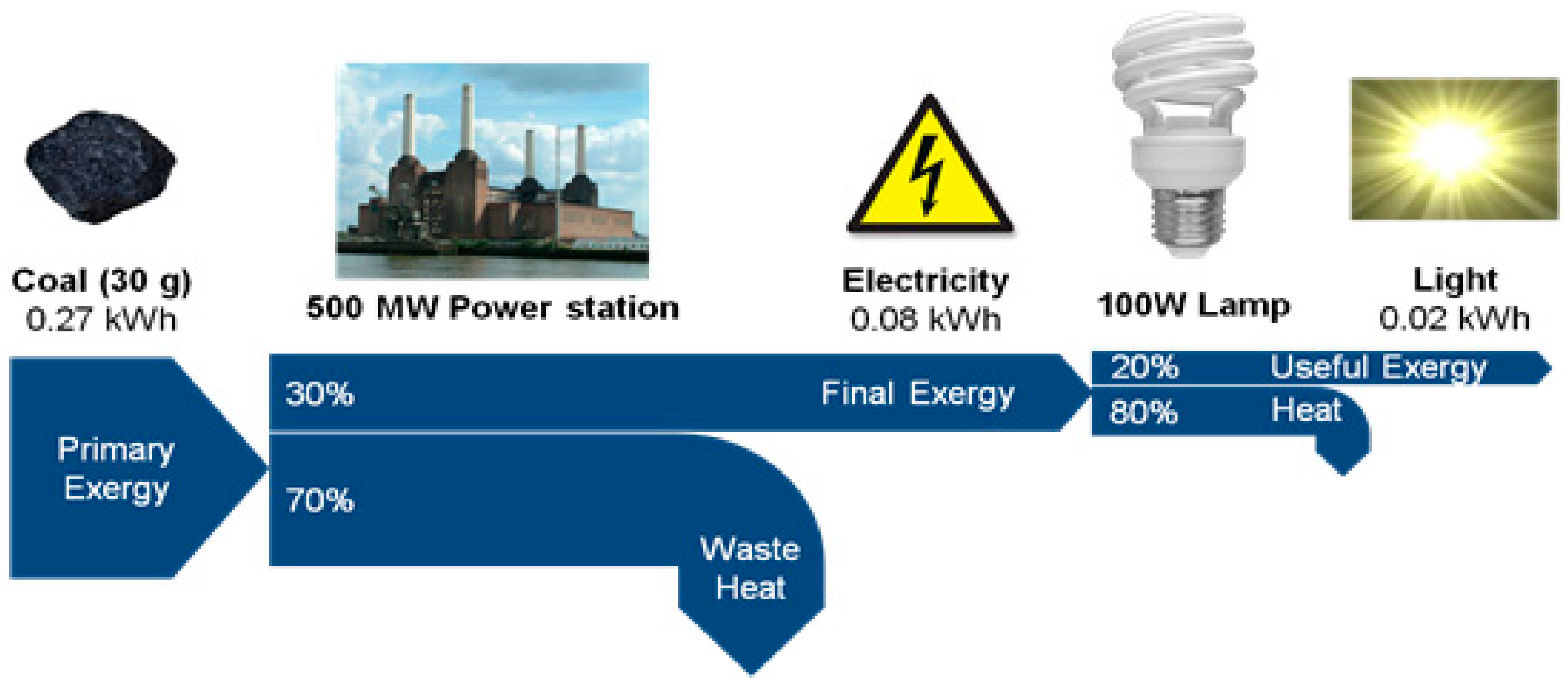
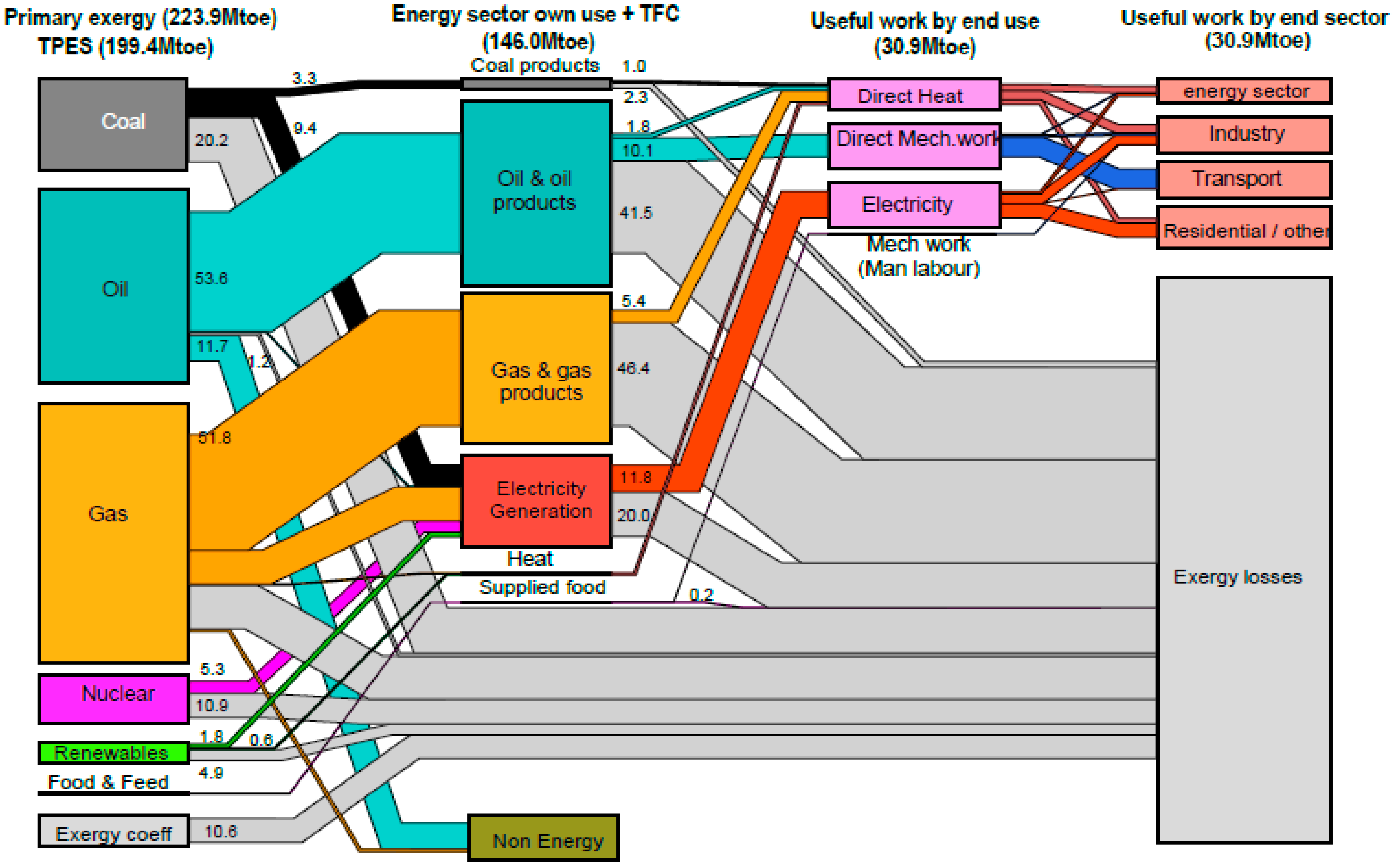
1.3. The Response: An Exergy-Based Approach to Estimate National Energy Rebound
2. Methods and Data
2.1. Step 1: Selecting the Aggregate Production Function
2.2. Step 2: Specifying and Estimating the Exergy-Based CES Function Parameters
2.2.1. The Exergy-Based CES Function
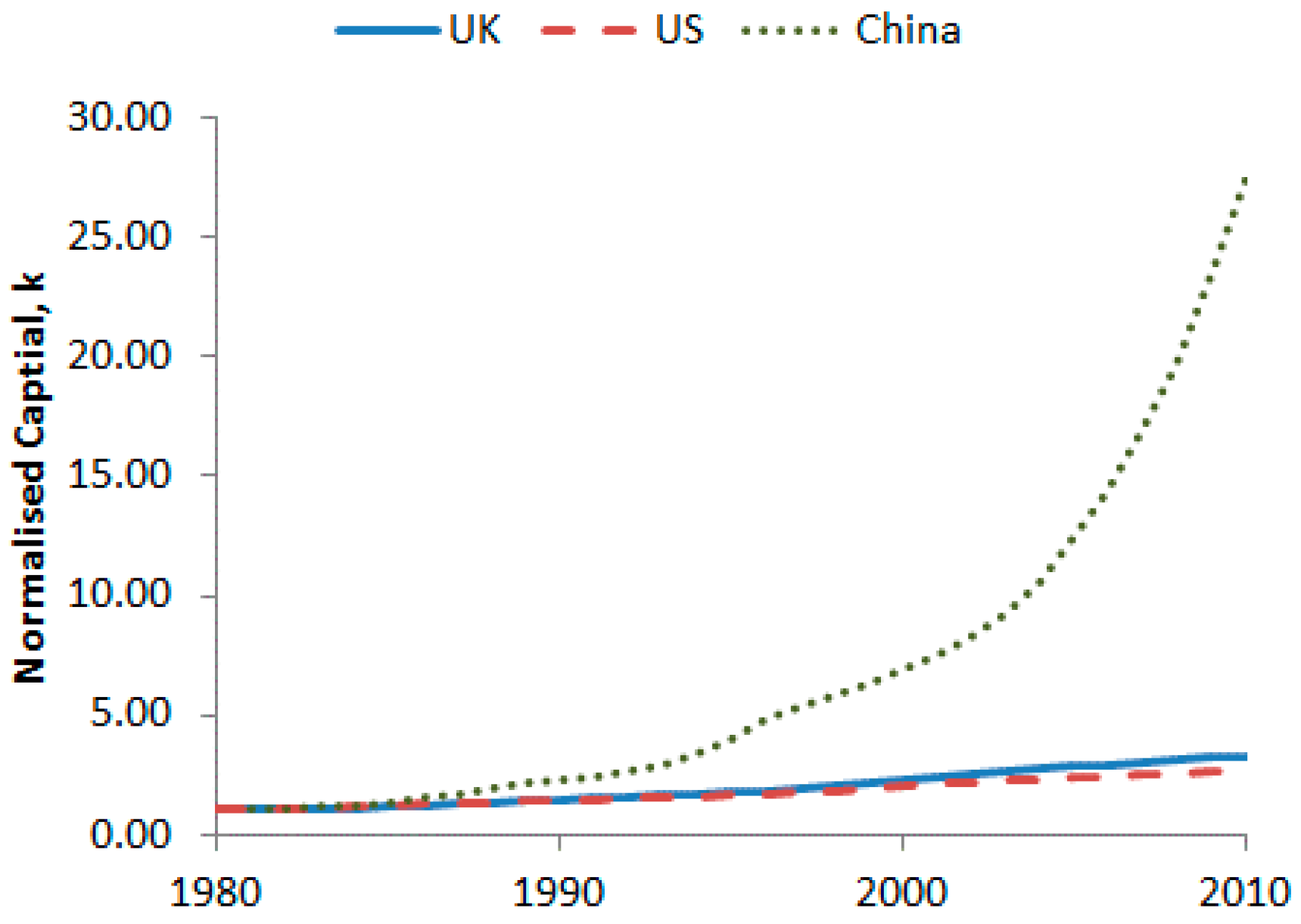
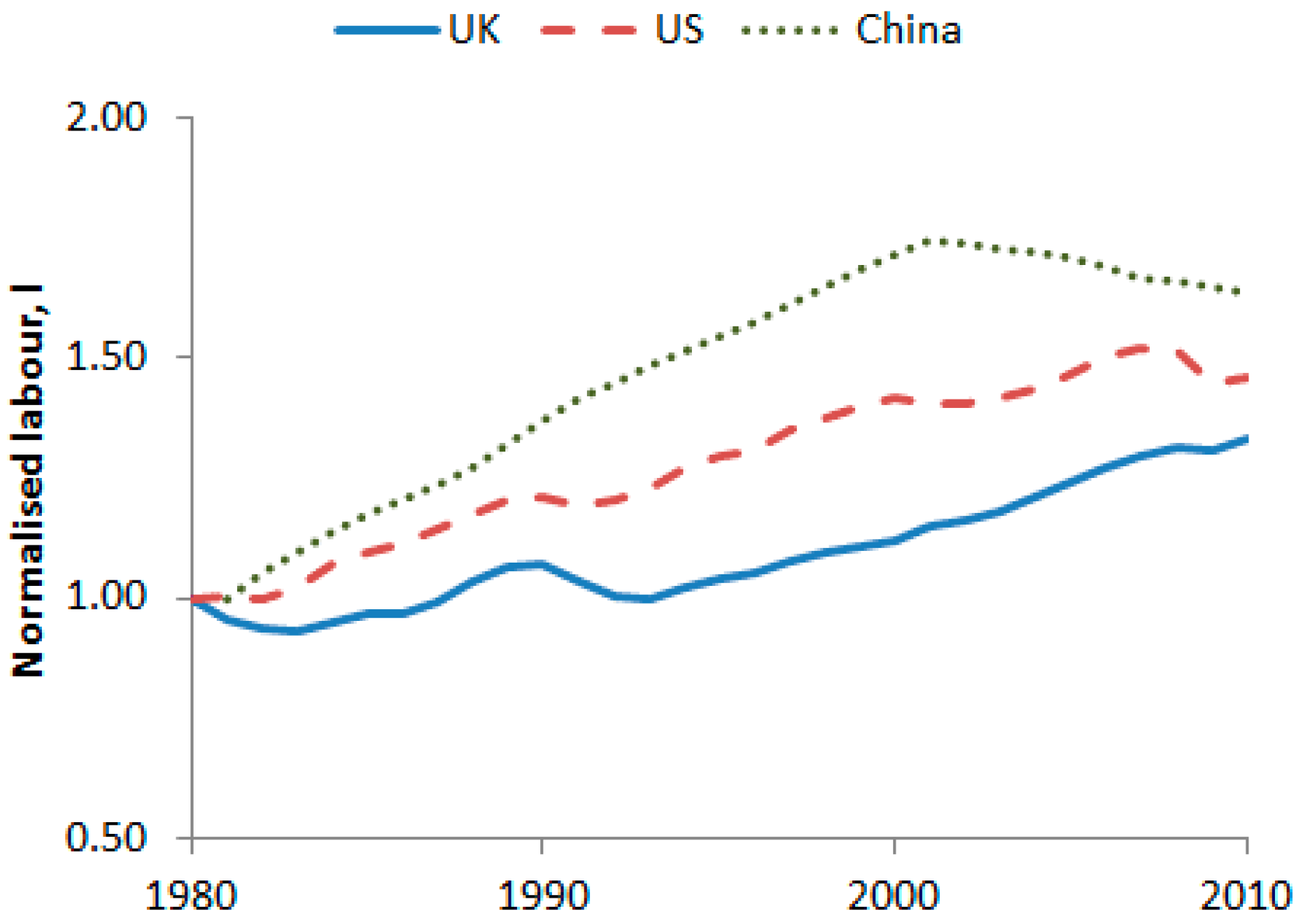
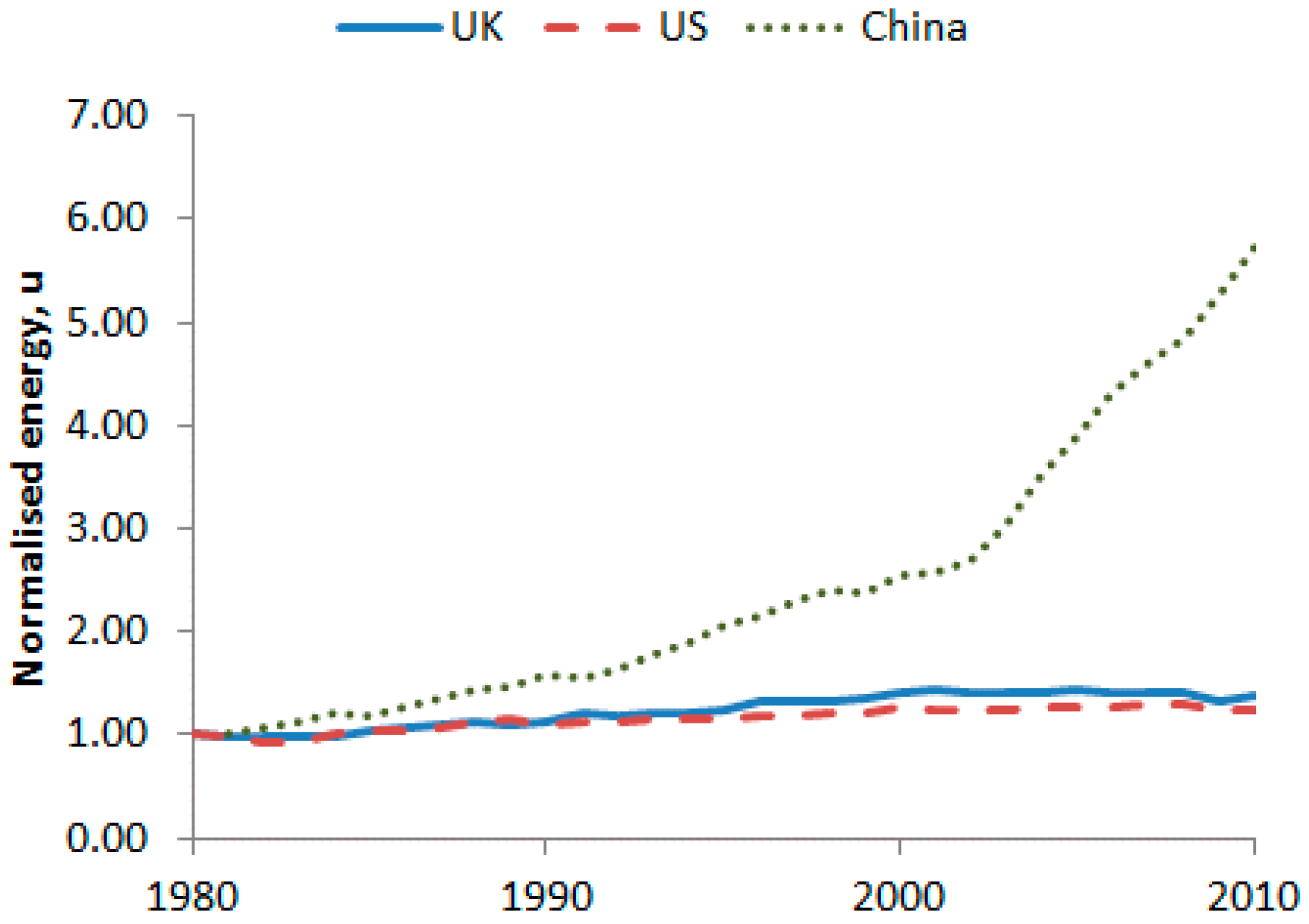
2.2.2. Input Data
2.2.3. Econometric Fitting of the CES Aggregate Production Function
2.3. Step 3: Derive Equations for Estimation of National Energy Rebound
2.3.1. Method 1: Ratio of Actual to Potential Energy Savings (AES/PES)
2.3.2. Method 2: Elasticity of Energy Use with Respect to Efficiency (EEE)
3. Results
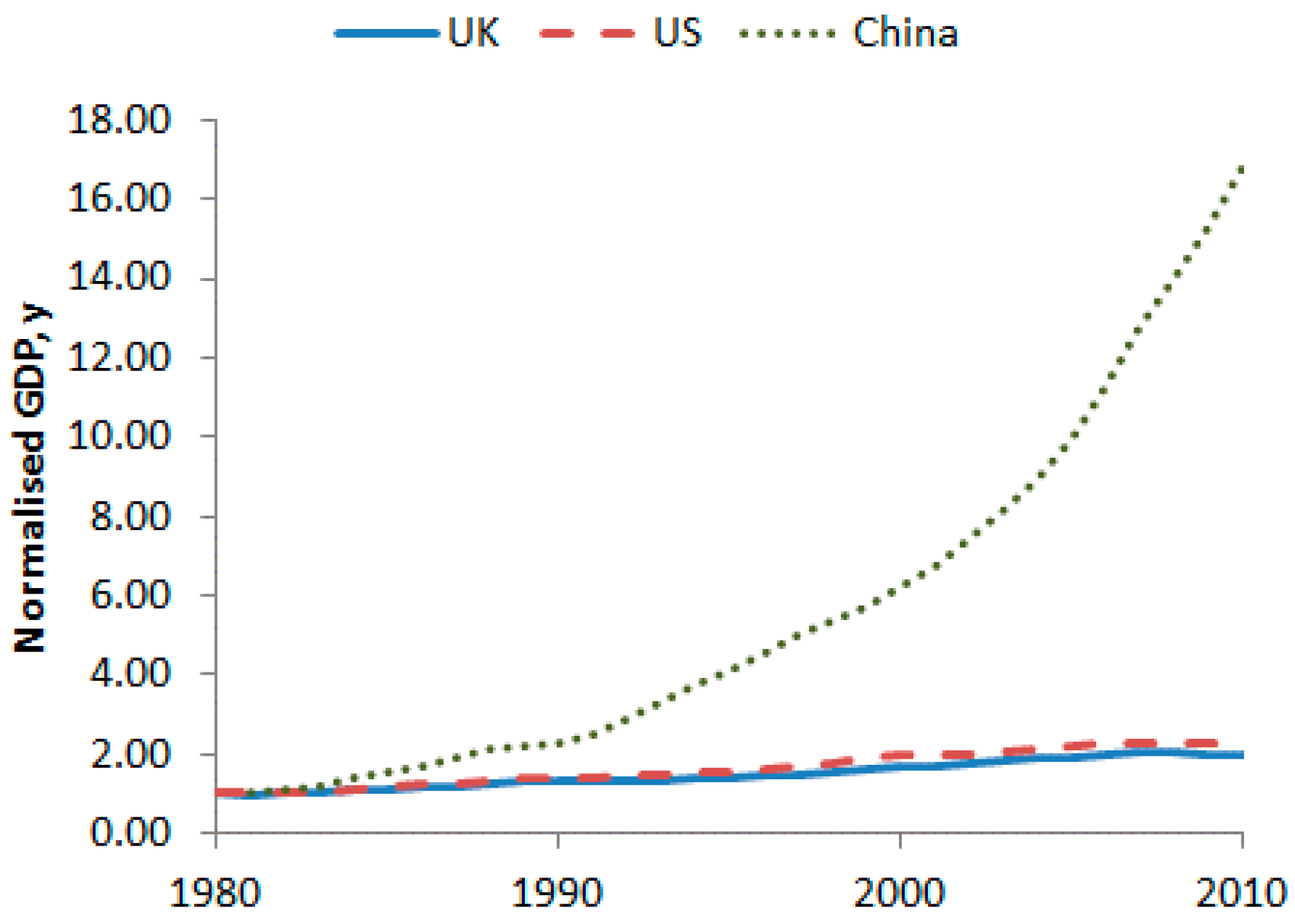
3.1. The CES Aggregate Production Function Results
3.2. Method 1 (AES/PES): Results
3.3. Method 2 (EEE): Results
4. Discussion
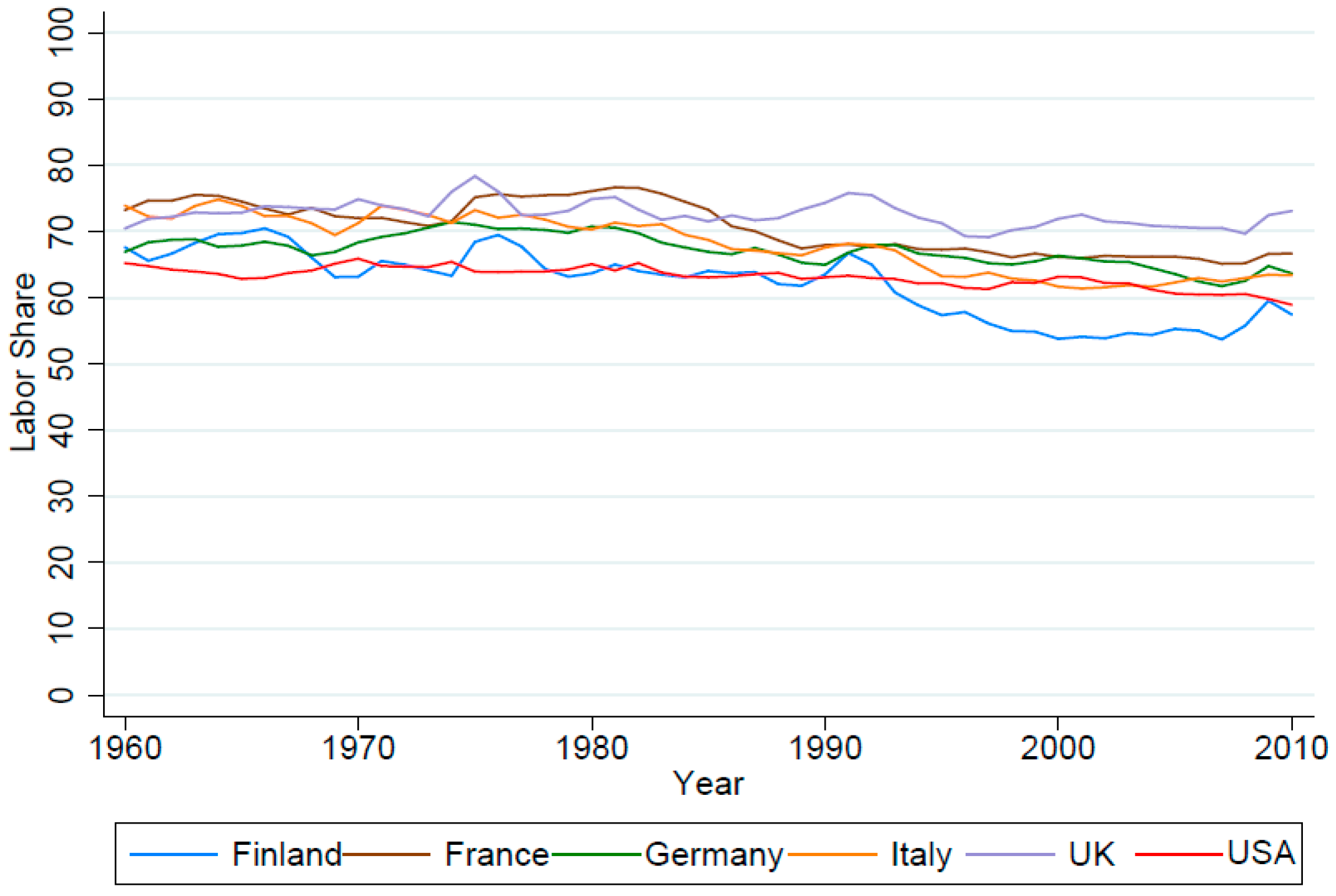
4.1. Comparison to Previous Studies
4.2. Interpretation
4.3. Reflections of the Exergy-Based Approaches
5. Conclusions
Supplementary Materials
Data Repository
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change (IPCC). Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2014. Summary for Policymakers; Intergovernmental Panel on Climate Change (IPCC): Cambridge, UK, 2014. [Google Scholar]
- European Parliament. Directive 2009/28/EC of the European Parliament and of the Council of 23 April 2009. Off. J. Eur. Union 2009, 140, 16–62. [Google Scholar]
- European Parliament. Directive 2012/27/EU of the European Parliament and of the Council of 25 October 2012 on energy efficiency. Off. J. Eur. Union 2012, 315, 1–56. [Google Scholar]
- Csereklyei, Z.; Stern, D.I. Global Energy Use: Decoupling or Convergence? Energy Econ. 2015, 51, 633–641. [Google Scholar] [CrossRef]
- Alcott, B. Impact caps: Why population, affluence and technology strategies should be abandoned. J. Clean. Prod. 2010, 18, 552–560. [Google Scholar] [CrossRef]
- Sorrell, S. Energy, economic growth and environmental sustainability: Five propositions. Sustainability 2010, 2, 1784–1809. [Google Scholar] [CrossRef]
- Redrawing the Energy-Climate Map; World Energy Outlook Special Report; International Energy Agency (IEA): Paris, France, 2013.
- Stern, D.I. The role of energy in economic growth. Ann. N. Y. Acad. Sci. 2011, 1219, 26–51. [Google Scholar] [CrossRef] [PubMed]
- Jevons, W.S. The Coal Question: An Inquiry Concerning the Progress of the Nation, and the Probable Exhaustion of Our Coal-Mines, 3rd ed.; Flux, A.W., Ed.; Augustus M. Kelley: New York, NY, USA, 1865. [Google Scholar]
- Saunders, H.D. Fuel conserving (and using) production functions. Energy Econ. 2008, 30, 2184–2235. [Google Scholar] [CrossRef]
- Wei, T. A general equilibrium view of global rebound effects. Energy Econ. 2010, 32, 661–672. [Google Scholar] [CrossRef]
- Greening, L.A.; Greene, D.L.; Difiglio, C. Energy efficiency and consumption—The rebound effect—A survey. Energy Policy 2000, 28, 389–401. [Google Scholar] [CrossRef]
- Jenkins, J.; Nordhaus, T.; Shellenberger, M. Energy Emergence: Rebound and Backfire as Emergent Phenomena; Breakthrough Institute: Oakland, CA, USA, 2011. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2014: Mitigation of Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Maxwell, D.; Owen, P.; McAndrew, L.; Mudgal, S.; Cachia, F.; Muehmel, K.; Neubauer, A. Addressing the Rebound Effect; Report for the European Commission; Directorate-General (DG) for Environment: Brussels, Belgium, 2011. [Google Scholar]
- Font Vivanco, D.; Kemp, R.; van der Voet, E. How to deal with the rebound effect? A policy-oriented approach. Energy Policy 2016, 94, 114–125. [Google Scholar] [CrossRef]
- UK Energy Bill; Her Majesty’s Government: London, UK, 2012.
- Nørgaard, J.S. Avoiding rebound through a steady-state economy. In Energy Efficiency and Sustainable Consumption: The Rebound Effect; Herring, H., Sorrell, S., Eds.; Palgrave Macmillan: Basingstoke, UK, 2008. [Google Scholar]
- Levett, R. Energy efficiency and sustainable consumption: The rebound effect. In Rebound and Rational Public Policy-Making; Herring, H., Sorrell, S., Eds.; Palgrave Macmillan (St. Martin’s Press): New York, NY, USA, 2009. [Google Scholar]
- Schaefer, S.; Wickert, C. The efficiency paradox in organization and management theory. In Proceedings of the 4th European Theory Development Workshop (EDTW), Cardiff, UK, 25–26 June 2015.
- Sorrell, S. The Rebound Effect: An Assessment of the Evidence for Economy-Wide Energy Savings from Improved Energy Efficiency. UKERC Research Report. Available online: http://www.efslearninghub.net.au/Portals/0/Resources/Publications/Files/565/UK ERC Rebound.pdf (accessed on 30 September 2016).
- Sorrell, S.; Dimitropoulos, J. Review of Evidence for the Rebound Effect Technical Report 2: Econometric Studies; UKERC Work Paper UKERC/WP/TPA/2007/010; The UK Energy Research Centre: London, UK, 2007. [Google Scholar]
- Broadstock, D.C.; Hunt, L.; Sorrell, S. Review of Evidence for the Rebound Effect Technical Report 3: Elasticity of Substitution Studies; UKERC Work Paper UKERC/WP/TPA/2007/011; The UK Energy Research Centre: London, UK, 2007. [Google Scholar]
- Allan, G.; Gilmartin, M.; Turner, K.; McGregor, P.; Swales, K. Review of Evidence for the Rebound Effect Technical Report 4: Computable General Equilibrium Modelling Studies; UKERC Work Paper UKERC/WP/TPA/2007/012; The UK Energy Research Centre: London, UK, 2007. [Google Scholar]
- Sorrell, S.; Dimitropoulos, J. Review of Evidence for the Rebound Effect Technical Report 5: Energy, Productivity and Economic Growth Studies; UKERC Work Paper UKERC/WP/TPA/2007/013; The UK Energy Research Centre: London, UK, 2007. [Google Scholar]
- Stapleton, L.; Sorrell, S.; Schwanen, T. Estimating direct rebound effects for personal automotive travel in Great Britain. Energy Econ. 2016, 54, 313–325. [Google Scholar] [CrossRef]
- Greene, D.L. Rebound 2007: Analysis of U.S. light-duty vehicle travel statistics. Energy Policy 2012, 41, 14–28. [Google Scholar] [CrossRef]
- Druckman, A.; Chitnis, M.; Sorrell, S.; Jackson, T. An Investigation into the Rebound and Backfire Effects from Abatement Actions by UK Households. Available online: http://epubs.surrey.ac.uk/729052/1/RESOLVE WP 05-10.pdf (accessed on 30 September 2016).
- Azevedo, I.L.; Sonnberger, M.; Thomas, B.; Morgan, G.; Renn, O. The Rebound Effect: Implications of Consumer Behaviour for Robust Energy Policies; International Risk Governance Council: Lausanne, Switzerland, 2013. [Google Scholar]
- Bentzen, J. Estimating the rebound effect in US manufacturing energy consumption. Energy Econ. 2004, 26, 123–134. [Google Scholar] [CrossRef]
- Saunders, H.D. Historical evidence for energy efficiency rebound in 30 US sectors and a toolkit for rebound analysts. Technol. Forecast. Soc. Chang. 2013, 80, 1317–1330. [Google Scholar] [CrossRef]
- Saunders, H.D. Recent Evidence for Large Rebound: Elucidating the Drivers and their Implications for Climate Change Models. Energy J. 2015, 36, 23–48. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, C.C. Estimating the Macroeconomic Rebound Effect in China. UC Davis Work Paper. 2013. Available online: http//www.des.ucdavis.edu/faculty/lin/china_rebound_effect_paper.pdf (accessed on 30 September 2016).
- Fouquet, R. Long-Run Demand for Energy Services: Income and Price Elasticities over Two Hundred Years. Rev. Environ. Econ. Policy 2014, 8, 186–207. [Google Scholar] [CrossRef]
- Fouquet, R.; Pearson, P.J.G. The Long Run Demand for Lighting: Elasticities and Rebound Effects in Different Phases of Economic Development. Econ. Energy Environ. Policy 2011, 1, 83–100. [Google Scholar]
- Tsao, J.Y.; Saunders, H.D.; Creighton, J.R.; Coltrin, M.E.; Simmons, J.A. Solid-state lighting: An energy-economics perspective. J. Phys. D Appl. Phys. 2010, 43, 354001. [Google Scholar] [CrossRef]
- HM Revenue and Customs. HMRC’s CGE Model Documentation. 2013. Available online: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/263652/CGE_model_doc_131204_new.pdf (accessed on 30 September 2016). [Google Scholar]
- Barker, T.; Dagoumas, A.; Rubin, J. The macroeconomic rebound effect and the world economy. Energy Effic. 2009, 2, 411–427. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). World Energy Model Documentation 2013 Version. Available online: http://www.worldenergyoutlook.org/media/weowebsite/2013/WEM_Documentation_WEO2013.pdf (accessed on 30 September 2016).
- Rant, Z. Exergy, a new word for “technical available work”. Forsch. Ing. 1956, 22, 36–37. [Google Scholar]
- Reistad, G. Available Energy Conversion and Utilization in the United States. ASME Trans. Ser. J. Eng. Power 1975, 97, 429–434. [Google Scholar] [CrossRef]
- Ford, K.W.; Rochlin, G.I.; Socolow, R.H.; Hartley, D.L.; Hardesty, D.R.; Lapp, M.; Dooher, J.; Dryer, F.; Berman, S.M.; Silverstein, S.D. Technical Aspects of the More Efficient Utilization of Energy: Chapter 2—Second law efficiency: The role of the second law of thermodynamics in assessing the efficiency of energy use. Am. Inst. Phys. Conf. 1975, 25, 25–51. [Google Scholar]
- Ford, K.W.; Rochlin, G.I.; Socolow, R.H.; Hartley, D.L.; Hardesty, D.R.; Lapp, M.; Dooher, J.; Dryer, F.; Berman, S.M.; Silverstein, S.D. Technical Aspects of the More Efficient Utilization of Energy: Chapter 4—The automobile. Am. Inst. Phys. Conf. 1975, 25, 99–120. [Google Scholar]
- Ford, K.W.; Rochlin, G.I.; Socolow, R.H.; Hartley, D.L.; Hardesty, D.R.; Lapp, M.; Dooher, J.; Dryer, F.; Berman, S.M.; Silverstein, S.D. Technical Aspects of the More Efficient Utilization of Energy: Chapter 5—Sample industrial processes. Am. Inst. Phys. Conf. 1975, 25, 122–159. [Google Scholar]
- Georgescu-Roegen, N. The Entropy Law and the Economic Process; Harvard University: Cambridge, MA, USA, 1971. [Google Scholar]
- Georgescu-Roegen, N. Energy and Economic Myths. South Econ. J. 1975, 41, 347–381. [Google Scholar] [CrossRef]
- Georgescu-Roegen, N. Energy Analysis and Economic Valuation. South Econ. J. 1979, 45, 1023–1058. [Google Scholar] [CrossRef]
- Ayres, R. The minimum complexity of endogenous growth models: The role of physical resource flows. Energy 2001, 26, 817–838. [Google Scholar] [CrossRef]
- Ayres, R.U.; Ayres, L.W.; Warr, B. Exergy, power and work in the US economy, 1900–1998. Energy 2003, 28, 219–273. [Google Scholar] [CrossRef]
- Ayres, R.U.; Warr, B. Accounting for growth: The role of physical work. Struct. Chang. Econ. Dyn. 2005, 16, 181–209. [Google Scholar] [CrossRef]
- Warr, B.; Ayres, R.U. Useful work and information as drivers of economic growth. Ecol. Econ. 2012, 73, 93–102. [Google Scholar] [CrossRef]
- Serrenho, A.C.; Warr, B.; Sousa, T.; Ayres, R.U. Structure and dynamics of useful work along the agriculture-industry-services transition: Portugal from 1856 to 2009. Struct. Chang. Econ. Dyn. 2016, 36, 1–21. [Google Scholar] [CrossRef]
- Brockway, P.E.; Barrett, J.R.; Foxon, T.J.; Steinberger, J.K. Divergence of trends in US and UK aggregate exergy efficiencies 1960–2010. Environ. Sci. Technol. 2014, 48, 9874–9881. [Google Scholar] [CrossRef] [PubMed]
- Ayres, R.; Voudouris, V. The economic growth enigma: Capital, labour and useful energy? Energy Policy 2014, 64, 16–28. [Google Scholar] [CrossRef]
- Serrenho, A.C.; Sousa, T.; Warr, B.; Ayres, R.U.; Domingos, T. Decomposition of useful work intensity: The EU (European Union)-15 countries from 1960 to 2009. Energy 2014, 76, 704–715. [Google Scholar] [CrossRef]
- Brockway, P.E.; Barrett, J.R.; Foxon, T.J.; Steinberger, J.K. Supporting Information—Divergence of trends in US and UK aggregate exergy efficiencies 1960–2010. Environ. Sci. Technol. 2014, 48, S1–S39. [Google Scholar] [CrossRef] [PubMed]
- Patterson, M.G. What is energy efficiency? Energy Policy 1996, 24, 377–390. [Google Scholar] [CrossRef]
- Malpede, M.; Verdolini, E. Rebound Effects in Europe. In Proceedings of the Fourth IAERE Annual Conference, Bologna, Italy, 11–12 February 2016.
- Szargut, J.; Morris, D.R.; Steward, F.R. Exergy Analysis of Thermal, Chemical and Metallurgical Processes; Hemisphere: New York, NY, USA, 1988. [Google Scholar]
- Warr, B.; Ayres, R.; Eisenmenger, N.; Krausmann, F.; Schandl, H. Energy use and economic development: A comparative analysis of useful work supply in Austria, Japan, the United Kingdom and the US during 100 years of economic growth. Ecol. Econ. 2010, 69, 1904–1917. [Google Scholar] [CrossRef]
- Lloyd, P.J. The Origins of the von Thünen-Mill-Wiksell-Cobb-Douglas Function. Hist. Polit. Econ. 2001, 33, 1–19. [Google Scholar] [CrossRef]
- Mishra, S.K. A Brief History of Production Functions. IUP J. Manag. Econ. 2010, VIII, 6–34. [Google Scholar] [CrossRef]
- Miller, E. An Assessment of CES and Cobb-Douglas Production Functions; US Congressional Budget Office Work Paper 2008-05; Congressional Budget Office: Washington, DC, USA, 2008.
- Solow, R.M. Technical Change and the Aggregate Production Function. Rev. Econ. Stat. 1957, 39, 312–320. [Google Scholar] [CrossRef]
- Denison, E.F. Accounting for Slower Economic Growth: The United States in the 1970’s; Brookings Institution Press: Washington, DC, USA, 1979. [Google Scholar]
- Barro, R.J. Notes on growth accounting. J. Econ. Growth 1999, 4, 119–137. [Google Scholar] [CrossRef]
- Manne, A.; Mendelsohn, R.; Richels, R. MERGE. A model for evaluating regional and global effects of GHG reduction policies. Energy Policy 1995, 23, 17–34. [Google Scholar] [CrossRef]
- Arora, V. An Evaluation of Macroeconomic Models for Use at EIA; U.S. Energy Information Administration: Washington, DC, USA, 2013.
- Klump, R.; Mcadam, P.; Willman, A. The Normalised CES Production Function: Theory and Empirics; European Central Bank Work Paper 1294; European Central Bank: Frankfurt, Germany, 2011. [Google Scholar]
- Growiec, J. On the Measurement of Technological Progress across Countries; National Bank of Poland Work Paper No. 73; National Bank of Poland: Warsaw, Poland, 2010. [Google Scholar]
- Groth, B.C.; Gutierrez-domenech, M.; Srinivasan, S. Measuring total factor productivity for the United Kingdom. Bank Engl. Q. Bull. Spring 2004, 2004, 63–73. [Google Scholar]
- Cambridge Centre for Climate Change Mitigation Research (4CMR). The Macro-Economic Rebound Effect and the UK Economy. 2006. Available online: http://ukerc.rl.ac.uk/pdf/ee01015_final_b.pdf (accessed on 30 September 2016).
- Shao, S.; Huang, T.; Yang, L. Using latent variable approach to estimate China’s economy-wide energy rebound effect over 1954–2010. Energy Policy 2014, 72, 235–248. [Google Scholar] [CrossRef]
- Sorrell, S. Energy Substitution, Technical Change and Rebound Effects. Energies 2014, 7, 2850–2873. [Google Scholar] [CrossRef]
- Van der Werf, E. Production functions for climate policy modeling: An empirical analysis. Energy Econ. 2008, 30, 2964–2979. [Google Scholar] [CrossRef]
- Warr, B.S.; Ayres, R.U. Evidence of causality between the quantity and quality of energy consumption and economic growth. Energy 2010, 35, 1688–1693. [Google Scholar] [CrossRef]
- Voudouris, V.; Ayres, R.; Serrenho, A.C.; Kiose, D. The economic growth enigma revisited: The EU-15 since the 1970s. Energy Policy 2015, 86, 812–832. [Google Scholar] [CrossRef]
- Temple, J. The calibration of CES production functions. J. Macroecon. 2012, 34, 294–303. [Google Scholar] [CrossRef]
- Feenstra, R.C.; Inklaar, R.; Timmer, M.P. Penn World Tables 8.1. 2015. Available online: http://www.rug.nl/research/ggdc/data/pwt/pwt-8.1 (accessed on 30 September 2016).
- Nilsen, Ø.A.; Raknerud, A.; Rybalka, M.; Skjerpen, T. The importance of skill measurement for growth accounting. Rev. Income Wealth 2011, 57, 293–305. [Google Scholar] [CrossRef]
- Daude, C. Understanding Solow Residuals in Latin America. Economia 2014, 13, 109–138. [Google Scholar]
- Hájková, D.; Hurník, J. Cobb-Douglas production function: The case of a converging economy. Czech J. Econ. Financ. 2007, 57, 465–476. [Google Scholar]
- Barro, R.; Lee, J.-W. Barro-Lee Educational Attainment Dataset Version 2.0. 2014. Available online: http://www.barrolee.com/ (accessed on 30 September 2016).
- Wu, H.X. China’s Growth and Productivity Performance Debate Revisited—Accounting for China’s Sources of Growth with a New Data Set. 2014. Available online: https//www.conference-board.org/pdf_free/workingpapers/EPWP1401.pdf (accessed on 30 September 2016).
- Wallis, G.; Oulton, N. Integrated Estimates of Capital Stocks and Services for the United Kingdom: 1950–2013; CEP Discussion Papers, CEPDP1342; Centre for Economic Performance, London School of Economics and Political Science: London, UK.
- US Bureau of Labour Statistics. Total Economy Production Account and Costs, 1987 to 2013. 2015. Available online: http://www.bls.gov/mfp/special_requests/prod3.totecotable.zip (accessed on 30 September 2016). [Google Scholar]
- Schreyer, P.; Bignon, P.; Dupont, J. OECD Capital Services Estimates: Methodology and a First Set of Results; OECD Statistics Working Papers 2003/06; OECD Publishing: Paris, France, 2003. [Google Scholar]
- Wu, H.X. Constructing China’s Net Capital and Measuring Capital Services in China, 1980–2010; Discussion Papers 15-E-006; Research Institute of Economy, Trade and Industry (RIETI): Tokyo, Japan, 2015; pp. 1–39.
- Brockway, P.E.; Steinberger, J.K.; Barrett, J.R.; Foxon, T.J. Understanding China’s past and future energy demand: An exergy efficiency and decomposition analysis. Appl. Energy 2015, 155, 892–903. [Google Scholar] [CrossRef]
- Henningsen, A.; Henningsen, G. Econometric Estimation of the “Constant Elasticity of Substitution” Function in R: Package micEconCES; FOI Working Paper 2011/9; Institute of Food and Resource Economics, University of Copenhagen: Frederiksberg, Denmark, 2011. [Google Scholar]
- Henningsen, A.; Henningsen, G. On estimation of the CES production function—Revisited. Econ. Lett. 2012, 115, 67–69. [Google Scholar] [CrossRef]
- Heun, M.K.; Santos, J.; Brockway, P.E.; Pruim, R.; Domingos, T. From theory to econometrics to energy policy: Cautionary tales for policymaking using aggregate production functions. Energies 2016. submitted for publication. [Google Scholar]
- Lin, B.; Liu, X. Dilemma between economic development and energy conservation: Energy rebound effect in China. Energy 2012, 45, 867–873. [Google Scholar] [CrossRef]
- Li, L.; Lin, X. Regional Energy Rebound Effect in China Based on IPAT Equation. In Proceedings of the 2012 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; pp. 1–4.
- Li, L.; Yonglei, H. The Energy Efficiency Rebound Effect in China from Three Industries Perspective. Energy Procedia 2012, 14, 1105–1110. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). “Extended World Energy Balances”, IEA World Energy Statistics and Balances (Database). 2013. Available online: http://www.oecd-ilibrary.org/energy/data/iea-world-energy-statistics-and-balances/extended-world-energy-balances_data-00513-en (accessed on 30 September 2016).
- Hogan, W.W.; Manne, A.S. Energy-Economy Interactions: The Fable of the Elephant and the Rabbit? Stanford University: Stanford, CA, USA, 1977. [Google Scholar]
- Platchkov, L.M.; Pollitt, M.G. The Economics of Energy (and Electricity) Demand; Working Paper 1116; University of Cambridge Electricity Policy Research Group: Cambridge, UK, 2011. [Google Scholar]
- US Energy Information Administration (US EIA). Energy Consumption, Expenditures, and Emissions Indicators Estimates, Selected Years, 1949–2011. U.S. Energy Information Administration/Annual Energy Review 2011. Available online: http://www.eia.gov/totalenergy/data/annual/pdf/sec1_13.pdf (accessed on 30 September 2016).
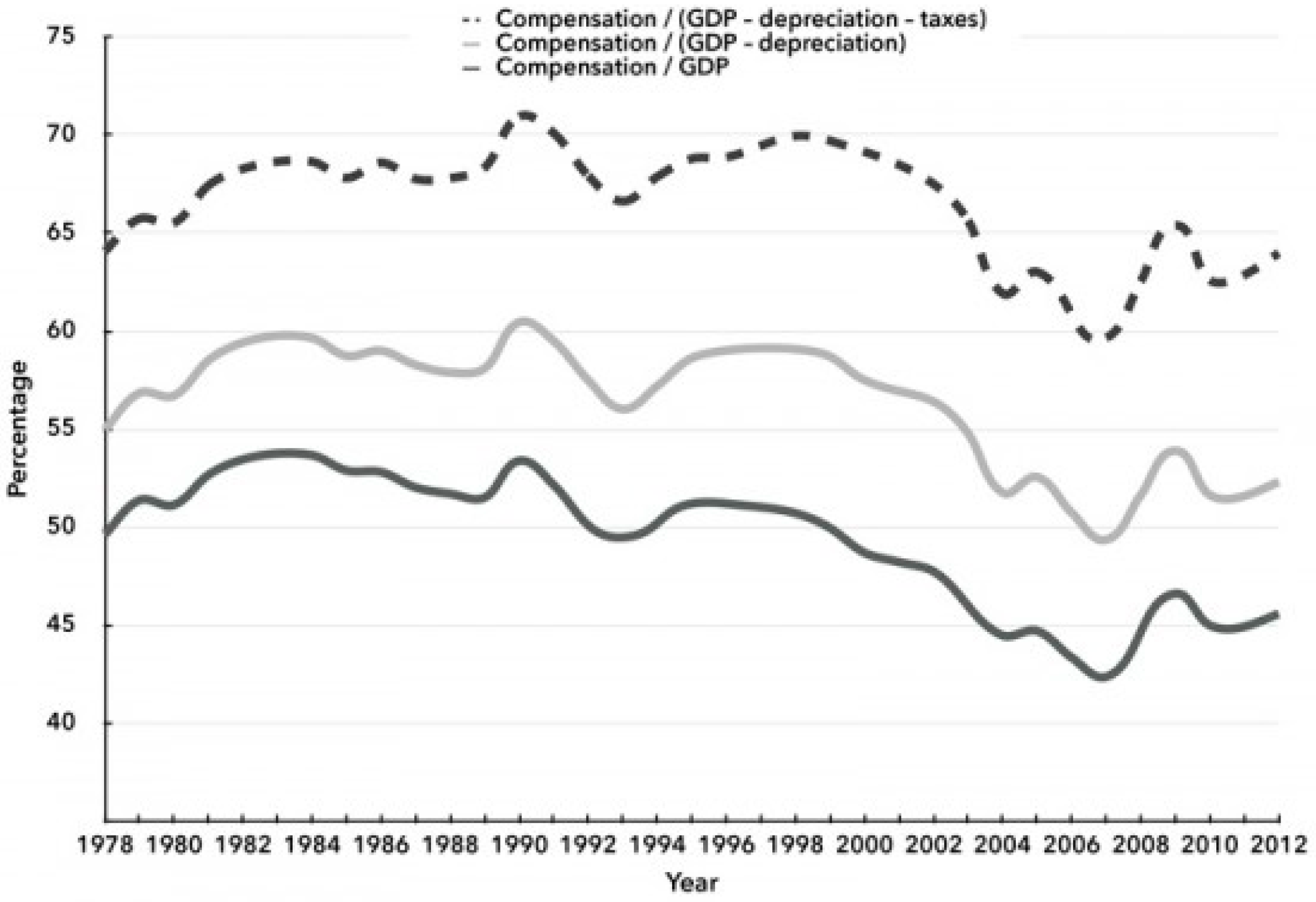
- Schneider, D. The Labor Share: A Review of Theory and Evidence. 2011. Available online: http://edoc.hu-berlin.de/series/sfb-649-papers/2011-69/PDF/69.pdf (accessed on 30 September 2016).
- Qi, H. The Labor share question in China. Available online: http://monthlyreview.org/2014/01/01/labor-share-question-china/ (accessed on 30 September 2016).
- Barker, T.; Ekins, P.; Foxon, T. The macro-economic rebound effect and the UK economy. Energy Policy 2007, 35, 4935–4946. [Google Scholar] [CrossRef]
- Sorrell, S. Jevons’ Paradox revisited: The evidence for backfire from improved energy efficiency. Energy Policy 2009, 37, 1456–1469. [Google Scholar] [CrossRef]
- Climate Change 2014: Mitigation of Climate Change; Working Group III Contribute to Fifth Assessment Report. Intergovernmental Panel Climate Change (IPCC). Available online: http://www.ipcc.ch/report/ar5/wg3/ (accessed on 30 September 2016).
- Van den Bergh, J.C.J.M. Energy Conservation More Effective With Rebound Policy. Environ. Resour. Econ. 2011, 48, 43–58. [Google Scholar] [CrossRef]
- Ouyang, J.; Long, E.; Hokao, K. Rebound effect in Chinese household energy efficiency and solution for mitigating it. Energy 2010, 35, 5269–5276. [Google Scholar] [CrossRef]
- Levinson, A. Offshoring Pollution: Is the United States Increasingly Importing Polluting Goods? Rev. Environ. Econ. Policy 2009, 4, 63–83. [Google Scholar] [CrossRef]
- Peters, G.P.; Minx, J.C.; Weber, C.L.; Edenhofer, O. Growth in emission transfers via international trade from 1990 to 2008. Proc. Natl. Acad. Sci. USA 2011, 108, 8903–8908. [Google Scholar] [CrossRef] [PubMed]
- Sousa, T.; Brockway, P.E.; Cullen, J.M.; Serrenho, A.C.; Henriques, S.T.; Domingos, T. Improving the Robustness of Societal Exergy Accounting. Energy 2016. submitted for publication. [Google Scholar]
- Miller, J.; Foxon, T.; Sorrell, S. Exergy Accounting: A Quantitative Comparison of Methods and Implications for Energy-Economy Analysis. Energies 2016, 9, 947. [Google Scholar] [CrossRef]
- Felipe, J.; Mccombie, J.S.L. How Sound are the Foundations of the Aggregate Production Function? East. Econ. J. 2005, 31, 467–488. [Google Scholar]
- Felipe, J.; McCombie, J.S.L. The Aggregate Production Function: “Not Even Wrong”. Rev. Polit. Econ. 2014, 26, 60–84. [Google Scholar] [CrossRef]
- Madlener, R.; Alcott, B. Energy rebound and economic growth: A review of the main issues and research needs. Energy 2009, 34, 370–376. [Google Scholar] [CrossRef]
- Ayres, R.U.; Warr, B. The Economic Growth Engine: How Energy and Work Drive Material Prosperity; Edward Elgar: Cheltenham, UK, 2010. [Google Scholar]
| Component of Energy Rebound | Origin/Mechanism | |
|---|---|---|
| Microeconomic rebound: these rebound mechanisms occur within the static economy, based on responses to the reduction in implicit price of an energy service. | Direct rebound: describes the direct response to the energy efficiency improvement. | Jenkins et al. [13] split into two sub-classes:
|
| Indirect rebound: this captures the indirect effects of direct energy rebound. | Jenkins et al. [13] split into two sub-classes:
| |
| Macroeconomic rebound | These mechanisms originate from the dynamic response of the economy to reach a stable equilibrium (between supply and demand for goods and energy services). | Greening et al. [12] split these into two sub-classes:
|
| State of Energy Rebound, (%) | ∆E, Change in Energy Use from 1% Efficiency Gain |
|---|---|
| Super-conservation ( < 0%) | ∆E < −1% |
| Zero ( = 0%) | ∆E = −1% |
| Partial (0% < < 100%) | −1% < ∆E < 0% |
| Full ( = 100%) | ∆E = 0% |
| Backfire ( > 100%) | ∆E > 0% |
| Country | Study Time-Scale | Cost Shares | |
|---|---|---|---|
| sE | sK | ||
| UK | 1980–2010 | 0.08 | 0.28 |
| US | 1980–2010 | 0.08 | 0.28 |
| China | 1981–2010 | 0.10 | 0.45 |
| Country | Value | Fitted Parameter Value | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| θ | λ | δ | σ | R2 | ||||||
| UK | 2.5% resampled | 0.996 | 0.0120 | 0.020 | 0.000 | −1.000 | 22.87 | ∞ | 0.042 | 0.998 |
| Base-fit | 1.014 | 0.0129 | 0.053 | 0.012 | −1.000 | 65.16 | ∞ | 0.015 | ||
| 97.5% resampled | 1.029 | 0.0137 | 0.859 | 0.771 | 171.2 | 1290 | 0.006 | 0.001 | ||
| US | 2.5% resampled | 0.974 | 0.0034 | 0.262 | 0.675 | −1.000 | −1.00 | ∞ | ∞ | 0.999 |
| Base-fit | 0.958 | 0.0093 | 0.338 | 1.000 | −1.000 | 84.78 | ∞ | 0.012 | ||
| 97.5% resampled | 0.994 | 0.0110 | 1.000 | 1.000 | 16.51 | 113.3 | 0.057 | 0.009 | ||
| China | 2.5% resampled | 0.959 | 0.0462 | 0.029 | 0.310 | −1.000 | −1.00 | ∞ | ∞ | 0.999 |
| Base-fit | 0.980 | 0.0559 | 1.000 | 0.532 | 228.1 | −0.52 | 0.004 | 2.082 | ||
| 97.5% resampled | 1.024 | 0.0606 | 1.000 | 0.724 | 548.5 | 1.07 | 0.002 | 0.484 | ||
| Rebound Equation Component | UK (1980–2010) | US (1980–2010) | China (1981–2010) | |
|---|---|---|---|---|
| (A1) | 0.512 | 0.121 | 0.452 | |
| (A2) | 0.551 | 0.332 | 0.546 | |
| (A3) | 0.585 | 0.390 | 0.592 | |
| (B) | 0.022 | 0.026 | 0.093 | |
| (C) | 0.023 | 0.022 | 0.066 | |
| 50% | 15% | 64% | ||
| 54% | 40% | 77% | ||
| 57% | 47% | 83% | ||
| Rebound Value | UK (1980–2010) | US (1980–2010) | China (1981–2010) |
|---|---|---|---|
| 12% | 13% | 58% | |
| 13% | 13% | 208% | |
| 16% | Infinity (∞) | Infinity (∞) |
| Source (Reference) | Time-Series | Method | Estimate of National Rebound |
|---|---|---|---|
| Shao et al. [73] | 1954–2010 | AES/PES | 37% |
| Zhang and Lin [33] | 1979–2004 | AES/PES | 41% |
| 1981–2009 | EEE | 52% (short term) | |
| Lin and Liu [93] | 1981–2009 | AES/PES | 53% |
| Li and Lin [94] | 1985–2008 | AES/PES | 67% |
| Li and Han [95] | 1997–2009 | AES/PES | 74% |
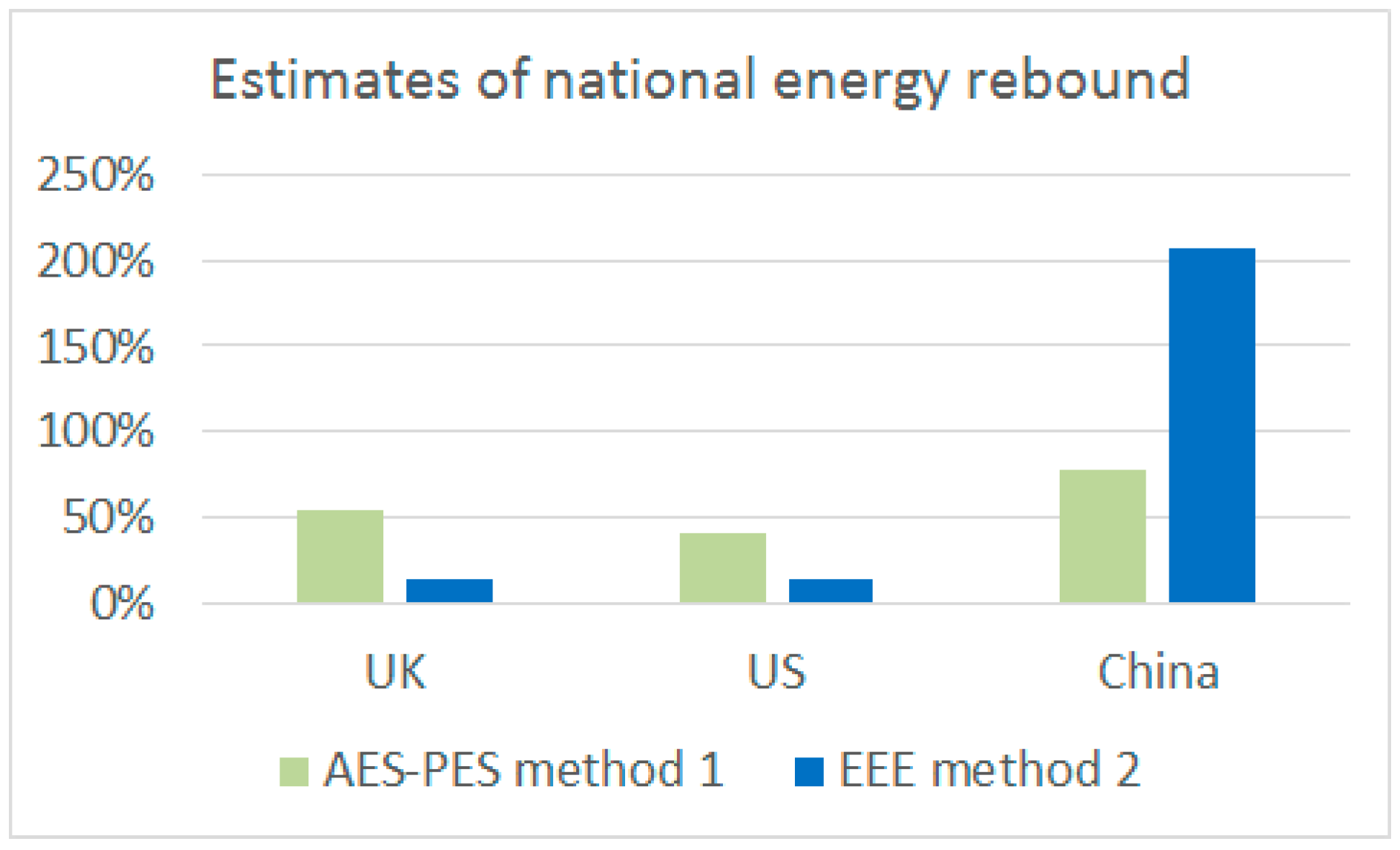
| Brockway et al. (this study) | 1981–2010 | AES/PES | 77% |
| Brockway et al. (this study) | 1981–2010 | EEE | 208% |
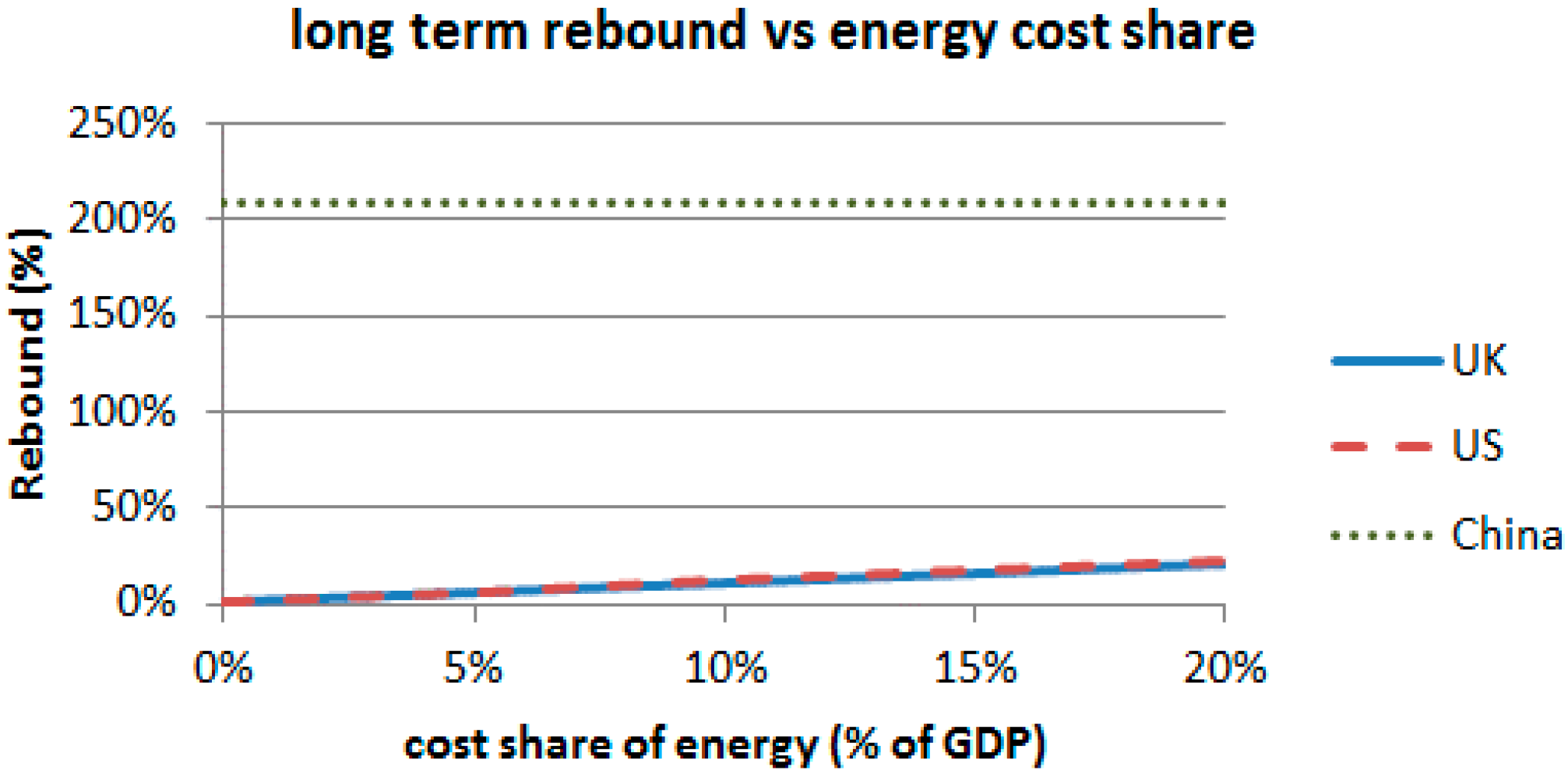
| Country | Substitution Effect | Re1 = 1 + (as Decimal Value) | Output Effect | Re = 1 + | |
|---|---|---|---|---|---|
| As Decimal Value | As % | ||||
| UK | −0.98 | 0.01 | 0.12 | 0.13 | 13% |
| US | −0.99 | 0.01 | 0.12 | 0.13 | 13% |
| China | 1.08 | 2.08 | 0.00 | 2.08 | 208% |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brockway, P.E.; Saunders, H.; Heun, M.K.; Foxon, T.J.; Steinberger, J.K.; Barrett, J.R.; Sorrell, S. Energy Rebound as a Potential Threat to a Low-Carbon Future: Findings from a New Exergy-Based National-Level Rebound Approach. Energies 2017, 10, 51. https://doi.org/10.3390/en10010051
Brockway PE, Saunders H, Heun MK, Foxon TJ, Steinberger JK, Barrett JR, Sorrell S. Energy Rebound as a Potential Threat to a Low-Carbon Future: Findings from a New Exergy-Based National-Level Rebound Approach. Energies. 2017; 10(1):51. https://doi.org/10.3390/en10010051
Chicago/Turabian StyleBrockway, Paul E., Harry Saunders, Matthew K. Heun, Timothy J. Foxon, Julia K. Steinberger, John R. Barrett, and Steve Sorrell. 2017. "Energy Rebound as a Potential Threat to a Low-Carbon Future: Findings from a New Exergy-Based National-Level Rebound Approach" Energies 10, no. 1: 51. https://doi.org/10.3390/en10010051
APA StyleBrockway, P. E., Saunders, H., Heun, M. K., Foxon, T. J., Steinberger, J. K., Barrett, J. R., & Sorrell, S. (2017). Energy Rebound as a Potential Threat to a Low-Carbon Future: Findings from a New Exergy-Based National-Level Rebound Approach. Energies, 10(1), 51. https://doi.org/10.3390/en10010051









