Conjugate Image Theory Applied on Capacitive Wireless Power Transfer
Abstract
:1. Introduction
- CPT has the ability to transfer energy through metal objects.
- Metal objects in the vicinity of the magnetic field generated by an IPT system cause power losses due to eddy currents. The power losses for CPT systems are generally significantly lower.
- Since the electric field lines of a CPT system extend far less than the magnetic field lines for a comparable IPT system, the electromagnetic interference can be less for CPT systems for short distances. This results in less health concerns, as well as decreased electromagnetic compatibility challenges.
- CPT does not require ferrite to guide the magnetic field, nor does it need litz wire to avoid the skin effect. This can significantly reduce the cost as well as the weight of the WPT system.
- The resistance in the windings of the coil in an IPT system may cause high temperatures. A CPT system will usually produce less heat.
- We determine the values of the compensating network at the input and output port of the wireless link as function of the characteristics of the capacitive wireless link (i.e., the working frequency and the value of the capacitances and their series resistance) to achieve maximum attainable efficiency.
- We determine the optimal values to achieve maximum efficiency for series and parallel topologies and compare our results for the CPT link to the IPT link.
- By introducing a new concept of “the coupling function”, we are able to describe the compensation network of a CPT and IPT system in only two elegant equations, valid for the series as the parallel topology as well. This allows us to better understand the fundamentals of the WPT link, necessary for the design of a WPT system.
2. Methodology
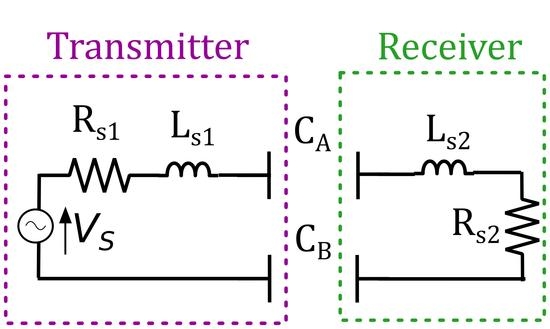
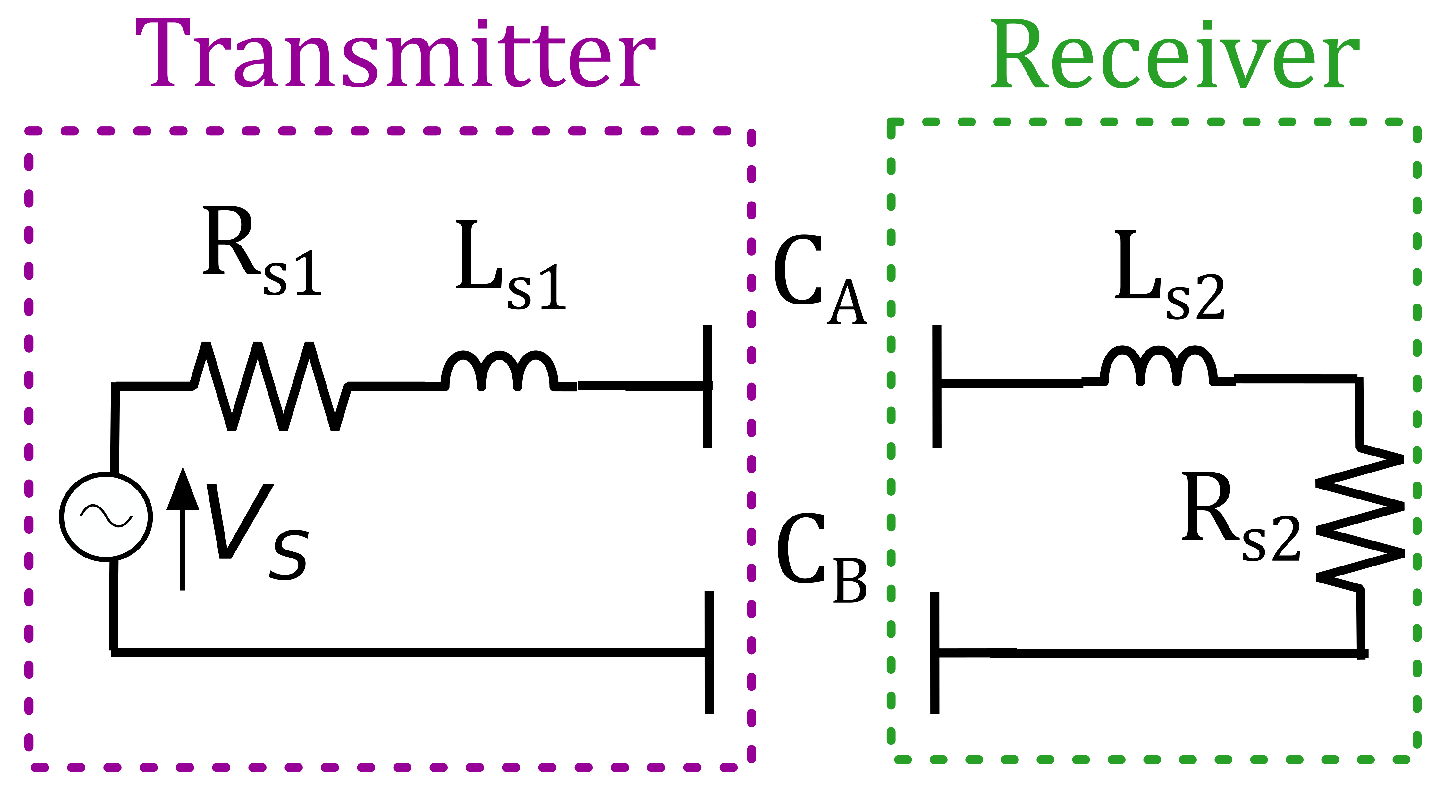
2.1. A General CPT System
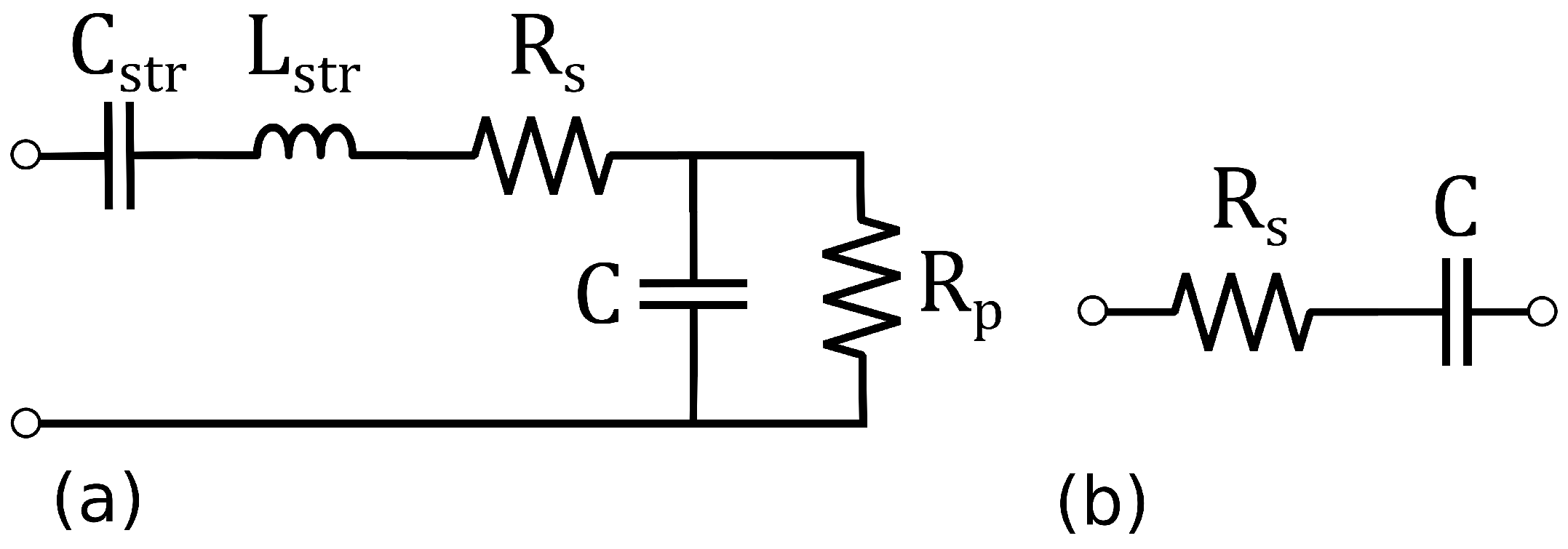
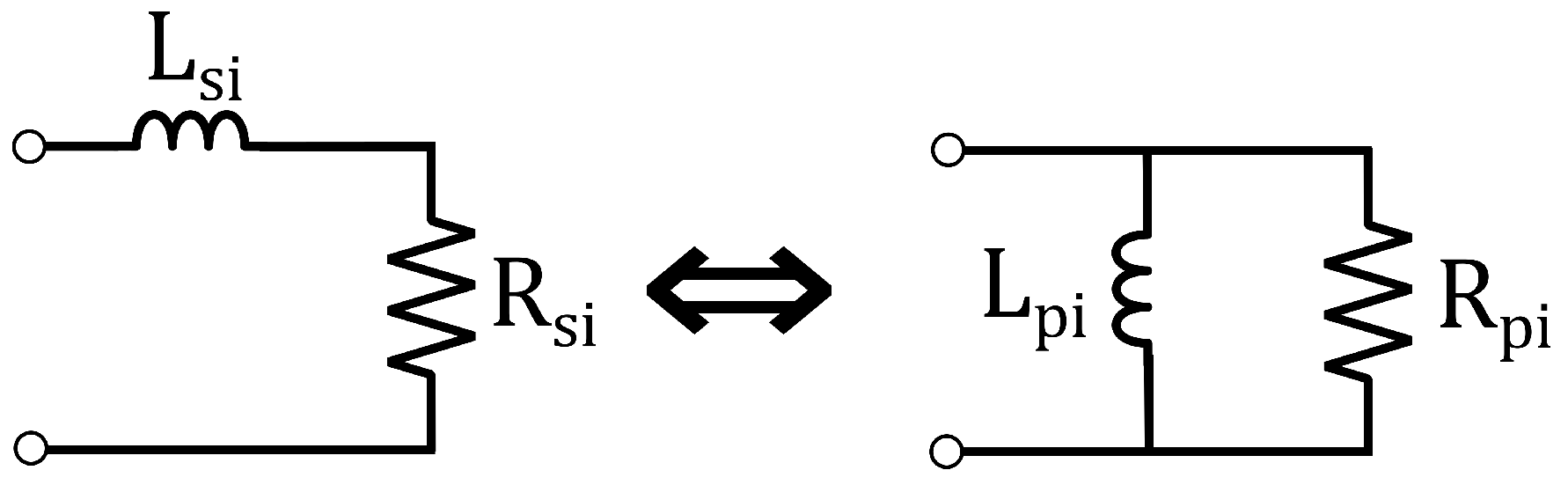
- A stray series capacitance , representing the terminal capacitance.
- A stray series inductance , caused by the leads and plates of the capacitor.
- The series resistance caused by the plates of and connections to the capacitor.
- The parallel resistance caused by the dielectric layer between the capacitor plates.
- The (ideal) capacitance C itself.
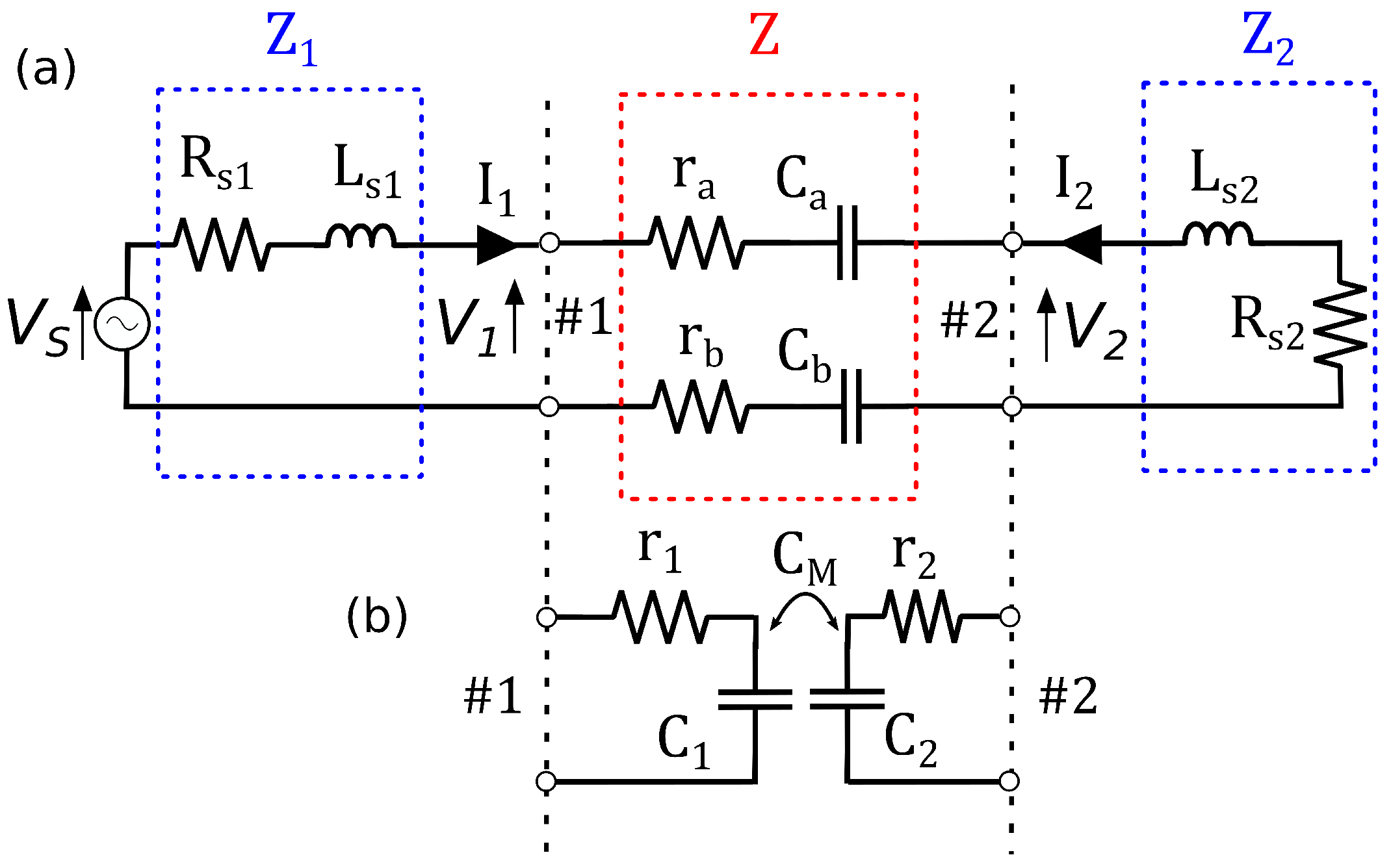
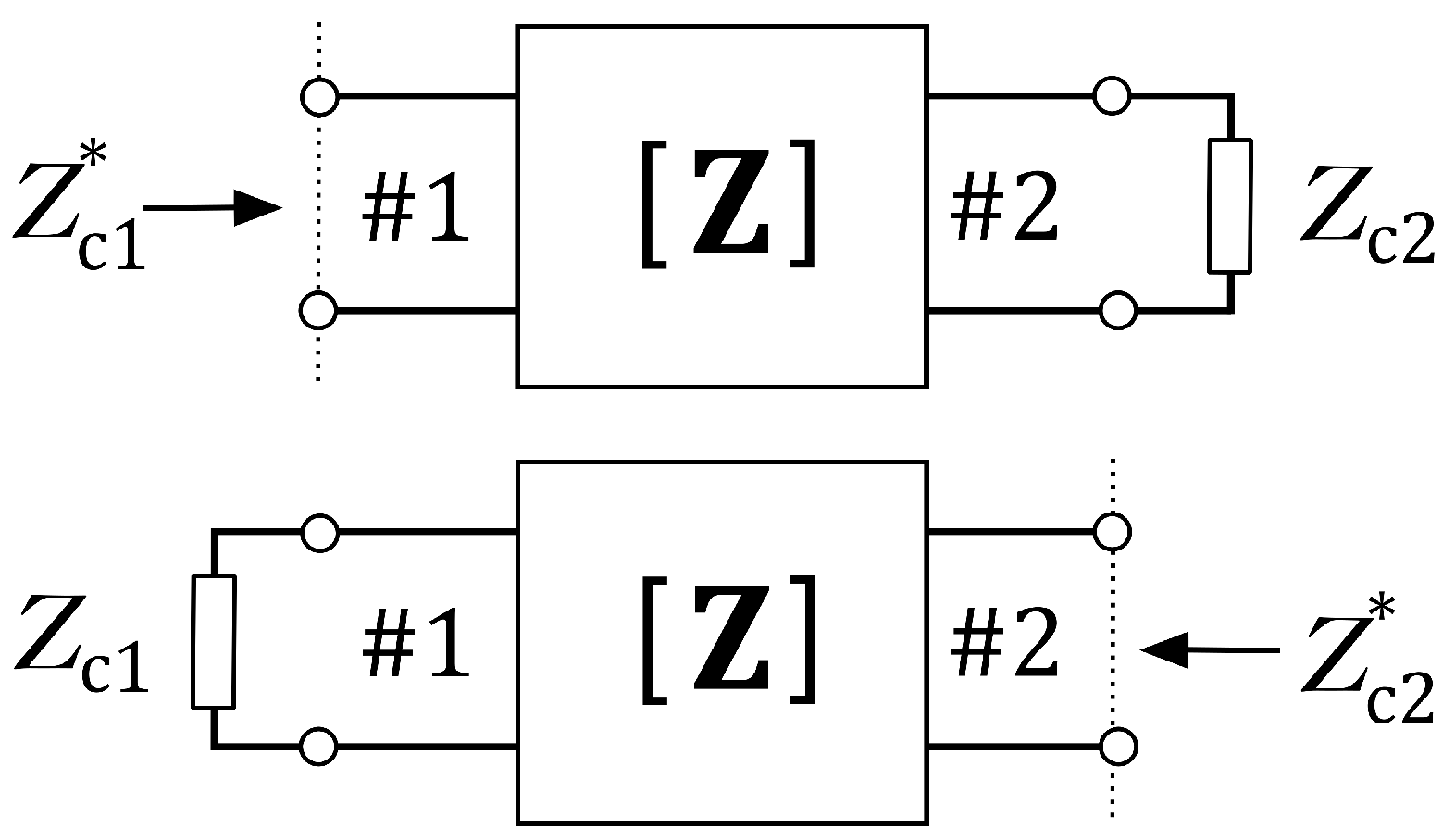
2.2. Conjugate Image Values for the Series Topology
- If we terminate port #2 with a load , the impedance as seen into port #1 is .
- If we terminate port #1 with an impedance , the impedance as seen into port #2 is .
2.3. Conjugate Image Values for the Parallel Topology
2.4. Lossless Approximation
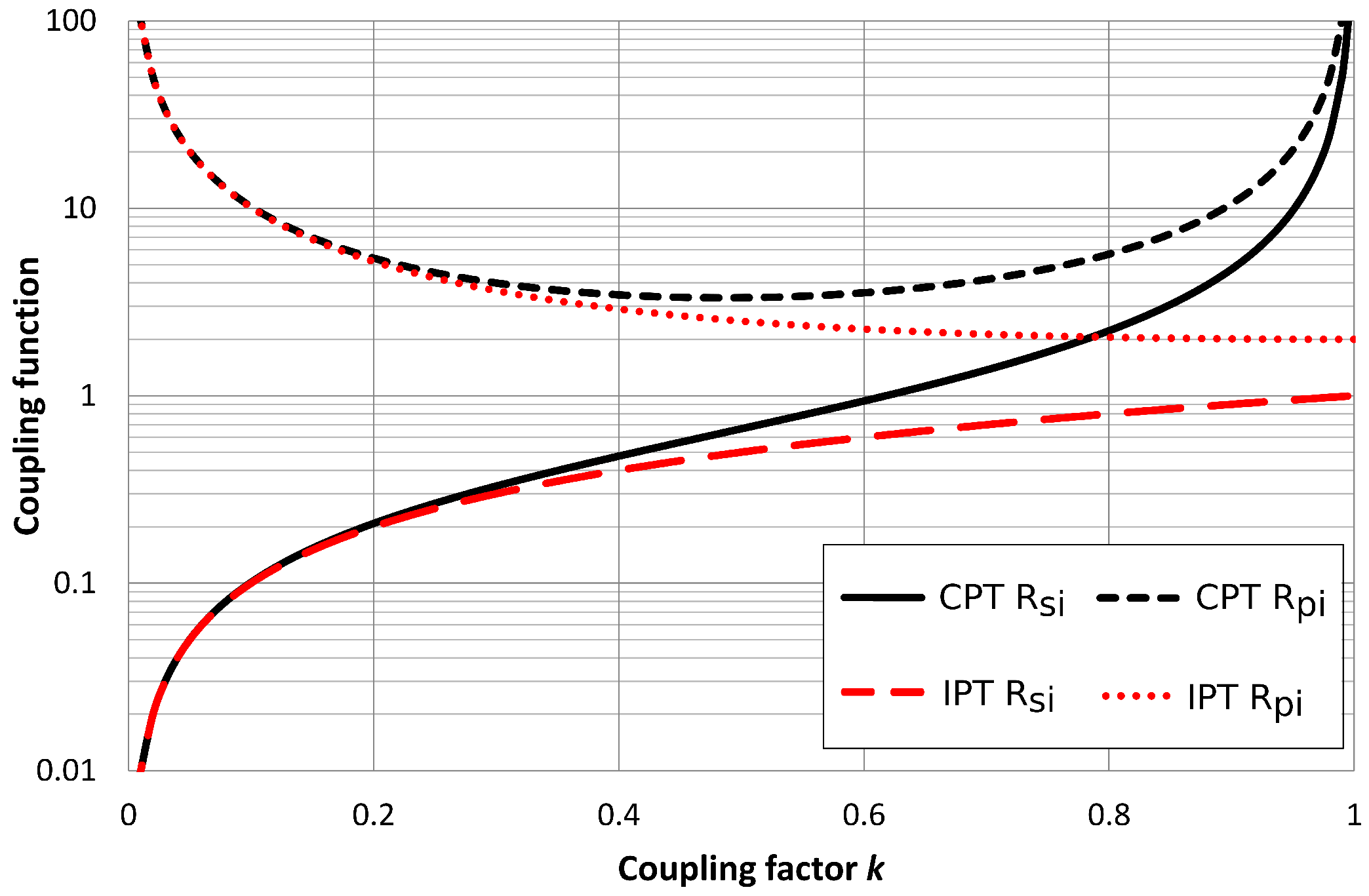
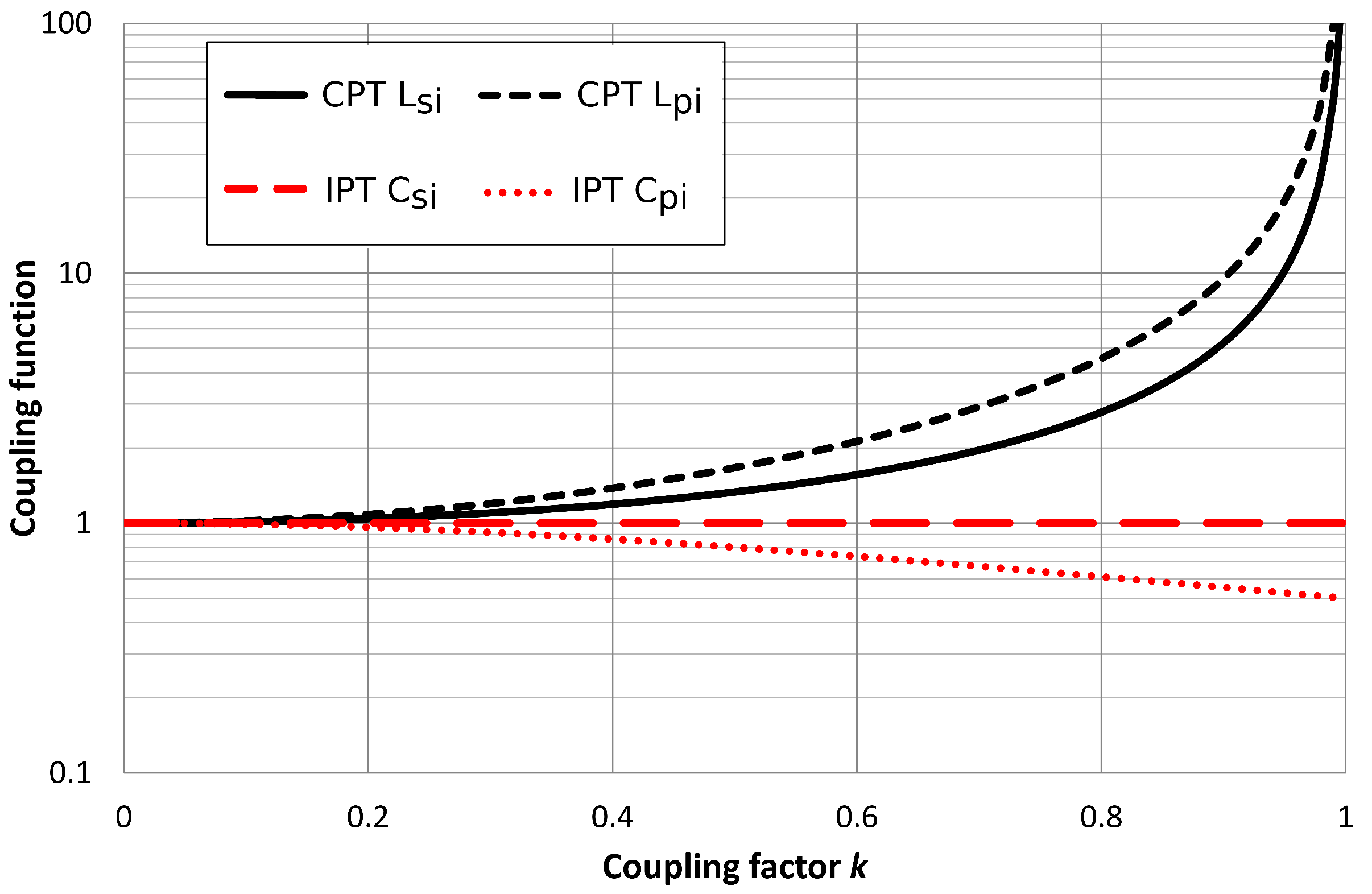
2.5. Comparison between CPT and IPT
3. Validation
3.1. Setup
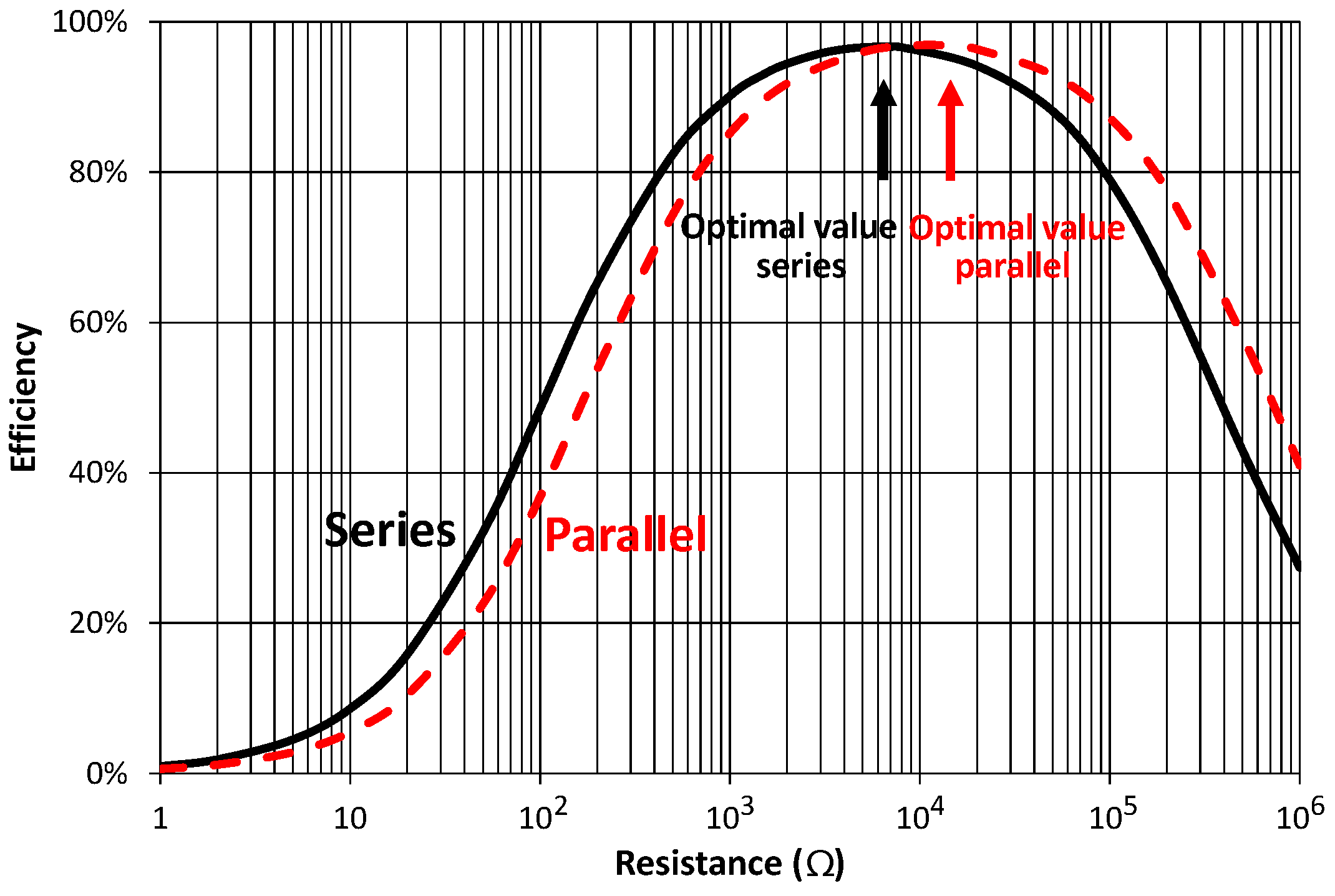
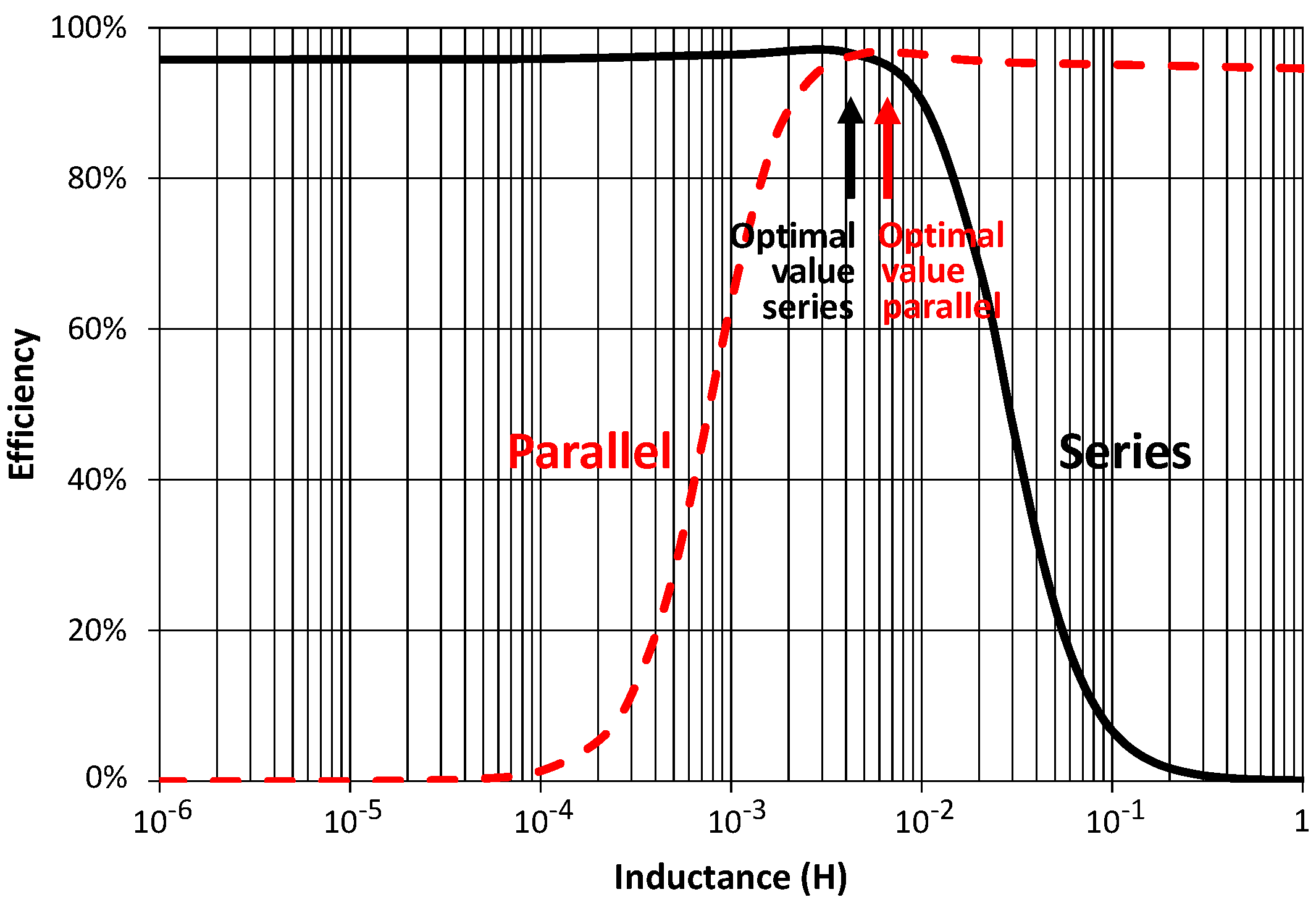
3.2. Series Topology
3.3. Parallel Topology
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CPT | Capacitive power transfer |
| IPT | Inductive power transfer |
| WPT | Wireless power transfer |
References
- Brown, W.C. The history of power transmission by radio waves. IEEE Trans. Microw. Theory Tech. 1984, 32, 1230–1242. [Google Scholar] [CrossRef]
- Roes, M.G.; Duarte, J.L.; Hendrix, M.A.; Lomonova, E.A. Acoustic energy transfer: A review. IEEE Trans. Ind. Electron. 2013, 60, 242–248. [Google Scholar] [CrossRef]
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Wireless charging technologies: Fundamentals, standards, and network applications. IEEE Commun. Surv. Tutor. 2015, 18, 1413–1452. [Google Scholar] [CrossRef]
- Kumar, A.; Pervaiz, S.; Chang, C.K.; Korhummel, S.; Popovic, Z.; Afridi, K.K. Investigation of power transfer density enhancement in large air-gap capacitive wireless power transfer systems. In Proceedings of the IEEE Wireless Power Transfer Conference, Boulder, CO, USA, 13–15 May 2015; pp. 1–4.
- Mi, C. High power capacitive power transfer for electric vehicle charging applications. In Proceedings of the 6th IEEE International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 15–17 December 2015; pp. 1–4.
- Hanazawa, M.; Ohira, T. Power transfer for a running automobile. In Proceedings of the IEEE MTT-S International Microwave Workshop Series on Innovative Wireless Power Transmission: Technologies, Systems, and Applications (IMWS 2011), Kyoto, Japan, 12–13 May 2011; pp. 77–80.
- Funato, H.; Kobayashi, H.; Kitabayashi, T. Analysis of transfer power of capacitive power transfer system. In Proceedings of the IEEE 10th International Conference on Power Electronics and Drive Systems (PEDS), Kitakyushu, Japan, 22–25 April 2013; pp. 1015–1020.
- Huang, L.; Hu, P.; Swain, A.; Su, Y. Z. Impedance compensation for wireless power transfer based on electric field coupling. IEEE Trans. Power Electron. 2016, 31, 7556–7563. [Google Scholar] [CrossRef]
- Komaru, T.; Akita, H. Positional characteristics of capacitive power transfer as a resonance coupling system. In Proceedings of the IEEE Wireless Power Transfer Conference, Perugia, Italy, 15–16 May 2013; pp. 218–221.
- Liu, C.; Hu, A.P.; Budhia, M. A generalized coupling model for capacitive power transfer systems. In Proceedings of the IECON 2010—36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 274–279.
- Liu, C.; Hu, A.P.; Nair, N.K.C. Coupling study of a rotary Capacitive Power Transfer system. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Churchill, Victoria, Australia, 10–13 February 2009; pp. 1–6.
- Xia, C.; Zhou, Y.; Zhang, J.; Li, C. Comparison of power transfer characteristics between CPT and IPT system and mutual inductance optimization for IPT system. J. Comput. 2012, 7, 2734–2741. [Google Scholar] [CrossRef]
- Inagaki, N. Theory of image impedance matching for inductively coupled power transfer systems. IEEE Trans. Microw. Theory Tech. 2014, 62, 901–908. [Google Scholar] [CrossRef]
- Monti, G.; Costanzo, A.; Mastri, F.; Mongiardo, M. Optimal design of a wireless power transfer link using parallel and series resonators. Wirel. Power Transf. 2016, 3, 105–116. [Google Scholar] [CrossRef]
- Malek, H.; Dadras, S.; Chen, Y. Fractional order ESR modeling of electrolytic capacitor and fractional order failure prediction with application to predictive maintenance. IET Power Electron. 2016, 9, 1608–1613. [Google Scholar] [CrossRef]
- Whitaker, J.C. AC Power Systems Handbook, 2nd ed.; Chemical Rubber Company (CRC) Press: Boca Raton, FL, USA, 2002; pp. 53–54. [Google Scholar]
- Bowick, C. RF Circuit Design Howard, 3rd ed.; Elsevier: Burlington, VT, USA, 1982; pp. 12–13. [Google Scholar]
- Hong, J.S.G.; Lancaster, M.J. Microstrip Filters for RF/Microwave Applications, 1st ed.; John Wiley & Sons: New York, NY, USA, 2001; pp. 235–253. [Google Scholar]
- Huang, L.; Hu, A.P. Defining the mutual coupling of capacitive power transfer for wireless power transfer. Electron. Lett. 2015, 51, 1806–1807. [Google Scholar] [CrossRef]
- Roberts, S. Conjugate-image impedances. Proc. IRE 1946, 34, 198–204. [Google Scholar] [CrossRef]
- Dionigi, M.; Mongiardo, M.; Perfetti, R. Rigorous network and full-wave electromagnetic modeling of wireless power transfer links. IEEE Trans. Microw. Theory Tech. 2015, 63, 65–75. [Google Scholar] [CrossRef]
- Dionigi, M.; Mongiardo, M.; Monti, G.; Perfetti, R. Modelling of wireless power transfer links based on capacitive coupling. Int. J. Numer. Model. 2016. [Google Scholar] [CrossRef]
- Costanzo, A.; Dionigi, M.; Masotti, D.; Mongiardo, M.; Monti, G.; Tarricone, L.; Sorrentino, R. Electromagnetic energy harvesting and wireless power transmission: A unified approach. Proc. IEEE 2014, 102, 1692–1711. [Google Scholar] [CrossRef]
- Aditya, K.; Youssef, M.; Williamson, S.S. Analysis of series-parallel resonant inductive coupling circuit using the two-port network theory. In Proceedings of the IEEE IECON 2015—41st Annual Conference of the Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 005402–005407.
- Ohira, T. Extended K-Q product formulas for capacitive-and inductive-coupling wireless power transfer schemes. IEICE Electron. Express 2014, 11. [Google Scholar] [CrossRef]
- Bavastro, D.; Canova, A.; Cirimele, V.; Freschi, F.; Giaccone, L.; Guglielmi, P.; Repetto, M. Design of wireless power transmission for a charge while driving system. IEEE Trans. Magn. 2014, 50, 965–968. [Google Scholar] [CrossRef]
- Pacini, A.; Mastri, F.; Trevisan, R.; Masotti, D.; Costanzo, A. Geometry optimization of sliding inductive links for position-independent wireless power transfer. In Proceedings of the IEEE Microwave Theory and Techniques Society (MTT-S) International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; pp. 1–4.
- Thoen, B.; Wielandt, S.; De Baere, J.; Goemaere, J.P.; De Strycker, L.; Stevens, N. Design of an inductively coupled wireless power system for moving receivers. In Proceedings of the IEEE Wireless Power Transfer Conference, Jeju City, Korea, 8–9 May 2014; pp. 48–51.
- Waters, B.H.; Sample, A.P.; Smith, J.R. Adaptive impedance matching for magnetically coupled resonators. In Proceedings of the 32nd Progress in Electromagnetics Research Symposium (PIERS), Moscow, Russia, 19–23 August 2012; pp. 694–701.

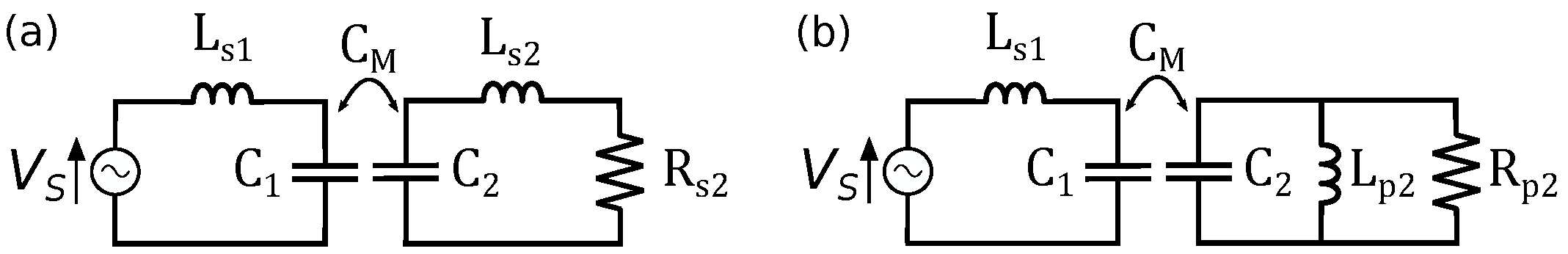
| R | L | |
|---|---|---|
| Series | ||
| Parallel |
| R | L | |
|---|---|---|
| Series | ||
| Parallel |
| CPT | IPT | |
|---|---|---|
| CPT | IPT | |
|---|---|---|
| k | ||
| 1 | ||
| Quantity | Value | Quantity | Value |
|---|---|---|---|
| 462 pF ± 0.5 pF | 17 Ω ± 0.5 Ω | ||
| 415 pF ± 0.5 pF | 17 Ω ± 0.5 Ω | ||
| 2.7 pF ± 0.5 pF | 220 pF ± 1.7 pF | ||
| 2.7 pF ± 0.5 pF | 220 pF ± 1.7 pF | ||
| 2.4 pF ± 0.5 pF | 20.0 V ± 0.05 V | ||
| 2.3 pF ± 0.5 pF | 16.4 V± 0.05 V | ||
| k | 82.9% ± 1.8% | 182 pF ± 2.8 pF |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minnaert, B.; Stevens, N. Conjugate Image Theory Applied on Capacitive Wireless Power Transfer. Energies 2017, 10, 46. https://doi.org/10.3390/en10010046
Minnaert B, Stevens N. Conjugate Image Theory Applied on Capacitive Wireless Power Transfer. Energies. 2017; 10(1):46. https://doi.org/10.3390/en10010046
Chicago/Turabian StyleMinnaert, Ben, and Nobby Stevens. 2017. "Conjugate Image Theory Applied on Capacitive Wireless Power Transfer" Energies 10, no. 1: 46. https://doi.org/10.3390/en10010046
APA StyleMinnaert, B., & Stevens, N. (2017). Conjugate Image Theory Applied on Capacitive Wireless Power Transfer. Energies, 10(1), 46. https://doi.org/10.3390/en10010046