Abstract
Accurate electric power demand forecasting plays a key role in electricity markets and power systems. The electric power demand is usually a non-linear problem due to various unknown reasons, which make it difficult to get accurate prediction by traditional methods. The purpose of this paper is to propose a novel hybrid forecasting method for managing and scheduling the electricity power. EEMD-SCGRNN-PSVR, the proposed new method, combines ensemble empirical mode decomposition (EEMD), seasonal adjustment (S), cross validation (C), general regression neural network (GRNN) and support vector regression machine optimized by the particle swarm optimization algorithm (PSVR). The main idea of EEMD-SCGRNN-PSVR is respectively to forecast waveform and trend component that hidden in demand series to substitute directly forecasting original electric demand. EEMD-SCGRNN-PSVR is used to predict the one week ahead half-hour’s electricity demand in two data sets (New South Wales (NSW) and Victorian State (VIC) in Australia). Experimental results show that the new hybrid model outperforms the other three models in terms of forecasting accuracy and model robustness.
1. Introduction
With economic and social development, more and more oil, coal, electricity power, natural gas and other energies are consumed. As a result, the world is facing serious energy resources shortage. It is high time to pay enough attention to make a saving plan with energy resources, which is a key point to ensure global economic sustainability and its healthy development. Electric energy, as an important sort of energy, is vital for a country’s security and social stability. So, accurate electric forecasting is a great asset. According to the research of Bunn and Farmer [1], the operating cost in electric managing will increase by 10 million pounds ever year for every 1% increase in the predicted error. However, since electricity demand is usually disturbed by various factors, such as unpredictable weather conditions, holidays and dynamic electricity prices, it is true that demand series often includes highly non-linear feature and complex factors which make it difficult to obtain accurate prediction [2].
To tackle this challenge and obtain more accurate electric demand forecasting, various models have been developed in the past several decades. Traditionally, researchers often adopt liner regression and time series methods. Bianco et al. [3] proposed linear regression models to forecast electricity consumption in Italy. Grey-based models [4,5] were applied to forecast various power demands. Taylor [6] used double seasonal exponential smoothing model for short-term electrical demand forecasting and obtained a good result. Auto regressive moving average (ARIMA) model as a classical statistic model was used to forecast the electric demand in Malaysia [7]. Tran [8] compared adaptive network based fuzzy inference system (ANFIS) and seasonal ARIMA (SARIMA) in electric demand prediction in Hanoi city, Vietnam, and stated that SARIMA was better. Wang et al. [9] presented a hybrid momentum threshold AR-GARCH model for short term load forecasting. In Nordic electric power market, Cifter [10] predicted electricity price volatility with Markov-switching GARCH model. In other methods of time series, chaotic time series method was used for electricity demand forecast in NSW, Australia [11]. Lack of non-linear consideration lets to inaccurate forecasting of those models because electric load is known to be nonlinear and complex.
To improve the performance of nonlinear electric demand forecasting, artificial intelligence techniques are employed [12]. Some researchers demonstrated the fact that an artificial neural network (ANN) improves the performance on forecasting electrical load [13,14,15,16]. Specht [17] proposed a new ANN model and named it general regression neural network (GRNN) in 1991. GRNN has been extensively applied by researchers in non-linear forecasting [18,19]. Naguib and Hamdy [18] applied GRNN to classify the label of prostate cancer, and Nose-Filho et al. [19] used GRNN to forecast short-term multinodal electric load forecasting. On the other hand, a novel machine learning method called support vector machine (SVM) was proposed by Cortes and Vapnik [20]. SVM for regression is abbreviated SVR. Guo et al. [21] applied SVM and stated that future electric load can be predicted and SVM is efficient for the forecasting. Sun and Liang [22] used an improved least-squares SVM (LSSVM) to predict short-term load forecasting and found that the mean absolute percentage error is less than 1.5%, and proved effectiveness of LSSVM in the short-term load forecasting.
In the latest several years, researchers proposed various and novel hybrid models for increasing forecasting accuracy of nonlinear electric demand. Generally, the combined and hybrid models not only include the advantage of individual models, but also theirs mean absolute error is lower than that of the individual models. Bouzerdoum et al. [23] combined seasonal autoregressive integrated moving average model (ARIMA) and SVM to forecast the short-term power demand and showed that the developed hybrid model performed better than both the single models. Zhao et al. [24] used time-varying weights updated by a high-order Markov chain model to forecast electricity consumption in china, and obtained the same conclusion. Combined time series modeling with adaptive particle swarm optimization was proposed by Wang et al. [25]. This hybrid model includes S-ARIMA, exponential smoothing model and SVM. The experimental results demonstrated that the hybrid model had excellent accuracy and higher level of reliability. Fan et al. [26] proposed a combined model called DEMD-SVR-AR to forecast electrical load in NSW market and the New York Independent System Operator (NYISO). Compared with the other methods, these hybrid models have great improvements in the performance of forecasting accuracy. In other filed, researchers [27,28,29,30] consistently reached a conclusion that hybrid model predicts more accurate than the single models.
The use of Neural Network or SVM and hybrid of them is also useful in the forecast of electricity price. For examples, Weron [31] reviewed abundant literatures of the electricity price forecasting and mentioned that many of the modeling and price forecasting approaches considered in the literature are hybrid solutions, combining techniques from two or more of the groups listed above; Cincotti et al. [32] analyzed electricity spot-prices of the Italian Power Exchange (IPEX) and the results showed that SVM methodology gives better forecasting accuracy for price time series; Another hybrid method which united wavelet transform and a combined forecast method is also proposed by Amjady and Keynia [33].
Almost all of the models mentioned above are chosen to model the original series, which simply ignores the influence of noise signal jamming, seasonal component and trend component. To remove the noise from a signal in the way of empirical mode decomposition (EMD), Guo et al. [34] suggested that the first intrinsic mode function (IMF) includes all of the noise. Nevertheless, EMD also has shortcomings, so we use an advanced EEMD to replace EMD for decomposing the series. The EEMD-based signal filtering has advantages which include extracting IMFs directly from the original sequence without any wavelet functions compared with wavelet decomposition methods and can easily be used to deal with nonlinear and nonstationary signals. In this paper, partial auto correlation function (PACF) also plays a vital role in recognizing noise series according to the truth that noise series does not have the correlation in short-term. The decomposition result of EEMD is split into noise component, waveform component and trend component. The method of seasonal adjustment is adopted to remove seasonal influence in the waveform component. Common season adjustment strategy is very effective to remove the seasonal component in the time series. Next we model the preprocessing waveform series and use the cross validation for GRNN (CGRNN) to train and test net. Later, use CGRNN to get the waveform prediction by adding the seasonal index back as the ultimate waveform prediction value. For the trend component, support vector regression machine optimized by the particle swarm optimization algorithm (PSVR) is selected to build model to formulate the trend series and obtain the predicted value. Finally, we recombine the results of forecasts for both waveform and trend as the ultimate electric demand predicted value.
The rest of this paper is organized as follows. Section 2 mainly describes EMD and EEMD-based signal filtering and PACF. In Section 3, seasonal adjustment, GRNN, cross validation (CV) and CGRNN are illustrated. particle swarm optimization (PSO) algorithm, SVR and PSVR are given in Section 4. The proposed model is presented in Section 5. Followed by the discussion of the experimental results in Section 6. Section 7 concludes this paper and discusses the contribution of this novel model.
2. EMD and EEMD Based Signal Filtering
2.1. Empirical Mode Decomposition Based Signal Filtering
Huang [35] proposed EMD in 1998. The idea of EMD is to decompose the original signal into a sum of IMFs. The decomposition of EMD for any original signal can be written as follows:
where n is the number of IMFs, the i- IMF, the final residual.
In general, noise exists in the first IMF. So, filtering the noise from the original signal by EMD method leads to the following equation:
2.2. Ensemble Empirical Mode Decomposition Based Signal Filtering
EEMD proposed by Wu and Huang [36] overcomes mode mixing on frequency in EMD. The main idea of EEMD is to add white noise into the original signal independently, repeating many times, and to obtain ensemble means of the corresponding IMFs.
2.3. Partial Auto Correlation Function (PACF)
PACF plays a vital role in recognizing noise series, because a noise series does not have the short-term correlation. For a time series , according to Wang and Zhao [30], the definition of PACF is described as follows. The covariance at lag k (if k = 0, it is the variance) is denoted by which are estimated as:
where is the mean of the series, the maximum lag, n the number of data in the time series.
Based on covariance, ACF (auto correlation function) at lag k is decided by:
Based on the covariance and ACF, we can define PACF at lag k denoted by , which is:
where , .
The principle of recognizing noise series is: If the partial autocorrelation at lag k is not out of 95% confidence interval, which is approximately, the series is different with white noise series.
3. The Processing Method of Waveform
3.1. Seasonal Adjustment
In this section, a new season adjustment is discussed. Given a data series ; , then:
For , represents the ith column cycle, the j-th position in the i-th column cycle, k the k-th position in the j-th row of the i-th column cycle. Then, we build a new matrix with size of from the i-th column cycle, which denotes as the matrix . The mean of each column is defined as follows: , so it is easy to obtain . Then use to compute the matrix . The seasonal index for all of column cycle are calculated by using when i from 1 to m. So we can acquire all of the seasonal index matrix for any of a column cycle denoted as . The seasonal index is used to remove the seasonal influence by the Equation (7).
3.2. General Regression Neural Network (GRNN)
The fundamental principle of GRNN is nonliner regression analysis, which is proposed in [18]. There is a main equation which represents the GRNN nonlinear regression formula:
From Equation (8), we know the estimated value is the weighted average with all the sample observed values. Each weight factor of the observed value is decided by corresponding the square of the distances between sample and X. The GRNN block diagram is drew in Figure 1.
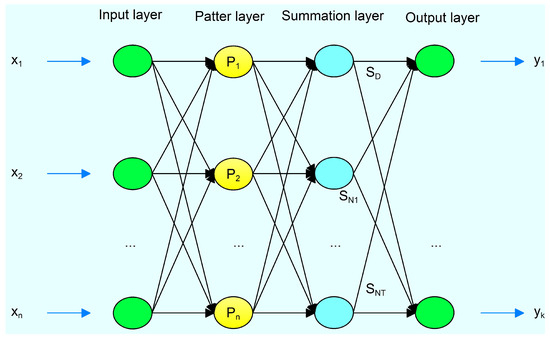
Figure 1.
The structure of general regression neural network (GRNN).
Where, , , , and is the j-th output value and it is decided as .
3.3. Cross Validation
The cross validation (CV) was proposed by Kohavi [37]. Randomly split the original data into k mutually exclusive subsets which have equal size. Let every subsets as a validation set respectively and the rest of subsets as the train sets, and then obtain a series accuracy of the parameters. In the end, every accurate value is decided by Equation (9) and denoted as accuracy (acc):
where n is the number of the validation, the value of the validation, the prediction value. The mean value of k times accuracy is an important criteria to select a better parameter and described in Equation (10). It’s obvious that the mean value of acc (macc) is much smaller, and the corresponding model is much better.
3.4. General Regression Neural Network Optimized by CV
The parameter optimization of GRNN is a problem that influences the accuracy of GRNN prediction. CV is an efficient method to search the optimal parameter of GRNN, because it makes full use of the information of the original sample data set.
Figure 2 is the flowchart of GRNN optimized by cross validation algorithm. Where macc represents mean of accuracy using k steps cross validation for a given parameter sigma. The best sigma is decided by the best macc.
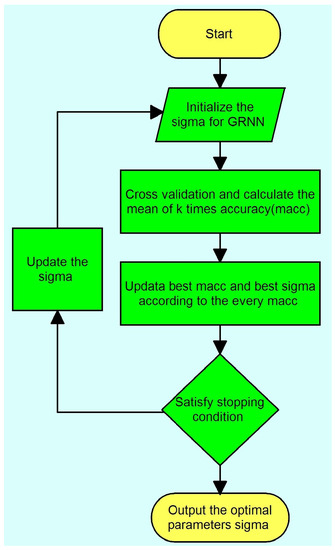
Figure 2.
The flowchart of GRNN optimized by CV algorithm.
4. The Processing Method of Trend Component
4.1. Support Vector Regression Machine
SVM was developed by Cortes and Vapnik [20]. Suppose we are given training data set , with as the input vector, the output value and N the number of the whole sample. The key idea of SVR is to map the input space into a higher dimensional feature space ℵ via nonlinearly mapping . In the higher dimensional feature space, training data is easily classifying and fitting. In SVR, is constructed to approximate linearly the unknown function relationship . The form of is denoted as the equation
where ω is the weight vector, and is a nonlinear mapping from input space to a higher dimensional feature, , and . In order to estimate the coefficients ω and b, the optimization problem is expressed in [20]. The solution is calculated in a form of:
where, is the kernel function. The Gaussian radial basis function (RBF) is an effective kernel function for nonlinear regression problems. Our model employs RBF, which can be expressed as:
4.2. Support Vector Regression Machine Optimized by Particle Swarm Optimization Algorithm
Inspired by foraging act of searching and observation about groups of birds, Kennedy and Eberhart [38] proposed a swarm intelligent optimization algorithm (PSO). PSO method can effectively solve many nonlinear and linear optimization problems.
In SVM, the positive constant parameter c and kernel parameter σ play a key role on the prediction accuracy. It’s important for SVR to select suitable parameter and optimization method. The following is a detailed description of the steps of SVR optimized by PSO.
- Step 1
- Initialization. Randomly generate N particles to make up an original population. The initial position and velocity of each particle are randomly assigned.
- Step 2
- Fitness evaluation. Calculate the fitness value of each particle. The fitness function is calculated in the following equation:where and represent the actual values and prediction values by SVR respectively. Update the local best position and the globe best position .
- Step 3
- Update and generate new particles for the next generation.
- Step 4
- Check whether the termination criteria is satisfied. If not, go back to step 2, otherwise, output the result.
5. The Proposed Method
In electric demand prediction, various factors affect the electric power demand data on different levels. To deal with the problem of noise data caused by the unknown factors, EEMD-based signal filtering and PACF identification approach are used. In addition, seasonal factor also influences the electric demand data. To eliminate the seasonal components and improve the forecasting accuracy, seasonal adjustment is used for processing waveform component after EEMD. GRNN optimizing parameter by CV on the processed data series is used to acquire the final waveform’s prediction by adding season index. PSVR is used to get the final trend’s prediction. In the end, recombined waveform and trend forecasting are used as the ultimate electric prediction. We call the newly established hybrid model EEMD-SCGRNN-PSVR.
The details of the novel model include three stages as follows:
- Stage 1
- Decomposition and noise reduction: EEMD is used to decompose the original electric demand data into a series of IMFs and one residual series. Then, PACF is used to identify noise interference from a number of IMFs and one residual series. In general, the first IMF includes the noise. The rest of IMFs are considered as the waveform component and the residual is considered as the trend component.
- Stage 2
- Single forecasting: On the one hand, the strategy of seasonal adjustment is used to reduce cycle components, GRNN using CV to forecast the processed waveform component series. The CGRNN obtains the final waveform’s prediction by adding corresponding season indexes, and the waveform prediction is noted as W. On the other hand, PSVR is used to obtain the trend forecasting values (T).
- Stage 3
- Ensemble forecasting: These respective estimates of waveform and trend component are combined into the final electric demand forecasts using the principle of ensemble. Equation (15) is the ensemble forecasting formula.
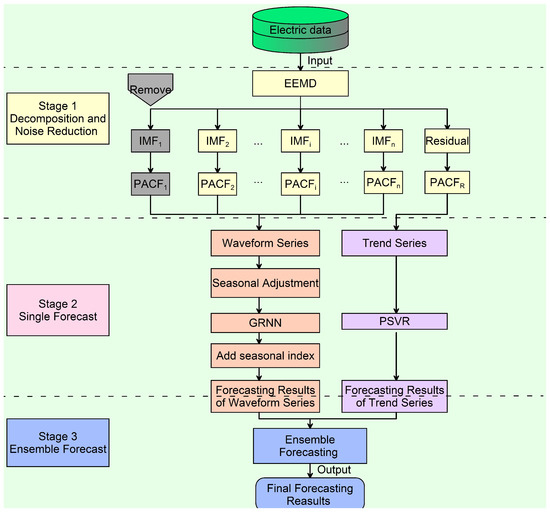
Figure 3.
Overall flowchart of EEMD-SCGRNN-PSVR. EEMD: combines ensemble empirical mode decomposition; IMF: intrinsic mode function; PACF: partial auto correlation function; PSVR: support vector regression machine optimized by the particle swarm optimization algorithm.
6. Simulation
6.1. Data Collection
The daily electricity demand data of New South Wales (NSW) and Victorian (VIC) in Australia used in this paper were collected from the website http://www.aemo.com.au/. The collected data in NSW and VIC covers a time span of 12 weeks in total (NSW: 1 April 2015–23 June 2015, VIC: 1 August 2015–23 October 2015 ), of which the first 11 weeks are used to predict the last one. Weekly predicted data are 336. With half-hour observation values starting from 0:30 to 24:00, there are 48 observation every day, which means a total of 3696 values for the 11 weeks as the training sets and the testing sets containing the remaining 336 data. The statistical properties of the data collected at NSW and VIC are given in Table 1. The original electricity demand data of 12 weeks in NSW are depicted in Figure 4.

Table 1.
Basic statistical properties of electric data sets. NSW: New South Wales; VIC: Victorian.
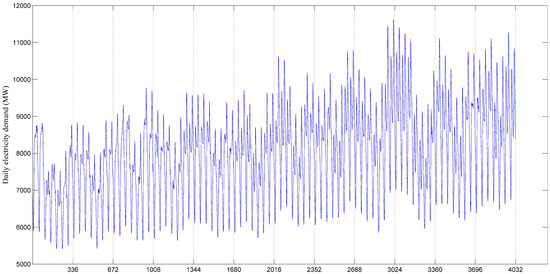
Figure 4.
Electricity demand of NSW from 1 April 2015 to 23 June 2015.
Figure 4 shows the data have an obvious periodic component. The different week data show that the weekly electricity demand is different. It has a seasonal component obviously. Trend component is also obvious, which is hidden in time series.
6.2. Statistical Measures of Forecasting Performance
In this paper, three criteria are employed to quantitatively determine the best model from the proposed models. They are the root mean square error (RMSE), mean absolute error (MAE) and mean absolute percentage error (MAPE), expressed in Equation (16)–(18):
where n is the number of periods of time, the actual value and the prediction value.
6.3. Different Processing Procedure of Four Predicted Models
In order to highlight the advantages of proposed model EEMD-SCGRNN-PSVR, three models are established to make a comparison in this research, i.e., CGRNN (cross validation for general regression neural network), EMD-CGRNN-PSVR (combined with empirical mode decomposition-based signal, cross validation for GRNN and PSO for support vector regression machine) and EEMD-CGRNN-PSVR (combined with ensemble empirical mode decomposition-based signal, cross validation for GRNN and PSO for support vector regression machine).
CGRNN uses the original electric series to build the model. The training function relationship about CGRNN is that the data of the previous weekday can be used to predict the data of the following corresponding weekday (e.g., one Monday to the next Monday, one Tuesday to the next Tuesday). Therefore, the model can directly predict the 336 half hour electric demand values of following week. The function relationship is also adopted by the other three models.
EMD-CGRNN-PSVR applies EMD to decompose the original electric demand data into a series of IMFs and one residual series. Then, PACF is used to identify and remove the noise interference from the IMFs and the residual series. The rest of IMFs as the waveform component and the residual as the trend component are adopted. Then, CGRNN is used to forecast the waveform component as the final waveform’s prediction. PSVR is used to forecast the trend component. In the end, the waveform component and the trend component are combined as the final electric demand forecasting.
The only difference between EEMD-CGRNN-PSVR and EMD-CGRNN-PSVR is that the former employs the method of EEMD to decompose the original electric demand data into a series of IMFs and one residual series. The following steps are same as in the EMD-CGRNN-PSVR.
6.4. Simulation and Experiment Result of EEMD-SCGRNN-PSVR in NSW
Figure 5 shows the decomposed results of EEMD and the high frequency information concentrated on the first several IMFs (a, b, c, d and e), and the low frequency information in the later several IMFs (f, g, h, i and j ). The last residual series (k) is the trend of the original electric series. According to the property that the noise series’ PACF value does not have the short-term correlation, we can identify the noise component.
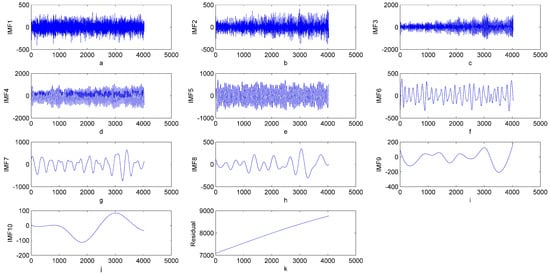
Figure 5.
Decomposition of the original electric demand by EEMD. (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) IMF6; (g) IMF7; (h) IMF8; (i) IMF9; (j) IMF10; and (k) Residual.
The results of the PACF are shown in Figure 6. It can be determined from Figure 6 that all of IMFs and the residual series have short-term correlation. Therefore, those original series just includes a little noise which can be ignored.
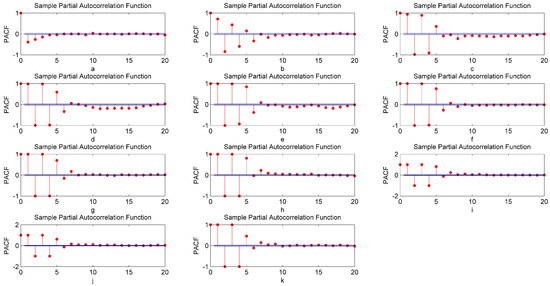
Figure 6.
Sample PACF of each IMF and one residual. (a) PACF of IMF1; (b) PACF of IMF2; (c) PACF of IMF3; (d) PACF of IMF4; (e) PACF of IMF5; (f) PACF of IMF6; (g) PACF of IMF7; (h) PACF of IMF8; (i) PACF of IMF9; (j) PACF of IMF10; and (k) PACF of Residual.
After decomposing and denoising, EEMD-SCGRNN-PSVR assembles IMFs as the waveform component and takes the residual as the trend component. The result of split waveform and trend component is show in Figure 7. Then for waveform, seasonal adjustment is used to eliminate the influences caused by seasonal factors. The detail of seasonal adjustment is introduced in Section 3.1. In this case, the data can compose a matrix , where . m presents the number of weeks for training data, n the seven days of one week, s the 48 half hours of one day. The following seasonal adjustment process is similar to Section 3.1. In the eliminated seasonal waveform series, two day series are depicted in Figure 8 as an example to show seasonal adjustment advantages. Figure 8 demonstrates that eliminated seasonal waveform component becomes more smooth and steady, which will make GRNN to obtain more accurate prediction. On the other hand, the method of PSO to optimize parameter of SVR is used to forecast the trend component series.
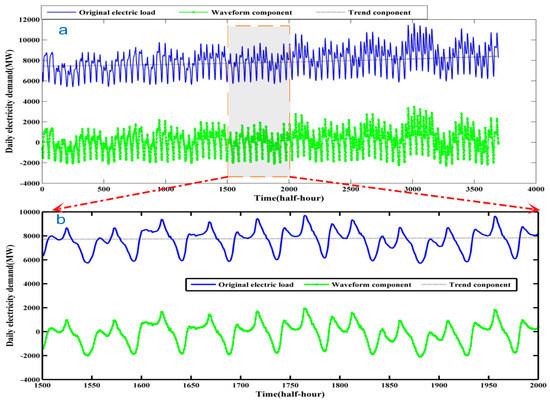
Figure 7.
Split waveform and trend component from original electric demand by using EEMD and PACF. (a) all of 11 weeks half-hour electric demand; (b) amplified the detailed half-hour electric demand between 1500th and 2000th.
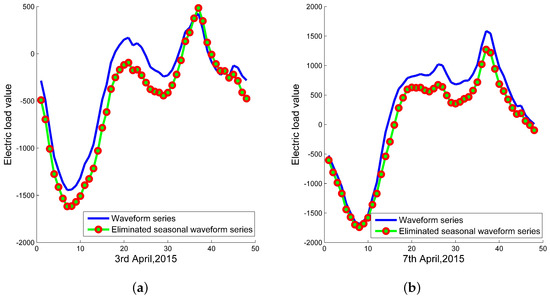
Figure 8.
Comparison of waveform component and eliminated seasonal waveform component in 3 April and 7 April 2015. (a) 3 April 2015; (b) 7 April 2015.
After that, EEMD-SCGRNN-PSVR uses ensemble forecasting. According to Equation (15), these respective estimations of waveform and trend component are combined as the final electric demand forecast value.
EEMD-SCGRNN-PSVR employs CGRNN with EEMD-based signal filtering, seasonal adjustment and PSVR to acquire forecasting value. To emphasize the advantages of EEMD-SCGRNN-PSVR model, the other three models in comparison all use CGRNN method. Contrasting with EEMD-SCGRNN-PSVR, CGRNN directly modeled with the original data. EMD-CGRNN-PSVR does not employ EEMD and seasonal adjustment. EEMD-CGRNN-PSVR does not employ seasonal adjustment.
6.5. Comparative Analysis
6.5.1. Comparative Model Accuracy Analysis
The four models (CGRNN, EMD-CGRNN-PSVR, EEMD-CGRNN-PSVR and EEMD-SCGRNN-PSVR) are respectively denoted as Model 1 to Model 4 for the convenience of discussion. Figure 9a,b shows the weekly ahead prediction values of these four models for NSW (17–23 June 2015) and VIC (17–23 October 2015), with an average value of 50 simulations. It can be seen from Figure 9 that EEMD-SCGRNN-PSVR is better than other models.
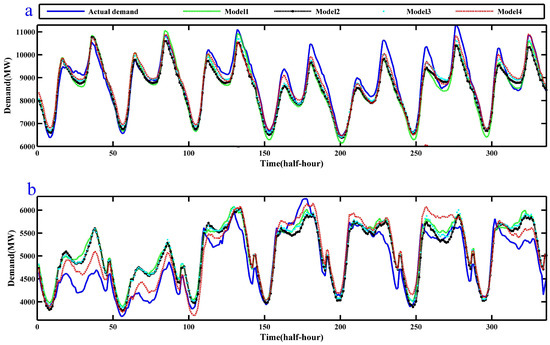
Figure 9.
One week ahead forecasting results of four models for two electricity demand data sets. (a) Next week electricity demand forecasting in NSW (17–23 June 2015); (b) in VIC (17–23 October 2015). This is a color figure, and the reader is referred to the electronic color version of this figure.
Table 2 shows the criteria values of RMSE, MAE and MAPE respectively for four models on one week ahead forecasting in NSW and VIC. When comparing EEMD-SCGRNN-PSVR and the other three models, we have the following observation from Table 2: For one week ahead forecasting in NSW area, three criteria show that the model of CGRNN performs the worst in accuracy (RMSE: 391.17, MAE: 293.38, MAPE: 3.78). However, EEMD-SCGRNN-PSVR has the smallest error value in four methods. When comparing EEMD-SCGRNN-PSVR with CGRNN, EEMD-SCGRNN-PSVR has reduced RMSE by 29.2%, MAE by 27.8%, MAPE by 30.5% in NSW. The other two methods, EMD-CGRNN-PSVR and EEMD-CGRNN-PSVR, have the medial performance. There are same results in VIC area. The optimal RMSE (258.22), MAE (220.46) and MAPE (4.54%) values come from EEMD-SCGRNN-PSVR. As shown in Table 2, compared with CGRNN, EEMD-SCGRNN-PSVR has reduced RMSE by 22.5%, MAE by 23.9%, MAPE by 26.5% in VIC. We can conclude that the advanced method EEMD-SCGRNN-PSVR can obtain much higher accurate electricity demand forecasting values than that of the other models.

Table 2.
Three statistical criteria of four models in two electric data sets.
6.5.2. Comparative Model Robustness Analysis
The robustness analysis of the four methods are given in Figure 10. According to Figure 10a,b, EEMD-SCGRNN-PSVR has the lowest average MAPE error in 50 times simulation, and its MAPE fluctuation is smaller than that of the other three methods. Moreover, the lowest lower and upper bounds of MAPE are given by EEMD-SCGRNN-PSVR method. Broadly speaking, in the two actual cases, the robustness of EEMD-SCGRNN-PSVR model is superior to the other three models.
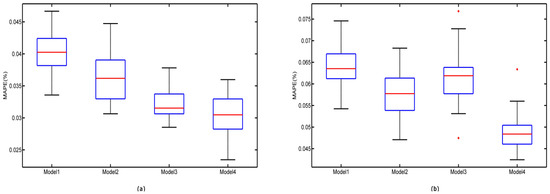
Figure 10.
Box plots of one week ahead forecasting MAPE distribution (50 times simulation) for four models in two electricity demand data sets: (a) NSW (17–23 June 2015); (b) VIC (17–23 October 2015).
All in all, the contrastive experiment carried out EEMD-SCGRNN-PSVR model outperforms the other three models in terms of forecasting accuracy and model stability. EEMD-SCGRNN-PSVR also has the ability to do well in managing and making plan for electricity demand forecasting.
In above experiments, we choose 11 weeks as the training period. Do the results change with the training period? We designed another experiment to evaluate the influence of training period on the accuracy of forecasting. We tried a few of training periods to explain the problem (Using training period as 9, 10, 11, 12, 13, 14 weeks). The experimental results are listed in Table 3. We can see that as the training period changing, the performance of the hybrid model also changes. The best performance is an 11 week training period in both two data sets. However, we cannot give the conclusion that 11 weeks is the best training period. Perhaps it is depending on data set. The performance of EEMD-SCGRNN-PSVM is also very good on all these training periods.

Table 3.
MAPE statistical criteria of EEMD-SCGRNN-PSVM in two electric data sets (NSW, VIC) under different training periods.
7. Conclusions
This paper proposed a forecasting model named EEMD-SCGRNN-PSVR for one week ahead electricity demand forecasting. The main innovate idea of EEMD-SCGRNN-PSVR is that we forecast waveform component and trend component respectively to substitute directly forecasting original electric demand. We applied some advanced techniques into the hybrid model. For example, PACF is used to identify whether original electric demand contains white noise; Seasonal adjustment is taken into account to deal with seasonal factor in the waveform component; GRNN and SVR are used to respectively forecast the waveform and trend. Combining the respectively predicted results as the final electric demand prediction is more accurate than the directly forecasting model (CGRNN), non seasonal adjusting model(EMD-CGRNN-PSVM) and non EEMD decomposing model (EMD-SCGRNN-PSVM). Experiments with three criteria (RMSE, MAE and MAPE) clearly demonstrate that EEMD-SCGRNN-PSVR significantly improves the accuracy and stability of prediction, and this new model can be used to schedule electricity energy demand forecasting in electric market. Moreover, this hybrid model can also be applied to forecast electric price, wind speed, tourism demand and other energy demand. Seemingly complex, the experiment results on two datasets show that the EEMD-SCGRNN-PSVR does not have the over-fitting problem. In contrast, the new hybrid model performs more robust than the other three models. Of course, EEMD-SCGRNN-PSVR has some shortcomings to be overcome. For instance, when using it to forecast electric demand, more time is needed with respected to the simple models. It’s sophisticated model, which will use large memory space on computing. But with the development of computing ability, the new hybrid model can quickly cover the problem.
Acknowledgments
This study is supported by NSFC (Grand No: 41571016). The authors are grateful to Yujing Lu, an English professor in Lanzhou University, for her proof reading.
Author Contributions
Weide Li mainly suggested the idea and significantly contributed manuscript preparation and modification; Xuan Yang contributed to the most analysis work of the study, performed the data experiment and wrote the manuscript; Hao li draw figures and tables for manuscript; Lili Su helped to search the related reference literatures and companied to do data experiment. All the authors are contributed on the research work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bunn, D.W.; Farmer, E.D. Comparative Models for Electrical Load Forecasting; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Zhu, S.; Wang, J.; Zhao, W.; Wang, J. A seasonal hybrid procedure for electricity demand forecasting in China. Appl. Energy 2011, 88, 3807–3815. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S. Electricity consumption forecasting in Italy using linear regression models. Energy 2009, 34, 1413–1421. [Google Scholar] [CrossRef]
- Hsu, C.C.; Chen, C.Y. Applications of improved grey prediction model for power demand forecasting. Energy Convers. Manag. 2003, 44, 2241–2249. [Google Scholar] [CrossRef]
- Xie, N.M.; Yuan, C.Q.; Yang, Y.J. Forecasting China’s energy demand and self-sufficiency rate by grey forecasting model and Markov model. Int. J. Electr. Power Energy Syst. 2015, 66, 1–8. [Google Scholar] [CrossRef]
- Taylor, J.W. Short-term electricity demand forecasting using double seasonal exponential smoothing. J. Oper. Res. Soc. 2003, 54, 799–805. [Google Scholar] [CrossRef]
- Mohamed, N.; Ahmad, M.H.; Ismail, Z. Double seasonal ARIMA model for forecasting load demand. Matematika 2010, 2, 217–231. [Google Scholar]
- Tran, V. One week hourly electricity load forecasting using neuro-fuzzy and seasonal ARIMA models. In Proceedings of the Power Plants and Power Systems Control, Toulouse, France, 2–5 September 2012; pp. 97–102.
- Wang, Y.; Li, F.; Wan, Q.; Chen, H. Hybrid momentum TAR-GARCH models for short term load forecasting. In Proceedings of the Power and Energy Society General Meeting, Detroit, MI, USA, 24–29 July 2011.
- Cifter, A. Forecasting electricity price volatility with the Markov-switching GARCH model: Evidence from the Nordic electric power market. Electr. Power Syst. Res. 2013, 102, 61–67. [Google Scholar] [CrossRef]
- Wang, J.; Chi, D.; Wu, J.; Lu, H.Y. Chaotic time series method combined with particle swarm optimization and trend adjustment for electricity demand forecasting. Expert Syst. Appl. 2011, 38, 8419–8429. [Google Scholar] [CrossRef]
- Hong, W.C. Chaotic particle swarm optimization algorithm in a support vector regression electric load forecasting model. Energy Convers. Manag. 2009, 50, 105–117. [Google Scholar] [CrossRef]
- Gotman, N.; Shumilova, G.; Starceva, T. Electric Load Forecasting Using an Artificial Neural Networks; LAP LAMBERT Academic Publishing: Saarbrucken, Germany, 2014. [Google Scholar]
- Zealand, C.M.; Burn, D.H.; Simonovic, S.P. Short term streamflow forecasting using artificial neural networks. J. Hydrol. 1999, 214, 32–48. [Google Scholar] [CrossRef]
- Bhattacharyya, S.C.; Thanh, L.T. Short-term electric load forecasting using an artificial neural network: Case of Northern Vietnam. Int. J. Energy Res. 2004, 28, 463–472. [Google Scholar] [CrossRef]
- Hamid, M.A.; Rahman, T.A. Short term load forecasting using an artificial neural network trained by artificial immune system learning algorithm. In Proceedings of the Uksim, International Conference on Computer Modelling and Simulation, Cambridge, UK, 24–26 March 2010; pp. 408–413.
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Naguib, R.N.G.; Hamdy, F.C. A general regression neural network analysis of prognostic markers in prostate cancer. Neurocomputing 1998, 19, 145–150. [Google Scholar] [CrossRef]
- Nose-Filho, K.; Lotufo, A.D.P.; Minussi, C.R. Short-term multinodal load forecasting using a modified general regression neural network. IEEE Trans. Power Deliv. 2011, 26, 2862–2869. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Guo, X.C.; Liang, Y.C.; Wu, C.G.; Wang, H.Y. Electric load forecasting using SVMS. In Proceedings of the IEEE 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006; pp. 4213–4215.
- Sun, W.; Liang, Y. Least-squares support vector machine based on improved imperialist competitive algorithm in a short-term load forecasting model. J. Energy Eng. 2014, 141, 04014037. [Google Scholar] [CrossRef]
- Bouzerdoum, M.; Mellit, A.; Pavan, A.M. A hybrid model (SARIMA–SVM) for short-term power forecasting of a small-scale grid-connected photovoltaic plant. Sol. Energy 2013, 98, 226–235. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, J.; Lu, H. Combining forecasts of electricity consumption in China with time-varying weights updated by a high-order Markov chain model. Omega 2014, 45, 80–91. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, S.; Zhang, W.; Lu, H. Combined modeling for electric load forecasting with adaptive particle swarm optimization. Energy 2010, 35, 1671–1678. [Google Scholar] [CrossRef]
- Fan, G.F.; Peng, L.L.; Hong, W.C.; Sun, F. Electric load forecasting by the SVR model with differential empirical mode decomposition and auto regression. Neurocomputing 2015, 173, 958–970. [Google Scholar] [CrossRef]
- Guo, Z.H.; Wu, J.; Lu, H.Y.; Wang, J.Z. A case study on a hybrid wind speed forecasting method using BP neural network. Knowl.-Based Syst. 2011, 24, 1048–1056. [Google Scholar] [CrossRef]
- Kran, M.S.; Ozceylan, E.; Gunduz, M.; Paksoy, T. A novel hybrid approach based on Particle Swarm Optimization and Ant Colony Algorithm to forecast energy demand of Turkey. Energy Convers. Manag. 2012, 53, 75–83. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Li, Y.F. Comparison of two new ARIMA-ANN and ARIMA-Kalman hybrid methods for wind speed prediction. Appl. Energy 2012, 98, 415–424. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, W. ARIMA model estimated by particle swarm optimization algorithm for consumer price index forecasting. In Proceedings of the Artificial Intelligence and Computational Intelligence, International Conference (AICI 2009), Shanghai, China, 7–8 November 2009; pp. 48–58.
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Cincotti, S.; Gallo, G.; Ponta, L.; Raberto, M. Modeling and forecasting of electricity spot-prices: Computational intelligence vs. classical econometrics. AI Commun. 2014, 27, 301–314. [Google Scholar]
- Amjady, N.; Keynia, F. Day ahead price forecasting of electricity markets by a mixed data model and hybrid forecast method. Int. J. Electr. Power Energy Syst. 2008, 30, 533–546. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, W.; Lu, H.; Wang, J. Multi-step forecasting for wind speed using a modified EMD-based artificial neural network model. Renew. Energy 2012, 37, 241–249. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2011, 1, 1–41. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1143.
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948.
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).