Particle Swarm Optimization for Outdoor Lighting Design
Abstract
:1. Introduction
2. Outdoor Lighting
2.1. Energy Efficiency Classification
- Functional street lighting: It encompasses lighting installations for motorways, dual carriageways, urban streets and roads.
- Ambient street lighting: It is generally placed on low supports in urban areas for lighting pedestrian and commercial areas, pavements, parks and gardens, historic centers and roads with low speeds limits.
2.2. Lighting Systems
3. Particle Swarm Optimization for Outdoor Lighting Optimization
- 1.
- First of all, the algorithm has to initialize the population with random positions, as in Equation (3), and velocities, as in Equation (4), in the search space.
- 2.
- Analyze value of each particle according to a fitness function, selecting the particle with the best solution as the leader.
- 3.
- Update the velocity of each particle according to the following Equation (5):
- 4.
- Update the position of each particle according to Equation (6):
- 5.
- Evaluate the quality of each particle according to a fitness function, which is also the objective function, in our case the function which calculates the energy efficiency of the outdoor lighting installation.
- 6.
- Check the quality of the particle result. In case the quality of the solution is better than the best particle result, it will be updated with the value of the current particle.
- 7.
- In case one of the solutions reached by any of the particles is better than the current leader, the leader of the swarm is updated.
- 8.
- Check if the maximum number of iterations has been reached or if the best solution fits the fitness value. In case the maximum number of iterations is not reached, the algorithm will go to the third step again.
4. Experiments and Discussion
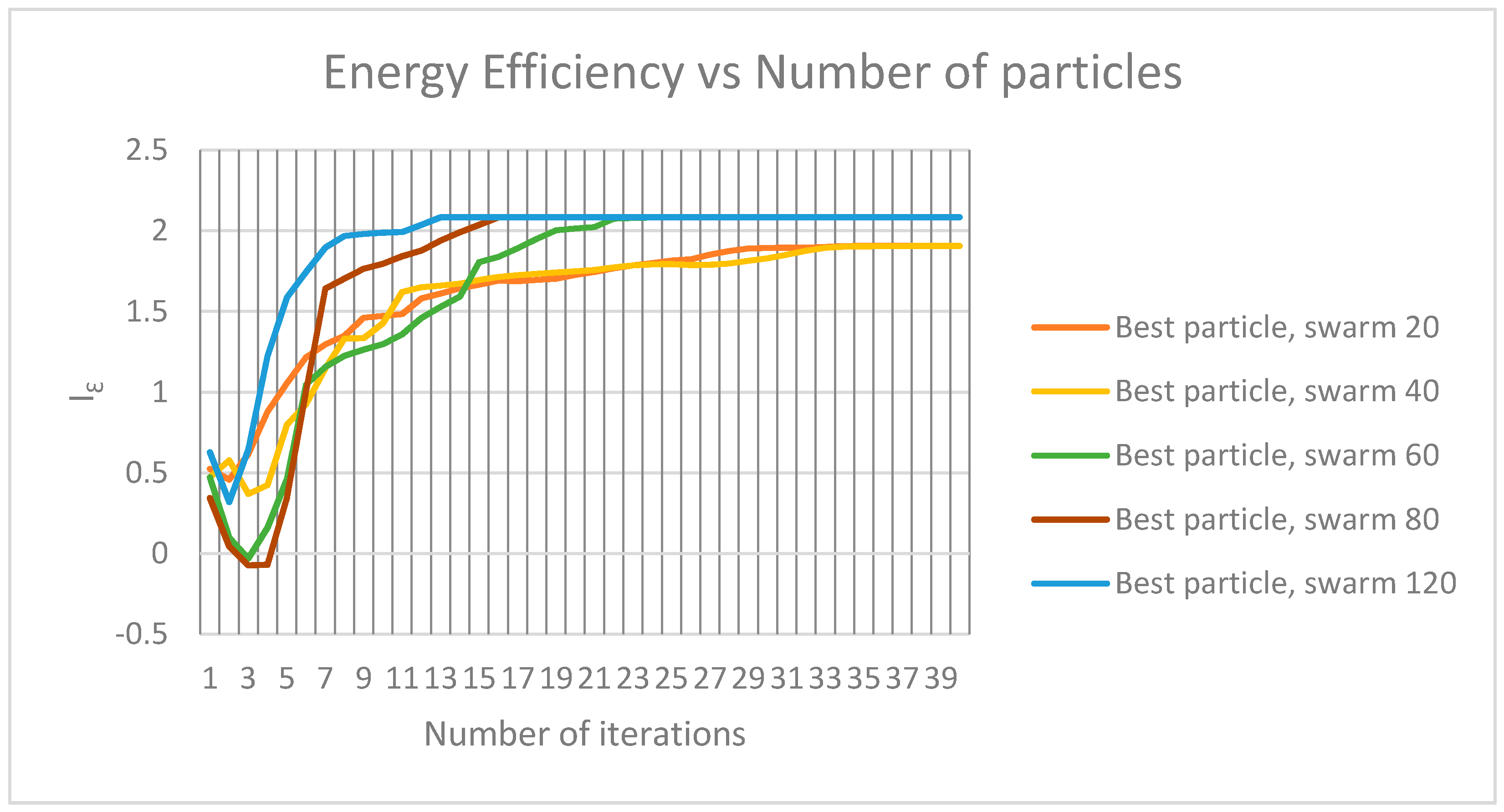
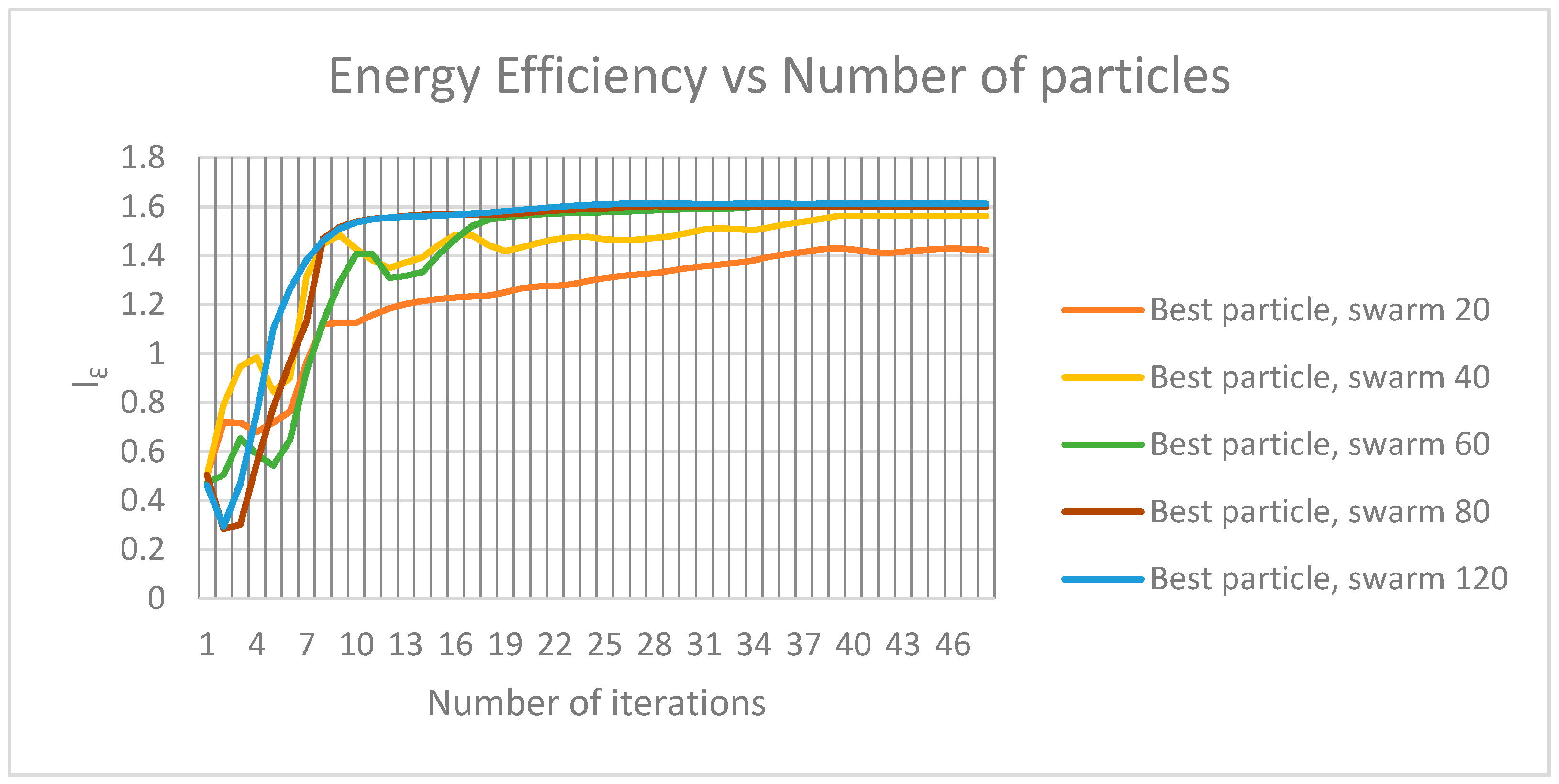
- Number of particles in swarm = {20, 30, 40, 50, 60, 70, 80, 100, 120}.
- Number of iterations = {1–60}.
- Inertia weight (ω) = {0.1, 0.3, 0.5, 0.7, 0.8, 0.9, 1.1, 1.3, 1.5, 1.7}.
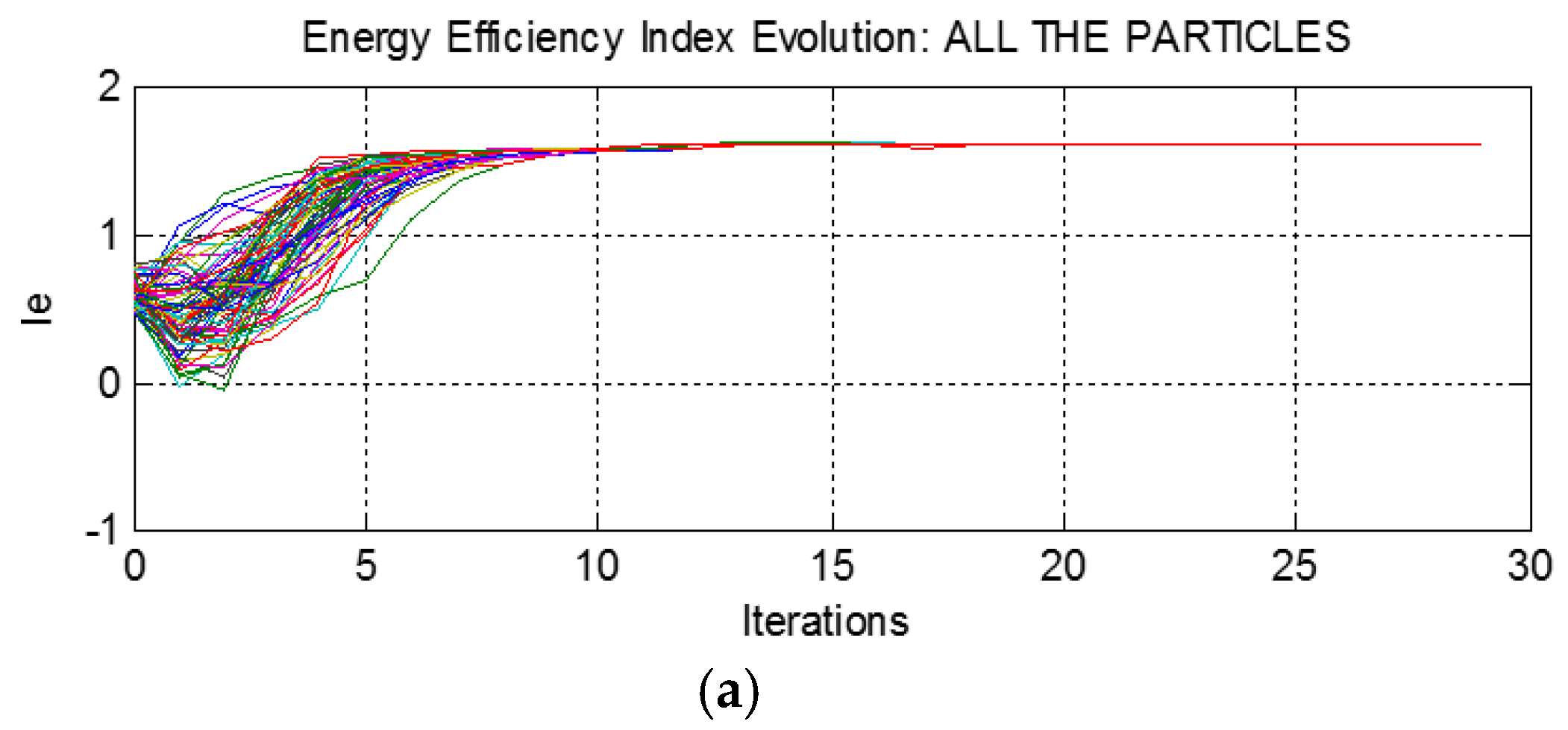
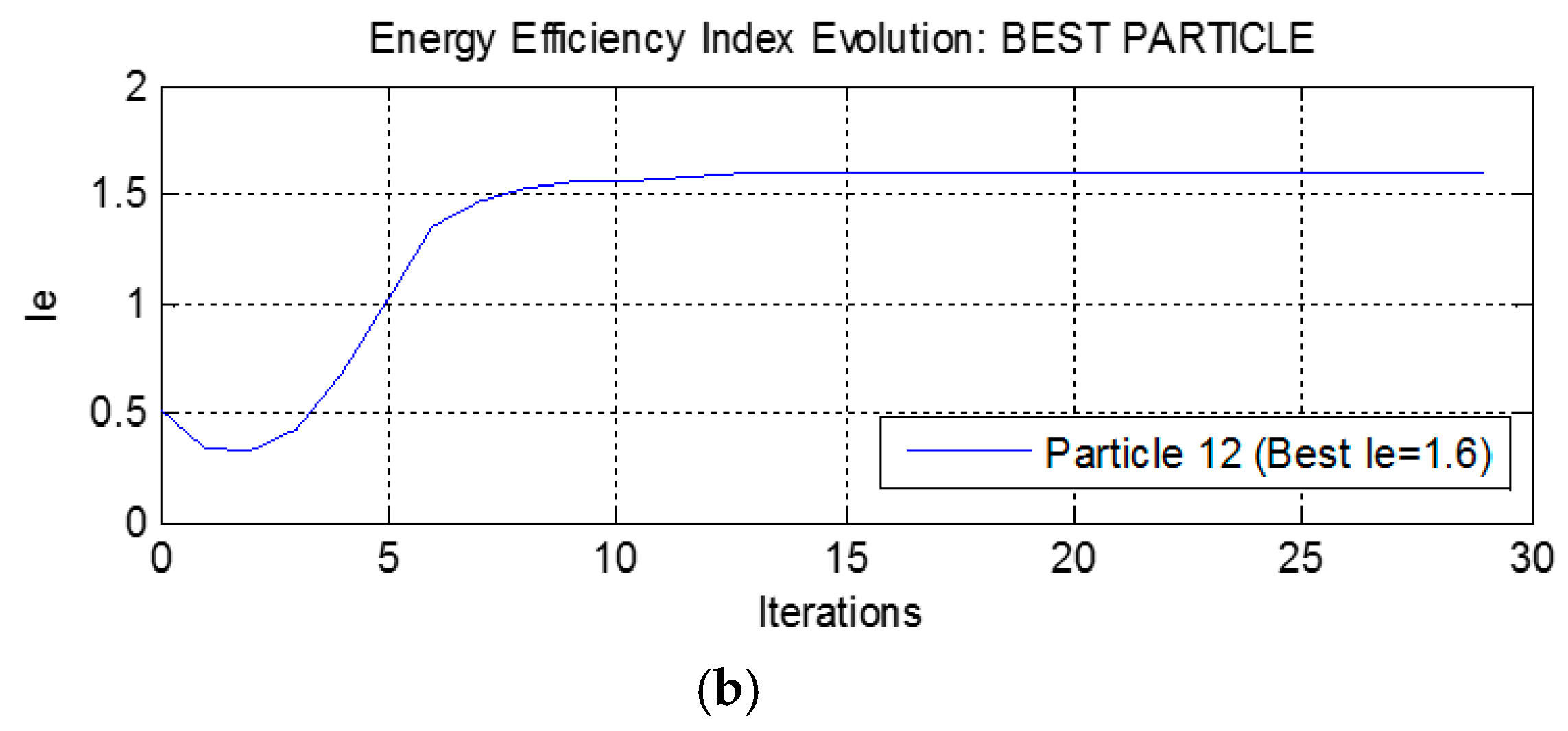
4.1. Experiment 1
4.2. Experiment 2
4.3. Algorithm Validation
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Lorenc, T.; Petticrew, M.; Whitehead, M.; Neary, D.; Clayton, S.; Wright, K.; Thomson, H.; Cummins, S.; Sowden, A.; Renton, A. Environmental interventions to reduce fear of crime: Systematic review of effectiveness. Syst. Rev. 2013, 2. [Google Scholar] [CrossRef] [PubMed]
- Reusel, K.V. A look ahead at energy-efficient electricity applications in a modern world. In Proceedings of the Energy Climate Technology 2008, Bergen, Norway, 17–18 April 2008.
- AAE—Agencia Andaluza de la Energía. Guía de ahorro y Eficiencia Energética en Municipios (Guide for Savings and Energy Efficiency un Municipalities). Aviliable online: https://www.agenciaandaluzadelaenergia.es/sites/default/files/guia_de_ahorro_y_eficiencia_energxtica_web_def1.pdf (accessed on 14 November 2014).
- Spanish Government. Royal Decree 1890/2008 Energy Efficiency for Outdoor Lighting Installations; Spanish Government: Madrid, Spain, 2008.
- De Miguel, A.S.; Zamorano, J.; Castaño, J.G.; Pascual, S. Evolution of the energy consumed by street lighting in Spain estimated with DMSP-OLS data. J. Quant. Spectrosc. Radiat. Transf. 2014, 139, 109–117. [Google Scholar] [CrossRef]
- Herranz, C. Entrevista con Alfonso Beltrán García-Echaniz, Director General del Instituto para la Diversificación y Ahorro de la Energía (IDAE). Física y Sociedad. 2011, Volume 21, pp. 26–29. Available online: http://www.cofis.es/pdf/fys/fys21/fys21_26-29.pdf (accessed on 19 January 2017).
- Gómez-Lorente, D.; Rabaza, O.; Estrella, A.E.; Peña-García, A. A new methodology for calculating roadway lighting design based on a multi-objective evolutionary algorithm. Expert Syst. Appl. 2013, 40, 2156–2164. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Swarm Intelligence; Morgan Kaufmann Publishers: San Mateo, CA, USA, 2001. [Google Scholar]
- Alba, E.; Garcia-Nieto, J.; Taheri, J.; Zomaya, A. New research in nature inspired algorithms for mobility management in GSM networks. In Applications of Evolutionary Computing; Springer: Berlin, Germany, 2008; pp. 1–10. [Google Scholar]
- Parsopoulos, K.E.; Vrahatis, F.M. Unified particle swarm optimization for solving constrained engineering optimization problems. In Advances in Natural Computation; Springer: Berlin, Germany, 2005; pp. 582–591. [Google Scholar]
- Alba, E.; Garcia-Nieto, J.; Jourdan, L.; Talbi, E.-G. Gene selection in cancer classification using PSO/SVM and GA/SVM hybrid algorithms. In Proceedings of the IEEE Congress of Evolutionary Computation, Singapore, 25–28 September 2007; pp. 284–290.
- Garcia-Nieto, J.; Toutouh, J.; Alba, E. Automatic tuning of communication protocols for vehicular ADOC networks using metaheuristics. Eng. Appl. Artif. Intel. 2010, 23, 795–805. [Google Scholar] [CrossRef]
- Martins, M.S.R.; Fuchs, S.C.; Pando, L.U.; Lüders, R.; Delgado, M.R. PSO with path relinking for resource allocation using simulation optimization. Comput. Ind. Eng. 2013, 65, 322–330. [Google Scholar] [CrossRef]
- Khare, A.; Rangnekar, S. A review of particle swarm optimization and its applications in Solar Photovoltaic system. Appl. Soft Comput. 2013, 13, 2997–3006. [Google Scholar] [CrossRef]
- AlRashidi, M.R.; El-Hawary, M.E. A survey of particle swarm optimization applications in electric power systems. IEEE Trans. Evolut. Comput. 2009, 13, 913–918. [Google Scholar] [CrossRef]
- Jeffery, C.R. Crime Prevention through Environmental Design; Sage Publications: Beverly Hills, CA, USA, 1971. [Google Scholar]
- De la Paz Gómez, F.; Sanhueza, P.; Díaz Castro, J. Practical Guide for Outdoor Lighting; Instituto de Astrofísica de Canarias (IAC)/Quality Protection Technical Office (OTPC): Tenerife, Spain, 2010. [Google Scholar]
- Dully, M. Traffic Safety Evaluation of Future Road Lighting Systems. Aviliable online: http://www.diva-portal.org/smash/get/diva2:667217/FULLTEXT01.pdf (accessed on 14t November 2014).
- Jackett, M.; Frith, W. Quantifying the impact of road lighting on road safety—A New Zealand study. IATSS Res. 2013, 36, 139–145. [Google Scholar] [CrossRef]
- Lighting against Crime. A Guide for Crime Reduction Professionals. Aviliable online: http://www.securedbydesign.com/pdfs/110107_LightingAgainstCrime.pdf (accessed on 14 November 2014).
- Corcione, M.; Fontana, L. Optimal design of outdoor lighting systems by genetic algorithms. Lighting Res. Technol. 2003, 35, 261–280. [Google Scholar] [CrossRef]
- Kostic, M.; Djokic, L. Recommendations for energy efficient and visually acceptable street lighting. Energy 2009, 34, 1565–1572. [Google Scholar] [CrossRef]
- Sȩdziwy, A.; Kozién-Woၺniak, M. Computational Support for Optimizing Street Lighting Design; Springer: Berlin, Germany, 2012; pp. 241–255. [Google Scholar]
- Kennedy, J. The particle swarm: Social adaptation of knowledge. In Proceedings of the IEEE International Conference on Evolutionary Computation, Indianapolis, IN, USA, 13–16 April 1997; pp. 303–308.
- Eberhart, R.C.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948.
- Eberhart, R.C.; Shi, Y.; Kennedy, J. Swarm Intelligence; Morgan Kaufmann Publishers: Burlington, MA, USA, 2001. [Google Scholar]
- Kennedy, J. Thinking is social: Experiments with the adaptive culture model. J. Confl. Resolut. 1998, 42, 56–76. [Google Scholar] [CrossRef]
- Rezaee Jordehi, A.; Jasni, J. Parameter selection in particle swarm optimization: A survey. J. Exp. Theor. Artif. Intel. 2013, 25, 527–542. [Google Scholar] [CrossRef]


| Inertia Weight (ω) | Maximum Energy Efficiency Index () | Do the Particles Converge? |
|---|---|---|
| 0.1 | 0.85 | Yes |
| 0.3 | 1.32 | Yes |
| 0.5 | 1.66 | Yes |
| 0.7 | 1.71 | Yes |
| 0.9 | 1.69 | Yes |
| 1.1 | 1.69 | No |
| 1.3 | 1.68 | No |
| 1.5 | 1.67 | No |
| 1.7 | 1.64 | No |
| Particle Swarm Size | Maximum Value (Mean) | Convergence Iteration | Memory Used (Bytes) |
|---|---|---|---|
| 20 | 1.904 | 35–40 | 127,192 |
| 30 | 1.954 | 30–35 | 147,856 |
| 40 | 2.017 | 30–35 | 168,552 |
| 50 | 2.030 | 20–25 | 189,216 |
| 60 | 2.083 | 20–25 | 209,912 |
| 70 | 2.083 | 15–20 | 230,576 |
| 80 | 2.083 | 15–20 | 251,272 |
| 100 | 2.084 | 15–20 | 292,632 |
| 120 | 2.084 | 10–15 | 333,992 |
| Spacing between Luminaires | (DIALux) | (algorithm) | Deviation |
|---|---|---|---|
| 17 | 0.763 | 0.747 | −2.09% |
| 27 | 0.821 | 0.799 | −2.67% |
| 30 | 0.820 | 0.814 | −1.21% |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo-Martinez, A.; Ramon Almagro, J.; Gutierrez-Escolar, A.; Del Corte, A.; Castillo-Sequera, J.L.; Gómez-Pulido, J.M.; Gutiérrez-Martínez, J.-M. Particle Swarm Optimization for Outdoor Lighting Design. Energies 2017, 10, 141. https://doi.org/10.3390/en10010141
Castillo-Martinez A, Ramon Almagro J, Gutierrez-Escolar A, Del Corte A, Castillo-Sequera JL, Gómez-Pulido JM, Gutiérrez-Martínez J-M. Particle Swarm Optimization for Outdoor Lighting Design. Energies. 2017; 10(1):141. https://doi.org/10.3390/en10010141
Chicago/Turabian StyleCastillo-Martinez, Ana, Jose Ramon Almagro, Alberto Gutierrez-Escolar, Antonio Del Corte, José Luis Castillo-Sequera, José Manuel Gómez-Pulido, and José-María Gutiérrez-Martínez. 2017. "Particle Swarm Optimization for Outdoor Lighting Design" Energies 10, no. 1: 141. https://doi.org/10.3390/en10010141
APA StyleCastillo-Martinez, A., Ramon Almagro, J., Gutierrez-Escolar, A., Del Corte, A., Castillo-Sequera, J. L., Gómez-Pulido, J. M., & Gutiérrez-Martínez, J.-M. (2017). Particle Swarm Optimization for Outdoor Lighting Design. Energies, 10(1), 141. https://doi.org/10.3390/en10010141