State of Charge and State of Health Estimation of AGM VRLA Batteries by Employing a Dual Extended Kalman Filter and an ARX Model for Online Parameter Estimation
Abstract
:1. Introduction
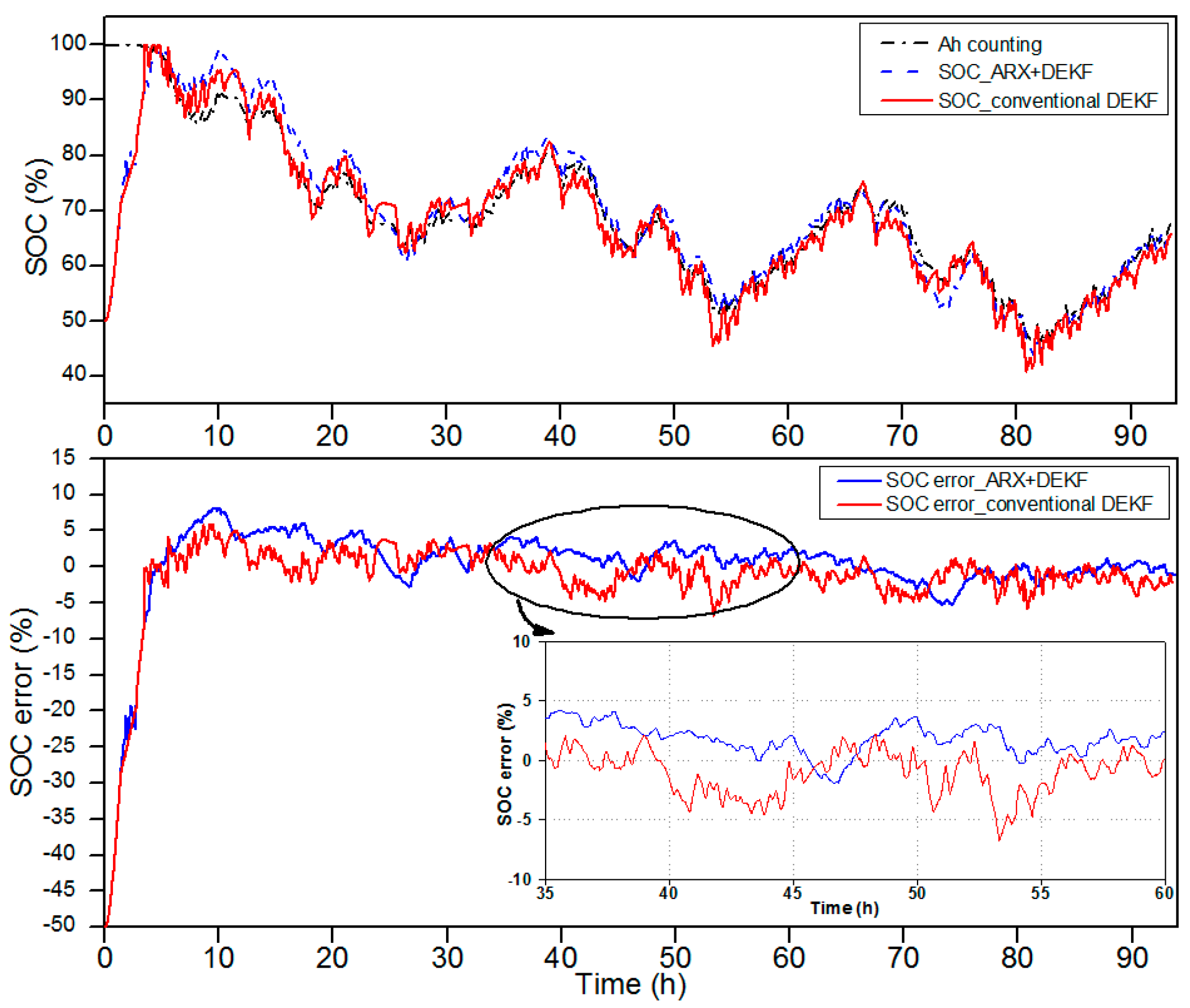
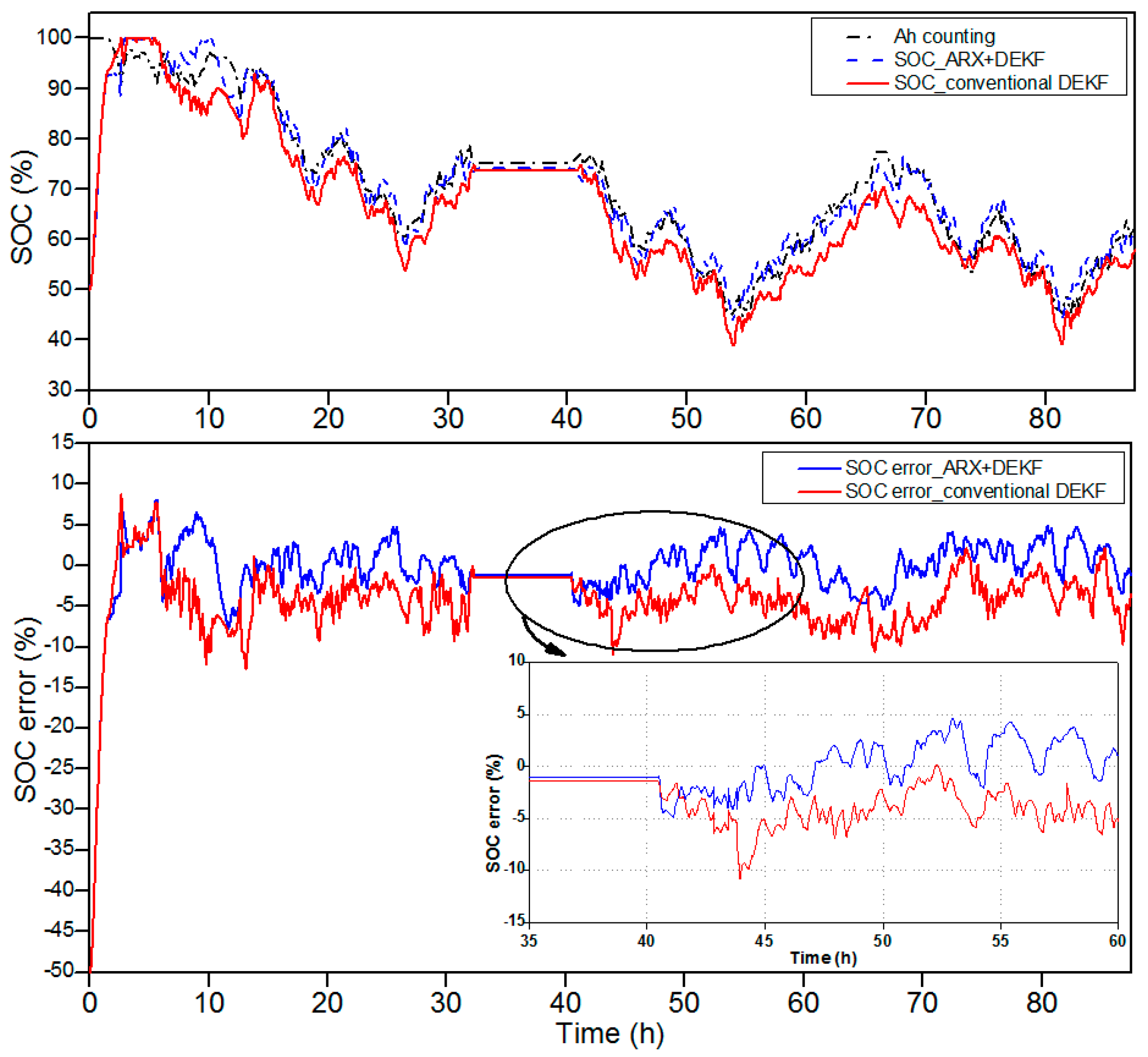
- The nonlinear characteristics of lead-acid batteries such as the hysteresis and diffusion effects have been modeled accurately and the error in the SOC estimation is less than 5%.
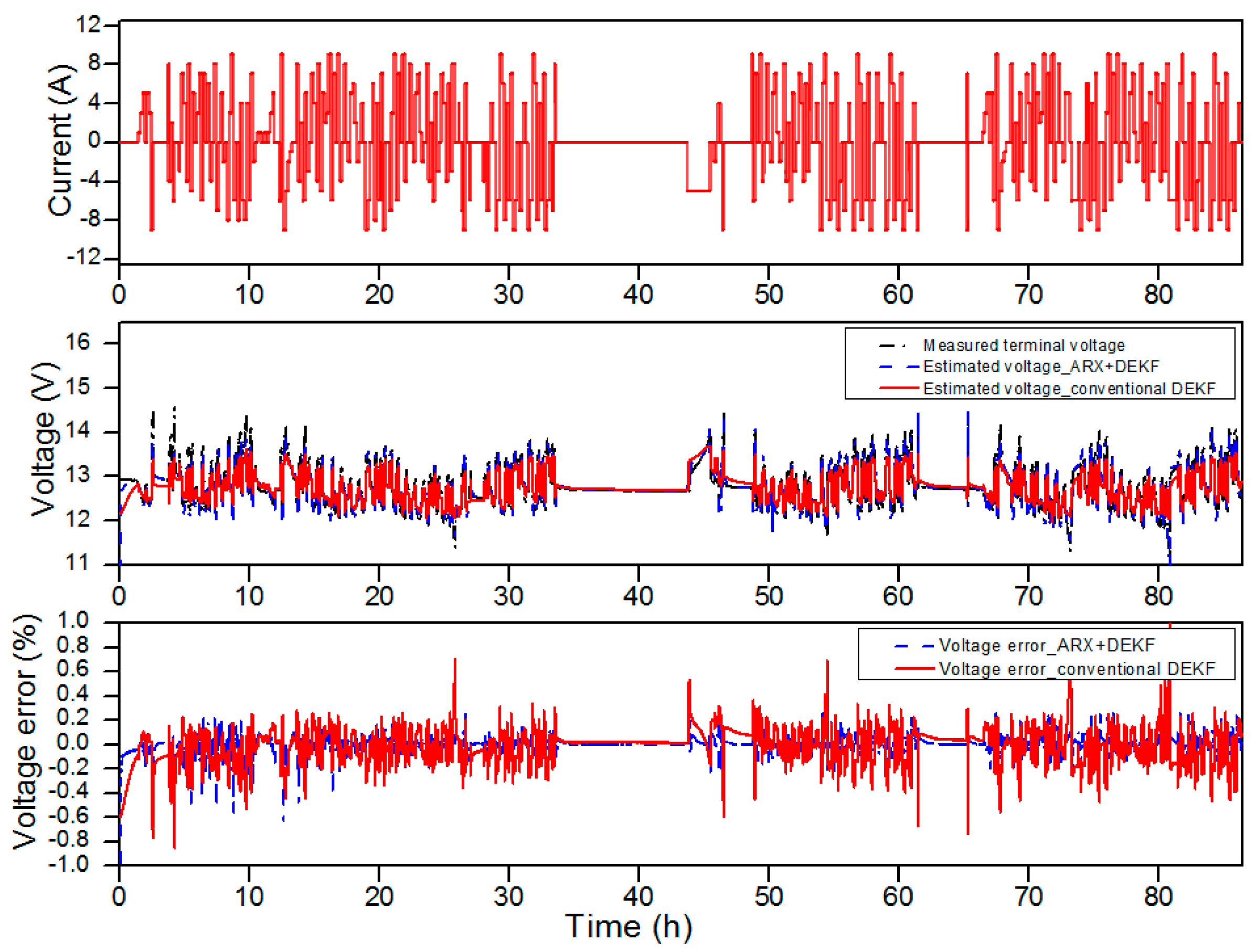
- Unlike the conventional approaches, the SOC and SOH estimation performance has been tested with batteries with different aging levels under the varying temperature conditions and reliable results have been obtained under extensive variations in temperature, SOC and current.
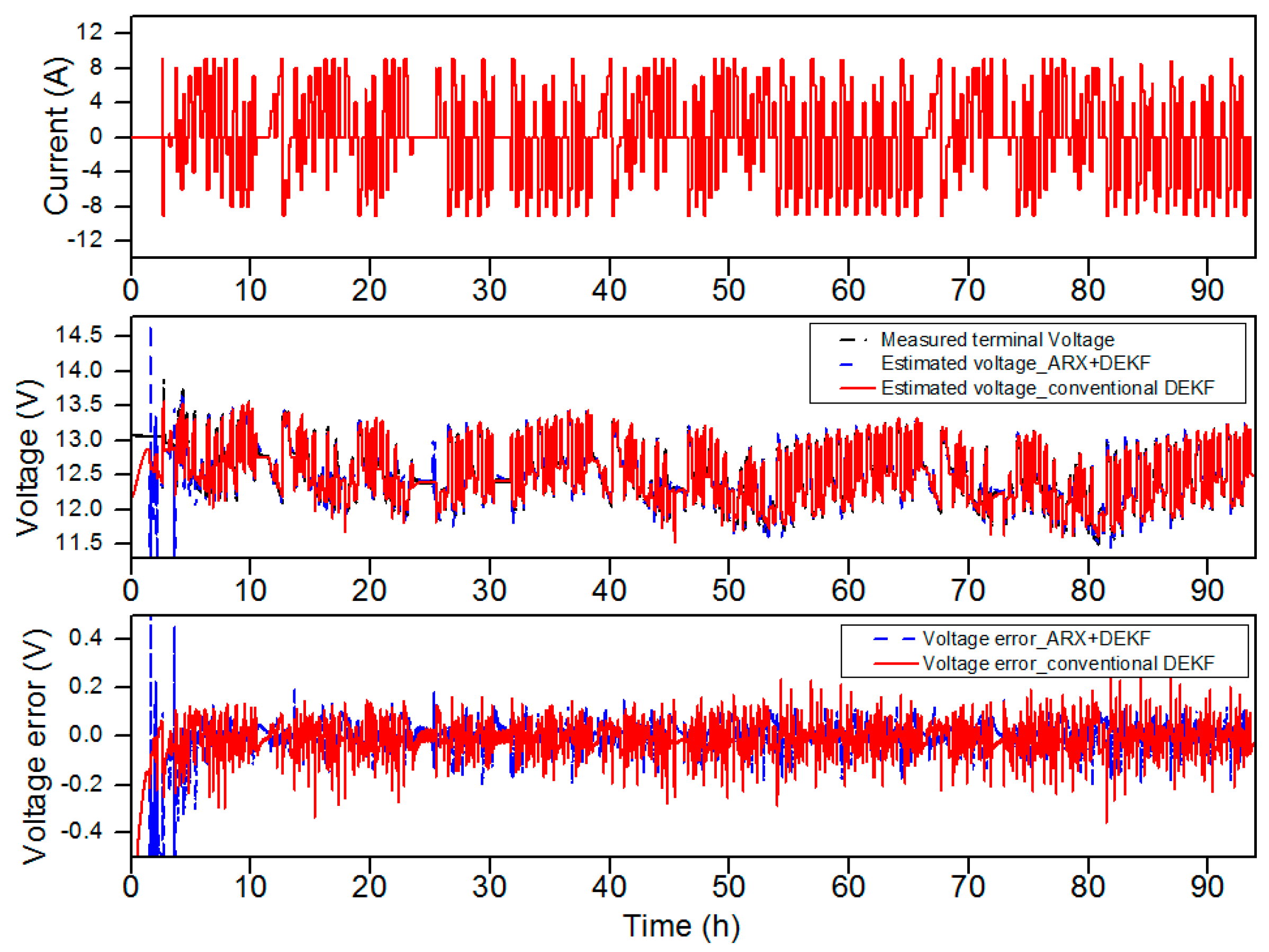
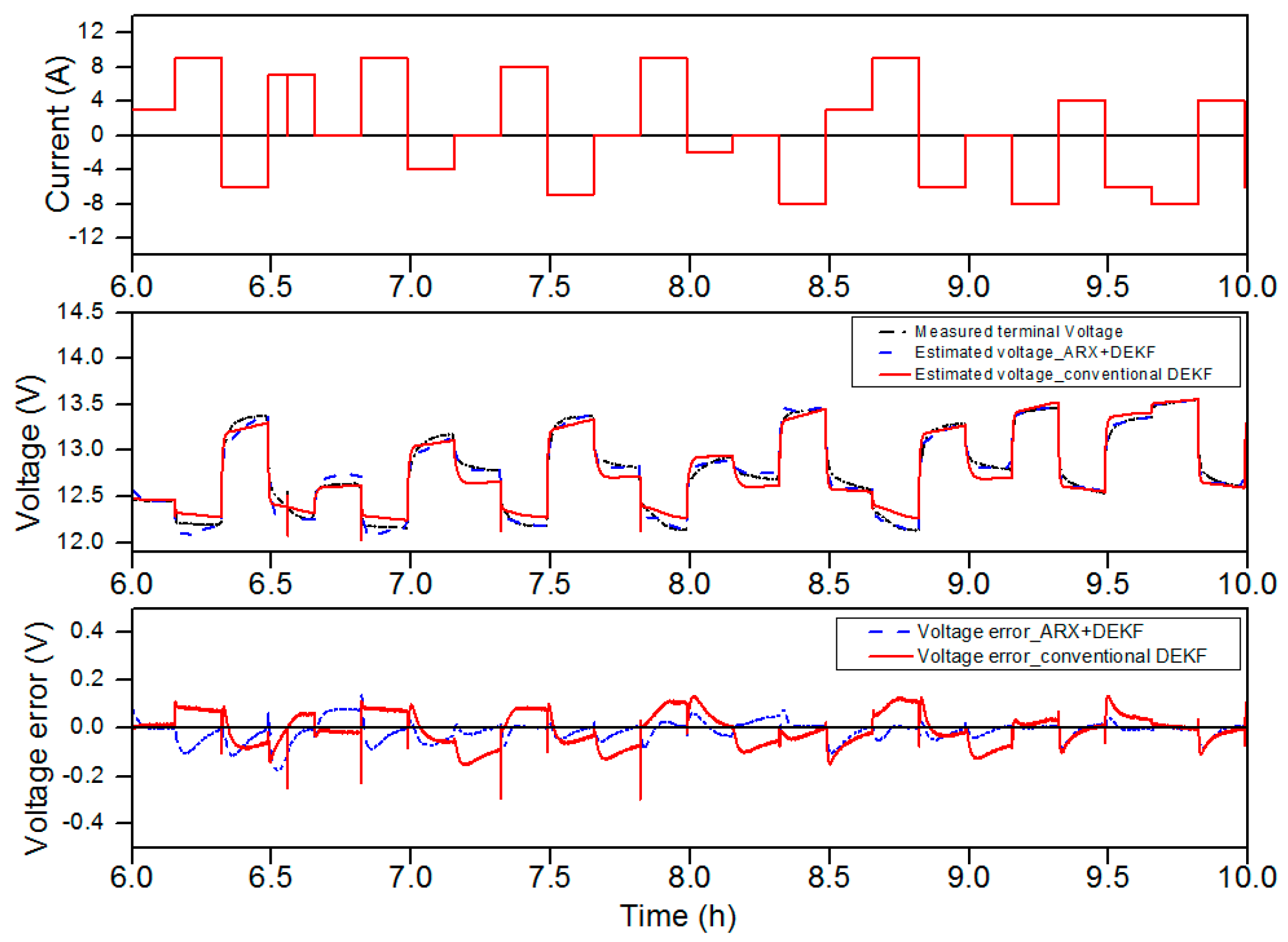
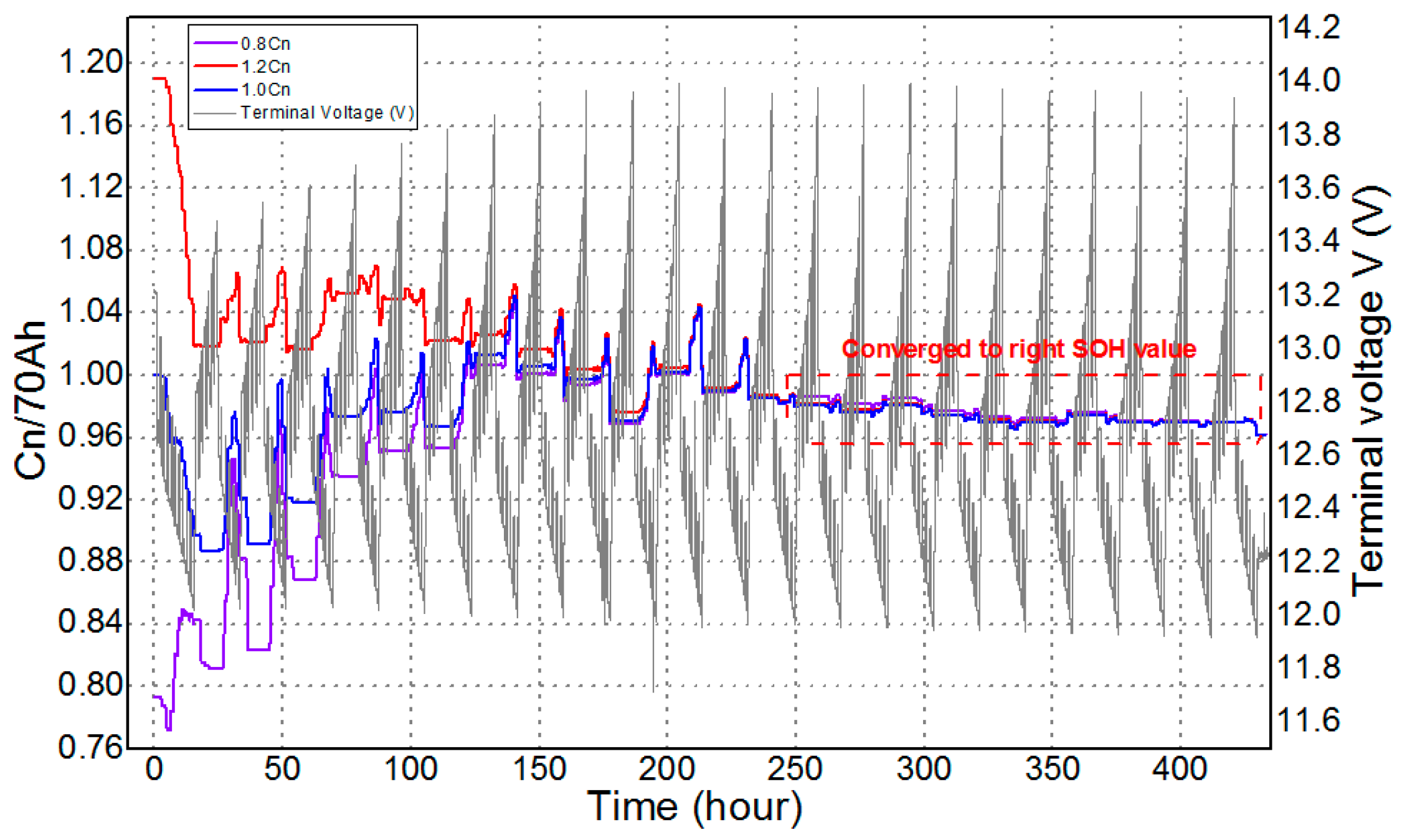
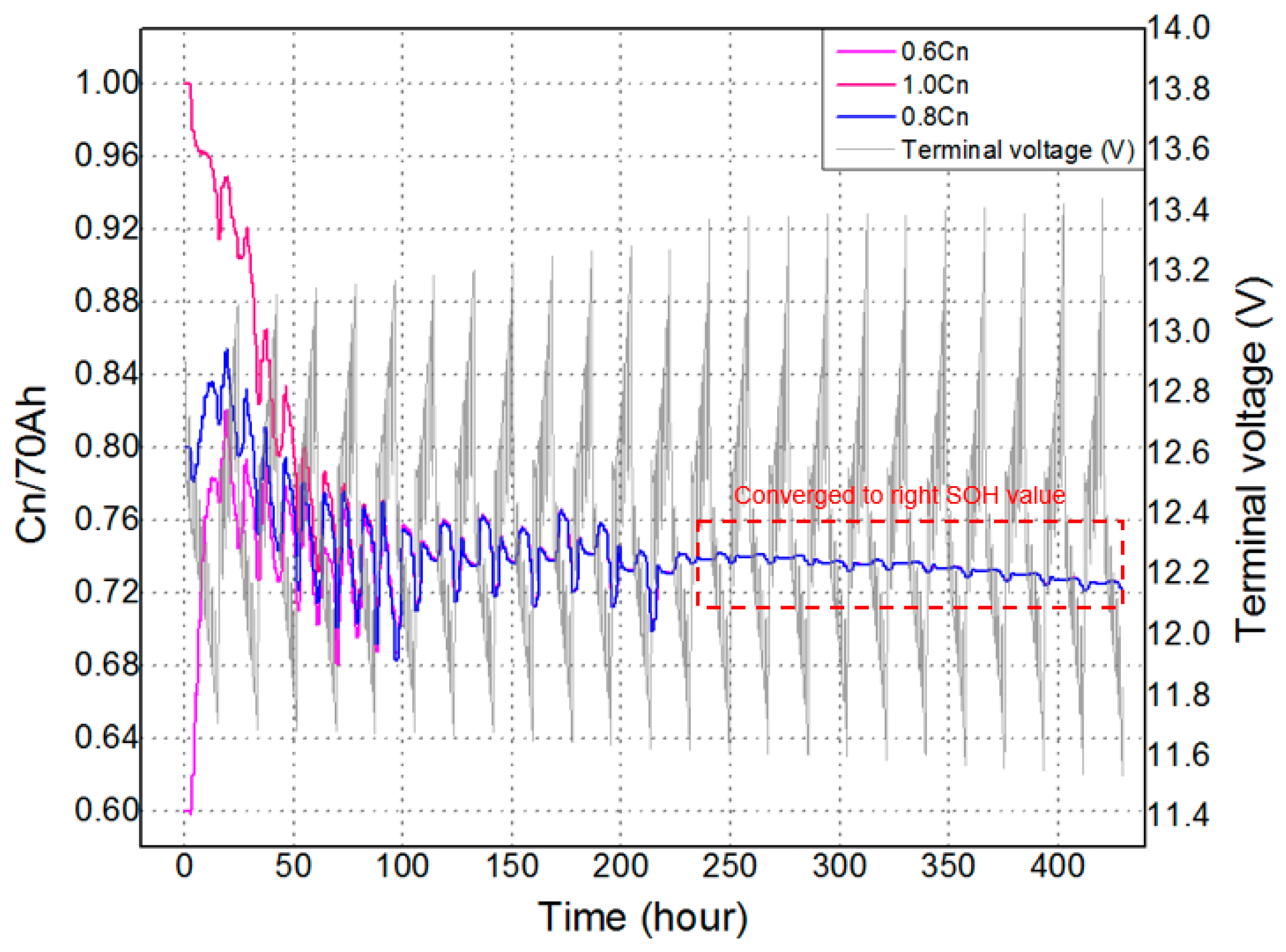
- The reliability of the proposed method in terms of estimating the SOC and SOH have been verified through very long test profiles (about 100 h for the SOC estimation and 440 h for the SOH estimation) with both the charging and discharging cycles.
- To test the performance in estimating the SOH, three different initial values have been given to verify its convergence characteristics by using a 440 h test profile.
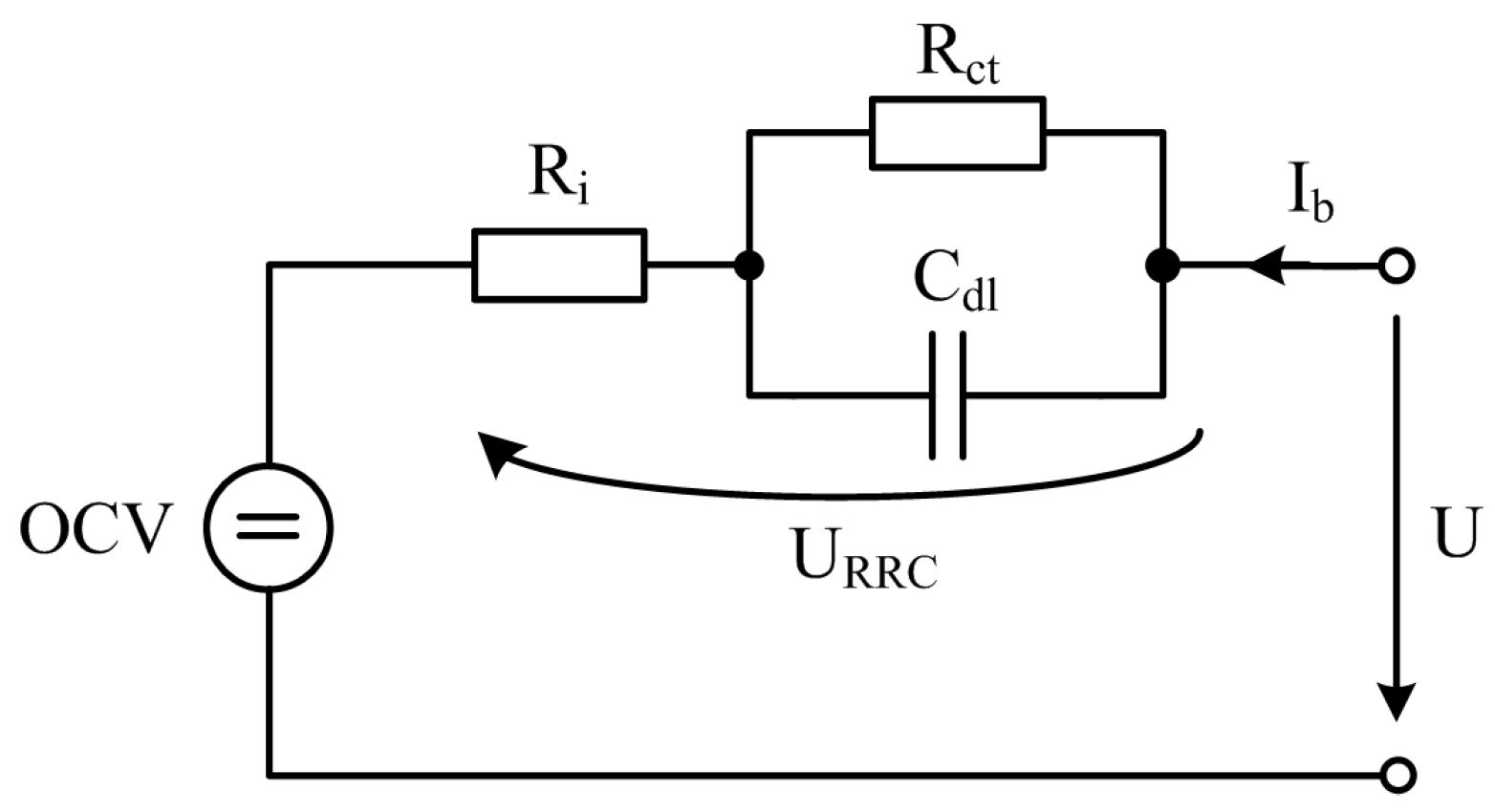
2. Battery Model
3. Battery Parameters Estimation
3.1. ARX Model
3.2. Parameters Estimation Algorithm
4. Combination of a Dual Extended Kalman Filter and an ARX Model for SOC and SOH Estimation
5. Experimental Validation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Le, D.; Sisk, B. Lead-Acid state of charge estimation for start-stop applications. SAE Int. J. Altern. Power 2013, 2, 172–178. [Google Scholar] [CrossRef]
- Duong, V.H.; Tran, N.T.; Park, Y.J.; Choi, W. Novel estimation technique for the state-of-charge of the lead-acid battery by using EKF considering diffusion and hysteresis phenomenon. Trans. Korean Inst. Power Electron. 2014, 19, 139–148. [Google Scholar] [CrossRef]
- Duong, V.H.; Tran, N.T.; Choi, W.; Kim, D.W. State estimation technique for VRLA batteries for automotive applications. J. Power Electron. 2016, 16, 238–248. [Google Scholar] [CrossRef]
- Anbuky, A.H.; Pascoe, P.E. VRLA battery state-of-charge estimation in telecommunication power systems. IEEE Trans. Ind. Electron. 2000, 47, 565–573. [Google Scholar] [CrossRef]
- Coleman, M.; Lee, C.K.; Zhu, C.; Hurley, W.G. State-of-charge determination from EMF voltage estimation: Using impedance, terminal voltage, and current for lead-acid and lithium-ion batteries. IEEE Trans. Ind. Electron. 2007, 54, 2550–2557. [Google Scholar] [CrossRef]
- Coleman, M.; Hurley, W.G.; Lee, C.K. An improved battery characterization method using a two-pulse load test. IEEE Trans. Energy Convers. 2008, 23, 708–713. [Google Scholar] [CrossRef]
- Bhangu, B.S.; Bentley, P.; Stone, D.A.; Bingham, C.M. Nonlinear observers for predicting state-of-charge and state-of-health of lead-acid batteries for hybrid-electric vehicles. EEE Trans. Veh. Technol. 2005, 54, 783–794. [Google Scholar] [CrossRef]
- Shahriari, M.; Farrokhi, M. Online state-of-health estimation of VRLA batteries using state of charge. IEEE Trans. Ind. Electron. 2013, 60, 191–202. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Gong, X.; Gao, C. A data-driven based adaptive state of charge estimator of lithium-ion polymer battery used in electric vehicles. Appl. Energy 2014, 113, 1421–1433. [Google Scholar] [CrossRef]
- Yuan, S.; Wu, H.; Yin, C. State of charge estimation using the extended Kalman filter for battery management systems based on the ARX battery model. Energies 2013, 6, 444–470. [Google Scholar] [CrossRef]
- Dong, G.; Wei, J.; Zhang, C.; Chen, Z. Online state of charge estimation and open circuit voltage hysteresis modeling of LiFePO4 battery using invariant imbedding method. Appl. Energy 2016, 162, 163–171. [Google Scholar] [CrossRef]
- He, H.; Zhang, X.; Xiong, R.; Xu, Y.; Guo, H. Online model-based estimation of state-of-charge and open-circuit voltage of lithium-ion batteries in electric vehicles. Energy 2012, 39, 310–318. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Xiong, R.; Gong, X.; Mi, C.C.; Sun, F. A robust state-of-charge estimator for multiple types of lithium-ion batteries using adaptive extended Kalman filter. J. Power Sources 2013, 243, 805–816. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. state and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Kong-Soon, N.; Yao-Feng, H.; Chin-Sien, M.; Yao-Ching, H. An enhanced coulomb counting method for estimating state-of-charge and state-of-health of lead-acid batteries. In Proceedings of the 31st Telecommunications Energy Conference, Incheon, Korea, 18–22 October 2009; pp. 1–5.
- Ho-Ta, L.; Tsomg-Juu, L.; Shih-Ming, C. Estimation of battery state of health using probabilistic neural network. IEEE Trans. Ind. Inform. 2013, 9, 679–685. [Google Scholar]
- Zhang, C.; Yuhong, F.; Mi, C.C. State of charge estimation of lithium-ion batteries in electric drive vehicles using extended kalman filtering. IEEE Trans. Veh. Technol. 2013, 62, 1020–1030. [Google Scholar]
- Chen, Q.; Jiang, J.; Liu, S.; Zhang, C. A novel sliding mode observer for state of charge estimation of EV lithium batteries. J. Power Electron. 2016, 16, 1131–1140. [Google Scholar] [CrossRef]
- Piao, C.; Li, Z.; Lu, S.; Jin, Z.; Cho, C. Analysis of real-time estimation method based on hidden Markov models for battery system states of health. J. Power Electron. 2016, 1, 217–226. [Google Scholar] [CrossRef]
- Kang, L.; Zhao, X.; Ma, J. A new neural network model for the state-of-charge estimation in the battery degradation process. Appl. Energy 2014, 121, 20–27. [Google Scholar] [CrossRef]
- Weigert, T.; Tian, Q.; Lian, K. State-of-charge prediction of batteries and battery–supercapacitor hybrids using artificial neural networks. J. Power Sources 2011, 196, 4061–4066. [Google Scholar] [CrossRef]
- Salkind, A.J.; Fennie, C.; Singh, P.; Atwater, T.; Reisner, D.E. Determination of state-of-charge and state-of-health of batteries by fuzzy logic methodology. J. Power Sources 1999, 80, 293–300. [Google Scholar] [CrossRef]
- Shen, W.X.; Chan, C.C.; Lo, E.W.C.; Chau, K.T. Adaptive neuro-fuzzy modeling of battery residual capacity for electric vehicles. IEEE Trans. Ind. Electron. 2002, 49, 677–684. [Google Scholar] [CrossRef]
- Ming-Fa, T.; Yi-Yuan, P.; Chung-Shi, T.; Nan-Sin, L. Modeling and estimation of state of charge for lithium-ion batteries using ANFIS architecture. In Proceedings of the IEEE International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 863–868.
- Zenati, A.; Desprez, P.; Razik, H. Estimation of the SOC and the SOH of li-ion batteries, by combining impedance measurements with the fuzzy logic inference. In Proceedings of the 36th Annual Conference of Industrial Electronic Society, Glendale, AZ, USA, 7–10 November 2010; pp. 1773–1778.
- Lee, J.; Nam, O.; Cho, B.H. Li-ion battery SOC estimation method based on the reduced order extended kalman filtering. J. Power Sources 2007, 174, 9–15. [Google Scholar] [CrossRef]
- Vasebi, A.; Bathaee, S.M.T.; Partovibakhsh, M. Predicting state of charge of lead-acid batteries for hybrid electric vehicles by extended Kalman filter. Energy Convers. Manag. 2008, 49, 75–82. [Google Scholar] [CrossRef]
- Waag, W.; Kabitz, S.; Sauer, D.U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application. Appl. Energy 2013, 102, 885–897. [Google Scholar] [CrossRef]
- Shuo, T.; Munan, H.; Minggao, O. An experimental study and nonlinear modeling of discharge behavior of valve-regulated lead acid batteries. IEEE Trans. Energy Convers. 2009, 24, 452–458. [Google Scholar] [CrossRef]
- Achaibou, N.; Haddadi, M.; Malek, A. Modeling of lead acid batteries in PV systems. Energy Procedia 2012, 18, 538–544. [Google Scholar] [CrossRef]
- Ljung, L. System Identification Theory for the User; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1999. [Google Scholar]


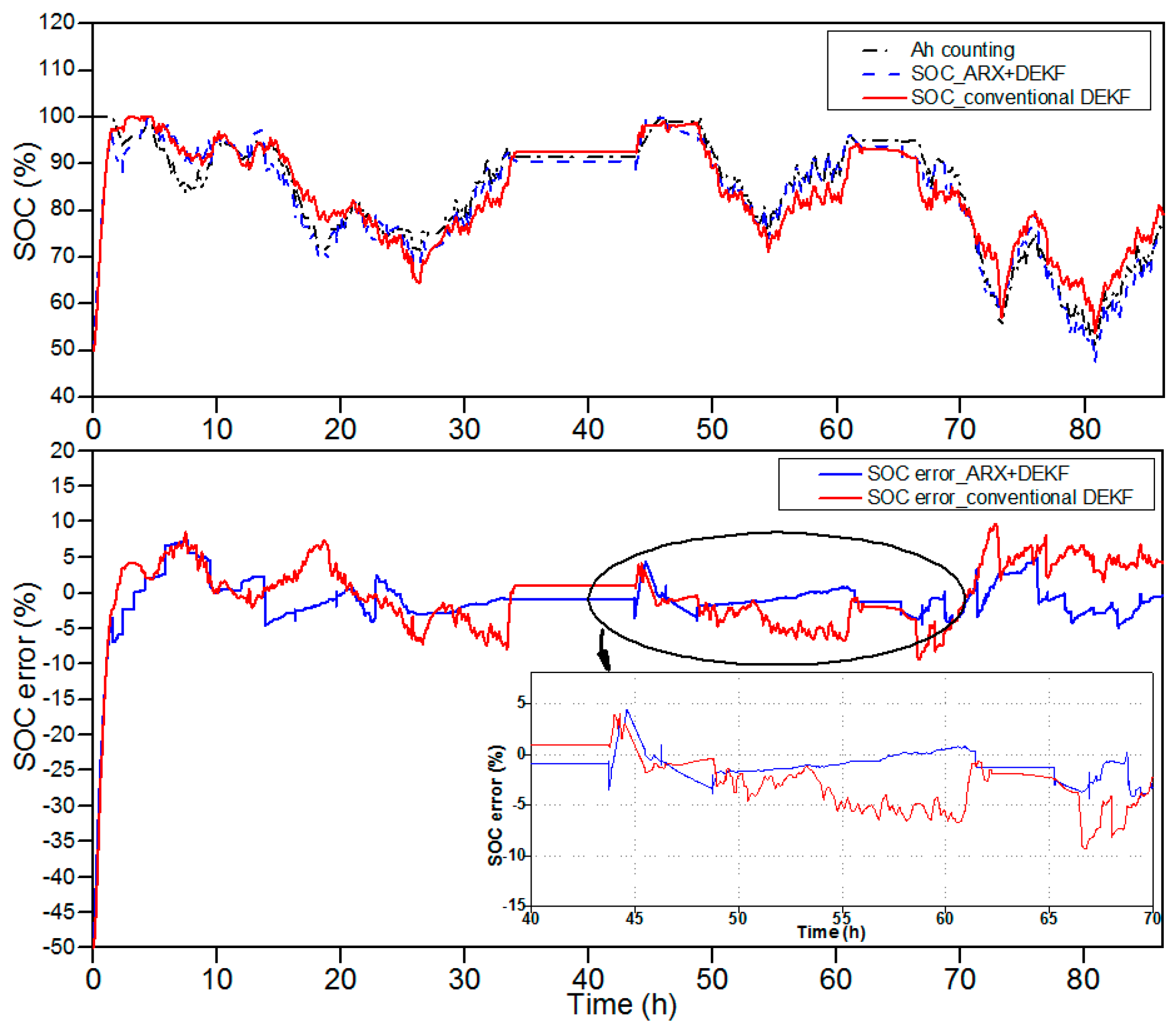
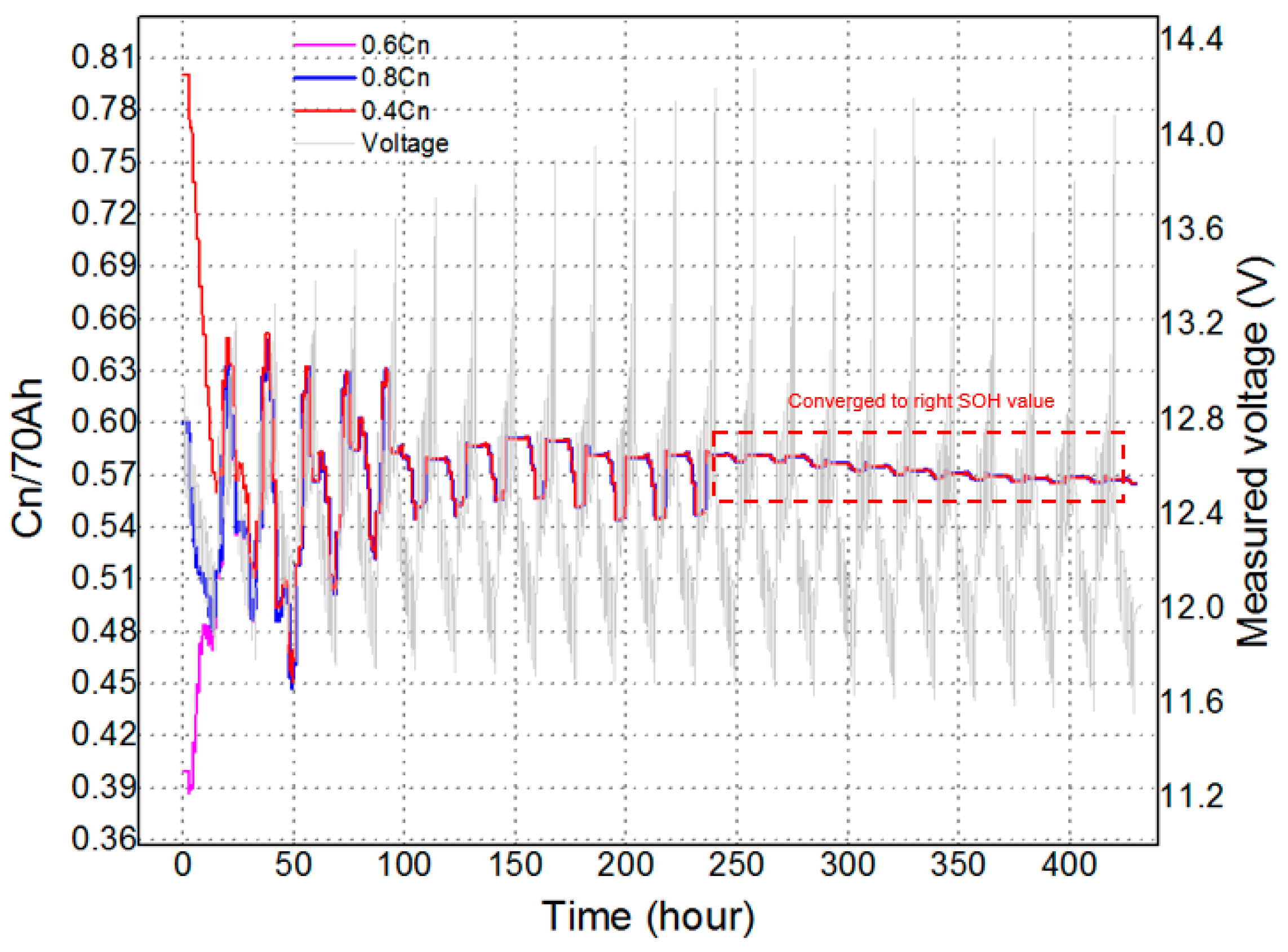
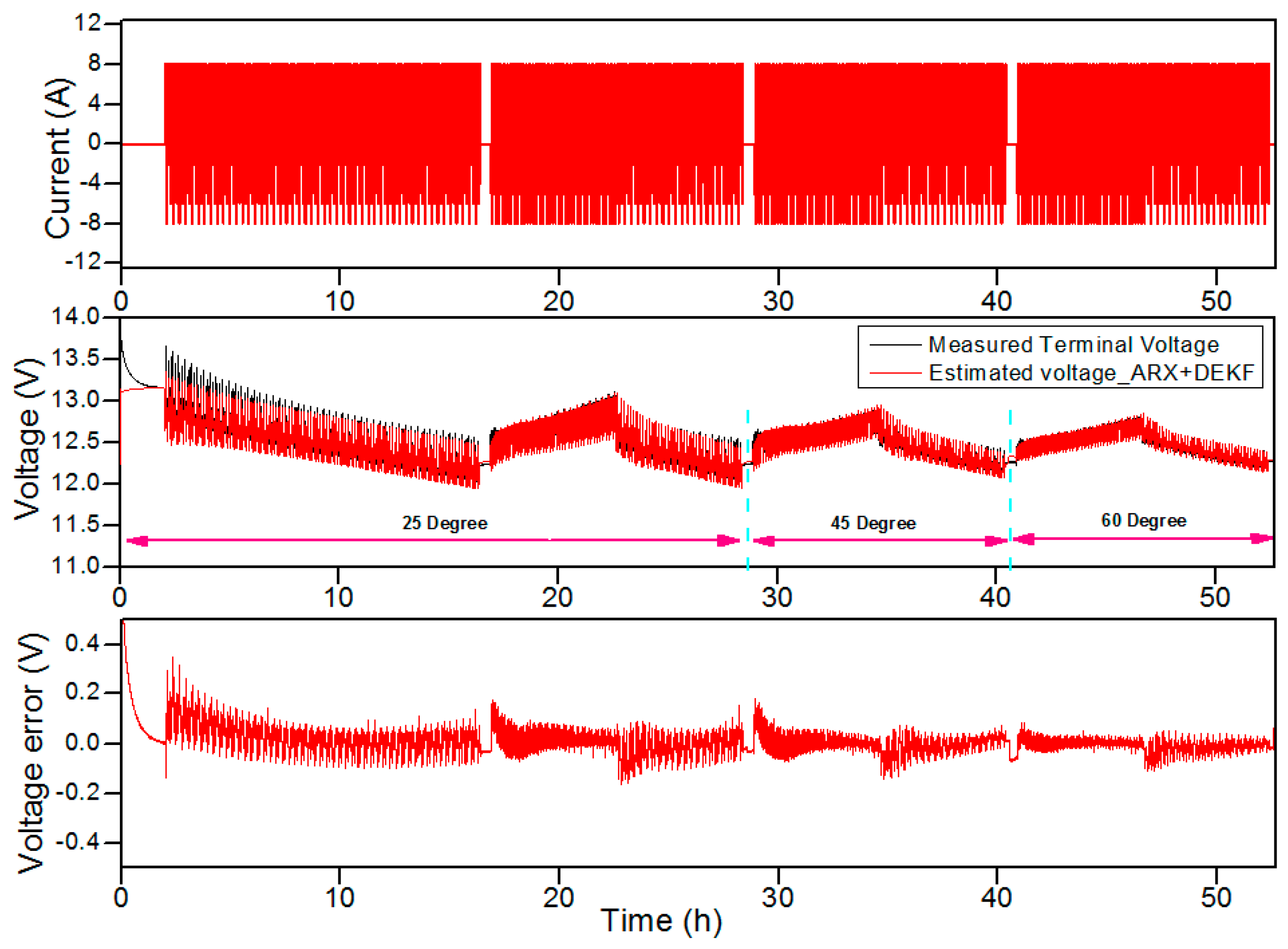
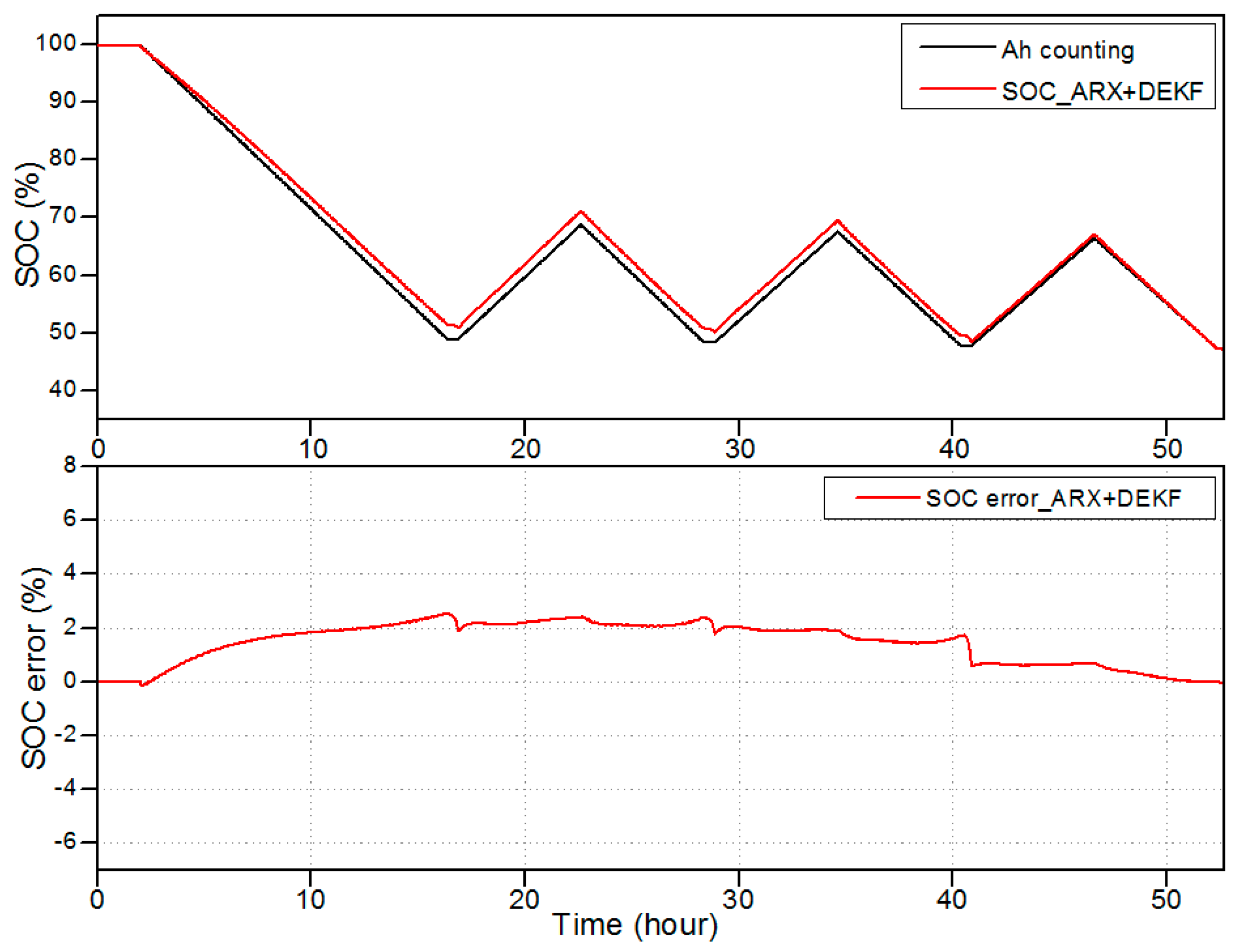
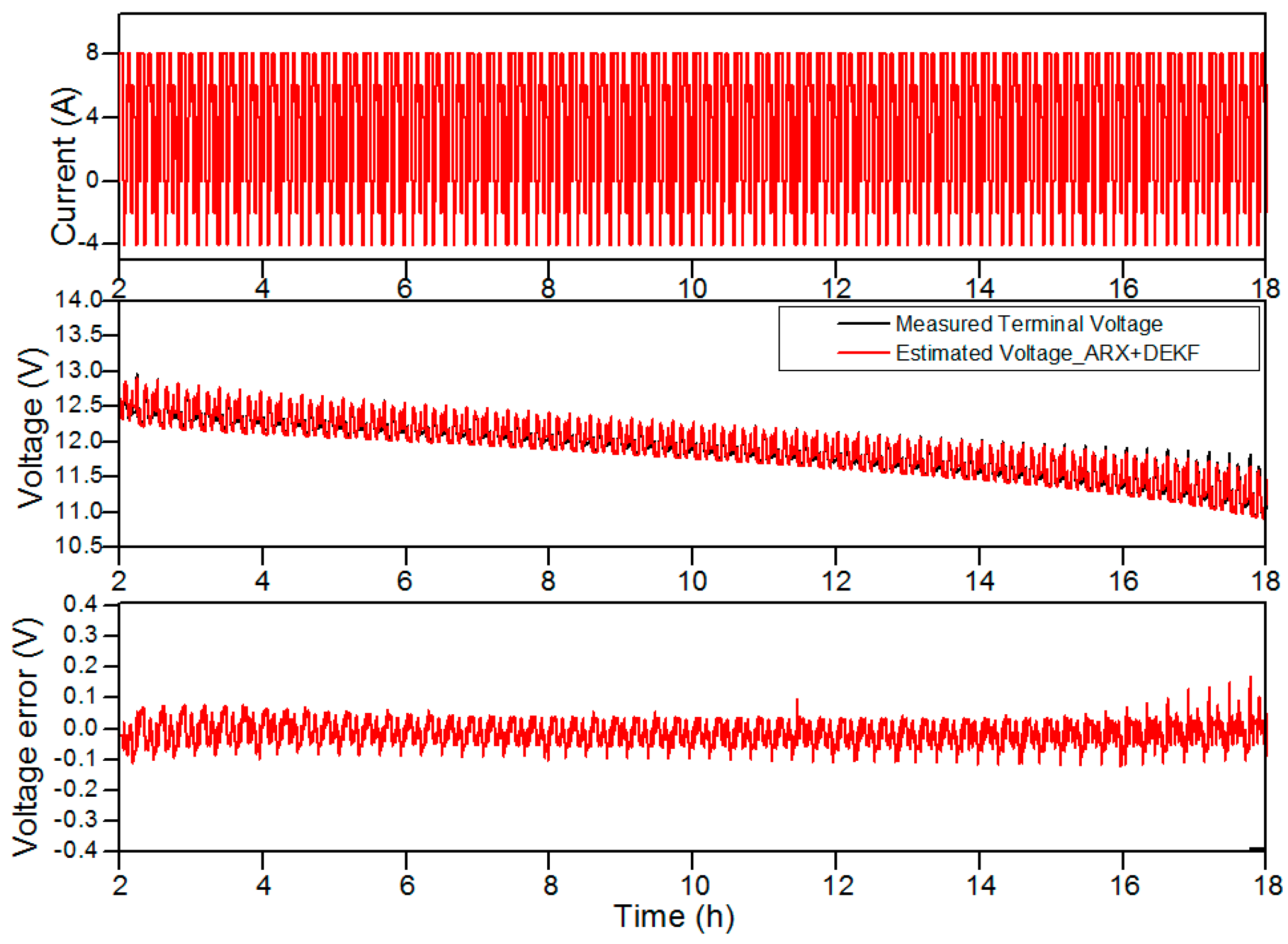
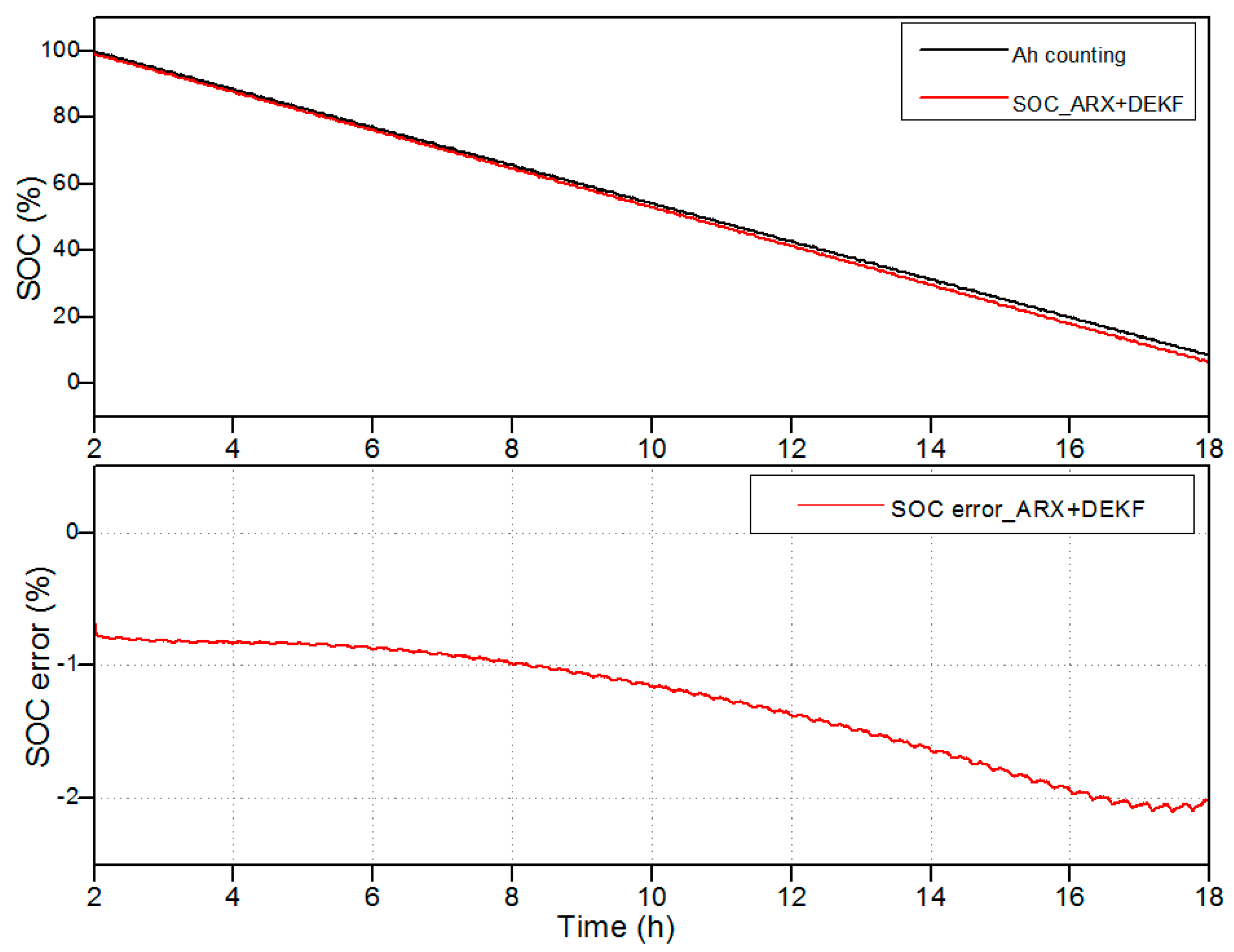
| Measured Capacity (%) | RMSE of Voltage (V) by Proposed Method | RMSE of Voltage (V) by Conventional Method | RMSE SOC (%) by Proposed Method | RMSE SOC (%) by Conventional Method |
|---|---|---|---|---|
| 98.0 | 0.0626 | 0.1015 | 4.5812 | 5.4202 |
| 75.6 | 0.0515 | 0.1234 | 4.4289 | 6.1276 |
| 60.3 | 0.0586 | 0.1252 | 4.2348 | 7.2234 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, N.-T.; Khan, A.B.; Choi, W. State of Charge and State of Health Estimation of AGM VRLA Batteries by Employing a Dual Extended Kalman Filter and an ARX Model for Online Parameter Estimation. Energies 2017, 10, 137. https://doi.org/10.3390/en10010137
Tran N-T, Khan AB, Choi W. State of Charge and State of Health Estimation of AGM VRLA Batteries by Employing a Dual Extended Kalman Filter and an ARX Model for Online Parameter Estimation. Energies. 2017; 10(1):137. https://doi.org/10.3390/en10010137
Chicago/Turabian StyleTran, Ngoc-Tham, Abdul Basit Khan, and Woojin Choi. 2017. "State of Charge and State of Health Estimation of AGM VRLA Batteries by Employing a Dual Extended Kalman Filter and an ARX Model for Online Parameter Estimation" Energies 10, no. 1: 137. https://doi.org/10.3390/en10010137
APA StyleTran, N.-T., Khan, A. B., & Choi, W. (2017). State of Charge and State of Health Estimation of AGM VRLA Batteries by Employing a Dual Extended Kalman Filter and an ARX Model for Online Parameter Estimation. Energies, 10(1), 137. https://doi.org/10.3390/en10010137







