Quantile-Time-Frequency Connectedness in Global Equity Markets: Evidence from BRICS and G7 Economies

Abstract

We examine the quantile-time-frequency connectedness of stock returns among BRICS and G7 markets over the period January 2000 to January 2024, employing the Quantile Vector Autoregression (QVAR) model. Our findings reveal that spillover effects intensify during periods of extreme market conditions, compared to more tranquil phases. Furthermore, the stock markets of France, Germany, the United States, the United Kingdom, Italy, and Canada emerge as primary sources of contagion, whereas the BRICS markets and Japan primarily act as recipients across all quantile regimes. The frequency-quantile decomposition reveals that short-term dynamics primarily drive the net transmission of shocks at both the median and upper quantiles, whereas long-term dynamics are dominant at the lower quantile, indicating more persistent effects during market downturns. Finally, we construct investment portfolios based on the Minimum Connectedness Portfolio (MCP) approach and evaluate them through average portfolio weights and Hedging Effectiveness (HE) ratios. The results demonstrate that G7-based portfolios tend to have lower average weights and higher hedging efficiency, implying greater diversification benefits and enhanced risk mitigation performance compared to BRICS-based portfolios.

1. Introduction

The BRICS group, which comprises Brazil, Russia, India, China, and South Africa, is an economic consortium made up of five of the world’s largest emerging economies. On the other hand, the G7, which includes the United States, Germany, France, Canada, the United Kingdom, Italy, and Japan, is a coalition of the seven leading developed economies. Although the BRICS and the G7 share similar economic objectives, they are often perceived as competing entities on the global geopolitical scene. The BRICS represents a counterweight to the G7 nations, challenging their economic and political dominance. The rivalry between the BRICS and the G7 reflects shifts in the global power balance. Mensi et al. (2017) emphasized the pivotal role of BRICS markets within the global economy, citing their position as the fastest-growing economies in the world. They specifically noted the swift expansion of BRICS stock markets, particularly regarding their size and transaction volumes. According to Hammoudeh et al. (2013), the BRICS countries are responsible for 40% of the global population and are projected to contribute 41% of global market capitalization. These nations are ranked among the largest and most influential countries of the 21st century. El Khoury et al. (2024) note that the G7 countries hold significant economic power and strategic influence on the global stage. This distinctive position enables them to initiate change and serve as role models both domestically and internationally. As some of the wealthiest and most technologically advanced nations, they play a pivotal role in debates on global economic governance.

In recent years, the trend toward the integration of the global economy and financial systems has led to increased interconnectedness among the stock markets of different countries. This has resulted in a tendency for contagion to cause markets to rise and fall together, especially during major global events. Spillovers and interconnections between markets have important implications for portfolio design and investment decisions. Investors and portfolio managers can use information on cross-market spillovers to identify markets that are most susceptible to external shocks, as well as those that act as primary sources of transmission. By analyzing contagion effects and inter-market connectedness, portfolios can be better managed, risks more effectively hedged, and asset returns optimized (Fengler & Gisler, 2015; Lovcha & Perez-Laborda, 2020). Consequently, the accurate measurement of risk transmission facilitates improved cross-market forecasting and supports more optimal investment decisions.

Building on this discussion, it is important to clarify the conceptual distinctions in the literature. While interdependence generally refers to a stable and continuous relationship between markets during so-called “normal” periods, co-movement is linked to situations where a regime shift in a dominant market triggers, with some delay, corresponding changes in more dependent markets (Jung & Maderitsch, 2014). However, the notion of contagion remains far less straightforward, as scholars have yet to converge on a single theoretical or empirical definition. This lack of consensus makes the debate over contagion not merely an academic matter but also a practical one, with significant implications for both its measurement and the design of appropriate policy responses.

Although no universal definition exists, several widely accepted interpretations appear in the literature. For example, Pericoli and Sbracia (2003) identify five of the most representative definitions. Building on this foundation, our study adopts the following perspective: contagion is defined as the spread of asset price volatility from a crisis-affected country to other nations, thereby capturing the transmission of uncertainty across international financial markets.

Financial risk management increasingly emphasizes the study of extreme events in the tails of asset return distributions, where low-probability shocks can generate disproportionately large impacts. Traditional models, which focus on the overall distribution, often fail to capture these tail risks accurately, leaving systemic vulnerabilities underestimated.

In this context, analyzing extreme return connectedness between G7 and BRICS stock markets provides a powerful framework to assess asymmetric shock transmissions and contagion during rare but impactful market events, such as financial crises or abrupt bullish surges. Focusing on the tails allows us to identify hidden interdependencies and potential risks that are not observable under normal market conditions, offering actionable insights for both portfolio construction and risk management.

This paper examines risk transmission and quantile-frequency connectedness between the G7 stock markets (USA, Germany, France, Canada, United Kingdom, Italy, and Japan) and the BRICS markets (including Brazil, Russia, India, China, and South Africa) during periods of extreme shocks. Firstly, employing the Quantile Vector Autoregressive (QVAR) method developed by Ando et al. (2022). We assess the risk of spillovers between stock markets at different quantile levels. Quantile connectedness is a powerful tool for addressing problems of interconnectedness, spillovers, and risk transfer paths between BRICS and G7 stock markets. Secondly, we apply the methodology proposed by Chatziantoniou et al. (2022), which introduces a novel econometric framework known as the quantile-frequency connectedness approach. Given the increased political instability and heightened geopolitical risk, studying connectedness according to market conditions has become essential to produce relevant results, whereas traditional methods such as VAR may no longer provide precise outcomes. The main advantage lies in the frequency-domain approach. allows the study of asymmetric spillover effects across different time frequencies, providing a more detailed perspective than traditional time-domain methods. This enables the capture of spillover effects that may not be apparent in a conventional temporal analysis.

Moreover, the frequency-domain method allows for the decomposition of realized volatility into asymmetric risks, such as “good” and “bad” volatility. This decomposition offers a deeper understanding of the impact of economic policy uncertainty on stock markets, highlighting the differentiated effects on upside and downside risks.

In addition, the frequency-domain approach enables the analysis of dynamic connectedness between variables at different quantiles, providing a more comprehensive view of the interactions between stock markets and international economic policy uncertainty.

Our results show that market connectedness is more intense during extreme events, which means that the dynamic variation of connectedness measures in the tails differs from those at the median. Specifically, we observe a high level of connectedness between the BRICS and G7 stock markets at the extreme quantiles. The G7 markets, excluding Japan, act as transmitters, while the BRICS markets and Japan consistently serve as receivers of contagion effects under all three market conditions. We also observe from the frequency-quantile connectedness that short-term dynamics are solely determined by whether each market acts as a net transmitter or receiver of shocks.

The MCP results highlight the practical relevance of connectivity-based portfolio construction for mitigating market risk. The higher weights assigned to G7 markets across quantiles, coupled with their strong hedging effectiveness, indicate that these markets not only provide central roles in systemic exposure but also offer robust risk absorption within a portfolio context. In contrast, BRICS markets, despite their higher individual hedging efficiency in countries like Russia and Brazil, contribute less to overall portfolio stability due to their varying volatility profiles and lower average weights. The quantile-dependent variation in hedging effectiveness suggests that the MCP approach effectively adapts to different market regimes, providing enhanced risk management during extreme market conditions while maintaining diversification. Overall, these findings imply that investors can exploit the MCP methodology to construct portfolios that are both resilient to extreme shocks and optimized for risk-adjusted performance across G7 and BRICS markets.

Our study provides several distinct contributions to the literature on international stock market connectedness. First, we combine quantile-based analysis with frequency-domain decomposition, allowing us to capture both the intensity and timing of extreme spillovers across short-, medium-, and long-term horizons—a perspective rarely addressed in prior research. Second, we apply these insights to portfolio construction through the Minimum Connectivity Portfolio (MCP) approach, demonstrating how connectivity-informed strategies can mitigate systemic risk and enhance diversification under extreme market conditions. Third, our findings provide new evidence on the asymmetric roles of G7 and BRICS markets as net transmitters and receivers of shocks, offering a deeper understanding of market interdependencies in both normal and stressed states. Collectively, these contributions advance the literature by linking time-frequency dynamics, extreme tail risk, and practical portfolio applications, providing both methodological innovation and actionable insights for investors and policymakers.

The remainder of the article is structured as follows: Section 2 provides a review of the existing literature. Section 3 outlines the methodology employed in this study. Section 4 presents a detailed discussion of the results, and Section 5 offers the conclusions.

2. Literature Review

The review of the existing literature highlights several significant trends while also underscoring the limitations of previous studies. Prior research has mainly focused on the connectedness of BRICS and G7 stock markets and their linkages with energy, commodity, and sustainable finance indices. However, three major gaps can be identified.

First, most studies examine either BRICS or G7 in isolation, but very few compare the dynamics of extreme risk connectedness between these two groups of economies. For example, Shi (2021) examined the time-frequency spillovers among the five stock markets of the BRICS countries. One of the most interesting findings is that return spillover effects decreased significantly with a decrease in frequency, while volatility contagion effects increased with lower frequency. Moreover, the dynamics of connectedness were influenced by major systematic risk events, revealing certain common patterns in spillovers across various frequency bands. The Chinese and Russian stock markets played influential roles in return spillovers and volatility connectedness within the emerging markets.

In a related contribution, Billah et al. (2022) explored the return and volatility linkages between energy markets and BRIC markets using the QVAR approach. Their results show that periods of economic uncertainty and high intensity shape return and volatility interconnectedness in both energy and BRIC markets. These time-varying characteristics were further validated by major disruptive events such as the Global Financial Crisis, the shale oil revolution, and the COVID-19 pandemic, all of which amplified contagion effects.

Extending the focus to G7 markets, El Khoury et al. (2024) examined the quantile time-frequency connectedness among clean energy indices and G7 stock markets. They found high volatility connectedness between all markets, except clean fuels, which exhibited the least integration. Furthermore, they noted greater dynamic contagion effects under extreme market conditions compared to normal ones, with the US market serving as the primary transmitter of connectedness during bullish periods. In addition, their findings emphasize the importance of accounting for the time-varying aspects of connectedness, highlighting notable differences across short-, medium-, and long-run spillovers.

Second, although many works employ methodologies such as Diebold–Yilmaz spillover indices, ADCC-EGARCH, or TVP-VAR. Lang et al. (2024) used a TVP-VAR methodology to study the connectedness of tail risk between G7 stock markets. They showed fluctuating extreme risk connectedness in the G7 markets during the pandemic, interventions, logistics issues, and investor sentiment. Italy and the UK were major emitters of extreme risk, while Japan primarily took on risk, showcasing its vulnerability. There is still limited evidence on quantile-frequency connectedness (QVAR) that explicitly captures the asymmetric transmission of shocks under different market regimes (bullish, bearish, or normal). Chatziantoniou et al. (2022) introduced a novel method for quantile-frequency connectedness, combining the QVAR approach with the frequency connectivity approach to consider connectedness measures over time, frequencies, and quantiles. The authors examined the dynamic interplay and return propagation of four environmental financial indices. They found that the S&P Global Clean Energy Index and the S&P Green Bond Index generally act as net recipients of both short- and long-term shocks, whereas the Dow Jones Sustainability Index World and the MSCI Global Environment Index serve as transmitters of these shocks. They discovered that TCIs fluctuate over time and are influenced by economic events.

Third, prior research has primarily focused on traditional asset classes (oil, energy, and commodities), while the interplay between extreme risk transmission and geopolitical tensions remains underexplored. Chen & Qi (2024) investigated the dynamic connectedness between news related to the COVID-19 pandemic and its effect on Chinese commodity futures by employing time-frequency connectedness methodologies. Based on static interconnectedness, they found that energy futures and petrochemicals were the main beneficiaries and contributors within the studied sample. Both short- and long-term datasets consistently indicate that COVID-19 uncertainty acts as a beneficiary and exerts heterogeneous impacts on commodities. Interestingly, the Coronavirus Media Hype Index and the Coronavirus Panic Index exerted the most significant influence on commodities. Moreover, dynamic data show that the extent of market connectedness changes substantially over time, with short-term linkages surpassing those in the long term.

In a related line of research, Le (2023) examined the volatility connectedness between energy and cryptocurrency markets during the Ukraine–Russia conflict, utilizing the frequency QVAR approach. This study revealed significant time variations in connectedness, driven not only by the COVID-19 pandemic but also by the war in Ukraine. The results further indicate that the Crypto Volatility Index predominantly absorbs shocks in the short term while maintaining a similar role over the long run, except at the beginning of 2022, when it became a net source of shocks due to the outbreak of the conflict. Additionally, wind energy was identified as a shock emitter, whereas clean energy acted as a net recipient of shocks in the short run.

Extending this literature, Jiang and Chen (2024) examined the effect of the Russian–Ukrainian war on return connectivity between agricultural, metals, and energy markets in China using the frequency QVAR approach. Their findings demonstrate that the conflict not only increases connectedness in both tails but also amplifies short-run median quantile connectedness. Energy commodities consistently emerge as the main emitters and receivers of connectedness, except under certain extreme market situations. Furthermore, the study highlights the growing long-term importance of oil crops and seed oils, underscoring the structural shifts induced by geopolitical shocks.

Accordingly, our study addresses these shortcomings by focusing on extreme risk transmission and contagion between BRICS and G7 stock markets using the QVAR approach. By doing so, we contribute to the literature in two ways: (i) by providing new evidence on how shocks propagate asymmetrically across advanced and emerging markets, and (ii) by identifying the role of major crises in shaping the dynamics of connectedness.

3. Econometric Methodology

3.1. QVAR Approach

In this research, we adopt the quantile connectedness framework introduced by Ando et al. (2022), which extends the Diebold and Yilmaz (2012) methodology. While the D&Y model measures average spillover effects, it may obscure critical information in the tails of the distribution. For effective risk management and systemic risk assessment, it is therefore more relevant to focus on extreme losses. To this end, we implement a Quantile VAR (QVAR) model based on the quantile regression approach of Koenker and Bassett (1978), estimating VARs at both the upper and lower quantiles. This approach allows us to map the connectedness network associated with extreme positive and negative shocks, specifically those at the 95th (bullish periods) and 5th (bearish periods) percentiles of the shock distribution, providing richer insights into tail spillovers than conventional mean-based analyses. The QVAR($p$) model with n variables is given by:

$$y_t=\mu (\tau )+\sum _{j=1}^p{\phi }_j\left(\tau \right)y_{t-j}+{\epsilon }_t\left(\tau \right)$$

where $y_t$ et $y_{t-1}$ are vectors of the endogenous variables of dimension K × 1, $\tau$ is an interval whose range is [0, 1] and represents the quantile, and $p$ is the lag length of the QVAR model. The conditional mean is denoted by $\mu \left(\tau \right)$which is a vector of intercepts of dimension K × 1. ${\phi }_j\left(\tau \right)$ is the $j$th matrix of autoregressive parameters of dimension k × k and $\epsilon \left(\tau \right)$ is a vector of error terms of dimension K × k.

To acquire the estimated coefficient matrices $\widehat{\phi }$, from Koenker and Xiao (2006), the errors ${\epsilon }_t$ were presumed to adhere to the population quantile constraints $Q_{\tau }\left({\epsilon }_t |{ y}_{t-1},\dots ,y_{t-p}\right)=0$. These constraints indicate that the reactions of the population of $y$ at quantiles $\tau$ are defined by:

$$Q_{\tau }\left(y_t|y_{t-1},\dots ,y_{t-p}\right)=\mu \left(\tau \right)+\sum _{j=1}^P{\widehat{\phi }}_j\left(\tau \right)y_{t-j}$$

According to Koenker and Xiao (2006), $\widehat{\phi }\left(\tau \right)$ are called autoregression quantiles.

To convert the QVAR(p) to its QVMA (∞) representation, we employ the Wold theorem:

$$y_t=\mu \left(\tau \right)+\sum _{j=1}^p{\phi }_i\left(\tau \right)y_{t-j}+{\epsilon }_t\left(\tau \right)=\mu \left(\tau \right)+\sum _{j=1}^{\mathrm{\infty }}{B}_j\left(\tau \right){\epsilon }_{t-j}(\tau )$$

where $B_j\left(\tau \right)={\phi }_1\left(\tau \right)B_{j-1}\left(\tau \right)+{\phi }_2\left(\tau \right)B_{j-2}\left(\tau \right)+\cdots . \mathrm{F}\mathrm{o}\mathrm{r} j=\mathrm{1,2},\dots$ With $B_0\left(\tau \right)=I_m$ and $B_j\left(\tau \right)=0 \mathrm{f}\mathrm{o}\mathrm{r} \mathcal{l}<0$.

It is assumed that ${\epsilon }_{it}=\mathsf{\Lambda }{f}_t+{\upsilon }_t$, where $f_t$ denotes a vector of common factors, $\mathsf{\Lambda }=({\lambda }_1^{\prime },{\lambda }_2^{\prime },\dots ,{\lambda }_n^{\prime })\prime$ is a matrix of heterogeneous factor loadings, and ${\upsilon }_t=({\lambda }_{1t}^{\prime },{\lambda }_{2t}^{\prime },\dots ,{\lambda }_{nt}^{\prime })\prime$ comprises the idiosyncratic components of ${\epsilon }_t$.

Subsequently, the H-step ahead Generalized Forecast Error Variance Decomposition (GFEVD) developed by Koop et al. (1996) and Pesaran and Shin (1998) is calculated to demonstrate the effect of a shock in series j on series i. Under the assumption that ${\upsilon }_t\left(\tau \right)~iid\left(0,\Omega \right),$ where $\mathsf{\Omega }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(w_{11},w_{22},\dots ,w_{mm}$), is such that $w_{ii}^{-1}\mathsf{\Omega }{e}_i=e_i$, we have:

$$FEVD\left(y_{jt};{\mu }_{it}\left(\tau \right),h\right)={\displaystyle \frac{w_{ii}^{-1}\sum _{\mathcal{l}=0}^h{e}_j^{\prime }\left(B_{\mathcal{l}}\left(\tau \right)\Omega e_i{e^{\prime }}_i\Omega {B^{\prime }}_{\mathcal{l}}\left(\tau \right)\right)e_j}{\sum _{\mathcal{l}=0}^h{e}_j^{\prime }{B_{\mathcal{l}}\left(\tau \right)\Omega {B^{\prime }}_{\mathcal{l}}\left(\tau \right)e}_j}}={\displaystyle \frac{w_{ii}^{-1}\sum _{\mathcal{l}=0}^h{\left(e_j^{\prime }{B}_{\mathcal{l}}\left(\tau \right)\mathsf{\Omega }{e}_i\right)}^2}{\sum _{\mathcal{l}=0}^h{(e}_j^{\prime }{B_{\mathcal{l}}\left(\tau \right)\mathsf{\Omega }{B^{\prime }}_{\mathcal{l}}\left(\tau \right)e}_j)}}$$

For $\mathcal{l}=\mathrm{0,1},\dots ,h$ and $i,j=1,\dots ,m.$ Where $w_{ii}$ represents the standard deviation for the error term of the variable, $e_j$ selects the predicted variable and $e_i$ selects the source innovation. To simplify the notation, we have $d_{j\leftarrow i}^{\left(h\right)}\left(\tau \right)=FEVD\left(y_{jt};{\mu }_{it}\left(\tau \right),h\right)$ where $d_{j\leftarrow i}^{\left(h\right)}\left(\tau \right)$ assesses the propagation of shocks influencing variable i into variable j.

The normalized variance decomposition matrix is defined by the formula:

$${\tilde{d}}_{j\leftarrow i}^h\left(\tau \right)={\displaystyle \frac{d_{j\leftarrow i}^{\left(h\right)}\left(\tau \right)}{\sum _{j=1}^k{d}_{j\leftarrow i}^{\left(h\right)}\left(\tau \right)}}$$

The h-step ahead m × m connectedness matrix for $y_t$, evaluated at the conditional $\tau$th quantile, can be expressed as follows

$${\mathsf{A}}^h\left(\tau \right)=\left[\begin{array}{ccc}\begin{array}{cc}{d}_{1\leftarrow 1}^{\left(h\right)}\left(\tau \right)& d_{1\leftarrow 2}^{\left(h\right)}\left(\tau \right)\\ d_{2\leftarrow 1}^{\left(h\right)}\left(\tau \right)& d_{2\leftarrow 2}^{\left(h\right)}\left(\tau \right)\end{array}& \dots & \begin{array}{c}{d}_{1\leftarrow m}^{\left(h\right)}\left(\tau \right)\\ d_{2\leftarrow m}^{\left(h\right)}\left(\tau \right)\end{array}\\ \begin{array}{cc} ⋮ & ⋮\end{array}& \ddots & ⋮\\ \begin{array}{cc}{d}_{m\leftarrow 1}^{\left(h\right)}\left(\tau \right)& d_{m\leftarrow 2}^{\left(h\right)}\left(\tau \right)\end{array}& \dots & d_{m\leftarrow m}^{\left(h\right)}\left(\tau \right)\end{array}\right]$$

Based on ${\mathsf{A}}^h\left(\tau \right)$, we can construct a set of summary statistics that characterize the underlying network topology at the conditional τth quantile, thereby providing a comprehensive assessment of the directional spillovers and interdependencies among the variables.

The total impact of variable i on the other variables j is a significant aspect of this research; the total directional connectedness “TO” the others is captured:

$${TO}_{.\leftarrow i}^{\left(h\right)}\left(\tau \right)=\sum _{j=1,j\ne i}^n {\tilde{d}}_{j\leftarrow i}^h\left(\tau \right)$$

Conversely, the impact of the perturbation of all other variables j on variable i can also be gauged by the total directional interconnectedness “FROM” other:

$${FROM}_{i\leftarrow .}^{\left(h\right)}\left(\tau \right)=\sum _{j=1,j\ne i}^n{\tilde{d}}_{j\leftarrow i}^h\left(\tau \right)$$

To gain deeper insights into the net transmission dynamics between the TO and FROM measures, the net directional connectedness is formally defined as follows:

$${NET}_{i\leftarrow i}^{\left(h\right)}\left(\tau \right)={TO}_{.\leftarrow i}^{\left(h\right)}\left(\tau \right)-{FROM}_{i\leftarrow .}^{\left(h\right)}\left(\tau \right)$$

This metric captures the balance between shocks transmitted to other variables and those received from them, thereby providing a refined measure of each variable’s net contribution to the overall system.

To explore in more detail the net effect between TO and FROM, net directional connectedness is defined as follows:

$$TCI\left(\tau \right)={\displaystyle \frac{\sum _{i,j=1,j\ne i}^n{\tilde{d}}_{j\leftarrow i}^h\left(\tau \right)}{k-1}}$$

The previous equation is the adjusted total connectedness index (TCI) of Chatziantoniou and Gabauer (2021), which is between [0, 1]. In general, this indicator serves as a proxy for market risk, as a higher TCI implies a greater degree of interconnectedness within the system, thereby signaling a stronger potential for shock transmission and systemic vulnerability.

The net pairwise directional connectedness transmitted from j to i is as follows.

$${NPDC}_{ij}={\tilde{d}}_{j\leftarrow i}^h\left(\tau \right)-{\tilde{d}}_{i\leftarrow j}^h\left(\tau \right)$$

The main advantage of the Quantile Vector Autoregressive (QVAR) model over other methods is that it allows for the analysis of spillover effects arising from extreme market conditions (both upper and lower tails) and enables the dynamic connectedness between variables to be captured across different quantiles (Long et al., 2022). Moreover, given heightened political instability and geopolitical risk, investigating connectedness according to market conditions has become essential to produce relevant results, whereas traditional methods such as VAR may no longer provide precise outcomes. Thus, the choice of the 0.05, 0.5, and 0.95 quantiles is based on previous studies, and there is an almost consensus in the literature: most of the research uses these values as reference quantiles.

3.2. Frequency-Based QVAR

Frequency QVAR is an enhancement of the QVAR methodology by merging the traditional QVAR technique of Chatziantoniou and Gabauer (2021) with the frequency-domain interconnectedness approach of Baruník and Křehlík (2018). By employing the spectral decomposition method outlined by Stiassny (1996), we can analyze the interconnectedness relationship in the frequency domain. The frequency response function can be expressed as: $\mathrm{B}\left(e^{-iw}\right)=\sum _{h=0}^{\infty }{e}^{-iw}{ B}_h$, Whereas $i=\sqrt{-1}$ and ω indicates the rate at which the spectral density of y_t persists at frequency ω. This can be described as the Fourier transform of the QVMA (∞) representation:

$$S_x\left(w\right)=\sum _{h=-\mathrm{\infty }}^{\mathrm{\infty }}E\left(y_t{y}_{t-h}^{\prime }\right)e^{-iwh}=\mathrm{B}\left(e^{-iw}\right){\mathsf{\Omega }}_t\mathrm{B}\left(e^{+iw}\right)$$

Significantly, the generalized decomposition frequency of the variance of forecasting errors, which includes both spectral density and GFEVD components, warrants particular attention. Similar to the time domain, it is necessary to normalize the frequency GFEVD. This normalization procedure can be outlined as follows:

$$\begin{gathered} {\theta }_{ij}\left(w\right)={\displaystyle \frac{{\mathsf{\Omega }\left(\tau \right)}_{jj}^{-1}\left|\sum _{h=0}^{\mathrm{\infty }}{\left(\mathrm{B}\left(\tau \right)\left(e^{-iw}\right){\mathsf{\Omega }\left(\tau \right)}_{ij})\right)}^2\right|}{\sum _{h=0}^{\mathrm{\infty }}{\mathrm{B}\left(e^{-iw}\right)\mathsf{\Omega }\left(\tau \right)\mathrm{B}\left(\tau \right)\left(e^{-iw}\right)}_{ ii}}} \\ {\tilde{\theta }}_{ij}\left(w\right)={\displaystyle \frac{{\theta }_{ij}\left(w\right)}{\sum _{k=1}^N{\theta }_{ij}\left(w\right)}} \end{gathered}$$

${\tilde{\theta }}_{ij}$(ω) denotes the portion of the spectrum of the ith series at a specified frequency ω that can be ascribed to a shock in the jth series. It can be attributed to an intra-frequency indicator.

To evaluate interconnectedness in the short-, medium-, and long-term, we chose a specific classification of all frequencies, rather than single-frequency connectedness; d = (a, b): a, b ∈ (−π, π), a < b

$${\tilde{\theta }}_{ij}\left(d\right)={\int }_a^b{\tilde{\theta }}_{ij}\left(w\right)dw$$

At this juncture, we can derive the same interconnectedness metrics as in Diebold and Yilmaz (2012, 2014), which can be understood in a similar way. Nevertheless, in this situation, they are frequency-connectedness metrics that offer insights into spillovers within specific frequency bands.

$$\begin{gathered} {{NPDC}_{ij}}^{\left(d\right)}={\tilde{\theta }}_{ij}\left(d\right)-{\tilde{\theta }}_{ji}\left(d\right) \\ {TO}_{.\leftarrow i}^{\left(d\right)}\left(\tau \right)=\sum _{j=1,j\ne i}^n{\tilde{\theta }}_{j\leftarrow i}^{\left(d\right)}\left(\tau \right) \\ {FROM}_{i\leftarrow .}^{\left(d\right)}\left(\tau \right)=\sum _{j=1,j\ne i}^n{\tilde{\theta }}_{i\leftarrow j}^{\left(h\right)}\left(\tau \right) \\ {NET}_{i\leftarrow i}^{\left(d\right)}\left(\tau \right)={TO}_{.\leftarrow i}^{\left(d\right)}\left(\tau \right)-{FROM}_{i\leftarrow .}^{\left(d\right)}\left(\tau \right) \\ {TCI}^{\left(d\right)}\left(\tau \right)=N^{-1}\sum _{i=1}^N{TO}_{.\leftarrow i}^{\left(d\right)}\left(\tau \right)=N^{-1}\sum _{i=1}^N{FROM}_{i\leftarrow .}^{\left(d\right)}\left(\tau \right) \end{gathered}$$

In this instance, there are three frequency bands representing short, medium, and long-term dynamics covering 1 to 5 days: d₁ = (π/5, π), from 6 to 16 days; d₂ = (π/16, π/5), and from 16 to infinite days; d₃ = (0, π/16).

${{NPDC}_{ij}}^{\left(d1\right)},{{NPDC}_{ij}}^{\left(d2\right)}{{,NPDC}_{ij}}^{\left(d3\right)}$: show net pairwise directional connectedness over the short, medium, and long term, respectively. ${\mathrm{T}\mathrm{O}}_{.\leftarrow \mathrm{i}}^{\left(\mathrm{d}1\right)}, {\mathrm{T}\mathrm{O}}_{.\leftarrow \mathrm{i}}^{\left(\mathrm{d}2\right)},{\mathrm{T}\mathrm{O}}_{.\leftarrow \mathrm{i}}^{\left(\mathrm{d}3\right)}:$ Represent, respectively the total directional connectedness in the short, medium, and long-term TO others, ${\mathrm{F}\mathrm{R}\mathrm{O}\mathrm{M}}_{\mathrm{i}\leftarrow .}^{\left(\mathrm{d}1\right)}{,\mathrm{F}\mathrm{R}\mathrm{O}\mathrm{M}}_{\mathrm{i}\leftarrow .}^{\left(\mathrm{d}2\right)}{,\mathrm{F}\mathrm{R}\mathrm{O}\mathrm{M}}_{\mathrm{i}\leftarrow .}^{\left(\mathrm{d}3\right)}$: Show respectively Total directional connectedness in the short, medium, and long-term FROM others. ${\mathrm{N}\mathrm{E}\mathrm{T}}_{\mathrm{i}\leftarrow \mathrm{i}}^{\left(\mathrm{d}1\right)}{,\mathrm{N}\mathrm{E}\mathrm{T}}_{\mathrm{i}\leftarrow \mathrm{i}}^{\left(\mathrm{d}2\right)},{\mathrm{N}\mathrm{E}\mathrm{T}}_{\mathrm{i}\leftarrow \mathrm{i}}^{\left(\mathrm{d}3\right)}$: Represent the total NET directional connectedness in the short, medium, and long term, respectively. ${\mathrm{T}\mathrm{C}\mathrm{I}}^{\left(\mathrm{d}1\right)},{\mathrm{T}\mathrm{C}\mathrm{I}}^{\left(\mathrm{d}2\right)},{\mathrm{T}\mathrm{C}\mathrm{I}}^{\left(\mathrm{d}3\right)}$ Illustrent respectivement l’indice de connectivité totale à court terme, à moyen terme et à long terme.

The link between the measurements of the frequency bands of Baruník and Křehlík (2018) and the measures of the Diebold and Yilmaz time range (Diebold & Yilmaz, 2012, 2014) is highlighted:

$$\begin{gathered} {{NPDC}_{ij}}^{\left(h\right)}=\sum _{j=1,j\ne i}^n{{NPDC}_{ij}}^{\left(d\right)}\left(\tau \right) \\ {TO}_{.\leftarrow i}^{\left(h\right)}\left(\tau \right)=\sum _{j=1,j\ne i}^n{TO}_{.\leftarrow i}^{\left(d\right)}\left(\tau \right) \\ {FROM}_{i\leftarrow .}^{\left(h\right)}\left(\tau \right)=\sum _{j=1,j\ne i}^n{FROM}_{i\leftarrow .}^{\left(d\right)}\left(\tau \right) \\ {NET}_{i\leftarrow i}^{\left(h\right)}\left(\tau \right)=\sum _{j=1,j\ne i}^n{NET}_{i\leftarrow i}^{\left(d\right)}\left(\tau \right) \\ {TCI}^{\left(h\right)}\left(\tau \right)=\sum _{j=1,j\ne i}^n{TCI}^{\left(d\right)}\left(\tau \right) \end{gathered}$$

Overall, this approach makes it possible to examine the time-frequency connectedness of the quantiles between the G7 and BRICS stock markets in the normal market condition (at the median).

3.3. Portfolio Management

In this part, we apply the minimum connectivity portfolio (MCP) method using all pairwise connectivity indices, as proposed by Broadstock et al. (2022). Reducing the interconnectivity of variables and therefore their impacts makes it possible to form a portfolio less vulnerable to network shocks, or more resilient to them. This approach aims to limit the transmission of shocks across assets, thereby reducing the overall portfolio risk.

$$\underset{\mathrm{W}}{\min }\mathrm{W}\prime \mathrm{M}\mathrm{W} s.t. {\mathrm{W}}^{\prime }I=1$$

where $\mathrm{I}$ is an N*1 vector with all elements equal to one, and $\mathrm{M}$ denotes the matrix of pairwise connectedness indices.

Thus, variables without significant influence on the others and not influenced by them will receive a greater weighting in the portfolio. This can be articulated as follows:

$$W_{Rt}={\displaystyle \frac{{PCI}_t^{-1}I}{I{PCI}_t^{-1}I}}$$

where I is the identity matrix, and PCI_t is the pairwise connectivity index matrix,

$${PCI}_t=\left(\begin{array}{cccc}{CD}_{1\to 1}^h& {CD}_{2\to 1}^h& \dots & {CD}_{N\to 1}^h\\ {CD}_{1\to 2}^h& {CD}_{2\to 2}^h& \dots & {CD}_{N\to 2}^h\\ ⋮& ⋮& \ddots & ⋮\\ {CD}_{1\to T}^h& {CD}_{2\to T}^h& \dots & {CD}_{N\to T}^h\end{array}\right)$$

where ${CD}_{i\to j}^h$ denotes the pairwise directional connectedness transmitted to variable j from variable i. The minimum-connectedness portfolio weights, $\mathrm{W}$, are obtained by analyzing the first-order conditions derived from the minimization problem. Specifically, the weight vector is determined by solving the first-order conditions for $\mathrm{W}$.

3.4. The Hedging Effectiveness Ratio

According to Ederington (1979), the Hedging Effectiveness Ratio is given by:

$$HE=1-{\displaystyle \frac{{Var(R}_{hedged})}{{Var(R}_{\mathrm{u}\mathrm{n}\mathrm{h}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d}})}}$$

R_Unhedged and R_Hedged are the returns on the unhedged and hedged portfolios, respectively. The greater the HE, the more substantial the risk reduction, and conversely.

4. Empirical Results and Discussion

4.1. Data

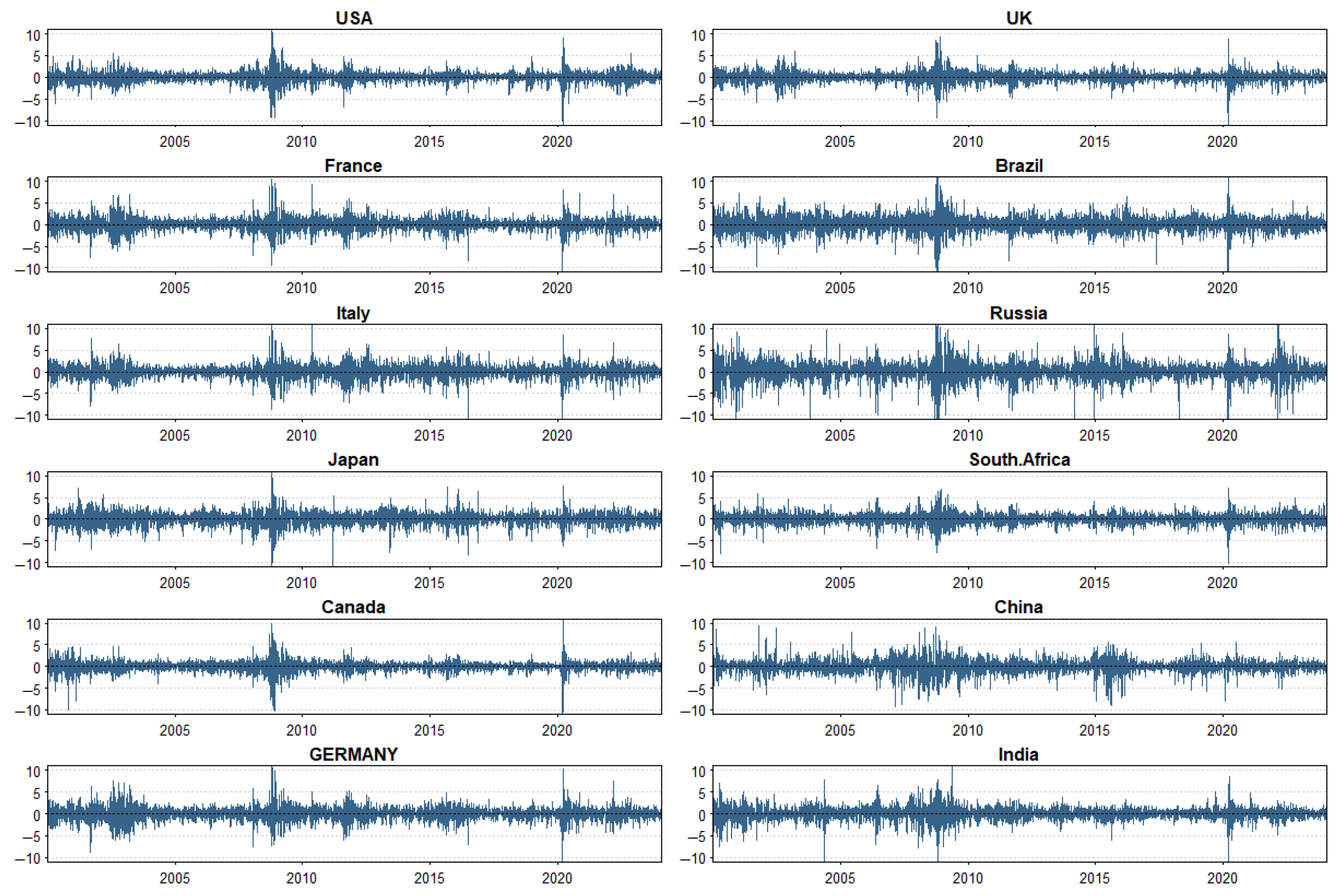
To measure extreme risk and the effect of quantile connectedness among BRICS and G7 stock market returns, we collected the daily stock prices of 12 indices of these stock markets from the Data Stream database for the period from 1 January 2000 to 22 January 2024. All original datasets are expressed in dollars. Percentage daily returns are calculated by transforming each set of data into logarithmic differences of two consecutive prices. The stock market indices studied in this empirical study include the following indices: BRICS stock markets: Russia (RTS Index), Brazil (Bovespa Index), China (SSE Composite), India (BSE SENSEX), and South Africa (FTSE/JSE All Share Index); G7 stock markets: Japan (Nikkei 225), United States (S&P 500), Canada (S & P/TSX Composite Index), Italy (MIB), Germany (DAX 30), United Kingdom (FTSE 100), and France (CAC 40).

Figure 1 shows the movements of the G7 and BRICS stock index return for the period from 1 January 2000 to 22 January 2024.

Table 1. Descriptive statistical analysis.

	USA	France	UK	Germany	Japan	Italy	Canada	Brazil	Russia	India	China	South Africa
Moyenne	0.019	0.003	0.001	0.013	0.010	−0.005	0.014	0.031	0.029	0.042	0.01	0.034
Maximum	10.957	10.594	9.384	10.797	13.234	10.874	11.680	13.678	23.204	15.989	9.399	7.261
Median	0.026	0.01	0.006	0.042	0.000	0.028	0.038	0.000	0.045	0.026	0.000	0.010
Minimum	−12.76	−13.098	−11.51	−13.054	−12.111	−18.54	−13.364	−15.99	−48.29	−14.10	−9.256	−10.23
Écart type	1.214	1.390	1.144	1.427	1.404	1.484	1.137	1.709	2.180	1.379	1.431	1.431
skewness	−0.382	−0.205	−0.349	−0.158	−0.372	−0.594	−0.841	−0.365	−2.033	−0.374	−0.386	−0.301
Kurtosis	10.772	6.620	8.314	6.148	6.796	9.246	17.241	7.175	47.506	10.359	6.021	5.041
Jarque_Bera	30,523 ***	11,517 ***	18,220 ***	9922.8 ***	12,237 ***	22,746 ***	778,538 ***	13,616 ***	594,905 ***	28,235 ***	9646.6 ***	6749 ***
Q2 (20)	8514.9 ***	4294.8 ***	5653 ***	4427.3 ***	55,514.7 ***	1946.5 ***	7160.8 ***	6309.2 ***	512.1 ***	2759.4 ***	1913.4 ***	5583.4 ***
ADF	−18.60 ***	−19.15 ***	−19.82 ***	−19.06 ***	−18.31 ***	−18.51 ***	−19.19 ***	−17.29 ***	−18.49 ***	−17.24 ***	−17.52 ***	−19.35 ***
Number of Observation	6277	6277	6277	6277	6277	6277	6277	6277	6277	6277	6277	6277

Note: Q² (20) denotes the Ljung-Box Q statistics up to 20th-order autocorrelation. The Jarque-Bera statistics represent the normality test of the sample data. The ADF test represents the Dickey-Fuller augmented unit root test. *** indicates significance at the 1% level.

provides descriptive statistics of the daily returns of the stock market indices for the G7 and BRICS nations over the period from 1 January 2000 to 22 January 2024. The daily returns of the stock market index are positive for all markets, with a mean of between 0.001% and 0.042%, except for the slightly negative FTSE MIB mean. Russia’s RTS index has the highest mean return. In terms of risk, we can see that the standard deviation is relatively high, indicating a large variation in returns, with BRICS stock indices proving riskier than the G7 countries. Among these stock markets, Russia tops the list in risk, followed by Brazil and Italy. Conversely, South Africa’s stock market is the least volatile.

The Jarque-Bera test rejects the hypothesis that returns follow a normal distribution. This indicates that returns are not uniformly distributed around the mean. On the other hand, the Ljung-Box test reveals the presence of autocorrelations in the return since the null hypothesis is rejected. The ADF test confirms that the returns are stationary.

Figure 2 provides a visual representation of the correlation matrix among various assets. The color and intensity of the shaded boxes denote the correlation levels: blue signifies a positive correlation, while red denotes a negative correlation.

The pairwise correlation coefficients indicate that France has the highest correlated market to the others. In contrast, China has the lowest correlation with its pairs.

We notice a markedly robust positive correlation between the major stock markets in the G7 countries, indicating a high likelihood of interconnectedness between these markets. France is significantly linked with all other stock markets, suggesting that the transmission of risk among these stock markets is probably substantial. More importantly, the stock market portfolio is unlikely to offer any diversification advantage to investors, as the matrix shows that G7 stock markets are generally positively correlated with each other. This means that if one G7 market falls, the other G7 markets tend to fall as well.

Japan exhibits a low positive correlation with the majority of G7 stock markets and a negative correlation with the S&P500. This low correlation of the NIKKEI 225 index with other stock markets suggests potential diversification advantages for investors. Our results also indicate that China’s and India’s stock markets have negative and low correlations with other stock markets, indicating a prospective diversification opportunity for investors.

4.2. Static Connectedness Analysis

Since our objective is to prove connectedness return across the extreme, and under previous studies, we employ τ = 0.05 for the left quantile, τ = 0.50 for the median quantile, and τ = 0.95 for the right quantile. For the parameterization of the connected model, we follow Ando et al. (2022); utilizing a rolling QVAR window of 200 days to examine time-varying connectedness, we select an order of 1 for the VAR lag length based on the Bayesian Information criterion (BIC) and using a 20-step forecast variance decomposition to estimate spillover.

Table 2. Quantile total connectedness table.

	USA	France	Italy	Japan	Canada	Germany	UK	Brazil	Russia	SA	Chine	India
Panel A: Static connectedness of returns at the median quantile (τ = 0.50)
TO	88.70	107.21	92.66	19.52	77.51	102.65	95.00	53.73	41.84	57.42	10.14	27.13
FROM	69.99	79.05	76.37	65.22	68.72	78.10	76.99	57.44	55.81	67.23	27.26	51.31
Net	18.71	28.15	16.29	−45.69	8.79	24.55	18.01	−3.72	−13.97	−9.82	−17.12	−24.18
TCI	64.46
Panel B: Static connectedness of returns at the at the lower quantile (τ = 0.05)
TO	95.88	95.04	94.43	80.30	92.67	93.12	92.38	88.21	81.77	88.63	81.33	87.89
FROM	89.03	89.76	89.57	89.82	89.27	90.03	89.89	88.95	89.33	89.45	87.94	88.62
Net	6.84	5.28	4.86	−9.51	3.40	3.09	2.50	−0.74	−7.56	−0.82	−6.60	−0.73
TCI	89.30
Panel C: Static connectedness of returns at the at the upper quantile (τ = 0.95)
TO	92.69	97.19	94.30	79.00	90.41	96.71	93.65	88.44	81.75	88.74	74.82	81.88
FROM	88.48	89.11	88.87	88.64	88.25	88.95	89.17	87.58	87.88	88.58	86.42	87.63
Net	4.21	8.09	5.43	−9.64	2.16	7.76	4.48	0.85	−6.13	0.16	−11.61	−5.75
TCI	88.30

,

Table 3. Frequency connectedness at the 0.5 quantile.

	USA	France	Italy	Japan	Canada	Germany	UK	Brazil	Russia	SA	Chine	India
Panel A: short term: 1–4 days
TO	61.10	78.63	68.23	14.51	54.46	75.05	69.79	37.43	30.70	42.09	7.97	20.22
FROM	54.39	59.44	57.47	42.89	51.46	58.40	57.29	43.53	38.42	46.15	18.94	31.80
Net	6.71	19.19	10.75	−28.38	3.00	16.65	12.50	−6.10	−7.71	−4.06	−10.97	−11.59
TCI	46.68
Panel B: medium term: 4–16 days
TO	19.79	20.52	17.55	3.60	16.54	19.83	18.11	11.71	8.02	11.02	1.57	4.98
FROM	11.28	14.16	13.59	15.96	12.43	14.17	14.20	10.01	12.48	15.14	5.98	13.83
Net	8.52	6.36	3.96	−12.36	4.11	5.66	3.91	1.69	−4.46	−4.13	−4.40	−8.85
TCI	12.77
Panel C: long term: 16–Inf days
TO	7.80	8.06	6.88	1.41	6.51	7.77	7.10	4.59	3.12	4.31	0.60	1.94
FROM	4.33	5.46	5.31	6.37	4.83	5.53	5.50	3.90	4.92	5.94	2.35	5.68
Net	3.48	2.61	1.58	−4.96	1.68	2.24	1.60	0.69	−1.80	−1.63	−1.75	−3.74
TCI	5.01

and

Table 4. Quantile frequency connectedness results.

	USA	France	Italy	Japan	Canada	Germany	UK	Brésil	Russie	AS	Chine	India
Frequency interconnectedness at the 0.05 quantile
Panel A: short term: 1–4 days
TO	55.02	56.19	57.16	47.10	53.40	54.40	53.69	52.34	48.10	53.14	48.46	50.62
FROM	55.45	54.27	55.13	46.79	54.69	54.45	53.03	56.28	51.19	50.88	50.09	47.36
Net	−0.43	1.92	2.03	0.31	−1.30	−0.05	0.66	−3.94	−3.09	2.26	−1.63	3.26
TCI	52.47
Panel B: medium term: 4–16 days
TO	22.70	21.76	21.51	18.26	21.82	22.05	21.52	20.26	18.75	19.73	17.61	19.72
FROM	18.22	19.70	18.98	24.30	19.01	19.72	20.06	17.98	21.37	21.96	21.57	22.82
Net	4.48	2.06	2.54	−6.04	2.80	2.32	1.47	2.28	−2.62	−2.23	−3.97	−3.10
TCI	20.47
Panel C: long Term: 16–Inf days
TO	18.16	17.09	15.75	14.94	17.46	16.68	17.17	15.61	14.93	15.75	15.27	17.55
FROM	15.36	15.79	15.46	18.73	15.57	15.86	16.80	14.68	16.77	16.61	16.27	18.44
Net	2.80	1.30	0.29	−3.79	1.89	0.82	0.37	0.92	−1.84	−0.85	−1.00	−0.89
TCI	16.36
Frequency interconnectedness at the 0.95 quantile
Panel A: short term: 1–4 days
TO	70.96	74.25	72.79	62.25	69.84	74.70	73.06	67.78	63.50	68.53	58.65	64.30
FROM	73.83	71.48	72.82	62.01	71.32	71.00	70.03	69.54	66.34	65.73	63.32	63.21
Net	−2.88	2.77	−0.03	0.24	−1.47	3.70	3.03	−1.76	−2.84	2.80	−4.67	1.10
TCI	68.38
Panel B: medium term: 4–16 days
TO	14.72	14.97	14.33	10.95	13.85	14.64	14.07	13.47	12.03	13.05	10.33	11.50
FROM	9.59	11.75	10.41	17.96	11.06	11.93	12.72	11.67	14.26	15.33	15.11	16.12
Net	5.13	3.22	3.92	−7.01	2.79	2.71	1.35	1.80	−2.23	−2.28	−4.78	−4.62
TCI	13.16
Panel C: long Term: 16–Inf days
TO	7.02	7.98	7.18	5.80	6.71	7.37	6.52	7.19	6.22	7.16	5.83	6.08
FROM	5.06	5.88	5.65	8.67	5.87	6.02	6.42	6.38	7.29	7.52	7.99	8.30
Net	1.96	2.09	1.53	−2.87	0.84	1.35	0.10	0.81	−1.07	−0.36	−2.16	−2.22
TCI	6.75

report the static connectedness matrix between G7 and BRICS country index returns at the quantile level, specifically showing the results for the lower, median, and upper quantiles.

We find significant additional return connectedness in the extremes compared to the median. This finding aligns with Mensi et al. (2023), who showed high extreme quantile connectedness between bear and bull markets compared to median connectedness. The total connectedness index (TCI) underwent significant changes across various quantiles. The lowest TCI is 64.46%, occurring at τ = 0.5. The two highest TCI values are 89.30% in the inferior quantile and 88.30% in the superior quantile. Notably, in both the lower and upper tails, the contributions to and from others were more important than the median. This implies that BRICS and G7 countries are closely linked during periods of financial stress.

We begin by interpreting the connectedness of returns when the market is normal (τ = 0.5). Table 2, Panel A, displays the connectedness results between markets at the median quantile, utilizing QVAR models; France, the UK, Germany, and Italy are strongly linked to the other variables at the median quantile. These stock markets receive more than 76% of the system’s shocks. At the same time, they are the largest contributor to other markets, transmitting 107.21%, 95.00%, 102.65%, and 92.66% of shocks to the system, respectively. On the other hand, China is the least affected by spillovers from other stock markets and is the least linked to other variables.

However, regarding net transmissions, all G7 countries except Japan show positive results, while the five BRICS countries and Japan display negative net connectivity. This indicates that these six countries “Italy, United States, United Kingdom, Canada, France, and Germany”—are net transmitters within the system, given that their contributions to other markets surpass what they receive from other markets at the median quantile.

The strong connectedness of France, the UK, Germany, USA, and Italy at the median quantile underlines their central role in shaping global financial dynamics. These markets reflected their high integration with international capital markets. This systemic importance means that shocks in these economies can rapidly spill over to others, amplifying global volatility and reducing diversification opportunities for international investors. In contrast, China’s relative isolation suggests that it is less synchronized with global markets, which, from a portfolio allocation perspective, highlights its potential as a risk-mitigating asset during normal market conditions.

Table 2, Panel B illustrates the connectedness between variables at extremely low quantile (τ = 0.05). For tail spillover measures, the 12 countries under consideration receive a spillover index between 87.94% (China) and 90.03% (Germany). Similarly, directional connectedness to others ranges from 80.30% (Japan) to 95.88% (USA).

At this extremely low percentage for the BRICS countries, South Africa is the largest emitter (88.63%), followed by Brazil with 88.21%. South Africa is also the largest receiver of the return connectedness (89.45%), followed by Russia with 89.33%. At the static connectedness level of the 0.05 quantile, all BRICS countries are receivers, but India, Brazil, and South Africa have the lowest net connectedness (−0.73%, −0.74%, and 0.82%, respectively). Nevertheless, the contribution percentages for the BRICS are greater at the lower and upper quantiles than at the median quantile.

The pronounced connectedness observed at the extreme lower quantile (τ = 0.05) highlights the heightened vulnerability of global stock markets to downside risks. Conversely, the fact that all BRICS markets act as net receivers, with India, Brazil, and South Africa displaying negative net connectedness, indicates that these markets are highly susceptible to contagion effects and external shocks rather than exerting influence over others. From a portfolio allocation perspective, the higher spillovers at the tails suggest that the benefits of diversification between BRICS and G7 markets are significantly reduced during extreme downturns, as cross-market correlations intensify. This asymmetry in connectedness across quantiles has direct implications for portfolio risk management, indicating that strategies based on median dependence may underestimate systemic risk in extreme bearish conditions.

Table 2, Panel C shows the findings on connectedness at the 0.95 quantile among these 12 stock market indices. For the analysis of spillover effects at the bullish tail level, China is the least receiver (86.42%) and the least emitter (74.82%). Considering the sign and direction of the measures of net connectedness, our results show that Japan and the nations act as net recipients of shocks within the system. whereas the remaining G7 are net transmitters of shocks.

At the upper quantile (τ = 0.95), the results reveal an asymmetry of spillover dynamics during bullish market conditions. The finding that G7 markets act predominantly as net transmitters of shocks reflects their systemic importance and dominant role in driving global equity cycles during expansions. In contrast, Japan and several other markets behaving as net receivers indicates their stronger dependence on external capital flows and global sentiment in upward phases, rather than being sources of contagion themselves. The position of China as both the least emitter and the least receiver further reinforces its partial segmentation from the global system, suggesting that, despite its market size, structural or regulatory factors may dampen its integration in bullish states.

Importantly, Brazil’s consistently low net connectedness across bearish, bullish, and normal regimes implies that it retains unique diversification properties for international portfolios. This suggests that, unlike other BRICS members that are highly vulnerable to external spillovers, Brazil provides a relatively uncorrelated investment opportunity, which could be strategically exploited in global asset allocation to mitigate contagion risk.

4.3. Analysis of Dynamic Connectedness

As highlighted by Jena et al. (2022) and Yousaf et al. (2022), conducting a detailed analysis of the connectedness of time-varying returns across different quantiles is crucial for distinguishing between positive and negative shocks. Such an analysis can also equip portfolio managers with valuable insights.

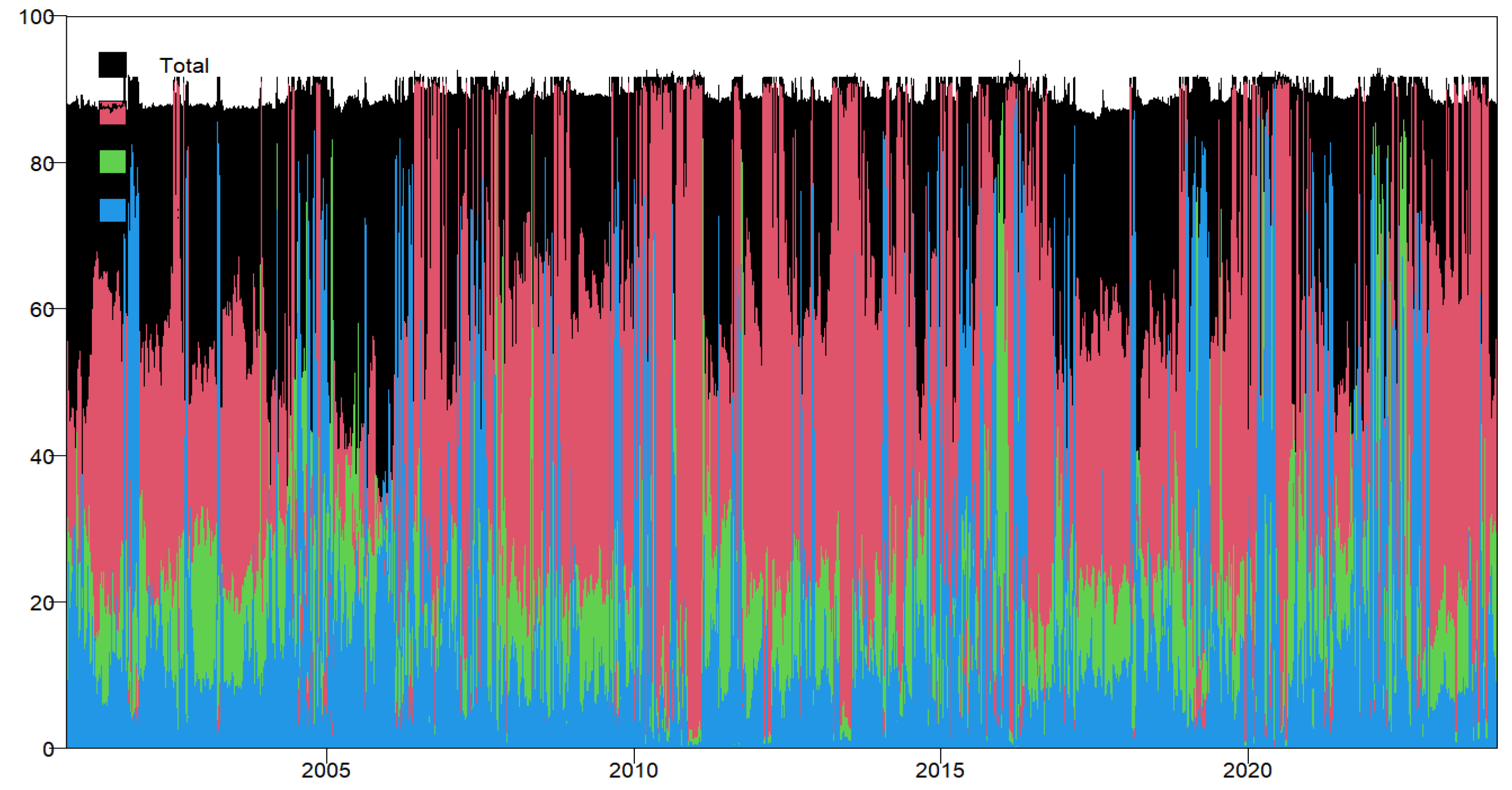
So, it is crucial to investigate the dynamic variation of return connectedness at various quantiles and over different times. Figure 2, Figure 3 and Figure 4 represent the time-varying total connectedness index over three quantiles: the middle (τ = 0.5) and the extremes of the distribution (lower, τ = 0.05 and upper, τ = 0.95, quantiles), measured with 200-day rolling windows.

From Figure 3, Figure 4 and Figure 5, it is possible to see that in the 0.5 quantile, the TCI shows considerable variations in response to different shocks, ranging from a low of 55% to a high nearing 85%. However, when concentrating on the tails of the return distribution, there is a more pronounced fluctuation in connectedness, indicating greater sensitivity of the BRICS and G7 stock markets to extreme upper and lower events. The TCI ranges from 95% to 99.98% in the 0.05 quantile and from 85% to 99% in the τ = 0.95 quantile. Practically, the proportion of total connectedness at both extremes is greater than at the median (85% to 99% versus 55% to 85%). This indicates that BRICS and G7 indices are more affected by extreme positive and negative shocks as opposed to median shocks. Interestingly, the TCI remains consistently elevated in the lower quantile across our full sample. However, the TCI for the upper quantile rises to levels like the extreme lower tail during crises, notably the 2008 global financial crisis, COVID-19, and the conflict in Ukraine. Finally, the TCI for the median quantile also increases in 2020, likely due to the heightened uncertainty caused by COVID-19.

According to Figure 3, the TCI rose to a new record of 89% after the onset of COVID-19 in February 2020; the pandemic exerted a major influence on the global economy and financial markets. Subsequently, the TCI declined in 2021 and remained almost stable for most of the year. It reached a new peak of 78% just during the Ukrainian War. We observe a significant increase in total system connectedness in stock markets when a major economic crisis breaks out. According to El Khoury et al. (2024), it is notable that the COVID-19 pandemic had a significantly larger impact than other crises, highlighting its substantial and unmatched economic impact on sustainability-focused financial markets.

Contrary to the median, the TCI varies in the high and low quantiles, ranging from 85% to 100% in 2010. There is a visible increase in 2019, with peaks in early 2020 and significant variations between 2020 and 2023. This consistent rise in the TCI at the lower and upper quantiles suggests that investors are growing more responsive to major positive and negative shocks. Connectedness at the lower market has been dominant, as reflected in the fact that 5th quantile connectedness exceeds the values seen in the 95th quantile counterparts.

Figure 4 shows that overall connectedness between the BRICS and G7 stock markets reached 100% in 2010–2011 after the sovereign debt crisis. This index reached a level of 100% during COVID-19 and a peak of 102% following the Russo-Ukrainian War. Figure 5 shows that dynamic connectivity between this market is also higher during periods of growth. This observation is particularly relevant during the stock market booms from 2003 to 2007. During this period, the dynamic connectedness between the stock market returns of these two groups reached an unprecedented level. The degree of connectedness intensifies even further during market downturns caused by events such as the global financial crisis, the European debt crisis, and COVID-19. After the global financial crisis, the TCI value of these 12 stock market returns has grown from the previous level, reaching a peak of 97%.

These findings demonstrate a substantial degree of connectedness in the system and a strong susceptibility to global political and economic events during both bullish and bearish market conditions. They imply that investors should also consider extreme scenarios when making investment or regulatory decisions.

4.4. Net Directional Connectedness

In this section, we will evaluate the net directional connectedness at three quantile levels. This connectedness is determined by calculating the difference between “TO” directional connectedness and “FROM” directional connectedness. Figure 6, Figure 7 and Figure 8 show the progression of total return net connectedness for each BRICS and G7 country positive (negative). Net overall connectedness signifies that the market is a net sender (recipient) of spillovers.

A visual analysis of Figure 6 reveals three distinct groups of markets: the first group comprises stock markets that recorded positive net connectedness for almost the entire sample period, meaning they were net return transmitters. These markets are the USA, France, Germany, Italy, and the UK. We can see that these five markets, which belong to the G7 countries, served as net senders of returns for nearly the entire period (1 January 2020–22 January 2024). The second group consists of stock markets that have experienced negative net connectedness during most of the sampling period. This implies that they are net receivers of connectedness in terms of returns. India, China, Russia, South Africa, and Japan fall into this category as net receivers of return spillovers. The third group comprises stock markets that alternated between being net transmitters and net receivers of return connectedness. These markets are Brazil and Canada.

During extreme events, the pattern of net connectedness shifts markedly in both tails, with no stock market consistently acting as a net sender or recipient of returns over the whole period. Most stock markets can be net transmitters during some periods, while in other periods they are net receivers, as shown in Figure 7 and Figure 8. There are significant variations in connectedness between G7 and BRICS stock markets over time. These variations can be attributed to various factors, including political events, economic changes, and technological innovations.

During extreme incidents, investors should stay vigilant regarding the contagion effects of return shocks in stock indices. Investors ought to evaluate their risks at the bearish and bullish extremes of the distribution. This knowledge can help them in optimizing their asset allocation strategies and reducing risks. Research indicates that market interconnectedness is higher during bear and bull markets compared to calm periods.

4.5. Network Representation of the Net Directional Pairwise Shock Connectedness

In this part, we visualize a pairwise net directional connectedness network among BRICS and G7 stock market returns across the extreme lower, extreme upper quantiles, and the middle quantile of the joint distribution. Our goal is to identify which markets function as net transmitters or net receivers of shock spillovers within the entire system. By examining the network plot, we can observe the intensity and direction of shock transmission between variables. The border represents the direction in which shocks are transmitted between markets, while the size of each border indicates the intensity of net connectedness. The intensity of connectivity among markets is represented by the thickness of the border: thicker borders signify stronger connectedness. Each node, varying in size and color, signifies the magnitude and overall strength of shock transmissions. Blue (yellow) denotes the net transmitter (receiver) of risk contagion. Figure 9 presents the results as network diagrams for bear (Figure 9A), normal (Figure 9B), and bull markets (Figure 9C), respectively. Each of these networks displays the net directional connectedness of shocks to each market throughout the system.

First, we investigate the net connectedness of returns at the median quantile (τ = 0.5) as illustrated in Figure 9B. The network graph displays very thin boards, signifying low net connectedness between stock market returns. The exception has been registered between the USA-Japan pairs, as well as between the France-Japan, Germany-Japan, and Italy-Japan pairs. In addition, the Japanese stock market emerges as the largest recipient of net connectedness from shocks in other markets. At the 0.5 quantile, France emerges as the primary net transmitter of connectedness, transmitting most of the shocks to the Russian, South African, and Japanese markets, followed by the German and US stock markets. As a result, net shock transmission is lower during periods of normal market conditions. We find a relatively limited risk transmission between these markets and the stock market in China; the yellow color of China’s node shows that its stock market is a net recipient of shocks, and this market has no border with the other markets, indicating the low net connectedness with those markets.

From Figure 9A,C, we can see that the lower and upper quantiles exhibit very similar net connectedness behavior in terms of shock directions and intensities. As panel A shows, the greatest shock effect was exerted by six markets in Group 7 (France, USA, Germany, Italy, UK, and Canada). This result indicates that these markets significantly influenced Japan and the BRICS markets in an extremely bearish market context. China’s and Japan’s stock markets emerge as the primary net recipients of shocks from the other G7 nations’ markets. According to panel C, at the extreme upper quantile (τ = 0.95), the G7 countries (Italy, Germany, the UK, Canada, France, and the USA) are identified as the primary transmitters of strong net connectedness to the other markets. China stands out as the largest recipient of net connectedness from France, Germany, and the UK, followed by Japan, which receives even greater net connectedness from the US and France. Investors need to understand the robust dynamic connectedness among the BRICS and G7 stock markets during boom times. This indicates that the stock market returns of these two groups are likely to be more closely linked during these periods. Investors should consider diversifying their portfolios by including stock markets from both groups.

Taking our interpretation further, we observe that in all three cases, BRICS stock markets are always net receivers of connectedness. They are net transmitters of shocks in the three extreme quantiles. Remarkably, net connectedness is more pronounced in bear and bull market scenarios.

The static connectedness network visualization of the normal market (Figure 9B) allows us to draw the following conclusions: three distinct market segmentations can be identified. The first group consists of the G7 countries, due to the intensity of spillovers they exchange with each other. These markets are net emitters of financial shocks to other markets, allowing us to form a dominant cluster in terms of externalities.

The second cluster comprises the markets of Brazil, Russia, South Africa, India, and Japan, which have moderate interconnectedness between them while acting as net receivers of shocks from the G7 markets. Finally, the third cluster consists solely of the Chinese stock market, which is notable for its segmentation and relative isolation compared to the other markets analyzed.

The results reveal heightened connectedness among the markets under tail conditions, encompassing both bullish and bearish regimes. In particular, the evidence indicates that the stock markets of the G7 and BRICS exhibit strong integration across these extreme states, highlighting significant tail dependence and the potential for systemic risk spillovers.

4.6. Quantile Frequency Connectedness Analysis in the Middle Distribution

Table 3 details the degree of connectedness among BRICS and G7 stock markets across different time frames within normal market conditions. The table is divided into three panels: Panel A focuses on short-term connectedness, Panel B examines medium-term connectedness, and Panel C addresses long-term connectedness.

After examining the connectedness index in Table 3, we find that short-term dynamics have a much higher impact, accounting for 46.68% of the total, which is more than three times greater than the influence of medium-term and long-term connectedness, which have 12.77% and 5.01%, respectively. We observe that the French stock market serves as the primary net transmitter of shocks, with a value of 28.15%. It also leads in short-term shock transmission, with 19.19%. But the US stock market, though also a significant net transmitter with an overall value of 18.71%, is the predominant transmitter in medium-term and long-term connectedness, with values of 8.52% and 3.48%, respectively. Among the series of returns for the markets studied, all the BRICS markets and Japan are net receivers of connectedness. The Japanese stock market is the chief recipient of shocks, with −45.69%, followed by India with −24.18%.

The frequency-domain analysis also reveals the existence of three distinct clusters, similar to those identified under the time-domain approach, particularly during periods of market stability. The dominance of short-term connectedness indicates that global equity shocks are primarily transmitted through high-frequency channels, underscoring the need for rapid response strategies in risk management. France’s role as the main short-term transmitter highlights its systemic importance within Europe, while the United States’ stronger influence over medium- and long-term horizons reflects its global financial centrality. Conversely, the BRICS markets and Japan, as net receivers, appear more vulnerable to external shocks, suggesting limited capacity to propagate systemic risk. This asymmetric connectedness implies that, even under normal market conditions, geographic diversification benefits may be constrained, and investors should consider frequency-based hedging to mitigate exposure to short-term volatility. Moreover, the identification of three distinct clusters supports the use of cluster-based portfolio allocation strategies, enabling better management of interconnectedness risk across regions.

Figure 10 shows the evolution of total frequency dynamic connectedness at the median quantile, derived using a QVAR model with a 200-day sliding window size, an order-one lag length (determined by BIC), and a generalized 100-step forecast error variance decomposition. Figure 10 divides the total connectedness dynamics into three frequency bands and a total period connectedness band based on QVAR. The black region represents the dynamic connectedness values over the total period, while the red, green, and blue areas correspond to short-, medium-, and long-term results. The analysis reveals a significant level of interconnectedness within the lower frequency band.

We observe that the peak value of long-term TCI was reached in 2022, while there was a decline in short-term TCI during the same period. Hence, it is important to separately analyze short-term and long-term dynamics. Considering the onset of COVID-19 in 2020, frequency analysis indicates that the upsurge in total TCI is mainly driven by short-term dynamics rather than long-term ones. This holds significance for investors because, as noted by Chatziantoniou and Gabauer (2021), a change in the variation of long-term TCI typically indicates a significant change in the overall market structure. Additionally, according to Antonakakis et al. (2020), further insights into the dynamics of short- and long-term TCI suggest that the overall dynamic TCI is chiefly influenced by short-term dynamics, which are generally more volatile than long-term dynamics. The frequency-quantile connectedness indices reveal that short-term dynamics predominantly account for the net transmission behavior within the study network. However, it is important to note that, over time, variables may switch roles, transitioning between being network transmitters and receivers.

The next step is to examine the time-frequency connectedness among the BRICS and the G7 markets over short, medium, and long-term periods at the extreme quantiles.

4.7. Time-Frequency Connectedness Analysis at the Extreme Quantiles

Table 4 shows the results for the lower and upper quantiles. Regarding the short term, the total connectedness of the returns is 52.47% and 68.38% at the 0.05 and 0.95 quantiles, respectively. This result indicates that total connectedness is most strongly affected by the dynamics of short-term frequency (1–4 days). This frequency plays a particularly important role in the transmission of extreme shocks between these markets.

However, only 20.47% and 13.16% of the TCI are attributable to the medium-term frequency (5–16 days) at the lower and upper quantiles, respectively, suggesting a reduction in connectedness. While the total long-term results (16–Inf days) reach 16.36% and 6.75 in bearish and bullish market conditions, respectively, showing a decrease in long-term connectedness. However, only 20.47% and 13.16% of the Total Connectivity Index (TCI) are attributable to medium-term frequency (5–16 days) at the 0.05 and 0.95 quantiles, respectively, suggesting a reduction in connectivity. While the total long-term results (16–Inf days) reach 16.36% and 6.75% under bearish and bullish market conditions, respectively, showing a decrease in long-term connectivity.

By examining the results of frequency connectedness at the bearish market level, the stock markets of the G7, including the United States, Italy, France, and Canada, are mostly net transmitters, especially over medium- and long-term horizons. In contrast, the markets of Japan and the BRICS countries, such as China, Russia, Brazil, and India, are net receivers in these same bands.

By analyzing the results of frequency connectedness under the bullish market condition (τ = 0.95) for stock markets across three-time horizons, we observe the following: In the short term, the main net transmitters are Germany with 3.70, the United Kingdom with 3.03, South Africa with 2.80, and France with 2.77, indicating significant influence on other stock markets during extreme upward movements. Conversely, China (−4.67), the United States (−2.88), and Russia (−2.84) are the primary net receivers, meaning they are more influenced by other markets in the short term. In the medium term, the United States has a net transmission of 5.13, followed by Italy (3.72) and France (3.22), making them major transmitters of shock propagation. However, Japan (−7.01), China (−4.78), and India (−4.62) are the main markets receiving shocks from others. For long-term connectedness, France (2.09), Germany (1.35), and the USA (1.96) act as primary net transmitters, while Japan (−2.87), India (−2.22), and China (−2.16) continue to receive contagion effects from other markets.

Our results indicate that the stock markets of the G7 and BRICS are highly integrated, a factor that investors must incorporate into their asset allocation strategies and risk management decisions.

Figure 11 and Figure 12 illustrate the dynamic evolution of the frequency connectedness of stock markets over various time horizons for the extreme quantiles. These figures decompose the total dynamic connectedness into 3 frequency bands; the red zone represents short-term, the green zone illustrates medium-term connectedness, and the blue zone shows long-term connectedness, along with a black band showing the total dynamic connectedness.

By comparing Figure 10, which shows frequency-dynamic connectivity at the median level, with Figure 11 and Figure 12, we can make the following remarks: Firstly, connectedness is significantly weaker in the case of the median quantile. Firstly, short-term connectedness (in red) constitutes a significant part of the base of total connectedness (in black). It is more stable at the median level (Figure 10), whereas it varies notably at the lower (Figure 11) and upper (Figure 12) quantile levels. Although long-term connectedness (in blue) is constant in all figures, it is more pronounced at the lower quantile levels. Secondly, the connectedness is significantly less in the case of the median quantile.

At the upper quantile level, Figure 12 illustrates that the BRICS and G7 stock markets react very rapidly and intensely in the short-term, characterized by high connectedness that varies with high responsiveness. In contrast, medium- and long-term connectedness play a stabilizing role after the shock, allowing the markets to change gradually. At the lower quantile level, the BRICS and G7 stock markets show a rapid and more intense reaction to short-term international shocks compared to medium- and long-term ones. During a crisis, short-term connectedness prevails, whereas long-term connectedness is essential for stabilization in the aftermath of the crisis.

4.8. Sensitivity Analysis

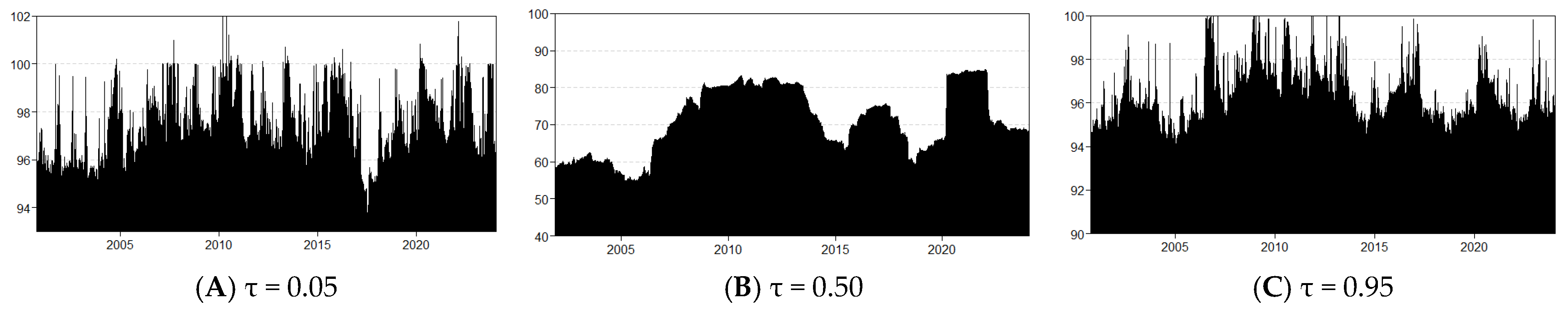
To validate the robustness of our analyses, we conduct a sensitivity assessment with respect to the rolling window size and the choice of the forecasting horizon. Specifically, we use a 500-day rolling window and a 10-day forecasting horizon, and then re-estimate the models presented in our article.

The analysis of Figure 13 reveals that the level of the TCI decreases slightly, although its dynamics, which are the focus of our study, remain largely unchanged. The results for total dynamic connectedness across different quantiles are still similar; indeed, the same features persist when the models are evaluated at the median and in the tails. Moreover, total connectedness remains high in the tails, significantly higher than at the median. Overall, these findings confirm the robustness of our results, which are not affected by the rolling-window size or the choice of forecasting horizon.

4.9. Minimum Connectedness Portfolio

In this section, we present optimal investment portfolios constructed using the Minimum Connectivity Portfolio (MCP) method by examining variations in average portfolio weights (W) and efficiency ratios (HE) to assess the relative performance of each portfolio. The MCP technique aims to minimize pairwise connectivity and, therefore, spillovers among the markets of the G7 and BRICS as determined by the QVAR model. The outcomes are detailed in

Table 5. Minimum Connectedness Portfolio.

QUANTILE	0.05		0.5		0.95
	W	HE	W	HE	W	HE
USA	0.09	0.43	0.08	0.47	0.09	0.43
France	0.08	0.56	0.06	0.59	0.08	0.56
Italy	0.07	0.62	0.06	0.64	0.07	0.62
Japan	0.10	0.57	0.12	0.60	0.09	0.57
Canada	0.10	0.35	0.09	0.39	0.11	0.35
Germany	0.08	0.59	0.06	0.61	0.08	0.59
UK	0.10	0.36	0.08	0.40	0.10	0.36
Brazil	0.06	0.71	0.06	0.73	0.06	0.71
Russia	0.06	0.82	0.06	0.83	0.06	0.82
South Africa	0.10	0.40	0.09	0.44	0.09	0.40
China	0.08	0.59	0.13	0.62	0.08	0.59
India	0.09	0.56	0.10	0.59	0.09	0.56

, which displays the values of average portfolio weights (W) and hedging efficiency ratios across different quantiles (0.05, 0.5, 0.95).

For the minimum connectivity portfolio, we examine the average portfolio weights for the G7 and BRICS stock markets across various quantile levels. Portfolio weights vary between 6% and 10% at the lower tail level and between 6% and 11% at the upper tail, giving the G7 stock markets a combined average weight of 62% for these two quantiles. At the median, weights range from 6% to 13%, with a combined average weighting of 55% for the G7 stock markets. Among the different stock markets, Canada has the highest weighting in the extreme quantiles, while Japan has the highest weighting at the median.

In terms of hedge effectiveness ratios, the results of the minimum connectivity portfolio (MCP) method at the median suggest that if we invested on average 8% in the US stock market, 6% in France’s market, 6% in Italy’s market, 12% in Japan’s market, 9% in Canada’s market, 6% in Germany’s market, and 8% in the UK’s market, then the volatility of each asset within this portfolio would be statistically significantly decreased by 47%, 59%, 64%, 60%, 39%, 61%, and 40%, respectively.

Adopting the MCP approach at the lower quantile level, it is suggested that the average allocation in various assets be distributed as follows: 9% in the US market, 8% in the French market, 7% in the Italian market, 10% in the Japanese market, 10% in the Canadian market, 8% in the German market, and 10% in the British market. This distribution would lead to a notable statistical decrease in the volatility of each asset in the portfolio by 43%, 56%, 62%, 57%, 35%, 59%, and 36%, respectively.

We can also see that hedging effectiveness ratios vary depending on quantile. For most countries, hedge effectiveness ratios are slightly higher at the 0.5 quantile, suggesting better hedging performance in average market conditions.

The hedging effectiveness (HE) of the G7 countries (Italy, Canada, USA, Japan, France, Germany, and the UK) shows varying performances. Germany, France, and Italy exhibit higher and more stable HE. Germany maintains a high and stable coverage efficiency (HE) around 0.59 to 0.61. Italy has a high HE, around 0.62 to 0.64, indicating robust coverage performance. Japan shows a slight variation in hedging effectiveness but remains high overall (0.57 to 0.60). The USA’s Hedging Effectiveness is stable around 0.43 to 0.47 for all quantiles, indicating relatively consistent hedging performance across different market conditions. On the other hand, Canada has lower HE values, around 0.35 to 0.39, indicating less effective hedging compared to other countries.

The BRICS countries (Brazil, Russia, South Africa, China, and India) also show varied performance in terms of hedging effectiveness (HE), with Russia and Brazil having the highest HE; Russia holds the highest hedging effectiveness (HE) value among all countries, hovering around 0.82 to 0.83. Brazil has a very high hedging efficiency with HE around 0.71 to 0.73. On the other hand, South Africa has lower HE, like Canada and the United Kingdom.

The findings from the MCP approach highlight the strategic role of connectivity-informed portfolio construction in enhancing risk management. G7 markets, with relatively lower portfolio weights but consistently high hedging effectiveness, serve as reliable anchors that stabilize the portfolio across different market conditions. BRICS markets, while showing high hedging efficiency in certain cases (notably Russia and Brazil), display more variability, reflecting their higher exposure to market-specific shocks. The dependence of hedge effectiveness on quantile levels illustrates the adaptability of the MCP method to both extreme and average market scenarios, making it particularly suitable for tail risk mitigation.

The results of this analysis indicate that the MCP method can be effectively used to construct high-performance investment portfolios for the G7 and BRICS stock markets. Portfolios constructed using this method are generally diversified and efficient, with high hedging efficiency ratios.

Examining the connectedness between financial assets is a crucial step in building an optimal investment strategy. Based on the connectedness results, the investor can construct an optimal portfolio. In our case, the results indicate that the least connected stock markets, such as Brazil and China under normal market conditions and Brazil and South Africa during bullish and bearish markets, are considered diversification assets. Indeed, in times of crisis and extreme shocks, these assets are only weakly affected. Therefore, when constructing a portfolio, the investor should include Chinese equities under normal market conditions, and during periods of extreme stress, should add Brazilian and South African equities. These assets help absorb the decline of other portfolio components, and potential losses can be offset thanks to their low level of connectedness.

Furthermore, the connectedness results provide a general overview of optimal portfolio management strategies. However, to deepen the analysis and propose a truly optimal investment strategy, we apply the minimum connectedness portfolios (MCoP) approach. This method, in contrast, aims to decrease pairwise connectedness, thereby limiting bilateral externalities between stock markets.

We compute the average portfolio weights across the 12 stock markets of the G7 and BRICS countries using the three market conditions: bear market, normal market, and bull market. In bear and bull markets, the portfolio weightings suggest allocating 62% to G7 stock markets to implement an effective investment strategy. In contrast, in a normal market, it is recommended to allocate only 55% to G7 stock markets, indicating that, in this context, they do not represent solid diversification assets.

More specifically, China has the highest weightings according to the normal and bull markets, confirming its role as the most effective asset for portfolio diversification and risk minimization. In comparison, Canada has the highest weighting according to the bear market. Based on these findings, investors are advised to allocate their capital to the least connected stock indices to minimize downside risk.

G7 markets benefit from higher liquidity, deeper market structure, and well-developed derivative instruments—factors that enhance the availability and effectiveness of traditional hedging tools such as gold. In contrast, BRICS markets, being more segmented, exposed to structural instability, and less integrated, tend to exhibit higher correlations and less reliable hedging outcomes.

Taken together, the comparative findings from both our study and prior research such as Izadi and Hassan (2018) support the view that structural market characteristics and asset-specific hedging properties drive the consistently higher hedging effectiveness observed in G7 portfolios compared to those of the BRICS.

5. Conclusions

This study focuses on quantile market risk between BRICS and G7 stock markets to emphasize the connectedness of returns at the middle, lower, and upper quantiles using a dynamic connectedness approach based on the newly developed QVAR by Ando et al. (2022) and Chatziantoniou et al. (2022) over a period from 1 January 2000 to 22 January 2024 that covered many financial shocks and events, such as the financial crisis 2008, the sovereign debt crisis, the COVID-19 pandemic, and the recent Russo-Ukrainian conflict, all of which have impacted global economic issues.

The principal findings from both static and dynamic connectedness analyses reveal that return connectedness is determined by the magnitude of the shock. It should be noted that shock transmissions in the upper and lower tails have a more substantial impact on the connectedness system compared to median shocks. Consequently, this results in the dynamic variation of connectedness measures in the tails being different from those at the median. Additionally, there is a difference in the total connectedness index over time under bear and bull market conditions. At the tails of the distribution, the connectedness between the G7 and BRICS stock markets remains substantial, with the G7 markets, apart from Japan, acting as principal net transmitters of tail-risk spillovers, while the BRICS markets consistently emerge as net receivers of contagion and volatility shocks.

By dividing the total net directional connectedness into short-, medium-, and long-term dynamics, we observe that short-term dynamics are predominantly responsible for the market being a net transmitter or receiver of shocks during the median and upper extreme quantiles. But the long-term can be considered responsible for a net transmitter of shocks at the lower quantile level.

In terms of investment policy, under normal market conditions in G7 and BRICS countries, our results highlight a segmentation across markets. This implies that investors can achieve diversification and, consequently, enhance their hedging strategies through exposure to Asian markets, particularly the Chinese market.

During periods of extreme market conditions, whether in bullish or bearish phases, a strong degree of interconnectedness is observed across markets. Our results suggest that the stock markets of the G7 and BRICS countries are highly integrated in both regimes.

Considering that market linkages are typically stronger during times of financial stress compared to calm periods (Ang & Bekaert, 2002), it is understandable that extremely low quantiles display a heightened level of connectedness. However, the variation in TCI between extreme quantiles (both lower and higher) and the median indicates that the degree of connectedness escalates with the severity of the shock, encompassing both extremely positive and negative events. This finding aligns with previous research on contagion, such as Mensi et al. (2023), which has demonstrated that extreme events can significantly impact both the upper and lower quantiles.

The MCP analysis demonstrates the effectiveness of constructing portfolios based on connectivity patterns to mitigate systemic risk. The prominence of G7 markets in portfolio weights, combined with their high hedging effectiveness, underscores their dual role as both central nodes in global market dynamics and stabilizing components in a diversified portfolio. While some BRICS markets, particularly Russia and Brazil, exhibit very strong hedging efficiency, their overall contribution to portfolio stability is moderated by lower average weights and heterogeneous volatility. The variation of hedge effectiveness across quantiles indicates that the MCP method successfully adjusts allocations according to different market conditions, providing robust protection against extreme market movements. These findings suggest that portfolios built using the MCP approach can achieve both high diversification and superior risk-adjusted performance across G7 and BRICS stock markets.