Can Including Cryptocurrencies with Stocks in Portfolios Enhance Returns in Small Economies? An Analysis of Fiji’s Stock Market
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Basic Knowledge of the Utilized Portfolio Models
3.2. Data Description
4. Experimental Results
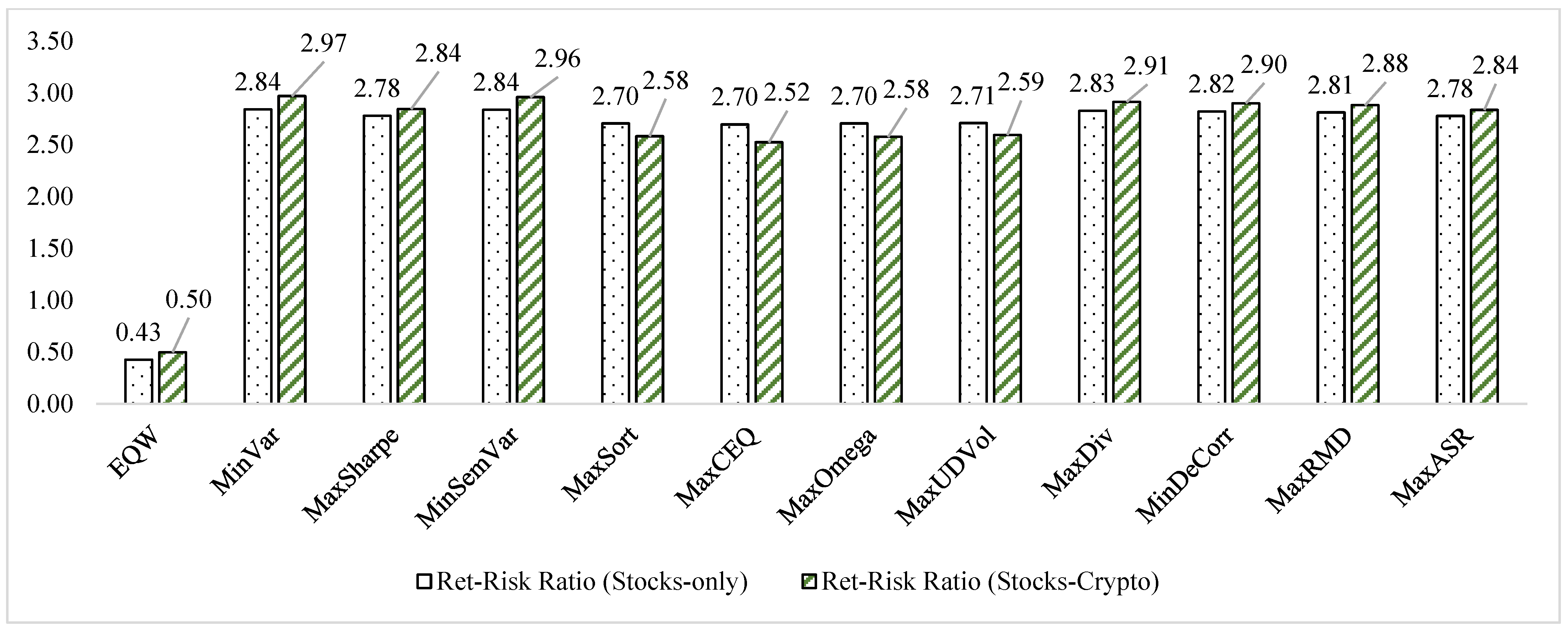
4.1. The Stocks-Only Versus Stocks-Cryptocurrencies Portfolios
4.2. Stocks-Cryptocurrencies Portfolio: Out-of-Sample Forecast Analysis
4.3. Stocks-Cryptocurrencies Portfolio: Monte Carlo Simulation Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Ticker | Mean | Standard Error | Median | Mode | Standard Deviation | Sample Variance | Kurtosis | Skewness | Range | Minimum | Maximum | Sum |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APP | 0.00881 | 0.00532 | 0.00000 | 0.00000 | 0.04480 | 0.00201 | 14.42227 | 2.49697 | 0.35398 | −0.09237 | 0.26161 | 0.62527 |
| ATH | −0.00779 | 0.00685 | 0.00000 | 0.00000 | 0.05775 | 0.00333 | 2.41866 | −0.35220 | 0.36593 | −0.19637 | 0.16956 | −0.55339 |
| BCN | 0.00485 | 0.00526 | 0.00000 | 0.00000 | 0.04431 | 0.00196 | 4.52847 | 0.75084 | 0.29380 | −0.14630 | 0.14750 | 0.34421 |
| CFL | 0.00044 | 0.00164 | 0.00000 | 0.00000 | 0.01382 | 0.00019 | 26.77761 | 3.84237 | 0.12586 | −0.03489 | 0.09097 | 0.03092 |
| FBL | 0.00607 | 0.00695 | 0.00000 | 0.00000 | 0.05857 | 0.00343 | 14.23349 | 0.29018 | 0.54382 | −0.27871 | 0.26511 | 0.43078 |
| FHL | −0.00856 | 0.04942 | −0.00976 | 0.00000 | 0.41644 | 0.17343 | 29.05617 | −0.26836 | 4.71966 | −2.40795 | 2.31172 | −0.60799 |
| FIL | 0.03372 | 0.00637 | 0.01380 | 0.00000 | 0.05370 | 0.00288 | 1.59472 | 1.26046 | 0.28535 | −0.07128 | 0.21407 | 2.39393 |
| FMF | −0.00287 | 0.01079 | 0.00000 | 0.00000 | 0.09094 | 0.00827 | 29.59665 | 2.33435 | 0.99330 | −0.41567 | 0.57763 | −0.20375 |
| FTV | −0.02492 | 0.01161 | 0.00000 | 0.00000 | 0.09780 | 0.00956 | 7.43202 | −0.31108 | 0.78885 | −0.39354 | 0.39531 | −1.76929 |
| KFL | 0.00363 | 0.00691 | −0.00858 | 0.00000 | 0.05819 | 0.00339 | 2.82057 | 0.57758 | 0.35148 | −0.18443 | 0.16705 | 0.25783 |
| KGF | 0.00546 | 0.00254 | 0.00000 | 0.00000 | 0.02143 | 0.00046 | 26.73681 | 4.91766 | 0.14310 | 0.00000 | 0.14310 | 0.38745 |
| PBP | 0.01572 | 0.00717 | 0.00000 | 0.00000 | 0.06039 | 0.00365 | 17.89386 | 3.59763 | 0.49627 | −0.12921 | 0.36706 | 1.11640 |
| PDM | 0.00665 | 0.00604 | 0.00000 | 0.00000 | 0.05094 | 0.00259 | 5.46851 | 1.96378 | 0.30316 | −0.09309 | 0.21007 | 0.47191 |
| RBG | 0.00849 | 0.00783 | 0.00000 | 0.00000 | 0.06598 | 0.00435 | 36.40201 | 5.44725 | 0.55593 | −0.08264 | 0.47329 | 0.60309 |
| RCF | 0.00244 | 0.00438 | 0.00000 | 0.00000 | 0.03687 | 0.00136 | 32.18154 | 4.56608 | 0.35341 | −0.09963 | 0.25378 | 0.17290 |
| TTS | 0.00337 | 0.00446 | 0.00000 | 0.00000 | 0.03759 | 0.00141 | 29.19315 | 4.29627 | 0.35341 | −0.09963 | 0.25378 | 0.23944 |
| VBH | 0.00697 | 0.00569 | 0.00000 | 0.00000 | 0.04798 | 0.00230 | 11.98466 | 2.55580 | 0.36108 | −0.10976 | 0.25131 | 0.49508 |
| VIL | −0.00312 | 0.00306 | 0.00000 | 0.00000 | 0.02582 | 0.00067 | 8.57772 | −0.79285 | 0.19783 | −0.11778 | 0.08004 | −0.22143 |
| Ticker | APP | ATH | BCN | CFL | FBL | FHL | FIL | FMF | FTV | KFL | KGF | PBP | PDM | RBG | RCF | TTS | VBH | VIL |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APP | 1.0000 | |||||||||||||||||
| ATH | 0.0654 | 1.0000 | ||||||||||||||||
| BCN | 0.1657 | 0.0416 | 1.0000 | |||||||||||||||
| CFL | 0.5825 | 0.2299 | −0.0397 | 1.0000 | ||||||||||||||
| FBL | 0.3841 | 0.1264 | −0.0331 | 0.0925 | 1.0000 | |||||||||||||
| FHL | −0.0298 | 0.0767 | 0.0431 | 0.1009 | −0.2065 | 1.0000 | ||||||||||||
| FIL | −0.0561 | −0.1046 | −0.0462 | −0.0318 | −0.0373 | 0.0095 | 1.0000 | |||||||||||
| FMF | −0.1464 | 0.0404 | 0.0618 | 0.0038 | −0.3365 | 0.1307 | 0.1547 | 1.0000 | ||||||||||
| FTV | −0.0304 | 0.1051 | 0.0070 | 0.2165 | 0.0639 | −0.0697 | −0.0558 | 0.0269 | 1.0000 | |||||||||
| KFL | −0.0027 | 0.0061 | 0.1968 | −0.0655 | 0.0552 | −0.1019 | −0.1079 | 0.1339 | 0.1167 | 1.0000 | ||||||||
| KGF | −0.0458 | 0.0060 | 0.2502 | −0.0939 | 0.0067 | −0.0902 | −0.1078 | −0.0241 | −0.1905 | 0.0065 | 1.0000 | |||||||
| PBP | 0.1959 | −0.0358 | −0.0143 | 0.0380 | 0.0750 | −0.0065 | −0.0090 | −0.0807 | 0.0018 | 0.0037 | 0.0539 | 1.0000 | ||||||
| PDM | 0.0084 | −0.1353 | 0.0380 | 0.0964 | 0.0381 | −0.0398 | −0.1060 | −0.0180 | 0.1074 | 0.1265 | −0.0717 | −0.0275 | 1.0000 | |||||
| RBG | −0.0460 | 0.1571 | 0.0935 | 0.0361 | 0.0964 | −0.0741 | −0.0270 | −0.0213 | 0.2379 | 0.1220 | −0.0433 | −0.0425 | 0.1228 | 1.0000 | ||||
| RCF | 0.0637 | −0.0983 | 0.0103 | −0.0194 | −0.0424 | 0.0076 | 0.0671 | 0.0334 | 0.0562 | 0.0653 | −0.0508 | −0.0181 | 0.0087 | 0.0920 | 1.0000 | |||
| TTS | 0.0575 | −0.0800 | 0.0309 | 0.0088 | −0.0442 | 0.0080 | 0.0500 | 0.0361 | 0.0652 | 0.0543 | −0.0562 | −0.0244 | 0.0832 | 0.0869 | 0.9790 | 1.0000 | ||
| VBH | 0.0604 | −0.0680 | 0.0072 | 0.0013 | 0.0965 | −0.0043 | 0.0065 | 0.0706 | 0.0594 | 0.2184 | 0.0084 | 0.0076 | 0.1113 | −0.0197 | 0.0833 | 0.0780 | 1.0000 | |
| VIL | 0.0732 | 0.0178 | −0.0354 | 0.0285 | 0.0087 | −0.0553 | −0.0708 | −0.0268 | 0.0871 | 0.1060 | −0.0110 | 0.0157 | −0.0247 | −0.0415 | −0.4702 | −0.4581 | −0.1195 | 1.0000 |
| Ticker | APP | ATH | BCN | CFL | FBL | FHL | FIL | FMF | FTV | KFL | KGF | PBP | PDM | RBG | RCF | TTS | VBH | VIL |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APP | 0.0241 | |||||||||||||||||
| ATH | 0.0020 | 0.0400 | ||||||||||||||||
| BCN | 0.0039 | 0.0013 | 0.0236 | |||||||||||||||
| CFL | 0.0043 | 0.0022 | −0.0003 | 0.0023 | ||||||||||||||
| FBL | 0.0121 | 0.0051 | −0.0010 | 0.0009 | 0.0412 | |||||||||||||
| FHL | −0.0067 | 0.0221 | 0.0095 | 0.0070 | −0.0604 | 2.0811 | ||||||||||||
| FIL | −0.0016 | −0.0039 | −0.0013 | −0.0003 | −0.0014 | 0.0025 | 0.0346 | |||||||||||
| FMF | −0.0072 | 0.0025 | 0.0030 | 0.0001 | −0.0215 | 0.0594 | 0.0091 | 0.0993 | ||||||||||
| FTV | −0.0016 | 0.0071 | 0.0004 | 0.0035 | 0.0044 | −0.0341 | −0.0035 | 0.0029 | 0.1148 | |||||||||
| KFL | −0.0001 | 0.0002 | 0.0061 | −0.0006 | 0.0023 | −0.0296 | −0.0040 | 0.0085 | 0.0080 | 0.0406 | ||||||||
| KGF | −0.0005 | 0.0001 | 0.0029 | −0.0003 | 0.0001 | −0.0097 | −0.0015 | −0.0006 | −0.0048 | 0.0001 | 0.0055 | |||||||
| PBP | 0.0064 | −0.0015 | −0.0005 | 0.0004 | 0.0032 | −0.0019 | −0.0003 | −0.0053 | 0.0001 | 0.0002 | 0.0008 | 0.0438 | ||||||
| PDM | 0.0002 | −0.0048 | 0.0010 | 0.0008 | 0.0014 | −0.0101 | −0.0035 | −0.0010 | 0.0064 | 0.0045 | −0.0009 | −0.0010 | 0.0311 | |||||
| RBG | −0.0016 | 0.0072 | 0.0033 | 0.0004 | 0.0045 | −0.0244 | −0.0011 | −0.0015 | 0.0184 | 0.0056 | −0.0007 | −0.0020 | 0.0050 | 0.0522 | ||||
| RCF | 0.0013 | −0.0025 | 0.0002 | −0.0001 | −0.0011 | 0.0014 | 0.0016 | 0.0013 | 0.0024 | 0.0017 | −0.0005 | −0.0005 | 0.0002 | 0.0027 | 0.0163 | |||
| TTS | 0.0012 | −0.0021 | 0.0006 | 0.0001 | −0.0012 | 0.0015 | 0.0012 | 0.0015 | 0.0029 | 0.0014 | −0.0005 | −0.0007 | 0.0019 | 0.0026 | 0.0163 | 0.0170 | ||
| VBH | 0.0016 | −0.0023 | 0.0002 | 0.0000 | 0.0033 | −0.0010 | 0.0002 | 0.0037 | 0.0033 | 0.0073 | 0.0001 | 0.0003 | 0.0033 | −0.0007 | 0.0018 | 0.0017 | 0.0276 | |
| VIL | 0.0010 | 0.0003 | −0.0005 | 0.0001 | 0.0002 | −0.0071 | −0.0012 | −0.0008 | 0.0026 | 0.0019 | −0.0001 | 0.0003 | −0.0004 | −0.0008 | −0.0054 | −0.0053 | −0.0018 | 0.0080 |
| Ticker | Mean | Standard Error | Median | Mode | Standard Deviation | Sample Variance | Kurtosis | Skewness | Range | Minimum | Maximum | Sum |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APP | 0.0089 | 0.0054 | 0.0000 | 0.0000 | 0.0451 | 0.0020 | 14.1811 | 2.4737 | 0.3540 | −0.0924 | 0.2616 | 0.6253 |
| ATH | −0.0083 | 0.0069 | 0.0000 | 0.0000 | 0.0580 | 0.0034 | 2.3988 | −0.3283 | 0.3659 | −0.1964 | 0.1696 | −0.5842 |
| BCN | 0.0043 | 0.0053 | 0.0000 | 0.0000 | 0.0444 | 0.0020 | 4.6189 | 0.7860 | 0.2938 | −0.1463 | 0.1475 | 0.3016 |
| CFL | 0.0002 | 0.0016 | 0.0000 | 0.0000 | 0.0138 | 0.0002 | 27.8076 | 3.9577 | 0.1259 | −0.0349 | 0.0910 | 0.0145 |
| FBL | 0.0062 | 0.0071 | 0.0000 | 0.0000 | 0.0590 | 0.0035 | 14.0082 | 0.2838 | 0.5438 | −0.2787 | 0.2651 | 0.4308 |
| FHL | −0.0087 | 0.0501 | −0.0098 | 0.0000 | 0.4194 | 0.1759 | 28.6339 | −0.2656 | 4.7197 | −2.4079 | 2.3117 | −0.6080 |
| FIL | 0.0342 | 0.0064 | 0.0151 | 0.0000 | 0.0539 | 0.0029 | 1.5349 | 1.2388 | 0.2854 | −0.0713 | 0.2141 | 2.3939 |
| FMF | −0.0030 | 0.0109 | 0.0000 | 0.0000 | 0.0916 | 0.0084 | 29.2021 | 2.3252 | 0.9933 | −0.4157 | 0.5776 | −0.2129 |
| FTV | −0.0256 | 0.0118 | 0.0000 | 0.0000 | 0.0983 | 0.0097 | 7.3537 | −0.2910 | 0.7888 | −0.3935 | 0.3953 | −1.7918 |
| KFL | 0.0040 | 0.0070 | −0.0082 | 0.0000 | 0.0585 | 0.0034 | 2.7544 | 0.5590 | 0.3515 | −0.1844 | 0.1671 | 0.2776 |
| KGF | 0.0055 | 0.0026 | 0.0000 | 0.0000 | 0.0216 | 0.0005 | 26.3253 | 4.8804 | 0.1431 | 0.0000 | 0.1431 | 0.3874 |
| PBP | 0.0159 | 0.0073 | 0.0000 | 0.0000 | 0.0608 | 0.0037 | 17.6021 | 3.5674 | 0.4963 | −0.1292 | 0.3671 | 1.1164 |
| PDM | 0.0044 | 0.0057 | 0.0000 | 0.0000 | 0.0477 | 0.0023 | 6.8212 | 2.0534 | 0.3032 | −0.0931 | 0.2101 | 0.3102 |
| RBG | 0.0086 | 0.0079 | 0.0000 | 0.0000 | 0.0664 | 0.0044 | 35.8606 | 5.4068 | 0.5559 | −0.0826 | 0.4733 | 0.6031 |
| RCF | 0.0025 | 0.0044 | 0.0000 | 0.0000 | 0.0371 | 0.0014 | 31.7047 | 4.5328 | 0.3534 | −0.0996 | 0.2538 | 0.1729 |
| TTS | 0.0071 | 0.0058 | 0.0000 | 0.0000 | 0.0483 | 0.0023 | 11.7715 | 2.5328 | 0.3611 | −0.1098 | 0.2513 | 0.4960 |
| VBH | −0.0032 | 0.0031 | 0.0000 | 0.0000 | 0.0260 | 0.0007 | 8.4220 | −0.7825 | 0.1978 | −0.1178 | 0.0800 | −0.2214 |
| VIL | −0.0008 | 0.0082 | 0.0000 | 0.0000 | 0.0682 | 0.0047 | 10.6244 | 0.5281 | 0.5570 | −0.2806 | 0.2764 | −0.0590 |
| BTC | 0.0344 | 0.0220 | 0.0308 | - | 0.1839 | 0.0338 | 0.1151 | −0.2131 | 0.8648 | −0.4743 | 0.3905 | 2.4091 |
| ETH | 0.0381 | 0.0283 | 0.0261 | - | 0.2367 | 0.0560 | 0.0564 | −0.0438 | 1.1767 | −0.5988 | 0.5779 | 2.6684 |
| ALG | −0.0114 | 0.0394 | −0.0460 | - | 0.3299 | 0.1088 | 3.1597 | 0.9222 | 2.1239 | −0.7702 | 1.3537 | −0.7991 |
| ADA | 0.0363 | 0.0399 | −0.0374 | - | 0.3335 | 0.1112 | 3.6756 | 1.6692 | 1.7752 | −0.4421 | 1.3331 | 2.5429 |
| HBA | 0.0073 | 0.0450 | −0.0334 | - | 0.3762 | 0.1415 | 3.0586 | 1.0880 | 2.1880 | −0.8911 | 1.2968 | 0.5090 |
| QNT | 0.0423 | 0.0338 | 0.0000 | - | 0.2824 | 0.0798 | 1.2999 | 0.6498 | 1.6175 | −0.6128 | 1.0047 | 2.9585 |
| XLM | 0.0190 | 0.0396 | −0.0237 | - | 0.3314 | 0.1098 | 10.3836 | 2.5090 | 2.1927 | −0.4576 | 1.7351 | 1.3313 |
| XDC | 0.0689 | 0.0509 | −0.0017 | - | 0.4260 | 0.1815 | 4.0744 | 1.6462 | 2.2352 | −0.6159 | 1.6193 | 4.8228 |
| XRP | 0.0308 | 0.0422 | −0.0081 | - | 0.3534 | 0.1249 | 4.1655 | 0.9939 | 2.4457 | −1.1060 | 1.3397 | 2.1561 |
| Ticker | APP | ATH | BCN | CFL | FBL | FHL | FIL | FMF | FTV | KFL | KGF | PBP | PDM | RBG | RCF | TTS | VBH | VIL | BTC | ETH | ALG | ADA | HBA | QNT | XLM | XDC | XRP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APP | 1.000 | ||||||||||||||||||||||||||
| ATH | 0.068 | 1.000 | |||||||||||||||||||||||||
| BCN | 0.169 | 0.034 | 1.000 | −0.055 | |||||||||||||||||||||||
| CFL | 0.592 | 0.222 | −0.055 | 1.000 | |||||||||||||||||||||||
| FBL | 0.384 | 0.128 | −0.032 | 0.095 | 1.000 | ||||||||||||||||||||||
| FHL | −0.030 | 0.077 | 0.043 | 0.102 | −0.206 | 1.000 | |||||||||||||||||||||
| FIL | −0.058 | −0.099 | −0.039 | −0.022 | −0.038 | 0.010 | 1.000 | ||||||||||||||||||||
| FMF | −0.146 | 0.039 | 0.061 | 0.002 | −0.336 | 0.131 | 0.156 | 1.000 | |||||||||||||||||||
| FTV | −0.029 | 0.101 | 0.001 | 0.211 | 0.065 | −0.070 | −0.052 | 0.026 | 1.000 | ||||||||||||||||||
| KFL | −0.004 | 0.010 | 0.203 | −0.059 | 0.055 | −0.102 | −0.112 | 0.135 | 0.120 | 1.000 | |||||||||||||||||
| KGF | −0.047 | 0.008 | 0.255 | −0.091 | 0.006 | −0.090 | −0.111 | −0.024 | −0.189 | 0.005 | 1.000 | ||||||||||||||||
| PBP | 0.195 | −0.033 | −0.011 | 0.043 | 0.075 | −0.006 | −0.011 | −0.080 | 0.004 | 0.002 | 0.053 | 1.000 | |||||||||||||||
| PDM | 0.018 | −0.178 | 0.001 | 0.049 | 0.046 | −0.044 | −0.084 | −0.026 | 0.093 | 0.155 | −0.065 | −0.017 | 1.000 | ||||||||||||||
| RBG | −0.046 | 0.159 | 0.096 | 0.039 | 0.096 | −0.074 | −0.028 | −0.021 | 0.239 | 0.121 | −0.044 | −0.043 | 0.138 | 1.000 | |||||||||||||
| RCF | 0.064 | −0.098 | 0.011 | −0.018 | −0.043 | 0.008 | 0.067 | 0.034 | 0.057 | 0.065 | −0.051 | −0.018 | 0.013 | 0.092 | 1.000 | ||||||||||||
| TTS | 0.060 | −0.067 | 0.009 | 0.004 | 0.096 | −0.004 | 0.005 | 0.071 | 0.060 | 0.218 | 0.008 | 0.007 | 0.127 | −0.020 | 0.083 | 1.000 | |||||||||||
| VBH | 0.074 | 0.017 | −0.037 | 0.027 | 0.009 | −0.055 | −0.070 | −0.027 | 0.086 | 0.107 | −0.011 | 0.016 | −0.032 | −0.041 | −0.470 | −0.119 | 1.000 | ||||||||||
| VIL | 0.034 | 0.108 | 0.106 | 0.014 | 0.081 | 0.010 | −0.066 | −0.023 | 0.112 | −0.312 | 0.105 | 0.000 | −0.075 | 0.267 | −0.151 | −0.341 | −0.022 | 1.000 | |||||||||
| BTC | −0.053 | −0.173 | −0.027 | −0.067 | −0.117 | −0.042 | 0.235 | 0.108 | 0.002 | 0.166 | −0.013 | 0.063 | −0.063 | −0.173 | 0.087 | 0.214 | 0.047 | −0.072 | 1.000 | ||||||||
| ETH | −0.037 | −0.107 | −0.045 | −0.042 | −0.159 | −0.101 | 0.142 | 0.097 | 0.044 | −0.040 | −0.084 | 0.036 | −0.011 | −0.136 | 0.104 | 0.152 | 0.047 | −0.081 | 0.778 | 1.000 | |||||||
| ALG | 0.201 | −0.102 | 0.035 | 0.057 | −0.069 | −0.041 | 0.082 | 0.058 | −0.004 | −0.007 | −0.084 | 0.087 | −0.152 | −0.050 | 0.045 | 0.120 | 0.108 | 0.014 | 0.614 | 0.667 | 1.000 | ||||||
| ADA | 0.004 | −0.096 | 0.069 | −0.067 | −0.066 | −0.087 | 0.237 | 0.037 | 0.003 | 0.164 | −0.085 | −0.035 | −0.023 | −0.089 | 0.165 | 0.157 | 0.105 | −0.148 | 0.603 | 0.635 | 0.732 | 1.000 | |||||
| HBA | 0.138 | −0.131 | 0.133 | 0.035 | −0.148 | −0.006 | 0.078 | 0.085 | −0.060 | −0.037 | 0.119 | 0.042 | −0.084 | −0.295 | −0.015 | 0.057 | 0.157 | −0.175 | 0.556 | 0.596 | 0.752 | 0.547 | 1.000 | ||||
| QNT | −0.014 | −0.203 | 0.126 | 0.073 | −0.247 | 0.083 | 0.186 | 0.041 | −0.129 | −0.104 | −0.034 | 0.000 | −0.085 | −0.108 | −0.013 | −0.068 | 0.182 | −0.085 | 0.419 | 0.508 | 0.517 | 0.433 | 0.524 | 1.000 | |||
| XLM | −0.106 | −0.222 | −0.113 | −0.137 | −0.081 | −0.058 | 0.023 | 0.020 | −0.004 | 0.112 | −0.126 | −0.034 | −0.002 | −0.138 | 0.059 | 0.286 | 0.086 | −0.302 | 0.585 | 0.661 | 0.750 | 0.754 | 0.584 | 0.448 | 1.000 | ||
| XDC | 0.073 | −0.185 | 0.008 | −0.034 | −0.016 | −0.091 | 0.249 | −0.075 | −0.015 | 0.001 | 0.021 | −0.045 | 0.022 | −0.066 | 0.094 | 0.002 | 0.048 | −0.193 | 0.356 | 0.405 | 0.440 | 0.594 | 0.262 | 0.330 | 0.480 | 1.000 | |
| XRP | −0.123 | −0.183 | −0.013 | −0.184 | −0.069 | −0.065 | −0.096 | −0.003 | −0.057 | 0.062 | 0.038 | −0.020 | 0.019 | −0.199 | 0.029 | 0.296 | −0.024 | −0.376 | 0.433 | 0.595 | 0.594 | 0.549 | 0.511 | 0.413 | 0.846 | 0.481 | 1.000 |
| Ticker | APP | ATH | BCN | CFL | FBL | FHL | FIL | FMF | FTV | KFL | KGF | PBP | PDM | RBG | RCF | TTS | VBH | VIL | BTC | ETH | ALG | ADA | HBA | QNT | XLM | XDC | XRP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APP | 0.024 | ||||||||||||||||||||||||||
| ATH | 0.002 | 0.040 | |||||||||||||||||||||||||
| BCN | 0.004 | 0.001 | 0.024 | ||||||||||||||||||||||||
| CFL | 0.004 | 0.002 | 0.000 | 0.002 | |||||||||||||||||||||||
| FBL | 0.012 | 0.005 | −0.001 | 0.001 | 0.042 | ||||||||||||||||||||||
| FHL | −0.007 | 0.022 | 0.010 | 0.007 | −0.061 | 2.111 | |||||||||||||||||||||
| FIL | −0.002 | −0.004 | −0.001 | 0.000 | −0.001 | 0.003 | 0.035 | ||||||||||||||||||||
| FMF | −0.007 | 0.003 | 0.003 | 0.000 | −0.022 | 0.060 | 0.009 | 0.101 | |||||||||||||||||||
| FTV | −0.002 | 0.007 | 0.000 | 0.003 | 0.005 | −0.035 | −0.003 | 0.003 | 0.116 | ||||||||||||||||||
| KFL | 0.000 | 0.000 | 0.006 | −0.001 | 0.002 | −0.030 | −0.004 | 0.009 | 0.008 | 0.041 | |||||||||||||||||
| KGF | −0.001 | 0.000 | 0.003 | 0.000 | 0.000 | −0.010 | −0.002 | −0.001 | −0.005 | 0.000 | 0.006 | ||||||||||||||||
| PBP | 0.006 | −0.001 | 0.000 | 0.000 | 0.003 | −0.002 | 0.000 | −0.005 | 0.000 | 0.000 | 0.001 | 0.044 | |||||||||||||||
| PDM | 0.000 | −0.006 | 0.000 | 0.000 | 0.002 | −0.011 | −0.003 | −0.001 | 0.005 | 0.005 | −0.001 | −0.001 | 0.027 | ||||||||||||||
| RBG | −0.002 | 0.007 | 0.003 | 0.000 | 0.005 | −0.025 | −0.001 | −0.002 | 0.019 | 0.006 | −0.001 | −0.002 | 0.005 | 0.053 | |||||||||||||
| RCF | 0.001 | −0.003 | 0.000 | 0.000 | −0.001 | 0.001 | 0.002 | 0.001 | 0.002 | 0.002 | 0.000 | 0.000 | 0.000 | 0.003 | 0.017 | ||||||||||||
| TTS | 0.002 | −0.002 | 0.000 | 0.000 | 0.003 | −0.001 | 0.000 | 0.004 | 0.003 | 0.007 | 0.000 | 0.000 | 0.004 | −0.001 | 0.002 | 0.028 | |||||||||||
| VBH | 0.001 | 0.000 | −0.001 | 0.000 | 0.000 | −0.007 | −0.001 | −0.001 | 0.003 | 0.002 | 0.000 | 0.000 | 0.000 | −0.001 | −0.005 | −0.002 | 0.008 | ||||||||||
| VIL | 0.001 | 0.005 | 0.004 | 0.000 | 0.004 | 0.004 | −0.003 | −0.002 | 0.009 | −0.015 | 0.002 | 0.000 | −0.003 | 0.015 | −0.005 | −0.013 | 0.000 | 0.056 | |||||||||
| BTC | −0.005 | −0.022 | −0.003 | −0.002 | −0.015 | −0.039 | 0.028 | 0.022 | 0.000 | 0.021 | −0.001 | 0.009 | −0.007 | −0.025 | 0.007 | 0.023 | 0.003 | −0.011 | 0.406 | ||||||||
| ETH | −0.005 | −0.018 | −0.006 | −0.002 | −0.027 | −0.120 | 0.022 | 0.025 | 0.012 | −0.007 | −0.005 | 0.006 | −0.002 | −0.026 | 0.011 | 0.021 | 0.004 | −0.016 | 0.407 | 0.672 | |||||||
| ALG | 0.036 | −0.023 | 0.006 | 0.003 | −0.016 | −0.069 | 0.018 | 0.021 | −0.002 | −0.002 | −0.007 | 0.021 | −0.029 | −0.013 | 0.007 | 0.023 | 0.011 | 0.004 | 0.447 | 0.625 | 1.306 | ||||||
| ADA | 0.001 | −0.022 | 0.012 | −0.004 | −0.016 | −0.146 | 0.051 | 0.014 | 0.001 | 0.038 | −0.007 | −0.008 | −0.004 | −0.024 | 0.024 | 0.030 | 0.011 | −0.040 | 0.443 | 0.601 | 0.966 | 1.334 | |||||
| HBA | 0.028 | −0.034 | 0.027 | 0.002 | −0.039 | −0.012 | 0.019 | 0.035 | −0.027 | −0.010 | 0.012 | 0.011 | −0.018 | −0.089 | −0.002 | 0.013 | 0.018 | −0.054 | 0.461 | 0.637 | 1.120 | 0.823 | 1.698 | ||||
| QNT | −0.002 | −0.040 | 0.019 | 0.003 | −0.049 | 0.118 | 0.034 | 0.013 | −0.043 | −0.021 | −0.003 | 0.000 | −0.014 | −0.024 | −0.002 | −0.011 | 0.016 | −0.020 | 0.261 | 0.408 | 0.578 | 0.489 | 0.668 | 0.957 | |||
| XLM | −0.019 | −0.051 | −0.020 | −0.008 | −0.019 | −0.098 | 0.005 | 0.007 | −0.002 | 0.026 | −0.011 | −0.008 | 0.000 | −0.037 | 0.009 | 0.055 | 0.009 | −0.082 | 0.428 | 0.622 | 0.984 | 1.000 | 0.874 | 0.503 | 1.318 | ||
| XDC | 0.017 | −0.055 | 0.002 | −0.002 | −0.005 | −0.194 | 0.069 | −0.035 | −0.008 | 0.000 | 0.002 | −0.014 | 0.005 | −0.022 | 0.018 | 0.000 | 0.006 | −0.067 | 0.334 | 0.490 | 0.741 | 1.012 | 0.503 | 0.477 | 0.813 | 2.178 | |
| XRP | −0.024 | −0.045 | −0.002 | −0.011 | −0.017 | −0.116 | −0.022 | −0.001 | −0.024 | 0.015 | 0.003 | −0.005 | 0.004 | −0.056 | 0.005 | 0.061 | −0.003 | −0.109 | 0.337 | 0.597 | 0.831 | 0.776 | 0.816 | 0.494 | 1.188 | 0.869 | 1.499 |
| Ticker | Mean | Standard Error | Median | Mode | Standard Deviation | Sample Variance | Kurtosis | Skewness | Range | Minimum | Maximum | Sum |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APP | 0.0086 | 0.0040 | 0.0000 | 0.0000 | 0.0389 | 0.0015 | 19.8068 | 2.8738 | 0.3540 | −0.0924 | 0.2616 | 0.8106 |
| ATH | −0.0075 | 0.0052 | −0.0048 | 0.0000 | 0.0500 | 0.0025 | 4.2101 | −0.4319 | 0.3659 | −0.1964 | 0.1696 | −0.7014 |
| BCN | 0.0039 | 0.0039 | 0.0000 | 0.0000 | 0.0383 | 0.0015 | 7.1565 | 0.9412 | 0.2938 | −0.1463 | 0.1475 | 0.3627 |
| CFL | 0.0004 | 0.0012 | 0.0000 | 0.0000 | 0.0119 | 0.0001 | 37.3237 | 4.5075 | 0.1259 | −0.0349 | 0.0910 | 0.0370 |
| FBL | 0.0054 | 0.0052 | 0.0000 | 0.0000 | 0.0508 | 0.0026 | 19.4842 | 0.3743 | 0.5438 | −0.2787 | 0.2651 | 0.5041 |
| FHL | −0.0051 | 0.0373 | 0.0051 | 0.0000 | 0.3613 | 0.1306 | 38.7581 | −0.3363 | 4.7197 | −2.4079 | 2.3117 | −0.4807 |
| FIL | 0.0281 | 0.0049 | 0.0104 | 0.0000 | 0.0476 | 0.0023 | 3.2869 | 1.6868 | 0.2854 | −0.0713 | 0.2141 | 2.6395 |
| FMF | −0.0040 | 0.0082 | −0.0044 | 0.0000 | 0.0791 | 0.0063 | 39.2578 | 2.6940 | 0.9933 | −0.4157 | 0.5776 | −0.3742 |
| FTV | −0.0531 | 0.0359 | 0.0000 | 0.0000 | 0.3477 | 0.1209 | 35.6753 | −4.7873 | 3.6106 | −2.6532 | 0.9574 | −4.9903 |
| KFL | 0.0030 | 0.0052 | 0.0000 | 0.0000 | 0.0505 | 0.0025 | 4.6984 | 0.6997 | 0.3515 | −0.1844 | 0.1671 | 0.2853 |
| KGF | 0.0048 | 0.0019 | 0.0000 | 0.0000 | 0.0186 | 0.0003 | 36.2969 | 5.7043 | 0.1431 | 0.0000 | 0.1431 | 0.4525 |
| PBP | 0.0142 | 0.0054 | 0.0000 | 0.0000 | 0.0525 | 0.0028 | 24.6313 | 4.1935 | 0.4963 | −0.1292 | 0.3671 | 1.3305 |
| PDM | 0.0031 | 0.0042 | −0.0006 | 0.0000 | 0.0412 | 0.0017 | 10.2599 | 2.4511 | 0.3032 | −0.0931 | 0.2101 | 0.2958 |
| RBG | 0.0058 | 0.0059 | −0.0025 | 0.0000 | 0.0574 | 0.0033 | 48.8431 | 6.3128 | 0.5559 | −0.0826 | 0.4733 | 0.5428 |
| RCF | 0.0012 | 0.0033 | 0.0000 | 0.0000 | 0.0321 | 0.0010 | 43.2604 | 5.3091 | 0.3534 | −0.0996 | 0.2538 | 0.1082 |
| TTS | 0.0066 | 0.0043 | 0.0000 | 0.0000 | 0.0416 | 0.0017 | 16.6756 | 2.9533 | 0.3611 | −0.1098 | 0.2513 | 0.6194 |
| VBH | −0.0031 | 0.0023 | 0.0000 | 0.0000 | 0.0224 | 0.0005 | 12.1441 | −0.9126 | 0.1978 | −0.1178 | 0.0800 | −0.2898 |
| VIL | −0.0010 | 0.0061 | −0.0011 | 0.0000 | 0.0588 | 0.0035 | 15.0311 | 0.6163 | 0.5570 | −0.2806 | 0.2764 | −0.0937 |
| BTC | 0.0278 | 0.0164 | 0.0089 | - | 0.1588 | 0.0252 | 1.1097 | −0.1179 | 0.8648 | −0.4743 | 0.3905 | 2.6176 |
| ETH | 0.0312 | 0.0211 | 0.0124 | - | 0.2043 | 0.0417 | 1.0775 | 0.0523 | 1.1767 | −0.5988 | 0.5779 | 2.9371 |
| ALG | −0.0286 | 0.0296 | −0.0579 | - | 0.2866 | 0.0822 | 5.2014 | 1.2099 | 2.1239 | −0.7702 | 1.3537 | −2.6861 |
| ADA | 0.0288 | 0.0297 | 0.0045 | - | 0.2876 | 0.0827 | 6.0494 | 1.9970 | 1.7752 | −0.4421 | 1.3331 | 2.7034 |
| HBA | 0.0065 | 0.0334 | 0.0040 | - | 0.3240 | 0.1050 | 5.0762 | 1.2614 | 2.1880 | −0.8911 | 1.2968 | 0.6067 |
| QNT | 0.0342 | 0.0251 | 0.0106 | - | 0.2436 | 0.0594 | 2.8176 | 0.8455 | 1.6175 | −0.6128 | 1.0047 | 3.2191 |
| XLM | 0.0152 | 0.0294 | 0.0038 | - | 0.2855 | 0.0815 | 14.8622 | 2.9303 | 2.1927 | −0.4576 | 1.7351 | 1.4244 |
| XDC | 0.0540 | 0.0379 | 0.0100 | - | 0.3678 | 0.1353 | 6.6393 | 2.0064 | 2.2352 | −0.6159 | 1.6193 | 5.0748 |
| XRP | 0.0247 | 0.0314 | 0.0070 | - | 0.3046 | 0.0928 | 6.5972 | 1.2041 | 2.4457 | −1.1060 | 1.3397 | 2.3251 |
| Ticker | APP | ATH | BCN | CFL | FBL | FHL | FIL | FMF | FTV | KFL | KGF | PBP | PDM | RBG | RCF | TTS | VBH | VIL | BTC | ETH | ALG | ADA | HBA | QNT | XLM | XDC | XRP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APP | 1.000 | ||||||||||||||||||||||||||
| ATH | 0.067 | 1.000 | |||||||||||||||||||||||||
| BCN | 0.169 | 0.033 | 1.000 | ||||||||||||||||||||||||
| CFL | 0.591 | 0.222 | −0.055 | 1.000 | |||||||||||||||||||||||
| FBL | 0.384 | 0.127 | −0.031 | 0.094 | 1.000 | ||||||||||||||||||||||
| FHL | −0.030 | 0.077 | 0.043 | 0.102 | −0.207 | 1.000 | |||||||||||||||||||||
| FIL | −0.054 | −0.103 | −0.033 | −0.027 | −0.031 | 0.006 | 1.000 | ||||||||||||||||||||
| FMF | −0.146 | 0.039 | 0.061 | 0.001 | −0.335 | 0.130 | 0.156 | 1.000 | |||||||||||||||||||
| FTV | −0.006 | 0.020 | 0.003 | 0.048 | 0.019 | −0.019 | 0.016 | 0.008 | 1.000 | ||||||||||||||||||
| KFL | −0.003 | 0.009 | 0.204 | −0.060 | 0.055 | −0.102 | −0.102 | 0.135 | 0.033 | 1.000 | |||||||||||||||||
| KGF | −0.045 | 0.006 | 0.256 | −0.092 | 0.008 | −0.091 | −0.093 | −0.022 | −0.037 | 0.007 | 1.000 | ||||||||||||||||
| PBP | 0.196 | −0.035 | −0.010 | 0.041 | 0.076 | −0.007 | 0.002 | −0.079 | 0.008 | 0.004 | 0.057 | 1.000 | |||||||||||||||
| PDM | 0.019 | −0.179 | 0.002 | 0.048 | 0.047 | −0.045 | −0.070 | −0.024 | 0.030 | 0.157 | −0.061 | −0.014 | 1.000 | ||||||||||||||
| RBG | −0.045 | 0.156 | 0.097 | 0.036 | 0.098 | −0.075 | −0.009 | −0.019 | 0.070 | 0.124 | −0.038 | −0.038 | 0.142 | 1.000 | |||||||||||||
| RCF | 0.064 | −0.100 | 0.013 | −0.020 | −0.041 | 0.006 | 0.081 | 0.035 | 0.023 | 0.067 | −0.046 | −0.014 | 0.016 | 0.097 | 1.000 | ||||||||||||
| TTS | 0.060 | −0.067 | 0.009 | 0.003 | 0.097 | −0.005 | 0.009 | 0.071 | 0.017 | 0.218 | 0.009 | 0.008 | 0.127 | −0.018 | 0.084 | 1.000 | |||||||||||
| VBH | 0.074 | 0.017 | −0.037 | 0.027 | 0.009 | −0.055 | −0.070 | −0.027 | 0.020 | 0.107 | −0.011 | 0.016 | −0.033 | −0.042 | −0.469 | −0.119 | 1.000 | ||||||||||
| VIL | 0.034 | 0.108 | 0.106 | 0.014 | 0.081 | 0.010 | −0.063 | −0.021 | 0.027 | −0.312 | 0.105 | 0.000 | −0.074 | 0.267 | −0.150 | −0.341 | −0.022 | 1.000 | |||||||||
| BTC | −0.052 | −0.174 | −0.026 | −0.069 | −0.115 | −0.043 | 0.244 | 0.109 | 0.010 | 0.168 | −0.008 | 0.067 | −0.059 | −0.166 | 0.091 | 0.215 | 0.047 | −0.072 | 1.000 | ||||||||
| ETH | −0.037 | −0.108 | −0.044 | −0.044 | −0.157 | −0.101 | 0.151 | 0.099 | 0.018 | −0.038 | −0.080 | 0.039 | −0.008 | −0.130 | 0.107 | 0.152 | 0.047 | −0.080 | 0.779 | 1.000 | |||||||
| ALG | 0.201 | −0.104 | 0.037 | 0.054 | −0.065 | −0.043 | 0.103 | 0.058 | −0.005 | −0.003 | −0.076 | 0.093 | −0.145 | −0.041 | 0.051 | 0.121 | 0.107 | 0.014 | 0.614 | 0.666 | 1.000 | ||||||
| ADA | 0.005 | −0.097 | 0.069 | −0.068 | −0.065 | −0.088 | 0.241 | 0.037 | 0.007 | 0.165 | −0.081 | −0.032 | −0.020 | −0.085 | 0.167 | 0.157 | 0.104 | −0.148 | 0.604 | 0.635 | 0.730 | 1.000 | |||||
| HBA | 0.139 | −0.131 | 0.133 | 0.035 | −0.148 | −0.006 | 0.077 | 0.085 | −0.014 | −0.037 | 0.119 | 0.042 | −0.084 | −0.294 | −0.014 | 0.058 | 0.157 | −0.175 | 0.555 | 0.595 | 0.746 | 0.546 | 1.000 | ||||
| QNT | −0.013 | −0.204 | 0.127 | 0.071 | −0.245 | 0.082 | 0.194 | 0.042 | −0.024 | −0.102 | −0.030 | 0.003 | −0.082 | −0.102 | −0.009 | −0.066 | 0.181 | −0.084 | 0.421 | 0.510 | 0.518 | 0.434 | 0.524 | 1.000 | |||
| XLM | −0.105 | −0.223 | −0.113 | −0.138 | −0.081 | −0.059 | 0.028 | 0.020 | 0.002 | 0.113 | −0.124 | −0.033 | −0.001 | −0.136 | 0.061 | 0.286 | 0.086 | −0.302 | 0.585 | 0.661 | 0.746 | 0.754 | 0.584 | 0.449 | 1.000 | ||
| XDC | 0.073 | −0.187 | 0.010 | −0.035 | −0.014 | −0.092 | 0.258 | −0.074 | 0.006 | 0.003 | 0.025 | −0.041 | 0.025 | −0.060 | 0.098 | 0.003 | 0.048 | −0.192 | 0.359 | 0.407 | 0.442 | 0.595 | 0.261 | 0.333 | 0.481 | 1.000 | |
| XRP | −0.122 | −0.184 | −0.012 | −0.185 | −0.068 | −0.066 | −0.086 | −0.002 | −0.009 | 0.063 | 0.040 | −0.018 | 0.021 | −0.195 | 0.031 | 0.297 | −0.024 | −0.376 | 0.434 | 0.595 | 0.592 | 0.549 | 0.511 | 0.414 | 0.846 | 0.482 | 1.000 |
| Ticker | APP | ATH | BCN | CFL | FBL | FHL | FIL | FMF | FTV | KFL | KGF | PBP | PDM | RBG | RCF | TTS | VBH | VIL | BTC | ETH | ALG | ADA | HBA | QNT | XLM | XDC | XRP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APP | 0.018 | ||||||||||||||||||||||||||
| ATH | 0.002 | 0.030 | |||||||||||||||||||||||||
| BCN | 0.003 | 0.001 | 0.018 | ||||||||||||||||||||||||
| CFL | 0.003 | 0.002 | 0.000 | 0.002 | |||||||||||||||||||||||
| FBL | 0.009 | 0.004 | −0.001 | 0.001 | 0.031 | ||||||||||||||||||||||
| FHL | −0.005 | 0.017 | 0.007 | 0.005 | −0.046 | 1.567 | |||||||||||||||||||||
| FIL | −0.001 | −0.003 | −0.001 | 0.000 | −0.001 | 0.001 | 0.027 | ||||||||||||||||||||
| FMF | −0.005 | 0.002 | 0.002 | 0.000 | −0.016 | 0.045 | 0.007 | 0.075 | |||||||||||||||||||
| FTV | −0.001 | 0.004 | 0.000 | 0.002 | 0.004 | −0.029 | 0.003 | 0.002 | 1.450 | ||||||||||||||||||
| KFL | 0.000 | 0.000 | 0.005 | 0.000 | 0.002 | −0.022 | −0.003 | 0.006 | 0.007 | 0.031 | |||||||||||||||||
| KGF | 0.000 | 0.000 | 0.002 | 0.000 | 0.000 | −0.007 | −0.001 | 0.000 | −0.003 | 0.000 | 0.004 | ||||||||||||||||
| PBP | 0.005 | −0.001 | 0.000 | 0.000 | 0.002 | −0.002 | 0.000 | −0.004 | 0.002 | 0.000 | 0.001 | 0.033 | |||||||||||||||
| PDM | 0.000 | −0.004 | 0.000 | 0.000 | 0.001 | −0.008 | −0.002 | −0.001 | 0.005 | 0.004 | −0.001 | 0.000 | 0.020 | ||||||||||||||
| RBG | −0.001 | 0.005 | 0.003 | 0.000 | 0.003 | −0.019 | 0.000 | −0.001 | 0.017 | 0.004 | 0.000 | −0.001 | 0.004 | 0.040 | |||||||||||||
| RCF | 0.001 | −0.002 | 0.000 | 0.000 | −0.001 | 0.001 | 0.001 | 0.001 | 0.003 | 0.001 | 0.000 | 0.000 | 0.000 | 0.002 | 0.012 | ||||||||||||
| TTS | 0.001 | −0.002 | 0.000 | 0.000 | 0.002 | −0.001 | 0.000 | 0.003 | 0.003 | 0.006 | 0.000 | 0.000 | 0.003 | −0.001 | 0.001 | 0.021 | |||||||||||
| VBH | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | −0.005 | −0.001 | −0.001 | 0.002 | 0.001 | 0.000 | 0.000 | 0.000 | −0.001 | −0.004 | −0.001 | 0.006 | ||||||||||
| VIL | 0.001 | 0.004 | 0.003 | 0.000 | 0.003 | 0.003 | −0.002 | −0.001 | 0.007 | −0.011 | 0.001 | 0.000 | −0.002 | 0.011 | −0.003 | −0.010 | 0.000 | 0.041 | |||||||||
| BTC | −0.004 | −0.017 | −0.002 | −0.002 | −0.011 | −0.030 | 0.022 | 0.016 | 0.006 | 0.016 | 0.000 | 0.007 | −0.005 | −0.018 | 0.006 | 0.017 | 0.002 | −0.008 | 0.303 | ||||||||
| ETH | −0.003 | −0.013 | −0.004 | −0.001 | −0.020 | −0.090 | 0.018 | 0.019 | 0.015 | −0.005 | −0.004 | 0.005 | −0.001 | −0.018 | 0.008 | 0.016 | 0.003 | −0.012 | 0.303 | 0.501 | |||||||
| ALG | 0.027 | −0.018 | 0.005 | 0.002 | −0.011 | −0.053 | 0.017 | 0.016 | −0.006 | −0.001 | −0.005 | 0.017 | −0.020 | −0.008 | 0.006 | 0.017 | 0.008 | 0.003 | 0.335 | 0.468 | 0.986 | ||||||
| ADA | 0.001 | −0.017 | 0.009 | −0.003 | −0.011 | −0.109 | 0.040 | 0.010 | 0.009 | 0.029 | −0.005 | −0.006 | −0.003 | −0.017 | 0.019 | 0.023 | 0.008 | −0.030 | 0.331 | 0.448 | 0.722 | 0.992 | |||||
| HBA | 0.021 | −0.026 | 0.020 | 0.002 | −0.029 | −0.009 | 0.014 | 0.026 | −0.019 | −0.007 | 0.009 | 0.009 | −0.013 | −0.066 | −0.002 | 0.009 | 0.014 | −0.040 | 0.342 | 0.473 | 0.831 | 0.611 | 1.260 | ||||
| QNT | −0.002 | −0.030 | 0.014 | 0.002 | −0.036 | 0.087 | 0.027 | 0.010 | −0.024 | −0.015 | −0.002 | 0.000 | −0.010 | −0.017 | −0.001 | −0.008 | 0.012 | −0.014 | 0.196 | 0.305 | 0.434 | 0.365 | 0.496 | 0.712 | |||
| XLM | −0.014 | −0.038 | −0.015 | −0.006 | −0.014 | −0.073 | 0.005 | 0.006 | 0.003 | 0.020 | −0.008 | −0.006 | 0.000 | −0.027 | 0.007 | 0.041 | 0.007 | −0.061 | 0.318 | 0.462 | 0.732 | 0.743 | 0.648 | 0.374 | 0.978 | ||
| XDC | 0.013 | −0.041 | 0.002 | −0.002 | −0.003 | −0.146 | 0.054 | −0.026 | 0.009 | 0.001 | 0.002 | −0.009 | 0.005 | −0.015 | 0.014 | 0.001 | 0.005 | −0.050 | 0.251 | 0.367 | 0.559 | 0.755 | 0.374 | 0.358 | 0.606 | 1.624 | |
| XRP | −0.017 | −0.034 | −0.002 | −0.008 | −0.013 | −0.087 | −0.015 | −0.001 | −0.012 | 0.012 | 0.003 | −0.003 | 0.003 | −0.041 | 0.004 | 0.045 | −0.002 | −0.081 | 0.252 | 0.445 | 0.620 | 0.577 | 0.605 | 0.368 | 0.883 | 0.648 | 1.113 |
| Ticker | APP | ATH | BCN | CFL | FBL | FHL | FIL | FMF | FTV | KFL | KGF | PBP | PDM | RBG | RCF | TTS | VBH | VIL | BTC | ETH | ALG | ADA | HBA | QNT | XLM | XDC | XRP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APP | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ATH | 0.068 | 0.998 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| BCN | 0.169 | 0.022 | 0.985 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| CFL | 0.592 | 0.182 | −0.161 | 0.769 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FBL | 0.384 | 0.102 | −0.101 | −0.217 | 0.886 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FHL | −0.030 | 0.079 | 0.047 | 0.146 | −0.188 | 0.966 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FIL | −0.058 | −0.095 | −0.027 | 0.034 | −0.002 | 0.012 | 0.993 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FMF | −0.146 | 0.049 | 0.085 | 0.121 | −0.283 | 0.049 | 0.151 | 0.922 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FTV | −0.029 | 0.103 | 0.004 | 0.273 | 0.141 | −0.096 | −0.051 | 0.039 | 0.939 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| KFL | −0.004 | 0.010 | 0.207 | −0.033 | 0.077 | −0.096 | −0.104 | 0.176 | 0.101 | 0.943 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| KGF | −0.047 | 0.012 | 0.266 | −0.029 | 0.049 | −0.095 | −0.103 | −0.018 | −0.219 | −0.053 | 0.924 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| PBP | 0.195 | −0.047 | −0.044 | −0.093 | −0.023 | 0.015 | −0.003 | −0.045 | 0.049 | 0.016 | 0.092 | 0.967 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| PDM | 0.018 | −0.179 | 0.001 | 0.093 | 0.087 | −0.027 | −0.104 | 0.018 | 0.070 | 0.138 | −0.059 | −0.018 | 0.955 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| RBG | −0.046 | 0.162 | 0.101 | 0.069 | 0.138 | −0.080 | −0.014 | −0.008 | 0.186 | 0.068 | −0.048 | −0.018 | 0.126 | 0.934 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| RCF | 0.064 | −0.103 | 0.003 | −0.048 | −0.075 | 0.011 | 0.063 | 0.024 | 0.102 | 0.067 | −0.012 | −0.047 | −0.008 | 0.110 | 0.971 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| TTS | 0.060 | −0.071 | 0.000 | −0.025 | 0.085 | 0.023 | 0.002 | 0.118 | 0.065 | 0.198 | 0.039 | −0.014 | 0.080 | −0.050 | 0.062 | 0.955 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| VBH | 0.074 | 0.012 | −0.051 | −0.035 | −0.038 | −0.055 | −0.065 | −0.007 | 0.100 | 0.104 | 0.024 | −0.013 | −0.056 | −0.054 | −0.500 | −0.119 | 0.831 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| VIL | 0.034 | 0.106 | 0.099 | −0.013 | 0.072 | 0.014 | −0.051 | −0.002 | 0.099 | −0.374 | 0.079 | −0.004 | −0.018 | 0.263 | −0.153 | −0.265 | −0.106 | 0.799 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| BTC | −0.053 | −0.170 | −0.015 | −0.009 | −0.094 | −0.047 | 0.217 | 0.059 | 0.040 | 0.192 | 0.036 | 0.060 | −0.093 | −0.149 | 0.054 | 0.170 | 0.085 | 0.166 | 0.875 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ETH | −0.037 | −0.105 | −0.037 | −0.009 | −0.158 | −0.124 | 0.131 | 0.046 | 0.076 | −0.036 | −0.054 | 0.040 | −0.008 | −0.123 | 0.087 | 0.158 | 0.118 | 0.048 | 0.733 | 0.561 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ALG | 0.201 | −0.116 | 0.004 | −0.052 | −0.164 | −0.051 | 0.086 | 0.045 | 0.052 | −0.004 | −0.056 | 0.041 | −0.163 | 0.011 | −0.007 | 0.128 | 0.109 | 0.090 | 0.576 | 0.265 | 0.657 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ADA | 0.004 | −0.097 | 0.071 | −0.053 | −0.070 | −0.091 | 0.234 | −0.008 | 0.043 | 0.176 | −0.072 | −0.042 | −0.041 | −0.097 | 0.128 | 0.117 | 0.197 | 0.045 | 0.487 | 0.269 | 0.426 | 0.550 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| HBA | 0.138 | −0.141 | 0.114 | −0.004 | −0.198 | −0.034 | 0.076 | 0.040 | −0.015 | −0.047 | 0.115 | 0.002 | −0.077 | −0.246 | −0.027 | 0.056 | 0.156 | −0.115 | 0.527 | 0.200 | 0.443 | −0.087 | 0.505 | 0.000 | 0.000 | 0.000 | 0.000 |
| QNT | −0.014 | −0.203 | 0.134 | 0.181 | −0.190 | 0.031 | 0.164 | −0.069 | −0.126 | −0.068 | −0.072 | 0.023 | −0.093 | −0.037 | −0.028 | −0.023 | 0.242 | −0.045 | 0.385 | 0.256 | 0.217 | −0.033 | 0.056 | 0.690 | 0.000 | 0.000 | 0.000 |
| XLM | −0.106 | −0.216 | −0.092 | −0.065 | −0.047 | −0.041 | −0.003 | 0.022 | 0.037 | 0.130 | −0.100 | −0.029 | −0.060 | −0.112 | 0.035 | 0.262 | 0.132 | −0.117 | 0.518 | 0.298 | 0.463 | 0.180 | −0.033 | 0.030 | 0.417 | 0.000 | 0.000 |
| XDC | 0.073 | −0.191 | 0.000 | −0.054 | −0.041 | −0.076 | 0.239 | −0.101 | 0.038 | 0.039 | 0.057 | −0.087 | 0.014 | −0.039 | 0.048 | −0.021 | 0.075 | −0.168 | 0.326 | 0.186 | 0.235 | 0.318 | −0.252 | 0.058 | 0.021 | 0.681 | 0.000 |
| XRP | −0.123 | −0.175 | 0.012 | −0.101 | −0.027 | −0.047 | −0.116 | 0.012 | −0.023 | 0.046 | 0.011 | −0.014 | −0.017 | −0.180 | 0.039 | 0.286 | 0.016 | −0.263 | 0.424 | 0.374 | 0.364 | 0.055 | −0.088 | 0.090 | 0.326 | 0.117 | 0.385 |
| Portfolio | EQW | MinVar | MaxSharpe | MinSemVar | MaxSort | MaxCEQ | MaxOmega | MaxUDVol | MaxDiv | MinDeCorr | MaxRMD | MaxASR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
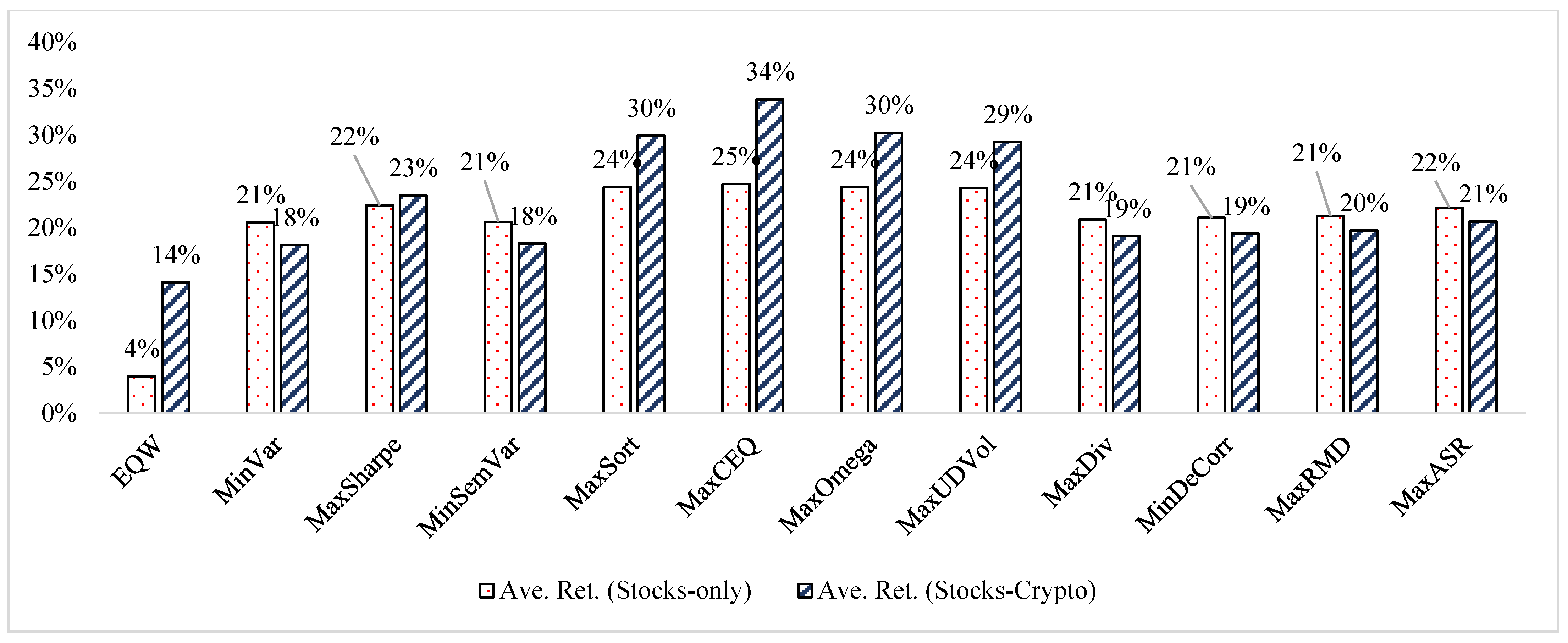
| Ave. Ret. | 0.181 | 0.198 | 0.260 | 0.209 | 0.260 | 0.354 | 0.222 | 0.247 | 0.217 | 0.222 | 0.232 | 0.256 |
| Std. Dev. | 0.272 | 0.070 | 0.095 | 0.074 | 0.098 | 0.141 | 0.084 | 0.092 | 0.078 | 0.080 | 0.084 | 0.096 |
| Skewness | −0.170 | 0.542 | 0.275 | 0.566 | 0.438 | −0.008 | 0.592 | 0.666 | 0.524 | 0.438 | 0.461 | 0.345 |
| Kurtosis | −0.006 | 2.249 | 1.841 | 2.349 | 1.786 | 1.332 | 1.872 | 2.109 | 2.573 | 2.120 | 2.390 | 1.024 |
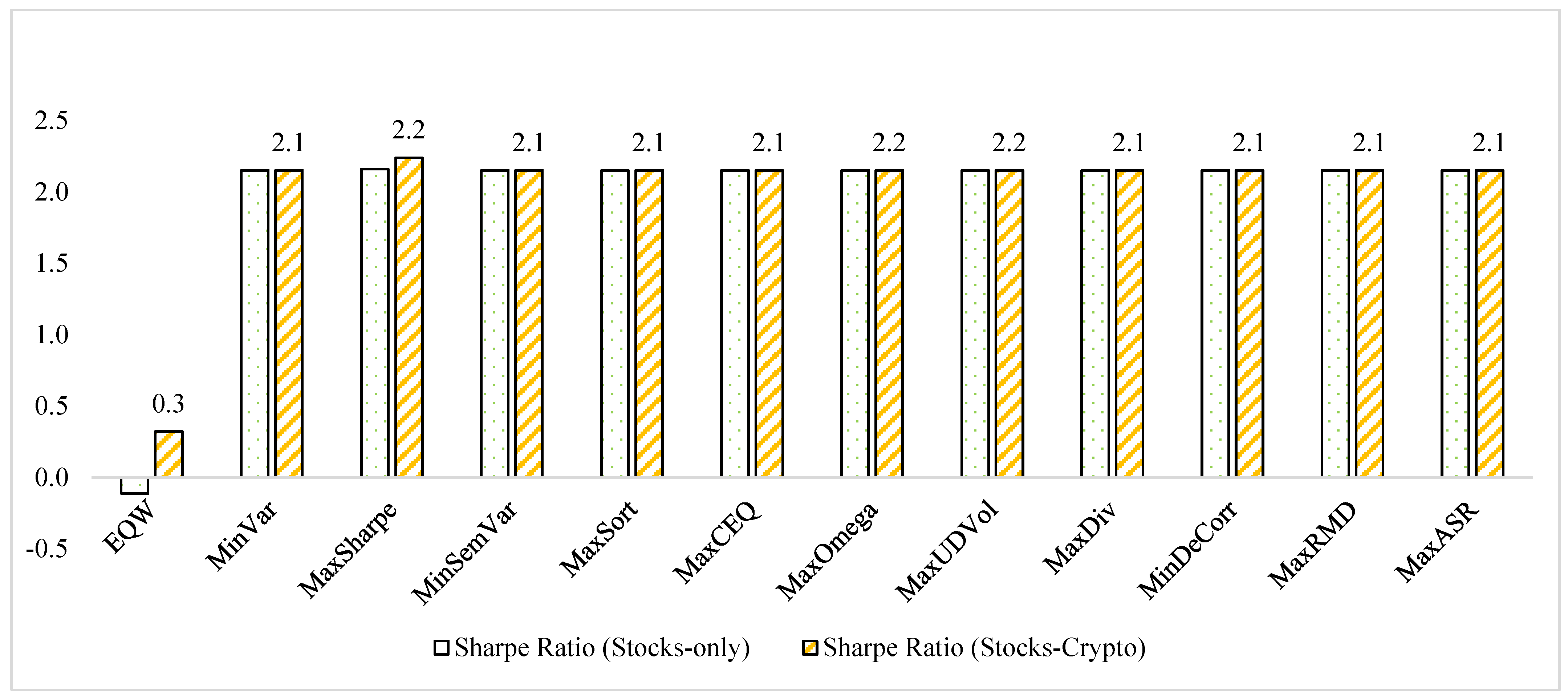
| Sharpe | 0.482 | 2.120 | 2.199 | 2.150 | 2.150 | 2.150 | 2.050 | 2.150 | 2.150 | 2.150 | 2.150 | 2.150 |
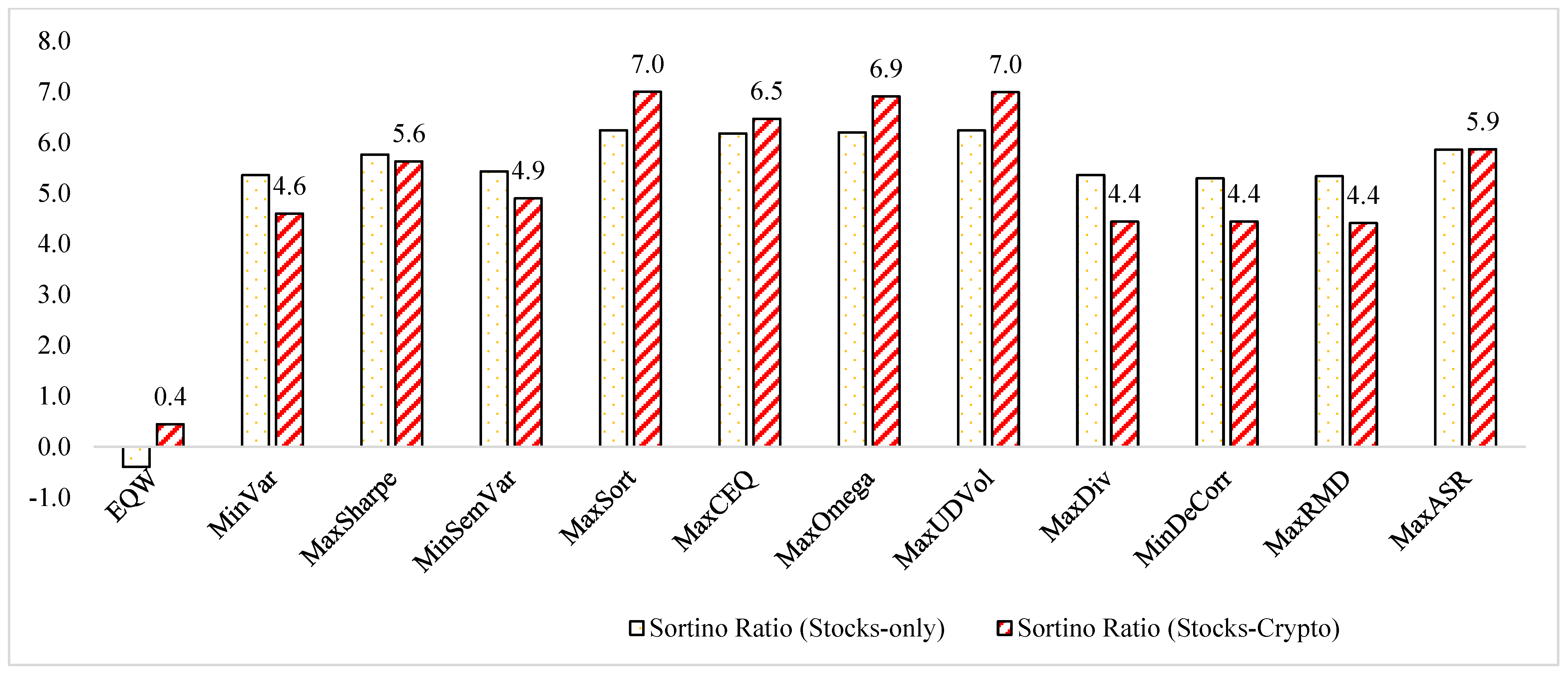
| Sortino | 0.631 | 4.558 | 4.828 | 4.752 | 4.878 | 4.531 | 4.598 | 5.216 | 4.680 | 4.708 | 4.710 | 4.940 |
| Ret-Risk Ratio | 0.666 | 2.835 | 2.723 | 2.828 | 2.661 | 2.504 | 2.647 | 2.695 | 2.793 | 2.774 | 2.742 | 2.671 |
| Assets | ||||||||||||
| APP | 0.037 | 0.128 | 0.101 | 0.128 | 0.177 | 0.039 | 0.193 | 0.132 | 0.123 | 0.123 | 0.116 | 0.103 |
| ATH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| BCN | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| CFL | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FBL | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FHL | 0.037 | 0.006 | 0.008 | 0.006 | 0.007 | 0.012 | 0.010 | 0.002 | 0.011 | 0.009 | 0.010 | 0.001 |
| FIL | 0.037 | 0.277 | 0.371 | 0.292 | 0.396 | 0.524 | 0.369 | 0.364 | 0.285 | 0.299 | 0.292 | 0.408 |
| FMF | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FTV | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| KFL | 0.037 | 0.000 | 0.006 | 0.017 | 0.000 | 0.000 | 0.003 | 0.000 | 0.029 | 0.027 | 0.030 | 0.064 |
| KGF | 0.037 | 0.281 | 0.157 | 0.257 | 0.138 | 0.000 | 0.160 | 0.138 | 0.219 | 0.183 | 0.153 | 0.136 |
| PBP | 0.037 | 0.099 | 0.152 | 0.103 | 0.130 | 0.226 | 0.110 | 0.102 | 0.119 | 0.121 | 0.144 | 0.100 |
| PDM | 0.037 | 0.027 | 0.000 | 0.005 | 0.000 | 0.000 | 0.000 | 0.000 | 0.004 | 0.033 | 0.014 | 0.002 |
| RBG | 0.037 | 0.078 | 0.070 | 0.079 | 0.113 | 0.037 | 0.100 | 0.099 | 0.091 | 0.088 | 0.083 | 0.047 |
| RCF | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.011 | 0.000 |
| TTS | 0.037 | 0.088 | 0.104 | 0.093 | 0.000 | 0.110 | 0.029 | 0.128 | 0.091 | 0.085 | 0.112 | 0.110 |
| VBH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.005 | 0.000 | 0.000 |
| VIL | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.001 | 0.006 | 0.000 |
| BTC | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ETH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ALG | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ADA | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| HBA | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| QNT | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| XLM | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| XDC | 0.037 | 0.014 | 0.029 | 0.015 | 0.021 | 0.053 | 0.000 | 0.025 | 0.018 | 0.022 | 0.026 | 0.028 |
| XRP | 0.037 | 0.002 | 0.002 | 0.006 | 0.018 | 0.000 | 0.027 | 0.010 | 0.008 | 0.003 | 0.003 | 0.000 |
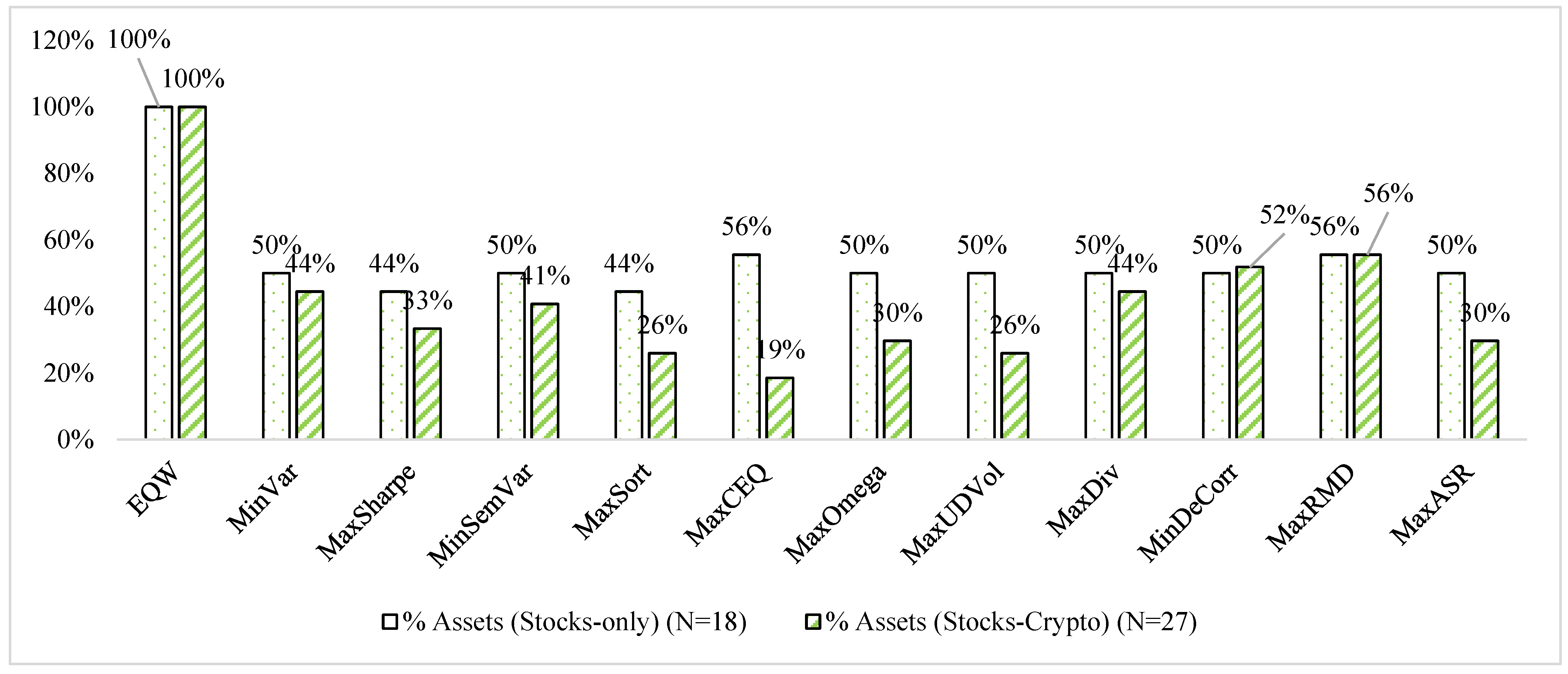
| % Assets | 100% | 41% | 37% | 44% | 41% | 30% | 56% | 33% | 78% | 59% | 48% | 70% |
| Portfolio | EQW | MinVar | MaxSharpe | MinSemVar | MaxSort | MaxCEQ | MaxOmega | MaxUDVol | MaxDiv | MinDeCorr | MaxRMD | MaxASR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ave. Ret. | 0.109 | 0.155 | 0.261 | 0.162 | 0.279 | 0.360 | 0.242 | 0.278 | 0.174 | 0.191 | 0.187 | 0.244 |
| Std. Dev. | 0.249 | 0.050 | 0.088 | 0.052 | 0.098 | 0.144 | 0.083 | 0.101 | 0.058 | 0.065 | 0.064 | 0.083 |
| Skewness | 0.181 | −0.001 | 0.145 | 0.262 | 0.454 | 0.284 | 0.214 | 0.536 | −0.096 | 0.276 | 0.219 | 0.331 |
| Kurtosis | 0.132 | −0.266 | −0.035 | −0.212 | −0.419 | −0.402 | −0.315 | −0.334 | −0.414 | −0.547 | −0.577 | −0.882 |
| Sharpe | 0.236 | 2.120 | 2.397 | 2.150 | 2.332 | 2.150 | 2.304 | 2.257 | 2.150 | 2.150 | 2.150 | 2.341 |
| Sortino | 0.246 | 4.036 | 5.949 | 4.643 | 7.115 | 5.591 | 5.878 | 7.016 | 4.174 | 5.105 | 4.882 | 6.863 |
| Ret-Risk Ratio | 0.436 | 3.125 | 2.965 | 3.112 | 2.840 | 2.497 | 2.903 | 2.751 | 3.015 | 2.914 | 2.932 | 2.943 |
| Assets | ||||||||||||
| APP | 0.037 | 0.045 | 0.000 | 0.058 | 0.055 | 0.000 | 0.033 | 0.098 | 0.030 | 0.021 | 0.052 | 0.017 |
| ATH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| BCN | 0.037 | 0.018 | 0.034 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.056 | 0.000 |
| CFL | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.000 |
| FBL | 0.037 | 0.095 | 0.183 | 0.095 | 0.165 | 0.186 | 0.258 | 0.141 | 0.124 | 0.109 | 0.098 | 0.180 |
| FHL | 0.037 | 0.004 | 0.003 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.010 | 0.001 | 0.000 | 0.000 |
| FIL | 0.037 | 0.128 | 0.278 | 0.105 | 0.205 | 0.149 | 0.143 | 0.212 | 0.131 | 0.108 | 0.112 | 0.126 |
| FMF | 0.037 | 0.031 | 0.033 | 0.037 | 0.038 | 0.000 | 0.050 | 0.041 | 0.063 | 0.053 | 0.029 | 0.058 |
| FTV | 0.037 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.002 | 0.000 | 0.007 | 0.000 | 0.012 | 0.000 |
| KFL | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| KGF | 0.037 | 0.270 | 0.000 | 0.286 | 0.000 | 0.000 | 0.047 | 0.000 | 0.183 | 0.102 | 0.083 | 0.124 |
| PBP | 0.037 | 0.097 | 0.169 | 0.103 | 0.189 | 0.220 | 0.161 | 0.176 | 0.116 | 0.133 | 0.125 | 0.173 |
| PDM | 0.037 | 0.023 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.028 | 0.047 | 0.034 | 0.000 |
| RBG | 0.037 | 0.134 | 0.248 | 0.143 | 0.232 | 0.302 | 0.178 | 0.222 | 0.154 | 0.152 | 0.123 | 0.201 |
| RCF | 0.037 | 0.074 | 0.000 | 0.068 | 0.000 | 0.000 | 0.067 | 0.000 | 0.031 | 0.077 | 0.083 | 0.000 |
| TTS | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.026 | 0.047 | 0.000 |
| VBH | 0.037 | 0.025 | 0.000 | 0.032 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.044 | 0.023 | 0.000 |
| VIL | 0.037 | 0.024 | 0.001 | 0.030 | 0.045 | 0.000 | 0.000 | 0.038 | 0.077 | 0.066 | 0.062 | 0.047 |
| BTC | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ETH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ALG | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ADA | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| HBA | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| QNT | 0.037 | 0.008 | 0.000 | 0.012 | 0.013 | 0.068 | 0.032 | 0.005 | 0.001 | 0.017 | 0.021 | 0.028 |
| XLM | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| XDC | 0.037 | 0.001 | 0.007 | 0.001 | 0.024 | 0.044 | 0.000 | 0.031 | 0.006 | 0.010 | 0.011 | 0.014 |
| XRP | 0.037 | 0.024 | 0.044 | 0.025 | 0.035 | 0.032 | 0.027 | 0.035 | 0.037 | 0.034 | 0.026 | 0.031 |
| % Assets | 100% | 63% | 41% | 59% | 48% | 30% | 81% | 37% | 63% | 74% | 70% | 56% |
| Portfolio | EW-1 | EW-2 | EW-3 | EW-4 | EW-5 | EW-6 | MS-1 | MS-2 | MS-3 | MS-4 | MS-5 | MS-6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ave. Ret. | 0.191 | 0.401 | 0.139 | 0.257 | 0.271 | 0.189 | 0.289 | 0.310 | 0.250 | 0.201 | 0.217 | 0.217 |
| Std. Dev. | 0.291 | 0.336 | 0.306 | 0.275 | 0.285 | 0.307 | 0.096 | 0.106 | 0.078 | 0.039 | 0.071 | 0.050 |
| Skewness | 0.324 | 0.036 | 0.376 | 0.327 | −0.255 | −0.074 | 0.155 | −0.331 | 0.137 | −0.042 | 0.128 | 0.248 |
| Kurtosis | −0.462 | −0.026 | −0.192 | 0.462 | −0.662 | 0.053 | −0.581 | −0.144 | −0.210 | 0.360 | 0.348 | −0.284 |
| Sharpe | 0.485 | 1.045 | 0.291 | 0.751 | 0.775 | 0.454 | 2.485 | 2.450 | 2.571 | 3.836 | 2.371 | 3.317 |
| Sortino | 0.715 | 1.760 | 0.372 | 1.207 | 1.152 | 0.607 | 6.772 | 5.366 | 6.761 | 11.784 | 5.360 | 8.402 |
| Ret-Risk Ratio | 0.657 | 1.194 | 0.455 | 0.932 | 0.951 | 0.617 | 3.005 | 2.922 | 3.214 | 5.106 | 3.079 | 4.312 |
| Assets | ||||||||||||
| APP | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.108 | 0.001 | 0.001 | 0.147 | 0.027 | 0.066 |
| ATH | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| BCN | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.101 | 0.000 | 0.042 | 0.000 | 0.000 | 0.000 |
| CFL | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FBL | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.033 | 0.000 | 0.052 | 0.026 | 0.157 | 0.000 |
| FHL | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.000 | 0.017 | 0.008 | 0.005 | 0.006 |
| FIL | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.429 | 0.345 | 0.335 | 0.263 | 0.266 | 0.212 |
| FMF | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.017 |
| FTV | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| KFL | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.089 | 0.000 | 0.000 | 0.111 | 0.004 | 0.028 |
| KGF | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.000 | 0.258 | 0.043 | 0.152 | 0.278 |
| PBP | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.136 | 0.316 | 0.099 | 0.006 | 0.149 | 0.085 |
| PDM | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.000 | 0.000 | 0.134 | 0.057 | 0.093 |
| RBG | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.251 | 0.132 | 0.000 | 0.073 | 0.023 |
| RCF | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.031 | 0.000 | 0.000 | 0.085 | 0.000 | 0.075 |
| TTS | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.007 | 0.000 | 0.038 | 0.040 | 0.002 | 0.000 |
| VBH | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| VIL | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.043 | 0.001 | 0.001 | 0.101 | 0.093 | 0.090 |
| BTC | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ETH | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.017 | 0.012 | 0.008 | 0.009 | 0.000 |
| ALG | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ADA | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| HBA | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.000 | 0.014 | 0.000 | 0.000 | 0.000 |
| QNT | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.010 | 0.055 | 0.000 | 0.000 | 0.000 | 0.000 |
| XLM | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| XDC | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.013 | 0.000 | 0.000 | 0.001 | 0.000 | 0.008 |
| XRP | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.001 | 0.015 | 0.000 | 0.028 | 0.006 | 0.021 |
| % Assets | 100% | 100% | 100% | 100% | 100% | 100% | 44% | 33% | 52% | 52% | 48% | 48% |
| 1 | For recent developments on digital assets in Vanuatu and Tuvalu, refer to: https://fca.vu/vanuatu-passes-virtual-asset-service-providers-vasp-act/#:~:text=The%20Parliament%20of%20Vanuatu%20has,growth%20and%20additional%20revenue%20streams, and https://bsvblockchain.org/tuvalus-national-digital-ledger/, respectively. The webpages were accessed on 9 July 2025. |
| 2 | https://www.westpac.com.fj/personal/cards/exchange-control-limits/; and https://www.rbf.gov.fj/press-release-no-08-rbf-cautions-public-on-the-use-of-and-investment-in-cryptocurrencies-and-virtual-assets/. The webpages were accessed on 9 July 2025. |
| 3 | Of course, by overcoming the limitations of Fiji’s stock market (in the long-term), other trading strategies can be examined. |
| 4 | Readers are requested to refer to Kumar and Stauvermann (2022), Kumar et al. (2022, 2024), the references therein, for a background on Fiji’s stock market. |
| 5 | For readings on ISO20022 compliant technologies, please refer to: https://tangem.com/en/blog/post/iso-compliant-cryptocurrencies/; https://bloxbytes.com/iso-20022-coins/; https://101blockchains.com/iso-20022-compliant-crypto-list/; https://99bitcoins.com/cryptocurrency/best-iso-20022-cryptos/; https://coincodex.com/article/27964/iso-20022-crypto/. The webpages were accessed on 9 July 2025. |
| 6 | See: Crypto Carbon Footprint List: https://www.cryptowisser.com/crypto-carbon-footprint/ and CCRI Crypto Sustainability Metrics—https://indices.carbon-ratings.com/. The webpages were accessed on 9 July 2025. |
| 7 | https://etfdb.com/etfs/currency/cryptocurrency/#etfs&sort_name=assets_under_management&sort_order=desc&page=1. The webpage was accessed on 9 July 2025. |
| 8 | See: https://www.thestreet.com/crypto/innovation/companies-holding-bitcoin-on-their-balance-sheets-a-strategic-investment- and https://www.coingecko.com/en/public-companies-bitcoin. The webpages were accessed on 9 July 2025. |
| 9 | We set equal to the monthly target return. |
| 10 | Two stocks, FHL and RBG, went through share splits of 1:10 and 1:5 prior to 9 January 2019 and 13 November 2019, respectively. Since the period of split only affected our sample of RBG, we have adjusted its price accordingly. |
| 11 | https://www.schwab.com/learn/story/calculate-sharpe-ratio-to-gauge-risk. The webpages was accessed on 9 July 2025. |
| 12 | In the case of optimized portfolios based on stocks-only and stocks-cryptocurrencies portfolios, and based on stocks-cryptocurrencies with out-of-sample, whenever we obtain , we added an additional constraint and , respectively. |
| 13 | The author thanks an anonymous reviewer for suggesting that we run Monte Carlo simulations to strengthen the robustness of the main results. |
| 14 | While not financial advice, the information can be useful for stocks-only investors focusing on asset diversification, and/or even rebalancing portfolios. |
| 15 | We thank an anonymous reviewer for suggesting these measures as alternatives. |
| 16 | |
| 17 | As a caveat, please note that since stable coins are often used to trade cryptocurrencies, the price and often the returns from the stable coins (e.g., USDT) varies with the performance of the market for cryptocurrencies. |
References
- Akhtaruzzaman, M., Sensoy, A., & Corbet, S. (2020). The influence of Bitcoin on portfolio diversification and design. Finance Research Letters, 37, 101344. [Google Scholar] [CrossRef]
- Aliu, F., Bajra, U., & Preniqi, N. (2022). Analysis of diversification benefits for cryptocurrency portfolios before and during the COVID-19 pandemic. Studies in Economics and Finance, 39(3), 444–457. [Google Scholar] [CrossRef]
- Aliu, F., Nuhiu, A., Krasniqi, B. A., & Jusufi, G. (2021). Modeling the optimal diversification opportunities: The case of crypto portfolios and stocks portfolios. Studies in Economics and Finance, 38(1), 50–66. [Google Scholar] [CrossRef]
- Almeida, J., & Gonçalves, T. C. (2022). Portfolio diversification, hedge and safe-haven properties in cryptocurrency investments and financial economics: A systematic literature review. Journal of Risk and Financial Management, 16(1), 3. [Google Scholar] [CrossRef]
- Ardia, D., Boudt, K., & Fleury, J. P. G. (2017). RiskPortfolios: Computation of risk-based portfolios in R. Journal of OpenSource Software, 10(2). Available online: https://bookdown.org/shenjian0824/portr/port-opt.html (accessed on 9 July 2025). [CrossRef]
- Bai, L., & Newsom, P. (2011). Teaching utility theory with an application in modern portfolio optimization. Decision Sciences Journal of Innovative Education, 9(1), 107–112. [Google Scholar] [CrossRef]
- Batten, D. (2025, June 27). How the IMF prevents global bitcoin adoption (and why they do it). Bitcoin Magazine. Available online: https://bitcoinmagazine.com/featured/how-the-imf-prevents-global-bitcoin-adoption-and-why-they-do-it (accessed on 1 July 2025).
- Baur, D. G., Karlsen, J. R., Smales, L. A., & Trench, A. (2024). Digging deeper-Is bitcoin digital gold? A mining perspective. Journal of Commodity Markets, 34, 100406. [Google Scholar] [CrossRef]
- Bielstein, P., Jaegers, J.-P., & Wesson, P. (2023, October 11). A novel way to diversify portfolio weights. Wilmott Magazine. Available online: https://wilmott.com/wilmott-magazine-november-2023-issue/ (accessed on 29 August 2024).
- Booth, G., & Broussard, J. P. (2016). The Sortino ratio and extreme value theory: An application to asset allocation. In Extreme events in finance: A handbook of extreme value theory and its applications (pp. 443–464). John Wiley & Sons, Inc. [Google Scholar]
- Bouri, E., Lucey, B., & Roubaud, D. (2020). Cryptocurrencies and the downside risk in stocks investments. Finance Research Letters, 33, 101211. [Google Scholar] [CrossRef]
- Brauneis, A., & Mestel, R. (2019). Cryptocurrency-portfolios in a mean-variance framework. Finance Research Letters, 28, 259–264. [Google Scholar] [CrossRef]
- Burggraf, T. (2019). Risk-based portfolio optimization in the cryptocurrency world. SSRN, 3454764. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3454764 (accessed on 9 July 2025).
- Charfeddine, L., Benlagha, N., & Maouchi, Y. (2020). Investigating the dynamic relationship between cryptocurrencies and conventional assets: Implications for financial investors. Economic Modelling, 85, 198–217. [Google Scholar] [CrossRef]
- Choueifaty, Y., & Coignard, Y. (2008). Toward maximum diversification. The Journal of Portfolio Management, 35, 40–51. [Google Scholar] [CrossRef]
- Christoffersen, P., Errunza, V., Jacobs, K., & Langlois, H. (2012). Is the potential for international diversification disappearing? A dynamic copula approach. The Review of Financial Studies, 25(12), 3711–3751. [Google Scholar] [CrossRef]
- Clarke, R., De Silva, H., & Thorley, S. (2006). Minimum-variance portfolios in the US equity market. Journal of Portfolio Management, 33(1), 10–24. [Google Scholar]
- Corbet, S., Meegan, A., Larkin, C., Lucey, B., & Yarovaya, L. (2018). Exploring the dynamic relationships between cryptocurrencies and other financial assets. Economics Letters, 165, 28–34. [Google Scholar] [CrossRef]
- Čuljak, M., Tomić, B., & Žiković, S. (2022). Benefits of sectoral cryptocurrency portfolio optimization. Research in International Business and Finance, 60, 101615. [Google Scholar] [CrossRef]
- DeMiguel, V., Garlappi, L., & Uppal, R. (2009). Optimal versus naive diversification: How inefficient is the 1/N portfolio strategy? The Review of Financial Studies, 22(5), 1915–1953. [Google Scholar] [CrossRef]
- Elton, E., & Gruber, M. (1997). Modern portfolio theory, 1950 to date. Journal of Banking and Finance, 21, 1743–1759. [Google Scholar] [CrossRef]
- Estrada, J. (2008). Mean-semivariance optimization: A heuristic approach. Journal of Applied Finance (Formerly Financial Practice and Education), 18(1), 57–82. [Google Scholar] [CrossRef]
- Ghanbari, H., Mohammadi, E., Fooeik, A. M. L., Kumar, R. R., Stauvermann, P. J., & Shabani, M. (2024). Cryptocurrency portfolio allocation under credibilistic CVaR criterion and practical constraints. Risks, 12(10), 163. [Google Scholar] [CrossRef]
- Gladstein, A. (2021, June 23). Fighting monetary colonialism with open-source code. Bitcoin Magazine. Available online: https://bitcoinmagazine.com/culture/bitcoin-a-currency-of-decolonization (accessed on 1 July 2025).
- Harlow, W. V., & Rao, R. (1989). Asset-pricing in a generalized mean-LPM framework: Theory and evidence. Journal of Financial and Quantitative Analysis, 24, 285–311. [Google Scholar] [CrossRef]
- Haugen, R., & Baker, N. (1991). The efficient market inefficiency of capitalization-weighted stock portfolios. Journal of Portfolio Management, 17(3), 35–40. [Google Scholar] [CrossRef]
- Huffman, E. (2025). ISO 20022 crypto: Top list of compliant coins in 2025. Cryptonews, Cryptocurrency.com. Available online: https://cryptonews.com/cryptocurrency/iso-20022-crypto/#:~:text=global%20financial%20ecosystem.-,How%20Will%20ISO%2020022%20Change%20Crypto?,due%20to%20their%20increased%20safety (accessed on 27 August 2025).
- Jarrow, R., & Zhao, F. (2006). Downside loss aversion and portfolio management. Management Science, 52(4), 558–566. [Google Scholar] [CrossRef]
- Jutel, O. (2021). Blockchain imperialism in the Pacific. Big Data & Society, 8(1), 2053951720985249. [Google Scholar] [CrossRef]
- Jutel, O. (2022). Blockchain humanitarianism and crypto-colonialism. Patterns, 3(1), 100422. [Google Scholar] [CrossRef] [PubMed]
- Jutel, O. (2023). Blockchain financialization, neo-colonialism, and Binance. Frontiers in Blockchain, 6, 1160257. [Google Scholar] [CrossRef]
- Kalash, S. Y. (2025). Policy pathways for integrating fast payment systems with digital currencies. Policy brief No. 200—March 2025. Center for International Governance Innovation. Available online: https://www.cigionline.org/static/documents/Kalash_8fTzU9T.pdf (accessed on 27 August 2025).
- Kapsos, M., Christofides, N., & Rustem, B. (2014). Worst-case robust Omega ratio. European Journal of Operational Research, 234(2), 499–507. [Google Scholar] [CrossRef]
- Keating, C., & Shadwick, W. (2002). A universal performance measure. Journal of Performance Measurement, 6(3), 59–84. [Google Scholar]
- Krause, D. (2024, June 6). Unlocking ethereum’s potential: The rise of spot ETFs in cryptocurrency investment. Available online: https://ssrn.com/abstract=4856380 (accessed on 1 July 2025). [CrossRef]
- Kumar, R. R., Ghanbari, H., & Stauvermann, P. J. (2024). Application of a Robust Maximum Diversified Portfolio to a Small Economy’s Stock Market: An Application to Fiji’s South Pacific Stock Exchange. Journal of Risk and Financial Management, 17(9), 388. [Google Scholar] [CrossRef]
- Kumar, R. R., & Stauvermann, P. J. (2022). Portfolios under different methods and scenarios: A case of Fiji’s South Pacific Stock Exchange. Journal of Risk and Financial Management, 15(12), 549. [Google Scholar] [CrossRef]
- Kumar, R. R., Stauvermann, P. J., & Samitas, A. (2022). An application of portfolio mean-variance and semi-variance optimization techniques: A case of Fiji. Journal of Risk and Financial Management, 15(5), 190. [Google Scholar] [CrossRef]
- Kwok, A. O. J., & Treiblmaier, H. (2024). Blockchain technology as a driver of economic development in small economies: A dynamic capabilities framework. Journal of Decision Systems, 33(3), 413–438. [Google Scholar] [CrossRef]
- Letho, L., Chelwa, G., & Alhassan, A. L. (2022). Cryptocurrencies and portfolio diversification in an emerging market. China Finance Review International, 12(1), 20–50. [Google Scholar] [CrossRef]
- Li, J.-P., Naqvi, B., Rizvi, S. K. A., & Chang, H.-L. (2021). Bitcoin: The biggest financial innovation of fourth industrial revolution and a portfolio’s efficiency booster. Technological Forecasting and Social Change, 162, 120383. [Google Scholar] [CrossRef]
- Ma, Y., Ahmad, F., Liu, M., & Wang, Z. (2020). Portfolio optimization in the era of digital financialization using cryptocurrencies. Technological Forecasting and Social Change, 161, 120265. [Google Scholar] [CrossRef]
- Maillard, S., Roncalli, T., & Teïletche, J. (2010). The properties of equally weighted risk contribution portfolios. Journal of Portfolio Management, 36(4), 60–70. [Google Scholar] [CrossRef]
- Markowitz, H. M. (1952a). Portfolio selection. The Journal of Finance, 7, 77–91. [Google Scholar]
- Markowitz, H. M. (1952b). The Utility of Wealth. Journal of Political Economy, 60, 43–50. [Google Scholar] [CrossRef]
- Markowitz, H. M. (1991). Foundations of portfolio theory. The Journal of Finance, 46, 469–477. [Google Scholar] [CrossRef]
- Markowitz, H. M. (2010). Portfolio theory: As I still see it. Annual Review of Financial Economics, 2, 1–23. [Google Scholar] [CrossRef]
- Matkovskyy, R., Jalan, A., Dowling, M., & Bouraoui, T. (2021). From bottom ten to top ten: The role of cryptocurrencies in enhancing portfolio return of poorly performing stocks. Finance Research Letters, 38, 101405. [Google Scholar] [CrossRef]
- Petukhina, A., Trimborn, S., Härdle, W. K., & Elendner, H. (2021). Investing with cryptocurrencies–evaluating their potential for portfolio allocation strategies. Quantitative Finance, 21(11), 1825–1853. [Google Scholar] [CrossRef]
- Pézier, J., & White, A. (2008). The relative merits of alternative investments in passive portfolios. The Journal of Alternative Investments, 10(4), 37–49. [Google Scholar] [CrossRef]
- Platanakis, E., Sutcliffe, C., & Urquhart, A. (2018). Optimal vs. naïve diversification in cryptocurrencies. Economics Letters, 171(2018), 93–96. [Google Scholar] [CrossRef]
- Platanakis, E., & Urquhart, A. (2020). Should investors include bitcoin in their portfolios? A portfolio theory approach. The British Accounting Review, 52(4), 100837. [Google Scholar] [CrossRef]
- Reserve Bank of Fiji (RBF). (2024). RBF press release No. 8. Available online: https://www.rbf.gov.fj/press-release-no-08-rbf-cautions-public-on-the-use-of-and-investment-in-cryptocurrencies-and-virtual-assets/ (accessed on 30 June 2025).
- Salo, A., Doumpos, M., Liesiö, J., & Zopounidis, C. (2024). Fifty years of portfolio optimization. European Journal of Operational Research, 318(1), 1–18. [Google Scholar] [CrossRef]
- Schellinger, B. (2020). Optimization of special cryptocurrency portfolios. The Journal of Risk Finance, 21(2), 127–157. [Google Scholar] [CrossRef]
- Sharpe, W. (1966). Mutual fund performance. The Journal of Business, 39(1), 119–138. [Google Scholar] [CrossRef]
- Smetters, K., & Zhang, X. (2013). A sharper ratio: A general measure for correctly ranking non-normal investment risks. No. w19500. National Bureau of Economic Research. Available online: https://www.nber.org/system/files/working_papers/w19500/w19500.pdf (accessed on 9 July 2025).
- Sortino, F., & van der Meer, R. (1991). Downside Risk. Journal of Portfolio Management, 17, 27–31. [Google Scholar] [CrossRef]
- South Pacific Stock Exchange (SPX). (2025). Market reports. SPX, Suva, Fiji. Available online: https://marketreports.spx.com.fj/Company.aspx?code= (accessed on 9 July 2025).
- Surtee, T., & Alagidede, I. P. (2023). A novel approach to using modern portfolio theory. Borsa Istanbul Review, 23(3), 527–540. [Google Scholar] [CrossRef]
- Symitsi, E., & Chalvatzis, K. (2019). The economic value of Bitcoin: A portfolio analysis of currencies, gold, oil and stocks. Research in International Business and Finance, 48, 97–110. [Google Scholar] [CrossRef]
- Tangem Team. (2025). Top ISO-compliant cryptocurrencies in August 2025. Tangem. Available online: https://tangem.com/en/blog/post/iso-compliant-cryptocurrencies/ (accessed on 27 August 2025).
- UNDP. (2024). Small island digital states: How digital can catalyse SIDS development. UNDP Global SIDS Team. [Google Scholar]
- Waller, L. G., & Johnson, S. (2022). The possible contributive value of cryptocurrencies to Small Island Developing States. International Journal of Blockchains and Cryptocurrencies, 3(1), 60–79. [Google Scholar] [CrossRef]
- Wang, F., & Yan, X. S. (2021). Downside risk and the performance of volatility-managed portfolios. Journal of Banking & Finance, 131, 106198. [Google Scholar] [CrossRef]
- Yan, L., & Garcia, P. (2017). Portfolio investment: Are commodities useful? Journal of Commodity Markets, 8, 43–55. [Google Scholar] [CrossRef]
- You, L., & Daigler, R. T. (2013). A Markowitz optimization of commodity futures portfolios. Journal of Futures Markets, 33(4), 343–368. [Google Scholar] [CrossRef]
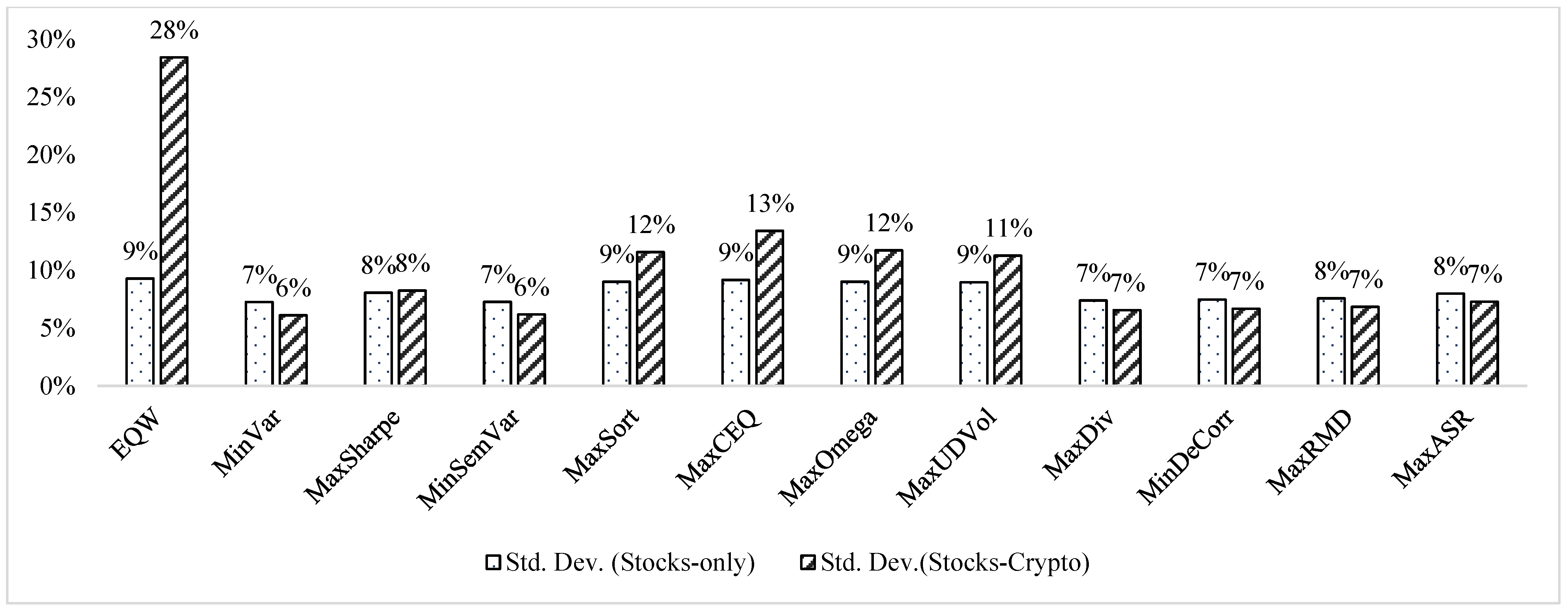
| Portfolio | EQW | MinVar | MaxSharpe | MinSemVar | MaxSort | MaxCEQ | MaxOmega | MaxUDVol | MaxDiv | MinDeCorr | MaxRMD | MaxASR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ave. Ret. | 0.040 | 0.206 | 0.224 | 0.206 | 0.244 | 0.247 | 0.244 | 0.243 | 0.209 | 0.211 | 0.213 | 0.222 |
| Std. Dev. | 0.093 | 0.072 | 0.081 | 0.073 | 0.090 | 0.092 | 0.090 | 0.090 | 0.074 | 0.075 | 0.076 | 0.080 |
| Skewness | −0.596 | 0.395 | 0.530 | 0.421 | 0.692 | 0.670 | 0.684 | 0.692 | 0.392 | 0.372 | 0.392 | 0.550 |
| Kurtosis | 12.635 | −0.076 | 0.181 | −0.062 | 0.462 | 0.423 | 0.436 | 0.459 | −0.077 | −0.071 | −0.047 | 0.061 |
| Sharpe | −0.112 | 2.150 | 2.159 | 2.150 | 2.150 | 2.150 | 2.150 | 2.150 | 2.150 | 2.150 | 2.150 | 2.150 |
| Sortino | −0.394 | 5.355 | 5.762 | 5.430 | 6.238 | 6.175 | 6.198 | 6.237 | 5.359 | 5.292 | 5.333 | 5.855 |
| Ret-Risk Ratio | 0.426 | 2.840 | 2.779 | 2.838 | 2.704 * | 2.695 * | 2.704 * | 2.707 * | 2.827 | 2.819 | 2.810 | 2.776 |
| Assets | ||||||||||||
| APP | 0.056 | 0.094 | 0.091 | 0.094 | 0.087 | 0.087 | 0.089 | 0.087 | 0.096 | 0.100 | 0.099 | 0.100 |
| ATH | 0.056 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| BCN | 0.056 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.005 | 0.000 |
| CFL | 0.056 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FBL | 0.056 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FHL | 0.056 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.001 | 0.000 | 0.002 | 0.000 | 0.000 | 0.001 |
| FIL | 0.056 | 0.359 | 0.409 | 0.361 | 0.465 | 0.472 | 0.466 | 0.463 | 0.366 | 0.369 | 0.373 | 0.400 |
| FMF | 0.056 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FTV | 0.056 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| KFL | 0.056 | 0.020 | 0.014 | 0.018 | 0.002 | 0.008 | 0.010 | 0.002 | 0.024 | 0.025 | 0.022 | 0.018 |
| KGF | 0.056 | 0.273 | 0.227 | 0.282 | 0.205 | 0.168 | 0.193 | 0.211 | 0.243 | 0.223 | 0.213 | 0.247 |
| PBP | 0.056 | 0.096 | 0.108 | 0.095 | 0.116 | 0.123 | 0.117 | 0.115 | 0.102 | 0.104 | 0.109 | 0.113 |
| PDM | 0.056 | 0.080 | 0.079 | 0.075 | 0.064 | 0.077 | 0.063 | 0.062 | 0.083 | 0.087 | 0.083 | 0.048 |
| RBG | 0.056 | 0.048 | 0.048 | 0.048 | 0.047 | 0.047 | 0.043 | 0.048 | 0.053 | 0.055 | 0.055 | 0.061 |
| RCF | 0.056 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| TTS | 0.056 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| VBH | 0.056 | 0.029 | 0.024 | 0.027 | 0.013 | 0.016 | 0.020 | 0.013 | 0.031 | 0.036 | 0.041 | 0.011 |
| VIL | 0.056 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| % of Asset | 100% | 50% | 44% | 50% | 44% | 56% | 50% | 50% | 50% | 50% | 56% | 50% |
| Portfolio | EQW | MinVar | MaxSharpe | MinSemVar | MaxSort | MaxCEQ | MaxOmega | MaxUDVol | MaxDiv | MinDeCorr | MaxRMD | MaxASR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ave. Ret. | 0.141 | 0.181 | 0.235 | 0.183 | 0.299 | 0.338 | 0.302 | 0.292 | 0.191 | 0.194 | 0.197 | 0.207 |
| Std. Dev. | 0.284 | 0.061 | 0.083 | 0.062 | 0.116 | 0.134 | 0.117 | 0.113 | 0.066 | 0.067 | 0.068 | 0.073 |
| Skewness | 0.928 | 0.108 | 0.394 | 0.248 | 0.888 | 0.777 | 0.885 | 0.888 | 0.003 | 0.007 | 0.006 | 0.517 |
| Kurtosis | 2.106 | −0.313 | 0.300 | −0.284 | 0.902 | 0.949 | 0.943 | 0.903 | −0.162 | −0.138 | −0.035 | −0.197 |
| Sharpe | 0.321 | 2.150 | 2.238 | 2.150 | 2.150 | 2.150 | 2.150 | 2.150 | 2.150 | 2.150 | 2.150 | 2.150 |
| Sortino | 0.442 | 4.596 | 5.626 | 4.896 | 6.997 | 6.467 | 6.907 | 6.991 | 4.437 | 4.440 | 4.410 | 5.866 |
| Ret-Risk Ratio | 0.497 ** | 2.969 ** | 2.844 ** | 2.958 ** | 2.582 | 2.523 | 2.576 | 2.593 | 2.913 ** | 2.899 ** | 2.881 ** | 2.836 ** |
| Assets | ||||||||||||
| APP | 0.037 | 0.108 | 0.114 | 0.107 | 0.105 | 0.059 | 0.132 | 0.105 | 0.108 | 0.107 | 0.100 | 0.118 |
| ATH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| BCN | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.016 | 0.000 |
| CFL | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FBL | 0.037 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.014 | 0.009 | 0.021 | 0.000 |
| FHL | 0.037 | 0.003 | 0.001 | 0.003 | 0.001 | 0.000 | 0.000 | 0.001 | 0.007 | 0.003 | 0.002 | 0.003 |
| FIL | 0.037 | 0.287 | 0.416 | 0.294 | 0.608 | 0.695 | 0.616 | 0.593 | 0.310 | 0.314 | 0.317 | 0.354 |
| FMF | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FTV | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| KFL | 0.037 | 0.039 | 0.020 | 0.034 | 0.000 | 0.000 | 0.004 | 0.000 | 0.055 | 0.056 | 0.042 | 0.020 |
| KGF | 0.037 | 0.315 | 0.222 | 0.342 | 0.102 | 0.000 | 0.083 | 0.129 | 0.223 | 0.177 | 0.164 | 0.341 |
| PBP | 0.037 | 0.075 | 0.107 | 0.072 | 0.121 | 0.160 | 0.107 | 0.114 | 0.088 | 0.096 | 0.106 | 0.086 |
| PDM | 0.037 | 0.055 | 0.031 | 0.040 | 0.000 | 0.000 | 0.000 | 0.000 | 0.053 | 0.064 | 0.058 | 0.000 |
| RBG | 0.037 | 0.056 | 0.072 | 0.056 | 0.056 | 0.058 | 0.047 | 0.053 | 0.064 | 0.063 | 0.065 | 0.074 |
| RCF | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.009 | 0.014 | 0.000 |
| TTS | 0.037 | 0.020 | 0.000 | 0.014 | 0.000 | 0.000 | 0.000 | 0.000 | 0.010 | 0.035 | 0.040 | 0.000 |
| VBH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| VIL | 0.037 | 0.026 | 0.000 | 0.027 | 0.000 | 0.000 | 0.000 | 0.000 | 0.048 | 0.048 | 0.035 | 0.000 |
| BTC | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ETH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ALG | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ADA | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| HBA | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| QNT | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.000 | 0.000 | 0.002 | 0.003 | 0.000 |
| XLM | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| XDC | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| XRP | 0.037 | 0.013 | 0.018 | 0.012 | 0.007 | 0.027 | 0.009 | 0.006 | 0.021 | 0.018 | 0.016 | 0.003 |
| % Assets | 100% | 44% | 33% | 41% | 26% | 19% | 30% | 26% | 44% | 52% | 56% | 30% |
| Portfolio | EQW | MinVar | MaxSharpe | MinSemVar | MaxSort | MaxCEQ | MaxOmega | MaxUDVol | MaxDiv | MinDeCorr | MaxRMD | MaxASR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ave. Ret. | 0.091 | 0.208 | 0.212 | 0.209 | 0.217 | 0.2190 | 0.218 | 0.217 | 0.210 | 0.211 | 0.209 | 0.211 |
| Std. Dev. | 0.250 | 0.080 | 0.082 | 0.080 | 0.084 | 0.0853 | 0.085 | 0.084 | 0.081 | 0.081 | 0.080 | 0.081 |
| Skewness | 1.141 | 0.938 | 0.943 | 0.945 | 1.006 | 0.996 | 1.005 | 1.005 | 0.934 | 0.954 | 0.934 | 0.960 |
| Kurtosis | 3.608 | 1.482 | 1.506 | 1.495 | 1.653 | 1.649 | 1.660 | 1.646 | 1.476 | 1.528 | 1.476 | 1.501 |
| Sharpe | 0.165 | 1.981 | 1.981 | 1.981 | 1.981 | 1.981 | 1.981 | 1.981 | 1.981 | 1.981 | 1.981 | 1.981 |
| Sortino | 0.157 | 5.282 | 5.291 | 5.298 | 5.456 | 5.426 | 5.453 | 5.455 | 5.280 | 5.319 | 5.271 | 5.346 |
| Ret-Risk Ratio | 0.365 | 2.606 | 2.593 | 2.605 | 2.574 | 2.567 | 2.572 | 2.576 | 2.601 | 2.596 | 2.603 | 2.596 |
| Assets | ||||||||||||
| APP | 0.037 | 0.144 | 0.147 | 0.144 | 0.145 | 0.146 | 0.144 | 0.145 | 0.145 | 0.141 | 0.144 | 0.150 |
| ATH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| BCN | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| CFL | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FBL | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FHL | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 |
| FIL | 0.037 | 0.449 | 0.459 | 0.449 | 0.477 | 0.481 | 0.477 | 0.475 | 0.452 | 0.458 | 0.450 | 0.456 |
| FMF | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FTV | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| KFL | 0.037 | 0.012 | 0.013 | 0.011 | 0.007 | 0.008 | 0.006 | 0.007 | 0.013 | 0.013 | 0.012 | 0.015 |
| KGF | 0.037 | 0.189 | 0.167 | 0.190 | 0.168 | 0.157 | 0.167 | 0.171 | 0.180 | 0.178 | 0.181 | 0.177 |
| PBP | 0.037 | 0.126 | 0.129 | 0.126 | 0.132 | 0.135 | 0.133 | 0.131 | 0.128 | 0.126 | 0.128 | 0.127 |
| PDM | 0.037 | 0.005 | 0.009 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | 0.005 | 0.006 | 0.006 | 0.000 |
| RBG | 0.037 | 0.054 | 0.053 | 0.054 | 0.053 | 0.053 | 0.053 | 0.053 | 0.056 | 0.054 | 0.055 | 0.055 |
| RCF | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| TTS | 0.037 | 0.002 | 0.004 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.004 | 0.004 | 0.000 |
| VBH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| VIL | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| BTC | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ETH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ALG | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ADA | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| HBA | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| QNT | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| XLM | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| XDC | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| XRP | 0.037 | 0.019 | 0.019 | 0.019 | 0.019 | 0.020 | 0.019 | 0.019 | 0.020 | 0.019 | 0.019 | 0.019 |
| % Assets | 100% | 33% | 33% | 33% | 26% | 26% | 26% | 26% | 33% | 33% | 33% | 26% |
| Portfolio | EQW | MinVar | MaxSharpe | MinSemVar | MaxSort | MaxCEQ | MaxOmega | MaxUDVol | MaxDiv | MinDeCorr | MaxRMD | MaxASR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ave. Ret. | 0.044 | 0.141 | 0.175 | 0.145 | 0.196 | 0.223 | 0.194 | 0.191 | 0.150 | 0.158 | 0.161 | 0.164 |
| Std. Dev. | 0.274 | 0.043 | 0.055 | 0.044 | 0.067 | 0.081 | 0.070 | 0.066 | 0.046 | 0.050 | 0.052 | 0.053 |
| Skewness | −0.268 | −0.147 | −0.091 | −0.100 | −0.023 | −0.085 | 0.107 | 0.028 | −0.094 | −0.084 | −0.052 | −0.003 |
| Kurtosis | −0.170 | −0.504 | −0.316 | −0.432 | −0.600 | −0.249 | 0.391 | −0.654 | −0.027 | 0.019 | 0.191 | −0.884 |
| Sharpe | −0.023 | 2.120 | 2.256 | 2.150 | 2.179 | 2.150 | 2.050 | 2.150 | 2.150 | 2.150 | 2.150 | 2.154 |
| Sortino | −0.117 | 3.686 | 4.436 | 3.851 | 4.598 | 4.308 | 4.046 | 4.574 | 3.825 | 3.924 | 3.974 | 4.355 |
| Ret-Risk Ratio | 0.160 | 3.281 | 3.160 | 3.283 | 2.927 | 2.771 | 2.762 | 2.911 | 3.229 | 3.149 | 3.120 | 3.102 |
| Assets | ||||||||||||
| APP | 0.037 | 0.166 | 0.164 | 0.169 | 0.176 | 0.124 | 0.038 | 0.192 | 0.172 | 0.147 | 0.136 | 0.183 |
| ATH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| BCN | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.026 | 0.000 |
| CFL | 0.037 | 0.009 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.018 | 0.011 | 0.000 |
| FBL | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FHL | 0.037 | 0.012 | 0.018 | 0.014 | 0.022 | 0.029 | 0.026 | 0.024 | 0.014 | 0.016 | 0.017 | 0.018 |
| FIL | 0.037 | 0.182 | 0.254 | 0.180 | 0.304 | 0.388 | 0.250 | 0.290 | 0.182 | 0.196 | 0.195 | 0.225 |
| FMF | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| FTV | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| KFL | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| KGF | 0.037 | 0.235 | 0.154 | 0.235 | 0.017 | 0.000 | 0.056 | 0.022 | 0.170 | 0.123 | 0.120 | 0.223 |
| PBP | 0.037 | 0.054 | 0.084 | 0.059 | 0.072 | 0.132 | 0.150 | 0.058 | 0.071 | 0.086 | 0.099 | 0.022 |
| PDM | 0.037 | 0.073 | 0.096 | 0.073 | 0.150 | 0.159 | 0.162 | 0.147 | 0.088 | 0.097 | 0.114 | 0.124 |
| RBG | 0.037 | 0.111 | 0.136 | 0.116 | 0.164 | 0.144 | 0.125 | 0.167 | 0.120 | 0.138 | 0.121 | 0.128 |
| RCF | 0.037 | 0.106 | 0.077 | 0.107 | 0.078 | 0.000 | 0.169 | 0.085 | 0.104 | 0.100 | 0.105 | 0.064 |
| TTS | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| VBH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| VIL | 0.037 | 0.039 | 0.001 | 0.033 | 0.000 | 0.000 | 0.000 | 0.000 | 0.058 | 0.055 | 0.035 | 0.000 |
| BTC | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ETH | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ALG | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| ADA | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| HBA | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| QNT | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 |
| XLM | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| XDC | 0.037 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| XRP | 0.037 | 0.013 | 0.016 | 0.013 | 0.018 | 0.024 | 0.021 | 0.015 | 0.020 | 0.023 | 0.021 | 0.012 |
| % Assets | 100% | 44% | 41% | 41% | 44% | 30% | 67% | 33% | 52% | 44% | 44% | 67% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, R.R.; Ghanbari, H.; Stauvermann, P.J. Can Including Cryptocurrencies with Stocks in Portfolios Enhance Returns in Small Economies? An Analysis of Fiji’s Stock Market. J. Risk Financial Manag. 2025, 18, 484. https://doi.org/10.3390/jrfm18090484
Kumar RR, Ghanbari H, Stauvermann PJ. Can Including Cryptocurrencies with Stocks in Portfolios Enhance Returns in Small Economies? An Analysis of Fiji’s Stock Market. Journal of Risk and Financial Management. 2025; 18(9):484. https://doi.org/10.3390/jrfm18090484
Chicago/Turabian StyleKumar, Ronald Ravinesh, Hossein Ghanbari, and Peter Josef Stauvermann. 2025. "Can Including Cryptocurrencies with Stocks in Portfolios Enhance Returns in Small Economies? An Analysis of Fiji’s Stock Market" Journal of Risk and Financial Management 18, no. 9: 484. https://doi.org/10.3390/jrfm18090484
APA StyleKumar, R. R., Ghanbari, H., & Stauvermann, P. J. (2025). Can Including Cryptocurrencies with Stocks in Portfolios Enhance Returns in Small Economies? An Analysis of Fiji’s Stock Market. Journal of Risk and Financial Management, 18(9), 484. https://doi.org/10.3390/jrfm18090484









