Hot-Hand Belief and Loss Aversion in Individual Portfolio Decisions: Evidence from a Financial Experiment

Abstract

We investigate whether a belief in trend continuation, often associated with the so-called “hot-hand effect,” can be endogenously triggered by personal performance feedback in a controlled financial experiment. Participants allocated funds across assets with randomly generated prices, under conditions of known probabilities and varying levels of risk. In a two-stage setup, participants were first exposed to random price sequences to learn the task and potentially develop perceptions of personal success. They then faced additional price paths under incentivized conditions. Our findings show that participants initially increased purchases following gains—consistent with a feedback-driven belief in momentum—but this pattern faded over time. When facing sustained losses, loss aversion dominated decision-making, overriding early optimism. These results highlight how cognitive heuristics and emotional biases interact dynamically, suggesting that belief in trend continuation is context-sensitive and constrained by the reluctance to realize losses.

1. Introduction

This paper investigates whether individuals develop a belief in trend continuation based on their own experience with past outcomes, what is sometimes referred to in the literature as the “hot-hand” effect. While the traditional notion of the hot hand involves an actual increase in the probability of success following a streak, often studied in contexts such as sports or mutual fund performance (Hendricks et al., 1993; Sirri & Tufano, 1998), we focus instead on the formation of a subjective belief that recent success implies continued favorable outcomes. We thank an anonymous referee for highlighting the importance of distinguishing this belief from the traditional notion of the hot hand, which motivated us to refine our conceptual framing throughout the revised version. Recent studies show that such beliefs not only persist in complex, real-world decision environments like televised game shows, but are also frequently exaggerated relative to the true statistical effect (Kukavica & Narayanan, 2024). Moreover, meta-analyses have documented robust evidence of belief-based illusions across diverse settings, reinforcing the behavioral relevance of this phenomenon beyond sports (Miller & Sanjurjo, 2024). Specifically, we test whether this belief can be endogenously triggered by perceived personal success in asset selection, even in an environment where asset prices follow a purely random path.

To investigate this belief-formation process, we designed a controlled laboratory experiment simulating a financial market with transparent, random price dynamics. Participants allocated resources among four assets with varying degrees of risk, all of which had prices generated through known probabilistic rules. The experiment followed a two-stage structure. In the first stage, participants interacted with sequences of randomly fluctuating asset prices to familiarize themselves with the task and potentially experience patterns of perceived success. In the second stage, they made incentivized decisions under similar conditions, allowing us to observe whether earlier performance influenced subsequent portfolio choices.

Our approach makes a distinct contribution to the literature by isolating the endogenous formation of belief-driven behavioral patterns in a controlled environment. Rather than assigning beliefs externally, as in studies where participants respond to the performance of third-party agents, our design allows for subjective interpretations to emerge from participants’ own interactions with random sequences. This setup avoids confounding influences and highlights how small differences in early outcomes can shape perceptions and guide subsequent decisions, even in contexts governed entirely by chance.

In our framework, the belief in trend continuation manifests as an increased tendency to repurchase assets after observing prior gains or upward price movements. This behavior reflects a subjective expectation of momentum, even when outcomes are governed by randomness. In contrast, loss aversion is characterized by a reluctance to sell depreciating assets and a tendency to prematurely sell appreciating ones. While early perceived success led participants to pursue continuation strategies, this pattern faded over time. When confronted with persistent negative trends, loss aversion became more salient, overriding earlier optimism and reshaping portfolio decisions.

This study contributes to the behavioral finance literature by showing that belief in trend continuation can emerge endogenously from feedback-driven interactions with random outcomes, and that its influence is shaped by evolving investment conditions. Importantly, our results indicate that this belief is not expressed in isolation, but interacts dynamically with loss aversion, a well-documented feature of investor behavior. As participants experienced sustained losses, the reluctance to realize them gradually outweighed any optimism derived from prior gains. These findings offer new insights into how cognitive heuristics and emotional biases jointly influence financial decision-making under risk, underscoring the limitations of models based solely on rational expectations.

The remainder of this paper is structured as follows. Section 2 reviews the theoretical foundations and related literature. Section 3 details the experimental design, procedures, and behavioral hypotheses. Section 4 presents and interprets the empirical findings. Finally, Section 5 summarizes the main contributions and outlines directions for future research.

2. Literature Review and Theoretical Background

Expected Utility Theory (EU) has long served as the standard framework for modeling investor behavior under risk. It posits that rational agents evaluate risky alternatives based on the expected value of a utility function, adhering to axioms such as completeness, transitivity, continuity, and independence (Bernoulli, 1954/1738; Myerson, 2013; Savage, 1954; Von Neumann & Morgenstern, 1947). Despite its normative appeal and internal consistency, EU has encountered persistent empirical challenges. Numerous studies have documented systematic violations of its axioms, particularly when individuals display inconsistent attitudes toward risk. For example, preferences often reverse depending on whether outcomes are framed as gains or losses, and people frequently exhibit risk aversion in the gain domain and risk-seeking behavior in the loss domain, patterns that contradict EU predictions (Ellsberg, 1961; MacCrimmon & Larsson, 1979; Slovic & Tversky, 1974).

To account for these empirical inconsistencies, Kahneman and Tversky (1979) proposed Prospect Theory (PT), which has since become a cornerstone of behavioral economics. PT models decision-making under risk as a function of changes in wealth relative to a reference point, rather than absolute final outcomes. Its core components include a value function that is concave for gains, convex for losses, and steeper in the loss domain—capturing the phenomenon of loss aversion, where losses loom larger than equivalent gains. In addition, PT introduces a probability weighting function that overweights small probabilities and underweights large ones, departing from the linear treatment assumed in EU. These features enable PT to explain a range of behavioral anomalies, such as the certainty effect, isolation effect, and framing effects (Allais, 1953; Fox & Poldrack, 2009; Swalm, 1966).

Loss aversion plays a central role in explaining behavioral patterns such as the disposition effect—the tendency of investors to sell winning assets too early and hold on to losing ones for too long (Shefrin & Statman, 1985; Weber & Camerer, 1998). Within the framework of PT, this effect emerges because individuals evaluate outcomes relative to a reference point, typically the purchase price. Investors tend to be risk-averse when facing gains, prompting them to lock in profits, and risk-seeking when facing losses, encouraging them to hold declining assets in the hope of a rebound. Consequently, portfolio decisions are shaped not only by expected utility or probabilistic reasoning, but also by emotional reactions to perceived gains and losses.

Empirical evidence for the disposition effect has been consistently documented in both real-world trading data and controlled laboratory settings (Arora & Rajendran, 2023; Odean, 1998). This bias appears robust across contexts and is often associated with suboptimal portfolio performance, particularly in volatile markets. While PT offers a foundational explanation, subsequent refinements, most notably Cumulative Prospect Theory (CPT) (Tversky & Kahneman, 1992), have deepened our understanding of decision-making under risk. CPT incorporates nonlinear probability weighting and predicts a four-fold pattern of risk attitudes: individuals are risk-averse for gains with high probability, risk-seeking for losses with high probability, and reverse these preferences when probabilities are low. Such patterns can also account for the reluctance to realize losses. However, belief-driven behaviors may coexist with or even counteract these tendencies. One such belief is the expectation that recent success will persist—a heuristic commonly referred to as the hot-hand belief, even in the absence of objective autocorrelation. Understanding how such cognitive heuristics interact with emotional biases like loss aversion is essential for capturing the complexity of investor behavior in dynamic environments.

Initially examined in the context of sports performance, the belief that recent success is likely to continue, often labeled the hot-hand belief, has been linked to the representativeness heuristic, whereby individuals expect short random sequences to mirror the statistical properties of longer runs (Tversky & Kahneman, 1971, 1974). Under this heuristic, people tend to overinfer from small samples, interpreting recent outcomes as indicative of skill or momentum, even in environments governed by chance. This can lead to the expectation of continued success following streaks, regardless of the objective statistical structure of the underlying process.

The tendency to perceive patterns or momentum in purely random sequences is often attributed to the misperception of randomness, a phenomenon rooted in the representativeness heuristic and the overinterpretation of short-term trends (Tversky & Kahneman, 1971). In this framework, beliefs such as the hot hand may arise when individuals anchor their judgments on recent outcomes and exhibit overconfidence in perceived personal performance (Kahneman et al., 1982). These mechanisms are well established in cognitive psychology and help explain how expectations of trend continuation can emerge even in environments characterized by objective unpredictability. Crucially, when individuals receive performance feedback that appears to confirm their expectations, such beliefs may be reinforced and persist despite a lack of statistical justification.

One of the most influential empirical investigations of the hot-hand belief was conducted by Gilovich, Vallone, and Tversky (Gilovich et al., 1985). Analyzing player statistics from professional basketball games and survey responses from fans and coaches, the authors tested whether success in prior shots increased the probability of subsequent success. Although many participants believed that players could experience performance streaks, the analysis found no evidence of positive autocorrelation in shooting outcomes. The authors interpreted this as a cognitive illusion stemming from the misperception of randomness and introduced the term “hot-hand fallacy” to describe the mismatch between belief and observed data. Their study became a foundational reference in the literature on judgment under uncertainty and helped establish the notion that individuals often overinfer patterns in stochastic environments.

More than three decades after the original study, Miller and Sanjurjo (Miller & Sanjurjo, 2018) revisited the statistical methods employed by Gilovich, Vallone, and Tversky and identified a subtle but systematic bias in their analysis. Specifically, they showed that in finite sequences, the empirical probability of success following a streak is expected to be lower than the true underlying probability—even under independence—due to a selection bias in how conditional probabilities are calculated. Once this bias was accounted for, Miller and Sanjurjo found statistically significant evidence of a hot-hand effect in the original basketball dataset. Their findings renewed scholarly interest and prompted a broader reexamination of how such beliefs are measured, interpreted, and contextualized. More recent work by the same authors extends this reassessment to a variety of domains, offering robust empirical evidence that belief in the hot hand may align with subtle, but real, performance streaks in certain environments (Miller & Sanjurjo, 2024).

In the domain of finance, the hot-hand belief has been examined primarily in contexts where individuals evaluate the past performance of third parties, such as fund managers or financial “experts.” Empirical studies have shown that investors tend to allocate more capital to mutual funds that have recently outperformed, a behavior often interpreted as reflecting belief in trend continuation or managerial skill (Hendricks et al., 1993; Sirri & Tufano, 1998). In such settings, the belief is exogenous to the decision-maker: the investor attributes predictive power to the past success of others, rather than to their own actions. This perspective mirrors the sports context, where observers believe that athletes who are “hot” are more likely to sustain strong performance. Experimental evidence also supports this view; for example, Huber et al. (2010) show that individuals prefer options associated with recent success, even when outcomes are generated by chance.

Whereas prior research has predominantly examined the hot-hand belief as an exogenous perception about others’ performance, our study explores whether such a belief can arise endogenously from individuals’ own investment experiences. Rather than evaluating the outcomes of external agents, participants in our experiment make repeated portfolio choices and receive direct feedback on the results of their decisions. This controlled setting allows us to examine whether perceived personal streaks—despite occurring in a random environment—lead to expectations of continued success. The design further enables us to track the persistence or dissipation of this belief over time, particularly in interaction with other behavioral forces such as loss aversion.

3. Experimental Design

3.1. Design Overview

The experimental task was implemented using the z-Tree software package (Fischbacher, 2007), version 3.6.7. It was designed to simulate a simplified investment environment in which participants made repeated portfolio decisions under controlled risk conditions. The experiment featured two distinct stages, combining a total of 28 rounds and 16 portfolio decisions. Participants allocated resources among four assets with varying risk profiles: a high-risk asset (A), a medium-risk asset (B), a low-risk asset (C), and a risk-free alternative (cash). In the first stage, participants made six investment decisions without monetary consequences. Each of these decisions remained fixed for three consecutive rounds, allowing them to observe the results over short sequences of price changes. In the second stage, participants made ten additional decisions, with one decision made in each round. In this stage, decisions had financial consequences linked to the final portfolio value. This design approach combines automatic liquidation with structured decision phases, drawing on established methodologies in experimental finance (Kroll & Levy, 1992; Kroll et al., 1988a, 1988b; Weber & Camerer, 1992, 1998). It also ensures a gradual learning process for participants.

In every round, participants could purchase any quantity of the available assets at the displayed prices. All holdings were automatically liquidated at the end of each round, regardless of whether a new investment decision was made. Asset prices were then updated according to a predefined random mechanism. In the first stage, although participants maintained the same portfolio for three consecutive rounds, the automatic liquidation and price updates continued to occur after each round. In the second stage, participants made a new portfolio decision at every round. This structure created a controlled and repetitive decision environment that allowed us to examine how participants adapted their behavior in response to sequences of random outcomes, a key aspect for studying belief formation and adaptive responses.

At the beginning of each round, participants received an endowment of BRL 5000, which could be allocated among the available assets or kept in cash. The cash option functioned as a risk-free asset and did not accrue interest. Participants were not permitted to borrow or to take short positions. The endowment was provided at every round throughout the experiment, regardless of whether the investment decision was newly made or maintained from a previous round. Participants’ gains and losses within each round were not carried over to subsequent rounds; each round started afresh with the same endowment of BRL 5000, independent of previous outcomes. Only the final accumulated portfolio value at the end of the incentivized stage was used to calculate potential monetary payments. If the total value of a participant’s portfolio reached zero at any point, the session was automatically terminated for that individual. For reference, the nominal value of BRL 5000 corresponded to approximately USD 1199, based on the exchange rate of BRL 4.17 per US dollar on 12 November 2019 (Banco Central do Brasil, 2019).

After each investment decision, participants were shown the updated value of their portfolios in the subsequent round, allowing them to monitor their performance over time. In the first stage, although investment decisions were made only once every three rounds, feedback on portfolio value was provided after each round. Participants also received informational feedback during this stage, comparing their current outcome to their own historical average performance. Specifically, the system displayed the message “You have outperformed your average game performance” when their return exceeded their average up to that point, and “You underperformed your average game performance” otherwise. These feedback messages served as standardized cues to signal “success” or “failure” within the task.

In contrast to settings like sports, where success has a clear and objective definition such as scoring a basket, financial decision-making involves multiple potential definitions of success, including portfolio appreciation, outperforming others, or correctly predicting asset movements. In our experiment, we defined success behaviorally and consistently through personal portfolio gains and relative improvement over one’s own past performance. This was captured by both the monetary returns and the explicit feedback messages provided throughout the experiment, regardless of whether decisions were newly made or maintained from previous rounds. This approach allowed us to isolate the endogenous formation of belief-driven behavior, independent of comparisons with others or external benchmarks.

At the beginning of each session, participants received standardized instructions outlining the rules of the experiment, including the mechanics of decision-making and the functioning of the price system. The instructor adhered to a predefined script to ensure consistency across all sessions. Participants were also guided through the interface, including how to observe asset prices, input decisions, and execute transactions within the game environment. The full version of the experimental instructions is provided in Supplementary Materials.

Participants were informed about the price-formation process using simplified and standardized language. They were told that all assets would start at the same initial price, and that future changes in prices would occur randomly. At each round, prices could either increase or decrease with equal probability, and the magnitude of the change varied across assets according to their risk classification: high, medium, or low. The underlying structure was based on a two-step random draw, as detailed in the next subsection.

Asset prices were generated by a fixed algorithm that remained constant throughout the experiment. All assets began at BRL 100 in the first round. In each subsequent period, prices were updated through a two-step random process. First, the direction of the price change (increase or decrease) was determined independently for each asset, with equal probability ($p=0.5$). Second, the magnitude of the change was randomly selected from three equally likely values, specific to each asset: BRL 21, 23, or 25 for asset A (high risk); BRL 11, 13, or 15 for asset B (medium risk); and BRL 1, 3, or 5 for asset C (low risk). Both the direction and magnitude of the price variation were drawn independently. The resulting distributions are summarized in

Table 1. Probability distribution of price changes for each asset (from the initial price of BRL 100).

Asset	Increase (+)	Decrease (−)	Possible Variation Values (BRL)
A	0.5	0.5	21, 23, 25
B	0.5	0.5	11, 13, 15
C	0.5	0.5	1, 3, 5

Note: Each value has the same probability and is drawn independently (i.i.d.).

.

The choice of assets with zero expected returns was deliberate and aimed at isolating belief-based behaviors. By removing objective return differences, we ensured that investment decisions reflected subjective expectations rather than rational responses to structural incentives. This approach follows prior experimental research on cognitive biases and trend perception under risk-neutral conditions (e.g., Huber et al., 2010). Our goal was not to simulate a realistic financial market, but to create a controlled setting for analyzing the endogenous formation of behavioral patterns such as the hot-hand belief and loss aversion.

The price distributions were chosen to serve two primary purposes. First, they ensured that any belief in price autocorrelation would reflect a subjective interpretation, since all assets had an equal probability of increasing or decreasing. This neutrality implies that any perception of trend persistence, which is central to the hot-hand belief, would arise not from the price-generating process itself but from the participant’s reading of observed outcomes. Second, the use of three distinct values for price variation in each asset enabled participants to identify apparent trends without requiring advanced analytical skills. This feature was intended to reduce the familiarity bias, which occurs when individuals feel overly confident in evaluating simple or repetitive lotteries (Chew & Sagi, 2008; Ergin & Gul, 2009; Fox & Tversky, 1995). As in coin-tossing tasks, investors may perceive patterns even in environments where probabilities are symmetric (Ayton & Fischer, 2004). By employing a random walk structure with multiple variation levels, we created a setting that was simultaneously unpredictable and suggestive of structure. This strategy builds on the design proposed by Huber et al. (2010), replacing abstract betting choices with portfolio decisions involving assets of varying volatility.

An additional advantage of our design is that the resulting distributions of multi-asset portfolio returns were approximately normal. This property allowed asset performance to be characterized using only mean and variance, thereby avoiding the complexities associated with non-quadratic utility functions. The assumption of normally distributed returns is consistent with prior experimental studies in finance, such as Weber and Camerer (1992).

The experimental design also aimed to mitigate ambiguity bias while maintaining control over familiarity. Ambiguity, as originally discussed by Ellsberg (1961), refers to the uncertainty experienced when individuals face complex or ill-defined probability distributions. Unlike previous studies such as Weber and Camerer (1998), which offered seven purchase options, our design limited choices to three risky assets and one risk-free alternative. Each risky asset was associated with a clearly defined risk and return profile: high, medium, or low. This structure enabled participants to make decisions within a well-specified environment, thereby reducing ambiguity in portfolio selection.

Balancing familiarity and ambiguity in the multi-asset environment was essential to establishing the relevant information set for the formation of subjective expectations. Building on the approach proposed by Ayton and Fischer (2004), our design allowed participants to develop beliefs about trend continuation based on observed price dynamics, rather than on explicit cues or instructions. Investment decisions were guided by graphical displays of past asset prices, along with summary indicators such as recent averages, historical maxima, and minima. These elements were presented directly on the interface and served as visual references for individual expectations about future performance.

The price series generated by our algorithm behaved as expected and exhibited approximately normal distributions. All assets passed the Shapiro–Wilk normality test, with p-values above 0.05, indicating no significant deviation from normality. Figure 1 displays the time series produced by the simulation. Asset A is shown as a solid line with circular markers, Asset B as a dotted line with square markers, and Asset C as a dash-dotted line with cross markers.

3.2. Procedure and Treatments

The experiment received approval from two Research Ethics Committees: decision No. 2.558.540 at the University of Brasília (UnB) and decision No. 2.850.741 at the Federal University of Tocantins (UFT). Prior to full implementation, we conducted pilot sessions to evaluate the clarity of the on-screen instructions, participants’ understanding of the task, and the functionality of key design components. One of the objectives was to assess whether participants’ behavior would vary depending on their awareness of the price-generation process, as suggested by Barberis and Thaler (2003).

The pilot sessions included two groups of 14 undergraduate students from UFT. One group received explicit information about the risk structure of each asset, while the other group was only informed that prices would be determined randomly. In the informed group, the instructor explained that asset A involved high risk, asset B medium risk, and asset C low risk, with gains and losses corresponding to these categories. Participants in this group displayed more differentiated purchasing behavior following price increases or decreases, consistent with the behavioral dynamics under investigation. Based on these observations, we adopted the known-distribution format described by Weber and Camerer (1998) for the final experiment. The pilot sessions also supported the refinement of the experimental instructions, validation of the on-screen information, and definition of the optimal number of rounds.

A total of 226 undergraduate students from various academic programs at UFT and UnB were recruited to participate in the experiment. After applying exclusion criteria, the final sample comprised 208 participants. We applied an exclusion criterion to remove participants who demonstrated a fundamental misunderstanding of the task. Specifically, participants who believed that only a single asset or a single unit could be purchased per round were excluded from the final sample. This misunderstanding was identified through their observed behavior during the experimental sessions. In total, 18 participants were excluded based on this criterion. The full dataset from the validated sample is publicly available on Mendeley Data (Morais, 2025). Although we collected basic demographic data (age, gender, academic program, and academic semester), we deliberately chose not to include these variables in the analysis, as our focus was on behavioral patterns related to the experimental manipulations. These data are available in our repository for potential future analyses.

The experimental sessions were conducted between August 2018 and May 2019 in computer laboratories at both universities. Each session included a maximum of 20 participants, who were seated at individual workstations to prevent communication. All participants signed a written informed consent form before the beginning of the activity. Each session lasted approximately 30 min.

Participants were informed that only one-third of them would be randomly selected to receive monetary compensation at the end of the session. For those selected, the payment was determined as 0.02% of the accumulated portfolio value from the incentivized stage, provided the final amount was positive. This procedure allowed us to maintain a performance-based incentive while controlling for budget limitations. The full details of this payment mechanism were explicitly communicated in the experimental instructions and consent forms provided to participants. Payments ranged from BRL 9.50 to BRL 11.00, depending on the participant’s final portfolio value.

3.3. Hypotheses Tested

The central behavioral hypothesis of the experiment was whether participants would exhibit portfolio decisions consistent with the hot-hand belief. To evaluate this, we constructed two individual-level indices that capture whether asset purchases tended to increase following signals of recent success, consistent with the idea of perceived momentum. This approach follows the methodology proposed by Weber and Camerer (1998).

The first index, ${\theta }_1^i$, measures whether participant i was more likely to purchase assets after a price increase ($U_i$) than after a price decrease ($D_i$). It is defined as the normalized difference between the two conditions: ${\theta }_1^i=(U_i-D_i)/(U_i+D_i)$.

The second index, ${\theta }_2^i$, is based on participant i’s own outcomes. It compares the quantity of assets purchased after a gain ($G_i$) to the quantity purchased after a loss ($L_i$), and is defined as ${\theta }_2^i=(G_i-L_i)/(G_i+L_i)$. While ${\theta }_1^i$ captures reactions to market-level price movements, ${\theta }_2^i$ reflects whether participants increased their purchases after experiencing personal gains, which may signal perceived self-generated success. Both indices are designed to detect behavioral patterns in which perceived positive outcomes lead to increased investment activity.

The values of ${\theta }_1^i$ and ${\theta }_2^i$ range from $-1$ to 1. A value of 1 indicates that the participant made purchases exclusively after positive outcomes (price increases or gains), while a value of $-1$ indicates that purchases occurred only after negative outcomes. A value of zero reflects symmetric behavior across conditions, that is, $U_i=D_i$ or $G_i=L_i$. Positive values of either index suggest that the participant was more likely to invest following signals of success, which is consistent with the hot-hand belief.

To assess whether this pattern holds at the group level, we computed the average index values across all participants. This led to the following hypothesis:

Hypothesis 1:

${\overline{\theta }}_j>0$, with $j\in \{1,2\}$, where ${\overline{\theta }}_j$ denotes the average of the individual index values ${\theta }_j^i$.

We also investigated whether participants’ decisions to hold or repurchase assets were influenced by reference-dependent evaluations of gains and losses, as described in Prospect Theory. Since asset prices were exogenously determined, we used descriptive statistics to examine how individuals reacted to different pricing scenarios. Following Barberis et al. (2001), we considered three commonly used reference points in behavioral finance: the asset’s purchase price (i.e., the most recent transaction price), the recent average price, and the maximum historical price observed during the task. Hypotheses 2, 3, and 4 test whether participants were more likely to retain or repurchase assets when the current price exceeded each of these benchmarks.

Hypothesis 2 (Purchase price reference point):

Participants are more likely to hold or repurchase assets when the current price is above the price they previously paid than when it is below.

Hypothesis 3 (Recent average price reference point):

Participants are more likely to hold or repurchase assets when the current price is above the recent average price than when it is below.

Hypothesis 4 (Maximum price reference point):

Participants are more likely to hold or repurchase assets when the current price is above the maximum price observed than when it is below.

In addition to responses to individual price and performance signals, we examined whether participants exhibited inertia in their portfolio decisions following favorable outcomes. Specifically, we tested whether success in prior rounds increased the likelihood of repeating or maintaining the same asset allocation. This behavior would reflect a reinforcement mechanism consistent with the hot-hand belief applied at the portfolio level.

Hypothesis 5 (Portfolio-level reinforcement):

Participants are more likely to repeat or maintain a portfolio configuration after a sequence of successful results.

Together, these five hypotheses capture the central behavioral mechanisms explored in the experiment. They allow us to test for decision patterns consistent with the hot-hand belief, the role of reference-dependent evaluation, and the persistence of choice strategies under perceived success. The next section presents the empirical results derived from this framework.

4. Results and Discussion

The descriptive statistical analysis of both stages, as presented in

Table A1. Descriptive statistics.

Period	Variable		N	Mean	St. Dev.	Min	Max
−17	Shares Purchased	A	208	8.264	7.904	0	50
		B	208	9.933	8.163	0	50
		C	208	9.587	8.322	0	50
		Total	208	27.784	17.003	0	50
	Shares Cost	A	208	829.327	789.885	0	5000
		B	208	993.269	816.291	0	5000
		C	208	955.288	833.577	0	5000
		Total	208	2777.885	1700.324	0	5000
−14	Shares Purchased	A	208	8.058	7.536	0	40
		B	208	9.538	8.825	0	46
		C	208	10.361	8.554	0	45
		Total	208	27.957	15.551	2	54
	Shares Cost	A	208	1003.514	944.965	0	4920
		B	208	848.923	785.142	0	4094
		C	208	1130.351	931.651	0	4905
		Total	208	2982.788	1642.812	178	5000
−11	Shares Purchased	A	208	8.005	7.480	0	33
		B	208	9.375	11.087	0	64
		C	208	10.019	9.286	0	47
		Total	208	27.399	15.574	1	64
	Shares Cost	A	208	1184.712	1107.100	0	4884
		B	208	730.500	863.961	0	4992
		C	208	1061.529	983.913	0	4982
		Total	208	2976.740	1627.623	78	5000
−8	Shares Purchased	A	208	7.986	8.314	0	40
		B	208	10.399	14.444	0	72
		C	208	10.904	10.174	0	45
		Total	208	29.288	17.343	2	72
	Shares Cost	A	208	998.197	1039.271	0	5000
		B	208	717.534	996.609	0	4968
		C	208	1185.899	1105.996	0	4905
		Total	208	2901.630	1619.813	138	5000
−5	Shares Purchased	A	208	15.769	22.094	0	92
		B	208	8.760	9.222	0	58
		C	208	11.596	10.993	0	41
		Total	208	36.125	23.371	1	92
	Shares Cost	A	208	851.538	1193.093	0	4968
		B	208	683.250	719.349	0	4524
		C	208	1298.769	1231.239	0	4592
		Total	208	2833.558	1618.966	54	5000
−2	Shares Purchased	A	208	7.024	7.417	0	42
		B	208	6.236	5.772	0	30
		C	208	11.928	10.280	0	42
		Total	208	25.188	13.930	0	42
	Shares Cost	A	208	821.812	867.843	0	4914
		B	208	766.976	709.907	0	3690
		C	208	1419.418	1223.334	0	4998
		Total	208	3008.207	1662.491	0	5000
1	Shares Purchased	A	208	5.538	6.083	0	35
		B	208	7.024	6.666	0	46
		C	208	12.139	10.183	0	45
		Total	208	24.702	13.764	0	46
	Shares Cost	A	208	775.385	851.625	0	4900
		B	208	760.154	719.283	0	4968
		C	208	1334.808	1119.861	0	4950
		Total	208	2870.346	1586.954	0	4994
2	Shares Purchased	A	208	6.625	8.298	0	43
		B	208	7.721	8.582	0	50
		C	208	11.827	9.860	0	43
		Total	208	26.173	14.302	2	53
	Shares Cost	A	208	761.875	952.373	0	4945
		B	208	717.620	798.507	0	4650
		C	208	1359.543	1133.617	0	4945
		Total	208	2839.038	1539.845	230	4995
3	Shares Purchased	A	208	5.413	5.922	0	36
		B	208	9.587	11.916	0	60
		C	208	12.274	9.724	0	40
		Total	208	27.274	14.313	2	60
	Shares Cost	A	208	740.808	807.714	0	4896
		B	208	785.702	977.086	0	4920
		C	208	1473.462	1166.841	0	4800
		Total	208	2999.971	1496.792	240	4998
4	Shares Purchased	A	208	7.168	8.609	0	44
		B	208	8.572	9.249	0	52
		C	208	11.053	10.205	0	40
		Total	208	26.793	13.905	2	52
	Shares Cost	A	208	810.014	972.859	0	4972
		B	208	812.067	877.660	0	4940
		C	208	1359.505	1255.245	0	4920
		Total	208	2981.587	1546.876	190	5000
5	Shares Purchased	A	208	4.933	6.526	0	36
		B	208	9.620	12.259	0	62
		C	208	11.298	9.985	0	40
		Total	208	25.851	14.998	0	62
	Shares Cost	A	208	670.846	887.496	0	4896
		B	208	769.615	980.758	0	4960
		C	208	1378.365	1218.216	0	4880
		Total	208	2818.827	1573.459	0	5000
6	Shares Purchased	A	208	8.562	9.823	0	44
		B	208	11.034	15.345	0	72
		C	208	10.784	9.948	0	39
		Total	208	30.380	17.088	0	72
	Shares Cost	A	208	967.019	1110.210	0	4972
		B	208	761.322	1058.834	0	4968
		C	208	1369.524	1263.396	0	4953
		Total	208	3097.865	1567.239	0	4999
7	Shares Purchased	A	208	5.457	7.925	0	36
		B	208	16.731	23.345	0	86
		C	208	9.442	9.575	0	40
		Total	208	31.630	22.493	0	86
	Shares Cost	A	208	752.365	1092.756	0	4968
		B	208	970.385	1354.023	0	4988
		C	208	1151.962	1168.194	0	4880
		Total	208	2874.712	1646.133	0	5000
8	Shares Purchased	A	208	5.923	6.730	0	31
		B	208	23.188	33.908	0	116
		C	208	8.231	8.675	0	31
		Total	208	37.341	31.751	0	116
	Shares Cost	A	208	941.769	1068.993	0	4929
		B	208	997.062	1458.053	0	4988
		C	208	979.462	1032.292	0	3689
		Total	208	2918.293	1643.294	0	4999
9	Shares Purchased	A	208	5.303	6.630	0	35
		B	208	15.635	20.607	0	86
		C	208	10.293	9.093	0	40
		Total	208	31.231	20.907	0	86
	Shares Cost	A	208	731.798	914.982	0	4830
		B	208	906.808	1195.220	0	4988
		C	208	1255.779	1109.340	0	4880
		Total	208	2894.385	1641.567	0	5000
10	Shares Purchased	A	208	5.072	6.213	0	31
		B	208	13.490	16.088	0	72
		C	208	10.423	10.527	0	41
		Total	208	28.986	17.743	0	72
	Shares Cost	A	208	808.096	999.632	0	4991
		B	208	940.788	1123.333	0	4968
		C	208	1255.375	1276.803	0	4961
		Total	208	3004.260	1679.705	0	4998

, reveals distinct patterns in the number of shares purchased and their associated monetary value. In the first stage, the average number of shares purchased ranges from 25.18 to 36.12, with several instances reaching up to 50. The average monetary values range from 683.25 to 1419.41 units, and the data exhibit substantial dispersion, with standard deviations frequently exceeding 800 in purchase values. The second stage shows a higher average number of shares purchased, particularly in period 8, where the average reaches 37.34. Standard deviations remain elevated in periods 9 and 10, with values averaging over 20 shares. Monetary values during this stage also span a broader range, with averages between 670.84 and 1378.36 units per period. Overall, the second stage is marked by an increase in the number of shares purchased and more moderate monetary value fluctuations compared to the first.

To test Hypothesis 1, we analyzed the average values of the two indices, ${\theta }_1^i$ and ${\theta }_2^i$, which capture whether participants tended to increase their asset purchases following recent gains in price or personal performance. These indices reflect behavioral patterns consistent with the hot-hand belief, as defined in the experimental framework. Since the Shapiro–Wilk test indicated that the distributions of both indices significantly deviated from normality ($p<0.01$), we applied the Wilcoxon signed-rank test with continuity correction to assess whether the median values differed from zero.

The analysis was structured into five time blocks to capture the evolution of participants’ behavior throughout the experiment. The first block included all six decisions made during the initial, non-incentivized stage (labeled “<1”), in which each decision applied to three consecutive rounds. The following three blocks covered sequential intervals of decisions in the second, incentivized stage: decisions 1 to 4, 5 to 7, and 8 to 10. The final block aggregated all decisions from the entire second stage (decisions 1 to 10). The results are summarized in

Table 2. Wilcoxon signed-rank test for the average values of both indices.

Rounds	${\overline{\mathit{\theta }}}_1$	${\overline{\mathit{\theta }}}_2$
<1	0.27 ***	0.28 ***
	(0.73)	(0.73)
1–4	0.28 ***	0.32 ***
	(0.58)	(0.59)
4–7	−0.42 ***	−0.41 ***
	(0.57)	(0.60)
7–10	0.14 ***	0.11 ***
	(0.66)	(0.70)
1–10	−0.001	−0.007
	(0.68)	(0.70)

Note: *** $p\le 0.01$, standard deviation in parentheses.

.

In the first stage, both indices exhibited positive median values that were statistically different from zero. The median for ${\theta }_1^i$ was 0.27, and for ${\theta }_2^i$, 0.28. These results suggest that participants were more likely to increase their purchases following either a price increase or a personal gain than after a decrease or a loss. This behavior is consistent with decision patterns predicted by the hot-hand belief during the early phase of the experiment.

These results suggest that participants’ buying behavior was moderately influenced by recent outcomes, with a tendency to increase purchases following prior success. This feedback-driven behavior was more pronounced in the early stages, when the frequency of positive outcomes was higher. As participants were increasingly exposed to persistent negative price trends, however, this pattern weakened. Loss aversion began to play a more dominant role, leading individuals to adjust their portfolios in ways that overrode initial reinforcement-based responses. These shifts reflect a dynamic learning process, in which portfolio rebalancing is shaped by evolving performance signals and emotional responses to gains and losses.

Our approach to capturing hot-hand-consistent behavior differs substantially from previous studies such as Hendricks et al. (1993), Sundali and Croson (2006), and Huber et al. (2010). These works typically investigate belief in streaks by observing participants’ responses to the past performance of third-party agents, such as mutual fund managers or simulated “experts.” In contrast, our experiment was specifically designed to examine whether individuals form such beliefs based on their own performance in a multi-asset portfolio environment. This conceptual shift—from attributing skill to others toward forming expectations through personal feedback—required a different empirical strategy and behavioral framework.

In a dynamic portfolio environment with multiple assets and automatic liquidation, participants do not make one-time choices among fixed options. Rather, they continuously reallocate resources in response to observed outcomes and perceived asset trends. To capture this adaptive behavior, we constructed indices that measure the relative difference in asset purchases following gains versus losses, or after price increases versus decreases. These metrics align with the experimental structure and reflect how individuals incorporate personal feedback into decision-making. Although our method differs from traditional formulations used in studies of the disposition effect, it yields consistent and interpretable results. For instance, in the first stage, the average values of ${\theta }_1$ and ${\theta }_2$ exceeded the benchmark reported by Weber and Camerer (1998) (0.155), reinforcing the robustness and relevance of our approach.

At the beginning of the second stage, the indices remained statistically positive, indicating a continuation of the behavioral pattern observed in the initial phase—participants were still more likely to invest following perceived success. However, this tendency reversed between rounds 4 and 7, with both indices turning negative on average. In the final block (rounds 7–10), the indices recovered slightly, returning to positive values, though at lower levels than those recorded earlier. When aggregated across the entire second stage (rounds 1–10), the average values of both indices approached zero, suggesting that hot-hand-consistent behavior had progressively diminished over time.

These findings indicate that hot-hand-consistent behavior was not sustained throughout the experiment. Although participants initially adjusted their portfolios in response to perceived patterns of success, prior gains no longer shaped decisions as the task progressed. The decline in the indices reflects a reduced tendency to increase purchases after favorable outcomes. This behavioral shift aligns with the predictions of Prospect Theory, which suggests that individuals are generally reluctant to realize losses and tend to hold onto underperforming assets while selling winners too early. As we show in the following analyses, this transition becomes particularly salient in the case of asset B, whose persistent price decline during the second stage appears to have triggered a loss-averse adjustment in portfolio choices.

Hypothesis 2 proposes that participants are more likely to retain or repurchase assets when the current price is above the original purchase price—a classic reference point in Prospect Theory. In the context of automatic liquidation between rounds, this behavior manifests as a greater tendency to repurchase an asset following a gain than after a loss.

Table 3. Number and percentage of assets repurchased after gains and losses, by asset and round.

	Rounds	A		B		C		Overall
		Total	%	Total	%	Total	%	Total	%
Gain	<1	3522	40	4095	48	9475	89	17,092	61
	1–4	969	30	1522	32	7037	100	9528	64
	4–7	1807	61	0	0	2117	35	3924	24
	7–10	1846	66	5765	57	1823	34	9434	52
	1–10	4622	51	7287	33	10,977	59	22,886	46
Loss	<1	5192	60	4354	52	1203	11	10,749	39
	1–4	2247	70	3185	68	0	0	5432	36
	4–7	1151	39	7107	100	3973	65	12,231	76
	7–10	958	34	4349	43	3515	66	8822	48
	1–10	4356	49	14,641	67	7488	41	26,485	54

presents the total number of shares repurchased under both conditions. The results mirror the patterns observed under Hypothesis 1, particularly during the early rounds, and are consistent with hot-hand-influenced behavior reinforced by perceived success.

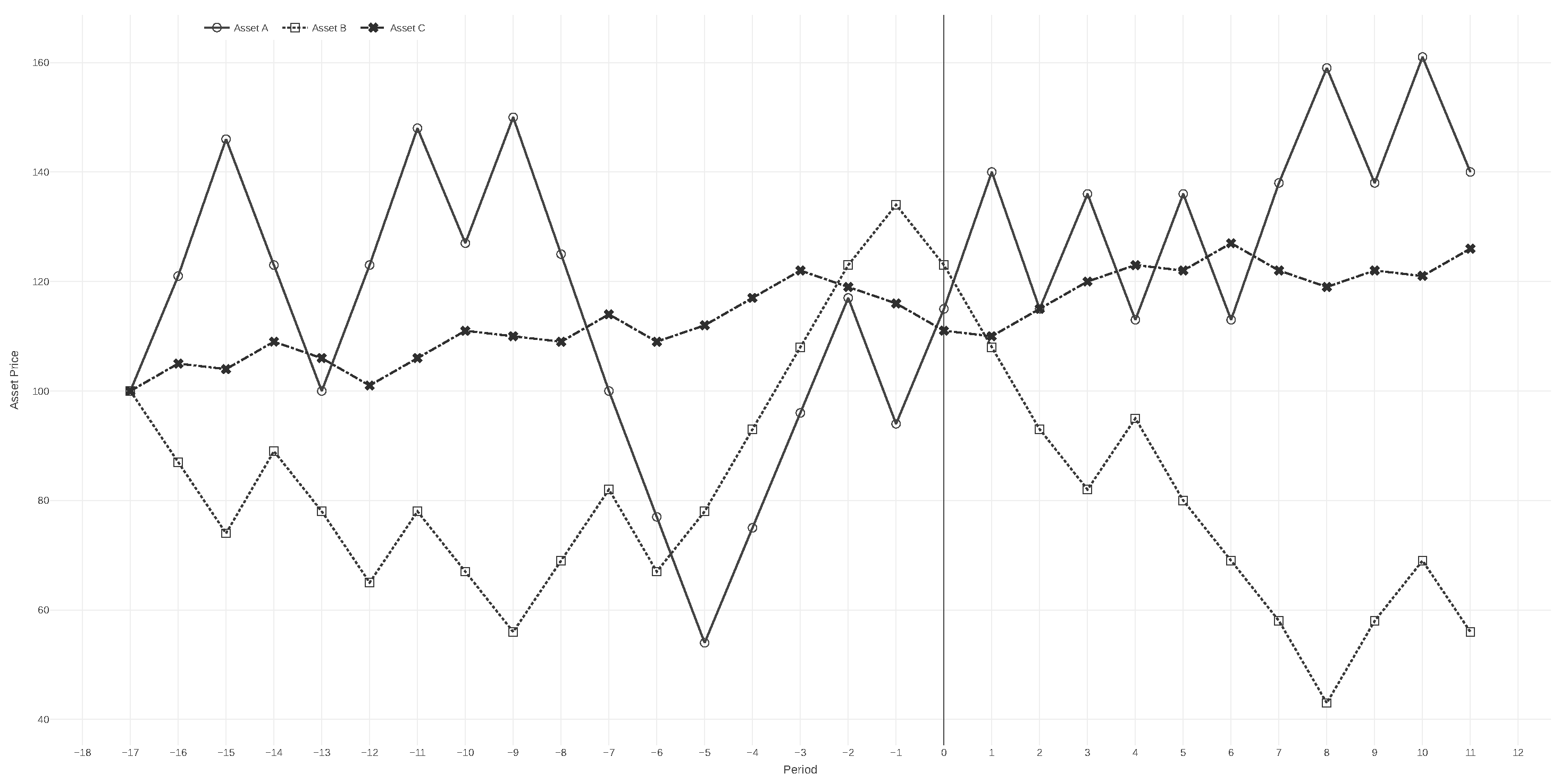
During the first stage and the initial rounds of the second stage, participants repurchased more than 60% of assets following gains, compared to just under 40% following losses. This asymmetry is consistent with hot-hand-influenced behavior, in which favorable outcomes reinforce the expectation of continued success. The effect was particularly pronounced for the low-risk asset (C), for which approximately 90% of acquisitions occurred after a gain. Asset C exhibited a predominantly positive price trajectory during the first stage, with only a minor decline in one early round (see Figure 1). In contrast, asset B followed a downward trend in the early rounds before recovering, while asset A showed the highest price variability across all rounds.

The distribution of purchases following gains and losses reflects the distinct volatility profiles of the three assets. Asset C, which had the lowest price variation and the highest frequency of gains, attracted the greatest volume of repurchases overall. It was followed by asset B, and then asset A, whose high volatility may have discouraged consistent buying. This pattern indicates that price stability and the recurrence of favorable outcomes reinforced participants’ confidence and willingness to repurchase, particularly in cases where recent gains appeared more predictable.

The data in Table 3 also illustrate how hot-hand-consistent behavior interacted with loss aversion across different assets. Although such behavior was evident in early rounds, it did not persist uniformly throughout the experiment. Instead, the patterns observed align with a broader prediction of Prospect Theory: a reluctance to realize losses. This tendency is particularly apparent when comparing repurchase behavior after gains versus losses. For assets A and C, participants generally repurchased more frequently following favorable outcomes—consistent with reinforcement-driven expectations. In contrast, asset B exhibited the opposite pattern, with repurchases increasing even amid persistent price declines, suggesting that participants were unwilling to realize losses and continued investing in hopes of recovery.

This pattern becomes even clearer when analyzing participants’ selling behavior and the associated profit outcomes. Specifically, we compared assets that were sold at any point during the experiment with those that were consistently repurchased and held until the end. The analysis revealed that participants were more likely to sell assets after gains and to continue holding those with declining values. This asymmetry reflects a classic manifestation of loss aversion: the tendency to avoid realizing losses, even when doing so leads to suboptimal portfolio performance.

Table 4. Average profit of assets sold at any point and of assets kept until the end, by asset and round.

	Rounds	A (BRL)	B (BRL)	C (BRL)	Overall (BRL)
Kept	<1	−20.9	14	13.6	7.7
	1–4	−35.0	−17	21.2	−12.4
	4–7	32.4	−50	−1.6	−12.9
	7–10	1.9	−2	4.9	3.9
	1–10	0.0	−21	7.8	−6.0
Sold	<1	−171.3	47	15.9	−54.1
	1–4	10.6	−51	18.0	−7.5
	4–7	38.0	−87	−10.8	−18.3
	7–10	−28.9	84	21.0	37.9
	1–10	9.3	−12	9.0	3.6

summarizes the average profit for sold versus held assets across experimental blocks.

The data in

Table 5. Number and percentage of assets purchased after price increases and decreases, by asset and round.

Trend	Rounds	A		B		C		Overall
		Total	%	Total	%	Total	%	Total	%
+	<1	3704	38	4384	48	10,133	89	18,221	60
	1–4	1126	28	1783	33	7312	100	10,221	61
	4–7	2161	55	0	0	2243	34	4404	24
	7–10	2287	67	6058	56	2141	36	10,486	52
	1–10	5574	49	7841	33	11,696	59	25,111	45
−	<1	6039	62	4832	52	1267	11	12,138	40
	1–4	2869	72	3600	67	0	0	6469	39
	4–7	1781	45	7776	100	4314	66	13,871	76
	7–10	1103	33	4823	44	3880	64	9806	48
	1–10	5753	51	16,199	67	8194	41	30,146	55

provide further insight into how participants adjusted their purchasing behavior in response to recent price trends. In general, individuals tended to increase their buying activity after positive trends and reduce it after negative ones. However, this behavior was not purely mechanical. Participants appeared to require repeated favorable signals before reinforcing a belief in trend continuation, indicating a cautious and selective expression of hot-hand-consistent behavior.

This pattern was particularly pronounced for asset B during rounds 1 to 8, when purchases following losses dominated the portfolio composition. Such behavior aligns with loss aversion, suggesting that participants were reluctant to realize losses despite observing unfavorable price trends. Although the proportion of purchases following gains increased slightly in the final block (rounds 7–10), the persistently negative performance of asset B likely dampened the overall effect. Specifically, 67% of purchases of asset B followed losses, compared to only 33% after gains. By contrast, assets A and C showed more balanced patterns, with post-gain purchases representing 51% and 59% of total purchases, respectively. Among the three, asset C provided the strongest indication of hot-hand-consistent behavior, as reflected in its stable upward trajectory and concentration of purchases after positive outcomes.

A more nuanced pattern emerges when considering the total number of shares repurchased in relation to recent price movements, as detailed in Table 5. The data confirm the predominance of asset B in participants’ portfolios, particularly through purchases made after price declines. Specifically, 67% of asset B acquisitions occurred following a decrease, while only 33% followed an increase. Asset A exhibited an even more pronounced asymmetry, with 72% of purchases following declines and just 28% after increases. These patterns suggest that rather than responding to short-term positive trends, participants often increased their exposure to assets experiencing losses, consistent with a reluctance to realize losses.

We further examined whether participants’ decisions to retain or sell assets were associated with realized profits. Specifically, we compared the average profit of assets that were purchased but never repurchased (classified as sold) with those that were repurchased in every subsequent round until the end of the experiment (classified as kept). Under Hypothesis 2, hot-hand-consistent behavior would imply keeping assets that had previously generated gains and selling those associated with losses. In contrast, loss aversion would lead participants to hold on to underperforming assets in an attempt to avoid realizing losses. Table 4 presents the average profits across these two categories.

This pattern was primarily driven by the behavior observed with asset B. When held until the end, asset B yielded an average loss of BRL 21, compared to a smaller average loss of BRL 12 when sold earlier. This suggests that participants who maintained positions in asset B experienced more substantial losses, potentially reinforcing their reluctance to realize them. Rather than exiting unprofitable positions, many continued to repurchase the asset, possibly in the hope of recovery. This behavior is more consistent with loss aversion than with a hot-hand expectation. By contrast, assets A and C exhibited positive average returns in both categories—sold and kept—indicating that asset-specific performance shaped the manifestation of behavioral biases across the portfolio.

To further examine how short-term trends influenced asset disposal, we analyzed cases in which participants sold an asset in period t and did not repurchase it in the subsequent one or two rounds. These instances offer a window into participants’ responses to recent price dynamics. As shown in

Table 6. Number of sales in period t, conditional on price changes in the two previous periods.

Rounds	Price Trend		Sales	Units Sold	%
	${\mathit{t}}_{-2}$	${\mathit{t}}_{-1}$
<1	U	U	255	3294	32.39
	D	U	514	3916	38.50
	–	U	769	7210	70.89
	U	D	227	1571	15.45
	D	D	205	1390	13.67
	–	D	432	2961	29.11
1–4	U	U	169	1235	24.92
	D	U	220	2122	42.83
	–	U	389	3357	67.75
	U	D	147	773	15.60
	D	D	141	825	16.65
	–	D	288	1598	32.25
4–7	U	U	0	0	0.00
	D	U	282	2454	44.55
	–	U	282	2454	44.55
	U	D	305	2207	40.06
	D	D	109	848	15.39
	–	D	414	3055	55.45
7–10	U	U	125	1430	21.22
	D	U	212	2901	43.04
	–	U	337	4331	64.26
	U	D	157	1056	15.67
	D	D	164	1353	20.07
	–	D	321	2409	35.74
1–10	U	U	294	2665	15.49
	D	U	714	7477	43.46
	–	U	1008	10,142	58.95
	U	D	609	4036	23.46
	D	D	414	3026	17.59
	–	D	1023	7062	41.05

, we classified the price sequences preceding each sale into four categories based on the direction of price changes in the two prior periods ($t-1$ and $t-2$): two consecutive increases (UU), a decrease followed by an increase (DU), an increase followed by a decrease (UD), and two consecutive decreases (DD).

According to Hypothesis 2, if participants were guided by the hot-hand belief, we would expect fewer sales after price sequences suggesting upward momentum, such as two consecutive increases (UU) or a decrease followed by an increase (DU).

The data from the second stage reveal that participants’ selling behavior was indeed responsive to recent trends. Notably, sales were most frequent following DU sequences, in which a price increase was preceded by a decline—accounting for 43.46% of all cases. In contrast, only 23.46% of sales occurred after UD sequences (increase followed by a decrease). When grouped by the final signal, sequences ending in an increase (UU and DU) represented 58.95% of all sales, while those ending in a decrease (UD and DD) accounted for 41.05%.

A closer look at consistent price trends reveals an informative asymmetry. Participants sold less frequently after two consecutive increases (UU: 15.49%) than after two consecutive decreases (DD: 17.59%). This suggests that persistent upward trends were less likely to prompt asset liquidation, whereas sustained declines more often triggered sales. The pattern offers partial support for hot-hand-consistent behavior, as positive streaks appear to reduce selling pressure. At the same time, it reflects a degree of caution: participants did not respond mechanically to short sequences, indicating that belief in trend continuation was selectively applied.

The findings above suggest that the last observed price may have functioned as an inverted reference point in participants’ decisions. Instead of reinforcing the hot-hand effect, this benchmark appeared to activate loss aversion, increasing the likelihood that participants would retain assets after losses and sell them after gains. Such behavior dampens hot-hand-consistent patterns and underscores the influence of emotional biases—particularly the reluctance to realize losses—even in the absence of economic rationale.

To further investigate this mechanism, we tested Hypotheses 3 and 4, which introduce alternative reference points grounded in historical price benchmarks. Hypothesis 3 examines whether participants are more likely to hold assets when the current price exceeds the recent average, while Hypothesis 4 considers the maximum price observed up to the previous period.

Table 7. Sales in period t, by whether the current price is above or below the average or maximum observed until $t_{-1}$.

Rounds	Price Trend	Average			Maximum
		Sales	Units Sold	%	Sales	Units Sold	%
<1	U	800	7341	72.18	153	926	10.47
	D	401	2830	27.82	884	7920	89.53
1–4	U	389	3357	67.75	26	209	4.71
	D	288	1598	32.25	580	4230	95.29
4–7	U	449	3762	68.29	21	219	4.35
	D	247	1747	31.71	617	4821	95.65
7–10	U	426	2962	43.95	31	250	4.31
	D	232	3778	56.05	483	5556	95.69
1–10	U	1264	10,081	58.60	78	678	4.44
	D	767	7123	41.40	1680	14,607	95.56

Note: The trend is defined relative to the reference values accumulated up to period $t_{-1}$.

presents the number of sales in period t according to whether the current price was above or below these respective benchmarks.

The results reveal a pattern consistent with the interpretation of the recent average price as an inverted reference point. Participants sold more frequently when the current price was above the recent average—exceeding 56% of sales in most blocks—than when it was below. This asymmetry suggests that price recoveries may have prompted realization of gains. In contrast, no such asymmetry was observed for the maximum price. When the current price was below the historical maximum, sales were concentrated following price declines. In the second stage alone, over 90% of these sales occurred after a decrease, indicating that the maximum price likely functioned not as an inverted reference but rather as a psychological ceiling or anchor influencing participants’ expectations.

Finally, we tested whether participants were more likely to maintain a given portfolio composition following a sequence of favorable outcomes than after unfavorable ones. This behavior, predicted by the hot-hand hypothesis, reflects reinforcement learning, whereby recent success leads to the continuation or replication of previous choices. An investor influenced by such belief would increase exposure to assets with upward trends and low variability, while reducing or avoiding positions in more volatile or declining assets. In this framework, past success is taken as a signal of future success, whereas past failure suggests future underperformance.

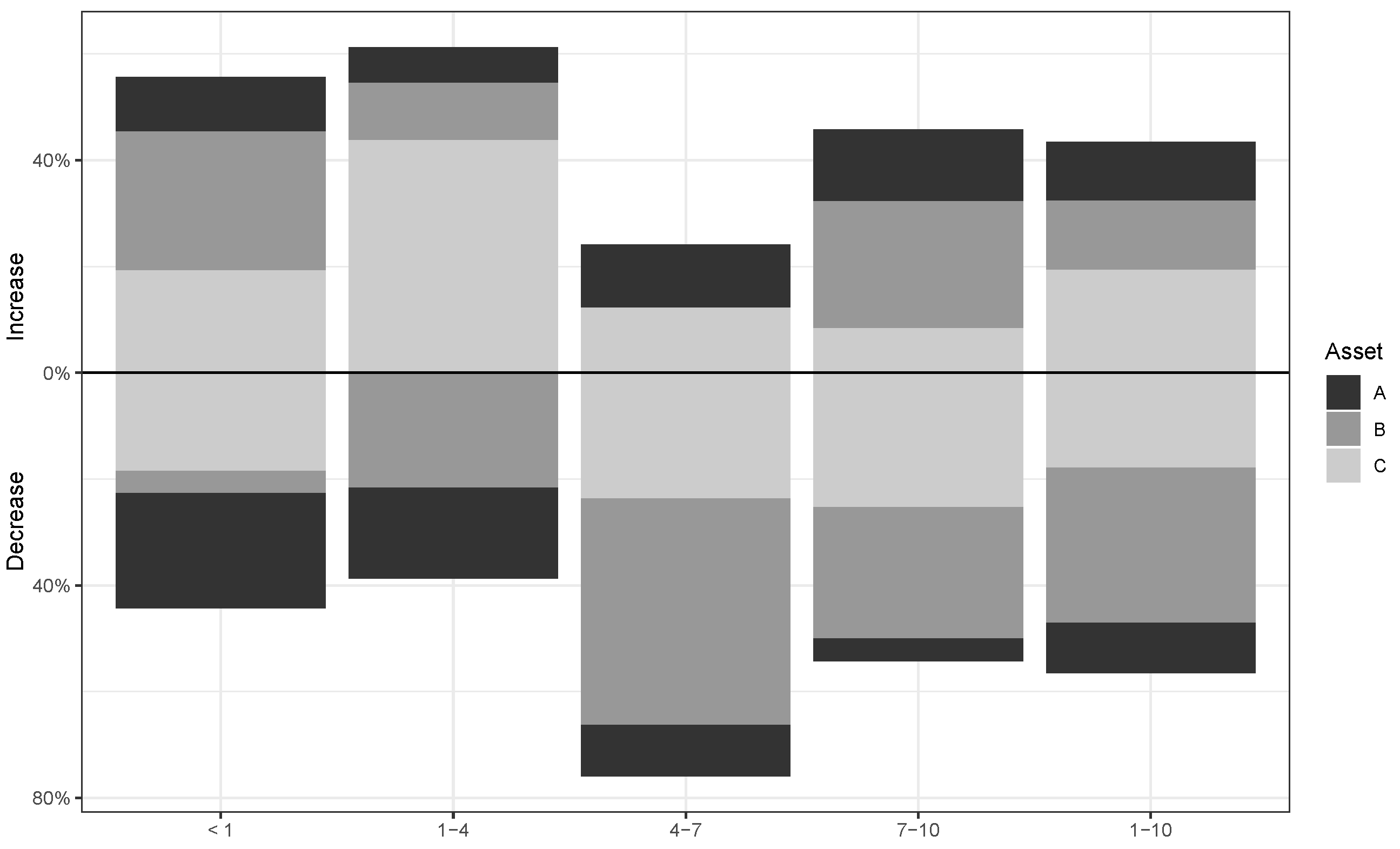
Figure 2 illustrates the evolution of portfolio composition over time, displaying the proportion of each asset purchased after price increases or decreases. The data are grouped by blocks of rounds, allowing for a comparison of behavioral patterns across different phases of the experiment.

In the first stage (<1) and during the initial block of the second stage (rounds 1–4), participants’ decisions were consistent with the hot-hand effect. Most purchases occurred after price increases, as indicated by the predominance of positive bars in Figure 2. In this early phase, asset C represented 43.8% of all acquisitions, reflecting its relatively stable and upward-trending price path. In contrast, asset B exhibited a downward trajectory, while asset A showed substantial volatility. As a result, purchases of assets B and A were markedly lower, accounting for just 10.7% and 6.7% of the total, respectively.

However, this pattern shifted markedly in the middle and final blocks. Between rounds 4 and 7, nearly 43% of all purchases were allocated to asset B, despite its persistent negative trend. During this phase, most acquisitions of both assets B and C followed losses, amounting to approximately two-thirds of total purchases. This behavior continued in the final block (rounds 7–10), with asset B consistently repurchased after unfavorable outcomes. In total, asset B represented 29.2% of acquisitions across the second stage, notwithstanding its higher volatility and poor performance. This sustained preference suggests a reluctance to realize losses—a hallmark of loss aversion—and helps explain the reduced expression of hot-hand-consistent behavior in the later rounds.

The average portfolio composition further illustrates a departure from hot-hand behavior, particularly in response to the negative performance of asset B. Faced with repeated losses and elevated price volatility, participants increased their holdings in asset B, despite its deteriorating outlook. This pattern points to a dominant role of loss aversion, as individuals appeared unwilling to realize losses and instead reinforced their positions in anticipation of a rebound.

In contrast, portfolio adjustments involving assets A and C were more consistent with hot-hand behavior. Participants increased exposure to these assets when price trends were favorable and reduced allocations when volatility intensified. These contrasting patterns help explain the divergent portfolio trajectories: while assets A and C followed a behaviorally adaptive path, asset B remained prominent due to a reluctance to acknowledge realized losses.

To reinforce these observed patterns, we applied the Wilcoxon rank-sum test to compare the average number of purchases made after price increases versus decreases. The test results indicated statistically significant differences in most blocks, confirming that participants’ investment decisions were influenced by recent price trends. The only exception occurred in the aggregated block encompassing rounds 1–10, where statistical significance was found solely for asset C. This outcome strengthens the interpretation that hot-hand behavior was more pronounced for asset C, whose price dynamics were relatively stable and consistently upward-trending.

Overall, participants adjusted their portfolio composition in response to recent price trends, increasing exposure to assets following gains and reducing it when price variance rose. This behavior explains the divergent trajectories of assets A and C, whose allocations shifted according to market signals, versus the sustained allocation to asset B, despite its poor performance. These patterns support the interpretation that hot-hand belief influenced investment decisions in the presence of consistent gains, while loss aversion played a more prominent role when facing sustained losses. Taken together, the results offer a nuanced view of how cognitive and emotional biases interact in dynamic portfolio settings, a theme further explored in the concluding section.

5. Conclusions

We conducted a laboratory experiment to examine whether the hot-hand belief, typically framed as an exogenous perception, can arise endogenously from an investor’s own performance feedback. Departing from previous studies that investigate beliefs about external agents, such as fund managers or “experts,” our approach focused on belief formation grounded in personal investment experience. By isolating this mechanism within a controlled financial environment with random price sequences, we offer new evidence on how internally generated cognitive biases can influence portfolio choices.

Participants initially displayed behavior consistent with the hot-hand belief, increasing their asset purchases following prior gains or price increases. However, this pattern weakened as the experiment progressed and losses accumulated, particularly in the case of asset B, which exhibited a persistent negative trend and high volatility. Under these conditions, loss aversion dominated: participants continued to allocate resources to declining assets, suggesting reluctance to realize losses, even when doing so compromised portfolio performance.

These results contribute to the behavioral finance literature by demonstrating that the hot-hand belief can emerge from self-generated performance cues and that its influence is not uniform. It is contingent on contextual feedback and interacts with emotional biases such as loss aversion. By capturing both the formation and attenuation of belief-driven behavior within a dynamic portfolio setting, the study offers a more complete understanding of how cognitive heuristics and emotional responses shape decision-making under risk.

Although the experimental setting enabled precise control of price dynamics and feedback mechanisms, it has some limitations. Participants were undergraduate students recruited through convenience sampling at two public universities in Brazil, which limits the socioeconomic and demographic diversity of the sample. Their behavior may not fully reflect that of experienced investors or the broader population. In addition, although we collected basic demographic variables such as age, gender, academic program, and academic semester, we did not use them in the analyses, as our primary focus was on the experimental manipulations. The sample also involved self-selection, which further limits external generalizability.

Moreover, although we employed a monetary incentive mechanism, in which one-third of participants were randomly selected to receive payments based on their portfolio performance, the stakes were relatively modest. This feature may not fully replicate the psychological effects of real-world financial decisions. Future research could address these limitations by employing higher and more uniform monetary stakes, using more heterogeneous samples, and adopting longitudinal designs that capture learning and adaptation over time.

Understanding how belief formation and emotional responses jointly drive financial decisions remains a central challenge in behavioral economics. Our findings provide novel insights into the conditions under which the hot-hand belief emerges and persists, and how it interacts with loss aversion in portfolio contexts. These insights may inform not only theoretical debates on investor psychology but also the design of educational, institutional, or technological tools aimed at reducing behavioral distortions in financial choices.