Stock Return Prediction on the LQ45 Market Index in the Indonesia Stock Exchange Using a Machine Learning Algorithm Based on Technical Indicators

Abstract

Stock return prediction in emerging markets remains difficult due to the gap between theoretical efficiency and empirical irregularities. This study assesses the statistical and economic performance of Linear Regression, Ridge Regression, Random Forest, and XGBoost in forecasting 5-day and 21-day returns for six LQ45 stocks (2016–2025). Momentum, volatility, trend, and volume indicators are used as predictors, while model performance is evaluated using MAE, RMSE, R², and backtested trading metrics that include transaction costs. All models yield near-zero or negative R², directional accuracy of 49–54%, and AUC around 0.50–0.53, indicating weak signals overshadowed by noise. XGBoost offers the lowest statistical errors, but Ridge Regression achieves slightly better risk-adjusted outcomes (Sharpe 0.1232), although every strategy underperforms Buy & Hold. SHAP results show volatility and volume features as most influential, but with minimal absolute impact. Overall, the LQ45 market exhibits semi-efficiency: patterns exist but fail to translate into profitable trading once real-world frictions are considered, underscoring the gap between statistical predictability and economic viability in algorithmic trading. This research was conducted in order to support the achievement of various goals through SDG 8 (Decent Work and Economic Growth).

1. Introduction

Stock price movements in financial markets often reflect rapid macroeconomic shifts, evolving market sentiment, and heterogeneous investor behavior. In Indonesia, these dynamics are particularly pronounced among the large-cap, highly liquid equities included in the LQ45 index, a benchmark closely monitored by domestic and international investors. The fast-moving and imperfectly informed nature of this segment demands analytical approaches capable of capturing non-linear relationships, complex variable interactions, and regime shifts. Under such conditions, forecasting stock returns remains a key challenge, situated between the theoretical limits of market efficiency and the empirical potential of machine learning (ML) to uncover hidden patterns (Saberironaghi et al., 2025; Bustos et al., 2025).

This research problem is shaped by two fundamental issues. First, although the Efficient Market Hypothesis (EMH) states that asset prices fully account for available information (Fama, 1970), extensive empirical evidence documents persistent technical, value, and momentum anomalies across emerging market stock markets, including Indonesia (Rouwenhorst, 1999; Cakici et al., 2013; Zaremba & Szyszka, 2016; Azevedo & Hoegner, 2023; Peng & Yao, 2023). Rouwenhorst (1999) identified momentum effects across various emerging stock markets, while Cakici et al. (2013) found that value and momentum factors consistently yield significant returns across 18 emerging economies. More recently, Zaremba and Szyszka (2016) documented momentum in over 100 equity anomalies in the Polish emerging market. These findings imply that information frictions, behavioral biases, and heterogeneous investor reactions hinder full price efficiency, creating room for data-driven predictive modeling. Second, much of the existing machine learning (ML) literature emphasizes statistical performance, typically using R², RMSE, and MAE, without evaluating whether these predictions produce economically meaningful results. In practice, investors prioritize profitability, stability, and risk-adjusted returns, rather than simply predictive accuracy. This gap highlights the need for more comprehensive evaluations that integrate statistical and economic perspectives. Driven by this gap, this study evaluates the performance of four ML algorithms: Linear Regression, Ridge Regression, Random Forest, and XGBoost in forecasting LQ45 stock returns over the short (5-day) and medium (21-day) periods. The selection of these timeframes reflects two commonly used investment cycles: the 5-day timeframe captures short-term trading volatility, while the 21-day timeframe approximates the monthly adjustment period commonly used in institutional portfolio rebalancing. Furthermore, this study focuses on six LQ45 constituents that provide complete historical price and volume data, are continuously listed, and exhibit minimal corporate action distortion, ensuring consistent feature availability and comparability throughout the analysis period. The primary objective is to bridge the gap between statistical predictability and economic profitability in ML-based return forecasting in partially efficient emerging markets.

To achieve this objective, this study answers the following research questions:

• RQ1: Which ML algorithm achieves the highest statistical accuracy for short- and medium-term return prediction?
• RQ2: Does higher statistical accuracy lead to superior economic profitability when applied to realistic trading strategies with transaction costs?
• RQ3: Which technical indicators contribute most strongly to predictive performance, and how do these contributions differ between linear and nonlinear models?

These research questions establish a coherent analytical framework that connects theoretical motivation, empirical design, and performance evaluation across statistical and economic dimensions. This research leverages advances in the ML-finance literature demonstrating the capacity of ML models to capture nonlinear dependencies, enhance predictive stability, and improve portfolio performance. Evidence from Azevedo and Hoegner (2023), Peng and Yao (2023), and Chun et al. (2024) suggests that ensemble models and regularized linear models often provide robust predictive results across a variety of market environments. Furthermore, recent contributions in ML-based portfolio construction emphasize the importance of integrating prediction, risk management, and economic evaluation to support more effective investment decisions (Sukono et al., 2024a; Fransisca et al., 2024; Sukono et al., 2024b).

This study makes four key contributions. First, it provides new empirical evidence on ML-based return prediction in Indonesia, an emerging market that exhibits partial market efficiency and remains underrepresented in quantitative finance research. Second, it introduces an integrated evaluation framework that combines statistical accuracy with economic performance measures such as the Sharpe ratio, total return, and maximum drawdown, thus aligning model assessments more closely with real-world investment objectives. Third, the findings demonstrate that higher model complexity does not necessarily yield superior economic results: regularized linear models such as Ridge Regression can match or outperform more complex ensemble methods such as XGBoost, underscoring the importance of parsimony and robustness in noisy market environments. Fourth, it incorporates SHAP-based interpretability to identify the most influential technical indicators, offering practical value for feature engineering, model governance, and the development of AI-assisted trading systems.

2. Literature Review

2.1. Basic Concepts of Stock Return Prediction

Stock return prediction is a central topic in modern finance because it is directly related to market efficiency and optimal portfolio formation. Conceptually, stock returns describe the level of profit an investor obtains from changes in stock prices and dividends over a specific period. According to the Efficient Market Hypothesis (EMH) introduced by Fama (1970), market prices always reflect all available information, making it impossible for investors to consistently obtain abnormal returns through historical analysis. However, various empirical studies have subsequently shown that market efficiency is relative, and the existence of market anomalies such as momentum, size, and calendar effects creates opportunities for quantitative and machine learning (ML) approaches to identify hidden patterns in stock price data (Alzyadat & Asfoura, 2021; Salur & Ekinci, 2023).

Stock return ($R_t$) is generally defined as the logarithmic change in stock price between two time periods:

$$R_t=\ln \left({\displaystyle \frac{P_t}{P_{t-1}}}\right)$$

(1)

where $p_t$ is the stock price at time $t$, and $p_{t-1}$ is the previous price. This formula is often used in financial time series analysis because it has the property of additivity, which facilitates aggregation and statistical modeling (Rouwenhorst, 1999). Predicted returns are usually categorized into two main time horizons: short-term returns (1–5 days) and medium-term returns (10–21 days), depending on the investment objective and trading strategy employed.

In practice, stock returns are influenced by a combination of fundamental factors (company financial performance, macroeconomic conditions) and technical factors (historical price patterns, trading volume, volatility). Because the relationships between these variables are complex and not always linear, conventional statistical approaches such as linear regression often fail to adequately explain return variations. This has led to the emergence of machine learning (ML) as a more flexible approach to studying non-linear patterns and high interactions between market variables (Azevedo & Hoegner, 2023).

The general relationship between future stock returns ($R_{t+h}$) and its predictor variables ($x_t$) can be represented in the form of a non-parametric function (Rapach et al., 2013; Mullainathan & Spiess, 2017; Gu et al., 2020):

$$R_{t+h}=f\left(X_t\right)+{\mathsf{\epsilon }}_t$$

(2)

where $f\left(X_t\right)$ is the function learned by the ML model, and ${\epsilon }_t$ represents the error component or market noise. Unlike classical regression, which assumes a linear form for $f$, ML approaches allow for highly flexible forms, such as decision trees, ensembles, or neural networks.

According to research by Bustos et al. (2025), ensemble models such as Random Forest and XGBoost can reduce short-term return prediction errors by 15–25% compared to linear regression. This suggests that nonlinear patterns and interactions between technical indicators play a significant role in stock price formation in modern markets. Furthermore, Peng and Yao (2023) in Empirical Economics, found that stock markets in developing countries, including South Korea, tend to exhibit semi-efficient characteristics that is, information is not fully reflected in stock prices. In these conditions, machine learning-based models with interaction learning capabilities, such as Random Forest and XGBoost, have been shown to significantly improve predictions of the direction and magnitude of returns, particularly in volatile market conditions influenced by systemic risk factors.

Thus, while the EMH theory remains the primary conceptual foundation for understanding price formation mechanisms, modern ML-based approaches provide a computational framework capable of transcending the limitations of linearity and stationarity assumptions. The combination of the two not only enriches academic studies on market efficiency but also opens up opportunities for practical application of quantitative trading strategies in the Indonesian stock market, particularly the LQ45 index, which reflects the highest liquidity and market capitalization on the Indonesia Stock Exchange (IDX).

2.2. Machine Learning in Stock Return Prediction

Machine Learning (ML) approaches have become a dominant paradigm in modern financial research due to their ability to identify non-linear patterns and complex relationships between market variables that cannot be explained by traditional econometric models (Azevedo & Hoegner, 2023). ML functions to approximate the mapping function $f\left(X_t\right)$ that links a set of technical indicators to future returns $R_{t+h}$, without having to explicitly specify a specific function form. Thus, ML is able to capture market dynamics that are non-stationary, highly fluctuating, and often influenced by investor behavior (investor sentiment).

In the literature, ML models used in stock prediction can be grouped into two broad categories: regularized linear models and ensemble-based non-linear models. Linear models maintain high interpretability and statistical efficiency, while non-linear models excel at handling complex data with strong interactions between features (Vu & Ko, 2024).

2.3. EMH, Random Walk, Short-Term Predictability

The Efficient Market Hypothesis (EMH) posits that asset prices fully and immediately reflect available information (Fama, 1970). In its strong form, price movements follow a random walk, making historical data useless for forecasting (Malkiel, 2003; Fama & French, 2010):

$$P_t=P_{t-1}+{\epsilon }_t$$

(3)

where ${\mathsf{\epsilon }}_t$ is white noise, implying that technical analysis offers no predictive power.

Empirical research, however, frequently challenges this view. Lo and MacKinlay (1988) documented positive serial correlation in returns using the variance ratio test, contradicting the independence assumption of the random walk. Lim and Brooks (2011) reported that emerging markets generally exhibit weaker information efficiency, with predictable returns even after adjusting for transaction costs. Timmermann and Granger (2004) further showed that market efficiency varies over time, with shifts between efficient periods and episodes of strong predictability during high-volatility regimes.

Behavioral finance provides theoretical grounding for these deviations. Kahneman and Tversky (1979) identified systematic cognitive biases overconfidence, anchoring, and loss aversion that generate predictable market patterns. The momentum anomaly is a key example: Jegadeesh and Titman (1993, 2001) reported strong 3–12 month momentum gains that traditional risk models cannot explain. In emerging markets, limited information flow and heterogeneous investor sophistication amplify such effects (Bekaert et al., 2007). Lesmond et al. (2004) argued that higher transaction costs slow information diffusion, improving momentum profitability, consistent with the gradual diffusion hypothesis of Hong and Stein (1999).

Short-term predictability (days to weeks) shows the strongest empirical support. Hasbrouck and Seppi (2001) found that order flow imbalances carry information about future short-term returns, while Chordia et al. (2005) showed predictability intensifies during periods of high trading volume and volatility.

From a machine learning standpoint, these inefficiencies create exploitable non-linear signals that ML models can detect through adaptive learning and regime sensitivity, particularly relevant in emerging markets where structural breaks and non-stationarity are common (Harvey et al., 2016; Gu et al., 2020). Still, Campbell and Thompson (2008) stress that statistical predictability does not guarantee economic profitability once costs and risks are considered. Welch and Goyal (2008) similarly found that many in-sample predictors fail to deliver consistent out-of-sample performance, underscoring overfitting risks.

2.4. Related Research in Emerging Markets

Emerging markets exhibit higher volatility, lower liquidity, greater information asymmetry, and stronger behavioral biases than developed markets (Bekaert & Harvey, 2002). These characteristics increase noise in financial data, challenging ML modeling but also creating exploitable inefficiencies that can improve strategy profitability. Research applying machine learning to emerging markets is limited but growing. Nti et al. (2020) conducted a systematic review identifying Random Forest, SVM, and artificial neural networks as the most common algorithms, with ensemble methods yielding 8–15% higher accuracy than single models. In Asian markets, Wang et al. (2023) improved volatility forecasting in China using ML, noting that momentum and volume-based indicators were the dominant predictors, while valuation metrics contributed only slightly to short-term performance.

Research in Indonesia is less limited but growing. Shen and Shafiq (2020) showed that combining technical and sentiment features in a hybrid deep learning model improves predictive accuracy, although they did not evaluate economic profitability or focus on individual index constituents. In Brazil, Krauss et al. (2017) reported that deep neural networks and gradient boosted trees produced superior Sharpe ratios compared to traditional buy-and-hold and factor models, reflecting the benefits of high volatility and partial inefficiency features comparable to the Indonesian market. Fischer and Krauss (2018) further demonstrated that LSTM networks capture temporal dependencies overlooked by traditional methods, thus achieving consistent predictive advantages across markets. Evidence from Central Europe reinforces these patterns. Ballings et al. (2015) compared seven ML classifiers and found that Random Forest achieved the highest AUC, with ML-based trading strategies generating excess returns during volatile regimes but underperforming in trending markets, highlighting regime sensitivity in model performance.

Recent studies have further emphasized interpretability. Carta et al. (2021) noted that black-box ML models face regulatory and risk management challenges and proposed an interpretable framework that maintains accuracy while enhancing transparency. Lundberg et al. (2020) introduced SHAP values as a unified approach to explaining ML predictions, allowing for clearer validation of feature contributions. Insights from cryptocurrency markets also offer parallels. Gradojevic and Tsiakas (2021) found that ML models outperformed econometric benchmarks in predicting crypto returns, with microstructural and sentiment variables dominating technical indicators. While structurally different from equities, these results suggest that tree-based ensemble methods can be effective in volatile and information-poor environments, which are typical of emerging markets.

2.5. Gaps and Research Opportunities

Although prior studies demonstrate the potential of machine learning to enhance stock return predictability in emerging markets, most research continues to evaluate model performance primarily through statistical metrics such as RMSE, MAE, or directional accuracy, without linking these measures to economically meaningful outcomes. Insights from Campbell and Thompson (2008) and Welch and Goyal (2008) highlight that statistical improvements rarely guarantee economic profitability once transaction costs, volatility, and drawdown risks are incorporated. This disconnect leaves unresolved whether ML-based forecasts provide tangible value in real-world investment settings, particularly in markets characterized by high frictions such as Indonesia.

Research on the Indonesian equity market remains limited and often focuses on aggregated indices rather than stock-level predictability. Such an approach overlooks the distinct liquidity profiles, volatility patterns, sector sensitivities, and microstructure characteristics of individual LQ45 constituents, making it unclear whether ML models perform consistently across different market conditions. Moreover, interpretability has received minimal attention, even though methods such as SHAP introduced by Lundberg et al. (2020) can clarify the contribution of technical indicators and support model governance, transparency, and feature validation especially important in volatile and partially efficient markets.

Another gap arises from the choice of forecasting horizons. Existing studies frequently emphasize very short horizons (intraday or one-day) or long horizons (monthly or quarterly), leaving intermediate horizons such as 5-day and 21-day returns underexplored, despite their alignment with actual trading cycles and institutional rebalancing practices. Additionally, comparative evidence on the relative effectiveness of linear versus non-linear models remains scarce. While ensemble methods like Random Forest and XGBoost often show strong statistical results, it is still unclear whether their higher complexity consistently delivers superior economic performance in noisy emerging markets, or whether regularized linear models can offer more stable and parsimonious forecasts. These gaps underscore the need for a more comprehensive research framework that integrates statistical and economic evaluation, examines stock-specific predictability within the LQ45 index, incorporates interpretability, and systematically compares linear and non-linear models across realistic investment horizons.

3. Methods

3.1. Research Framework and Procedure

This research adopts a quantitative-predictive framework that applies machine learning (ML) to model the relationship between historical market information and future stock returns (Zaremba & Szyszka, 2016). Four predictive models are used: Linear Regression, Ridge Regression, Random Forest, and XGBoost, representing interpretable linear approaches and adaptive nonlinear methods. The framework is based on the predictive return function in Equation (2), where future returns $R_{t+h}$ are expressed as a function of technical features $X_t,$ allowing for the capture of dynamic patterns that traditional econometric models often fail to represent. Beyond statistical accuracy, this research emphasizes economic relevance through backtesting simulations to evaluate the profitability and stability of signals in semi-efficient market conditions like Indonesia.

The research procedure follows a structured computational flow consisting of five sequential stages, as illustrated in Figure 1.

The process begins with Data Collection and Preprocessing, which involves obtaining stock price data, converting prices to logarithms, and handling missing values. This process continues with Feature Engineering, which includes the development of technical indicators and normalization. Model Development is then carried out by training the four models with their respective optimal parameters. The fourth stage, Validation and Evaluation, compares the statistical accuracy and economic performance of each model. Finally, Backtesting and Interpretation involves trading simulations and per-stock visualizations to assess the robustness and consistency of predictive signals across sectors and forecasting horizons.

3.2. Data and Sampling

The research data was obtained from Yahoo Finance using the Python 3.10 library $yfinance$, covering the period from 1 January 2016 to 30 September 2025. The sample consists of six LQ45 index issuers BBCA.JK (Bank Central Asia), BBRI.JK (Bank Rakyat Indonesia), BMRI.JK (Bank Mandiri), ASII.JK (Astra International), ICBP.JK (Indofood CBP Sukses Makmur), and UNVR.JK (Unilever Indonesia) (Yahoo Finance, 2025).

These issuers were selected purposively based on liquidity, trading continuity, and cross-sector representation, ensuring that the dataset reflects the structural diversity of the Indonesian capital market. Each stock contains approximately 2416–2417 daily observations, indicating balanced and continuous trading activity.

Table 1. Sample of LQ45 issuers and number of daily observations.

Ticker	Obs	Mean	Std Dev	Min	Max	Vol. (Ann.)	Skew.	Kurt	JB Stat	JB p-Value
BBCA.JK	2420	0.0005546	0.0146187	−0.0891527	0.1598490	0.232065	0.5081	9.0114	8253.9	0.0000
BBRI.JK	2420	0.0004511	0.0196741	−0.1067330	0.1864120	0.312317	0.3208	5.8133	3432.1	0.0000
BMRI.JK	2420	0.0004763	0.0202250	−0.1391720	0.1467210	0.321062	−0.0219	4.5987	2121.5	0.0000
ASII.JK	2419	0.0002088	0.0191734	−0.1216450	0.1196230	0.304369	0.1487	3.1183	983.4	0.0000
ICBP.JK	2419	0.0001443	0.0168663	−0.0938584	0.1350360	0.267744	0.1684	4.9787	2497.0	0.0000
UNVR.JK	2420	−0.0003213	0.0210455	−0.1674330	0.1771690	0.334087	0.7514	9.4359	9163.6	0.0000

summarizes the composition of the dataset across issuers.

To provide an initial understanding of market behavior, adjusted closing price trends for the six issuers are visualized, as shown in Figure 2. All issuers exhibited a long-term upward movement from 2016 to 2024, punctuated by a sharp decline in 2020 that coincided with the global COVID-19 pandemic and the resulting temporary market contraction. Following this disruption, prices gradually recovered, with the banking sector (BBCA, BBRI, BMRI) exhibiting a faster stabilization compared to the consumer goods (UNVR, ICBP) and automotive (ASII) sectors. This descriptive visualization confirms that the selected stocks maintained an active and representative trading pattern, validating their suitability for yield forecasts.

The adjusted close transformation ensures that the series reflects corporate actions such as dividends and stock splits, providing a realistic measure of capital gains. Subsequently, price transformation was applied using logarithmic returns, which stabilize variance and preserve the additive property of price changes, as expressed in Equation (1). Furthermore, forecast targets were defined as cumulative returns for five-day and twenty-one-day horizons, corresponding to weekly and monthly intervals, respectively, following Equation (3) (Rapach et al., 2013):

$$TARGE{T}_h={\displaystyle \frac{P_{t+h}-P_t}{P_t}},h\in \{1,5,21\}$$

(4)

where $P_t$ denotes the asset price at time $t$, and $P_{t+h}$ is the price after $h$ trading days. The horizons $h=1$, $h=5$ and $h=21$ correspond to weekly and monthly prediction intervals, respectively. This formulation captures the short- and medium-term dynamics of asset price movements and serves as the dependent variable in the return forecasting model.

It is important to note the distinction between the return definitions used in this study. For feature construction and model training, we employ logarithmic returns as defined in Equation (1), which provide desirable statistical properties including time-additivity and variance stabilization. However, for the target variable (dependent variable) used in prediction, we use cumulative simple returns as defined in Equation (4). This choice maintains interpretability for economic evaluation and backtesting simulations, as simple returns directly correspond to capital gains that investors realize in practice.

3.3. Feature Construction and Preprocessing

Feature engineering is applied to transform raw price and volume data into a set of technical indicators that capture momentum, volatility, trend, and volume pressure. The indicators constructed in this study consist of lagged returns ($RE{T}_{LAG1},RE{T}_{LAG5},RE{T}_{LAG10}),$ a short-term momentum measure ($MOMENTU{M}_5$), a volatility indicator ($VOLA{T}_{21}$), trend-based indicators (EMA10, EMA30, $EM{A}_{RATIO}$), oscillators (RSI14, MACD, $MAC{D}_{SIG},MAC{D}_{HIST}$), and a volume-based signal ($OB{V}_Z$). Together, these features provide a comprehensive representation of short- and medium-term market behavior.

To ensure data stability and reduce the influence of extreme observations, two preprocessing techniques are applied: winsorization and Z-score normalization. The winsorized variable $X_i^{\ast }$ is defined as follows:

$$X_i^{\ast }=\left\{\begin{array}{cc}\hfill Q_{0.01},& if X_i < Q_{0.01}\hfill \\ \hfill Q_{0.99},& if X_i > Q_{0.99}\hfill \\ \hfill X_i,& otherwise\hfill \end{array}\right.$$

(5)

This transformation limits the effect of outliers by capping extreme values below the 1st percentile and above the 99th percentile, effectively stabilizing the data distribution without discarding any observations. After winsorization, all features are standardized using Z-score normalization, expressed as:

$$Z_i={\displaystyle \frac{X_i-{\mu }_X}{{\sigma }_X}}$$

(6)

where $\mu X$ and $\sigma X$ denote the mean and standard deviation of variable $X$, respectively. This normalization rescales the variables to have a mean of zero and a standard deviation of one, allowing for comparability among features with different units and magnitudes. The combination of winsorization and Z-score normalization ensures that the model training process becomes more robust and less sensitive to skewness or heteroscedasticity in the input data.

3.4. Machine Learning Models

The machine learning models applied in this study combine linear and nonlinear approaches to capture different structural patterns in return dynamics. Each model offers distinct advantages in terms of interpretability, robustness, and the ability to learn complex interactions in financial data. The following subsections describe the theoretical foundations and practical motivations for each model used in the forecasting framework.

3.4.1. Linear Regression

Linear regression is a basic model that assumes a deterministic relationship between stock returns and technical variables:

$$R_{t+h}={\mathsf{\beta }}_0+{\sum }_{j=1}^p{\mathsf{\beta }}_j{X}_{j,t}+{\mathsf{\epsilon }}_t$$

(7)

This model remains the starting point in various stock price prediction studies due to its interpretability and ease of estimation. However, its linearity assumption and sensitivity to multicollinearity make it less effective when dealing with dynamic market data.

3.4.2. Ridge Regression

Ridge Regression, proposed by Hoerl and Kennard (1970), introduces L₂ regularization to mitigate overfitting and multicollinearity by penalizing large coefficient values. Its objective function is formulated as follows:

$$\underset{\mathsf{\beta }}{\mathrm{m}\mathrm{i}\mathrm{n}}(||R-X\mathsf{\beta }{||}_2^2+\mathsf{\lambda }||\mathsf{\beta }{|}_2^2)$$

(8)

where $\lambda$ is a regularization parameter that controls model complexity. Ridge Regression is able to stabilize the model when there is high correlation between features (multicollinearity), and prevents overfitting without eliminating important variables. Huang et al. (2019) showed that Ridge Regression has strong predictive performance for high-dimensional financial data, especially when technical indicators are correlated.

3.4.3. Random Forest (RF)

Random Forest is an ensemble bagging algorithm that combines many independent decision trees. Each tree is trained on a random subset of the data and features (Breiman, 2001):

$$\widehat{R_{t+h}}={\displaystyle \frac{1}{B}}{\sum }_{b=1}^B{T}_b\left(X_t\right)$$

(9)

Each tree is constructed from a random subset of data and features, making the final results more robust against outliers and noise. Peng and Yao (2023) found that RF reduced prediction errors by up to 20% compared to conventional linear models, especially in volatile and non-stationary market conditions.

3.4.4. XGBoost (Extreme Gradient Boosting)

XGBoost is a development of the gradient boosting algorithm that combines decision trees in stages by minimizing the cumulative prediction error (Chen & Guestrin, 2016):

$$\mathcal{L}={\sum }_{i=1}^{n}l\left(y_i,\widehat{y_i}\right)+{\sum }_{k=1}^K\Omega \left(f_k\right),\Omega \left(f_k\right)=\mathsf{\gamma }T+{\displaystyle \frac{1}{2}}\mathsf{\lambda }||w{\left|\right|}^2$$

(10)

This model is computationally efficient, robust to multicollinearity, and capable of capturing complex nonlinear relationships between variables. Bustos et al. (2025) demonstrated that XGBoost significantly improves out-of-sample R² and significantly reduces forecast error in stock price prediction across global markets.

3.5. Backtesting Framework

The backtesting framework is designed to evaluate whether improvements in statistical accuracy translate into economically meaningful trading performance. All simulations follow a strictly time-ordered expanding-window Time-Series Cross-Validation (TSCV) scheme to avoid forward-looking bias. For each fold, the model is trained exclusively on past data and used to generate predictions for the next out-of-sample window, ensuring that every trading decision relies solely on information available at the time the prediction is made.

For each forecasted return $\widehat{R_{t+h}}$, a trading position is opened at time ttt and held for the corresponding horizon of 5 days or 21 days. The realized return for each trade is computed using log returns (Hudson & Gregoriou, 2015):

$$r_{t+h}=\mathrm{I}\mathrm{n}\left({\displaystyle \frac{P_{t+h}}{P_t}}\right)$$

(11)

which provides time-additive consistency. Based on the model’s prediction, the trading signal is defined as (Sullivan et al., 1999):

$$s_t=\left\{\begin{array}{cc}1,\hfill & \widehat{R_{t+h}}>0,\hfill \\ 0,\hfill & \widehat{R_{t+h}} \le 0\hfill \end{array}\right.$$

(12)

and the strategy’s realized return is given by (Fama & French, 1988):

$$R_{t+h}^{\mathrm{strategy}}=s_t·r_{t+h}$$

(13)

To account for real-world frictions, all returns are adjusted for transaction costs using (Lesmond et al., 2004):

$$R_{t+h}^{\mathrm{net}}=s_t·r_{t+h}-c$$

(14)

where $c$ represents the proportional round-trip trading cost. In markets where short-selling is restricted, the signal may be constrained to $s_t\in \{0,1\}$ as in Equation (14), but the baseline analysis in this study applies the unrestricted long-short specification.

To evaluate long-run trading performance, cumulative returns are computed by compounding net returns across all trades (Bailey & López de Prado, 2012):

$$R_T^{cum}=\prod _{t=1}^T\left(1+r_t^{\mathrm{net}}\right)-1$$

(15)

while risk-adjusted profitability is assessed using the Sharpe ratio (Sharpe, 1994):

$$\mathrm{Sharpe}={\displaystyle \frac{{\overline{r}}^{net}-r_f}{\sigma \left({\overline{r}}^{net}\right)}}$$

(16)

where $R_f$ is set to zero due to the negligible daily risk-free rate. Downside risk is quantified using maximum drawdown, defined as (Chekhlov et al., 2005):

$$MDD=\underset{t\in \left|0,T\right|}{\max }\left[{\displaystyle \frac{\underset{t\in \left|0,T\right|}{\mathrm{m}\mathrm{a}\mathrm{x}}{V}_s-V_t}{\underset{t\in \left|0,T\right|}{\mathrm{m}\mathrm{a}\mathrm{x}}{V}_s}}\right]$$

(17)

These evaluation components provide a comprehensive measure of economic value, capturing profitability, volatility, and capital preservation. By integrating prediction, trading execution, transaction costs, and risk-adjusted evaluation, the backtesting framework offers a robust assessment of the practical utility of machine learning models in the Indonesian equity market.

3.6. Training, Validation, and Baseline Models

The training and validation procedure follows a strictly time-ordered structure to prevent look-ahead bias and ensure that all model evaluations reflect realistic investment conditions. The historical data are divided chronologically, with the 2016–2022 period serving as the training set and the 2023–2025 period reserved exclusively for out-of-sample testing. This temporal separation guarantees that future information is never used to estimate model parameters.

To strengthen the robustness of the estimation, model training is further supported by an expanding-window Time-Series Cross-Validation (TSCV) framework. In each fold, the model is trained on an incrementally growing historical window and validated on the immediately subsequent period, allowing performance to be assessed across multiple market regimes while fully avoiding data leakage. This approach reflects practical investment settings, where only past information is available at any decision point.

For comparison purposes, the machine learning models are evaluated against two baseline forecasting rules. The first baseline is the historical mean return, which represents a naïve but common benchmark in financial prediction studies. The second baseline uses a random-walk assumption, implying that the best forecast for future returns equals the most recent observed return. These baselines provide reference points to assess whether the selected machine learning models offer meaningful improvements beyond simple statistical heuristics.

3.7. Evaluation Metrics

The evaluation of forecasting performance is conducted using both statistical and economic metrics to provide a comprehensive assessment of each model’s predictive accuracy and practical investment value. Statistical metrics quantify the closeness between predicted and realized returns, while economic metrics assess whether these predictions translate into profitable and risk-efficient trading outcomes.

3.7.1. Statistical Metrics

Previous studies have commonly employed statistical indicators such as the Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and the Coefficient of Determination (R²) to measure predictive accuracy (Saberironaghi et al., 2025; Bustos et al., 2025; Fama, 1970).

These metrics evaluate the magnitude of prediction error and the proportion of variance explained by the model (Hyndman & Koehler, 2006):

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|y_i-\widehat{y_i}\right|$$

(18)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}$$

(19)

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}$$

(20)

These metrics comprehensively evaluate the deviation between actual and predicted returns as well as the proportion of data variance explained by the model. However, achieving high statistical accuracy (low MAE/RMSE and high R²) does not always guarantee practical usefulness, as models may fit historical data without effectively anticipating future price movements.

To further assess the model’s capacity to predict the direction of stock price movement, a binary classification framework is applied using a Confusion Matrix and Receiver Operating Characteristic (ROC) analysis. The Confusion Matrix quantifies correct classifications (True Positives, True Negatives) versus incorrect ones (False Positives, False Negatives). From this, four key metrics are derived Accuracy, Precision, Recall, and F1-score as shown in Equations (21)–(24) (Kohavi & Provost, 1998):

$$Accuracy={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(21)

$$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(22)

$$Recall={\displaystyle \frac{TP}{TP+FN}}$$

(23)

$$F_1=2\times {\displaystyle \frac{Precision\times Recall}{Precision+Recall}}$$

(24)

Precision measures how effectively the model avoids false alarms, Recall captures its sensitivity to true market movements, and the F1-score represents the harmonic balance between both particularly important when the dataset is imbalanced between up and down movements.

The discriminative power of the models is further examined through the Area Under the ROC Curve (AUC), which measures the ability of the model to distinguish between positive and negative signals at various classification thresholds (Fawcett, 2006):

$$TPR={\displaystyle \frac{TP}{TP+FN}},FPR={\displaystyle \frac{FP}{FP+TN}},AUC={\int }_0^{1}TPR\left(FPR\right)\hspace{0.17em}d\left(FPR\right)$$

(25)

An AUC value of 0.5 implies random classification, whereas a value close to 1.0 indicates excellent discriminatory performance. In the context of stock return prediction, AUC reflects the model’s robustness against market noise and non-stationary volatility.

3.7.2. Economic Evaluation

Beyond statistical accuracy, economic metrics are employed to evaluate the real-world profitability of the predictions. The Total Return (TR), Sharpe Ratio (SR), and Win Rate (WR) are used to assess the economic significance of the generated trading signals, as formulated in Equations (25)–(27) (Sharpe, 1966; Lo, 2002):

$$TotalReturn=\sum _{t=1}^T{R}_t·signa{l}_t$$

(26)

$$SR={\displaystyle \frac{E\left[R_p-R_f\right]}{{\mathsf{\sigma }}_p}}$$

(27)

$$WR={\displaystyle \frac{\mathrm{Number} \mathrm{of} \mathrm{profitable} \mathrm{transactions}}{\mathrm{Total} \mathrm{number} \mathrm{of} \mathrm{transactions}}}$$

(28)

The Total Return quantifies the cumulative profit or loss generated by the trading strategy, the Sharpe Ratio evaluates the risk-adjusted return relative to a risk-free benchmark, and the Win Rate measures the proportion of profitable trades. These economic metrics provide a more realistic assessment of model performance within a live trading environment.

This dual evaluation approach statistical and economic follows the methodology of Chun et al. (2024), who demonstrated that integrating risk-adjusted performance measures such as the Sharpe Ratio and cumulative returns yields a more comprehensive view of model performance in financial forecasting.

3.8. Hyperparameter Search Space

Hyperparameter tuning is conducted using a 5-fold Time-Series Cross-Validation (TSCV) procedure with an expanding-window design to ensure chronological integrity and prevent any form of look-ahead bias. The optimization objective is the Negative Mean Squared Error (Neg MSE), which aligns the hyperparameter search by minimizing out-of-sample forecasting error.

The search space for each model is summarized in

Table 2. Summary of the Hyperparameter Search Space for Each Model.

Model	Hyperparameter	Search Space
Linear Regression	-	No tuning (default settings)
Ridge Regression	alpha	(0.01, 0.1, 1, 10, 100, 1000)
Random Forest	n_estimators	(50, 100, 200, 300)
	max_depth	(5, 10, 15, 20, None)
	max_features	$(sqrt$, log2, 0.3, 0.5)
	min_samplesleaf	(1, 2, 4, 8)
	min_samplesplit	(2, 5, 10)
XGBoost	learning_rate	(0.01, 0.05, 0.1, 0.2)
	max_depth	(3, 5, 7, 9)
	subsample	(0.6, 0.8, 1.0)
	colsample_bytree	(0.6, 0.8, 1.0)
	gamma	(0, 0.1, 0.2, 0.5)
	reg_alpha	(0, 0.1, 0.5, 1)
	reg_lambda	(0, 0.1, 0.5, 1)
	n_estimators	(100, 200, 300)

. Linear Regression is included as a baseline without tuning, while Ridge Regression, Random Forest, and XGBoost are optimized over a comprehensive grid of model-specific parameters to balance flexibility, predictive accuracy, and computational efficiency.

3.9. Additional Statistical Tests

To ensure the suitability of the daily log-return series for predictive modeling, several standard statistical diagnostics are employed to examine the fundamental characteristics of financial time series. These tests assess whether returns satisfy key assumptions related to stationarity, independence, and the Random Walk behavior, all of which directly influence the validity of forecasting models.

First, the Augmented Dickey–Fuller (ADF) and KPSS tests are used jointly to examine the stationarity of the log-return process. The ADF test evaluates the presence of unit roots, while the KPSS test assesses trend-stationarity under the reverse null hypothesis. Applying both tests provides a robust verification that the return series is sufficiently stable for model estimation and avoids spurious regression issues often found in non-stationary data. Second, serial dependence is assessed using the Ljung–Box test across multiple lags. This test examines whether past returns contain statistically meaningful autocorrelation. Detecting short-horizon dependence is important because it provides the theoretical basis for employing machine learning models that exploit temporal patterns and nonlinear interactions. Finally, the Variance Ratio (VR) test is used to assess deviations from the Random Walk hypothesis. The VR test evaluates whether return variances scale proportionally with time, where departures from unity indicate potential predictability and departures from weak-form market efficiency. This test complements the autocorrelation diagnostics and provides a broader understanding of whether machine learning models are theoretically justified in capturing return dynamics.

4. Results

4.1. Comparison with Baseline

An initial comparison was conducted to assess the performance of two baseline models: Naive Drift and Random Walk, which serve as reference points before evaluating machine learning models. A summary of the performance of both baselines can be seen in

Table 3. Baseline Summary Statistics per Model and Horizon.

Model	Horizon	MAE	RMSE	R2	Direction Acc
Naive Drift	1D	0.0134	0.0189	−0.0010	0.4903
	5D	0.0135	0.0190	−0.0008	0.4915
	21D	0.0135	0.0189	−0.0008	0.4925
Random Walk	1D	0.0134	0.0189	−0.0004	0.5637
	5D	0.0134	0.0190	−0.0004	0.5635
	21D	0.0134	0.0189	−0.0004	0.5630

.

Table 3 shows that both Naive Drift and Random Walk produce very similar error rates across all horizons, with MAE values ranging from 0.0134 to 0.0135 and RMSE values around 0.0189–0.0190. R² values approaching zero to negative indicate that neither model has significant predictive ability, consistent with the characteristics of a market approaching a random walk, where short-term price changes tend to be random and difficult to predict. A more striking difference is seen in the accuracy of price movement direction. As shown in Table 3, Random Walk consistently produces higher directional accuracy (≈56%) than Naive Drift (≈49%). A more detailed visualization of this pattern can be seen in Figure 1, which shows a comparison of the performance of the two baselines over a 5-day horizon for six LQ45 stocks.

Figure 3 shows that Random Walk outperforms all tickers, particularly large-cap stocks like BBCA and BMRI, while Naive Drift remains near the 50% threshold indicating random performance. However, the difference is relatively small and statistically within the range of market noise commonly found on short-term horizons. This finding has important implications for further analysis. First, the negative R² value indicates that any developed prediction model must be able to outperform a very conservative baseline, namely the natural uncertainty of daily returns. Second, the stable directional accuracy of Random Walk at around 0.56 indicates the presence of a slight short-term pattern in stock prices, but this pattern is not strong enough to generate profitable trading signals without the support of a more complex model. To determine whether deeper predictability patterns exist, a series of statistical tests were performed, summarized in

Table 4. Market Predictability Test Results.

Ticker	Ljung–Box	Sig VR Rejections	Stationary (ADF)	Predictable
BBCA	20/20	4/4	Yes	Yes
BBRI	19/20	0/4	Yes	Yes
BMRI	19/20	3/4	Yes	Yes
ASII	20/20	3/4	Yes	Yes
ICBP	20/20	4/4	Yes	Yes
UNVR	7/20	0/4	Yes	Yes

.

Table 4 shows that the Ljung–Box test rejects the hypothesis of no autocorrelation for almost all tickers (except UNVR), indicating the presence of short-term dependencies that can be exploited by a non-linear model. The Variance Ratio test also rejects the random walk hypothesis, particularly for BBCA, ASII, ICBP, and BMRI, suggesting the possible existence of mean-reversion or short-term momentum patterns. The ADF test confirms that all return series are stationary, making them valid for use in predictive modeling.

The results in Table 3 and Table 4, and Figure 1 indicate that the LQ45 market is semi-efficient. Although price movements are dominated by random components, there are weak patterns in the form of autocorrelation and small deviations from random walk that can be captured by more complex models. Therefore, the main challenge for machine learning models in the next section is to determine whether they are able to exploit these subtle patterns and produce statistically and economically significant performance.

4.2. Experimental Results

The experimental results for all ticker-horizon model combinations are summarized in

Table 5. Summary of Model Performance Results.

Ticker	Horizon	Model	MAE	RMSE	R2
ASII	1D	XGBoost	0.012076	0.016537	−0.001830
	5D	RandomForest	0.012290	0.016644	−0.011846
	21D	XGBoost	0.012044	0.016464	−0.002786
BBCA	1D	RandomForest	0.010678	0.014614	0.016572
	5D	Ridge	0.010749	0.014784	−0.000376
	21D	XGBoost	0.010735	0.014674	−0.000986
BBRI	1D	Ridge	0.013966	0.018932	0.001119
	5D	XGBoost	0.013854	0.018925	−0.000784
	21D	Ridge	0.013820	0.018843	0.003982
BMRI	1D	XGBoost	0.014066	0.019488	0.005006
	5D	XGBoost	0.014200	0.019693	−0.009002
	21D	XGBoost	0.013928	0.019345	−0.000041
ICPB	1D	RandomForest	0.012135	0.017027	0.013081
	5D	XGBoost	0.012198	0.017149	−0.000310
	21D	XGBoost	0.012200	0.017119	−0.000567
UNVR	1D	XGBoost	0.017628	0.026617	0.001071
	5D	Ridge	0.017801	0.026935	−0.006006
	21D	Linear	0.018161	0.026934	0.013083

.

Table 5 shows that the performance of the machine learning models varies substantially across stocks and horizons, with no single model dominating across all conditions. Generally, MAE and RMSE values are within a consistent range, but the performance differences between models are more pronounced in the R² values, which provide an indication of the models’ relative ability to capture return variation.

As shown in Figure 4, Figure 5 and Figure 6, the heatmaps for the 1D, 5D, and 21D horizons show that most R² values are in the negative region or close to zero. Figure 4 shows that at the 1D horizon, only a few ticker-model combinations (e.g., BBCA–RandomForest and ICPB–RandomForest) produce a positive R², albeit a small one (≈0.01). A similar trend is seen at the 5D horizon in Figure 5, where almost all models fail to achieve a stable positive R². At the 21D horizon in Figure 6, the Ridge and XGBoost models show slight improvements for some stocks, such as BBRI and UNVR, but overall predictive performance remains limited.

The findings in Table 5 are consistent with this visual pattern. For example, for the BBCA ticker, Random Forest provides the highest R² at the 1D horizon (0.0166), but loses its lead at the 5D and 21D horizons, where XGBoost becomes the best-performing model, although the R² value approaches zero again. Conversely, for the BMRI ticker, XGBoost dominates across all horizons, but the R² value remains relatively small, indicating that model complexity does not provide a significant increase in predictability beyond the baseline. For UNVR, the simple linear model even outperforms the other models at the 21D horizon, as indicated by an R² value of 0.0131, one of the few positive values at long horizons.

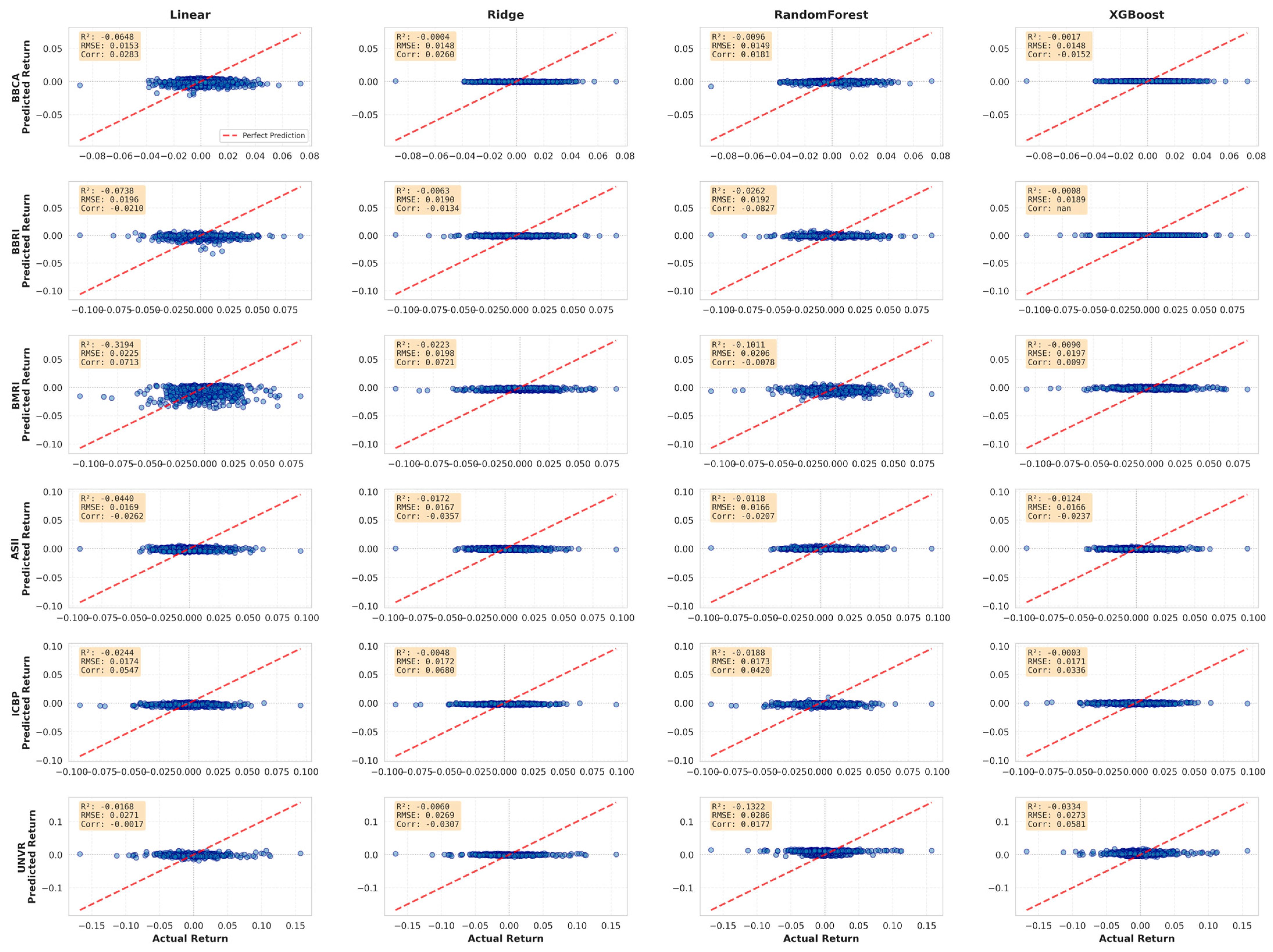
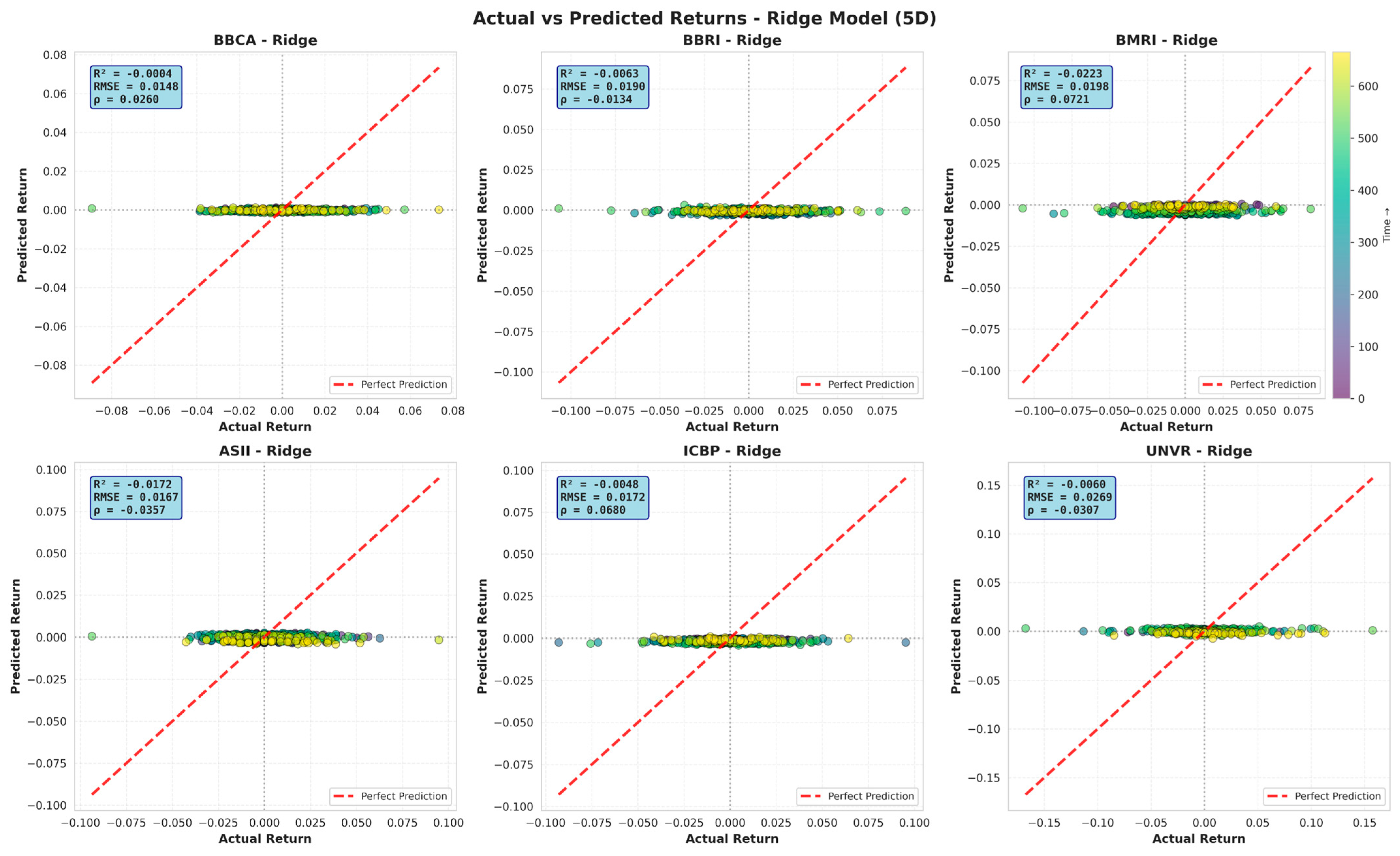
Visualizing the actual–predicted relationship for the 5D horizon in Figure 7 highlights the limitations of these predictions. For a comprehensive view across all models (Linear, Ridge, Random Forest, and XGBoost), see Figure A1 in Appendix A.

Figure 7 shows that most predictions for the Ridge model are concentrated around zero and fail to track the variability of actual returns. The “horizontal” distribution pattern, far from the perfect prediction line (marked by the red dashed line), indicates that the model tends to estimate shrunken values, a common characteristic of penalized regression when the predictive signal is weak or unstable. This supports the interpretation that short-term stock returns are dominated by noise, rendering nonlinear models like Random Forest and XGBoost incapable of capturing meaningful predictive structure. To test whether the differences between models are statistically significant, the results of the Diebold–Mariano (DM) Test for the 5D horizon are presented in

Table 6. Results of the Diebold–Mariano (DM) Test for the 5-day Horizon.

Ticker	Horizon	Model 1	Model 2	DM (Stat)	p (Value)	Significant (5%)
BBCA	5D	Linear	Ridge	2.7058	0.0068	True
		Linear	RandomForest	1.7759	0.0758	False
		Linear	XGBoost	2.4721	0.0134	True
		Ridge	RandomForest	−1.6438	0.1002	False
		Ridge	XGBoost	−0.2783	0.7808	False
		RandomForest	XGBoost	1.4331	0.1518	False
BBRI	5D	Linear	Ridge	3.9081	0.000093	True
		Linear	RandomForest	2.6223	0.00873	True
		Linear	XGBoost	3.5219	0.000428	True
		Ridge	RandomForest	−2.8627	0.00420	True
		Ridge	XGBoost	0.8396	0.4012	False
		RandomForest	XGBoost	2.5522	0.0107	True
BMRI	5D	Linear	Ridge	5.6387	1.71 × 10−8	True
		Linear	RandomForest	4.0570	4.97 × 10−5	True
		Linear	XGBoost	5.1701	2.34 × 10−7	True
		Ridge	RandomForest	−3.9534	0.000077	True
		Ridge	XGBoost	1.8038	0.07127	False
		RandomForest	XGBoost	3.9652	0.000073	True
ASII	5D	Linear	Ridge	3.3392	0.00084	True
		Linear	RandomForest	2.7726	0.00556	True
		Linear	XGBoost	2.5448	0.01093	True
		Ridge	RandomForest	1.1319	0.2577	False
		Ridge	XGBoost	0.8209	0.4117	False
		RandomForest	XGBoost	−0.1917	0.8480	False
ICPB	5D	Linear	Ridge	2.2822	0.02248	True
		Linear	RandomForest	0.5841	0.5592	False
		Linear	XGBoost	1.3655	0.1721	False
		Ridge	RandomForest	−1.6255	0.1040	False
		Ridge	XGBoost	0.4274	0.6691	False
		RandomForest	XGBoost	1.2252	0.2205	False
UNVR	5D	Linear	Ridge	1.1156	0.2646	False
		Linear	RandomForest	−3.3316	0.000864	True
		Linear	XGBoost	−1.0104	0.3123	False
		Ridge	RandomForest	−3.8990	0.000096	True
		Ridge	XGBoost	−1.6990	0.08933	False
		RandomForest	XGBoost	4.7241	2.31 × 10−6	True

.

Table 6 shows that several model comparisons show significant differences at the 5% confidence level. For example, on BBCA stock, the Linear model significantly differs from Ridge (p = 0.0068) and XGBoost (p = 0.0134), as indicated by the positive DM statistic. A similar trend is observed for BBRI and BMRI tickers, where the linear model often differs significantly from the non-linear model. However, in many other comparisons, such as Ridge vs. XGBoost or RandomForest vs. XGBoost, the performance differences are insignificant (p > 0.05), indicating that despite slight variations in numerical performance, the predictive ability between models remains essentially identical. The experimental results in Table 5, Figure 4, Figure 5, Figure 6 and Figure 7, and Table 6 lead to a consistent conclusion: machine learning is capable of generating performance variations between stocks and across horizons, but the predictive signal obtained is very weak, with most R² values approaching zero. This confirms the hypothesis that short-term LQ45 stock returns tend to be random and difficult to predict, so that performance improvements between models reflect algorithmic variation more than the existence of a truly robust predictive pattern.

4.3. Evaluation of Price Movement Direction Classification

A performance evaluation of price movement direction classification was conducted to assess the model’s ability to distinguish positive and negative returns on 1D, 5D, and 21D time horizons. A summary of the results is presented in

Table 7. Evaluation Results by Model.

Model	MAE	RMSE	R2	Acc	F1	AUC
Linear	0.01398	0.01953	−0.06596	0.5339	0.3241	0.5235
RandomForest	0.01419	0.01952	−0.05145	0.5205	0.3545	0.5157
Ridge	0.01353	0.01898	−0.00421	0.5386	0.2832	0.5239
XGBoost	0.01351	0.01897	−0.00296	0.4930	0.4667	0.5116

, which shows that all Linear, Ridge, Random Forest, and XGBoost models achieved accuracy values in the range of 0.49–0.54, only slightly higher than the random baseline (50%).

As shown in Table 7, the Ridge model achieved the highest accuracy (0.5386) with a relatively better R² value than the other models, while XGBoost demonstrated the lowest accuracy (0.4930) despite producing the highest F1-score (0.4667), indicating an imbalance between positive and negative errors.

Next, a comparison based on horizon is shown in

Table 8. Evaluation Results by Horizon.

Horizon	MAE	RMSE	R2	Acc	F1	AUC
1D	0.013823	0.019253	−0.033331	0.5300	0.3837	0.5336
5D	0.013876	0.019364	−0.039902	0.5174	0.3360	0.5065
21D	0.013703	0.019134	−0.020195	0.5170	0.3517	0.5159

.

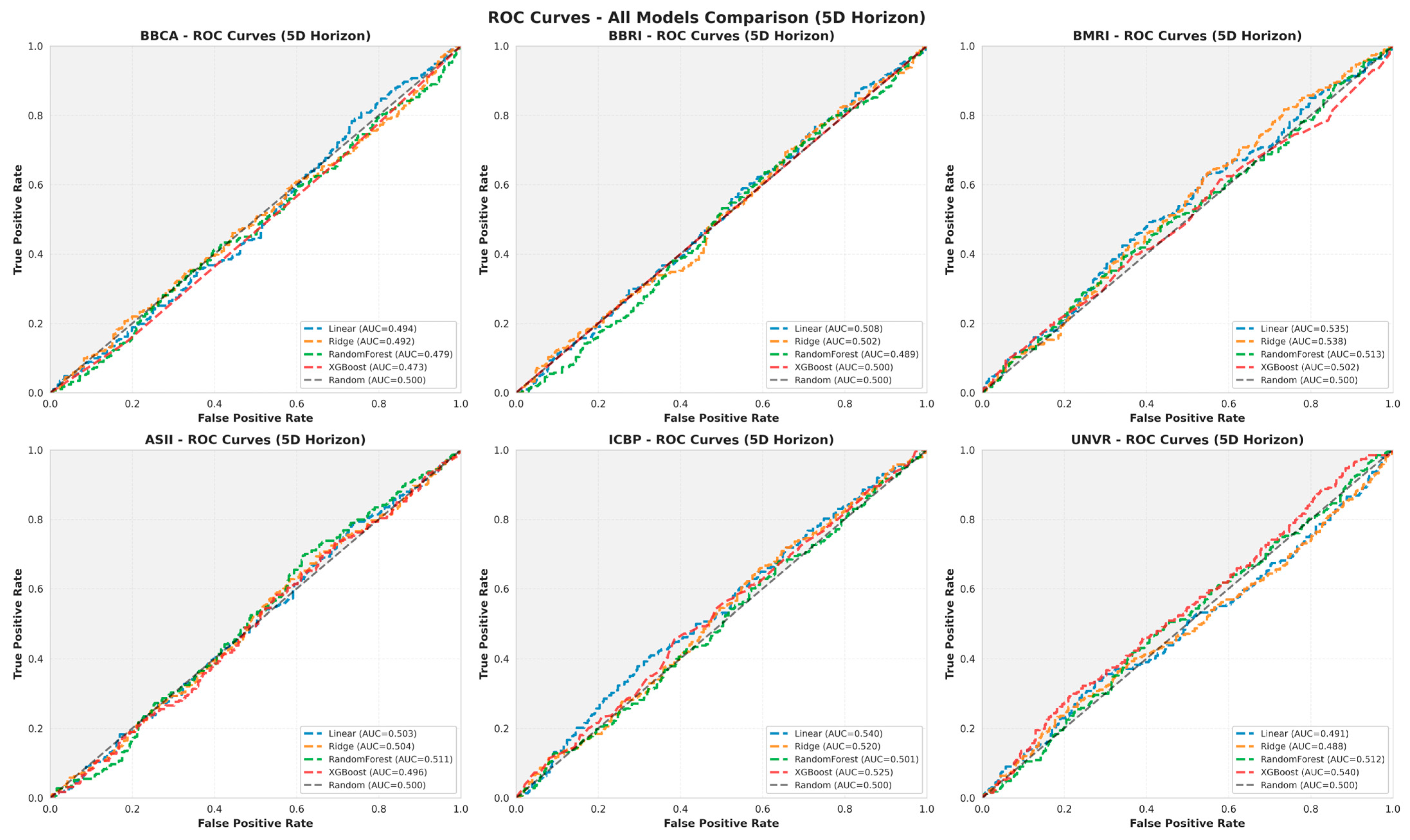
Table 8 shows that classification accuracy tends to decline at longer horizons, with values for 1D = 0.5300, 5D = 0.5174, and 21D = 0.5170. Although the MAE and RMSE are relatively stable across horizons, the AUC value remains around 0.50–0.53, indicating the model’s discrimination ability is nearly equivalent to random guessing. This finding confirms that the return direction signal in the LQ45 market is very weak, making it difficult for the model to consistently distinguish between upward and downward movements. These performance characteristics are visualized through the ROC curves in Figure 8, which show a comparison of the four models over a 5-day horizon for the BBCA ticker. Corresponding ROC curves for the other five tickers (BBRI, BMRI, ASII, ICBP, and UNVR) are presented in Figure A2 in Appendix A.

Figure 8 shows that all ROC curves are very close to the 45-degree diagonal line (random classifier), with AUCs ranging from 0.49 to 0.53. This pattern indicates a low predictive signal in the daily return data, where the model is unable to form a clear separation between positive and negative classes. This nearly random performance is consistent with the weak-form efficiency hypothesis, where historical information does not provide a strong directional signal. To deepen our understanding of the relationship between regression and classification performance, Figure 9 presents two scatterplots: (i) the relationship between classification accuracy and R² value, and (ii) the relationship between F1-score and RMSE.

Figure 9 shows that there is no significant correlation between the model’s ability to predict return values (through a mostly negative R²) and its ability to predict return direction. The dense scatterplots near the vertical line R² = 0 confirm that the regression model has almost no explanatory power, but its classification accuracy remains around 50–55%. This indicates that although the model is unable to approximate return values well, it can still capture a small number of binary patterns (up/down), albeit at a marginal level. The results in Table 7 and Table 8, Figure 8 and Figure 9 lead to one important conclusion: the machine learning model is unable to consistently outperform the random baseline in predicting the price direction of LQ45 stocks. The low AUC values and accuracy of only slightly above 50% confirm that the short-term return direction structure is highly random and dominated by noise, making it very difficult to exploit to generate reliable predictive signals. This finding aligns with market characteristics approaching weak-form efficiency.

4.4. Model Economic Performance Evaluation (Backtesting and Trading Strategy Simulation)

Economic performance evaluation was conducted through backtesting simulations incorporating transaction costs and slippage to ensure the results reflected real market conditions. The backtesting parameters were set as follows: initial capital of USD 100,000, transaction costs of 0.15%, and slippage of 0.07%, resulting in a total cost per transaction of 0.22%. This approach ensured that strategies that appeared theoretically profitable were thoroughly tested against real market frictions. A summary of the average performance of each model is shown in

Table 9. Average Performance by Model.

Model	Total Return	CAGR	Sharpe Ratio	Max Drawdown	Volatility
Buy_Hold	0.0363	0.0043	0.1916	−0.4312	0.3008
Linear	−0.0624	−0.0261	−0.0001	−0.2329	0.1518
RandomForest	−0.0727	−0.0331	−0.0527	−0.2957	0.1597
Ridge	−0.0370	−0.0189	0.1232	−0.2107	0.1437
XGBoost	−0.1536	−0.0635	−0.1935	−0.3994	0.2402

.

As seen in Table 9, none of the machine learning models outperformed the Buy & Hold strategy when transaction costs were taken into account. The Buy & Hold strategy generated a total return of 3.63%, a CAGR of 0.43%, and a Sharpe Ratio of 0.1916, despite experiencing a substantial maximum drawdown of −43.12%. Conversely, all ML models performed negatively, with XGBoost performing the worst (total return of −15.36%, Sharpe Ratio of −0.1935). The Ridge model showed the smallest loss (−3.70%) and the highest Sharpe Ratio among the ML models (0.1232), but remained below Buy & Hold.

The performance of the equal-weight portfolio is presented in

Table 10. Equal-Weight Portfolio Performance Results.

Model/Strategi	Return (%)	CAGR (%)	Sharpe	Max Drawdown (%)
Buy & Hold	3.63	1.28	0.166	−28.33
Linear	−6.24	−2.27	−0.334	−10.38
Ridge	−3.70	−1.33	−0.163	−13.79
RandomForest	−7.27	−2.65	−0.365	−18.06
XGBoost	−15.36	−5.76	−0.401	−26.15

.

Table 10 shows that all ML-based strategies again performed inferiorly to Buy & Hold. Although the ML model’s annual volatility was lower, for example, in Linear (0.1518) and Ridge (0.1437), this decrease in volatility was not enough to offset the lower returns. Consequently, the overall risk-return ratio deteriorated, reflected by negative Sharpe Ratios for almost all models. A visualization of individual portfolio performance for each stock can be seen in Figure 10.

Figure 10 shows that the ML strategy’s returns move in a “step-like” pattern, reflecting the nature of direction-based switching strategies: the model only enters positions when the predicted return is above zero, and exits when the prediction is negative. This pattern results in high transaction frequency, resulting in transaction costs significantly eroding profitability. For stocks like ASII and UNVR, the model’s performance fell significantly below that of Buy & Hold due to a combination of weak forecast signals and high price volatility. Conversely, for BMRI and BBCA, ML performance was slightly more stable, but still unable to provide a meaningful economic advantage. A comparison of the contribution of each model relative to the Buy & Hold strategy is visualized in Figure 11.

Figure 11 shows that in the total return and Sharpe Ratio metrics, almost all bars of the ML model are in the negative area, indicating consistent underperformance. On the risk dimension, particularly maximum drawdown and annual volatility, some models, such as Ridge and Linear, provided limited improvement compared to Buy & Hold, but this improvement did not translate into better returns. In other words, the reduction in risk was not commensurate with the reduction in return, so risk-adjusted performance remained low. The backtesting results in Table 9 and Table 10, Figure 10 and Figure 11 indicate that the machine learning strategy is unable to deliver competitive profitability when applied to LQ45 data, especially after considering transaction costs. This suggests that while the ML model is capable of capturing small numerical patterns in the data (as shown in the regression and DM significance test sections), these patterns are not robust enough to generate economic returns in a real trading context. This finding is consistent with the literature emphasizing the dominance of noise in short-term returns and the weakness of predictive signals in semi-efficient markets like Indonesia.

4.5. Interpretation of Non-Linear Models with SHAP

Model interpretation was conducted to understand how technical features influence return predictions, particularly in the XGBoost model, which represents a non-linear model, and Ridge Regression, which represents a linear-regularized model.

4.5.1. Non-Linear Model Interpretation: XGBoost

As shown in

Table 11. Top 15 Features Based on Mean Absolute SHAP Value (XGBoost).

Feature	Mean SHAP	Std	Min	Max
ATR_14	0.000390	0.000505	0.0	0.001174
Stoch_D	0.000358	0.000432	0.0	0.001031
BB_Width	0.000346	0.000628	0.0	0.001624
OBV_norm	0.000331	0.000348	0.0	0.000962
EMA_10	0.000303	0.000478	0.0	0.001256
BB_High	0.000279	0.000283	0.0	0.000587
Volatility_21D	0.000249	0.000386	0.0	0.001016
Momentum_5D	0.000213	0.000311	0.0	0.000798
Volume_Ratio	0.000209	0.000157	0.0	0.000436
RSI_14	0.000187	0.000278	0.0	0.000726
MACD_Hist	0.000182	0.000249	0.0	0.000667
BB_Low	0.000169	0.000225	0.0	0.000620
EMA_Ratio	0.000152	0.000173	0.0	0.000427
EMA_30	0.000147	0.000124	0.0	0.000322
Stoch_K	0.000146	0.000157	0.0	0.000423

, the features with the highest mean absolute SHAP values, indicating the largest contribution to model output, are dominated by short-term volatility indicators and oscillators. ATR_14 (Average True Range) emerged as the most important feature (mean SHAP = 0.000390), followed by Stoch_D, BB_Width, and OBV_norm. This pattern indicates that the non-linear model is highly sensitive to market volatility dynamics and short-term momentum changes.

4.5.2. Linear Model Interpretation: Ridge Regression

In contrast to XGBoost, the Ridge Regression model exhibits a more stable and symmetrical feature importance structure. According to

Table 12. Top 15 Features Based on Ridge Regression Coefficients.

Feature	Coeff. Mean	Coeff. Std	Abs Mean	Abs Std	Abs Min	Abs Max
OBV_norm	0.000021	0.000420	0.000320	0.000232	0.000003	0.000558
Volume_Ratio	0.000239	0.000310	0.000303	0.000235	0.000065	0.000702
Volatility_21D	−0.000023	0.000365	0.000296	0.000169	0.000113	0.000528
Momentum_5D	0.000014	0.000455	0.000295	0.000321	0.000029	0.000785
Volume_MA_20	0.000157	0.000218	0.000212	0.000153	0.000048	0.000493
MACD_Hist	−0.000194	0.000211	0.000207	0.000196	0.000037	0.000558
ATR_14	−0.000170	0.000164	0.000193	0.000130	0.000069	0.000429
RSI_14	0.000118	0.000155	0.000176	0.000062	0.000076	0.000264
EMA_Ratio	−0.000124	0.000163	0.000154	0.000128	0.000045	0.000366
Stoch_D	−0.000153	0.000161	0.000153	0.000161	0.000026	0.000467
EMA_30	−0.000150	0.000101	0.000151	0.000100	0.000002	0.000274
EMA_10	−0.000150	0.000092	0.000150	0.000092	0.000008	0.000273
BB_High	−0.000138	0.000107	0.000147	0.000092	0.000026	0.000248
BB_Width	−0.000080	0.000158	0.000142	0.000091	0.000031	0.000287
BB_Mid	−0.000134	0.000096	0.000141	0.000082	0.000022	0.000239

, the most dominant features based on absolute coefficient values are OBV_norm, Volume_Ratio, Volatility_21D, and Momentum_5D. These four features are nearly identical to the top features in the XGBoost version, indicating structural consistency between the models despite their different mathematical approaches. However, their contribution patterns can differ. This is evident from the positive/negative coefficients on MACD_Hist, ATR_14, EMA_Ratio, and Stoch_D, which in the Ridge model indicate a linear relationship between the feature signature and the predicted signature.

4.5.3. XGBoost vs. Ridge Regression Interpretation Comparison

A comparison of the two models shown in Figure 12 shows that although the order of the most important features is relatively consistent, particularly volatility and volume, the direction and shape of their influence differ. The XGBoost model captures the nonlinear relationship between volatility changes and returns, while Ridge only captures a more muted linear relationship. This is why the nonlinear model appears more responsive to market fluctuations, although its performance remains economically insignificant, as shown in the backtesting section. One key finding from this section is that both the linear and nonlinear models identified that the most informative predictive signals come from short-term volatility, volume pressure, and oscillator dynamics, rather than from long-term trends. This is consistent with the characteristics of a semi-efficient market, where daily returns are dominated by noise and the emerging predictive signals are weak and unstable.

The findings in Table 11 and Table 12, and Figure 12 explain the relatively low predictive performance of the models in the previous section. Although the models can identify frequently contributing features, the magnitude of their contribution is very small (mean SHAP < 0.0004). This confirms that the predictive structure in short-term LQ45 returns is very limited, and although volatility patterns and volume pressure can be somewhat helpful, these signals are not strong enough to produce significant predictions either statistically or economically.

5. Discussion

The empirical findings of this study reveal a fundamental tension between statistical prediction capability and the economic reality of trading in semi-efficient emerging markets. All machine learning models produced R² values predominantly near zero or negative across all horizons, with the highest positive R² reaching only 0.016 (BBCA, 1D horizon, Random Forest), consistent with weak-form market efficiency where historical price information is already incorporated into current prices (Fama, 1970; Malkiel, 2003; Fama & French, 2010). While the Ljung–Box test rejected the hypothesis of no autocorrelation for most tickers and the Variance Ratio test identified deviations from the random walk in several stocks, the magnitude of these deviations proved insufficient to generate economically exploitable signals. The superior statistical performance of XGBoost achieving the lowest MAE and RMSE in most cases failed to translate into economic profitability, highlighting the critical distinction between in-sample fitting and out-of-sample utility emphasized by Campbell and Thompson (2008) and Welch and Goyal (2008). Near-random directional accuracy (49–54% across models) and AUC values hovering around 0.50–0.53 further reinforce that short-term return direction signals are extremely weak in the LQ45 market, suggesting the market processes information efficiently enough to prevent systematic directional forecasting at daily to monthly horizons.

The backtesting results reveal a counterintuitive but theoretically important finding: simpler regularized linear models, particularly Ridge Regression, delivered superior risk-adjusted performance compared to complex ensemble methods despite lower statistical accuracy. Ridge achieved a Sharpe Ratio of 0.1232 and total return of −3.70%, compared to XGBoost’s Sharpe Ratio of −0.1935 and total return of −15.36%, while all ML-based strategies underperformed the Buy & Hold benchmark (Total Return: 3.63%, Sharpe Ratio: 0.1916). This superiority of parsimony can be explained through several mechanisms: regularized linear models impose constraints on coefficient magnitudes that limit responsiveness to noise; tree-based ensemble methods are highly adaptive and can overfit to spurious patterns that do not persist out-of-sample as demonstrated by Huang et al. (2019) and transaction costs (0.22% per round-trip) disproportionately affect complex models that generate frequent trading signals. Ridge exhibited the lowest annual volatility (0.1437) and maximum drawdown of −21.07%, compared to XGBoost’s volatility of 0.2402 and drawdown of −39.94%, demonstrating that in practical investment contexts where drawdown risk is critically important, simpler models provide superior stability even if they sacrifice potential upside. The SHAP-based interpretability analysis reveals that the most influential features were volatility indicators (ATR_14, BB_Width, Volatility_21D) and volume-based metrics (OBV_norm, Volume_Ratio), while trend-following indicators (EMA_10, EMA_30) and oscillators (RSI_14, MACD_Hist) contributed less, suggesting that in the LQ45 market, price trends are less stable than commonly assumed, consistent with weak momentum effects documented by Rouwenhorst (1999) in emerging markets. Critically, mean absolute SHAP values across all features remain extremely small (<0.0004), quantifying the fundamental challenge: while technical indicators contain some signal, the signal-to-noise ratio is too low to support reliable forecasting.

These findings contribute to the ongoing debate about market efficiency in emerging economies by supporting a nuanced view of semi-efficiency: the LQ45 market is not perfectly efficient (evidenced by significant statistical test rejections), but it is efficient enough that exploitable inefficiencies do not translate into reliable economic profits after accounting for implementation costs. This interpretation aligns with behavioral finance perspectives of Kahneman and Tversky (1979), which emphasize that cognitive biases create predictable patterns but do not necessarily persist strongly enough to overcome market frictions. While the momentum anomaly documented by Jegadeesh and Titman (1993, 2001) and the gradual information diffusion hypothesis of Hong and Stein (1999) suggest emerging markets should exhibit stronger predictability due to information asymmetries and heterogeneous investor sophistication, our results indicate that in Indonesia’s increasingly liquid and institutionalized capital market, these advantages have narrowed substantially (Bekaert et al., 2007). For practitioners, this study offers critical insights that recalibrate expectations for ML-based trading: investors should approach machine learning predictions with realistic expectations, recognizing that patterns may be too weak to overcome transaction costs; simpler regularized models may offer better risk-adjusted performance than complex ensemble methods; volatility and volume indicators provide stronger predictive signals than traditional trend-following indicators; transaction cost awareness is critical as even small costs (0.22% per round trip) can eliminate apparent profitability; and the consistent outperformance of passive Buy & Hold suggests that in markets exhibiting near-random-walk behavior, passive exposure may be the most cost-effective approach, with active trading reserved for scenarios where investors possess genuine informational advantages beyond publicly available technical indicators.

While this research provides valuable insights into machine learning-based stock return prediction in the Indonesian LQ45 market, several methodological and contextual limitations should be acknowledged to properly contextualize the findings. The analysis focused on six LQ45 constituents rather than the full 45-stock index, selected primarily for liquidity and data quality considerations, which restricts the generalizability of conclusions across different market capitalization levels, sectoral characteristics, and liquidity profiles. The out-of-sample testing period spanning approximately two years (2023–2025) may not capture sufficient regime diversity including bull markets, bear markets, high-volatility crises, and stable growth periods to fully assess model robustness across varying market conditions. The study relied exclusively on price- and volume-based technical indicators, excluding fundamental factors such as earnings quality and valuation ratios, macroeconomic variables including interest rates and GDP growth, as well as alternative data sources such as news sentiment and social media activity, any of which might complement technical signals and improve predictive performance. The examination of only two forecasting horizons (5-day and 21-day returns) leaves open the question of whether predictability varies systematically with holding period, potentially missing optimal trading frequencies at very short-term or intermediate-term horizons. The single-market focus on Indonesia limits the ability to distinguish Indonesia-specific institutional features from broader emerging market dynamics, while transaction cost assumptions at 0.22% per round trip may not fully capture heterogeneity in actual implementation costs that vary by broker commission structures, trade size, and market conditions during periods of stress when liquidity evaporates and bid-ask spreads widen substantially.

Despite these limitations, the study makes important contributions by providing integrated statistical-economic evaluation, demonstrating the superiority of parsimonious models in noisy environments, and offering SHAP-based interpretability analysis that bridges the gap between model predictions and economic intuition. Future research should address these limitations through expansion to the full LQ45 universe with cross-sectional analysis identifying stock-specific predictability patterns, incorporation of fundamental and alternative data sources to complement technical signals, development of regime-dependent models that adapt to changing market conditions as suggested by Timmermann and Granger (2004) and Ballings et al. (2015), application of deep learning architectures such as LSTM networks and Transformer models that can capture longer-term temporal dependencies, implementation of multi-horizon joint forecasting that exploits cross-horizon dependencies, integration of portfolio-level optimization techniques that combine ML-based return forecasts with mean-variance or risk parity frameworks, employment of causal inference techniques to identify structural relationships between technical indicators and returns, conducting live paper trading experiments to reveal practical challenges not captured by historical backtesting, systematic comparison across multiple emerging markets to clarify whether findings generalize or reflect Indonesia-specific features, and development of explainable AI frameworks that satisfy regulatory requirements while maintaining predictive performance. These research directions would collectively advance both theoretical understanding of market efficiency in emerging economies and practical implementation of algorithmic trading strategies, while addressing the gap between statistical predictability and economic profitability that remains a central challenge in financial machine learning research.

6. Conclusions

This study examines the application of machine learning algorithms to predict stock returns in Indonesia’s LQ45 index using four models, Linear Regression, Ridge Regression, Random Forest, and XGBoost, across 5-day and 21-day forecasting horizons. Analyzing six representative LQ45 constituents from 2016 to 2025, the research adopts an integrated evaluation framework combining statistical accuracy metrics with economic performance assessment through realistic backtesting incorporating transaction costs. The empirical findings reveal three key insights. First, all models produced R² values near zero or negative with directional accuracy of 49–54% and AUC values around 0.50–0.53, demonstrating that short-term return patterns are dominated by unpredictable noise rather than systematic exploitable signals, consistent with weak-form market efficiency. Second, while XGBoost achieved the lowest MAE and RMSE, the simpler Ridge Regression delivered superior risk-adjusted economic performance with a Sharpe Ratio of 0.1232 versus XGBoost’s −0.1935, revealing that model parsimony and robustness dominate complexity in high-noise environments, though all ML strategies ultimately underperformed passive Buy & Hold. Third, SHAP analysis showed that short-term volatility indicators (ATR, BB_Width, Volatility_21D) and volume metrics (OBV, Volume_Ratio) provide the strongest predictive signals, yet even these features exhibit extremely small mean absolute SHAP values below 0.0004, quantifying that while certain indicators are relatively more important, their absolute predictive power remains insufficient for reliable forecasting or profitable trading.

For practitioners, machine learning offers advantages including flexibility to capture non-linear relationships, adaptability to regime shifts, scalability, transparency through interpretability tools, and systematic discipline, but these must be weighed against significant disadvantages including weak signal-to-noise ratios limiting profitability, overfitting risks, transaction cost erosion from high-frequency trading, model instability, implementation complexity, and regulatory risks. Practitioners should maintain realistic expectations, recognizing that statistical accuracy does not guarantee economic profitability once frictions are incorporated. When implementing quantitative strategies in emerging markets, simpler regularized models may outperform complex ensembles by prioritizing robustness, technical systems should weight volatility and volume indicators more heavily than traditional trend-following signals, and transaction cost awareness is paramount. While ML models struggled with directional prediction, they may prove valuable in alternative applications such as volatility forecasting, portfolio optimization, and risk management. The consistent outperformance of passive Buy & Hold suggests that for most investors in near-random-walk markets, low-cost passive exposure may be most cost-effective, with active trading reserved for genuine informational advantages.

While this research provides valuable insights into machine learning-based stock return prediction in the Indonesian LQ45 market, several important limitations should be acknowledged. First and most critically, the analysis focused on six LQ45 constituents rather than the full 45-stock index, selected primarily for liquidity, data completeness, and minimal corporate action distortion. While this purposive sampling ensures robust and consistent data quality throughout the 2016–2025 analysis period, it fundamentally restricts the generalizability of conclusions across different market capitalization levels, sectoral characteristics, and liquidity profiles within the broader LQ45 universe. Cross-sectional heterogeneity in predictability patterns potentially associated with firm size, volatility, trading volume, or sector membership cannot be comprehensively assessed with the current sample of six stocks. This represents the most important limitation and the highest priority direction for future research. Expanding to all 45 LQ45 constituents would enable rigorous statistical inference about cross-sectional heterogeneity in predictability, revealing whether stock characteristics including size, book-to-market ratios, profitability, momentum, volatility, liquidity, or sector membership systematically associate with forecast accuracy and economic profitability. Cross-sectional regression could identify firm-level attributes predicting ML success, while panel data methods could disentangle stock-specific from common market factors, and portfolio construction across the full universe could reveal whether aggregate performance exceeds individual results through diversification. Second, the out-of-sample testing period spanning approximately two years (2023–2025) may not capture sufficient regime diversity to fully assess model robustness across varying market conditions. Third, the study relied exclusively on price- and volume-based technical indicators, excluding fundamental factors, macroeconomic variables, and alternative data sources that might complement technical signals. Fourth, the examination of only two forecasting horizons (5-day and 21-day returns) leaves open questions about whether predictability varies systematically with holding period. Finally, the single-market focus on Indonesia limits the ability to distinguish Indonesia-specific institutional features from broader emerging market dynamics.