Bayesian Estimation of Extreme Quantiles and the Distribution of Exceedances for Measuring Tail Risk
Abstract
1. Introduction
2. Unconditional Quantile Estimation
2.1. Bayesian and ML Quantile Estimation
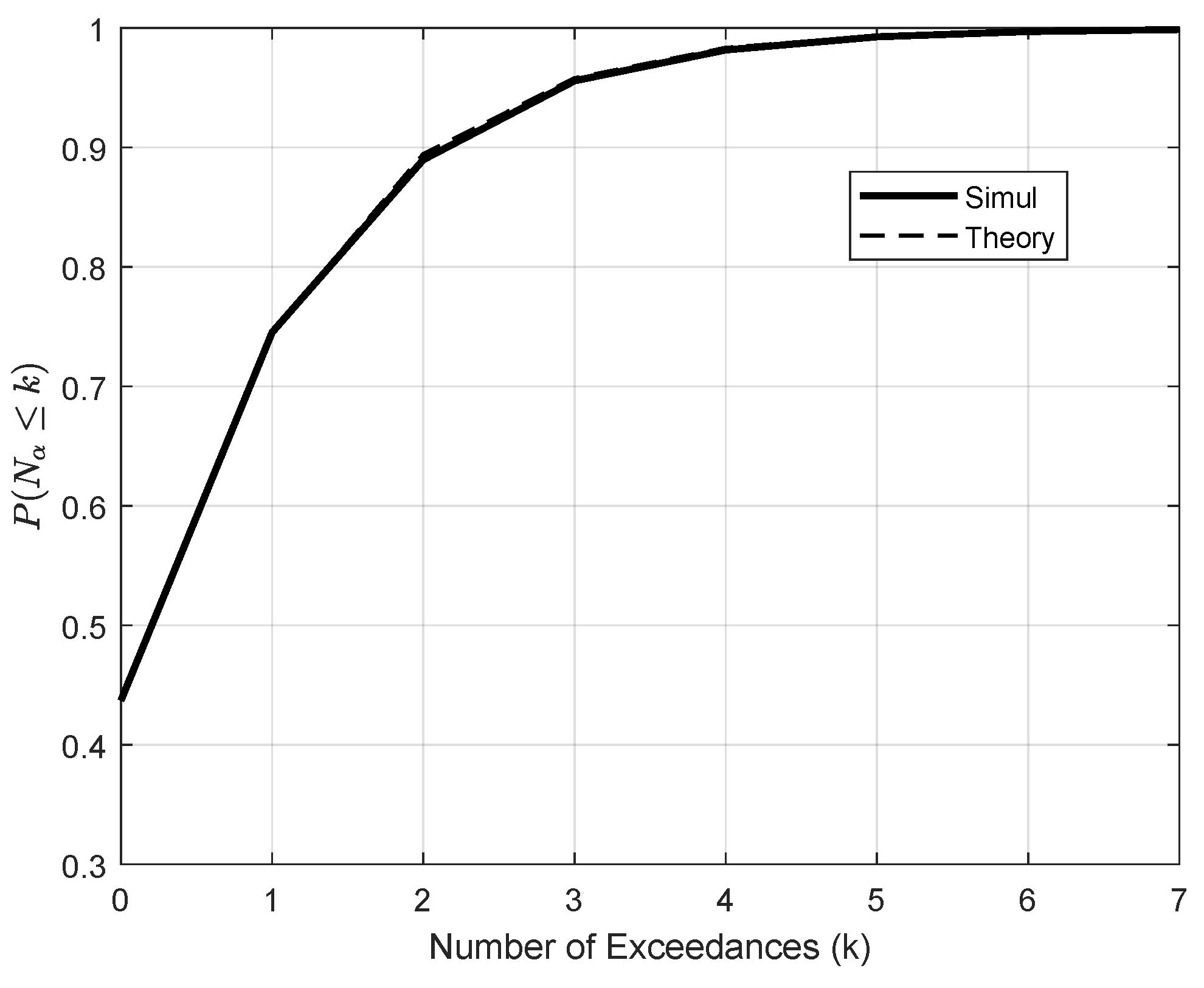
2.2. The Distribution of Exceedances
2.3. Extending the Exponential Distribution
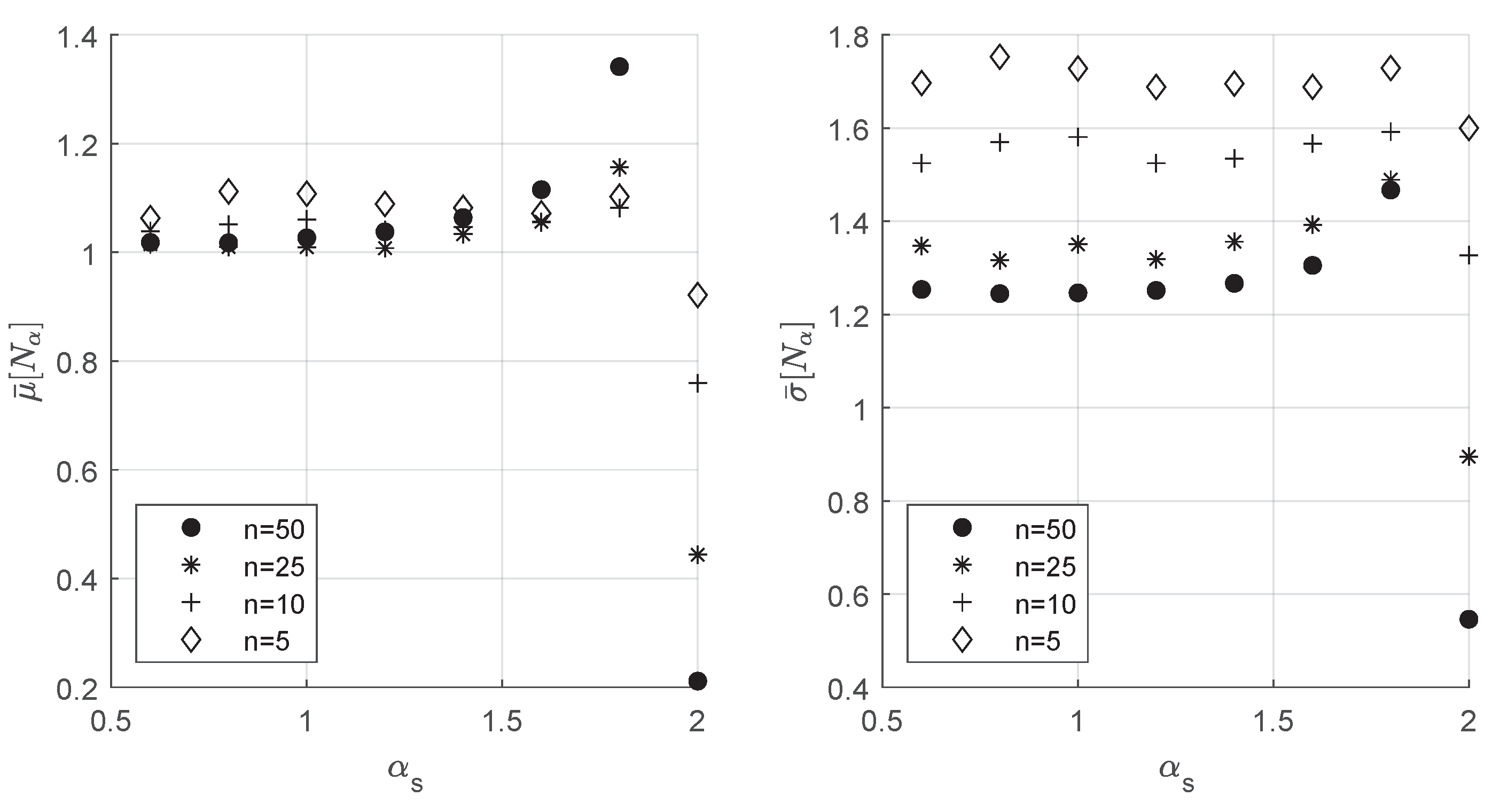
3. ZCE Quantile Estimation for Paretian Tails
3.1. Extreme Value Theory
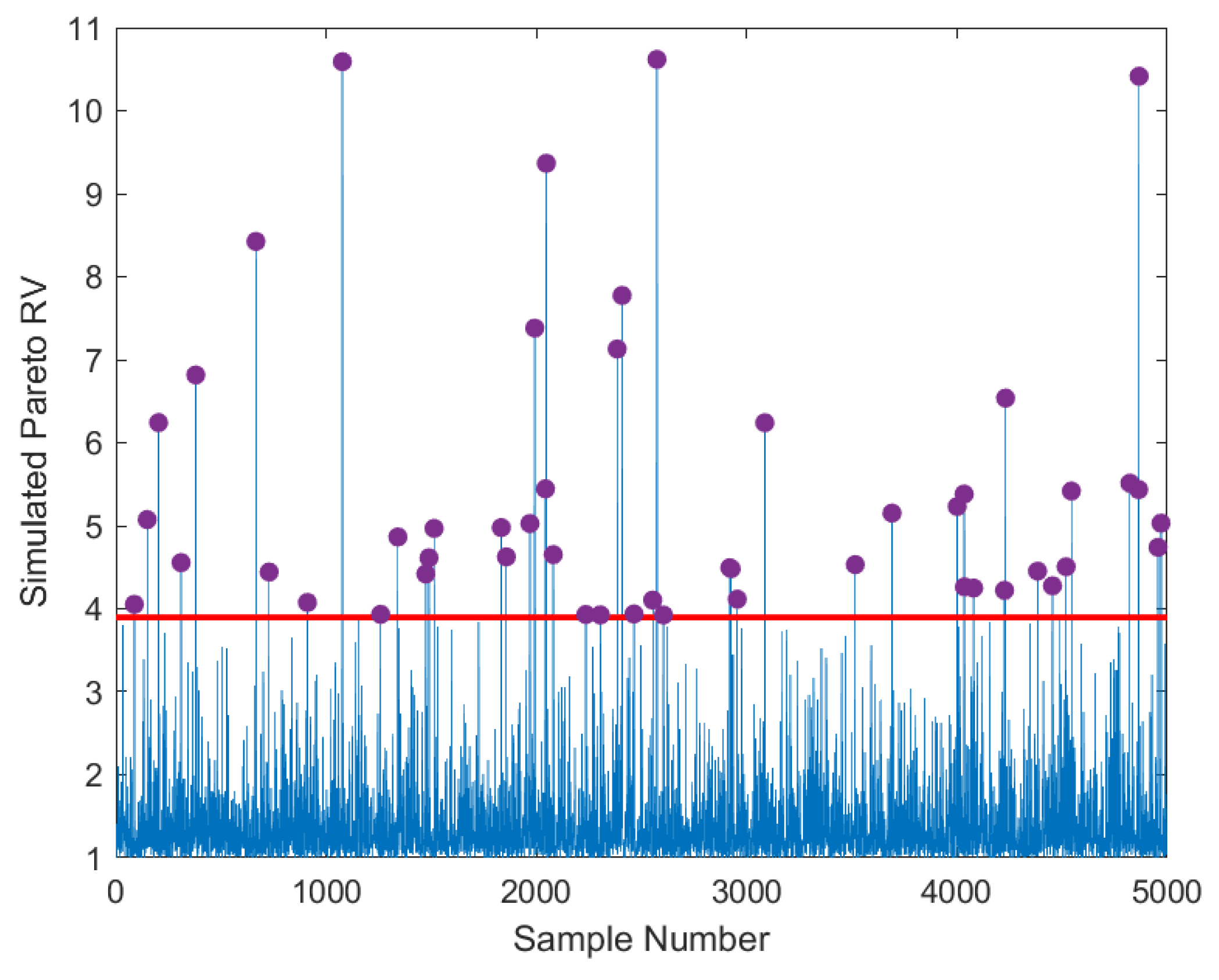
3.2. Data Definition and Solution
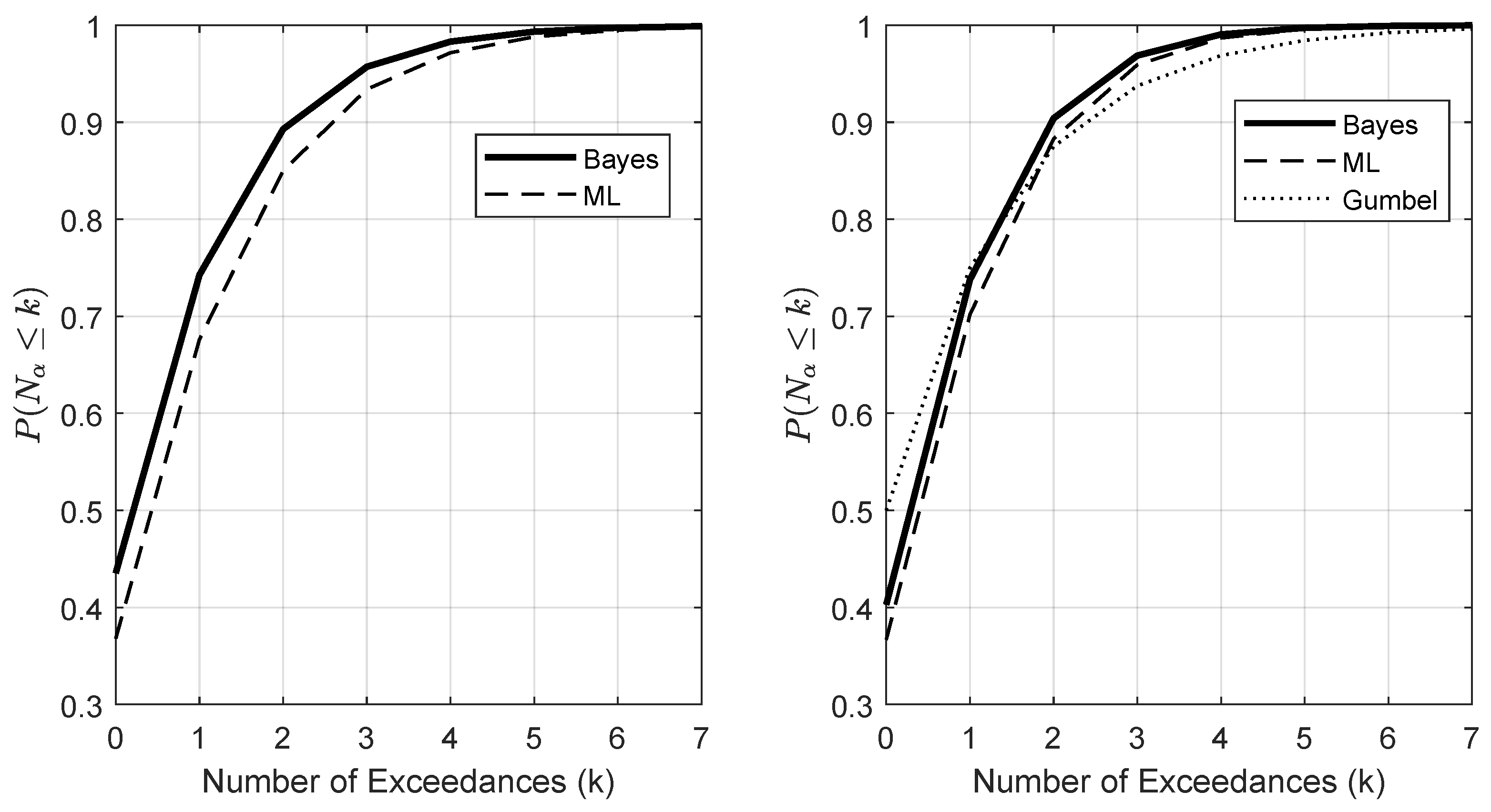
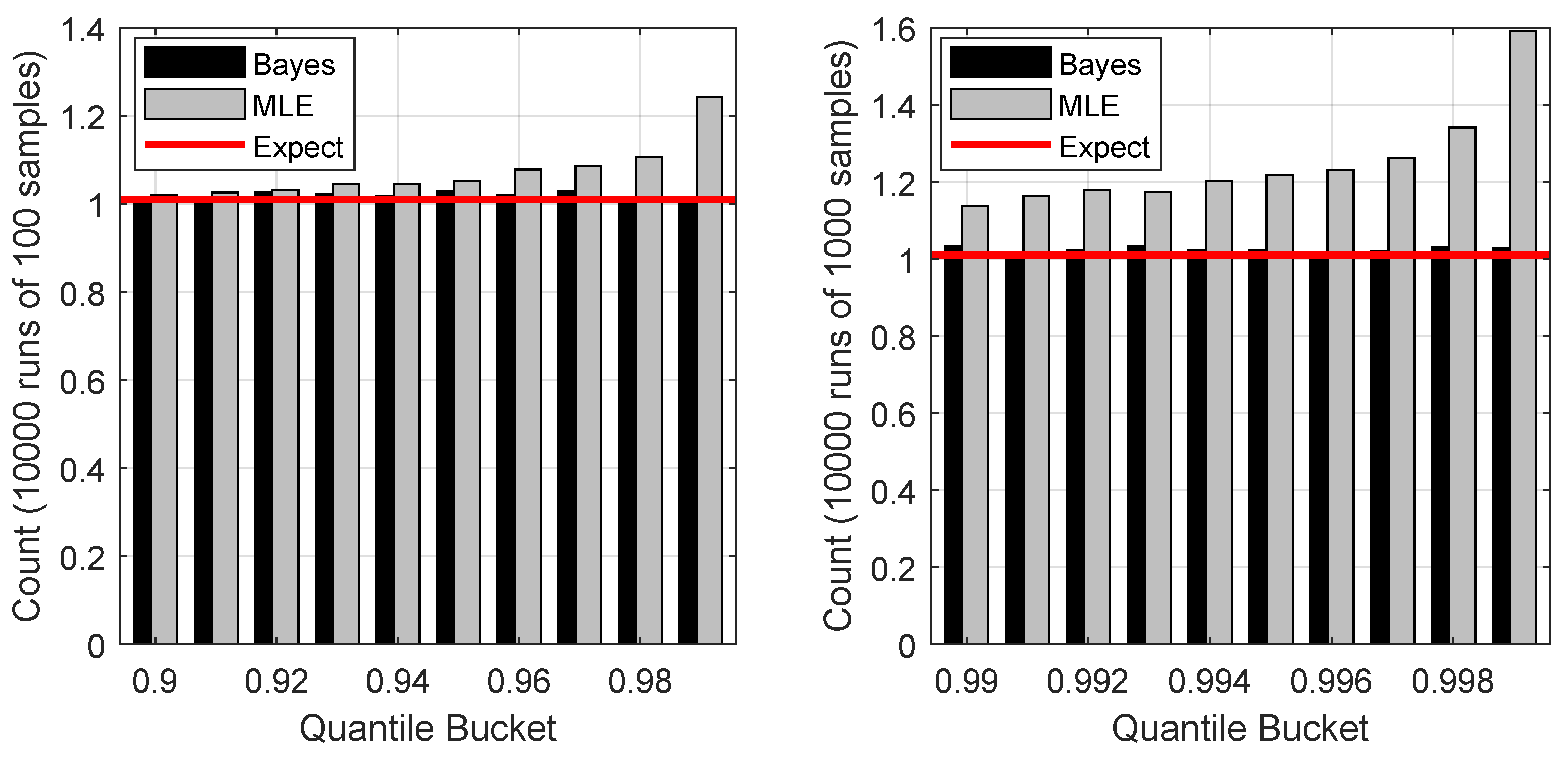
4. Simulation Results
5. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BEG | Binomial-Exponential-Gamma |
| GEV | Generalized extreme value |
| GPD | Generalized Pareto distribution |
| MDA | Maximum domain of attraction |
| ML | Maximum likelihood |
| MLM | Maximum likelihood method |
| POT | Peaks over threshold |
| RV | Random variable |
| VaR | Value at risk |
| ZCE | Zero coverage error |
References
- Bairamov, I. G. (1996). Some distribution free properties of statistics based on record values and characterizations of the distributions through records. Journal of Applied Statistical Science, 5(1), 17–25. [Google Scholar]
- Balkema, A., & de Haan, L. (1974). Residual life time at great age. Annals of Probability, 2(5), 792–804. [Google Scholar] [CrossRef]
- Broadwater, J. B., & Chellappa, R. (2010). Adaptive threshold estimation via extreme value theory. IEEE Transactions on Signal Processing, 58(2), 490–500. [Google Scholar] [CrossRef]
- Buishand, T. A. (1989). The partial duration series method with a fixed number of peaks. Journal of Hydrology, 109(1–2), 1–9. [Google Scholar] [CrossRef]
- Coles, S. (2004). An introduction to statistical modeling of extreme values. Springer. [Google Scholar]
- Coles, S. G., & Dixon, M. J. (1999). Likelihood-based inference for extreme value models. Extremes, 2(1), 5–23. [Google Scholar] [CrossRef]
- Coles, S. G., & Powell, E. A. (1996). Bayesian methods in extreme value modelling: A review and new developments. International Statistical Review, 64(1), 119–136. [Google Scholar] [CrossRef]
- Datta, G. S., Mukerjee, R., Ghosh, M., & Sweeting, T. J. (2000). Bayesian prediction with approximate frequentist validity. The Annals of Statistics, 28(5), 1414–1426. [Google Scholar] [CrossRef]
- Dekkers, A. L. M., & de Haan, L. (1989). On the estimation of the extreme-value index and large quantile estimation. Annals of Statistics, 17(4), 1795–1832. [Google Scholar] [CrossRef]
- DuMouchel, W. H. (1983). Estimating the stable index α in order to measure tail thickness: A critique. The Annals of Statistics, 11(4), 1019–1031. [Google Scholar] [CrossRef]
- Embrechts, P., Kluppelberg, C., & Mikosch, T. (2003). Modelling extremal events. Springer. [Google Scholar]
- Fofack, H., & Nolan, J. P. (1999). Tail behavior, modes and other characteristics of stable distributions. Extremes, 2, 39–58. [Google Scholar] [CrossRef]
- Gumbel, E. J. (1958). Statistics of extremes. Columbia University Press. [Google Scholar]
- Gumbel, E. J., & von Schelling, H. (1950). The distribution of the number of exceedances. The Annals of Mathematical Statistics, 21(2), 247–262. [Google Scholar] [CrossRef]
- Hall, P., & Rieck, A. (2001). Improving coverage accuracy of non-parametric prediction intervals. Journal of the Royal Statistical Society B, 63(4), 717–725. [Google Scholar] [CrossRef]
- Hill, B. M. (1975). A simple general approach to inference about the tail of a distribution. Annals of Statistics, 3(5), 1163–1174. [Google Scholar] [CrossRef]
- Hosking, J. R. M., & Wallis, J. R. (1987). Parameter and quantile estimation for the generalized Pareto distribution. Technometrics, 29(3), 339–349. [Google Scholar] [CrossRef]
- Johnston, D. E., & Djurić, P. M. (2011). The science behind risk management: A signal processing perspective. IEEE Signal Processing Magazine, 28(5), 26–36. [Google Scholar]
- Johnston, D. E., & Djurić, P. M. (2020, May 4–8). A recursive Bayesian solution for the excess over threshold distribution with stochastic parameters. ICASSP 2020, Barcelona, Spain. [Google Scholar]
- Johnston, D. E., & Djurić, P. M. (2021, June 6–11). Baysian estimation of a tail-index with marginalized threshold. ICASSP 2021 (pp. 5569–5573), Toronto, ON, Canada. [Google Scholar]
- Leadbetter, M. R. (1991). On a basis for ‘Peaks over Threshold’ modeling. Statistics and Probability Letters, 12(4), 357–362. [Google Scholar] [CrossRef]
- McNeil, A., Frey, R., & Embrechts, P. (2005). Quantitative risk management. Princeton University Press. [Google Scholar]
- Nerantzaki, S. D., & Papalexiou, S. M. (2022). Assessing extremes in hydroclimatology: A review on probabilistic methods. Journal of Hydrology, 605, 1–20. [Google Scholar] [CrossRef]
- Northrop, P. J., Attalides, N., & Jonathan, P. (2017). Cross-validatory extreme value threshold selection and uncertainty with application to ocean storm severity. Journal of the Royal Statistical Society: Applied Statistics, 66(1), 93–120. [Google Scholar] [CrossRef]
- Pickands, J. (1975). Statistical inference using extreme order statistics. Annals of Statistics, 3(1), 119–131. [Google Scholar]
- Resnick, S. I., & Rootzeń, H. (2000). Self-similar communication models and very heavy tails. Annals of Applied Probability, 10(3), 753–778. [Google Scholar] [CrossRef]
- Roberts, S. J. (2000). Extreme value statistics for novelty detection in biomedical data processing. IEE Proceedings-Science, Measurement and Technology, 147(6), 363–367. [Google Scholar]
- Shenoy, S., & Gorinevsky, D. (2015). Estimating long tail models for risk trends. IEEE Signal Processing Letters, 22(7), 968–972. [Google Scholar] [CrossRef]
- Smith, R. L. (1987). Estimating tails of probability distributions. The Annals of Statistics, 15(3), 1174–1207. [Google Scholar] [CrossRef]
- van Dantzig, D. (1954, September 2–9). Mathematical problems raised by the flood disaster of 1953. International Congress of Mathematicians (pp. 218–239), Amsterdam, Denmark. [Google Scholar]
- Weron, R. (2001). Levy-stable distributions revisited: Tail index > 2 does not exclude the Levy-stable regime. International Journal of Modern Physics, 12(2), 209–223. [Google Scholar] [CrossRef]
- Wesolowski, J., & Ahsanullah, M. (1998). Distributional properties of exceedance statistics. Annals of the Institute of Statistical Mathematics, 50(3), 543–565. [Google Scholar] [CrossRef]
- Yu, K., & Ally, A. (2009). Improving prediction intervals: Some elementary methods. The American Statistician, 63(1), 17–19. [Google Scholar] [CrossRef]
- Yu, K., & Moyeed, R. A. (2001). Bayesian quantile regression. Statistics and Probability Letters, 54(4), 437–447. [Google Scholar]

| Exp () | Lognormal (, ) | |||||||
| n = 5 | n = 10 | n = 25 | n = 50 | n = 5 | n = 10 | n = 25 | n = 50 | |
| 0.13 | 0.14 | 0.16 | 0.18 | 0.28 | 0.29 | 0.32 | 0.34 | |
| 0.05 | 0.04 | 0.03 | 0.02 | 0.12 | 0.09 | 0.06 | 0.04 | |
| 0.95 | 0.78 | 0.48 | 0.25 | 0.98 | 0.90 | 0.71 | 0.53 | |
| 1.67 | 1.37 | 0.93 | 0.60 | 1.60 | 1.45 | 1.12 | 0.88 | |
| 0.21 | 0.18 | 0.10 | 0.04 | 0.23 | 0.22 | 0.17 | 0.11 | |
| StdPar ( = 0.1) | GEV ( = 0.5, = 1, = 0) | |||||||
| n = 5 | n = 10 | n = 25 | n = 50 | n = 5 | n = 10 | n = 25 | n = 50 | |
| 0.10 | 0.10 | 0.10 | 0.10 | 0.52 | 0.51 | 0.53 | 0.54 | |
| 0.04 | 0.03 | 0.02 | 0.01 | 0.23 | 0.16 | 0.10 | 0.07 | |
| 1.08 | 1.04 | 1.03 | 1.0 | 1.05 | 1.03 | 0.94 | 0.88 | |
| 1.70 | 1.53 | 1.37 | 1.22 | 1.70 | 1.50 | 1.30 | 1.14 | |
| 0.26 | 0.25 | 0.26 | 0.26 | 0.25 | 0.25 | 0.23 | 0.23 | |
| StudentT () | StudentT () | |||||||
| n = 5 | n = 10 | n = 25 | n = 50 | n = 5 | n = 10 | n = 25 | n = 50 | |
| 0.50 | 0.50 | 0.50 | 0.51 | 0.14 | 0.15 | 0.17 | 0.18 | |
| 0.23 | 0.16 | 0.10 | 0.07 | 0.06 | 0.04 | 0.03 | 0.02 | |
| 1.08 | 1.04 | 1.0 | 0.95 | 1.02 | 0.86 | 0.64 | 0.40 | |
| 1.71 | 1.57 | 1.34 | 1.19 | 1.69 | 1.39 | 1.07 | 0.73 | |
| 0.25 | 0.25 | 0.25 | 0.24 | 0.24 | 0.20 | 0.14 | 0.08 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johnston, D.E. Bayesian Estimation of Extreme Quantiles and the Distribution of Exceedances for Measuring Tail Risk. J. Risk Financial Manag. 2025, 18, 659. https://doi.org/10.3390/jrfm18120659
Johnston DE. Bayesian Estimation of Extreme Quantiles and the Distribution of Exceedances for Measuring Tail Risk. Journal of Risk and Financial Management. 2025; 18(12):659. https://doi.org/10.3390/jrfm18120659
Chicago/Turabian StyleJohnston, Douglas E. 2025. "Bayesian Estimation of Extreme Quantiles and the Distribution of Exceedances for Measuring Tail Risk" Journal of Risk and Financial Management 18, no. 12: 659. https://doi.org/10.3390/jrfm18120659
APA StyleJohnston, D. E. (2025). Bayesian Estimation of Extreme Quantiles and the Distribution of Exceedances for Measuring Tail Risk. Journal of Risk and Financial Management, 18(12), 659. https://doi.org/10.3390/jrfm18120659






