Normalizing Pandemic Data for Credit Scoring

Abstract

The COVID-19 pandemic created abnormal credit risk conditions that did not align well with pre-2020 credit scores. Since the pandemic, most organizations have either excluded the period 2020–2021 from their modeling or included it without adjustment, leaving it as noise in the data. Model validators and examiners have been divided about requiring one of these approaches or defaulting to model developer judgment. None of this is ideal from a model development perspective. This paper presents a unique technical solution that allows for the inclusion of pandemic data while constructing credit scores and actually produces scores that perform better and have long-term stability across the entire economic cycle. This result negates the common belief that credit scores must be frequently rebuilt in order to maintain rank order accuracy. This analysis uses lifecycle and environment outputs from an Age-Period-Cohort analysis as fixed offsets to credit score development. Panel data is used, so the credit score is developed with a discrete time survival model approach. Logistic regression and stochastic gradient boosted regression trees were tested as estimators with the panel data and APC inputs.

1. Introduction

The COVID-19 pandemic created unprecedented economic conditions that fundamentally disrupted traditional credit risk assessment. According to research on marketplace lending, the probability of loan default increased from 0.056 in the pre-pandemic period to 0.079 during the pandemic. This significant shift occurred despite massive government intervention programs designed to stabilize the economy (Bose et al., 2021).

These intervention programs, while beneficial for short-term economic stability, created additional challenges for credit risk assessment. Studies have found that default intensities shifted from long-range to short-range dependence during the COVID-19 period (Aït-Sahalia et al., 2022; Gerardi et al., 2022), making historical credit performance much less relevant for credit prediction. This phenomenon contrasts sharply with previous financial crises, where long-memory patterns remained relatively stable. The current research appears to present a solution to this challenge.

Financial institutions faced significant challenges in implementing credit risk models during this period. The disconnect between economic conditions and credit performance led many institutions to replace advanced credit scores with simple bureau score-based decision trees.

Traditional credit scoring models faced particular challenges during the pandemic for several reasons. The rapid implementation of forbearance programs Cherry et al. (2021) artificially suppressed delinquencies Basel Committee on Banking Supervision (2022), creating a disconnect between observed credit performance and actual credit risk. Consumer spending patterns changed dramatically as lockdowns limited discretionary spending opportunities, leading to decreased credit utilization and paradoxically improved credit scores during a period of economic distress. The impact of the pandemic was heterogeneous across different segments of borrowers, with certain industries and geographic regions experiencing more severe effects Li and Strahan (2021).

A fundamental limitation of traditional credit scoring approaches is their reliance on cross-sectional data rather than panel data. Cross-sectional models provide only a snapshot at a single point in time, failing to capture the dynamic nature of credit risk as it changes through a loan’s lifecycle and across different economic environments.

Panel data approaches, which track the same borrowers over multiple time periods, offer several advantages for credit risk modeling (Singer & Willett, 2003; Thomas & Crook, 2007). By knowing when a loan defaults, the model can be designed to distinguish between defaults that occur due to the maturing of the loan, shifts in the economic environment, or the intrinsic credit risk of the loan. During economic shocks like the pandemic, these advantages become even more critical as they allow models to adapt to changing conditions and capture time-varying effects that cross-sectional approaches cannot address.

This paper introduces a method to normalize pandemic data for use in credit scoring. The lifecycle and environment functions from an Age-Period-Cohort (APC) model are used to normalize panel-structured performance data. With this normalization, logistic regression and stochastic gradient boosted trees are created on Fannie Mae and Freddie Mac mortgage data to create origination scores that maintain predictive power despite the pandemic’s unprecedented conditions.

2. Literature Review

The challenge of maintaining predictive credit models through economic disruptions has been a persistent concern in financial risk management. This literature review examines the progression of approaches to credit scoring under stressed conditions, the development of survival analysis techniques in credit risk, and the specific challenges posed by the COVID-19 pandemic.

2.1. Traditional Credit Scoring and Economic Shocks

Traditional credit scoring models, pioneered by Fair Isaac Corporation in the 1950s and 1960s, rely primarily on cross-sectional data snapshots that capture borrower characteristics at a single point in time (Thomas & Crook, 2007). While these models have proven effective under stable economic conditions, their performance degrades significantly during periods of macroeconomic stress. Anderson (2007) documented substantial prediction errors in FICO scores during the 2001 recession, attributing these failures to the models’ inability to capture time-varying default intensities.

The 2008 financial crisis exposed fundamental limitations in traditional credit risk frameworks. Bellotti and Crook (2009) found that credit scores developed before 2007 experienced dramatic rank-ordering failures when applied to 2008-2009 vintages, with Gini coefficients declining by as much as 0.15 in some portfolios. This led many institutions to implement ad-hoc adjustments or segmented underwriting approaches (Siddiqi, 2012). However, these reactive solutions lacked theoretical foundations and proved difficult to validate.

Breeden (2011) introduced the concept of “Macroeconomic Adverse Selection,” demonstrating that economic conditions systematically influence the risk characteristics of loan applicants in ways not captured by traditional credit attributes. During periods of rising interest rates or economic uncertainty, the pool of applicants shifts toward riskier borrowers who cannot be distinguished using conventional credit scores. This phenomenon has been empirically validated across multiple product types, including mortgages Breeden and Canals-Cerdá (2018), auto loans Breeden and Leonova (2023a) and home equity lines of credit Calem et al. (2011).

2.2. Survival Analysis in Credit Risk Modeling

The application of survival analysis to credit risk emerged as researchers recognized that default is fundamentally a time-to-event phenomenon rather than a binary outcome. Narain (1992) proposed using survival models for credit scoring, arguing that the dynamic nature of credit risk required temporal modeling frameworks. This insight gained traction in academic research throughout the 1990s and 2000s.

Cox proportional hazards models Cox (1972); Therneau and Grambsch (2000) became the dominant approach for incorporating survival concepts into credit scoring Malik and Thomas (2012); Stepanova and Thomas (2002). These semi-parametric models allow estimation of time-varying default risk without specifying a baseline hazard function. However, researchers have identified significant limitations. Breeden et al. (2023) demonstrated that Cox models exhibit coefficient instability in credit applications due to violations of the proportional hazards assumption, particularly during economic transitions. The assumption that hazard ratios remain constant over time proves unrealistic for credit risk, where idiosyncratic factors, loan seasoning, and macroeconomic conditions influence default intensities, creating the same ambiguities first identified via Age-Period-Cohort models. Discrete-time survival models offer an alternative estimation approach that addresses some limitations of Cox regression. By treating time as discrete intervals (typically months), these models allow for more flexible specification of time-varying effects through panel logistic regression (Allison, 1982).

More recent research has extended survival analysis frameworks using machine learning techniques. Xia et al. (2021) developed survival gradient boosting models that outperformed traditional approaches for Chinese consumer loans. Norell (2023) combined survival regression with gradient boosting for corporate credit ratings, while Archetti and Noci (2024) proposed fully parametric gradient boosting methods. These approaches demonstrate the potential for machine learning to capture complex, nonlinear relationships in survival data, though questions remain about interpretability and stability across economic regimes.

2.3. Age-Period-Cohort Modeling

Age-Period-Cohort (APC) analysis originated in epidemiology and demography as a method for disentangling lifecycle effects, period effects, and cohort quality T. R. Holford (1983). The framework decomposes outcomes into three components: age effects that vary with individual maturation, period effects reflecting contemporaneous environmental conditions, and cohort effects capturing characteristics of birth or origination groups.

Application of APC methods to credit risk began with Breeden (2007), who used APC to demonstrate the effectiveness of APC models for stress testing and loss forecasting during the financial crisis. The approach proved valuable for separating the effects of vintage quality (cohort) from loan maturation (age) and macroeconomic deterioration (period). Subsequent research demonstrated that APC models could improve out-of-sample prediction accuracy compared to traditional approaches (Breeden, 2018).

A fundamental challenge in APC modeling is the identification problem: age, period, and cohort are linearly dependent (age = period − cohort), making unique parameter estimation impossible without constraints Fu (2018); Yang and Land (2014). Various solutions have been proposed, including imposing equality constraints, using intrinsic estimators, or specifying one component as a known function. For credit risk applications, the work comparing APC and Cox Ph estimation Breeden et al. (2023) demonstrated that the trend specification problem in APC models is expressed as a multicollinearity problem in Cox PH and regression models. The problem originates within the structure of the data and is simply expressed differently within each model.

2.4. COVID-19 Pandemic and Credit Risk

The COVID-19 pandemic created unprecedented disruptions to credit markets that challenged existing modeling frameworks. The speed and severity of economic contraction in March-April 2020 had no modern parallel, with unemployment spiking from 3.5% to 14.7% in a single month, although the report footnote states that it was probably as high as 19.8% Bureau of Labor Statistics (2020). Simultaneously, massive government intervention programs, including enhanced unemployment benefits, stimulus payments, and loan forbearance programs, created artificial support for consumer finances that decoupled credit performance from traditional macroeconomic indicators.

Research on pandemic credit effects has documented several key phenomena. Bose et al. (2021) found that default probabilities increased significantly in marketplace lending despite government support, rising from 5.6% pre-pandemic to 7.9% during 2020. Aït-Sahalia et al. (2022) demonstrated that credit default intensities shifted from long-range to short-range dependence during COVID-19, breaking historical correlation patterns that credit models relied upon. This contrasts sharply with previous financial crises, where long-memory patterns remained relatively stable.

The heterogeneous impact of the pandemic across industries and demographics further complicated modeling efforts. Li and Strahan (2021) showed that relationship lending through small banks provided better outcomes for Paycheck Protection Program loans than automated lending by fintech firms, suggesting that soft information became more valuable during the crisis. Geographic and sectoral variations in economic impact meant that portfolio-level models masked substantial underlying risk variation.

Financial institutions responded to pandemic disruptions by reverting to simplified decision rules. Many lenders replaced sophisticated credit scores with bureau score cutoffs and simple decision trees, effectively abandoning years of model development (Board of Governors of the Federal Reserve System, 2020). Model validators and regulators were divided on appropriate treatments: some required excluding 2020–2021 data entirely, others mandated macroeconomic adjustments, while still others deferred to model developer judgment. None of these approaches proved fully satisfactory from a statistical perspective.

2.5. Research Gap and Contribution

Despite extensive research on credit scoring, survival analysis, APC modeling, and pandemic effects, no prior work has demonstrated a systematic method for normalizing pandemic data to enable its inclusion in credit score development. Existing approaches either exclude anomalous periods (reducing sample size and eliminating valuable information) or include them without adjustment (introducing noise that degrades model performance). The current research addresses this gap by integrating APC lifecycle and environment functions as fixed offsets in discrete-time survival models, providing a theoretically grounded and empirically validated approach to pandemic data normalization.

3. Model Architecture

Many lending analysts have tried to create macroeconomic indices to measure the actual impact of the pandemic on consumers (Cavallo, 2020; Diewert & Fox, 2022). The author tried creating an index of “persons receiving income”, which would include employed people and those receiving government support. Although this and other indices made sense, none could capture the impacts of the various forbearance programs and benefits. Rather than a macroeconomic-based approach to normalization, the most effective method was to measure the net impact via age-period cohort modeling and then adjust the score estimation to use the observed environmental impacts for normalization.

3.1. Fundamentals of APC Modeling

Age-Period-Cohort (APC) analysis provides an effective framework for modeling default risk over time (Fu, 2018; Yang & Land, 2014). Originally developed in epidemiology and sociology T. Holford (2005), APC models have been used in loss forecasting and stress testing Breeden et al. (2008). These models decompose credit performance into three fundamental components: lifecycle effects versus age of the account, environmental impacts versus calendar date, and credit quality by vintage.

The basic APC model can be expressed as

$$\log \text{-}\mathrm{odds}PD(a,t,v)=F\left(a\right)+G\left(v\right)+H\left(t\right)$$

(1)

$PD$ is defined in this context as Ever 60+ DPD Rate, meaning a “default” is recorded on the first occurrence of an account becoming 60 or more days past due. a is the age of the loan, t is the calendar time, v is the vintage date, $F\left(a\right)$ represents the lifecycle function, $H\left(t\right)$ represents the environment function, and $G\left(v\right)$ represents the vintage quality function.

This decomposition allows researchers to separate the effects of vintage quality from loan aging and macroeconomic conditions. During economic shocks like the COVID-19 pandemic, the environment function captures the impact of changing consumer financial conditions, while the vintage function reflects changes in borrower quality. The ability to measure actual impacts via $H\left(t\right)$, rather than trying to explain calendar date impacts purely from macroeconomic factors, was a key to success during the pandemic.

One challenge in APC modeling is the identification problem arising from the linear relationship $a=t-v$ (T. R. Holford, 1983). Various approaches have been proposed to address this issue, including imposing constraints on the functions. In credit risk applications, a common approach is to represent the model as

$$log\left(\mathrm{PD}(a,t,v)\right)=b_0+b_{1}a+b_{2}v+F^{\prime }\left(a\right)+G^{\prime }\left(v\right)+H^{\prime }\left(t\right)$$

(2)

where $F^{\prime }\left(a\right)$, $G^{\prime }\left(v\right)$, and $H^{\prime }\left(t\right)$ are nonlinear functions with zero mean and no linear component. This formulation resolves the linear trend ambiguity. The analyst must then decide how best to allocate the trend, considering the details of the problem. For the analysis here, the environment function is chosen to have zero trend, which is most appropriate for long time histories spanning more than one recession. If less than one economic cycle had been available, fitting to economic factors while allowing for a secular trend can resolve the environmental trend uncertainty.

The functions are estimated using a Bayesian Age-Period-Cohort algorithm (Schmid & Held, 2007), in order to constrain the estimates for recent vintages and older dates where few observations are available.

3.2. Panel Logistic Regression with APC Inputs

Many credit scoring techniques exist that leverage survival modeling principles (Dirick et al., 2017; Djeundje & Crook, 2019; Shang et al., 2025; Thackham, 2022). The most common of these is Cox proportional hazards (Cox, 1972; Sargent, 1997; Therneau & Grambsch, 2000), which is widely used but suffers from instability in credit scoring applications (Breeden et al., 2023).

To implement discrete time survival models with APC inputs, panel logistic regression is used with an augmented model matrix (Breeden & Leonova, 2023b). One row is created per account per month active and no more than one entry for a default event. Censoring the data after default implicitly means that the denominator for $PD$ will be the previous month’s open accounts. This structure allows the analyst to include a parallel model of the probability of prepayment in order to consider competing risks (Deng et al., 2000; Fine & Gray, 1999).

The model matrix becomes

$$X_i=\left[\begin{array}{ccccccc}0& F\left(1\right)& H\left(t_1\right)& s_{i1}& s_{i2}& \cdots & s_{ik}\\ 0& F\left(2\right)& H\left(t_2\right)& s_{i1}& s_{i2}& \cdots & s_{ik}\\ ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& F\left(a_i\right)& H\left(t_i\right)& s_{i1}& s_{i2}& \cdots & s_{ik}\end{array}\right]$$

(3)

where the first column is the default indicator, the second column is the lifecycle at each age, the third column is the environment function at each time, and the remaining columns are scoring covariates. During model estimation, the coefficients for the lifecycle and environment columns are fixed at $1.0$.

By including the APC lifecycle and environment functions as fixed inputs, the panel logistic regression model can be expressed as:

$$log\left({\displaystyle \frac{\mathrm{PD}(a,v,t,i)}{1-\mathrm{PD}(a,v,t,i)}}\right)=F\left(a\right)+H\left(t\right)+\sum _j{c}_j{s}_{ij}+\sum _v{\beta }_v\delta \left(v\right)+\epsilon (a,v,t,i)$$

(4)

where $s_{ij}$ are the available attributes at origination for account i, and $c_j$ are the coefficients to be estimated. This approach allows $F\left(a\right)+H\left(t\right)$ to specify the mean of the distribution at each forecast month, with the logistic regression model estimating the distribution of account risk centered about that mean. In other words, the credit score models the residual risk after adjusting for lifecycle and environment, thus normalizing the performance data for account age and the pandemic conditions.

This approach significantly improves out-of-time performance compared to traditional credit scoring methods (Breeden & Leonova, 2023b). By providing lifecycle and environment functions as fixed inputs to the model, more stable coefficients can be achieved for risk factors, and the impact of changing economic conditions is better captured.

3.3. Stochastic Gradient Boosted Trees

Machine learning methods, particularly gradient boosted trees, have gained popularity in credit scoring due to their ability to capture complex, non-linear relationships in data. Stochastic Gradient Boosted Regression Trees (SGBTs) combine bagging with gradient boosting to create an ensemble of trees (Davis et al., 2019; Friedman, 2002; Hothorn et al., 2006; Ridgeway, 1999).

The basic idea of gradient boosting is to build subsequent models on the residuals of previous models, computing the gradient of a fitness function to provide weights to each model trained. Stochastic gradient boosting adds randomization to this process, building different gradient boosted ensembles for each data subsample.

$$F_K\left(x\right)=c+\sum _{k=1}^K\nu h_k\left(x\right)$$

(5)

where each $h_k\left(x\right)$ is a model and $\nu$ is a learning rate parameter. This approach can significantly reduce computation times while maintaining acceptable accuracy.

When regression models are used for the $h_k\left(x\right)$, then lifecycle and environment may be included as fixed offsets, just as was done for the discrete time survival model (Breeden & Leonova, 2023b). The input data is again structured as a panel, so the resulting forecasts are monthly, conditional $PD$. Other researchers have developed combinations of survival modeling and stochastic gradient boosted trees (Archetti & Noci, 2024; Barnwal et al., 2021; Chen et al., 2013; Norell, 2023; Xia et al., 2021), although for the current problem, the APC approach of incorporating an empirical environment function is preferred for normalization of the credit score development.

4. Fannie Mae and Freddie Mac Data for Origination Scores

To demonstrate the approach, loan-level data from Fannie Mae and Freddie Mac were analyzed. The Freddie Mac Single Family Loan-Level Dataset covers approximately 53.8 million mortgages originated between 1 January 1999, and 30 June 2024, with monthly loan performance data through 30 September 2024 (Freddie Mac, 2025). Comparable data from the Fannie Mae Single-Family Loan Performance Data was prepared for modeling Fannie Mae (2020):

For this analysis, only fixed-rate, 30-year mortgages were analyzed. Loans with the full range of origination FICO scores were included. As will be shown in the tables of results, only loans originated between 2016 and 2024 were included in the credit scoring analysis, but all available loans starting with 1999 were included in the Age-Period-Cohort modeling.

The origination scoring variables available from both Fannie Mae and Freddie Mac are given in

Table 1. Variables for credit scoring.

Variable Name
Borrower Credit Score At Origination
Loan Purpose
Number Of Borrowers
Original Combined Loan-To-Value Ratio (CLTV)
Original Debt-To-Income Ratio (DTI)
Original Interest Rate
Property Type

.

This set of variables is sufficient to demonstrate the approach but not to highlight the nonlinear modeling capabilities of the stochastic gradient boosted regression trees.

To prepare the data for our panel modeling approach, an augmented data matrix is created where each loan has multiple observations corresponding to different points in its lifecycle. For each observation, both static variables (such as bureau credit score and LTV at origination) and the values of the APC functions are included.

5. Results

5.1. Age-Period-Cohort Model

For the APC analysis, the full Fannie Mae data was analyzed. This was necessary in order to estimate the environment function over the full date range. For all in-sample and out-of-sample test results, the actual environment function was used. This means that out-of-sample or out-of-time refers to the data used for training the score. This approach is called an “ideal scenario validation”, so as to avoid confusing our scoring model tests with errors from predicting the environment function using macroeconomic variables.

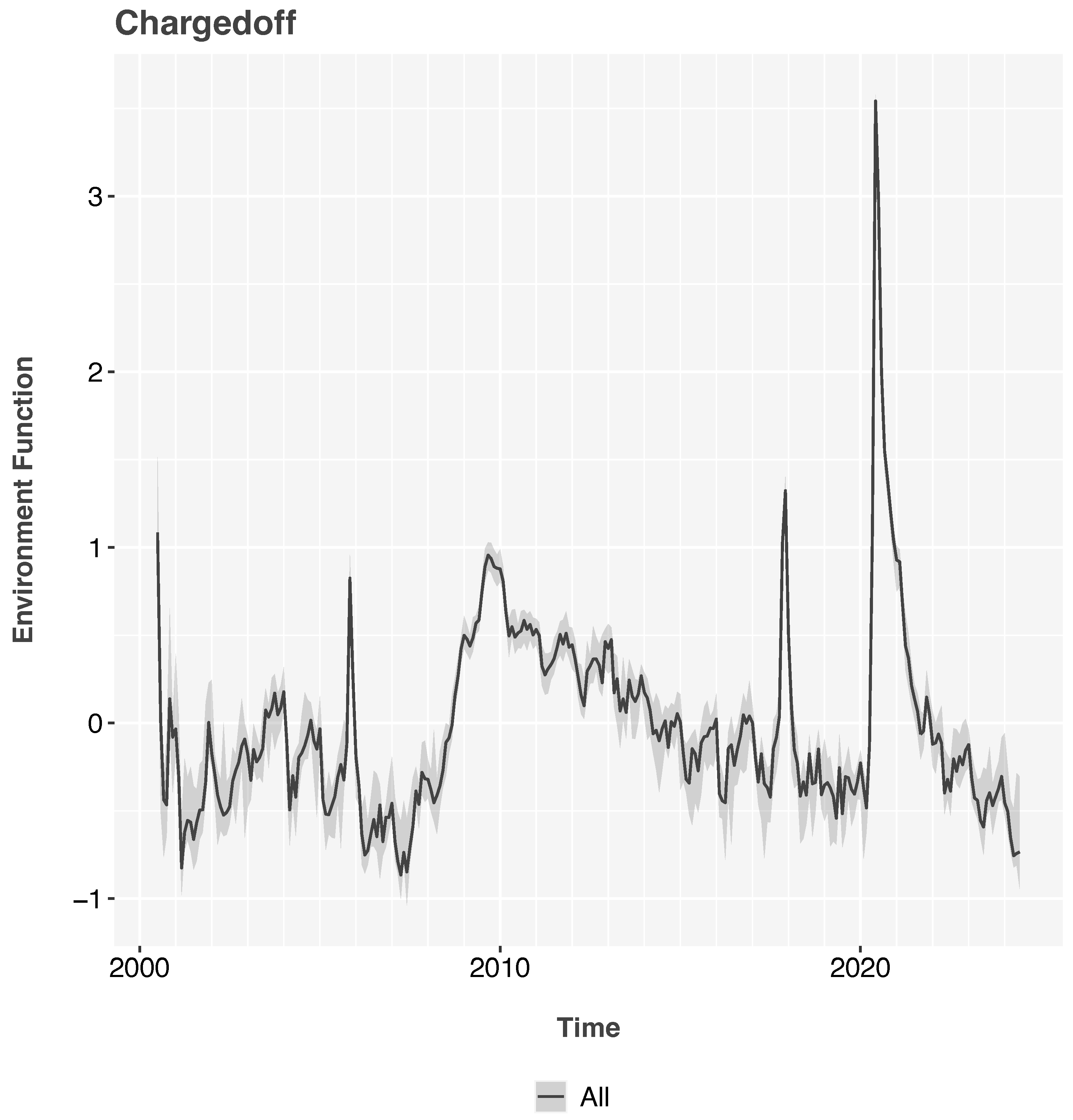
The environment function clearly shows the 2001 and 2009 recessions and the 2020 pandemic, Figure 1. The lifecycle functions, Figure 2, mirror those observed previously Breeden (2018).

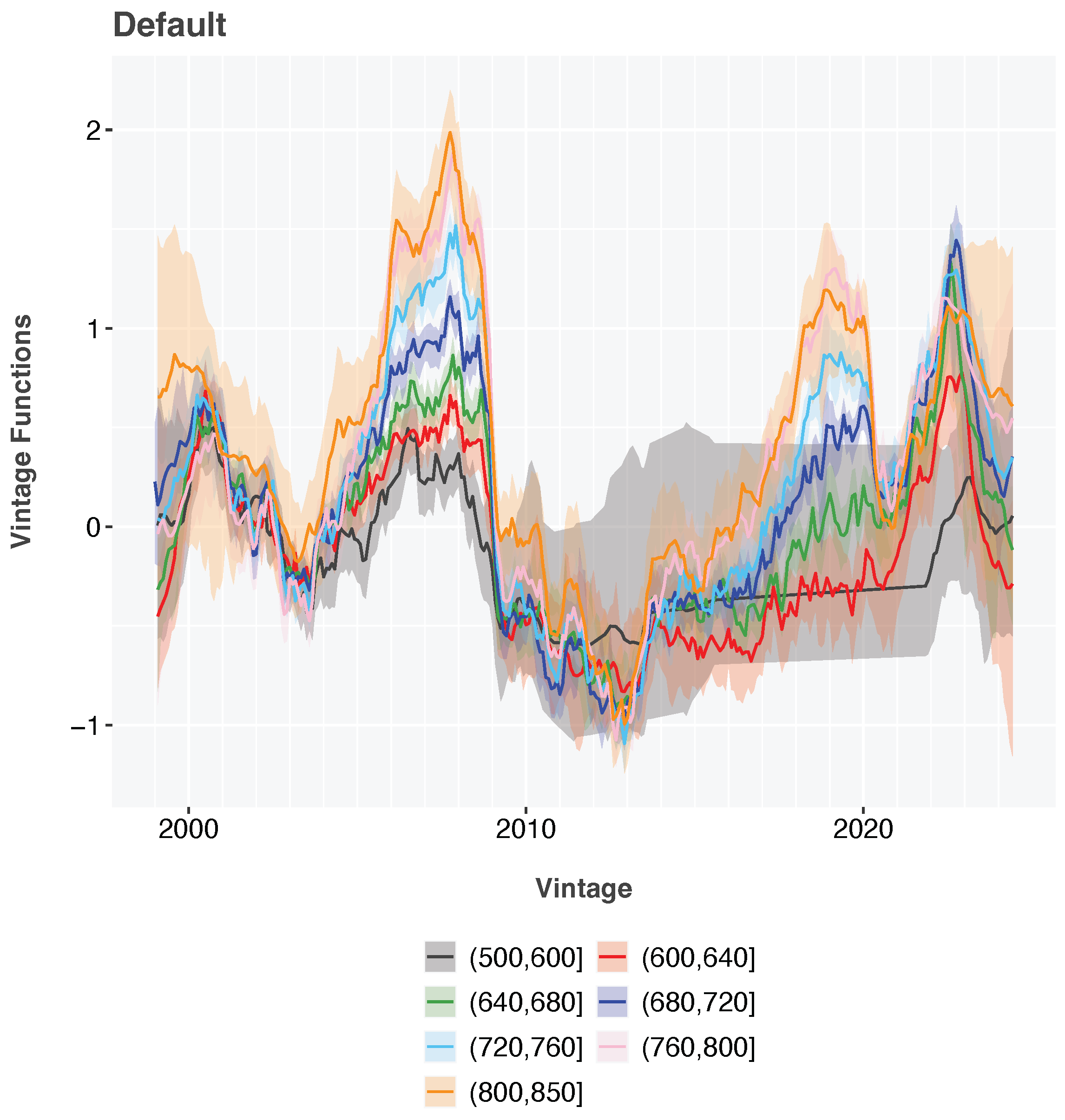
The APC vintage functions, Figure 3, clearly show the strong periods of adverse selection from 2006 through 2008 (Breeden & Canals-Cerdá, 2018) and more recently from 2022 through 2024. These periods have previously been explained as arising from sudden shifts in interest rates, causing a shift in the intrinsic risk of the loan applicants in ways not visible from standard scoring attributes. This effect was also observed in auto loans Breeden and Leonova (2023a) and other consumer loans Calem et al. (2011).

For purposes of demonstrating normalizing pandemic data for scoring, the vintage function was not included in the credit score, and macroeconomic adverse selection was not estimated after score construction. If these models were put into production, researchers should continuously track vintage residuals and include these in the forecast in order to align the credit score forecasts from different periods. Vintage residuals are not exactly the same as the APC vintage function. Conceptually, they are equivalent to subtracting the credit score aggregated by vintage from the vintage function.

5.2. Credit Scores

To test the credit scoring approach, models were estimated on two-year periods and tested on all other two-year periods. For each type of credit score, this process created four separate models plus a fifth model spanning the entire range.

A panel logistic regression model was created with lifecycle and environment as fixed offsets, as discussed earlier. All of the scoring variables from Table 1 were significant and retained in all models.

Table 2. Logistic regression comparisons. Bold values are in-sample, in-time. All off-diagonal values are out-of-time. All Freddie Mac outputs are out-of-sample. The results demonstrate that all logistic regression scores using the APC lifecycle and environment as inputs perform significantly better during the pandemic. The performance is also confirmed on the completely out-of-sample Freddie Mac data.

Fannie Mae		Test Period
		No Offset						With Offset						Difference
		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024
Train Period	2016–2017	0.60	0.59	0.46	0.54	0.49		0.65	0.59	0.73	0.52	0.70		0.05	0.00	0.28	−0.02	0.21
	2018–2019	0.60	0.59	0.45	0.55	0.49		0.65	0.60	0.73	0.52	0.70		0.05	0.00	0.28	−0.03	0.22
	2020–2021	0.58	0.56	0.47	0.51	0.49		0.59	0.53	0.74	0.50	0.69		0.01	−0.03	0.27	0.00	0.21
	2022–2023	0.56	0.56	0.42	0.56	0.48		0.62	0.57	0.74	0.54	0.71		0.06	0.00	0.31	−0.02	0.23
	2016–2024	0.58	0.57	0.45	0.55	0.49		0.62	0.56	0.74	0.52	0.70		0.03	−0.01	0.28	−0.03	0.21
Freddie Mac		Test Period
		No Offset						With Offset						Difference
		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024
Train Period	2016–2017	0.48	0.49	0.41	0.48	0.42		0.53	0.49	0.64	0.46	0.59		0.045	0.009	0.23	−0.019	0.18
	2018–2019	0.48	0.49	0.40	0.50	0.42		0.53	0.50	0.64	0.47	0.59		0.050	0.012	0.24	−0.023	0.18
	2020–2021	0.46	0.45	0.42	0.45	0.41		0.46	0.42	0.64	0.45	0.58		−0.002	−0.030	0.22	0.001	0.17
	2022–2023	0.44	0.46	0.37	0.51	0.40		0.50	0.47	0.65	0.49	0.60		0.059	0.010	0.27	−0.019	0.20
	2016–2024	0.46	0.47	0.40	0.49	0.42		0.50	0.46	0.65	0.47	0.59		0.040	−0.005	0.24	−0.023	0.18
Source Comparison		Test Period
		No Offset						With Offset
		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024
Train Period	2016–2017	0.12	0.10	0.045	0.057	0.074		0.12	0.098	0.088	0.051	0.11
	2018–2019	0.12	0.10	0.044	0.054	0.072		0.12	0.097	0.087	0.050	0.11
	2020–2021	0.12	0.11	0.051	0.063	0.079		0.13	0.11	0.096	0.057	0.12
	2022–2023	0.12	0.10	0.048	0.051	0.074		0.12	0.096	0.088	0.052	0.11
	2016–2024	0.12	0.10	0.051	0.057	0.077		0.11	0.098	0.091	0.054	0.11

shows the Gini coefficients for each model. In-sample test values are shown in bold. Out-of-time test values are shown in regular type. The table is designed to facilitate the comparison of panel logistic regression models with and without the APC offsets. As shown in the Difference section, the difference is insignificant except for the period 2020–2021, in which case the model with an offset had a Gini coefficient on average 0.28 higher than the panel regression without an offset. The model built on the entire span had a comparable gain, presumably because of the inclusion of the 2020–2021 period.

The section for Freddie Mac was included as a fully out-of-sample test, since none of this data was included in the model. The comparison of Freddie Mac to Fannie Mae could give an idea as to how much a score would degrade if built on Fannie Mae data and then applied to a lender’s in-house loan origination. The Freddie Mac results generally show a reduction in Gini of 0.08 relative to Fannie Mae but with the same pattern regarding the 2020–2021 period.

For the second test, a panel stochastic gradient boosted regression tree (SGBRT) was created. The SGBRT models were estimated on 60% of the in-sample data with 40% as a cross-validation hold-out sample. The meta-parameters for the SGBRT algorithm (number of leaves, tree depth, learning rate, number of trees) were optimized in-sample on the 2016–2017 time slice and used throughout. One model was given the APC lifecycle and environment as fixed offsets, and the other was not. Those results are shown in

Table 3. Stochastic gradient boosted regression tree comparisons. Bold values along the diagonal are in-time. All off-diagonal values are out-of-time. All Freddie Mac outputs are out-of-sample. The results demonstrate that all stochastic gradient boosted regression tree scores using the APC lifecycle and environment as inputs perform significantly better during the pandemic. The performance is also confirmed on the completely out-of-sample Freddie Mac data.

Fannie Mae		Test Period
		No Offset						With Offset						Difference
		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024
Train Period	2016–2017	0.62	0.59	0.45	0.54	0.48		0.67	0.61	0.73	0.52	0.70		0.05	0.01	0.28	−0.02	0.22
	2018–2019	0.60	0.61	0.45	0.54	0.49		0.66	0.62	0.73	0.55	0.71		0.06	0.01	0.28	0.01	0.23
	2020–2021	0.53	0.53	0.52	0.42	0.49		0.61	0.55	0.75	0.52	0.71		0.08	0.02	0.23	0.10	0.22
	2022–2023	0.57	0.58	0.43	0.58	0.49		0.64	0.60	0.74	0.58	0.72		0.07	0.02	0.30	−0.00	0.23
	2016–2024	0.58	0.57	0.50	0.54	0.52		0.64	0.59	0.75	0.56	0.72		0.07	0.02	0.25	0.01	0.21
Freddie Mac		Test Period
		No Offset						With Offset						Difference
		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024
Train Period	2016–2017	0.58	0.56	0.43	0.50	0.45		0.61	0.55	0.71	0.48	0.66		0.04	−0.01	0.28	−0.03	0.21
	2018–2019	0.57	0.56	0.44	0.50	0.45		0.63	0.58	0.72	0.51	0.69		0.06	0.02	0.28	0.02	0.23
	2020–2021	0.46	0.45	0.49	0.37	0.43		0.55	0.47	0.72	0.47	0.66		0.09	0.02	0.23	0.10	0.23
	2022–2023	0.50	0.51	0.40	0.53	0.44		0.61	0.56	0.73	0.53	0.70		0.12	0.05	0.32	0.00	0.26
	2016–2024	0.52	0.51	0.47	0.50	0.47		0.61	0.54	0.73	0.51	0.69		0.09	0.02	0.26	0.02	0.22
Source Comparison		Test Period
		No Offset						With Offset
		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024		2016–2017	2018–2019	2020–2021	2022–2023	2016–2024
Train Period	2016–2017	0.04	0.03	0.02	0.03	0.03		0.05	0.05	0.02	0.05	0.04
	2018–2019	0.03	0.05	0.02	0.04	0.04		0.03	0.05	0.01	0.03	0.03
	2020–2021	0.06	0.08	0.03	0.05	0.05		0.06	0.08	0.03	0.05	0.05
	2022–2023	0.08	0.07	0.03	0.05	0.05		0.03	0.04	0.01	0.04	0.03
	2016–2024	0.06	0.06	0.02	0.05	0.05		0.04	0.06	0.02	0.04	0.03

with the same format as for the panel logistic regression outputs.

The panel SGBRT models show slightly better performance than panel logistic regression in all tests, but the difference is not significant. The pattern across test periods is again the same as for Table 2, with the 2020–2021 period showing the greatest when including the APC inputs. The Freddie Mac out-of-sample testing was even closer to the Fannie Mae results.

Previous studies have shown improvement when using APC inputs, in-sample and most notably out-of-sample. The mortgage data is different, because it is a very large data set with a wide range of vintages. When modeled over a short, two-year time window in a calm economic period with a limited set of available scoring variables, the advantages of APC inputs largely disappear. For smaller, more dynamic portfolios of shorter-term loans, the APC lifecycle will be an important contributor.

The lack of significant improvement from SGBRT as compared to LR is not a surprise. Much has been written trying to determine which modeling algorithm is best without paying sufficient attention to the data being modeled. This mortgage data, where the scoring attributes are either linearized or predefined discrete factor levels, eliminates the need for SGBRT’s nonlinear flexibility.

Overall, these results confirm that incorporating APC inputs into both panel logistic regression and stochastic gradient boosted regression trees significantly improves model performance during economic transitions, particularly the unprecedented conditions of the COVID-19 pandemic. This approach not only allowed for the inclusion of pandemic data in the modeling but actually improved the resulting scores compared to excluding that data.

6. Discussion

6.1. Interpretation of Key Findings

The results presented in Table 2 and Table 3 demonstrate an unexpected benefit of APC normalization in credit scoring. The most striking finding is the dramatic improvement in model performance during the pandemic period (2020–2021), where Gini coefficients increased by approximately 0.28 when APC offsets were included. This improvement occurred consistently across models from all training periods with both modeling approaches (logistic regression and SGBRT), suggesting a robust and fundamental benefit rather than a statistical artifact.

Notably, the improvement from APC normalization appears minimal during calm economic periods. Models trained on 2016–2017 or 2018–2019 data and tested on similar periods showed virtually identical performance with or without APC inputs (differences of 0.00 to 0.05 in Gini). This pattern reflects an important characteristic of the mortgage dataset: it is large, encompasses a wide range of vintages, and the available scoring variables are already well-specified for stable economic conditions. Under these circumstances, traditional cross-sectional approaches capture most available predictive information, leaving little room for temporal adjustments to add value.

The mechanism by which APC normalization improves pandemic-period performance deserves careful consideration. The environment function does not directly impact rank-ordering statistics like the Gini coefficient during testing, since it applies as a parallel shift to all accounts at any given point in time. Instead, the benefit arises during model training. By including lifecycle and environment as fixed offsets, the logistic regression or SGBRT algorithm learns to predict residual, account-level idiosyncratic risk after controlling for temporal effects. This forces the model to focus on the stable, borrower-specific risk factors that distinguish good credits from bad credits within each time period, rather than conflating borrower quality with environmental conditions.

During the pandemic, defaults were artificially suppressed by forbearance programs and economic support measures. A traditional cross-sectional model trained on this period would learn that most borrowers performed well, potentially overweighting variables that happened to correlate with the specific pandemic circumstances. In contrast, the APC-normalized model, having removed the environmental component, learned which borrowers were intrinsically riskier even though observed default rates were low. When tested out-of-sample, these models maintained their predictive power because they had learned transferable risk patterns rather than period-specific correlations.

6.2. Portfolio Characteristics and Model Selection

The mortgage data analyzed here represents a best-case scenario for traditional modeling approaches: millions of observations, decades of history spanning multiple economic cycles, and borrowers with well-established credit histories. Under these favorable conditions, the marginal benefit of APC normalization outside crisis periods was minimal. However, internal analyses conducted on smaller, more dynamic portfolios tell a different story.

For shorter-term consumer products such as personal loans, credit cards, and auto loans, the lifecycle component of APC modeling provides substantial value even in stable economic periods. These products typically have steeper lifecycle curves with most defaults occurring in the first 12–24 months, making accurate lifecycle estimation critical. Additionally, portfolios for these products often span only a few years of origination history, making it difficult for traditional models to learn lifecycle patterns through observation of fully-matured loans. The explicit APC lifecycle function provides this information directly, improving model accuracy from origination forward.

Similarly, portfolios at smaller financial institutions or for newer products face sample size constraints that amplify the value of APC inputs. With limited data, traditional models struggle to estimate stable coefficients while simultaneously learning lifecycle and environmental patterns. By providing lifecycle and environment as known functions derived from broader data sources or regulatory models, the institution’s specific model can focus its limited sample on estimating borrower-level risk factors.

The choice between panel logistic regression and stochastic gradient boosted regression trees (SGBRT) showed minimal performance differences in this analysis. SGBRT models demonstrated slightly higher Gini coefficients (typically 0.01–0.03 higher), but this advantage was not consistent across all time periods and came with substantially higher computational costs and reduced interpretability. This finding may surprise practitioners who have observed larger advantages for machine learning approaches in other contexts.

The explanation lies in the structure of available variables. The Fannie Mae and Freddie Mac datasets provide credit scores, debt-to-income ratios, and loan-to-value ratios—variables that are either pre-linearized (credit score) or have well-established monotonic relationships with default risk. This eliminates the primary advantage of tree-based methods: their ability to discover complex nonlinear relationships and interactions without manual feature engineering. When variables require significant transformation or when important interactions exist but are unknown, SGBRT and similar machine learning approaches can substantially outperform logistic regression. However, for the limited set of well-specified variables available in this analysis, logistic regression proved nearly as effective and far more interpretable.

6.3. Comparison to Industry Practices

Current industry approaches to handling pandemic data fall into three categories: exclusion, inclusion without adjustment, and ad-hoc normalization. Many institutions excluded 2020–2021 originations entirely from model development, arguing that anomalous conditions made this data uninformative. While this approach avoids contaminating models with unusual patterns, it discards valuable information and leaves models untested against the most severe recent stress period. Our results demonstrate that proper normalization allows pandemic data to improve rather than degrade model performance.

Other institutions included pandemic data without adjustment, treating 2020–2021 as simply another historical period. This approach maximizes sample size but introduces significant noise, as evidenced by the “No Offset” results showing Gini coefficients 0.28 lower during the pandemic period. Models trained this way learn correlations specific to pandemic conditions that fail to generalize to normal periods, creating prediction errors in both directions depending on when the model is applied.

Some institutions implemented ad-hoc adjustments such as reweighting observations, segmenting time periods, or including macroeconomic variables as model inputs. While these approaches recognize the need for normalization, reweighting is not normalization. Simply reducing the relative importance of pandemic data does not adjust for changes in the environment. Direct inclusion of macroeconomic variables fails, because the consumer environment, as driven by government support and lender forbearance programs, actually moved opposite to key traditional economic indicators such as unemployment.

7. Conclusions

The fragility of traditional credit scores to economic changes has often been accepted as an intrinsic feature to be worked around and monitored Machado et al. (2025); Sousa et al. (2014). This paper demonstrates that credit scores can be designed to be resilient through economic volatility and, in fact, benefit from volatility. The keys to this resilience are (1) using panel data (one observation per account per month) rather than cross-sectional data (one observation per account for the full training window) and (2) integrating the Age-Period-Cohort lifecycle and environment into credit score estimation, whether via traditional logistic regression or machine learning.

This approach was quite effective in terms of being able to model data from the worst economic period of the COVID-19 pandemic. One particularly powerful aspect is that no macroeconomic variables were used. The pandemic is notorious for breaking the traditional correlations between macroeconomic factors and loan defaults due to the unprecedented government intervention and forbearance programs. The APC environment function can quantify what the environment was during any given time period without needing to explain what caused that environment in macroeconomic terms.

Although the current research focused on modeling defaults, the same methods can be applied to other key metrics, most commonly prepayment, attrition, and recovery rates. Although survival models are designed to model terminal events, the APC approach applies to any variable. For products such as credit cards, this can include modeling purchase, payment, utilization, and revolving balance rates.

The work here was performed on Fannie Mae and Freddie Mac mortgage default data. Similar analysis for auto, credit card, and personal loans internally at banks with proprietary data has shown even more dramatic benefits because of the smaller, more dynamic portfolios being modeled.

The specific combination of APC and credit scoring is one of a family of algorithms that could be employed to achieve similar goals. Broadly speaking, combining discrete time survival models and logistic regression or machine learning models can overcome many shortcomings of today’s credit scores.