Using Carbon Tax to Reach the U.S.’s 2050 NDCs Goals—A CGE Model of Firms, Government, and Households
Abstract
1. Introduction
2. Literature Review
- A carbon tax can help governments fiscally.
- A carbon tax can significantly reduce local pollutants and CO2 emissions.
- A carbon tax can help the government design and monitor long-term emissions reduction targets.
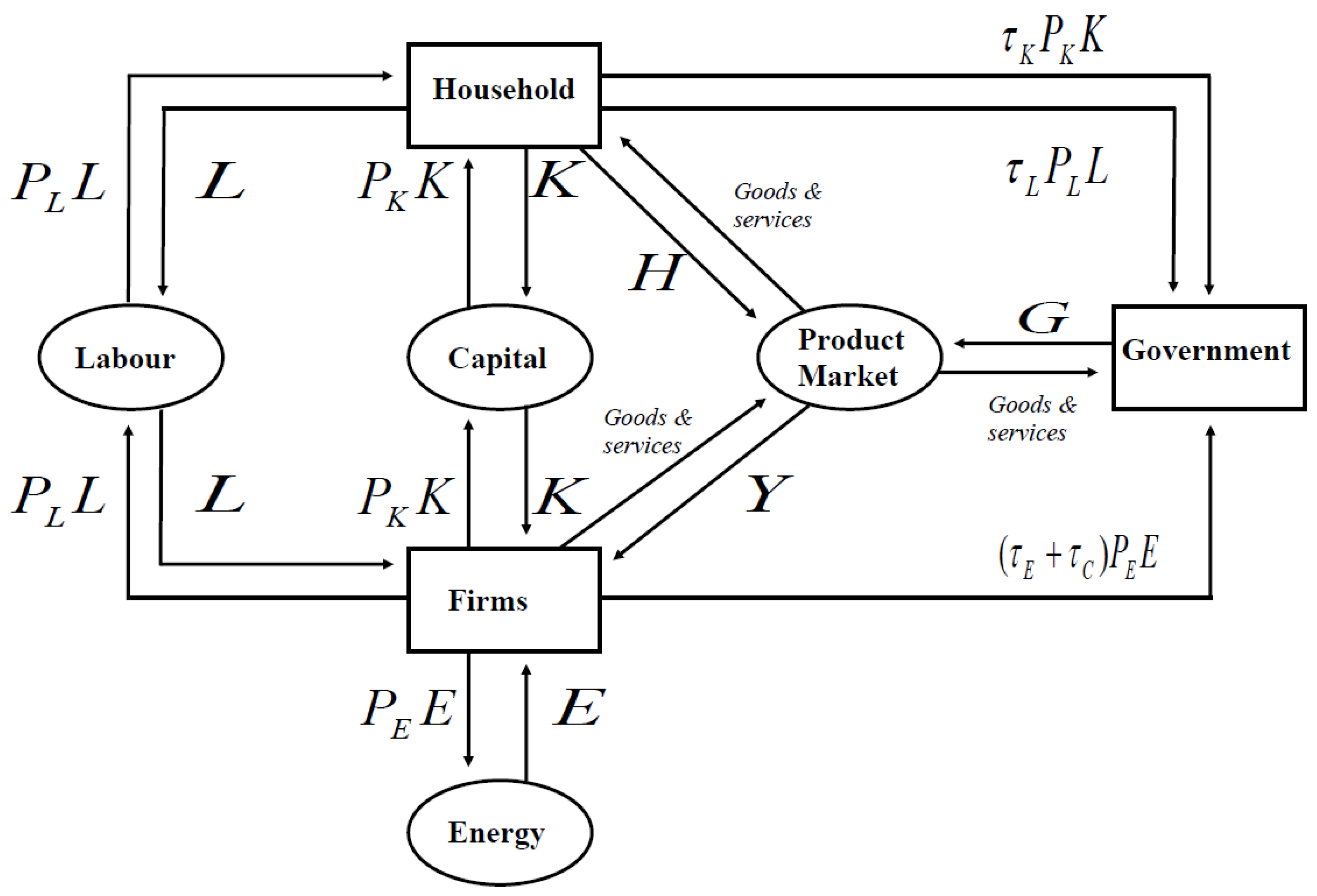
3. Methodology
4. Empirical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | Primary energy consumption is the same as direct method measures energy statistics in their raw form: how much coal, oil, and gas energy are consumed as inputs to the energy system. |
| 2 | Despite the U.S. return to the Paris Agreement in 2021, political factors create a great uncertainty about U.S. environmental policy. |
| 3 | The U.S. Climate Alliance is a coalition committed to reducing GHG emissions in line with the goals of the Paris Agreement |
| 4 | A carbon tax can reduce economic growth and increase spending by businesses and households. These effects would have a direct impact on the price of labour, capital, and energy (Winkler and Marquard 2011). In the CGE model, equilibrium is characterised by the set of prices and production levels in each industry, such that the market demand for all goods is equal to the supply. Moreover, the Cobb–Douglas production function was created by Cobb and Douglas (1928) to describe the relationship between manufacturing output, labour input, and capital input for the period 1889–1922 in the U.K. Thus, when these two models are combined, the balance between the carbon tax and governments’, firms’, and households’ expenditure is well-solved. |
| 5 | A maximum threshold of carbon tax rate is to protect the fiscal neutral, if the carbon tax rate exceeds this threshold, the fiscal neutral will disappear. |
| 6 | A fiscal neutral form of revenue neutrality is that when fiscal revenues from carbon taxes are increased, fiscal revenues from other taxes will decrease, but the government budgetary position will remain unchanged, and the overall tax burden will remain the same. |
| 7 | All the parameters are estimated by the method of maximum likelihood estimation (MLE). |
| 8 | Prices of labour, capital, and energy are estimated by maximum likelihood estimation (MLE) as endogenous variables. |
| 9 | The tax rates including , and are endogenous variables, the values of these variables are estimated by the method of maximum likelihood estimation. |
References
- Abrell, Jan, Anta Ndoye, and Georg Zachmann. 2011. Assessing the Impact of the EU ETS Using Firm Level Data. Bruegel Working Paper 2011/08. Brussels: Bruegel. Available online: https://www.bruegel.org/sites/default/files/wp-content/uploads/imported/publications/WP_2011_08_ETS_01.pdf (accessed on 1 June 2023).
- Aghion, Philippe, Ufuk Akcigit, and Jesús Fernández-Villaverde. 2013. Optimal Capital versus Labor Taxation with Innovation-Led Growth. NBER Working Paper No. 19086, (Abrell 2011). pp. 1–38. Available online: https://www.nber.org/papers/w19086 (accessed on 1 June 2023).
- Andersen, Mikael S. 2016. An Introductory Note on Carbon Taxation in Europe: A Vermont Briefing. Aarhus: Aarhus University. [Google Scholar]
- Andersson, Julius J. 2019. Carbon taxes and CO2 emissions: Sweden as a case study. Economic Policy 11: 1–30. [Google Scholar] [CrossRef]
- Atalla, T., and Patrick Bean. 2017. Determinants of energy productivity in 39 countries: An empirical investigation. Energy Economics 62: 217–29. [Google Scholar] [CrossRef]
- Bai, Yunfan, and Xing Yang. 2016. The research on the economic effect of market-based environmental policy instruments. Open Journal of Social Sciences 4: 38–47. [Google Scholar] [CrossRef]
- Baranzini, Andrea, José Goldemberg, and Stefan Speck. 2000. Survey—A future for carbon taxes. Ecological Economics 32: 395–412. [Google Scholar] [CrossRef]
- Baumol, William J. 1972. On taxation and the control of externalities. The American Economic Review 62: 307–22. [Google Scholar]
- Baumol, William. J., and Wallace E. Oates. 1971. The use of standards and prices for protection of the environment. The Swedish Journal of Economics 73: 42–54. [Google Scholar] [CrossRef]
- Bloomberg New Energy Finance. 2016. Global Trends in Renewable Energy Finance. Available online: https://www.actu-environnement.com/media/pdf/news-26477-rapport-pnue-enr.pdf (accessed on 1 June 2023).
- Bonetti, Shanes, and Felix FitzRoy. 1999. Environmental tax reform and government expenditure. Environmental and Resource Economics 13: 289–308. [Google Scholar] [CrossRef]
- BP Statistic Review of Global Energy. 2020. Available online: http://www.bp.com/statisticalreview (accessed on 1 June 2023).
- Carl, Jeremy, and David Fedor. 2016. Tracking global carbon revenues: A survey of carbon taxes versus cap-and-trade in the real world. Energy Policy 96: 50–77. [Google Scholar] [CrossRef]
- Chan, Hei, Shanjun S. Li, and Fan Zhang. 2013. Firm competitiveness and the European Union emissions trading scheme. Energy Policy 63: 1056–64. [Google Scholar] [CrossRef]
- Cobb, Charles W., and Paul H. Douglas. 1928. A Theory of Production. American Economic Review 18: 139–65. [Google Scholar]
- Commins, N., Seán Lyons, Marc Schiffbauer, and Richard Tol. 2011. Climate policy and corporate behavior. The Energy Journal 32: 51–68. [Google Scholar] [CrossRef]
- Convery, Frank J., and Luke Redmond. 2007. Market and Price Developments in the European Union Emissions Trading Scheme. Review of Environmental Economics and Policy 1: 88–111. [Google Scholar] [CrossRef]
- Davis, Lucas W., and Lutz Kilian. 2009. Estimating the Effect of a Gasoline Tax on Carbon Emissions. NBER Working Paper No (14685). Cambridge: National Bureau of Economic Research, p. 1. Available online: https://www.nber.org/papers/w14685 (accessed on 1 June 2023).
- Dissou, Yazid, Lilia Karnizova, and Qian Sun. 2015. Industry-level econometric estimates of energy-capital-labor substitution with a nested CES production function. International Atlantic Economic Society: Atlantic Economic Journal 43: 107–21. [Google Scholar] [CrossRef]
- Ellerman, Denny A., and Barabara Buchner. 2007. The European Union Emissions Trading Scheme: Origins, Allocation, and Early Results. Review of Environmental Economics 1: 66–87. [Google Scholar] [CrossRef]
- Global Carbon Project. 2019. Supplemental Data of Global Carbon Budget 2019 (Version 1.0). Available online: https://doi.org/10.18160/gcp-2019 (accessed on 1 June 2023).
- Goulder, Lawrence. 1995. Environmental Taxation and the ‘Double Dividend’: A Reader’s Guide. International Tax and Public Finance 2: 157–83. [Google Scholar] [CrossRef]
- Huynh, Bao T. 2016. Macroeconomic effects of energy price shocks on the business cycle. Macroeconomic Dynamics 20: 623–42. [Google Scholar] [CrossRef]
- IPCC. 2019. United Nations Environment Programme (UNEP) Emissions Gap Report. Available online: https://www.unenvironment.org/resources/emissions-gap-report2019 (accessed on 1 June 2019).
- Jorgenson, D. 2014. Time to Tax Carbon. Harvard Magazine. pp. 52–56, 78–79. Available online: http://bit.ly/1dDlxtI (accessed on 1 June 2023).
- Jorgenson Dale, Richard Goettle, Ho Mun, and Peter Wilcoxen. 2013. Double Dividend: Environmental Taxes and Fiscal Reform in the United States. Cambridge and London: MIT Press. [Google Scholar]
- Jorgenson, Dale W., Daniel T. Slesnick, Peter J. Wilcoxen, Paul L. Joskow, and Raymond Kopp. 1992. Carbon taxes and economic welfare. Brookings Papers on Economic Activity 1992: 393–454. [Google Scholar] [CrossRef]
- Krupnick, Alan, Ian Parry, Margaret Walls, Tony Knowles, and Kristin Hayes. 2010. Towards a New National Energy Policy: Assessing the Options. Washington, DC: Resources for the Future and National Energy Policy Institute. [Google Scholar]
- Lai, C. F. 2016. Examining the double dividend effect of energy tax with the overlapping generations model. International Journal of Energy Economics and Policy 6: 53–57. [Google Scholar]
- Larsen, Kate, Trevor Houser, and Shashank Mohan. 2019. Sizing Up a Potential Fuel Economy Standards Freeze. Available online: htpps://rhg.com/research/sizing-up-a-potential-fuel-economy-standards-freeze (accessed on 29 June 2023).
- Li, Wei, and Zhijie J. Jia. 2017. Carbon tax, emission trading, or the mixed policy: Which is the most effective strategy for climate change mitigation in China? Mitigation and Adaption Strategies for Global Change 22: 973–92. [Google Scholar] [CrossRef]
- Liang, Q. M., and Y. M. Wei. 2012. Distributional impacts of taxing carbon in China: Results from the CEEPA model. Applied Energy 92: 545–51. [Google Scholar] [CrossRef]
- Mankiw, N. Gregory, David Romer, and David N. Weil. 1992. A contribution to the empirics of economic growth. The Quarterly Journal of Economics 107: 407–37. [Google Scholar] [CrossRef]
- Mardones, C., and B. Flores. 2018. Effectiveness of a CO2 tax on industrial emissions. Energy Economics 71: 370–82. [Google Scholar] [CrossRef]
- Marron, Donald, and Eric J. Toder. 2014. Tax policy issues in designing a carbon tax. American Economic Review: Papers & Proceedings 104: 563–68. [Google Scholar]
- Marron, Donald, Eric J. Toder, and Lydia Austin. 2015. Taxing Carbon: What, Why and How. Washington, DC: Tax Policy Center. Urban Institute Brooking Institution, pp. 1–28. [Google Scholar]
- Martin, Ralf, Mirabelle Muûls, and Ulrich Wagner. 2016. The Impact of the European Union Emissions Trading Scheme on Regulated Firms: What Is the Evidence after Ten Years? Review of Environmental Economics and Policy 10: 129–48. [Google Scholar] [CrossRef]
- Masanjala, Winford H., and Chris Papageorgiou. 2004. The Solow model with CES technology: Nonlinearities and parameter heterogeneity. Journal of Applied Econometrics 19: 171–201. [Google Scholar] [CrossRef]
- Masoud, Yahoo, and Jamal Othman. 2017. Carbon and energy taxation for CO2 mitigation: A CGE model of Malaysia. Environmental Development and Sustainability 19: 239–62. [Google Scholar]
- McKibbin, Warwick, Adele C. Morris, Peter J. Wilcoxen, and Yiyong Y. Cai. 2015. Carbon taxes and U.S. fiscal reform. National Tax Journal 68: 139–56. [Google Scholar] [CrossRef]
- McKitrick, Ross, Elmira Aliakbari, and Ashley Stedman. 2019. The Impact of the Federal Carbon Tax on the Competitiveness of Canadian Industries. Fraser Institute, August 22. Available online: https://www.fraserinstitute.org/studies/impact-of-the-federal-carbon-tax-on-the-competitiveness-of-canadian-industries (accessed on 1 June 2023).
- Meng, Xanming, Mahinda Siriwardana, and Judith McNeill. 2015. The environmental and employment effect of Australian carbon tax. International Journal of Social Science and Humanity 5: 514–19. [Google Scholar] [CrossRef][Green Version]
- Miller, Sebastián J., and Mauricio A. Vela. 2013. Are Environmentally Related Taxes Effective? IDB Working Paper Series No. IDB-WP-467. Inter-American Development Bank, pp. 1–27. Available online: https://core.ac.uk/display/19456380 (accessed on 1 June 2023).
- Natural Resources Defense Council. 2018. Comments of the Natural Resources Defense Council on EPA’s Proposed Emission Guidelines for Greenhouse Gas Emissions From Existing Electric Utility Generating Units; Revisions to Emission Guideline Implementing Regulations. Available online: https://www.nrdc.org/sites/default/files/nrdc-ace-comments-20181031.pdf (accessed on 1 June 2023).
- Nordhaus, William. 2010. Carbon Taxes to Move Toward Fiscal Sustainability. The Economists’ Voice 7: 3. Available online: http://bit.ly/1LUcSxO (accessed on 1 June 2023). [CrossRef]
- Nunavut. 2019. The Carbon Tax in Nunavut Frequently Asked Questions. FAQ-Carbon Tax in Nunavut. Available online: https://gov.nu.ca/finance/documents/carbon-tax-frequently-asked-questions (accessed on 1 June 2023).
- Nurdianto, Ditya A., and Budy Resosudarmo. 2016. The economy-wide impact of a uniform carbon tax in ASEAN. Journal of Southeast Asian Economies 33: 1–22. [Google Scholar] [CrossRef]
- Oberndorfer, Ulrich, and Klauss Rennings. 2007. Costs and Competitiveness Effects of the European Union Emissions Trading Scheme. European Environment 17: 1–17. [Google Scholar] [CrossRef]
- Othman, Jamal, and Masoud Yahoo. 2014. Reducing CO2 emissions in Malaysia: Do carbon taxes work? Prosiding Persidangan Kebangsaan Ekonomi Malaysia Ke 9: 175–82. [Google Scholar]
- Pang, Y. 2019. Taxing pollution and profits: A bargaining approach. Energy Economics 78: 278–88. [Google Scholar] [CrossRef]
- Pearce, David. 1991. The Role of Carbon Taxes in Adjusting to Global Warming. Economic Journal 101: 938–48. [Google Scholar] [CrossRef]
- Pereira, Alfredo M., Rui M. Pereira, and Pedro G. Rodrigues. 2016. A new carbon tax in Portugal: A missed opportunity to achieve the triple dividend? Energy Policy 9: 110–18. [Google Scholar] [CrossRef]
- Poterba, James M. 1991. Tax Policy to Combat Global Warming: On Designing a Carbon Tax. MIT-CEPR 91-003WP. MIT Center for Energy and Environmental Policy Research, March. Available online: https://www.nber.org/papers/w3649 (accessed on 1 June 2023).
- Rosenberg, Joseph, Eric Toder, and Chenxi Lu. 2018. Distributional Implications of a Carbon Tax. New York: Center on Global Energy Policy, p. 3. [Google Scholar]
- Rosendahl, Knut E. 1995. Carbon Taxes and the Petroleum Wealth; Cleveland: International Association for Energy Economics. Available online: https://www.osti.gov/biblio/416359-carbon-taxes-petroleum-wealth (accessed on 1 June 2023).
- Saboori, Behnaz, and Jamalludin B. Sulaiman. 2013. Environmental degradation, economic growth and energy consumption: Evidence of the environmental Kuznets curve in Malaysia. Energy Policy 60: 892–905. [Google Scholar] [CrossRef]
- Schneider, Uwe A., and Bruce A. McCarl. 2005. Implications of a Carbon Based Energy Tax for U.S. Agriculture. Agricultural and Resource Economics Review 34: 265–79. [Google Scholar] [CrossRef]
- Scrimgeour, Frank G., Les Oxley, and Koli Fatai. 2004. Reducing carbon emissions? The relative effectiveness of different types of environmental tax: The case of New Zealand. Paper presented at 2nd International Congress on Environmental Modeling and Software, Osnabruck, Germany, June 10–14; Available online: https://scholarsarchive.byu.edu/iemssconference/2004/all/172/ (accessed on 1 June 2023).
- Solow, R. M. 1956. A contribution to the theory of economic growth. The Quarterly Journal of Economics 71: 65–94. [Google Scholar] [CrossRef]
- Stern, Nicholas. 2007. The Economics of Climate Change: The Stern Review. Cambridge: Cambridge University Press. [Google Scholar]
- Stern, Todd. 2010. United States Association with Copenhagen Accord. Washington, DC: United States Department of State, Office of the Special Envoy for Climate Change, January 28, Available online: https://unfccc.int/files/meetings/cop_15/copenhagen_accord/application/pdf/unitedstatescphaccord_app.1.pdf (accessed on 1 June 2019).
- Swan, Trevor W. 1956. Economic growth and capital accumulation. Economic Record 32: 334–61. [Google Scholar] [CrossRef]
- Symons, Elizabeth, John Proops, and Philip Gay. 1994. Carbon taxes, consumer demand and carbon dioxide emissions: A simulation analysis for the UK. Fiscal Studies 15: 19–43. [Google Scholar] [CrossRef]
- Tol, Richard S. J. 2012. Leviathan carbon taxes in the short run: A letter. Climatic Change 114: 409–15. [Google Scholar] [CrossRef]
- Torrie, Ralph D., Christopher Stone, and David B. Layzell. 2016. Understanding energy systems change in Canada: 1. Decomposition of total energy intensity. Energy Economics 5: 101–6. [Google Scholar] [CrossRef]
- United Nations. 2016. Paris Agreement. Available online: https://unfccc.int/sites/default/files/english_paris_agreement.pdf (accessed on 1 June 2023).
- Upmann, Thorsten. 2009. A positive analysis of labor-market institutions and tax reforms. International Tax and Public Finance 16: 621–46. [Google Scholar] [CrossRef]
- US Energy Information Administration (EIA). 2021. Energy Explained, Your Guide to Understanding. Available online: https://www.eia.gov/energyexplained (accessed on 1 June 2023).
- Wara, Michael. 2015. Instrument choice, carbon emissions, and information. Michigan Journal of Environmental and Administrative Law 4: 261–302. [Google Scholar] [CrossRef]
- Winkler, Harald, and Andrew Marquard. 2011. Analysis of the economic implications of a carbon tax. Journal of Energy in Southern Africa 22: 55–68. [Google Scholar] [CrossRef]
- World Bank. 2020. Data Indicators from the Website of The World Bank. Available online: https://data.worldbank.org/indicator (accessed on 1 June 2023).
- Yukon. 2019. Proposed Framework: Yukon Government Carbon Price Rebate. Yukon Government. January 17. Available online: https://yukon.ca/en/proposed-framework-government-yukon-carbon-price-rebate (accessed on 1 June 2023).
- Zachariadis, Theodoros. 2015. How can Cyprus meet its energy and climate policy commitments? The importance of a carbon tax. December. Cyprus Economic Policy Review 9: 3–20. [Google Scholar]
- Zhang, Kezhong, Juan Wang, and Yongming Huang. 2011. Estimating the effect of carbon tax on CO2 emissions of coal in China. Journal of Environmental Protection 2: 1101–07. [Google Scholar] [CrossRef]
- Zhao, Yibing, Can Wang, Yuwei Sun, and Xianbing Liu. 2018. Factors influencing companies’ willingness to pay for carbon emissions: Emission trading schemes in China. Energy Economics 75: 357–67. [Google Scholar] [CrossRef]


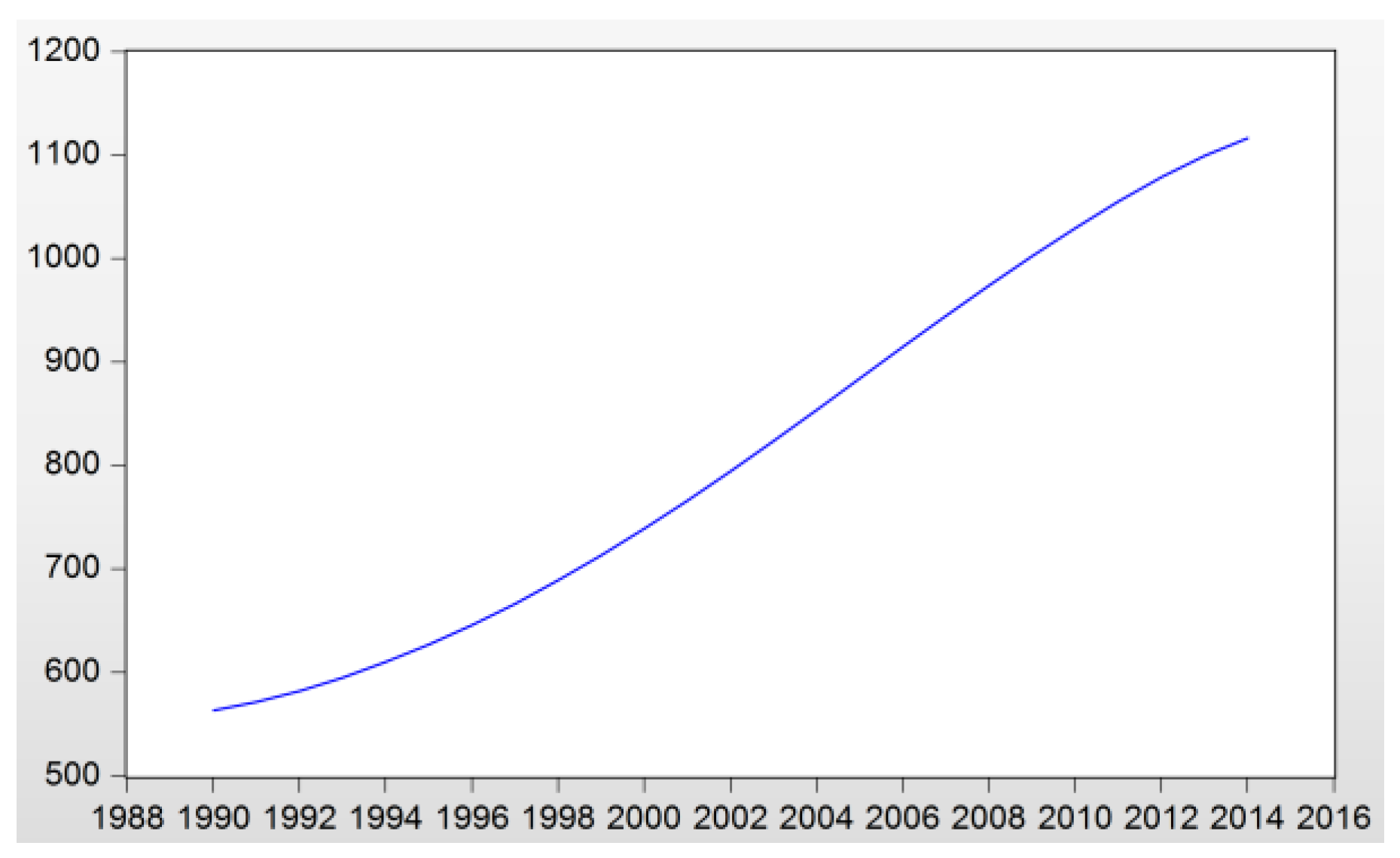

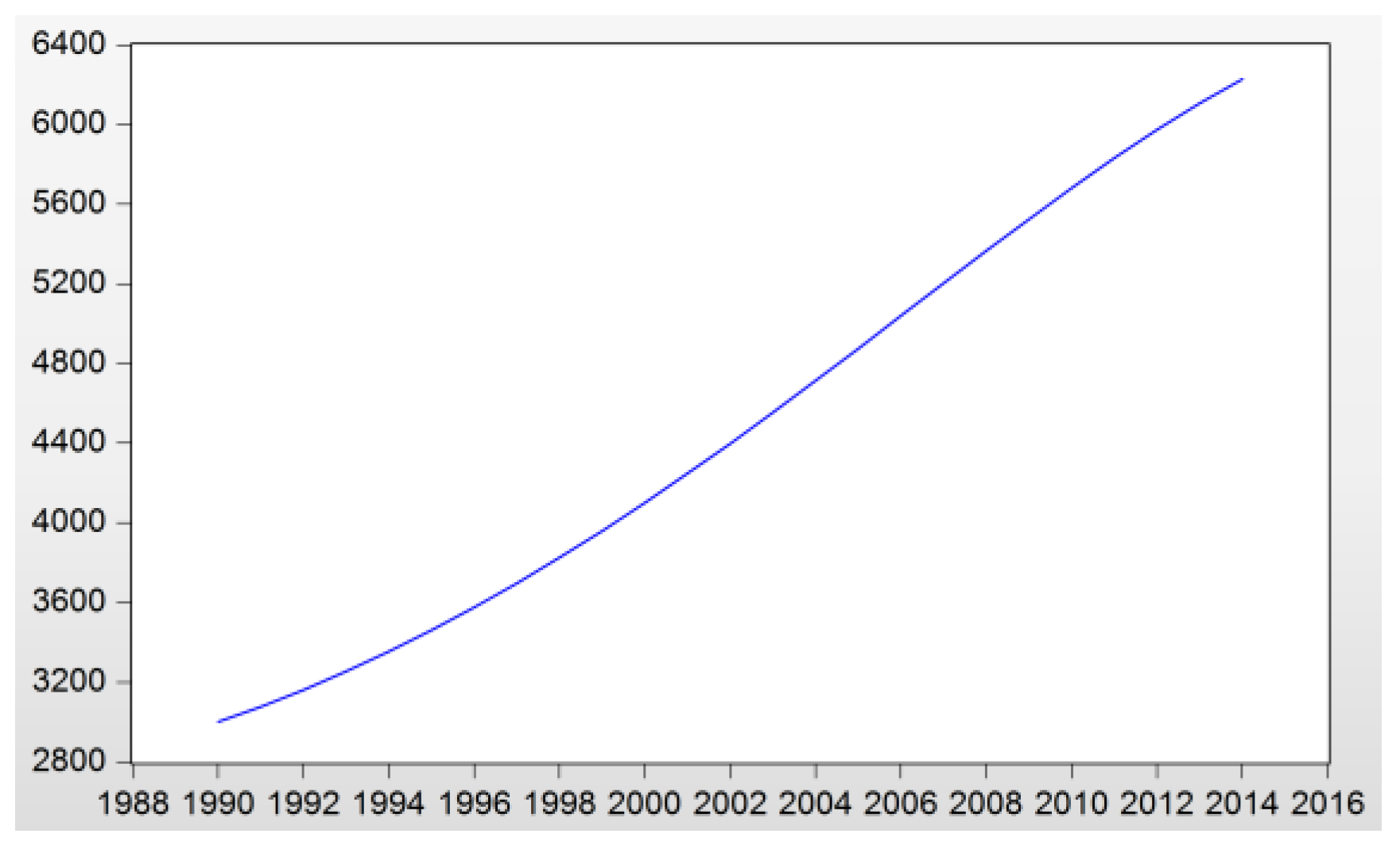

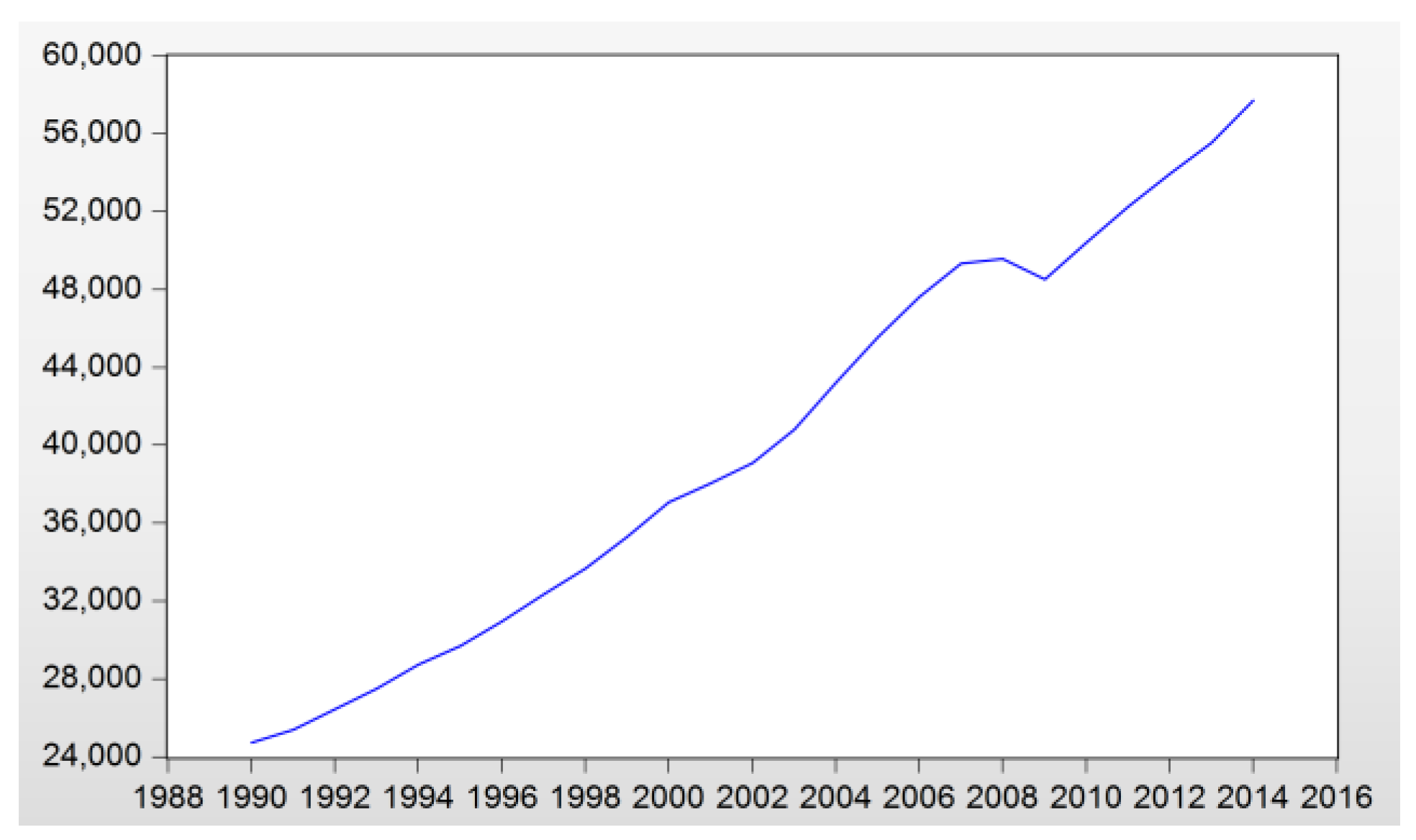
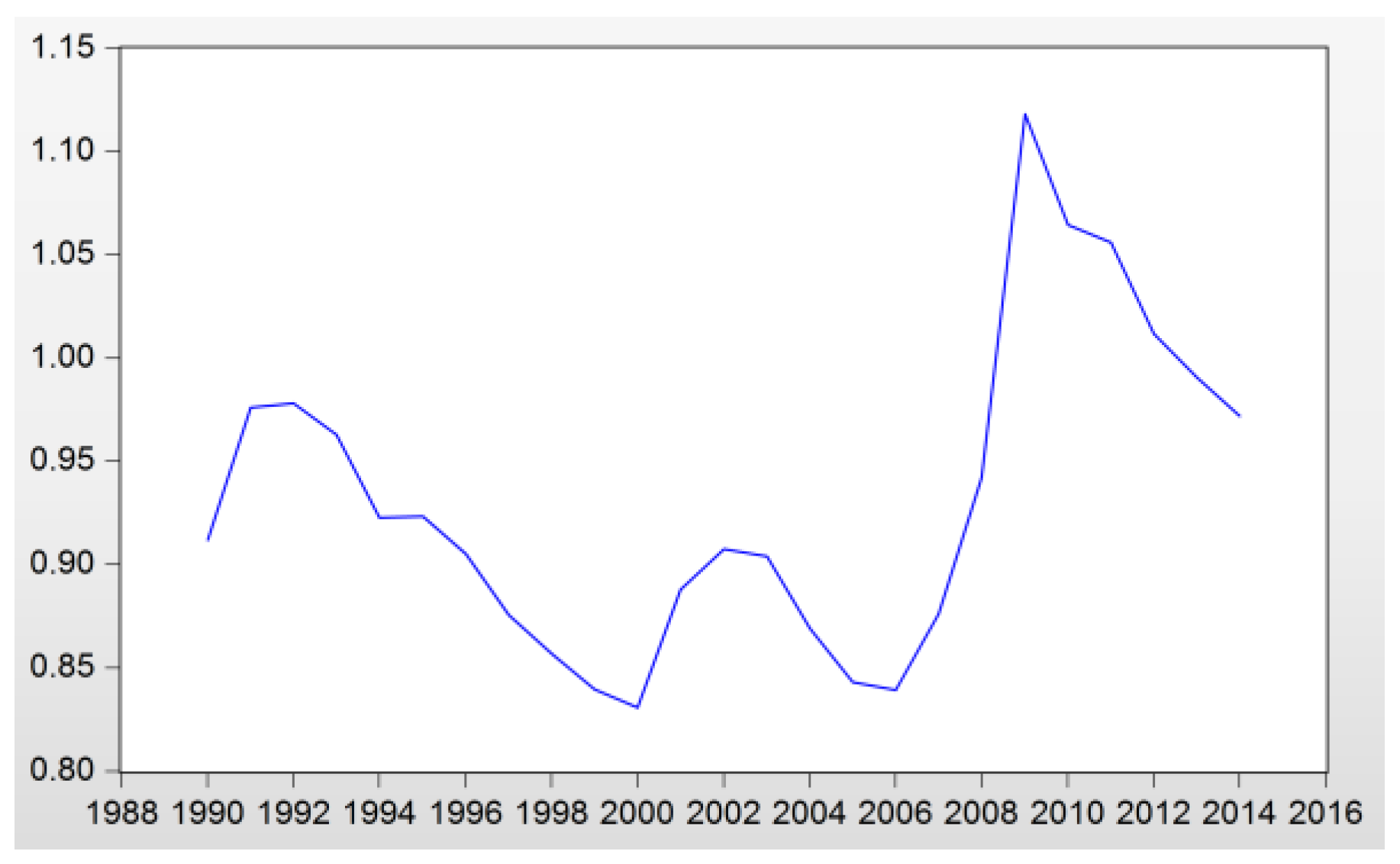

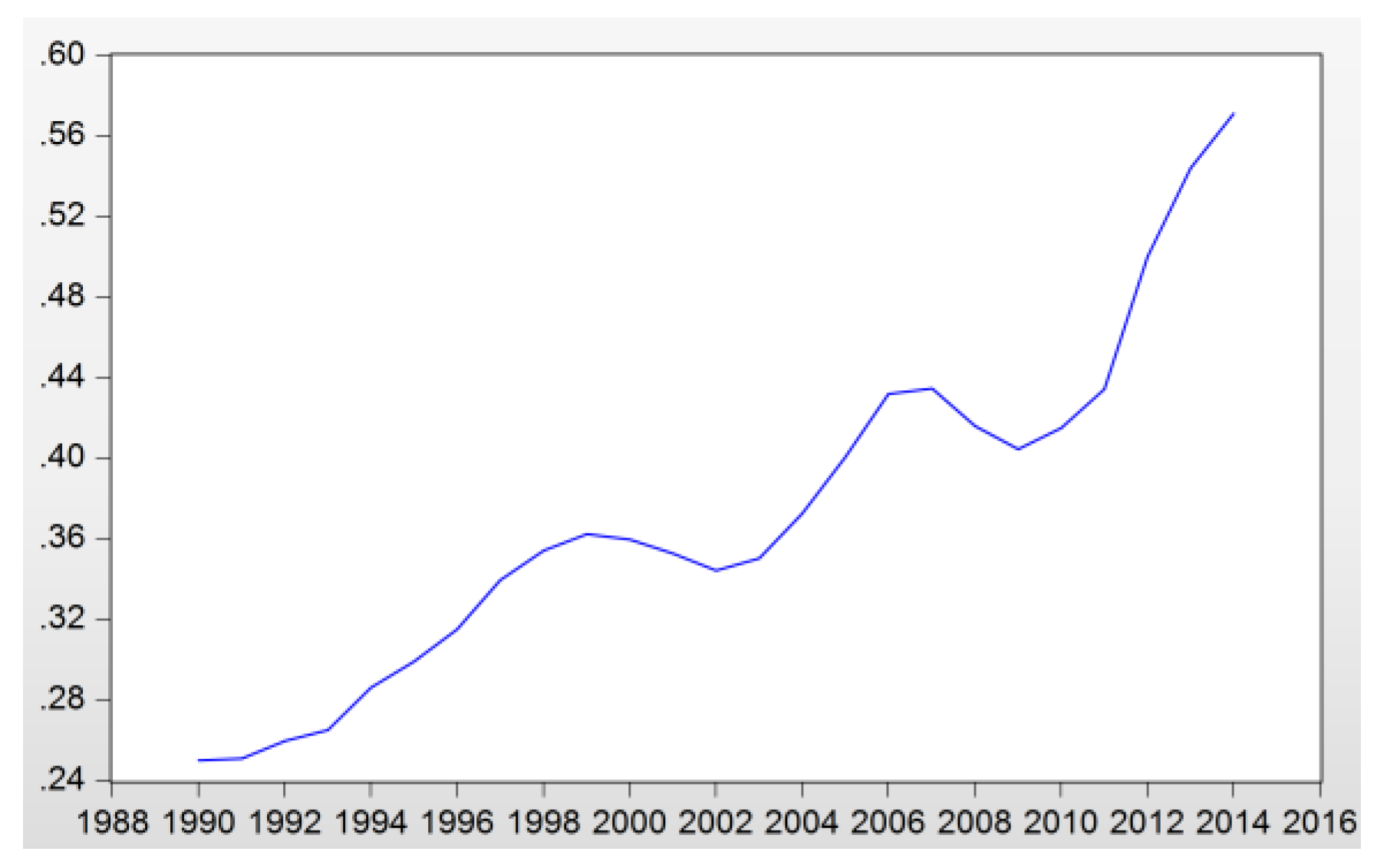
| Year | ||||||||
|---|---|---|---|---|---|---|---|---|
| GDP USD in Billions | Govt USD in Billions | Household Cons USD in Billions | Labor in Millions | Gross Capital USD in Billions | Energy KGs in Billions | KGs in Billions | kg per kg of Energy | |
| 1990 | 5979.59 | 947.99 | 3825.63 | 127.94 | 1283.82 | 1915.05 | 4823.40 | 2.52 |
| 1991 | 6174.04 | 1004.07 | 3960.15 | 128.70 | 1238.44 | 1930.62 | 4820.85 | 2.50 |
| 1992 | 6539.30 | 1049.25 | 4215.65 | 130.85 | 1309.13 | 1969.36 | 4909.53 | 2.49 |
| 1993 | 6878.72 | 1074.18 | 4471.00 | 132.28 | 1398.71 | 2003.84 | 5028.67 | 2.51 |
| 1994 | 7308.76 | 1109.57 | 4741.02 | 134.62 | 1550.66 | 2041.29 | 5094.35 | 2.50 |
| 1995 | 7664.06 | 1144.48 | 4984.18 | 136.50 | 1625.16 | 2067.32 | 5132.92 | 2.48 |
| 1996 | 8100.20 | 1176.50 | 5268.07 | 138.42 | 1752.01 | 2113.25 | 5252.11 | 2.49 |
| 1997 | 8608.52 | 1224.63 | 5560.72 | 140.84 | 1925.13 | 2134.52 | 5368.72 | 2.52 |
| 1998 | 9089.17 | 1272.11 | 5903.03 | 142.83 | 2076.73 | 2152.68 | 5401.01 | 2.51 |
| 1999 | 9660.62 | 1357.57 | 6307.02 | 144.82 | 2252.66 | 2210.90 | 5504.67 | 2.49 |
| 2000 | 10,284.78 | 1444.17 | 6792.40 | 146.77 | 2424.01 | 2273.34 | 5693.68 | 2.50 |
| 2001 | 10,621.82 | 1545.13 | 7103.10 | 147.74 | 2342.27 | 2230.70 | 5595.79 | 2.51 |
| 2002 | 10,977.51 | 1651.36 | 7384.05 | 148.57 | 2368.57 | 2255.94 | 5641.31 | 2.50 |
| 2003 | 11,510.67 | 1755.59 | 7765.53 | 149.18 | 2493.21 | 2261.17 | 5675.70 | 2.51 |
| 2004 | 12,274.93 | 1868.94 | 8260.02 | 150.26 | 2765.14 | 2307.77 | 5756.08 | 2.49 |
| 2005 | 13,093.73 | 1980.05 | 8794.11 | 152.12 | 3040.75 | 2318.77 | 5789.73 | 2.50 |
| 2006 | 13,855.89 | 2089.85 | 9303.99 | 153.99 | 3233.00 | 2296.82 | 5697.29 | 2.48 |
| 2007 | 14,477.64 | 2209.72 | 9750.51 | 155.29 | 3235.95 | 2337.00 | 5789.03 | 2.48 |
| 2008 | 14,718.58 | 2368.57 | 10,013.65 | 157.09 | 3059.44 | 2277.08 | 5614.11 | 2.47 |
| 2009 | 14,418.74 | 2442.06 | 9846.97 | 157.20 | 2525.14 | 2164.82 | 5263.51 | 2.43 |
| 2010 | 14,964.37 | 2522.21 | 10,202.19 | 157.02 | 2752.64 | 2215.22 | 5395.53 | 2.44 |
| 2011 | 15,517.93 | 2530.86 | 10,689.30 | 157.13 | 2877.76 | 2190.42 | 5289.68 | 2.41 |
| 2012 | 16,155.26 | 2544.15 | 11,050.63 | 158.43 | 3126.14 | 2156.98 | 5119.44 | 2.37 |
| 2013 | 16,691.52 | 2523.73 | 11,361.17 | 159.01 | 3298.62 | 2182.58 | 5159.16 | 2.36 |
| 2014 | 17,427.61 | 2562.69 | 11,863.67 | 159.80 | 3510.76 | 2216.19 | 5254.28 | 2.37 |
| Variance | is from the Equation of | |||
|---|---|---|---|---|
| Variable | ||||||||
|---|---|---|---|---|---|---|---|---|
| Year | ||||||||
| 1990 | 24,737 | 0.9121 | 0.6297 | 92.5589 | 2.2038 | 0.5821 | 2.5187 | 0.2500 |
| 1991 | 25,391 | 0.9763 | 0.6267 | 92.1063 | 2.1930 | 0.5793 | 2.4971 | 0.2510 |
| 1992 | 26,451 | 0.9782 | 0.6471 | 95.1134 | 2.2646 | 0.5982 | 2.4930 | 0.2596 |
| 1993 | 27,523 | 0.9631 | 0.6655 | 97.8151 | 2.3289 | 0.6152 | 2.5095 | 0.2652 |
| 1994 | 28,736 | 0.9230 | 0.7143 | 104.9948 | 2.4999 | 0.6603 | 2.4957 | 0.2862 |
| 1995 | 29,716 | 0.9235 | 0.7427 | 109.1637 | 2.5991 | 0.6866 | 2.4829 | 0.2991 |
| 1996 | 30,972 | 0.9054 | 0.7835 | 115.1533 | 2.7417 | 0.7242 | 2.4853 | 0.3152 |
| 1997 | 32,350 | 0.8757 | 0.8541 | 125.5426 | 2.9891 | 0.7896 | 2.5152 | 0.3396 |
| 1998 | 33,680 | 0.8571 | 0.8891 | 130.6866 | 3.1116 | 0.8219 | 2.5090 | 0.3544 |
| 1999 | 35,306 | 0.8398 | 0.9028 | 132.6975 | 3.1595 | 0.8346 | 2.4898 | 0.3626 |
| 2000 | 37,089 | 0.8309 | 0.9010 | 132.4260 | 3.1530 | 0.8329 | 2.5045 | 0.3597 |
| 2001 | 38,052 | 0.8881 | 0.8847 | 130.0405 | 3.0962 | 0.8179 | 2.5085 | 0.3527 |
| 2002 | 39,107 | 0.9076 | 0.8609 | 126.5338 | 3.0127 | 0.7958 | 2.5006 | 0.3443 |
| 2003 | 40,837 | 0.9041 | 0.8799 | 129.3259 | 3.0792 | 0.8134 | 2.5101 | 0.3505 |
| 2004 | 43,237 | 0.8693 | 0.9299 | 136.6769 | 3.2542 | 0.8596 | 2.4942 | 0.3728 |
| 2005 | 45,558 | 0.8433 | 1.0003 | 147.0323 | 3.5008 | 0.9247 | 2.4969 | 0.4006 |
| 2006 | 47,623 | 0.8393 | 1.0719 | 157.5553 | 3.7513 | 0.9909 | 2.4805 | 0.4321 |
| 2007 | 49,342 | 0.8762 | 1.0772 | 158.3284 | 3.7697 | 0.9958 | 2.4771 | 0.4349 |
| 2008 | 49,590 | 0.9421 | 1.0260 | 150.8089 | 3.5907 | 0.9485 | 2.4655 | 0.4162 |
| 2009 | 48,545 | 1.1182 | 0.9838 | 144.5980 | 3.4428 | 0.9094 | 2.4314 | 0.4046 |
| 2010 | 50,442 | 1.0646 | 1.0112 | 148.6240 | 3.5387 | 0.9347 | 2.4357 | 0.4152 |
| 2011 | 52,270 | 1.0560 | 1.0490 | 154.1853 | 3.6711 | 0.9697 | 2.4149 | 0.4344 |
| 2012 | 53,971 | 1.0120 | 1.1871 | 174.4776 | 4.1542 | 1.0973 | 2.3734 | 0.5001 |
| 2013 | 55,559 | 0.9909 | 1.2859 | 189.0063 | 4.5002 | 1.1887 | 2.3638 | 0.5440 |
| 2014 | 57,722 | 0.9721 | 1.3542 | 199.0489 | 4.7393 | 1.2519 | 2.3709 | 0.5712 |
| Variable | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Year | % | % | % | ||||||
| 1990 | 6.08% | 15.78% | 53.21% | 3164.82 | 1171.00 | 1205.97 | 192.41 | 184.73 | 641.64 |
| 1991 | 6.24% | 16.18% | 55.34% | 3267.74 | 1209.08 | 1209.82 | 203.79 | 195.66 | 669.49 |
| 1992 | 6.15% | 15.97% | 54.20% | 3461.06 | 1280.60 | 1274.39 | 212.96 | 204.47 | 690.68 |
| 1993 | 5.99% | 15.54% | 51.99% | 3640.71 | 1347.07 | 1333.54 | 218.02 | 209.32 | 693.34 |
| 1994 | 5.82% | 15.11% | 49.82% | 3868.31 | 1431.29 | 1458.17 | 225.20 | 216.22 | 726.53 |
| 1995 | 5.73% | 14.86% | 48.61% | 4056.37 | 1500.87 | 1535.40 | 232.29 | 223.02 | 746.42 |
| 1996 | 5.57% | 14.45% | 46.66% | 4287.20 | 1586.28 | 1655.63 | 238.78 | 229.26 | 772.55 |
| 1997 | 5.46% | 14.16% | 45.27% | 4556.24 | 1685.82 | 1823.17 | 248.55 | 238.64 | 825.32 |
| 1998 | 5.37% | 13.93% | 44.21% | 4810.64 | 1779.95 | 1914.02 | 258.19 | 247.89 | 846.26 |
| 1999 | 5.39% | 13.98% | 44.47% | 5113.09 | 1891.86 | 1996.03 | 275.53 | 264.55 | 887.69 |
| 2000 | 5.38% | 13.97% | 44.42% | 5443.44 | 2014.09 | 2048.21 | 293.11 | 281.42 | 909.88 |
| 2001 | 5.58% | 14.48% | 46.77% | 5621.83 | 2080.09 | 1973.59 | 313.60 | 301.10 | 923.00 |
| 2002 | 5.77% | 14.97% | 49.15% | 5810.08 | 2149.75 | 1942.10 | 335.16 | 321.80 | 954.50 |
| 2003 | 5.85% | 15.18% | 50.17% | 6092.27 | 2254.16 | 1989.55 | 356.32 | 342.11 | 998.20 |
| 2004 | 5.84% | 15.15% | 50.04% | 6496.77 | 2403.82 | 2145.97 | 379.32 | 364.20 | 1073.90 |
| 2005 | 5.80% | 15.05% | 49.53% | 6930.13 | 2564.17 | 2319.57 | 401.87 | 385.85 | 1148.97 |
| 2006 | 5.78% | 15.01% | 49.34% | 7333.52 | 2713.43 | 2462.05 | 424.16 | 407.24 | 1214.80 |
| 2007 | 5.85% | 15.19% | 50.23% | 7662.60 | 2835.19 | 2517.41 | 448.49 | 430.60 | 1264.42 |
| 2008 | 6.17% | 16.01% | 54.44% | 7790.12 | 2882.37 | 2336.37 | 480.73 | 461.56 | 1271.97 |
| 2009 | 6.49% | 16.85% | 58.98% | 7631.42 | 2823.65 | 2129.71 | 495.64 | 475.88 | 1256.18 |
| 2010 | 6.46% | 16.77% | 58.53% | 7920.21 | 2930.50 | 2239.97 | 511.91 | 491.50 | 1311.08 |
| 2011 | 6.25% | 16.23% | 55.58% | 8213.19 | 3038.91 | 2297.77 | 513.67 | 493.18 | 1277.19 |
| 2012 | 6.04% | 15.67% | 52.66% | 8550.51 | 3163.72 | 2560.48 | 516.36 | 495.77 | 1348.46 |
| 2013 | 5.80% | 15.05% | 49.52% | 8834.34 | 3268.73 | 2806.62 | 512.22 | 491.79 | 1389.91 |
| 2014 | 5.64% | 14.63% | 47.52% | 9223.93 | 3412.88 | 3001.25 | 520.13 | 499.39 | 1426.11 |
| Variable | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Year | Target % | Yearly % | % | % | |||||
| 2005 | 5724.11 | 0.585% | 2318.77 | 2.4969 | |||||
| 2006 | −1.133% | −1.133% | 5658.50 | −1.133% | 2296.82 | 2.4922 | |||
| 2007 | −1.133% | −2.267% | 5592.88 | −1.146% | 2337.00 | 2.4213 | |||
| 2008 | −1.133% | −3.400% | 5527.27 | −1.160% | 2277.08 | 2.4562 | |||
| 2009 | −1.133% | −4.533% | 5461.65 | −1.173% | 2164.82 | 2.5532 | |||
| 2010 | −1.133% | −5.666% | 5396.04 | −1.187% | 2215.22 | 2.4655 | 6.68 | 0.0030 | |
| 2011 | −1.133% | −6.800% | 5330.42 | −1.201% | 2190.42 | 2.4635 | 8.40 | 0.0038 | |
| 2012 | −1.133% | −7.933% | 5264.81 | −1.216% | 2156.98 | 2.4712 | 1.50 | 0.0007 | |
| 2013 | −1.133% | −9.066% | 5199.19 | −1.231% | 2182.58 | 2.4122 | 53.64 | 0.0246 | |
| 2014 | −1.133% | −10.200% | 5133.58 | −1.246% | 2216.19 | 2.3460 | 113.77 | 0.0513 | |
| 2015 | −1.133% | −11.333% | 5067.96 | −1.262% | 2229.54 | 2.3025 | 153.66 | 0.0689 | |
| 2016 | −1.133% | −12.466% | 5002.35 | −1.278% | 2242.98 | 2.2595 | 193.63 | 0.0863 | |
| 2017 | −1.133% | −13.600% | 4936.73 | −1.295% | 2256.49 | 2.2169 | 233.68 | 0.1036 | |
| 2018 | −1.133% | −14.733% | 4871.12 | −1.312% | 2270.09 | 2.1747 | 273.81 | 0.1206 | |
| 2019 | −1.133% | −15.866% | 4805.47 | −1.329% | 2283.77 | 2.1329 | 314.02 | 0.1375 | |
| 2020 | −17.00% | −1.133% | −17.000% | 4654.94 | −1.348% | 2297.53 | 2.0916 | 354.33 | 0.1542 |
| 2021 | −2.600% | −19.600% | 4504.41 | −3.133% | 2311.38 | 2.0139 | 429.04 | 0.1856 | |
| 2022 | −2.600% | −22.200% | 4353.87 | −3.234% | 2325.31 | 1.9371 | 503.84 | 0.2167 | |
| 2023 | −2.600% | −24.800% | 4203.34 | −3.342% | 2339.32 | 1.8612 | 578.73 | 0.2474 | |
| 2024 | −2.600% | −27.400% | 4052.81 | −3.457% | 2353.41 | 1.7861 | 653.70 | 0.2778 | |
| 2025 | −30.00% | −2.600% | −30.000% | 3913.86 | −3.581% | 2367.60 | 1.7118 | 728.75 | 0.3078 |
| 2026 | −2.400% | −32.400% | 3774.90 | −3.429% | 2381.86 | 1.6432 | 799.20 | 0.3355 | |
| 2027 | −2.400% | −34.800% | 3635.95 | −3.550% | 2396.22 | 1.5754 | 869.75 | 0.3630 | |
| 2028 | −2.400% | −37.200% | 3497.00 | −3.681% | 2410.66 | 1.5083 | 940.38 | 0.3901 | |
| 2029 | −2.400% | −39.600% | 3358.04 | −3.822% | 2425.18 | 1.4420 | 1011.09 | 0.4169 | |
| 2030 | −42.00% | −2.400% | −42.000% | 3239.35 | −3.974% | 2439.80 | 1.3764 | 1081.89 | 0.4434 |
| 2031 | −2.050% | −44.050% | 3120.66 | −3.534% | 2454.50 | 1.3198 | 1144.59 | 0.4663 | |
| 2032 | −2.050% | −46.100% | 3001.97 | −3.664% | 2469.29 | 1.2638 | 1207.38 | 0.4890 | |
| 2033 | −2.050% | −48.150% | 2883.28 | −3.803% | 2484.17 | 1.2084 | 1270.25 | 0.5113 | |
| 2034 | −2.050% | −50.200% | 2764.59 | −3.954% | 2499.14 | 1.1537 | 1333.22 | 0.5335 | |
| 2035 | −2.050% | −52.250% | 2645.91 | −4.116% | 2514.20 | 1.0996 | 1396.27 | 0.5554 | |
| 2036 | −2.050% | −54.300% | 2527.22 | −4.293% | 2529.35 | 1.0461 | 1459.42 | 0.5770 | |
| 2037 | −2.050% | −56.350% | 2408.53 | −4.486% | 2544.59 | 0.9932 | 1522.65 | 0.5984 | |
| 2038 | −2.050% | −58.400% | 2289.84 | −4.696% | 2559.93 | 0.9409 | 1585.98 | 0.6195 | |
| 2039 | −2.050% | −60.450% | 2171.15 | −4.928% | 2575.35 | 0.8891 | 1649.40 | 0.6405 | |
| 2040 | −2.050% | −62.500% | 2052.46 | −5.183% | 2590.87 | 0.8380 | 1712.92 | 0.6611 | |
| 2041 | −2.050% | −64.550% | 1933.77 | −5.467% | 2606.48 | 0.7874 | 1776.52 | 0.6816 | |
| 2042 | −2.050% | −66.600% | 1815.08 | −5.783% | 2622.19 | 0.7375 | 1840.23 | 0.7018 | |
| 2043 | −2.050% | −68.650% | 1696.39 | −6.138% | 2637.99 | 0.6881 | 1904.02 | 0.7218 | |
| 2044 | −2.050% | −70.700% | 1577.70 | −6.539% | 2653.89 | 0.6392 | 1967.91 | 0.7415 | |
| 2045 | −2.050% | −72.750% | 1459.01 | −6.997% | 2669.88 | 0.5909 | 2031.90 | 0.7610 | |
| 2046 | −2.050% | −74.800% | 1340.32 | −7.523% | 2685.97 | 0.5432 | 2095.98 | 0.7803 | |
| 2047 | −2.050% | −76.850% | 1221.63 | −8.135% | 2702.15 | 0.4960 | 2160.16 | 0.7994 | |
| 2048 | −2.050% | −78.900% | 1102.94 | −8.855% | 2718.44 | 0.4494 | 2224.44 | 0.8183 | |
| 2049 | −2.050% | −80.950% | 984.25 | −9.716% | 2734.82 | 0.4033 | 2288.82 | 0.8369 | |
| 2050 | −83.00% | −2.050% | −83.000% | 5724.11 | −10.761% | 2751.30 | 0.3577 | 2353.29 | 0.8553 |
| Variable | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Year | % | % | % | % | % | Ratio | |||
| 2005 | 0.0000 | 0.0 | 0.00% | 49.53% | 0.00% | 100.00% | 49.53% | 0.4006 | 0.0000 |
| 2006 | 0.0024 | 2.4 | 0.55% | 47.88% | 1.13% | 98.87% | 48.43% | 0.4301 | 0.0115 |
| 2007 | 0.0048 | 4.8 | 1.07% | 46.29% | 2.27% | 97.73% | 47.36% | 0.4449 | 0.0232 |
| 2008 | 0.0072 | 7.2 | 1.74% | 49.30% | 3.40% | 96.60% | 51.03% | 0.4177 | 0.0352 |
| 2009 | 0.0098 | 9.8 | 2.54% | 53.45% | 4.53% | 95.47% | 55.99% | 0.3853 | 0.0475 |
| 2010 | 0.0124 | 12.4 | 3.02% | 50.21% | 5.67% | 94.33% | 53.23% | 0.4101 | 0.0601 |
| 2011 | 0.0150 | 15.0 | 3.53% | 48.36% | 6.80% | 93.20% | 51.89% | 0.4258 | 0.0730 |
| 2012 | 0.0177 | 17.7 | 3.69% | 42.87% | 7.93% | 92.07% | 46.57% | 0.4804 | 0.0862 |
| 2013 | 0.0205 | 20.5 | 3.85% | 38.63% | 9.07% | 90.93% | 42.48% | 0.5331 | 0.0997 |
| 2014 | 0.0234 | 23.4 | 4.05% | 35.68% | 10.20% | 89.80% | 39.73% | 0.5773 | 0.1136 |
| 2015 | 0.0263 | 26.3 | 6.60% | 51.63% | 11.33% | 88.67% | 58.23% | 0.3988 | 0.1278 |
| 2016 | 0.0293 | 29.3 | 7.22% | 50.67% | 12.47% | 87.53% | 57.88% | 0.4064 | 0.1424 |
| 2017 | 0.0324 | 32.4 | 7.82% | 49.71% | 13.60% | 86.40% | 57.54% | 0.4143 | 0.1574 |
| 2018 | 0.0356 | 35.6 | 8.43% | 48.77% | 14.73% | 85.27% | 57.19% | 0.4223 | 0.1728 |
| 2019 | 0.0388 | 38.8 | 9.02% | 47.83% | 15.87% | 84.13% | 56.85% | 0.4306 | 0.1886 |
| 2020 | 0.0422 | 42.2 | 9.61% | 46.90% | 17.00% | 83.00% | 56.51% | 0.4391 | 0.2048 |
| 2021 | 0.0502 | 50.2 | 11.01% | 45.16% | 19.60% | 80.40% | 56.17% | 0.4560 | 0.2438 |
| 2022 | 0.0588 | 58.8 | 12.40% | 43.44% | 22.20% | 77.80% | 55.84% | 0.4741 | 0.2853 |
| 2023 | 0.0679 | 67.9 | 13.76% | 41.74% | 24.80% | 75.20% | 55.50% | 0.4934 | 0.3298 |
| 2024 | 0.0777 | 77.7 | 15.12% | 40.05% | 27.40% | 72.60% | 55.17% | 0.5142 | 0.3774 |
| 2025 | 0.0883 | 88.3 | 16.45% | 38.39% | 30.00% | 70.00% | 54.84% | 0.5365 | 0.4286 |
| 2026 | 0.0987 | 98.7 | 17.66% | 36.85% | 32.40% | 67.60% | 54.51% | 0.5589 | 0.4793 |
| 2027 | 0.1099 | 109.9 | 18.86% | 35.33% | 34.80% | 65.20% | 54.18% | 0.5829 | 0.5337 |
| 2028 | 0.1220 | 122.0 | 20.04% | 33.82% | 37.20% | 62.80% | 53.86% | 0.6089 | 0.5924 |
| 2029 | 0.1350 | 135.0 | 21.20% | 32.34% | 39.60% | 60.40% | 53.54% | 0.6369 | 0.6556 |
| 2030 | 0.1491 | 149.1 | 22.35% | 30.86% | 42.00% | 58.00% | 53.22% | 0.6672 | 0.7241 |
| 2031 | 0.1621 | 162.1 | 23.30% | 29.60% | 44.05% | 55.95% | 52.90% | 0.6958 | 0.7873 |
| 2032 | 0.1761 | 176.1 | 24.24% | 28.34% | 46.10% | 53.90% | 52.58% | 0.7267 | 0.8553 |
| 2033 | 0.1912 | 191.2 | 25.17% | 27.10% | 48.15% | 51.85% | 52.26% | 0.7599 | 0.9286 |
| 2034 | 0.2076 | 207.6 | 26.08% | 25.87% | 50.20% | 49.80% | 51.95% | 0.7960 | 1.0080 |
| 2035 | 0.2253 | 225.3 | 26.98% | 24.66% | 52.25% | 47.75% | 51.64% | 0.8352 | 1.0942 |
| 2036 | 0.2447 | 244.7 | 27.87% | 23.46% | 54.30% | 45.70% | 51.33% | 0.8779 | 1.1882 |
| 2037 | 0.2659 | 265.9 | 28.75% | 22.27% | 56.35% | 43.65% | 51.02% | 0.9247 | 1.2910 |
| 2038 | 0.2891 | 289.1 | 29.62% | 21.10% | 58.40% | 41.60% | 50.72% | 0.9761 | 1.4038 |
| 2039 | 0.3148 | 314.8 | 30.48% | 19.94% | 60.45% | 39.55% | 50.41% | 1.0328 | 1.5284 |
| 2040 | 0.3432 | 343.2 | 31.32% | 18.79% | 62.50% | 37.50% | 50.11% | 1.0959 | 1.6667 |
| 2041 | 0.3750 | 375.0 | 32.15% | 17.66% | 64.55% | 35.45% | 49.81% | 1.1662 | 1.8209 |
| 2042 | 0.4106 | 410.6 | 32.98% | 16.54% | 66.60% | 33.40% | 49.51% | 1.2453 | 1.9940 |
| 2043 | 0.4510 | 451.0 | 33.79% | 15.43% | 68.65% | 31.35% | 49.22% | 1.3347 | 2.1898 |
| 2044 | 0.4969 | 496.9 | 34.59% | 14.33% | 70.70% | 29.30% | 48.92% | 1.4367 | 2.4130 |
| 2045 | 0.5498 | 549.8 | 35.38% | 13.25% | 72.75% | 27.25% | 48.63% | 1.5541 | 2.6697 |
| 2046 | 0.6113 | 611.3 | 36.16% | 12.18% | 74.80% | 25.20% | 48.34% | 1.6906 | 2.9683 |
| 2047 | 0.6836 | 683.6 | 36.93% | 11.12% | 76.85% | 23.15% | 48.05% | 1.8514 | 3.3197 |
| 2048 | 0.7701 | 770.1 | 37.68% | 10.08% | 78.90% | 21.10% | 47.76% | 2.0435 | 3.7393 |
| 2049 | 0.8751 | 875.1 | 38.43% | 9.04% | 80.95% | 19.05% | 47.47% | 2.2771 | 4.2493 |
| 2050 | 1.0055 | 1005.5 | 39.17% | 8.02% | 83.00% | 17.00% | 47.19% | 2.5671 | 4.8824 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, K.; Gupta, R.; Maheshwari, S. Using Carbon Tax to Reach the U.S.’s 2050 NDCs Goals—A CGE Model of Firms, Government, and Households. J. Risk Financial Manag. 2023, 16, 317. https://doi.org/10.3390/jrfm16070317
Yan K, Gupta R, Maheshwari S. Using Carbon Tax to Reach the U.S.’s 2050 NDCs Goals—A CGE Model of Firms, Government, and Households. Journal of Risk and Financial Management. 2023; 16(7):317. https://doi.org/10.3390/jrfm16070317
Chicago/Turabian StyleYan, Kejia, Rakesh Gupta, and Suneel Maheshwari. 2023. "Using Carbon Tax to Reach the U.S.’s 2050 NDCs Goals—A CGE Model of Firms, Government, and Households" Journal of Risk and Financial Management 16, no. 7: 317. https://doi.org/10.3390/jrfm16070317
APA StyleYan, K., Gupta, R., & Maheshwari, S. (2023). Using Carbon Tax to Reach the U.S.’s 2050 NDCs Goals—A CGE Model of Firms, Government, and Households. Journal of Risk and Financial Management, 16(7), 317. https://doi.org/10.3390/jrfm16070317








