An Empirical Study of Volatility in Cryptocurrency Market
Abstract
1. Introduction
2. Data
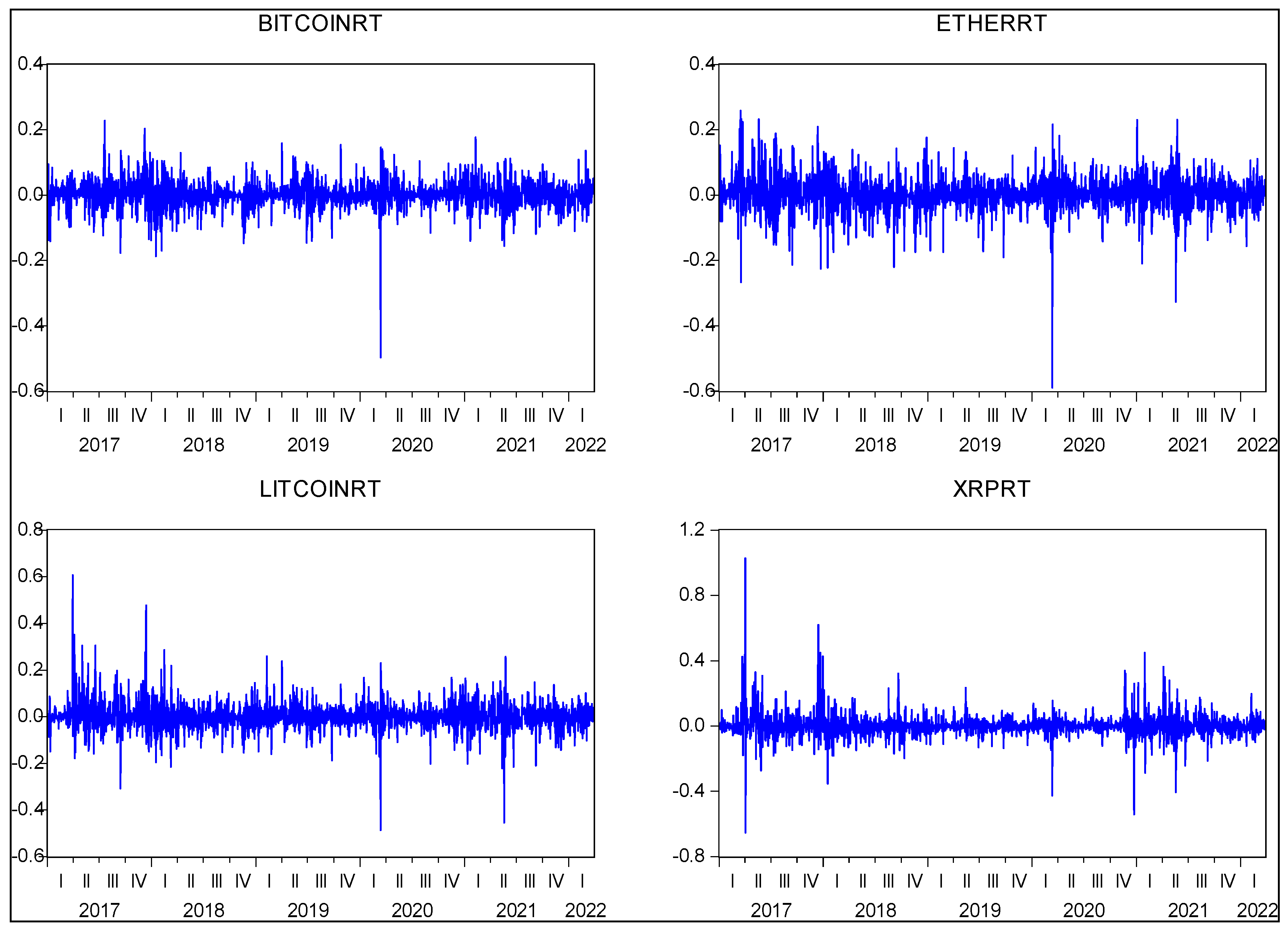
Descriptive Statistics
- Rit = Daily log return of cryptocurrency at day t;
- Pit = Closing price of crypto at day t;
- Pi,t−1 = Closing price of crypto at day t − 1.
3. Data Analysis
3.1. Unit Root Test
3.2. ARCH Effect Test
3.3. Granger Causality
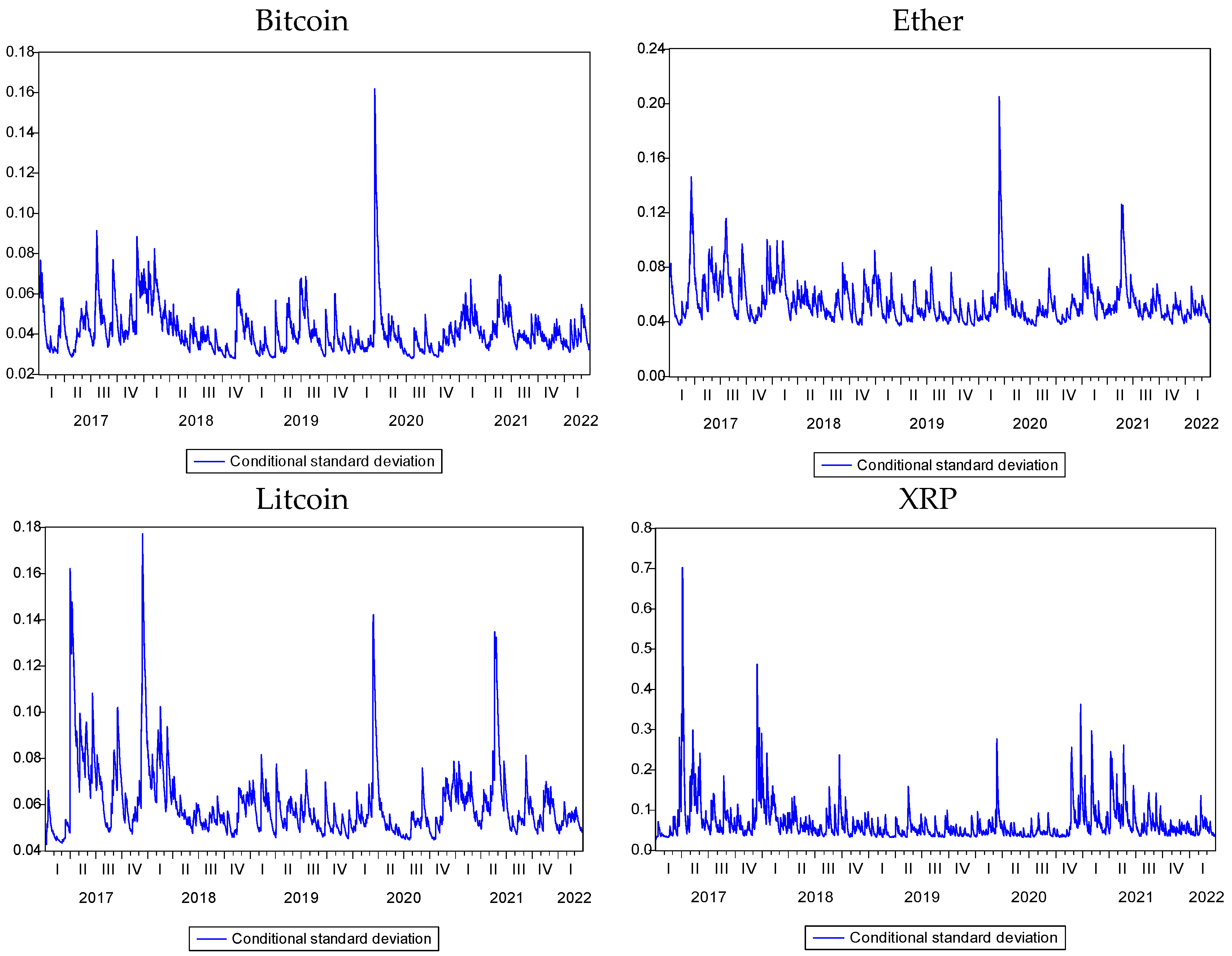
3.4. GARCH Model
3.5. EGARCH Model
3.6. GARCH in Mean (GARCH-M) Model
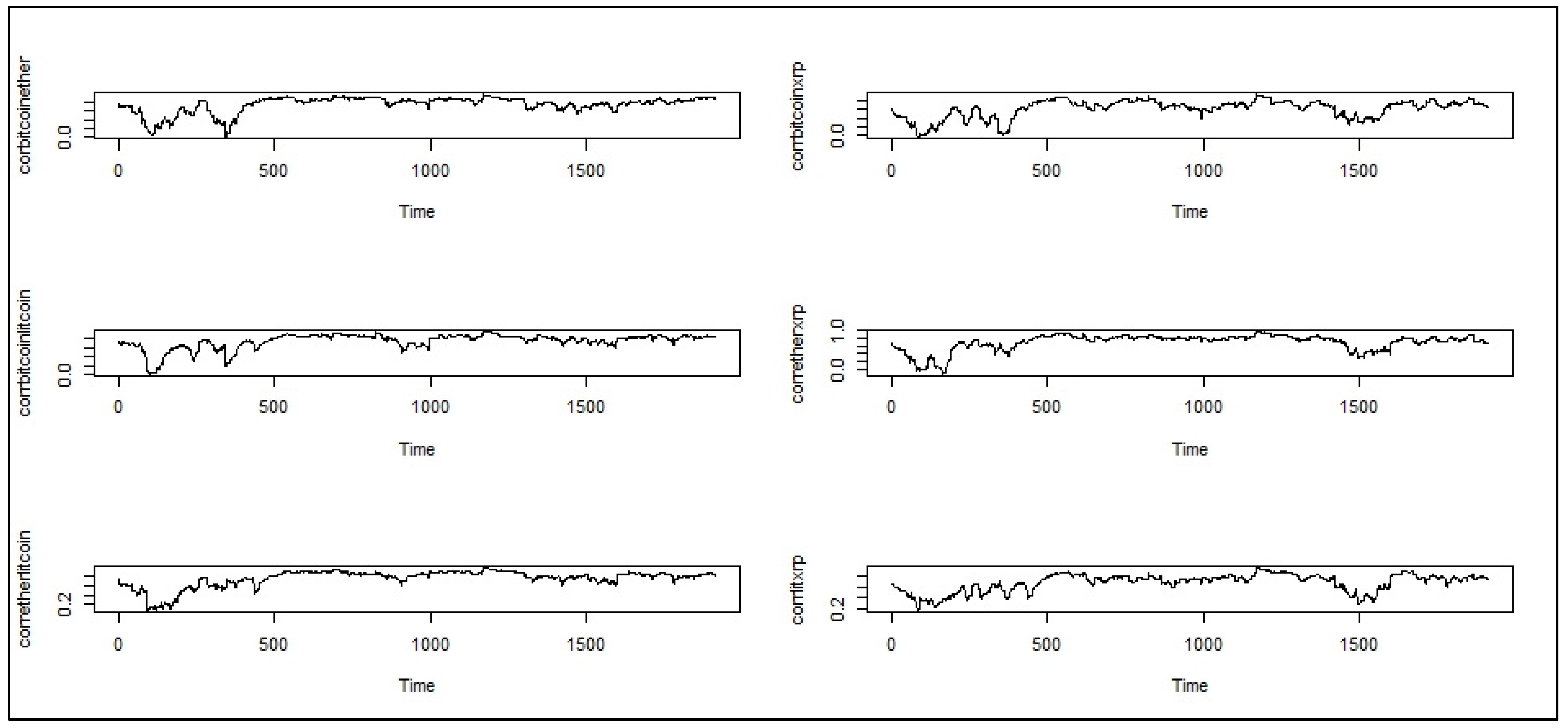
3.7. DCC(1,1) Model
- Rt:
- represents the dynamic conditional correlation (DCC) matrix.
- Dt:
- represents the diagonal matrix from the covariance matrix Ht.
- Dt−1:
- the inverse of the Dt Matrix.
- Qt
- indicates Covariance Matrix
- Gt
- indicates the diagonal matrix of the covariance matrix Qt,
- Qt−1
- indicates the inverse matrix of the matrix Qt.
- Ct
- indicates Correlation Matrix
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abakah, Emmanuel Joel Aikins, Luis Alberiko Gil-Alana, Godfrey Madigu, and Fatima Romero-Rojo. 2020. Volatility persistence in cryptocurrency markets under structural breaks. International Review of Economics & Finance 69: 680–91. [Google Scholar]
- Baur, Dirk G. 2012. Asymmetric volatility in the gold market. The Journal of Alternative Investments 14: 26–38. [Google Scholar] [CrossRef]
- Baur, Dirk G., and Thomas Dimpfl. 2018. Asymmetric volatility in cryptocurrencies. Economics Letters 173: 148–51. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bouri, Elie, Tareq Saeed, Xuan Vinh Vo, and David Roubaud. 2021. Quantile connectedness in the cryptocurrency market. Journal of International Financial Markets, Institutions and Money 71: 101302. [Google Scholar] [CrossRef]
- Brooks, Chris, and Alistair G. Rew. 2002. Testing for a unit root in a process exhibiting a structural break in the presence of GARCH errors. Computational Economics 20: 157–76. [Google Scholar] [CrossRef]
- Brooks, Chris, Olan T. Henry, and Gita Persand Persand. 2002. The effect of asymmetries on optimal hedge ratios. The Journal of Business 75: 333–52. [Google Scholar] [CrossRef]
- Campbell, John Y., and Ludger Hentschel. 1992. No news is good news: An asymmetric model of changing volatility in stock returns. Journal of Financial Economics 31: 281–318. [Google Scholar] [CrossRef]
- Chaudhary, Rashmi, Priti Bakhshi, and Hemendra Gupta. 2020. Volatility in international stock markets: An empirical study during COVID-19. Journal of Risk and Financial Management 13: 208. [Google Scholar] [CrossRef]
- Christie, Andrew A. 1982. The stochastic behavior of common stock variances: Value, leverage and interest rate effects. Journal of Financial Economics 10: 407–32. [Google Scholar] [CrossRef]
- Chu, Jeffrey, Stephen Chan, Saralees Nadarajah, and Joerg Osterrieder. 2017. GARCH modelling of cryptocurrencies. Journal of Risk and Financial Management 10: 17. [Google Scholar] [CrossRef]
- Ciaian, Pavel, Miroslava Rajcaniova, and d’Artis Kancs. 2016. The economics of BitCoin price formation. Applied Economics 48: 1799–815. [Google Scholar] [CrossRef]
- Ciaian, Pavel, Miroslava Rajcaniova, and Artis Kancs. 2018. Virtual relationships: Short- and long-run evidence from BitCoin and altcoin markets. Journal of International Financial Markets, Institutions & Money 52: 173–95. [Google Scholar]
- Corbet, Shaen, Andrew Meegan, Charles Larkin, Brian Lucey, and Larisa Yarovaya. 2018. Exploring the dynamic relationships between cryptocurrencies and other financial assets. Economics Letters 165: 28–34. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1981. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica: Journal of the Econometric Society 49: 1057–72. [Google Scholar] [CrossRef]
- Dutta, Anupam, and Elie Bouri. 2022. Outliers and Time-Varying Jumps in the Cryptocurrency Markets. Journal of Risk and Financial Management 15: 128. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica: Journal of the Econometric Society 50: 987–1007. [Google Scholar] [CrossRef]
- Engle, Robert. 2001. GARCH 101: The use of ARCH/GARCH models in applied econometrics. Journal of Economic Perspectives 15: 157–68. [Google Scholar] [CrossRef]
- Engle, Robert F., David M. Lilien, and Russell P. Robins. 1987. Estimating time varying risk premia in the term structure: The ARCH-M model. Econometrica: Journal of the Econometric Society 55: 391–407. [Google Scholar] [CrossRef]
- Fry, John, and Eng-Tuck Cheah. 2016. Negative bubbles and shocks in cryptocurrency markets. International Review of Financial Analysis 47: 343–52. [Google Scholar] [CrossRef]
- Gupta, Hemendra, Rashmi Chaudhary, Kajal Srivastava, and Suneel Gupta. 2022. Volatility modelling of asset classes: An empirical study during different phases of COVID-19. Academy of Accounting and Financial Studies Journal 26: 1–19. [Google Scholar]
- Horpestad, Jone B., Štefan Lyócsa, Peter Molnár, and Torbjørn B. Olsen. 2019. Asymmetric volatility in equity markets around the world. The North American Journal of Economics and Finance 48: 540–54. [Google Scholar] [CrossRef]
- Ji, Qiang, Elie Bouri, Chi Keung Marco Lau, and David Roubaud. 2019. Dynamic connectedness and integration in cryptocurrency markets. International Review of Financial Analysis 63: 257–72. [Google Scholar] [CrossRef]
- Kaya Soylu, Pınar, Mustafa Okur, Özgür Çatıkkaş, and Z. Ayca Altintig. 2020. Long memory in the volatility of selected cryptocurrencies: Bitcoin, Ethereum and Ripple. Journal of Risk and Financial Management 13: 107. [Google Scholar] [CrossRef]
- Lahajnar, Sebastian, and Alenka Rozanec. 2020. The correlation strength of the most important cryptocurrencies in the bull and bear market. Investment Management and Financial Innovations 17: 67–81. [Google Scholar] [CrossRef]
- Ljung, G.M., and G. E. Box. 1978. On a measure of lack of fit in time series models. Biometrika 65: 297–303. [Google Scholar] [CrossRef]
- Nelson, Daniel B. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica: Journal of the Econometric Society 59: 347–70. [Google Scholar] [CrossRef]
- Phillip, Andrew, Jennifer S. K. Chan, and Shelton Peiris Peiris. 2018. A new look at cryptocurrencies. Economics Letters 163: 6–9. [Google Scholar] [CrossRef]
- Rastogi, Shailesh. 2014. The financial crisis of 2008 and stock market volatility–analysis and impact on emerging economies pre and post crisis. Afro-Asian Journal of Finance and Accounting 4: 443–59. [Google Scholar] [CrossRef]
- Schilling, Linda, and Harald Uhlig. 2019. Some simple bitcoin economics. Journal of Monetary Economics 106: 16–26. [Google Scholar] [CrossRef]
- Sensoy, Ahmet, Thiago Christiano Silva, Shaen Corbet, and Benjamin Miranda Tabak. 2021. High-frequency return and volatility spillovers among cryptocurrencies. Applied Economics 53: 4310–28. [Google Scholar] [CrossRef]
- Shahzad, Syed Jawad Hussain, Elie Bouri, David Roubaud, Ladislav Kristoufek, and Brian Lucey. 2019. Is Bitcoin a better safe-haven investment than gold and commodities? International Review of Financial Analysis 63: 322–30. [Google Scholar] [CrossRef]
- Shahzad, Syed Jawad Hussain, Elie Bouri, David Roubaud, and Ladislav Kristoufek. 2020. Safe haven, hedge and diversification for G7 stock markets: Gold versus bitcoin. Economic Modelling 87: 212–24. [Google Scholar] [CrossRef]
- Sharpe, William F. 1963. A simplified model for portfolio analysis. Management Science 9: 277–93. [Google Scholar] [CrossRef]
- Stavroyiannis, Stavros. 2018. A note on the Nelson-Cao inequality constraints in the GJR-GARCH model: Is there a leverage effect? International Journal of Economics and Business Research 16: 442–52. [Google Scholar] [CrossRef]
- Yan, Kejia, Huqin Yan, and Rakesh Gupta. 2022. Are GARCH and DCC values of 10 cryptocurrencies affected by COVID-19? Journal of Risk and Financial Management 15: 113. [Google Scholar] [CrossRef]
| Currency | Market Cap |
|---|---|
| Bitcoin | USD 377.53B |
| Ether | USD 129.53B |
| Litecoin | USD 3.79B |
| XRP | USD 16.02B |
| BITCOINRT | ETHERRT | LITECOINRT | XRPRT | |
| Mean | 0.20% | 0.32% | 0.18% | 0.26% |
| Median | 0.23% | 0.22% | −0.03% | 0.00% |
| Minimum | −0.4973 | −0.5896 | −0.4868 | −0.653 |
| Maximum | 0.2276 | 0.2586 | 0.607 | 1.028 |
| Std.Dev. | 4% | 6% | 6% | 8% |
| Skewness | −0.8444 | −0.6056 | 0.6600 | 1.8551 |
| Kurtosis | 15.0827 | 11.9877 | 15.5543 | 32.6549 |
| Observations | 1913 | 1913 | 1913 | 1913 |
| Jarque-Bera | 11,864.2 | 6555.72 | 12,701.7 | 71,193.7 |
| Probability | 0 | 0 | 0 | 0 |
| BITCOINRT | ETHERRT | LITECOINRT | XRPRT | |
| BITCOINRT | 1.0000 | |||
| ETHERRT | 0.7210 | 1.0000 | ||
| LITECOINRT | 0.6825 | 0.6931 | 1.0000 | |
| XRPRT | 0.4676 | 0.5083 | 0.5235 | 1.0000 |
| One-Year Return | ||||
| BITCOIN | ETHER | LITECOIN | XRP | |
| Mean | 175% | 595% | 1092% | 334% |
| Med | 61% | 65% | 24% | 22% |
| Max | 1832% | 14,171% | 44,380% | 6921% |
| Min | −83% | −92% | −87% | −93% |
| SD | 277% | 1733% | 4630% | 1075% |
| Three-Year Return | ||||
| Mean | 78% | 86% | 36% | 31% |
| Med | 79% | 66% | 20% | 18% |
| Max | 149% | 267% | 280% | 178% |
| Min | −0.12% | −15.52% | −56.74% | −40.37% |
| SD | 34% | 74% | 67% | 45% |
| Five-Year Return | ||||
| Mean | 94% | 133% | 96% | 63% |
| Med | 102% | 132% | 99% | 73% |
| Max | 121% | 239% | 171% | 108% |
| Min | 49% | 23% | 1% | −1% |
| SD | 22% | 63% | 66% | 37% |
| BITCOINRT | ETHERRT | LITECOINRT | XRPRT | |
| T Stat | −47.051 | −46.831 | −46.98 | −30.04 |
| Prob. | 0.0001 | 0.0001 | 0.0001 | 0.0001 |
| BITCOINRT | ETHERRT | LITECOINRT | XRPRT | |
| F-Stats | 9.7978 | 25.1836 | 36.7409 | 133.5966 |
| Prob. | 0.00 | 0.00 | 0.00 | 0.00 |
Null Hypothesis:  Indicates Does Not Granger Cause Indicates Does Not Granger Cause | F-Statistic | Prob. | Type of Causality |
|---|---|---|---|
ETHERRT  BITCOINRT BITCOINRT | 8.5385 | 0.0002 * | Unidirectional |
BITCOINRT  ETHERRT ETHERRT | 0.0623 | 0.9396 | No causality |
LITECOINRT  BITCOINRT BITCOINRT | 1.0697 | 0.3433 | No causality |
BITCOINRT  LITECOINRT LITECOINRT | 2.2198 | 0.1089 | No causality |
XRPRT  BITCOINRT BITCOINRT | 4.6675 | 0.0095 * | Unidirectional |
BITCOINRT  XRPRT XRPRT | 0.6506 | 0.5218 | No causality |
LITECOINRT  ETHERRT ETHERRT | 0.2374 | 0.7887 | No causality |
ETHERRT  LITECOINRT LITECOINRT | 0.9367 | 0.3921 | No causality |
XRPRT  ETHERRT ETHERRT | 2.9438 | 0.0429 ** | Unidirectional |
ETHERRT  XRPRT XRPRT | 0.3821 | 0.6825 | No causality |
XRPRT  LITECOINRT LITECOINRT | 0.5818 | 0.559 | No causality |
LITECOINRT  XRPRT XRPRT | 1.1575 | 0.3145 | No causality |
| BITCOIN RT | ETHER RT | LITECOIN RT | XRP RT | |||||
| Coeff. | Prob. | Coeff. | Prob. | Coeff. | Prob. | Coeff. | Prob. | |
| c | 0.0015 | 0.1076 | 0.0024 | 0.0478 | 0.0012 | 0.3621 | 0.0020 | 0.2155 |
| AR(1) | −0.7508 | 0.0000 | −0.8053 | 0.0000 | −0.7799 | 0.0000 | −0.4235 | 0.1371 |
| MA(1) | 0.7131 | 0.0000 | 0.7637 | 0.0000 | 0.7419 | 0.0000 | 0.3634 | 0.2148 |
| BITCOINRT | ETHERRT | LITECOINRT | XRPRT | |||||
| Coeff. | Prob. | Coeff. | Prob. | Coeff. | Prob. | Coeff. | Prob. | |
| C | 0.0001 | 0.0010 | 0.0003 | 0.0010 | 0.0002 | 0.0010 | 0.0004 | 0.0010 |
| ARCH () | 0.1008 | 0.0010 | 0.0927 | 0.0010 | 0.0673 | 0.0010 | 0.3923 | 0.0010 |
| GARCH () | 0.8376 | 0.0010 | 0.7961 | 0.0010 | 0.8737 | 0.0010 | 0.6304 | 0.0010 |
| BITCOINRT | ETHERRT | LITECOINRT | XRPRT | |||||
| Coeff. | Prob. | Coeff. | Prob. | Coeff. | Prob. | Coeff. | Prob. | |
| −0.6223 | 0.001 | −0.5334 | 0.001 | −0.438 | 0.001 | −0.7695 | 0.001 | |
| 0.1701 | 0.001 | 0.2075 | 0.001 | 0.1557 | 0.001 | 0.4378 | 0.001 | |
| λ | −0.0649 | 0.001 | −0.0226 | 0.0031 | 0.0274 | 0.001 | 0.0697 | 0.001 |
| β | 0.9214 | 0.001 | 0.9343 | 0.001 | 0.9411 | 0.001 | 0.9159 | 0.001 |
| BITCOINRT | ETHERRT | LITECOINRT | XRPRT | |||||
| Coeff. | Prob. | Coeff. | Prob. | Coeff. | Prob. | Coeff. | Prob. | |
| Δ | 0.0413 | 0.7360 | 0.1186 | 0.3143 | 0.1363 | 0.3360 | 0.0182 | 0.7593 |
| C | 0.0001 | 0.0010 | 0.0002 | 0.0010 | 0.0002 | 0.0010 | 0.0003 | 0.0010 |
| A | 0.1009 | 0.0010 | 0.1128 | 0.0010 | 0.0678 | 0.0010 | 0.3626 | 0.0010 |
| Β | 0.8373 | 0.0010 | 0.8223 | 0.0010 | 0.8725 | 0.0010 | 0.6538 | 0.0010 |
| BITCOINRT | ETHERRT | LITECOINRT | XRPRT | |
| BITCOINRT | 1.0000 | |||
| ETHERRT | 0.7210 | 1.0000 | ||
| LITECOINRT | 0.7379 | 0.7456 | 1.0000 | |
| XRPRT | 0.6143 | 0.6869 | 0.6818 | 1.0000 |
| Estimate | t-Value | Pr(>|t|) | ||
|---|---|---|---|---|
| All Currencies | α | 0.033 | 7.815 | 0.000 |
| β | 0.963 | 186.198 | 0.000 | |
| Bitcoin–Ether | α | 0.058 | 2.330 | 0.020 |
| β | 0.934 | 27.697 | 0.000 | |
| Bitcoin–XRP | α | 0.037 | 3.337 | 0.001 |
| β | 0.956 | 66.737 | 0.000 | |
| Bitcoin–Litcoin | α | 0.048 | 3.615 | 0.000 |
| β | 0.948 | 62.468 | 0.000 | |
| Ether–Litcoin | α | 0.038 | 5.163 | 0.000 |
| β | 0.962 | 128.784 | 0.000 | |
| Ether–XRP | α | 0.034 | 2.882 | 0.004 |
| β | 0.962 | 64.787 | 0.000 | |
| Litcoin–XRP | α | 0.034 | 3.421 | 0.001 |
| β | 0.965 | 86.364 | 0.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, H.; Chaudhary, R. An Empirical Study of Volatility in Cryptocurrency Market. J. Risk Financial Manag. 2022, 15, 513. https://doi.org/10.3390/jrfm15110513
Gupta H, Chaudhary R. An Empirical Study of Volatility in Cryptocurrency Market. Journal of Risk and Financial Management. 2022; 15(11):513. https://doi.org/10.3390/jrfm15110513
Chicago/Turabian StyleGupta, Hemendra, and Rashmi Chaudhary. 2022. "An Empirical Study of Volatility in Cryptocurrency Market" Journal of Risk and Financial Management 15, no. 11: 513. https://doi.org/10.3390/jrfm15110513
APA StyleGupta, H., & Chaudhary, R. (2022). An Empirical Study of Volatility in Cryptocurrency Market. Journal of Risk and Financial Management, 15(11), 513. https://doi.org/10.3390/jrfm15110513







