A Discount Technique-Based Inventory Management on Electronics Products Supply Chain
Abstract
:1. Introduction and Literature Review
- It critically evaluates when one needs to impose a discount and when to not, especially when a bulk purchase has been made by a retailer with a huge investment in a limited storage shop in a highly expensive location.
- A synergy between stock, price, and time-dependent demand and implications of discount policy has been meticulously explained.
- A sensitivity analysis with some theoretical findings has been suggesting to achieve the maximum profit in the chain for the managers of the industry and shown a threshold point of discount offered time.
1.1. Literature Review
1.1.1. Influence of Stock Dependent Demand on Traditional Inventory Model
1.1.2. Influence of Price Sensitive Demand on Tradition Inventory Model
1.1.3. Influence of Sensitiveness of Time on Traditional Inventory Mode
1.1.4. Impacts of Discount Policy on Electronic Products
2. Assumption and Notations
2.1. Assumptions
- The replenishment rate is infinite and Lead-time is negligible.
- This model is for a single type of item.
- The planning horizon is considered infinite.
- In this paper, the demand function comprises price, time, and stock-dependence in the form ofwhere,is the initial rate of demandis the rate decrease demand on pricesis the product priceis the discount rate on price of productis the rate with which the demand rate increases on timeis the rate of changes of rate on time in the demand rate itselfis the rate depending on stock,
- There are no shortages considered in this model.
2.2. Notations
3. Mathematical Formulation for Proposed Electronics Product Inventory Model
3.1. Solution of Differential Equations from (1) and (2)
3.2. The Total Cost per Unit Time per Cycle
- (a)
- Ordering cost per cycle =
- (b)
- Holding cost (HC) =i.e.,
- (c)
- Purchase cost (PC) =
- (d)
- Transportation cost (TC) =
- (e)
- Sales revenue (SR) =
4. Theoretical Derivations
4.1. Algorithms
4.1.1. Algorithm for Single Decision Variable
- Step 1.
- Input all the parameters value ().
- Step 2.
- Evaluate the value of from Equation (13).
- Step 3.
- Evaluate the value of ω from Equation (12) using all the parameters and the value of p*.
- Step 4.
- Output the value of p* and ω.
- Step 5.
- End.
4.1.2. Algorithm for Double Decision Variable
- Step 1.
- Declare and from Equations (18) and (19).
- Step 2.
- Input all the parameters value ().
- Step 3.
- Take where and iterative variable .
- Step 4.
- Find
- Step 5.
- IF and , Go to Setp 3. And IF and Go to Step 10.
- Step 6.
- Find and
- Step 7.
- Set and .
- Step 8.
- If and , Go to Step 10 ( is small value).
- Step 9.
- Update and . Go to Step 4.
- Step 10.
- Evaluate from Equation (12).
- Step 11.
- Output the value of and .
- Step 12.
- End.
4.2. Case Study
4.3. Numerical Illustration:
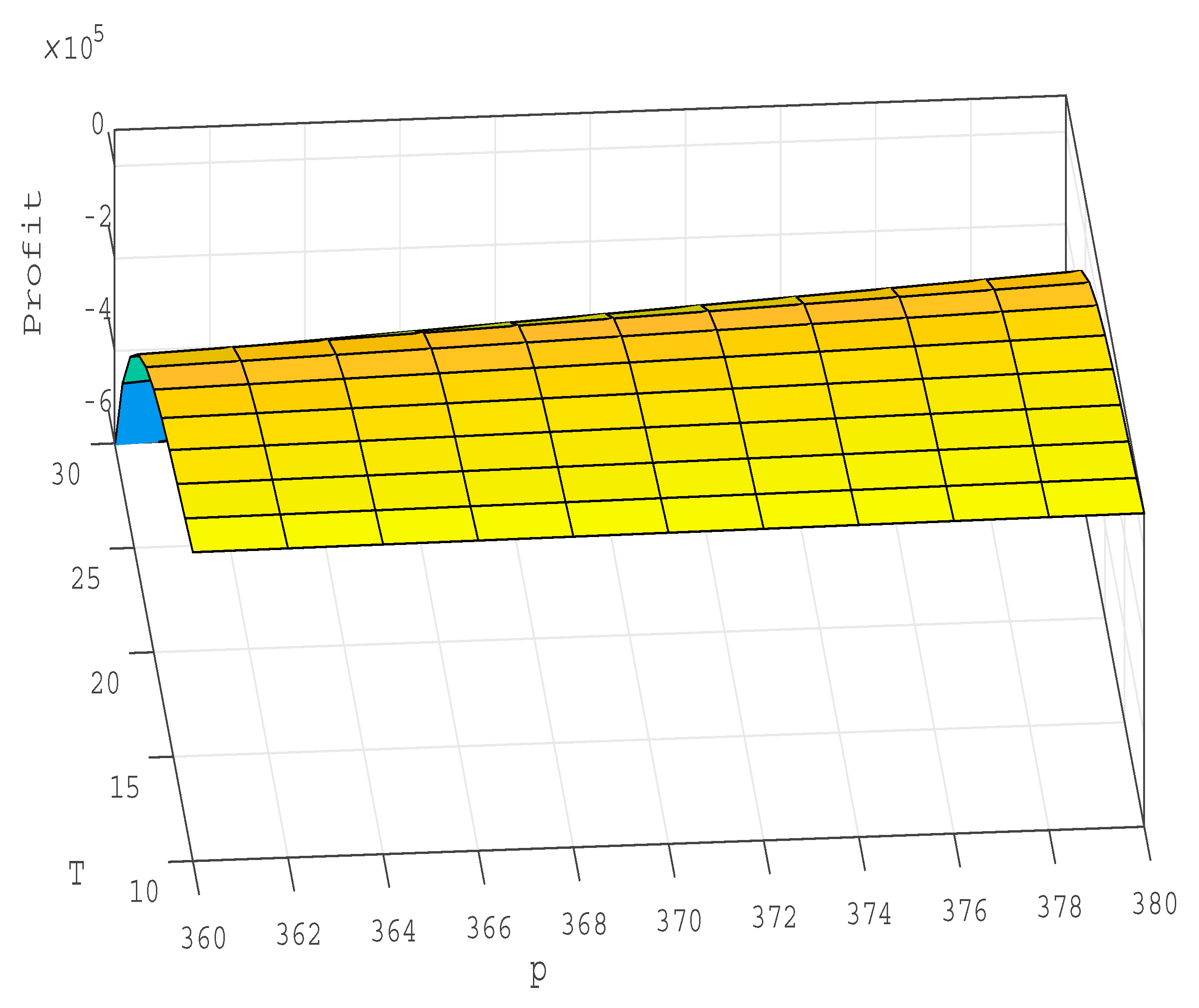
4.4. Sensitivity Analysis
- When the ordering cost (C) of the system increased, the selling price (p) and as well as the cycle length (T) of the chain were raised. This happens because a higher ordering cost brings a more considerable lot and intensifies the total cost of the business. As a result, the retailer will need to sell his products at a comparatively higher selling price, and as the lot is massive so it is challenging to sell the products quickly. However, the profits without discount and with discount were increased.
- With the intensification of purchase costs, the profit was decreasing. However, the selling price and total cycle length also increased. If a retailer purchased any item at a high price to maintain the profit margin, he needs to sell it at a high price. Moreover, an increase in stock provides fluctuations in the profit and selling price of the system.
- The profit becomes lower with the upsurge of the per-unit holding cost of the item. Moreover, it increases the selling price (p) and cycle length (T) of the system. Furthermore, the increase in initial demand parameter (a) provides a more significant profit than usual. In contrast, an increase in another parameter (b) will give a decrease in profit.
- The increase of the rate of change of demand rate () provides a lower profit for the system while it is vice versa for the increasing rate of demand parameter (). The profit of the chain decreased with the increase of the period (). However, the rate depending on stock (s) when increased the system’s profit has been reduced. A significant change in profit has been noticed with variable transportation () and fixed transportation (). However, for both costs, the retailer’s profit margin slightly drops due to the excessive expenses in the transportation system.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Adak, Sudip, and G. S. Mahapatra. 2020. Effect of reliability on multi-item inventory system with shortages and partial backlog incorporating time dependent demand and deterioration. Annals of Operations Research 11: 1–21. [Google Scholar] [CrossRef]
- Ahn, Hyun-Soo, Mehmet Gümüş, and Philip Kaminsky. 2009. Inventory, discounts, and the timing effect. Manufacturing and Service Operations Management 11: 613–29. [Google Scholar] [CrossRef] [Green Version]
- Bhaula, Bhaskar, Jayanta Kumar Dash, and M. Rajendra Kumar. 2019. An optimal inventory model for perishable items under successive price discounts with permissible delay in payments. OPSEARCH 56: 261–81. [Google Scholar] [CrossRef]
- Cambini, Alberto, and Laura Martein. 2009. Generalized Convexity of Some Classes of Fractional Functions. Generalized Convexity and Optimization: Theory and Applications 616: 137–57. [Google Scholar]
- Cárdenas-Barrón, Leopoldo Eduardo, Ali Akbar Shaikh, Sunil Tiwari, and Gerardo Treviño-Garza. 2020. An EOQ inventory model with nonlinear stock dependent holding cost, nonlinear stock dependent demand and trade credit. Computers & Industrial Engineering 139: 105557. [Google Scholar]
- Chandra, Sujan. 2017. An inventory model with ramp type demand, time varying holding cost and price discount on backorders. Uncertain Supply Chain Management 5: 52–58. [Google Scholar] [CrossRef]
- Chang, Chun-Tao, Jinn-Tsair Teng, and Suresh Kumar Goyal. 2010. Optimal replenishment policies for non-instantaneous deteriorating items with stock-dependent demand. International Journal of Production Economics 123: 62–68. [Google Scholar] [CrossRef]
- Chang, Horng-Jinh, and Chung-Yuan Dye. 1999. An EOQ model for deteriorating items with time varying demand and partial backlogging. Journal of the Operational Research Society 50: 1176–82. [Google Scholar]
- Datta, Tapan Kumar, Karabi Paul, and Ashis Kumar Pal. 1998. Demand promotion by upgradation under stock-dependent demand situation—A model. International Journal of Production Economics 55: 31–38. [Google Scholar] [CrossRef]
- De-la-Cruz-Márquez, Cynthia Griselle, Leopoldo Eduardo Cárdenas-Barrón, and Buddhadev Mandal. 2021. An Inventory Model for Growing Items with Imperfect Quality When the Demand Is Price Sensitive under Carbon Emissions and Shortages. Mathematical Problems in Engineering 2021: 6649048. [Google Scholar] [CrossRef]
- Donaldson, W. A. 1977. Inventory Replenishment Policy for a Linear Trend in Demand—An Analytical Solution. Operational Research Quarterly (1970–1977) 28: 663–70. [Google Scholar] [CrossRef]
- Gupta, Rakesh, and Prem Vrat. 1986. Inventory model for stock-dependent consumption rate. Opsearch 23: 6. [Google Scholar]
- Halim, Mohammad Abdul, A. Paul, Mona Mahmoud, B. Alshahrani, Atheelah Y. M. Alazzawi, and Gamal M. Ismail. 2021. An overtime production inventory model for deteriorating items with nonlinear price and stock dependent demand. Alexandria Engineering Journal 60: 2779–86. [Google Scholar] [CrossRef]
- Harris, Ford W. 1990. How Many Parts to Make at Once. Operations Research 38: 947–50. [Google Scholar] [CrossRef]
- Hasan, Md. Rakibul, Yosef Daryanto, Tutul Chandra Roy, and Yi Feng. 2020. Inventory management with online payment and preorder discounts. Industrial Management and Data Systems 120: 2001–23. [Google Scholar] [CrossRef]
- Latha, K. F. Mary, Ganesh Kumar M, and Uthayakumar Ramasamy. 2021. Two echelon economic lot sizing problems with geometric shipment policy backorder price discount and optimal investment to reduce ordering cost. OPSEARCH 12: 1–31. [Google Scholar] [CrossRef]
- Limansyah, Taufik, Dharma Lesmono, and Ign Sandy. 2020. Economic order quantity model with deterioration factor and all-units discount. Journal of Physics: Conference Series 1490: 012052. [Google Scholar] [CrossRef]
- Liu, Lu, Qiuhong Zhao, and Mark Goh. 2021. Perishable material sourcing and final product pricing decisions for two-echelon supply chain under price-sensitive demand. Computers & Industrial Engineering 156: 107260. [Google Scholar]
- Macías-López, Adrián, Leopoldo Eduardo Cárdenas-Barrón, Rodrigo E. Peimbert-García, and Buddhadev Mandal. 2021. An Inventory Model for Perishable Items with Price-, Stock-, and Time-Dependent Demand Rate considering Shelf-Life and Nonlinear Holding Costs. Mathematical Problems in Engineering 2021: 6630938. [Google Scholar] [CrossRef]
- Manna, Amalesh Kumar, Md Akhtar, Ali Akbar Shaikh, and Asoke Kumar Bhunia. 2021. Optimization of a deteriorated two-warehouse inventory problem with all-unit discount and shortages via tournament differential evolution. Applied Soft Computing 107: 107388. [Google Scholar] [CrossRef]
- Mashud, Abu Hashan Md, Hui-Ming Wee, Biswajit Sarkar, and Yu-Hua Chiang Li. 2021. A sustainable inventory system with the advanced payment policy and trade-credit strategy for a two-warehouse inventory system. Kybernetes 50: 1321–48. [Google Scholar] [CrossRef]
- Md Mashud, Abu Hashan, Dipa Roy, Yosef Daryanto, and Mohd Helmi Ali. 2020. A Sustainable Inventory Model with Imperfect Products, Deterioration, and Controllable Emissions. Mathematics 8: 2049. [Google Scholar] [CrossRef]
- Pando, Valentín, Luis A. San-José, and Joaquín Sicilia. 2021. An Inventory Model with Stock-Dependent Demand Rate and Maximization of the Return on Investment. Mathematics 9: 844. [Google Scholar] [CrossRef]
- Papachristos, Sotirios, and Konstantina Skouri. 2000. An optimal replenishment policy for deteriorating items with time-varying demand and partial—exponential type—backlogging. Operations Research Letters 27: 175–84. [Google Scholar] [CrossRef]
- Paul, Asim, Magfura Pervin, Sankar Kumar Roy, Gerhard Wilhelm Weber, and Abolfazl Mirzazadeh. 2021. Effect of price-sensitive demand and default risk on optimal credit period and cycle time for a deteriorating inventory model. RAIRO: Recherche Opérationnelle 55: S2575–S2592. [Google Scholar] [CrossRef]
- Rana, Ranveer Singh, Dinesh Kumar, and Kanika Prasad. 2021. Two warehouse dispatching policies for perishable items with freshness efforts, inflationary conditions and partial backlogging. Operations Management Research 5: 1–8. [Google Scholar] [CrossRef]
- San-José, Luis A., Joaquín Sicilia, Manuel González-de-la-Rosa, and Jaime Febles-Acosta. 2021. Profit maximization in an inventory system with time-varying demand, partial backordering and discrete inventory cycle. Annals of Operations Research 4: 1–21. [Google Scholar] [CrossRef]
- Shah, Nita H., and Monika K. Naik. 2018. Inventory policies for price-sensitive stock-dependent demand and quantity discounts. International Journal of Mathematical, Engineering and Management Sciences 3: 245–57. [Google Scholar] [CrossRef]
- Shaikh, Ali Akbar, Al-Amin Khan, Gobinda Chandra Panda, and Ioannis Konstantaras. 2019. Price discount facility in an EOQ model for deteriorating items with stock-dependent demand and partial backlogging. International Transactions in Operational Research 26: 1365–95. [Google Scholar] [CrossRef]
- Zhou, Youjun. 2012. The bi-ramp type demand and price discount inventory model for deteriorating items. Paper presented at World Congress on Intelligent Control and Automation (WCICA), Beijing, China, July 6–8; pp. 3298–304. [Google Scholar]
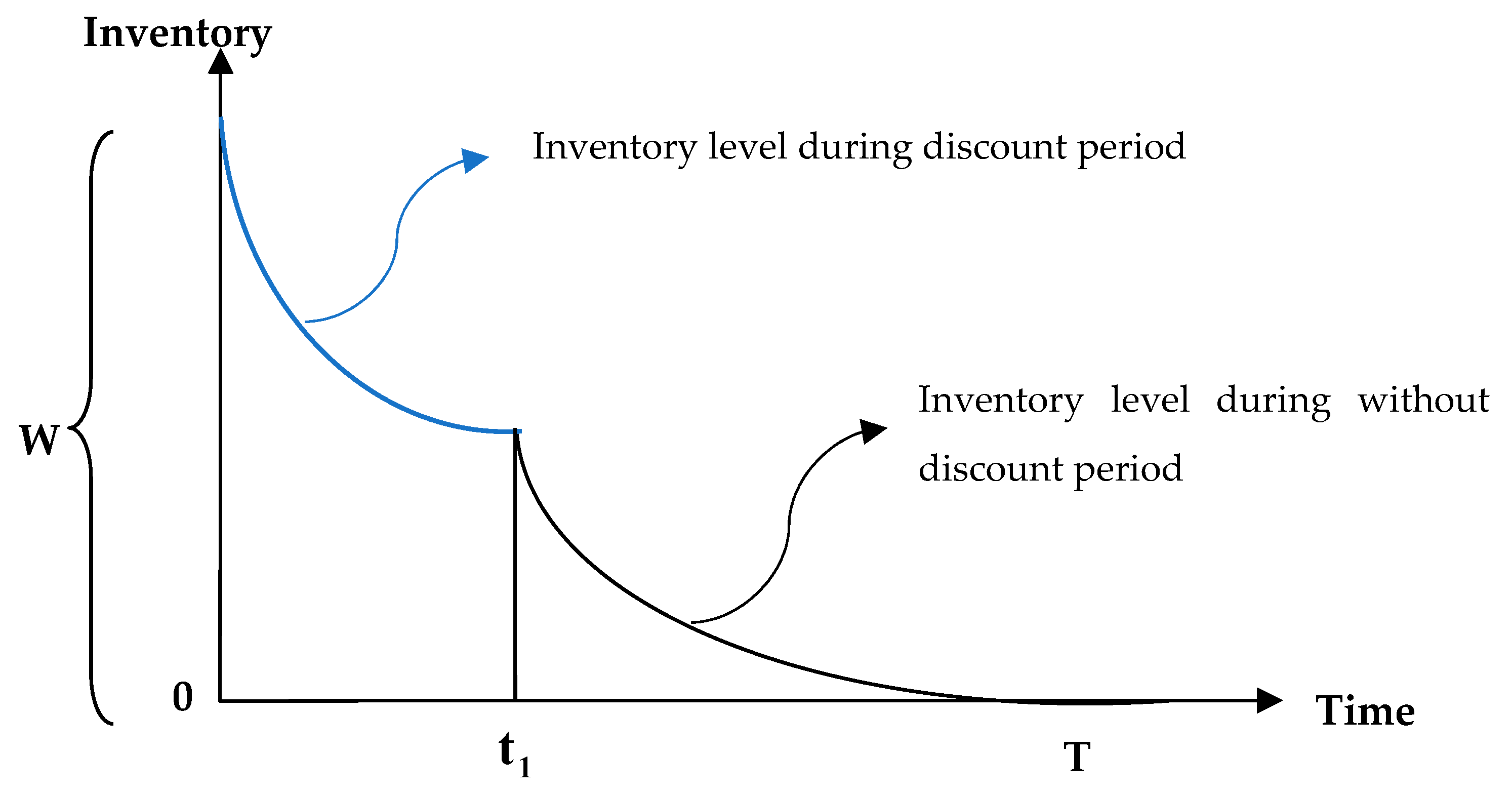

| Notations | Units | Description |
|---|---|---|
| $/Cycle | Ordering cost per cycle | |
| $/Unit | Purchasing cost per unit | |
| $/Unit | Holding cost per unit per unit time | |
| Units/Cycle | Ordering quantity per cycle | |
| $/Cycle | Fixed transportation cost | |
| $/unit | Variable transportation cost | |
| Months | Discount time from the beginning of cycle | |
| Units | Demand function | |
| Units | inventory level at any time t where when i = 1, when i = 2 | |
| Constant | Discount rate on price of product | |
| $/Month | Total profit per unit time | |
| Decision variables | ||
| $/Unit | Selling price per unit of product | |
| Months | replenishment time. | |
| Optimal Solutions | |||
|---|---|---|---|
| 0 | 369.559 | 18.027 | 14,462.310 |
| 0.5 | 373.951 | 18.737 | 11,531.170 |
| 1 | 380.394 | 19.984 | 8643.954 |
| 1.5 | 392.878 | 23.020 | 5872.356 |
| 2 | 847.031 | 90.767 | 5190.119 |
| 2.5 | 648.980 | 70.028 | 2489.949 |
| 3 | 575.141 | 60.376 | 217.017 |
| 3.5 | … | … | … |
| N.B. (…) means infeasible solution | |||
| Parameter | % Change | With Discount | Without Discount | |||
|---|---|---|---|---|---|---|
| −20 | 372.922 | 18.560 | 12,122.700 | 14,470.070 | −16.22% | |
| −10 | 372.937 | 18.563 | 12,118.930 | 14,466.190 | −16.23% | |
| 10 | 372.966 | 18.568 | 12,111.390 | 14,458.430 | −16.23% | |
| 20 | 372.980 | 18.571 | 12,107.620 | 14,454.540 | −16.24% | |
| −20 | 370.786 | 17.408 | 9576.597 | 12,056.410 | −20.57% | |
| −10 | 371.828 | 18.004 | 10,858.480 | 13,266.230 | −18.15% | |
| 10 | 374.111 | 19.095 | 13,351.800 | 15,647.190 | −14.67% | |
| 20 | 372.951 | 18.566 | 12,115.160 | 16,822.770 | −27.98% | |
| −20 | 352.280 | 15.439 | 18,783.750 | 21,230.690 | −11.53% | |
| −10 | 362.195 | 16.765 | 15,297.790 | 17,712.490 | −13.63% | |
| 10 | 386.700 | 21.553 | 9294.282 | 11,516.450 | −19.30% | |
| 20 | … | … | … | … | … | |
| −20 | 372.902 | 18.556 | 12,145.900 | 14,496.270 | −16.21% | |
| −10 | 372.927 | 18.561 | 12,130.530 | 14,479.290 | −16.22% | |
| 10 | 372.976 | 18.570 | 12,099.800 | 14,445.330 | −16.24% | |
| 20 | 373.000 | 18.575 | 12,084.430 | 14,428.360 | −16.25% | |
| −20 | … | … | … | … | … | |
| −10 | 356.797 | 23.530 | 8425.492 | 10,169.700 | −17.15% | |
| 10 | 396.470 | 16.294 | 16,417.390 | 19,396.440 | −15.36% | |
| 20 | 421.316 | 14.743 | 21,174.930 | 24,849.270 | −14.79% | |
| −20 | 440.256 | 15.430 | 23,542.580 | 26,605.330 | −11.51% | |
| −10 | 402.391 | 16.758 | 17,024.210 | 19,709.090 | −13.62% | |
| 10 | 351.622 | 21.574 | 8430.589 | 10,448.790 | −19.32% | |
| 20 | … | … | … | … | … | |
| −20 | 372.562 | 18.559 | 12,069.910 | 14,412.980 | −16.26% | |
| −10 | 372.757 | 18.562 | 12,092.530 | 14,437.640 | −16.24% | |
| 10 | 373.146 | 18.569 | 12,137.790 | 14,486.980 | −16.22% | |
| 20 | 373.341 | 18.573 | 12,160.430 | 14,511.660 | −16.20% | |
| −20 | 368.712 | 18.256 | 11,801.260 | 14,129.450 | −16.48% | |
| −10 | 370.784 | 18.405 | 11,957.220 | 14,294.920 | −16.35% | |
| 10 | 375.226 | 18.739 | 12,275.230 | 14,631.730 | −16.11% | |
| 20 | 377.627 | 18.928 | 12,437.600 | 14,803.340 | −15.98% | |
| −20 | 372.370 | 20.753 | 12,731.030 | 14,804.060 | −14.00% | |
| −10 | 372.435 | 19.538 | 12,496.160 | 14,709.430 | −15.05% | |
| 10 | 373.801 | 17.786 | 11,596.440 | 14,070.370 | −17.58% | |
| 20 | 374.922 | 17.169 | 10,948.390 | 13,540.900 | −19.15% | |
| −20 | 365.411 | 17.276 | 14,929.950 | 16,843.630 | −11.36% | |
| −10 | 368.994 | 17.861 | 13,503.730 | 15,639.110 | −13.65% | |
| 10 | 377.446 | 19.446 | 10,770.670 | 13,315.880 | −19.11% | |
| 20 | 382.828 | 20.617 | 9479.562 | 12,203.190 | −22.32% | |
| −20 | 372.948 | 18.565 | 12,116.020 | 14,463.200 | −16.23% | |
| −10 | 372.950 | 18.565 | 12,115.590 | 14,462.750 | −16.23% | |
| 10 | 372.953 | 18.566 | 12,114.730 | 14,461.860 | −16.23% | |
| 20 | 372.955 | 18.566 | 12,114.300 | 14,461.420 | −16.23% | |
| −20 | 372.928 | 18.561 | 12,121.190 | 14,468.520 | −16.22% | |
| −10 | 372.940 | 18.564 | 12,118.180 | 14,465.410 | −16.23% | |
| 10 | 372.963 | 18.568 | 12,112.150 | 14,459.200 | −16.23% | |
| 20 | 372.974 | 18.570 | 12,109.130 | 14,456.100 | −16.24% | |
| N.B. (…) means infeasible solution | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miah, M.S.; Islam, M.M.; Hasan, M.; Mashud, A.H.M.; Roy, D.; Sana, S.S. A Discount Technique-Based Inventory Management on Electronics Products Supply Chain. J. Risk Financial Manag. 2021, 14, 398. https://doi.org/10.3390/jrfm14090398
Miah MS, Islam MM, Hasan M, Mashud AHM, Roy D, Sana SS. A Discount Technique-Based Inventory Management on Electronics Products Supply Chain. Journal of Risk and Financial Management. 2021; 14(9):398. https://doi.org/10.3390/jrfm14090398
Chicago/Turabian StyleMiah, Md. Sujan, Md. Mominul Islam, Mahmudul Hasan, Abu Hashan Md. Mashud, Dipa Roy, and Shib Sankar Sana. 2021. "A Discount Technique-Based Inventory Management on Electronics Products Supply Chain" Journal of Risk and Financial Management 14, no. 9: 398. https://doi.org/10.3390/jrfm14090398
APA StyleMiah, M. S., Islam, M. M., Hasan, M., Mashud, A. H. M., Roy, D., & Sana, S. S. (2021). A Discount Technique-Based Inventory Management on Electronics Products Supply Chain. Journal of Risk and Financial Management, 14(9), 398. https://doi.org/10.3390/jrfm14090398









