The Incidence of Spillover Effects during the Unconventional Monetary Policies Era
Abstract
1. Introduction
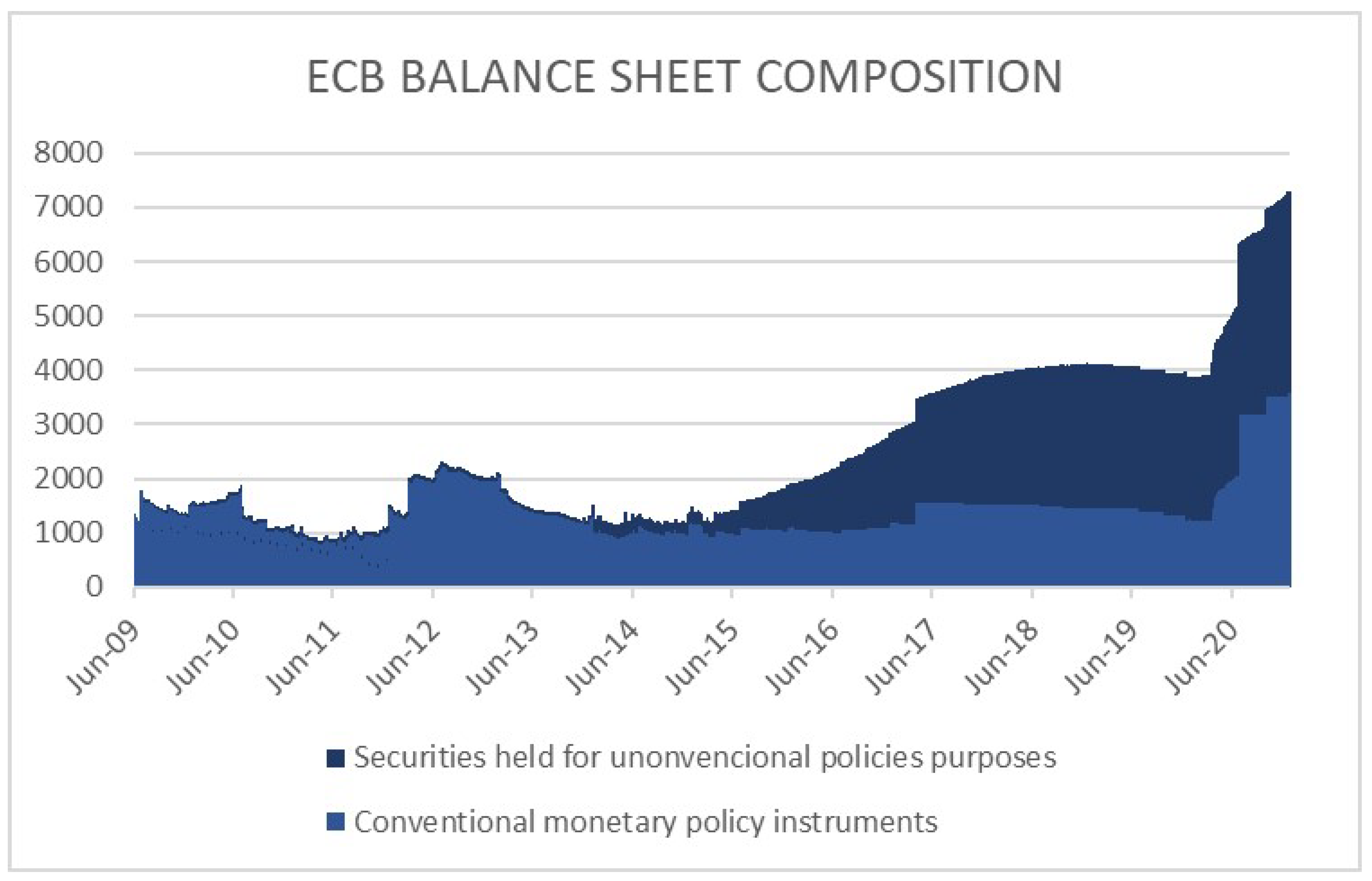
2. A Brief Overview of the ECB’s Unconventional Monetary Policy
3. The Multiplicative Error Model
3.1. The MS-AMEMX
4. Empirical Application
4.1. The Dataset
4.2. Estimation Results
4.3. Out-of-Sample Analysis
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | |
| 2 | The program—consisting of outright transactions of government bond with a maturity up to 3 years in the secondary market—was never implemented because of the tight conditions it required. In particular, according to the “conditionality condition”, a Eurozone country could have requested for entry in the program if it had been in serious and blatant macroeconomic distress. |
| 3 | It concerned corporate bonds issued by companies different from credit institutions with a minimum BBB rating and a remaining maturity between 6 months and 30 years. |
| 4 | Including both central and local government bonds. |
| 5 | In any case, the program will last up to the end of March 2022. |
| 6 | Given this assumption, the error term has a unit conditional mean, whereas its variance is equal to . |
| 7 | Actually, this condition for stationarity could be considered too strong. Indeed, Gallo and Otranto (2018) show how—given the properties of stationarity and ergodicity of the MS GARCH model (Francq et al. (2001))—the necessary condition for the MS-AMEM to be stationary and ergodic is , where represents the ergodic probability of each regime. |
| 8 | Given that in the MEM framework one does not need to resort to logs, the GJR–GARCH model should be preferred to other GARCH specifications such as the EGARCH. As regards other specifications, the GJR-GARCH coincides with the TGARCH (Zakoian 1994) when the squared variables are considered. |
| 9 | All the data are provided by the Oxford Man’s Institute: https://realized.oxford-man.ox.ac.uk/data/download. |
| 10 | Quantitative data are available at: https://www.ecb.europa.eu/stats/policy_and_exchange_rates/minimum_reserves/html/index.en.html. |
| 11 | Information on monetary policy announcements is available at: https://www.ecb.europa.eu/press/pr/activities/mopo/html/index.en.html. |
| 12 | In particular, on these days, the value of the belongs to the last percentile of the series. |
| 13 | As given by . |
| 14 | The smoothed probabilities are defined as an ex post measure of how likely the volatility process is in a certain state at time t, given the full information set (Hamilton 1994, chp. 22). |
| 15 | Estimation results obtained from the two sub-samples are available upon request. In general, results do not change significantly, with coefficients ( and , in particular) that are still significant and enter the model with the expected sign. We interpret this result as a robustness check about the sensitivity of the estimated coefficients. |
| 16 | This conclusion is supported by the fact that, by estimating our model through the ECB’s total asset growth as a proxy for the balance sheet size, we obtain a non-significant coefficient. Estimation results are available upon request. |
References
- Altavilla, Carlo, Domenico Giannone, and Michele Lenza. 2014. The Financial and Macroeconomic Effects of OMT. announcements. ECB Working Paper No. 1707. Rome: European Central Bank. [Google Scholar]
- Apostolou, Apostolos, and John Beirne. 2017. Volatility Spillovers of Federal Reserve and ECB Balance Sheet Expansions to Emerging Market Economies. ECB Working Paper No. 2044. Rome: European Central Bank. [Google Scholar]
- Baele, Lieven. 2005. Volatility spillover effects in european equity markets. Journal of Financial and Quantitative Analysis 40: 373–401. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., Peter Reinhard Hansen, Asger Lunde, and Neil Shephard. 2008. Designing realised kernels to measure the ex-post variation of equity prices in the presence of noise. Econometrica 76: 1481–536. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bomfim, Antulio N. 2003. Pre-announcement effects, news effects, and volatility: Monetary policy and the stock market. Journal of Banking & Finance 27: 133–51. [Google Scholar]
- Brownlees, Christian T., Fabrizio Cipollini, and Giampiero M. Gallo. 2011. Intra-daily volume modeling and prediction for algorithmic trading. Journal of Financial Econometrics 9: 489–518. [Google Scholar] [CrossRef]
- Brownlees, Christian T., Fabrizio Cipollini, and Giampiero M. Gallo. 2012. Multiplicative Error Models. In Volatility Models and Their Applications. Edited by Luc Bauwens, Christian M. Hafner and Sébastien Laurent. Hoboken: John Wiley & Sons, pp. 223–47. [Google Scholar]
- Burriel, Pablo, and Alessandro Galesi. 2018. Uncovering the heterogeneous effects of ECB unconventional monetary policies across euro area countries. European Economic Review 101: 210–29. [Google Scholar] [CrossRef]
- Chan, Kam F., and Philip Gray. 2018. Volatility jumps and macroeconomic news announcements. Journal of Futures Markets 38: 881–97. [Google Scholar] [CrossRef]
- Chen, Han, Vasco Cúrdia, and Andrea Ferrero. 2012. The macroeconomic effects of large-scale asset purchase programmes. The Economic Journal 122: F289–F315. [Google Scholar] [CrossRef]
- Ciarlone, Alessio, and Andrea Colabella. 2018. Asset Price Volatility in EU-6 Economies: How Large Is the Role Played by the ECB? Bank of Italy Temi di Discussione Working Paper No. 1175. Rome: Banca D’italia. [Google Scholar]
- Curdia, Vasco, and Michael Woodford. 2011. The central-bank balance sheet as an instrument of monetary policy. Journal of Monetary Economics 58: 54–79. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Roberto S. Mariano. 1995. Comparing predictive accuracy. Journal of Business & Economic Statistics 13: 253–63. [Google Scholar]
- Diebold, Francis X., and James A. Nason. 1990. Nonparametric exchange rate prediction? Journal of International Economics 28: 315–32. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2009. Measuring financial asset return and volatility spillovers, with application to global equity markets. The Economic Journal 119: 158–71. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2012. Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting 28: 57–66. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yılmaz. 2014. On the network topology of variance decompositions: Measuring the connectedness of financial firms. Journal of Econometrics 182: 119–34. [Google Scholar] [CrossRef]
- Edwards, Sebastian. 1998. Interest rate volatility, contagion and convergence: An empirical investigation of the cases of Argentina, Chile and Mexico. Journal of Applied Economics 1: 55–86. [Google Scholar] [CrossRef][Green Version]
- Edwards, Sebastian, and Raul Susmel. 2001. Volatility dependence and contagion in emerging equity markets. Journal of Development Economics 66: 505–32. [Google Scholar] [CrossRef]
- Edwards, Sebastian, and Raul Susmel. 2003. Interest-rate volatility in emerging markets. Review of Economics and Statistics 85: 328–48. [Google Scholar] [CrossRef]
- Engle, Robert F. 2002. New frontiers for ARCH models. Journal of Applied Econometrics 17: 425–46. [Google Scholar] [CrossRef]
- Engle, Robert F., and Giampiero M. Gallo. 2006. A multiple indicators model for volatility using intra-daily data. Journal of Econometrics 131: 3–27. [Google Scholar] [CrossRef]
- Engle, Robert F., Giampiero M. Gallo, and Margherita Velucchi. 2012. Volatility spillovers in East Asian financial markets: A MEM based approach. Review of Economics and Statistics 94: 222–33. [Google Scholar] [CrossRef]
- Engle, Robert F., Takatoshi Ito, and Wen-Ling Lin. 1990. Meteor showers or heat waves?: Heteroskedastic intra daily volatility in the foreign exchange market. Econometrica 58: 1749–78. [Google Scholar] [CrossRef]
- Eser, Fabian, and Bernd Schwaab. 2016. Evaluating the impact of unconventional monetary policy measures: Empirical evidence from the ECB’s securities markets programme. Journal of Financial Economics 119: 147–67. [Google Scholar] [CrossRef]
- Forbes, Kristin J., and Roberto Rigobon. 2002. No contagion, only interdependence: Measuring stock market comovements. The Journal of Finance 57: 2223–61. [Google Scholar] [CrossRef]
- Francq, Christian, Michel Roussignol, and Jean-Michel Zakoïan. 2001. Conditional heteroskedasticity driven by hidden Markov chains. Journal of Time Series Analysis 22: 197–220. [Google Scholar] [CrossRef]
- Fratzscher, Marcel, Marco Lo Duca, and Roland Straub. 2016. ECB unconventional monetary policy: Market impact and international spillovers. IMF Economic Review 64: 36–74. [Google Scholar] [CrossRef]
- Gallo, Giampiero M., and Edoardo Otranto. 2008. Volatility spillovers, interdependence and comovements: A Markov switching approach. Computational Statistics & Data Analysis 52: 3011–26. [Google Scholar] [CrossRef]
- Gallo, Giampiero M., and Edoardo Otranto. 2015. Forecasting realized volatility with changing average levels. International Journal of Forecasting 31: 620–34. [Google Scholar] [CrossRef]
- Gallo, Giampiero M., and Edoardo Otranto. 2018. Combining sharp and smooth transitions in volatility dynamics: A fuzzy regime approach. Journal of the Royal Statistical Society: Series C (Applied Statistics) 67: 549–73. [Google Scholar] [CrossRef]
- Gambacorta, Leonardo, Boris Hofmann, and Gert Peersman. 2014. The effectiveness of unconventional monetary policy at the zero lower bound: A cross-country analysis. Journal of Money, Credit and Banking 46: 615–42. [Google Scholar] [CrossRef]
- Georgiadis, Georgios, and Johannes Gräb. 2016. Global financial market impact of the announcement of the ECB’s asset purchase programme. Journal of Financial Stability 26: 257–65. [Google Scholar] [CrossRef]
- Ghysels, Eric, Julien Idier, Simone Manganelli, and Olivier Vergote. 2017. A high-frequency assessment of the ECB Securities Markets Programme. Journal of the European Economic Association 15: 218–43. [Google Scholar] [CrossRef]
- Giudici, Paolo, Paolo Pagnottoni, and Gloria Polinesi. 2020. Network models to enhance automated cryptocurrency portfolio management. Frontiers in Artificial Intelligence 3: 22. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., Ravi Jagannanthan, and David E. Runkle. 1993. On the relation between the expected value and the volatility of the nominal excess return on stocks. The Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Hamilton, James D. 1989. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 57: 357–84. [Google Scholar] [CrossRef]
- Hamilton, James D. 1994. Time Series Analysis. Princeton: Princeton University Press. [Google Scholar]
- Hansen, Peter Reinhard. 2010. A winner’s curse for econometric models: On the joint distribution of in-sample fit and out-of-sample fit and its implications for model selection. Research Paper 1: 39. [Google Scholar]
- Joyce, Michael, Ana Lasaosa, Ibrahim Stevens, and Matthew Tong. 2011. The financial market impact of quantitative easing in the UK. International Journal of Central Banking 7: 113–61. [Google Scholar]
- Kapetanios, George, Haroon Mumtaz, Ibrahim Stevens, and Konstantinos Theodoridis. 2012. Assessing the economy-wide effects of quantitative easing. The Economic Journal 122: F316–F347. [Google Scholar] [CrossRef]
- Kenourgios, Dimitris, Stephanos Papadamou, and Dimitrios Dimitriou. 2015. Intraday exchange rate volatility transmissions across QE announcements. Finance Research Letters 14: 128–34. [Google Scholar] [CrossRef]
- Khalifa, Ahmed A. A., Shawkat Hammoudeh, and Edoardo Otranto. 2014. Patterns of volatility transmissions within regime switching across GCC and global markets. International Review of Economics & Finance 29: 512–24. [Google Scholar]
- Kim, Chang-Jin. 1994. Dynamic linear models with Markov switching. Journal of Econometrics 60: 1–22. [Google Scholar] [CrossRef]
- Krishnamurthy, Arvind, Stefan Nagel, and Annette Vissing-Jorgensen. 2018. ECB policies involving government bond purchases: Impact and channels. Review of Finance 22: 1–44. [Google Scholar] [CrossRef]
- Lacava, Demetrio, Giampiero M. Gallo, and Edoardo Otranto. 2020. Measuring the Effects of Unconventional Policies on Stock Market Volatility. CRENoS Working Paper 202006. Sardinia: Centre for North South Economic Research, Universiy of Cagliari and Sassari. [Google Scholar]
- Lane, Philip R. 2012. The european sovereign debt crisis. Journal of Economic Perspectives 26: 49–68. [Google Scholar] [CrossRef]
- Otranto, Edoardo. 2015. Capturing the spillover effect with multiplicative error models. Communications in Statistics-Theory and Methods 44: 3173–91. [Google Scholar] [CrossRef]
- Pagnottoni, Paolo. 2019. Neural network models for Bitcoin option pricing. Frontiers in Artificial Intelligence 2: 5. [Google Scholar] [CrossRef]
- Papadamou, Stephanos, Nikolaos A. Kyriazis, and Panayiotis G. Tzeremes. 2019a. Spillover effects of US QE and QE tapering on African and middle eastern stock indices. Journal of Risk and Financial Management 12: 57. [Google Scholar] [CrossRef]
- Papadamou, Stephanos, Nikolaos A. Kyriazis, and Panayiotis G. Tzeremes. 2019b. Unconventional monetary policy effects on output and inflation: A meta-analysis. International Review of Financial Analysis 61: 295–305. [Google Scholar] [CrossRef]
- Papadamou, Stephanos, Nikolaos A. Kyriazis, and Panayiotis G. Tzeremes. 2019c. USnon-linear causal effects on global equity indices in normal times versus unconventional eras. International Economics and Economic Policy 17: 1–27. [Google Scholar]
- Patton, Andrew J. 2011. Volatility forecast comparison using imperfect volatility proxies. Journal of Econometrics 160: 246–56. [Google Scholar] [CrossRef]
- Peersman, Gert. 2011. Macroeconomic Effects of Unconventional Monetary Policy in the Euro Area. CESifo Working Paper Series No. 3589. Available online: https://ideas.repec.org/p/ces/ceswps/_3589.html (accessed on 26 November 2020).
- Peralta, Gustavo, and Abalfazl Zareei. 2016. A network approach to portfolio selection. Journal of Empirical Finance 38: 157–80. [Google Scholar] [CrossRef]
- Pichler, Anton, Sebastian Poledna, and Stefan Thurner. 2021. Systemic risk-efficient asset allocations: Minimization of systemic risk as a network optimization problem. Journal of Financial Stability 52: 100809. [Google Scholar] [CrossRef]
- Shogbuyi, Abiodun, and James M. Steeley. 2017. The effect of quantitative easing on the variance and covariance of the UK and US equity markets. International Review of Financial Analysis 52: 281–91. [Google Scholar] [CrossRef]
- Steeley, James M., and Alexander Matyushkin. 2015. The effects of quantitative easing on the volatility of the gilt-edged market. International Review of Financial Analysis 37: 113–28. [Google Scholar] [CrossRef]
- White, Halbert. 1982. Maximum likelihood estimation of misspecified models. Econometrica 50: 1–25. [Google Scholar] [CrossRef]
- Wu, Jing Cynthia, and Fan Dora Xia. 2016. Measuring the macroeconomic impact of monetary policy at the zero lower bound. Journal of Money, Credit and Banking 48: 253–91. [Google Scholar] [CrossRef]
- Zakoian, Jean-Michel. 1994. Threshold heteroskedastic models. Journal of Economic Dynamics and Control 18: 931–55. [Google Scholar] [CrossRef]



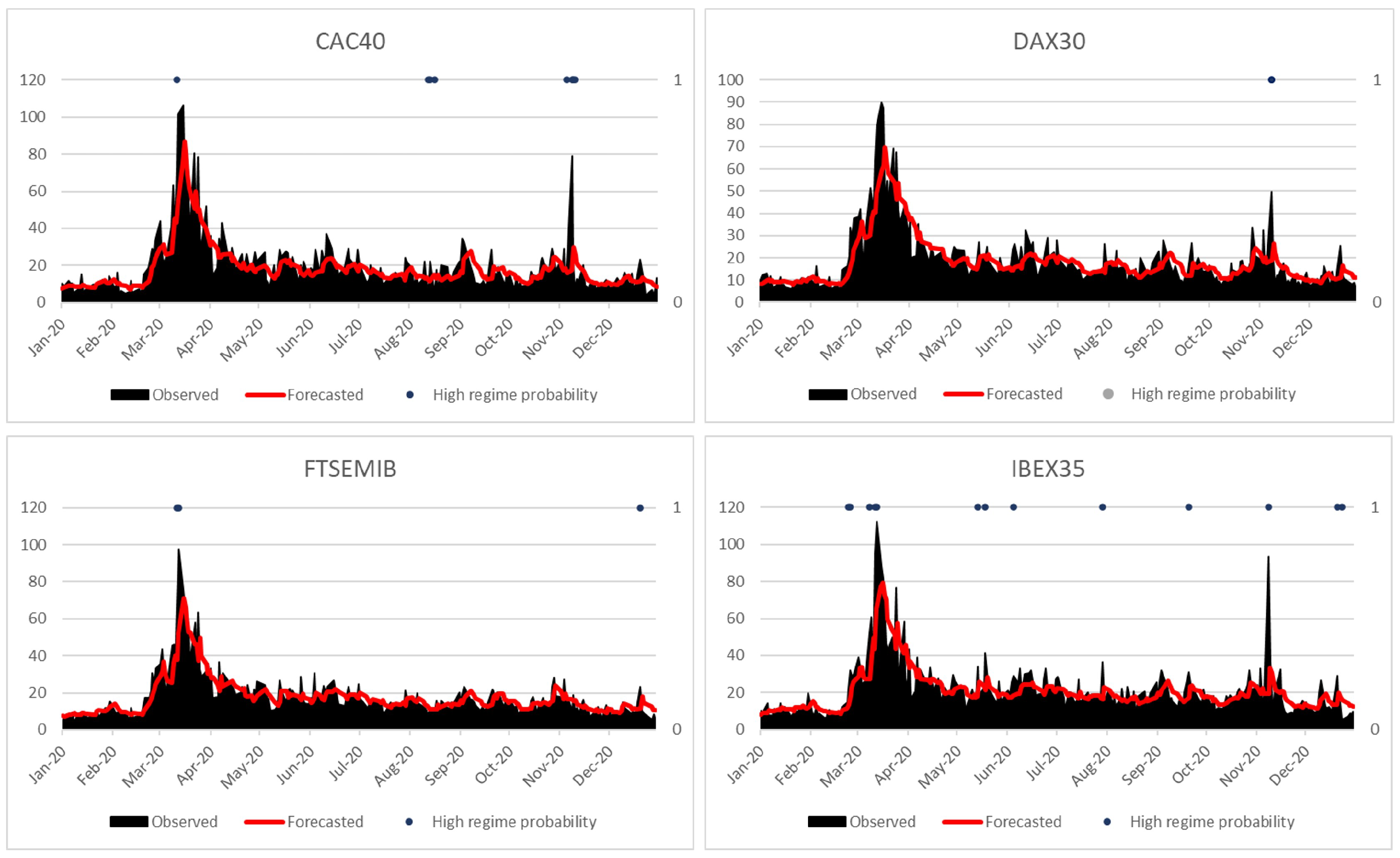
| CAC40 | DAX30 | FTSEMIB | IBEX35 | |
|---|---|---|---|---|
| Mean | 14.16 | 14.369 | 15.569 | 17.024 |
| Min | 1.102 | 2.141 | 1.578 | 2.974 |
| Max | 106.37 | 89.92 | 97.699 | 148.61 |
| St.Dev. | 8.616 | 8.031 | 8.243 | 9.768 |
| Skewness | 3.106 | 2.761 | 2.458 | 3.379 |
| Kurtosis | 18.797 | 14.823 | 11.432 | 24.285 |
| N. observations | 2882 | 2853 | 2857 | 2877 |
| CAC40 | DAX30 | FTSEMIB | IBEX35 | |
|---|---|---|---|---|
| 0.920 | 0.957 | 1.224 | 1.092 | |
| (0.198) | (0.249) | (0.291) | (0.243) | |
| 0.188 | 0.119 | 0.286 | 0.236 | |
| (0.026) | (0.225) | (0.028) | (0.028) | |
| 0.69 | 0.693 | 0.594 | 0.662 | |
| (0.032) | (0.024) | (0.035) | (0.034) | |
| 0.104 | 0.092 | 0.074 | 0.066 | |
| (0.013) | (0.011) | (0.011) | (0.012) | |
| 7.474 | 9.795 | 10.807 | 9.113 | |
| (0.256) | (0.542) | (0.509) | (0.342) | |
| p-values for Ljung-Box statistics | ||||
| Ljung–Box 1 | 0.019 | 0.053 | 0.105 | 0.002 |
| Ljung–Box 5 | 0.08 | 0.023 | 0.723 | 0.017 |
| Ljung–Box 10 | 0.118 | 0.008 | 0.871 | 0.102 |
| CAC40 | DAX30 | FTSEMIB | IBEX35 | |
|---|---|---|---|---|
| 1.358 | 1.136 | 1.876 | 1.739 | |
| (0.264) | (0.294) | (0.37) | (0.232) | |
| 0.156 | 0.178 | 0.286 | 0.215 | |
| (0.024) | (0.022) | (0.025) | (0.028) | |
| 0.633 | 0.666 | 0.517 | 0.611 | |
| (0.041) | (0.029) | (0.041) | (0.043) | |
| 0.112 | 0.091 | 0.074 | 0.072 | |
| (0.013) | (0.011) | (0.012) | (0.012) | |
| 0.069 | 0.036 | 0.052 | 0.047 | |
| (0.018) | (0.013) | (0.014) | (0.014) | |
| −0.853 | −0.448 | −1.337 | −1.305 | |
| (0.21) | (0.183) | (0.316) | (0.282) | |
| 1.48 | 1.104 | 2.228 | 2.042 | |
| (0.453) | (0.373) | (0.493) | (0.494) | |
| 7.74 | 9.991 | 11.371 | 9.513 | |
| (0.252) | (0.524) | (0.492) | (0.351) | |
| p-values for Ljung-Box statistics | ||||
| Ljung–Box 1 | 0.335 | 0.188 | 0.813 | 0.052 |
| Ljung–Box 5 | 0.324 | 0.087 | 0.899 | 0.073 |
| Ljung–Box 10 | 0.086 | 0.006 | 0.517 | 0.232 |
| CAC40 | DAX30 | FTSEMIB | IBEX35 | |
|---|---|---|---|---|
| 1.103 | 0.705 | 1.436 | 1.396 | |
| (0.184) | (0.109) | (0.239) | (0.242) | |
| 0.139 | 0.172 | 0.279 | 0.155 | |
| (0.02) | (0.018) | (0.025) | (0.029) | |
| 0.677 | 0.701 | 0.551 | 0.689 | |
| (0.037) | (0.027) | (0.04) | (0.041) | |
| 0.113 | 0.088 | 0.069 | 0.073 | |
| (0.011) | (0.008) | (0.01) | (0.009) | |
| 0.047 | 0.038 | 0.043 | 0.01 | |
| (0.016) | (0.011) | (0.014) | (0.019) | |
| 0.182 | 0.278 | 0.214 | 0.241 | |
| (0.11) | (0.119) | (0.081) | (0.069) | |
| −0.737 | −0.251 | −0.948 | −1.047 | |
| (0.158) | (0.102) | (0.206) | (0.209) | |
| 1.061 | 0.641 | 1.717 | 1.342 | |
| (0.387) | (0.305) | (0.398) | (0.374) | |
| 9.14 | 11.288 | 14.406 | 13.228 | |
| (0.513) | (0.429) | (1.338) | (1.105) | |
| 2.879 | 0.769 | 3.124 | 8.403 | |
| (0.909) | (0.785) | (1.888) | (1.259) | |
| 0.969 | 0.994 | 0.955 | 0.844 | |
| (0.032) | (0.005) | (0.038) | (0.086) | |
| 0.583 | 0.286 | 0.33 | 0.252 | |
| (0.381) | (0.238) | (0.201) | (0.154) | |
| p-values for Ljung-Box statistics | ||||
| Ljung–Box 1 | 0.417 | 0.529 | 0.875 | 0.004 |
| Ljung–Box 5 | 0.369 | 0.977 | 0.855 | 0.015 |
| Ljung–Box 10 | 0.424 | 0.994 | 0.977 | 0.127 |
| (a) | Spillover Effect | ||
|---|---|---|---|
| Full Sample | Sub-Sample | Sub-Sample | |
| 2009–2014 | 2015–2019 | ||
| CAC40 | 0.542 | 1.105 | 0.452 |
| DAX30 | 0.412 | 0.574 | 0.469 |
| FTSEMIB | 0.5 | 0.844 | 0.507 |
| IBEX35 | 0.268 | 0.46 | 0.475 |
| (b) | Unconventional Policy Effect | ||
| Full Sample | Sub-Sample | Sub-Sample | |
| 2009–2014 | 2015–2019 | ||
| CAC40 | −0.212 | −0.12 | −1.248 |
| DAX30 | −0.072 | −0.002 | −0.852 |
| FTSEMIB | −0.273 | 0.003 | −0.934 |
| IBEX35 | −0.301 | −0.121 | −1.53 |
| (c) | Net Effect | ||
| Full Sample | Sub-Sample | Sub-Sample | |
| 2009–2014 | 2015–2019 | ||
| CAC40 | 0.33 | 0.985 | −0.795 |
| DAX30 | 0.34 | 0.572 | −0.383 |
| FTSEMIB | 0.227 | 0.841 | −0.428 |
| IBEX35 | −0.033 | 0.339 | −1.055 |
| CAC40 | DAX30 | |||||
|---|---|---|---|---|---|---|
| AMEM | AMEMX | MS-AMEMX | AMEM | AMEMX | MS-AMEMX | |
| LogLik | −7712.012 | −7663.943 | −7627.295 | −7365.365 | −7338.932 | −7254.689 |
| AIC | 5.853 | 5.819 | 5.794 | 5.643 | 5.626 | 5.564 |
| BIC | 5.864 | 5.837 | 5.821 | 5.655 | 5.643 | 5.591 |
| MSE | 30.357 | 29.222 | 29.481 | 23.847 | 23.352 | 23.17 |
| QLIKe | 0.068 | 0.066 | 0.066 | 0.052 | 0.051 | 0.052 |
| FTSEMIB | IBEX35 | |||||
| AMEM | AMEMX | MS-AMEMX | AMEM | AMEMX | MS-AMEMX | |
| LogLik | −7514.834 | −7446.347 | −7373.76 | −7970.565 | −7911.763 | −7860.52 |
| AIC | 5.749 | 5.699 | 5.647 | 6.065 | 6.023 | 5.987 |
| BIC | 5.76 | 5.717 | 5.674 | 6.076 | 6.041 | 6.014 |
| MSE | 28.327 | 27.47 | 27.817 | 42.957 | 41.452 | 41.859 |
| QLIKe | 0.047 | 0.045 | 0.045 | 0.056 | 0.053 | 0.054 |
| CAC40 | DAX30 | |||
|---|---|---|---|---|
| Model 1/Model 2 | t-Statistics | p-Value | t-Statistics | p-Value |
| AMEM/AMEMX | 1.999 | 0.023 | 1.792 | 0.037 |
| AMEM/MS-AMEMX | 1.349 | 0.089 | 0.846 | 0.199 |
| AMEMX/MS-AMEMX | 0.307 | 0.379 | -0.035 | 0.514 |
| FTSEMIB | IBEX35 | |||
| Model 1/Model 2 | t-Statistics | p-Value | t-Statistics | p-Value |
| AMEM/AMEMX | 1.548 | 0.062 | 2.233 | 0.013 |
| AMEM/MS-AMEMX | 1.355 | 0.088 | 1.328 | 0.093 |
| AMEMX/MS-AMEMX | 0.967 | 0.167 | 0.752 | 0.226 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lacava, D.; Scaffidi Domianello, L. The Incidence of Spillover Effects during the Unconventional Monetary Policies Era. J. Risk Financial Manag. 2021, 14, 242. https://doi.org/10.3390/jrfm14060242
Lacava D, Scaffidi Domianello L. The Incidence of Spillover Effects during the Unconventional Monetary Policies Era. Journal of Risk and Financial Management. 2021; 14(6):242. https://doi.org/10.3390/jrfm14060242
Chicago/Turabian StyleLacava, Demetrio, and Luca Scaffidi Domianello. 2021. "The Incidence of Spillover Effects during the Unconventional Monetary Policies Era" Journal of Risk and Financial Management 14, no. 6: 242. https://doi.org/10.3390/jrfm14060242
APA StyleLacava, D., & Scaffidi Domianello, L. (2021). The Incidence of Spillover Effects during the Unconventional Monetary Policies Era. Journal of Risk and Financial Management, 14(6), 242. https://doi.org/10.3390/jrfm14060242





