An Artificial Intelligence Approach to the Valuation of American-Style Derivatives: A Use of Particle Swarm Optimization
Abstract
1. Introduction
2. Monte Carlo in American-Style Derivative Pricing
2.1. The Longstaff–Schwartz Model
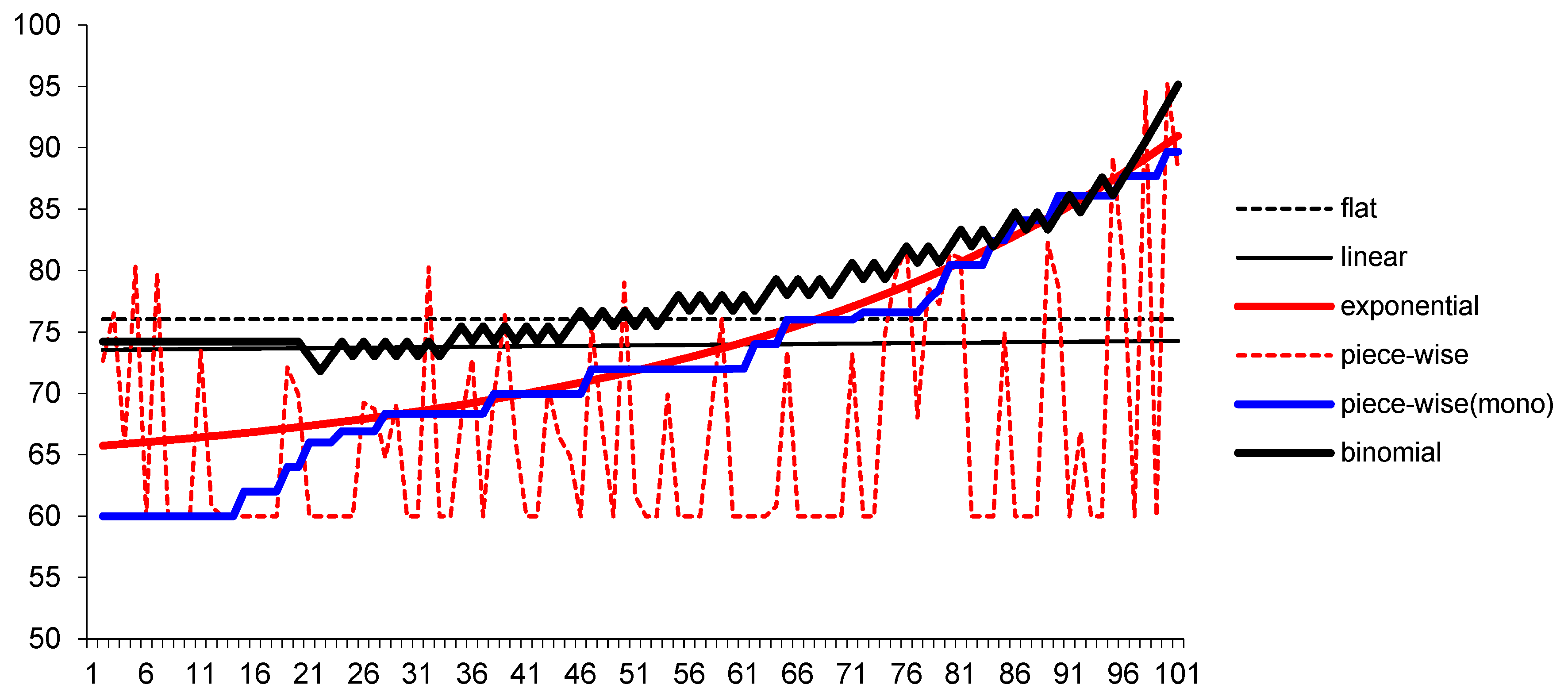
2.2. Explicit Boundary Method
- Constant: ;
- Linear: ;
- Exponential: ;
- Exponential-constant: ;
- Polynomial: ;
- Carr et al. (2008): .
3. Swarm Intelligence
3.1. What is AI?
- Swarm intelligence (birds, ants, bees, fish);
- Genetic algorithm (genes);
- Neural networks (neurons);
- Reinforcement learning (mice in a maze).
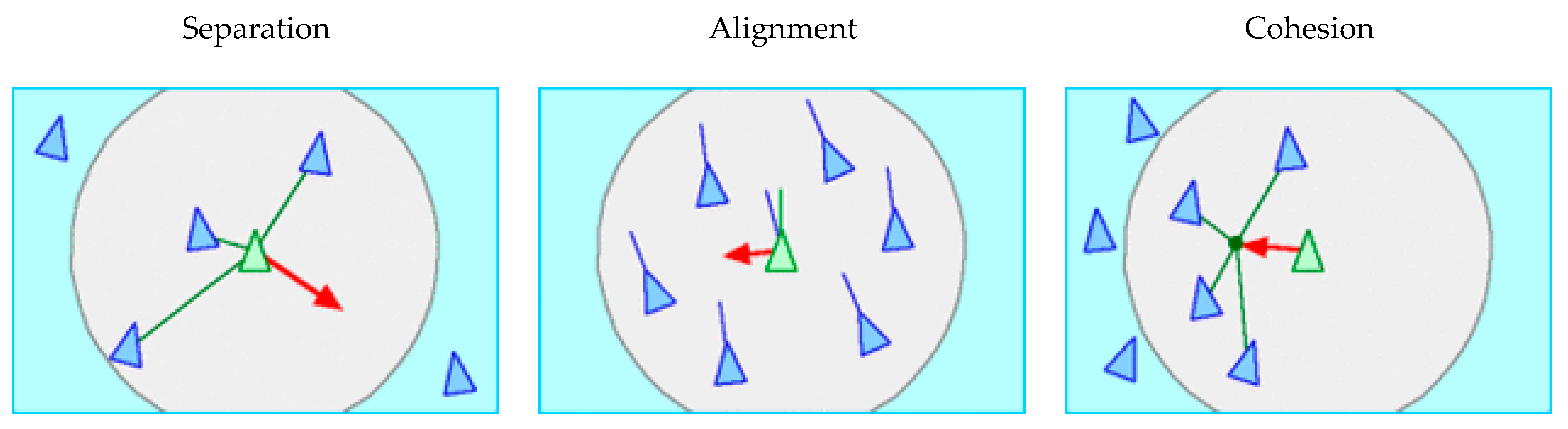
3.2. Swarm Intelligence
- be the th bird at time ;
- be a vector in the space representing the velocity of the th bird;
- be a vector in space representing the position (coordinates) of the th bird.
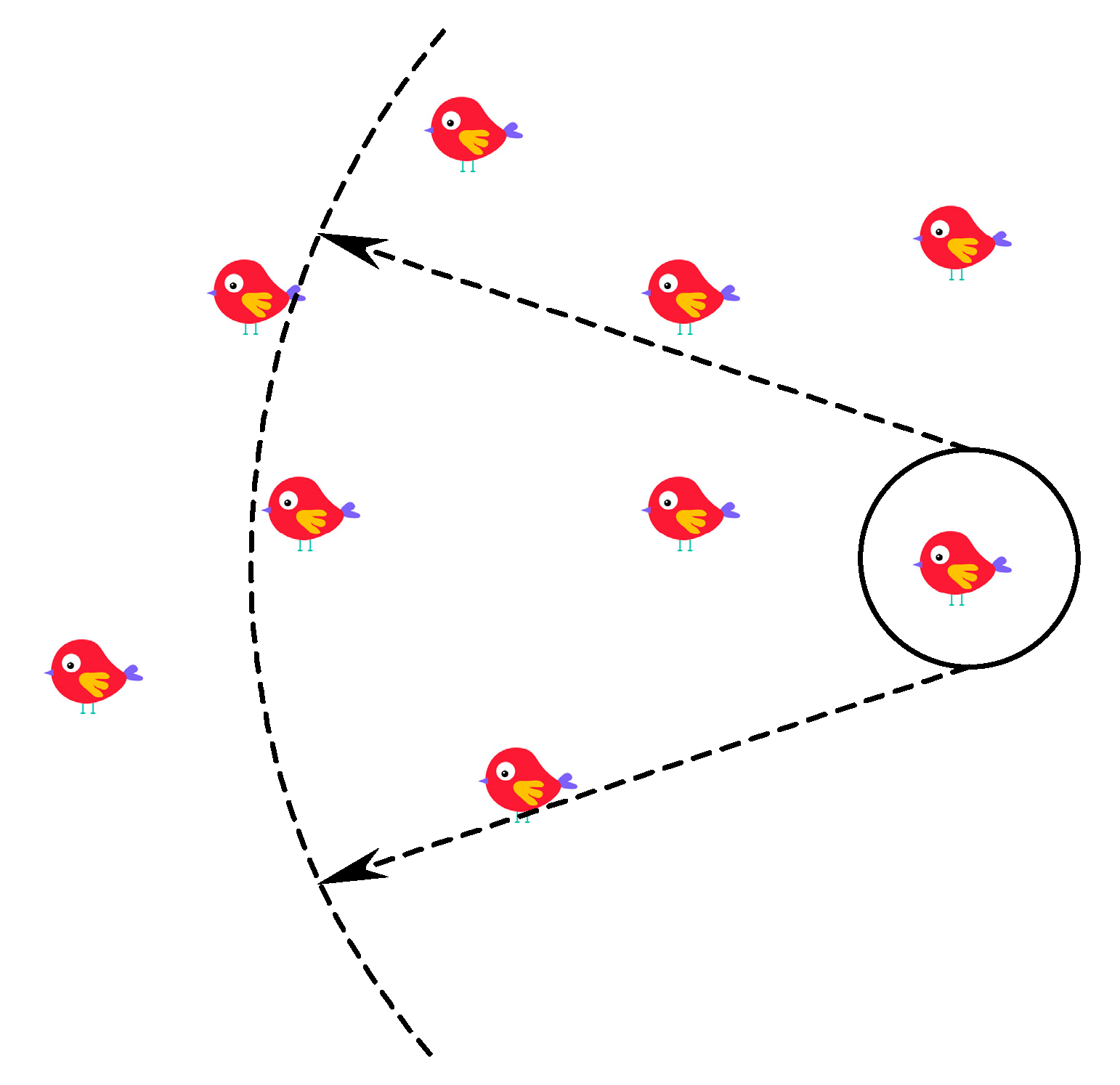 where the circled bird is referencing three nearby birds by the angle and the radius. The alignment and cohesion (we ignore the separation parameter for the moment) parameters are calculated as follows10:
where the circled bird is referencing three nearby birds by the angle and the radius. The alignment and cohesion (we ignore the separation parameter for the moment) parameters are calculated as follows10:3.3. Particle Swarm Optimization
- Modifications;16
- Population topology;17
- Hybridization;18
- Extensions;19
- Theoretical analysis;20
- Parallel implementation.21
4. American-style Derivative Pricing
4.1. Univariate
| Scheme 100. | 100 |
| strike price | 100 |
| volatility | 0.3 |
| risk-free rate | 0.03 |
| time to maturity | 1 |
| time steps | 100 |
| Monte Carlo paths | 10,000 |
4.2. Multivariate
| asset 1 | asset 2 | |
| price | 40 | 40 |
| volatility | 0.2 | 0.3 |
| strike | 35 | |
| time to maturity | 7/12 | |
| risk free rate | 0.03 | |
| correlation | 0.5 |
4.3. Path-Dependent
4.4. Computational Efficiency
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. American Call Option on Min/Max Will Never be Exercised Early
Appendix A.2. Option on Min/Max
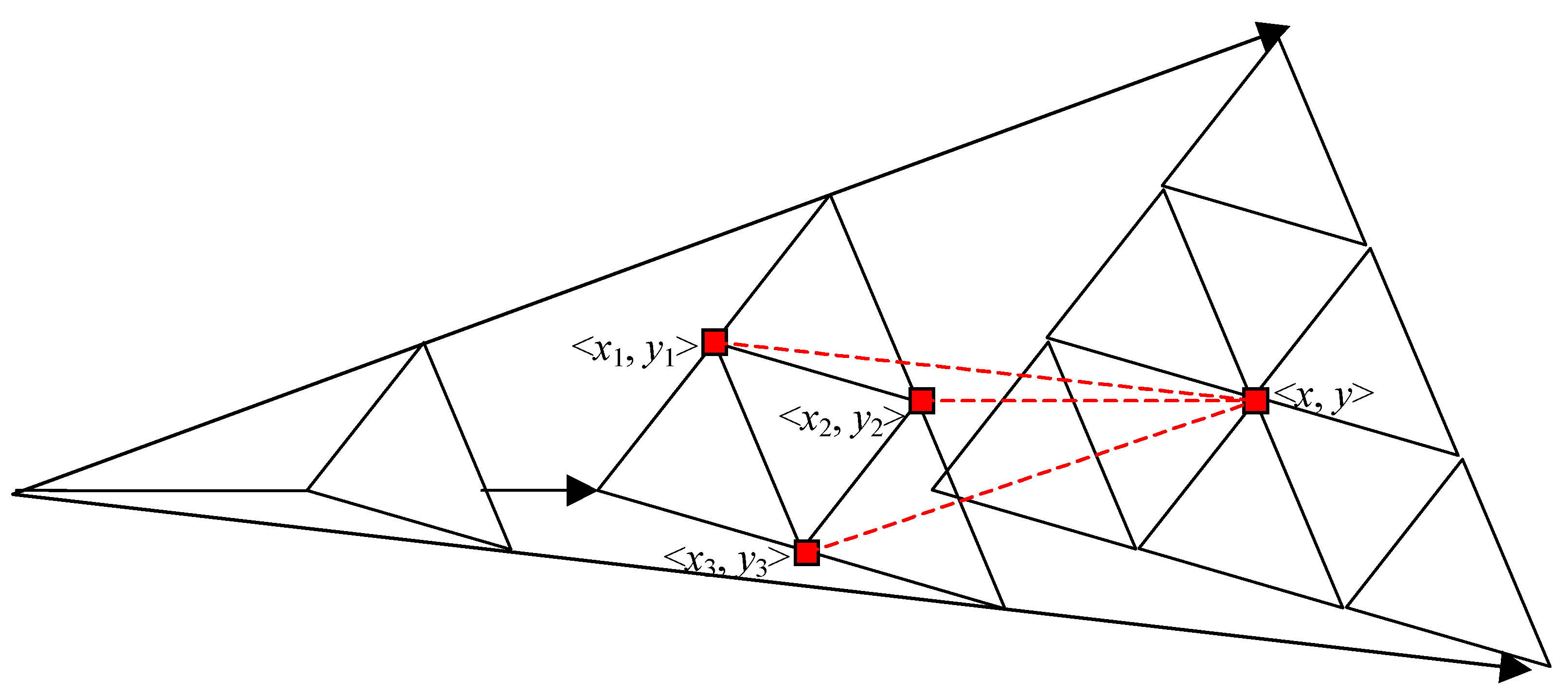
Appendix A.3. Illustration of the Chen–Chung–Yang Model
| num of assets | m = 1 | m = 2 | m = 3 | … | m = m |
| i | j | j | j | j | |
| 0 | 1 | 1 | 1 | 1 | |
| 1 | 2 | 3 | 4 | 5 | |
| 2 | 3 | 6 | 10 | 15 | |
| 3 | 4 | 10 | 20 | 35 | |
| … | |||||
| n | … |
References
- Boyle, Phelim P. 1988. A Lattice Framework for Option Pricing with Two State Variables. Journal of Financial And Quantitative Analysis 23: 1–12. [Google Scholar] [CrossRef]
- Boyle, Phelim P., Jeremy Evnine, and Stephen Gibbs. 1989. Numerical Evaluation of Multivariate Contingent Claims. The Review of Financial Studies 2: 241–50. [Google Scholar] [CrossRef]
- Carr, Peter. 1998. Randomizing and the American Put. Review of Financial Studies 11: 597–626. [Google Scholar] [CrossRef]
- Carr, Peter, Robert Jarrow, and Ravi Myneni. 2008. Alternative Characterizations of American Put Options. Financial Derivatives Pricing 2: 85–103. [Google Scholar]
- Chen, Ren-Raw, San-Lin Chung, and Tyler T. Yang. 2002. Option Pricing in a Multi-Asset, Complete Market Economy. The Journal of Financial and Quantitative Analysis 37: 649–66. [Google Scholar] [CrossRef][Green Version]
- Cox, John C., Stephen A. Ross, and Mark Rubinstein. 1979. Option Pricing, a Simplified Approach. Journal of Financial Economics 7: 229–63. [Google Scholar] [CrossRef]
- Dorigo, Marco, and Luca Maria Gambardella. 1997. Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem. IEEE Transactions on Evolutionary Computation 1: 53–66. [Google Scholar] [CrossRef]
- Dorigo, Marco, Vittorio Maniezzo, and Alberto Colorni. 1991. Ant System: An Autocatalytic Optimizing Process. Technical Report. Milano: Politecnico di Milano Department of Electronics, pp. 91–016. [Google Scholar]
- Eberhart, Russell C., and James Kennedy. 1995. A New Optimizer Using Particle Swarm Theory. Paper presented at the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, October 4–6. [Google Scholar]
- Eberhart, Russell C., and Yuhui Shi. 1998. A Modified Particle Swarm Pptimizer. Paper presented at 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, May 4–9. [Google Scholar]
- Huang, Kaihua. 2019. Particle Swarm Optimization Central Mass on Portfolio Construction. New York: Gabelli School of Business, Fordham University. [Google Scholar]
- Hull, John. 2015. Options, Futures and Other Derivatives. Upper Saddle River: Prentice Hall. [Google Scholar]
- Jamous, Razan A., Al-Aguizy Tharwat, Essam El Seidy, and Bayoumi Ibrahim Bayoumi. 2015. A New Particle Swarm with Center of Mass Optimization. International Journal of Engineering Research and Technology 4: 312–17. [Google Scholar]
- Kamrad, Bardia, and Peter Ritchken. 1991. Multinomial Approximating Models for Options with k State Variables. Management Science 37: 1640–52. [Google Scholar] [CrossRef]
- Kumar, Sajjan, Susmita Sau, Diptendu Pal, Bhimsen Tudu, Swadhin K. Mandal, and Nilanjan Chakraborty. 2013. “Parametric Performance Evaluation of Different Types of Particle Swarm Optimization Techniques Applied in Distributed Generation System. Paper presented at the International Conference on Frontiers of Intelligent Computing: Theory and Applications (FICTA), Odisa, India, January 14–16; pp. 349–56. [Google Scholar]
- Longstaff, Francis, and Eduardo Schwartz. 2001. Valuing American-style derivatives by Simulation. The Review of Financial Studies I 4: 113–47. [Google Scholar] [CrossRef]
- Nunes, João Pedro Vidal. 2009. Pricing American options under the constant elasticity of variance model and subject to bankruptcy. Journal of Financial and Quantitative Analysis 44: 1231–63. [Google Scholar] [CrossRef]
- Reynolds, Craig. 1987. Flocks, herds and schools: A distributed behavioral model. Paper presented the 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, July 27–31; Association for Computing Machinery. pp. 25–34. [Google Scholar]
- Stulz, Rene. 1982. Options on the Minimum or the Maximum of Two Risky Assets: Analysis and Applications. Journal of Financial Economics 10: 161–85. [Google Scholar] [CrossRef]
- Zhang, Yudong, Shuihua Wang, and Genlin Ji. 2015. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications. Mathematical Problems in Engineering 2015: 38. [Google Scholar] [CrossRef]
| 1 | By efficient, we refer to the balance between speed and accuracy. |
| 2 | For recent work, see Carr et al. (2008). See also Nunes (2009) for a nice review/comparison of various boundaries. |
| 3 | As a reminder, a continuation value in the option literature refers to the expected value of future maximum payoff at any given point in time. Since the continuation value is the expected future payoff, it is compared to the exercise value at the given time to see if (early) exercise is worthwhile. |
| 4 | In the case of put options, the quadratic function works very well. Yet, in other forms of payoff, Longstaff and Schwartz do not provide any guidance. |
| 5 | |
| 6 | |
| 7 | According to Wikipedia (footnote 6), Reynold created Boid in 1986: “Boids is an artificial life program, developed by Craig Reynolds in 1986, which simulates the flocking behaviour of birds.” |
| 8 | For example, see Google Scholar: https://scholar.google.com/scholar?q=boids+flocking+algorithm&hl=en&as_sdt=0&as_vis=1&oi=scholart |
| 9 | These reference birds are like “my leaders” for a given bird. |
| 10 | We ignore separation in our model because in our applications, particles can take the same coordinates (i.e., collision is allowed). |
| 11 | While this is out of the scope of this paper, we encourage the readers to view a popular YouTube clip on how drones use an artificial swarm: “Skynet’Drones Work Together for ‘Homeland Security” (https://www.youtube.com/watch?v=oDyfGM35ekc). |
| 12 | Similar to PSO, an ACO (ant colony optimization) by Dorigo et al. (1991) and ACS (ant colony system) by Dorigo and Gambardella (1997) are both based upon swarm intelligence. The first ant system was first developed by Dorigo et al. (1991) and then popularized by Dorigo and Gambardella (1997). |
| 13 | A brief analysis of the min/max option is provided in the Appendix A. |
| 14 | The reason is that as a particle is approaching the global best, the velocity should approach 0 (i.e., the particle should no longer move at the global optimum). |
| 15 | PSO can also vary in terms of parameterization such as center mass (see Jamous et al. 2015). |
| 16 | This includes quantum-behaved PSO, bare-bones PSO, chaotic PSO, and fuzzy PSO. |
| 17 | This includes von Neumann, ring, star, random, among others. |
| 18 | This is to combine PSO with genetic algorithm, simulated annealing, Tabu search, artificial immune system, ant colony algorithm, artificial bee colony, differential evolution, harmonic search, and biogeography-based optimization. |
| 19 | This includes multi-objective, constrained, discrete, and binary optimization. |
| 20 | This includes parameter selection and tuning, and convergence analysis. |
| 21 | This involves multi-core, multiprocessor, GPU, and cloud computing forms. |
| 22 | They are electrical and electronic engineering, automation control systems, communication theory, operations research, mechanical engineering, fuel and energy, medicine, chemistry, and biology. |
| 23 | Kumar et al. (2013) examines the performance of various PSO algorithms: Canonical PSO, Hierarchical PSO (HPSO), Time varying acceleration coefficient (TVAC) PSO, Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients (HPSO-TVAC), Stochastic inertia weight (Sto-IW) PSO, and Time varying inertia weight (TVIW) PSO have been used for comparative study. These versions of PSO vary only in parameterization. |
| 24 | |
| 25 | Certainly, we can increase the number of periods in the binomial model to achieve more accurate American values; however, this is not our main focus. |
| 26 | Note that time step 100, or , is equal to the maturity time, which is 1 (year) in the example. Hence, T26 = 0.26 and T74 = 0.74. |
| 27 | As mentioned in footnote 25, we can increase the number of steps in the binomial model to smooth the exercise boundary further. |
| 28 | For 4 assets, it requires over 1.6 billion nodes. |
| 29 | This problem has been solved by Chen et al. (2002). Later, we adopt their model as the benchmark for options on multiple assets. |
| 30 | We assume the readers are fairly familiar with the standard binomial model of Cox et al. (1979). The notation used here is quite standard (e.g., see Hull 2015) and straightforward. |
| 31 | Note that even in the simplest independence case, the number of nodes at the time step n is (n + 1)m. For example, for three periods, a four-asset model has 256 nodes as opposed to 35 nodes in the CCY model. |
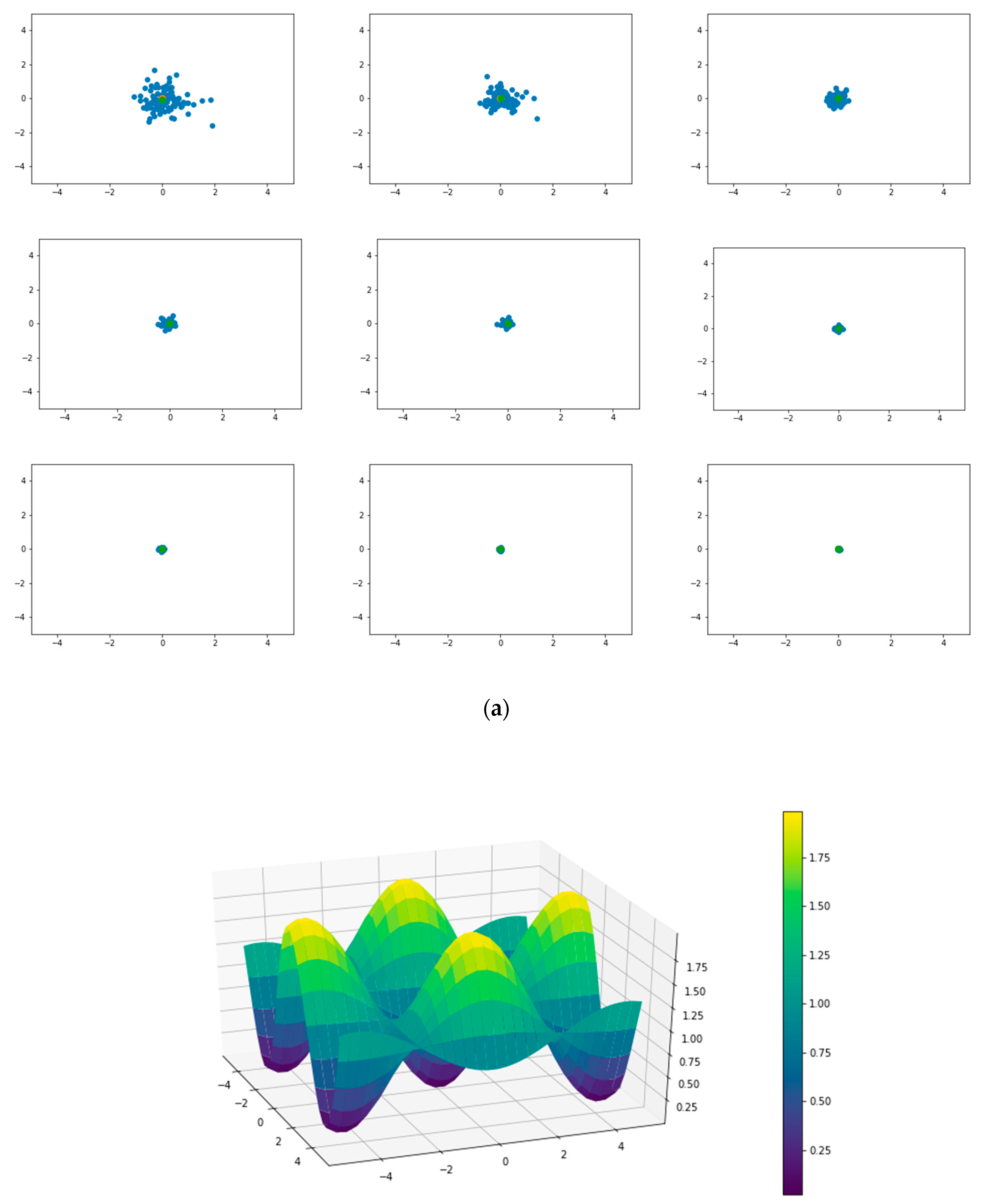

| stock price | 100 | |
| strike price | 100 | |
| volatility | 0.3 | |
| risk-free rate | 0.03 | |
| time to maturity | 1 | |
| time steps | 100 | |
| Monte Carlo paths | 10,000 | |
| Put Option | ||
| European | American | |
| Black–Scholes | 10.3278 | N.A |
| binomial (CRR) | 10.2984 | 10.5917 |
| Longstaff–Schwartz | 10.3656 | 10.6217 |
| PSO-flat | 10.3656 | 10.5591 |
| PSO-linear | 10.3656 | 10.5621 |
| PSO-exponential | 10.3656 | 10.6647 |
| PSO-piecewise | 10.3656 | 10.7714 |
| PSO-piecewise(restricted) | 10.3656 | 10.6908 |
| asset 1 | asset 2 | |
| price | 40 | 40 |
| volatility | 0.2 | 0.3 |
| strike | 35 | |
| time to maturity | 7/12 | |
| risk free rate | 0.03 | |
| correlation | 0.5 | |
| Min/Max Option | ||
| European | American | |
| BS | 0.1948 | N.A |
| binomial (CCY) | 0.1884 | 0.2557 |
| Longstaff–Schwartz | 0.1974 | 0.2386 |
| PSO-flat | 0.1974 | 0.2318 |
| PSO-linear | 0.1974 | 0.2349 |
| PSO-exponential | 0.1974 | 0.2361 |
| PSO-piecewise | 0.1974 | 0.2426 |
| PSO-piecewise(restricted) | 0.1974 | 0.2352 |
| Average Option | ||
|---|---|---|
| European | American | |
| Longstaff–Schwartz | 9.0109 | 9.2415 |
| PSO-flat | 9.0109 | 9.0117 |
| PSO-linear | 9.0109 | 9.0117 |
| PSO-exponential | 9.0109 | 9.0117 |
| PSO-piecewise | 9.0109 | 9.1925 |
| PSO-piecewise(restricted) | 9.0109 | 9.1912 |
| (A) Put Option (1-asset) | |||||||||||||
| Value ($) | |||||||||||||
| Seed | 69,905 | 80,302 | 8249 | 26,795 | 967 | 12,128 | 81,917 | 26,488 | 3143 | 41,675 | Mean | Max | Min |
| Swarm Size | |||||||||||||
| 50 | 10.0368 | 9.7001 | 10.2470 | 10.1109 | 9.8039 | 10.1586 | 10.2712 | 10.5006 | 9.3164 | 9.4168 | 9.9562 | 10.5006 | 9.3164 |
| 100 | 10.0388 | 10.4329 | 9.2902 | 10.0156 | 10.5760 | 10.2345 | 10.5512 | 10.2584 | 9.8404 | 9.7683 | 10.1006 | 10.5760 | 9.2902 |
| 200 | 10.0744 | 9.7776 | 9.8149 | 10.5076 | 10.3039 | 10.6329 | 10.0999 | 10.7066 | 10.5164 | 9.8415 | 10.2276 | 10.7066 | 9.7776 |
| 500 | 10.5811 | 10.0202 | 10.5791 | 10.7459 | 10.7074 | 10.5237 | 10.4950 | 10.6977 | 10.7714 | 10.4127 | 10.5534 | 10.7714 | 10.0202 |
| Computation Time (seconds) | |||||||||||||
| Seed | 69,905 | 80,302 | 8249 | 26,795 | 967 | 12,128 | 81,917 | 26,488 | 3143 | 41,675 | Mean | Max | Min |
| Swarm Size | |||||||||||||
| 50 | 19.6829 | 18.8187 | 18.8304 | 18.5710 | 18.3021 | 18.9599 | 18.8633 | 19.2746 | 18.8743 | 19.0645 | 18.9242 | 19.6829 | 18.3022 |
| 100 | 37.3748 | 36.9218 | 38.1397 | 36.7419 | 37.8845 | 37.1103 | 37.9693 | 37.1976 | 37.7589 | 37.7402 | 37.4839 | 38.1397 | 36.7419 |
| 200 | 75.1492 | 75.1461 | 77.2891 | 75.0346 | 74.6849 | 75.8589 | 76.6391 | 73.8078 | 76.6213 | 73.0110 | 75.3242 | 77.2891 | 73.0110 |
| 500 | 186.9830 | 185.8080 | 178.4430 | 182.4440 | 186.9290 | 185.8810 | 184.2930 | 183.5500 | 185.3380 | 178.0620 | 183.7732 | 186.9831 | 178.0624 |
| (B) Min/Max Option (2-asset) | |||||||||||||
| Value ($) | |||||||||||||
| Seed | 69,905 | 80,302 | 8249 | 26,795 | 967 | 12,128 | 81,917 | 26,488 | 3143 | 41,675 | Mean | Max | Min |
| Swarm Size | |||||||||||||
| 50 | 0.2268 | 0.2358 | 0.2350 | 0.2368 | 0.2374 | 0.2347 | 0.2383 | 0.2393 | 0.2257 | 0.2353 | 0.2345 | 0.2393 | 0.2257 |
| 100 | 0.2334 | 0.2344 | 0.2398 | 0.2379 | 0.2364 | 0.2342 | 0.2342 | 0.2381 | 0.2384 | 0.2382 | 0.2365 | 0.2398 | 0.2334 |
| 200 | 0.2383 | 0.2380 | 0.2368 | 0.2315 | 0.2374 | 0.2335 | 0.2338 | 0.2387 | 0.2409 | 0.2320 | 0.2361 | 0.2409 | 0.2315 |
| 500 | 0.2359 | 0.2342 | 0.2366 | 0.2412 | 0.2413 | 0.2426 | 0.2414 | 0.2392 | 0.2416 | 0.2362 | 0.2390 | 0.2426 | 0.2342 |
| Computation Time (seconds) | |||||||||||||
| Seed | 69,905 | 80,302 | 8249 | 26,795 | 967 | 12,128 | 81,917 | 26,488 | 3143 | 41,675 | Mean | Max | Min |
| Swarm Size | |||||||||||||
| 50 | 10.7312 | 20.6707 | 20.5986 | 20.5549 | 20.7069 | 16.1223 | 20.6824 | 20.6649 | 6.97153 | 20.7073 | 17.8411 | 20.7073 | 6.9715 |
| 100 | 41.1003 | 44.5624 | 45.634 | 41.0282 | 41.201 | 40.7916 | 41.1614 | 40.6881 | 25.1049 | 46.8837 | 40.8156 | 46.8837 | 25.1049 |
| 200 | 87.6694 | 73.1363 | 78.1617 | 83.9155 | 86.7515 | 73.6531 | 81.172 | 86.2793 | 81.5649 | 40.9068 | 77.3211 | 87.6694 | 40.9068 |
| 500 | 203.568 | 202.788 | 219.504 | 229.666 | 222.398 | 202.404 | 210.968 | 203.651 | 207.758 | 202.525 | 210.5230 | 229.6660 | 202.4040 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.-R.; Huang, J.; Huang, W.; Yu, R. An Artificial Intelligence Approach to the Valuation of American-Style Derivatives: A Use of Particle Swarm Optimization. J. Risk Financial Manag. 2021, 14, 57. https://doi.org/10.3390/jrfm14020057
Chen R-R, Huang J, Huang W, Yu R. An Artificial Intelligence Approach to the Valuation of American-Style Derivatives: A Use of Particle Swarm Optimization. Journal of Risk and Financial Management. 2021; 14(2):57. https://doi.org/10.3390/jrfm14020057
Chicago/Turabian StyleChen, Ren-Raw, Jeffrey Huang, William Huang, and Robert Yu. 2021. "An Artificial Intelligence Approach to the Valuation of American-Style Derivatives: A Use of Particle Swarm Optimization" Journal of Risk and Financial Management 14, no. 2: 57. https://doi.org/10.3390/jrfm14020057
APA StyleChen, R.-R., Huang, J., Huang, W., & Yu, R. (2021). An Artificial Intelligence Approach to the Valuation of American-Style Derivatives: A Use of Particle Swarm Optimization. Journal of Risk and Financial Management, 14(2), 57. https://doi.org/10.3390/jrfm14020057





