Abstract
The aim of this study is to test the ability of the yield curve on US government bonds to forecast the future evolution in the prices of commodities often used in as raw materials. We consider the monthly prices of nine commodities for more than 30 years. Our findings, confirmed by several parametric and non-parametric tests, are robust and indicate that the ability to forecast future performance changes over time. Specifically, between 1986 and the early 2000s the yield curve was quite successful in forecasting monthly changes in commodity prices, but that success diminished in the period following. One possible explanation for this outcome is the increased flow of capital into the commodity market resulting in stronger correlations with the equity markets and a breakdown of the obvious relationship between commodities and business cycle. Our findings are important for asset pricing, commodity traders and policy makers.
JEL Classification:
C53; E3; E4; Q02
1. Introduction
The literature regards the term structure curve, which plots the yield of government bonds against their maturity, as an indicator with valuable information about the current and future states of the economy (e.g., Harvey 1989; Abdymomunov 2013; Gogas et al. 2015; McMillan 2021b). The U.S. Federal Reserve, among other policymakers and institutional market participants, has always looked at the difference between the yields on long- and short-term sovereign bonds as an indication of where the economy is heading. Thus, the forecasting ability of the yield spread has become something of a stylized fact among macroeconomists.
Many studies, detailed in the literature review section, have demonstrated the ability of yield spreads to predict future economic situations effectively. They have established that the spreads contain a great deal of information about future economic activity and are accurate predictors of economic growth. However, there have been fewer comprehensive attempts to understand the dynamic relationships between the evolution in the prices of commodities and the shape of the yield curve. This question has become particularly relevant in the wake of the unconventional monetary policy used in the last two decades, which has not been employed since the Great Depression during 1930s. Thus, our goal is to fill this gap by exploring the ability of the term structure to forecast the future evolution in the prices of commodities. To accomplish this task, we use 30 years of data about nine commodities often used as raw materials: coal, gold, silver, oil, platinum, palladium, zinc, ethanol, and natural gas. We also use various proxies for the yield spread combined from 30-year, 10-year, 2-year, 1-year and 3-month interest rates.
Our findings indicate that yield spreads are generally positively correlated with future changes in the price of commodities. Our results are robust to controlling for real economic and financial variables. Adding any or all of these potential alternative explanatory variables only marginally affects the coefficients or their statistical significance. In our analysis, we also utilize the Engle’s (2002) dynamic conditional correlation procedure (DCC). The overall picture confirms the existence of time-varying correlation between the yield spread and future price movements in commodities. To determine why this result emerged, we consider sub-samples that are determined endogenously using the Bai and Perron (2003) tests. These structural break tests confirm that the positive correlation is economically and statistically significant mainly for the period prior to 2004. On the other hand, in the period following (2004–2020) it seems that the yield spread has been unable to predict changes in commodities in any significant way.
The weakening correlation between the variables of interest may be related to the massive capital inflows from individual and institutional investors into the commodity market in the early 2000s (e.g., Tang and Xiong 2012). Many studies justified these inflows to commodities by their relatively low correlation with financial markets and, accordingly, the potential diversification benefits (e.g., Gorton and Rouwenhorst 2006; Daskalaki et al. 2017). However, the considerable inclusion of commodities in investors’ portfolios resulted in the financialization of commodities, yielding a strong correlation between commodity prices and equity markets (e.g., Hu et al. 2020) and a breakdown of the obvious relationship between commodities and cyclical phases of the economy.
Lastly, between 1986 and December 2020, we found eight periods during which the yield spread was negative or equal to zero. The non-parametric tests conducted to track the future evolution in commodity prices following flat or downward-sloped yield curves indicate that such situations can be a successful timing to embark on long positions in several commodities for investors planning to hold for a relatively long period of time. Recently, with the outbreak of the Coronavirus late in February 2020, the U.S. 1-year yield was 1.43%, and the 10-year was about flat (1.46%). Tracking the commodity prices in the few months following indicate significant shrink in prices. However, the prices recovered sharply after 2–4 quarters. This recent case, among the others observed, confirms that specific shapes of the yield curve may generate abnormal returns for investors (see Table A1 in the online Appendix A).
The mechanism underlying our conjecture here accords with the empirical evidence confirming a strong relationship between the business cycle and commodity prices (Labys et al. 1999; Chevallier et al. 2014). In addition, the literature has established that financial markets, including the yield curve, move more quickly than real markets (Saar and Yagil 2015). Accordingly, one should observe a causal relationship from this macro-financial predictor to the commodity market.
The paper contributes to the existing literature in several ways. First, our study sheds light on the link between yield spreads and long-term prices in the commodity market. While previous studies have focused on interest rates in level rather than the difference between long and short-term sovereign bond yields (e.g., Dai and Kang 2021), little is known about the information content of the term structure for commodities. Second, we add to the literature documenting the time-varying relationship between real economic and financial variables by examining the structural breaks in the long-term correlation between yield spreads and the commodity market (e.g., Chinn and Kucko 2015). Third, our findings are especially useful for policy makers and central banks because long-term predictions about commodity prices are essential in targeting inflation and promoting overall economic stability (e.g., Garner 1989; Orlowski 2017; Fasanya and Awodimila 2020). Finally, modeling and forecasting future innovations in commodity prices are important for both market participants and scholars. Predictions in this area play a vital role in portfolio optimization and risk management. Indeed, investors are attracted to commodities due to their inflation-hedging properties (e.g., Beckmann and Czudaj 2013; Bampinas and Panagiotidis 2015; Levine et al. 2018; Umar et al. 2019), and their possible contribution to diversifying risks (e.g., Gagnon et al. 2020).
The remainder of this study proceeds as follows. Section 2 reviews the literature. Section 3 describes the data and the construction of the key variables. Section 4 presents the methodology. Section 5 details the empirical findings and discusses the results. Section 6 checks the robustness of the findings, and Section 7 concludes.
2. Literature Review
The macroeconomic literature has established that future real economic growth is positively correlated with lagged interest spreads (e.g., Stock and Watson 1989; Estrella and Hardouvelis 1991; Plosser and Rouwenhorst 1994; McMillan 2021a). In parallel, the link between interest rates and commodities has been also investigated and can be classified into two categories. The first addresses the effect of the interest rate level on commodity prices. This line of literature has established that commodity prices increase significantly in response to reductions in real interest rates (Akram 2009; Arango et al. 2011). The second category explores the effect of shocks in the commodity market (mainly oil prices) on long-term interest rates (e.g., Ioannidis and Ka 2018). Recent studies use the Granger (1969) causality test and provide evidence that not only do interest rates drive commodity prices, but also that commodity prices drive income and interest rates (e.g., Harvey et al. 2017). Despite these extensive efforts, the examination of the ability of yield spreads to predict future innovations in commodity prices has attracted relatively less attention in the literature.
The literature points to several reasons why yield spreads forecast future real economic activity. One reason relates to the expectation theory, according to which when the yield curve flattens, market participants expect short-term interest rates to fall due to a recession. This expectation translates into a drop in long-term interest rates, as deteriorating market conditions during recessions might explain the decline in short-term rates. Indeed, economic depressions are often associated with job loss, increased uncertainty, business failures, and credit line contractions. Consequently, if people anticipate a slowdown in economic activity, there will likely be a drop in the demand for credit, which in turn leads to a decline in long-term interest rates. On the other hand, if market participants anticipate an upturn in the economy, future short-term interest rates will be expected to rise, leading to a steepening of the yield curve. Thus, while falling yield spreads preceding recessions are caused by both aforementioned factors, the decline in expectations about short-term rates is the more important one (Hamilton and Kim 2002).
The second explanation is related to the countercyclical monetary policy according to which economic expansion is accompanied by inflation. To control inflation, central banks follow a countercyclical monetary policy by raising short-term interest rates. Tight monetary policies are used to stabilize output growth and cause the yield spread to drop. This measure is aimed at reducing the anticipation of inflation to levels below the current inflation rate. Consequently, short-term interest rates rise more than long-term interest rates do, and the yield curve flattens. As real interest rates remain high, spending decreases, causing an economic slowdown. Estrella (2005) provided a theoretical model wherein the yield spread explains both output and inflation. The author showed that the predictive ability of the yield spread depends upon the reaction of the given monetary policy. By the same logic, in a recessionary economy, central banks will reduce short-term interest rates as part of a countercyclical monetary policy. Thus, a lower yield spread or a flat yield curve is a harbinger of economic downturn.
The third explanation of why the yield curve slope is a leading indicator of economic output is referred to as the inter-temporal consumption model. As per Harvey (1989), during expansionary periods people have a stable level of consumption, whereas during recessions, when income is falling, they tend to reduce their consumption. Hence, if people anticipate a decline in economic activity, they have an incentive to save in the current period by selling short-term assets and buying bonds, which will ensure a stable income during the low-income period. As a result, long-term bond prices rise, which in turn reduces their yields, and short-term bonds trade at increased rates.
Finally, there are various empirical works dealing with the relationship between the factors affecting macroeconomic fundamentals and commodity prices. Variables such as an increase in economic activity (e.g., Duarte et al. 2021), economic uncertainty (Qadan and Nama 2018), the exchange rate of the dollar (e.g., Churchill et al. 2019) and the market index (Kagraoka 2016) are capable of affecting commodity prices. Considering the ability of the spread in bond yields to anticipate future economic activity, it is very important to have some understanding of its role in providing information about the future prices of commodities.
3. Data
Our sample consists of monthly data on nine commodities—oil, silver, gold, platinum, palladium, zinc, ethanol, coal, and natural gas—obtained based on the availability of the data. These commodities are used in many industries as raw materials. Data about silver and gold come from the Chicago Mercantile Exchange (CME). Data about platinum palladium and natural gas come from the New York Mercantile Exchange (NYMEX). The data on zinc and copper come from the London Bullion Market Association (LBMA). Information about coal comes from the International Exchange (ICE), whereas the data on WTI oil are taken from the Federal Reserve Bank of St. Louis.
The largest sample period used is that for oil, gold and silver, and ranges from January 1986 to December 2020, while the smallest sample is that for coal and ranges from January 2009 to December 2020. Our starting point for each commodity is simply due to the availability of information about their prices. We use the International Monetary Fund’s International Financial Statistics database for the rates for the 3-month, 1-year, 2-year, 10-year and 30-year Treasury bills. Table 1 reports the descriptive statistics of the key variables used in this study and outlines the sample period. Panel A reports the descriptive statistics of the six proxies used to capture the yield spread, while Panel B reports the descriptive statistics of the commodities employed here.

Table 1.
Descriptive Statistics. Panel A—yield rates. Panel B—commodities.
4. Method
The empirical economic literature defines the yield spread as the difference between the yield rates on long-term and short-term government bonds. In fact, there is no precise theory that defines how the yield spread should be calculated, and the choice of creating a proxy for the yield spread is somewhat arbitrary. Indeed, the literature provides many proxies for the yield spread including the difference between the yields on 10-year bonds and 3-month bonds (Estrella and Hardouvelis 1991), the difference between 10-year and 1-year interest rates (Stock and Watson 1989) and the difference between yields on 30-year and 3-month bonds (Duffee 1998). Given the mixed definitions of the yield spread, we utilize as broad a spectrum of bonds as possible, specifically, the differences in the yields on 10-year and 3-month Treasury bonds, 10-year and 1-year bonds, 10-year and 2-year bonds, 30-year and 3-month bonds, 30-year and 1-year bonds and 30-year and 2-year bonds.
We formulate the following model to trace the effect of the current yield spread (at time t) on the cumulative rate of change in the “h” subsequent months or quarters.
where
is the rate of change in the price of the commodity in annual terms. If, for example, h = 1, then captures the cumulative return of one period (say, a quarter) ahead. If h = 4, then captures the cumulative returns for the coming twelve months (four quarters). The difference between the yield rates on long-term and short-term government bonds is given by and is the forecast error. Given the possibility that the forecast error might be correlated, we use Newey and West’s (1987) corrected covariance estimator. The estimated coefficients guarantee consistency in the presence of both heteroscedasticity and autocorrelation (HAC) of unknown form. denotes a matrix of additional explanatory variables. In line with the literature, we use the U.S. dollar exchange rate (Churchill et al. 2019), the S&P500 (Kagraoka 2016), the industrial production index (Duarte et al. 2021) and the economic policy uncertainty index (Huang et al. 2021).
To depict the dynamic correlation between the current yield spread and the future price direction of commodities, we use the established multivariate concept of dynamic conditional correlation generalized autoregressive conditional heteroscedasticity (DCC GARCH). Engle (2002) developed this state-of-the-art method, which has been used extensively to quantify dynamic relationships over time. In the following, we provide a very basic description of this methodology.1
The dynamic conditional correlation estimator is an extension of the constant conditional correlation model suggested by Bollerslev (1990). According to Bollerslev’s procedure, the correlation matrix ρ is constant. That is, where and represents the i-th univariate (G)ARCH(p, q) process. In other words,
According to Engle (2002), ρ is allowed to vary in time t. Thus,
The correlation matrix is then given by:
The correlation matrix is a positive definite one because of the positive nature of Ht. Given that , then:
where are the standardized residuals from the (G)ARCH model, is a n × n matrix and represents the unconditional variance matrix of the standardized error terms ηt and computed as . α and β are non-negative scalars and satisfy the mean-revering assumption (i.e., α + β < 1). is a positive definite matrix that determines the structure of dynamics and normalizes the elements in ;
In order to estimate the parameters of specifically , the following log-likelihood function is maximized:
5. Empirical Findings
Table 2 reports the estimation results of the reduced form of Equation (1). That is, future commodity returns () are regressed against the current yield spread only. . In this table, we utilize the difference between 10-year and 3-month bond yields (Y10-Y3M) as a proxy for the yield spread. We also use four forecasting horizons (h; h = 1, 2, 3 and 4) where h = 1 indicates forecasting of one quarter ahead and h = 4 indicates forecasting four quarters ahead. Panel A of the table reports the estimation results with respect to the entire sample, Panel B covers 1986 to 2003, and Panel C covers 2004 to 2020.

Table 2.
Estimation results of Equation (1) with the Y10-Y3M indicator. Panel A: entire sample. Panel B: sample period 1986–2003. Panel C: sample period 2004–2020.
The picture that emerges indicates an insignificant positive tendency of the yield spread to forecast future changes in the commodities used. Panel B, however, presents a different picture. Except for oil and palladium, we find that, when considering 1986–2003, the yield spread has a positive effect on the future prices of the rest of the commodities. The ability of the current yield spread to predict future innovations in commodity prices is manifested in both the statically significant positive coefficients and the relatively high R2 (for example, R2 values are 6%, 7%, 11.2%, 11.4% and 26% for gold, natural gas, platinum, silver and zinc, respectively.). A steeper yield curve is always viewed as an indication that the growth in future output is about to rise. Thus, the positive correlation detected indicates that an increase in the slope at time t will have a positive impact on the future prices of commodities.
While Table 2 regresses the commodity returns against the yield spread only, in Table 3 we present the full estimation of Equation (1) after controlling for additional explanatory variables. The sample period considered in Table 3 is for 1986–2003. The results for the entire sample and the period after 2004 appear in Table A2 (in the online Appendix A). The overall picture is maintained as evident by the significant positive coefficients of the yield spreads even after controlling for real and financial economic variables in the period prior to 2004. The results hold true for all commodities except for oil and palladium.

Table 3.
Estimation results of Equation (1) for the period 1986–2003.
The statistically significant positive coefficients accord with the empirical literature postulating that commodity prices (specifically silver, gold, platinum, zinc and natural gas) are tightly linked with the business cycle and the state of the economy (e.g., Batten et al. 2010; Kucher and McCoskey 2017; Jahan and Serletis 2019). This economically and statistically significant relationship confirms that these metals are used extensively in various industries, making them more exposed to the expected phases in the economic cycle.
In investigating whether the relationship between yield spreads and future innovations in commodity prices is stable over time, we made two major findings. The first is that the correlation between commodity prices and yield spreads is not stable over time. This finding is evident in Engle’s (2002) dynamic conditional correlations depicted in Figure 1, Figure 2 and Figure 3, which illustrate the dynamic conditional correlation between the yield spreads and the commodity prices two, three and four quarters ahead. This finding accords with recent studies maintaining time-varying relationship between yield spread and future economic output (e.g., Kuosmanen et al. 2019; Chinn and Kucko 2015).
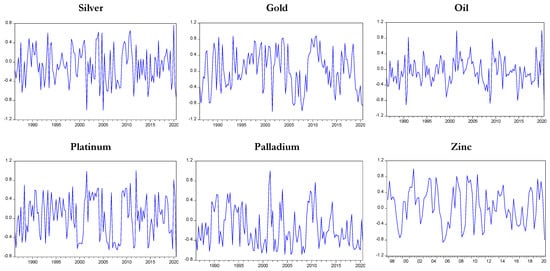
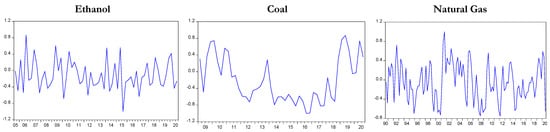
Figure 1.
Dynamic correlation between the yield spread and two quarters ahead.
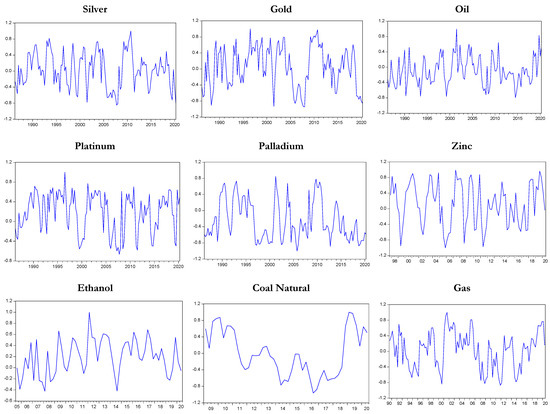
Figure 2.
Dynamic correlation between the yield spread and three quarters ahead.
Figure 3.
Dynamic correlation between the yield spread and four quarters ahead.
Second, using the Bai and Perron (2003) structural break test we find that the early 2000s is the period associated with structural breaks in the relationship between the yield curve and the prices of commodities. Table 4 presents the results of this test and indicates the dates detected as structural break points. In general, the findings of Bai and Perron (2003) test point to the 2003–3004 as the period in which there was a structural break in the relationship between yield spreads and future commodity prices. These findings accord with earlier studies that date the start of the financialization commodities to the early 2000s (Hamilton and Wu 2015; Henderson et al. 2015). In other words, this period marks the start of the increased exposure of portfolio managers, individuals and hedge funds to commodities.

Table 4.
Bai and Perron (2003) multiple break-point test.
This finding is in line with prior studies documenting the weakening ability of the term structure to predict future economic activity. Early on, Stock and Watson (2003) and Giacomini and Rossi (2006) maintained that the yield spread’s ability to forecast economic expansion has weakened since the 1980s, but its predictive ability remains strong only for recessions. Other works raise questions regarding the stability of the term spread’s predictive content (e.g., Wheelock and Wohar 2009). Evgenidis et al. (2020) confirm the time-varying nature of the yield spread’s predictive ability, mainly during the 2000s.
One possible factor explaining this break between commodities and the most reliable indicator of future economic activity is the financialization of commodities. For a long time, commodities were viewed as a segmented market offering significant diversification benefits in light of the low—even negative—correlation between their returns and the stock market (e.g., Bodie and Rosansky 1980; Demiralay et al. 2019). This characteristic prompted traders, financial institutions and institutional investors to consider this new asset class as a useful diversifier in their portfolios. A byproduct of this development is the acceleration in the financialization of these commodities, which in turn fueled a rapid increase in their co-movements with equity markets (e.g., Qadan et al. 2019). This evolution may explain the breakdown of the obvious relationship between commodities and the expected economic evolution.
We also test the extent to which the dynamic correlation of commodity “i” co-moves with that of commodity “j.” A quick glance at Figure 1, Figure 2 and Figure 3 shows the apparent co-movements between some of these commodities. Table 5 presents the simple correlation between the DCC values. Some of the correlation values are negative and statistically significant. For example, we detect a negative correlation between the prices of ethanol and gold, gold and natural gas, natural gas and palladium, oil, and palladium. On the other hand, the majority of the other cases are associated with statistically significant positive correlations, particularly for precious metals. For example, the correlation between the DCC values of gold and silver is 0.73, and that between gold and platinum is 0.534. Overall, this picture reveals that the conditional slope among commodities is largely connected—a clear indication of their similar reaction to the current yield spread.

Table 5.
Pearson’s correlation between the DCC values of the commodities.
6. Robustness Checks
6.1. Additional Proxies for Yield
Previous studies suggested capturing the yield spread using different proxies. To develop a broader picture regarding the interaction between the yield spread and the future evolution in commodity prices, we depart from the standard yield spread used in the literature (Y10-Y3M) and test other proxies: the difference between 10-year and 1-year interest rates (Y10-Y1), between 10-year and 2-year yields (Y10-Y2), between 30-year and 3-months yields (Y30-Y3M), between 30-year and 1-year bond yields (Y30-Y1) and between 30-year and 2-year bond yields (Y30-Y2).
Table 6, Table 7, Table 8, Table 9 and Table 10 report the estimation results of the prediction model. Table 6 presents the estimation results given Y10-Y1 as the yield spread. In Table 7, Y10-Y2 proxies for the yield spread. In Table 8, Y30-Y3M proxies for the yield spread. Table 9 utilizes Y30-Y1 as the yield spread, and Table 10 utilizes Y30-Y2 to proxy for the yield spread. The overall picture is maintained as evident by the significant positive coefficients in the period prior to 2004 (Panel B in each table), but the insignificant results in the period that follows (Panels C). The regression results that include the other explanatory variables reflect very similar picture. They appear in Table A3, Table A4, Table A5, Table A6 and Table A7 in the online Appendix A.

Table 6.
Estimation results of Equation (1) with the Y10-Y1 indicator. Panel A: entire sample. Panel B: sample period 1986–2003. Panel C: sample period 2004–2020.

Table 7.
Estimation results of Equation (1) with the Y10-Y2 indicator. Panel A: entire sample. Panel B: sample period 1986–2003. Panel C: sample period 2004–2020.

Table 8.
Estimation results of Equation (1) with the Y30-Y3M indicator. Panel A: entire sample. Panel B: sample period 1986–2003. Panel C: sample period 2004–2020.

Table 9.
Estimation results of Equation (1) with the Y30-Y1 indicator. Panel A: entire sample. Panel C: sample period 2004–2020.

Table 10.
Estimation results of Equation (1) with the Y30-Y2 indicator. Panel A: entire sample. Panel B: sample period 1986–2003. Panel C: sample period 2004–2020.
A closer glance at the results in Panel B of Table 6 confirms that the yield spread, defined as Y10-Y1, is an efficient predictor of the future prices of silver, gold, platinum and zinc. The resulting R2 for silver ranges between 0.03 when forecasting one quarter ahead (h = 1), and 0.19 when forecasting the prices one year ahead (h = 4). We find that the regression R2 for gold ranges between 0.04 (for h = 1) and 0.15 (for h = 4), for platinum it ranges between 0.01 (for h = 1) and 0.12 (for h = 4), and finally it ranges between 0.09 (for h = 1) and 0.26 for zinc (h = 4). This picture is essentially replicated in Table 7, Table 8, Table 9 and Table 10. Moreover, Panel B of Table 10 provides strong support for these findings. The resulting R2 for zinc ranges between 0.08 (for h = 1), and 0.34 (for h = 4). By and large, these findings confirm the premise that metal prices are positively correlated with macroeconomic activity (e.g., Fama and French 1988).
6.2. Commodity Prices following Periods of Non-Positive Yield Spreads
What happens to the price of commodities in the months following downward-sloped or flat yield curves? To answer this question, we track the evolution in the price of the sampled commodities throughout the sample period. The period between 1986 and December 2020 witnessed eight periods during which the yield spread (10-year minus 1-year yields) was negative or equal to zero. The left-hand side of Table 11 lists the dates when the yield spread became non-positive. For each commodity, we calculate the returns accumulated 1, 2, 3, 4, 5 and 6 quarters following these non-positive yield spread periods.

Table 11.
Commodity prices in the periods following non-positive yield spread. Panel A: oil. Panel B: silver. Panel C: gold. Panel D: platinum. Panel E: palladium. Panel F: zinc. Panel G: ethanol. Panel H: coal. Panel I: natural gas.
Oil, silver, gold, platinum, palladium, and natural gas prices surged strongly in the quarters following the periods associated with equality in long and short-term Treasury yields. For example, tracking the prices of these commodities three quarters after an end in the zero slope in the bond term structure reveals significant positive returns on average (oil 11.22%; silver 13.43%; gold 16.26%; platinum 19.82%; palladium 26.32%; ethanol 5.85%; natural gas 24%). In contrast, coal and zinc prices present a mixed and inconclusive picture with a tendency to negative returns. This finding emphasizes that investors should note that flat or downward-sloped yield curves seem to be reasonable points at which to take long positions in several commodities that they plan to hold for a relatively long period of time.
Our findings are even more pronounced if we consider the recent relatively flat yield curve observed during the last week in February 2020 due to the outbreak of the coronavirus. However, we did not include the findings in the table because the difference between the 10-year and 1-year bond interest rates was 0.03% (0.0003). While quite small, it is not a non-positive yield. In addition, prices recovered sharply after two to four quarters. Nevertheless, the findings in Table A1 in the online Appendix A lend support to our conjecture.
7. Conclusions
We investigated an important, yet barely discussed, issue: Can yield spreads forecast future innovations in the commodity market? If so, is this long-term correlation stable over time? Despite the extensive research linking economic real activity to lagged yield spreads, the predictive ability of the yield curve has not been proven with regard to commodities often used in as raw materials.
Our findings can be summarized as follows. First, the prediction ability of the yield curve is evident mainly in the period before the financialization of commodities era, but is absent between 2004 and 2020. Second, structural break tests confirm the changes in the correlation between the six yield spreads proposed and future commodity prices. Third, the findings of the dynamic conditional correlation confirm the time-varying nature of the yield spread in predicting the future evolution in commodity prices. One explanation might be the increased flow of money into the commodity market and the increased correlation between it and equity markets. These changes disconnected the prices of commodities from the economic cycle.
The structural breaks and the fading correlation between the variables of interest are critical for those involved in risk management and investment diversification. Furthermore, our results may be useful for policy makers who must make decisions about policies to target and control inflation. Future research can extend the standing literature by addressing the interplay between the shape of the term structure and future evolution of asset prices in the wake of pandemic outbreaks and the massive monetary intervention conducted by central banks under severe economic conditions.
Author Contributions
Conceptualization, Y.I.-B. and M.Q.; methodology, Y.I.-B. and M.Q.; software, Y.I.-B. and M.Q.; validation, Y.I.-B. and M.Q.; formal analysis, Y.I.-B. and M.Q.; investigation, Y.I.-B. and M.Q.; resources, M.Q.; data curation, Y.I.-B. and M.Q.; writing—original draft preparation, Y.I.-B. and M.Q.; writing—review and editing, Y.I.-B. and M.Q.; visualization, Y.I.-B. and M.Q.; supervision, M.Q.; project administration, M.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Evolution in the commodity prices following the relatively flat curve witnessed in February 2020.
Table A1.
Evolution in the commodity prices following the relatively flat curve witnessed in February 2020.
| Accumulated Returns after: | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 Month | 2 Months | 3 Months | 4 Months | 5 Months | 6 Months | 7 Months | 8 Months | 9 Months | 10 Months | |
| Oil | −50.9% | −66.1% | −33.4% | −22.4% | −17.3% | −13.1% | −19.3% | −22.7% | −8.4% | −1.6% |
| Silver | −18.4% | −16.1% | −2.9% | −1.6% | 25.4% | 44.4% | 26.5% | 34.2% | 28.4% | 42.6% |
| Gold | −0.8% | 4.7% | 5.4% | 7.0% | 15.2% | 16.1% | 12.8% | 15.5% | 9.6% | 14.5% |
| PLTNM | −20.0% | −17.0% | −4.9% | −13.9% | 1.7% | 0.2% | −9.7% | −6.4% | 4.0% | 11.9% |
| PLDM | −14.0% | −25.0% | −25.3% | −31.1% | −13.4% | −18.0% | −16.6% | −10.5% | −11.5% | −10.8% |
| Zinc | −9.4% | −7.1% | −1.6% | 1.3% | 9.9% | 22.2% | 16.9% | 25.4% | 35.9% | 41.7% |
| Ethanol | −29.6% | −27.5% | −14.3% | −12.0% | −10.9% | −0.4% | 1.6% | 21.5% | 6.2% | 2.3% |
| Coal | −2.3% | −10.0% | −23.5% | −21.6% | −23.4% | −26.7% | −22.2% | −14.6% | −6.1% | 17.8% |
| Nat.Gas | −10.2% | −5.5% | −6.3% | −19.8% | −2.1% | 34.8% | 15.8% | 63.7% | 56.8% | 46.2% |
Notes: With the outbreak of the COVID−19 pandemic in February 2020, the U.S. 1-year yield was 1.43% while the 10-year was 1.46%. That is, the yield spread was 0.03%. The table reports the evolution in the prices of commodities in the few months following this relatively flat curve. Though we discuss one case, the overall picture is clear and shows that the current yield spread is a relatively good predictor of the future evolution in commodity prices.

Table A2.
Estimation results of model 5 with the Y10-Y3M indicator. Panel A: entire sample. Panel B: sample period 2004–2020.
Table A2.
Estimation results of model 5 with the Y10-Y3M indicator. Panel A: entire sample. Panel B: sample period 2004–2020.
| Panel A | ||||||||||||||||
| Forecast Horizon | Oil (1986:01–2020:12) | Silver (1986:01–2020:12) | ||||||||||||||
| h | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 5.92 | −0.79 | −0.55 | 9.32 | −14.07b | 0.11 | 0.03 | 139 | 1.67 | 1.06 | −0.85 | −10.29 | −4.90 | 0.06 | −0.01 | 139 |
| (0.45) | (−0.12) | (−0.08) | (0.56) | (−2.43) | (1.08) | (0.21) | (0.28) | (−0.21) | (−1.04) | (−1.44) | (0.99) | |||||
| 2 | 7.33 | −1.74 | −5.23 | 2.47 | −3.76 | 0.04 | −0.01 | 138 | 3.12 | 1.40 | −3.50 | −6.35 | −4.05c | −0.05 | 0.02 | 138 |
| (0.84) | (−0.41) | (−1.16) | (0.22) | (−0.99) | (0.66) | (0.58) | (0.54) | (−1.26) | (−0.93) | (−1.73) | (−1.10) | |||||
| 3 | 4.84 | −0.54 | −5.93 | −9.86 | −5.02 | −0.02 | 0.04 | 137 | −0.37 | 2.76 | −2.12 | −8.83 | −5.06a | −0.03 | 0.05 | 137 |
| (0.75) | (−0.17) | (−1.81) | (−1.23) | (−1.75) | (−0.35) | (−0.09) | (1.32) | (−0.96) | (−1.64) | (−2.62) | (−0.77) | |||||
| 4 | 4.49 | −1.48 | −2.40 | −5.33 | 6.23 | −0.01 | −0.01 | 136 | 0.69 | 2.56 | −3.33c | −0.55 | −0.82 | −0.04 | 0.02 | 136 |
| (0.84) | (−0.56) | (−0.85) | (−0.80) | (1.17) | (−0.25) | (0.19) | (1.42) | (−1.71) | (−0.12) | (−0.23) | (−1.38) | |||||
| Forecast Horizon | Gold (1986:01–2020:12) | Platinum (1986:04–2020:12) | ||||||||||||||
| h | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 3.73 | 0.54 | 1.61 | −1.05 | −2.52 | 0.01 | −0.02 | 138 | 3.32 | −0.56 | −3.60 | −8.25 | −1.92 | 0.02 | −0.02 | 139 |
| (0.86) | (0.26) | (0.73) | (−0.20) | (−1.37) | (0.45) | (0.46) | (−0.16) | (−0.96) | (−0.91) | (−0.61) | (0.4) | |||||
| 2 | 5.19c | 0.43 | −2.09 | 2.21 | −1.25 | −0.03 | 0.01 | 137 | 3.83 | −0.31 | −6.05b | −5.14 | 0.50 | −0.03 | 0.02 | 138 |
| (1.76) | (0.30) | (−1.37) | (0.60) | (−0.97) | (−1.14) | (0.79) | (−0.13) | (−2.43) | (−0.84) | (0.24) | (−0.87) | |||||
| 3 | 4.68c | 0.33 | −0.91 | 1.45 | −1.05 | −0.02 | −0.01 | 136 | 0.63 | 1.01 | −2.32 | −7.80c | −1.71 | −0.04 | 0.02 | 137 |
| (1.84) | (0.27) | (−0.71) | (0.46) | (−0.93) | (−0.85) | (0.17) | (0.55) | (−1.21) | (−1.66) | (−1.02) | (−1.44) | |||||
| 4 | 5.25b | 0.38 | −1.91 | 3.31 | −2.83 | −0.02 | 0.01 | 135 | 1.19 | 0.56 | −1.71 | −0.17 | 4.16 | −0.04c | 0.02 | 136 |
| (2.34) | (0.34) | (−1.61) | (1.19) | (−1.27) | (−1.22) | (0.38) | (0.36) | (−1.03) | (−0.04) | (1.34) | (−1.8) | |||||
| Forecast Horizon | Palladium (1986:04–2020:12) | Zinc (1997:08–2020:12) | ||||||||||||||
| h | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 19.89c | −6.40 | −12.07b | −7.36 | 8.63c | 0.03 | 0.03 | 139 | −1.27 | 0.56 | −6.60 | −15.05 | 0.07 | 0.17b | 0.01 | 93 |
| (1.94) | (−1.29) | (−2.27) | (−0.57) | (1.93) | (0.37) | (−0.13) | (0.11) | (−1.3) | (−1.07) | (0.02) | (2.03) | |||||
| 2 | 16.52b | −4.10 | −7.36c | −10.51 | 4.02 | −0.05 | 0.02 | 138 | −2.35 | 2.75 | −2.46 | −11.65 | −0.71 | 0.03 | −0.03 | 92 |
| (2.16) | (−1.11) | (−1.87) | (−1.1) | (1.21) | (−0.92) | (−0.3) | (0.7) | (−0.61) | (−1.05) | (−0.23) | (0.45) | |||||
| 3 | 11.65c | −1.77 | −0.97 | −5.21 | 2.92 | −0.03 | −0.02 | 137 | −6.15 | 5.27 | −2.60 | −5.86 | −2.95 | 0.02 | −0.01 | 91 |
| (1.78) | (−0.56) | (−0.29) | (−0.64) | (1) | (−0.69) | (−0.91) | (1.59) | (−0.77) | (−0.63) | (−1.07) | (0.43) | |||||
| 4 | 9.71c | −1.60 | 0.49 | −1.63 | 13.19b | −0.03 | 0.01 | 136 | −6.83 | 6.04b | −1.16 | 7.09 | 3.45 | 0.02 | 0.01 | 90 |
| (1.72) | (−0.57) | (0.16) | (−0.23) | (2.35) | (−0.72) | (−1.14) | (2.05) | (−0.37) | (0.86) | (0.57) | (0.38) | |||||
| Forecast Horizon | Ethanol (2005:06–2020:12) | Coal (2009:01–2020:12) | ||||||||||||||
| h | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | −1.39 | −0.65 | 3.71 | 47.44c | −7.37 | 0.20 | 0.07 | 62 | 4.07 | −0.18 | −3.93 | −14.93 | 9.82b | −0.12 | 0.10 | 48 |
| (−0.07) | (−0.07) | (0.35) | (1.95) | (−1.12) | (1.35) | (0.26) | (−0.03) | (−0.54) | (−0.84) | (2.45) | (−1.11) | |||||
| 2 | −5.25 | −0.63 | 1.61 | −2.20 | −7.50c | 0.13 | 0.02 | 61 | −1.02 | 2.98 | −5.38 | −16.73 | 5.05c | −0.20b | 0.15 | 47 |
| (−0.43) | (−0.1) | (0.25) | (−0.15) | (−1.85) | (1.47) | (−0.09) | (0.55) | (−1.02) | (−1.29) | (1.72) | (−2.42) | |||||
| 3 | −5.53 | 0.68 | −0.35 | −8.83 | −5.12c | 0.01 | −0.03 | 60 | −13.96 | 7.81 | −1.61 | −12.06 | −1.60 | −0.13c | 0.07 | 46 |
| (−0.63) | (0.16) | (−0.08) | (−0.83) | (−1.7) | (0.12) | (−1.34) | (1.66) | (−0.36) | (−1.1) | (−0.61) | (−1.84) | |||||
| 4 | −3.89 | 0.66 | −3.32 | 2.19 | 0.06 | −0.02 | −0.07 | 59 | −12.55 | 6.48 | −1.08 | −7.51 | 1.56 | −0.06 | −0.01 | 45 |
| (−0.58) | (0.2) | (−0.87) | (0.27) | (0.01) | (−0.33) | (−1.3) | (1.48) | (−0.24) | (−0.74) | (0.23) | (−0.93) | |||||
| Forecast Horizon | Natural gas (1990:05–2020:12) | |||||||||||||||
| h | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | ||||||||
| 1 | 5.82 | −3.09 | 15.11c | 15.35 | 1.91 | 0.00 | 0.00 | 122 | ||||||||
| (0.36) | (−0.4) | (1.87) | (0.74) | (0.29) | (−0.01) | |||||||||||
| 2 | −0.62 | 0.29 | 2.48 | −14.15 | −3.37 | 0.02 | −0.03 | 121 | ||||||||
| (−0.06) | (0.05) | (0.45) | (−1) | (−0.73) | (0.22) | |||||||||||
| 3 | −6.55 | 2.69 | −0.25 | −26.80b | −5.08 | 0.06 | 0.02 | 120 | ||||||||
| (−0.75) | (0.65) | (−0.06) | (−2.46) | (−1.38) | (0.85) | |||||||||||
| 4 | −5.93 | 1.55 | 1.67 | −16.60c | 12.51c | 0.04 | 0.03 | 119 | ||||||||
| (−0.86) | (0.47) | (0.47) | (−1.93) | (1.85) | (0.7) | |||||||||||
| Panel B | ||||||||||||||||
| Forecast Horizon | Oil (2004:01–2020:12) | Silver (2004:01–2020:12) | ||||||||||||||
| h | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | −0.10 | −0.53 | 0.86 | 16.77 | −15.95b | 0.17 | 0.04 | 68 | 11.98 | −4.06 | −2.96 | −13.37 | −4.65 | 0.11 | −0.03 | 68 |
| (0.00) | (−0.05) | (0.07) | (0.61) | (−2.11) | (1.01) | (0.86) | (−0.6) | (−0.4) | (−0.77) | (−0.98) | (1.09) | |||||
| 2 | 3.69 | −2.15 | 0.72 | 9.54 | −5.95 | 0.08 | −0.03 | 67 | 16.38c | −4.37 | −7.96 | −11.18 | −3.03 | −0.06 | 0.06 | 67 |
| (0.25) | (−0.3) | (0.09) | (0.52) | (−1.2) | (0.73) | (1.77) | (−0.98) | (−1.63) | (−0.98) | (−0.97) | (−0.9) | |||||
| 3 | −0.32 | 0.45 | −6.34 | −16.19 | −6.44c | −0.02 | 0.03 | 66 | 9.86 | −1.47 | −4.98 | −11.62 | −4.22 | −0.03 | 0.05 | 66 |
| (−0.03) | (0.08) | (−1.1) | (−1.21) | (−1.68) | (−0.27) | (1.29) | (−0.4) | (−1.26) | (−1.27) | (−1.6) | (−0.54) | |||||
| 4 | −0.25 | −0.17 | −1.22 | −1.81 | 8.51 | −0.03 | −0.05 | 65 | 10.70c | −0.62 | −6.94c | 3.41 | −0.20 | −0.06 | 0.03 | 65 |
| (−0.03) | (−0.04) | (−0.24) | (−0.17) | (1.04) | (−0.44) | (1.7) | (−0.21) | (−1.98) | (0.45) | (−0.03) | (−1.23) | |||||
| Forecast Horizon | Gold (2004:01–2020:12) | Platinum (2004:01–2020:12) | ||||||||||||||
| h | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 13.40b | −2.83 | −0.20 | 3.97 | −1.68 | 0.02 | −0.03 | 68 | 7.99 | −5.32 | −5.15 | 0.76 | −1.60 | 0.13 | −0.02 | 68 |
| (2.15) | (−0.94) | (−0.06) | (0.51) | (−0.79) | (0.45) | (0.66) | (−0.9) | (−0.79) | (0.05) | (−0.39) | (1.41) | |||||
| 2 | 15.01a | −2.91 | −3.22 | 0.05 | −0.50 | −0.03 | 0.02 | 67 | 11.86 | −5.76 | −10.43b | −1.19 | 1.81 | −0.01 | 0.05 | 67 |
| (3.24) | (−1.31) | (−1.31) | (0.01) | (−0.32) | (−0.96) | (1.44) | (−1.45) | (−2.4) | (−0.12) | (0.65) | (−0.17) | |||||
| 3 | 14.24a | −2.59 | −1.62 | 1.16 | −0.16 | −0.02 | −0.02 | 66 | 7.39 | −3.57 | −4.49 | −9.43 | −1.74 | −0.05 | 0.05 | 66 |
| (3.44) | (−1.31) | (−0.76) | (0.23) | (−0.11) | (−0.67) | (1.16) | (−1.17) | (−1.36) | (−1.23) | (−0.79) | (−1.04) | |||||
| 4 | 15.03a | −2.38 | −2.94 | 5.51 | −1.90 | −0.03 | 0.06 | 65 | 7.35 | −3.13 | −3.70 | 2.13 | 2.23 | −0.05 | 0.02 | 65 |
| (4.32) | (−1.42) | (−1.52) | (1.31) | (−0.6) | (−1.29) | (1.43) | (−1.26) | (−1.29) | (0.34) | (0.47) | (−1.31) | |||||
| Forecast Horizon | Palladium (2004:01–2020:12) | Zinc (2004:01–2020:12) | ||||||||||||||
| h | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 25.75 | −8.22 | −8.27 | −5.39 | 6.03 | 0.15 | −0.01 | 68 | 8.68 | −4.06 | −15.79b | −15.38 | 2.54 | 0.22b | 0.06 | 68 |
| (1.66) | (−1.09) | (−0.99) | (−0.28) | (1.14) | (1.26) | (0.66) | (−0.63) | (−2.23) | (−0.93) | (0.56) | (2.19) | |||||
| 2 | 29.00a | −8.33 | −8.79 | −15.25 | 2.57 | −0.06 | 0.03 | 67 | 5.83 | −0.67 | −6.85 | −9.64 | 0.78 | 0.03 | −0.05 | 67 |
| (2.64) | (−1.58) | (−1.51) | (−1.13) | (0.69) | (−0.73) | (0.53) | (−0.13) | (−1.19) | (−0.72) | (0.21) | (0.37) | |||||
| 3 | 23.67b | −5.24 | −2.35 | −12.46 | 0.92 | −0.07 | −0.01 | 66 | −0.61 | 3.31 | −5.75 | −3.17 | −1.63 | 0.01 | −0.04 | 66 |
| (2.54) | (−1.18) | (−0.49) | (−1.11) | (0.29) | (−1.06) | (−0.06) | (0.73) | (−1.17) | (−0.28) | (−0.5) | (0.13) | |||||
| 4 | 21.04a | −3.07 | −3.58 | −4.10 | 1.08 | −0.07 | −0.02 | 65 | −2.05 | 4.53 | −2.82 | 10.35 | 3.08 | 0.00 | −0.03 | 65 |
| (2.65) | (−0.8) | (−0.81) | (−0.43) | (0.15) | (−1.26) | (−0.24) | (1.12) | (−0.6) | (1.02) | (0.4) | (0) | |||||
| Forecast Horizon | Natural gas (2004:01–2020:12) | |||||||||||||||
| h | C | (Y10-Y3M) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | ||||||||
| 1 | 4.42 | −5.06 | 17.53c | 29.15 | 0.44 | −0.03 | −0.01 | 68 | ||||||||
| (0.23) | (−0.54) | (1.68) | (1.2) | (0.07) | (−0.2) | |||||||||||
| 2 | 1.56 | −5.31 | 2.90 | −6.76 | −4.44 | 0.06 | −0.05 | 67 | ||||||||
| (0.11) | (−0.77) | (0.38) | (−0.38) | (−0.92) | (0.58) | |||||||||||
| 3 | −1.68 | −4.13 | −1.47 | −18.22 | −5.65 | 0.04 | −0.01 | 66 | ||||||||
| (−0.15) | (−0.75) | (−0.25) | (−1.32) | (−1.43) | (0.51) | |||||||||||
| 4 | −0.06 | −5.29 | −0.68 | −10.39 | 11.01 | 0.03 | −0.01 | 65 | ||||||||
| (−0.01) | (−1.23) | (−0.14) | (−0.96) | (1.35) | (0.42) | |||||||||||
Notes: The forecast horizon (h) is in quarters. Y10-Y3M denotes the yield spread calculated as the difference between the yield rates on 10-year and 3-month government bonds. The table reports the estimation results of Equation (1) with the Newey and West (1987) procedure. The sample period appears separately for each commodity. Figures in parentheses denote estimated standard errors. a, b and c denote statistical significance at the 1%, 5%, and 10% levels, respectively.

Table A3.
Estimation results of Equation (1) with the Y10-Y1 indicator. Panel A: sample period 1986–2003. Panel B: sample period 2004–2020.
Table A3.
Estimation results of Equation (1) with the Y10-Y1 indicator. Panel A: sample period 1986–2003. Panel B: sample period 2004–2020.
| Panel A | ||||||||||||||||
| Forecast Horizon | Oil (1986:01–2003:12) | Silver (1986:01–2003:12) | ||||||||||||||
| h | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 10.68 | −5.04 | 0.38 | −2.13 | 10.18 | 0.04 | −0.06 | 72 | −12.36 | 10.33 ** (0.03) | 0.09 | −11.41 | −3.41 | 0.06 | 0.02 | 72 |
| 2 | 9.29 | −2.61 | −9.56 * (0.07) | −5.23 | 9.22 | 0.00 | 0.00 | 72 | −10.04 * (0.05) | 8.40 *** (0.01) | 0.54 | −6.30 | −1.82 | −0.01 | 0.05 | 72 |
| 3 | 7.75 | −0.90 | −5.37 | −4.32 | 1.16 | 0.03 | −0.03 | 72 | −10.75 *** (0.01) | 8.55 *** (0.00) | 0.40 | −9.64 * (0.09) | −2.06 | 0.00 | 0.13 | 72 |
| 4 | 6.47 | −0.83 | −3.00 | −7.62 | 1.38 | 0.04 | −0.03 | 72 | −10.23 *** (0.00) | 8.30 *** (0.00) | −0.13 | −7.98 * (0.09) | −1.94 | 0.00 | 0.18 | 72 |
| Forecast Horizon | Gold (1986:01–2003:12) | Platinum (1986:04–2003:12) | ||||||||||||||
| h | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | −8.47 | 5.17 | 4.41 | −10.64 | 3.55 | 0.01 | 0.03 | 70 | −3.87 | 4.24 | −1.97 | −22.85 | 7.19 | −0.07 | 0.05 | 72 |
| 2 | −4.65 | 5.43 *** (0.01) | −1.55 | 2.89 | −4.56 | −0.01 | 0.07 | 70 | −4.31 | 4.94 * (0.08) | −1.66 | −14.42 ** (0.03) | 3.87 | −0.03 | 0.07 | 72 |
| 3 | −4.99 * (0.05) | 4.71 *** (0.00) | −0.59 | 0.26 | −2.62 | −0.01 | 0.09 | 70 | −5.63 | 5.03 ** (0.02) | 0.32 | −10.42 * (0.05) | 6.87 | −0.01 | 0.11 | 72 |
| 4 | −5.03 ** (0.03) | 4.71 *** (0.00) | −0.98 | −0.86 | −3.38 | −0.01 | 0.12 | 70 | −5.16 | 5.25 *** (0.01) | −0.22 | −5.71 | 5.58 | −0.02 | 0.11 | 72 |
| Forecast Horizon | Palladium (1986:04–2003:12) | Zinc (1997:08–2003:12) | ||||||||||||||
| h | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 11.59 | −7.16 | −14.61 * (0.05) | −12.90 | 33.00 ** (0.04) | −0.09 | 0.08 | 72 | −21.33 * (0.06) | 9.16 | 8.23 | −25.35 | 11.31 | 0.03 | 0.10 | 26 |
| 2 | 7.05 | −5.81 | −3.70 | −11.63 | 31.04 *** (0.01) | −0.07 | 0.06 | 72 | −16.97 ** (0.04) | 7.48 | 6.01 | −27.80 | 6.11 | 0.01 | 0.16 | 26 |
| 3 | 3.32 | −4.93 | 3.38 | −4.13 | 36.35 *** (0.00) | −0.02 | 0.14 | 72 | −15.35 ** (0.02) | 7.55 ** (0.04) | 3.84 | −25.00 * (0.09) | −0.50 | 0.08 | 0.23 | 26 |
| 4 | 1.79 | −3.31 | 3.58 | −4.30 | 30.21 *** (0.00) | −0.02 | 0.11 | 72 | −15.03 *** (0.01) | 8.66 *** (0.01) | 2.34 | −12.80 | 3.54 | 0.09 | 0.28 | 26 |
| Forecast Horizon | Natural gas (1990:05–2003:12) | |||||||||||||||
| h | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | ||||||||
| 1 | 4.59 | −4.38 | 18.18 | −12.43 | 36.19 | 0.01 | −0.04 | 55 | ||||||||
| 2 | −3.53 | 3.48 | 5.06 | −33.81 | 22.93 | −0.03 | −0.03 | 55 | ||||||||
| 3 | −12.73 | 7.90 | 5.30 | −49.78 *** (0.00) | 23.53 * (0.09) | 0.11 | 0.15 | 55 | ||||||||
| 4 | −9.98 | 8.53 | 4.29 | −31.91 ** (0.02) | 14.60 | 0.09 | 0.10 | 55 | ||||||||
| Panel B | ||||||||||||||||
| Forecast Horizon | Oil (2004:01–2020:12) | Silver (2004:01–2020:12) | ||||||||||||||
| h | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 0.01 | −0.71 | 0.87 | 16.72 | −15.96 ** (0.04) | 0.17 | 0.04 | 67 | 13.07 | −6.08 | −2.52 | −14.07 | −4.75 | 0.08 | −0.03 | 67 |
| 2 | 3.06 | −2.22 | 0.81 | 9.33 | −6.02 * (0.09) | 0.07 | −0.03 | 66 | 15.64 * (0.09) | −4.56 | −7.99 | −11.44 | −3.10 | −0.06 | 0.06 | 66 |
| 3 | 2.19 | −1.56 | −6.05 | −16.46 | −6.38 | −0.04 | 0.04 | 65 | 10.99 | −2.58 | −4.89 | −11.82 | −4.20 | −0.04 | 0.06 | 65 |
| 4 | 1.64 | −1.67 | −1.05 | −1.99 | 8.65 | −0.04 | −0.05 | 64 | 11.94 * (0.05) | −1.64 | −6.86 * (0.06) | 3.29 | −0.10 | −0.06 | 0.03 | 64 |
| Forecast Horizon | Gold (2004:01–2020:12) | Platinum (2004:01–2020:12) | ||||||||||||||
| h | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 12.91 ** (0.03) | −2.92 | −0.23 | 3.82 | −1.73 | 0.02 | −0.03 | 67 | 6.12 | −5.08 | −5.07 | 0.34 | −1.76 | 0.12 | −0.03 | 67 |
| 2 | 14.64 *** (0.00) | −3.10 | −3.25 | −0.10 | −0.54 | −0.03 | 0.02 | 66 | 9.76 | −5.21 | −10.51 ** (0.02) | −1.47 | 1.68 | −0.01 | 0.04 | 66 |
| 3 | 14.14 *** (0.00) | −2.91 | −1.65 | 1.01 | −0.19 | −0.02 | −0.02 | 65 | 7.63 | −4.39 | −4.44 | −9.72 | −1.78 | −0.05 | 0.06 | 65 |
| 4 | 15.12 *** (0.00) | −2.78 | −2.98 | 5.36 | −2.01 | −0.03 | 0.07 | 64 | 7.83 | −4.00 | −3.69 | 1.85 | 2.06 | −0.05 | 0.03 | 64 |
| Forecast Horizon | Palladium (2004:01–2020:12) | Zinc (2004:01–2020:12) | ||||||||||||||
| h | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 24.57 * (0.09) | −9.53 | −7.76 | −6.41 | 5.78 | 0.10 | −0.02 | 67 | 9.45 | −5.33 | −15.72 ** (0.03) | −15.73 | 2.51 | 0.21 ** (0.04) | 0.06 | 67 |
| 2 | 26.18 ** (0.02) | −7.80 | −8.83 | −15.73 | 2.36 | −0.06 | 0.02 | 66 | 6.95 | −1.46 | −6.89 | −9.66 | 0.83 | 0.03 | −0.05 | 66 |
| 3 | 23.33 *** (0.01) | −5.92 | −2.31 | −12.83 | 0.82 | −0.07 | −0.01 | 65 | 2.55 | 1.68 | −5.68 | −3.06 | −1.41 | 0.01 | −0.05 | 65 |
| 4 | 21.35 *** (0.00) | −3.68 | −3.65 | −4.26 | 1.01 | −0.07 | −0.02 | 64 | 1.63 | 2.63 | −2.57 | 10.56 | 3.89 | −0.01 | −0.05 | 64 |
| Forecast Horizon | Natural Gas (2004:01–2020:12) | |||||||||||||||
| h | C | (Y10-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | ||||||||
| 1 | 1.86 | −3.96 | 17.37 | 28.99 | 0.32 | −0.02 | −0.01 | 67 | ||||||||
| 2 | −0.63 | −4.66 | 2.84 | −7.03 | −4.58 | 0.06 | −0.05 | 66 | ||||||||
| 3 | −2.01 | −4.66 | −1.41 | −18.54 | −5.74 | 0.04 | −0.01 | 65 | ||||||||
| 4 | −1.42 | −5.19 | −0.79 | −10.76 | 10.45 | 0.03 | −0.01 | 64 | ||||||||
Notes: The forecast horizon (h) is in quarters. Y10-Y1 denotes the yield spread calculated as the difference between the yield rates on 10-year and 1-year government bonds. The table reports the estimation results of Equation (1) with the Newey and West (1987) procedure. The sample period appears separately for each commodity. Figures in parentheses denote estimated standard errors. ***, ** and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.

Table A4.
Estimation results of Equation (1) with the Y10-Y2 indicator. Panel A: sample period 1986–2003. Panel B: sample period 2004–2020.
Table A4.
Estimation results of Equation (1) with the Y10-Y2 indicator. Panel A: sample period 1986–2003. Panel B: sample period 2004–2020.
| Panel A | ||||||||||||||||
| Forecast Horizon | Oil (1986:01–2003:12) | Silver (1986:01–2003:12) | ||||||||||||||
| h | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 10.51 | −6.94 | 0.47 | −2.11 | 9.52 | 0.04 | −0.06 | 72 | −11.02 | 13.14 ** (0.02) | −0.01 | −11.22 | −1.76 | 0.06 | 0.03 | 72 |
| 2 | 8.54 | −2.87 | −9.57 * (0.07) | −5.37 | 8.69 | 0.00 | 0.00 | 72 | −9.15 * (0.05) | 10.90 *** (0.00) | 0.44 | −6.19 | −0.53 | −0.01 | 0.07 | 72 |
| 3 | 6.92 | −0.37 | −5.42 | −4.51 | 0.81 | 0.03 | −0.03 | 72 | −10.21 *** (0.01) | 11.50 *** (0.00) | 0.26 | −9.61 * (0.08) | −0.86 | 0.00 | 0.17 | 72 |
| 4 | 5.07 | 0.34 | −3.11 | −7.94 | 0.88 | 0.04 | −0.03 | 72 | −9.70*** (0.00) | 11.15 *** (0.00) | −0.26 | −7.95 * (0.08) | −0.77 | 0.00 | 0.23 | 72 |
| Forecast Horizon | Gold (1986:01–2003:12) | Platinum (1986:04–2003:12) | ||||||||||||||
| h | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | −8.04 | 6.88 * (0.08) | 4.32 | −10.59 | 4.28 | 0.01 | 0.04 | 70 | −3.70 | 5.81 | −2.05 | −22.86 ** (0.03) | 7.76 | −0.07 | 0.05 | 72 |
| 2 | −4.12 | 7.13 *** (0.00) | −1.63 | 2.96 | −3.76 | −0.01 | 0.09 | 70 | −3.63 | 6.24 * (0.07) | −1.71 | −14.32 ** (0.03) | 4.67 | −0.03 | 0.07 | 72 |
| 3 | −4.85 ** (0.03) | 6.54 *** (0.00) | −0.69 | 0.25 | −2.02 | −0.01 | 0.13 | 70 | −5.00 | 6.41 ** (0.02) | 0.27 | −10.32 * (0.05) | 7.67 * (0.07) | −0.01 | 0.12 | 72 |
| 4 | −4.94 *** (0.01) | 6.59 *** (0.00) | −1.08 | −0.89 | −2.80 | −0.01 | 0.18 | 70 | −4.48 | 6.69 *** (0.01) | −0.27 | −5.61 | 6.42 * (0.09) | −0.02 | 0.12 | 72 |
| Forecast Horizon | Palladium (1986:04–2003:12) | Zinc (1997:08–2003:12) | ||||||||||||||
| h | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 9.00 | −7.31 | −14.69 | −13.43 | 31.39 | −0.09 | 0.07 | 72 | −19.80 * (0.06) | 10.45 | 8.30 | −24.92 | 12.87 | 0.03 | 0.10 | 26 |
| 2 | 6.24 | −7.35 | −3.65 | −11.75 | 30.10 | −0.07 | 0.06 | 72 | −16.40 ** (0.04) | 9.25 * (0.08) | 5.98 | −27.08 | 7.58 | 0.00 | 0.17 | 26 |
| 3 | 2.72 | −6.32 | 3.43 | −4.21 | 35.57 | −0.02 | 0.14 | 72 | −14.85 ** (0.02) | 9.42 ** (0.03) | 3.79 | −24.23 * (0.09) | 1.01 | 0.08 | 0.26 | 26 |
| 4 | 1.38 | −4.23 | 3.61 | −4.36 | 29.68 | −0.02 | 0.11 | 72 | −14.53 *** (0.01) | 10.91 *** (0.00) | 2.28 | −11.87 | 5.29 | 0.08 | 0.33 | 26 |
| Forecast Horizon | Natural Gas (1990:05–2003:12) | |||||||||||||||
| h | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | ||||||||
| 1 | 4.28 | −5.76 | 18.25 | −12.59 | 35.60 | 0.01 | −0.04 | 55 | ||||||||
| 2 | −0.05 | 1.51 | 5.22 | −32.94 | 23.99 | −0.04 | −0.03 | 55 | ||||||||
| 3 | −8.32 | 6.74 | 5.43 | −48.61 *** (0.01) | 25.29 * (0.07) | 0.10 | 0.13 | 55 | ||||||||
| 4 | −6.13 | 8.14 | 4.38 | −30.86 ** (0.03) | 16.34 | 0.08 | 0.08 | 55 | ||||||||
| Panel B | ||||||||||||||||
| Forecast Horizon | Oil (2004:01–2020:12) | Silver (2004:01–2020:12) | ||||||||||||||
| h | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 0.64 | −1.32 | 0.90 | 16.67 | −15.94 ** (0.04) | 0.17 | 0.04 | 67 | 12.44 | −6.54 | −2.47 | −14.23 | −4.82 | 0.08 | −0.03 | 67 |
| 2 | 2.39 | −2.04 | 0.81 | 9.29 | −6.07 | 0.07 | −0.03 | 66 | 15.43 * (0.09) | −5.12 | −7.94 | −11.58 | −3.15 | −0.06 | 0.05 | 66 |
| 3 | 2.44 | −2.01 | −6.02 | −16.53 | −6.38 * (0.09) | −0.04 | 0.04 | 65 | 12.12 | −3.87 | −4.83 | −11.96 | −4.17 | −0.04 | 0.06 | 65 |
| 4 | 2.98 | −2.99 | −0.97 | −2.09 | 8.80 | −0.04 | −0.05 | 64 | 13.44 ** (0.03) | −3.08 | −6.78 * (0.06) | 3.18 | 0.08 | −0.06 | 0.04 | 64 |
| Forecast Horizon | Gold (2004:01–2020:12) | Platinum (2004:01–2020:12) | ||||||||||||||
| h | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 12.82 ** (0.04) | −3.31 | −0.20 | 3.73 | −1.76 | 0.02 | −0.03 | 67 | 4.78 | −4.82 | −5.04 | 0.25 | −1.84 | 0.12 | −0.03 | 67 |
| 2 | 14.76 *** (0.00) | −3.68 | −3.21 | −0.21 | −0.56 | −0.03 | 0.02 | 66 | 8.53 | −5.06 | −10.48 ** (0.02) | −1.57 | 1.59 | −0.01 | 0.04 | 66 |
| 3 | 14.61 *** (0.00) | −3.74 | −1.60 | 0.89 | −0.20 | −0.02 | −0.01 | 65 | 7.96 | −5.35 | −4.37 | −9.88 | −1.82 | −0.05 | 0.06 | 65 |
| 4 | 15.67 *** (0.00) | −3.66 * (0.09) | −2.93 | 5.24 | −2.01 | −0.03 | 0.08 | 64 | 8.58 * (0.09) | −5.23 | −3.62 | 1.69 | 2.05 | −0.05 | 0.04 | 64 |
| Forecast Horizon | Palladium (2004:01–2020:12) | Zinc (2004:01–2020:12) | ||||||||||||||
| h | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 23.20 | −9.94 | −7.69 | −6.65 | 5.65 | 0.10 | −0.02 | 67 | 10.90 | −7.32 | −15.61 ** (0.03) | −15.98 | 2.51 | 0.21 ** (0.04) | 0.06 | 67 |
| 2 | 25.65 ** (0.02) | −8.61 | −8.75 | −15.96 | 2.27 | −0.06 | 0.02 | 66 | 9.24 | −3.49 | −6.80 | −9.83 | 0.89 | 0.03 | −0.05 | 66 |
| 3 | 24.84 *** (0.01) | −8.04 | −2.20 | −13.10 | 0.83 | −0.08 | 0.00 | 65 | 5.34 | −0.22 | −5.64 | −3.14 | −1.25 | 0.01 | −0.05 | 65 |
| 4 | 23.42 *** (0.00) | −5.90 | −3.52 | −4.47 | 1.21 | −0.07 | −0.01 | 64 | 4.68 | 0.63 | −2.45 | 10.55 | 4.42 | −0.01 | −0.06 | 64 |
| Forecast Horizon | Natural Gas (2004:01–2020:12) | |||||||||||||||
| h | C | (Y10-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | ||||||||
| 1 | 2.17 | −4.83 | 17.42 | 28.85 | 0.30 | −0.02 | −0.01 | 67 | ||||||||
| 2 | −0.89 | −5.19 | 2.89 | −7.17 | −4.63 | 0.06 | −0.05 | 66 | ||||||||
| 3 | −1.55 | −5.77 | −1.34 | −18.72 | −5.77 | 0.04 | −0.01 | 65 | ||||||||
| 4 | −1.25 | −6.14 | −0.74 | −10.95 | 10.32 | 0.03 | −0.01 | 64 | ||||||||
Notes: The forecast horizon (h) is in quarters. Y10-Y2 denotes the yield spread calculated as the difference between the yield rates on 10-year and 2-year government bonds. The table reports the estimation results of Equation (1) with the Newey and West (1987) procedure. The sample period appears separately for each commodity. Figures in parentheses denote estimated standard errors. ***, ** and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.

Table A5.
Estimation results of Equation (1) with the Y30-Y3M indicator. Panel A: sample period 1986–2003. Panel B: sample period 2004–2020.
Table A5.
Estimation results of Equation (1) with the Y30-Y3M indicator. Panel A: sample period 1986–2003. Panel B: sample period 2004–2020.
| Panel A | ||||||||||||||||
| Forecast Horizon | Oil (1986:01–2003:12) | Silver (1986:01–2003:12) | ||||||||||||||
| h | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 12.77 | −4.45 | 0.56 | −1.91 | 11.52 | 0.04 | −0.06 | 72 | −13.32 | 7.41 ** (0.03) | −0.04 | −11.21 | −4.69 | 0.05 | 0.01 | 72 |
| 2 | 9.63 | −1.93 | −9.52 * (0.07) | −5.25 | 9.60 | 0.00 | 0.00 | 72 | −11.32 ** (0.04) | 6.28 *** (0.01) | 0.39 | −6.24 | −3.08 | −0.02 | 0.05 | 72 |
| 3 | 8.10 | −0.78 | −5.34 | −4.29 | 1.39 | 0.03 | −0.03 | 72 | −12.25 *** (0.01) | 6.50 *** (0.00) | 0.24 | −9.61 * (0.09) | −3.43 | −0.01 | 0.14 | 72 |
| 4 | 6.17 | −0.41 | −3.02 | −7.71 | 1.32 | 0.04 | −0.03 | 72 | −11.34 *** (0.00) | 6.13 *** (0.00) | −0.26 | −7.89 * (0.09) | −3.12 | −0.01 | 0.17 | 72 |
| Forecast Horizon | Gold (1986:01–2003:12) | Platinum (1986:04–2003:12) | ||||||||||||||
| h | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | −7.98 | 3.22 | 4.39 | −10.34 | 3.31 | 0.01 | 0.02 | 70 | −5.10 | 3.47 | −2.09 | −22.94 | 6.29 | −0.07 | 0.05 | 72 |
| 2 | −4.92 | 3.77 *** (0.01) | −1.60 | 3.03 | −5.13 | −0.02 | 0.06 | 70 | −5.62 | 3.98 * (0.06) | −1.79 | −14.49 ** (0.03) | 2.88 | −0.04 | 0.08 | 72 |
| 3 | −5.12 * (0.06) | 3.22 *** (0.01) | −0.63 | 0.41 | −3.06 | −0.02 | 0.07 | 70 | −6.89 * (0.08) | 4.02 *** (0.01) | 0.20 | −10.48 ** (0.04) | 5.88 | −0.01 | 0.12 | 72 |
| 4 | −4.96 ** (0.04) | 3.11 *** (0.00) | −1.00 | −0.68 | −3.73 | −0.01 | 0.09 | 70 | −6.42 * (0.07) | 4.17 *** (0.01) | −0.34 | −5.76 | 4.59 | −0.02 | 0.12 | 72 |
| Forecast Horizon | Palladium (1986:04–2003:12) | Zinc (1997:08–2003:12) | ||||||||||||||
| h | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 10.62 | −4.30 | −14.65 * (0.05) | −13.36 | 33.17 ** (0.04) | −0.08 | 0.07 | 72 | −21.63 * (0.07) | 6.28 | 7.90 | −25.51 | 9.97 | 0.03 | 0.09 | 26 |
| 2 | 7.04 | −3.89 | −3.67 | −11.85 | 31.52 *** (0.01) | −0.07 | 0.06 | 72 | −18.24 ** (0.04) | 5.68 * (0.09) | 5.59 | −27.52 | 5.02 | 0.01 | 0.17 | 26 |
| 3 | 3.00 | −3.14 | 3.38 | −4.38 | 36.62 *** (0.00) | −0.01 | 0.13 | 72 | −17.30 *** (0.01) | 6.09 ** (0.02) | 3.31 | −24.44 * (0.09) | −1.61 | 0.08 | 0.27 | 26 |
| 4 | 0.66 | −1.64 | 3.51 | −4.65 | 29.98 *** (0.00) | −0.02 | 0.11 | 72 | −17.16 *** (0.01) | 6.94 *** (0.00) | 1.75 | −12.20 | 2.27 | 0.09 | 0.34 | 26 |
| Forecast Horizon | Natural Gas (1990:05–2003:12) | |||||||||||||||
| h | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | ||||||||
| 1 | 7.71 | −4.40 | 18.39 | −11.95 | 37.52 | 0.01 | −0.04 | 55 | ||||||||
| 2 | −3.67 | 2.41 | 5.02 | −33.69 | 22.62 | −0.03 | −0.03 | 55 | ||||||||
| 3 | −14.50 | 6.16 | 5.13 | −49.82 *** (0.00) | 22.36 | 0.10 | 0.15 | 55 | ||||||||
| 4 | −13.07 | 7.20 * (0.07) | 4.04 | −32.21 ** (0.02) | 12.97 | 0.09 | 0.11 | 55 | ||||||||
| Panel B | ||||||||||||||||
| Forecast Horizon | Oil (2004:01–2020:12) | Silver (2004:01–2020:12) | ||||||||||||||
| h | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | −3.50 | 1.08 | 0.76 | 16.84 | −16.06 ** (0.04) | 0.17 | 0.04 | 67 | 15.85 | −5.05 | −2.31 | −14.20 | −4.77 | 0.08 | −0.03 | 67 |
| 2 | 2.08 | −0.98 | 0.81 | 9.35 | −6.09 | 0.07 | −0.03 | 66 | 17.66 * (0.08) | −3.76 | −7.83 | −11.53 | −3.12 | −0.06 | 0.06 | 66 |
| 3 | 0.66 | −0.34 | −6.05 | −16.43 | −6.48 * (0.09) | −0.04 | 0.04 | 65 | 13.20 | −2.58 | −4.77 | −11.91 | −4.17 | −0.04 | 0.06 | 65 |
| 4 | 0.65 | −0.63 | −1.06 | −1.98 | 8.48 | −0.04 | −0.05 | 64 | 13.85 * (0.05) | −1.87 | −6.70 * (0.06) | 3.26 | 0.23 | −0.06 | 0.04 | 64 |
| Forecast Horizon | Gold (2004:01–2020:12) | Platinum (2004:01–2020:12) | ||||||||||||||
| h | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 15.19 ** (0.03) | −2.83 | −0.11 | 3.73 | −1.71 | 0.02 | −0.03 | 67 | 9.44 | −4.65 | −4.86 | 0.20 | −1.75 | 0.12 | −0.02 | 67 |
| 2 | 16.84 *** (0.00) | −2.91 | −3.12 | −0.19 | −0.52 | −0.03 | 0.04 | 66 | 12.79 | −4.61 | −10.31 ** (0.02) | −1.60 | 1.68 | −0.01 | 0.05 | 66 |
| 3 | 16.44 *** (0.00) | −2.83 * (0.08) | −1.52 | 0.92 | −0.16 | −0.02 | 0.01 | 65 | 9.74 | −3.69 | −4.28 | −9.82 | −1.80 | −0.05 | 0.07 | 65 |
| 4 | 17.09 *** (0.00) | −2.63 * (0.05) | −2.79 | 5.32 | −1.67 | −0.03 | 0.09 | 64 | 9.50 * (0.09) | −3.28 | −3.48 | 1.81 | 2.35 | −0.05 | 0.04 | 64 |
| Forecast Horizon | Palladium (2004:01–2020:12) | Zinc (2004:01–2020:12) | ||||||||||||||
| h | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 29.84 * (0.07) | −8.31 | −7.40 | −6.65 | 5.77 | 0.10 | −0.01 | 67 | 8.58 | −2.99 | −15.64 ** (0.03) | −15.73 | 2.41 | 0.21 | 0.05 | 67 |
| 2 | 30.47 *** (0.01) | −6.79 | −8.53 | −15.93 | 2.35 | −0.06 | 0.03 | 66 | 5.39 | −0.25 | −6.91 | −9.61 | 0.76 | 0.03 | −0.05 | 66 |
| 3 | 26.31 *** (0.01) | −5.03 | −2.10 | −12.97 | 0.81 | −0.07 | 0.00 | 65 | −0.13 | 2.21 | −5.79 | −2.97 | −1.49 | 0.01 | −0.04 | 65 |
| 4 | 22.79 *** (0.01) | −2.97 | −3.46 | −4.30 | 1.26 | −0.07 | −0.02 | 64 | −1.41 | 3.00 | −2.82 | 10.61 | 3.38 | −0.01 | −0.04 | 64 |
| Forecast Horizon | Natural gas (2004:01–2020:12)) | |||||||||||||||
| h | C | (Y30-M3) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | ||||||||
| 1 | 0.34 | −1.84 | 17.39 | 29.02 | 0.22 | −0.02 | −0.01 | 67 | ||||||||
| 2 | −1.16 | −2.72 | 2.91 | −7.04 | −4.67 | 0.06 | −0.06 | 66 | ||||||||
| 3 | −2.99 | −2.55 | −1.33 | −18.55 | −5.89 | 0.04 | −0.01 | 65 | ||||||||
| 4 | −1.73 | −3.17 | −0.66 | −10.78 | 10.40 | 0.03 | −0.02 | 64 | ||||||||
Notes: The forecast horizon (h) is in quarters. Y30-Y3M denotes the yield spread calculated as the difference between the yield rates on 10-year and 3-month government bonds. The table reports the estimation results of Equation (1) with the Newey and West (1987) procedure. The sample period appears separately for each commodity. Figures in parentheses denote estimated standard errors. ***, ** and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.

Table A6.
Estimation results of Equation (1) with the Y30-Y1 indicator. Panel A: sample period 1986–2003. Panel B: sample period 2004–2020.
Table A6.
Estimation results of Equation (1) with the Y30-Y1 indicator. Panel A: sample period 1986–2003. Panel B: sample period 2004–2020.
| Panel A | ||||||||||||||||
| Forecast Horizon | Oil (1986:01–2003:12) | Silver (1986:01–2003:12) | ||||||||||||||
| h | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 11.73 | −4.60 | 0.50 | −1.93 | 10.11 | 0.04 | −0.06 | 72 | −13.51 * (0.08) | 8.82 *** (0.01) | −0.08 | −11.60 | −2.95 | 0.06 | 0.03 | 72 |
| 2 | 9.08 | −1.93 | −9.55 * (0.07) | −5.29 | 8.95 | 0.00 | 0.00 | 72 | −11.34 ** (0.03) | 7.39 *** (0.00) | 0.37 | −6.54 | −1.56 | −0.01 | 0.08 | 72 |
| 3 | 7.17 | −0.36 | −5.41 | −4.46 | 0.90 | 0.03 | −0.03 | 72 | −12.32 *** (0.00) | 7.68 *** (0.00) | 0.21 | −9.93 * (0.07) | −1.88 | 0.00 | 0.19 | 72 |
| 4 | 5.40 | −0.01 | −3.08 | −7.86 | 0.97 | 0.04 | −0.04 | 72 | −11.52 *** (0.00) | 7.31 *** (0.00) | −0.30 | −8.22 * (0.07) | −1.69 | 0.00 | 0.24 | 72 |
| Forecast Horizon | Gold (1986:01–2003:12) | Platinum (1986:04–2003:12) | ||||||||||||||
| h | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | −8.48 | 4.09 | 4.35 | −10.60 | 3.93 | 0.01 | 0.03 | 70 | −4.59 | 3.77 | −2.06 | −22.99 ** (0.03) | 7.30 | −0.07 | 0.06 | 72 |
| 2 | −4.99 | 4.49 *** (0.00) | −1.62 | 2.85 | −4.25 | −0.01 | 0.09 | 70 | −4.77 | 4.17 * (0.06) | −1.74 | −14.49 ** (0.03) | 4.12 | −0.03 | 0.08 | 72 |
| 3 | −5.71 ** (0.02) | 4.16 *** (0.00) | −0.69 | 0.14 | −2.48 | −0.01 | 0.13 | 70 | −6.35 * (0.08) | 4.39 *** (0.01) | 0.22 | −10.54 ** (0.04) | 7.05 * (0.09) | −0.01 | 0.13 | 72 |
| 4 | −5.69 *** (0.01) | 4.11 *** (0.00) | −1.07 | −0.97 | −3.23 | −0.01 | 0.16 | 70 | −5.93 * (0.07) | 4.60 *** (0.00) | −0.32 | −5.85 | 5.76 | −0.02 | 0.13 | 72 |
| Forecast Horizon | Palladium (1986:04–2003:12) | Zinc (1997:08–2003:12) | ||||||||||||||
| h | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 10.57 | −5.02 | −14.64 * (0.05) | −13.17 | 32.11 ** (0.04) | −0.09 | 0.08 | 72 | −21.84 * (0.06) | 6.90 | 8.09 | −25.65 | 11.71 | 0.03 | 0.10 | 26 |
| 2 | 7.38 | −4.78 | −3.63 | −11.59 | 30.69 *** (0.01) | −0.07 | 0.07 | 72 | −18.30 ** (0.03) | 6.16 * (0.08) | 5.78 | −27.69 | 6.57 | 0.00 | 0.18 | 26 |
| 3 | 3.17 | −3.79 | 3.40 | −4.19 | 35.91 *** (0.00) | −0.02 | 0.14 | 72 | −17.09 *** (0.01) | 6.44 ** (0.02) | 3.55 | −24.73 * (0.08) | 0.02 | 0.08 | 0.28 | 26 |
| 4 | 1.10 | −2.19 | 3.55 | −4.48 | 29.72 *** (0.00) | −0.02 | 0.11 | 72 | −17.03 *** (0.00) | 7.41 *** (0.00) | 2.01 | −12.49 | 4.14 | 0.08 | 0.35 | 26 |
| Forecast Horizon | Natural gas (1990:05–2003:12) | |||||||||||||||
| h | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | ||||||||
| 1 | 6.68 | −4.48 | 18.32 | −12.18 | 36.38 | 0.01 | −0.04 | 55 | ||||||||
| 2 | −1.62 | 1.67 | 5.15 | −33.25 | 23.58 | −0.04 | −0.03 | 55 | ||||||||
| 3 | −11.31 | 5.34 | 5.33 | −49.12 *** (0.01) | 24.34 * (0.08) | 0.10 | 0.14 | 55 | ||||||||
| 4 | −8.91 | 6.01 | 4.30 | −31.30 ** (0.03) | 15.38 | 0.09 | 0.09 | 55 | ||||||||
| Panel B | ||||||||||||||||
| Forecast Horizon | Oil (2004:01–2020:12) | Silver (2004:01–2020:12) | ||||||||||||||
| h | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | −3.42 | 1.15 | 0.77 | 16.91 | −16.04 ** (0.04) | 0.17 | 0.04 | 67 | 14.08 | −4.73 | −2.40 | −14.42 | −4.86 | 0.08 | −0.03 | 67 |
| 2 | 0.85 | −0.50 | 0.77 | 9.36 | −6.13 | 0.07 | −0.03 | 66 | 16.73 * (0.09) | −3.71 | −7.89 | −11.72 | −3.19 | −0.06 | 0.06 | 66 |
| 3 | 1.44 | −0.75 | −6.04 | −16.50 | −6.46 * (0.09) | −0.04 | 0.04 | 65 | 13.60 * (0.09) | −3.04 | −4.77 | −12.10 | −4.19 | −0.03 | 0.06 | 65 |
| 4 | 1.53 | −1.12 | −1.02 | −2.06 | 8.57 | −0.04 | −0.05 | 64 | 14.52 ** (0.03) | −2.39 | −6.70 * (0.06) | 3.10 | 0.22 | −0.06 | 0.04 | 64 |
| Forecast Horizon | Gold (2004:01–2020:12) | Platinum (2004:01–2020:12) | ||||||||||||||
| h | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 14.67 ** (0.03) | −2.87 | −0.14 | 3.57 | −1.76 | 0.02 | −0.03 | 67 | 6.63 | −3.78 | −4.97 | 0.07 | −1.86 | 0.12 | −0.03 | 67 |
| 2 | 16.43 *** (0.00) | −3.02 | −3.15 | −0.36 | −0.57 | −0.03 | 0.04 | 66 | 10.72 | −4.10 | −10.40 ** (0.02) | −1.77 | 1.58 | −0.01 | 0.04 | 66 |
| 3 | 16.26 *** (0.00) | −3.04 * (0.07) | −1.54 | 0.74 | −0.21 | −0.02 | 0.01 | 65 | 9.37 | −3.91 | −4.31 | −10.04 | −1.87 | −0.05 | 0.07 | 65 |
| 4 | 17.07 *** (0.00) | −2.89 ** (0.04) | −2.83 | 5.14 | −1.82 | −0.03 | 0.10 | 64 | 9.44 * (0.08) | −3.58 * (0.09) | −3.53 | 1.58 | 2.15 | −0.05 | 0.05 | 64 |
| Forecast Horizon | Palladium (2004:01–2020:12) | Zinc (2004:01–2020:12) | ||||||||||||||
| h | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 25.07 | −6.88 | −7.61 | −6.89 | 5.57 | 0.11 | −0.02 | 67 | 8.66 | −3.34 | −15.66 ** (0.03) | −15.93 | 2.38 | 0.21 ** (0.04) | 0.05 | 67 |
| 2 | 27.23 ** (0.02) | −5.95 | −8.68 | −16.16 | 2.20 | −0.06 | 0.02 | 66 | 6.70 | −0.90 | −6.87 | −9.71 | 0.79 | 0.03 | −0.05 | 66 |
| 3 | 25.42 *** (0.01) | −5.14 | −2.15 | −13.24 | 0.70 | −0.07 | 0.00 | 65 | 2.66 | 1.13 | −5.71 | −2.99 | −1.35 | 0.01 | −0.05 | 65 |
| 4 | 23.11 *** (0.00) | −3.43 | −3.49 | −4.53 | 1.13 | −0.07 | −0.02 | 64 | 1.69 | 1.82 | −2.61 | 10.69 | 4.00 | −0.01 | −0.05 | 64 |
| Forecast Horizon | Natural gas (2004:01–2020:12)) | |||||||||||||||
| h | C | (Y30-Y1) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | ||||||||
| 1 | −1.61 | −1.10 | 17.31 | 29.03 | 0.16 | −0.02 | −0.01 | 67 | ||||||||
| 2 | −3.34 | −1.97 | 2.82 | −7.08 | −4.75 | 0.06 | −0.06 | 66 | ||||||||
| 3 | −3.84 | −2.42 | −1.37 | −18.66 | −5.96 | 0.04 | −0.01 | 65 | ||||||||
| 4 | −3.23 | −2.78 | −0.79 | −10.94 | 10.00 | 0.03 | −0.02 | 64 | ||||||||
Notes: The forecast horizon (h) is in quarters. Y30-Y1 denotes the yield spread calculated as the difference between the yield rates on 10-year and 1-year government bonds. The table reports the estimation results of Equation (1) with the Newey and West (1987) procedure. The sample period appears separately for each commodity. Figures in parentheses denote estimated standard errors. ***, ** and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.

Table A7.
Estimation results of Equation (1) with the Y30-Y2 indicator. Panel A: sample period 1986–2003. Panel B: sample period 2004–2020.
Table A7.
Estimation results of Equation (1) with the Y30-Y2 indicator. Panel A: sample period 1986–2003. Panel B: sample period 2004–2020.
| Panel A | ||||||||||||||||
| Forecast Horizon | Oil (1986:01–2003:12) | Silver (1986:01–2003:12) | ||||||||||||||
| h | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 11.32 | −5.65 | 0.56 | −1.99 | 9.36 | 0.04 | −0.06 | 72 | −11.97 * (0.09) | 10.26 *** (0.01) | −0.13 | −11.33 | −1.33 | 0.06 | 0.04 | 72 |
| 2 | 8.40 | −1.97 | −9.57 * (0.07) | −5.43 | 8.52 | 0.00 | 0.00 | 72 | −10.23 ** (0.03) | 8.73 *** (0.00) | 0.31 | −6.35 | −0.24 | −0.01 | 0.09 | 72 |
| 3 | 6.51 | 0.05 | −5.46 | −4.60 | 0.70 | 0.03 | −0.03 | 72 | −11.45 *** (0.00) | 9.29 *** (0.00) | 0.12 | −9.80 * (0.07) | −0.58 | 0.00 | 0.22 | 72 |
| 4 | 4.35 | 0.81 | −3.17 | −8.10 | 0.73 | 0.04 | −0.03 | 72 | −10.68 *** (0.00) | 8.84 *** (0.00) | −0.38 | −8.09 * (0.07) | −0.44 | 0.00 | 0.28 | 72 |
| Forecast Horizon | Gold (1986:01–2003:12) | Platinum (1986:04–2003:12) | ||||||||||||||
| h | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | −7.86 | 4.87 * (0.09) | 4.29 | −10.48 | 4.62 | 0.01 | 0.03 | 70 | −4.23 | 4.62 | −2.11 | −22.94 ** (0.03) | 7.92 | −0.07 | 0.06 | 72 |
| 2 | −4.30 | 5.30 *** (0.00) | −1.66 | 2.97 | −3.45 | −0.01 | 0.10 | 70 | −4.00 | 4.81 * (0.05) | −1.76 | −14.35 ** (0.03) | 4.89 | −0.04 | 0.08 | 72 |
| 3 | −5.34 ** (0.02) | 5.13 *** (0.00) | −0.75 | 0.19 | −1.82 | −0.01 | 0.16 | 70 | −5.61 * (0.09) | 5.12 *** (0.01) | 0.19 | −10.41 ** (0.04) | 7.85 * (0.06) | −0.01 | 0.13 | 72 |
| 4 | −5.36 *** (0.00) | 5.10 *** (0.00) | −1.14 | −0.92 | −2.58 | −0.01 | 0.21 | 70 | −5.15 * (0.09) | 5.36 *** (0.00) | −0.35 | −5.71 | 6.60 * (0.08) | −0.02 | 0.14 | 72 |
| Forecast Horizon | Palladium (1986:04–2003:12) | Zinc (1997:08–2003:12) | ||||||||||||||
| h | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 8.32 | −4.76 | −14.73 ** (0.04) | −13.64 | 30.87 ** (0.04) | −0.08 | 0.07 | 72 | −20.44 * (0.07) | 7.38 | 8.17 | −25.51 | 12.79 | 0.03 | 0.09 | 26 |
| 2 | 6.49 | −5.51 | −3.60 | −11.75 | 29.80 *** (0.01) | −0.07 | 0.07 | 72 | −17.71 ** (0.03) |
7.05 * (0.07) | 5.76 | −27.27 | 7.72 | 0.00 | 0.19 | 26 |
| 3 | 2.48 | −4.39 | 3.43 | −4.32 | 35.21 *** (0.00) | −0.02 | 0.14 | 72 | −16.55 *** (0.01) | 7.43 ** (0.02) | 3.52 | −24.26 * (0.09) | 1.24 | 0.08 | 0.30 | 26 |
| 4 | 0.64 | −2.48 | 3.56 | −4.56 | 29.30 *** (0.00) | −0.02 | 0.11 | 72 | −16.49 *** (0.00) | 8.59 *** (0.00) | 1.96 | −11.91 | 5.56 | 0.08 | 0.39 | 26 |
| Forecast Horizon | Natural Gas (1990:05–2003:12) | |||||||||||||||
| h | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | ||||||||
| 1 | 6.22 | −5.39 | 18.38 | −12.43 | 35.71 | 0.01 | −0.04 | 55 | ||||||||
| 2 | 1.23 | 0.21 | 5.31 | −32.64 | 24.24 | −0.04 | −0.03 | 55 | ||||||||
| 3 | −7.52 | 4.24 | 5.48 | −48.20 *** (0.01) | 25.63 * (0.07) | 0.10 | 0.13 | 55 | ||||||||
| 4 | −5.53 | 5.36 | 4.41 | −30.44 ** (0.03) | 16.70 | 0.08 | 0.07 | 55 | ||||||||
| Panel B | ||||||||||||||||
| Forecast Horizon | Oil (2004:01–2020:12) | Silver (2004:01–2020:12) | ||||||||||||||
| h | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | −3.48 | 1.30 | 0.75 | 16.95 | −16.03 ** (0.04) | 0.17 | 0.04 | 67 | 13.47 | −4.90 | −2.36 | −14.55 | −4.93 | 0.08 | −0.03 | 67 |
| 2 | −0.15 | −0.03 | 0.74 | 9.42 | −6.15 | 0.07 | −0.03 | 66 | 16.55 * (0.09) | −4.01 | −7.84 | −11.85 | −3.23 | −0.06 | 0.06 | 66 |
| 3 | 1.47 | −0.84 | −6.02 | −16.53 | −6.47 * (0.09) | −0.04 | 0.04 | 65 | 14.86 * (0.07) | −4.02 | −4.68 | −12.32 | −4.20 | −0.03 | 0.07 | 65 |
| 4 | 2.57 | −1.79 | −0.95 | −2.18 | 8.67 | −0.04 | −0.05 | 64 | 16.11 ** (0.02) | −3.48 | −6.58 * (0.06) | 2.90 | 0.34 | −0.06 | 0.05 | 64 |
| Forecast Horizon | Gold (2004:01–2020:12) | Platinum (2004:01–2020:12) | ||||||||||||||
| h | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 14.78 ** (0.03) | −3.23 | −0.09 | 3.45 | −1.79 | 0.02 | −0.03 | 67 | 5.38 | −3.52 | −4.97 | 0.03 | −1.93 | 0.12 | −0.03 | 67 |
| 2 | 16.70 *** (0.00) | −3.48 | −3.10 | −0.50 | −0.60 | −0.03 | 0.04 | 66 | 9.64 | −3.96 | −10.39 ** (0.02) | −1.84 | 1.51 | −0.01 | 0.04 | 66 |
| 3 | 16.88 *** (0.00) | −3.69 * (0.05) | −1.48 | 0.58 | −0.24 | −0.02 | 0.02 | 65 | 9.76 | −4.53 | −4.24 | −10.22 | −1.92 | −0.05 | 0.07 | 65 |
| 4 | 17.75 *** (0.00) | −3.55 ** (0.03) | −2.76 | 4.97 | −1.83 | −0.03 | 0.11 | 64 | 10.18 * (0.06) | −4.35 * (0.07) | −3.45 | 1.39 | 2.12 | −0.05 | 0.05 | 64 |
| Forecast Horizon | Palladium (2004:01–2020:12) | Zinc (2004:01–2020:12) | ||||||||||||||
| h | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N |
| 1 | 23.62 | −6.84 | −7.57 | −7.03 | 5.47 | 0.11 | −0.03 | 67 | 9.55 | −4.16 | −15.58 ** (0.03) | −16.12 | 2.35 | 0.21 ** (0.04) | 0.05 | 67 |
| 2 | 26.66 ** (0.03) | −6.28 | −8.62 | −16.34 | 2.11 | −0.06 | 0.02 | 66 | 8.53 | −1.96 | −6.79 | −9.89 | 0.81 | 0.04 | −0.05 | 66 |
| 3 | 26.79 *** (0.01) | −6.41 | −2.03 | −13.55 | 0.66 | −0.07 | 0.01 | 65 | 5.05 | 0.00 | −5.65 | −3.13 | −1.27 | 0.01 | −0.05 | 65 |
| 4 | 24.98 *** (0.00) | −4.78 | −3.35 | −4.79 | 1.26 | −0.07 | −0.01 | 64 | 4.33 | 0.61 | −2.48 | 10.59 | 4.39 | −0.01 | −0.06 | 64 |
| Forecast Horizon | Natural Gas (2004:01–2020:12) | |||||||||||||||
| h | C | (Y30-Y2) | ∆SP | ∆EX | ∆IP | ∆EPU | R2 | N | ||||||||
| 1 | −2.07 | −0.97 | 17.31 | 29.02 | 0.14 | −0.02 | −0.01 | 67 | ||||||||
| 2 | −4.18 | −1.73 | 2.81 | −7.08 | −4.79 | 0.06 | −0.06 | 66 | ||||||||
| 3 | −3.91 | −2.64 | −1.33 | −18.75 | −6.00 | 0.04 | −0.01 | 65 | ||||||||
| 4 | −3.57 | −2.90 | −0.78 | −11.03 | 9.87 | 0.03 | −0.03 | 64 | ||||||||
Notes: The forecast horizon (h) is in quarters. Y30-Y2 denotes the yield spread calculated as the difference between the yield rates on 10-year and 2-year government bonds. The table reports the estimation results of Equation (1) with the Newey and West (1987) procedure. The sample period appears separately for each commodity. Figures in parentheses denote estimated standard errors. ***, ** and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
Note
| 1 | The conditional correlation between two random variables y1 and y2 is . It is acceptable to present returns as the conditional standard deviation times the standardized disturbance. . This is because . For each series i, is a standardized disturbance with a mean of zero and a variance of one. Accordingly, the conditional correlation can be presented as . Hence, the conditional correlation is also the conditional covariance between the standardized disturbances. This is the spirit of the DCC method. |
References
- Abdymomunov, Azamat. 2013. Predicting output using the entire yield curve. Journal of Macroeconomics 37: 333–44. [Google Scholar] [CrossRef]
- Akram, Farooq. 2009. Commodity prices, interest rates and the dollar. Energy Economics 31: 838–51. [Google Scholar] [CrossRef] [Green Version]
- Arango, Luis, Fernando Arias, and Adriana Flórez. 2011. Determinants of commodity prices. Applied Economics 44: 135–45. [Google Scholar] [CrossRef]
- Bai, Jushan, and Pierre Perron. 2003. Critical values for multiple structural change tests. Econometrics Journal 6: 72–78. [Google Scholar] [CrossRef]
- Bampinas, Georgios, and Theodore Panagiotidis. 2015. Are gold and silver a hedge against inflation? A two century perspective. International Review of Financial Analysis 41: 267–76. [Google Scholar] [CrossRef] [Green Version]
- Batten, Jonathan, Cetin Ciner, and Brian Lucey. 2010. The macroeconomic determinants of volatility in precious metals markets. Resources Policy 35: 65–71. [Google Scholar] [CrossRef]
- Beckmann, Joscha, and Robert Czudaj. 2013. Gold as an inflation hedge in a time-varying coefficient framework. North American Journal of Economics and Finance 24: 208–22. [Google Scholar] [CrossRef] [Green Version]
- Bodie, Zvi, and Victor Rosansky. 1980. Risk and return in commodity futures. Financial Analysts Journal 36: 27–39. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1990. Modelling the coherence in short-run nominal exchange rates: A multivariate generalized ARCH model. Review of Economics and Statistics 72: 498–505. [Google Scholar] [CrossRef]
- Chevallier, Julien, Mathieu Gatumel, and Florian Ielpo. 2014. Commodity markets through the business cycle. Quantitative Finance 14: 1597–618. [Google Scholar] [CrossRef]
- Chinn, Menzie, and Kavan Kucko. 2015. The predictive power of the yield curve across countries and time. International Finance 18: 129–56. [Google Scholar] [CrossRef]
- Churchill, Sefa, John Inekwe, Kris Ivanovski, and Russell Smyth. 2019. Dynamics of oil price, precious metal prices and the exchange rate in the long-run. Energy Economics 84: 104508. [Google Scholar] [CrossRef]
- Dai, Zhifeng, and Jie Kang. 2021. Bond yield and crude oil prices predictability. Energy Economics 97: 105205. [Google Scholar] [CrossRef]
- Daskalaki, Charoula, George Skiadopoulos, and Nikolas Topaloglou. 2017. Diversification benefits of commodities: A stochastic dominance efficiency approach. Journal of Empirical Finance 44: 250–69. [Google Scholar] [CrossRef]
- Demiralay, Sercan, Selcuk Bayraci, and Gaye Gencer. 2019. Time-varying diversification benefits of commodity futures. Empirical Economics 56: 1823–53. [Google Scholar] [CrossRef]
- Duarte, Angelo, Wagner Gaglianone, Osmani de Carvalho Guillén, and João Issler. 2021. Commodity Prices and Global Economic Activity: A derived-demand approach. Energy Economics 96: 105120. [Google Scholar] [CrossRef]
- Duffee, Gregory. 1998. The relation between treasury yields and corporate bond yield spreads. Journal of Finance 53: 2225–41. [Google Scholar] [CrossRef]
- Engle, Robert. 2002. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business & Economic Statistics 20: 339–50. [Google Scholar]
- Estrella, Arturo. 2005. Why does the yield curve predict output and inflation? Economic Journal 115: 722–44. [Google Scholar] [CrossRef]
- Estrella, Arturo, and Gikas Hardouvelis. 1991. The term structure as a predictor of real economic activity. Journal of Finance 46: 555–76. [Google Scholar] [CrossRef]
- Evgenidis, Anastasios, Stephanos Papadamou, and Costas Siriopoulos. 2020. The yield spread’s ability to forecast economic activity: What have we learned after 30 years of studies? Journal of Business Research 106: 221–32. [Google Scholar] [CrossRef]
- Fama, Eugene, and Kenneth French. 1988. Business cycles and the behavior of metals prices. The Journal of Finance 43: 1075–93. [Google Scholar] [CrossRef]
- Fasanya, Ismail, and Crystal Awodimila. 2020. Are commodity prices good predictors of inflation? The African perspective. Resources Policy 69: 101802. [Google Scholar] [CrossRef]
- Gagnon, Marie, Guillaume Manseau, and Gabriel Power. 2020. They’re back! Post-financialization diversification benefits of commodities. International Review of Financial Analysis 71: 101515. [Google Scholar] [CrossRef]
- Garner, Alan. 1989. Commodity prices: Policy target or information variable?: Note. Journal of Money, Credit and Banking 21: 508–14. [Google Scholar] [CrossRef]
- Giacomini, Raffaella, and Barbara Rossi. 2006. How stable is the forecasting performance of the yield curve for output growth? Oxford Bulletin of Economics and Statistics 68: 783–95. [Google Scholar] [CrossRef]
- Gogas, Periklis, Theophilos Papadimitriou, Maria Matthaiou, and Efthymia Chrysanthidou. 2015. Yield curve and recession forecasting in a machine learning framework. Computational Economics 45: 635–45. [Google Scholar]
- Gorton, Gary, and Geert Rouwenhorst. 2006. Facts and fantasies about commodity futures. Financial Analysts Journal 62: 47–68. [Google Scholar] [CrossRef] [Green Version]
- Granger, Clive. 1969. Investigating causal relations by econometric models and cross-spectral methods. Econometrica: Journal of the Econometric Society 37: 424–38. [Google Scholar] [CrossRef]
- Hamilton, James, and Dong Kim. 2002. A reexamination of the predictability of economic activity using the yield spread. Journal of Money, Credit, and Banking 34: 340–60. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, James, and Jing Wu. 2015. Effects of index-fund investing on commodity futures prices. International Economic Review 56: 187–205. [Google Scholar] [CrossRef] [Green Version]
- Harvey, Campbell. 1989. Forecasts of economic growth from the bond and stock markets. Financial Analysts Journal 45: 38–45. [Google Scholar] [CrossRef]
- Harvey, David, Neil Kellard, Jakob Madsen, and Mark Wohar. 2017. Long-run commodity prices, economic growth, and interest rates: 17th century to the present day. World Development 89: 57–70. [Google Scholar] [CrossRef] [Green Version]
- Henderson, Brian, Neil Pearson, and Li Wang. 2015. New evidence on the financialization of commodity markets. Review of Financial Studies 28: 1285–311. [Google Scholar] [CrossRef] [Green Version]
- Hu, Conghui, Zhibing Li, and Xiaoyu Liu. 2020. Liquidity shocks, commodity financialization, and market comovements. Journal of Futures Markets 40: 1315–36. [Google Scholar] [CrossRef]
- Huang, Jianbai, Yingli Li, Hongwei Zhang, and Jinyu Chen. 2021. The effects of uncertainty measures on commodity prices from a time-varying perspective. International Review of Economics & Finance 71: 100–14. [Google Scholar]
- Ioannidis, Christos, and Kook Ka. 2018. The impact of oil price shocks on the term structure of interest rates. Energy Economics 72: 601–20. [Google Scholar] [CrossRef] [Green Version]
- Jahan, Sayeeda, and Apostolos Serletis. 2019. Business cycles and hydrocarbon gas liquids prices. The Journal of Economic Asymmetries 19: e00115. [Google Scholar] [CrossRef] [Green Version]
- Kagraoka, Yusho. 2016. Common dynamic factors in driving commodity prices: Implications of a generalized dynamic factor model. Economic Modelling 52: 609–17. [Google Scholar] [CrossRef]
- Kucher, Oleg, and Suzanne McCoskey. 2017. The long-run relationship between precious metal prices and the business cycle. Quarterly Review of Economics and Finance 65: 263–75. [Google Scholar] [CrossRef]
- Kuosmanen, Petri, Jaana Rahko, and Juuso Vataja. 2019. Predictive ability of financial variables in changing economic circumstances. North American Journal of Economics and Finance 47: 37–47. [Google Scholar] [CrossRef]
- Labys, Walter, Aymad Achouch, and Michael Terraza. 1999. Metal prices and the business cycle. Resources Policy 25: 229–38. [Google Scholar] [CrossRef]
- Levine, Ari, Yao Ooi, Matthew Richardson, and Caroline Sasseville. 2018. Commodities for the long run. Financial Analysts Journal 74: 55–68. [Google Scholar] [CrossRef] [Green Version]
- McMillan, David. 2021a. Predicting GDP growth with stock and bond markets: Do they contain different information? International Journal of Finance and Economics 26: 3651–75. [Google Scholar] [CrossRef]
- McMillan, David. 2021b. When and Why Do Stock and Bond Markets Predict Economic Growth? Quarterly Review of Economics and Finance 80: 331–43. [Google Scholar] [CrossRef]
- Newey, Whitney, and Kenneth West. 1987. Hypothesis testing with efficient method of moments estimation. International Economic Review 28: 777–87. [Google Scholar] [CrossRef]
- Orlowski, Lucjan. 2017. Volatility of commodity futures prices and market-implied inflation expectations. Journal of International Financial Markets, Institutions and Money 51: 133–41. [Google Scholar] [CrossRef]
- Plosser, Charles, and Geert Rouwenhorst. 1994. International term structures and real economic growth. Journal of Monetary Economics 33: 133–55. [Google Scholar] [CrossRef]
- Qadan, M., and H. Nama. 2018. Investor sentiment and the price of oil. Energy Economics 69: 42–58. [Google Scholar] [CrossRef]
- Qadan, Mahmoud, David Aharon, and Ron Eichel. 2019. Seasonal patterns and calendar anomalies in the commodity market for natural resources. Resources Policy 63: 101435. [Google Scholar] [CrossRef]
- Saar, Dan, and Yossi Yagil. 2015. Forecasting growth and stock performance using government and corporate yield curves: Evidence from the European and Asian markets. Journal of International Financial Markets, Institutions and Money 37: 27–41. [Google Scholar] [CrossRef]
- Stock, James, and Mark Watson. 1989. New indexes of coincident and leading economic indicators. NBER Macroeconomics Annual 4: 351–94. [Google Scholar] [CrossRef]
- Stock, James, and Mark Watson. 2003. Forecasting output and inflation: The role of asset prices. Journal of Economic Literature 41: 788–829. [Google Scholar] [CrossRef]
- Tang, Ke, and Wei Xiong. 2012. Index investment and the financialization of commodities. Financial Analysts Journal 68: 54–74. [Google Scholar] [CrossRef]
- Umar, Zaghum, Syed Shahzad, and Dimitris Kenourgios. 2019. Hedging US metals & mining Industry’s credit risk with industrial and precious metals. Resources Policy 63: 101472. [Google Scholar]
- Wheelock, David, and Mark Wohar. 2009. Can the term spread predict output growth and recessions? A survey of the literature. Federal Reserve Bank of St. Louis Review 91: 419–40. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).