1. Introduction
Bitcoin was initially designed to be a digital currency, but evolved more and more to an investment which is comparatively risky due to the high volatility of the Bitcoin price. Therefore, substantial effort is made to understand the properties and the sources of volatility in Bitcoin and other cryptocurrency markets. Thus far, research has either considered model based estimates of Bitcoin volatility (
Aharon and Qadan 2019;
Baur and Dimpfl 2018;
Chu et al. 2017;
Katsiampa 2017), relied on realized volatility (
Aalborg et al. 2019;
Catania and Sandholdt 2019;
Ma et al. 2020) or other non-parametric measures (
Bleher and Dimpfl 2019) to construct daily or higher-frequency time series of volatility. In this article, we contribute to the literature with a trading perspective on volatility. In particular, we follow
Engle and Russell (
1998) and model the durations, i.e., the time elapsed between two consecutive price changes, in order to assess the riskiness of trading in Bitcoin markets. In doing so, we lift the restriction of a fixed time grid to estimate GARCH models or realized volatility and descend to high-frequency properties of irregularly spaced transaction data. This is particularly interesting as Bitcoin is traded continuously 24 h a day. In the stock market, in contrast, trading is restricted to the operating hours of the stock exchange and it is well-documented that trading intensities vary over the day. For example,
Manganelli (
2005) and
Liu and Maheu (
2012) report an inverted U-shaped pattern for trade durations for stocks traded on the New York stock exchange and the Shanghai and Shenzhen stock exchanges, respectively. To the best of our knowledge, trading intensity on Bitcoin markets has not been studied yet. Recently,
Baur et al. (
2019) documented an intraday pattern of Bitcoin returns and trading volume, which gives rise to the assumption that trading intensities also vary during the day. Therefore, trading Bitcoin is not equally risky during the 24 h that an exchange is open and we provide a characterization of the risk profile over the day.
The literature which analyses Bitcoin is broad and considers all facets of trading. For example,
Pieters and Vivanco (
2017) showing that prices across Bitcoin exchanges differ substantially and conclude that the law of one price does not hold which gives rise to arbitrage opportunities as documented by
Makarov and Schoar (
2020).
Urquhart (
2017) and
Bariviera (
2017) show that price and volatility clustering, respectively, are key features of a Bitcoin market.
Blau (
2017) considers speculative trading but does not find evidence for an association between the unusual volatility levels and speculation in Bitcoin. Other studies like
Nadarajah and Chu (
2017) focus on market efficiency considering Bitcoin as an asset traded in an unregulated market. Efficiency is also related to market microstructure such as the technical mechanism and the frameworks of trading (
Brauneis et al. 2020;
Koutmos 2018) as well as the market organization in general (
Easley et al. 2019).
The purpose of this paper is to shed light on the microstructure of Bitcoin trading using a transaction based approach. This makes our study different from
Koutmos (
2018) or
Brauneis et al. (
2020) who, on one hand, focus on liquidity, and, on the other hand, use regularly spaced transaction data for their analysis. Still, the link to this branch of the microstructure literature is the idea that trading conveys information. In our case, the time elapsed between trades is considered informative as advocated by
Easley and O’Hara (
1992) and
Easley et al. (
1997). In other words, a longer spell of constant prices is associated with a lack of new information. Empirically, this conjecture is analysed using autoregressive conditional duration (ACD) models based on
Engle and Russell (
1998) and
Engle (
2000), for example by
Bauwens and Giot (
2000),
Fernandes and Grammig (
2006), or
Ghysels and Jasiak (
1998). Hence, we contribute to the literature with an analysis of Bitcoin trading at the transaction level. We extract the risk of non-trading based on an ACD model and calculate the instantaneous, implied volatility. This allows us to identify risk patterns across the 24 h of bitcoin trading. In a second step, we aggregate the thus obtained volatility to a daily measure and investigate how institutional features of the Bitcoin blockchain are related to price durations and volatility. Since
Clark (
1973) introduced the mixture of distribution hypothesis which postulates a relationship between information flow and trading, the relationship between price volatility and volume has been studied extensively (
Giot et al. 2010;
Louhichi 2011). We show how blockchain features interact with our information measures (durations and volatility) and investigate whether traders account for blockchain characteristics (such as long confirmation times or high fees paid to miners) when placing their orders. If they do, blockchain characteristics should be good predictors of future intensity and volatility.
Our findings based on Bitcoin price data of Kraken and Bitfinex may be summarized as follows. We find decisive variation of price durations over time and within the day. Long durations are usually observed for periods when the European and U.S. stock markets are closed, suggesting that investors on these exchanges are to the greatest extent based in Europe and the USA. The intraday pattern of volatility obtained from the duration analysis reflects the same time zone pattern. The analysis of blockchain characteristics shows that there is a contemporaneous relation between volatility, duration, and on-chain characteristics. However, the predictive power on a day-to-day basis is very weak, which shows that traders account for changes much faster than our analysis can reveal. Only higher costs per transaction turn out to significantly increase future volatility which indicates that Bitcoin traders are price-sensitive.
The remainder of the paper is structured as follows:
Section 2 illustrates the ACD model.
Section 3 presents the available data, their transformation and descriptive statistics.
Section 4 presents the results of the ACD model estimation, the intradaily volatility, and analyses the interaction of durations and volatility with the blockchain. Lastly,
Section 5 provides the conclusions.
2. Methodology
Conceptually, our irregularly spaced transaction data can be conceived as being generated by a dependent point process so that we can estimate the instantaneous probability that a bitcoin price change event occurs. The irregular arrival of such events can then be related to the instantaneous volatility at every point in time during the day, such that we transform the irregular transaction price change events to volatility on an equally-spaced time grid. To achieve this goal, we consider a self-exciting point process which is estimated using an Autoregressive Conditional Duration (ACD) model developed by
Engle and Russell (
1998).
To define a generic point process, let
X be the time continuum {t:
} which might, for example, represent a day. The point process is the ordered sequence of arrival times of events {
} during that day (with
), which is a subset of
X. According to this definition, {
} is a sequence of
occurrence times, in contrast to the related sequence {
} of
interarrival times, i.e., the random time between two consecutive events with time stamps
and
such that
. Furthermore, the number of events which have occurred up to time
t evolves according to a count process
with
.
is conditionally orderly and evolves with after effects. These properties mean that no two events happen at exactly the same point in time and that past occurrences may influence the conditional probability of future occurrences which allows for clustering of events.
1 In addition,
is a step-function which is non-decreasing in time and continuous from the left (
Engle and Russell 1997).
Conditionally, orderly point processes are completely characterized by the conditional intensity
The conditional intensity, or hazard function, can also be interpreted as an approximation of the conditional probability that an event occurs in the (infinitesimal) interval
(
Snyder and Miller 2012). The ACD model provides a way to estimate the conditional intensity, starting from the (non-negative) durations
, in our case the realizations of the interarrival times computed from the realizations of occurrence times.
The main assumption of the ACD model is that the time dependence of the durations is fully characterized by the conditional expected duration
as follows:
where
is the conditional information set and
and
are variation-free
2. In other words, it is assumed that the conditional expectation of the durations is a function
of the parameters in
and of the past durations. Furthermore, the duration
deviates from the function of its conditional expectation
by a multiplicative term,
. The random variables
are assumed to be
iid and their distribution must have a non-negative support as neither the durations nor their conditional expectation can be negative.
Given a particular distribution assumption for
, the conditional density of the durations can be computed based on Equation (
3) as
Based on the assumption in Equation (
2), it is possible to formulate the conditional density of the durations as a function of
; accordingly, the conditional likelihood is also defined. Likewise, the unconditional and the conditional intensities are directly derived from the intensity of
. The baseline hazard rate is
, with
and
the density and the distribution function of
, respectively. The conditional intensity follows as
The distribution assumption for
defines the shape of the conditional intensity distribution. Overall, different specifications of the ACD model are obtained by assuming a different functional form of
in Equation (
2) and various distributions for
in Equation (
4). In this paper, we assume the parametric conditional mean equation for the ACD(
) model to be linear such that
A sufficient, albeit not necessary set of conditions for the non-negativity of the durations imposes boundaries and during the estimation process, while assures stationarity.
Furthermore, we use the exponential distribution to model
. Therefore, the conditional distribution of the durations is exponential as well, and the model is the Exponential Autoregressive Conditional Duration model (EACD(
)) of
Engle and Russell (
1998) with
and conditional log-likelihood function
with
for
and
.
To evaluate the goodness of fit of the model, we apply the tests proposed by
Engle and Russell (
1998). First, we assess whether the i.i.d. assumption outlined in Equation (4) holds for the standardized durations
. To do so, a Ljung-Box test is applied on
including 15 lags. The square of the standardized durations and higher moments are also tested for autocorrelation in the same manner. Second, we check whether the distribution of
exhibits excess dispersion, testing whether the standard deviation of
differs from the theoretical value of 1. The test is one-sided under the null hypothesis of no excess dispersion (
). The test statistic is calculated as
, where
is the sample variance of the standardized durations, and
is the standard deviation of
, which should be equal to
under
. The test has a limiting normal distribution under
.
Under the assumptions outlined above, the quasi-maximum likelihood (QML) estimator of
obtained by maximizing the log-likelihood function in Equation (
7) is consistent and asymptotically normal distributed (
Engle 2000). This is the reason why the exponential model was chosen over others. A shortcoming of the exponential assumption, though, is that the baseline hazard is constant and equal to the
’s mean, implying a constant conditional intensity from an event until the next one. This is evident from Equation (
5) shrinking to
. While this is a strong assumption, the QML estimate is consistent and, combined with a non-parametric estimate of the baseline hazard in Equation (
5), provides a consistent semiparametric estimate of the conditional hazard (
Engle and Russell 1998) that would not have a predefined shape anymore. The non-parametric estimate of the baseline hazard is built upon a cubic spline smoothing of the
k-th nearest neighbor estimator derived by
Engle and Russell (
1998):
where
denotes the empirical residual of the upper bound of the
i-th 5% quantile, and the empirical residuals are the empirical standardized residuals used for the diagnosis checks. It is worth noting that, as i indicates the
i-th 5% quantile, the last i will be 20 and
. Thus, for the last quantile, the denominator of the first term in Equation (8) will be zero. To avoid this problem, the formula is computed for all but the last quantile.
An important remark is due. The basic ACD model includes every transaction time in the occurrence time sequence. The model applied here, instead, does not, as it includes only those that carry some price information. The price associated with the occurrence times is a key element for the volatility, and is taken into account here by “thinning” the point process accordingly to the associated price information. The new sequence of occurrence times is created by including only those transaction events that embed a consecutive price change. This way, the sequence of price change events is created. As in
Engle and Russell (
1998), price change events include only price changes greater than or equal to a threshold c in which the next price has not come back to the previous one, to avoid considering errant and insignificant price changes.
To shed light on the intraday pattern of duration induced volatility, we need to link their conditional intensity with instantaneous volatility. As shown by
Engle and Russell (
1998), the conditional instantaneous variance is defined as
where
is the price at time
t and
c is the threshold for the price change as described above.
is the conditional intensity, i.e., an approximation of the probability of a price change in the next second. The term in parentheses is proportional to the squared return. Therefore, Equation (
9) is the expected conditional volatility per second in the next instant. To provide a more intuitive measure, we follow
Engle and Russell (
1997) and compute an annualized version of the instantaneous volatility. To this end,
in Equation (9) is multiplied by the number of seconds in a year based on 365 days of uninterrupted trading.
3. Data and Preliminary Analysis
We use data on Bitcoin transaction prices in U.S. dollar from two major Bitcoin exchanges, Bitfinex and Kraken. The data range from 7 Mach 2017 to 7 January 2019 for Bitfinex or till 1 April 2019 for Kraken are obtained via the API of the respective exchange. During this time period, Bitfinex and Kraken had a combined market share of 45% on average, but never less than 30% of all Bitcoins traded in USD
3. The database consists of 50,924,494 entries for Bitfinex and 12,621,000 for Kraken. Each entry consists of a Unix timestamp (with a precision of 1/100 of a millisecond), the transaction price in USD, the traded volume, and an indicator whether the transaction was buyer or seller initiated.
While the platforms are generally open 24-7, there are periods of downtime, usually scheduled for maintenance and updates. For Bitfinex, we identify 14 interruptions of more than 15 min in our dataset which can be matched with the official recordings on Bitfinex’ websites about downtime. For Kraken, the same 15 min interval would identify 126 interruptions. However, the number of transactions in the Bitfinex sample is almost five times higher (accounting for the differing time periods considered), and therefore longer than 15 min interruptions on Kraken might also be possible in continuous trading. We therefore set the threshold in the Kraken sample to 30 min which results in 31 interruptions. We are able to match most of the identified downtime periods with incident announcements on the official Kraken status website. The most important platform problems occurred on Tuesday 6 November 2018, after which the platform did not open again until Friday 16 November 2018, and on Thursday 13 December 2018, when the platform closed until Saturday 15 December 2018. When implementing the estimation, we remove one hour of data after each interruption in order to avoid any impact of re-starting trading as there is no opening auction as in a stock market. The likelihood function is re-initialized anew each time.
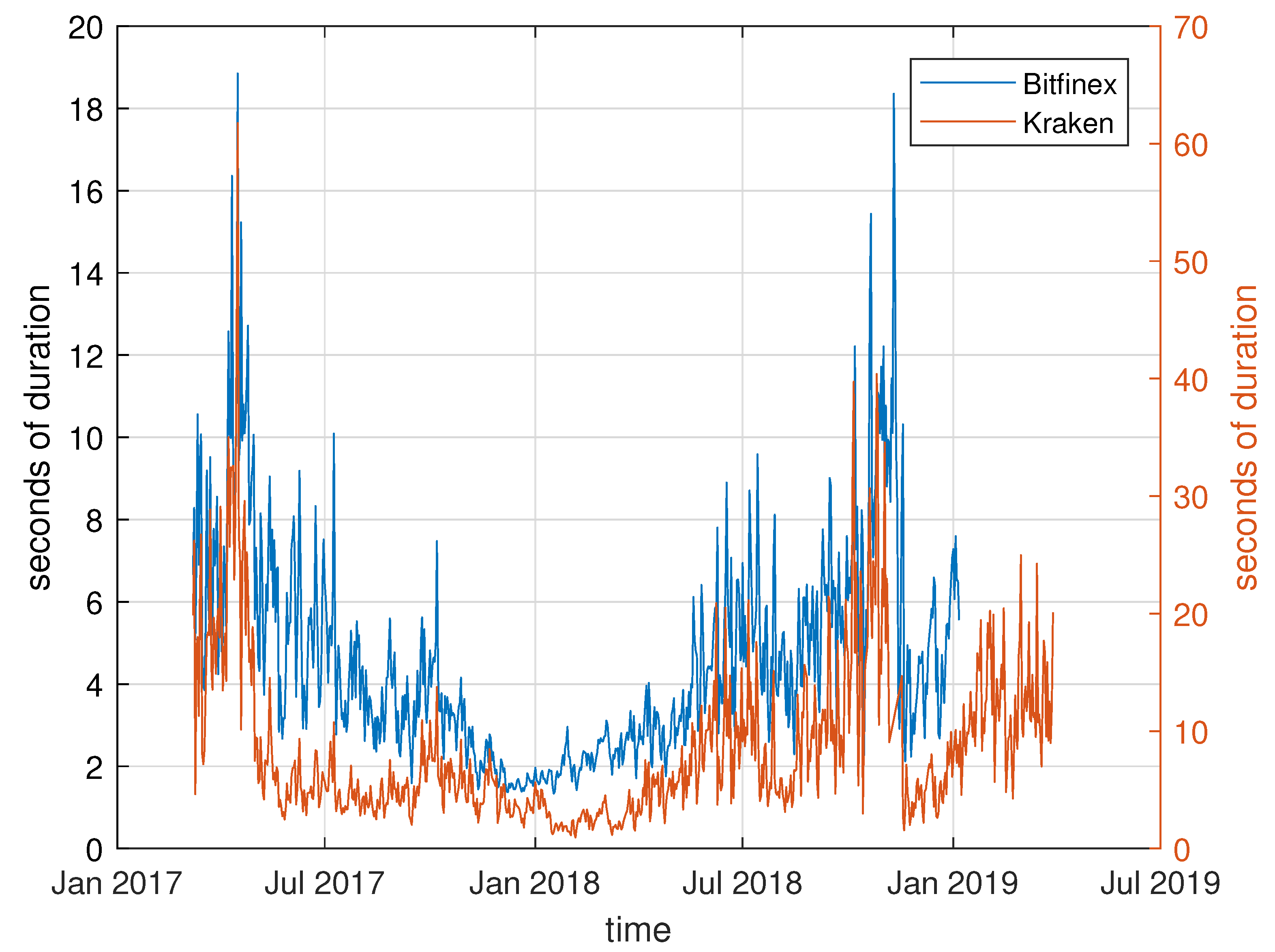
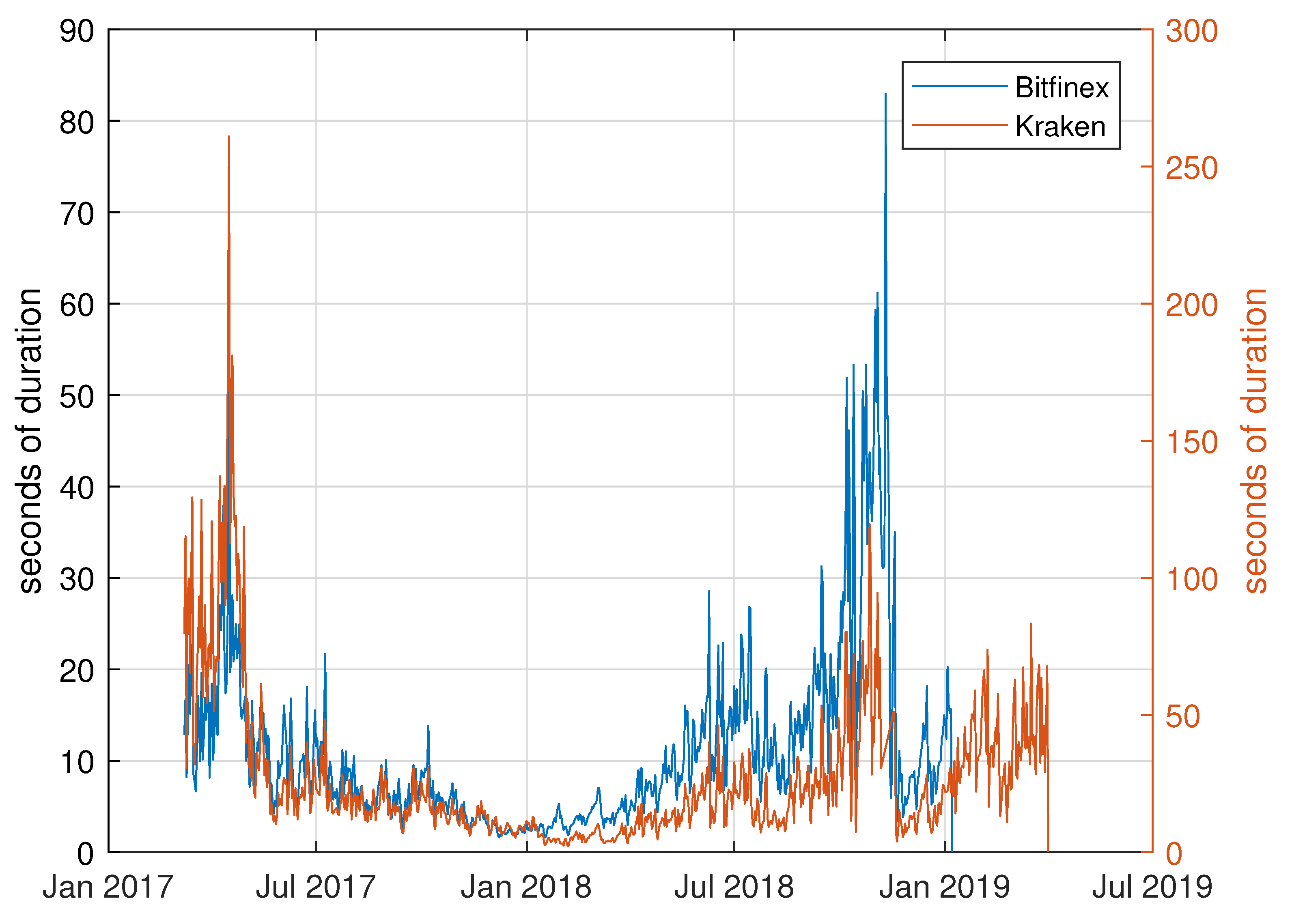
To give a first impression of our dataset,
Figure 1 presents the average daily transaction duration over the sample period for the unfiltered data (excluding durations which are exactly zero). The pattern clearly reflects the increasing appeal and rising demand of Bitcoin during 2017 which culminated in the record price of nearly 20,000 USD on 17 December 2017. The shortest trade durations are also observed around this date. The downturn during early 2018 which was accompanied by less trading and hence longer spells with no transactions on both platforms, are also visible. Furthermore, the time between two consecutive transactions is clearly longer on Kraken than on Bitfinex. This is in line with the market shares of each exchange as the share of Bitfinex is about five times higher than Kraken’s market share.
While the time-stamp of the data would allow for a finer distinction, we chose one second as the baseline precision for time. Hence, all durations will be measured in seconds rather than milliseconds. Durations, in turn, are computed as price durations, i.e., the time between two consecutive transactions which do not occur at the same price. Following
Engle and Russell (
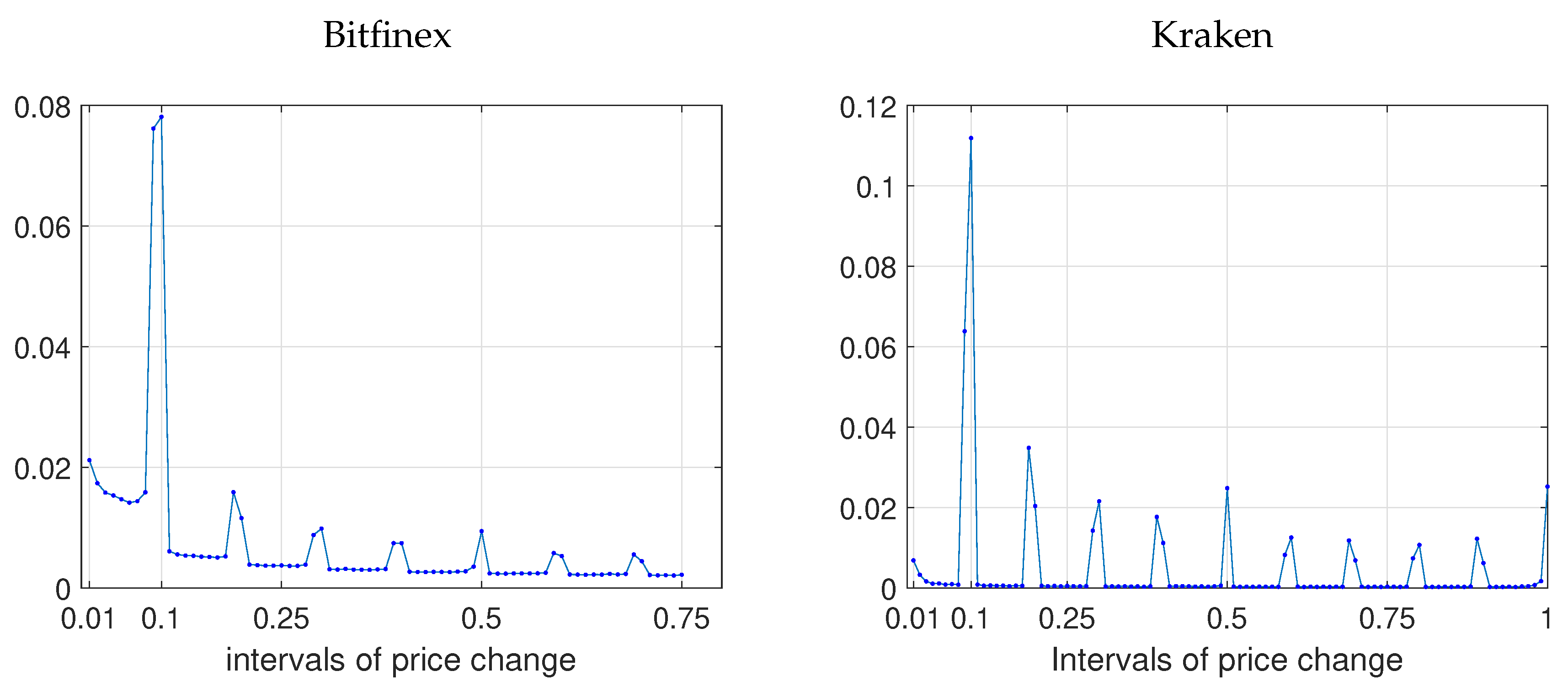
1998), we only include price changes which exceed a certain threshold and which do not qualify as “errant” according to their definition. Therefore, the datasets are cleaned in the following way. First, we aggregate contemporaneous transactions. If there are multiple trades at the same time stamp (at the highest available precision), we calculate a volume-weighted average price for this trade observation. Second, we filter the data using a price change threshold to identify informational price changes. The threshold is determined using the distribution of all cleaned transaction price changes, excluding price changes of zero which is common practice in the literature. This way, meaningful price changes are considered only. For both Bitfinex and Kraken, we chose a threshold
USD. This value corresponds to the most frequent change observed in our dataset as can be seen from
Figure 2. Consequently, we lose about 7% (14%) of all non-zero price change observations of Kraken (Bitfinex). Third, “errant” quotes, i.e., transactions which lead to price changes which are immediately reverted to the previous price, are dropped from the sample.
Subsequently, price durations are computed as the time elapsed between the selected price change events. The thus thinned sample consists of 9,159,554 observations for Bitfinex and 4,775,659 for Kraken, about half of the respective sample of trade durations (including price changes of zero) for Bitfinex and 40% for Kraken. Corresponding to the price duration events, we extract further characteristics of the trading process as follows. First, we measure the trading intensity associated with each price duration interval. To this end, we count the number of actual trades which happened during the interval, including the last transaction in the counts, but not the very first (which pertains to the last interval), and divide it by the price duration. Second, the average volume per duration is calculated as the average traded volume during the duration spell.
Summary statistics of price durations and associated average volume and trading intensity are presented in
Table 1. The average price duration is about 6 seconds for Bitfinex and 13 for Kraken, with a maximum of slightly less than an hour for Bitfinex and less than two hours for Kraken. Note that these are periods where prices were stable, but there was still trading on the platform. The trading intensity is on average around one transaction every 1.5 s for Bitfinex. For Kraken, in contrast, trading intensity is rather high: on average, we observe 77 trades per second during a price duration. This is probably due to the finer time grid of Kraken which might split up orders of the same customer into multiple smaller ones. Furthermore, the standard deviation, minimum, and maximum indicate that trading intensity is more stable for Bitfinex while it varies a lot for Kraken. The average volume per transaction associated with the transactions within a price event, though, is far lower for Kraken than for Bitfinex: about 0.35 bitcoin on Kraken in contrast to 1.72 on Bitfinex. In addition, the standard deviation of the average volume is very low for Kraken.
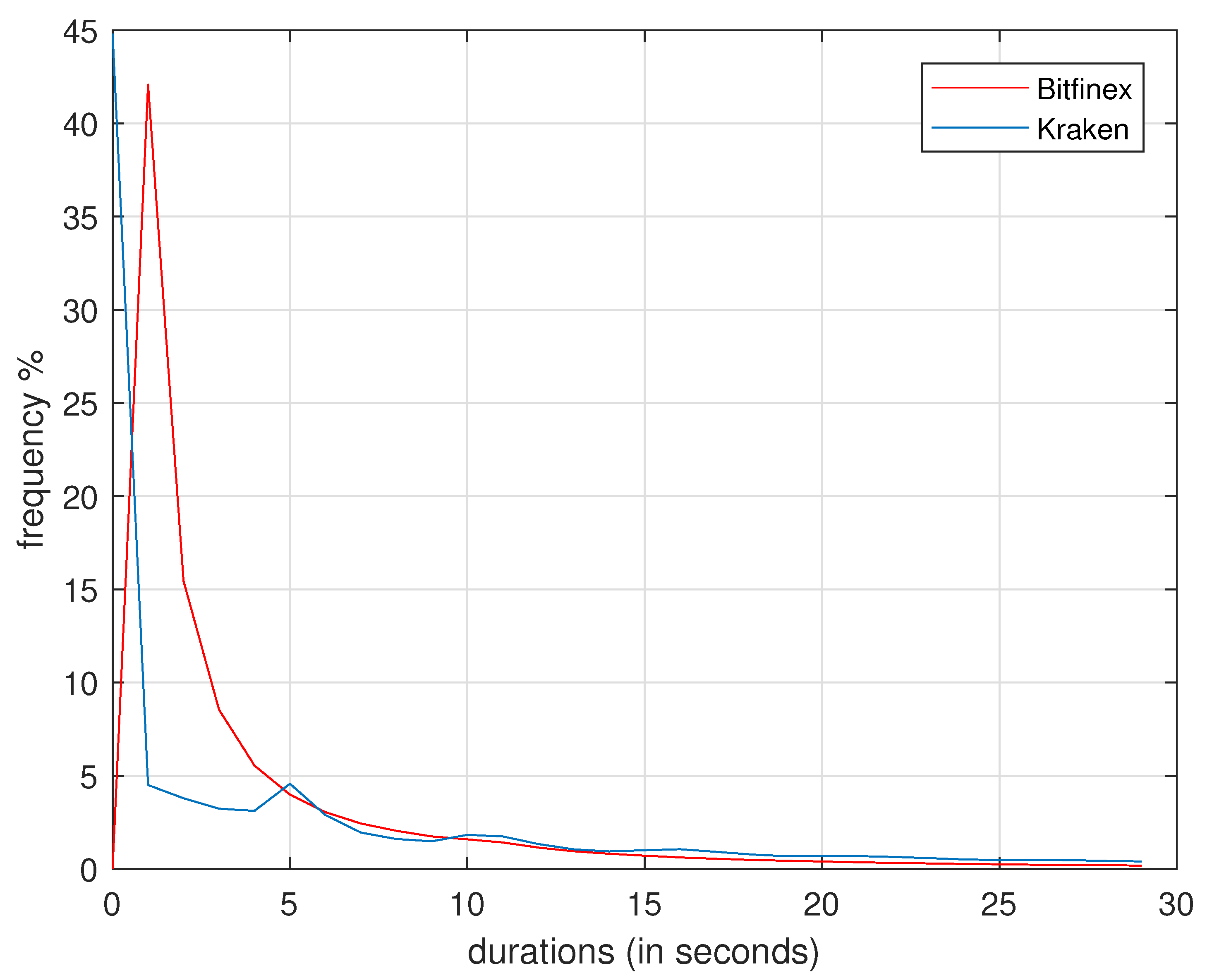
Figure 3 presents the distribution of price durations for Bitfinex and Kraken, cut off at 30 s for visibility. The pattern reflects the original sample size in that Bitfinex price durations are usually much shorter which stems from a greater number of trades. In contrast, Kraken durations are on average longer which is visible in that the blue line drops faster and lies consistently above the red line from 10 s onward. The median of roughly 2 s durations is clearly visible for Bitfinex. Considering the minimum durations in
Table 1 and the shape of the distribution in
Figure 3, it seems that Kraken makes better use of the fine time grid compared to Bitfinex when recording transactions. In the latter sample, durations of less than one second are scarce while this seems to be a substantial part of durations on Kraken. This observation is the reason why we decided to use one second as the baseline frequency. Overall, the timing is comparable, however, as the median duration on both exchanges is roughly 2 s.
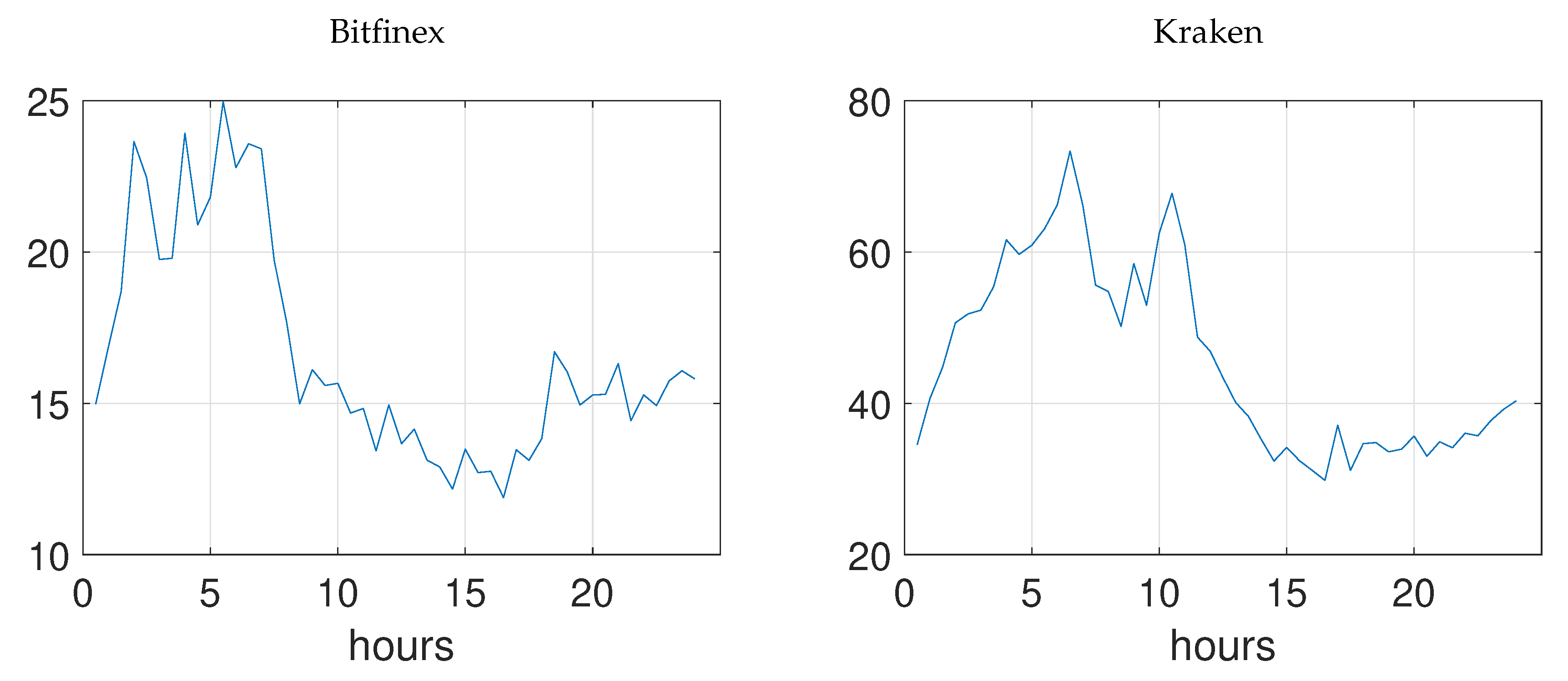
Figure 4 sheds light on the intraday development of price durations. We split the day in 30 min intervals and calculate the average across the whole sample for the respective interval. As can be seen, there is a pronounced time-of-day effect on both exchanges: Price durations are substantially lower in the period from 8:00 a.m. UTC (Bitfinex) or 10:00 a.m. UTC (Kraken) till 12:00 a.m. UTC. These times correspond roughly to the trading times of European and U.S. stock markets. As we have Bitcoin prices denoted in U.S. dollar, this pattern is sensible. It is also in line with the findings of
Baur et al. (
2019) who document increased traded volume on exchanges trading in U.S. dollar during these times.
The evolution of price durations over time is depicted in
Figure 5 which presents the average price duration per day. It also reflects the increase of trading intensity until the end of 2017 and the subsequent decay in 2018, similar to
Figure 1. All in all, the pattern is similar to the development of trade durations depicted in
Figure 1 which shows that the thinning of the data did not substantially discriminate against a particular feature inherent in the duration process or substantially alter the relation between Bitfinex and Kraken.
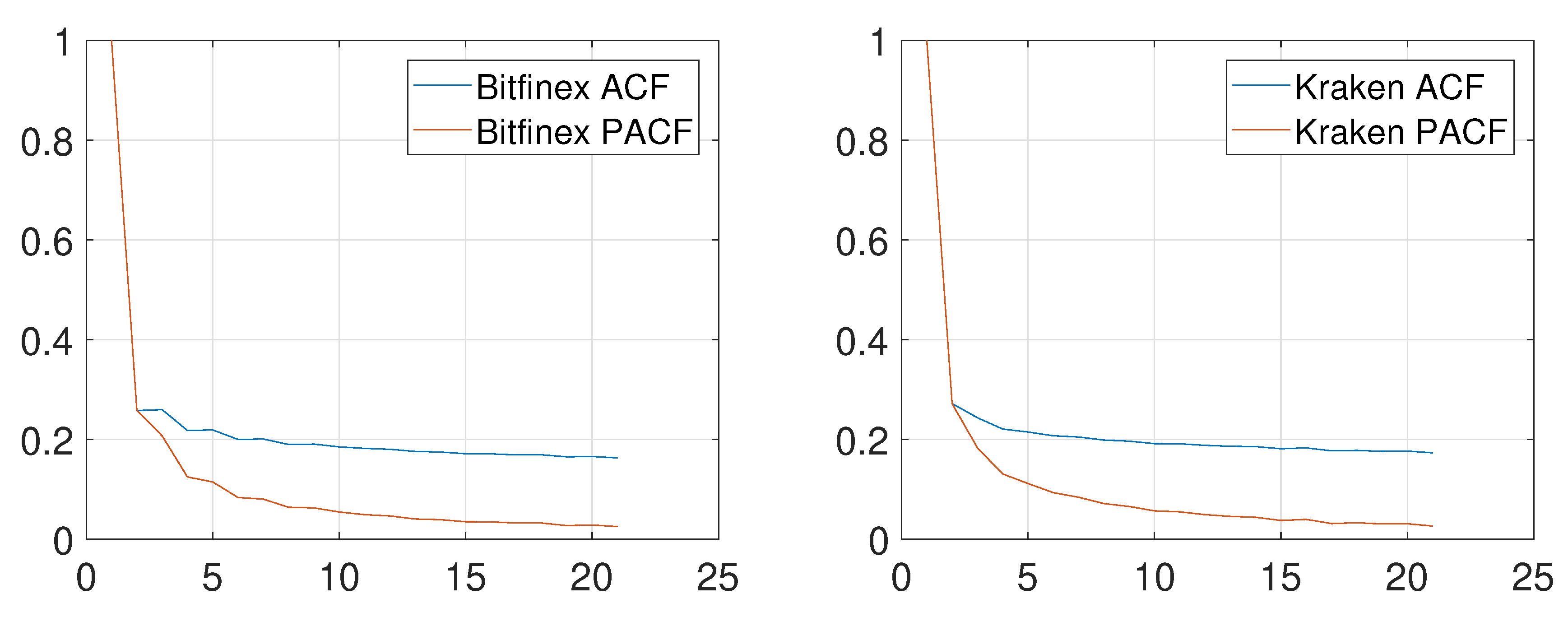
Autocorrelation and partial autocorrelation functions of durations computed on the full samples for Bitfinex and Kraken are displayed in
Figure 6. While they decay quickly, they strongly suggest that price durations are dependent on their past history which advocates for the application of an ACD model. The finding is supported by a Ljung–Box test (detailed results not reported) as we can reject the null hypothesis of no autocorrelation of the first 15 lags. Nevertheless, the daily averages of the price durations displayed in
Figure 5 suggest a substantial heterogeneity of the trading from one day to the next. Therefore, we implement the ACD model for each day instead of the full sample. As we require that the data are stationary, we conduct augmented Dickey-Fuller tests on each of the daily price duration samples. We reject the null hypothesis of a unit root in 663 out of 671 cases for Bitfinex, and 717 out of 741 for Kraken. The non-rejections are most likely false negative test results and we therefore treat all daily samples as stationary. To back this proceeding, we also run the unit root test of
Phillips and Perron (
1988). Here, we always reject the unit root null hypothesis. Reject H0 with both ADF and Phillips-Perron tests.
4. Results
4.1. Duration-Based Volatility
Due to the strong time pattern of durations displayed in
Figure 5, the analysis is conducted on a per day basis for the two samples of Bitfinex and Kraken. We apply a parsimoniously parameterized EACD(1,1) to analyze price durations as the partial autocorrelation functions in
Figure 6 decay substantially from lag 1 to lag 2. To find suitable starting values for the optimization of the likelihood function, we follow again
Engle and Russell (
1998) and implement a GARCH (1, 1) model for the square root of the durations.
4 For all daily samples, convergence is achieved without errors.
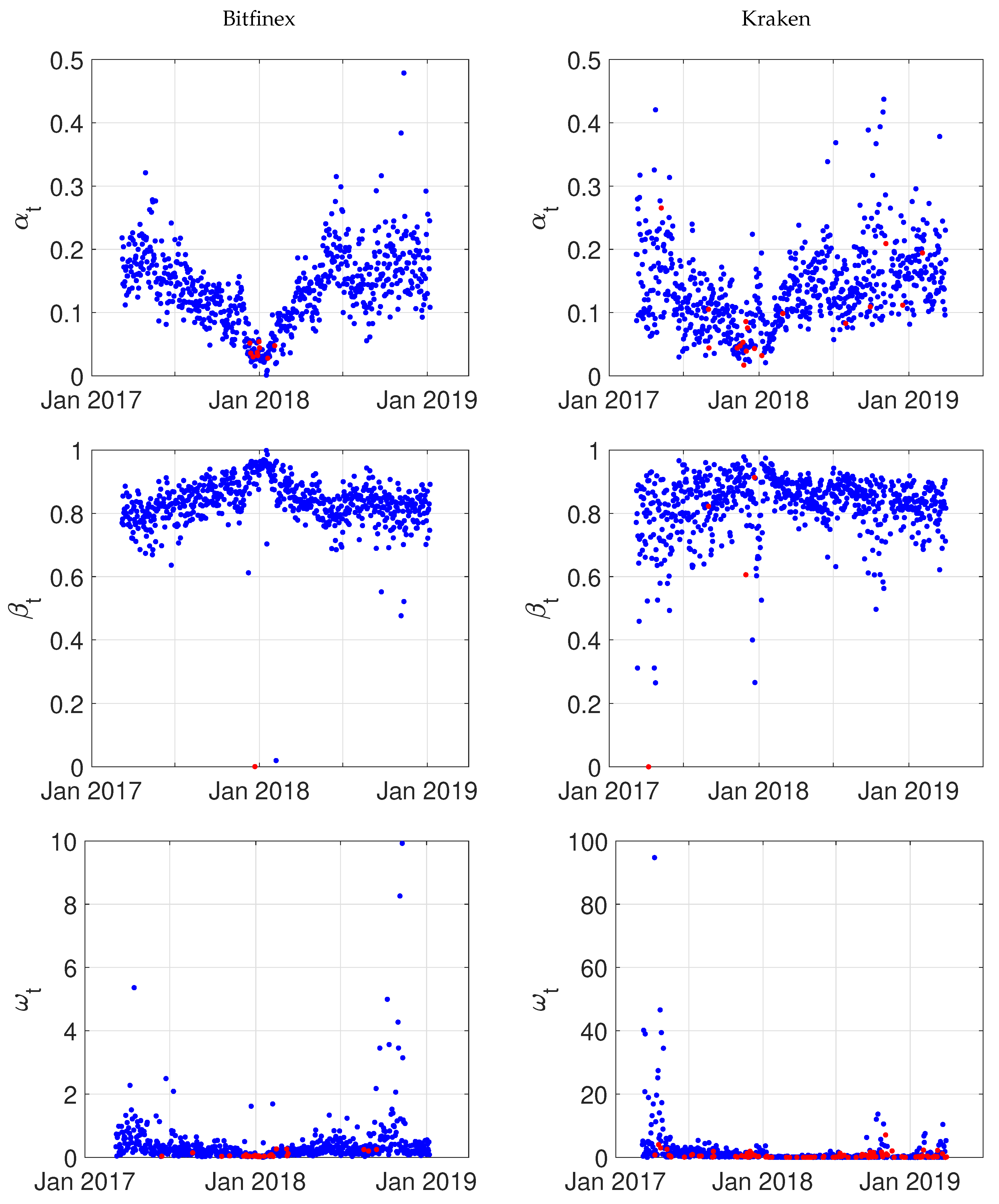
As we conduct in total 1412 estimations
5, we resort to a graphical illustration of the results rather than tables
6. The estimates of the model parameters
,
, and
are presented in
Figure 7. Overall, the estimates are compatible with a stationary autoregressive duration process, i.e.,
. Again, the pattern over time corresponds to the increased attention that Bitcoin trading received until the end of 2017: the persistence parameter
slightly increases from around 0.8 towards 0.99 (with a few exceptions) at the end of 2017 and then starts to decay again. This reflects the self-enforcing property of the process that the intensity level clusters (just like volatility in a GARCH process). The parameter
shows the opposite behavior which indicates that short-run innovations in the duration process were not that important at the end of 2017. The constant
is the most volatile of our parameters. This is sensible as the unconditional mean of the (stationary) process
is strongly driven by the constant which ultimately has to reflect the unconditional distribution of average durations over time as depicted in
Figure 5.
The estimated parameters (, ) are statistically significant on a 5% significance level in 98.66% (99.85%, 96.13%) of all daily samples for Bitfinex and in 97.57% (99.46%, 87.45%) of all samples for Kraken. The overdispersion test leads us to reject the hypothesis that the model is correctly specified using an exponential distribution. Due to the high number of observations, we rely on the asymptotic results of QML which establish that the parameter estimates are consistent, albeit with a larger standard error. Based on the Ljung-Box statistic, we reject the hypothesis of residual autocorrelation in 380 out of 741 cases for Kraken. Using higher orders in the test to check whether higher moments are independent, we reject the null hypothesis of dependence in no less than 678 cases. For Bitfinex, the null hypothesis of autocorrelated residuals is rejected in nearly half of all cases. For tests of higher order, we reject the null hypothesis in no less than 639 out of 671 cases. Overall, the model seems to provide a good fit with some exceptions.
Based on the parameter estimates displayed in
Figure 7, we can then compute the intradaily volatility as in Equation (
9) for every day. The measure is computed on a 1-second basis and the values are annualized.
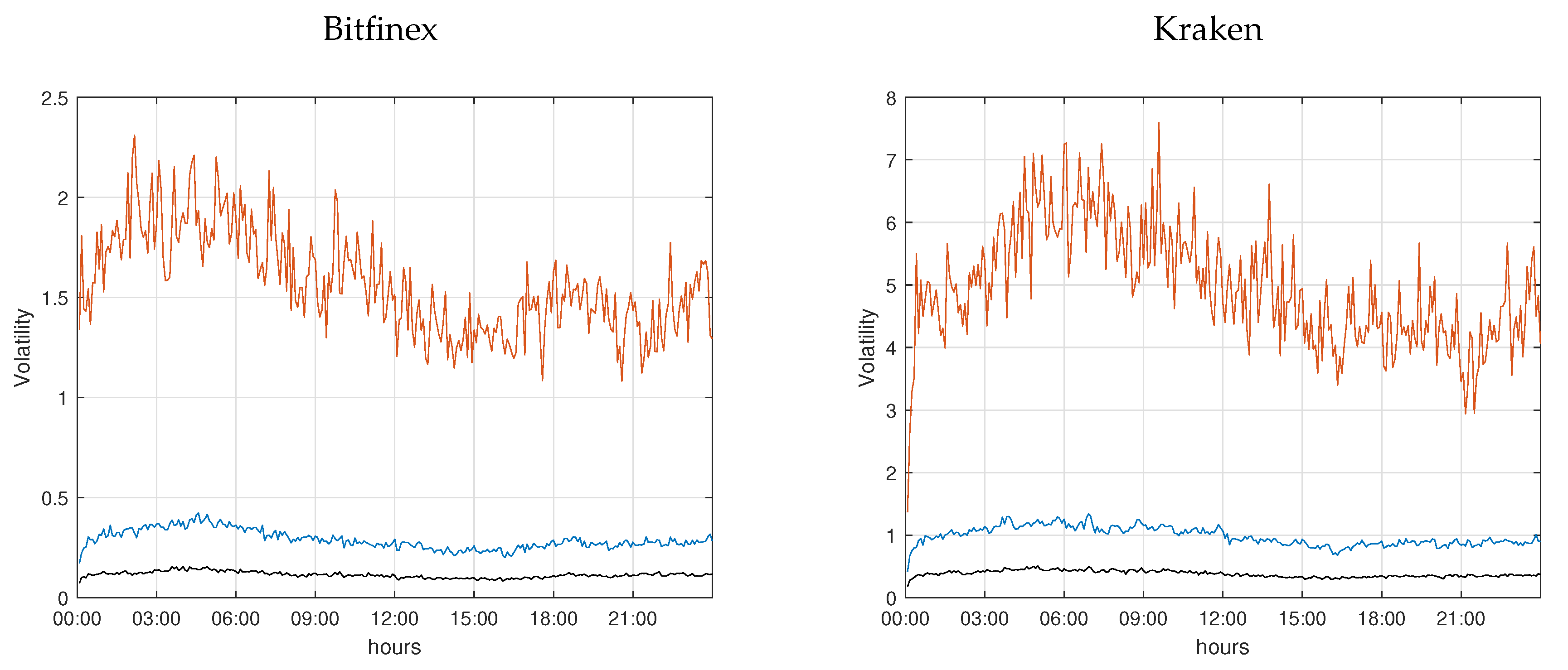
To visualize the time series, we aggregate the thus obtained instantaneous volatility to five minute intervals by taking the interval average.
Figure 8 presents for all five-minute intervals during a day the median and the 70% and 90% quantiles of volatility across days. As can be seen, the median of average volatility is comparatively low and does not vary substantially over the day. Hence, we may say that, on a median day, the volatility is almost constant over time. In contrast, on a volatile day, i.e., a day with a volatility level which is higher by roughly a factor 10, there is a pronounced pattern as can be seen from the 90% quantile. As before, the pattern corresponds to trading and non-trading times of European and U.S. stock markets.
The results presented in
Figure 8 have a direct implication for the microstructure of Kraken and Bitfinex. Our estimates show that, on average, the information flow in Bitcoin markets is clustered during the day. The higher volatility from 12:00 a.m. to 9:00 a.m. UCT shows that information flow and trading activity are low, and therefore the risk of no informational price changes which is tantamount to no new information is high. Our results complement the findings of
Eross et al. (
2019) who show that liquidity is lowest during the same period (based on
Amihud’s (
2002) illiquidity measure). In other words, price risk is highest during the European night. A single, sufficiently large transaction would have the ability to induce large price swings as in general the risk of no price change is high during this period.
This observation has two important implications. On the one hand, when an investor wants to sell a substantial amount of Bitcoin, she is well-advised to split her orders in a way that the execution time does not include this nightly period. A simple TWAP order placement strategy, i.e., sending a new order with the same order volume after every pre-defined interval, would be exposed to substantial price risk if the time for execution is not limited to the identified low risk period. While a VWAP strategy could account for the available volume, it would still be riskier from 12:00 a.m. to 9:00 a.m. UCT than during the rest of the day. On the other hand, a high price risk offers the opportunity to manipulate the market. A trader might try to push prices down and take the opposite standpoint in the Bitcoin derivatives markets to make money. Such a strategy is easier implemented during the night than the day.
4.2. Durations and the Blockchain
The time in-between consecutive trades carries information about the price as well as about liquidity. If durations are long, this corresponds to a period of low liquidity and slow generation of new information. As trading on Bitfinex and Kraken is organized as a limit order book, limit orders submitted by investors provide the necessary liquidity on the exchanges. However, there is an additional factor which is not an issue in the stock market: the blockchain. While exchanges net a substantial amount of trading on their platform, we assume that they are not be able to cross all trades internally. Hence, it will be necessary to submit some orders to the blockchain which triggers the post-processing industry: miners are paid and orders wait in the pool to be confirmed and added to a block. Thus, on a contemporaneous basis, we would expect that days with shorter durations require more computational efforts on the blockchain. If investors are rational, they might take these factors into account, however. If time is not pressing, they might delay a transaction if fees are high and wait for the next day when trading might be slower. All of these considerations entail a risk component and should therefore also be reflected in the volatility estimated based on price durations. Therefore, we will consider the contemporaneous relationship of selected features of the blockchain with durations and volatility as well as a predictive regression to evaluate whether traders account for blockchain characteristics and adjust their trading intensity accordingly.
The blockchain feature set considered includes the following variables: daily traded volume (in billion USD); the average block size (in megabytes); the cost per transaction (in USD); the hash rate (exahashes per second); the median confirmation time (in minutes); the aggregate number of confirmed transactions per day (Mempool Count); the aggregate size of transactions waiting to be confirmed (in megabytes, Mempool Size); the revenue of miners (coinbase block rewards and transaction fees in USD paid to miners); the average number of transactions per block (in thousands); the number of confirmed transactions (per day, in thousands); the total transaction fees paid (in USD); and the number of transactions added to the mempool per second (Transaction Rate). All data are obtained via the Blockchain Charts & Statistics API of Blockchain.com
7 and rescaled to the order of magnitude described above.
Table 2 presents contemporaneous correlations between the volatility and duration time series of Bitfinex and Kraken and the blockchain characteristics. Regarding volume, we find a negative relation with price durations which is sensible as higher volume is also associated with more transactions which lead to shorter durations. We also find a negative relationship between volume and volatility, which is in contrast to findings documented by
Giot et al. (
2010) and
Louhichi (
2011) who find a positive relationship between volume and volatility. It should be noted, however, that our volatility measure first and foremost indicates the risk of non-trading, i.e., liquidity risk. Of course, liquidity risk should be lower when volume is high and, thus, a negative association in this case is sensible.
As regards the remaining variables, average block size shows the weakest link to durations. Only in the case of Bitfinex do we find a slightly negative relation with durations that indicate that longer durations are associated with smaller blocks. As there is less to be recorded in case that durations are longer, this association is sensible, even though it does not seem to hold in the case of Kraken where we find a positive, albeit not statistically significant correlation. The correlation between cost per transaction and miner revenue and durations is negative as less transactions that need to be paid for reducing the volume dependent price that miners receive and, thus, their income. The relation with volatility is also negative which reflects the fact that lower execution risk comes at the cost of higher fees paid to miners. The relation to total transaction fees is similar. For the hash rate, we would have expected a negative relation with durations as shorter durations, associated with more transactions, should increase the necessary hashes the Bitcoin network needs to perform. Hence, the positive relation to Bitfinex durations cannot be explained. While the sign of Kraken durations is as expected, the estimate is not statistically significant. The relation to volatility is negative, which reflects again the relation between more traffic and reduced execution risk. The time from order submission to order execution is positively related to volatility and negatively to durations: A higher confirmation time is associated with a higher liquidity risk and more traffic in the sense of shorter durations jamming the blockchain so that confirmation times rise.
Both the growth and the existing size of the mempool are negatively related to durations, but not to volatility. Both measures reflect the demand for the blockchain and miner services which increases if the transaction frequency increases and, thus, price durations decrease. Lastly, the number of transactions per block, the number of confirmed transactions, and the transaction rate are positively related to volatility and negatively to durations. Again, higher durations require less computing power from the blockchain and are therefore negatively related to these measures. In contrast, lower values of these measures are associated with higher liquidity risk.
In order to evaluate whether traders account for these features when considering to submit a new order, we estimate a linear regression model to explain current volatility and durations with the previous day’s blockchain characteristics. Note that there cannot be a feedback effect from today’s on-exchange measures to yesterday’s blockchain characteristics. As a number of the features considered is related to the same underlying relationship, we reduce the variables for the predictive regression, also to avoid multicollinearity issues. Therefore, we drop miner revenue and total transaction fees, the average block size, the transaction rate, and the Mempool Count variables. As
Figure 5 and
Figure 8 show that both price durations and volatility have a strong time-varying pattern, the regression includes a level and squared time trend variable. The trend is implemented in such a way that the variable increases from 0 to 1 in the course of a year. Statistical significance is evaluated using heteroskedasticity and autocorrelation robust standard errors.
The results are presented in
Table 3. It turns out that most of the blockchain variables do not predict future duration averages or volatility. Hence, traders seem to take these features as given and only consider them of minor importance when taking the decision to trade. This is in particular true for the cost per transaction which does not predict duration. Hence, traders do not delay any orders based on a fear that high transaction fees might occur. However, transaction fees are related to liquidity, and higher fees indeed predict higher volatility.
The only variable which is consistently statistically significant is the hash rate. A higher hash rate predicts both longer durations and higher volatility. The hash rate is the speed at which new blocks can be created and it has steadily increased over time. Hence, the sign in the predictive regression is unexpected: one might assume that a better performing network would reduce risk and also set an incentive for traders to trade at a higher frequency (maybe by reducing order size). This is, however, not what we find. The parameter estimates are all positive and would indicate that a higher hash rate is associated with less favorable terms of trading. This is an unexpected result, but one should keep in mind that the explanatory power of the hash rate is still weak, albeit the parameter being statistically significant. Overall, adding the blockchain characteristics increases the adjusted by no more than two basis points in the volatility models and less than one basis point in the duration models.
The variables which explain a substantial proportion of the variance of volatility and durations are the time trend and its square. Of course, these are deterministic functions and their explanatory power is at odds with the idea of efficient markets. However, in the special case of Bitcoin and in the time period considered, the trend variables pick up attention.
Figure 5 and
Figure 8 suggest a decisive u-shape of durations and volatility, respectively, over time. This pattern coincides with the increase and decrease of interest in Bitcoin markets as measured, for example, by the search volume of Google. The latter peaked in the week of 17 December 2017, the day with the highest Bitcoin price ever recorded. As the price began to fall, interest dissipated as well. Hence, it seems that, along with the issues which are known from market microstructure theory to influence price volatility and liquidity, in Bitcoin markets, there is an additional, important component: Attention as fostered by the media and picked up by the trend function in our regression.