Pricing and Hedging American-Style Options with Deep Learning
Abstract
1. Introduction
2. Calculating a Candidate Optimal Stopping Strategy
- (i)
- Simulate5 paths , , of the underlying process .
- (ii)
- Set for all k.
- (iii)
- For , approximate with by minimizing the sum
- (iv)
- Set
- (v)
- Define , and set constantly equal to .
- denotes the depth and the numbers of nodes in the different layers;
- are affine functions;
- For , is of the form for a given activation function .
3. Pricing
3.1. Lower Bound
3.2. Upper Bound, Point Estimate and Confidence Intervals
4. Hedging
4.1. Hedging Until the First Possible Exercise Date
4.2. Hedging Until the Exercise Time
5. Example
5.1. Pricing Results
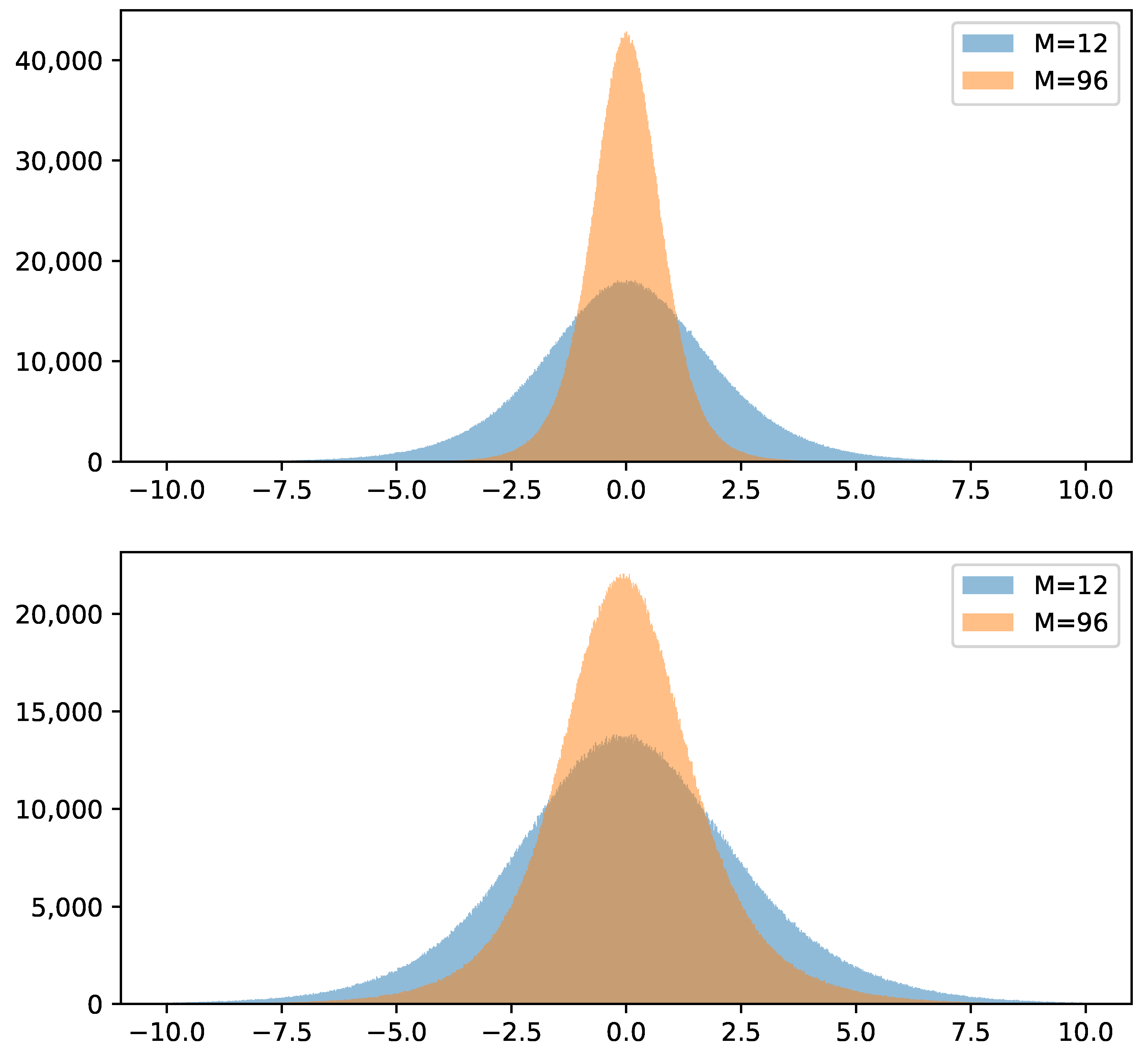
5.2. Hedging Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Andersen, Leif. 2000. A simple approach to the pricing of Bermudan swaptions in the multifactor LIBOR market model. The Journal of Computational Finance 3: 5–32. [Google Scholar] [CrossRef]
- Bally, Vlad, Gilles Pagès, and Jacques Printems. 2005. A quantization tree method for pricing and hedging multidimensional American options. Mathematical Finance 15: 119–68. [Google Scholar] [CrossRef]
- Barraquand, Jérôme, and Didier Martineau. 1995. Numerical valuation of high dimensional multivariate American securities. The Journal of Financial and Quantitative Analysis 30: 383–405. [Google Scholar] [CrossRef]
- Becker, Sebastian, Patrick Cheridito, and Arnulf Jentzen. 2019a. Deep optimal stopping. Journal of Machine Learning Research 20: 1–25. [Google Scholar]
- Becker, Sebastian, Patrick Cheridito, Arnulf Jentzen, and Timo Welti. 2019b. Solving high-dimensional optimal stopping problems using deep learning. arXiv arXiv:1908.01602. [Google Scholar]
- Berridge, Steffan J., and Johannes M. Schumacher. 2008. An irregular grid approach for pricing high-dimensional American options. Journal of Computational and Applied Mathematics 222: 94–111. [Google Scholar] [CrossRef]
- Bouchard, Bruno, and Xavier Warin. 2012. Monte-Carlo valuation of American options: Facts and new algorithms to improve existing methods. In Numerical Methods in Finance. Berlin and Heidelberg: Springer, pp. 215–255. [Google Scholar]
- Broadie, Mark, and Menghui Cao. 2008. Improved lower and upper bound algorithms for pricing American options by simulation. Quantitative Finance 8: 845–61. [Google Scholar] [CrossRef]
- Broadie, Mark, and Paul Glasserman. 2004. A stochastic mesh method for pricing high-dimensional American options. Journal of Computational Finance 7: 35–72. [Google Scholar] [CrossRef]
- Bru, Bernard, and Henri Heinich. 1985. Meilleures approximations et médianes conditionnelles. Annales de l’I.H.P. Probabilités et Statistiques 21: 197–224. [Google Scholar]
- Buehler, Hans, Lukas Gonon, Josef Teichmann, and Ben Wood. 2019. Deep hedging. Quantitative Finance 19: 1271–91. [Google Scholar] [CrossRef]
- Carriere, Jacques F. 1996. Valuation of the early-exercise price for options using simulations and nonparametric regression. Insurance: Mathematics and Economics 19: 19–30. [Google Scholar] [CrossRef]
- Chen, Yangang, and Justin W.L. Wan. 2019. Deep neural network framework based on backward stochastic differential equations for pricing and hedging American options in high dimensions. arXiv arXiv:1909.11532. [Google Scholar]
- Egloff, Daniel, Michael Kohler, and Nebojsa Todorovic. 2007. A dynamic look-ahead Monte Carlo algorithm for pricing Bermudan options. Annals of Applied Probability 17: 1138–71. [Google Scholar] [CrossRef]
- Forsyth, Peter A., and Ken R. Vetzal. 2002. Quadratic convergence for valuing American options using a penalty method. SIAM Journal on Scientific Computing 23: 2095–122. [Google Scholar] [CrossRef]
- García, Diego. 2003. Convergence and biases of Monte Carlo estimates of American option prices using a parametric exercise rule. Journal of Economic Dynamics and Control 27: 1855–79. [Google Scholar] [CrossRef]
- Glorot, Xavier, and Yoshua Bengio. 2010. Understanding the difficulty of training deep feedforward neural networks. Paper Presented at Thirteenth International Conference on Artificial Intelligence and Statistics, PMLR, Sardinia, Italy, May 13–15, vol. 9, pp. 249–256. [Google Scholar]
- Han, Jiequn, Arnulf Jentzen, and Weinan E. 2018. Solving high-dimensional partial differential equations using deep learning. Proceedings of the National Academy of Sciences of the United States of America 115: 8505–10. [Google Scholar] [CrossRef]
- Haugh, Martin B., and Leonid Kogan. 2004. Pricing American options: a duality approach. Operations Research 52: 258–70. [Google Scholar] [CrossRef]
- Hull, John C. 2003. Options, Futures and Other Derivatives. London: Pearson. Upper Saddle River: Prentice Hall. [Google Scholar]
- Ioffe, Sergey, and Christian Szegedy. 2015. Batch normalization: accelerating deep network training by reducing internal covariate shift. Paper presented at 32nd International Conference on Machine Learning, ICML 2015, Lille, France, July 6–11, vol. 37, pp. 448–456. [Google Scholar]
- Jain, Shashi, and Cornelis W. Oosterlee. 2015. The stochastic grid bundling method: efficient pricing of Bermudan options and their Greeks. Applied Mathematics and Computation 269: 412–31. [Google Scholar] [CrossRef]
- Kingma, Diederik P., and Jimmy Ba. 2015. Adam: A method for stochastic optimization. Paper Presented at International Conference on Learning Representations, San Diego, CA, USA, May 7–9. [Google Scholar]
- Kohler, Michael, Adam Krzyżak, and Nebojsa Todorovic. 2010. Pricing of high-dimensional American options by neural networks. Mathematical Finance 20: 383–410. [Google Scholar] [CrossRef]
- Kolodko, Anastasia, and John Schoenmakers. 2006. Iterative construction of the optimal Bermudan stopping time. Finance and Stochastics 10: 27–49. [Google Scholar] [CrossRef]
- Lapeyre, Bernard, and Jérôme Lelong. 2019. Neural network regression for Bermudan option pricing. arXiv arXiv:1907.06474. [Google Scholar]
- Longstaff, Francis A., and Eduardo S. Schwartz. 2001. Valuing American options by simulation: a simple least-squares approach. The Review of Financial Studies 14: 113–47. [Google Scholar] [CrossRef]
- Reisinger, Christoph, and Jan H. Witte. 2012. On the use of policy iteration as an easy way of pricing American options. SIAM J. Financial Math. 3: 459–78. [Google Scholar] [CrossRef]
- Rogers, Chris. 2002. Monte Carlo valuation of American options. Mathematical Finance 12: 271–86. [Google Scholar] [CrossRef]
- Rogers, Chris. 2010. Dual valuation and hedging of Bermudan options. SIAM Journal on Financial Mathematics 1: 604–8. [Google Scholar] [CrossRef]
- Sirignano, Justin, and Konstantinos Spiliopoulos. 2018. DGM: A deep learning algorithm for solving partial differential equations. Journal of Computational Physics 375: 1339–64. [Google Scholar] [CrossRef]
- Tilley, James A. 1993. Valuing American options in a path simulation model. Transactions of the Society of Actuaries 45: 83–104. [Google Scholar]
- Tsitsiklis, John N., and Benjamin Van Roy. 2001. Regression methods for pricing complex American-style options. IEEE Transactions on Neural Networks 12: 694–703. [Google Scholar] [CrossRef]
| 1. | Meaning feedforward networks with a single hidden layer. |
| 2. | This covers Bermudan options as well as American options that can only be exercised at a given time each day. Continuously exercisable options must be approximated by discretizing time. |
| 3. | That is, is -measurable, and for all and every measurable function such that is integrable. |
| 4. | The main difference between this algorithm and the one of Longstaff and Schwartz (2001) is the use of neural networks instead of linear combinations of basis functions. In addition, the sum in (3) is over all simulated paths, whereas in Longstaff and Schwartz (2001), only in-the-money paths are considered to save computational effort. While it is enough to use in-the-money paths to determine a candidate optimal stopping rule, we need accurate approximate continuation values for all to construct good hedging strategies in Section 4. |
| 5. | As usual, we simulate the paths , , independently of each other. |
| 6. | Generated independently of , |
| 7. | The use of nested simulation ensures that are unbiased estimates of , which is crucial for the validity of the upper bound. In particular, we do not directly approximate with the estimated continuation value functions . |
| 8. | Discounting is done with respect to the savings account. Then, the discounted value of money invested in the savings account stays constant. |
| 9. | That is, is -measurable and for all and every measurable function such that is integrable. |
| 10. | |
| 11. | Independent of , . |
| 12. | The computations were performed on a NVIDIA GeForce RTX 2080 Ti GPU. The underlying system was an AMD Ryzen 9 3950X CPU with 64 GB DDR4 memory running Tensorflow 2.1 on Ubuntu 19.10. |
| 13. | Bermudan max-call options are a benchmark example in the literature on numerical methods for high-dimensional American-style options; see, e.g., Longstaff and Schwartz (2001); Rogers (2002); García (2003); Broadie and Glasserman (2004); Haugh and Kogan (2004); Broadie and Cao (2008); Berridge and Schumacher (2008); Jain and Oosterlee (2015); Becker et al. (2019a, 2019b). |
| 14. | That is, for all and . |
| 15. | Simulation based methods work for any price dynamics that can efficiently be simulated. Prices of max-call options on underlying assets with different price dynamics were calculated in Broadie and Cao (2008) and Becker et al. (2019a). |
| 16. | The hyperparamters were chosen as in Kingma and Ba (2015). The stepsize was specified as , , and according to a deterministic schedule. |
| d | Point Est. | CI | DOS CI | |||||
|---|---|---|---|---|---|---|---|---|
| 5 | 90 | 132 | 8 | |||||
| 5 | 100 | 134 | 8 | |||||
| 5 | 110 | 133 | 8 | |||||
| 10 | 90 | 136 | 8 | |||||
| 10 | 100 | 136 | 7 | |||||
| 10 | 110 | 135 | 8 |
| IHE | IHS | IHS/ | T1 | HE | HS | HS/ | T2 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 90 | 12 | 102 | 379 | ||||||
| 5 | 90 | 24 | 129 | 473 | ||||||
| 5 | 90 | 48 | 234 | 839 | ||||||
| 5 | 90 | 96 | 436 | |||||||
| 5 | 100 | 12 | 102 | 407 | ||||||
| 5 | 100 | 24 | 131 | 512 | ||||||
| 5 | 100 | 48 | 252 | 931 | ||||||
| 5 | 100 | 96 | 470 | |||||||
| 5 | 110 | 12 | 102 | 380 | ||||||
| 5 | 110 | 24 | 130 | 511 | ||||||
| 5 | 110 | 48 | 262 | 950 | ||||||
| 5 | 110 | 96 | 471 | |||||||
| 10 | 90 | 12 | 111 | 414 | ||||||
| 10 | 90 | 24 | 145 | 534 | ||||||
| 10 | 90 | 48 | 269 | 958 | ||||||
| 10 | 90 | 96 | 506 | |||||||
| 10 | 100 | 12 | 111 | 414 | ||||||
| 10 | 100 | 24 | 152 | 531 | ||||||
| 10 | 100 | 48 | 271 | 978 | ||||||
| 10 | 100 | 96 | 512 | |||||||
| 10 | 110 | 12 | 112 | 410 | ||||||
| 10 | 110 | 24 | 146 | 530 | ||||||
| 10 | 110 | 48 | 269 | 965 | ||||||
| 10 | 110 | 96 | 507 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Becker, S.; Cheridito, P.; Jentzen, A. Pricing and Hedging American-Style Options with Deep Learning. J. Risk Financial Manag. 2020, 13, 158. https://doi.org/10.3390/jrfm13070158
Becker S, Cheridito P, Jentzen A. Pricing and Hedging American-Style Options with Deep Learning. Journal of Risk and Financial Management. 2020; 13(7):158. https://doi.org/10.3390/jrfm13070158
Chicago/Turabian StyleBecker, Sebastian, Patrick Cheridito, and Arnulf Jentzen. 2020. "Pricing and Hedging American-Style Options with Deep Learning" Journal of Risk and Financial Management 13, no. 7: 158. https://doi.org/10.3390/jrfm13070158
APA StyleBecker, S., Cheridito, P., & Jentzen, A. (2020). Pricing and Hedging American-Style Options with Deep Learning. Journal of Risk and Financial Management, 13(7), 158. https://doi.org/10.3390/jrfm13070158




