Life after Debt: The Effects of Overleveraging on Conventional and Islamic Banks
Abstract
1. Introduction
2. Literature Review
3. Empirical Approach and Definition of Variables
3.1. Background
3.2. Theoretical Model
4. Empirical Analysis
4.1. Graphical Results and Analysis: Actual vs. Optimal Debt
4.2. Graphical Results and Analysis: Excess Debt
5. Policy Implication
6. Conclusions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Mathematical Derivation of Stein’s Optimal Debt
Appendix A.1.1. Model I
Appendix A.1.2. Model II
Appendix B
| Bank Name | Type | Country |
|---|---|---|
| Bank of Bahrain and Kuwait | Conventional Bank | Bahrain |
| National Bank of Bahrain | Conventional Bank | Bahrain |
| Salam Bank | Islamic Bank | Bahrain |
| Shamil Bank | Islamic Bank | Bahrain |
| National Bank of Kuwait | Conventional Bank | Kuwait |
| Gulf Bank of Kuwait | Conventional Bank | Kuwait |
| Boubyan Bank | Islamic Bank | Kuwait |
| Kuwait Finance House | Islamic Bank | Kuwait |
| United Overseas Bank | Conventional Bank | Malaysia |
| MayBank | Conventional Bank | Malaysia |
| Bank Islam Berhad | Islamic Bank | Malaysia |
| Bank Muamalat | Islamic Bank | Malaysia |
| Bank of America | Conventional Bank | United States |
| Wells Fargo | Conventional Bank | United States |
| Bank of Whittier | Islamic Bank | United States |
| University Bank Corp | Islamic Bank | United States |
| Barclays | Conventional Bank | United Kingdom |
| Lloyds | Conventional Bank | United Kingdom |
| Bank of London and the Middle East | Islamic Bank | United Kingdom |
| Islamic Bank of Britain | Islamic Bank | United Kingdom |
Appendix C
| Bank | Year | Capital Gains/ (losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bank of Bahrain and Kuwait | 2000 | 0.035948 | 0.0209 | 0.025349 | (0.009) | 0.001 | 0.33 | 0.0001 | (0.0416) | (0.0000) | 0.0112 | 0.1543 | (0.0000) | 0.166 | 0.29 | 0.87 | 0.236872 | (0.37) | (1.24) |
| 2001 | 0.041504 | 0.0267 | 0.032331 | (0.002) | 0.001 | 0.33 | 0.0059 | (0.0360) | (0.0001) | 0.0112 | 0.1543 | (0.0001) | 0.166 | 0.29 | 0.86 | 0.254565 | (0.34) | (1.20) | |
| 2002 | 0.073967 | 0.018 | 0.003159 | (0.031) | 0.003 | 0.34 | (0.0028) | (0.0035) | 0.0000 | 0.0112 | 0.1543 | 0.0000 | 0.165 | 0.53 | 1.13 | 0.69835 | 0.56 | (0.57) | |
| 2003 | 0.138663 | 0.011 | 0.033255 | (0.001) | 0.010 | 0.34 | (0.0098) | 0.0611 | (0.0002) | 0.0112 | 0.1543 | (0.0004) | 0.166 | 0.92 | 1.57 | 0.205046 | (0.44) | (2.01) | |
| 2004 | 0.088788 | 0.013 | 0.037132 | 0.003 | 0.004 | 0.37 | (0.0078) | 0.0113 | (0.0000) | 0.0112 | 0.1543 | (0.0001) | 0.166 | 0.64 | 1.26 | 0.070744 | (0.71) | (1.97) | |
| 2005 | 0.063932 | 0.033 | 0.031825 | (0.002) | 0.002 | 0.39 | 0.0122 | (0.0136) | (0.0001) | 0.0112 | 0.1543 | (0.0001) | 0.166 | 0.38 | 0.96 | 0.235672 | (0.38) | (1.34) | |
| 2006 | 0.430349 | 0.049 | 0.034116 | (0.000) | 0.093 | 0.41 | 0.0282 | 0.3528 | 0.0041 | 0.0112 | 0.1543 | 0.0081 | 0.157 | 2.08 | 2.88 | 1.387948 | 1.96 | (0.92) | |
| 2007 | −0.0284 | 0.037 | 0.036741 | 0.003 | 0.000 | (0.04) | 0.0162 | (0.1059) | 0.0001 | 0.0112 | 0.1543 | 0.0002 | 0.165 | (0.19) | 0.32 | 0.8 | 0.77 | 0.45 | |
| 2008 | −0.05395 | 0.0295 | 0.052763 | 0.019 | 0.001 | 0.09 | 0.0087 | (0.1315) | (0.0001) | 0.0112 | 0.1543 | (0.0002) | 0.166 | (0.31) | 0.19 | 1.52585 | 2.24 | 2.05 | |
| 2009 | 0.019355 | 0.0159 | 0.039745 | 0.006 | 0.000 | 0.37 | (0.0049) | (0.0582) | 0.0001 | 0.0112 | 0.1543 | 0.0002 | 0.165 | 0.23 | 0.79 | 1.078156 | 1.33 | 0.54 | |
| 2010 | −0.30252 | 0.0133 | 0.045063 | 0.011 | 0.046 | 0.38 | (0.0075) | (0.3800) | 0.0011 | 0.0112 | 0.1543 | 0.0022 | 0.163 | (2.00) | (1.72) | 0.346702 | (0.15) | 1.57 | |
| 2011 | 0.17931 | 0.0225 | 0.044219 | 0.010 | 0.016 | 0.65 | 0.0017 | 0.1018 | 0.0001 | 0.0112 | 0.1543 | 0.0002 | 0.165 | 1.06 | 1.73 | 0.117191 | (0.62) | (2.35) | |
| 2012 | 0.152295 | 0.0159 | 0.03695 | 0.003 | 0.012 | 0.67 | (0.0049) | 0.0748 | (0.0002) | 0.0112 | 0.1543 | (0.0005) | 0.166 | 0.96 | 1.61 | 0.061531 | (0.73) | (2.34) | |
| 2013 | 0.093535 | 0.0082 | 0.033621 | (0.001) | 0.004 | 0.67 | (0.0126) | 0.0160 | (0.0001) | 0.0112 | 0.1543 | (0.0003) | 0.166 | 0.69 | 1.32 | 0.029262 | (0.79) | (2.11) | |
| 2014 | −0.05067 | 0.007 | 0.032519 | (0.002) | 0.001 | 0.68 | (0.0138) | (0.1282) | 0.0012 | 0.0112 | 0.1543 | 0.0024 | 0.163 | (0.14) | 0.37 | 0.059426 | (0.73) | (1.11) | |
| 2015 | 0.239627 | 0.012 | 0.033432 | (0.001) | 0.029 | (1.00) | (0.0088) | 0.1621 | 0.0014 | 0.0112 | 0.1543 | 0.0029 | 0.163 | 1.44 | 2.16 | 0.027358 | (0.80) | (2.96) | |
| 2016 | 0.196 | 0.0209 | 0.028069 | (0.006) | 0.019 | (1.00) | 0.0001 | 0.1185 | (0.0000) | 0.0112 | 0.1543 | (0.0000) | 0.003 | 1.21 | 1.90 | 0.025771 | (0.80) | (2.70) |
| Bank | Year | Capital Gains/(Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| National Bank of Bahrain | 2000 | 0.166589 | 0.0209 | 0.0531 | (0.007) | 0.014 | (0.51) | 0.0001 | 0.0951 | (0.0000) | 0.0112 | 0.0682 | (0.0000) | 0.079 | 2.41 | 1.16 | 0.194007 | (0.76) | (1.92) |
| 2001 | 0.041728 | 0.0267 | 0.057698 | (0.002) | 0.001 | (0.51) | 0.0059 | (0.0298) | 0.0001 | 0.0112 | 0.0682 | 0.0002 | 0.079 | 0.93 | (0.43) | 0.195552 | (0.74) | (0.31) | |
| 2002 | 0.072756 | 0.018 | 0.054797 | (0.005) | 0.003 | (0.51) | (0.0028) | 0.0012 | 0.0000 | 0.0112 | 0.0682 | 0.0000 | 0.079 | 1.41 | 0.08 | 0.206507 | (0.64) | (0.72) | |
| 2003 | 0.14795 | 0.011 | 0.056187 | (0.004) | 0.011 | (0.51) | (0.0098) | 0.0764 | 0.0004 | 0.0112 | 0.0682 | 0.0008 | 0.079 | 2.37 | 1.12 | 0.217089 | (0.54) | (1.66) | |
| 2004 | 0.108767 | 0.013 | 0.058259 | (0.002) | 0.006 | (0.51) | (0.0078) | 0.0372 | 0.0001 | 0.0112 | 0.0682 | 0.0003 | 0.079 | 1.89 | 0.60 | 0.211194 | (0.60) | (1.20) | |
| 2005 | 0.017907 | 0.033 | 0.057255 | (0.003) | 0.000 | (0.51) | 0.0122 | (0.0536) | 0.0003 | 0.0112 | 0.0682 | 0.0007 | 0.079 | 0.57 | (0.83) | 0.203157 | (0.67) | 0.15 | |
| 2006 | 0.084808 | 0.049 | 0.048394 | (0.011) | 0.004 | (0.51) | 0.0282 | 0.0133 | (0.0002) | 0.0112 | 0.0682 | (0.0004) | 0.080 | 1.15 | (0.20) | 0.447588 | 1.62 | 1.82 | |
| 2007 | −0.12275 | 0.037 | 0.048615 | (0.011) | 0.008 | (0.51) | 0.0162 | (0.1943) | 0.0016 | 0.0112 | 0.0682 | 0.0032 | 0.076 | (1.39) | (2.94) | 0.48535 | 1.98 | 4.92 | |
| 2008 | −0.01062 | 0.0295 | 0.043831 | (0.016) | 0.000 | (0.51) | 0.0087 | (0.0822) | 0.0004 | 0.0112 | 0.0682 | 0.0007 | 0.079 | 0.25 | (1.17) | 0.455625 | 1.70 | 2.87 | |
| 2009 | 0.062447 | 0.0159 | 0.033267 | (0.027) | 0.002 | (0.51) | (0.0049) | (0.0091) | (0.0000) | 0.0112 | 0.0682 | (0.0000) | 0.079 | 1.31 | (0.02) | 0.447103 | 1.62 | 1.64 | |
| 2010 | 0.116453 | 0.0133 | 0.039456 | (0.020) | 0.007 | (0.51) | (0.0075) | 0.0449 | 0.0002 | 0.0112 | 0.0682 | 0.0003 | 0.079 | 1.98 | 0.69 | 0.233302 | (0.39) | (1.08) | |
| 2011 | 0.088381 | 0.0225 | 0.028235 | (0.032) | 0.004 | (0.51) | 0.0017 | 0.0168 | (0.0000) | 0.0112 | 0.0682 | (0.0000) | 0.079 | 1.53 | 0.21 | 0.239318 | (0.33) | (0.55) | |
| 2012 | 0.034268 | 0.0159 | 0.047863 | (0.012) | 0.001 | (0.51) | (0.0049) | (0.0373) | (0.0001) | 0.0112 | 0.0682 | (0.0002) | 0.080 | 0.97 | (0.39) | 0.23483 | (0.37) | 0.02 | |
| 2013 | 0.060448 | 0.0082 | 0.042752 | (0.017) | 0.002 | (0.51) | (0.0126) | (0.0111) | (0.0001) | 0.0112 | 0.0682 | (0.0001) | 0.080 | 1.38 | 0.05 | 0.227359 | (0.44) | (0.50) | |
| 2014 | 0.113977 | 0.007 | 0.242594 | 0.183 | 0.006 | (0.51) | (0.0138) | 0.0424 | 0.0003 | 0.0112 | 0.0682 | 0.0006 | 0.079 | 2.04 | 0.76 | 0.236065 | (0.36) | (1.12) | |
| 2015 | 0.117358 | 0.012 | 0.059611 | (0.000) | 0.007 | (0.51) | (0.0088) | 0.0458 | 0.0002 | 0.0112 | 0.0682 | 0.0004 | 0.079 | 2.01 | 0.72 | 0.224724 | (0.47) | (1.19) | |
| 2016 | 0.115698 | 0.0209 | 0.044737 | (0.015) | 0.007 | (0.51) | 0.0001 | 0.0442 | (0.0000) | 0.0112 | 0.0682 | (0.0000) | 0.079 | 1.86 | 0.57 | 0.210441 | (0.60) | (1.17) |
| Bank | Year | Capital Gains/ (Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Salam | 2006 | 0.28948 | 0.049 | 0.090492 | (0.549) | 0.042 | 0.29 | 0.0280 | 0.4546 | 0.0037 | 0.0129 | 0.9810 | 0.0073 | 0.987 | 0.85 | 0.37 | 0.037723 | (0.48) | (0.85) |
| 2007 | 0.093897 | 0.037 | 0.206722 | (0.433) | 0.004 | 0.29 | 0.0160 | 0.2590 | 0.0012 | 0.0129 | 0.9810 | 0.0024 | 0.992 | 0.70 | 0.31 | 0.153804 | 1.12 | 0.82 | |
| 2008 | −0.48842 | 0.0295 | 0.214255 | (0.425) | 0.119 | 0.29 | 0.0085 | (0.3233) | (0.0008) | 0.0129 | 0.9810 | (0.0016) | 0.995 | 0.00 | 0.00 | 0.174155 | 1.40 | 1.40 | |
| 2009 | −0.25221 | 0.0159 | 0.087267 | (0.552) | 0.032 | 0.29 | (0.0051) | (0.0871) | 0.0001 | 0.0129 | 0.9810 | 0.0003 | 0.994 | 0.34 | 0.15 | 0.155421 | 1.15 | 0.99 | |
| 2010 | 0.013407 | 0.0133 | 0.07927 | (0.560) | 0.000 | 0.29 | (0.0077) | 0.1785 | (0.0004) | 0.0129 | 0.9810 | (0.0008) | 0.995 | 0.64 | 0.28 | 0.169291 | 1.34 | 1.05 | |
| 2011 | 0.006393 | 0.0225 | 0.148245 | (0.491) | 0.000 | 0.29 | 0.0015 | 0.1715 | 0.0001 | 0.0129 | 0.9810 | 0.0001 | 0.994 | 0.63 | 0.28 | 0.01643 | (0.77) | (1.05) | |
| 2012 | 0.682094 | 0.0159 | 0.207661 | (0.432) | 0.233 | 0.29 | (0.0051) | 0.8472 | (0.0012) | 0.0129 | 0.9810 | (0.0025) | 0.996 | 1.08 | 0.47 | 0.01547 | (0.79) | (1.26) | |
| 2013 | −2.96427 | 0.0082 | 1.040925 | 0.401 | 4.393 | 0.29 | (0.0128) | (2.7991) | 0.0103 | 0.0129 | 0.9810 | 0.0207 | 0.973 | (6.90) | (2.99) | 0.023331 | (0.68) | 2.31 | |
| 2014 | 0.070685 | 0.007 | 1.354018 | 0.715 | 0.002 | 0.29 | (0.0140) | 0.2358 | (0.0010) | 0.0129 | 0.9810 | (0.0019) | 0.996 | 0.70 | 0.31 | 0.018723 | (0.74) | (1.05) | |
| 2015 | 0.406731 | 0.012 | 1.742688 | 1.103 | 0.083 | 0.29 | (0.0090) | 0.5719 | (0.0015) | 0.0129 | 0.9810 | (0.0030) | 0.997 | 0.95 | 0.42 | 0.018835 | (0.74) | (1.16) | |
| 2016 | 0.32568 | 0.0209 | 1.862311 | 1.223 | 0.053 | 0.29 | (0.0001) | 0.4908 | (0.0000) | 0.0129 | 0.9810 | (0.0000) | 0.994 | 0.90 | 0.39 | 0.013584 | (0.81) | (1.21) |
| Bank | Year | Capital Gains/(Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shamil | 2004 | −0.06515 | 0.013 | 0.137938 | (0.005) | 0.002 | 0.06 | (0.0083) | (0.2037) | 0.0001 | 0.0125 | 0.5135 | 0.0002 | 0.526 | 0.12 | (0.21) | 0.038924 | (1.49) | (1.28) |
| 2005 | 0.838895 | 0.033 | 0.123874 | (0.019) | 0.352 | 0.06 | 0.0117 | 0.7003 | 0.0005 | 0.0125 | 0.5135 | 0.0010 | 0.525 | 1.14 | 1.50 | 0.018369 | (1.68) | (3.19) | |
| 2006 | 0.23448 | 0.049 | 0.075787 | (0.067) | 0.027 | 0.06 | 0.0277 | 0.0959 | 0.0002 | 0.0125 | 0.5135 | 0.0003 | 0.526 | 0.57 | 0.55 | 0.105952 | (0.85) | (1.40) | |
| 2007 | 0.16803 | 0.037 | 0.195192 | 0.052 | 0.014 | 0.06 | 0.0157 | 0.0295 | 0.0000 | 0.0125 | 0.5135 | 0.0001 | 0.526 | 0.49 | 0.42 | 0.115486 | (0.76) | (1.18) | |
| 2008 | −0.14689 | 0.0295 | 0.093179 | (0.050) | 0.011 | 0.06 | 0.0082 | (0.2854) | (0.0001) | 0.0125 | 0.5135 | (0.0003) | 0.526 | (0.08) | (0.55) | 0.335118 | 1.32 | 1.88 | |
| 2009 | −0.02378 | 0.0159 | 0.109571 | (0.033) | 0.000 | 0.06 | (0.0054) | (0.1623) | 0.0001 | 0.0125 | 0.5135 | 0.0001 | 0.526 | 0.20 | (0.08) | 0.286356 | 0.86 | 0.94 | |
| 2010 | −0.63694 | 0.0133 | 0.137254 | (0.006) | 0.203 | 0.06 | (0.0080) | (0.7755) | 0.0004 | 0.0125 | 0.5135 | 0.0008 | 0.525 | (1.35) | (2.69) | 0.292248 | 0.92 | 3.60 | |
| 2011 | −0.02243 | 0.0225 | 0.121374 | (0.021) | 0.000 | 0.06 | 0.0012 | (0.1610) | (0.0000) | 0.0125 | 0.5135 | (0.0000) | 0.526 | 0.19 | (0.10) | 0.279813 | 0.80 | 0.90 | |
| 2012 | −0.0387 | 0.0159 | 0.258069 | 0.115 | 0.001 | 0.06 | (0.0054) | (0.1772) | 0.0001 | 0.0125 | 0.5135 | 0.0001 | 0.526 | 0.17 | (0.13) | 0.099477 | (0.91) | (0.78) | |
| 2013 | 1.47713 | 0.0082 | 0.142039 | (0.001) | 1.091 | 0.06 | (0.0131) | 1.3386 | (0.0011) | 0.0125 | 0.5135 | (0.0021) | 0.528 | 0.98 | 1.24 | 0.250673 | 0.52 | (0.72) | |
| 2014 | −0.07402 | 0.007 | 0.169908 | 0.027 | 0.003 | 0.06 | (0.0143) | (0.2126) | 0.0002 | 0.0125 | 0.5135 | 0.0004 | 0.526 | 0.11 | (0.22) | 0.253831 | 0.55 | 0.77 | |
| 2015 | 0.069478 | 0.012 | 0.154903 | 0.012 | 0.002 | 0.06 | (0.0093) | (0.0691) | 0.0000 | 0.0125 | 0.5135 | 0.0001 | 0.526 | 0.38 | 0.22 | 0.239775 | 0.42 | 0.20 | |
| 2016 | 0.020982 | 0.0209 | 0.137954 | (0.005) | 0.000 | 0.06 | (0.0004) | (0.1176) | 0.0000 | 0.0125 | 0.5135 | 0.0000 | 0.526 | 0.27 | 0.04 | 0.228215 | 0.31 | 0.26 |
| Bank | Year | Capital Gains/ (Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt RATIO | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| National Bank of Kuwait | 2000 | 0.297217 | 0.0209 | 0.064684 | (0.001) | 0.044 | (0.17) | (0.0003) | 0.2393 | 0.0000 | 0.0113 | 0.2373 | 0.0000 | 0.249 | 1.20 | 1.24 | 0.045879 | 1.26 | 0.02 |
| 2001 | 0.104353 | 0.0267 | 0.062055 | (0.003) | 0.005 | (0.17) | 0.0055 | 0.0464 | (0.0000) | 0.0113 | 0.2373 | (0.0001) | 0.249 | 0.55 | 0.35 | 0.044998 | 1.20 | 0.85 | |
| 2002 | 0.486797 | 0.018 | 0.055328 | (0.010) | 0.118 | (0.17) | (0.0032) | 0.4289 | 0.0002 | 0.0113 | 0.2373 | 0.0005 | 0.248 | 1.68 | 1.90 | 0.041164 | 0.94 | (0.97) | |
| 2003 | −0.04097 | 0.011 | 0.062038 | (0.003) | 0.001 | (0.17) | (0.0102) | (0.0989) | (0.0002) | 0.0113 | 0.2373 | (0.0004) | 0.249 | 0.05 | (0.34) | 0.06483 | 2.56 | 2.90 | |
| 2004 | 0.734127 | 0.013 | 0.074002 | 0.009 | 0.269 | (0.17) | (0.0082) | 0.6762 | 0.0010 | 0.0113 | 0.2373 | 0.0019 | 0.247 | 2.10 | 2.49 | 0.027306 | (0.01) | (2.50) | |
| 2005 | −0.05141 | 0.033 | 0.088201 | 0.023 | 0.001 | (0.17) | 0.0118 | (0.1093) | 0.0002 | 0.0113 | 0.2373 | 0.0004 | 0.248 | (0.08) | (0.52) | 0.015636 | (0.81) | (0.29) | |
| 2006 | −0.07181 | 0.049 | 0.06037 | (0.005) | 0.003 | (0.17) | 0.0278 | (0.1297) | 0.0006 | 0.0113 | 0.2373 | 0.0013 | 0.247 | (0.23) | (0.73) | 0.024639 | (0.20) | 0.54 | |
| 2007 | 0.034653 | 0.037 | 0.044478 | (0.021) | 0.001 | (0.17) | 0.0158 | (0.0233) | 0.0001 | 0.0113 | 0.2373 | 0.0001 | 0.248 | 0.25 | (0.07) | 0.030955 | 0.24 | 0.30 | |
| 2008 | −0.02344 | 0.0295 | 0.036688 | (0.029) | 0.000 | (0.17) | 0.0083 | (0.0814) | 0.0001 | 0.0113 | 0.2373 | 0.0002 | 0.248 | 0.05 | (0.34) | 0.022845 | (0.32) | 0.03 | |
| 2009 | 0.017498 | 0.0159 | 0.028306 | (0.037) | 0.000 | (0.17) | (0.0053) | (0.0404) | (0.0000) | 0.0113 | 0.2373 | (0.0001) | 0.249 | 0.27 | (0.04) | 0.024198 | (0.23) | (0.18) | |
| 2010 | −0.14862 | 0.0133 | 0.02959 | (0.036) | 0.011 | (0.17) | (0.0079) | (0.2066) | (0.0003) | 0.0113 | 0.2373 | (0.0006) | 0.249 | (0.43) | (1.01) | 0.014284 | (0.91) | 0.11 | |
| 2011 | −0.14298 | 0.0225 | 0.019768 | (0.046) | 0.010 | (0.17) | 0.0013 | (0.2009) | 0.0000 | 0.0113 | 0.2373 | 0.0001 | 0.249 | (0.44) | (1.03) | 0.012775 | (1.01) | 0.02 | |
| 2012 | −0.02679 | 0.0159 | 0.026635 | (0.039) | 0.000 | (0.17) | (0.0053) | (0.0847) | (0.0001) | 0.0113 | 0.2373 | (0.0002) | 0.249 | 0.09 | (0.29) | 0.012212 | (1.05) | (0.76) | |
| 2013 | 0.07398 | 0.0082 | 0.059911 | (0.006) | 0.003 | (0.17) | (0.0130) | 0.0160 | 0.0000 | 0.0113 | 0.2373 | 0.0001 | 0.249 | 0.52 | 0.30 | 0.012956 | (1.00) | (1.30) | |
| 2014 | −0.07674 | 0.007 | 0.055254 | (0.010) | 0.003 | (0.17) | (0.0142) | (0.1347) | (0.0003) | 0.0113 | 0.2373 | (0.0007) | 0.249 | (0.09) | (0.53) | 0.017548 | (0.68) | (0.15) | |
| 2015 | −0.09038 | 0.012 | 0.174843 | 0.109 | 0.004 | (0.17) | (0.0092) | (0.1483) | (0.0002) | 0.0113 | 0.2373 | (0.0005) | 0.249 | (0.17) | (0.64) | 0.033052 | 0.38 | 1.02 | |
| 2016 | −0.09064 | 0.0275 | 0.170726 | 0.105 | 0.004 | (0.17) | 0.0063 | (0.1486) | 0.0002 | 0.0113 | 0.2373 | 0.0003 | 0.248 | (0.23) | (0.73) | 0.022339 | (0.35) | 0.37 |
| Bank | Year | Capital Gains/ (Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gulf Bank | 2000 | 0.742701 | 0.0209 | 0.057909 | (0.009) | 0.276 | (0.33) | (0.0003) | 0.5654 | 0.0001 | 0.0113 | 0.7205 | 0.0001 | 0.732 | 0.70 | 1.09 | 0.19577 | (0.33) | (1.42) |
| 2001 | 0.079908 | 0.0267 | 0.062263 | (0.004) | 0.003 | (0.33) | 0.0055 | (0.0974) | 0.0002 | 0.0113 | 0.7205 | 0.0004 | 0.731 | 0.16 | 0.31 | 0.190128 | (0.47) | (0.78) | |
| 2002 | 0.012333 | 0.018 | 0.077753 | 0.011 | 0.000 | (0.33) | (0.0032) | (0.1650) | (0.0002) | 0.0113 | 0.7205 | (0.0003) | 0.732 | 0.08 | 0.20 | 0.077616 | (3.33) | (3.53) | |
| 2003 | 2.537753 | 0.011 | 0.057003 | (0.010) | 3.220 | (0.33) | (0.0102) | 2.3604 | 0.0079 | 0.0113 | 0.7205 | 0.0158 | 0.716 | (0.86) | (1.17) | 0.172091 | (0.93) | 0.24 | |
| 2004 | 0.217287 | 0.013 | 0.0814 | 0.015 | 0.024 | (0.33) | (0.0082) | 0.0400 | 0.0001 | 0.0113 | 0.7205 | 0.0002 | 0.732 | 0.34 | 0.57 | 0.228009 | 0.49 | (0.07) | |
| 2005 | 0.240453 | 0.033 | 0.089881 | 0.023 | 0.029 | (0.33) | 0.0118 | 0.0631 | (0.0002) | 0.0113 | 0.7205 | (0.0005) | 0.732 | 0.33 | 0.56 | 0.249555 | 1.04 | 0.48 | |
| 2006 | 0.191106 | 0.049 | 0.069159 | 0.003 | 0.018 | (0.33) | 0.0278 | 0.0138 | (0.0001) | 0.0113 | 0.7205 | (0.0003) | 0.732 | 0.26 | 0.45 | 0.245373 | 0.93 | 0.48 | |
| 2007 | −0.95466 | 0.037 | 0.071458 | 0.005 | 0.456 | (0.33) | 0.0158 | (1.1320) | 0.0059 | 0.0113 | 0.7205 | 0.0118 | 0.720 | (1.91) | (2.68) | 0.215211 | 0.17 | 2.85 | |
| 2008 | −0.78633 | 0.0295 | 0.066017 | (0.001) | 0.309 | (0.33) | 0.0083 | (0.9636) | 0.0026 | 0.0113 | 0.7205 | 0.0053 | 0.727 | (1.45) | (2.02) | 0.248714 | 1.02 | 3.04 | |
| 2009 | −0.00223 | 0.0159 | 0.050728 | (0.016) | 0.000 | (0.33) | (0.0053) | (0.1795) | (0.0003) | 0.0113 | 0.7205 | (0.0006) | 0.732 | 0.07 | 0.17 | 0.217305 | 0.22 | 0.05 | |
| 2010 | 0.023587 | 0.0133 | 0.09094 | 0.024 | 0.000 | (0.33) | (0.0079) | (0.1537) | (0.0004) | 0.0113 | 0.7205 | (0.0008) | 0.733 | 0.10 | 0.23 | 0.21859 | 0.25 | 0.02 | |
| 2011 | 0.008343 | 0.0225 | 0.06105 | (0.006) | 0.000 | (0.33) | 0.0013 | (0.1690) | 0.0001 | 0.0113 | 0.7205 | 0.0001 | 0.732 | 0.07 | 0.18 | 0.226227 | 0.45 | 0.27 | |
| 2012 | 0.023444 | 0.0159 | 0.067841 | 0.001 | 0.000 | (0.33) | (0.0053) | (0.1539) | (0.0003) | 0.0113 | 0.7205 | (0.0005) | 0.732 | 0.10 | 0.22 | 0.21843 | 0.25 | 0.03 | |
| 2013 | 0.06693 | 0.0082 | 0.060188 | (0.006) | 0.002 | (0.33) | (0.0130) | (0.1104) | (0.0005) | 0.0113 | 0.7205 | (0.0009) | 0.733 | 0.17 | 0.32 | 0.21373 | 0.13 | (0.19) | |
| 2014 | 0.052106 | 0.007 | 0.055726 | (0.011) | 0.001 | (0.33) | (0.0142) | (0.1252) | (0.0006) | 0.0113 | 0.7205 | (0.0012) | 0.733 | 0.15 | 0.29 | 0.214306 | 0.14 | (0.15) | |
| 2015 | 0.235851 | 0.012 | 0.056378 | (0.010) | 0.028 | (0.33) | (0.0092) | 0.0585 | 0.0002 | 0.0113 | 0.7205 | 0.0004 | 0.731 | 0.36 | 0.60 | 0.211711 | 0.08 | (0.52) | |
| 2016 | 0.325687 | 0.0275 | 0.055836 | (0.011) | 0.053 | (0.33) | 0.0063 | 0.1484 | (0.0003) | 0.0113 | 0.7205 | (0.0006) | 0.732 | 0.43 | 0.69 | 0.204606 | (0.10) | (0.79) |
| Bank | Year | Capital Gains/ (Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bounyan | 2004 | 0.054486 | 0.0330 | 0.136908 | 0.069 | 0.001 | (0.02) | 0.0096 | (0.2134) | 0.0000 | 0.0127 | 0.6086 | 0.0001 | 0.621 | 0.14 | (0.07) | 0.67 | (2.18) | (2.11) |
| 2005 | 0.383606 | 0.033 | 0.106337 | 0.039 | 0.074 | (0.02) | 0.0096 | 0.1158 | (0.0000) | 0.0127 | 0.6086 | (0.0000) | 0.621 | 0.55 | 0.93 | 0.083325 | 4.96 | 4.02 | |
| 2006 | 0.029426 | 0.049 | 0.122643 | 0.055 | 0.000 | (0.02) | 0.0256 | (0.2384) | 0.0001 | 0.0127 | 0.6086 | 0.0002 | 0.621 | 0.08 | (0.22) | 0.157232 | (3.28) | (3.06) | |
| 2007 | −0.41181 | 0.037 | 0.033597 | (0.034) | 0.085 | (0.02) | 0.0136 | (0.6797) | 0.0002 | 0.0127 | 0.6086 | 0.0003 | 0.621 | (0.75) | (2.23) | 0.123655 | (17.54) | (15.31) | |
| 2008 | 2.107361 | 0.0295 | 0.055545 | (0.012) | 2.220 | (0.02) | 0.0061 | 1.8395 | (0.0002) | 0.0127 | 0.6086 | (0.0004) | 0.622 | (0.12) | (0.70) | 0.20333 | (6.69) | (5.99) | |
| 2009 | −0.11167 | 0.0159 | 0.064079 | (0.004) | 0.006 | (0.02) | (0.0075) | (0.3795) | (0.0001) | 0.0127 | 0.6086 | (0.0001) | 0.621 | (0.11) | (0.67) | 0.220452 | (6.45) | (5.78) | |
| 2010 | 0.125712 | 0.0133 | 0.081265 | 0.014 | 0.008 | (0.02) | (0.0101) | (0.1421) | (0.0000) | 0.0127 | 0.6086 | (0.0001) | 0.621 | 0.28 | 0.26 | 0.214478 | 0.17 | (0.09) | |
| 2011 | −0.23026 | 0.0225 | 0.011053 | (0.057) | 0.027 | (0.02) | (0.0009) | (0.4981) | (0.0000) | 0.0127 | 0.6086 | (0.0000) | 0.621 | (0.34) | (1.24) | 0.233164 | (10.48) | (9.25) | |
| 2012 | 0.223031 | 0.0159 | 0.053347 | (0.014) | 0.025 | (0.02) | (0.0075) | (0.0448) | (0.0000) | 0.0127 | 0.6086 | (0.0000) | 0.621 | 0.40 | 0.56 | 0.222369 | 2.33 | 1.76 | |
| 2013 | 0.134721 | 0.0082 | 0.052563 | (0.015) | 0.009 | (0.02) | (0.0152) | (0.1331) | (0.0000) | 0.0127 | 0.6086 | (0.0001) | 0.621 | 0.30 | 0.31 | 0.226835 | 0.53 | 0.22 | |
| 2014 | 0.441024 | 0.007 | 0.052981 | (0.015) | 0.097 | (0.02) | (0.0164) | 0.1732 | 0.0001 | 0.0127 | 0.6086 | 0.0001 | 0.621 | 0.65 | 1.17 | 0.235979 | 6.62 | 5.45 | |
| 2015 | 0.38 | 0.012 | 0.055116 | (0.013) | 0.072 | (0.02) | (0.0114) | 0.1122 | 0.0000 | 0.0127 | 0.6086 | 0.0000 | 0.621 | 0.59 | 1.01 | 0.229718 | 5.48 | 4.47 | |
| 2016 | 0.356426 | 0.0275 | 0.055116 | (0.013) | 0.064 | (0.02) | 0.0041 | 0.0886 | (0.0000) | 0.0127 | 0.6086 | (0.0000) | 0.621 | 0.54 | 0.89 | 0.253754 | 4.63 | 3.75 |
| Bank | Year | Capital Gains/(Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kuwait Finance House | 2000 | 0.06000 | 0.0209 | 0.11050 | 0.008 | 0.002 | (0.03) | (0.0003) | (0.0208) | (0.0000) | 0.0113 | 0.1114 | (0.0000) | 0.123 | 1.14 | (0.14) | 0.112308 | 2.08 | 2.22 |
| 2001 | 0.05000 | 0.0267 | 0.10691 | 0.004 | 0.001 | (0.03) | 0.0055 | (0.0308) | 0.0000 | 0.0113 | 0.1114 | 0.0000 | 0.123 | 1.02 | (0.30) | 0.100397 | 1.73 | 2.03 | |
| 2002 | 0.05000 | 0.018 | 0.11158 | 0.009 | 0.001 | (0.03) | (0.0032) | (0.0308) | (0.0000) | 0.0113 | 0.1114 | (0.0000) | 0.123 | 1.09 | (0.21) | 0.085928 | 1.30 | 1.51 | |
| 2003 | 0.09000 | 0.011 | 0.10418 | 0.002 | 0.004 | (0.03) | (0.0102) | 0.0092 | 0.0000 | 0.0113 | 0.1114 | 0.0000 | 0.123 | 1.45 | 0.26 | 0.070202 | 0.84 | 0.58 | |
| 2004 | 0.40000 | 0.013 | 0.10600 | 0.004 | 0.080 | (0.03) | (0.0082) | 0.3192 | 0.0001 | 0.0113 | 0.1114 | 0.0001 | 0.123 | 3.34 | 2.73 | 0.065811 | 0.71 | (2.02) | |
| 2005 | 0.12000 | 0.033 | 0.06114 | (0.041) | 0.007 | (0.03) | 0.0118 | 0.0392 | (0.0000) | 0.0113 | 0.1114 | (0.0000) | 0.123 | 1.49 | 0.31 | 0.062056 | 0.60 | 0.29 | |
| 2006 | 0.07721 | 0.049 | 0.05775 | (0.045) | 0.003 | (0.03) | 0.0278 | (0.0036) | 0.0000 | 0.0113 | 0.1114 | 0.0000 | 0.123 | 1.04 | (0.27) | 0.043158 | 0.04 | 0.31 | |
| 2007 | 0.14686 | 0.037 | 0.16676 | 0.064 | 0.011 | (0.03) | 0.0158 | 0.0660 | (0.0000) | 0.0113 | 0.1114 | (0.0001) | 0.123 | 1.64 | 0.51 | 0.025858 | (0.47) | (0.99) | |
| 2008 | −0.08542 | 0.0295 | 0.14760 | 0.045 | 0.004 | (0.03) | 0.0083 | (0.1662) | 0.0000 | 0.0113 | 0.1114 | 0.0001 | 0.123 | (0.13) | (1.79) | 0.018906 | (0.68) | 1.11 | |
| 2009 | 0.02752 | 0.0159 | 0.12135 | 0.019 | 0.000 | (0.03) | (0.0053) | (0.0533) | (0.0000) | 0.0113 | 0.1114 | (0.0000) | 0.123 | 0.93 | (0.42) | 0.019352 | (0.67) | (0.25) | |
| 2010 | 0.00368 | 0.0133 | 0.10600 | 0.004 | 0.000 | (0.03) | (0.0079) | (0.0771) | (0.0000) | 0.0113 | 0.1114 | (0.0000) | 0.123 | 0.76 | (0.64) | 0.017893 | (0.71) | (0.07) | |
| 2011 | 0.08195 | 0.0225 | 0.11836 | 0.016 | 0.003 | (0.03) | 0.0013 | 0.0011 | (0.0000) | 0.0113 | 0.1114 | (0.0000) | 0.123 | 1.29 | 0.06 | 0.017788 | (0.71) | (0.77) | |
| 2012 | 0.26946 | 0.0159 | 0.11747 | 0.015 | 0.036 | (0.03) | (0.0053) | 0.1886 | 0.0000 | 0.0113 | 0.1114 | 0.0001 | 0.123 | 2.61 | 1.77 | 0.014952 | (0.80) | (2.57) | |
| 2013 | 0.00037 | 0.0082 | 0.09071 | (0.012) | 0.000 | (0.03) | (0.0130) | (0.0805) | (0.0000) | 0.0113 | 0.1114 | (0.0001) | 0.123 | 0.77 | (0.62) | 0.016026 | (0.76) | (0.14) | |
| 2014 | −0.00036 | 0.007 | 0.07709 | (0.025) | 0.000 | (0.03) | (0.0142) | (0.0812) | (0.0000) | 0.0113 | 0.1114 | (0.0001) | 0.123 | 0.77 | (0.62) | 0.013876 | (0.83) | (0.21) | |
| 2015 | 0.04049 | 0.012 | 0.07487 | (0.028) | 0.001 | (0.03) | (0.0092) | (0.0403) | (0.0000) | 0.0113 | 0.1114 | (0.0000) | 0.123 | 1.06 | (0.24) | 0.013793 | (0.83) | (0.59) | |
| 2016 | 0.04216 | 0.0275 | 0.06403 | (0.038) | 0.001 | (0.03) | 0.0063 | (0.0387) | 0.0000 | 0.0113 | 0.1114 | 0.0000 | 0.123 | 0.95 | (0.39) | 0.013909 | (0.83) | (0.44) |
| Bank | Year | Capital Gains/(Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| United Overseas | 2000 | −0.19685 | 0.0391 | 0.039856 | (0.006) | 0.019 | 0.06 | (0.0004) | (0.2501) | 0.0000 | 0.0035 | 0.1097 | 0.0000 | 0.113 | (1.85) | (2.34) | 0.039746 | (1.09) | 1.26 |
| 2001 | −0.20171 | 0.0416 | 0.035023 | (0.011) | 0.020 | 0.06 | 0.0021 | (0.2550) | (0.0000) | 0.0035 | 0.1097 | (0.0001) | 0.113 | (1.92) | (2.42) | 0.037871 | (1.16) | 1.26 | |
| 2002 | 0.009804 | 0.03208 | 0.051201 | 0.005 | 0.000 | 0.06 | (0.0074) | (0.0434) | 0.0000 | 0.0035 | 0.1097 | 0.0000 | 0.113 | 0.21 | (0.26) | 0.021904 | (1.76) | (1.50) | |
| 2003 | 0.186584 | 0.0429 | 0.049871 | 0.004 | 0.017 | 0.06 | 0.0034 | 0.1333 | 0.0000 | 0.0035 | 0.1097 | 0.0001 | 0.113 | 1.53 | 1.07 | 0.029477 | (1.47) | (2.54) | |
| 2004 | 0.139542 | 0.04045 | 0.043946 | (0.002) | 0.010 | 0.06 | 0.0010 | 0.0863 | 0.0000 | 0.0035 | 0.1097 | 0.0000 | 0.113 | 1.20 | 0.74 | 0.0457 | (0.86) | (1.60) | |
| 2005 | 0.151762 | 0.04045 | 0.046927 | 0.001 | 0.012 | 0.06 | 0.0010 | 0.0985 | 0.0000 | 0.0035 | 0.1097 | 0.0000 | 0.113 | 1.29 | 0.83 | 0.079222 | 0.41 | (0.42) | |
| 2006 | 0.024766 | 0.0377 | 0.047331 | 0.001 | 0.000 | 0.06 | (0.0018) | (0.0285) | 0.0000 | 0.0035 | 0.1097 | 0.0000 | 0.113 | 0.29 | (0.18) | 0.070013 | 0.06 | 0.24 | |
| 2007 | −0.02798 | 0.0416 | 0.050572 | 0.004 | 0.000 | 0.06 | 0.0021 | (0.0812) | (0.0000) | 0.0035 | 0.1097 | (0.0000) | 0.113 | (0.21) | (0.69) | 0.071952 | 0.13 | 0.82 | |
| 2008 | 0.091431 | 0.03208 | 0.052854 | 0.007 | 0.004 | 0.06 | (0.0074) | 0.0382 | (0.0000) | 0.0035 | 0.1097 | (0.0000) | 0.113 | 0.90 | 0.43 | 0.084251 | 0.60 | 0.17 | |
| 2009 | 0.105458 | 0.0429 | 0.0528 | 0.006 | 0.006 | 0.06 | 0.0034 | 0.0522 | 0.0000 | 0.0035 | 0.1097 | 0.0000 | 0.113 | 0.91 | 0.45 | 0.066177 | (0.09) | (0.54) | |
| 2010 | 0.053334 | 0.04045 | 0.049271 | 0.003 | 0.001 | 0.06 | 0.0010 | 0.0001 | 0.0000 | 0.0035 | 0.1097 | 0.0000 | 0.113 | 0.51 | 0.04 | 0.059585 | (0.34) | (0.38) | |
| 2011 | 0.139186 | 0.03696 | 0.043851 | (0.002) | 0.010 | 0.06 | (0.0025) | 0.0859 | (0.0000) | 0.0035 | 0.1097 | (0.0000) | 0.113 | 1.23 | 0.77 | 0.082314 | 0.52 | (0.24) | |
| 2012 | 0.073253 | 0.035 | 0.04673 | 0.000 | 0.003 | 0.06 | (0.0045) | 0.0200 | (0.0000) | 0.0035 | 0.1097 | (0.0000) | 0.113 | 0.72 | 0.26 | 0.074773 | 0.24 | (0.02) | |
| 2013 | 0.106115 | 0.04149 | 0.043242 | (0.003) | 0.006 | 0.06 | 0.0020 | 0.0529 | 0.0000 | 0.0035 | 0.1097 | 0.0000 | 0.113 | 0.93 | 0.47 | 0.089484 | 0.80 | 0.33 | |
| 2014 | 0.037805 | 0.0413 | 0.04432 | (0.002) | 0.001 | 0.06 | 0.0018 | (0.0154) | (0.0000) | 0.0035 | 0.1097 | (0.0000) | 0.113 | 0.37 | (0.10) | 0.090892 | 0.85 | 0.95 | |
| 2015 | 0.114067 | 0.04224 | 0.046395 | 0.000 | 0.007 | 0.06 | 0.0028 | 0.0608 | 0.0000 | 0.0035 | 0.1097 | 0.0000 | 0.113 | 0.99 | 0.52 | 0.103088 | 1.31 | 0.79 | |
| 2016 | 0.098654 | 0.04238 | 0.043214 | (0.003) | 0.005 | 0.06 | 0.0029 | 0.0454 | 0.0000 | 0.0035 | 0.1097 | 0.0000 | 0.113 | 0.86 | 0.40 | 0.117099 | 1.84 | 1.44 |
| Bank | Year | Capital Gains/ (Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Maybank | 2000 | −0.27543 | 0.0377 | 0.130869 | 0.027 | 0.038 | (0.06) | (0.0017) | (0.3400) | (0.0000) | 0.0035 | 0.1600 | (0.0001) | 0.164 | (1.51) | 2.25 | 0.083725 | 0.31 | (1.94) |
| 2001 | 0.197485 | 0.0416 | 0.128838 | 0.025 | 0.020 | (0.06) | 0.0022 | 0.1329 | (0.0000) | 0.0035 | 0.1600 | (0.0000) | 0.164 | 1.47 | (0.78) | 0.073852 | (0.13) | 0.65 | |
| 2002 | −0.012 | 0.03208 | 0.117896 | 0.014 | 0.000 | (0.06) | (0.0073) | (0.0766) | (0.0000) | 0.0035 | 0.1600 | (0.0001) | 0.164 | 0.36 | 0.34 | 0.071222 | (0.24) | (0.59) | |
| 2003 | 0.178033 | 0.0429 | 0.115088 | 0.012 | 0.016 | (0.06) | 0.0035 | 0.1135 | (0.0000) | 0.0035 | 0.1600 | (0.0000) | 0.164 | 1.36 | (0.67) | 0.075972 | (0.03) | 0.64 | |
| 2004 | 0.115484 | 0.04045 | 0.108391 | 0.005 | 0.007 | (0.06) | 0.0011 | 0.0509 | (0.0000) | 0.0035 | 0.1600 | (0.0000) | 0.164 | 1.05 | (0.36) | 0.072978 | (0.17) | 0.19 | |
| 2005 | 0.001701 | 0.04045 | 0.107693 | 0.004 | 0.000 | (0.06) | 0.0011 | (0.0629) | 0.0000 | 0.0035 | 0.1600 | 0.0000 | 0.164 | 0.40 | 0.31 | 0.065124 | (0.51) | (0.82) | |
| 2006 | 0.148666 | 0.0377 | 0.105344 | 0.002 | 0.011 | (0.06) | (0.0017) | 0.0841 | 0.0000 | 0.0035 | 0.1600 | 0.0000 | 0.164 | 1.24 | (0.55) | 0.092949 | 0.71 | 1.27 | |
| 2007 | −0.26264 | 0.0416 | 0.110047 | 0.007 | 0.034 | (0.06) | 0.0022 | (0.3272) | 0.0000 | 0.0035 | 0.1600 | 0.0001 | 0.163 | (1.44) | 2.17 | 0.099787 | 1.01 | (1.16) | |
| 2008 | 0.213565 | 0.03208 | 0.112024 | 0.009 | 0.023 | (0.06) | (0.0073) | 0.1490 | 0.0001 | 0.0035 | 0.1600 | 0.0001 | 0.163 | 1.60 | (0.92) | 0.10026 | 1.04 | 1.95 | |
| 2009 | 0.28137 | 0.0429 | 0.099333 | (0.004) | 0.040 | (0.06) | 0.0035 | 0.2168 | (0.0000) | 0.0035 | 0.1600 | (0.0001) | 0.164 | 1.85 | (1.17) | 0.116252 | 1.74 | 2.91 | |
| 2010 | 0.22493 | 0.04045 | 0.108948 | 0.005 | 0.025 | (0.06) | 0.0011 | 0.1604 | (0.0000) | 0.0035 | 0.1600 | (0.0000) | 0.164 | 1.61 | (0.92) | 0.111218 | 1.52 | 2.44 | |
| 2011 | 0.167897 | 0.03696 | 0.04516 | (0.058) | 0.014 | (0.06) | (0.0024) | 0.1033 | 0.0000 | 0.0035 | 0.1600 | 0.0000 | 0.164 | 1.35 | (0.66) | 0.087565 | 0.48 | 1.13 | |
| 2012 | 0.15071 | 0.035 | 0.076368 | (0.027) | 0.011 | (0.06) | (0.0044) | 0.0861 | 0.0000 | 0.0035 | 0.1600 | 0.0000 | 0.164 | 1.27 | (0.58) | 0.068514 | (0.36) | 0.22 | |
| 2013 | −0.02989 | 0.04149 | 0.092691 | (0.011) | 0.000 | (0.06) | 0.0021 | (0.0945) | 0.0000 | 0.0035 | 0.1600 | 0.0000 | 0.164 | 0.19 | 0.52 | 0.044073 | (1.44) | (1.96) | |
| 2014 | −0.04044 | 0.0413 | 0.094364 | (0.009) | 0.001 | (0.06) | 0.0019 | (0.1050) | 0.0000 | 0.0035 | 0.1600 | 0.0000 | 0.164 | 0.13 | 0.58 | 0.045215 | (1.39) | (1.97) | |
| 2015 | 0.01933 | 0.04224 | 0.102306 | (0.001) | 0.000 | (0.06) | 0.0029 | (0.0452) | 0.0000 | 0.0035 | 0.1600 | 0.0000 | 0.164 | 0.49 | 0.21 | 0.051097 | (1.13) | (1.34) | |
| 2016 | 0.018962 | 0.04238 | 0.104143 | 0.001 | 0.000 | (0.06) | 0.0030 | (0.0456) | 0.0010 | 0.0035 | 0.1600 | 0.0020 | 0.162 | 0.50 | 0.20 | 0.044977 | (1.40) | (1.60) |
| Bank | Year | Capital Gains/ (Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation And Variances Of Interest And Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Islam-Malaysia | 2000 | 0.090845 | 0.0377 | 0.041633 | (0.047) | 0.004 | 0.12 | (0.0017) | 0.3758 | (0.0001) | 0.0035 | 1.3605 | (0.0001) | 1.364 | 0.10 | 0.27 | 0.006709 | (0.72) | (0.98) |
| 2001 | 0.068085 | 0.0416 | 0.076135 | (0.013) | 0.002 | 0.12 | 0.0022 | 0.3530 | 0.0001 | 0.0035 | 1.3605 | 0.0002 | 1.364 | 0.08 | 0.26 | 0.037485 | 2.46 | 2.20 | |
| 2002 | 0.061241 | 0.03208 | 0.072885 | (0.016) | 0.002 | 0.12 | (0.0073) | 0.3462 | (0.0003) | 0.0035 | 1.3605 | (0.0006) | 1.365 | 0.08 | 0.26 | 0.036902 | 2.40 | 2.13 | |
| 2003 | 0.005881 | 0.0429 | 0.04455 | (0.044) | 0.000 | 0.12 | 0.0035 | 0.2908 | 0.0001 | 0.0035 | 1.3605 | 0.0002 | 1.364 | 0.04 | 0.25 | 0.009001 | (0.48) | (0.73) | |
| 2004 | −0.22877 | 0.04045 | 0.045453 | (0.043) | 0.026 | 0.12 | 0.0011 | 0.0562 | 0.0000 | 0.0035 | 1.3605 | 0.0000 | 1.364 | (0.15) | 0.20 | 0.007486 | (0.64) | (0.83) | |
| 2005 | −1.27373 | 0.04045 | 0.106761 | 0.018 | 0.811 | 0.12 | 0.0011 | (0.9888) | (0.0001) | 0.0035 | 1.3605 | (0.0003) | 1.364 | (1.49) | (0.18) | 0.012166 | (0.16) | 0.03 | |
| 2006 | −5.36689 | 0.0377 | 0.132537 | 0.044 | 14.402 | 0.12 | (0.0017) | (5.0820) | 0.0010 | 0.0035 | 1.3605 | 0.0020 | 1.362 | (14.48) | (3.86) | 0.013757 | 0.01 | 3.86 | |
| 2007 | 0.238326 | 0.0416 | 0.10066 | 0.012 | 0.028 | 0.12 | 0.0022 | 0.5233 | 0.0001 | 0.0035 | 1.3605 | 0.0003 | 1.364 | 0.19 | 0.29 | 0.012912 | (0.08) | (0.37) | |
| 2008 | 0.114532 | 0.03208 | 0.096257 | 0.007 | 0.007 | 0.12 | (0.0073) | 0.3995 | (0.0003) | 0.0035 | 1.3605 | (0.0007) | 1.365 | 0.12 | 0.27 | 0.009166 | (0.46) | (0.74) | |
| 2009 | 0.537893 | 0.0429 | 0.077692 | (0.011) | 0.145 | 0.12 | 0.0035 | 0.8228 | 0.0003 | 0.0035 | 1.3605 | 0.0007 | 1.363 | 0.32 | 0.33 | 0.014325 | 0.07 | (0.26) | |
| 2010 | 0.15185 | 0.04045 | 0.132735 | 0.044 | 0.012 | 0.12 | 0.0011 | 0.4368 | 0.0001 | 0.0035 | 1.3605 | 0.0001 | 1.364 | 0.14 | 0.28 | 0.006768 | (0.71) | (0.99) | |
| 2011 | 0.112064 | 0.03696 | 0.095143 | 0.006 | 0.006 | 0.12 | (0.0024) | 0.3970 | (0.0001) | 0.0035 | 1.3605 | (0.0002) | 1.364 | 0.12 | 0.27 | 0.009465 | (0.43) | (0.70) | |
| 2012 | 0.111997 | 0.035 | 0.098173 | 0.009 | 0.006 | 0.12 | (0.0044) | 0.3969 | (0.0002) | 0.0035 | 1.3605 | (0.0004) | 1.364 | 0.12 | 0.27 | 0.010971 | (0.28) | (0.55) | |
| 2013 | 0.127038 | 0.04149 | 0.097262 | 0.008 | 0.008 | 0.12 | 0.0021 | 0.4120 | 0.0001 | 0.0035 | 1.3605 | 0.0002 | 1.364 | 0.12 | 0.27 | 0.005326 | (0.86) | (1.13) | |
| 2014 | 0.255644 | 0.0413 | 0.098339 | 0.010 | 0.033 | 0.12 | 0.0019 | 0.5406 | 0.0001 | 0.0035 | 1.3605 | 0.0002 | 1.364 | 0.20 | 0.29 | 0.004463 | (0.95) | (1.24) | |
| 2015 | 0.071459 | 0.04224 | 0.098497 | 0.010 | 0.003 | 0.12 | 0.0029 | 0.3564 | 0.0001 | 0.0035 | 1.3605 | 0.0002 | 1.364 | 0.08 | 0.26 | 0.01918 | 0.57 | 0.31 | |
| 2016 | 0.078562 | 0.04238 | 0.095527 | 0.007 | 0.003 | 0.12 | 0.0030 | 0.3635 | 0.0001 | 0.0035 | 1.3605 | 0.0003 | 1.364 | 0.09 | 0.26 | 0.016287 | 0.27 | 0.01 |
| Bank | Year | Capital Gains/(Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Muamalat | 2000 | 0.063992 | 0.0377 | 0.128634 | 0.035 | 0.002 | (1.00) | (0.0017) | (0.0697) | (0.0001) | 0.0035 | 0.2240 | (0.0002) | 0.228 | 0.52 | (0.25) | 0.010201 | (0.85) | (0.60) |
| 2001 | 0.052955 | 0.0416 | 0.089128 | (0.005) | 0.001 | (1.00) | 0.0022 | (0.0807) | 0.0002 | 0.0035 | 0.2240 | 0.0004 | 0.227 | 0.46 | (0.34) | 0.011149 | (0.79) | (0.45) | |
| 2002 | −0.00807 | 0.03208 | 0.085301 | (0.009) | 0.000 | (1.00) | (0.0073) | (0.1418) | (0.0010) | 0.0035 | 0.2240 | (0.0021) | 0.230 | 0.23 | (0.68) | 0.006934 | (1.07) | (0.39) | |
| 2003 | 0.408393 | 0.0429 | 0.085591 | (0.008) | 0.083 | (1.00) | 0.0035 | 0.2747 | (0.0010) | 0.0035 | 0.2240 | (0.0019) | 0.229 | 1.63 | 1.41 | 0.008151 | (0.99) | (2.40) | |
| 2004 | 0.10417 | 0.04045 | 0.08294 | (0.011) | 0.005 | (1.00) | 0.0011 | (0.0295) | 0.0000 | 0.0035 | 0.2240 | 0.0001 | 0.227 | 0.67 | (0.03) | 0.005021 | (1.20) | (1.17) | |
| 2005 | 0.752409 | 0.04045 | 0.087489 | (0.006) | 0.283 | (1.00) | 0.0011 | 0.6187 | (0.0007) | 0.0035 | 0.2240 | (0.0013) | 0.229 | 2.28 | 2.37 | 0.006899 | (1.07) | (3.45) | |
| 2006 | 0.035759 | 0.0377 | 0.08857 | (0.005) | 0.001 | (1.00) | (0.0017) | (0.0979) | (0.0002) | 0.0035 | 0.2240 | (0.0003) | 0.228 | 0.40 | (0.43) | 0.027526 | 0.29 | 0.72 | |
| 2007 | 0.025604 | 0.0416 | 0.104129 | 0.010 | 0.000 | (1.00) | 0.0022 | (0.1081) | 0.0002 | 0.0035 | 0.2240 | 0.0005 | 0.227 | 0.34 | (0.51) | 0.043045 | 1.32 | 1.84 | |
| 2008 | 0.5673 | 0.03208 | 0.104992 | 0.011 | 0.161 | (1.00) | (0.0073) | 0.4336 | 0.0032 | 0.0035 | 0.2240 | 0.0063 | 0.221 | 2.13 | 2.15 | 0.062654 | 2.62 | 0.47 | |
| 2009 | 0.014106 | 0.0429 | 0.104028 | 0.010 | 0.000 | (1.00) | 0.0035 | (0.1196) | 0.0004 | 0.0035 | 0.2240 | 0.0008 | 0.227 | 0.29 | (0.59) | 0.021625 | (0.10) | 0.50 | |
| 2010 | 0.0154 | 0.04045 | 0.104028 | 0.010 | 0.000 | (1.00) | 0.0011 | (0.1183) | 0.0001 | 0.0035 | 0.2240 | 0.0003 | 0.227 | 0.30 | (0.57) | 0.021625 | (0.10) | 0.47 | |
| 2011 | 0.139182 | 0.03696 | 0.082125 | (0.012) | 0.010 | (1.00) | (0.0024) | 0.0055 | 0.0000 | 0.0035 | 0.2240 | 0.0000 | 0.228 | 0.82 | 0.20 | 0.029567 | 0.43 | 0.23 | |
| 2012 | 0.050793 | 0.035 | 0.081588 | (0.012) | 0.001 | (1.00) | (0.0044) | (0.0829) | (0.0004) | 0.0035 | 0.2240 | (0.0007) | 0.228 | 0.47 | (0.32) | 0.036215 | 0.87 | 1.19 | |
| 2013 | 0.038553 | 0.04149 | 0.088164 | (0.006) | 0.001 | (1.00) | 0.0021 | (0.0951) | 0.0002 | 0.0035 | 0.2240 | 0.0004 | 0.227 | 0.40 | (0.43) | 0.029608 | 0.43 | 0.86 | |
| 2014 | 0.078632 | 0.0413 | 0.092115 | (0.002) | 0.003 | (1.00) | 0.0019 | (0.0551) | 0.0001 | 0.0035 | 0.2240 | 0.0002 | 0.227 | 0.56 | (0.18) | 0.026321 | 0.21 | 0.40 | |
| 2015 | −0.03193 | 0.04224 | 0.088276 | (0.006) | 0.001 | (1.00) | 0.0029 | (0.1656) | 0.0005 | 0.0035 | 0.2240 | 0.0010 | 0.227 | 0.09 | (0.89) | 0.024219 | 0.08 | 0.97 | |
| 2016 | −0.03459 | 0.04238 | 0.098245 | 0.004 | 0.001 | (1.00) | 0.0030 | (0.1683) | 0.0005 | 0.0035 | 0.2240 | 0.0010 | 0.227 | 0.07 | (0.91) | 0.021659 | (0.09) | 0.82 |
| Bank | Year | Capital Gains/(Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BOA | 2000 | 0.572191 | 0.06 | 0.127479 | 0.055 | 0.164 | 0.07 | 0.0232 | 0.4429 | 0.0007 | 0.0124 | 0.4125 | 0.0014 | 0.423 | 1.00 | 1.17 | 0.680095 | 0.00 | (1.17) |
| 2001 | 0.443747 | 0.05 | 0.10036 | 0.028 | 0.098 | 0.07 | 0.0132 | 0.3144 | 0.0003 | 0.0124 | 0.4125 | 0.0006 | 0.424 | 0.87 | 0.99 | 0.710113 | 0.13 | (0.86) | |
| 2002 | −0.16062 | 0.05 | 0.083624 | 0.011 | 0.013 | 0.07 | 0.0132 | (0.2899) | (0.0003) | 0.0124 | 0.4125 | (0.0005) | 0.425 | (0.36) | (0.77) | 1.40984 | 3.01 | 3.78 | |
| 2003 | 0.587322 | 0.04 | 0.277929 | 0.205 | 0.172 | 0.07 | 0.0032 | 0.4580 | 0.0001 | 0.0124 | 0.4125 | 0.0002 | 0.425 | 1.05 | 1.25 | 0.066463 | (2.52) | (3.77) | |
| 2004 | −5.3E−05 | 0.04 | 0.072195 | (0.000) | 0.000 | 0.07 | 0.0032 | (0.1294) | (0.0000) | 0.0124 | 0.4125 | (0.0001) | 0.425 | 0.08 | (0.15) | 0.645631 | (0.14) | 0.01 | |
| 2005 | 0.265024 | 0.04 | 0.099294 | 0.027 | 0.035 | 0.07 | 0.0032 | 0.1357 | 0.0000 | 0.0124 | 0.4125 | 0.0001 | 0.425 | 0.62 | 0.63 | 0.569288 | (0.45) | (1.08) | |
| 2006 | −0.21368 | 0.05 | 0.121422 | 0.049 | 0.023 | 0.07 | 0.0132 | (0.3430) | (0.0003) | 0.0124 | 0.4125 | (0.0006) | 0.426 | (0.50) | (0.98) | 0.575 | (0.43) | 0.55 | |
| 2007 | −0.01956 | 0.05 | 0.099201 | 0.027 | 0.000 | 0.07 | 0.0132 | (0.1489) | (0.0001) | 0.0124 | 0.4125 | (0.0003) | 0.425 | 0.01 | (0.25) | 0.661609 | (0.07) | 0.18 | |
| 2008 | −0.27296 | 0.04 | 0.052829 | (0.020) | 0.037 | 0.07 | 0.0032 | (0.4023) | (0.0001) | 0.0124 | 0.4125 | (0.0002) | 0.425 | (0.65) | (1.20) | 0.650165 | (0.12) | 1.08 | |
| 2009 | −0.51764 | 0.03 | 0.034936 | (0.038) | 0.134 | 0.07 | (0.0068) | (0.6469) | 0.0003 | 0.0124 | 0.4125 | 0.0006 | 0.424 | (1.43) | (2.32) | 0.664126 | (0.06) | 2.26 | |
| 2010 | −0.13178 | 0.03 | 0.020823 | (0.052) | 0.009 | 0.07 | (0.0068) | (0.2611) | 0.0001 | 0.0124 | 0.4125 | 0.0002 | 0.425 | (0.23) | (0.59) | 0.73245 | 0.22 | 0.81 | |
| 2011 | 1.239467 | 0.03 | 0.018721 | (0.054) | 0.768 | 0.07 | (0.0068) | 1.1102 | (0.0005) | 0.0124 | 0.4125 | (0.0011) | 0.426 | 1.21 | 1.47 | 0.745874 | 0.28 | (1.20) | |
| 2012 | 0.049365 | 0.02 | 0.01743 | (0.055) | 0.001 | 0.07 | (0.0168) | (0.0799) | 0.0001 | 0.0124 | 0.4125 | 0.0002 | 0.425 | 0.24 | 0.08 | 0.712678 | 0.14 | 0.06 | |
| 2013 | 0.263485 | 0.0173 | 0.028183 | (0.044) | 0.035 | 0.07 | (0.0195) | 0.1342 | (0.0002) | 0.0124 | 0.4125 | (0.0004) | 0.425 | 0.67 | 0.70 | 0.668887 | (0.04) | (0.74) | |
| 2014 | 0.156146 | 0.032 | 0.018238 | (0.054) | 0.012 | 0.07 | (0.0048) | 0.0268 | (0.0000) | 0.0124 | 0.4125 | (0.0000) | 0.425 | 0.43 | 0.36 | 0.669359 | (0.04) | (0.40) | |
| 2015 | −0.05628 | 0.025 | 0.030221 | (0.042) | 0.002 | 0.07 | (0.0118) | (0.1856) | 0.0002 | 0.0124 | 0.4125 | 0.0003 | 0.425 | (0.02) | (0.29) | 0.686567 | 0.03 | 0.32 | |
| 2016 | −0.00599 | 0.0219 | 0.031617 | (0.041) | 0.000 | 0.07 | (0.0149) | (0.1353) | 0.0001 | 0.0124 | 0.4125 | 0.0003 | 0.425 | 0.11 | (0.11) | 0.693327 | 0.06 | 0.17 |
| Bank | Year | Capital Gains/(Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wellsfargo | 2000 | −0.22568 | 0.06 | 0.138929 | 0.025 | 0.025 | (0.35) | 0.0232 | (0.3039) | 0.0025 | 0.0124 | 0.1759 | 0.0050 | 0.183 | (1.06) | (2.03) | 0.117632 | (0.61) | 1.42 |
| 2001 | 0.072185 | 0.05 | 0.126259 | 0.012 | 0.003 | (0.35) | 0.0132 | (0.0060) | 0.0000 | 0.0124 | 0.1759 | 0.0001 | 0.188 | 0.71 | (0.03) | 0.117356 | (0.62) | (0.59) | |
| 2002 | 0.265502 | 0.05 | 0.134078 | 0.020 | 0.035 | (0.35) | 0.0132 | 0.1873 | (0.0009) | 0.0124 | 0.1759 | (0.0017) | 0.190 | 1.55 | 0.92 | 0.135511 | (0.09) | (1.01) | |
| 2003 | 0.0532 | 0.04 | 0.13446 | 0.020 | 0.001 | (0.35) | 0.0032 | (0.0250) | 0.0000 | 0.0124 | 0.1759 | 0.0001 | 0.188 | 0.67 | (0.07) | 0.164111 | 0.74 | 0.82 | |
| 2004 | −0.00237 | 0.04 | 0.129088 | 0.015 | 0.000 | (0.35) | 0.0032 | (0.0806) | 0.0001 | 0.0124 | 0.1759 | 0.0002 | 0.188 | 0.38 | (0.40) | 0.171977 | 0.97 | 1.37 | |
| 2005 | 0.142572 | 0.04 | 0.126144 | 0.012 | 0.010 | (0.35) | 0.0032 | 0.0644 | (0.0001) | 0.0124 | 0.1759 | (0.0001) | 0.188 | 1.10 | 0.41 | 0.165375 | 0.78 | 0.37 | |
| 2006 | −0.17085 | 0.05 | 0.135534 | 0.021 | 0.015 | (0.35) | 0.0132 | (0.2490) | 0.0012 | 0.0124 | 0.1759 | 0.0023 | 0.186 | (0.64) | (1.56) | 0.1808 | 1.23 | 2.79 | |
| 2007 | −0.01517 | 0.05 | 0.126856 | 0.012 | 0.000 | (0.35) | 0.0132 | (0.0934) | 0.0004 | 0.0124 | 0.1759 | 0.0009 | 0.187 | 0.26 | (0.53) | 0.172725 | 0.99 | 1.53 | |
| 2008 | 0.425788 | 0.04 | 0.059591 | (0.055) | 0.091 | (0.35) | 0.0032 | 0.3476 | (0.0004) | 0.0124 | 0.1759 | (0.0008) | 0.189 | 2.16 | 1.62 | 0.203994 | 1.91 | 0.29 | |
| 2009 | 0.166774 | 0.03 | 0.131109 | 0.017 | 0.014 | (0.35) | (0.0068) | 0.0886 | 0.0002 | 0.0124 | 0.1759 | 0.0004 | 0.188 | 1.26 | 0.60 | 0.163922 | 0.74 | 0.14 | |
| 2010 | −0.10878 | 0.03 | 0.12322 | 0.009 | 0.006 | (0.35) | (0.0068) | (0.1870) | (0.0005) | 0.0124 | 0.1759 | (0.0009) | 0.189 | (0.16) | (1.02) | 0.124775 | (0.40) | 0.61 | |
| 2011 | 0.238475 | 0.03 | 0.111448 | (0.003) | 0.028 | (0.35) | (0.0068) | 0.1603 | 0.0004 | 0.0124 | 0.1759 | 0.0008 | 0.188 | 1.57 | 0.95 | 0.095408 | (1.26) | (2.21) | |
| 2012 | 0.326 | 0.02 | 0.109027 | (0.005) | 0.053 | (0.35) | (0.0168) | 0.2478 | 0.0015 | 0.0124 | 0.1759 | 0.0029 | 0.185 | 1.99 | 1.42 | 0.089516 | (1.43) | (2.85) | |
| 2013 | 0.187531 | 0.0173 | 0.098985 | (0.015) | 0.018 | (0.35) | (0.0195) | 0.1093 | 0.0008 | 0.0124 | 0.1759 | 0.0015 | 0.187 | 1.43 | 0.79 | 0.100425 | (1.11) | (1.91) | |
| 2014 | −0.02339 | 0.032 | 0.090178 | (0.024) | 0.000 | (0.35) | (0.0048) | (0.1016) | (0.0002) | 0.0124 | 0.1759 | (0.0003) | 0.189 | 0.31 | (0.48) | 0.109026 | (0.86) | (0.38) | |
| 2015 | −0.00011 | 0.025 | 0.086938 | (0.027) | 0.000 | (0.35) | (0.0118) | (0.0783) | (0.0003) | 0.0124 | 0.1759 | (0.0007) | 0.189 | 0.47 | (0.30) | 0.11162 | (0.79) | (0.49) | |
| 2016 | −0.00252 | 0.0219 | 0.082927 | (0.031) | 0.000 | (0.35) | (0.0149) | (0.0807) | (0.0004) | 0.0124 | 0.1759 | (0.0008) | 0.189 | 0.47 | (0.30) | 0.132156 | (0.19) | 0.11 |
| Bank | Year | Capital Gains/(Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bank of Whittier | 2003 | 0.111111 | 0.0400 | −0.00107 | (0.009) | 0.006 | 0.31 | 0.0067 | 0.0517 | 0.0001 | 0.0104 | 0.0739 | 0.0002 | 0.084 | 0.87 | 0.69 | 0.206012 | 0.38 | (0.31) |
| 2004 | −0.03333 | 0.0400 | −0.00116 | (0.009) | 0.001 | 0.31 | 0.0067 | (0.0928) | (0.0002) | 0.0104 | 0.0739 | (0.0004) | 0.085 | (0.78) | (1.53) | 0.331706 | 2.04 | 3.57 | |
| 2005 | 0.27931 | 0.0400 | 0.007237 | (0.001) | 0.039 | 0.31 | 0.0067 | 0.2199 | 0.0005 | 0.0104 | 0.0739 | 0.0009 | 0.083 | 2.51 | 2.89 | 0.351468 | 2.30 | (0.59) | |
| 2006 | 0.123989 | 0.0500 | 0.012775 | 0.005 | 0.008 | 0.31 | 0.0167 | 0.0646 | 0.0003 | 0.0104 | 0.0739 | 0.0007 | 0.084 | 0.90 | 0.72 | 0.168669 | (0.12) | (0.84) | |
| 2007 | 0.028777 | 0.0500 | 0.01443 | 0.006 | 0.000 | 0.31 | 0.0167 | (0.0307) | (0.0002) | 0.0104 | 0.0739 | (0.0003) | 0.085 | (0.16) | (0.70) | 0.149226 | (0.37) | 0.33 | |
| 2008 | 0.044289 | 0.0400 | 0.006398 | (0.002) | 0.001 | 0.31 | 0.0067 | (0.0151) | (0.0000) | 0.0104 | 0.0739 | (0.0001) | 0.084 | 0.14 | (0.30) | 0.212467 | 0.46 | 0.76 | |
| 2009 | 0.046875 | 0.0300 | 0.007358 | (0.001) | 0.001 | 0.31 | (0.0033) | (0.0126) | 0.0000 | 0.0104 | 0.0739 | 0.0000 | 0.084 | 0.28 | (0.10) | 0.153424 | (0.32) | (0.22) | |
| 2010 | 0.008529 | 0.0300 | 0.007421 | (0.001) | 0.000 | 0.31 | (0.0033) | (0.0509) | 0.0001 | 0.0104 | 0.0739 | 0.0001 | 0.084 | (0.16) | (0.70) | 0.141217 | (0.48) | 0.22 | |
| 2011 | 0.035941 | 0.0300 | 0.005337 | (0.003) | 0.001 | 0.31 | (0.0033) | (0.0235) | 0.0000 | 0.0104 | 0.0739 | 0.0000 | 0.084 | 0.16 | (0.27) | 0.140527 | (0.49) | (0.22) | |
| 2012 | 0.046939 | 0.0200 | 0.010253 | 0.002 | 0.001 | 0.31 | (0.0133) | (0.0125) | 0.0001 | 0.0104 | 0.0739 | 0.0001 | 0.084 | 0.41 | 0.06 | 0.143844 | (0.44) | (0.51) | |
| 2013 | 0.02729 | 0.0173 | 0.011071 | 0.003 | 0.000 | 0.31 | (0.0160) | (0.0321) | 0.0002 | 0.0104 | 0.0739 | 0.0003 | 0.084 | 0.21 | (0.20) | 0.124627 | (0.70) | (0.50) | |
| 2014 | 0.037951 | 0.0320 | 0.007544 | (0.001) | 0.001 | 0.31 | (0.0013) | (0.0215) | 0.0000 | 0.0104 | 0.0739 | 0.0000 | 0.084 | 0.16 | (0.27) | 0.11651 | (0.81) | (0.54) | |
| 2015 | 0.034735 | 0.0250 | 0.014742 | 0.007 | 0.001 | 0.31 | (0.0083) | (0.0247) | 0.0001 | 0.0104 | 0.0739 | 0.0001 | 0.084 | 0.21 | (0.21) | 0.110298 | (0.89) | (0.68) | |
| 2016 | 0.039653 | 0.0219 | 0.012521 | 0.004 | 0.001 | 0.31 | (0.0114) | (0.0198) | 0.0001 | 0.0104 | 0.0739 | 0.0001 | 0.084 | 0.30 | (0.08) | 0.134526 | (0.57) | (0.49) |
| Bank | Year | Capital Gains/(Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| University Bank Corp | 2000 | 0.045825 | 0.06 | −0.02448 | (0.217) | 0.001 | 0.00 | 0.0232 | (0.0833) | (0.0000) | 0.0124 | 0.3095 | (0.0000) | 0.322 | 0.55 | (0.39) | 0.918632 | 1.09 | 1.48 |
| 2001 | 0.062903 | 0.05 | −0.01147 | (0.203) | 0.002 | 0.00 | 0.0132 | (0.0662) | (0.0000) | 0.0124 | 0.3095 | (0.0000) | 0.322 | 0.63 | (0.20) | 0.409539 | (1.89) | (1.69) | |
| 2002 | 0.056146 | 0.05 | 0.00841 | (0.184) | 0.002 | 0.00 | 0.0132 | (0.0730) | (0.0000) | 0.0124 | 0.3095 | (0.0000) | 0.322 | 0.61 | (0.24) | 0.386312 | (2.02) | (1.78) | |
| 2003 | −0.15924 | 0.04 | 0.002512 | (0.190) | 0.013 | 0.00 | 0.0032 | (0.2884) | (0.0000) | 0.0124 | 0.3095 | (0.0000) | 0.322 | (0.06) | (1.79) | 0.810897 | 0.46 | 2.25 | |
| 2004 | 1.263458 | 0.04 | −0.01819 | (0.210) | 0.798 | 0.00 | 0.0032 | 1.1343 | 0.0000 | 0.0124 | 0.3095 | 0.0000 | 0.322 | 1.92 | 2.76 | 0.902737 | 1.00 | (1.76) | |
| 2005 | 0.024538 | 0.04 | 0.028364 | (0.164) | 0.000 | 0.00 | 0.0032 | (0.1046) | (0.0000) | 0.0124 | 0.3095 | (0.0000) | 0.322 | 0.55 | (0.39) | 0.825355 | 0.54 | 0.93 | |
| 2006 | 0.150454 | 0.05 | −0.00473 | (0.197) | 0.011 | 0.00 | 0.0132 | 0.0213 | 0.0000 | 0.0124 | 0.3095 | 0.0000 | 0.322 | 0.87 | 0.36 | 0.888708 | 0.92 | 0.56 | |
| 2007 | −0.01068 | 0.05 | 0.126045 | (0.066) | 0.000 | 0.00 | 0.0132 | (0.1398) | (0.0000) | 0.0124 | 0.3095 | (0.0000) | 0.322 | 0.41 | (0.71) | 0.571265 | (0.94) | (0.23) | |
| 2008 | 0.065285 | 0.04 | 0.103717 | (0.088) | 0.002 | 0.00 | 0.0032 | (0.0639) | (0.0000) | 0.0124 | 0.3095 | (0.0000) | 0.322 | 0.67 | (0.11) | 0.627158 | (0.61) | (0.50) | |
| 2009 | 0.065539 | 0.03 | 0.234591 | 0.043 | 0.002 | 0.00 | (0.0068) | (0.0636) | 0.0000 | 0.0124 | 0.3095 | 0.0000 | 0.322 | 0.70 | (0.04) | 0.757978 | 0.15 | 0.19 | |
| 2010 | 0.116171 | 0.03 | 0.247119 | 0.055 | 0.007 | 0.00 | (0.0068) | (0.0130) | 0.0000 | 0.0124 | 0.3095 | 0.0000 | 0.322 | 0.84 | 0.29 | 0.761034 | 0.17 | (0.12) | |
| 2011 | 0.150917 | 0.03 | 0.21595 | 0.024 | 0.011 | 0.00 | (0.0068) | 0.0218 | (0.0000) | 0.0124 | 0.3095 | (0.0000) | 0.322 | 0.94 | 0.50 | 0.849694 | 0.69 | 0.18 | |
| 2012 | 0.109367 | 0.02 | 0.496317 | 0.304 | 0.006 | 0.00 | (0.0168) | (0.0198) | 0.0000 | 0.0124 | 0.3095 | 0.0000 | 0.322 | 0.86 | 0.32 | 0.696964 | (0.21) | (0.52) | |
| 2013 | 0.02348 | 0.0173 | 0.548799 | 0.357 | 0.000 | 0.00 | (0.0195) | (0.1057) | 0.0000 | 0.0124 | 0.3095 | 0.0000 | 0.322 | 0.61 | (0.24) | 0.606863 | (0.73) | (0.50) | |
| 2014 | −0.10965 | 0.032 | 0.473758 | 0.282 | 0.006 | 0.00 | (0.0048) | (0.2388) | 0.0000 | 0.0124 | 0.3095 | 0.0000 | 0.322 | 0.14 | (1.33) | 0.656979 | (0.44) | 0.89 | |
| 2015 | 0.301272 | 0.025 | 0.398736 | 0.207 | 0.045 | 0.00 | (0.0118) | 0.1721 | (0.0000) | 0.0124 | 0.3095 | (0.0000) | 0.322 | 1.31 | 1.37 | 0.983059 | 1.47 | 0.10 | |
| 2016 | 0.039656 | 0.0219 | 0.438981 | 0.247 | 0.001 | 0.00 | (0.0149) | (0.0895) | 0.0000 | 0.0124 | 0.3095 | 0.0000 | 0.322 | 0.65 | (0.16) | 0.792741 | 0.35 | 0.51 |
| Bank | Year | Capital Gains/(Losses), (r) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Barclays | 2000 | 0.229472 | 0.05211 | 0.066601 | 0.021 | 0.026 | 0.80 | 0.0155 | 0.1564 | 0.0019 | 0.0132 | 0.1410 | 0.0039 | 0.150 | 1.32 | 1.07 | 0.22829 | (1.17) | (2.24) |
| 2001 | 0.115182 | 0.04924 | 0.06848 | 0.023 | 0.007 | 0.80 | 0.0126 | 0.0421 | 0.0004 | 0.0132 | 0.1410 | 0.0008 | 0.153 | 0.68 | 0.28 | 0.229723 | (1.15) | (1.43) | |
| 2002 | 0.091569 | 0.04834 | 0.062823 | 0.018 | 0.004 | 0.80 | 0.0117 | 0.0185 | 0.0002 | 0.0132 | 0.1410 | 0.0003 | 0.154 | 0.55 | 0.11 | 0.226876 | (1.18) | (1.29) | |
| 2003 | 0.040994 | 0.04479 | 0.063656 | 0.018 | 0.001 | 0.80 | 0.0081 | (0.0321) | (0.0002) | 0.0132 | 0.1410 | (0.0004) | 0.155 | 0.26 | (0.25) | 0.222299 | (1.23) | (0.98) | |
| 2004 | 0.209629 | 0.04863 | 0.064504 | 0.019 | 0.022 | 0.80 | 0.0120 | 0.1366 | 0.0013 | 0.0132 | 0.1410 | 0.0026 | 0.152 | 1.22 | 0.96 | 0.1786 | (1.67) | (2.62) | |
| 2005 | 0.137991 | 0.04371 | 0.037897 | (0.007) | 0.010 | 0.80 | 0.0071 | 0.0649 | 0.0004 | 0.0132 | 0.1410 | 0.0007 | 0.153 | 0.85 | 0.49 | 0.366701 | 0.22 | (0.27) | |
| 2006 | 0.228487 | 0.04507 | 0.043293 | (0.002) | 0.026 | 0.80 | 0.0084 | 0.1554 | 0.0010 | 0.0132 | 0.1410 | 0.0021 | 0.152 | 1.34 | 1.10 | 0.351386 | 0.06 | (1.04) | |
| 2007 | 0.37721 | 0.05004 | 0.034189 | (0.011) | 0.071 | 0.80 | 0.0134 | 0.3041 | 0.0033 | 0.0132 | 0.1410 | 0.0065 | 0.148 | 2.06 | 2.01 | 0.315039 | (0.30) | (2.31) | |
| 2008 | 0.080593 | 0.04431 | 0.020411 | (0.025) | 0.003 | 0.80 | 0.0077 | 0.0075 | 0.0000 | 0.0132 | 0.1410 | 0.0001 | 0.154 | 0.51 | 0.06 | 0.558934 | 2.14 | 2.08 | |
| 2009 | 0.060747 | 0.03626 | 0.041678 | (0.004) | 0.002 | 0.80 | (0.0004) | (0.0123) | 0.0000 | 0.0132 | 0.1410 | 0.0000 | 0.154 | 0.44 | (0.03) | 0.409835 | 0.65 | 0.67 | |
| 2010 | −0.05002 | 0.03463 | 0.040014 | (0.005) | 0.001 | 0.80 | (0.0020) | (0.1231) | 0.0002 | 0.0132 | 0.1410 | 0.0004 | 0.154 | (0.26) | (0.91) | 0.396496 | 0.51 | 1.42 | |
| 2011 | 0.030525 | 0.02987 | 0.035011 | (0.010) | 0.000 | 0.80 | (0.0068) | (0.0425) | 0.0002 | 0.0132 | 0.1410 | 0.0005 | 0.154 | 0.30 | (0.21) | 0.436523 | 0.91 | 1.12 | |
| 2012 | 0.072838 | 0.0182 | 0.036942 | (0.008) | 0.003 | 0.80 | (0.0185) | (0.0002) | 0.0000 | 0.0132 | 0.1410 | 0.0000 | 0.154 | 0.63 | 0.21 | 0.412953 | 0.68 | 0.47 | |
| 2013 | −0.06163 | 0.02352 | 0.040416 | (0.005) | 0.002 | 0.80 | (0.0131) | (0.1347) | 0.0014 | 0.0132 | 0.1410 | 0.0028 | 0.151 | (0.27) | (0.91) | 0.339012 | (0.06) | 0.85 | |
| 2014 | 0.002773 | 0.02452 | 0.036194 | (0.009) | 0.000 | 0.80 | (0.0121) | (0.0703) | 0.0007 | 0.0132 | 0.1410 | 0.0014 | 0.153 | 0.16 | (0.38) | 0.402511 | 0.57 | 0.96 | |
| 2015 | −0.16425 | 0.01808 | 0.043828 | (0.001) | 0.013 | 0.80 | (0.0186) | (0.2373) | 0.0035 | 0.0132 | 0.1410 | 0.0071 | 0.147 | (1.00) | (1.83) | 0.375769 | 0.31 | 2.14 | |
| 2016 | −0.15986 | 0.01183 | 0.0334 | (0.012) | 0.013 | 0.80 | (0.0248) | (0.2329) | 0.0046 | 0.0132 | 0.1410 | 0.0093 | 0.145 | (0.93) | (1.75) | 0.416357 | 0.71 | 2.46 |
| Bank | Year | Capital Gains/(Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half Square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation And Variances Of Interest And Capital Gain | Std. Deviation of Interest Rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lloyds | 2000 | 0.064103 | 0.05211 | 0.074401 | (0.004) | 0.002 | (0.17) | 0.0155 | 0.0159 | (0.0000) | 0.0132 | 0.3545 | (0.0001) | 0.368 | 0.24 | 0.19 | 0.233145 | 0.47 | 0.28 |
| 2001 | −0.40241 | 0.04924 | 0.071379 | (0.007) | 0.081 | (0.17) | 0.0126 | (0.4506) | 0.0010 | 0.0132 | 0.3545 | 0.0019 | 0.366 | (1.24) | (1.56) | 0.196116 | (0.01) | 1.55 | |
| 2002 | 0.012097 | 0.04834 | 0.067126 | (0.011) | 0.000 | (0.17) | 0.0117 | (0.0361) | 0.0001 | 0.0132 | 0.3545 | 0.0001 | 0.367 | 0.12 | 0.04 | 0.039976 | (2.00) | (2.04) | |
| 2003 | 0.055777 | 0.04479 | 0.075332 | (0.003) | 0.002 | (0.17) | 0.0081 | 0.0076 | (0.0000) | 0.0132 | 0.3545 | (0.0000) | 0.368 | 0.24 | 0.19 | 0.043809 | (1.95) | (2.14) | |
| 2004 | 0.033962 | 0.04863 | 0.064758 | (0.014) | 0.001 | (0.17) | 0.0120 | (0.0142) | 0.0000 | 0.0132 | 0.3545 | 0.0001 | 0.368 | 0.17 | 0.11 | 0.137198 | (0.76) | (0.87) | |
| 2005 | 0.175182 | 0.04371 | 0.14206 | 0.064 | 0.015 | (0.17) | 0.0071 | 0.1270 | (0.0002) | 0.0132 | 0.3545 | (0.0003) | 0.368 | 0.53 | 0.53 | 0.18771 | (0.11) | (0.64) | |
| 2006 | −0.17081 | 0.04507 | 0.110801 | 0.032 | 0.015 | (0.17) | 0.0084 | (0.2190) | 0.0003 | 0.0132 | 0.3545 | 0.0006 | 0.367 | (0.41) | (0.59) | 0.212856 | 0.21 | 0.79 | |
| 2007 | 0.142322 | 0.05004 | 0.099669 | 0.021 | 0.010 | (0.17) | 0.0134 | 0.0942 | (0.0002) | 0.0132 | 0.3545 | (0.0004) | 0.368 | 0.44 | 0.42 | 0.247441 | 0.65 | 0.23 | |
| 2008 | −0.08938 | 0.04431 | 0.031467 | (0.047) | 0.004 | (0.17) | 0.0077 | (0.1375) | 0.0002 | 0.0132 | 0.3545 | 0.0004 | 0.367 | (0.16) | (0.29) | 0.274883 | 1.00 | 1.29 | |
| 2009 | 0.383518 | 0.03626 | 0.08456 | 0.006 | 0.074 | (0.17) | (0.0004) | 0.3354 | 0.0000 | 0.0132 | 0.3545 | 0.0000 | 0.368 | 0.96 | 1.04 | 0.300523 | 1.33 | 0.29 | |
| 2010 | −0.60145 | 0.03463 | 0.083713 | 0.005 | 0.181 | (0.17) | (0.0020) | (0.6496) | (0.0002) | 0.0132 | 0.3545 | (0.0004) | 0.368 | (2.01) | (2.47) | 0.309867 | 1.45 | 3.91 | |
| 2011 | 0.890884 | 0.02987 | 0.05272 | (0.026) | 0.397 | (0.17) | (0.0068) | 0.8427 | 0.0010 | 0.0132 | 0.3545 | 0.0019 | 0.366 | 1.49 | 1.66 | 0.286808 | 1.15 | (0.51) | |
| 2012 | 0.670227 | 0.0182 | 0.07966 | 0.001 | 0.225 | (0.17) | (0.0185) | 0.6221 | 0.0019 | 0.0132 | 0.3545 | 0.0039 | 0.364 | 1.40 | 1.55 | 0.214093 | 0.22 | (1.33) | |
| 2013 | −0.03871 | 0.02352 | 0.08571 | 0.007 | 0.001 | (0.17) | (0.0131) | (0.0869) | (0.0002) | 0.0132 | 0.3545 | (0.0004) | 0.368 | 0.04 | (0.05) | 0.176945 | (0.25) | (0.20) | |
| 2014 | −0.03627 | 0.02452 | 0.066074 | (0.012) | 0.001 | (0.17) | (0.0121) | (0.0844) | (0.0002) | 0.0132 | 0.3545 | (0.0003) | 0.368 | 0.05 | (0.04) | 0.158454 | (0.49) | (0.44) | |
| 2015 | −0.14452 | 0.01808 | 0.054237 | (0.024) | 0.010 | (0.17) | (0.0186) | (0.1927) | (0.0006) | 0.0132 | 0.3545 | (0.0012) | 0.369 | (0.26) | (0.40) | 0.163222 | (0.43) | (0.02) | |
| 2016 | −0.12589 | 0.01183 | 0.091416 | 0.013 | 0.008 | (0.17) | (0.0248) | (0.1740) | (0.0007) | 0.0132 | 0.3545 | (0.0015) | 0.369 | (0.18) | (0.31) | 0.160272 | (0.46) | (0.15) |
| Bank | Year | Capital Gains/ (Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta Variance (αy(t)) | Half square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest Rate Variance | Capital Gain Variance | Correlation and Variances of Interest and Capital Gain | Std. Deviation of Interest Rate | Std. Deviation Of Capital Gain | 2 x (Correlation and Variances of Interest and Capital Gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal debt Ratio | Actual Debt Ratio | Normalized Actual debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bank of London and the ME | 2007 | 0.416576 | 0.037 | 0.074163 | (0.051) | 0.087 | 0.65 | 0.0188 | 0.3771 | 0.0046 | 0.0095 | 0.1593 | 0.0091 | 0.160 | 2.64 | 2.17 | 0.001444 | (0.73) | (2.90) |
| 2008 | −0.03746 | 0.0295 | 0.079447 | (0.045) | 0.001 | 0.65 | 0.0113 | (0.0770) | (0.0006) | 0.0095 | 0.1593 | (0.0011) | 0.170 | 0.33 | (0.56) | 0.000593 | (0.79) | (0.23) | |
| 2009 | 0.014437 | 0.0159 | 0.087611 | (0.037) | 0.000 | 0.65 | (0.0023) | (0.0251) | 0.0000 | 0.0095 | 0.1593 | 0.0001 | 0.169 | 0.73 | (0.09) | 0.001044 | (0.76) | (0.67) | |
| 2010 | −0.04321 | 0.0133 | 0.118387 | (0.006) | 0.001 | 0.65 | (0.0049) | (0.0827) | 0.0003 | 0.0095 | 0.1593 | 0.0005 | 0.168 | 0.40 | (0.48) | 0.001518 | (0.73) | (0.25) | |
| 2011 | 0.012255 | 0.0225 | 0.113426 | (0.011) | 0.000 | 0.65 | 0.0043 | (0.0272) | (0.0001) | 0.0095 | 0.1593 | (0.0002) | 0.169 | 0.68 | (0.16) | 0.002186 | (0.68) | (0.53) | |
| 2012 | −0.00079 | 0.0159 | 0.108883 | (0.016) | 0.000 | 0.65 | (0.0023) | (0.0403) | 0.0001 | 0.0095 | 0.1593 | 0.0001 | 0.169 | 0.64 | (0.20) | 0.010814 | (0.09) | 0.10 | |
| 2013 | −0.21454 | 0.0082 | 0.106047 | (0.019) | 0.023 | 0.65 | (0.0100) | (0.2540) | 0.0016 | 0.0095 | 0.1593 | 0.0033 | 0.165 | (0.72) | (1.81) | 0.011308 | (0.06) | 1.75 | |
| 2014 | 0.06978 | 0.007 | 0.29993 | 0.175 | 0.002 | 0.65 | (0.0112) | 0.0303 | (0.0002) | 0.0095 | 0.1593 | (0.0004) | 0.169 | 1.09 | 0.33 | 0.018203 | 0.41 | 0.07 | |
| 2015 | 0.081756 | 0.012 | 0.132536 | 0.008 | 0.003 | 0.65 | (0.0062) | 0.0423 | (0.0002) | 0.0095 | 0.1593 | (0.0003) | 0.169 | 1.13 | 0.38 | 0.032835 | 1.41 | 1.03 | |
| 2016 | 0.096235 | 0.0209 | 0.127406 | 0.003 | 0.005 | 0.65 | 0.0027 | 0.0567 | 0.0001 | 0.0095 | 0.1593 | 0.0002 | 0.169 | 1.16 | 0.41 | 0.041943 | 2.03 | 1.61 |
| Bank | Year | Capital gains/ (Losses), (r ) | Interest Rate (i) | Beta (Productivity of Capital, β) | Beta variance (αy(t)) | Half square of Capital Gain Variance | Correlation of Interest and Capital Gain Variables | Interest rate Variance | Capital gain Variance | Correlation and Variances of Interest and Capital Gain | std. deviation of Interest rate | Std. Deviation of Capital Gain | 2 x (Correlation and Variances of Interest and Capital gain) | Risk | Optimal Debt Ratio, ƒ*(t) | Normalized Optimal Debt Ratio | Actual Debt Ratio | Normalized Actual Debt Ratio | Excess Debt |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IB of Britain | 2004 | −0.13823 | 0.04863 | 0.011541 | (0.026) | 0.010 | (0.33) | 0.0157 | (0.3728) | 0.0019 | 0.0129 | 0.9213 | 0.0039 | 0.930 | (0.17) | 0.04 | 0.036566 | 2.52 | 2.48 |
| 2005 | −0.21533 | 0.04371 | 0.034007 | (0.004) | 0.023 | (0.33) | 0.0107 | (0.4499) | 0.0016 | 0.0129 | 0.9213 | 0.0032 | 0.931 | (0.26) | (0.11) | 0.011311 | (0.31) | (0.21) | |
| 2006 | −0.21574 | 0.04507 | 0.040216 | 0.002 | 0.023 | (0.33) | 0.0121 | (0.4503) | 0.0018 | 0.0129 | 0.9213 | 0.0036 | 0.931 | (0.26) | (0.11) | 0.018532 | 0.50 | 0.61 | |
| 2007 | −0.23549 | 0.05004 | 0.049504 | 0.012 | 0.028 | (0.33) | 0.0171 | (0.4701) | 0.0027 | 0.0129 | 0.9213 | 0.0053 | 0.929 | (0.29) | (0.16) | 0.018025 | 0.44 | 0.60 | |
| 2008 | −0.09666 | 0.04431 | 0.049343 | 0.012 | 0.005 | (0.33) | 0.0113 | (0.3313) | 0.0012 | 0.0129 | 0.9213 | 0.0025 | 0.932 | (0.11) | 0.13 | 0.019253 | 0.58 | 0.45 | |
| 2009 | 0.542116 | 0.03626 | 0.026957 | (0.011) | 0.147 | (0.33) | 0.0033 | 0.3075 | (0.0003) | 0.0129 | 0.9213 | (0.0007) | 0.935 | 0.42 | 1.01 | 0.017505 | 0.38 | (0.63) | |
| 2010 | −0.34628 | 0.03463 | 0.025304 | (0.012) | 0.060 | (0.33) | 0.0017 | (0.5809) | 0.0003 | 0.0129 | 0.9213 | 0.0006 | 0.934 | (0.43) | (0.39) | 0.015202 | 0.12 | 0.51 | |
| 2011 | 0.169176 | 0.02987 | 0.028315 | (0.009) | 0.014 | (0.33) | (0.0031) | (0.0654) | (0.0001) | 0.0129 | 0.9213 | (0.0001) | 0.934 | 0.17 | 0.60 | 0.017419 | 0.37 | (0.23) | |
| 2012 | 0.209329 | 0.0182 | 0.034336 | (0.003) | 0.022 | (0.33) | (0.0148) | (0.0253) | (0.0001) | 0.0129 | 0.9213 | (0.0002) | 0.934 | 0.22 | 0.68 | 0.009052 | (0.57) | (1.25) | |
| 2013 | 3.197765 | 0.02352 | 0.042347 | 0.005 | 5.113 | (0.33) | (0.0095) | 2.9632 | 0.0093 | 0.0129 | 0.9213 | 0.0186 | 0.916 | (2.07) | (3.05) | 0.006707 | (0.83) | 2.22 | |
| 2014 | 0.056658 | 0.02452 | 0.043702 | 0.006 | 0.002 | (0.33) | (0.0085) | (0.1779) | (0.0005) | 0.0129 | 0.9213 | (0.0010) | 0.935 | 0.07 | 0.44 | 0.005141 | (1.01) | (1.44) | |
| 2015 | 0.076536 | 0.01808 | 0.051524 | 0.014 | 0.003 | (0.33) | (0.0149) | (0.1581) | (0.0008) | 0.0129 | 0.9213 | (0.0016) | 0.936 | 0.10 | 0.48 | 0.004414 | (1.09) | (1.57) | |
| 2016 | 0.045895 | 0.01183 | 0.054336 | 0.017 | 0.001 | (0.33) | (0.0211) | (0.1887) | (0.0013) | 0.0129 | 0.9213 | (0.0027) | 0.937 | 0.07 | 0.44 | 0.004167 | (1.12) | (1.55) |
References
- Abdullah, Fikriyah, Taufiq Hassan, and Shamsher Mohamad. 2007. Investigation of Performance of Malaysian Islamic Unit Trust Funds: Comparison with Conventional Unit Trust Funds. Managerial Finance 33: 142–53. [Google Scholar] [CrossRef]
- Abdul-Rahman, Yahia. 2010. The art of Islamic finance and Banking: Tools and Techniques for Community-Based Banking. Hoboken: Wiley. [Google Scholar]
- Amin, Muslim, Zaidi Isa, and Rodrigue Fontaine. 2013. Islamic banks. International Journal of Bank Marketing 31: 79–97. [Google Scholar] [CrossRef]
- Bashir, Abdel-Hameed M. 2001. Assessing the performance of Islamic banks: Some evidence from the Middle East. Topics in Middle Eastern and North African Economies 3: 1–11. [Google Scholar]
- Beck, Thorsten, Demirgüç-Kunt Asli, and Ouarda Merrouche. 2010. Islamic vs. Conventional Banking: Business Model, Efficiency and Stability. The World Bank: Available online: https://elibrary.worldbank.org/doi/abs/10.1596/1813-9450-5446 (accessed on 22 June 2020).
- Bitar, Mohammad, Mr Sami Ben Naceur, Rym Ayadi, and Thomas Walker. 2017. Basel Compliance and Financial Stability: Evidence from Islamic Banks. IMF Working Papers. Washington, DC: International Monetary Fund, vol. 17. [Google Scholar]
- Brunnermeier, Markus K. 2009. Deciphering the Liquidity and Credit Crunch 2007–2008. Journal of Economic Perspectives 23: 77–100. [Google Scholar] [CrossRef]
- Brunnermeier, Markus K., and Yuliy Sannikov. 2014. A Macroeconomic Model with a Financial Sector. American Economic Review 104: 379–421. [Google Scholar] [CrossRef]
- Chapra, M. Umer. 2008. The Global Financial Crisis: Can Islamic Finance Help Minimize the Severity and Frequency of Such a Crisis in the Future? Paper presented at the Forum on the Global Financial Crisis, Jeddah, Saudi Arabia, October 25. [Google Scholar]
- Ebisike, Obioma. 2014. Inquiry into U.S. Banks Exposures to Mortgage Securities. New York: The New School, Proquest. [Google Scholar]
- El Said, Ayah, and Rachel Ziemba. 2009. Stress-Testing Islamic Finance. New York: Roubini Global Economics. [Google Scholar]
- Fayed, Mona Esam. 2013. Comparative performance study of conventional and Islamic banking in Egypt. Journal of Applied Finance and Banking 3: 1–14. [Google Scholar]
- Febianto, Irawan. 2012. Adapting risk management for profit and loss sharing financing of Islamic banks. Modern Economy 3: 16808. [Google Scholar] [CrossRef]
- Gross, Marco, Jerome Henry, and Willi Semmler. 2017. Destabilizing Effects of Bank Overleveraging on Real Activity—An Analysis Based on a Threshold MCS-GVAR. Macroeconomic Dynamics 22: 1750–68. [Google Scholar] [CrossRef]
- Hasan, Maher, and Jemma Dridi. 2010. The Effects of the Global Crisis on Islamic and Conventional Banks: A Comparative Study. Washington, DC: International Monetary Fund. [Google Scholar]
- Hibbs, Douglas A., Jr. 1977. Political Parties and Macroeconomic Policy. The American Political Science Review 71: 1467–87. [Google Scholar] [CrossRef]
- Hidayat, Sutan Emir, and Muhammad Abduh. 2012. Does financial crisis give impacts on Bahrain Islamic banking performance? A panel regression analysis. International Journal of Economics and Finance 4: 79–87. [Google Scholar] [CrossRef]
- Khan, Feisal. 2010. How ‘Islamic’ is Islamic Banking? Journal of Economic Behavior & Organization 76: 805–20. [Google Scholar]
- Kusuma, Hadri, and Ariza Ayumardani. 2016. The corporate governance efficiency and Islamic bank performance: An Indonesian evidence. Polish Journal of Management Studies 13: 111–20. [Google Scholar] [CrossRef]
- Mishkin, Frederic S. 2007. The Economics of Money, Banking, and Financial Markets. London: Pearson education. [Google Scholar]
- Mittnik, Stefan, and Willi Semmler. 2012. Regime Dependence of the Multiplier. Journal of Economic Behavior and Organization 83: 502–52. [Google Scholar] [CrossRef]
- Mittnik, Stefan, and Willi Semmler. 2013. The Real Consequences of Financial Stress. Journal of Economic Dynamics and Control 37: 1479–99. [Google Scholar] [CrossRef]
- Osborn, David P. J., Gus Levy, Irwin Nazareth, Irene Petersen, Amir Islam, and Michael B. King. 2007. Relative Risk of Cardiovascular and Cancer Mortality in People with Severe Mental Illness from the United Kingdom’s General Practice Research Database. Archives of General Psychiatry 64: 242–49. [Google Scholar] [CrossRef]
- Parashar, Sat Paul, and Jyothi Venkatesh. 2012. How Did Islamic Banks Do During Global Financial Crisis. Banks and Bank Systems 5: 54–62. [Google Scholar]
- Pratomo, Wahyu Ario, and Abdul Ghafar Ismail. 2006. Islamic Bank Performance and Capital Structure. Munich: University Library of Munich, Germany. [Google Scholar]
- Samad, Abdus. 2004. Performance of Interest-Free Islamic Banks Vis-À-Vis Interest-Based Conventional Banks of Bahrain. International Journal of Economics, Management and Accounting 12. Available online: https://journals.iium.edu.my/enmjournal/index.php/enmj/article/view/99 (accessed on 23 June 2020).
- Samad, Abdus, and M Kabir Hassan. 2006. The Performance of Malaysian Islamic Bank During 1984–1997: An Exploratory Study. Thoughts on Economics 10: 7–26. [Google Scholar] [CrossRef]
- Schleer, Frauke, and Willi Semmler. 2016. Banking Overleveraging and Macro Instability: A Model and VSTAR Estimations. Jahrbücher für Nationalökonomie und Statistik 236: 609–38. [Google Scholar] [CrossRef]
- Shabsigh, Ghiath, Abdullah Haron, and Mohamed Afzal Norat. 2017. In Won Song, Mariam El Hamiani Khatat, Diarmuid Murphy and Artak Harutyunyan. Ensuring Financial Stability In Countries With Islamic Banking. International Monetary Fund 5. Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwiy2Pnn9JbqAhVQeXAKHYJRD6MQFjAAegQIARAB&url=https%3A%2F%2Fwww.imf.org%2F~%2Fmedia%2FFiles%2FPublications%2FPP%2FPP-Ensuring-Financial-Stability-in-Countries-with-Islamic-Banking.ashx&usg=AOvVaw2rI2XZCuLk8SngDngCZjo5 (accessed on 23 June 2020).
- Sole, Mr Juan. 2007. Introducing Islamic Banks into Coventional Banking Systems (Epub). Washington, DC: International Monetary Fund. [Google Scholar]
- Stein, Jerome L. 2008. A Tale of Two Debt Crises: A Stochastic Optimal Control Analysis. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1092397#maincontent (accessed on 22 June 2020).
- Stein, Jerome L. 2011. The Diversity of the Debt Crisis in Europe. CESifo Working Paper No. 3348 2011: 1–20. [Google Scholar]
- Stein, Jerome L. 2012a. Stochastic Optimal Control and the US Financial Debt Crisis. Économie Publique/Public Economics 26–27: 271–79. [Google Scholar] [CrossRef]
- Stein, Jerome L. 2012b. The diversity of debt crises in Europe. In Stochastic Optimal Control and the US Financial Debt Crisis. Boston: Springer, pp. 133–54. [Google Scholar]
- Sufian, Fadzlan. 2014. The nexus between economic freedom and Islamic bank performance: Empirical evidence from the MENA banking sectors. Contemporary Review of the Middle East 1: 411–39. [Google Scholar] [CrossRef]
- The Economist. 2009. Middle East Finance: Shine Comes Off Islamic Banks. The Economist, September 24. [Google Scholar]
- Turk-Ariss, Rima. 2009. Competitive Behavior in Middle East and North Africa Banking Systems. The Quarterly Review of Economics and Finance 49: 693–710. [Google Scholar] [CrossRef]
- Wilson, Rodney. 1999. Challenges and Opportunities for Islamic Banking and Finance in the West: The United Kingdom Experience. Thunderbird International Business Review 41: 421–44. [Google Scholar] [CrossRef]
| 1 | Meaning increases in housing prices. |
| 2 | See “The Art of Riba-Free (RF) Islamic Banking and Finance”, published by Wiley (first e. 2010 and second e. 2014) by Dr. Yahia Abdul-Rahman. |
| 3 | If the rate is much lower than the accepted return in the market, say 4–5%, they do not invest/finance. If the rate is high, then they finance, but reduce the rent such that the monthly payment would be competitive with that of other banks in the market. |
| 4 | This source of instability is also discussed by Brunnermeier and Sannikov (2014). |
| 5 | |
| 6 | The list of banks’ names and types is provided in Appendix B. |
| 7 | |
| 8 | Variables in the first two columns, capital gain/loss and interest rate, form the uncertainty of the model. The two variables are stochastic in the model and can move in different directions. |
| 9 | The reason that total capital is calculated this way is because capital investments in a company are made up of equity capital and debt financing; hence, a company has two types of stakeholders: equity and debt holders. |
| 10 | In the calculation, this correlation is a constant value over the period. |
| 11 | The optimal-debt ratio is positive only if the net return is greater than the risk premium. |
| 12 | They were normalized such that each variable had a mean of zero. |
| 13 | Such as cash, accounts receivable, investments in other firms, properties, and intangible assets. |
| 14 | See BOA annual report for 2001. |
| 15 | |
| 16 | See Schleer and Semmler (2016) for a Moving Average (1,1) smoothing technique. |
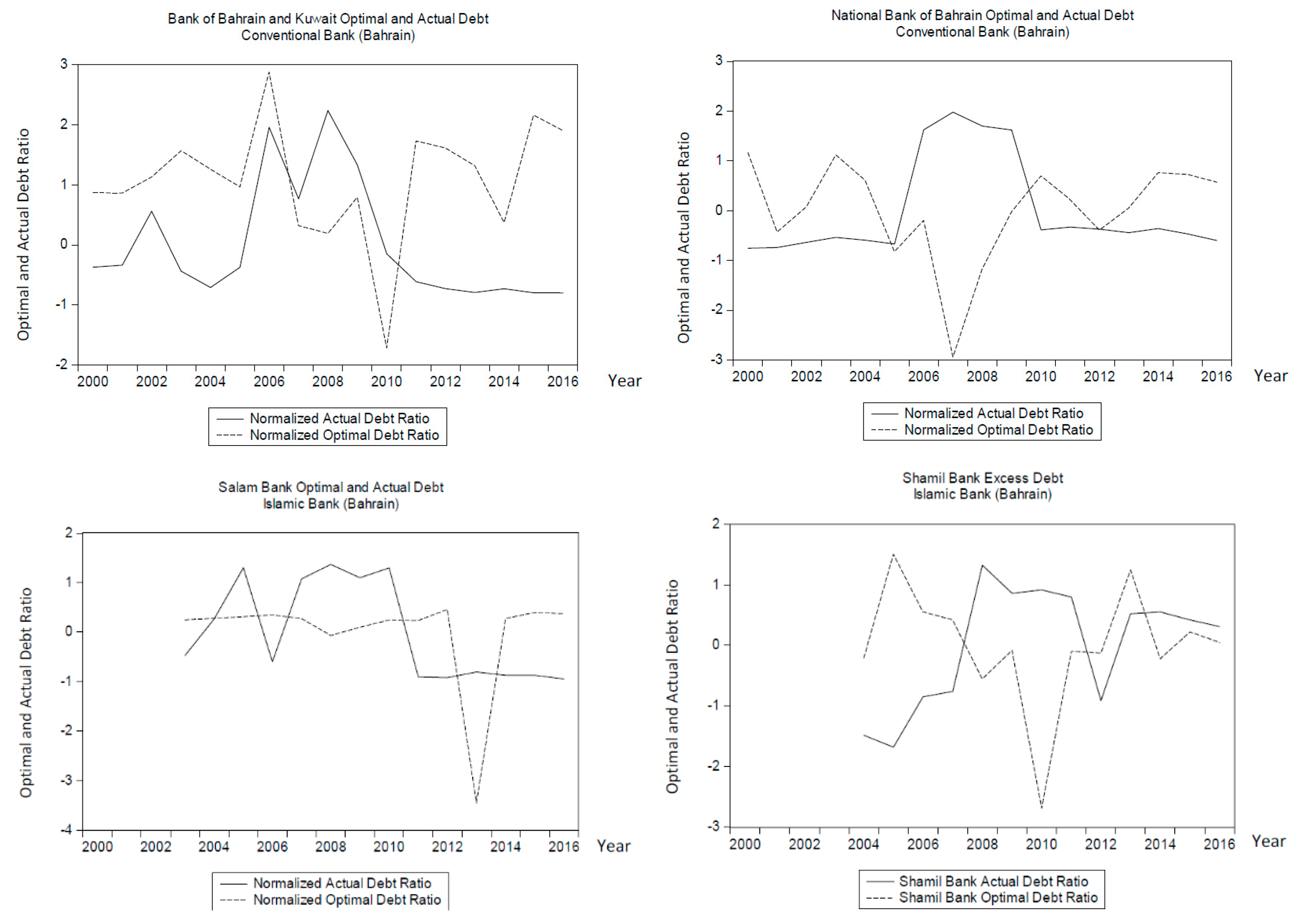
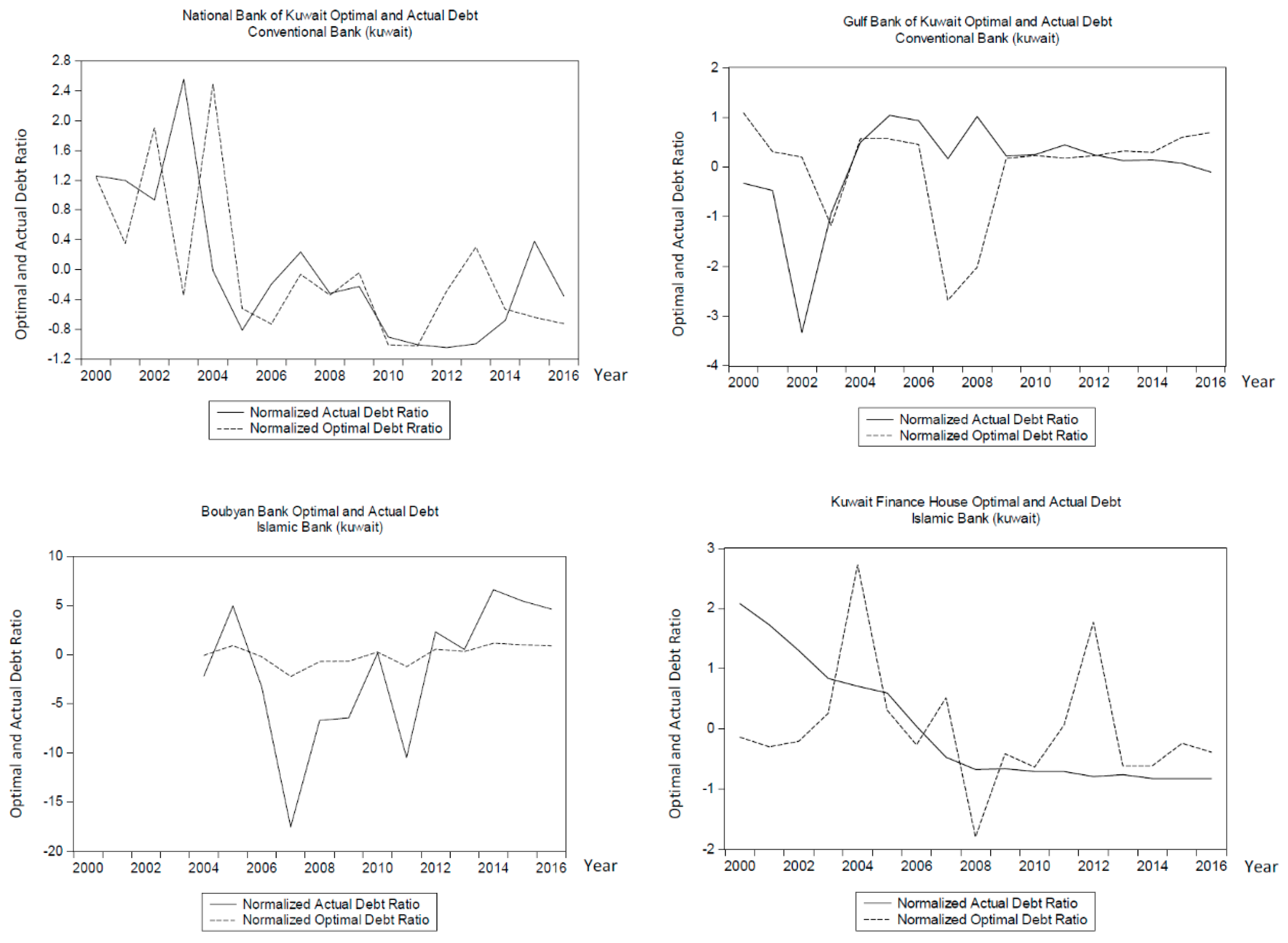


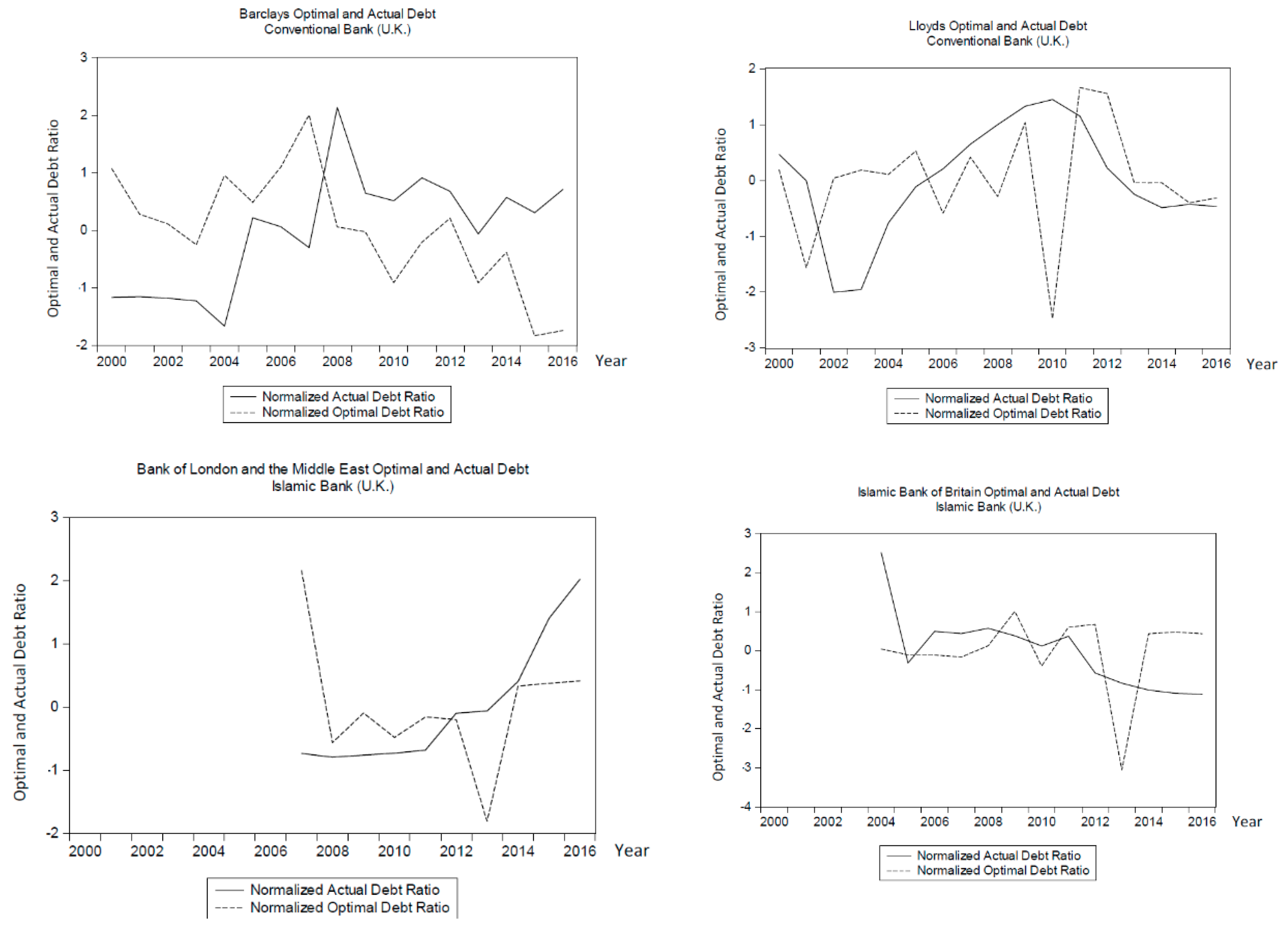
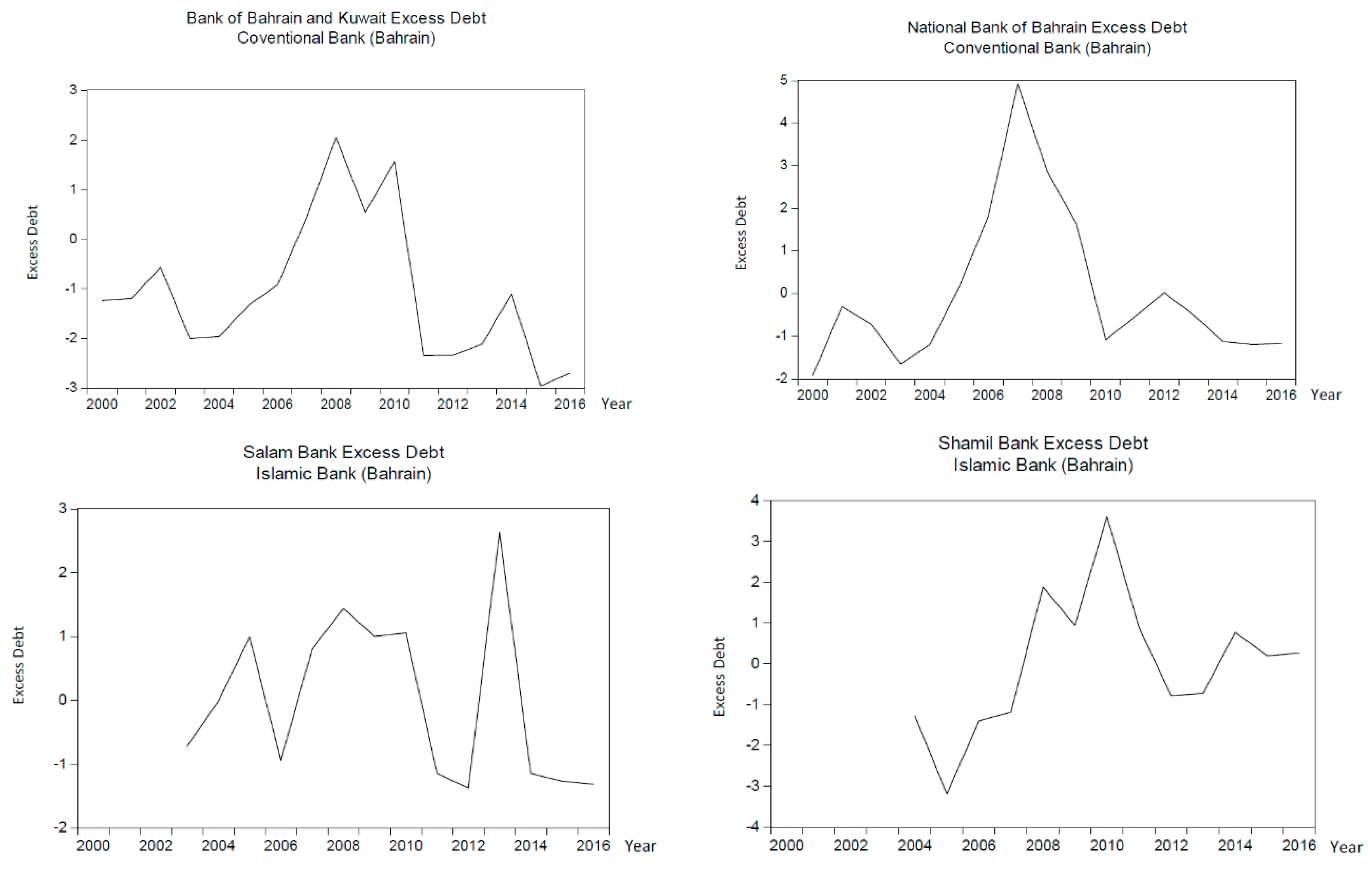

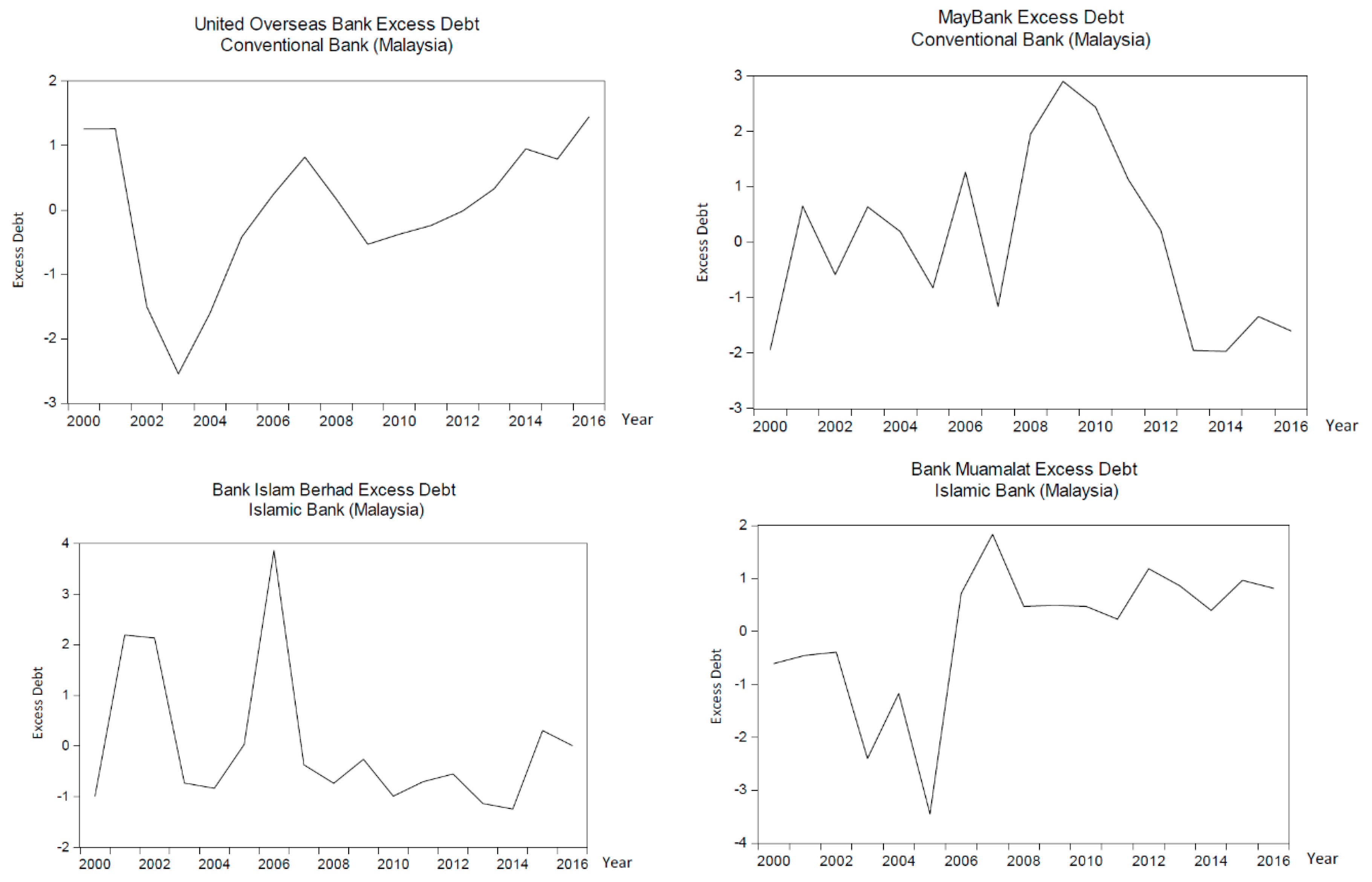
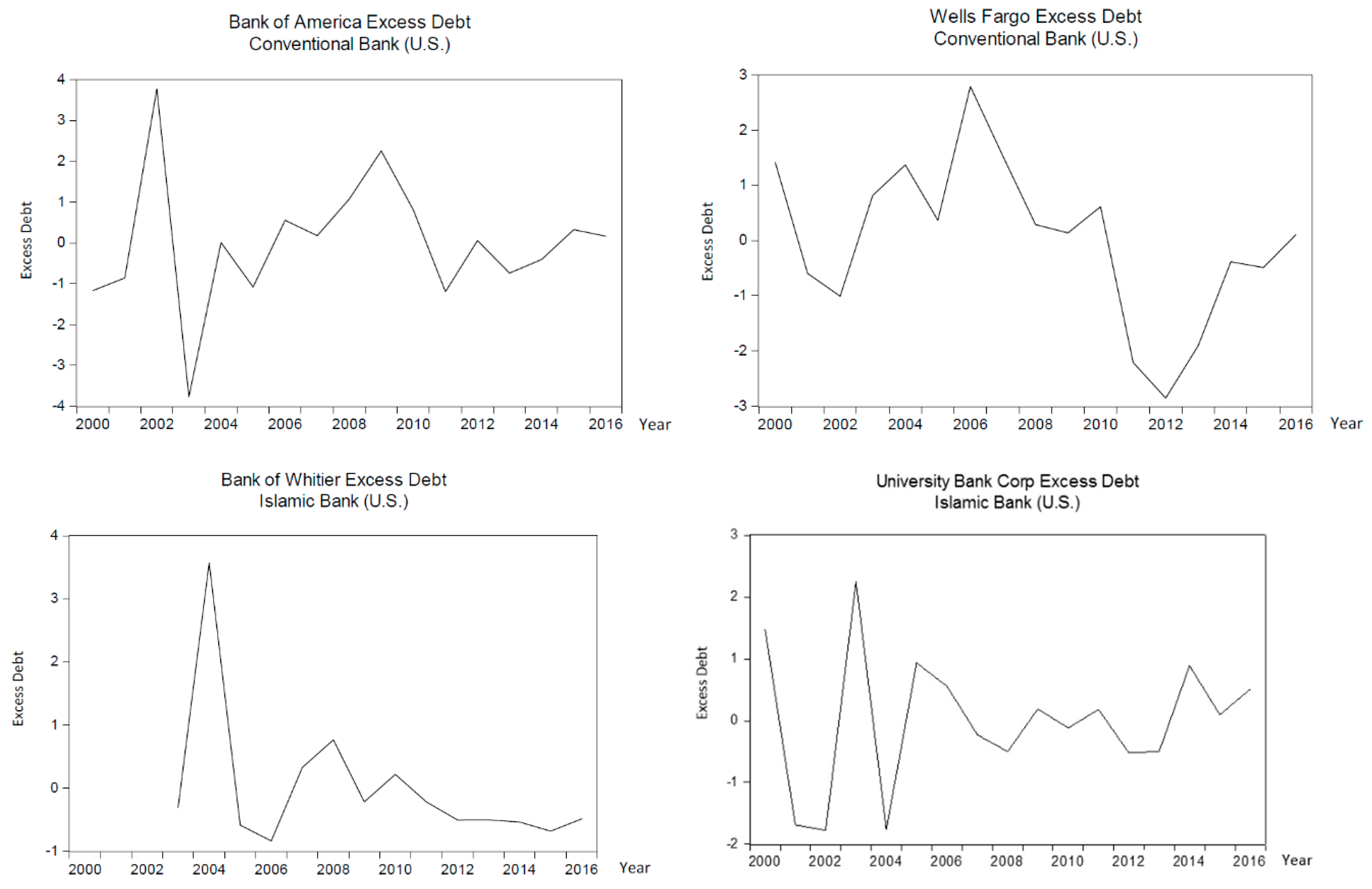
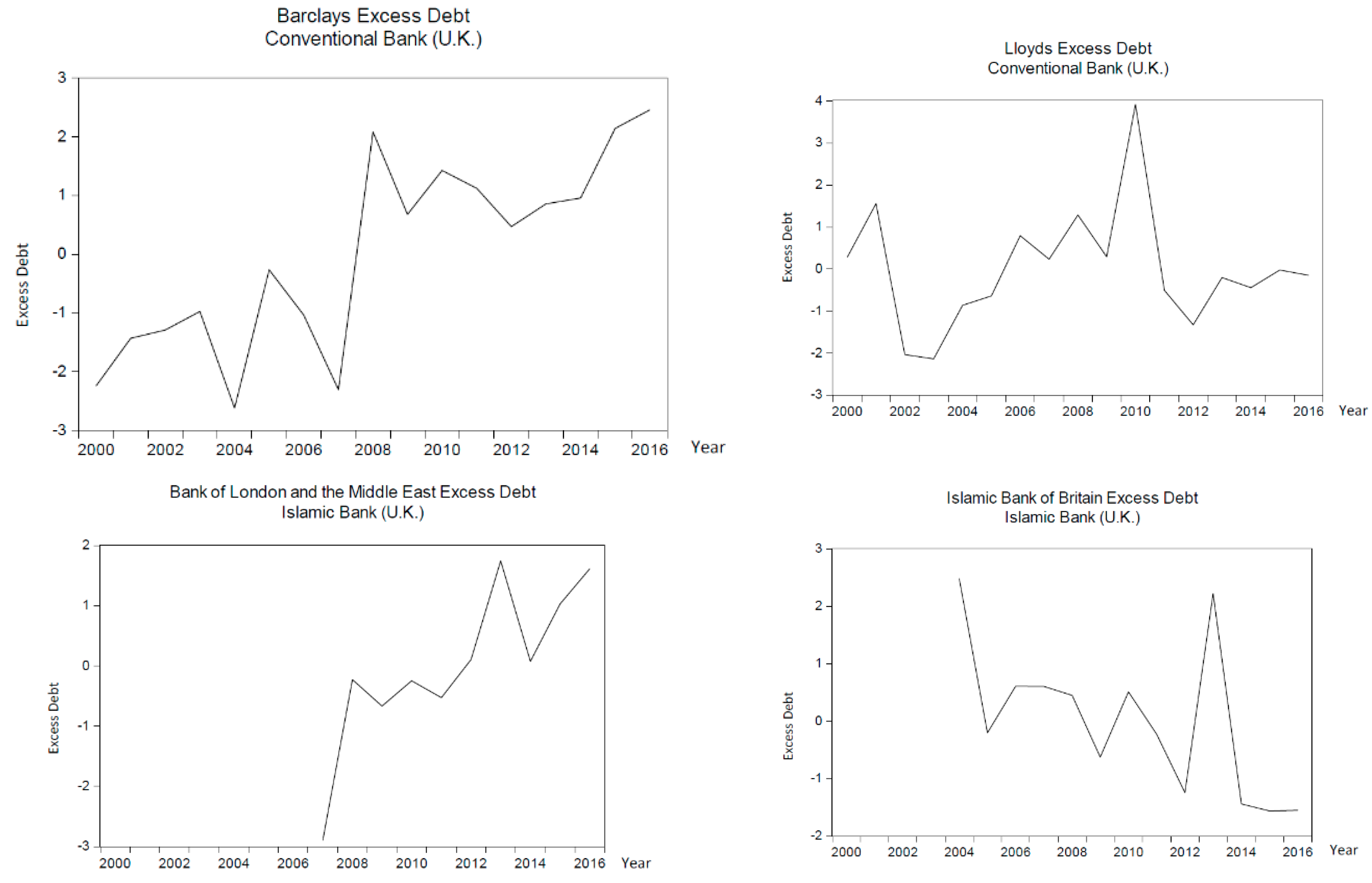
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Issa, S. Life after Debt: The Effects of Overleveraging on Conventional and Islamic Banks. J. Risk Financial Manag. 2020, 13, 137. https://doi.org/10.3390/jrfm13060137
Issa S. Life after Debt: The Effects of Overleveraging on Conventional and Islamic Banks. Journal of Risk and Financial Management. 2020; 13(6):137. https://doi.org/10.3390/jrfm13060137
Chicago/Turabian StyleIssa, Samar. 2020. "Life after Debt: The Effects of Overleveraging on Conventional and Islamic Banks" Journal of Risk and Financial Management 13, no. 6: 137. https://doi.org/10.3390/jrfm13060137
APA StyleIssa, S. (2020). Life after Debt: The Effects of Overleveraging on Conventional and Islamic Banks. Journal of Risk and Financial Management, 13(6), 137. https://doi.org/10.3390/jrfm13060137




