Intraday Jumps, Liquidity, and U.S. Macroeconomic News: Evidence from Exchange Traded Funds
Abstract
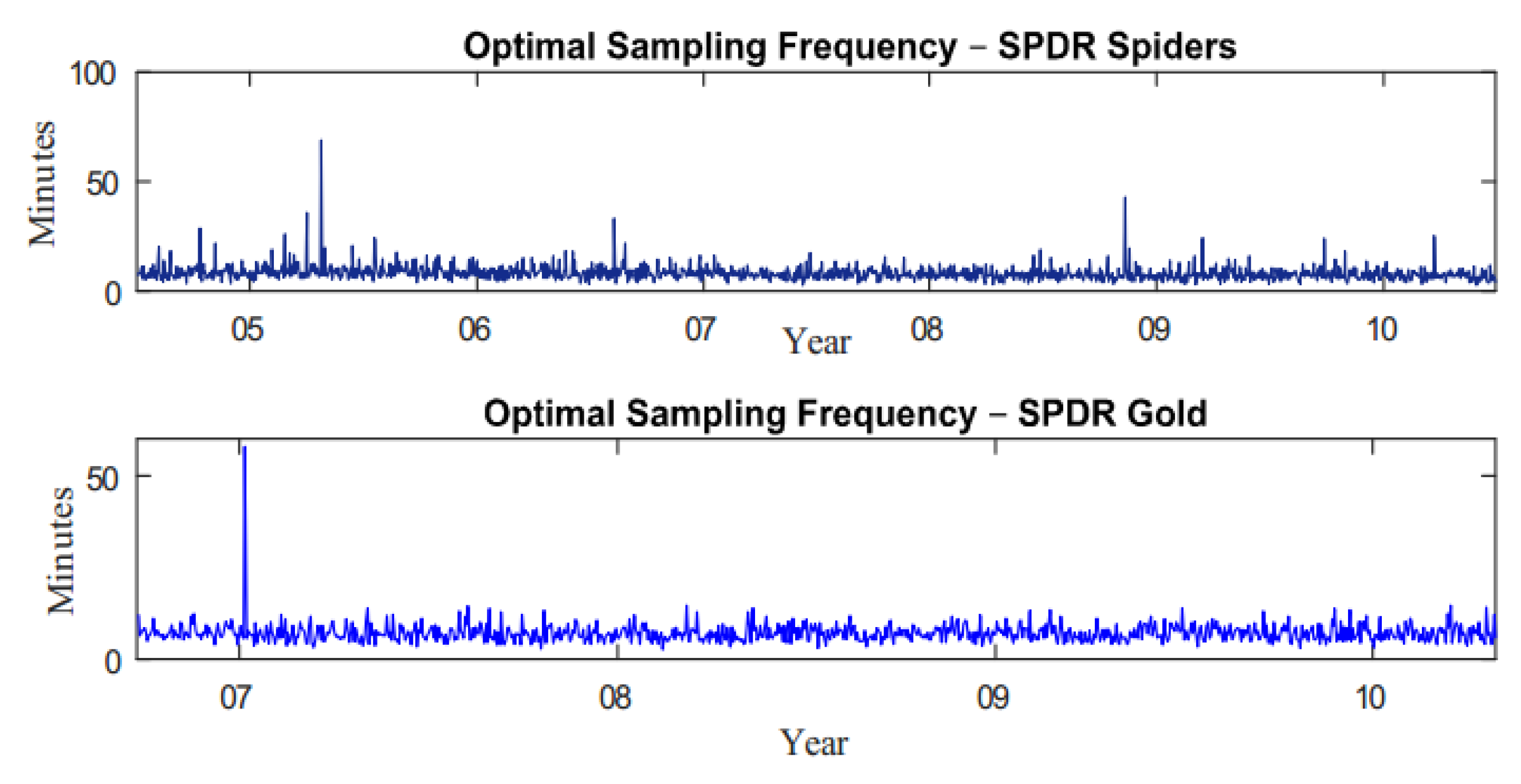
1. Introduction
2. Relevant Literature
3. Methodology
3.1. Identifying Intraday Jumps
3.2. Mitigating Market Microstructure Noise
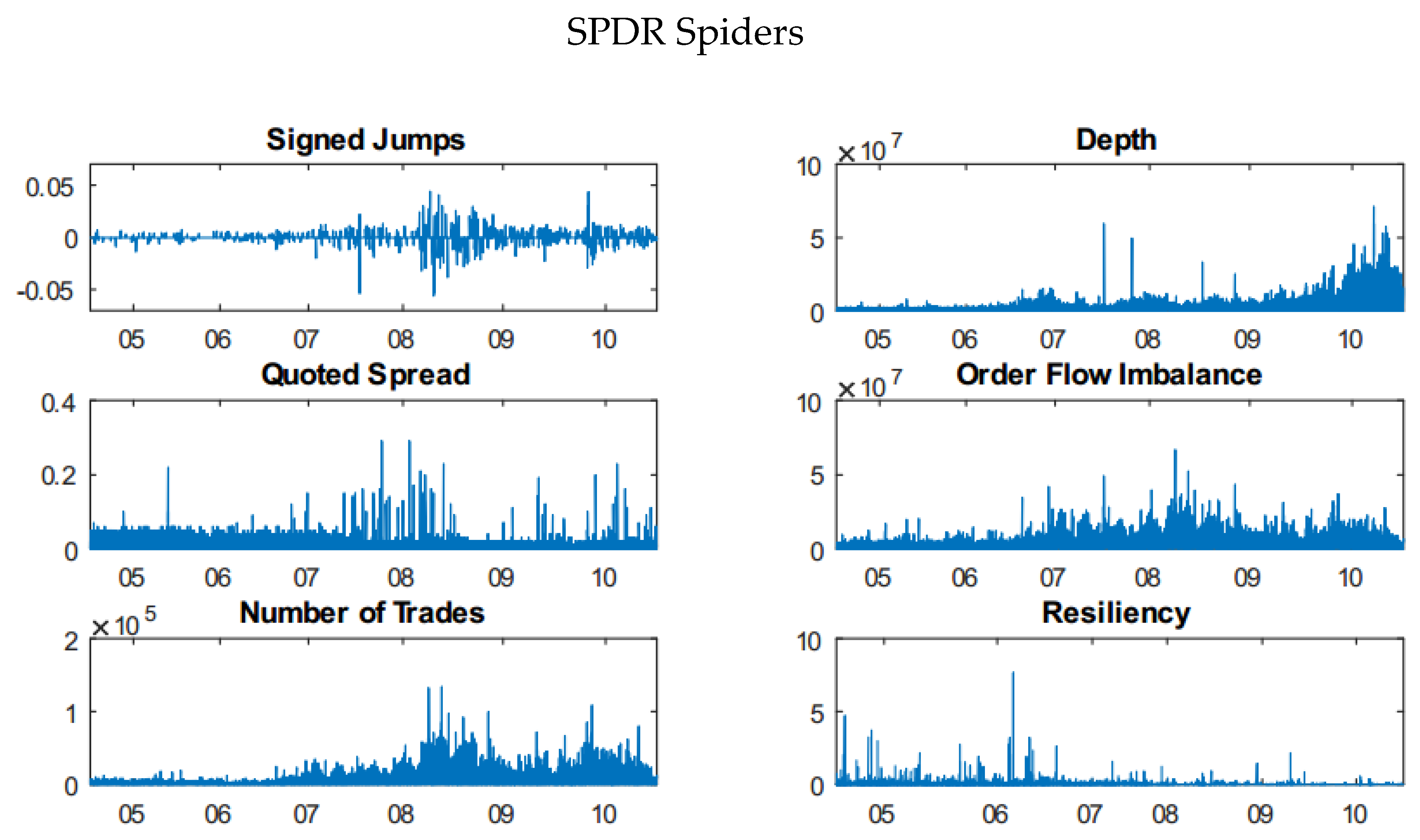
3.3. Variable Definitions
3.4. Econometric Model
4. Data
5. Empirical Results
5.1. Intraday Jumps and Liquidity Dynamics
5.2. Intraday Jumps, Liquidity, and Macroeconomic Announcement Surprises
5.3. Cojumps Analysis
5.4. Post-Jump Price Discovery
6. Conclusions
Funding
Conflicts of Interest
References
- Ackert, Lucy F., and Yisong S. Tian. 2000. Arbitrage and Valuation in the Market for Standard and Poor’s Depositary Receipts. Financial Management 29: 71–87. [Google Scholar] [CrossRef]
- Agrrawal, Pankaj, John M. Clark, Rajat Agarwal, and Jivendra K. Kale. 2014. An Intertemporal Study of ETF Liquidity and Underlying Factor Transition, 2009–2014. The Journal of Trading 9: 69–78. [Google Scholar] [CrossRef]
- Amihud, Yakov. 2002. Illiquidity and stock returns: Cross-section and time-series effects. Journal of Financial Markets 5: 31–56. [Google Scholar] [CrossRef]
- Andersen, Torben G., and Tim Bollerslev. 1998. Answering the skeptics: Yes, standard volatility models do provide accurate forecasts. International Economic Review 39: 885–905. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Clara Vega. 2003. Micro effects of macro announcements: Real-time price discovery in foreign exchange. American Economic Review 93: 38–62. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, and Francis X. Diebold. 2007a. Roughing it up: Including jump components in the measurement, modeling, and forecasting of return volatility. The Review of Economics and Statistics 89: 701–20. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, and Dobrislav Dobrev. 2007b. No-arbitrage semi-martingale restrictions for continuous-time volatility models subject to leverage effects, jumps and i.i.d. noise: Theory and testable distributional implications. Journal of Econometrics 138: 125–80. [Google Scholar] [CrossRef]
- Balduzzi, Pierluigi, Edwin J. Elton, and T. Clifton Green. 2001. Economic news and bond prices: Evidence from the U.S. Treasury market. Journal of Financial and Quantitative Analysis 36: 523–43. [Google Scholar] [CrossRef]
- Bandi, Federico M., and Jeffrey R. Russell. 2006. Separating microstructure noise from volatility. Journal of Financial Economics 79: 655–92. [Google Scholar] [CrossRef]
- Bandi, Federico M., and Jeffrey R. Russell. 2008. Microstructure noise, realized variance, and optimal sampling. Review of Economic Studies 75: 339–69. [Google Scholar] [CrossRef]
- Bandi, Federico M., Jeffrey R. Russell, and Yinghua Zhu. 2008. Using High-Frequency Data in Dynamic Portfolio Choice. Econometric Review 27: 163–98. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2002a. Econometric analysis of realized volatility and its use in estimating stochastic volatility models. Journal of Royal Statistical Society Series B 64: 253–80. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2004. Power and bipower variation with stochastic volatility and jumps. Journal of Financial Econometrics 2: 1–37. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2006. Econometrics of testing for jumps in financial economics using bipower variation. Journal of Financial Econometrics 4: 1–30. [Google Scholar] [CrossRef]
- Baur, Dirk G., and Brian M. Lucey. 2010. Is Gold a hedge or a safe haven? An analysis of Stocks, Bonds and Gold. Financial Review 45: 217–29. [Google Scholar] [CrossRef]
- Bessembinder, Hendrik. 2003. Trade execution costs and market quality after decimalization. Journal of Financial and Quantitative Analysis 38: 747–77. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Jia Li, and Yuan Xue. 2018. Volume, volatility, and public news announcements. Review of Economic Studies 85: 2005–41. [Google Scholar] [CrossRef]
- Boudt, Kris, and Mikael Petitjean. 2014. Intraday liquidity dynamics and news releases around price jumps: Evidence from the DJIA stocks. Journal of Financial Markets 17: 121–49. [Google Scholar] [CrossRef]
- Chan, Choon Chat, and Wai Mun Fong. 2006. Realized volatility and transactions. Journal of Banking and Finance 30: 2063–85. [Google Scholar] [CrossRef]
- Chu, Quentin C., and Dan Zhou. 2010. Does the “spiders” market attract uninformed trading volume? Journal of Business & Economics Research 8: 1–19. [Google Scholar]
- Copeland, Thomas E., and Dan Galai. 1983. Information effects on the bid-ask spread. Journal of Finance 38: 1457–69. [Google Scholar] [CrossRef]
- Das, Sanjiv R. 2002. The surprise element: Jumps in interest rates. Journal of Econometrics 106: 27–65. [Google Scholar] [CrossRef]
- Dungey, Mardi, Michael McKenzie, and L. Vanessa Smith. 2009. Empirical evidence on jumps in the term structure of the U.S. Treasury Market. Journal of Empirical Finance 16: 430–45. [Google Scholar] [CrossRef]
- Ellis, Katrina, Roni Michaely, and Maureen O’Hara. 2000. The accuracy of trade classification rules: Evidence from NASDAQ. Journal of Financial and Quantitative Analysis 35: 529–51. [Google Scholar] [CrossRef]
- Eraker, Bjørn, Michael Johannes, and Nicholas Polson. 2003. The impact of jumps in volatility and returns. Journal of Finance 58: 1269–300. [Google Scholar] [CrossRef]
- Evans, Kevin P. 2011. Intraday jumps and U.S. macroeconomic news announcements. Journal of Banking and Finance 35: 2511–27. [Google Scholar] [CrossRef]
- Fair, Ray C. 2002. Events that shook the market. Journal of Business 75: 713–32. [Google Scholar] [CrossRef]
- Giot, Pierre, Sébastien Laurent, and Mikael Petitjean. 2010. Trading activity realized volatility and jumps. Journal of Empirical Finance 17: 168–75. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., and Paul R. Milgrom. 1985. Bid and ask and transaction prices in a specialist market with heterogeneously informed traders. Journal of Financial Economics 14: 71–100. [Google Scholar] [CrossRef]
- Grossman, Sanford J. 1992. The information role of upstairs and downstairs trading. Journal of Business 65: 509–28. [Google Scholar] [CrossRef]
- Harris, Lawrence. 1990. Liquidity, Trading Rules, and Electronic Trading Systems. Salomon Brothers Center Monograph Series in Finance and Economics; New York: New York University. [Google Scholar]
- Huang, Xin, and George Tauchen. 2005. The relative contribution of jumps to total price variation. Journal of Financial Econometrics 3: 456–99. [Google Scholar] [CrossRef]
- Huang, Xin. 2018. Macroeconomic News Announcements, Systemic Risk, Financial Market Volatility, and Jumps. Journal of Futures Markets 38: 513–34. [Google Scholar] [CrossRef]
- Jiang, George J., Ingrid Lo, and Adrien Verdelhan. 2011. Information shocks, liquidity shocks, jumps, and price discovery: Evidence from the U.S. Treasury market. Journal of Financial and Quantitative Analysis 46: 527–51. [Google Scholar] [CrossRef]
- Johannes, Michael. 2004. The statistical and economic role of jumps in continuous-time interest rate models. Journal of Finance 59: 227–60. [Google Scholar] [CrossRef]
- Jones, Charles M., Gautam Kaul, and Marc L. Lipson. 1994. Transactions, volume, and volatility. Review of Financial Studies 7: 631–51. [Google Scholar] [CrossRef]
- Kyle, Albert S. 1985. Continuous auctions and insider trading. Econometrica 53: 1315–36. [Google Scholar] [CrossRef]
- Lahaye, Jérôme, Sébastien Laurent, and Christopher J. Neely. 2011. Jumps, cojumps, and macro announcements. Journal of Applied Econometrics 26: 893–921. [Google Scholar] [CrossRef]
- Lee, Suzanne S., and Per A. Mykland. 2008. Jumps in Financial Markets: A New Nonparametric Test and Jump Dynamics. Review of Financial Studies 21: 2535–63. [Google Scholar] [CrossRef]
- Lee, Charles M. C., and Mark J. Ready. 1991. Inferring trade direction from intraday data. Journal of Finance 46: 733–46. [Google Scholar] [CrossRef]
- Liao, Yin. 2013. The benefit of modeling jumps in realized volatility for risk prediction: Evidence from Chinese mainland stocks. Pacific-Basin Finance Journal 23: 25–48. [Google Scholar] [CrossRef]
- Marshall, Ben R., Nhut H. Nguyen, and Nuttawat Visaltanachoti. 2013. ETF arbitrage: Intraday evidence. Journal of Banking and Finance 37: 3486–98. [Google Scholar] [CrossRef]
- Morscheck, Justin David. 2018. Overreaction in trading: Evidence from the intraday trading of SPDRs during the 2008 financial crisis. International Journal of Finance & Banking Studies 7: 21–37. [Google Scholar]
- Pan, Jun. 2002. The jump-risk premia implicit in options: Evidence from an integrated timeseries study. Journal of Financial Economics 63: 3–50. [Google Scholar] [CrossRef]
- Patton, Andrew J., and Kevin Sheppard. 2015. Good volatility, bad volatility: Signed jumps and the persistence of volatility. The Review of Economics and Statistics 97: 683–97. [Google Scholar] [CrossRef]
- Piccotti, Louis R. 2018. Jumps, cojumps, and efficiency in the spot foreign exchange market. Journal of Banking and Finance 87: 49–67. [Google Scholar] [CrossRef]
- Roache, Shaun K., and Marco Rossi. 2010. The effects of economic news on commodity prices. The Quarterly Review of Economics and Finance 50: 377–85. [Google Scholar] [CrossRef]
- Rosa, Carlo. 2011. The high-frequency response of exchange rates to monetary policy actions and statements. Journal of Banking and Finance 35: 478–89. [Google Scholar] [CrossRef]
- Schlossberg, Jessica, and Norman R. Swanson. 2018. Jump Spillover and Risk Effects on Excess Returns in the United States during the Great Recession. Available online: http://dx.doi.org/10.2139/ssrn.3208759 (accessed on 1 June 2020).
- Seppi, Duane J. 1997. Liquidity provision with limit orders and a strategic specialist. Review of Financial Studies 10: 103–50. [Google Scholar] [CrossRef]
- Sun, Bianxia, and Yang Gao. 2020. Market liquidity and macro announcement around intraday jumps: Evidence from Chinese stock index futures markets. Physica A: Statistical Mechanics and its Applications 541: 123308. [Google Scholar] [CrossRef]
- Wallace, Damien G., Petko S. Kalev, and Guanghua Lian. 2019. The evolution of price discovery in us equity and derivatives markets. J Futures Markets 39: 1122–36. [Google Scholar] [CrossRef]
- Wan, Die, Xianhua Wei, and Xiaoguang Yang. 2017. Liquidity dynamics around intraday price jumps in Chinese stock market. J Syst Sci Complex 30: 434–63. [Google Scholar] [CrossRef]
- Wu, Chunchi, and Xiaoqing Eleanor Xu. 2000. Return volatility, trading imbalance and the information content of volume. Review of Quantitative Finance and Accounting 14: 131–53. [Google Scholar] [CrossRef]
| 1 | Agrrawal et al. (2014) use a four-factor liquidity scoring algorithm to rank 462 ETFs, based on all four factors. They show that liquid ETFs are characterized by large market capitalization and lower bid–ask spreads. These ETFs attract a large trading volume and have a lower expense ratio. |
| 2 | Bandi et al. (2008) evaluate economic implications of the optimal sampling theory to investors. They show that the economic utility of a risk averse investor is improved when relying on variance forecasts constructed using the optimal sampling frequency rather than the 5 or 15-minute forecasts that are commonly used in the literature to mitigate market microstructure noise. |
| 3 | Balduzzi et al. (2001) find that the median is an efficient and unbiased predictor of macroeconomic announcement figures. |
| 4 | Occasionally, data are obtained for timestamps prior to 8:01 a.m. when the optimal sampling frequency is relatively low. This is necessary to match returns with macroeconomic announcements occurring at 8:30 a.m. |
| 5 | Occasionally, there are days where the optimal sampling interval exceeds 15 minutes. For these days, the sample is extended to include observations prior to 8:00 a.m. such that 2 observations are always included in the record before announcement times. |
| 6 | The results in the table are based on sampling all variables at the optimal frequency by starting at 8:01 a.m. on each day. |
| 7 | Estimate of probit models which include macroeconomic news surprises and liquidity variables show similar results to the ones reported in Table 5. Consumer confidence, initial claims, and leading indicators announcements remain significant. News variables do not subsume the information contained in liquidity variables. These results are not reported here for brevity. |

| Indicator | Freq | Time | μs | σs | μA |
|---|---|---|---|---|---|
| Business inventories | M | 10:00 * | 0.028 | 1.582 | 27 |
| Capacity utilization | M | 9:15 | −0.272 | 1.989 | 29 |
| Construction spending | M | 10:00 | 0.290 | 2.369 | 25 |
| Consumer confidence | M | 10:00 | −0.002 | 3.260 | 27 |
| Consumer credit | M | 15:00 | −0.291 | 3.258 | 20 |
| Consumer price index (CPI) | M | 8:30 | −0.106 | 1.358 | 30 |
| Durable orders | M | 8:30 | −0.064 | 2.341 | 29 |
| Factory orders | M | 10:00 | 0.300 | 1.629 | 22 |
| GDP advance report | Q | 8:30 | −0.203 | 1.721 | 31 |
| GDP second report | Q | 8:30 | 0.201 | 1.426 | 31 |
| GDP third report | Q | 8:30 | −0.660 | 2.308 | 30 |
| Housing starts | M | 8:30 | −0.180 | 2.703 | 29 |
| Industrial production | M | 9:15 | −0.214 | 2.11 | 29 |
| Initial jobless claims | W | 8:30 | 0.317 | 3.916 | 16 |
| Leading indicators | M | 8:30 | −0.041 | 1.157 | 26 |
| New home sales | M | 10:00 | −0.265 | 2.978 | 30 |
| Personal consumption expenditures | M | 8:30 | 0.062 | 1.013 | 29 |
| Personal income | M | 8:30 | 0.192 | 1.792 | 29 |
| Producers price index (PPI) | M | 8:30 | 0.278 | 2.204 | 30 |
| Private nonfarm payrolls | M | 8:30 | −0.609 | 2.201 | 30 |
| Retail sales (ex-Auto) | M | 8:30 | 0.027 | 2.385 | 29 |
| Retail sales | M | 8:30 | 0.006 | 2.299 | 29 |
| Treasury budget | M | 14:00 | 0.059 | 1.538 | 15 |
| Unemployment rate | M | 8:30 | −0.156 | 2.615 | 28 |
| Institute for Supply Management survey (ISM) | M | 10:00 | 0.241 | 2.370 | 28 |
| ISM non-manufacturing | M | 10:00 | 0.070 | 2.402 | 27 |
| Panel A | SPDR Spiders (SPY) | ||||||
|---|---|---|---|---|---|---|---|
| 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | All | |
| Number of Jumps | 29 | 44 | 64 | 65 | 99 | 93 | 394 |
| Number of Positive Jumps | 17 | 28 | 33 | 45 | 49 | 58 | 230 |
| Number of Negative Jumps | 12 | 16 | 31 | 20 | 50 | 35 | 164 |
| E (jump size | jumps) (%) | 0.48 | 0.41 | 0.61 | 1.66 | 1.1 | 0.84 | 0.93 |
| SD (jump size | jump) (%) | 0.22 | 0.12 | 0.34 | 1.26 | 0.63 | 0.62 | 0.79 |
| P (jumps | announcements) (%) | 3.58 | 6.8 | 5.55 | 4.32 | 6.63 | 5.43 | 5.39 |
| P (news | jumps) (%) | 6.48 | 11.92 | 8.19 | 7.47 | 9.7 | 7.46 | 8.64 |
| P (jumps, announcements) (%) | 0.05 | 0.09 | 0.04 | 0.04 | 0.07 | 0.05 | 0.06 |
| Panel B | SPDR Gold (GLD) | ||||||
| 2007 | 2008 | 2009 | 2010 | All | |||
| Number of Jumps | 68 | 118 | 130 | 116 | 432 | ||
| Number of Positive Jumps | 45 | 66 | 76 | 71 | 258 | ||
| Number of Negative Jumps | 23 | 52 | 54 | 45 | 174 | ||
| E (jump size | jumps) (%) | 0.81 | 1.37 | 0.93 | 0.74 | 0.98 | ||
| SD (jump size | jump) (%) | 0.44 | 0.62 | 0.39 | 0.32 | 0.52 | ||
| P (jumps | announcements) (%) | 2.45 | 1.02 | 0.49 | 1.01 | 1.11 | ||
| P (news | jumps) (%) | 3.44 | 1.33 | 0.63 | 0.01 | 1.48 | ||
| P (jumps, announcements) (%) | 0.02 | 0.01 | 0.005 | 0.01 | 0.01 | ||
| Model | 1 | 2 | 3 | 4 | 5 | 6 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dep. Variable | P(JSpiders = 1|x) | P(JGold = 1|x) | ||||||||||
| Coef | S.E. | Coef | S.E. | Coef | S.E. | Coef | S.E. | Coef | S.E. | Coef | S.E. | |
| Constant | −2.879 *** | 0.032 | −3.028 *** | 0.029 | −3.152 *** | 0.032 | −2.459 *** | 0.039 | −2.563 *** | 0.043 | −2.762 *** | 0.055 |
| Depth shocks | −0.041 *** | 0.015 | −0.041 ** | 0.018 | −0.035 | 0.023 | 0.053 *** | 0.015 | 0.038 *** | 0.018 | 0.059 *** | 0.021 |
| ES shock | 0.048 *** | 0.016 | 0.045 *** | 0.019 | 0.039 * | 0.023 | 0.148 *** | 0.015 | 0.126 *** | 0.019 | 0.151 * | 0.021 |
| RQS shocks | 0.078 *** | 0.020 | 0.036 * | 0.021 | 0.119 *** | 0.031 | 0.073 *** | 0.018 | 0.088 *** | 0.021 | 0.041 * | 0.025 |
| NT | 0.142 *** | 0.011 | 0.121 ** | 0.024 | 0.136 *** | 0.013 | −0.037 * | 0.021 | −0.035 | 0.024 | −0.002 | 0.032 |
| Resiliency | 0.640 * | 0.359 | 0.725 * | 0.374 | −0.022 | 0.063 | −0.233 | 0.358 | 0.054 | 0.081 | −0.976 *** | 0.34 |
| OF Imbalance | 0.038 *** | 0.007 | 0.031 *** | 0.009 | 0.037 *** | 0.009 | 0.077 *** | 0.015 | 0.078 *** | 0.019 | 0.061 *** | 0.021 |
| Volatility | −0.028 *** | 0.01 | −0.020 * | 0.011 | −0.034 *** | 0.010 | −0.078 *** | 0.025 | −0.125 *** | 0.03 | −0.025 ** | 0.029 |
| McFadden R2 | 7.06 | 5.19 | 8.15 | 3.9 | 4.08 | 4.84 | ||||||
| Model | 1 | 2 | 3 | 4 | 5 | 6 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dep. Variable | P(JSpiders = 1|x) | P(JGold = 1|x) | ||||||||||
| Coef | SE | Coef | SE | Coef | SE | Coef | SE | Coef | SE | Coef | S.E. | |
| Constant | −2.880 *** | 0.023 | −3.030 *** | 0.029 | −2.718 *** | 0.021 | −2.597 *** | 0.027 | −2.742 *** | 0.034 | −2.931 *** | 0.036 |
| Depth shocks | −0.043 *** | 0.015 | −0.043 ** | 0.189 | −0.039 | 0.023 | 0.027 * | 0.014 | 0.025 | 0.018 | 0.024 | 0.023 |
| ES shock | 0.048 *** | 0.016 | 0.045 ** | 0.199 | 0.039 * | 0.023 | 0.126 *** | 0.014 | 0.104 *** | 0.018 | 0.132 *** | 0.018 |
| RQS shocks | 0.079 *** | 0.020 | 0.036 * | 0.021 | 0.119 *** | 0.029 | 0.098 *** | 0.016 | 0.068 *** | 0.020 | 0.122 *** | 0.023 |
| NT | 0.142 *** | 0.011 | 0.121 *** | 0.014 | 0.137 *** | 0.013 | 0.074 *** | 0.014 | 0.073 *** | 0.015 | 0.064 *** | 0.019 |
| Resiliency | 0.640 * | 0.359 | 0.725 ** | 0.370 | 0.022 | 0.063 | −0.007 | 0.013 | 0.001 | 0.007 | 0.279 *** | 0.003 |
| OF Imbalance | 0.038 *** | 0.007 | 0.031 *** | 0.009 | 0.037 *** | 0.009 | 0.036 *** | 0.007 | 0.029 *** | 0.009 | 0.038 *** | 0.011 |
| Volatility | −0.287 *** | 0.103 | −0.206 | 0.128 | −0.349 *** | 0.105 | −0.791 *** | 0.134 | −0.864 *** | 0.195 | −0.578 *** | 0.167 |
| Consumer confidence | −0.060 *** | 0.014 | −0.055 *** | 0.013 | −0.054 *** | 0.013 | −0.049 *** | 0.014 | −0.045 | 0.013 | −0.044 *** | 0.012 |
| Construction spending | −0.064 ** | 0.029 | −0.057 ** | 0.026 | −0.060 ** | 0.027 | −0.100 *** | 0.038 | −0.095 *** | 0.035 | −0.091 *** | 0.034 |
| GDP second report | −0.097 * | 0.053 | −0.107 ** | 0.050 | ||||||||
| GDP third report | 0.066 * | 0.037 | 0.059 * | 0.034 | 0.065 * | 0.036 | ||||||
| Initial claims | 0.205 ** | 0.092 | 0.205 ** | 0.092 | ||||||||
| Leading indicators | −0.177 * | 0.100 | ||||||||||
| Nonfarm payroll | −0.286 ** | 0.145 | −0.332 ** | 0.147 | ||||||||
| Personal income | −0.039 * | 0.019 | −0.032 * | 0.019 | 0.831 ** | 0.199 | 0.640 *** | 0.217 | 1.311 *** | 0.172 | ||
| PPI | −0.872 *** | 0.196 | −0.686 *** | 0.213 | −1.335 *** | 0.171 | ||||||
| Treasury Budget | −0.146 * | 0.085 | −0.167 * | 0.090 | ||||||||
| Other announcements | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES |
| McFadden R2(%) | 7.25 | 5.51 | 8.17 | 5.08 | 4.02 | 5.79 | ||||||
| Model | 1 | 2 | 3 | |||
|---|---|---|---|---|---|---|
| Panel A | ||||||
| Dep. Variable | P(cojump = 1|x) | P(cojump+ = 1|x) | P(cojump− = 1|x) | |||
| Coef | SE | Coef | SE | Coef | S.E. | |
| Constant | −2.703 *** | 0.02 | −2.994 *** | 0.03 | −3.079 *** | 0.034 |
| Consumer Confidence | −0.037 *** | 0.011 | −0.034 *** | 0.01 | −0.033 *** | 0.01 |
| Initial Jobless Claims | 0.107 ** | 0.055 | 0.167 ** | 0.069 | ||
| Leading Indicators | 0.574 * | 0.313 | 0.736 ** | 0.349 | ||
| Other announcements | YES | YES | YES | YES | YES | YES |
| McFadden R2(%) | 1.00 | 0.09 | 4.00 | |||
| Panel B | ||||||
| Dep. variable | P(cojump = 1|x) | P(cojump+ = 1|x) | P(cojump− = 1|x) | |||
| Coef | SE | Coef | SE | Coef | S.E. | |
| Constant | −3.193 *** | 0.167 | −3.793 *** | 0.266 | −3.105 *** | 0.184 |
| Depth shocks Spiders | −0.133 *** | 0.018 | −0.113 *** | 0.02 | −0.113 *** | 0.024 |
| RQS shocks Spiders | 0.022 *** | 0.005 | −0.007 | 0.023 | 0.025 *** | 0.006 |
| NT Spiders | 0.258 *** | 0.029 | 0.192 *** | 0.029 | 0.206 *** | 0.058 |
| Resiliency Spiders | −0.031 *** | 0.005 | −0.040 *** | 0.007 | −0.036 *** | 0.008 |
| OF Imbalance Spiders | 0 | 0.001 | −0.0007 | <0.0001 | 0.002 | 0.001 |
| Volatility Spiders | 0.019 *** | 0.123 | 0.075 | 0.161 | 0.032 | 0.03 |
| Depth shocks Gold | −0.493 *** | 0.106 | −0.687 *** | 0.155 | −0.229 * | 0.013 |
| RQS shocks Gold | 0.004 *** | 0.001 | 0.004 *** | 0.001 | 0.003 *** | 0.001 |
| NT Gold | −1.138 *** | 0.203 | −0.647 *** | 0.194 | −1.336 *** | 0.303 |
| Resiliency Gold | 0.038 ** | 0.018 | 0.026 | 0.023 | 0.058 *** | 0.04 |
| OF Imbalance Gold | −0.001 ** | 0 | −0.0005 | 0.001 | −0.001 ** | 0.0005 |
| Volatility Gold | −0.060 * | 0.034 | −0.032 | 0.033 | −0.107 | 0.126 |
| McFadden R2(%) | 37.98 | 37.02 | 31.67 | |||
| Model | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Dep. Variable | ||||||||
| −0.004 | −0.0006 | |||||||
| 0.256 | 0.254 | |||||||
| −0.007 | −0.008 | |||||||
| 0.007 | 0.008 | |||||||
| −0.365 | ||||||||
| 0.353 | ||||||||
| 0.377 | ||||||||
| 0.371 | ||||||||
| −0.009 | ||||||||
| 0.009 | ||||||||
| −0.003 | ||||||||
| 0.015 | ||||||||
| 0.009 | 0.009 ** | |||||||
| 0.897 | 0.897 | |||||||
| −0.0001 | −1.9 × 10−5 | −0.0001 | −0.0001 | −0.00001 | −2.9 × 10−5 | |||
| 0.0001 | 0.0001 | 6.78 × 10−5 | 0.0001 | 0.0001 | 0.0001 | |||
| −0.0009 ** | −0.003 | −0.0008 | −0.0009 ** | −0.003 | −0.004 | |||
| 0.0004 | 0.003 | 0.0005 | 0.0004 | 0.003 | 0.003 | |||
| 0.023 * | 0.023 * | 0.033 *** | 0.022 * | |||||
| 0.013 | 0.013 | 0.011 | 0.012 | |||||
| 0.307 *** | 0.263 ** | 0.298 *** | 0.263 ** | |||||
| 0.071 | 0.107 | 0.089 | 0.107 | |||||
| 0.036 ** | 0.037 *** | |||||||
| 0.014 | 0.014 | |||||||
| −0.008 | 0.002 | |||||||
| 0.022 | 0.019 | |||||||
| 0.509 *** | 0.564 *** | |||||||
| 0.101 | 0.14 | |||||||
| −2.552 *** | −3.076 ** | |||||||
| 0.901 | 1.31 | |||||||
| Constant | 0.0012 | 0.001 *** | 0.004 | 0.001 ** | 0.001 | 0.001 | 0.004 | 0.005 |
| 0.002 | 0.001 | 0.003 | 0.0007 | 0.002 | 0.0006 | 0.003 | 0.003 | |
| R2 (%) | 0.01 | 0.3 | 0.3 | 3.7 | 1.8 | 2.01 | 0.3 | 1.8 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jurdi, D.J. Intraday Jumps, Liquidity, and U.S. Macroeconomic News: Evidence from Exchange Traded Funds. J. Risk Financial Manag. 2020, 13, 118. https://doi.org/10.3390/jrfm13060118
Jurdi DJ. Intraday Jumps, Liquidity, and U.S. Macroeconomic News: Evidence from Exchange Traded Funds. Journal of Risk and Financial Management. 2020; 13(6):118. https://doi.org/10.3390/jrfm13060118
Chicago/Turabian StyleJurdi, Doureige J. 2020. "Intraday Jumps, Liquidity, and U.S. Macroeconomic News: Evidence from Exchange Traded Funds" Journal of Risk and Financial Management 13, no. 6: 118. https://doi.org/10.3390/jrfm13060118
APA StyleJurdi, D. J. (2020). Intraday Jumps, Liquidity, and U.S. Macroeconomic News: Evidence from Exchange Traded Funds. Journal of Risk and Financial Management, 13(6), 118. https://doi.org/10.3390/jrfm13060118





